Oxygen diffusion in the fluorite-type oxides CeO2, ThO2, UO2, PuO2, and (U, Pu)O2

This study evaluates the self-diffusion and chemical diffusion coefficients of oxygen in the fluorite-type oxides CeO₂, ThO₂, UO₂, PuO₂, and (U, Pu)O₂ using point defect chemistry (oxygen vacancies and interstitials). The self-diffusion coefficient changed in proportion to the 1/n power of oxygen partial pressure, similar to the defect concentration. All parameters used to represent the diffusion coefficients were determined, and the experimental data were accurately stated. The defect formation and migration energies of the oxides were compared, and the change in Frenkel defect concentration was found to affect the high-temperature heat capacities of CeO₂ and ThO₂. The oxygen chemical diffusion was evaluated in the oxides, excluding the line compound ThO₂, and the coefficients increased dramatically around the stoichiometric composition, i.e., the chemical diffusion coefficient was much higher at stoichiometric composition, with the oxygen-to-metal ratio equal to 2.00, than in low oxygen-to-metal oxides. This difference altered the mechanism of the reduction and oxidation processes. In the reduction process, the chemical diffusion control rate was dominant and a new phase with the oxygen-to-metal ratio equal to 2.00 was formed, which then expanded from the surface in the oxidation process from a low oxygen-to-metal ratio to the stoichiometric composition.

1 Introduction

Understanding diffusion phenomena in nuclear oxide fuels is important for its research and development for two reasons. The first is to understand and describe various behavior at high temperatures, such as phase transformation, precipitation, oxidation, reduction, creep, sintering, solid–gas reaction, grain growth, thermal recovery of irradiation defects, and formation of fission product gas bubbles (Suzuki et al., 2007; Lösönen, 2017; Forsberg et al., 2020; Watanabe and Seki, 2021). The second is to understand the behavior of oxygen vacancy and interstitial point defects (Kato et al., 2017a; Kato et al., 2017b; Cooper et al., 2018; Watanabe et al., 2021). It is important to understand the mechanism of basic properties at high temperatures because the concentration of point defects is strongly related to various properties, such as oxygen potential, thermal conductivity, heat capacity, and electrical conductivity. The defect concentration of vacancy and interstitial atoms in oxygen sites is much greater than that of cation sites because fluorite-type oxides are nonstoichiometric oxygen compounds (Cooper et al., 2018). Therefore, understanding the chemical and thermal properties of the materials requires knowledge of oxygen diffusion behavior.

Oxygen self-diffusion and chemical diffusion coefficients were measured and explained using defect concentration and migration mechanisms (Kröger and Vink, 1956; Matzke, 1987; Stan and Cristea, 2005; Kato et al., 2017a; Kato et al., 2017b; Watanabe et al., 2021; Kato, 2022). Defect concentration is related to the oxygen potential, heat capacity, thermal conductivity, and electric conduction mechanisms (Kofstad, 1972; Kato, 2022). This study used defect concentration to determine the diffusion coefficients of CeO₂, ThO₂, UO₂, PuO₂, and (U, Pu)O₂ with fluorite-type crystal structures. The oxygen potential and diffusion coefficients of the materials, excluding ThO₂, were measured, along with their defect equilibria using the gas equilibrium method. The diffusion coefficient and defect concentration relationship were compared and evaluated based on defect chemistry. These results improve the understanding of the relationships between diffusion coefficient, properties, and redox behavior.

The aim of this study was to review oxygen diffusion coefficients in fluorite-type oxides and determine the relationships between the oxygen-to-metal (O/M) ratio, oxygen self-diffusion coefficients, and chemical diffusion coefficients using defect chemistry. This work contributes to a better understanding of the oxygen behavior in fuel technology and the mechanisms of high-temperature thermophysical properties.

2 Measurement techniques

Previous studies have measured oxygen self-diffusion and chemical diffusion coefficients (Watanabe et al., 2017; Vauchy et al., 2015; Sari, 1978; Murch and Catlow, 1987; Lorenzelli and El Sayed Ali, 1977; Kato et al., 2013; Kato et al., 2009; Garcia et al., 2010; Deaton and Wiedenheft, 1973; D'Annucci and Sari, 1977; Contamin et al., 1972; Breitung, 1978; Belle, 1969; Bayoglu and Lorenzelli, 1984; Bayoglu and Lorenzelli, 1979; Auskern and Belle, 1961; Ando et al., 1976; Watanabe and Kato, 2012; Kim and Olander, 1981; Floyd, 1973; Kamiya et al., 2000; Millot and Mierry, 1985; Gotte et al., 2007). The oxygen diffusion coefficients data set used in this review is shown in Table A1. The data were measured using various methods, such as the isotope method, thermogravimetry, electrical conductivity measurement, and thermal dilatometry. It was difficult to assess changes dependent on temperature and O/M ratio because the data were scattered (Floyd, 1973; Gotte et al., 2007; Kamiya et al., 2000; Millot and Mierry, 1985; Ando et al., 1976; Watanabe and Kato; Dornelas and Lacombe, 1967; Matzke, 1987; Ligeon et al., 1970; Dorado et al., 2011; Lay, 1970; Bittel et al., 1969; Ruello et al., 2004; Kato et al., 2013; Mullins, 1972; Deaton and Wiedenheft, 1973; Bayoglu et al., 1983; Bayoglu and Lorenzelli, 1979; Chereau and Wadier, 1973; Bayoglu and Lorenzelli, 1980; Bayoglu and Lorenzelli, 1984; D'Annucci and Sari, 1977; Kato et al., 2009; Watanabe et al., 2017; Watanabe et al., 2020; Vauchy et al., 2015).

Self-diffusion is the phenomenon in which oxygen ions move through oxygen vacancies and interstitial sites, i.e., without chemical gradient. The self-diffusion coefficient was measured using a gas containing an isotope of ¹⁸O. Isotope analyzers, such as the secondary ion micro spectrometer, have been used to determine the diffusion coefficient (Vauchy et al., 2015). Recently, Watanabe et al. (2020) used the weight difference between ¹⁶O and ¹⁸O to measure the oxygen self-diffusion coefficient of (U, Pu)O₂ by thermogravimetry. On the other hand, chemical diffusion is driven by the oxygen content change in nonstoichiometric composition. In measurement of the chemical diffusion coefficient, oxygen partial pressure in the measurement atmosphere is altered, and the rate of sample weight change is measured to determine the value. Therefore, oxygen potential data are required to control the oxygen partial pressure in this measurement. Also, in several studies, the oxygen potential of UO₂, (U, Pu)O₂, PuO₂, and CeO₂ were determined using the gas equilibrium method (H₂O/H₂ gas reaction), and defect equilibria were evaluated using a constructed Brouwer diagram (Brouwer, 1954; Kröger and Vink, 1956; Watanabe and Kato, 2012; Kato et al., 2017a; Kato et al., 2017b; Watanabe et al., 2021; Kato, 2022). These techniques were used to measure the self-diffusion and chemical diffusion coefficients. When change in sample weight during the measurement is observed from only the change in type O/M ratio, the diffusion coefficients can be determined from curves of the weight change using Eqs 1–3, which represent O/M changes in the sphere, cylinder, and plate-like samples, respectively (Jost, 1933).

$\frac{\overline{C}-C_f}{C_0-C_f}=\frac{6}{{\pi }^2}{\displaystyle \sum }_{n=1}^{\infty }\frac{1}{n^2}\exp \left(-D{n}^2{\pi }^{2}t/r^2\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e},(1)$

$\frac{\overline{C}-C_f}{C_0-C_f}={\displaystyle \sum }_{n=1}^{\infty }\frac{4}{{{\alpha }_n}^2}\exp \left[-\frac{D{{\alpha }_n}^{2}t}{r^2}\right]\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{y}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r},(2)$

$\frac{\overline{C}-C_f}{C_0-C_f}=\frac{8}{{\pi }^2}{\displaystyle \sum }_{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^2}\exp \left(-D{\left(2n+1\right)}^2{\pi }^{2}t/h^2\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e},(3)$

where $\overline{C}$, $C_0$, $C_f$, t, D, r, h, and ${\alpha }_n$ are the average O/M ratio, initial O/M ratio, final O/M ratio, time, diffusion coefficient, radius, diffusion distance, and the roots of the equation $J_o\left(x\right)=0$, respectively. $J_o\left(x\right)$ is the Bessel function of zero order. The diffusion coefficient can be determined by fitting the sample weight change curve with these equations. Figure 1 shows the three types of O/M change curves. Depending on the sample shape, the rate of change varies. Samples having various shapes have been prepared for diffusion coefficient measurement (Jost, 1933). Therefore, it is important to control sample shape and determine the O/M change curve during measurements to assess the diffusion mechanism. However, the O/M change curves have not been observed in initial studies on chemical diffusion coefficients. Therefore, the accuracy of the experimental data cannot be evaluated.

FIGURE 1

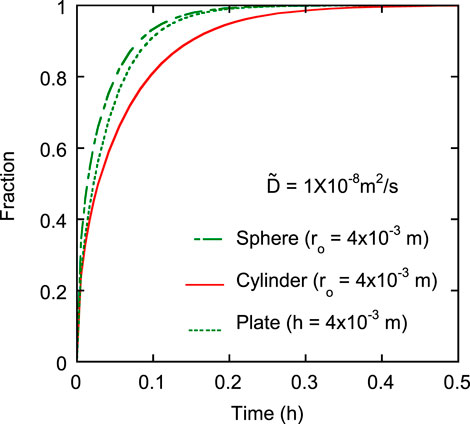
FIGURE 1. Changing fractions of the sphere-, cylinder-, and plate-like samples when diffusion coefficient and diffusion distance are 1 × 10^–8 m²/s and 4 × 10^–3 m, respectively. The three lines represent Eqs 1–3.

Previous studies have measured the chemical diffusion coefficient using O/M change curves of plate and cylinder-like samples (Kato et al., 2009; Kato et al., 2013). Oxidation and reduction curves were obtained between a low O/M ratio and O/M = 2.00, respectively. The reduction curve can be represented by Eqs 2, 3, but the oxidation curve cannot. It was assumed that the oxidation process was governed by a mechanism other than chemical diffusion, which will be discussed further.

The self-diffusion and chemical diffusion coefficients, $D^{*}$ and $\stackrel{\sim }{D}$, in nonstoichiometric oxides can be expressed by Eqs 4, 5:

$D^{*}=D_{Vo}^0\left[V_o\right]\mathit{exp}\left(-\frac{\Delta H_{Vo}^m}{RT}\right)+2D_{Oi}^0\left[O_i\right]\mathit{exp}\left(-\frac{\Delta H_{Oi}^m}{RT}\right),(4)$

$\stackrel{\sim }{D}=\frac{2\pm x}{2x}{D}^{*}\left(\pm \frac{\partial {logP}_{O2}}{\partial \mathit{log}x}\right),(5)$

where $\left[O_i\right]$, $\left[V_o\right]$, $D_{Vo}^0$, $\Delta H_{Vo}^m$, $D_{Oi}^0$, $\Delta H_{Oi}^m$, R, T, x, and $P_{O2}$ are oxygen vacancy concentration, interstitial oxygen concentration, the pre-exponential term for the oxygen vacancy, migration energy of oxygen vacancy, the pre-exponential term for the interstitial oxygen, migration energy of the interstitial oxygen, gas constant (8.3145 J/mol.K), temperature (K), deviation from stoichiometry in $M{O}_{2\pm x}$, and oxygen partial pressure, respectively. According to Eqs 4, 5, the concentrations of oxygen vacancy and interstitial oxygen, both dependent upon T and $P_{O2}$, are required in order to represent the diffusion coefficients.

3 Evaluation of diffusion coefficients

3.1 Point defect concentrations

As shown in Eqs 4, 5, defect concentrations are needed to represent the diffusion coefficients. Here, point defect concentration in each oxide was reviewed. In previous studies, the oxygen potentials of CeO₂, UO₂, PuO_2, and (U, Pu)O₂ were measured, and defect equilibria were evaluated (Komeno et al., 2012; Watanabe and Kato, 2012; Kato et al., 2017a; Kato et al., 2017b; Suzuki et al., 2018; Watanabe et al., 2021; Kato, 2022). The Brouwer diagram was used to derive the equations to represent $\left[O_i\right]$ and $\left[V_o\right]$. Recently, Kobayashi et al. (2022) evaluated the defect concentration in ThO₂ using the results obtained from molecular dynamic calculations. They estimated the $\left[V_o\right]$ and $D^{*}$ of ThO₂ depending on temperature. It is expected that the $\left[V_o\right]$ equals $\left[O_i\right]$, assuming that the O/M ratio does not change with temperature. The simulation result was used to derive the equation to represent $\left[V_o\right]$ and $\left[O_i\right]$ in ThO₂. Thus, the equations to evaluate $\left[V_o\right]$ and $\left[O_i\right]$ in each oxide can be expressed by Eqs 6–14:

(1) CeO₂

$\begin{array}{c}\left[V_O\right]=[{\left\{0.784596\cdot {\left(\mathit{exp}\left(\frac{\left(37.08\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{345,043}}{RT}\right)\right)}^{1/6}.P_{O_2}^{-\frac{1}{12}}\right\}}^{-8}{+{\left\{{\left(\mathit{exp}\left(\frac{\left(89.06\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{340,000}}{RT}\right)\right)}^{1/2}.P_{O_2}^{-\frac{1}{4}}\right\}}^{-8}+{\left\{0.5\right\}}^{-8}]}^{-1/8}\\ +{\left\{\mathit{exp}\left(\frac{165}{R}\right).\mathit{exp}\left(\frac{-\mathrm{413,000}}{RT}\right)\right\}}^{1/2},\end{array}(6)$

$\left[O_i\right]=\frac{\left[V_O\right]}{\left\{\mathit{exp}\left(\frac{165}{R}\right).\mathit{exp}\left(\frac{-\mathrm{413,000}}{RT}\right)\right\}}(7)$

(2) ThO₂

$\left[V_O\right]=\left[O_i\right]={\left\{\mathit{exp}\left(\frac{77.3}{R}\right)・\mathit{exp}\left(\frac{-\mathrm{650,000}}{RT}\right)\right\}}^{1/2}.(8)$

(3) UO₂

$\left[V_O\right]={\left\{{\left(\exp \left(\frac{32.0}{R}\right).\exp \left(-\frac{\mathrm{464,500}}{RT}\right).P_{O_2}^{-1/2}\right)}^{-5}+{\left({\left(2\exp \left(\frac{95.0}{R}\right).\exp \left(-\frac{\mathrm{1,079,100}}{RT}\right)\right)}^{1/3}.P_{O_2}^{-1/3}\right)}^{-5}\right\}}^{-1/5},(9)$

$\left[O_i\right]={\left\{{{\left(\exp \left(\frac{5.0}{R}\right).\exp \left(\frac{\mathrm{60,000}}{RT}\right)P_{O_2}^{1/2}\right)}^{-5}+\left(\left({\left(\exp \left(\frac{81.0}{R}\right).\exp \left(\frac{\mathrm{130,000}}{RT}\right)\right)}^{1/3}\right).P_{O_2}^{1/6}\right)}^{-5}\right\}}^{-1/5}.(10)$

(4) PuO₂

$\left[V_O\right]={[\left\{\mathit{exp}\left(\frac{55.5}{R}\right).\mathit{exp}\left(\frac{-\mathrm{305,700}}{RT}\right)\cdot P_{O_2}^{-\frac{1}{2}}\right\}}^{-5}{+{\left\{{\left(\mathit{exp}\left(\frac{\left(91.4\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{445,000}}{RT}\right)\right)}^{1/2}\cdot P_{O_2}^{-\frac{1}{4}}\right\}}^{-5}+{\left\{0.5\right\}}^{-5}]}^{-1/5},(11)$

$\left[O_i\right]=\mathit{exp}\left(\frac{\left(-4.7\right)}{R}\right)・\mathit{exp}\left(\frac{-\mathrm{159,300}}{RT}\right)\cdot P_{O_2}^{\frac{1}{2}}.(12)$

(5) (U, Pu)O₂

$\begin{array}{c}\left[V_O\right]={\left[\left\{\mathit{exp}\left(\frac{\left(42.3+48.3.{C_{\mathrm{P}\mathrm{u}}}^{\prime }+110.0.{C_{\mathrm{P}\mathrm{u}}}^2+99.4.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^3\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{372,000}}{RT}\right)\cdot P_{O_2}^{-\frac{1}{2}}\right\}\right.}^{-5}\\ +{\left\{\mathit{exp}\left(\frac{\left(125.8-745.1.{C_{\mathrm{P}\mathrm{u}}}^{\prime }+2678.5.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^2-3683.4.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^3+1792.7.{C_{\mathrm{P}\mathrm{u}}}^4\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{376,500}}{RT}\right)\cdot P_{O_2}^{-\frac{1}{2}}\right\}}^{-5}\\ +{\left\{\mathit{exp}\left(\frac{\left(91.6-63.7.C_{Pu}-54.0.{C_{Pu}}^2+99.4.{{C_{Pu}}^{\prime }}^3\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{306,000}}{RT}\right)\cdot P_{O_2}^{-\frac{1}{2}}\right\}}^{-5}\\ +{\left\{{\left(\mathit{exp}\left(\frac{\left(72.1+82.0.{C_{\mathrm{P}\mathrm{u}}}^{\prime }+164.0.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^2\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{511,000}}{RT}\right)\right)}^{1/2}\cdot P_{O_2}^{-\frac{1}{4}}\right\}}^{-5}\\ +{\left\{{\left(2\cdot \mathit{exp}\left(\frac{\left(275.7-1456.5.{C_{\mathrm{P}\mathrm{u}}}^{\prime }+5411.0.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^2-7466.2.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^3+3585.3.{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^4\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{892,000}}{RT}\right)\right)}^{1/3}\cdot P_{O_2}^{-\frac{1}{3}}\right\}}^{-5}\\ {+{\left\{{\left(\mathit{exp}\left(\frac{\left(121.4-30.0.{C_{\mathrm{P}\mathrm{u}}}^{\prime }\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{445,000}}{RT}\right)\right)}^{1/2}\cdot P_{O_2}^{-\frac{1}{4}}\right\}}^{-5}+{\left\{{C_{\mathrm{P}\mathrm{u}}}^{\prime }/2\right\}}^{-5}]}^{-1/5},\end{array}(13)$

$\left[O_i\right]=\left[{\left\{\mathit{exp}\left(\frac{\left(-20.0-112.2・{C_{\mathrm{P}\mathrm{u}}}^{\prime }+58.2・{{C_{\mathrm{P}\mathrm{u}}}^{\prime }}^2\right)}{R}\right).\mathit{exp}\left(\frac{\mathrm{105,000}}{RT}\right)\cdot P_{O_2}^{\frac{1}{2}}\right\}}^{-5}\right.{+{\left\{\mathit{exp}\left(\frac{\left(2595.3-\mathrm{2,600}.{C_{\mathrm{P}\mathrm{u}}}^{\prime }\right)}{R}\right).\mathit{exp}\left(\frac{-\mathrm{159,300}}{RT}\right)\cdot P_{O_2}^{\frac{1}{2}}\right\}}^{-5}]}^{-1/5},(14)$

where $C_{Pu}$ is Pu content in heavy metals (U + Pu).

Figure 2 shows the results obtained from the calculation of $\left[O_i\right]$ and $\left[V_o\right]$ at 1973 K. The cross points of [V] and [Oi] in UO₂, PuO₂, and (U, Pu)O₂ correspond to stoichiometric composition. The nuclear fuel pellets are sintered at approximately 1973 K. The figure shows the equilibrium condition during the sintering process. In CeO₂ and ThO₂, a region where $\left[O_i\right]$ = $\left[V_o\right]$ was observed, rather than a cross point. This difference between the groups is due to the stability of the point defect. Generally, the concentrations of electron-hole pairs and Frenkel defect pairs are known to be dominant in near stoichiometric composition in the former and latter groups, respectively (Brouwer, 1954; Kofstad, 1972). According to reports, their oxides exhibit electronic and ionic conduction mechanisms in electrical conductivity. Electronic conduction is assumed to be induced by 5f electrons. CeO₂ and ThO₂ are ionic conductors that lack valence electrons. Figure 2 shows the linear relationships observed between ln P _{O 2} and ln $\left[V_o\right]$ or ln $\left[O_i\right]$, which indicates that $\left[V_o\right]$ and $\left[O_i\right]$ are proportional to $P_{O_2}^{\frac{1}{2}}$ (Kofstad, 1972; Kato, 2022). In this case, values of n are constant depending on the defect type. It was observed that this same $P_{O_2}^{\frac{1}{2}}$ relationship also exists in the self-diffusion coefficient and electron conduction. The deviation x in $M{O}_{2+x}$ was obtained as follows:

$x=\left[O_i\right]-\left[V_o\right].(15)$

FIGURE 2

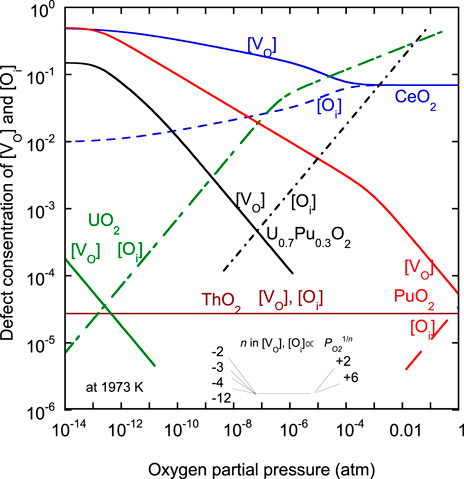
FIGURE 2. Point defect concentrations $\left[O_i\right]$ and $\left[V_o\right]$ in CeO₂, ThO₂, UO₂, PuO₂, and (U_0.7Pu_0.3)O₂ at 1973 K as a function of $p_{O2}$. Relationship of $\left[O_i\right]$ and $\left[V_o\right]\propto {p_{O2}}^{1/n}$ was observed. The value of n was dependent on defect type.

By substituting, Eqs 4–15 can be used to evaluate $D^{*}$ and $\stackrel{\sim }{D}$.

The parameters $D_{Vo}^0$, $\Delta H_{Vo}^m$, $D_{Oi}^0$, and $\Delta H_{Oi}^m$ are required to evaluate $D^{*}$ and $\stackrel{\sim }{D}$ using Eqs 4, 5. In previous studies, the values of $\Delta H_{Vo}^m$ and $\Delta H_{Oi}^m$ were determined using the ab initio approach (Kato et al., 2017a; Watanabe et al., 2021; Kobayashi et al., 2022). Other parameters were obtained by fitting the temperature dependences of $D^{*}$ and $\stackrel{\sim }{D}$. Table 1 shows the parameters used in this study, and $D^{*}$ and $\stackrel{\sim }{D}$ were determined and used to describe the lines in Figures 3–6 as functions of P _{O 2} and T. The figures show that $D^{*}$ is proportional to $P_{O_2}^{\frac{1}{2}}$, like $\left[V_o\right]$ and $\left[O_i\right]$. The calculated values agreed with the experimental data. The parameters used in the calculation were the same as those discovered in previous studies. However, the equations used to determine $\left[V_o\right]$ and $\left[O_i\right]$ differed from those used in previous evaluations. Eqs 6–14 demonstrate how a formula was used to represent the variation from multiple lines. These equations were improved in terms of representation near the boundary between regions with different values of n. Figure 6 shows the $D^{*}$ and $\stackrel{\sim }{D}$ of U_0.7Pu_0.3O₂, a nonstoichiometric compound that is stable in both hyper- and hypo-stoichiometric composition regions (Watanabe et al., 2020; Kato, 2022). $D^{*}$ becomes minimal in the near stoichiometric composition, and the changes in the range of composition of $D^{*}$ and $\stackrel{\sim }{D}$ can be seen in the figure.

TABLE 1

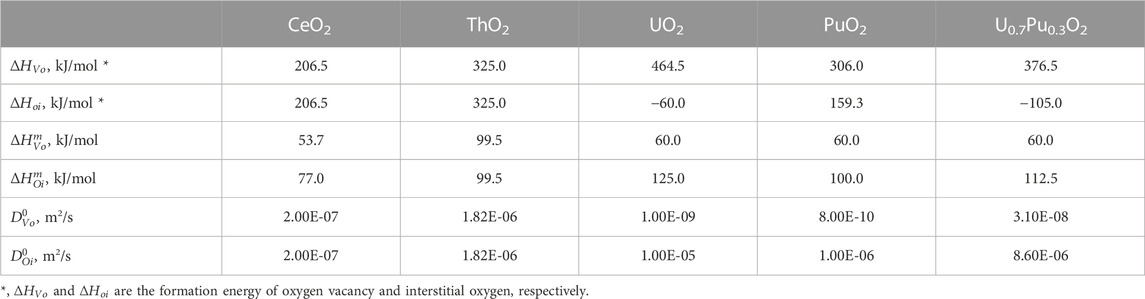
TABLE 1. List of parameters for Eq. 4.

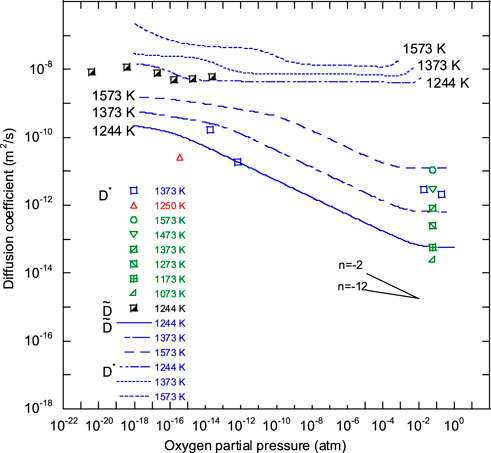
FIGURE 3

FIGURE 3. $D^{*}$ and $\stackrel{\sim }{D}$ of CeO₂ as functions of temperature and $p_{O2}$. Blue, red, green, and black symbols were reported by Floyd (1973), Gotte et al. (2007), Kamiya et al. (2000), and Millot and Mierry (1985), respectively.

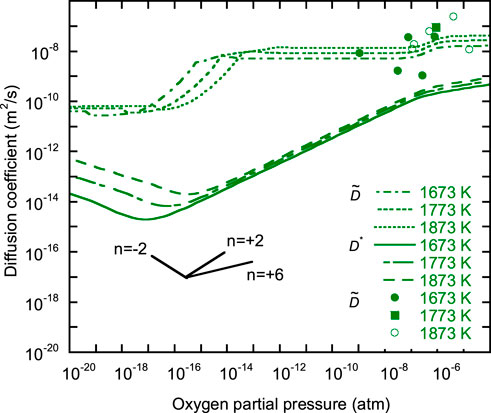
FIGURE 4

FIGURE 4. $D^{*}$ and $\stackrel{\sim }{D}$ of oxygen in UO₂ as functions of temperature and $p_{O2}$. The plotted data were reported by Watanabe and Kato.

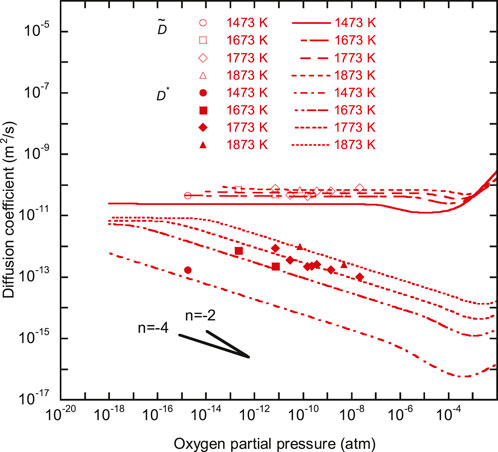
FIGURE 5

FIGURE 5. $D^{*}$ and $\stackrel{\sim }{D}$ of oxygen in PuO₂ as function of temperature and $p_{O2}$. The plotted data were reported by Kato et al. (2013).

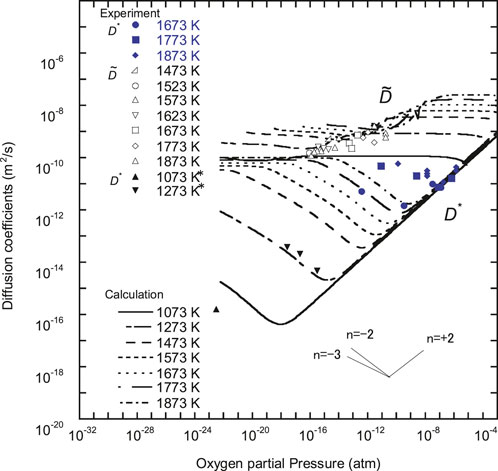
FIGURE 6

FIGURE 6. $D^{*}$ and $\stackrel{\sim }{D}$ of oxygen in U_0.7Pu_0.3O₂ as function of temperature and $p_{O2}$. Open symbols were reported by Watanabe et al. (2017) and Kato et al. (2009), and closed blue symbols were reported by Watanabe et al. (2020). Closed black symbols were reported by Vauchy et al. (2015), which were measured data in U_0.55Pu_0.45O₂.

3.2 Self-diffusion coefficients

Figure 7 shows O/M dependence of the oxygen self-diffusion coefficient ($D^{*}$) at 1773 K. The value decreases as the compound approaches stoichiometric composition. The minimum value of U_0.7Pu_0.3O₂ differs slightly from the O/M = 2.00 in terms of hypo-stoichiometric composition, which was calculated by using the equations reported previously (Kato, 2022). The large diffusion coefficient of O_i in comparison to V_o caused this deviation. Figure 8 shows $D^{*}$ at stoichiometric composition against 1/T with solid lines, which were determined using Eq. 4. The $D^{*}$ of ThO₂ was obtained using the simulation results reported by Kobayashi et al. (2022). The simulation results were evaluated using the following expression:

$D^{*}=D^0\mathit{exp}\left(-\frac{Q}{RT}\right),(16)$

where Q and $D^0$ are activation energy and the pre-exponential term of $D^{*}$, with the values 1.82E−06 and 424.48 kJ/mol, respectively. Of the materials assessed, CeO₂ had the highest $D^{*}$ value and ThO₂ had the lowest. The values of PuO₂ and UO₂ were nearly identical, and the value of the solid solution (U, Pu)O₂ was higher than that of either UO₂ or PuO₂. The data for $D^{*}$ are represented with broken lines. The $D^{*}$ of CeO₂ was in strong agreement with data from the current study and with that from prior research. However, the $D^{*}$ of the other oxides in this study differed from prior data. This difference was caused by a large change in $D^{*}$ near stoichiometric composition.

FIGURE 7

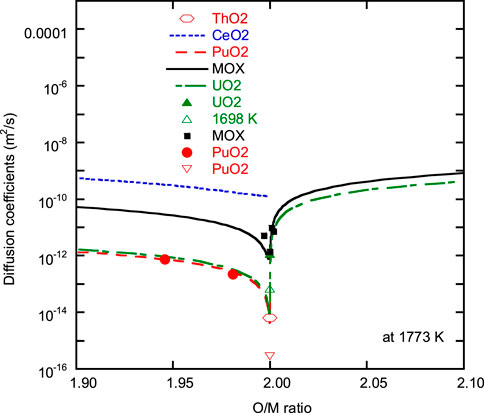
FIGURE 7. Comparison of O/M ratio dependence of $D^{*}$ for various oxides at 1773 K. The open symbol of ThO₂ was reported by Kobayashi et al. (2022). Closed green, black, and red symbols were reported by Matzke (1987), Watanabe et al. (2020), and Kato et al. (2013), respectively. Open red and green symbols were reported by Deaton and Wiedenheft (1973) and Hadari et al. (1971), respectively, and were measured at 1698 K.

FIGURE 8

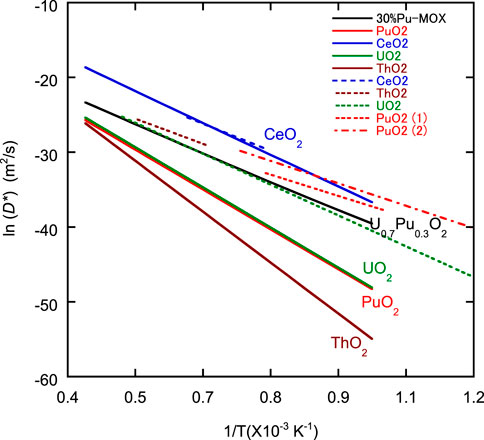
FIGURE 8. Plot of ln D* of oxygen in CeO₂, ThO₂, UO₂, PuO₂, and U_0.7Pu_0.3O₂ against 1/T. Data used to generate the solid lines were calculated using Eq. 4. The broken lines representing CeO₂, ThO₂, UO₂, PuO₂ (1), and PuO₂ (2) were reported by Kamiya et al. (2000), Ando et al. (1976), Breitung (1978), Deaton and Wiedenheft (1973), and Bayoglu et al. (1983), respectively.

Table 1 shows all the parameters required for the evaluation of $D^{*}$ and $\stackrel{\sim }{D}$. $\Delta H_{Vo}^m$ is approximately 60 kJ/mol in the oxides, excluding ThO₂. The $\Delta H_{Oi}^m$ of the oxides ranged from 77 to 112.5 kJ/mol. These migration energies and point defect concentrations can be used to evaluate $D^{*}$. The oxygen potential data were used to determine the point defect concentrations. It was observed that the diffusion coefficients were consistent with oxygen potential data. As shown in Figure 8 and Table 2, the D* and Q_sto. in the oxides at O/M = 2.00 were evaluated (Andersson et al., 2009; Zhang et al., 2019; Zamzamian et al., 2022). Of these oxides, the Q_sto of ThO₂ was found to be the highest. The activation energies, Q_Vo and Q_Oi, of $\left[V_o\right]$ and $\left[O_i\right]$ diffusion, respectively, are also compared in Table 2; these types of diffusion were dominant in hypo- and hyper-stoichiometric regions, respectively. The Q_Vo and Q_Oi were obtained using Eqs 17, 18, respectively.

$Q_{Vo}=∆{\mathit{H}}_{\mathit{V}\mathit{o}}/2+\mathit{\Delta }{H}_{Vo}^m,(17)$

$Q_{Oi}=∆{\mathit{H}}_{\mathit{O}\mathit{i}}/2+\mathit{\Delta }{H}_{Oi}^m.(18)$

TABLE 2

TABLE 2. Comparison of activation energy for diffusion.

The Q_Vo and Q_Oi of U_0.7Pu_0.3O₂ were expected to have properties related to the Q_Vo of PuO₂ and the Q_Oi of UO₂. Recently, diffusion mechanisms, such as ion migration route, have been studied using computational simulation. State-of-the-art simulation methods have added useful information to the discussion of oxygen diffusion mechanisms. However, many challenges remain in application of the methods to the analysis of high temperature diffusion in actinide oxides (Machida, 2022).

In general, the heat capacity of oxides with fluorite structures increases rapidly at high temperatures. This study attempted to evaluate the degree to which Frenkel defect formation contributed to the increase in heat capacity (Konings and Beneš, 2013; Konings et al., 2014; Kato, 2022). Eq. 19 represents the equilibrium constant of Frenkel defect formation $K_F$.

$K_F=\left[O_i\right]\left[V_o\right]=\exp \left(∆S_F/R\right).\exp \left(-∆H_F/RT\right),(19)$

where $∆S_F$ and $∆H_F$ are entropy and enthalpy of $K_F$, respectively. The $K_F$ of the oxides can be expressed using the following equations:

$K_F=\exp \left(165.0/R\right)\exp .\left(-\mathrm{413,000}/RT\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{C}\mathrm{e}{O}_{2,}(20)$

$K_F=\exp \left(154.0/R\right)\exp .\left(-\mathrm{650,000}/RT\right){\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{T}\mathrm{h}\mathrm{O}}_2,(21)$

$K_F=\exp \left(37.0/R\right)\exp .\left(-\mathrm{404,500}/RT\right)\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{U}\mathrm{O}}_2,(22)$

$K_F=\exp \left(50.8/R\right).\exp \left(-\mathrm{465,000}/RT\right)\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{P}\mathrm{u}\mathrm{O}}_2,(23)$

$K_F=\exp \left(9.98/R\right).\exp \left(-\mathrm{271,000}/RT\right)\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{U}}_{0.7}{\mathrm{P}\mathrm{u}}_{0.3}{\mathrm{O}}_2.(24)$

The contribution of Frenkel defect formation, $C_F$, to heat capacity can be expressed as follows:

$C_F=d\left({K_F}^{\frac{1}{2}}∆H_F\right)/dT.(25)$

Figure 9 shows the relationship between $C_F$ of oxides and temperature. At high temperatures, the $C_F$ of CeO₂ and ThO₂ increased rapidly to above 100 kJ/mol K. The Bredig transition limited the maximum value. This observation demonstrates the importance of the contribution of Frenkel defect formation in the $C_F$ of CeO₂ and ThO₂. However, the increase in the $C_F$ of UO₂, PuO₂, and U_0.7Pu_0.3O₂ was extremely low, at 5–10 kJ/mol K. This increase is significantly smaller when compared with other data. It has been observed that other mechanisms also play important roles in the heat capacity of UO₂, PuO₂, and (U_0.7Pu_0.3)O₂. For example, according to previous studies, the contribution of electronic defect formation in these oxides caused the high-temperature heat capacity (Hein et al., 1968; Fujino et al., 1993; Kato, 2022). Thus, the defect formation energies used in the evaluation of $D^{*}$ are strongly related to thermal properties. In order to ensure consistency with other properties, it is essential that $D^{*}$ is evaluated from defect formation energies.

FIGURE 9

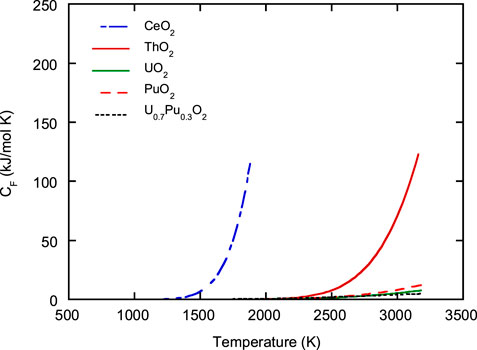
FIGURE 9. Contribution of Frenkel defect formation $C_F$ in heat capacity with temperature. The data were calculated using Eqs 18–23.

3.3 Chemical diffusion coefficients

Figure 10 shows the O/M dependence of chemical diffusion coefficients ($\stackrel{\sim }{D}$) at 1773 K. There were no significant observable change in the data in the region of low O/M ratio; however, near stoichiometric composition, the value suddenly increased. Between the range of hypo- and hyper-stoichiometric composition, $\stackrel{\sim }{D}$ varied by 1–4 orders of magnitude. Figure 11 shows the plot of $\ln \stackrel{\sim }{D}$ of low O/M and O/M = 2.00 materials against 1/T. In a previous study, the reduction and oxidation curves between PuO₂ and PuO_1.95 were measured, as shown in Figure 12. The reduction curve can be represented by Eq. 3, which is dominated by the chemical diffusion coefficient; the oxidation curve, however, cannot be represented by Eq. 3. This observation demonstrates the importance of other mechanisms in the oxidation process. Figure 13 shows the change in the O/M ratio during the reduction and oxidation reactions. In the reduction process, the sample’s O/M ratio was low at the pellet surface, as shown in Figure 13A. Because $\stackrel{\sim }{D}$ is lower at the surface than on the inside, the reduction process is dominated by $\stackrel{\sim }{D}$ at the surface, which is a chemical diffusion-controlling process. Whereas in the oxidation process, the O/M ratio at the surface is 2.00. Because $\stackrel{\sim }{D}$ is faster at the surface than on the inside, a new phase having O/M = 2.00 expands from the surface to the interior, which is diffusion in a system consisting of two phases, as shown in Figure 13B. The change in the O/M ratio in the oxidation process, as shown in Figure 13B, can be represented by the following equations (Jost, 1933):

$\frac{C_0-C_{II}}{C_{II}-C_s}=\sqrt{\pi }\gamma .\exp \left({\gamma }^2\right).\mathrm{erf}\left(\gamma \right),(26)$

$x_0={\gamma }^2\sqrt{\stackrel{\sim }{D}t}.(27)$

FIGURE 10

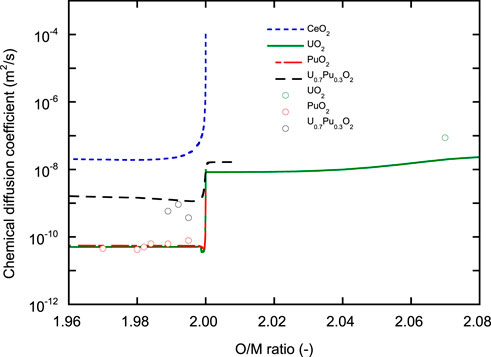
FIGURE 10. O/M ratio dependence of $\stackrel{\sim }{D}$ of oxygen in CeO₂, UO₂, PuO₂, and U_0.7Pu_0.3O₂ at 1773 K. The green, red, and black symbols were reported by Watanabe and Kato, Kato et al. (2013), and Watanabe et al. (2017), respectively.

FIGURE 11

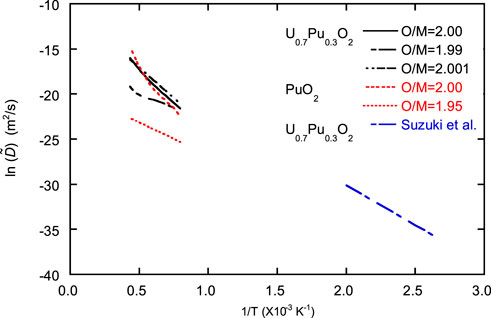
FIGURE 11. Inverse T dependence of ln $\stackrel{\sim }{D}$ of oxygen in PuO₂ and U_0.7Pu_0.3O₂. The blue line was reported by Suzuki et al. (2007).

FIGURE 12

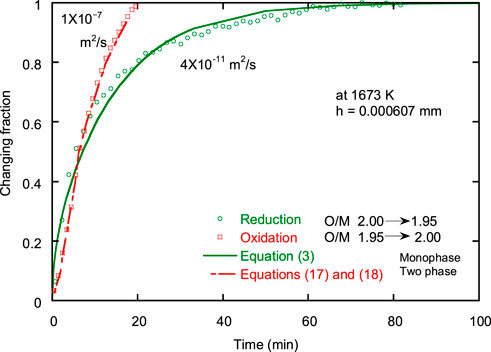
FIGURE 12. Reduction and oxidation curves between PuO₂ and PuO_1.95 at 1673 K. The data were obtained in a previous study by Kato et al. (2013) using the same sample.

FIGURE 13

FIGURE 13. O/M ratio gradients in the (A) reduction process and (B) oxidation process when $\stackrel{\sim }{D}atlow\frac{O}{M}$ and $\stackrel{\sim }{D}at\frac{O}{M}=2.00.$

Eqs 26, 27 were used to analyze the oxidation process, and it was discovered that $\stackrel{\sim }{D}$ and C_II were 1e−8 m²/s and O/M = 1.998–1.999, respectively. $\stackrel{\sim }{D}$ was in strong agreement with the results obtained, as shown in Figure 13. In early studies on the chemical diffusion of PuO₂ and MOX, $\stackrel{\sim }{D}$ was evaluated using an oxidation process, and the results yielded values higher than those of this study. Thus, the data were not accurate.

The nuclear fuel O/M ratio is an important parameter influencing fuel performance, and its value is controlled as one of the fuel specifications. In the pellet production process, the O/M ratio is adjusted, and the rate of change of the O/M ratio can be evaluated using the chemical diffusion coefficient. To remove additives from the pressed pellets, they were pre-sintered at about 1073 K. In this process, the pellets were adjusted to O/M = 2.00, and the final adjustment to the O/M ratio occurred via the chemical diffusion-controlling reduction in the sintering process. Assuming the pellet is an infinite cylinder, the change in the O/M ratio as a function of temperature, time, and P _{O 2} can be represented by Eq. 2. However, due to the difficulty in maintaining P _{O 2} in the atmosphere when many pellets are treated in engineering scale production, a longer sintering time is required in comparison with the evaluation results (Takano et al., 2011).

After sintering, low O/M sintered pellets were exposed to an oxidation atmosphere. In previous studies (Woodley and Gibby, 1973; Suzuki et al., 2007), it was discovered that low O/M pellets were oxidized at temperatures lower than 400 K. Suzuki et al. (2007) investigated low-temperature oxidation by diffusion in a two-phase system and estimated $\stackrel{\sim }{D}$ = 2.06e−16 m²/s at 373 K. The estimated data were consistent with those from this study, as shown in Figure 11. Thus, chemical diffusion coefficients are useful data for evaluating various phenomena in the fuel production process.

4 Summary

This study describes oxygen self-diffusion coefficients using the defect concentration $\left[V_o\right]$ and $\left[O_i\right]$ as functions of P _{O 2} and temperature. The diffusion coefficients of the fluorite-type crystals CeO₂, ThO₂, UO₂, PuO₂, and (U, Pu)O₂ were used to verify the relationship. Oxygen potential data was used to calculate the defect concentrations for the analysis of CeO₂, UO₂, PuO₂, and (U, Pu)O₂. The relationships between oxygen potential, the oxygen self-diffusion coefficient, and the chemical diffusion coefficient were represented by determining all parameters. The Frenkel defect concentration was used to evaluate the heat capacity increase observed at temperatures greater than 1500 K. The results revealed that Frenkel defect formation significantly impacts heat capacity in CeO₂ and ThO₂. However, the contribution for UO₂, PuO₂, and (U, Pu)O₂ was very small compared to other mechanisms, such as electronic defect formation.

The evaluation of chemical diffusion coefficients revealed that the mechanism of reduction in the reaction between O/M = 2.00 and hypo-stoichiometric composition differs from that of oxidation. It is proposed that the reduction process is dominated by a monophase chemical diffusion-controlling model, whereas the oxidation process occurs in a two-phase system wherein a new phase with O/M = 2.00 is formed at the surface and expands into the interior. These mechanisms are important for understanding the various behaviors of nuclear oxides during the production process.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MK made substantial contributions to the study concept or the data analysis or interpretation; MW, SH and RV drafted the manuscript or revised it critically for important intellectual content and agreed to be accountable for all aspects of the work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnuen.2022.1081473/full#supplementary-material

References

Andersson, D., Watanabe, T., Deo, C., and Uberuaga, B. (2009). Role of di-interstitial clusters in oxygen transport in UO_2+x from first principles. Phys. Rev. B 80, 060101. doi:10.1103/physrevb.80.060101

CrossRef Full Text | Google Scholar

Ando, K., Oishi, Y., and Hidaka, Y. (1976). Self-diffusion of oxygen in single crystal thorium oxide. J. Chem. Phys. 65, 2751–2755. doi:10.1063/1.433419

CrossRef Full Text | Google Scholar

Auskern, A. B., and Belle, J. (1961). Oxygen ion self-diffusion in uranium dioxide. J. Nucl. Mater. 3, 267–276. doi:10.1016/0022-3115(61)90194-5

CrossRef Full Text | Google Scholar

Bayoglu, A., and Lorenzelli, R. (1980). Chemical diffusion of oxygen in (U, Pu) O_2+x. J. Nucl. Mater. 88, 315–316. doi:10.1016/0022-3115(80)90289-5

CrossRef Full Text | Google Scholar

Bayoglu, A. S., Giordano, A., and Lorenzelli, R. (1983). Mesure de l'autodiffusion de l'oxygene dans PuO_2.00 par echange isotopique. J. Nucl. Mater. 113, 71–74. doi:10.1016/0022-3115(83)90168-x

CrossRef Full Text | Google Scholar

Bayoglu, A. S., and Lorenzelli, R. (1979). Etude de la diffusion chimique de l'oxygene dans PuO_2−x par dilatometrie et thermogravimetrie. J. Nucl. Mater. 82, 403–410. doi:10.1016/0022-3115(79)90022-9

CrossRef Full Text | Google Scholar

Bayoglu, A. S., and Lorenzelli, R. (1984). Oxygen diffusion in fcc fluorite type nonstoichiometric nuclear oxides MO_2±x. Solid State Ionics 12, 53–66. doi:10.1016/0167-2738(84)90130-9

CrossRef Full Text | Google Scholar

Belle, J. (1969). Oxygen and uranium diffusion in uranium dioxide (a review). J. Nucl. Mater. 30, 3–15. doi:10.1016/0022-3115(69)90163-9

CrossRef Full Text | Google Scholar

Berthinier, C., Rado, C., Chatillon, C., and Hodaj, F. (2013). Thermodynamic assessment of oxygen diffusion in non-stoichiometric UO_2±x from experimental data and Frenkel pair modeling. J. Nucl. Mater. 433, 265–286. doi:10.1016/j.jnucmat.2012.09.011

CrossRef Full Text | Google Scholar

Bittel, J., Sjodahl, L., and White, J. (1969). Steam oxidation kinetics and oxygen diffusion in UOz at high temperatures. J. Am. Ceram. Soc. 52, 446–451. doi:10.1111/j.1151-2916.1969.tb11976.x

CrossRef Full Text | Google Scholar

Breitung, W. (1978). Oxygen self and chemical diffusion coefficients in UO_2±x. J. Nucl. Mater. 74, 10–18. doi:10.1016/0022-3115(78)90527-5

CrossRef Full Text | Google Scholar

Brouwer, G. (1954). A general asymptotic solution of reaction equations common in solid-state chemistry. Philips Res. Rep. 9, 366–376.

Google Scholar

Chereau, P., and Wadier, J. F. (1973). Mesures de resistivite et de cinetique d'oxydation dans PuO_2−x. J. Nucl. Mater. 46, 1–8. doi:10.1016/0022-3115(73)90116-5

CrossRef Full Text | Google Scholar

Contamin, P., Bacmann, J. J., and Marin, J. F. (1972). Autodiffusion de l'oxygene dans le dioxyde d'uranium surstoechiometrique. J. Nucl. Mater. 42, 54–64. doi:10.1016/0022-3115(72)90007-4

CrossRef Full Text | Google Scholar

Cooper, M. W. D., Murphy, S. T., and Andersson, D. A. (2018). The defect chemistry of UO_2±x from atomistic simulations. J. Nucl. Mater. 504, 251–260. doi:10.1016/j.jnucmat.2018.02.034

CrossRef Full Text | Google Scholar

D'Annucci, F., and Sari, C. (1977). Oxygen diffusion in uranium-plutonium oxide fuels at low temperatures. J. Nucl. Mater. 68, 357–359. doi:10.1016/0022-3115(77)90265-3

CrossRef Full Text | Google Scholar

Deaton, R. L., and Wiedenheft, C. J. (1973). Self-diffusion of oxygen in ²³⁸PuO. Miamisburg, OH: Monsanto Research Corp.

Google Scholar

Dorado, B., Garcia, P., Carlot, G., Davoisne, C., Fraczkiewicz, M., Pasquet, B., et al. (2011). First-principles calculation and experimental study of oxygen diffusion in uranium dioxide. Phys. Rev. B 83, 035126. doi:10.1103/physrevb.83.035126

CrossRef Full Text | Google Scholar

Dornelas, W., and Lacombe, P. (1967). Application of diffusion in an electric field between 900 and 1100°C to the determination of the coefficient of diffusion of oxygen in the uranium oxide UO. C. R. Acad. Sci. Paris 265, C359.

Google Scholar

Floyd, J. M. (1973). Interpretation of transport phenomena in non-stoichiometric ceria. Indian J. Technol. 11, 589–594.

Google Scholar

Forsberg, K., Jernkvist, L. O., and Massih, A. R. (2020). Modeling oxygen redistribution in UO_2+x fuel pellet. J. Nucl. Mater. 528, 151829. doi:10.1016/j.jnucmat.2019.151829

CrossRef Full Text | Google Scholar

Fujino, T., Yamashita, T., Ohuchi, K., Naito, K., and Tsuji, T. (1993). High temperature electrical conductivity and conduction mechanism of (U, Pu)O_2±x at low oxygen partial pressures. J. Nucl. Mater. 202, 154–162. doi:10.1016/0022-3115(93)90038-z

CrossRef Full Text | Google Scholar

Garcia, P. H., Fraczkiewicz, M., Davoisne, C., Carlot, G., Pasquet, B., Baldinozzi, G., et al. (2010). Oxygen diffusion in relation to p-type doping in uranium dioxide. J. Nucl. Mater. 400, 112–118. doi:10.1016/j.jnucmat.2010.02.019

CrossRef Full Text | Google Scholar

Gotte, A., SpåNGBERG, D., Hermansson, K., and Baudin, M. (2007). Molecular dynamics study of oxygen self-diffusion in reduced CeO₂. Solid State Ionics 178, 1421–1427. doi:10.1016/j.ssi.2007.08.003

CrossRef Full Text | Google Scholar

Hadari, Z., Kroupp, M., and Wolfson, Y. (1971). Self-diffusion measurement of oxygen in UO₂ by the nuclear reaction ¹⁸O(p, γ)¹⁹F. J. Appl. Phys. 42, 534–535. doi:10.1063/1.1660058

CrossRef Full Text | Google Scholar

Hein, R. A., Flagella, P. N., and Conway, J. B. (1968). High-temperature enthalpy and heat of fusion of UO₂. J. Am. Ceram. Soc. 51, 291–292. doi:10.1111/j.1151-2916.1968.tb13863.x

CrossRef Full Text | Google Scholar

Jost, W. (1933). Diffusion and electrolytic conduction in crystals (ionic semiconductors). J. Chem. Phys. 1, 466–475. doi:10.1063/1.1749319

CrossRef Full Text | Google Scholar

Kamiya, M., Shimada, E., Ikuma, Y., Komatsu, M., and Haneda, H. (2000). Intrinsic and extrinsic oxygen diffusion and surface exchange reaction in cerium oxide. J. Electrochem. Soc. 147, 1222. doi:10.1149/1.1393340

CrossRef Full Text | Google Scholar

Kato, M., Morimoto, K., Tamura, T., Sunaoshi, T., Konashi, K., Aono, S., et al. (2009). Oxygen chemical diffusion in hypo-stoichiometric MOX. J. Nucl. Mater. 389, 416–419. doi:10.1016/j.jnucmat.2009.02.018

CrossRef Full Text | Google Scholar

Kato, M., Nakamura, H., Watanabe, M., Matsumoto, T., and Machida, M. (2017a). Defect chemistry and basic properties of non-stoichiometric PuO₂. Defect Diffusion Forum 375, 57–70. doi:10.4028/www.scientific.net/ddf.375.57

CrossRef Full Text | Google Scholar

Kato, M. (2022). “Properties,” in Materials science and fuel technologies of uranium and plutonium mixed oxide. Editors M. KATO,, and M. MACHIDA (Boca Raton, FL: CRC Press).

CrossRef Full Text | Google Scholar

Kato, M., Uchida, T., and Sunaoshi, T. (2013). Measurement of oxygen chemical diffusion in PuO_2-xand analysis of oxygen diffusion in PuO_2-x and (Pu, U)O_2-x. Phys. status solidi C. 10, 189–192. doi:10.1002/pssc.201200454

CrossRef Full Text | Google Scholar

Kato, M., Watanabe, M., Matsumoto, T., Hirooka, S., and Akashi, M. (2017b). Oxygen potentials, oxygen diffusion coefficients and defect equilibria of nonstoichiometric (U, Pu)O_2±x. J. Nucl. Mater. 487, 424–432. doi:10.1016/j.jnucmat.2017.01.056

CrossRef Full Text | Google Scholar

Kim, K. C., and Olander, D. R. (1981). Oxygen diffusion in UO_2−x. J. Nucl. Mater. 102, 192–199. doi:10.1016/0022-3115(81)90559-6

CrossRef Full Text | Google Scholar

Kobayashi, K., Okumura, M., Nakamura, H., Itakura, M., Machida, M., and Cooper, M. W. D. (2022). Machine learning molecular dynamics simulations toward exploration of high-temperature properties of nuclear fuel materials: Case study of thorium dioxide. Sci. Rep. 12, 9808. doi:10.1038/s41598-022-13869-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kofstad, P. (1972). Nonstoichiometry, diffusion, and electrical conductivity in binary metal oxides. Hoboken, New Jersey: Wiley-Interscience.

Google Scholar

Komeno, A., Kato, M., Hirooka, S., and Sunaoshi, T. (2012). Oxygen potentials of PuO_2-x. MRS Proc. 1444, 1162. doi:10.1557/opl.2012.1162

CrossRef Full Text | Google Scholar

Konings, R. J. M., Beneš, O., KováCS, A., Manara, D., Sedmidubske, D., Gorokhov, L., et al. (2014). The thermodynamic properties of thef-elements and their compounds. Part 2. The lanthanide and actinide oxides. J. Phys. Chem. Reference Data 43, 013101. doi:10.1063/1.4825256

CrossRef Full Text | Google Scholar

Konings, R. J. M., and Beneš, O. (2013). The heat capacity of NpO₂ at high temperatures: The effect of oxygen Frenkel pair formation. J. Phys. Chem. Solids 74, 653–655. doi:10.1016/j.jpcs.2012.12.018

CrossRef Full Text | Google Scholar

KröGER, F. A., and Vink, H. J. (1956). Solid state physics, New York: Academic Press, 307.

Google Scholar

Lay, K. (1970). Oxygen chemical diffusion coefficient of uranium dioxide. J. Am. Ceram. Soc. 53, 369–373. doi:10.1111/j.1151-2916.1970.tb12134.x

CrossRef Full Text | Google Scholar

Ligeon, E., Bontemps, A., and Contamin, P. (1970). Application de la réaction ¹⁸O(p, alpha) ¹⁵N à l’étude de l’autodiffusion de l’oxygène dans le dioxyde d’uranium’. Grenoble (France): Commissariat à l’Energie Atomique.

Google Scholar

Lorenzelli, R., and El Sayed Ali, M. (1977). Dilatation thermique d'oxydes mixtes (UPu)O_2−x en fonction de l'ecart a la stoechiometrie. J. Nucl. Mater. 68, 100–103. doi:10.1016/0022-3115(77)90221-5

CrossRef Full Text | Google Scholar

LöSöNEN, P. (2017). On the effect of irradiation-induced resolution in modelling fission gas release in UO₂ LWR fuel. J. Nucl. Mater. 496, 140–156. doi:10.1016/j.jnucmat.2017.09.015

CrossRef Full Text | Google Scholar

Machida, M. (2022). “Theoretical and computatinal works on oxide nuclear fuel materials,” in Materials science and fuel technologies of uranium and plutonium mixed oxide. Editors M. KATO,, and M. MACHIDA (Boca Raton, FL: CRC Press).

Google Scholar

Matzke, H. (1987). Atomic transport properties in UO₂ and mixed oxides (U, Pu)O₂. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 83, 1121–1142. doi:10.1039/f29878301121

CrossRef Full Text | Google Scholar

Millot, F., and Mierry, P. D. (1985). A new method for the study of chemical diffusion in oxides with application to cerium oxide CeO₂–_x. J. Phys. Chem. Solids 46, 797–801. doi:10.1016/0022-3697(85)90003-4

CrossRef Full Text | Google Scholar

Mullins, L. (1972). Preparation and evaluation of medical-grade $ sup 238$ Pu fuels. N. Mex: Los Alamos Scientific Lab.

Google Scholar

Murch, G. E., and Catlow, C. R. A. (1987). Oxygen diffusion in UO₂, ThO₂ and PuO₂. A review. J. Chem. Soc. Faraday Trans. 2, 83.

CrossRef Full Text | Google Scholar

Ruello, P., Chirlesan, G., Petot-Ervas, G., Petot, C., and Desgranges, L. (2004). Chemical diffusion in uranium dioxide–influence of defect interactions. J. Nucl. Mater. 325, 202–209. doi:10.1016/j.jnucmat.2003.12.007

CrossRef Full Text | Google Scholar

Sari, C. (1978). Oxygen chemical diffusion coefficient of uranium-plutonium oxides. J. Nucl. Mater. 78, 425–426. doi:10.1016/0022-3115(78)90465-8

CrossRef Full Text | Google Scholar

Stan, M., and Cristea, P. (2005). Defects and oxygen diffusion in PuO_2−x. J. Nucl. Mater. 344, 213–218. doi:10.1016/j.jnucmat.2005.04.044

CrossRef Full Text | Google Scholar

Suzuki, K., Kato, M., Sunaoshi, T., Uno, H., Carvajal-Nunez, U., Nelson, A. T., et al. (2018). Thermal and mechanical properties of CeO₂. J. Am. Ceram. Soc. 102, 1994. doi:10.1111/jace.16055

CrossRef Full Text | Google Scholar

Suzuki, K., Kato, M., Tamura, T., Aono, S., and Kashimura, M. (2007). The oxidation rate of (U_0.7Pu_0.3)O_2−x with two fcc phases. J. Alloys Compd. 444-445, 590–593. doi:10.1016/j.jallcom.2007.02.062

CrossRef Full Text | Google Scholar

Takano, T., Sudo, K., Takeuchi, K., Kihara, Y., and Kato, M. 2011. “Development of oxygen-to-metal ratio of MOX pellet adjustment technology for the simplified MOX pellet fabrication method in the FaCT project,” in Proceedings of GLOBAL 2011, Makuhari, Japan, December 11-16, 2011.

Google Scholar

Vauchy, R., Robisson, A. C., Bienvenu, P., Roure, I., Hodaj, F., and Garcia, P. (2015). Oxygen self-diffusion in polycrystalline uranium–plutonium mixed oxide U_0.55Pu_0.45O₂. J. Nucl. Mater. 467, 886–893. doi:10.1016/j.jnucmat.2015.11.003

CrossRef Full Text | Google Scholar

Watanabe, M., and Kato, M. (2012). Oxygen potential and defect equilibria in UO_2±x. Accepted in Frontiers in Nuclear Engineering Nuclear Materials.

Google Scholar

Watanabe, M., Kato, M., and Sunaoshi, T. (2020). Oxygen self-diffusion in near stoichiometric (U, Pu)O2 at high temperatures of 1673-1873 K. J. Nucl. Mater. 542, 152472. doi:10.1016/j.jnucmat.2020.152472

CrossRef Full Text | Google Scholar

Watanabe, M., Nakamura, H., Suzuki, K., Machida, M., and Kato, M. (2021). Defect equilibria and thermophysical properties of CeO_2-x based on experimental data and density functional theory calculation result. J. Am. Ceram. Soc. 105, 2248–2257. doi:10.1111/jace.18249

CrossRef Full Text | Google Scholar

Watanabe, M., and Seki, T. (2021). Initial sintering kinetics of non-stoichiometric CeO_2−x. Mater. Sci. Eng. B 272, 115369. doi:10.1016/j.mseb.2021.115369

CrossRef Full Text | Google Scholar

Watanabe, M., Sunaoshi, T., and Kato, M. (2017). Oxygen chemical diffusion coefficients of (U, Pu)O_2-x. Defect Diffusion Forum 375, 84–90. doi:10.4028/www.scientific.net/ddf.375.84

CrossRef Full Text | Google Scholar

Woodley, R. E., and Gibby, R. L. (1973). Room-temperature oxidation of (U,Pu)O_2–x. Richland, WA: Westinghouse Hanford Company Report.

Google Scholar

Zamzamian, S. M., Zolfaghari, A., and Kowsar, Z. (2022). Molecular dynamics investigation of xenon, uranium, and oxygen diffusion in UO₂ nuclear fuel. Comput. Mater. Sci. 211, 111553. doi:10.1016/j.commatsci.2022.111553

CrossRef Full Text | Google Scholar

Zhang, H., Wang, X., and Douglas, J. F. (2019). Localization model description of diffusion and structural relaxation in superionic crystalline UO₂. J. Chem. Phys. 151, 071101. doi:10.1063/1.5115067

PubMed Abstract | CrossRef Full Text | Google Scholar