Implementation and optimization of hybrid parallel strategy in HNET

For the self-developed three-dimensional whole-core High-fidelity NEutron Transport calculation program HNET, although the numerical acceleration algorithms can improve the computation performance of high-fidelity neutron transport in terms of algorithms and models, it still faces some critical issues such as long computing time and enormous memory requirement. The rapid development of high-performance clusters provides a foundation for the application of massively parallel computing. Most current MOC programs are based on a single-type variable to achieve efficient parallelism, and spatial domain decomposition methods are the most common parallel schemes. However, its parallelism is limited and cannot fully utilize the current state-of-the-art computer resources. To solve this problem, hybrid parallel strategies are implemented in HNET to further expand the parallel degree, improve the speed of computation, and reduce the memory requirement. A hybrid MPI/OpenMP method based on domain decomposition and characteristic rays is proposed for the method of characteristics (MOC). For domain decomposition, the simulation domain is divided into spatial subdomains, with each subdomain handled by different processes. On this basis, the characteristic ray parallelism is implemented taking advantage of the inherent parallelism of the characteristic rays. Meanwhile, the optimization of the hybrid parallel strategy further improves the computation speed by eliminating atomic operations and using private pointer arrays and other techniques. In addition, in the framework of generalized equivalence theory (GET) based two-level coarse mesh finite difference method (CMFD), there is also a certain time consumption in solving CMFD linear system. Hence, for CMFD, a hybrid MPI/OpenMP method based on domain decomposition and secondary domain decomposition can be used. Using the secondary domain decomposition method, each subdomain is divided into sub-subdomains, with each sub-subdomain handled by threads, which allows CMFD to utilize the resources of characteristic ray parallelism in MOC, and also increases the speed of CMFD computation. Numerical results show that for both steady-state and transient calculations, the hybrid MPI/OpenMP in HNET can further expand the parallelism and accelerate the computation. It can take full use of parallel resources and achieve large-scale parallelism.

1 Introduction

Over recent years, with the rapid development of new reactor core designs, the geometric complexity and heterogeneity of the cores are increasing, MOC for neutron transport calculations has gradually become a hot research issue and continues today. The method of characteristic is a deterministic method for neutron transport calculations, which is widely used in reactor physics calculations because of its powerful geometry processing capability, high accuracy, and inherent parallelism (Askew, 1972). In the meanwhile, MOC has become an indispensable neutron transport calculation method in domestic and international reactor physics analysis software such as HNET (Kang et al., 2020), NECP-X (Liu et al., 2018), SHARK (Zhang et al., 2022), DeCART (Joo et al., 2004), CRX-3D (Cho et al., 2002), PROTEUS-MOC (Jung et al., 2018), STREAM (Choi and Lee, 2020), MPACT (Kochunas et al., 2013; Collins et al., 2016) and OpenMOC (Boyd et al., 2014), etc. However, the high-fidelity whole-core neutron transport calculation faces serious challenges such as huge computation load and especially the runtime burden (Smith et al., 2013). In fact, the long computation time consumption is an internationally common problem. In order to crack this problem, enabling high-fidelity neutron transport acceleration algorithms has been studied at home and abroad. Among them, the coarse mesh finite difference method is a common global acceleration method, which provides a framework to accelerate the convergence of the eigenvalue problem, and a two-level gCMFD (generalized equivalence theory based on coarse mesh finite difference) acceleration algorithm is proposed, to achieve further efficiency performance (Xu and Downar. 2012).

Although the use of numerical acceleration algorithms can improve the computational efficiency of high-fidelity neutron transport in terms of algorithms and models, it still faces some critical problems such as long computing time and enormous memory requirements. Furthermore, the computational cost of solving the CMFD linear systems is not trivial, especially for the three-dimensional (3D) whole-core modeling with high-fidelity pin-resolved details. It constitutes a large portion of the computational effort (Yee et al., 2017).

In recent decades, the rapid development of massively parallel computing platforms provides a foundation for the application of parallel computing. The computationally intensive, time-consuming, and easily parallelized parts are solved in parallel using high-performance computing clusters (HPCs) and corresponding parallel algorithms, which can greatly increase the computational speed and reduce the computational time. Therefore, the massive parallelism is the inevitable course to accelerate the neutron transport calculation (Dangwei et al., 2019).

Parallel methods have been successfully applied to accelerate MOC and CMFD calculations, and most of them are based on a single-type variable to achieve parallelism, for example, Tsinghua University’s Tiger-3D program has achieved spatial parallelism (Wu et al., 2014), and Korea’s CRX-3D program has achieved angle parallelism (Cho et al., 2007). Among them, the domain decomposition method based on MPI (Message Passing Interface) of distributed storage architecture is the most common parallel scheme (Joo et al., 1996, Hongbo et al., 2013). The simulation domain is divided into subdomains that do not overlap with each other, with each subdomain being handled by separate processes, and these processes need to communicate with their nearest neighbors (Fitzgerald et al., 2019). Each process only stores data relevant to its subdomain, thus can decompose the memory pressure of the computer. However, the single-type variable parallelism has the following disadvantages: 1) the parallelism is limited, especially for energy groups and angles, which are small in actual calculation; 2) it cannot fully utilize the parallel resources of modern computer clusters; 3) there is a large amount of communication in MPI parallel mode, which may lead to communication delay phenomenon.

At present, the distributed-shared storage architecture is widely used in large-scale parallel computing platforms, and a new parallel algorithm needs to be developed. In addition, in order to further expand the parallel scale of computable problems, improve the computation speed, and achieve further acceleration, for MOC and CMFD calculations, a hybrid MPI/OpenMP (Open Multi-Processing) parallelism strategy is proposed in this work. Based on the domain decomposition method, for MOC, the characteristic ray parallelism in OpenMP is added. It can expand the parallel degree and improve the speed of computation (Chandra et al., 2001). In addition, the optimization of the hybrid parallel strategy further improves the computation speed. For CMFD, the secondary domain decomposition parallelism in OpenMP is also added, which allows the CMFD calculation to use the parallel resources when the characteristic rays are parallel, and achieve a certain speedup. The hybrid MPI/OpenMP parallel strategy is implemented to the MOC and CMFD solvers of the three-dimensional whole-core one-step high-fidelity transport calculation program HNET. The HNET code is independently developed in C language by Harbin Engineering University. Several problems such as the C5G7 benchmark problem (Boyarinov et al., 2016), and the QinShan real core problem are tested to verify the parallel efficiency of the hybrid MPI/OpenMP strategy.

This paper is organized as follows. Section 2 provides a detailed description of the MOC and CMFD solvers. In Section 3, the implementation and optimization of hybrid MPI/OpenMP in MOC and CMFD calculations are described. Section 4 demonstrates the analysis of the numerical results for the C5G7 benchmark problem, and the QinShan real core problem. Finally, the conclusions of this paper are listed in Section 5.

2 Transport methodology

The details of the equations for MOC and CMFD are demonstrated in this section. First the MOC transport equations, then the two-level gCMFD equations, and it is necessary to give a detailed introduction to some effective preconditioners.

2.1 MOC formulation

The method of characteristics is a numerical method to solve the neutron equation based on ray tracing. The basic idea is to handle both angular and spatial variables through coordinate transformation, then convert the neutron transport equation in partial differential form into a first-order ordinary differential equation along the neutron flight direction (Li L, 2013).

The steady neutron transport equation in Cartesian coordinate system as follows,

$\mathbf{\Omega }\cdot \nabla \phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)+{\mathrm{\Sigma }}_{\mathit{t}}\left(\mathit{r},\mathit{E}\right)\phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)=\mathit{q}\left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)(1)$

Using appropriate mathematical transformation of the first term on the left,

$\mathbf{\Omega }\cdot \nabla \phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)=\frac{\mathit{d}\phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)}{\mathit{d}\mathit{s}}(2)$

Bring Eq. 2 into Eq. 1, the characteristic ray equation can be expressed as,

$\frac{\mathit{d}\phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)}{\mathit{ds}}+{\mathrm{\Sigma }}_{\mathit{t}}\left(\mathit{r},\mathit{E}\right)\phi \left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)=\mathit{Q}\left(\mathit{r},\mathit{E},\mathbf{\Omega }\right)(3)$

where $\mathrm{r}$ is the position, E is the energy and $\Omega$ is the angle.

Discretization and approximation need to be introduced for each variable to numerically solve the characteristic ray equation. Among them, multi-group approximation is used for energy, and similar to the SN method, select a suitable quadrature group and directly discretize the angle space (Jarrett, 2018). The characteristic ray equation describes the neutron conservation relation along a specific direction, and the neutron flux density in this direction can be obtained by solving it.

Then, the multi-group characteristic ray equation with discrete angle can be obtained by the above processing,

$\frac{\mathit{d}{\phi }_{\mathit{g},\mathit{m}}\left(\mathit{r}\right)}{\mathit{d}\mathit{s}}+{\mathrm{\Sigma }}_{\mathit{t},\mathit{g}}\left(\mathit{r}\right){\phi }_{\mathit{g},\mathit{m}}\left(\mathit{r}\right)={\mathit{Q}}_{\mathit{g},\mathit{m}}\left(\mathit{r}\right)(4)$

Assuming the flat source approximation and giving the incident neutron angular flux density of the characteristic ray, the neutron angular flux density at any point on the characteristic ray can be obtained as follows:

${\phi }_{\mathit{i},\mathit{k},\mathit{m}}^{\mathit{o}\mathit{u}\mathit{t}}={\phi }_{\mathit{i},\mathit{k},\mathit{m}}^{\mathit{i}\mathit{n}}\exp \left(-{\sum }_{\mathit{t},\mathit{i}}{\mathit{s}}_{\mathit{i},\mathit{k}}^{\mathit{i}}\right)+\frac{{\mathit{Q}}_{\mathit{i},\mathit{k},\mathit{m}}}{{\sum }_{\mathit{t},\mathit{i}}}\left[1-\exp \left(-{\sum }_{\mathit{t},\mathit{i}}{\mathit{s}}_{\mathit{i},\mathit{k}}\right)\right](5)$

Integrating the neutron angular flux density over the length of the characteristic ray, the average neutron angular flux density on this characteristic ray is obtained,

${\overline{\phi }}_{\mathit{i},\mathit{k},\mathit{m}}=\frac{{\mathit{Q}}_{\mathit{i},\mathit{k},\mathit{m}}}{{\sum }_{\mathit{t},\mathit{i}}}+\frac{{\phi }_{\mathit{i},\mathit{k},\mathit{m}}^{\mathit{i}\mathit{n}}-{\phi }_{\mathit{i},\mathit{k},\mathit{m}}^{\mathit{o}\mathit{u}\mathit{t}}}{{\sum }_{\mathit{t},\mathit{i}}{\mathit{s}}_{\mathit{i},\mathit{k}}}(6)$

The average neutron angular flux density in this direction for the region can be calculated by using a volume-weighted averaging technique,

${\overline{\phi }}_{\mathit{i},\mathit{m}}=\frac{{\displaystyle \sum }_{\mathit{k}=1}^{\mathit{K}}{\overline{\phi }}_{\mathit{i},\mathit{k},\mathit{m}}{\mathit{s}}_{\mathit{i},\mathit{k}}\delta {\mathit{A}}_{\mathit{m}}}{{\mathit{V}}_{\mathit{i}}}(7)$

The average neutron angular flux density in all directions is summed according to the weight to obtain the neutron flux density on this pin cell,

${\mathit{\varphi }}_{\mathit{i}}={\displaystyle \sum }_{\mathit{m}=1}^{\mathit{M}}{\omega }_{\mathit{m}}{\overline{\phi }}_{\mathit{i},\mathit{m}}(8)$

2.2 Multi-level gCMFD formulation

The coarse mesh finite difference method was first proposed by K. Smith at MIT in the 1970s and 1980s. Due to its good acceleration effect, easy implementation, and wide application, it has been widely used to accelerate neutron transport calculations and has been successfully implemented in well-known neutronic calculation programs. However, the conventional CMFD has a computational instability or divergence problem, which will result in non-physical negative fluxes (Xu and Donwar, 2012). To overcome this drawback, the gCMFD has been studied and applied. The key feature of the gCMFD method is the use of two defined parameters, nodal discontinuity factor (NDF) and modified diffusion coefficient factor (MDF), to ensure the strict equivalence between CMFD and the transport solution and insure that only positive coupling coefficients would occur in the CMFD linear system.

CMFD starts with the 3D multi-group discrete diffusion equation as,

${\displaystyle \sum }_{\mathit{n}\in \mathit{n}\mathit{e}\mathit{i}\mathit{g}\mathit{h}\mathit{b}\mathit{o}\mathit{r}\mathit{s}}{\overline{\mathit{J}}}_{\mathit{g},\mathit{c},\mathit{n}}^{\mathit{k}}{\mathit{A}}_{\mathit{c},\mathit{n}}{+\mathit{V}}_{\mathit{c}}(-{\displaystyle \sum }_{{\mathit{g}}^{\prime }}{\sum }_{\mathit{g},{\mathit{g}}^{\prime },\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{{\mathit{g}}^{\mathit{i}},\mathit{c}}^{\mathit{k}}+{\sum }_{\mathit{t}\mathit{g},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{g},\mathit{c}}^{\mathit{k}}-\frac{{\chi }_{\mathit{g}}}{{\mathit{k}}_{\mathit{e}\mathit{f}\mathit{f}}}{\displaystyle \sum }_{{\mathit{g}}^{\prime }}\nu {\sum }_{\mathit{f}{\mathit{g}}^{\prime },\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{{\mathit{g}}^{\prime },\mathit{c}}^{\mathit{k}}){=\mathit{V}}_{\mathit{c}}{\overline{\mathit{S}}}_{\mathit{g},\mathit{c}}^{\mathit{k}-1}(9)$

Here, the conventional CMFD has a potential drawback of D’title’, it may be negative. In the new gCMFD, the D’title’ is defined as follows,

$\begin{array}{c}{\stackrel{\sim }{\mathit{D}}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}={\mathit{A}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}\frac{2{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{s}}}{\frac{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{s}}{\mathit{h}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}}{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{f}}{\mathit{D}}_{\mathit{g},\mathit{c}}}+\frac{{\mathit{f}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}^{\mathit{d}\mathit{i}\mathit{s}}{\mathit{h}}_{\mathit{n}\mathit{b}\mathit{r},\mathit{c}}}{{\mathit{f}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}^{\mathit{d}\mathit{i}\mathit{f}}{\mathit{D}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r}}}}\\ {\stackrel{\sim }{\mathit{D}}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}={\mathit{A}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}\frac{2{\mathit{f}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}^{\mathit{d}\mathit{i}\mathit{s}}}{\frac{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{s}}{\mathit{h}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}}{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{f}}{\mathit{D}}_{\mathit{g},\mathit{c}}}+\frac{{\mathit{f}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}^{\mathit{d}\mathit{i}\mathit{s}}{\mathit{h}}_{\mathit{n}\mathit{b}\mathit{r},\mathit{c}}}{{\mathit{f}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r},\mathit{c}}^{\mathit{d}\mathit{i}\mathit{f}}{\mathit{D}}_{\mathit{g},\mathit{n}\mathit{b}\mathit{r}}}}\end{array}(10)$

For the boundary node treatment, an albedo boundary condition is used and D’title’ is given as,

${\stackrel{\sim }{\mathit{D}}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{b}\mathit{o}\mathit{u}\mathit{n}\mathit{d}\mathit{a}\mathit{r}\mathit{y}}={\mathit{A}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}\frac{2{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{s}}}{\frac{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{s}}{\mathit{h}}_{\mathit{c},\mathit{n}\mathit{b}\mathit{r}}}{{\mathit{f}}_{\mathit{g},\mathit{c},\mathit{n}\mathit{b}\mathit{r}}^{\mathit{d}\mathit{i}\mathit{f}}{\mathit{D}}_{\mathit{g},\mathit{c}}}+\frac{2}{\stackrel{\sim }{\alpha }}}(11)$

where, ${\mathit{f}}^{\mathit{d}\mathit{i}\mathit{s}}$ and ${\mathit{f}}^{\mathit{d}\mathit{i}\mathit{f}}$ are refer to NDF and MDF respectively.

Another common drawback of the conventional CMFD method is that they exhibit the slow convergence and they incur a significant computational burden (Yuk et al., 2015). However, the one-group (1G) CMFD linear system is much cheaper to be solved. It is beneficial to utilize the fission source from 1G CMFD to accelerate the multi-group (MG) calculation. The 1G CMFD linear system can then be derived by collapsing MG CMFD over all every group. The cross section, flux and current of 1G CMFD can be calculated based on the corresponding information from MG CMFD, as following,

$\begin{array}{l}\mathit{V}\left({\sum }_{\mathit{a}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{c}}^{\mathit{k}}-{\lambda }^{\mathit{k}-1}\nu {\Sigma }_{\mathit{f}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{c}}^{\mathit{k}}\right)+\left(\begin{array}{l}{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{W}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{N}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{E}}^{\mathit{k}}\\ +{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{S}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{T}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{c},\mathit{N}}^{\mathit{k}}\end{array}\right){\overline{\mathit{\varphi }}}_{\mathit{c}}^{\mathit{k}}-\left(\begin{array}{l}{\stackrel{\sim }{\mathit{D}}}_{\mathit{W},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{W}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{N},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{N}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{E},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{E}}^{\mathit{k}}\\ +{\stackrel{\sim }{\mathit{D}}}_{\mathit{S},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{S}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{T},\mathit{c},}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{T}}^{\mathit{k}}+{\stackrel{\sim }{\mathit{D}}}_{\mathit{N},\mathit{c}}^{\mathit{k}}{\overline{\mathit{\varphi }}}_{\mathit{N}}^{\mathit{k}}\end{array}\right)\\ =\mathit{V}\left({\overline{\mathit{S}}}_{\mathit{c}}^{\mathit{k}-1}+\left({\lambda }^{\mathit{k}}-{\lambda }_{\mathit{s}}^{\mathit{k}-1}\right)\nu {\Sigma }_{\mathit{f}}^{\mathit{k}-1}{\overline{\mathit{\varphi }}}_{\mathit{c}}^{\mathit{k}-1}\right)\end{array}(12)$

It is generally accepted that the 3D CMFD is a large sparse non-symmetric linear system and can be represented using matrix notation as follows:

$\mathit{A}\mathit{x}=\mathit{b}(13)$

where $\mathit{A}$ is large sparse non-symmetric matrix with a dimension of hundreds of millions for high-fidelity neutron transport calculation, a huge amount of calculation is required. Normally, the GMRES (generalized minimal residual algorithm) method is chosen to solve this linear system which is a kind of Krylov subspace method (Y. Saad, 1996), it is very stable and can takes advantage of the sparsity of the coefficient matrix. The efficiency of the GMRES method depends on a good preconditioner, especially for the linear system with ill-conditioned or large condition numbers. So, an effective preconditioner is extremely important, to transform the original correlation coefficient matrix into a new matrix with small condition numbers.

Generally, the right preconditioning technique is utilized in GMRES method, which is then based on solving the linear system as:

$\begin{array}{c}\mathit{A}{\mathit{M}}^{-1}\omega =\mathit{b}\\ \omega =\mathit{M}\mathit{x}\end{array}(14)$

where, $\mathit{M}$ is the preconditioner.

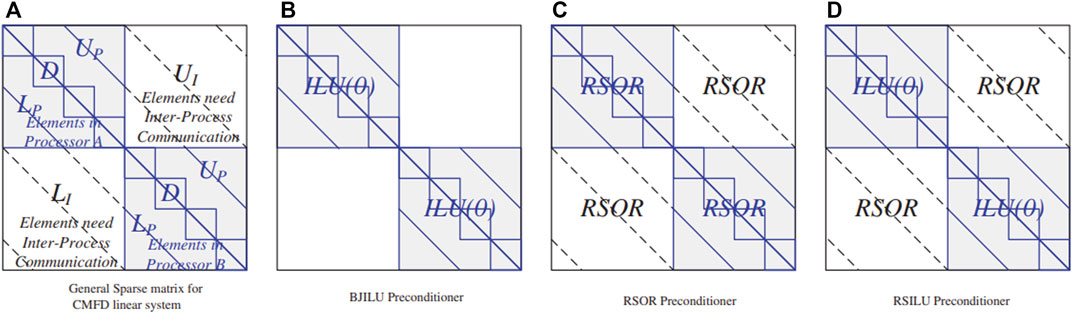
In serial computing, these preconditioners are widely used with high efficiency, such as Incomplete Low Upper (ILU), symmetric Successive Over-Relaxation (SSOR), approximate inverse algorithm and block algorithm. In parallel computing, a Red-Black ordering is required to achieve a good degree of parallelism for SOR or ILU preconditioners. However, The Red-Black ordering will introduce unnecessary queue waiting time and make development extremely complicated for code. In addition, the Block-Jacobi Incomplete Lower Upper (BJILU) preconditioner is easy to implement, but it only processes the elements in the respective CPUs, does not do any preprocessing for the elements that require information transfer between different cores. In order to solve this problem and further improve the preprocessing effect in parallel computing, a new Reduced SOR (RSOR) preconditioner and an innovative hybrid RSOR and ILU (RSILU) preconditioner are proposed, and these two preconditioners are described in more detail below (Xu et al., 2019).

2.2.1 The RSOR preconditioner

The coefficient matrix $\mathit{A}$ can be split into the sum of the following block matrices,

$\mathit{A}=\left[\begin{array}{cccc}{\mathit{D}}_1& {\mathit{U}}_{\mathit{A},1}& & \\ {\mathit{L}}_{\mathit{A},2}& {\mathit{D}}_2& & \\ & & ...& {\mathit{U}}_{\mathit{A},\mathit{n}-1}\\ & & {\mathit{L}}_{\mathit{A},\mathit{n}}& {\mathit{D}}_{\mathit{n}}\end{array}\right]={\mathit{L}}_{\mathit{A}}+\mathit{D}+{\mathit{U}}_{\mathit{A}}(15)$

where D are the diagonal blocks and L_A and U_A are strictly off-diagonal blocks, for application to the space and energy-dependent CMFD reactor problem, ${\mathit{D}}_{\mathit{i}}$ are $\mathit{G}\times \mathit{G}$ energy group full blocks, ${\mathit{L}}_{\mathit{A},\mathit{i}}$ and ${\mathit{U}}_{\mathit{A},\mathit{i}}$ are sparse matrices.

After the domain decomposition, combined with MPI parallel mode of distributed storage architecture. The coefficient matrix $\mathit{A}$ can be further expressed as follows,

$\mathit{A}={\mathit{L}}_{\mathit{I}}+{\mathit{L}}_{\mathit{P}}+\mathit{D}+{\mathit{U}}_{\mathit{P}}+{\mathit{U}}_{\mathit{I}}(16)$

where, ${\mathit{L}}_{\mathit{P}}$ and ${\mathit{U}}_{\mathit{P}}$ are strictly off-diagonal blocks stored in the current CPU, ${\mathit{L}}_{\mathit{I}}$ and ${\mathit{U}}_{\mathit{I}}$ are strictly off-diagonal blocks stored in different CPUs.

The RSOR preconditioner is proposed based on the well-known SOR preconditioner, which does not require the use of the Red-Black ordering for parallel computing. It is easy to implement and can significantly reduce the computing time. The RSOR preconditioner preserves symmetricity of solutions, and the iterative solution of GMRES with RSOR as preconditioner will be symmetric.

By approximating the SOR preconditioner, a new RSOR preconditioner can be generated. So, a brief review of SOR with multicolor ordering should first be introduced. The SOR preconditioner can be written as,

${\mathit{M}}_{\mathit{S}\mathit{O}\mathit{R}}=\left(\omega {\mathit{L}}_{\mathit{A}}{\mathit{D}}^{-1}+\mathit{I}\right)\left(\mathit{D}+\omega {\mathit{U}}_{\mathit{A}}\right)(17)$

The SOR preconditioner require the Red-Black ordering in parallel computing, and the structure of the coefficient matrix $\mathit{A}$ generated by this ordering is as follows,

$\mathit{A}=\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}& \mathit{U}\\ \mathit{L}& {\mathit{D}}_{\mathit{B}}\end{array}\right](18)$

Therefore, the SOR can be further expressed as,

${\mathit{M}}_{\mathit{S}\mathit{O}\mathit{R}}=\left[\begin{array}{cc}\mathit{I}& 0\\ \omega \mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}& \mathit{I}\end{array}\right]\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}& \omega \mathit{U}\\ 0& {\mathit{D}}_{\mathit{B}}\end{array}\right](19)$

Its inverse matrix format is as follows,

${\mathit{M}}_{\mathit{S}\mathit{O}\mathit{R}}^{-1}=\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}^{-1}+{\omega }^2{\mathit{D}}_{\mathit{R}}^{-1}\mathit{U}{\mathit{D}}_{\mathit{B}}^{-1}\mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}& -\omega {\mathit{D}}_{\mathit{R}}^{-1}\mathit{U}{\mathit{D}}_{\mathit{R}}^{-1}\\ -\omega {\mathit{D}}_{\mathit{B}}^{-1}\mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}& {\mathit{D}}_{\mathit{B}}^{-1}\end{array}\right](20)$

The analysis of the GMRES method shows that:

$\left[\begin{array}{c}{\mathit{z}}_{\mathit{R}}\\ {\mathit{z}}_{\mathit{B}}\end{array}\right]=\left[\begin{array}{c}{\mathit{D}}_{\mathit{R}}^{-1}\left({\mathit{v}}_{\mathit{R}}-\omega \mathit{U}{\mathit{D}}_{\mathit{B}}^{-1}\left({\mathit{v}}_{\mathit{B}}-\omega \mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}{\mathit{v}}_{\mathit{R}}\right)\right)\\ {\mathit{D}}_{\mathit{B}}^{-1}\left({\mathit{v}}_{\mathit{B}}-\omega \mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}{\mathit{v}}_{\mathit{R}}\right)\end{array}\right](21)$

For the red node in Eq. 20, if the term of $-\omega \mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}{\mathit{v}}_{\mathit{R}}$ is removed, a real symmetric form can be obtained,

$\left[\begin{array}{c}{\mathit{z}}_{\mathit{R}}\\ {\mathit{z}}_{\mathit{B}}\end{array}\right]=\left[\begin{array}{c}{\mathit{D}}_{\mathit{R}}^{-1}\left({\mathit{v}}_{\mathit{R}}-\omega \mathit{U}{\mathit{D}}_{\mathit{B}}^{-1}{\mathit{v}}_{\mathit{B}}\right)\\ {\mathit{D}}_{\mathit{B}}^{-1}\left({\mathit{v}}_{\mathit{B}}-\omega \mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}{\mathit{v}}_{\mathit{R}}\right)\end{array}\right](22)$

This approximation will produce a new RSOR preconditioner, which can be defined as,

${\mathit{M}}_{\mathit{R}\mathit{S}\mathit{O}\mathit{R}}^{-1}=\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}^{-1}& -\omega {\mathit{D}}_{\mathit{R}}^{-1}\mathit{U}{\mathit{D}}_{\mathit{B}}^{-1}\\ -\omega {\mathit{D}}_{\mathit{B}}^{-1}\mathit{L}{\mathit{D}}_{\mathit{R}}^{-1}& {\mathit{D}}_{\mathit{B}}^{-1}\end{array}\right](23)$

The RSOR can be rearranged as

${\mathit{M}}_{\mathit{R}\mathit{S}\mathit{O}\mathit{R}}^{-1}=\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}^{-1}& 0\\ 0& {\mathit{D}}_{\mathit{B}}^{-1}\end{array}\right]\left(\mathit{I}-\omega \left[\begin{array}{cc}0& \mathit{U}\\ \mathit{L}& 0\end{array}\right]\left[\begin{array}{cc}{\mathit{D}}_{\mathit{R}}^{-1}& 0\\ 0& {\mathit{D}}_{\mathit{B}}^{-1}\end{array}\right]\right)(24)$

As shown in this formula, it is not necessary to use the Red-Black ordering technique since the diagonal blocks and off-diagonal blocks are operated on separately. Therefore, the RSOR preconditioner can be rewritten as following:

${\mathit{M}}_{\mathit{R}\mathit{S}\mathit{O}\mathit{R}}^{-1}={\mathit{D}}^{-1}\left[\mathit{I}-\omega \left({\mathit{L}}_{\mathit{I}}+{\mathit{U}}_{\mathit{I}}\right){\mathit{D}}^{-1}\right](25)$

where, $\omega$ is relaxation factor.

2.2.2 The RSILU preconditioner

For RSOR preconditioner, the same preconditioner is used to preprocess the internal and the boundary elements that require inter-process communication, but its preconditioning effect on elements in each processor will be no better than that of ILU or SOR. Therefore, in order to take the full advantages of RSOR and the standard ILU preconditioner, based on the RSOR preconditioner and combined with ILU preconditioner, the effective hybrid RSILU preconditioner was innovatively proposed as illustrated in Figure 1. In addition, more on the theory and implementation of the RSILU preconditioner can be found in the cited paper (Xu at el., 2019).

FIGURE 1

FIGURE 1. A general sparse matrix and different preconditioners for CMFD linear system.

The RSILU preconditioner consists of the RSOR preconditioner and the ILU preconditioner, which do not need the Red-Black ordering. Among them, the ILU preconditioning technique efficiently process the elements in the respective CPUs, the standard ILU(0) preconditioner defined as follows:

${\mathit{M}}_{\mathit{I}\mathit{L}\mathit{U}}=\left({\mathit{L}}_{\mathit{A}}{\stackrel{\sim }{\mathit{D}}}^{-1}+\mathit{I}\right)\left(\stackrel{\sim }{\mathit{D}}+{\mathit{U}}_{\mathit{A}}\right)(26)$

where, $\stackrel{\sim }{\mathit{D}}$ is the diagonal block with only the diagonal elements modified as,

${\stackrel{\sim }{\mathit{D}}}_{\mathit{E},\mathit{i}}={\mathit{A}}_{\mathit{i}\mathit{i}}-{\displaystyle \sum }_{\mathit{j}=1}^{\mathit{i}-1}{\mathit{A}}_{\mathit{i}\mathit{j}}{\stackrel{\sim }{\mathit{D}}}_{\mathit{E},\mathit{j}}^{-1}{\mathit{A}}_{\mathit{j}\mathit{i}}(27)$

Combining Eqs. 24, 25, the RSILU preconditioner can then be written as

${\mathit{M}}_{\mathit{R}\mathit{S}\mathit{I}\mathit{L}\mathit{U}}^{-1}={\left(\stackrel{\sim }{\mathit{D}}+{\mathit{U}}_{\mathit{P}}\right)}^{-1}{\left({\mathit{L}}_{\mathit{P}}{\stackrel{\sim }{\mathit{D}}}^{-1}+\mathit{I}\right)}^{-1}\left[\mathit{I}-\omega \left({\mathit{L}}_{\mathit{I}}+{\mathit{U}}_{\mathit{I}}\right){\mathit{D}}^{-1}\right](28)$

To reduce the storage and computational burden of the RSILU preconditioner, replace ${\mathit{D}}_{\mathit{E}}$ in the above equation with $\mathit{D}$, where $\mathit{D}$ is the diagonal element of ${\mathit{D}}_{\mathit{E}}$. Finally, the RSILU preconditioner can be redefined as,

${\mathit{M}}_{\mathit{R}\mathit{S}\mathit{I}\mathit{L}\mathit{U}}^{-1}={\left(\stackrel{\sim }{\mathit{D}}+{\mathit{U}}_{\mathit{P}}\right)}^{-1}{\left({\mathit{L}}_{\mathit{P}}{\stackrel{\sim }{\mathit{D}}}^{-1}+\mathit{I}\right)}^{-1}\left[\mathit{I}-\omega \left({\mathit{L}}_{\mathit{I}}+{\mathit{U}}_{\mathit{I}}\right){\mathit{D}}_{\mathit{E}}^{-1}\right](29)$

3 Implementation of hybrid parallel strategy

The HNET code uses 2D/1D scheme under the gCMFD global acceleration framework, where MOC is used in the radial direction and two-node NEM is used in the axial direction. On the basis of spatial decomposition parallelism, this paper further studies the characteristic ray parallelism and the secondary domain decomposition parallelism for MOC and CMFD respectively. These parallel strategies will be introduced in detail below.

3.1 Spatial decomposition in HNET

In practical engineering applications, the high-fidelity whole-core neutron transport calculation faces the challenges of huge memory pressure and the long computational time. Using the domain decomposition method, the simulation domain is divided into subdomains that do not overlap with each other, with each subdomain being handled by separate processes. Therefore, each process only needs to store the information for the responsible subdomain, which can greatly relieve the memory pressure of the computer, especially for the large-scale real core problems.

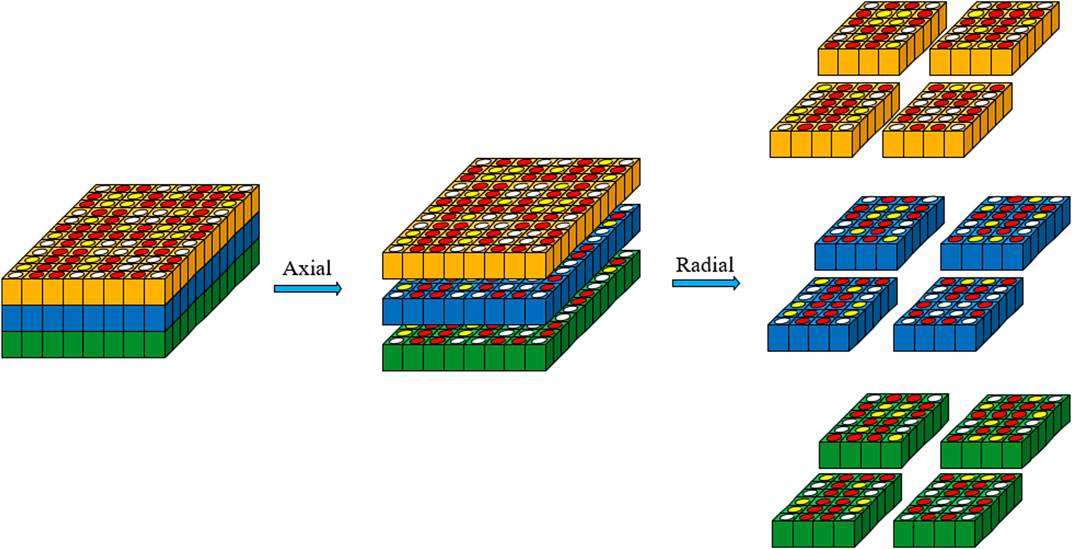
The spatial domain decomposition method of HNET is designed based on MPI parallel programming technique mode of distributed storage architecture. It can be achieved by two decompositions in radial and axial directions, as shown in Figure 2.

FIGURE 2

FIGURE 2. Spatial domain decomposition method.

For axial spatial decomposition, the number of layers on each CPU is obtained according to the number of axial layers and the number of axial domains to be decomposed. In order to ensure load-balance, the number of axial spatial domains is generally a divisor of the number of axial layers. For radial spatial decomposition, the number of horizontal and vertical reference divisions is manually set. This spatial decomposition method has greater flexibility, and allows users to understand the radial spatial decomposition results more intuitively. At the same time, to ensure load-balance, try to make the number of actual lattices contained in each subdomain in the radial direction consistent.

After the spatial domain decomposition. For MOC, each processor is responsible for processing the characteristic ray equations in the subdomain. For CMFD, each processor is responsible for processing the sparse matrix for different subdomain. Each processor communicates only with adjacent subdomains, there can be communication waiting issues. The non-blocking communication mode can help to promote the parallel computing efficiency compared with the blocking communication mode in MPI, so the non-blocking communication techniques are used in HNET to reduce communication time.

In addition, multi-dimensional arrays are usually used to represent physical parameters in HNET code, but the frequent calls lead to high time-consuming. Therefore, optimize the use of multi-dimensional arrays in loops, and use temporary variables to replace intermediate calculation results, which can improve the calculation speed.

All in all, the spatial domain decomposition method can decompose the memory pressure of the computer, expand the size of the computational problem, and the parallel efficiency is high.

3.2 The characteristic ray parallelism for MOC

With the rapid development of cluster hardware performance and computing power, currently, it is well-documented that large-scale parallel computing platforms all adopt the distributed-shared storage architecture. That is, the shared storage architecture is adopted in a single node, and the distributed storage architecture is adopted among different nodes. On the one hand, the degree of parallelism is limited to spatial decomposition. On the other hand, OpenMP parallel technology is based on shared memory and does not need communication between processes, it has the potential to further improve the parallel scale and efficiency. In summary, the application of high-performance clusters requires deeper research and optimization of the original parallel strategy.

By adding the characteristic ray parallelism to the parallel strategy based on the spatial domain decomposition, it will further expand the parallel scale and improve the computational speed. Moreover, the characteristic ray parallelism in OpenMP can reduce the memory requirement, accelerate the calculation, and take full advantage of the distributed-shared storage architecture computing systems.

The characteristic ray parallelism is to perform parallel acceleration of the core computing part of MOC calculation, the characteristic ray scanning part. Since the energy groups, discrete directions and characteristic rays are independent of each other, so, a parallel strategy can be designed from three aspects: angle, energy group, and characteristic ray. However, in the practical calculation, the number of energy groups and angles is usually small, compared with the angle and energy group parallel design, its limited parallel performance and the memory footprint increases greatly for large-scale problems, the parallel strategy is generally designed from the aspect of characteristic ray.

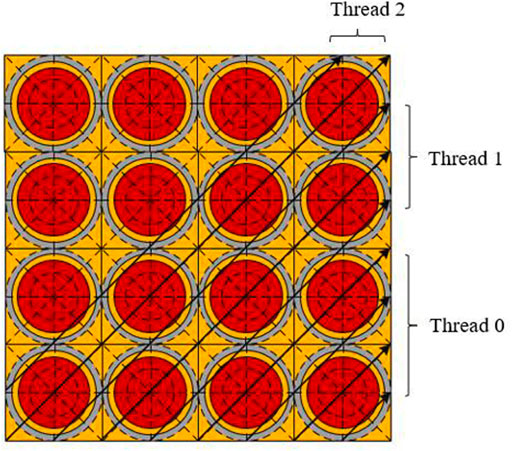
The characteristic ray parallelism is to assign long characteristic rays of all azimuth to different threads, thereby improving the calculation efficiency, as shown in Figure 3. This processing is equivalent to realizing the double parallel of the azimuth angle and the long characteristic ray. It should be noted that there is a potential load-balance problem in the characteristic ray parallelism, which is due to the fact that the number of characteristic ray segments allocated to each thread may vary. In order to reduce this potential load imbalance, HNET uses a static scheduling scheme to ensure the load balance among threads. Also, since the mapping of iterations on threads is determined at compile time, there is no scheduling overhead at runtime.

FIGURE 3

FIGURE 3. The characteristic ray parallelism scheme.

3.2.1 Implementation of the characteristic ray parallelism

The implementation of OpenMP parallelism is mainly composed of three parts: compilation guidance statements, library functions, and environment variables. For computationally intensive areas such as for loops that are suitable for parallelism, the loop iteration is divided into several parts by adding compilation guidance statements, and then evenly distributed to each thread, so as to realize multi-thread parallel computing within the same parallel scope. At the end of the parallel area, some thread stops execution and waits for all threads to complete, and then synchronizes the data to the main thread. The pseudo-code for the characteristic ray parallel implementation in the HNET code is shown below:

1 #pragma omp parallel private (pointer arrays)

2 {

3  #pragma omp for schedule (static)

4   for lt = 0, num_longtrack_halfspace-1

5   calculate boundary angular flux

6   for polar = 0, num_polar

7  for g = 0, ngroups

8 #pragma omp atomic

9   calculate scalar fluxes

10   end for

11  end for

12  update boundary condition

13 end for

14  {

There are two handling points in OpenMP parallelism of characteristic rays. First, when using the OpenMP parallelism, there is a problem of data write conflicts between different threads, such as summing the scalar fluxes of all threads to the main thread, the most common practice is to add locks to prevent simultaneous reading and writing by limiting the threads of reading and writing of data variables. There are three common locking operations in OpenMP: the omp_set_lock library function, critical instruction, and the atomic operation. The above three locking operations can achieve the same effect, but the atomic operation will be more efficient. Therefore, in order to implement the reduction operation, the atomic operation can be used, and it can be implemented by adding the “#pragma omp atomic” clause before the code block to calculate the scalar flux. Then, for the temporary arrays used in the transport scanning process, in order to prevent the write-read conflicts for data in OpenMP parallelism, the private pointer array processing scheme is adopted.

3.2.2 Optimization of the characteristic ray parallelism

The use of atomic operation leads to some overhead and code serialization, which is equivalent to the existence of an invisible fence, and may lead to a reduction in computational speed. To further improve the parallel efficiency of OpenMP, the atomic operation can be eliminated by adding dimensions to the scalar fluxes array to store the temporary calculation results of multiple threads simultaneously. The specific implementation scheme is as follows.

1 #pragma omp parallel private (pointer arrays)

2 {

3 #pragma omp for schedule(static)

4 for lt = 0, num_longtrack_halfspace-1

5  thread_rank = omp_get_thread_num ();

6  calculate boundary angular flux

7  for polar = 0, num_polar

8   for g = 0, ngroups

9   scalar_fluxes_thread [][g + NumGroups*thread_rank]

10   end for

11  end for

12  update boundary condition

13  end for

14 }

15 for thread_rank = 0, NumThreads

16  scalar_fluxes + = scalar_fluxes_thread

17 end for

By using the current thread number, the data operations between different threads are independent, thereby eliminating the atomic operation and further improving computing efficiency. In addition, due to the above operations, after OpenMP parallel computing, it is necessary to reduce the scalar fluxes under different threads.

Furthermore, in the process of MOC calculation, the source term calculation also has a certain amount of time. Therefore, OpenMP parallelism can be implemented for the source term calculation, and the collapse clause can expand the parallelism of the loop to further improve the parallel efficiency. The specific implementation scheme is as follows.

1 #pragma omp parallel for collapse (3)

2 for lay = 0, num_layers

3  for cell = 0, num_cells

4  for g = 0, ngroups

5    source term calculation

6  end for

7  end for

8 end for

3.3 The secondary domain decomposition parallelism for CMFD

In the HNET code, a multi-level gCMFD method is used to accelerate the neutron transport calculation. For gCMFD, it also has a certain amount of time, and it takes up a large proportion of transport time, especially for the transient problem. Therefore, it is necessary to use the parallel resources of characteristic ray parallelism to improve the efficiency of CMFD calculation. In summary, it is necessary to further implement OpenMP parallel strategy for CMFD as well.

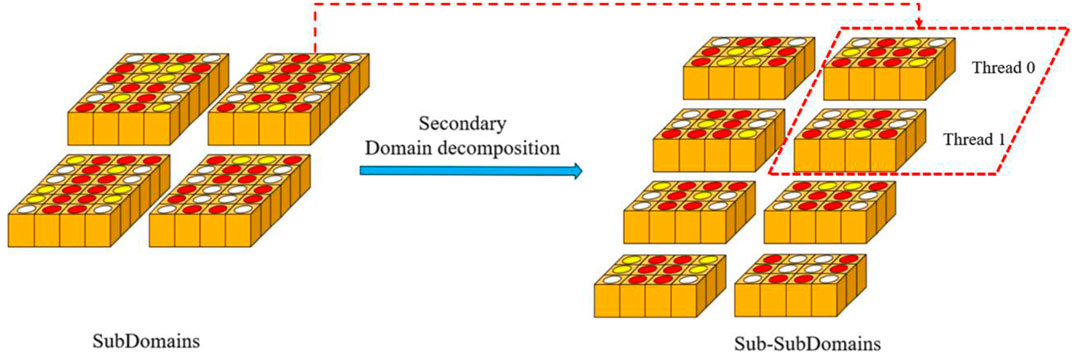
Referring to the introduction of the preconditioners in Section 2.2, it is known that there is a cyclic dependency issue in the implementation of pre-processing techniques. Therefore, to realize the OpenMP parallelism of CMFD, the subdomains in the radial direction can be further decomposition based on the idea of secondary domain decomposition, and a serial sub-subdomain can be obtained. Then, based on the above operations, each sub-subdomain can be handled by a separate OpenMP threads, as shown in Figure 4.

FIGURE 4

FIGURE 4. The secondary domain decomposition parallelism.

According to the above analysis, the pseudo-code for the secondary domain decomposition parallel implementation in the HNET code is shown below:

1 obtain the gCMFD linear system parameters for the subdomain

2 for the secondary domain decomposition, determine the number of horizontal and vertical in the radial direction, and represented by Nx and Ny, respectively

3 construct the linear system of each sub-subdomain

4 #pragma omp parallel for collapse(2)

5 for iter_ny = 0, Ny

6  for iter_nx = 0, Nx

7  solving the sub-subdomain linear system by GMRES

8  end for

9 end for

In addition, the collapse clause is used to extend the degree of parallelism. It should be noted that when solving the sub-subdomain linear system, some data needs to be transmitted between processes. At this time, it is necessary to insert the “#pragma omp master” clause, so that the information transmission between processes is only implemented on the main thread.

4 Numerical results

Numerical results are presented in this section. Two problems are tested to verify the parallel efficiency of the hybrid MPI/OpenMP method: 1) the 2D C5G7 benchmark problem for the steady transport calculation, and the C5G7-TD 5-1 benchmark problem for the transient event, 2) the QinShan problem for the application on the real core. All cases in this paper are simulated by the HNET code with the Shanhe HPC cluster at the National Supercomputing Center in Jinan, using the 2.70 GHz Intel(R) Xeon(R) Gold 6258 R CPU, which is configured with 56 cores per node, MPI and OpenMP are intel mpi 2017 and OpenMP 3.1 respectively.

First, using the C5G7 benchmark problem to verify the parallel efficiency of the spatial domain decomposition, the characteristic ray parallelism, and the secondary domain decomposition parallelism under steady and transient calculation respectively. And then, the parallel performance of the hybrid parallel strategy is further verified by using the QinShan real core.

4.1 C5G7 problem

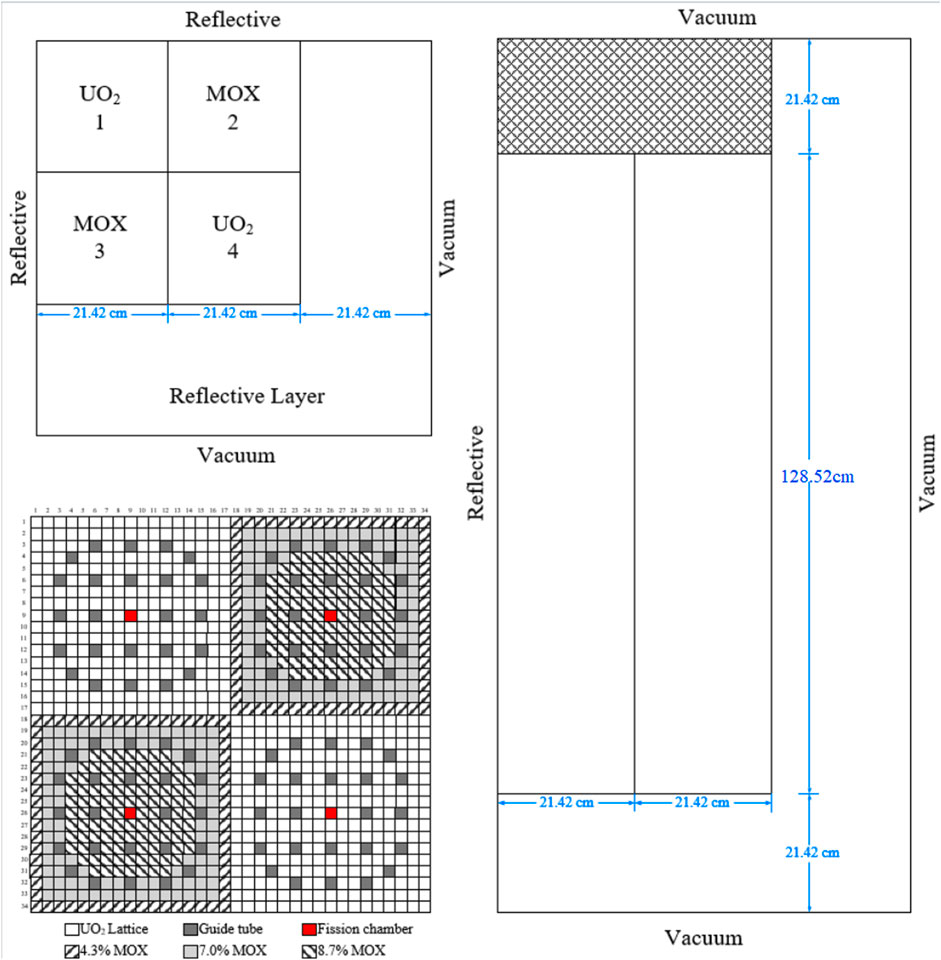
The first case considered is the 2D C5G7 benchmark, Figure 5 contains the pin layout of the 2D C5G7 core, which contains both UO₂ and MOX fuels. More detailed information can be found in the C5G7 benchmark report.

FIGURE 5

FIGURE 5. Assembly configuration and pin layout of the C5G7-TD benchmark problem.

The C5G7-TD 5-1 model is a moderator change transient event is used to further verify the applicability of the parallel strategy to transient problems, TD5-1 transient is initiated by the moderator density decrease in Assembly No.1 at the constant rate of 5% per second, and after 1 s into the transient the moderator density in Assembly No.3 starts to drop at the same rate. The moderator density starts to increase right after 2 s into the transient in both assemblies at the rate of 5% per second, and it returns to the nominal value within another 2 s and 1s respectively for Assembly No. 1 and 3, separately. The moderator density in Assembly No. 2 and 3 is not affected in this transient. Note that in this paper, the focus is on parallel efficiency, therefore, only the first 6s transient event can be simulated. The geometry of the C5G7-TD 5-1 core is same as illustrated in Figure 5.

For C5G7-TD 5-1 problem, this model is divided into 32 layers in the axial direction with each layer using a node for calculation, and the process and thread settings in the radial direction are the same as in the 2D C5G7 problem.

For the test of MPI parallel efficiency of spatial domain decomposition, 1, 2, 4, 8, and 16 processes were used for the calculation, and the results are shown as follows.

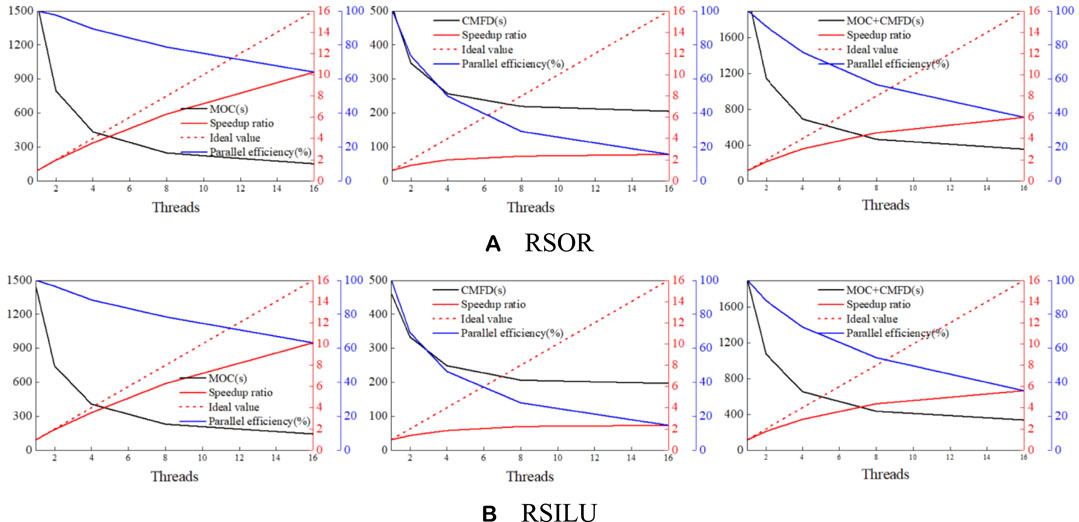
Figure 6 and Figure 7 are intended to present that MPI parallelism based on spatial domain decomposition has high parallel efficiency, and the parallel efficiency of MOC is higher than that of CMFD, this is due to the fact that the ration of communication and calculation is higher for CMFD. Furthermore, in this article, the AML-PCQM method is used for the transient calculation, that is, MG/CG CMFD time steps are added to the time step acceleration and CMFD iterative acceleration is introduced in different time steps. In short, the above reasons lead to a large ratio of communication and calculation for the transient problem, and the better CMFD MPI parallel efficiency for the C5G7-2D benchmark than C5G7-TD 5-1.

FIGURE 6

FIGURE 6. Calculation time, speedup and parallel efficiency. (A) RSOR. (B) RSILU. With different number of processes of 2D C5G7 problem.

FIGURE 7

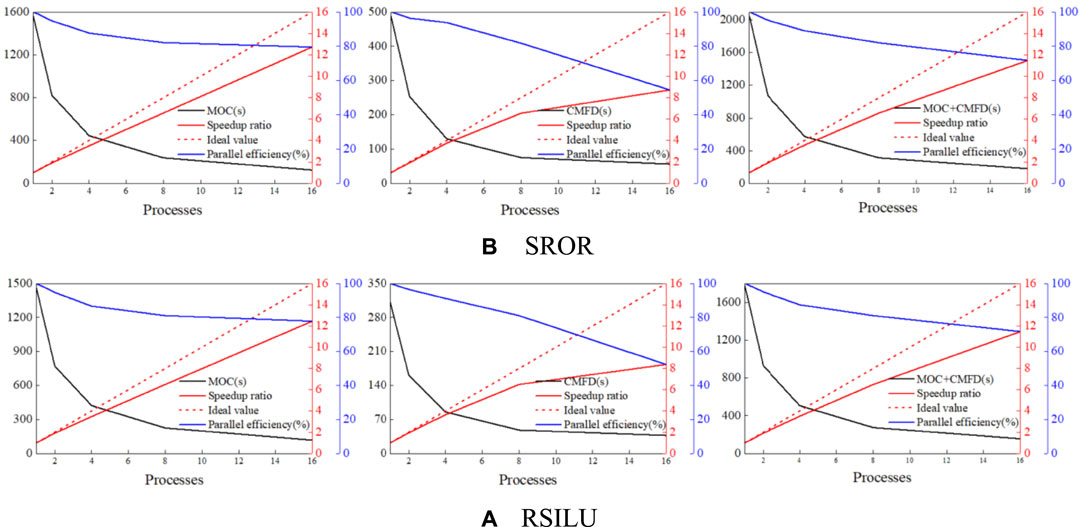
FIGURE 7. Calculation time, speedup and parallel efficiency. (A) SROR. (B) RSILU. With different number of processes of C5G7-TD 5-1 problem.

In addition, the speedup and parallel efficiency decrease along with the number of processes growth, but the decrease is not significant because each MPI process only communicates with processes in adjacent subdomains. So, the communication traffic of each MPI process does not increase linearly with the number of processes. It has good parallel scalability.

The 2D C5G7 benchmark was selected to verify the optimization capability of eliminating atomic operations. Using 1 thread for each of the two cases of using atomic operations and eliminating atomic operations, the results are shown in Table 1.

TABLE 1

TABLE 1. Results for parallel optimization of characteristic ray.

The numerical results in Table 1 show that eliminating atomic operations can greatly reduce the computation time and increase the computation speed. Therefore, in the following calculation, a parallel strategy with eliminates atomic operations is chosen.

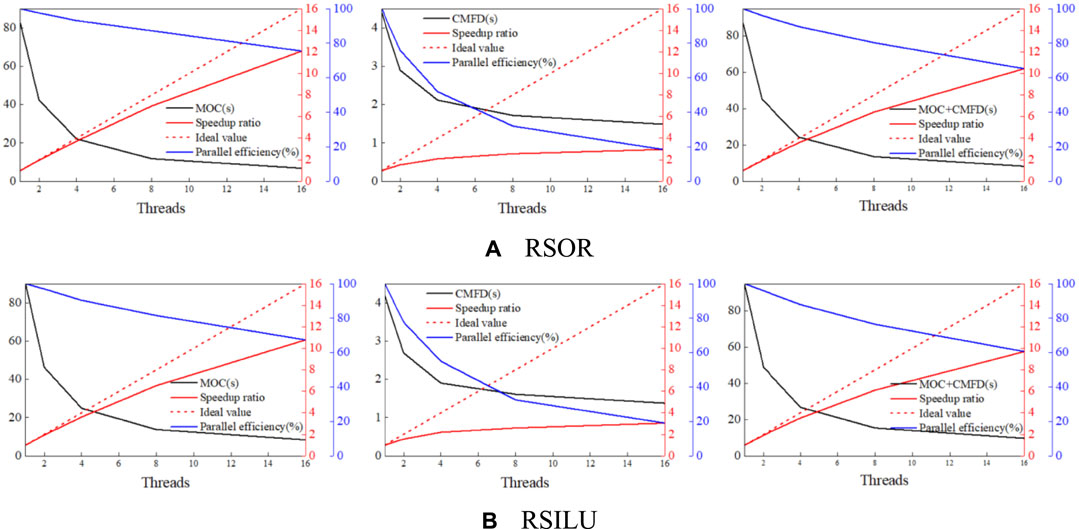
For the test of OpenMP parallel efficiency of characteristic ray parallelism and secondary domain decomposition parallelism, 1, 2, 4, 8, and 16 threads are selected for the calculation, and the results are shown in the following figure.

The analysis of Figure 8 and Figure 9 leads to the following conclusions. For MOC, OpenMP parallel efficiency is high when the number of threads is small, in particular, when the number of threads is smaller than or equal to 4, due to the fact that the load of each thread is completely balanced, the parallel efficiency is above 90%. However, as the number of threads increases, the computation time of the non-parallel part gradually increases, and the increase of threads increases the load imbalance of each thread, so, the parallel efficiency gradually decreases. For CMFD, OpenMP parallelism is currently implemented only for the GMRES function. There are a large number of “All_Allreduce” functions inside the entire CMFD function, and the number of sub-subdomains after the secondary domain decomposition is usually small, so that the degree of parallelism is limited. Those factors lead to low OpenMP parallel efficiency. Furthermore, for OpenMP parallelism, shared memory is used, and there is no communication. Therefore, the CMFD OpenMP parallel efficiency for C5G7-2D benchmark and C5G7-TD-5-1 is basically the same.

FIGURE 8

FIGURE 8. Calculation time, speedup and parallel efficiency. (A) RSOR. (B) RSILU.

FIGURE 9

FIGURE 9. Calculation time, speedup and parallel efficiency. (A) RSOR. (B) RSILU.

In addition, the results from Figure 8 and Figure 9 indicate that when OpenMP parallelism is implemented for characteristic rays, the secondary domain decomposition parallelism is implemented for CMFD at the same time. The CMFD can use the parallel resources of characteristic ray parallelism to reduce the CMFD computation time and achieve a certain degree of acceleration for CMFD calculation. On the other hand, the parallel efficiency is above 50% when the number of threads is smaller than or equal to 4, which is within the acceptable range.

4.2 QinShan real core problem

The QinShan real core model is a pressurized water reactor (PWR) whole core model, it contains 313 lattices, each of lattice is composed of $17\times 17$ cells, it is divided into 62 layers in the axial direction. The geometric schematic is shown in Figure 10.

FIGURE 10

FIGURE 10. The radial geometric schematic of QinShan real core.

The application of the hybrid MPI/OpenMP parallel strategy on the QinShan real core is analyzed, and the convergence criteria for eigenvalues and fission sources are ${10}^{-8}$ and ${10}^{-6}$. To further analyze the parallel efficiency of the hybrid MPI/OpenMP parallel strategy, 62 nodes are used for the calculation, each node calculates a layer of this real core problem. The number of processes and threads are varied when the total number of cores in the radial direction is fixed to 16.

First, using different preconditioners to calculate the Qinshan real core problem. The results are shown in Table 2.

TABLE 2

TABLE 2. Calculation time for each module using different preconditioner.

In Table 2, it can be seen that the computation time of CMFD is greatly reduced when using the RSILU preconditioner for the large-scale practical core problem. This shows the superiority of the RSILU preconditioner. Therefore, only the RSILU preconditioner is considered for the following QinShan real core problem verification. The numerical results are shown below.

Analysis of Figure 11 shows the following conclusions: 1) for the large-scale real reactor problem, the MPI parallel efficiency is lower than the C5G7 problem when the process is 16. For the QinShan core tested in this paper, the actual calculation amount in the edge region is significantly less than that in the internal region due to the spatial decomposition, which makes the load imbalance more serious; 2) for the hybrid MPI/OpenMP parallel strategy, the total number of cores is fixed, when the number of threads is smaller than or equal to 4, on the one hand, the load-balance between different threads, on the other hand, the increase in the number of threads leads to less communication between MPI processes, so that the speedup and parallel efficiency increase with the increase of the number of threads, and higher than those situations such as pure MPI and pure OpenMP; 3) it is known that the speedup of CMFD is low according to the research in the previous subsection, and the results in Table 2 show lower CMFD computation time. As a result, its impact on the transport computation time is not significant for large-scale problems.

FIGURE 11

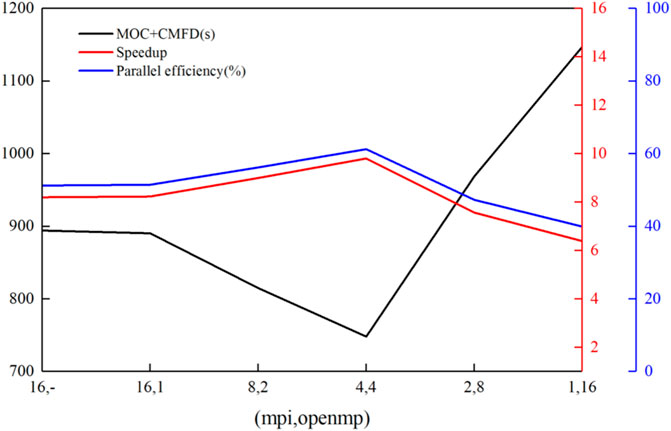
FIGURE 11. Calculation time, speedup, and parallel efficiency. With total number of radial cores is consistent of QinShan real core problem.

5 Conclusion

The principal contribution in this work is the implementation and optimization of the hybrid MPI/OpenMP parallel strategy in the three-dimensional whole-core one-step high-fidelity transport calculation program HNET. The spatial domain decomposition parallelism based on MPI can greatly reduce the memory burden, expand the scale of the problems, and achieve high parallel efficiency. For MOC, the characteristic ray parallelism based on OpenMP has better load-balance under the static scheduling scheme, and can better accelerate the calculation. At the same time, the source term calculation is also implemented in parallel. Afterwards, optimizing the characteristic ray parallelism by eliminating atomic operations further improves the computation efficiency, and can reduce the MOC computation time by 70% compared with using atomic operations. For CMFD, the secondary domain decomposition parallelism based on OpenMP is currently implemented only for the GMRES function. Implementing OpenMP parallelism for CMFD can use the parallel resources of characteristic ray parallelism to reduce the CMFD computation time and achieve a certain degree of acceleration for CMFD calculation, although it has a lower speedup and parallel efficiency than that of MOC.

Numerical results show that the hybrid parallel strategy can further expand the parallelism, accelerate the simulation, and fully utilize the parallel resources of modern computer clusters. In addition, the parallel efficiency of MOC and CMFD is above 90% and 50% respectively, when the number of threads is smaller than or equal to 4, especially for large-scale parallel computation problems, such as the Qinshan real core problem. The total speedup and parallel efficiency of MOC and CMFD can be higher when using the hybrid parallel strategy.

In summary, the hybrid MPI/OpenMP parallel strategy in HNET code can make full use of computational resources to achieve efficient parallel computation for large-scale problems. It has laid a solid foundation for practical nuclear engineering applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

For LP, the principal contribution in this work is the implementation and optimization of the hybrid MPI/OpenMP parallel strategy in the HNET code, and the parallel performance of the hybrid parallel strategy is verified by using the C5G7 benchmark and the QinShan real core problem. In the process, HC provided support on the transport methodology, LZ optimized the MPI parallel method, and LT provided computer support.

Funding

This study is supported by the Chinese National Natural Science Foundation Project 12075067 and the National Key R&D Program of China (2018YFE0180900).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Askew, J. (1972). A characteristics formulation of the neutron transport equation in complicated geometries. No. AEEW-M-1108. Abingdon, United Kingdom: United Kingdom Atomic Energy Authority.

Google Scholar

Boyarinov, V., Fomichenko, P., and Hou, J., (2016). Deterministic time-dependent neutron transport benchmark without spatial homogenization (C5G7-TD). Paris, France: Nuclear Energy Agency Organisation for Economic Co-operation and Development NEA-OECD.

Google Scholar

Boyd, W., Shaner, S., Li, L., Forget, B., and Smith, K. (2014). The OpenMOC method of characteristics neutral particle transport code. Ann. Nucl. Energy 68, 43–52. doi:10.1016/j.anucene.2013.12.012

CrossRef Full Text | Google Scholar

Chandra, R., Dagum, L., and Kohr, D., (2001). Parallel programming in OpenMP. Massachusetts, MA, USA: Morgan Kaufmann.

Google Scholar

Cho, J. Y., Kim, K. S., Lee, C. C., Zee, S. Q., and Joo, H. G. (2007). Axial SPN and radial MOC coupled whole core transport calculation. J. Nucl. Sci. Technol. 44 (9), 1156–1171. doi:10.1080/18811248.2007.9711359

CrossRef Full Text | Google Scholar

Cho, N. Z., Lee, G. S., and Park, C. J. (2002). Fusion of method of characteristics and nodal method for 3-D whole-core transport calculation. Trans. Am. Nucl. Soc. 87, 322–324.

Google Scholar

Choi, S. Y., and Lee, D. J. (2020). Three-dimensional method of characteristics/diamond-difference transport analysis method in STREAM for whole-core neutron transport calculation. Comput. Phys. Commun. 260, 107332. doi:10.1016/j.cpc.2020.107332

CrossRef Full Text | Google Scholar

Collins, B., Stimpson, S., Kelley, B. W., Young, M. T., Kochunas, B., Graham, A., et al. (2016). Stability and accuracy of 3D neutron transport simulations using the 2D/1D method in MPACT. J. Comput. Phys. 326, 612–628. doi:10.1016/j.jcp.2016.08.022

CrossRef Full Text | Google Scholar

Dangwei, M., Liu, Z., and Zhao, C., (2019). Multilevel parallel strategy and efficiency optimization in NECP-X. Atomic Energy Sci. Technol. 53 (5), 876. doi:10.7538/yzk.2018.youxian.0449

CrossRef Full Text | Google Scholar

Fitzgerald, A. P., Kochunas, B., Stimpson, S., and Downar, T. (2019). Spatial decomposition of structured grids for nuclear reactor simulations. Ann. Nucl. Energy 132, 686–701. doi:10.1016/j.anucene.2019.06.054

CrossRef Full Text | Google Scholar

Hongbo, Z., Hongchun, W., and Liangzhi, C., (2013). Two-dimensional matrix characteristics method based on Krylov subspace and domain decomposition theories. Nucl. Power Eng. 34. doi:10.3969/j.issn.0258-0926.2013.04.001

CrossRef Full Text | Google Scholar

Jarrett, M. G. (2018). A 2D/1D neutron transport method with improved angular coupling. Michigan, MI, USA: University of Michigan.

Google Scholar

Joo, H. G., Cho, J. Y., and Kim, K. S., (2004). Chicago, Illinois, US.Methods and performance of a three dimensional whole-core transport code DeCART, PHYSOR 2004–The Phys. Fuel Cycles Adv. Nucl. Syst.

Google Scholar

Joo, H. G., and Downar, T. J. (1996). An Incomplete domain decomposition preconditioning method for nonlinear nodal kinetics calculations. Nucl. Sci. Eng. 123 (3), 403–414. doi:10.13182/nse96-a24203

CrossRef Full Text | Google Scholar

Jung, Y. S., Lee, C., and Smith, M. A. (2018). PROTEUS-MOC user manual. Lemont, IL, USA: Argonne National Lab ANL.

Google Scholar

Kang, L., Hao, C., Qiang, Z., and Xu, Y. (2020). Two-level time-dependent GET based CMFD acceleration for 3D whole core transient transport simulation using 2D/1D method. Ann. Nucl. Energy 142, 107405. doi:10.1016/j.anucene.2020.107405

CrossRef Full Text | Google Scholar

Kochunas, B., Downar, T., and Liu, Z., 2013. Parallel 3-D method of characteristics in MPACT. M & C 2013: Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Sun Valley, Idaho, USA.

Google Scholar

Li, L. (2013). A low order acceleration scheme for solving the neutron transport equation. Massachusetts, MA, USA: Massachusetts Institute of Technology.

Google Scholar

Liu, Z., Liang, L., Chen, J., Zhao, C., and Wu, H. (2018). Accuracy and analysis of the iteratively coupling 2D/3D method for the three-dimensional transport calculations. Ann. Nucl. Energy 113, 130–138. doi:10.1016/j.anucene.2017.10.020

CrossRef Full Text | Google Scholar

Saad, Y. (2003). Iterative methods for sparse linear systems. Pennsylvania, PA, USA: Society for Industrial and Applied Mathematics.

Google Scholar

Smith, K., and Forget, B., 2013. Challenges in the development of high-fidelity LWR core neutronics tools. M & C 2013: Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Sun Valley, Idaho, USA.

Google Scholar

Wu, W., Li, Q., and Wang, K. (2015). Tiger-3D: 2D/1D coupled whole-core transport code based on large-scale parallel computation. React. Phys. Asia, 17–18.

Google Scholar

Xu, Y., and Downar, T. (2012). Convergence analysis of a CMFD method based on generalized equivalence theory. PHYSOR 2012. Illinois, IL, USA: American Nuclear Society.

Google Scholar

Xu, Y., and Hao, C. (2019). A novel and efficient hybrid RSILU preconditioner for the parallel GMRES solution of the coarse mesh finite difference equations for practical reactor simulations. Nucl. Sci. Eng. 194 (2), 104–119. doi:10.1080/00295639.2019.1657322

CrossRef Full Text | Google Scholar

Yee, B. C., Kochunas, B., and Larsen, E. W. (2017). A multilevel in space and energy solver for multigroup diffusion eigenvalue problems. Nucl. Eng. Technol. 49 (6), 1125–1134. doi:10.1016/j.net.2017.07.014

CrossRef Full Text | Google Scholar

Yuk, S., and Cho, N. Z. (2015). Whole-core transport solutions with 2-D/1-D fusion kernel viap-CMFD acceleration and p-CMFD embedding of nonoverlapping local/global iterations. Nucl. Sci. Eng. 181 (1), 1–16. doi:10.13182/nse14-88

CrossRef Full Text | Google Scholar

Zhang, H., Zhao, C., and Peng, X., (2022). Development of digital reactor high-fidelity neutronics code SHARK. Atomic Energy Sci. Technol. 56 (2), 334.

Google Scholar