Parallel schedules for MOC sweep in the neutron transport code PANDAS-MOC

Method of characteristics (MOC) is a commonly applied technique for solving the Boltzmann form of the neutron transport equation. In the PANDAS-MOC neutron transport code, MOC is used to determine the 2D radial solution. However, in the whole-code OpenMP threading hybrid model (WCP) of PANDAS-MOC, it is found that when using the classic parallelism, the MOC sweeping performance is restricted by the overhead incurred by the unbalanced workload and omp atomic clause. This article describes three parallel algorithms for the MOC sweep in the WCP model: the long-track schedule, equal-segment schedule, and no-atomic schedule. All algorithms are accomplished by updating the partition approach and rearranging the sweeping order of the characteristic rays, and their parallel performances are examined by the C5G7 3D core. The results illustrate that the no-atomic schedule can reach 0.686 parallel efficiency when using 36 threads, which is larger than the parallel efficiency obtained in the MPI-only parallelization model.

1 Introduction

In a general sense, parallel computing stands for the simultaneous use of multiple computational resources to solve a large and/or complex computational problem with a shorter time to completion and less memory consumption (Quinn, 2003). In the past several decades, with the rise of the supercomputers, parallel computing has been used to model complex problems in many science and engineering fields. One such example is the area of neutronics analysis, which needs significant amount of memory and is extremely time consuming due to the complex geometry and complicated physics interactions in nuclear reactors and, thus, makes the serial computing unpromising and improper for this kind of problem. On the contrary, parallelism partitions a large domain to multiple subdomains and assigns to individual computing nodes with a manageable size, and only the data corresponding to the assigned subdomain are stored in each node. Therefore, it has substantially decreased the memory requirement and makes the whole-core simulations possible. Moreover, since all nodes could run their jobs concurrently, the overall runtime decreases with the increasing number of devoted computing nodes/subdomains.

In neutron transport analysis, the method of characteristics (MOC) is the most popular deterministic method for solving the 3D Boltzmann neutron transport equation, which first discretizes the problem into several characteristic spaces and then tracks the characteristic rays for certain directions through the discretized domain. In 2003, the DeCART has demonstrated that MOC was applicable to the direct whole-core transport calculation (Joo et al., 2003), and then, this method has been widely implemented in the neutronics field. One capability that makes it more promising than the rest of the methods is that it can accurately handle arbitrary complicated geometries. However, to accurately simulate a 3D problem, the necessitated number of rays and of discretized regions has increased by the factor on the order of 1000 compared to solving a 2D problem. Consequently, MOC is usually considered as a 2D method for the neutronics analysis, and the solution to the third dimension is approximated by lower-order methods, given that there is less heterogeneity in the LWR geometry in the axial direction (1D) compared to the radial plane (2D). This method is referred to as the 2D/1D method. In real LWR reactors, the heterogeneity of the geometry design is quite large in the x–y plane and relatively small in the z-direction. Meanwhile, the 2D/1D method assumes the solution changes slightly in the axial direction, which allows coarse discretization in the z-direction and only does fine mesh discretization over the 2D radial domain. Therefore, the 2D/1D method could balance between the accuracy and computing time better than the direct 3D MOC method, which makes it a perfect candidate for such problem. Until now, the 2D/1D approximation technique has been applied to plentiful advanced neutronics simulation tools, such as DeCART (Joo et al., 2003), MPACT (Larsen et al., 2019), PROTEUS-MOC (Jung et al., 2018), nTRACER (Choi et al., 2018), NECP-X (Chen et al., 2018), OpenMOC (Boyd et al., 2014), and PANDAS-MOC (Tao and Xu, 2022c). Moreover, other deterministic methods, such as the variational nodal method (VNM), also exhibit the capability in handling arbitrarily complicated geometries and is developed and used in some prestigious neutronics codes, such as VITAS (Zhang et al., 2022).

The high-fidelity 3D neutron transport code PANDAS-MOC (Purdue Advanced Neutronics Design and Analysis System with Methods of Characteristics) is being developed at Purdue University (Tao and Xu, 2022c). Its essential method is the 2D/1D method, in which the 2D radial solution is solved by the MOC and the 1D axial solution is estimated by the nodal expansion method (NEM). To further improve its computing efficiency on large reactor problems, three parallel models were developed based on the nature of distributed and shared memory architectures, the pure MPI parallel model (PMPI), the segment OpenMP threading hybrid model (SGP), and the whole-code OpenMP threading hybrid model (WCP) (Tao and Xu, 2022b). As demonstrated in the previous study, in spite of the advantage of memory usage, the WCP model still needs further improvement in the multi-level coarse mesh finite different (ML-CMFD) solver and the MOC sweep in order to attain comparable, even exceptional, run-time performance to the pure MPI model. The improvement of the ML-CMFD solver is discussed by Tao and Xu (2022a), and this article concentrates on the optimization of the MOC sweep for hybrid MPI/OpenMP parallelization.

Until writing, the OpenMP parallelism in the MOC ray tracing is finished with the help of the omp atomic clause. For instance, in the nTRACER, the OpenMP is implemented in the levels of rotational ray sweep and energy group; then, the incoming and outgoing currents and the region scalar flux are atomically accumulated (Choi et al., 2018). Additionally, the parallel transport sweep algorithm of OpenMOC has two versions. One uses the omp atomic clause and the other does not use the omp atomic clause (Boyd et al., 2016). Nevertheless, the algorithm without an atomic clause is finished by introducing extra thread private arrays to store the intermediate scalar fluxes, and then, the FSR scalar fluxes are reduced across threads, which, however, costs significant amount of memory in this procedure.

This study is conducted based on the WCP model of PANDAS-MOC, and the detailed information could be found in Tao and Xu (2022b). This article is organized as follows. Section 2 describes the methodology of PANDAS-MOC. Section 3 introduces the parallelism and performance metrics. Section 4 gives the test problem and the key parameters defined for the geometry discretization and the numerical convergence. Section 5 presents three schedules designed to parallelize the MOC transport sweep in PANDAS-MOC using OpenMP and evaluates their performance. Section 6 is a brief discussion on the optimized WCP performance using the advanced ML-CMFD and MOC sweep solvers. Finally, a short summary and brief discussion of the future work are illustrated in Section 7.

2 Methodology

2.1 PANDAS-MOC methodology

This section will briefly introduce the methodology of PANDAS-MOC, highlighting the points that are most relevant for this work. The detailed derivations can be found in Tao and Xu (2022c). The transient method starts with the 3D time-dependent neutron transport equation (Eq. 1) and the precursor equations (Eq. 2):

$\begin{array}{ll}\hfill \frac{1}{v_g\left(r\right)}\frac{\partial {\phi }_g\left(r,\mathrm{\Omega },t\right)}{\partial t}& =-\mathrm{\Omega }\cdot \nabla {\phi }_g\left(r,\mathrm{\Omega },t\right)-{\mathrm{\Sigma }}_{tg}\left(r,t\right){\phi }_g\left(r,\mathrm{\Omega },t\right)+S_{sg}\left(r,\mathrm{\Omega },t\right)+\frac{{\chi }_g\left(r\right)}{4\pi }{S}_F\left(r,t\right)\hfill \\ \hfill & +\frac{1}{4\pi }\sum _k{\chi }_{\mathit{dgk}}\left({\lambda }_k{C}_k\left(r,t\right)-{\beta }_k{S}_F\left(r,t\right)\right),\hfill \end{array}(1)$

$\frac{\partial C_k\left(r,t\right)}{\partial t}={\beta }_k\left(r\right)S_F\left(r,t\right)-{\lambda }_k\left(r\right)C_k\left(r,t\right),k=\mathrm{1,2},\dots ,6,(2)$

where g is the energy group index, φ is the angular flux, Σ_tg is the total macroscopic cross section, β_k is the delayed neutron fraction, χ_g is the average fission spectra, which is a weighted average of the prompt fission spectra (χ_pg) and delayed fission spectra (χ_dgk) (Eq. 3), C_k is the density of delayed neutron precursors, S_sg is the scattered neutron source (Eq. 4), and S_F is the prompt fission neutron source (Eq. 5). The rest of the variables are in accordance with the standard definitions in nuclear reactor physics.

${\chi }_g={\chi }_{pg}+\sum _k{\beta }_k\left({\chi }_{\mathit{dgk}}-{\chi }_{pg}\right),(3)$

$S_{sg}\left(r,\mathrm{\Omega },t\right)=\sum _{g^{\prime }}{\int }_{4\pi }{\mathrm{\Sigma }}_{g^{\prime }g}\left(r,{\mathrm{\Omega }}^{\prime }\cdot \mathrm{\Omega },t\right){\phi }_{g^{\prime }}\left(r,{\mathrm{\Omega }}^{\prime },t\right)d{\mathrm{\Omega }}^{\prime },(4)$

$S_F\left(r,t\right)=\frac{1}{k_{\mathit{eff}}^s}\sum _{g^{\prime }}\nu {\mathrm{\Sigma }}_{f{g}^{\prime }}\left(r,t\right){\int }_{4\pi }{\phi }_{g^{\prime }}\left(r,\mathrm{\Omega },t\right)d\mathrm{\Omega }.(5)$

To numerically solve the transport equation, several approximations are considered.

1 Angular flux: Exponential transformation

2 Time derivative term: Implicit scheme of temporal integration method

3 Fission source: Exponential transformation and linear change in each time step

4 Densities of delayed neutron precursors: Integrating Eq.2 over time step

Accordingly, Eq. 1 can be transformed to the transient fix source equation, the Cartesian form of which is

$\left(\eta \frac{\partial }{\partial x}+ϵ\frac{\partial }{\partial y}+\mu \frac{\partial }{\partial z}\right){\phi }_g^n\left(r,\mathrm{\Omega }\right)+{\mathrm{\Sigma }}_{tg}^n\left(r\right){\phi }_g^n\left(r,\mathrm{\Omega }\right)=S_{sg}^n\left(r,\mathrm{\Omega }\right)+\frac{1}{4\pi }\left[{\chi }_g\left(r\right)S_F^n\left(r\right)+S_{\mathit{ntg}}^n\left(r\right)+S_{\mathit{trg}}^{n-1}\left(r\right)\right],(6)$

where

$\begin{array}{c}r=\left(x,y,z\right),\mathrm{\Omega }=\left(\mu ,\alpha \right),\eta =\sin \theta \cos \alpha ,ϵ=\sin \theta \sin \alpha \\ S_{\mathit{trg}}^{n-1}\left(r\right)=S_{\mathit{dcg}}^{n-1}\left(r\right)+S_{\mathit{dtg}}^{n-1}\left(r\right),S_{\mathit{dcg}}^{n-1}\left(r\right)=\sum _k{\chi }_{\mathit{dkg}}{\lambda }_k{\widehat{C}}_k^{n-1}\left(r\right)\\ S_{\mathit{dtg}}^{n-1}\left(r\right)=\frac{{\varphi }_g^{n-1}\left(r\right)}{E_g^n\left(r\right)\mathrm{\Delta }{t}_n{v}_g\left(r\right)},S_{\mathit{ntg}}^n\left(r\right)={\widehat{\chi }}_g{S}_F^n\left(r\right)-{\mathrm{\Sigma }}_{dg}^n{\varphi }_g^n\\ E_g^n\left(r\right)=e^{-{\alpha }_g^n\left(r\right)\mathrm{\Delta }{t}_n},{\alpha }_g^n=\left(\log P_n^{\mathit{tot}}-\log P_{n-1}^{\mathit{tot}}\right)/{\mathrm{\Delta }}_{n-1},{\mathrm{\Sigma }}_{dg}^n=\frac{{\alpha }_g^n}{v_g}+\frac{1}{\mathrm{\Delta }{t}_n{v}_g}\end{array}.$

Instead of directly resolving the computation-intensive 3D problem, it is converted to a radial 2D problem and an axial 1D problem, which is conventionally referred to as the 2D/1D method. The 2D equation is obtained by integrating Eq. 6 axially over the axial plane $({\int }_{z_b}^{z_t}dz)$ and solved by the MOC method, and the 1D equation is obtained by radially integrating over a box (∬_Adxdy) and solved by the NEM method. Then, the 2D radial solution and 1D axial solution are coupled by the transverse leakage. In addition, the multi-level coarse mesh finite difference (ML-CMFD) approach is implemented to accelerate the convergence for solutions to the transient fix source equation. Since this study concentrates on the performance improvement on the MOC sweep, the details of NEM and CMFD are omitted for brevity, and the details could be found in Xu and Downar (2012), Hao et al. (2018), and Tao and Xu (2020).

2.2 2D transient method of characteristics

2.2.1 Modular ray tracing

The method of characteristics (MOC) is developed to solve the first-order partial differential equations by transforming them into a system of ordinary differential equations. In neutron transport analysis, the MOC transforms the transport equation into the characteristic form by tracing the equation along the straight neutron flying paths over the spatial domain. This process is generally referred to as “ray tracing.” The setup of these tracks is substantial to the calculation accuracy and computational performance. In PANDAS-MOC, the modular ray tracing is implemented, which is the most straightforward approach to prepare the characteristic tracks.

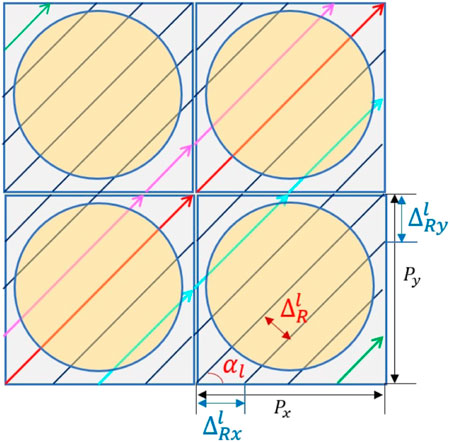
Considering that some structures are repeated throughout the reactor, such as the pin cells and assemblies, the transport problem is divided into multiple modules, which represents the fundamental small geometries in the large core. The ray-tracing information is then prepared for each module, and it is directly linked on the module interfaces using the direct neutron path linking technique (DNPL) (Kosaka and Saji, 2000). Next, the long tracks over the global domain are constructed by connecting the modular rays in adjacent geometries, as the red and magenta long tracks explained in Figure 1. Compared to arranging tracks over the entire reactor, modular ray tracing can significantly reduce the memory requirement for saving the ray data, which makes it very popular in MOC transport codes. Until now, PANDAS-MOC can handle rectangular fuel structures in LWR for the modular ray tracing.

FIGURE 1

FIGURE 1. Modular ray-tracing method.

In addition, the modular ray-tracing technique requires the number of tracks on the boundary as an integer. Given that the pitches P_x and P_y and the spacing between all parallel tracks (Δ_R) are constant, as illustrated in Figure 1, it further requires that all modules have the same spatial dimension to guarantee the long-track connection. For the lth azimuth angle, if the user-defined ray spacing is ${\mathrm{\Delta }}_R^{l0}$ and azimuthal angle is α_l0, the number of rays in x and y module boundaries are as follows:

$N_x=⌜\frac{P_x\sin {\alpha }_{l0}}{{\mathrm{\Delta }}_R^{l0}}⌝N_y=⌜\frac{P_y\sin {\alpha }_{l0}}{{\mathrm{\Delta }}_R^{l0}}⌝.(7)$

Then, the ray-spacing distance in x- and y-direction could be computed as follows:

${\mathrm{\Delta }}_{Rx}^l=\frac{P_x}{N_x}{\mathrm{\Delta }}_{Ry}^l=\frac{P_y}{N_y}.(8)$

Accordingly, the azimuthal angle is corrected to the true angle that satisfies the requirement of modular ray tracing, which is as follows:

${\alpha }_l=\arctan \frac{{\mathrm{\Delta }}_{Ry}^l}{{\mathrm{\Delta }}_{Rx}^l}=\arctan \frac{P_y{N}_x}{N_y{P}_x},(9)$

and the ray spacing is then adjusted to

${\mathrm{\Delta }}_R^l={\mathrm{\Delta }}_{Rx}^l\sin {\alpha }_l={\mathrm{\Delta }}_{Ry}^l\cos {\alpha }_l.(10)$

2.2.2 Method of characteristics sweep calculation

The MOC transforms the axially traversed 2D fix source equation into the characteristic form along various sorts of straight neutron paths (i.e., global characteristic long rays) over the spatial domain. Considering one inject line (r_in) passing through a point in direction Ω, any location along this ray is as follows:

$r=r_{in}+s\mathrm{\Omega }=r_{in}+\frac{l}{\sin \alpha }\mathrm{\Omega },(11)$

where l is the distance between the parallel tracks, α is the azimuthal angle of the characteristic ray, and s and l/sin α are the distance from the start point to the observe point along the track. Considering that the characteristic rays are separated to several segments based on the traversed constructs and materials along the path (Figure 1), the outgoing flux of one segment is the incident flux of the adjacent next segment along the neutron flying direction, and the sweep computation is performed on the level of such segments. The incident flux $({\phi }_p^{in}(\mathrm{\Omega }))$, outgoing flux $({\phi }_p^{\mathit{out}}(\mathrm{\Omega }))$, and the track-average flux $({\bar{\phi }}_p(\mathrm{\Omega }))$ over each segment of the ray are determined as follows:

${\phi }_p^{\mathit{out}}\left(\mathrm{\Omega }\right)={\phi }_p^{in}\left(\mathrm{\Omega }\right)+\frac{{\phi }_p^d\left(\mathrm{\Omega }\right)}{x}x,(12)$

$\frac{{\phi }_p^d\left(\mathrm{\Omega }\right)}{x}=\left[\frac{Q\left(\mathrm{\Omega }\right)}{{\mathrm{\Sigma }}_t}-{\phi }_p^{in}\left(\mathrm{\Omega }\right)\right]\frac{1-e^{-x}}{x},x={\mathrm{\Sigma }}_t\frac{l_p}{\sin \theta },(13)$

${\bar{\phi }}_p\left(\mathrm{\Omega }\right)=\frac{Q\left(\mathrm{\Omega }\right)}{{\mathrm{\Sigma }}_t}-\frac{{\phi }_p^d\left(\mathrm{\Omega }\right)}{x}.(14)$

The reason for using ${\varphi }_p^d(\mathrm{\Omega })/x$ here, instead of ${\varphi }_p^d(\mathrm{\Omega })$, is to avoid the potential loss of significance for very small x in Eqs 12, 13, 14. Given that there are abundant tracks with different azimuthal angles within each computational region, the overall average flux $(\bar{\phi }(\mathrm{\Omega }))$ in a flat-source region (FSR) can be determined by the average fluxes and the track spaces of all enclosed characteristic rays as follows:

$\bar{\phi }\left(\mathrm{\Omega }\right)=\frac{{\sum }_p{\bar{\phi }}_p\left(\mathrm{\Omega }\right)l_p\left(\mathrm{\Omega }\right)}{{\sum }_p{l}_p\left(\mathrm{\Omega }\right)}=\sum _p{\bar{\phi }}_p\left(\mathrm{\Omega }\right)l_p\left(\mathrm{\Omega }\right)\frac{C_{\mathrm{\Omega }}{\mathrm{\Delta }}_{\mathrm{\Omega }}}{A},(15)$

where C_Ω = A/(Δ_Ω ∑_pl_p(Ω)) and Δ_Ω is the ray-spacing distance for the direction Ω.

3 Parallelism

Parallel computing is more efficient regarding the run-time and memory than serial computing, since it breaks the problem into discrete parts in order to execute the code on multiple processors concurrently, which makes it a good choice for solving a problem that involves large memory and intensive computations (LLNL, 2022). Now, there are two primary parallel standards: the Message Passing Interface (MPI) and the Open Multi-Processing (OpenMP) (LLNL, 2022) (Quinn, 2003). MPI is used for distributed memory programming, indicating that the memory space that every parallel processor is working in is isolated from others, while OpenMP is applied for shared memory programming; in this way, every parallel thread can access all the shared data, which makes the communication between OpenMP threads faster than that between the MPI processors as it needs no internode message exchange. In addition, given that current parallel machines are having mixed distributed and shared memory, the hybrid MPI/OpenMP parallelization is also worth considering in order to take advantage of such memory architecture. Generally, the hybrid model uses MPI to communicate between the nodes and OpenMP for parallelism on the node. Therefore, it can eliminate the domain decomposition and provide automatic memory coherency at the node level and has lower memory latency and data movement with the node. The WCP model involved in this work is a hybrid MPI/OpenMP model, and the optimizations of the parallel schedules for MOC sweep are conducted on the OpenMP level in this work.

3.1 OpenMP application

To compile with the OpenMP, the pragmas must be inserted into the code so that the code can be transferred to a multithreaded version and then compiled into an executable file with the parallelism implemented by the OpenMP threads. The parallel constructs are established by pragmas provided by the OpenMP API according to the purpose of the parallelized regions, such as the parallel pragmas, tasking pragmas, work-sharing pragmas, and synchronization pragmas etc. For example, “omp parallel” is utilized to form a group of threads according to the specific number of threads and then execute those threads in parallel, and “omp for” defines a work-sharing loop and the iterations associated with it are performed in parallel by the threads in one team.

Given that OpenMP is programming for the shared memory, a thread’s temporary view of memory is not required to be in consistency with the memory at all times. Normally, a value written to a variable is kept in the thread’s temporary view until it is forced to the memory at a later time. Similarly, a read from a variable may get the value from the thread’s temporary view unless it is forced to read from memory. Thus, the consistency between a thread’s temporary view and memory for the shared variables is required in a race-free program, and it is guaranteed by the synchronization between the threads, which forces all threads to complete their work to a certain point before any thread is allowed to continue. In this work, two synchronization constructs are of critical concern (OpenMP, 2021).

The first one is “omp atomic.” If multiple threads need to access or modify the same variable, this directive allows them to touch this specific memory location atomically without causing any race conditions. Hence, atomic directive could help build more efficient concurrent algorithms with fewer locks. In addition, it has four clauses for different purposes, update (default), read, write, and capture. The other one is “omp barrier.” It specifies an explicit barrier at a point in the code where each thread must wait until all threads of the team have completed their explicit tasks in the associated region and arrived to this point.

3.2 Performance metrics

The measurement of parallel performance is the speedup, which is defined as the ratio of the sequential runtime (T_s) and the parallel runtime while using p processors (T_p) to solve the same problem. Also, efficiency (ϵ) is a metric of the use of the resources of the parallel system, the value of which is typically between 0 and 1.

$S_p=\frac{T_s}{T_p}=\frac{T_1}{T_p},{ϵ}_p=\frac{S_p}{p}.(16)$

According to Amdahl’s law (Quinn, 2003), the maximum speedup S_p that can be achieved when using p processors depends on the sequential fraction of the problem (f_s).

$S_p=\frac{1}{f_s+\frac{1-f_s}{p}}\to \underset{p\to \infty }{\lim }{S}_p=\frac{1}{f_s}.(17)$

For example, if 10% of work in a problem is remained serial, then the maximum speedup is limited to 10 times as fast even if more and more computing resources are devoted. Therefore, real applications generally have sublinear speedup (S_p < p), due to the parallel overhead, such as task start-up time, load balance, data communications and synchronizations, and redundant computations, etc.

4 Test problem

The parallel performance of designed codes in this work are determined by a steady-state problem, in which all control rods are kept out of the C5G7 3D core from the OECD/NEA deterministic time-dependent neutron transport benchmark, which is proposed to verify the ability and performance of the transient codes without neutron cross-section spatial homogenization above the fuel pin level (Boyarinov et al., 2016) (Hou et al., 2017). It is a miniature light water reactor with eight uranium oxide (UO₂) assemblies, eight mixed oxide (MOX) assemblies, and the surrounding water moderator/reflector. In addition, the C5G7 3D model is a quarter core, and fuel assemblies are arranged in the top-left corner. For the sake of symmetry, the reflected condition is used for the north and west boundaries, and the vacuum condition is considered for the rest six surfaces. Figure 2A shows the planar and axial configurations of the C5G7 core. The size of the 3D core is 64.26 cm × 64.26 cm × 171.36 cm, and the axial thickness is equally divided into 32 layers.

FIGURE 2

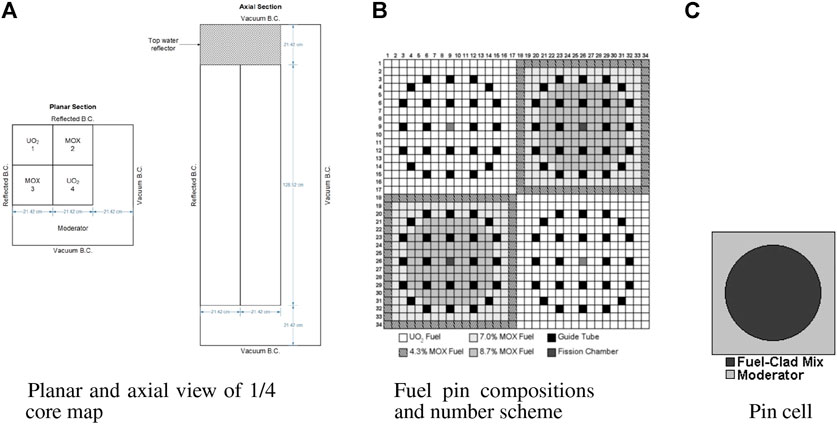
FIGURE 2. Geometry and composition of the C5G7-TD benchmark. (A) Planar and axial views of 1/4. (B) Fuel pin compositions and number scheme. (C) Pin cell.

Moreover, the UO₂ assemblies and MOX assemblies have the same geometry configurations. The assembly size is 21.42 cm × 21.42 cm. There are 289 pin cells in each assembly arranged as a 17 × 17 square (Figure 2B), including 264 fuel pins, 24 guide tubes, and 1 instrument tube for a fission chamber in the center of the assembly. The UO₂ assemblies contain only UO₂ fuel, while the MOX assemblies include MOX fuels with three levels of enrichment: 4.3%, 7.0%, and 8.7%. Moreover, each pin is simplified into two zones in this benchmark. Zone 1 is the homogenized fuel pin from the fuel, gap, and cladding materials, and zone 2 is the outside moderator (Figure 2C). The pin (zone 1) radius is 0.54 cm, and the pin pitch is 1.26 cm.

The MOC sweep was performed with the Tabuchi-Yamamoto quadrature set with 64 azimuthal angles and 3 polar angles, and the ray spacing was 0.03 cm. In addition, as for the geometry discretization, eight azimuthal flat source regions for each pin cell and three radial rings in the fuel regions were utilized for the spatial discretization. Differently, the moderator cells were divided into 1 × 1 coarse mesh or 6 × 6 fine mesh according to their locations in the core. The convergence criteria to the iterative functions are set as follows:

• Generalized minimal residual method (GMRES) in the ML-CMFD solver: 10^–10

• Eigenvalue (k_eff): 10^–6

• MOC flux: 10^–5

This study is conducted in the “Current” cluster at Purdue University, the mode of which is Intel(R) Xeon(R) Gold 6152 CPU @ 2.10GHz, and it has 2 nodes and 22 CPUs for each node.

5 Method of characteristics sweep parallelism

In the MOC technique, the calculation on each characteristic track is almost independent of others, which make it naturally parallel. Such ray decomposition is often implemented using the shared memory model, for example, OpenMP. However, it involves parallelizing the for-loops over the long tracks of all azimuth angles, and one of the major challenges is tackling with the load balance issue because the length of such tracks can be very different from one another. For example, the red track is significantly longer than the green track in Figure 1. Moreover, in order to update the average flux for each FSR (Eq. 15), the conventional hybrid MPI/OpenMP parallel approach is to have each thread compute the partial sums. While sweeping the long tracks associated with each azimuthal angle, the reduction operation is happening to accumulate the partial results on each thread, and this process has to be protected by the omp atomic clause. Nevertheless, it has been demonstrated in our previous research (Tao and Xu, 2022b) that the atomic operation itself has consumed more than 40% of the MOC sweeping time.

In this work, the parallelism of ray sweeping is optimized on the OpenMP schedule to take advantage of the shared memory architecture, and three parallel schedules on the MOC sweep will be explored. The first one is the long-track (LT) schedule, which is the typical parallelism of the MOC sweeping and used to demonstrate the aforementioned difficulties. The second one is the equal-segment (SEG) schedule, which provides the almost load-balanced partition. The third one is the no-atomic schedule, which bypasses the atomic operation through an innovative arrangement of the ray-sweeping sequence. All discussions in this section are based on the WCP model (Tao and Xu, 2022b) to take advantage of the minimal overhead of creating and destroying parallel regions, and the Flag-Save-Update reduction method developed by Tao and Xu (2022a) is used.

5.1 Long-track schedule

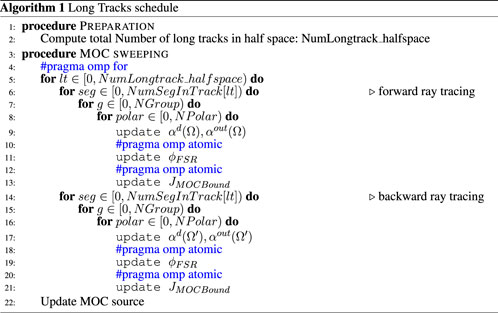
5.1.1 Design

This schedule is intuitive and classical. Since the MOC sweeping is carried out along all long tracks for all azimuth angles individually, the computation of the incident angular flux $({\phi }_p^{in}(\mathrm{\Omega }))$, the outgoing angular flux $({\phi }_p^{\mathit{out}}(\mathrm{\Omega }))$, and track-average angular flux $({\bar{\phi }}_p(\mathrm{\Omega }))$. Eqs 12, 13, 14 are performed on the segments of certain long tracks corresponding to one azimuth angle. In the code implementation, the flux array has four dimensions: azimuth angle, long-track index related to the azimuth angle, polar angle, and energy group. Therefore, the MOC sweeping loop could be partitioned by the “#pragma omp for” with a default schedule (i.e., static schedule) at the level of total long tracks of all azimuthal angles, as the Algorithm 1 suggests. For example, when applying six MPI processors and six OpenMP threads to the C5G7-3D core as illustrated in Figure 3, the number of long tracks and segments taken care by each thread is tabulated in Table 1. It is obvious that each thread manages a similar number of long tracks, but the number of segments could be greatly distinctive as long tracks could trespass different regions and have different segment lengths inside the reactor core as shown in Figure 1. Additionally, in order to update the flux for each FSR and the current on the domain boundaries, “#pragma omp atomic” is implemented to guarantee the correctness of data synchronization.

FIGURE 3

FIGURE 3. MPI partition in the C5G7 3D core when MPI-(x, y, z)= (3, 1, 2).

TABLE 1

TABLE 1. umber of long tracks and segments of the OpenMP thread for the LT schedule.

Algorithm 1

Algorithm 1. Long-track schedule.

5.1.2 Performance

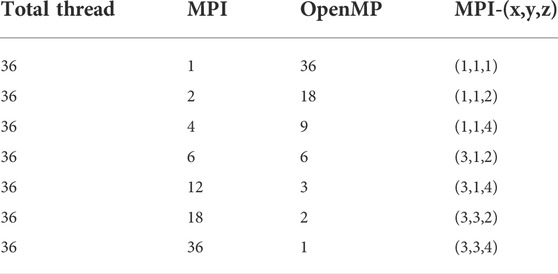
In order to compare the hybrid parallel performance, the tested total number of threads was fixed as 36, and all groups of number of MPI processor and OpenMP threads are tabulated in Table 2. Now that the C5G7 3D core has 51 × 51 assemblies in the x−y plane and 32 layers in the axial direction, the number of MPI processors in each direction is intentionally defined to evenly attribute the subdomains to each MPI processor. In addition, all tests were executed five times to minimize the measurement error, and the average run time was used for the further performance analysis.

TABLE 2

TABLE 2. Combinations of the tested number of MPI and OpenMP threads.

The measured run time for the MOC sweep is plotted in Figure 4A, and the speedup and efficiency are shown in Figure 4B, which are computed based on the run time for the MOC sweeping from the PMPI model with a single MPI processor (3938.421773 s) (Tao and Xu, 2022b). It is noticeable that all tests gave sublinear speedup, as the obtained speedup results are smaller than 36. Moreover, comparing the achieved speedup among all tests, (4,9) $>$ (2,18) $>$ (36,1), and the rest of the groups are slightly less than (36,1). There are several reasons for such unsatisfied behavior.

FIGURE 4

FIGURE 4. Performance of the MOC long-track schedule. (A) Run time. (B) Speedup and efficiency.

First is the unbalanced workload among spawn OpenMP threads. For tests with (1,36), (2,18), and (4,9), there are no MPI partition in the x−y plane and workload is approximately balanced for MPI processors in the axial direction; hence, all calculations related to the 2D MOC sweeping in each axial layer were accomplished by the OpenMP threads standalone. As mentioned before, the OpenMP separates the sweeping tasks on the total long track level, which makes the work per thread become more unbalanced when more threads were executed. For the MPI rank 0 at the center layer, the relative difference of the actual computed number of segment and the average number of segment, which is the number of perfect balanced distribution, on each launched OpenMP thread are computed as in Eq. 18 and depicted in Figure 5.

$R{E}_p=\left(\frac{{\text{Segment}}_p}{\frac{{\sum }_{p=0}^{P-1}{\text{Segment}}_p}{P}}-1\right)*100\%.(18)$

FIGURE 5

FIGURE 5. Segment relative deviation from the average number at the 0th MPI processor.

Apparently, the sweeping job is distributed in a more balanced way among the threads for (4,9) than for (2,18) and (1,36), although its relative error is in the range of [−11%, 8%], which is consistent with the speedup results (4.9) $>$ (2,18) $>$ (1,36).

Second is the overhead caused by the communication among spatial subdomains, especially in the x−y directions. Figure 4B shows that the speedup measured from test (2,18) is much larger than test (18,2). There are two significant differences in these two tests: 1) the load unbalanced issue is more severe when executing 18 OpenMP threads than that while using two OpenMP threads, and 2) there is additional domain decomposition in the x−y directions when running with 18 MPI processors, as stated in Table 2. As is well known, to perform the MOC sweeping along each long characteristic track, the outgoing angular flux at the previous subdomain is considered as the incident value for the next subdomain. Although all subdomains are allowed to solve their local problems concurrently, when having decomposition in the x−y plane, the interior subdomains will not have the boundary/interface conditions ready until they have been exchanged through all other subdomains across the interior interfaces and the problem boundaries, which means that the overhead brought by the data exchange across the subdomain interfaces is unavoidable. Particularly, the more synchronization points there are, the greater the synchronization execution latency overhead is. Therefore, the communication overhead is the major cause of the dissatisfied performance when having spatial partition in the 2D plane, such as in tests (18,2), (12,3), and (6,6), and it has overwhelmed the load balance problem in test (2,18).

Third is the overhead caused by the synchronization points. Figure 4B exhibits that test using (36,1) gave slightly larger speedup than (1,36). The data synchronization performed by the “#pragma omp atomic” statement in this solver is worth further investigation. To understand its significance, numerical experiments with “#pragma omp atomic” used or removed from the MOC sweeping part were conducted using the number of MPI processors and OpenMP threads equal to (1,1) and (36,1). Figure 8 shows the collected run time for the entire steady-state calculation and MOC sweeping solver along the run time of the PMPI model with an identical number of MPI processors. Even though there is only one OpenMP thread launched, when running without the “atomic” procedure, the measured run-time cost by the MOC sweep is only around 55% of the run time when the “atomic” is enacted. In other words, the access of a specific memory location atomically has consumed about 45% of run time all by itself even when there is only one thread enqueue. Furthermore, the run-time cost by the experiments without the atomic process is about 87% of the PMPI test. Therefore, the major factor that makes the speedup and efficiency unpromising could be the omp atomic structures defined in the MOC solver to avoid the race condition and ensure the correct data synchronization.

5.2 Equal-segment schedule

5.2.1 Design

As discussed in Section 5.1, it has great influence on the parallel performance that whether or not the workload distribution among the OpenMP threads is balanced. This section concentrates on a new schedule on the OpenMP partition, equal segment (SEG), that spreads the ray sweeping to all threads as unbiased as possible.

The fundamental unit of the calculations involved in the MOC sweep is the segment, which is the small chunk of the characteristic tracks intersected by the core geometries or materials. Due to the complex compositions within a reactor core, the number of segments for each long track could be significantly dissimilar as illustrated in Figure 1. Instead of directly separating the long tracks to each thread as in the long-track schedule, each OpenMP thread is expected to take care of a similar number of segments while sweeping on the characteristic long tracks, in this schedule.

In order to separate the segments as evened as possible, the total number of segments of all long tracks concerning all azimuthal angles is first tallied, and then, the average number of segments for each OpenMP thread is evaluated based on the executed number of OpenMP threads. With this average number, the thread-private start and end index of the long tracks associated to an individual thread could be determined. All of such manipulations could be finished right after the characteristic track construction of modular ray tracing in the geometry treatment, for that reason the for-loop partition finished by the “#pragma omp for” statement is eliminated from the MOC solver whenever it is called. With the thread private start and end track index known, the calculation fashion for the ray sweeping is maintained in an identical manner to that in the LT schedule. Nevertheless, the reduction operation is still secured by the omp atomic clauses for now. The detailed algorithm is listed in Algorithm 2.

Algorithm 2

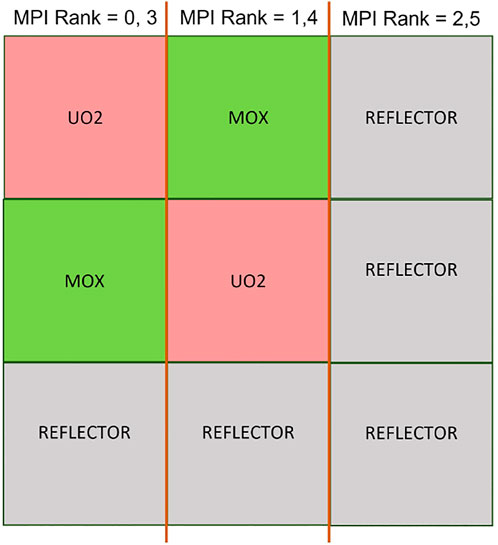
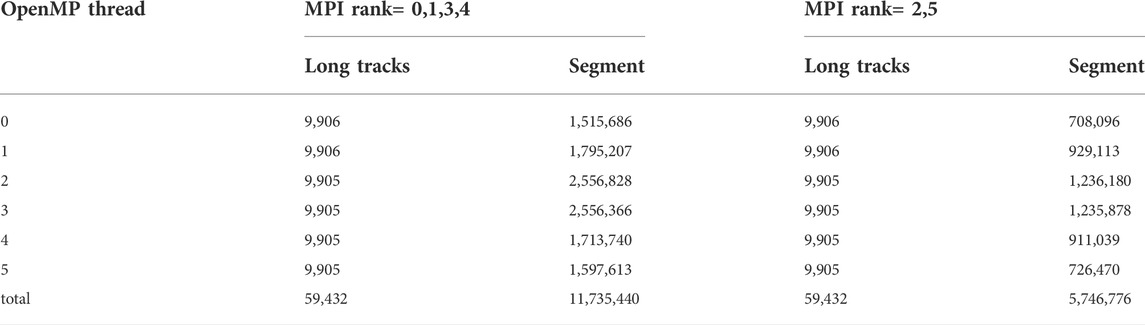
Applying six MPI processors and six OpenMP threads to the C5G7 3D reactor core as illustrated in Figure 3 and using this SEG schedule, the number of long tracks and segments per thread are tabulated in Table 3. The contrast between Tables 3,1 demonstrates the difference between the LT schedule and the SEG schedule. The SEG schedule provides an unequal number of long tracks but closer number of segments within each OpenMP thread, which yields more balanced workload among threads and, therefore, shorter waiting time for synchronization.

TABLE 3

TABLE 3. umber of long tracks and segments of the OpenMP thread for the SEG schedule.

5.2.2 Performance

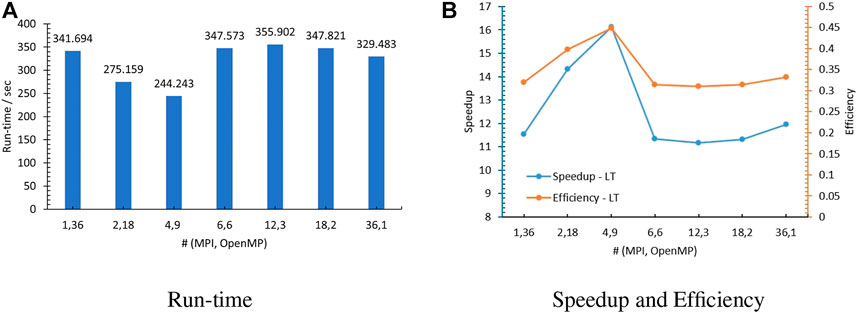
We repeat the numerical experiments using the same MPI processor and OpenMP thread groups as in Section 5.1. The measured run time of the MOC sweep is manifested in Figure 6A, and the speedup and efficiency are shown in Figure 6B, which are again computed based on the MOC time from the PMPI model with a single MPI processor (3938.421,773 s) (Tao and Xu, 2022b). It is revealed that all tests achieved larger speedup than (36,1), except that (18,2) is 4.8% smaller than (36,1). Similar to the LT schedule, (4,9) presented the best parallel performance among all groups.

FIGURE 6

FIGURE 6. Performance of the MOC equal-segment schedule. (A) Run time. (B) Speedup and efficiency.

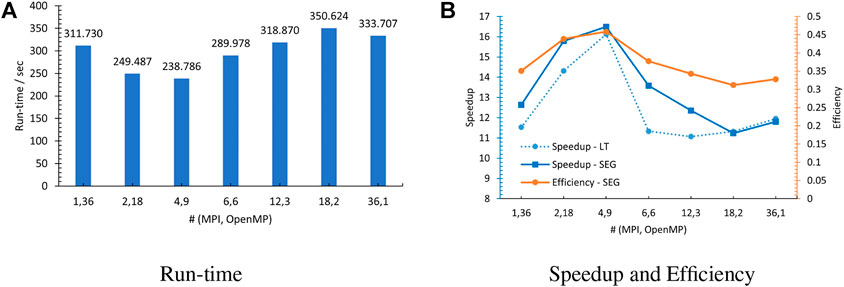
Moreover, a comparison of the speedup of the LT and SEG schedules demonstrates that they have similar speedup when running with (36,1) and (18,2) because their load balance situations are nearly equivalent in these circumstances. However, SEG has accomplished greater speedup for cases with number of OpenMP threads ≥3 because of the better workload distribution. According to Eq 18, the relative errors of the actual number of segments and the ideal number of segments in each thread are evaluated and drawn in Figure 7, and they are within the range of ±0.08%. It illustrates that the SEG schedule ensures that the task distribution among all threads is approximately balanced, and there is limited overhead introduced to the calculation by this factor.

FIGURE 7

FIGURE 7. Segment relative deviation from the average number at the 0th MPI processor.

However, the achieved optimal efficiency for the SEG schedule is 0.46, which indicates the overhead brought by the omp atomic clause is playing a vital role in restricting the speedup. The measured run time for the overall steady-state calculation and MOC sweeping solver by repeating the simulations with and without “^#pragma omp atomic” are plotted in Figure 8. Similar to the LT schedule, in spite of the number of MPI processors, the time consumed by the “#pragma omp atomic” here is about 45% of the MOC sweeping when there is only a single OpenMP thread undertaking the sweeping tasks.

FIGURE 8

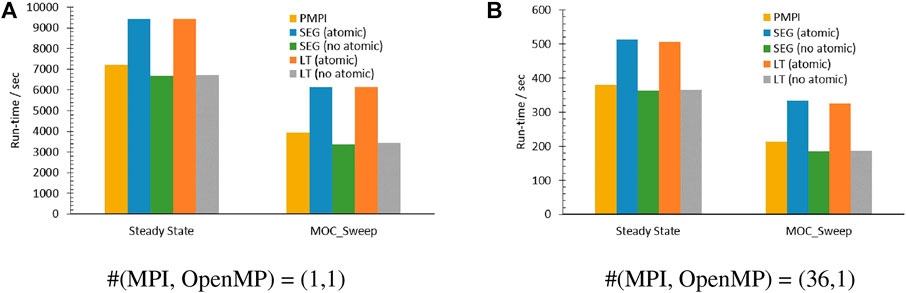
FIGURE 8. Performance with and without “^#pragma omp atomic.” (A) ^#(MPI, OpenMP)= (1,1). (B) ^#(MPI, OpenMP)= (36,1).

In short, the SEG schedule has alleviated the overhead brought by load unbalanced issue by pre-computing the start and end track index to equalize the number of segments in each executed thread, but the cost of the omp atomic operation in the calculations is still a significant issue that jeopardizes the parallel improvements.

5.3 No-atomic schedule

5.3.1 Design

In the OpenMP parallel, the atomic clause allows access of a specific memory location atomically and ensures that race conditions are avoided through direct control of concurrent threads that might read or write to or from the particular memory location (Quinn, 2003). In general, with the “#pragma omp atomic,” update will be a more efficient concurrent algorithm with fewer locks. However, in our tests discussed in the previous sections, the atomic operations within the MOC sweep can cost as much as 45% of the execution time all by itself, which is extremely inefficient and unaffordable for solving a whole-core pin-wise problem. Given that all the omp atomic clauses are utilized to protect the global quantities, such as flux of each FSR and current at subdomain boundaries, the essential task to eliminate such statements is to avoid sweeping the segments associated with the same FSR simultaneously in order to guarantee the race-free condition. In this part, this concept is accomplished by reshuffling the sweeping sequence of the long tracks for each OpenMP thread without using any additional memories or any revisions on the sweeping functions. This design is called no-atomic schedule, which will be explained with an example.

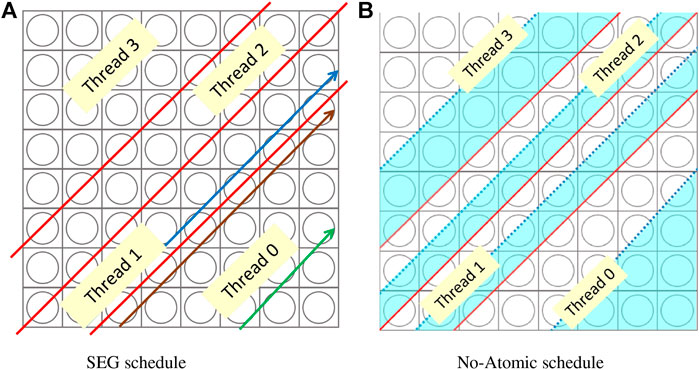
Figure 9A describes a partition of the long tracks using four threads utilizing the SEG schedule, in which OpenMP parallelizes all long tracks corresponding to all azimuthal angles together, and each thread takes care of a similar number of segments. The red lines stand for the splitting of the long tracks among threads. Given that the number of segment in each long track is significantly different, it is possible that thread 0 is working on the brown track while thread 1 is still on the blue track. Then, the same memory associated with one FSR might be touched by multiple threads at the same time. In this scenario, the “#pragma omp atomic” statement is necessary to protect the calculation from the potential race conditions. However, if thread 0 is handling the green track while thread 1 is on the blue track, all involved segments are related to different FSRs, which makes the race conditions non-existent. Consequently, the omp atomic clause now is unnecessary for the calculation correctness. Inspired by this observation, it is feasible to get rid of the omp atomic clause by deliberately scheduling the adjacent threads dealing with the segments or long tracks corresponding to different FSRs during the entire calculation.

FIGURE 9

FIGURE 9. Example of the no-atomic schedule. (A) SEG schedule. (B) No-atomic schedule.

In the previous LT and SEG schedules, the MOC sweeping is operated on a single layer of for-loop pertaining to the total number of long tracks accumulated from all azimuthal angles in half space. However, here, we break this effort to two layers: azimuthal angle and its corresponding long tracks, and the OpenMP parallelism is applied on the long-track layer related to the same azimuthal angle. For each azimuthal angle in half space, the long-track partition is prepared in the following steps:

1 We compute total number of segments (S_tot), average number of segments per thread (S_thd = S_tot/N_omp), and half average number of segments per thread (S_half = S_tot/(2*N_omp)), where N_omp is the number of launched OpenMP threads

2 We partition the long tracks based on the average number of segment per thread S_thd, which is similar to the concept of SEG

3 For each thread, its long tracks are further divided into two groups based on the half average number of segment per thread (S_half), which is the baseline for rearranging the track-sweeping sequence and assuring that the neighboring threads will not touch the same FSR simultaneously

For instance, in Figure 9B, starting from the SEG partition (red lines), after the aforementioned three steps, the long tracks are split into two equal-segment parts for each OpenMP thread, which are depicted as the blue and white parts. In this situation, if all threads are working on the blue part, then they will never read and update the same memory concurrently. Therefore, the atomic clause could be removed from the code. Nevertheless, the trade-off of this schedule is that an explicit barrier is required to make sure that all blue parts are finished sweeping before any threads start working on the white part. Eq. 19 is the coarse criterion of feasibility of the no-atomic schedule, where N_x and N_y are the number of rays in x and y pin cell boundaries, respectively, determined by Eq. 7. For each azimuthal angle, if S_half meets this requirement, when all threads are sweeping the same group of long tracks (e.g., the blue part in Figure 9B), the first long track of one thread and the last long track of the previous thread are guaranteed at least one pin cell away from each other, and in this manner, the memory associated with one FSR will be only accessed by a single thread at one time. On the contrary, if S_half fails to satisfy this formula, it cannot be claimed with full confidence that the race conditions have been exclusively eliminated from the MOC sweep solver. Accordingly, a smaller number of OpenMP threads will be advised, and the code will print a warning and be terminated immediately.

$S_{\mathit{half}}\left(\alpha \right)\ge N_x\left(\alpha \right)+N_y\left(\alpha \right).(19)$

In addition, the detailed algorithm of the no-atomic schedule is explained in Algorithm 3. In the actual design, the explicit barrier is included after each pair of forward and backward ray tracing to guarantee that all blue parts are finished before any threads shift to white parts in Figure 9B, which is the only synchronization point to avoid any potential race conditions.

Algorithm 3

Algorithm 3. No-atomic schedule

5.3.2 Performance

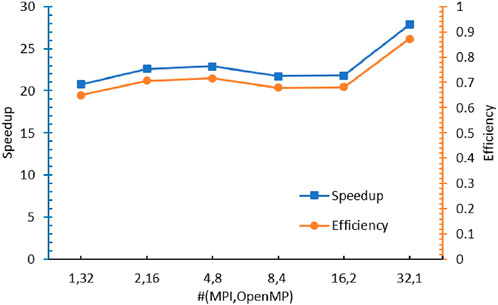
Repeating all the tests investigated in the previous sections using this newly developed no-atomic schedule, the measured run-time is plotted in Figure 10A, and the speedup and efficiency are shown in Figure 10B, which are evaluated using the MOC sweeping run-time from the PMPI model with a single MPI processor (3938.421,773 s) (Tao and Xu, 2022b). The speedup results of the LT schedule and SEG schedule are displayed in the figure altogether for comparison. Figure 10A illustrates that when using comparable computing resources, all tests are faster than (36,1), except (18,2), which is 9.45% slower. In addition, Figure 10B shows that the speedup obtained from the no-atomic schedule is about 1.5–1.8 times that from the SEG schedule, and now, the maximum parallel efficiency is 0.686 and the minimum efficiency is 0.529. On the contrary, the obtained efficiency for the MOC sweep in the PMPI code when using 36 MPI processors is 0.512. It indicates that the performance of the no-atomic schedule has exceeded the previous two schedules and the pure MPI parallel at all tests when executing the same total number of threads.

FIGURE 10

FIGURE 10. Performance of the no-atomic schedule. (A) Run time. (B) Speedup and efficiency.

The overhead in this schedule could be caused by the explicit omp barrier at line 24 in Algorithm 3 and spatial decomposition as discussed in Section 5.1.2. Since we already demonstrated in Section 5.2 that the sweeping workload has been distributed to threads as balanced as possible, the load balance problem is not a worry for the overhead anymore. As for the explicit barrier inserted in this schedule, it is an unavoidable trade-off between removing omp atomic clauses from the code and enforcing the data operated correctly. Thus, the principal issue left now is the communication between the MPI subdomain boundaries. To validate this assumption, additional tests were conducted using 32 threads, which is the number of axial layers of the C5G7 3D core. Also, all MPI processors are applied to the axial partition, so there is no MPI communicating overhead for MOC variables. The obtained speedup and efficiency are illustrated in Figure 11. In this situation, the maximum efficiency is 0.871 at (32.1), and the rest of the tests are having parallel efficiency around 0.70. Therefore, it hints that the communication among the x–y directional subdomains has created overhead for the parallelization in the aforementioned experiments using 36 threads.

FIGURE 11

FIGURE 11. Performance of the no-atomic schedule (total thread= 32).

6 Whole-code OpenMP optimizations

As explained by Tao and Xu (2022b), the parallel performance achieved from the WCP model is better than that from the SGP model, which is the conventional fashion of hybrid MPI/OpenMP parallelization, yet not comparable to the PMPI model. The improvement on the hybrid reduction in the ML-CMFD solver and parallelism of MOC sweeping are desired to optimize the WCP code and make it at least a match for the PMPI code. In this article, we have revolved the obstacle for the MOC sweep, and the measured speedup for the MOC sweep has outperformed the MOC sweep in the PMPI model using identical total number of threads (Figures 10, 12B). The improvement on the hybrid reduction in the ML-CMFD solver is thoroughly discussed by Tao and Xu (2022a), and here is a brief description.

FIGURE 12

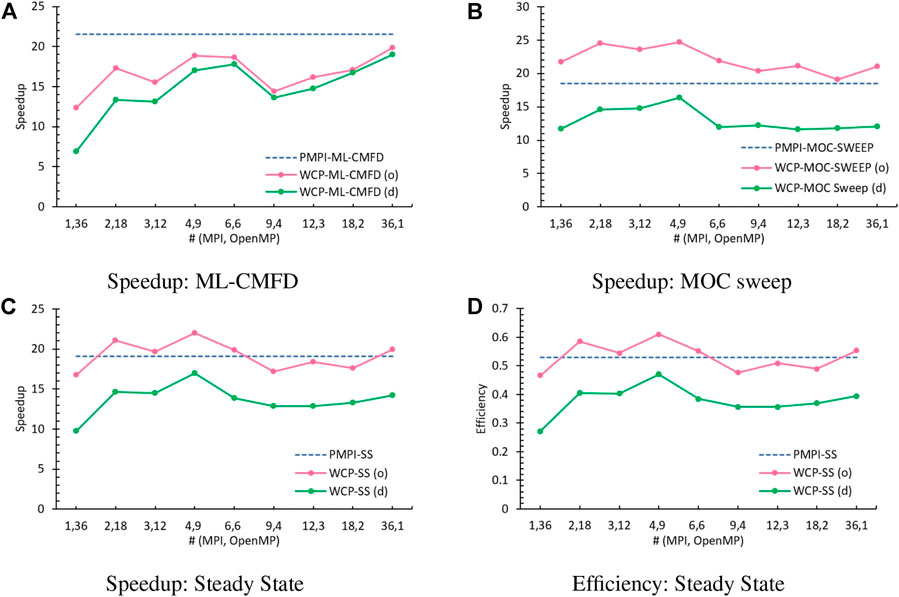
FIGURE 12. Performance comparison with total threads as 36 (o: optimized algorithm and d: default method). (A) Speedup: ML-CMFD. (B) Speedup: MOC sweep. (C) Speedup: steady state. (D) Efficiency: steady state.

The reduction in the hybrid MPI/OpenMP codes is generally completed by the omp reduction clause and MPI reduction routines, which contains implicit barriers to slow down the calculations. In order to get rid of such synchronization points, the Flag-Save-Update reduction algorithm was developed by Tao and Xu (2022a). In this algorithm, two global arrays are defined to store the partial results and the status flag of each OpenMP thread, and the threads are configured as a tree structure to favor the reduction procedure. Instead of waiting for all OpenMP threads to have their partial results ready, here, once the status flag shows the work in one thread is performed, its parent thread will collect this result immediately and flip the flag. When all partial results are collected, the MPI_Allreduce() routine is called to generate the global solution. Therefore, it contains no barriers, and the calculation flow it is controlled by the status flags. The detailed information could be found in Tao and Xu (2022a), in which we have demonstrated that the Flag-Save-Update reduction could provide better speedup than the conventional hybrid reduction algorithm, which nevertheless is still smaller than the MPI_Allreduce() standalone in the PMPI model.

The comparison of the performance obtained from the PMPI model (dashed blue line), the original WCP using default methods [green line, labeled as (d)], and the optimized WCP [pink line, labeled as (o)] is illustrated in Figure 12. When focusing on the improvement of ML-CMFD and MOC, Figure 12A illustrates that the optimized reduction algorithm can effectively improve the speedup when a large number of OpenMP threads is launched, but the performance of the CMFD solver is still affected by the overhead from load balance, communication, and also restricted by the hardware properties, such as cache size. Meanwhile, the no-atomic schedule can successfully enhance the parallel performance as demonstrated in this article. While The ML-CMFD solver using the Flag-Save-Update reduction is still not as efficient as PMPI using MPI_Allreduce() standalone, the advancement achieved from the optimized MOC sweep schedule is large enough to offset such weakness. Therefore, the steady state of the optimized WCP code has accomplished much better speedup and parallel efficiency than the original WCP code and comparable to or even greater than the PMPI code as explained in Figures 12C,D.

7 Summary and conclusion

In order to improve the parallel efficiency of the MOC sweep, this study presented the development and implementation of three different schedules for the MOC sweep module in the WCP model of PANDAS-MOC: the long-track (LT) schedule, equal-segment (SEG) schedule, and no-atomic schedule. All algorithms are accomplished by updating the partition approach and rearranging the sweeping order of the characteristic rays. In the LT and SEG schedules, the azimuthal angles and their associated characteristic tracks were condensed to a total number of long tracks, and then, the OpenMP partition was performed on this level. The LT schedule was straightforwardly adding the omp for directive on the long-track iteration, which led to a remarkable load-unbalanced issue for runs with a large number of OpenMP threads, and its parallel efficiency was found to be significantly affected by the omp atomic process as well, which was introduced for preventing the race conditions. Next, the SEG schedule deliberately separated the sweeping task according to the total number of segments and number of executed threads so that the workload was distributed among OpenMP threads as equalized as possible. In contrast to the LT schedule, its speedup has moderately improved yet still limited by the omp atomic directives. Finally, based on the SEG concept, the no-atomic schedule further removed all omp atomic clauses by the rearrangement of the sweeping sequence of long-track batches. Using the same numerical experiments, the no-atomic schedule has demonstrated much greater parallel performance than the previous two schedules. Its maximum parallel efficiency for the MOC sweeping was 0.686 when the total number of threads was 36 and 0.872 when using 32 threads and without MPI communication among subdomains in x–y directions. Particularly, when using 36 threads, all tested points have accomplished a better parallel efficiency than the PMPI code, and this improvement is large enough to compensate the deficiency in the hybrid MPI/OpenMP reduction in the ML-CMFD solver and makes the optimized WCP model more efficient than the PMPI model. In brief, the no-atomic schedule designed in this work can present performance beyond the pure MPI and traditional hybrid parallel styles without consuming extra memories. Future work could further decrease the overhead caused by the intro-node communications between the spatial subdomains for distributed memory parallelism for better efficiency.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

All authors contributed to the conception and methodology of the study. ST performed the coding and data analysis under the supervision of YX and wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boyarinov, V., Fomichenko, P., Hou, J., Ivanov, K., Aures, A., Zwermann, W., et al. (2016). Deterministic time-dependent neutron transport benchmark without spatial homogenization (c5g7-td). Paris, France: Nuclear Energy Agency Organisation for Economic Co-operation and Development.

Google Scholar

Boyd, W., Shaner, S., Li, L., Forget, B., and Smith, K. (2014). The openmoc method of characteristics neutral particle transport code. Ann. Nucl. Energy 68, 43–52. doi:10.1016/j.anucene.2013.12.012

CrossRef Full Text | Google Scholar

Boyd, W., Siegel, A., He, S., Forget, B., and Smith, K. (2016). Parallel performance results for the openmoc neutron transport code on multicore platforms. Int. J. High. Perform. Comput. Appl. 30, 360–375. doi:10.1177/1094342016630388

CrossRef Full Text | Google Scholar

Chen, J., Liu, Z., Zhao, C., He, Q., Zu, T., Cao, L., et al. (2018). A new high-fidelity neutronics code necp-x. Ann. Nucl. Energy 116, 417–428. doi:10.1016/j.anucene.2018.02.049

CrossRef Full Text | Google Scholar

Choi, N., Kang, J., and Joo, H. G. (2018). “Preliminary performance assessment of gpu acceleration module in ntracer,” in Transactions of the Korean Nuclear Society Autumn Meeting, Yeosu, Korea, October 24-26 2018.

Google Scholar

Hao, C., Xu, Y., and Downar, J. T. (2018). Multi-level coarse mesh finite difference acceleration with local two-node nodal expansion method. Ann. Nucl. Energy 116, 105–113. doi:10.1016/j.anucene.2018.02.002

CrossRef Full Text | Google Scholar

Hou, J. J., Ivanov, K. N., Boyarinov, V. F., and Fomichenko, P. A. (2017). Oecd/nea benchmark for time-dependent neutron transport calculations without spatial homogenization. Nucl. Eng. Des. 317, 177–189. doi:10.1016/j.nucengdes.2017.02.008

CrossRef Full Text | Google Scholar

Joo, H. G., Cho, J. Y., Kim, K. S., Lee, C., and Zee, S. Q. (2003). Parallelization of a three-dimensional whole core transport code decart. Available at: https://www.osti.gov/etdeweb/servlets/purl/20542391.

Google Scholar

Jung, Y. S., Lee, C., and Smith, M. A. (2018). PROTEUS-MOC user manual tech. Rep. ANL/NSE-18/10, nuclear science and engineering division. Illinois: Argonne National Laboratory.

Google Scholar

Kosaka, S., and Saji, E. (2000). Transport theory calculation for a heterogeneous multi-assembly problem by characteristics method with direct neutron path linking technique. J. Nucl. Sci. Technol. 37, 1015–1023. doi:10.1080/18811248.2000.9714987

CrossRef Full Text | Google Scholar

Larsen, E., Collins, B., Kochunas, B., and Stimpson, S. (2019). MPACT theory manual (version 4.1). Tech. Rep. CASL-U-2019-1874-001, University of Michigan, Oak Ridge National Laboratory.

Google Scholar

LLNL (2022). Introduction to parallel computing tutorial.

Google Scholar

OpenMP (2021). Openmp application programming interface (version 5.2).

Google Scholar

Quinn, M. (2003). Parallel programming in C with MPI and OpenMP. Boston: McGraw-Hill.

Google Scholar

Tao, S., and Xu, Y. (2020). “Hybrid parallel computing for solving 3d multi-group neutron diffusion equation via multi-level cmfd acceleration,” in Transactions of the American Nuclear Society (Virtual Conference).

Google Scholar

Tao, S., and Xu, Y. (2022a). Hybrid parallel reduction algorithms for the multi-level cmfd acceleration in the neutron transport code pandas-moc. [Manuscript submitted for publication].

Google Scholar

Tao, S., and Xu, Y. (2022b). Hybrid parallel strategies for the neutron transport code pandas-moc. [Manuscript submitted for publication].

Google Scholar

Tao, S., and Xu, Y. (2022c). Neutron transport analysis of c5g7-td benchmark with pandas-moc. Ann. Nucl. Energy 169, 108966. doi:10.1016/j.anucene.2022.108966

CrossRef Full Text | Google Scholar

Xu, Y., and Downar, T. (2012). “Convergence analysis of a cmfd method based on generalized equivalence theory,” in PHYSOR 2012: Conference on Advances in Reactor Physics - Linking Research, Industry, and Education, Knoxville, Tennessee, USA, Apr 15-20 2012.

Google Scholar

Zhang, T., Xiao, W., Yin, H., Sun, Q., and Liu, X. (2022). Vitas: A multi-purpose simulation code for the solution of neutron transport problems based on variational nodal methods. Ann. Nucl. Energy 178, 109335. doi:10.1016/j.anucene.2022.109335

CrossRef Full Text | Google Scholar