Department of Biomedical Engineering, Ben-Gurion University of the Negev, Israel
Motor control neuroscientists measure limb trajectories and extract the onset of the movement for a variety of purposes. Such trajectories are often aligned relative to the onset of individual movement before the features of that movement are extracted and their properties are inspected. Onset detection is performed either manually or automatically, typically by selecting a velocity threshold. Here, we present a simple onset detection algorithm that is more accurate than the conventional velocity threshold technique. The proposed method is based on a simple regression and follows the minimum acceleration with constraints model, in which the initial phase of the bell-shaped movement is modeled by a cubic power of the time. We demonstrate the performance of the suggested method and compare it to the velocity threshold technique and to manual onset detection by a group of motor control experts. The database for this comparison consists of simulated minimum jerk trajectories and recorded reaching movements.
Many neuroscientists consider the study of the motor system to be a window to the brain. Their work often involves tracking the position of a human or other mammalian limb under various experimental conditions. One essential parameter frequently extracted from the tracking data is the movement initiation time, or the onset time, which can also be used to assess other events, such as reaction time, peak velocity time, and target interception, among others. Correct onset detection, however, is also important for measuring other properties of the movement, such as the time difference between muscle activation and onset of the movement (Corcos et al., 1992
), or for measuring motor reaction time (Bekkering et al., 1994
). Although the onset time can be extracted using any one of a variety of methodologies, most studies employ the simple but inaccurate method of velocity threshold. Thus, the issue of accurately detecting the onset time via a simple algorithm is still a challenge (Soda et al., 2008
; Solnik et al., 2008
; Van Dijck et al., 2007
).
Onset detection time can be determined using a dedicated device such as a release switch (Mushiake et al., 1997
), but this usually limits the subjects to specific point in space and restricts the experimental setup. Alternately, onset detection time can be estimated from the tracked trajectory as measured by a tracking system, such as a magnetic/optical tracker (van Beers et al., 2004
), or via the encoder of a robot assistant device (Georgopoulos et al., 1982
; Shadmehr and Mussa-Ivaldi, 1994
). The recorded trajectory can then be manually analyzed offline by a skilled professional, which does not guarantee a perfect and consistent detection scheme, or it can be detected automatically by a dedicated onset detection algorithm.
Automatic onset detection algorithms usually involve calculating position (Bays et al., 2005
) or position derivatives, mainly velocity (Donchin et al., 1998
; Georgopoulos et al., 1982
; Moran and Schwartz, 1999
; Roby-Brami et al., 2000
; Scott et al., 2001
) or higher derivatives, such as acceleration or jerk (Wyatt, 1998
), and setting some upper threshold crossing point as the movement onset. These threshold techniques, however, tend to generate positive biases in the estimation of onset time. Other schemes, which strive to identify the transition time points between static episode and movement episode, have been suggested (Staude, 2001
; Staude et al., 1996
; Van Dijck et al., 2006
), but these require extensive modeling and computation, based on the optimal detection theory, and the fitting of additional, free parameters.
Here, we present a less complicated, alternative approach based on the notion that the point of movement onset can be regarded as a problem of change-point estimation between a static phase and a movement phase, both of which are corrupted by motor and tracking noises; however, this approach employs a simple, deterministic motor control model and a linear regression to estimate the deflection point. The issue of model estimation using the linear regression of non linear models has already been addressed (Li and Yu, 1999
), but as far as we know, it was never applied as a tool for onset detection.
We modeled the initial static trajectory using a constant term model and the movement phase using a simple polynomial function with one parameter. Numerous models exist that account for the typical bell-shaped speed profile of arm movement, such as the minimum-jerk trajectory model (Flash and Hogan, 1985
), which provides an analytical polynomial model, but for which multiple parameters must be estimated. Here, we use the minimum acceleration criterion with constraints (MACC) (Ben-Itzhak and Karniel, 2008
), which models the initial phase of the movement using a constant jerk, and as such, it requires the estimation of a single parameter that can be easily implemented via linear regression. Therefore, we named our approach the MACC-based onset detection method.
In addition to enabling precise onset detection, the technique we suggest may help elucidate the underlying mechanisms of motor control, such as the quantification of feedforward motor program changes. This may be accomplished by estimating the mean jerk at a very early stage of the movement when it is controlled solely by the feedforward mechanism (Carlton, 1981
; Elliott et al., 2001
) and before sensory feedback processes can intervene. Examples of such fundamental mechanisms may be the adaptation to force fields (Shadmehr and Mussa-Ivaldi, 1994
), adaptation to changes in the load force of a lifting task (Flanagan and Wing, 1997
; Flanagan et al., 1993
), the quantification of saccadic gain adaptation (Straube et al., 1997
; Wallman and Fuchs, 1998
), and the measurement of adaptation during visuomotor rotation (Rabe et al., 2009
). A recent example by Scheidt and Ghez (2007)
showed that adaptation to visuomotor rotation under special training may lead to curved movements. If the feedforward direction command is to be measured in such trials, it is vital that the correct onset be detected, the lack of which could cause the measured feedforward angle to deviate from its true value as a result of curved movement. Our technique may also be applicable when the timing between different actions must be measured, for example, when attempting to detect synergies among groups of muscles via their movement signals or between their principle components (Santello et al., 1998
; Thakur et al., 2008
). Finally, motor control studies of movements with lower signal to noise ratio as a result of shorter movement paths, such as movements of the fingers, the recording of signals from subjects suffering from bradykinesia, or measurements corrupted by severe noise conditions, may also benefit from our method.
We begin by explaining the methodology and then comparing its performance to that of other conventional methods. A Matlab code that implements the proposed algorithm is available online.
The MACC Based Onset Detection Algorithm
We assume that the trajectory has two distinct stages, a static stage followed by a movement stage, both of which are corrupted by normal zero mean Gaussian noise. We use two different models with an unknown change time point (t0) to describe this behavior. The first model is simply a constant position, x0, of a straight line having constant zero velocity. A variety of models exist for the second stage. One such model is the minimum jerk trajectory (MJT) model (Flash and Hogan, 1985
), given in Eq. 1:
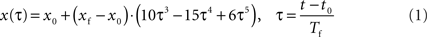
where x0 represents the end-effectors’ tracked position before the movement began and xf is its final position at time . In this model, the position at any given normalized time τ is a factor of the unknown parameters xf, x0, Tf, and t0. Therefore, to correctly detect the onset of the movement, all four parameters must be estimated. Furthermore, some of the parameters, such as xf and Tf are related to the final movement, which can be the result of several sub-movements. Correct identification of the sub-movements necessitates a preliminary process of movement segmentation (Fishbach et al., 2005
), but this process itself depends on onset detection.
In this work, we employ an alternative model that describes the initial phase of the movement trajectory (once x0 and t0 are known) with a single parameter, Um.
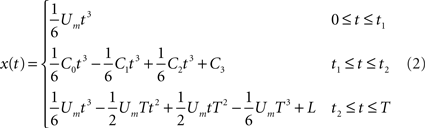
The model (Eq. 2) is based on the minimum acceleration trajectory with constraints criteria. This MACC model (Ben-Itzhak and Karniel, 2008
) asserts that the position x(t) is controlled by a series of three sign-alternating constant jerk segments (Um, C0, Um) with optimal switching times (t1, t2).
For onset detection, we are only interested in the initial phase of the movement (0 < t < t1), where the position depends solely on the cubic power of time, and a constant jerk Um. Thus, the remainder of our analysis ignores the other parameters of this model.
The derivation and justification of the MACC model were done by Ben-Itzhak and Karniel (2008)
. Early in the movement, however, when τ << 1, the MJT and the MACC are similar and the cubic power of time is the dominant factor. This observation is applicable to our onset detection method.
The joint model describes the initial static and movement phases, and it can be summarized as follows:
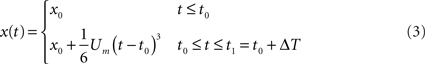
Four problems are inherent in the use of this model: (1) Estimation of the initial static position – x0; (2) Estimation of the initial jerk Um that best fits the data; (3) Estimation of the time change point t0; and (4) Identification of the time interval ΔT. We describe the mathematical solution using the signal that is sampled at a constant time interval, Ts, with a total of N sample points. The first three parameters are calculated through a method explained below, while the time interval ΔT should be set according to our prior knowledge of human reaction time and feedback loop delay. This issue and an analysis of parameter sensitivity are addressed later.
First we segment the trajectory and its appropriate time points into equal-sized segments denoted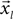 
and 
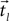, respectively (Eq. 4), each with m data points (m < N). Theoretically, the segmentation should be repeated for the entire sampled signal, but in this case, as justified later in the text, it was done only for that portion of the data in which we believe with high certainty that the onset resides.
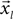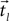and , respectively (Eq. 4), each with m data points (m < N). Theoretically, the segmentation should be repeated for the entire sampled signal, but in this case, as justified later in the text, it was done only for that portion of the data in which we believe with high certainty that the onset resides.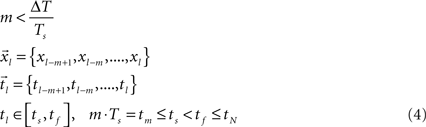
Our problem is thus redefined as a problem of estimating, which data segment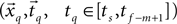 
best fits the static model and which adjacent data segment 
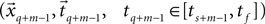best fits the constant jerk model. To that end, we estimate the model parameters (i.e., x0, t0, Um) for the entire segments and then select as a solution the set of parameters that best fits the data.
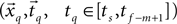best fits the static model and which adjacent data segment 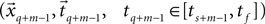best fits the constant jerk model. To that end, we estimate the model parameters (i.e., x0, t0, Um) for the entire segments and then select as a solution the set of parameters that best fits the data.The model for the static phase for each data segment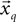 
(Eq. 5) is the simple mean of that segment, and it is an estimation of the true average (under reasonable assumptions of normal Gaussian zero mean additive noise).
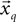(Eq. 5) is the simple mean of that segment, and it is an estimation of the true average (under reasonable assumptions of normal Gaussian zero mean additive noise).
The second term of the model (Eq. 3) is based on a constant jerk model that includes three parameters (x0, t0, Um). For every segment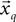 
, the estimation value of x0 is simply defined as the average value of the segment 
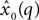, the value of t0 is defined as the end point of this segment tq, and finally, Um is defined as the best root-mean-square (RMS) solution that fits the data in the adjacent time segment 
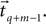These estimations and assumptions are summarized for a single onset point tq (Eq. 6).
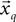, the estimation value of x0 is simply defined as the average value of the segment 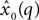, the value of t0 is defined as the end point of this segment tq, and finally, Um is defined as the best root-mean-square (RMS) solution that fits the data in the adjacent time segment 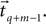These estimations and assumptions are summarized for a single onset point tq (Eq. 6).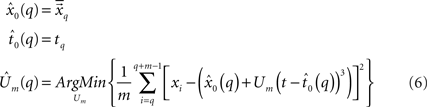
The fit quality of the joint model to the data is defined as the sum of the RMS errors between the data and the combined model (Eq. 7), which includes the static model (Eq. 5) and the constant jerk model (Eq. 6). Finally, the estimated onset point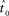 
is defined as the time point at which the sum of those RMS errors (Eq. 8) is minimized (a local minima exists), and the mean jerk, which describes the motor command, is simply 
.
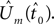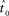is defined as the time point at which the sum of those RMS errors (Eq. 8) is minimized (a local minima exists), and the mean jerk, which describes the motor command, is simply .
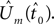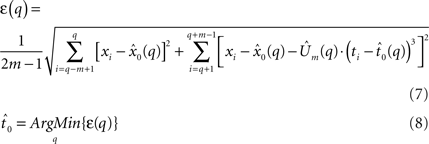
Theoretically, the minimum could be searched for within the entire signal. However, since the onset time clearly cannot be found near peak velocity, we limit the maximum search point tf by using the peak velocity threshold technique together with a relatively high threshold value. This technique assures with high certainty that the movement onset exists prior to this time point. In our implementation, we found that a threshold of 20% of the peak velocity is satisfactory, namely
In the event that more than one local minimum exists in the model, we simply select the latter as the onset point.
The suggested model has a single free parameter, m, which defines the durations of both the stationary and the initial movement trajectory segments. The selection of m is governed by two opposing factors: increasing m will both decrease (due to noise) and increase (due to misfit of the model) the error. Furthermore, if we assume that the model is adequate and that noise is independent, then the RMS error is simply the variance of the noise, which decreases as a function of the total sample size (i.e., in our case, the duration of 2m − 1 samples). On the other hand, higher m values may invalidate our assumptions, i.e., of a constant position prior to movement onset and a constant jerk in the initial portion of the movement, about the model.
In addition to these issues, we should also consider motor system physiology, specifically, a minimum reaction time (Carlton, 1981
; Paillard, 1996
) of an order of 100 ms, which may modify both the constant position term prior to the initiation of movement and the movement trajectory as a result of the sensory feedback loop. Likewise, it is important to emphasize that the model can also predict the feedforward initial jerk, Um, which may also be influenced by the feedback loop if the selected m is too large.
Theoretically, the duration could be defined differently for the two segments. However, as a result of a sensitivity analysis of this parameter and for the sake of simplicity, we chose to implement the model incorporating equal durations for both segments. These findings are summarized and addressed in “Results” and “Discussion” sections.
We provide an online Matlab code that implements the MACC model, and this code may be freely downloaded at http://www.bgu.ac.il/∼akarniel/pub/MACCInitV4.rar
Evaluation Method
We evaluated our proposed MACC-based onset detection algorithm by comparing its performance to those of other methods (velocity threshold technique and manual detection by a group of motor control experts) on a simulated movement and on real reaching movement databases.
Generated using Matlab R2008b software (MathWorks Corporation), the simulated movement database comprised movements that started with initial static segments and were followed by movement trajectories patterned after the minimum jerk trajectory. The static segment had a constant zero position value and duration, whereas the minimum jerk trajectory total movement path and total movement time parameters (xf, Tf, respectively) were selected from a unified probability distribution in the range xf ∈ [0.1, 0.5] m and Tf ∈ [1, 2.25] s. Using a sampling interval of 10 ms, we formed our main dataset by simulating 500 random movements based on these parameters. The simulation database included five similar datasets, each with an incrementally higher variance level of added zero mean white Gaussian noise. Altogether our database included 2500 movements, which were not preprocessed with a low pass filter and were analyzed as is.
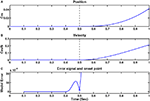
For each movement in the database, we compute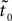d the estimated onset time 
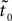using both the MACC model and the velocity threshold technique. Figure 1
shows an example of such a trajectory and the appropriate MACC model error and the estimated onset time.
using both the MACC model and the velocity threshold technique. Figure 1
shows an example of such a trajectory and the appropriate MACC model error and the estimated onset time.
Figure 1. Example of a single trajectory without noise and the estimated onset point using the MACC based onset detection model. (A) Position as a function of time; (B) velocity profile; (C) model error (blue) and its minima defined as the estimated onset point (blue circle). Black dashed vertical lines on the position and velocity illustrations mark the true onset time at 0.5 s.
The score of each method under each noise level was defined as the RMS difference between the true onset and the detected onset time across the dataset. Since the RMS errors are not necessarily Gaussian, we could not use a simple T distribution to compute the confidence intervals, and instead, we employed a bootstrap technique (p < 0.05) (Efron and Tibshirani, 1998
).
In addition, we compared manual onset detection of the motor control experts (experienced researchers in the BGU computational motor control laboratory) to the automatic methods mentioned previously. The database for this comparison was based on a subset of the previously mentioned database. Each expert analyzed the same 120 movements built from the identical set of 30 movements extracted from the first four datasets. The noisiest of the datasets was not included in this analysis. Movement positions and velocities were presented to the experts on a PC screen. Each movement profile was displayed with a different shift selected from a random unified distribution of 200 ms. Using a special tool written in Matlab, each expert selected the onset time.
In addition to that for synthetic movements, we created another database composed of recorded reaching movements. This additional database was specifically constructed to validate the efficacy of the MACC model on real movement with real noises and also to inspect whether the trend that we observed between the different methods on the synthetic database is also evident in the recorded movement database. Finally, the between-subjects variability of manual onset detection may be used to justify the use of automatic onset detection instead of manual segmentation.
The reaching database consisted of 100 reaching movements collected from 10 subjects after receiving their informed consent. Each subject was asked to perform 300 planned reaching movements of 12 cm while their hand position was tracked by a Phantom desktop (Sensable™) with dedicated software at 150 Hz. The criteria for selection of the 10 movements per subject were based on automatic measurements of signal noise levels. We only selected movements with noise levels similar to those in the fourth synthetic dataset. The noise level was defined as the RMS of the residual signal after its movement component was filtered. Two filters in series, the first a high-pass filter (51 taps, hamming window, cut-off 5 Hz) and the second a local detrend filter (median filter, 10 samples) constitute the filtering stage, which removed any local DC leftovers.
Another group of experts, comprising the former group of experts and one new recruit, performed additional onset detection tasks on the reaching movement database using the same Matlab tool as described before. Their results were compared to those from automatic detection of both the MACC and of the 5% velocity threshold.
We compared the performances of two automatic algorithms for the detection of movement onset using simulated movement and human reaching movement databases.
For MACC onset detection, the time windows for the segments (m) were defined as 15 sampling points, each with a duration of 150 ms. This value is short enough to capture early movement onset and to facilitate the use of the mean initial jerk as an estimator of the feedforward command. Later in “Results” section we describe the sensitivity analysis of this parameter.
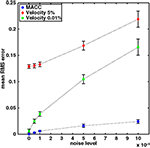
A performance comparison of the two automatic algorithms, in terms of RMS error, is provided in Figure 2
as a function of noise level. The results are presented as mean errors and confidence intervals (p < 0.05) for the MACC model and for the velocity threshold method at two different peak velocity threshold levels (5% and 0.01%). MACC model error is substantially lower than that of the velocity threshold technique, even without noise. This difference is the result of the inherent bias in the velocity threshold method and is related to threshold level. Therefore, we also compared the results of a lower peak velocity threshold of 0.01% that has a MACC-equivalent performance without noise. Although this threshold value was superior to the 5% value, its RMS error was consistently higher than that of the MACC model wherever noise level was increasing.
Figure 2. Mean performances of MACC onset and peak velocity methods under four levels of Gaussian noise. Markers and error bars show mean values and mean confidence intervals, respectively (p < 0.05). Blue circle: MACC model; Red diamond: 5% peak velocity threshold; Green square: 0.01% peak velocity threshold.
Algorithm performance was also compared to a motor control specialist’s manual segmentation, and their respective performances were, in turn, compared to the capacities of the automatic segmentation techniques. The results show (Figure 3
) that, in terms of mean error, MACC model performance was consistently better than the manual and the velocity threshold techniques, and that the experts performed better than the automatic velocity measurement technique. An examination of error behavior with increasing noise level shows that the error increases faster for manual onset detection than for MACC-based onset detection, which implies that MACC was less sensitive to noise. Note that at low noise levels, both manual detection and the velocity threshold methods exhibit biased detection, which is not evident in the MACC algorithm.
Figure 3. Mean onset error presenting the accuracy of the MACC onset detection method over manual onset detection by experts and automatic velocity-based onset detection. Bar represents mean value and error bar shows mean confidence intervals (p < 0.05). Gray: performances of six manual experts; Blue: automatic MACC model performance; Blue star: MACC model accurate performance without noise; Red: automatic 5% peak velocity threshold.
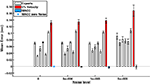
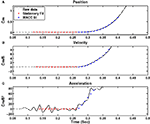
Another group of experts analyzed real reaching movements (Figure 4
, example of a single movement), taking the position and the velocity of the movement as explained in “Methods” section. Their performances were compared to those of the automatic MACC and velocity threshold techniques (Figure 5
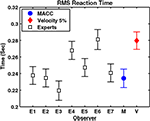
). The results reflect the wide variability that existed among the experts – although most expert analyses produced results in agreement with MACC, two expert computations yield results closer to the 5% velocity technique.
Figure 4. Example of a recorded reaching movement with onset detection according to MACC and to the 5% velocity threshold. (A) Recorded position along with onset detection method and the best MACC fit model. (B) Velocity. (C) Acceleration. The MACC defined onset point is 50 ms earlier than the onset point as determined by the 5% velocity threshold. Onset detections by the experts for this example ranged from 0.26 to 0.32 s, while the MACC onset detection was 0.26 s.
Figure 5. The RMS onset time of seven experts (E1 through E7) on a real database compared to MACC and 5% threshold techniques. Gray: individual mean expert performance; Blue: MACC mean onset detection; Red: 5% velocity threshold onset detection. Graph shows that the experts’ variabilities range between those of the MACC and of the velocity threshold techniques. Onset detection of five out of the seven experts does not differ statistically from the MACC. The onset detection trend present in the synthetic database between the three methods also exists in this database.
Relative to almost all the experts, the MACC model was negatively biased. Experiments with comparably simulated databases produced similar findings in which the true onset is known, a fact that reinforces our findings. These findings also suggest that manual onset detection, although largely in agreement with the MACC model, is positively biased.
We analyzed the sensitivity of the segment duration (m) using the synthetic database and explored both symmetric and asymmetric segment durations for the stationary and initial movement segments. Our findings show that when both segments are increased equivalently, the RMS onset error decreases as an inverse function of the time window size (observation discussed earlier). The minimum of this function is achieved in our simulated database at a value of 20 samples (i.e., a total time window of 390 ms). Further increases in window size cause the error to increase, probably because of the inadequacy of the model. Although the minimum is achieved at a segment size of 20 samples, we posit that our selection of a smaller window size of 15 samples is preferable since it may incorporate changes in the movements that are related to a feedforward mechanism and it could provide a better tool for detecting movement with a shorter reaction time. The extra mean RMS error in our sensitivity analysis due to this selection was about 10 ms. Our code accommodates the flexibility to define separate segment durations. Another theoretical possibility is to employ a multiple onset detection scheme based initially on a wide time window (larger m values) to make a rough detection of the onset time, after which the algorithm switches to a narrow search window focused around the approximated time point. This may improve algorithm accuracy and decrease its sensitivity to noises and sub-movements.
We present a simple yet efficient and accurate method for detecting movement onset. The method was shown to be superior to the conventional velocity threshold based method when tested on a simulated database that included minimum jerk movements corrupted with random Gaussian noise. It also performed better when used on actual recordings of reaching movements. A performance comparison with onset detection by experts using the same two databases revealed the presence of inconsistencies (absent when using automatic onset detection methods) between the expert evaluations. Finally MACC onset detection method performance on the synthetic database had smaller errors and earlier reaction times than the conventional velocity threshold technique. Because this trend was also evident in the database of recorded movements, we believe that our method is more accurate.
Our method does not assume that the constant term is known apriori, and therefore, its average value is estimated using the mean value of the segment, a process that leads to increases in the RMS error in the model. However, if the exact position in the experimental setup is known, then onset detection can be improved by omitting the use of the estimated average, thereby reducing the error.
In addition, our method assumes that the initial portion of the movement can be modeled by a third order power of the time series. This concept is consistent with the idea that the initial part of the movement can be modeled using a constant jerk, as suggested by the MACC model (Ben-Itzhak and Karniel, 2008
). The jerk signal has been used in the past for the detection of movement onset (Wyatt, 1998
), but in that case, it was used as a simple threshold similar to the velocity threshold.
The simulated database that we created was based on the assumption that human reaching movement can be depicted via the minimum jerk model (Eq. 1) (Flash and Hogan, 1985
; Shadmehr and Mussa-Ivaldi, 1994
; Wolpert et al., 1995
). The minimum jerk model can be regarded as a fifth order polynomial having null terms for time power series lower than three. Although the coefficient of the third order term is not the largest among the time power series, its contribution to the model in the early stage of the movement is higher than the other terms. The fit of a third order power series, therefore, seems appropriate even if the movement appears to be better modeled by the minimum jerk rather than by the MACC model. If one assumes that the constant jerk model accurately describes the initial movement phase and that the noise at each sampled position point is statistically independent, then the suggested algorithm, which uses linear regression, has a lower noise variance that is proportional to the inverse of the number of samples used in the regression. Even if the condition of independent noise is not entirely met, its partial fulfillment is an improvement, albeit to a lesser degree, over the use of a single threshold point.
The notion of movement onset detection using two separate models, one for the static phase and the other for the movement phase, has been previously suggested (Staude, 2001
). In that study, it was assumed that the noised model command drives a plant that can be represented as an all-pole filter; thus, in order to reveal the underlying motor command, a data-tuned inverse model was used and its output error was evaluated using a log likelihood ratio test. The final decision is made when the inverse filter error crosses some threshold. Although this technique produces accurate results, under the above assumptions, its difficult implementation and complexity prevent it from becoming a practical method for onset detection.
Very fast reaching movements, also called ballistic movements, are by definition controlled entirely by a pre-planned, feedforward controller. However, there is mounting evidence that practical reaching movements are also influenced by the feedback (Botzer and Karniel, 2008
; Desmurget and Grafton, 2000
; Ma-Wyatt and McKee, 2007
; Saunders and Knill, 2003
, 2005
). This emphasizes the importance of using a movement onset detection algorithm, such as that presented here, which uses only the initial portion of the movement where said movement is still dominated by the pre-planned, feedforward controller. As a consequence, when the proposed algorithm is used with the appropriate time window (m), it is superior to threshold techniques (e.g., velocity threshold) since it is insensitive to fragmentation of the movement (sub-movements) that may appear later. Moreover, the suggested model, which estimates the initial jerk (Ûm), may be used to estimate feedforward dynamics such as trial-by-trial adaptation during exposure to force fields, perturbation, or other imposed environmental changes.
We propose an onset detection method that provides an accurate estimation of the onset time and an average value for the initial feedforward motor command. The potential applications include reaction time evaluation, feedforward trial-by-trial adaptation analysis, and onset detection. The proposed tool is expected to be useful for analyzing reaching movements and similar movement profiles commonly measured in motor system studies.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The computational motor control laboratory is supported by the National Institute for Psychobiology in Israel; the Ministry of Science, Culture and Sport, Israel, and by the Ministry of Research, France; The United States – Israel Bi-National Science Foundation (BSF), Jerusalem, Israel; and the National Science Foundation (ISF), Israel.
Soda, P., Mazzoleni, S., Cavallo, G., Guglielmelli, E., and Iannello, G. (2008). A supervised pattern recognition approach for human movement onset detection. In: 21st IEEE International Symposium on Computer-Based Medical Systems, S. Puuronen, M. Pechenizkiy, A. Tsymbal and D. J. Lee, eds (Jyvaskyla, Finland), pp. 566–571.
Van Dijck, G., Van Hulle, M. M., and Van Vaerenbergh, J. (2007). A novel criterion for onset detection: differential information redundancy with application to human movement initiation. In: 7th IEEE International Conference on Data Mining, N. Ramakrishnan, O. R. Zaiane, Y. Shi, C. W. Clifton and X. D. Wu, eds (Omaha, NE), pp. 673–678.