
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Neurosci., 19 May 2023
Sec. Visual Neuroscience
Volume 17 - 2023 | https://doi.org/10.3389/fnins.2023.1191574
This article is part of the Research TopicNeuroscience-driven Visual RepresentationView all 12 articles
In this study, a multiple-constraint estimation algorithm is presented to estimate the 3D shape of a 2D image sequence. Given the training data, a sparse representation model with an elastic net, i.e., l1−norm and l2−norm constraints, is devised to extract the shape bases. In the sparse model, the l1−norm and l2−norm constraints are enforced to regulate the sparsity and scale of coefficients, respectively. After obtaining the shape bases, a penalized least-square model is formulated to estimate 3D shape and motion, by considering the orthogonal constraint of the transformation matrix, and the similarity constraint between the 2D observations and the shape bases. Moreover, an Augmented Lagrange Multipliers (ALM) iterative algorithm is adopted to solve the optimization of the proposed approach. Experimental results on the well-known CMU image sequences demonstrate the effectiveness and feasibility of the proposed model.
As an important component of computer vision, 3D shape reconstruction has been widely used in many applications (Li et al., 2016, 2018; Adamkiewicz et al., 2022; Chiang et al., 2022; Fombona-Pascual et al., 2022; Jang et al., 2022; Lu et al., 2022; Nian et al., 2022a,b; Wang et al., 2022; Wen et al., 2022). Among the various 3D shape reconstruction methods, non-rigid structure from motion (NRSFM) offers a technique to simultaneously recover the 3D structures and motions of an object, by using the 2D landmarks in a series of images (Graßhof and Brandt, 2022; Kumar and Van Gool, 2022; Song et al., 2022). Nevertheless, NRSFM is still an underconstrained and challenging issue because of lacking any prior knowledge of 3D structure deformation.
To alleviate the uncertainty, the various constraints are exploited constantly. Bregler et al. (2000), proposed a low-rank constraint-based approach to decompose the observation matrix into a motion factor and a shape basis. In order to reduce the number of the unknown variables proposed by Bregler et al. (2000), a point trajectory approach was presented by Akhter et al. (2010) by using the predefined bases of discrete cosine transform (DCT). However, the high-frequency deformation cannot be reconstructed well via this trajectory representation because of the low-rank constraint. Gotardo and Martinez (2011) modeled a smoothly deforming 3D shape as a single point moving along a smooth time trajectory within a linear shape space. In addition to the low-rank constraint, the higher frequency DCT was adopted to capture the high-frequency deformation.
For the low-rank constraint methods, it is difficult to determine the optimal number of shape bases or trajectory bases. To solve this problem, a Procrustean normal distribution (PND) model was presented by Lee et al. (2013) to separate the motion and deformation components strictly, without any additional constraints or prior knowledge. The experimental results demonstrate the performance of PND. Subsequently, the Procrustean Markov Process (PMP) algorithm was proposed by Lee et al. (2014), by combing in a first-order Markov model representing the smoothness between two adjacent frames with PND. Lee et al. (2016) reported a consensus of non-rigid reconstruction (CNR) approach to estimate 3D shapes based on local patches. However, the reconstruction performance of these methods may degrade significantly when the number of images becomes small, especially for a single image.
Referring to the active shape model (Cootes et al., 1995), a limb length constraint-based approach was presented by Wang et al. (2014) to estimate the 3D shape of an object from a single 2D image, by solving a l1−norm minimization problem. Zhou et al. (2013) proposed a sparse representation-based convex relaxation approach (CRA) to guarantee global optimality. The shape bases were extracted from a given training data by using a sparse representation model. The corresponding coefficients were obtained by adopting a convex relaxation assumption. A prominent advantage of CRA is that the algorithm can deal with a single image.
To further enhance the performance of the CRA algorithm, a multiple-constraint-based estimation approach is proposed to estimate the 3D shape of a 2D image sequence. Inspired by Zhang and Xing (2017), a dictionary learning model with l1−norm and l2−norm, i.e., elastic net, is constructed to extract more effective shape bases from a given training set. Referring to (Cheng et al., 2015), a penalized least-square model is constructed to estimate 3D shape and motion, by considering the orthogonal constraint of the transformation matrix and the similarity constraint between the 2D observations and the shape bases. In addition, an augmented Lagrange multipliers (ALM) iterative algorithm is developed to optimize the reconstruction model. The effectiveness and feasibility of the proposed algorithm are verified on the well-known CMU image sequences.
The rest of this article is organized as follows. A detailed description of the designed MCM-RR approach is introduced in Section 2. In Section 3, we report the experimental results. Finally, the article is concluded in Section 4.
According to the shape-space model by Zhou et al. (2013), the unknown 3D shape S ∈ ℝ3×p is constructed as a linear combination of a few shape bases , i.e.,
where p and K are the numbers of feature points and shape bases, respectively. The parameter ci and denote the coefficient and rotation matrix, respectively. In terms of the weak-perspective projection model, the corresponding 2D observations are modeled as a matrix W ∈ ℝ2×p,
The matrix can be represented as
where is the first two rows of Ri. Combining the orthogonal constraint, the matrix Mi satisfies
where is an identity matrix. The 3D shape, i.e., z−coordinates, and the motion parameters ci and Ri, are estimated by utilizing the observations W, i.e., the (x, y) coordinates of feature points.
In the proposed method, the shape bases B ∈ ℝ3K×p are extracted via a sparse model with the elastic net constraint. The B is the stacking of Bi(i = 1, ..., K). The matrix M are solved by a penalized least-square model. Given M, the parameters ci and Ri are derived via refinement decompose (Zhou et al., 2013). After obtaining ci, Ri and Bi, the unknown 3D shape can be computed via (1). The pseudocode of the proposed algorithm is summarized in 1. The pseudocode of the proposed algorithm is summarized in Algorithm 1.
For a given 3D training set A ∈ ℝ3p×F, i.e., the (x, y, z) coordinates of feature points of training images, the shape bases N ∈ ℝ3p×K and the coefficient matrix X ∈ ℝK×F can be obtained from the following sparse model:
where F and τ are the number of frames and a weight coefficient, respectively. The is the i-th column of N. The linear combination of l1−norm and l2−norm, called elastic net constraint, are enforced to constraint the sparsity of coefficients X as well as scale. The parameter λ is a trade-off parameter between the reconstruction error and the elastic net constraint.
For (5), we first compute the partial differentials of X and N, i.e.,
where IKF is a K × F identity matrix. Thereafter, X and N can be updated alternately as
where ϕ1 and ϕ2 are the step size of ∂X and ∂N, respectively. After convergence, the shape bases B can be obtained by a re-arrangement of N.
In terms of (2), the proposed penalized least-square model, including a relaxed orthogonality constraint (Zhou et al., 2013) and a similarity constraint (Cheng et al., 2015) can be formulated as
where Z ∈ ℝ2×3K is an auxiliary variable and , . The parameters α and β are used to weight the two regularization terms. The diagonal matrix D ∈ ℝ3K×3K is represented as
For the diagonal similarity matrix , the diagonal element di is computed as
where Π = [1, 0, 0;0, 1, 0], γ2 is the parameter of an exponential function.
With the ALM iterative algorithm, the penalized least-square model (10) can be reformulated as
where Y and μ are a dual variable and a weight of penalty term, respectively. In (13), there are four unknown variables , Z, Y, and μ. The solutions can be solved by the alternating direction method of multipliers (ADMM).
First, the optimal at the (t + 1)th iteration can be formulated as
where is the ith column-triple of . According to the proximal problem (Zhou et al., 2013), can be computed as
where . The operation denotes the projection of a vector to the unit l1−norm ball (Zhou et al., 2013).
Similarity, the optimal Z at the (t + 1)th iteration can be formulated as
We compute the one-order partial derivative of (16) with respect to Z and set it as zero. Thereafter, Zt+1 can be given by
Afterward, the optimal Y at the (t + 1)th iteration can be computed as
Given a weight τ, the coefficient μ at the (t + 1)th iteration can be given by
where
The iterations are repeated until
where ε is a small threshold value. After obtaining Mi, the unknown 3D shape can be reconstructed by refinement reconstruction (Zhou et al., 2013).
In the refinement reconstruction, we assume that the rotation matrices of each shape base are equal, denoted as . Thereafter, ci and can be estimated by the following rotation synchronization model
which can be solved via the alternating minimization (Zhou et al., 2013). Finally, the 3D shape S can be estimated after Mi is obtained.
The performance evaluation of the proposed 3D shape reconstruction model (denoted as MCM-RR) is carried out on eight motion categories (walk, run, jump, climb, box, dance, sit, and basketball) from the CMU motion capture dataset (Zhou et al., 2013). Figure 1 shows one frame of those eight categories.
In the experiments, the performance of several state-of-the-art 3D shape estimation methods are used to compare with the presented approach, including PND2 (Lee et al., 2013), CNR (Lee et al., 2016), PMP (Lee et al., 2014), and CRA (Zhou et al., 2013).
Mean error ξ of 3D shapes is calculated as the performance indicator to measure the estimation results:
where and are the reconstructed 3D structure and real 3D structure of tth frame, respectively.
Table 1 displays the mean and standard deviation (μ±σ) of reconstruction errors ξ of eight motion categories for the five methods, respectively. The best results are highlighted in red, whereas the second best is in blue.
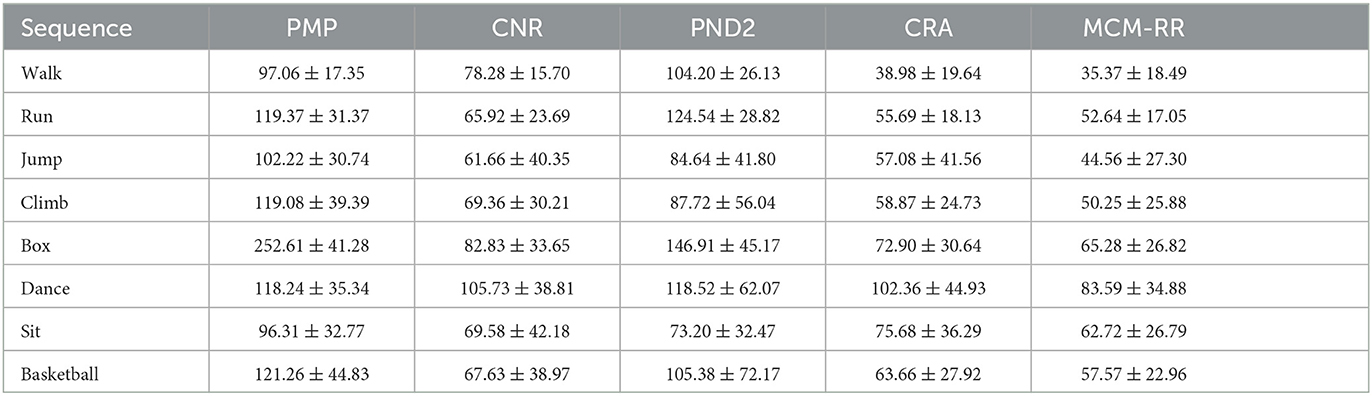
Table 1. Mean and standard deviation (μ±σ) of the 3D reconstruction errors ξ of eight motion categories for five methods.
Table 1 shows the estimation errors of the last two methods are clearly less than that of the first triple algorithms. Among eight categories, the mean reconstruction errors of MCM-RR are the lowest compared to CRA. Moreover, the standard deviations of MCM-RR are less than that of CRA among most categories. Therefore, compared to CRA, both accuracy and robustness are effectively improved for the proposed method.
Compared to CRA, the 3D reconstruction error decreased the percentage ξp(%) of MCM-RR can be computed as
From Table 2, we can see that the mean reconstruction errors of MCM-RR decreased about 5.48%∽21.93% compared to CRA. Thus, MCM-RR has a better 3D reconstruction performance than CRA for the eight motion categories.
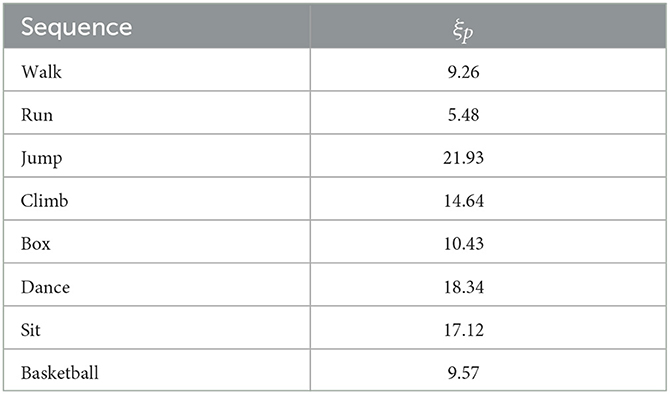
Table 2. Corresponding 3D reconstruction error decreasing percentage ξp(%) of MCM-RR compared to CRA for eight motion categories.
Take one frame of Jump as an example. Figure 2 displays a comparison of reconstructed shapes between MCM-RR and the other methods from three different viewpoints. From Figure 2, we can see that compared to other methods, most estimated shapes of MCM-RR are closer to real points than that of the other methods.

Figure 2. Comparisons of estimated shapes for single frame of Jump between MCM-RR and other methods from three different viewpoints. The symbol “°” denotes the observed real points, whereas “+” denotes reconstructed points.
In order to verify the feasibility of the proposed two strategies, the elastic net (denoted as CRA-EN) and similarity constraint (denoted as CRA-SC) are separately applied to the original algorithm CRA. Table 3 displays the mean and standard deviation (μ±σ) of 3D reconstruction errors ξ of eight motion categories for the four methods, respectively. Compared to CRA, both the elastic net and similarity constraint can decrease the 3D reconstruction errors. Therefore, the 3D reconstruction performance can be effectively improved once the two methods are simultaneously designed into CRA.
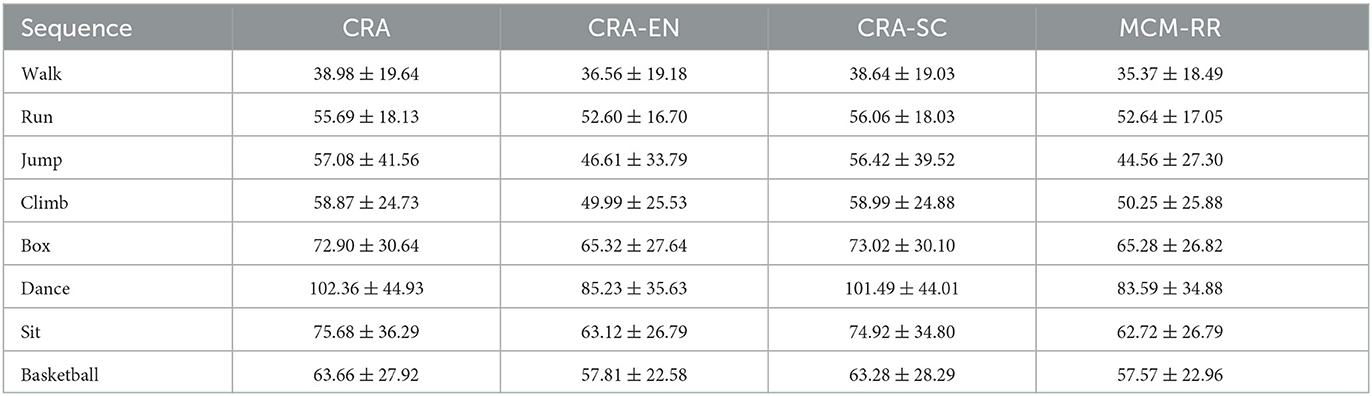
Table 3. Mean and standard deviation (μ±σ) of the 3D reconstruction errors ξ of eight motion categories for four methods.
In this study, a multiple-constraint algorithm is devised to estimate the 3D shape of a 2D image sequence. Experimental results on the well-known CMU datasets demonstrated that the proposed methods have higher accuracies and more robustness. Compared with CRA, the 3D reconstruction error is decreased by at least 5.48%.
The datasets used in this article is from a public datesets, and it can be found in the CMU Graphics Lab Motion Capture Database.
XC proposed the initial research idea, conducted the experiments, and wrote the manuscript. Z-LS supervised the work and advised the entire research process. YZ collected the dataset, analyzed the formal, and revised the manuscript. All authors reviewed and approved the final manuscript.
This work was supported by the National Natural Science Foundation of China (No. 61972002), the University Natural Science Research Project of Anhui Province (No. KJ2021A0180), Natural Science Foundation of Anhui Agricultural University (No. K2148001), Research Talents Stable Project of Anhui Agricultural University (No. rc482004), Key Laboratory of Intelligent Computing & Signal Processing, Ministry of Education (Anhui University) (No. 2020A002), Anhui Provincial Key Laboratory of Multimodal Cognitive Computation (Anhui University) (No. MMC202004), and the Anhui Provincial Natural Science Foundation (No. 2108085MC96).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Adamkiewicz, M., Chen, T., Caccavale, A., Gardner, R., Culbertson, P., Bohg, J., et al. (2022). Vision-only robot navigation in a neural radiance world. IEEE Robot. Automat. Lett. 7, 4606–4613. doi: 10.1109/LRA.2022.3150497
Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2010). Trajectory space: a dual representation for nonrigid structure from motion. IEEE Trans. Pattern Anal. Mach. Intell. 33, 1442–1456. doi: 10.1109/TPAMI.2010.201
Bregler, C., Hertzmann, A., and Biermann, H. (2000). “Recovering non-rigid 3d shape from image streams,” in Proceedings IEEE Conference on Computer Vision and Pattern Recognition (Hilton Head, SC: IEEE), 690–696.
Cheng, J., Yin, F., Wong, D. W. K., Tao, D., and Liu, J. (2015). Sparse dissimilarity-constrained coding for glaucoma screening. IEEE Trans. Biomed. Eng. 62, 1395–1403. doi: 10.1109/TBME.2015.2389234
Chiang, F.-K., Shang, X., and Qiao, L. (2022). Augmented reality in vocational training: a systematic review of research and applications. Comput. Hum. Behav. 129, 107125. doi: 10.1016/j.chb.2021.107125
Cootes, T. F., Taylor, C. J., Cooper, D. H., and Graham, J. (1995). Active shape models-their training and application. Comput. Vis. Image Understand. 61, 38–59.
Fombona-Pascual, A., Fombona, J., and Vicente, R. (2022). Augmented reality, a review of a way to represent and manipulate 3d chemical structures. J. Chem. Inform. Model. 62, 1863–1872. doi: 10.1021/acs.jcim.1c01255
Gotardo, P. F., and Martinez, A. M. (2011). Computing smooth time trajectories for camera and deformable shape in structure from motion with occlusion. IEEE Trans. Pattern Anal. Mach. Intell. 33, 2051–2065. doi: 10.1109/TPAMI.2011.50
Graßhof, S., and Brandt, S. S. (2022). “Tensor-based non-rigid structure from motion,” in Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition (Waikoloa, HI: IEEE), 3011–3020.
Jang, H., Sedaghat, S., Athertya, J. S., Moazamian, D., Carl, M., Ma, Y., et al. (2022). Feasibility of ultrashort echo time quantitative susceptibility mapping with a 3d cones trajectory in the human brain. Front. Neurosci. 16, 1033801. doi: 10.3389/fnins.2022.1033801
Kumar, S., and Van Gool, L. (2022). “Organic priors in non-rigid structure from motion,” in Proceedings of the European Conference on Computer Vision (Springer), 71–88.
Lee, M., Cho, J., Choi, C.-H., and Oh, S. (2013). “Procrustean normal distribution for non-rigid structure from motion,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Portland, OR: IEEE), 1280–1287.
Lee, M., Cho, J., and Oh, S. (2016). “Consensus of non-rigid reconstructions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE), 4670–4678.
Lee, M., Choi, C.-H., and Oh, S. (2014). “A procrustean markov process for non-rigid structure recovery,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Columbus, OH: IEEE), 1550–1557.
Li, T., Cheng, B., Ni, B., Liu, G., and Yan, S. (2016). Multitask low-rank affinity graph for image segmentation and image annotation. ACM Trans. Intell. Syst. Technol. 7, 1–18. doi: 10.1145/2856058
Li, T., Wang, Y., Hong, R., Wang, M., and Wu, X. (2018). PDisVPL: probabilistic discriminative visual part learning for image classification. IEEE MultiMedia 25, 34–45. doi: 10.1109/MMUL.2018.2873499
Lu, W., Li, Z., Li, Y., Li, J., Chen, Z., Feng, Y., et al. (2022). A deep learning model for three-dimensional nystagmus detection and its preliminary application. Front. Neurosci. 16, 930028. doi: 10.3389/fnins.2022.930028
Nian, F., Li, T., Bao, B.-K., and Xu, C. (2022a). Relative coordinates constraint for face alignment. Neurocomputing 395, 119–127. doi: 10.1016/j.neucom.2017.12.071
Nian, F., Sun, J., Jiang, D., Zhang, J., Li, T., and Lu, W. (2022b). Predicting dose-volume histogram of organ-at-risk using spatial geometric-encoding network for esophageal treatment planning. J. Ambient Intell. Smart Environ. 14, 25–37. doi: 10.3233/AIS-210084
Song, J., Patel, M., Jasour, A., and Ghaffari, M. (2022). A closed-form uncertainty propagation in non-rigid structure from motion. IEEE Robot. Automat. Lett. 7, 6479–6486. doi: 10.1109/LRA.2022.3173733
Wang, C., Wang, Y., Lin, Z., Yuille, A. L., and Gao, W. (2014). “Robust estimation of 3d human poses from a single image,” in Proceedings of the IEEE conference on Computer Vision and Pattern Recognition (Columbus, OH: IEEE), 2361–2368.
Wang, T., Chen, B., Zhang, Z., Li, H., and Zhang, M. (2022). Applications of machine vision in agricultural robot navigation: a review. Comput. Electron. Agric. 198, 107085. doi: 10.1016/j.compag.2022.107085
Wen, X., Zhou, J., Liu, Y.-S., Su, H., Dong, Z., and Han, Z. (2022). “3d shape reconstruction from 2d images with disentangled attribute flow,” in Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition (New Orleans, LA: IEEE), 3803–3813.
Zhang, S., and Xing, W. (2017). “Object tracking with adaptive elastic net regression,” in Proceedings of the IEEE International Conference on Image Processing (Honolulu, HI: IEEE), 2597–2601.
Keywords: non-rigid structure from motion, elastic net, similarity constraint, Augmented Lagrange multipliers, 3D reconstruction
Citation: Chen X, Sun Z-L and Zhang Y (2023) 3D shape reconstruction with a multiple-constraint estimation approach. Front. Neurosci. 17:1191574. doi: 10.3389/fnins.2023.1191574
Received: 22 March 2023; Accepted: 17 April 2023;
Published: 19 May 2023.
Edited by:
Fudong Nian, Hefei University, ChinaReviewed by:
Shengsheng Qian, Chinese Academy of Sciences (CAS), ChinaCopyright © 2023 Chen, Sun and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhan-Li Sun, emhsc3VuMjAwNkAxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.