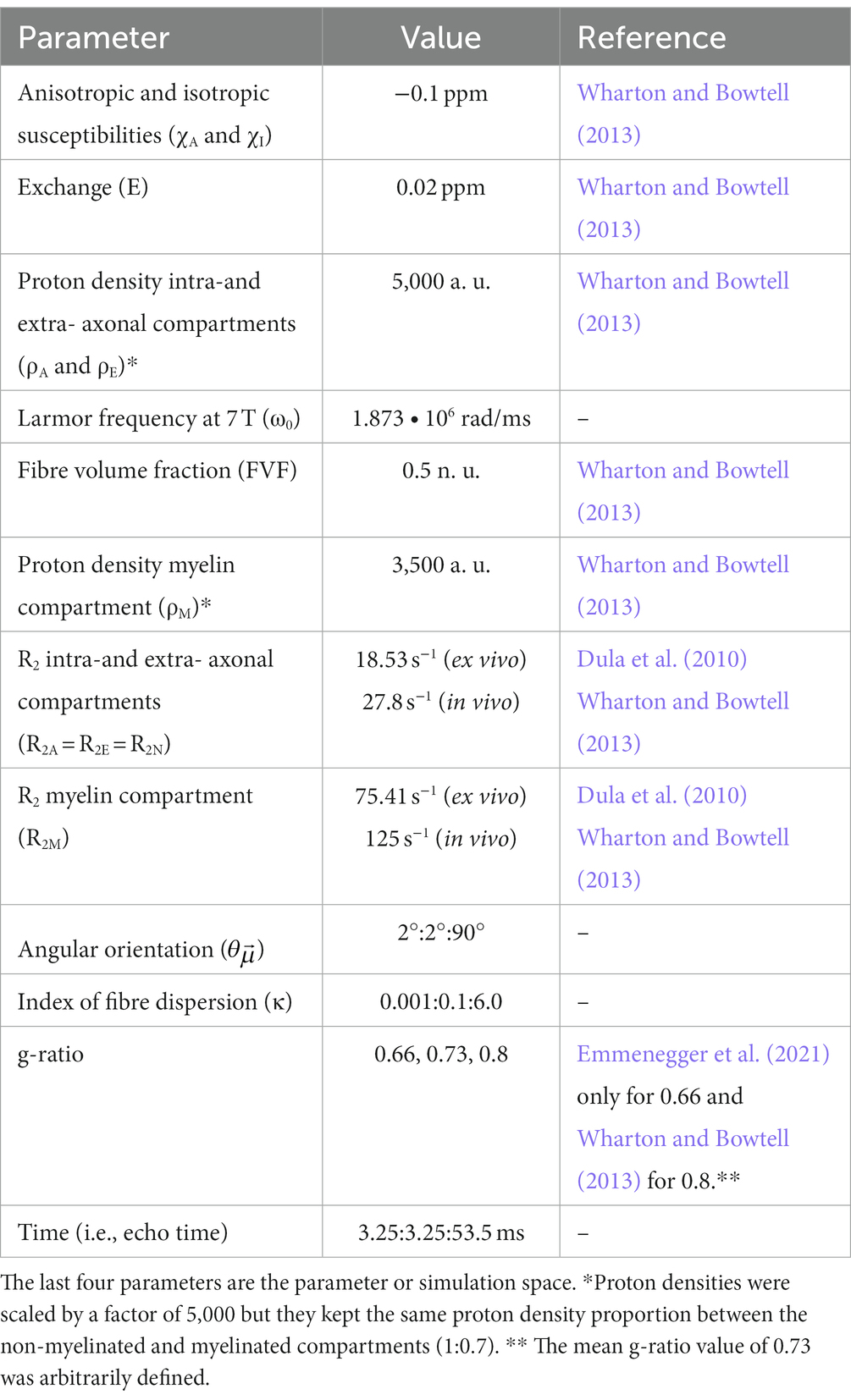
- 1Department of Systems Neurosciences, University Medical Center Hamburg-Eppendorf, Hamburg, Germany
- 2Berlin Ultrahigh Field Facility (B.U.F.F.), Max-Delbrueck-Center for Molecular Medicine in the Helmholtz Association, Berlin, Germany
- 3Paul Flechsig Institute – Center for Neuropathology and Brain Research, University of Leipzig, Leipzig, Germany
- 4Department of Neurophysics, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
- 5Wellcome Centre for Human Neuroimaging, UCL Queen Square Institute of Neurology, University College London, London, United Kingdom
- 6Felix Bloch Institute for Solid State Physics, Faculty of Physics and Earth Sciences, Leipzig University, Leipzig, Germany
- 7Max Planck Research Group MR Physics, Max Planck Institute for Human Development, Berlin, Germany
The effective transverse relaxation rate (R2*) is sensitive to the microstructure of the human brain like the g-ratio which characterises the relative myelination of axons. However, the fibre-orientation dependence of R2* degrades its reproducibility and any microstructural derivative measure. To estimate its orientation-independent part (R2,iso*) from single multi-echo gradient-recalled-echo (meGRE) measurements at arbitrary orientations, a second-order polynomial in time model (hereafter M2) can be used. Its linear time-dependent parameter, β1, can be biophysically related to R2,iso* when neglecting the myelin water (MW) signal in the hollow cylinder fibre model (HCFM). Here, we examined the performance of M2 using experimental and simulated data with variable g-ratio and fibre dispersion. We found that the fitted β1 can estimate R2,iso* using meGRE with long maximum-echo time (TEmax ≈ 54 ms), but not accurately captures its microscopic dependence on the g-ratio (error 84%). We proposed a new heuristic expression for β1 that reduced the error to 12% for ex vivo compartmental R2 values. Using the new expression, we could estimate an MW fraction of 0.14 for fibres with negligible dispersion in a fixed human optic chiasm for the ex vivo compartmental R2 values but not for the in vivo values. M2 and the HCFM-based simulations failed to explain the measured R2*-orientation-dependence around the magic angle for a typical in vivo meGRE protocol (with TEmax ≈ 18 ms). In conclusion, further validation and the development of movement-robust in vivo meGRE protocols with TEmax ≈ 54 ms are required before M2 can be used to estimate R2,iso* in subjects.
1. Introduction
The effective transverse relaxation rate (R2* = 1/T2*) is a nuclear magnetic resonance (NMR) relaxation property (Tofts, 2004) that enables non-invasive characterisation of the microstructure of the human brain (MacKay et al., 2006; Does, 2018; Weiskopf et al., 2021). The microstructural sensitivity of R2* makes it particularly interesting for neuroscience and clinical research studies (Langkammer et al., 2010; Draganski et al., 2011; Callaghan et al., 2014; Kirilina et al., 2020). This is because R2* is sensitive not only to free and myelin water pools in the brain (MacKay et al., 2006; Dula et al., 2010; Weiskopf et al., 2021) but also to microscopic perturbations in the main magnetic field ( ) (Chavhan et al., 2009). These microscopic perturbations are caused by the different magnetic susceptibilities of biological structures (Duyn and Schenck, 2017) like the diamagnetic myelin sheath (Kucharczyk et al., 1994; Duyn, 2014; Lee et al., 2017; Alonso-Ortiz et al., 2018) and paramagnetic iron deposits in glial cells (Ordidge et al., 1994; Li et al., 2009; Yao et al., 2009). Moreover, it has been shown that R2* is also strongly dependent on the angular orientation of the white matter fibre tracts relative to (Lee et al., 2011, 2012) confounding the mapping of R2* to the underlying microstructure. The impact of this confounding factor can be attenuated by decomposing the angular orientation dependence of R2* into an isotropic, i.e., angular-independent component (R2,iso*), and an angular-dependent component using either complex gradient-recalled echo (GRE) acquisitions at several angular orientations (Oh et al., 2013; Wharton and Bowtell, 2013; Rudko et al., 2014) or hybrid diffusion weighted imaging (DWI) and GRE acquisitions with reduced numbers of angular orientations (Gil et al., 2016). However, both methods are impractical for clinical research due to the constrained and inconvenient positioning of the patient’s head in the radiofrequency receiver coil needed to achieve the required distinct angular orientations.
A practical approach to estimate R2,iso* was recently proposed by Papazoglou et al. (2019). They showed that R2,iso* can be estimated from the magnitude signal of a single multi-echo GRE (meGRE) measurement using a second-order model in time hereafter denoted as M2. The model was derived from a two-pool system based on the hollow cylinder fibre model (HCFM) (Wharton and Bowtell, 2012, 2013). In M2, the linear component in time (β1) is a proxy for R2,iso* and the orientation-dependent part is regressed out by the second-order term in time (β2). Although M2 is just an approximation of the original HFCM multi-compartment model and thus less accurate, it is, to our knowledge, the only way of estimating R2,iso* from magnitude-only meGRE data with a single orientation of the head.
Another advantage of the M2 is its relation to the HCFM model, allowing for direct translation of the M2-proxy for R2,iso* (i.e., the β1 parameter) into microscopic tissue properties. However, a drawback of this model is the assumption in M2 that the signal contribution of the myelin water can be neglected, limiting the microscopic interpretability of the estimated β1 parameter. For example, the M2-based prediction of β1 depends only on the transverse relaxation rate of the free water molecules of the non-myelinated compartments (R2N) and thus is independent of any changes associated with the myelin water signal or the myelin water fraction (MWF). This model’s prediction could contradict experimental observations reporting that R2* (and presumably R2,iso*) is linearly dependent on MWF (see Lee et al., 2017; Kirilina et al., 2020; Milotta et al., 2023). Moreover, M2 assumes that axonal fibres are perfectly aligned or even described by one representative axon. However, most of the fibre bundles in the human brain possess a diverse range of topographies, i.e., show fanning and bending, or mildly to acute crossing (e.g., Schmahmann et al., 2007, 2009; Jeurissen et al., 2019) and different levels of relative myelination (e.g., Mohammadi et al., 2015). Besides that, the performance of M2 in estimating R2,iso* via β1 has only been tested with data acquired at very long maximum echo times up to ≈ 54 ms (Papazoglou et al., 2019). Such a long maximum echo time is unusual for in vivo meGRE measurements with whole-brain coverage (Weiskopf et al., 2013; Ziegler et al., 2019), because it increases the total scan time as well as the propensity for bulk and physiological motion.
This work explores the potential and pitfalls of using M2 to estimate R2,iso* via β1, from a single-orientation meGRE, while varying biological fibre properties and maximum echo times. To this end, we use simulated (hereafter in silico) data and ex vivo MRI. The in silico data are simulated using a three-pool system based on the HCFM to generate realistic meGRE datasets from an ensemble of myelinated axons, for which the ground truth biophysical parameters (i.e., g-ratio, fibre dispersion and angular orientation) are known and can be varied. The ex vivo dataset combines high-resolution DWI and multi-orientation meGRE imaging of a human optic chiasm to generate gold-standard datasets where the fibre orientation and dispersion can be estimated. Both datasets are used to perform the following analyses: First, we assess the performance of M2 to estimate R2,iso* via β1 for varying g-ratio values and fibre dispersions. Second, we assess the microstructural interpretability of β1. To this end, we test the model-prediction of M2 that β1 is independent of MWF by evaluating the deviation between the biophysically predicted β1 by M2 and the fitted β1 using the in silico data. Additionally, we perform the same comparison to the fitted β1 as above using a novel heuristic expression that incorporates the MWF dependence into the predicted β1. Third, we use the heuristic expression for β1 to calculate MWF from the β1 of the ex vivo data for two sets of compartmental R2 values, i.e., in vivo and ex vivo configurations. And fourth, we assess the performance of M2 to estimate R2,iso* via β1 for different echo times ranges.
2. Background
2.1. Overview of the hollow cylinder fibre model and the approximated log-quadratic model
The HCFM (Wharton and Bowtell, 2012, 2013) proposes an analytical approximation describing the dependence of the GRE signal on the angular orientation ( ) defined as the angle between the main magnetic field and the hollow-cylinder fibre ( ). This approximation establishes that the total MR signal comes from water molecules in an infinitely long and perfectly aligned hollow cylinder affected by the diamagnetic myelin sheath (Liu, 2010). The diamagnetic myelin sheath magnetically perturbs the water molecules in three distinct compartments: (1) the intra-axonal (SA), (2) myelin (SM) and (3) extra-cellular (SE) compartments (details in Supplementary material, section 2). When the signal of the water molecules in the myelin compartment is neglected (i.e., at long echo times: TE > T2 of myelin, T2M), the signal magnitude of the HCFM can be approximated by a log-quadratic model (M2) in time (Papazoglou et al., 2019):
where are the model parameters. In this model, the slope β1 is considered as a proxy for R2,iso* because it does not possess any dependence, whereas β2 contains all the dependent information of R2* (detailed derivation can be found in section 4, Supplementary Equations S17b,c).
Classically, R2* is estimated by the slope (α1) of the log-linear model (M1) (Elster, 1993):
where α1 is a function of R2,iso* and the dependent components of R2* e.g., (see Lee et al., 2011, 2012).
In this model, the offset parameter captures a large portion of the remaining information like contrast parameters, e.g., magnetisation transfer and longitudinal relaxation rate; and experimental parameters, e.g., transmit field. For M2, we assume that behaves in an identical fashion, i.e., this parameter captures all the remaining information as , even though this assumption is not explicitly shown in the HCFM [see Discussion in Wharton and Bowtell (2013)].
2.2. Myelin independence of β1 parameter as predicted by the log-quadratic model (M2)
The slope β1 of M2, which is a proxy for R2,iso*, is derived from the HCFM by assuming a two-pool system in the slow-exchange regime: a fast decaying water pool consisting of the myelin water with a relaxation rate and a non-myelin water pool with a relaxation rate . In this work, we assumed that this non-myelin water pool consisted of the intra and extra cellular water, based on the findings and simplifications of Dula et al. (2010) and Wharton and Bowtell (2013). The only source of dephasing in the HCFM is caused by the magnetic properties of the hollow-cylinder fibre. All potential other perturbers are ignored (e.g., non-local effects of susceptibility inhomogeneities due to cavities, vessels, iron molecules, and diffusion) as well as other anisotropic magnetic properties, e.g., the magnetisation transfer effects (Pampel et al., 2015), influencing transverse relaxation rate (Knight et al., 2017; Birkl et al., 2021; Tax et al., 2021) or longitudinal relaxation rate (Labadie et al., 2014; Schyboll et al., 2019; Chan and Marques, 2020; Kleban et al., 2021). In white matter, this simplification seems to be reasonable since the HCFM describes the orientation dependence of the meGRE signal to a great extend (Wharton and Bowtell, 2012). Consequently, in the approximation of M2 (Eq. 1), the predicted parameter (hereafter , where nm represents ‘no myelin contribution’) is given by the transverse relaxation rate of the non-myelin water pool ( ):
We hypothesise here that for realistic tissue composition where the myelin compartment cannot be neglected (i.e., g-ratio equal to or smaller than 0.8), Eq. 3 is invalid. This hypothesis is supported by previous observations showing that R2* (and presumably R2,iso*) depends on the myelin water fraction, MWF (e.g., Lee et al., 2017; Weber et al., 2020; Milotta et al., 2023).
Here, we propose an alternative heuristic biophysical expression of the predicted β1 parameter (hereafter , where m denotes ‘with myelin contribution’):
under the assumption that the proton densities of the non-myelinated compartments are equal (i.e., ρA = ρE ≡ ρN) and the volume of the non-myelinated compartment is defined as one minus the myelin compartment’s volume (= 1 – VM). The heuristic expression in Eq. 4 can be analytically derived under the condition that TE < T2 of the myelin compartment based on the HCFM (details can be found in section 4, Supplementary Equation S18).
In this case, can be re-written as a function of the myelin water fraction (MWF, Supplementary Equation S19a, section 4), R2N and R2M:
Consequently, the MWF can be calculated by re-ordering Eq. 5 as a function of the R2’s values:
Based on our hypothesis, we expect that the heuristic expression for can better describe the fitted β1 when varying the g-ratio, and thus is a better proxy of R2,iso*.
3. Materials and methods
This section explains the approaches used for data acquisition, data analysis and for comparing the results obtained from the ex vivo data and the findings derived from the in silico data.
3.1. Ex-vivo: optic chiasm
3.1.1. Sample and data acquisition
A human optic chiasm (OC) from a patient without any diagnosed neurological disorder was measured (male, 59 years, multi-organ failure, 48 h postmortem interval, ~80 days of fixation in phosphate buffered saline (PBS) pH 7.4 with 0.1% sodium acide NaN3 containing 3% paraformaldehyde +1% glutaraldehyde) with prior informed consent (Ethical approval #205/17-ek). Two MR techniques were used: multi-echo GRE (meGRE) and diffusion-weighted MRI (dMRI). The meGRE data used here have been in parts used already in Papazoglou et al. (2019).
All meGRE acquisitions were performed on a 7 T Siemens Magnetom MRI scanner (Siemens Healthcare GmbH, Erlangen, Germany) using a custom 2-channel transmit/receive circularly polarised (CP) coil with a diameter of 60 mm. The OC sample was fixed within an acrylic sphere of 60 mm diameter filled with agarose (1.5% Biozym Plaque low melting Agarose, Merck, Germany) dissolved in PBS (pH 7.4 + 0.1% sodium acide) and scanned at sixteen orientations (covering a solid angle, with azimuthal and elevation angles from 0° to 90°, Figure 1A) using the 3D meGRE MRI (hereafter: GRE dataset). For each angular meGRE measurement (Figure 1B), sixteen echoes were acquired at equally spaced echo times (TE) ranging from 3.4 to 53.5 ms (increment 3.34 ms) with a repetition time (TR) of 100 ms, a field of view (FoV) of (39.00 mm)3, a matrix size of 1123, resulting in an isotropic voxel resolution of (0.35 mm)3, non-selective RF excitation with a flip angle of 23° and a gradient readout bandwidth of 343 Hz/px.
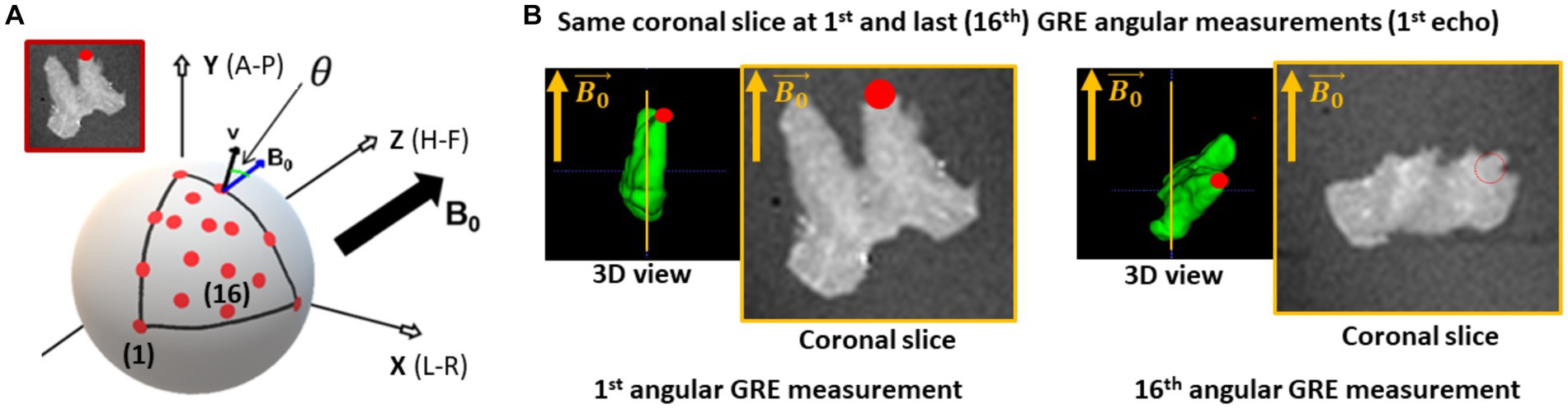
Figure 1. Acquisition of the multi-angular multi-echo gradient recalled echo (meGRE) ex vivo data. (A) An illustration of the different angular measurements performed on the optic chiasm (OC) specimen. The red dots show the position of the optical tracts (see inset) for the different measurements. The different coordinates (spatial, x-y-z and anatomical, anterior-head-right, A-H-R) are shown (adapted illustration from Papazoglou et al., 2019). (B) Illustration of the first echo meGRE image acquired at the first and last angular measurement. The 3D view shows the specimen position to the main magnetic field and the position of the optical tract (red dot). The yellow line shows the same coronal slice image.
The multi-shell dMRI data (hereafter: dMRI dataset), suitable for NODDI analysis, were acquired, three months later, on a 9.4 T small animal MR system (Bruker Biospec 94/20; Bruker Biospin, Ettlingen, Germany) using a 2-channel receiver cryogenically cooled quadrature transceiver surface RF coil (Bruker Biospin, Ettlingen, Germany) and a gradient system with Gmax = 700 mT/m per gradient axis. This dataset was acquired with a slice-selective (2D) pulsed-gradient spin-echo (PGSE) technique, consisting of four diffusion-weighting shells (number of directions) of b = 1,000 s/mm2 (60), 4,000 s/mm2 (60), 8,000 s/mm2 (60) and 12,000 s/mm2 (60) with 35 non-diffusion-weighted volumes (~ 0 s/mm2). The fixed diffusion parameters were diffusion time Δ = 13 ms, diffusion gradient duration δ = 6 ms. The remaining sequence parameters were TE = 27 ms, TR = 30 s (to acquire all the slices), FoV = 20.75 × 16.00 × 12.50 mm3, matrix size = 83 × 64 × 50, isotropic voxel resolution = (0.25 mm)3, slice selective pulses with flip angles of 90° (excitation) and 180° (refocusing) and receiver bandwidth of 9,411 Hz/px.
Note that we used different MR systems for dMRI and meGRE measurements, because it was intended to use the optimal system for the respective measurement. The dMRI dataset was acquired on a Bruker Biospec with cryo-coil to take advantage of the scanner’s high gradient strength, allowing for acquisition of high-resolution images at optimal b-values for ex vivo tissue [up to 12,000 s/mm2 (Roebroeck et al., 2018)]. Moreover, we used a TR of 30 s for dMRI measurements to ensure full magnetisation recovery and to reduce possible biases for diffusion analysis (section 3.1.2). The meGRE data was acquired on a human 7 T Siemens Magnetom MRI scanner because an optimised meGRE sequence was available on this system, including a self-built ex vivo sample coil.
Since the tissue sample was already fixed and immersed in PBS and sodium acide solution to preserve the tissue quality (Minassian and Huang, 1979), the time between the acquisitions (less than 2 weeks) did not affect the tissue quality.
3.1.2. Dispersion and mean fibre orientation estimation from dMRI dataset
To incorporate the voxel-wise information regarding the angular orientation of the fibres to and fibre’s dispersion, the dMRI datasets were corrected using a simple rigid-body registration to remove a potential drift of the sample during measurements. The dMRI data were analysed with two diffusion models: Neurite Orientation Dispersion and Density Imaging (NODDI) (Zhang et al., 2012) and Diffusion Tensor Imaging (DTI) (Basser et al., 1994). The NODDI toolbox was adjusted for ex vivo analysis (Wang et al., 2019) and used all the diffusion shells. The main neurite (hereafter fibre) orientation ( ), a measure of the fibre dispersion (κ), and fibre density (volume fraction of the intracellular compartment, ICVF) maps were estimated from this analysis. The DTI model used the first two diffusion shells (b-values: 1000 s/mm2 and 4,000 s/mm2) and was used only for estimating the fractional anisotropy (FA) map, which in turn was used only for diffusion-to-GRE coregistration (section 3.1.3). Note that eddy currents were small in this dMRI data because the data were acquired with a small FoV in the gradient-coil centre using the standard Bruker gradient coil. Moreover, the cryo-coil provided sufficiently high SNR values for unbiased dMRI model parameters (the mean SNR across the specimen was approximately 57 for the b-value = 0 s/mm2 images). The SNR was calculated by dividing the MR signal by the standard deviation of the background voxels of its corresponding image (Kellman and McVeigh, 2005).
3.1.3. Coregistration of the GRE angular measurements and dMRI results
To establish a voxel-to-voxel relationship between the meGRE signal at different angular orientations and the properties estimated from dMRI, i.e., κ, and ICVF, we coregistered the angular meGRE measurements and the dMRI measurement. To this end, we estimated two sets of transformation matrices: first, transformation matrices that coregister the i-th angular measurements in GRE space, (with i = 2… 16, see Figure 2A); and second, a transformation matrix that coregisters from GRE space to dMRI space, (see Figure 2B). The coordinate system of GRE space was defined by the first meGRE angular measurement. This reference was chosen due to the alignment of the optical nerves to and following the procedure adopted in a previous study (Papazoglou et al., 2019). The meGRE coregistration and estimation of were performed using the 3D Slicer software1 (Fedorov et al., 2012), while the GRE-to-diffusion transformation was performed using the coregistration module in SPM 12.2
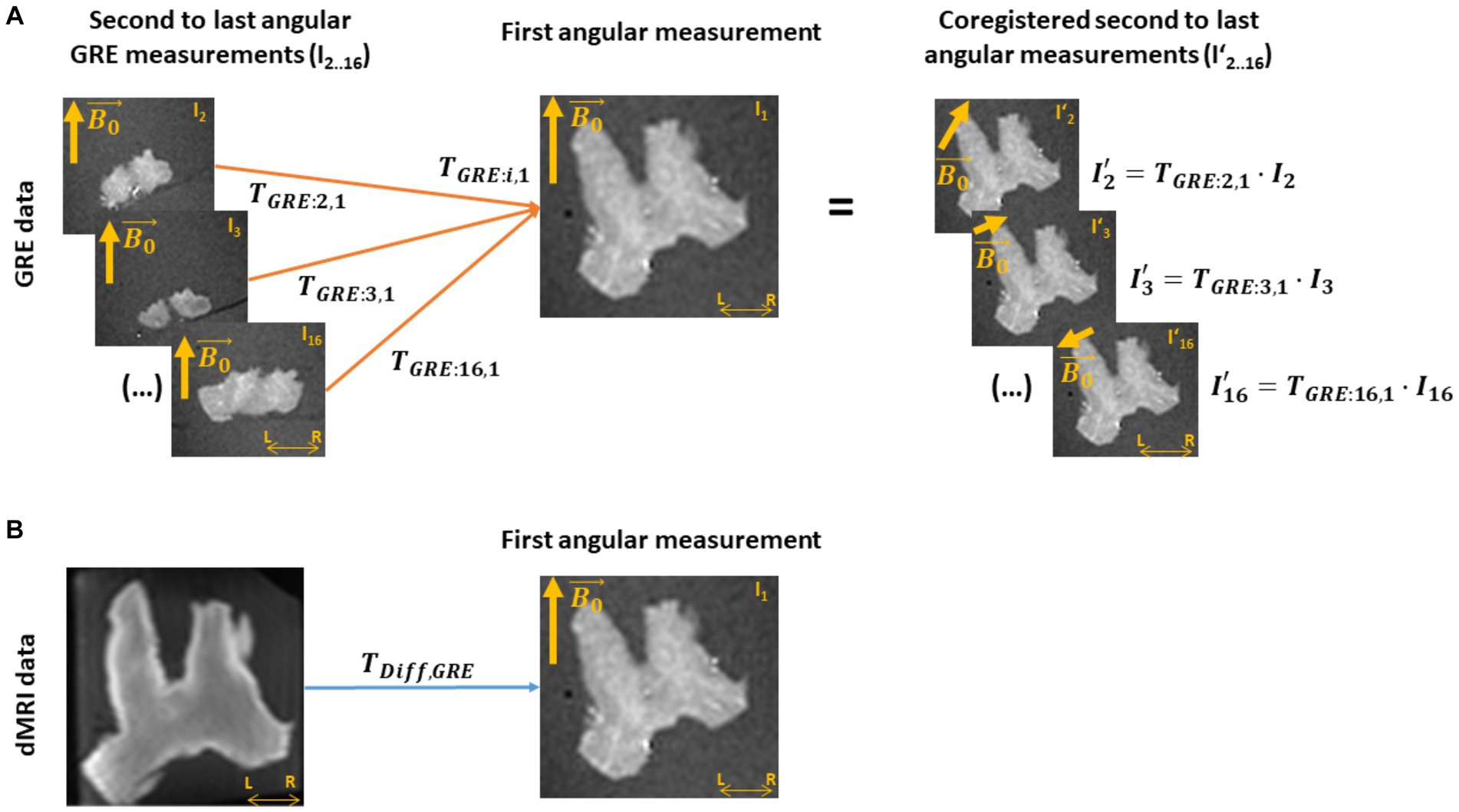
Figure 2. Coregistration of the ex vivo GRE and dMRI measurements. (A) A transformation matrix (TGRE) is obtained by coregistering all other multi-echo gradient-recall-echo (meGRE) datasets (I2.0.16) to the first measurement (I1, TGRE: i,1). This transformation matrices not only align, voxel-wise, the images of the meGRE datasets (I’2.0.16) to the first dataset, but also adjusts the directions of the main magnetic field ( ) per angular measurement to preserves their relative orientation with respect to the first meGRE dataset. (B) A transformation matrix (TDiff,GRE) is obtained by coregistering the diffusion MRI (dMRI) image to the first angular GRE measurement. This transformation will allow the coregistration of the NODDI analysis results to the GRE data.
3.1.4. Voxel-wise estimation of the angular orientation, , between fibres and
The angular orientation between fibres and for each meGRE angular measurement was calculated in dMRI space and the resulting maps mapped onto GRE space. For that, the arccosine of the inner product between and , i.e., was computed (Figure 3C). In this computation, is the resulting after the transformation from the i-th meGRE angular measurement to the first meGRE angular measurement ( ), and the transformation from GRE to dMRI space ( ) (Figure 3A). The main fibre direction was obtained by the map from the NODDI analysis (Figure 3B).
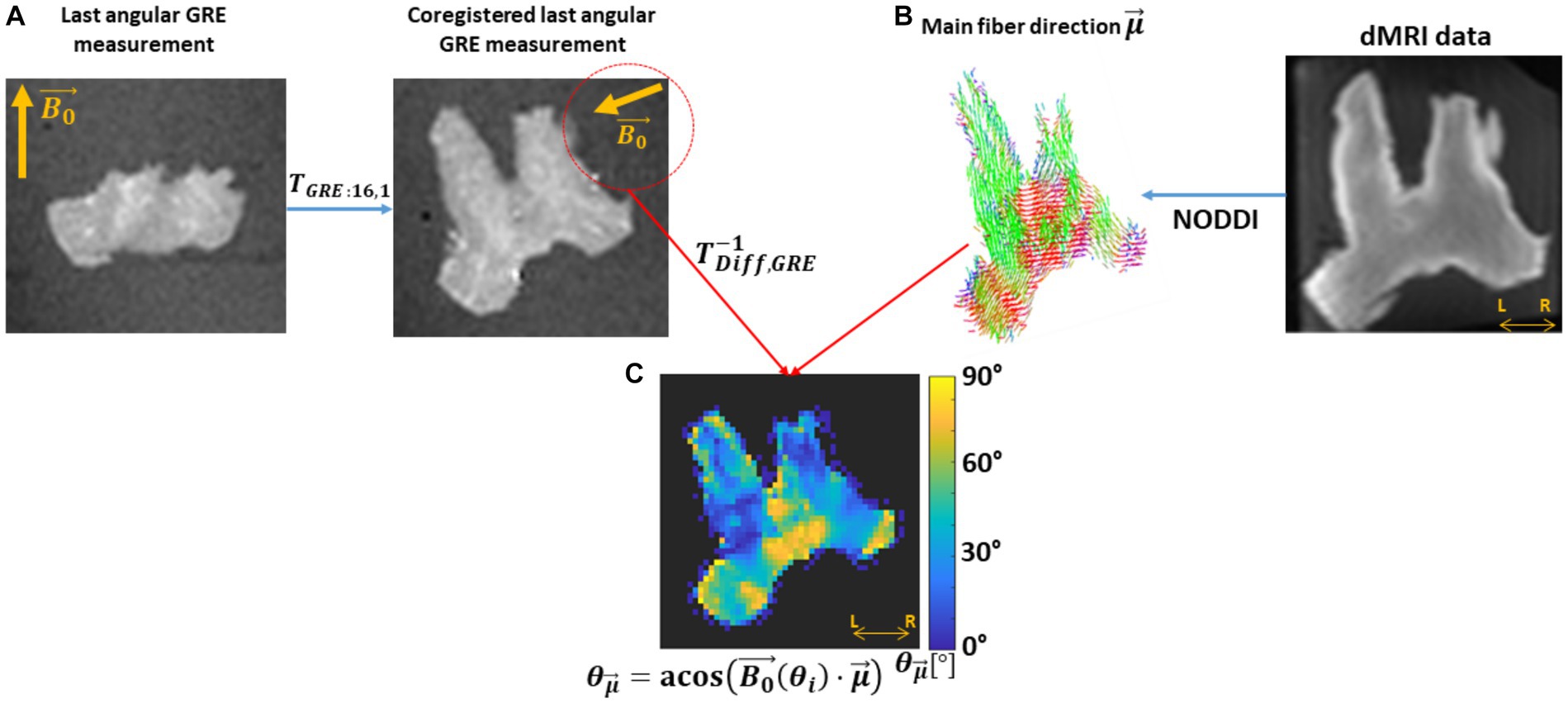
Figure 3. Estimation of the voxel-wise angular map. This estimation needed the B0 direction per angular GRE measurement ( ) in diffusion space and the main fibre direction. (A) The was estimated by applying to , first, the transformation matrix between GRE volumes (TGRE:i,1) and later from GRE-to-diffusion (T−1Diff,GRE). (B) The main fibre direction ( ) was acquired by analysing the dMRI data with the NODDI model. (C) Then, the voxel-wise per angular measurement was computed by the arccosine of the scalar product between the projected and the main diffusion direction ( ), . This sketch shows the steps for the last GRE angular measurement.
Note that was computed in dMRI space instead of GRE space to avoid undersampling and interpolation caused by transforming the dMRI-based to GRE space. These sources of error do not occur by transforming to dMRI space, i.e., computing , for each GRE angular measurement, since it is a global rather than a per-voxel measure. Finally, the maps together with the ICVF and κ maps (not shown in Figure 3) were transformed using . Exemplary maps in GRE space are shown in Supplementary Figure S1 (first row).
3.1.5. Masking and pooling the ex vivo data
Before analysis, the ex vivo data required further pre-processing to remove outliers and to ensure a robust assessment of the effect of fibre dispersion and on R2*. For that, the ex vivo data were masked using the coregistered ICVF map and later pooled across the sixteen coregistered meGRE angular measurements.
In this process, all voxels in the OC with an ICVF >0.8 were selected and pooled across all the meGRE angular measurements, hereafter referred to as cumulated data. The ICVF threshold was used because the extra-axonal space in the ex vivo specimen is reduced (e.g., Stikov et al., 2011). The application of this threshold reduced the number of voxels in the OC by 7.2% (~ 600 over 8,744 voxels). By pooling the data, the resulting cumulated data dependent on TE but also on from 0° to 90°, and on fibre dispersion assessed by κ from 0 to 6.
3.2. Simulated R2* signal decay from the HCFM
Multi-echo GRE signal decay was simulated as ground truth (hereafter, in silico data) to assess the impact on M2 of variable fibre orientation, dispersion and myelination (i.e., g-ratio). For that, we estimated averaged MR signals calculated from an ensemble of 1,500 hollow cylinders. The cylinders were evenly distributed on a sphere with defined spherical coordinates: an azimuthal angle φ rotating counter-clockwise from 0° to 359° starting aligned with the +X axis, and elevation angle θ rotating from 0° (+Z) to 180° (−Z). The signal contribution per hollow cylinder was modelled using the frequency-averaged signal equations from the HCFM for all the compartments including the myelin compartment (Supplementary Equations S1, S3, section 2).
In the simulation framework, three assumptions were made. First, the was fixed and oriented parallel to +Z (Figure 4A). Second, the approximated piece-wise function of DE in the SE signal was replaced by its analytical solution (Supplementary Equations S2b, S4, S7, S8, section 3; respectively), because a discontinuity in this piece-wise function was observed at the so-called critical time (Yablonskiy and Haacke, 1994; Wharton and Bowtell, 2013). See section 3 in Supplementary material for a detailed discussion. And third, we ignored the near-field effects between cylinders, therefore the total signal is the sum of all the complex signals from each cylinder as defined in Supplementary Equations S1–S3.
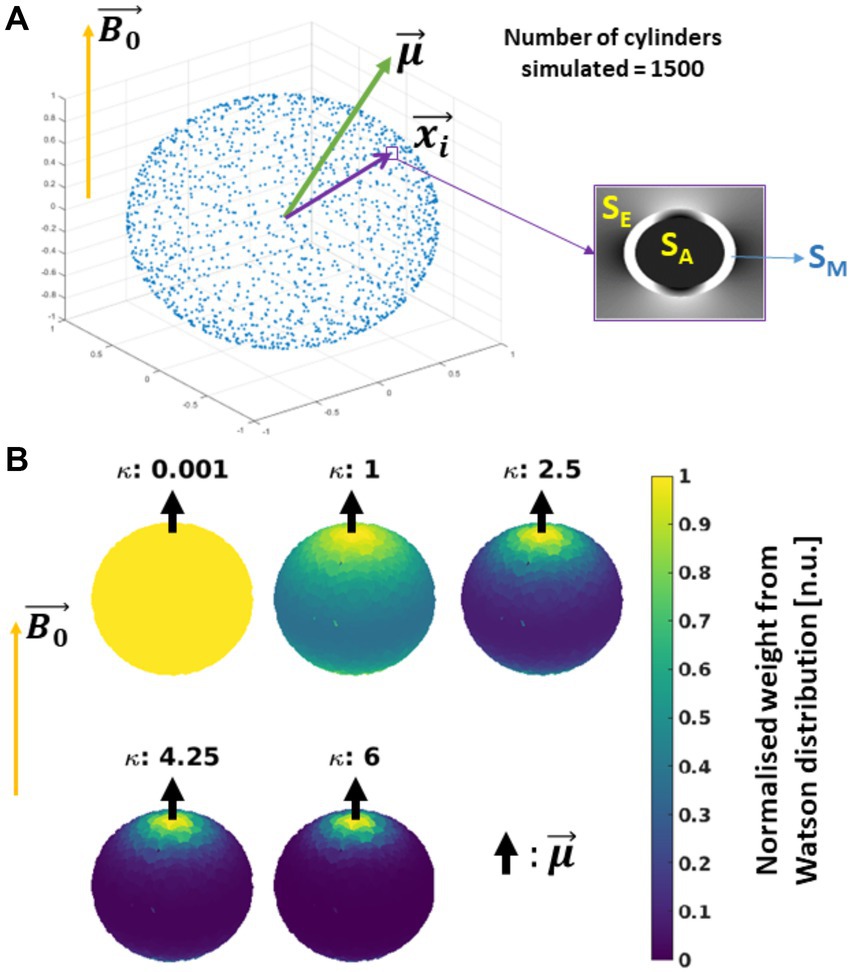
Figure 4. Schematics of the simulated in silico data: (A) Simulation: 1500 hollow cylinders, each of them defined by the vector , were distributed evenly on a sphere (see the blue dots). A mean orientation of the cylinders is defined, with the external magnetic field ( ) oriented parallel to the Z-axis. The signal contribution per cylinder was modelled using the Hollow Cylinder Fibre Model (HCFM) with the intra-axonal (SA), extra-axonal (SE) and myelin (SM) compartments (inset). (B) Addition of cylinder’s dispersion: the dispersion effect was added by weighting the signal coming from the cylinders by the parameter κ from the Watson distribution and (Eq. 8b). The parameter κ is limited from κ = 0 for isotropically dispersed to κ = infinity to fully parallel fibres. Here, is parallel to .
To incorporate the effect of fibre dispersion in the in silico data, the ensemble-average signal was calculated by weighting Sc with the Watson distribution (W) (Sra and Karp, 2013 and Eq. 8b). This weight from the Watson distribution was calculated using the position of each simulated cylinder, , and a mean fibre orientation , both defined with spherical coordinates (φ, θ) and ( , ), respectively (Figure 4A). For simplification, was restricted to an azimuthal angle of zero ( = 0°). Then, the analytical expression of the ensemble-average signal, SW, is defined as follows:
In Eq. 7b, () is the confluent hypergeometric function, which is the normalisation factor of the Watson distribution, and the exponent holds the norm of the inner product between each individual i-th cylinder and . The level of dispersion was modulated by the parameter κ (Zhang et al., 2012; Sra and Karp, 2013) as shown in Figure 4B for a few cases. It is important to note that the notation for the elevation angle of used here is equal to the one used to describe the fibre’s angular orientation in the ex vivo data (section 3.1.4). This is intentional since they stand for the same concept in both datasets. This simulation approach was used in previous conference publications [Fritz et al. (2020, 2021)].
With the ensemble averaged signal equation (Eq. 7a), a meGRE signal decay can be computed based on the relevant parameters listed in the following Table 1.
We tested the validity of M2 and its microstructural derivatives like MWF (Eq 6) for varying microstructural parameter settings. This included two different sets of compartmental R2 values (i.e., R2N and R2M) (Dula et al., 2010; Wharton and Bowtell, 2013). The sets represent two possible extremes of compartmental R2 values at 7 T: (1) ex vivo compartmental R2 values measured from an ex vivo rat spinal cord with similar tissue preparation procedure as the optic chiasm in this work [i.e., fixed with 4% PFA and hydrated in PBS (Dula et al., 2010)], and (2) in vivo compartmental R2 values obtained from in vivo human measurements (Wharton and Bowtell, 2013). The ex vivo compartmental R2 values are reported in the main manuscript whereas the in vivo compartmental R2 values are reported in the Supplementary material, Section 7.
Finally, each simulated meGRE signal decay was replicated 5,000 times with an additive Gaussian complex noise (Gudbjartsson and Patz, 1995) to approximate the SNR of the experimental ex vivo data (see Supplementary material, section 5). The experimental SNR was calculated by dividing the MR signal acquired at the first echo by the standard deviation of the background voxels of its corresponding image (Kellman and McVeigh, 2005), resulting in a mean SNR across the selected voxels of the OC of 112.
This simulation framework is publicly and freely available in Github.3
3.3. Data analysis
3.3.1. Data fitting and binning
The ex vivo data (section 3.1) and in silico data (each of 5,000 replicas per simulated meGRE signal decay, section 3.2) were analysed with the log-linear and log-quadratic models, M1 (Eq. 2) and M2 (Eq. 1), respectively. In both models, the α’s (α0 in arbitrary units, α1 in units of 1/s) from M1, and β’s (β0 in arbitrary units, β1 in units of 1/s and β2 in units of 1/s2) from M2, hereafter referred to as the α-parameters and β-parameters, were estimated. To fit the data, ordinary Least Square (OLS) optimization was used for both models in custom-made Matlab code. Three fittings were performed using three different meGRE subsets, that varied by their maximum TE (TEmax) values: TEmax = 54 ms (all 16 time points), TEmax = 36 ms (first 10 points) and TEmax = 18 ms (first 5 time points). The first meGRE subset with TEmax of 54 ms replicated the meGRE protocols of the ex vivo studies, while the meGRE subset with TEmax of 18 ms could be considered as a typical meGRE protocol for in vivo studies [at least with regards to the sample size and TE range used in the multi-parametric mapping protocol (Weiskopf et al., 2013)]. The meGRE subset with TEmax of 36 ms was chosen as an intermediate subset between both protocols.
To compare the α- and β-parameters between datasets as a function of fibre dispersion (κ) and , the fitted parameters were binned and averaged for the ex vivo cumulated data (section 3.1.5) and for the in silico data. The binning on the fitted parameters was performed to ensure: (1) a reduced effect size bias in the ex vivo cumulated data, given the unequal number of voxels at specific and κ (Figure 5); and (2) a better comparison between in silico and ex vivo data.
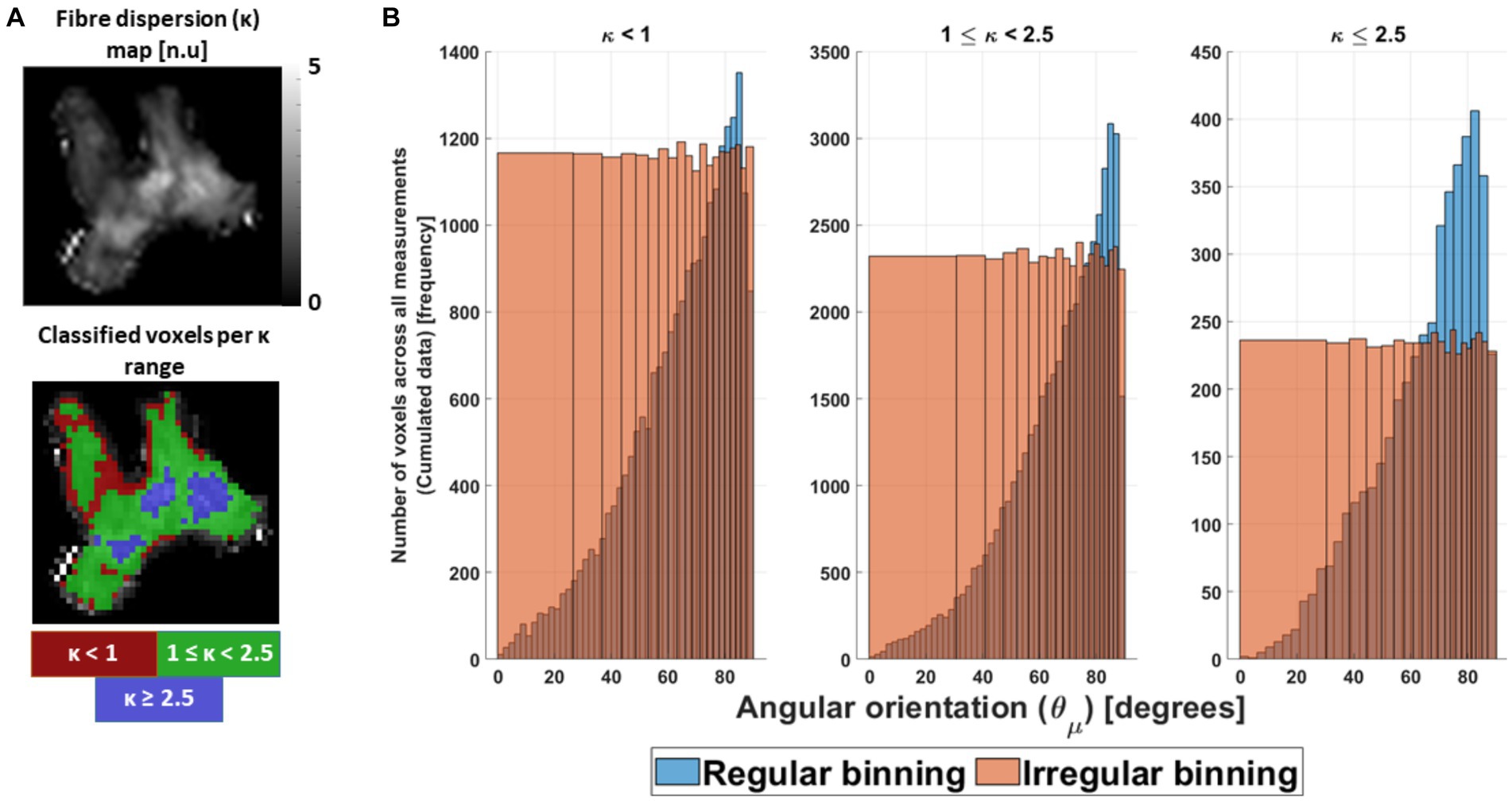
Figure 5. Preparation of the ex vivo data for analysis. (A) The cumulated ex vivo data were distributed first as a function of κ parameter, to ensure similar fibre dispersion. Heuristically it was divided in highly dispersed (κ < 1), mildly dispersed (1 ≤ κ < 2.5) and negligibly dispersed (κ ≥ 2.5) fibres. Coincidentally, this division enclosed specific areas in the OC (red, green and blue ROIs). (B) After division, the cumulated data were binned irregularly as a function of the estimated voxel-wise angular orientation ( ) per κ range (orange bars), to avoid a possible effect size bias caused by its non-uniform distribution (blue bars). The first angular irregular bin or angular offset was obtained and showed to be κ range dependent (Supplementary Table S1, section 5).
In the binning process, both datasets were distributed first as a function of κ, and later as a function of . The first distribution was performed to ensure a similar degree of fibre dispersion as observed in Figure 4B and in the work of Fritz et al. (2020). For that, three different fibre dispersion ranges were defined as a function of κ: κ < 1 for the highly dispersed fibres, 1 ≤ κ < 2.5 for the mildly dispersed fibres, and κ ≥ 2.5 for the negligibly dispersed fibres. Coincidentally, these fibre dispersion ranges depicted specific areas in the OC (Figure 5A). However, the in silico data required two extra averages on the fitted parameters to bin it as a function of the different fibre dispersion ranges: first, across the 5,000 replicas and, second, across the κ values within each fibre-dispersion range. The average across κ was performed in such a way that it resembled the frequency distribution of κ observed in the ex vivo cumulated data (for more detail, see Supplementary material, section 5). After separating the fitted parameters per fibre dispersion range for both datasets, the data were irregularly binned as a function of bins per defined κ range.
The irregular bins were introduced to avoid a bias due to the uneven distribution of voxels with azimuthal orientations across the 16 angular measurements (Figure 5B, blue bars). To determine the irregular bin sizes, a cumulated distribution of voxels was estimated and divided into 20 equally populated bins (Figure 5B, orange bars). The mean of the first angular irregular bin was defined as the angular offset . The range of values contained in each irregular bin and the values are shown in Supplementary Table S1, section 5.
After binning, the average and standard deviation (sd) of the α- and β-parameters between datasets was calculated per irregular bin in the ex vivo cumulated data. For the in silico data, the average and sd of the same parameters were obtained by weighting the distribution of in each bin in a similar way to that seen in the irregular bins in the ex vivo cumulated data (for more detail, see Supplementary material, section 5).
3.3.2. Quantitative analysis
Four different analyses were performed in order to study: (1) the effect of g-ratio and fibre dispersion, via κ, on the estimated angular-independent β1 parameter in M2, (2) the microstructural interpretability of β1 via the deviation between fitted β1 and its predicted counterparts from M2 (β1,nm, Eq. 3) and from the heuristic expression (β1,m, Eq. 4), (3) the possibility of calculating the MWF (Eq. 5) from the fitted β1 using the heuristic expression β1,m, and (4) the effect of TE, via the different meGRE subsets, on the performance of M2. The last analysis was divided into two parts, testing: (A) its capability to reduce the orientation dependence in β1 (and thus be a valid proxy for R2,iso*), and (B) if M2 can be better explained by the different meGRE subsets than M1. Using the simulation framework, the validity of M2 and its derived microstructural parameters were tested based on analyses 1, 2 and 4. While both datasets were used for the first and fourth analyses, only the in silico data were used for the second analysis while ex vivo data were only used for the third analysis.
3.3.2.1. First analysis: ability of M2 to obtain the angular-independent β1 parameter for varying g-ratio and fibre dispersion values
For the first analysis, the ability of M2 to estimate an orientation-independent effective transverse relaxation rate, R2,iso*, via the β1 parameter was assessed. Since R2,iso* by definition is the angular independent part of R2 * and according to the HCFM should be given by β1 parameter at , we assessed the residual dependence of the β1 parameter with respect to and compared it with its counterpart for α1, i.e., the proxy for the dependent R2*.
For this, we first calculated the dependence of each parameter with respect to using the normalised-root-mean-squared deviation (nRMSD, in %):
where varied slightly for each κ range (sub-index j) but was close to zero (see Supplementary Table S1) with 𝛾 ∈ {𝛼1, 𝛽1}.
To compare the nRMSD of each parameter, we calculated the difference between them, ΔnRMSD, as:
in percentage-points (%-points). If the ΔnRMSD is positive or higher than 0%-points, this implies that the dependency of β1 is similar or higher, in magnitude, to α1. The latter says therefore that M2 failed in estimating an angular-independent parameter from R2*. A negative ΔnRMSD in turn implies that the independence of has been reduced. A perfect orientation independence is achieved if and, consequently, .
3.3.2.2. Second analysis: assessment of the microstructural interpretability of β1
For the second analysis, the microstructural interpretation of β1 was quantitatively assessed by comparing the relative difference (ε) between estimated β1 at the angular orientation for the fitted in silico data ( ) and the predicted β1 ( ) using M2 or the heuristic expression:
where were defined in Eqs 5, 6, respectively. Additionally, the mean across angles was calculated as .
3.3.2.3. Third analysis: myelin water fraction and g-ratio estimation from ex vivo data using the heuristic expression of R2,iso* via β1,m
For the third analysis, the MWF was estimated from the fitted β1 in ex vivo data using the analytical expression for β1,m (Eq. 6). For that, we used the two sets of R2 values for the non-myelinated (R2N) and myelinated (R2M) compartments reported in Table 1. Only the ex vivo R2 values were reported in this section, while the in vivo R2 values were reported in Supplementary material, section 7.2.3.
3.3.2.4. Fourth analysis: the effect of echo time ranges on the performance of M2
In the fourth analysis, the performance of M2 was tested in two sub-analyses when using the meGRE datasets with different TE ranges (see section 3.3.1).
3.3.2.4.1. First sub-analysis: assessing the residual dependence in β1 for meGRE subsets with different maximum echo times
For the first sub-analysis, the orientation dependence of β1 was assessed for the different meGRE subsets from the ex vivo dataset and the in silico data for variable g-ratio. For that, α1 and β1 from M1 and M2 were compared once again as in the first analysis and the ΔnRMSD was calculated to assess the residual dependence of β1 in comparison to the dependence of α1.
3.3.2.4.2. Second sub-analysis: assessing if M2 is better explained by the data using meGRE subsets with different maximum echo times
For the second sub-analysis, the weighted-corrected Akaike Information Criterion (wAICc, Eq. 12) was introduced [more details can be found in Supplementary Equation S30, section 6 and Burnham et al. (2011)]. According to Burnham et al. (2011), the wAICc can be used to assess whether a given model (here M2) is better explained [or “supported” as introduced in Burnham et al. (2011)] by the data than a set of other models (here M1). In this work, we used the AICc (i.e., Akaike Information Criterion, AIC, with a correction for small sample sizes) instead of the AIC or the Bayesian Information Criterion (BIC) to better account for the small sample size in comparison to the number of model’s parameters. Note that to use the AIC the ratio between the sample size and the number of parameters (n/k) should be above 40 (Burnham and Anderson, 2002) and this condition was not always fulfilled in our data.
The wAICc for M2 is defined by:
where ΔAICc in Eq. 12 is the difference of the AICc for models M1 and M2:
The AICc and wAICc were estimated per voxel (for ex vivo) and replica (for in silico) from the previous analysis using the sum-of-squares error (SSE) from the fitting of each model (see Supplementary Equation S32, section 6) and for each of the three meGRE subsets. Note that the AICc and wAICc were estimated only ex vivo and in silico data with negligible fibre dispersion (κ ≥ 2.5). Then, the averaged wAICc as well as its standard deviation (sd) were calculated. In this work, we interpreted the range of possible wAICc values in a more conservative manner. Hereby, we mainly focused on the case AICc(M1) > AICc(M2) (Eq. 12), where the resulting wAICc (Eq. 11) is greater than 0.5: a wAICc >0.73 implies that M2 is better explained by the meGRE data than M1, and a wAICc between 0.5 and 0.73 implies that M2 and M1 are ambiguously explained by the data but M2 is still preferred. For the case of AICc(M1) ≤ AICc(M2), where wAICc ≤0.5, M2 was not explained by the data as compared to M1. More details regarding the calculations as well as the threshold of 0.73 can be found in the Supplementary material, section 6. Note that we were only reporting the average wAICc, thus the wAICc for some voxels (for ex vivo) or replicas (for in silico) might belong to a different range than the average wAICc, which can be observed by the estimated sd wAICc.
In the following sections, the dependence of the parameters under study, i.e., nRMSD( ), nRMSD( ), ΔnRMSD ( ), α1( ), β1( ) (Eqs 8, 9), (Eq. 10) and , to and were simplified for readability purposes. Therefore, these parameters will be hereafter nRMSD(α1), nRMSD(β1), ΔnRMSD, α1, β1, and , respectively.
4. Results
4.1. First analysis: ability of M2 to obtain the angular-independent β1 parameter for varying g-ratio and fibre dispersion values
Figure 6 shows the performance of M2 when estimating R2,iso* via β1 for variable g-ratio and fibre dispersion. To visualise this, we compared the dependence of α1 from M1 to the residual dependence of β1 from M2 (Figures 6A,B). Both dependencies were quantified in Figure 6C using their respective nRMSD (Eq. 8). The results are from the analysis performed on the ex vivo and in silico data. The in silico data was generated using the ex vivo compartmental R2 values (the corresponding results for the in vivo compartmental R2 values are presented in Supplementary Figure S4).
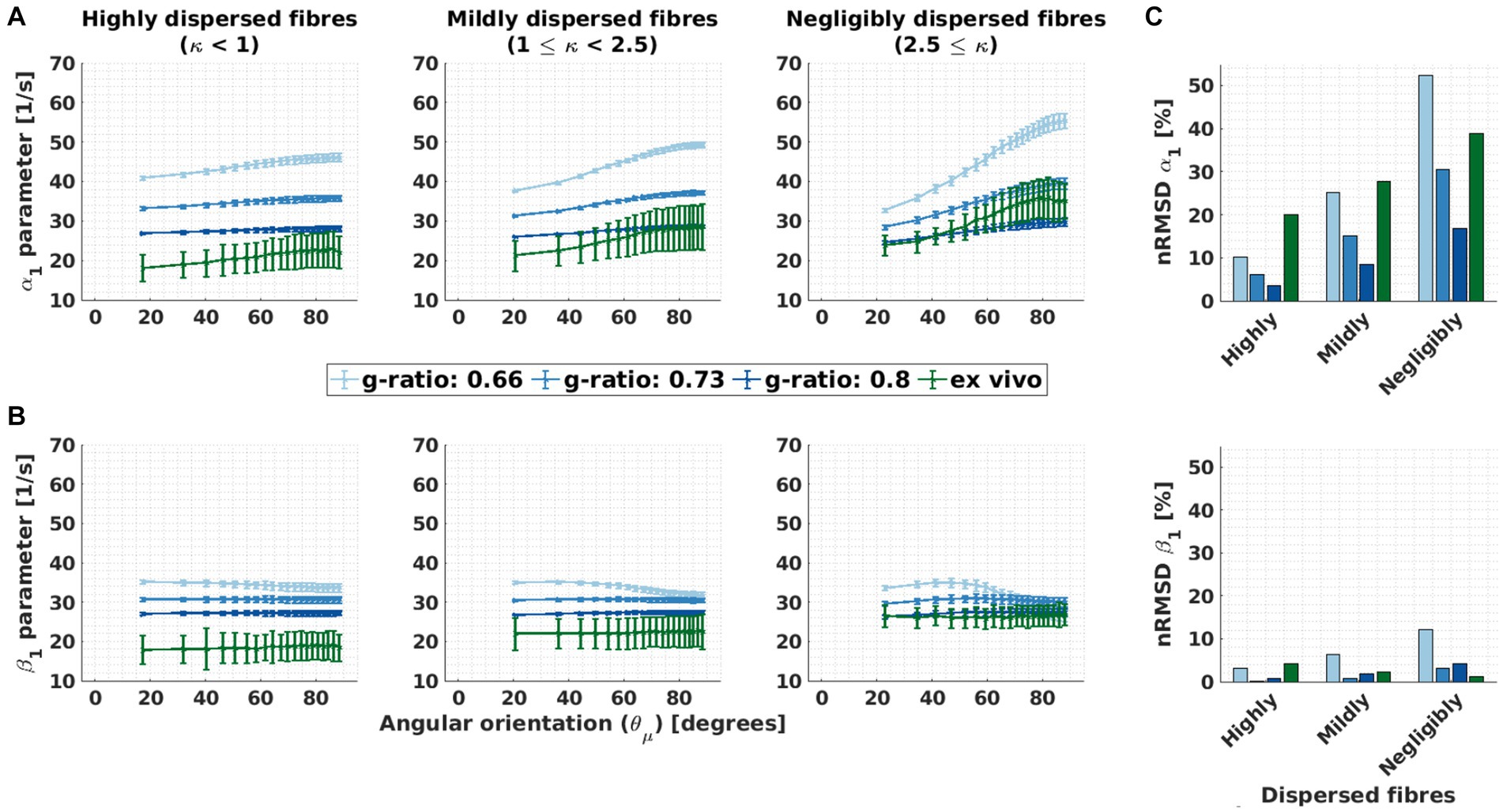
Figure 6. Orientation dependence of linear model parameters (α1 and β1) for varying g-ratio and fibre dispersion values. (A,B) Depicted is the α1 parameter of M1 (proxy for R2*) and β1 parameter of M2 (proxy for the isotropic part of R2*) as a function of the angle between the main magnetic field and the fibre orientation ( ) for different fibre dispersion and g-ratio values. The different columns depict different dispersion regimes: highly dispersed (κ < 1, first column), mildly dispersed (1 ≤ κ < 2.5, second column) and negligibly dispersed (κ ≥ 2.5, third column) fibres. Note that the smallest angle ( ) varied across dispersion regimes: 17.3° (κ < 1), 20.4° (1 ≤ κ < 2.5) and 22.9° (2.5 ≤ κ). This was caused by the irregular binning (see section 3.1.4) (C) Depicted is the normalised root-mean-squared deviation (nRMSD, Eq. 11 in %) of the α1 parameter of M1 (proxy for R2*) and β1 parameter of M2 (proxy for the isotropic part of R2*) for different fibre dispersion and g-ratio values. Across the entire figure, the distinct colours (blue and green curves and bars) distinguish between in silico data with variable g-ratios (increasing blue hue with increasing g-ratio) and ex vivo data (olive curve).
The ability of M2 to reduce the dependency of β1 varied with g-ratio and fibre dispersion. The dependency of α1 (and residual dependency of β1) was also strongly influenced by g-ratio and fibre dispersion: smaller g-ratio values and reduced fibre dispersion increased the dependency of α1 and (the residual dependency) of β1 (Figures 6A,B, respectively).
The fibre dispersion affected the performance of M2 the same between in silico and ex vivo datasets (Figure 6C). In both datasets, the improvement is largest for negligible dispersion (starting from ΔnRMSD = −12.0%-points for the in silico data with a g-ratio of 0.8 and ΔnRMSD = −37.4%-points for the ex vivo data). For the ex vivo data, the nRMSD(β1) was the lowest for the negligibly dispersed fibres (nRMSD(β1): 1.3% at κ ≥ 2.5). For the in silico data, the nRMSD(β1) was the lowest for the highly dispersed fibres and for a g-ratio of 0.73 (nRMSD(β1): 0.1%), and it increased with decreasing fibre dispersion (nRMSD(β1) up to 2.7%). For the g-ratios of 0.66 and 0.8, the nRMSD(β1) was higher but still below 12%.
The dependence of α1 on fibre dispersion was the same between in silico and ex vivo datasets (Figure 6C, top): the lower the dispersion the higher the nRMSD(α1). The dependence of α1 increased as the g-ratio decreased.
4.2. Second analysis: assessment of the microstructural interpretability of β1
Figures 7A,B report the angular-orientation ( ) dependent relative differences ( and , Eq. 10) between the fitted β1 from the in silico data and its predicted counterparts using M2 (Eq. 3) and the heuristic expression (Eq. 4). Figure 7C shows the mean and standard deviation of and across angles for ex vivo compartmental R2 values (the corresponding results for the in vivo R2 values are presented in Supplementary Figure S5).
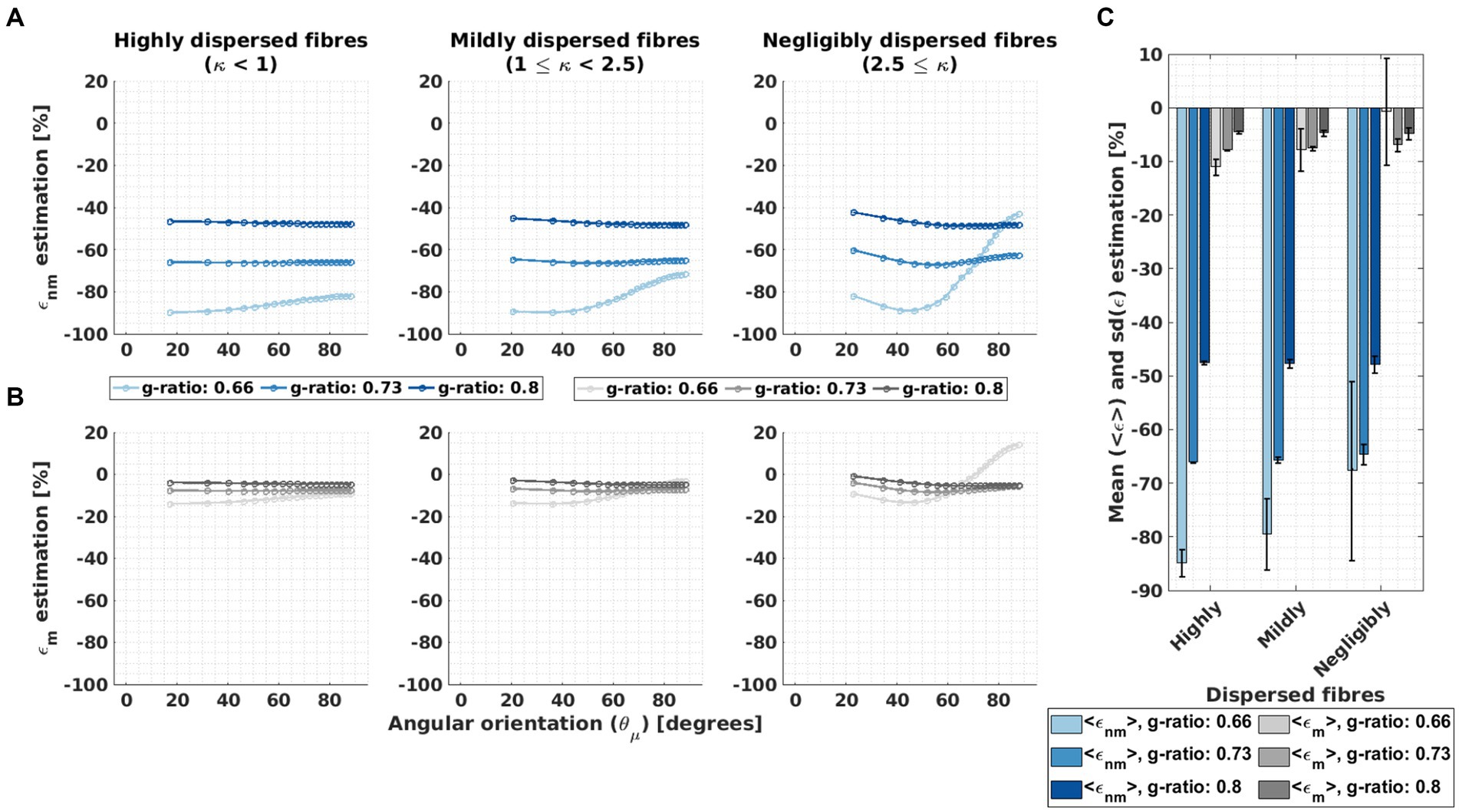
Figure 7. Assessment of the microstructural interpretability of β1 by the deviation between fitted and biophysically predicted β1. (A–B) The relative difference (ε, Equation 10) was calculated between the fitted β1 to the in silico data and two biophysically-modelled expressions for β1 based on the HCFM. The two expressions for β1 values were calculated from the original expression for M2, β1,nm (Equation 3, resulting in εnm, A) and the heuristic expression, β1,m (Equation 4, resulting in εm, B). This was calculated per g-ratio and fibre dispersion. (C) The corresponding mean, <ε>, and standard deviation, sd(ε), of the relative differences across the angular orientations ( ) were estimated. The hue intensity coding represents increasing g-ratio value for both error estimations.
was large, between −100% and − 40%, and varied strongly with g-ratio and fibre dispersion. showed the largest dependence where the largest deviation was observed (i.e., for the g-ratio of 0.66 and the lowest fibre dispersion, Figure 7A). was always smaller than and showed a smaller dependence across all the studied fibre dispersions and g-ratios. It varied between −20 and 20% and had the largest values and variation for the smallest g-ratio and negligibly fibre dispersion. For the average across angles, we found that negligibly dispersed fibres showed the smallest and per g-ratio.
The mean across angles for , , was up to −85% whereas the mean across angles for , , was only up to −12% (Figure 7C). On average across all g-ratios and fibre dispersion arrangements, was approximately 8 to 9 times larger than . Both relative mean differences became more negative with increasing g-ratio and decreasing fibre dispersion. The for the negligibly dispersed fibres at g-ratio 0.66 was close to −2% but accompanied by a large standard deviation across due to the strong -dependency of the corresponding fitted parameters. For both and , the variability (Figure 7C) across different values, and respectively, was highest when the fibre dispersion and g-ratio were lowest.
4.3. Third analysis: myelin water fraction estimation from ex vivo data using the heuristic expression of R2,iso* via β1,m
Figure 8 reports the MWF estimated from the ex vivo data by inverting the heuristic expression for β1,m (Eq. 6), using the ex vivo compartmental R2 values (the corresponding results for the in vivo R2 values are presented in Supplementary Figure S6). Figure 8A shows the estimated MWF as a function of while Figure 8B shows the median and standard deviation (sd) of the estimated MWF across .
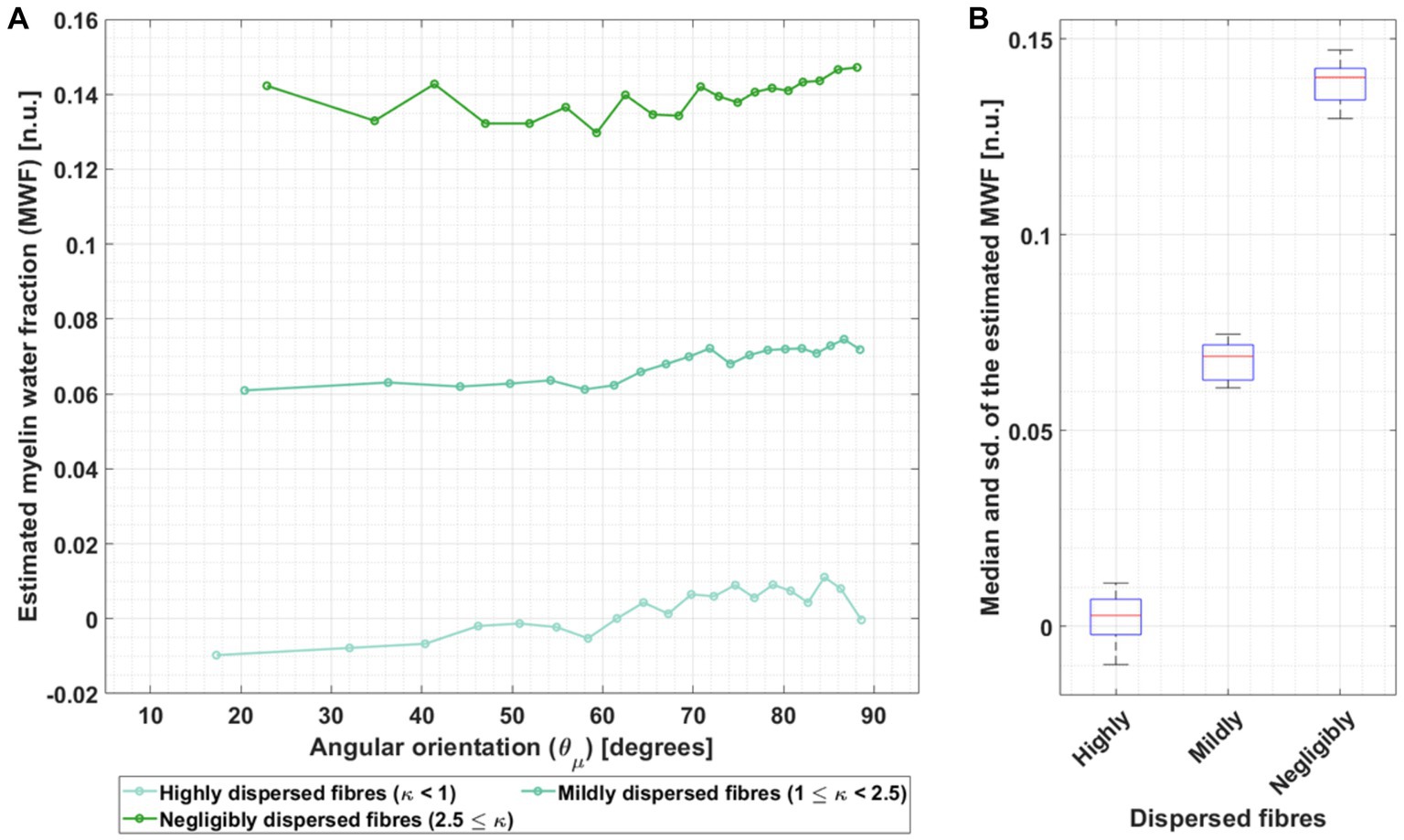
Figure 8. Dependence of the MWF estimation on angular orientation for three different fibre dispersion ranges in ex vivo data. (A) The MWF was estimated by using the heuristic analytical expression of β1 (β1,m, Eq. 4) and the fitted β1 for the ex vivo data using the compartmental R2 values from Dula et al. (2010) (hues of green) in Table 1. This calculation was performed per angle ( ) and for the three different fibre dispersion ranges: highly dispersed, mildly dispersed and negligibly dispersed. The increasing green hue represents decreasing fibre dispersion. (B) The corresponding median and standard deviation (sd) were estimated across per fibre dispersion range.
The estimated MWF was larger with decreasing fibre dispersion (Figure 8A). Moreover, there was a trend towards larger estimated MWF for larger . Across , the estimated median ex vivo MWF was 0.14 for fibres with negligible dispersion but moved towards to even lower and unrealistically small values (MWF: 0.069) for dispersed fibres (Figure 8B). The standard deviation across MWF was similar for different fibre dispersions, ranging from 0.0068 to 0.0104.
4.4. Fourth analysis: the effect of echo time ranges on the performance of M2
In this section, two sub-analyses were performed for in silico data at variable g-ratio and ex vivo data, both with negligibly dispersed fibres (i.e., κ ≥ 2.5), using the three meGRE subsets with different maximum echo time (TEmax) for ex vivo compartmental R2 values (the corresponding results for the in vivo R2 values are presented in Supplementary Figures S7, S8). In the first sub-analysis, its result is depicted similarly as in Figure 6, but for different TEmax and κ ≥ 2.5. In the second sub-analysis, it was assessed whether M2 was better explained by the different meGRE subsets than M1 using the average wAICc of M2 (Eq. 11).
4.4.1. First sub-analysis: assessing the residual dependence in β1 for meGRE subsets with different maximum echo times
Using the meGRE subsets with smaller TEmax (36 ms and 18 ms), M2 was less effective across all g-ratios (Figures 9A,B, second and third column). For some microstructural parameter settings, even an increased dependence was observed for β1 compared to α1: nRMSD(β1) went up by 5.6%-points at 36 ms (in silico, g-ratio: 0.8) and by 14.1%-points at 18 ms (ex vivo). Moreover, for the meGRE subset with the smallest TEmax (18 ms), an atypical dependence of β1 (and α1) was found in the ex vivo data: β1 (and α1) decreased with increasing up to approximately 55° (magic angle, dashed magenta lines in Figures 9A,B) and then slightly increased again. The dependence up to the magic angle was not observed in the in silico data at any investigated meGRE subset. Moreover, the dependence of α1 in the ex vivo data decreased when meGRE subsets with decreasing TEmax were used. This trend was mostly also observable in the in silico data (Figure 9A). Note that we investigated the orientation dependence of α1 and β1 also for mildly and highly dispersed fibres but did not find new trends in those datasets (data not shown).
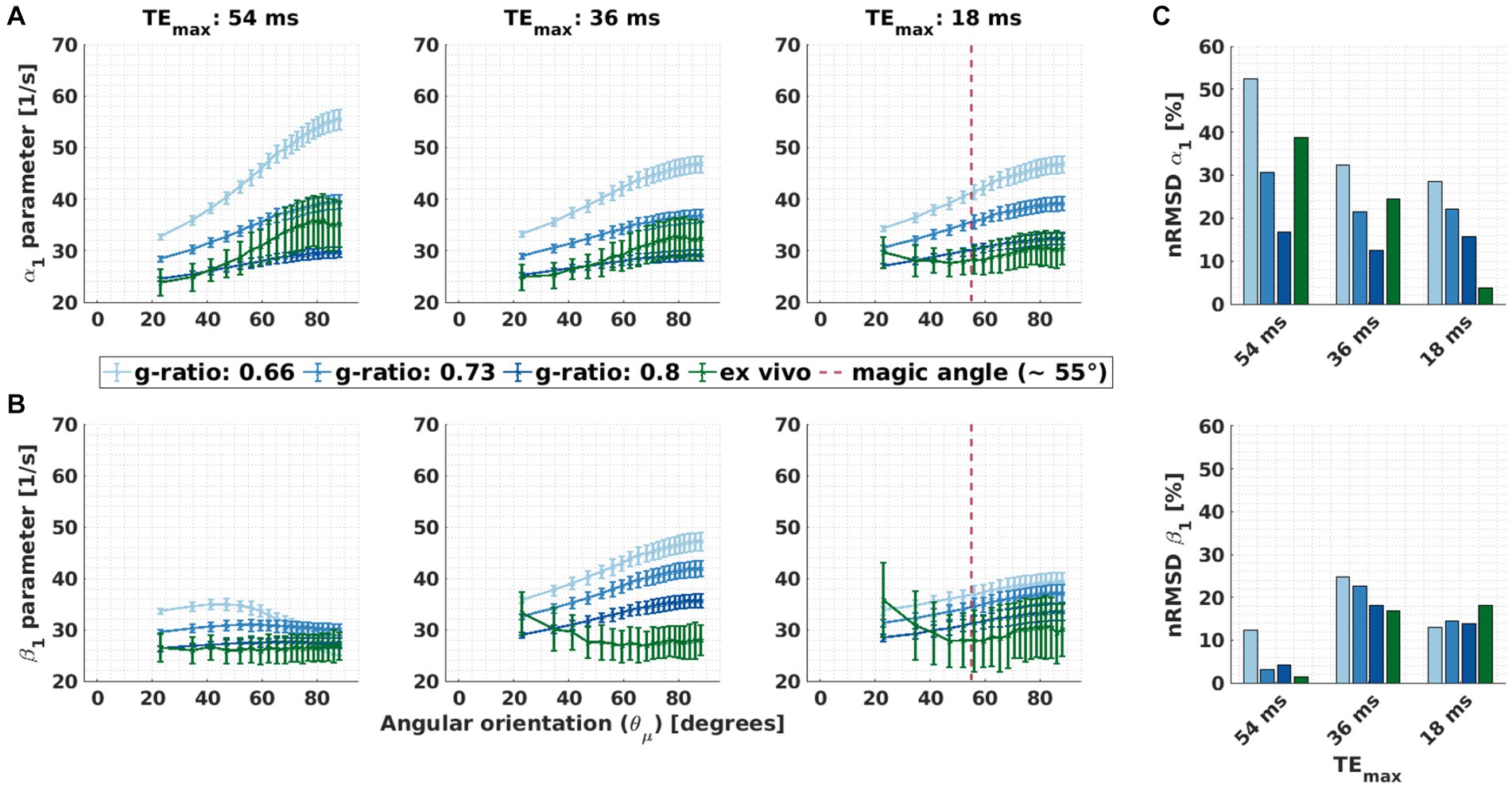
Figure 9. Effect of the maximal echo time, i.e., meGRE subsets with different maximum echo times, on the dependency of α1 and β1. (A,B) Angular orientation ( ) dependence of α1 in M1 and β1 in M2 for the three meGRE subsets with varying maximum TE (TEmax: 54 ms, 36 ms and 18 ms). Two datasets are compared: ex vivo (green curve) and in silico (blue curve) data at variable g-ratios. Only datasets of the negligibly dispersed fibres (κ ≥ 2.5) are presented. The magenta vertical lines in some of the subplots indicates the magic angle ( = 55°). (C) Depicted is the normalised root-mean-squared deviation (nRMSD, Eq. 8 in %) of the α1 parameter of M1 (proxy for R2*) and β1 parameter of M2 (proxy for the isotropic part of R2*) shown in (A) and (B), respectively.
4.4.2. Second sub-analysis: assessing if M2 is better explained by the data using meGRE subsets with different maximum echo times
The average wAICc showed different trends across the different meGRE subsets with varying TEmax for both datasets. For the ex vivo data, the average wAICc decreased when meGRE subsets with smaller TEmax were used. Using the meGRE subsets with the largest and intermediate TEmax (54 and 36 ms), the average wAICc indicated that M2 was better explained than M1 by the data with wAICc values in the ranges of wAICc >0.73 (TEmax = 54 ms) and 0.73 > wAICc >0.5 (TEmax = 36 ms), respectively. Interestingly, for the in silico data, the average wAICc decreased as a function of g-ratio for the meGRE subset with the largest TEmax, from wAICc: 0.71 to 0.44; but increased with increasing g-ratio for the meGRE subset with intermediate TEmax, from wAICc: 0.31 to 0.59. However, none of the highest wAICc overpassed the threshold of 0.73. Note that the large standard deviation of the reported wAICc per dataset indicates that the results are only valid on average whereas the wAICc for single voxels (ex vivo data) or replicas (in silico data) can be outside the reported ranges (see Figure 10).
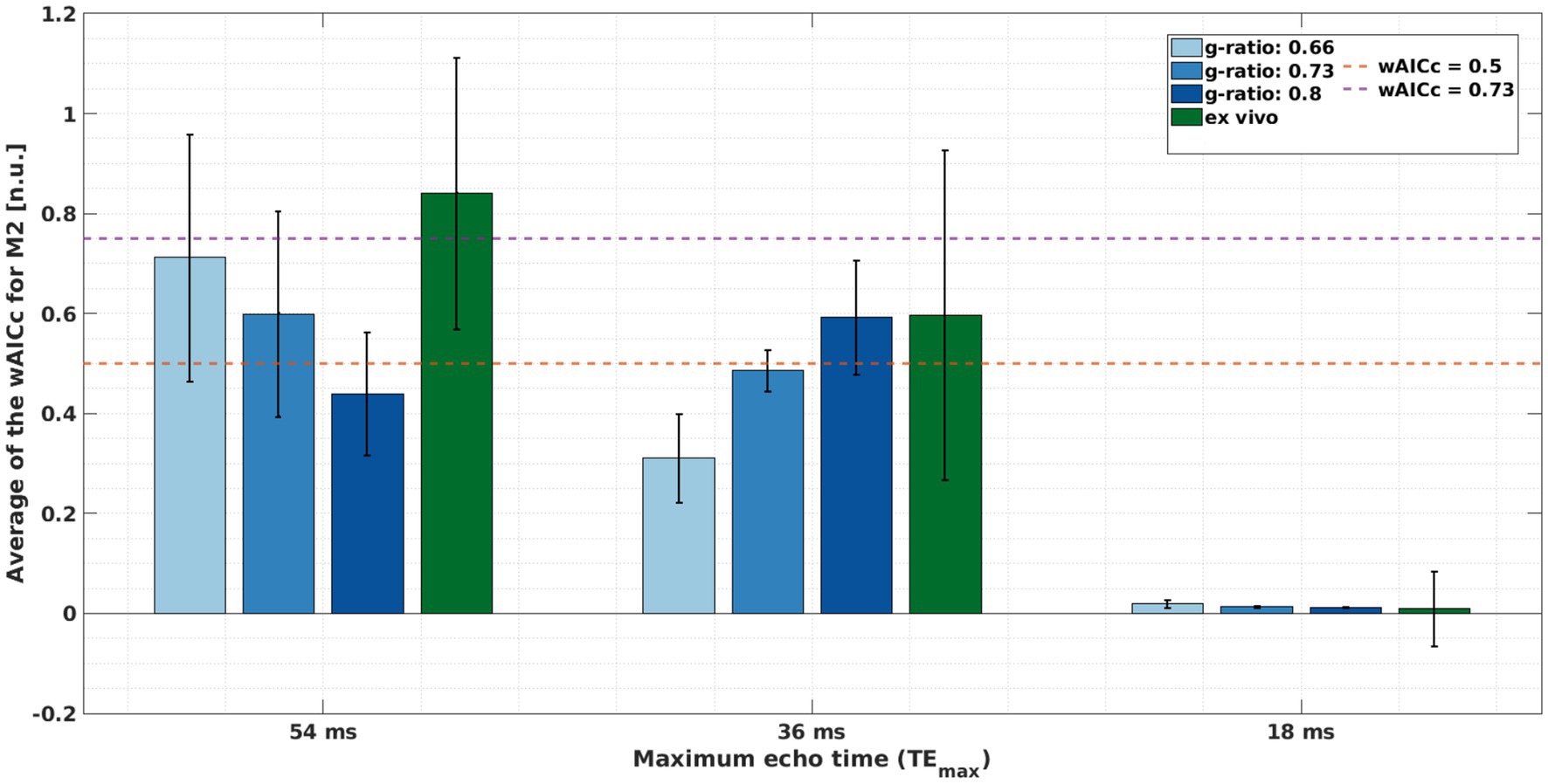
Figure 10. Assessing if model M2 is better explained by the meGRE signal decay than M1, quantified by the averaged wAICc for M2 (Eq. 11). This quantification was done per meGRE subsets with different maximum echo time (TEmax) for the in silico data at variable g-ratios (increased blue hue in bars, higher g-ratio) with R2 values from Dula et al. (2010); and ex vivo data (green bar) for negligibly dispersed fibres (κ > 2.5). The magenta and orange lines mark the following ranges: over the magenta line (wAICc = 0.73), M2 is better explained by the data; between the magenta and orange (wAICc = 0.5) lines, there is a preference for M2 but it is ambiguous whether M2 is better explained than M1 by the data; and bellow the orange line, M2 is not better explained by the data than M1.
5. Discussion
This work quantitatively evaluated the performance of the log-quadratic model (M2) for estimating the orientation-independent part of R2* (R2,iso*) via its linear parameter, β1, using a single-orientation multi-echo GRE (meGRE) measurement in simulations and in a human optic chiasm. We found that M2 can estimate R2,iso* via β1 when using meGRE with long maximum echo time (TEmax ≈ 54 ms) for all investigated fibre dispersion and g-ratios. Our simulation results show that the proposed heuristic expression for β1 better explained the fitted β1 for ex vivo compartmental R2 values than the M2-based prediction. Using this heuristic model, we estimated realistic MWF values from β1 fitted to the ex vivo data. However, we found that its validity depends on the choice of compartmental R2-values and we found that the heuristic model cannot be used for tissue with dispersed fibres. We created an openly available simulation framework to test the validity of the heuristic expression for different microstructural arrangements. We found that M2 cannot reduce the orientation dependence of β1, and therefore cannot be used as a proxy of R2,iso* when the meGRE subsets with shorter maximum echo times were used (TEmax ≈ 36 ms or 18 ms). For the meGRE subset with the shortest TEmax of 18 ms, we found that the orientation-dependence of the classical R2* showed the highest deviation between ex vivo and in silico data for angles below the magic angle (55°), indicating that, at short echo times, the mechanism for the orientation-dependence of R2* is not captured by our HCFM-based simulation.
5.1. Ability of M2 to estimate the angular independent β1 for varying g-ratio and fibre dispersion values
Our results show that M2 has the potential to estimate R2,iso* from a single-orientation meGRE via β1 for the ex vivo data of an optic chiasm tissue sample and the in silico data. We found that the performance of M2, assessed by the residual dependence of β1, varied for different g-ratios and fibre dispersions (Figure 5 and Supplementary Figure S4). For the ex vivo compartmental R2 values (Figure 5), the residual dependence of β1 was always less than 12% even if the dependence of the original R2* (using the α1 parameter of M1) was up to 50%. For the in vivo compartmental R2 values (Supplementary Figure S4), the residual dependence of β1 was always less than 20%. The comparison of the performance of M2 for different compartmental R2 values indicates that the performance of M2 might vary for tissue with different microstructural tissue properties such as the compartmental R2 values or the fibre volume fraction.
5.2. Assessment of the microstructural interpretability of β1
As hypothesised in the introduction, the fitted β1 parameter is an unsuitable proxy for estimating microscopic tissue parameters via the dependency of M2 on the biophysical HCFM (Eq. 3). Using the ex vivo compartmental R2 values to generate the in silico data, we obtained an error of up to −70% for the fibres with negligible dispersion (Figure 7C) between the fitted β1 and the β1 predicted using the biophysical relation in M2 (Eq. 3). With the proposed heuristic expression for β1 (Eq. 4), the relative error was reduced by a factor of about 10 and more for fibres with negligible dispersion (e.g., from −65% to −6% for a g-ratio of 0.73, Figure 7C), indicating that this expression is better suited for the biophysical interpretation of β1 than the M2-based expression. However, we also found that the heuristic expression is not valid for all microstructure parameters, e.g., for in vivo compartmental R2 values the error switched signed, e.g., it changed from −35 to 20% for a g-ratio of 0.73 and negligible fibre dispersion (Supplementary Figure S6). This shows that the validity of the new heuristic expression for β1 as a sum of the relaxation rates of the myelin and non-myelin water pools weighted by their signal fractions is constrained to a specific range of relaxation rate values.
In this manuscript, we provide a simulation framework that allows to test whether for a given set of microscopic parameters the validity of the heuristic expression is given.
Note that neither the proposed heuristic correction nor the previous M2-based expression account for the effect of fibre dispersion which might explain why the accuracy of the predictions decreased with increasing fibre dispersion (Figure 7). While the influence of fibre dispersion has been successfully incorporated into M2 in another study (Fritz et al., 2020), it remains an open task for future studies to also do this for the heuristic expression of β1.
5.3. Myelin water fraction estimation from ex vivo data using the heuristic expression for β1
Under the condition that M2 estimates an orientation-independent β1 and that the heuristic expression of β1 provides a valid biophysical interpretation, the myelin water fraction (MWF) can be estimated from the fitted β1 (Eq. 6). When using the ex vivo compartmental R2 values, we found a median (across orientation) MWF of 0.14 for fibres with negligible dispersion (Figure 8B), which is congruent with the mean value reported in white matter of 0.10 (Uddin et al., 2019). In the Supplementary materials section 7.2.3, we exemplified what happens if the MWF is calculated for a set of microscopic parameters for which the heuristic expression is invalid. We found that the resulting MWF is negative and thus implausible. As such, the estimation of the MWF through β1 seems a less effective method than existing MWF estimation approaches but might still be useful to estimate the MWF if magnitude-only meGRE data with a single head orientation are available.
5.4. The effect of echo time on the performance of M2
Our findings revealed that the ability of M2 to estimate β1 was reduced for meGRE subsets with shorter maximum echo time (TEmax). This was evidenced by: (i) an increased residual orientation dependence of β1, and (ii) M2 not being better explained by the meGRE data than M1. The performance of M2 decreased when the maximum TE (TEmax) also decreased. This was not only observed for meGRE subsets with TEmax values typically used for in vivo studies (i.e., TEmax = 18 ms), but also at the intermediate TEmax (= 36 ms). Note that these observations could also be driven by the reduced time points of the meGRE subsets at shorter TEmax: while the meGRE subset at TEmax = 54 ms contained 16 time points, the meGRE subset at TEmax = 18 ms only contained five time points. A limited sample size or number of time points, however, is an unsolved challenge for in vivo application of M2 because typical in vivo meGRE protocols, specifically MPM protocols, use short TEmax (~ 18 ms) and few echo times only (~ 6–8 echoes). Therefore, future studies should aim at increasing the TEmax and/or the time points. This will require highly accelerated acquisitions [e.g., like in Han et al. (2014) for spin echo sequences or Kim et al. (2019) for 3D-GRE sequences] and the correction of motion artefacts (Magerkurth et al., 2011), B0 fluctuations due to breathing (e.g., Vannesjo et al., 2015) and susceptibility artefacts (e.g., Port and Pomper, 2000), which are particularly strong at later echo times.
Interestingly, the biggest discrepancy between in silico and ex vivo results for β1 was seen for the meGRE subset with the shortest TEmax value at smaller than the magic angle (55°, Figure 9B). This is because β1 and α1 of the measured ex vivo data showed an atypical dependence in this range: they decreased as a function of increasing up to the magic angle. A similar observation was also made by Bartels et al. (2022) for the orientation dependence of R2. They suggested that a mechanism that could explain a reduction in R2 at the magic angle would be the Magic Angle Effect in highly structured molecules like myelin sheaths (see Bydder et al., 2007). Since, in our experiment, this phenomenon would be superimposed on the orientation dependence of R2*, it may be particularly evident when the latter effect is negligible, i.e., at low . Note that our finding was observed only for one tissue sample. Thus, further testing on different tissue samples is necessary to verify the generalisability of our finding.
5.5. Considerations
Our results indicate that the ability of M2 to estimate the orientation-independent component of R2* varies with echo time and strongly depends on microstructural parameters. As the space of parameters in the simulations are large, not all possible combinations could be investigated here. In future studies, we will test the performance of M2 in scenarios that map directly to in vivo meGRE experiments as opposed to the ex vivo case that was the focus of this study.
M2 can separate the orientation dependence of R2* leaving an orientation-independent parameter β1, but at the same time this estimated β1 cannot be predicted accurately based on the current analytical derivation of M2 (Supplementary Equations S15, S16, section 4). Future studies should aim to find a better derivation of M2 from the HCFM that does not neglect the contribution of the myelin water as well as incorporating other sources of dephasing, e.g., due to diffusion and near-field interactions. In fact, an analytical derivation without neglecting the contribution of the myelin compartment was performed in this manuscript (Supplementary material, section 4). However, this derivation is mathematically valid only for meGRE subsets with a maximal TE smaller than the T2 of the myelin compartment. Thus, the derived expression (Supplementary Equations S13, S14, section 4) does not hold for our simulated datasets because TEmax > T2 myelin for all meGRE subsets. This might also explain why the heuristic expression does not work for the in vivo compartmental R2 values, for which the T2 myelin is smaller. Nevertheless, it can be used to motivate our heuristic expression for β1 (Eq. 4) because it is the same expression as in Supplementary Equation S15b. This derivation might also be relevant for studies that are performed at lower magnetic fields, e.g., at 3 T, where the condition TEmax > T2 myelin could be fulfilled because the R2 from the myelinated and non-myelinated compartments are different (e.g., shorter) from the ones used in our current simulation.
Our simulations did not always show the same trend as the ex vivo data (e.g., Figures 6, 9) and were occasionally quantitatively different. This could be related to simplifications that were employed in our simulations and/or the underlying simplifications of the HCFM. The most important simplifications in our simulations were: First, the assumption that the R2 was the same for both intra- and extracellular compartments. Although, these R2 have been found to be different (e.g., Beaulieu et al., 1998; Assaf and Cohen, 2000; Does and Gore, 2000; Does, 2018; Veraart et al., 2018; Tax et al., 2021), we expect the differences not to play a substantial role at the short TEs that were used here [e.g., TEmax: 54 ms < T2 of the extra-axonal compartment ≈ 58 ms in Tax et al. (2021)]. Second, we assumed that the signal coming from multiple dispersed hollow cylinders is a superposition of the complex signal of multiple single hollow cylinders at different orientations, neglecting the near-field interaction of the cylinders. As compared to previous studies where near-field interaction was more faithfully described in two dimensions (Xu et al., 2018; Hédouin et al., 2021), our simulation framework allowed for better control over the fibre dispersion in three dimensions via the Watson distribution parameter κ. The most important simplifications of the HCFM are: (1) neglecting the orientation dependence of R2 with respect to the external magnetic field (Knight et al., 2017; Birkl et al., 2021; Tax et al., 2021) and (2) the different longitudinal magnetisation of the compartments which affects the longitudinal relaxation rate (R1) (see, e.g., Labadie et al., 2014; Shin et al., 2019; van Gelderen and Duyn, 2019; Chan and Marques 2020; Kleban et al., 2021). While the anisotropic part of R2 is three times smaller than the anisotropic part of R2* at 3 T (Gil et al., 2016) and could explain residual orientation dependence of β1, other assumptions requires further study, for example removing the R1 dependence in the estimated R2* (Milotta et al., 2023). Nevertheless, even with all the simplifications, the HCFM-based in silico data described the dependence of α1 and β1 similarly to the ex vivo data across all dispersion regimes when using the long maximal TE protocol.
The ex vivo data require further discussion. First, we investigated only one human optic chiasm tissue sample with relatively long postmortem interval of 48 h, which could explain parts of the differences that we found when comparing with the in silico dataset. Second, the coregistration of the diffusion and meGRE datasets (see section 3.1.4) might lead to image interpolation artefacts affecting the κ and estimates. Moreover, coregistration between meGRE images at different orientations could lead to additional blurring of the data. However, these coregistration steps are necessary to ensure maximal correspondence between the same voxels across maps. We expect that the additional coregistration-related blurring will only slightly reduce the variability when binning the data (e.g., the standard deviation along R2* in Figure 6). Third, the Watson dispersion from the NODDI model cannot describe all existing fibre arrangements in the brain accurately, e.g., the crossing fibre arrangement. However, in the optic chiasm specimen crossing-fibre arrangements were only found in a few regions, e.g., at the crossing of the optical tract and optic nerve. Therefore, the contribution of such crossing-fibre voxels with estimated κ values in the range of highly to mildly dispersed fibres will be averaged-out with the single-fibre orientation voxels with similar κ values during the irregular binning pre-processing (section 3.3.1). However, this could result in an increasing standard deviation in the estimated α-parameters in the log-linear model and β-parameters in the log-quadratic model.
6. Conclusion
We showed that our recently introduced biophysical log-quadratic model (M2) of the multi-echo gradient-recall echo (meGRE) signal can estimate the fibre-angular-orientation independent part of R2* (R2,iso*) for varying g-ratio values and fibre dispersions. Thus, the estimated linear time-dependent parameter of M2, β1, provides an attractive alternative for estimating R2,iso* to standard methods that require multiple acquisitions with distinct positioning of the sample in the head-coil. We also showed that β1 can be used to estimate the myelin water fraction (MWF) for ex vivo compartmental R2 values using a newly proposed heuristic expression relating β1 to microstructural tissue parameters including the myelin water signal. We provide a freely available simulation framework to test the validity of the heuristic expression for varying sets of microstructural parameters. We found that the heuristic expression cannot be used for in vivo compartmental R2 values.
Importantly, we found that an angular-independent β1 (and thus R2,iso*) cannot be estimated with the log-quadratic model for meGRE measurements with maximum shorter echo times, that are typically used for whole-brain in vivo meGRE experiments. Therefore, it indicates that we need to develop new meGRE protocols with longer echo times that remain time efficient and motion robust. This could be achieved by using highly accelerated acquisitions with a higher data sampling for shorter echo times. Finally, at echo time ranges of about 18 ms, an unexpected R2* orientation-dependence was found in the ex vivo dataset at angles below the magic angle: a decrease of R2* for increasing angles. However, more testing is required to confirm that our finding can be generalised to other brain regions and specimens since our results are based on thorough measurements of one human optic chiasm tissue sample.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
FF: conceptualization, MRI data analysis, in-silico data analysis and manuscript’s writer. LM and MC: manuscript review. MA: MRI data pre-processing and acquisition. JP and AP: MRI data acquisition and protocol design. MM: Ex-vivo specimen preparation and containment, manuscript review. CJ: Ex-vivo specimen preparation and containment. TN and NW: resources and manuscript review. KP: MRI data acquisition and protocol design, manuscript review. SM: conceptualization, funding acquisition, co-writer of the manuscript and manuscript review, supervision. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the German Research Foundation (DFG Priority Program 2041 “Computational Connectomics,” [AL 1156/2-1;GE 2967/1-1; MO 2397/5-1; MO 2249/3-1; MO 2397/5-2], by the Emmy Noether Stipend: MO 2397/4-1, MO 2397/4-2) and by the BMBF (01EW1711A and B) in the framework of ERA-NET NEURON and the Forschungszentrums Medizintechnik Hamburg (fmthh; grant 01fmthh2017). The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007–2013) / ERC grant agreement n° 616,905. MFC is supported by the MRC and Spinal Research Charity through the ERA-NET Neuron joint call (MR/R000050/1). The Wellcome Centre for Human Neuroimaging is supported by core funding from the Wellcome [203,147/Z/16/Z]. The Max Planck Institute for Human Cognitive and Brain Sciences has an institutional research agreement with Siemens Healthcare. NW holds a patent on acquisition of MRI data during spoiler gradients (US 10,401,453 B2). NW was a speaker at an event organized by Siemens Healthcare and was reimbursed for the travel expenses.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2023.1133086/full#supplementary-material
Footnotes
2. ^http://www.fil.ion.ucl.ac.uk/spm
3. ^https://github.com/quantitative-mri-and-in-vivo-histology/r2s_iso_estimation
References
Alonso-Ortiz, E., Levesque, I. R., and Pike, G. B. (2018). Impact of magnetic susceptibility anisotropy at 3 T and 7 T on T2*-based myelin water fraction imaging. NeuroImage 182, 370–378. doi: 10.1016/j.neuroimage.2017.09.040
Assaf, Y., and Cohen, Y. (2000). Assignment of the water slow-diffusing component in the central nervous system using q-space diffusion MRS: implications for fiber tract imaging. Magn. Reson. Med. 43, 191–199. doi: 10.1002/(SICI)1522-2594(200002)43:2<191::AID-MRM5>3.0.CO;2-B
Bartels, L. M., Doucette, J., Birkl, C., Zhang, Y., Weber, A. M., and Rauscher, A. (2022). Orientation dependence of R2 relaxation in the newborn brain. NeuroImage 264:119702. doi: 10.1016/j.neuroimage.2022.119702
Basser, P. J., Mattiello, J., and LeBihan, D. (1994). MR diffusion tensor spectroscopy and imaging. Biophys. J. 66, 259–267. doi: 10.1016/S0006-3495(94)80775-1
Beaulieu, C., Fenrich, F. R., and Allen, P. S. (1998). Multicomponent water proton transverse relaxation and T2-discriminated water diffusion in myelinated and nonmyelinated nerve. Magn. Reson. Imaging 16, 1201–1210. doi: 10.1016/s0730-725x(98)00151-9
Birkl, C., Doucette, J., Fan, M., Hernández-Torres, E., and Rauscher, A. (2021). Myelin water imaging depends on white matter fiber orientation in the human brain. Magn. Reson. Med. 85, 2221–2231. doi: 10.1002/mrm.28543
Burnham, K. P., and Anderson, D. R. (2002). Model selection and multimodel inference: a practical information-theoretic approach. Springer New York, NY: Springer Verlag.
Burnham, K. P., Anderson, D. R., and Huyvaert, K. P. (2011). AIC model selection and multimodel inference in behavioral ecology: some background, observations, and comparisons. Behav. Ecol. Sociobiol. 65, 23–35. doi: 10.1007/s00265-010-1029-6
Bydder, M., Rahal, A., Fullerton, G. D., and Bydder, G. M. (2007). The magic angle effect: a source of artifact, determinant of image contrast, and technique for imaging. J. Magn. Reson. Imaging 25, 290–300. doi: 10.1002/jmri.20850
Callaghan, M. F., Freund, P., Draganski, B., Anderson, E., Cappelletti, M., Chowdhury, R., et al. (2014). Widespread age-related differences in the human brain microstructure revealed by quantitative magnetic resonance imaging. Neurobiol. Aging 35, 1862–1872. doi: 10.1016/j.neurobiolaging.2014.02.008
Chan, K.-S., and Marques, J. P. (2020). Multi-compartment relaxometry and diffusion informed myelin water imaging – promises and challenges of new gradient echo myelin water imaging methods. NeuroImage 221:117159. doi: 10.1016/j.neuroimage.2020.117159
Chavhan, G. B., Babyn, P. S., Thomas, B., Shroff, M. M., and Haacke, E. M. (2009). Principles, techniques, and applications of T2*-based MR imaging and its special applications. Radiographics 29, 1433–1449. doi: 10.1148/rg.295095034
Does, M. D. (2018). Inferring brain tissue composition and microstructure via MR relaxometry. NeuroImage 182, 136–148. doi: 10.1016/j.neuroimage.2017.12.087
Does, M. D., and Gore, J. C. (2000). Compartmental study of diffusion and relaxation measured in vivo in normal and ischemic rat brain and trigeminal nerve. Magn. Reson. Med. 43, 837–844. doi: 10.1002/1522-2594(200006)43:6<837::aid-mrm9>3.0.co;2-o
Draganski, B., Ashburner, J., Hutton, C., Kherif, F., Frackowiak, R. S. J., Helms, G., et al. (2011). Regional specificity of MRI contrast parameter changes in normal ageing revealed by voxel-based quantification (VBQ). NeuroImage 55, 1423–1434. doi: 10.1016/j.neuroimage.2011.01.052
Dula, A. N., Gochberg, D. F., Valentine, H. L., Valentine, W. M., and Does, M. D. (2010). Multiexponential T2, magnetization transfer, and quantitative histology in white matter tracts of rat spinal cord. Magn. Reson. Med. 63, 902–909. doi: 10.1002/mrm.22267
Duyn, J. H. (2014). Frequency shifts in the myelin water compartment. Magn. Reson. Med. 71, 1953–1955. doi: 10.1002/mrm.24983
Duyn, J. H., and Schenck, J. (2017). Contributions to magnetic susceptibility of brain tissue. NMR Biomed. 30:e3546. doi: 10.1002/nbm.3546
Elster, A. D. (1993). Gradient-echo MR imaging: techniques and acronyms. Radiology 186, 1–8. doi: 10.1148/radiology.186.1.8416546
Emmenegger, T. M., David, G., Ashtarayeh, M., Fritz, F. J., Ellerbrock, I., Helms, G., et al. (2021). The influence of radio-frequency transmit field inhomogeneities on the accuracy of G-ratio weighted imaging. Front. Neurosci. 15:770. doi: 10.3389/fnins.2021.674719
Fedorov, A., Beichel, R., Kalpathy-Cramer, J., Finet, J., Fillion-Robin, J.-C., Pujol, S., et al. (2012). 3D slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imaging 30, 1323–1341. doi: 10.1016/j.mri.2012.05.001
Fritz, F. J., Ashtarayeh, M., Periquito, J., Pohlmann, A., Morawski, M., Jaeger, C., et al., (2021). Effects of fibre dispersion and myelin content on R2*: Simulations and post-mortem experiments. In: Proceedings of the 2021 ISMRM & SMRT Virtual Conference & Exhibition. Presented at the International Society of Magnetic Resonance Imaging (ISMRM).
Fritz, F. J., Edwards, L. J., Streubel, T., Pine, K. J., Weiskopf, N., and Mohammadi, S., (2020). Simulating the effect of axonal dispersion and noise on anisotropic R2* relaxometry in white matter. In: Proceedings of the 2020 ISMRM & SMRT Virtual Conference & Exhibition. Presented at the International Society of Magnetic Resonance Imaging (ISMRM).
Gil, R., Khabipova, D., Zwiers, M., Hilbert, T., Kober, T., and Marques, J. P. (2016). An in vivo study of the orientation-dependent and independent components of transverse relaxation rates in white matter. NMR Biomed. 29, 1780–1790. doi: 10.1002/nbm.3616
Gudbjartsson, H., and Patz, S. (1995). The rician distribution of noisy mri data. Magn. Reson. Med. 34, 910–914. doi: 10.1002/mrm.1910340618
Han, S. H., Cho, F. H., Song, Y. K., Paulsen, J., Song, Y. Q., Kim, Y. R., et al. (2014). Ultrafast 3D spin-echo acquisition improves gadolinium-enhanced MRI signal contrast enhancement. Sci. Rep. 4:5061. doi: 10.1038/srep05061
Hédouin, R., Metere, R., Chan, K.-S., Licht, C., Mollink, J., van Walsum, A.-M. C., et al. (2021). Decoding the microstructural properties of white matter using realistic models. NeuroImage 237:118138. doi: 10.1016/j.neuroimage.2021.118138
Jeurissen, B., Descoteaux, M., Mori, S., and Leemans, A. (2019). Diffusion MRI fiber tractography of the brain. NMR Biomed. 32:e3785. doi: 10.1002/nbm.3785
Kellman, P., and McVeigh, E. R. (2005). Image reconstruction in SNR units: a general method for SNR measurement. Magn. Reson. Med. 54, 1439–1447. doi: 10.1002/mrm.20713
Kim, T. H., Bilgic, B., Polak, D., Setsompop, K., and Haldar, J. P. (2019). Wave-LORAKS: combining wave encoding with structured low-rank matrix modeling for more highly accelerated 3D imaging. Magn. Reson. Med. 81, 1620–1633. doi: 10.1002/mrm.27511
Kirilina, E., Helbling, S., Morawski, M., Pine, K., Reimann, K., Jankuhn, S., et al. (2020). Superficial white matter imaging: contrast mechanisms and whole-brain in vivo mapping. Sci. Adv. 6:eaaz9281. doi: 10.1126/sciadv.aaz9281
Kleban, E., Gowland, P., and Bowtell, R. (2021). Probing the myelin water compartment with a saturation-recovery, multi-echo gradient-recalled echo sequence. Magn. Reson. Med. 86, 167–181. doi: 10.1002/mrm.28695
Knight, M. J., Dillon, S., Jarutyte, L., and Kauppinen, R. A. (2017). Magnetic resonance relaxation anisotropy: physical principles and uses in microstructure imaging. Biophys. J. 112, 1517–1528. doi: 10.1016/j.bpj.2017.02.026
Kucharczyk, W., Macdonald, P. M., Stanisz, G. J., and Henkelman, R. M. (1994). Relaxivity and magnetization transfer of white matter lipids at MR imaging: importance of cerebrosides and pH. Radiology 192, 521–529. doi: 10.1148/radiology.192.2.8029426
Labadie, C., Lee, J.-H., Rooney, W. D., Jarchow, S., Aubert-Frécon, M., Springer, C. S. Jr., et al. (2014). Myelin water mapping by spatially regularized longitudinal relaxographic imaging at high magnetic fields. Magn. Reson. Med. 71, 375–387. doi: 10.1002/mrm.24670
Langkammer, C., Krebs, N., Goessler, W., Scheurer, E., Ebner, F., Yen, K., et al. (2010). Quantitative MR imaging of brain iron: a postmortem validation study. Radiology 257, 455–462. doi: 10.1148/radiol.10100495
Lee, J., Shmueli, K., Kang, B.-T., Yao, B., Fukunaga, M., van Gelderen, P., et al. (2012). The contribution of myelin to magnetic susceptibility-weighted contrasts in high-field MRI of the brain. NeuroImage 59, 3967–3975. doi: 10.1016/j.neuroimage.2011.10.076
Lee, J., van Gelderen, P., Kuo, L.-W., Merkle, H., Silva, A. C., and Duyn, J. H. (2011). T2*-based fiber orientation mapping. NeuroImage 57, 225–234. doi: 10.1016/j.neuroimage.2011.04.026
Lee, J., Shin, H.-G., Jung, W., Nam, Y., Oh, S.-H., and Lee, J. (2017). An R2* model of white matter for fiber orientation and myelin concentration. NeuroImage 162, 269–275. doi: 10.1016/j.neuroimage.2017.08.050
Li, T.-Q., Yao, B., van Gelderen, P., Merkle, H., Dodd, S., Talagala, L., et al. (2009). Characterization of T2* heterogeneity in human brain white matter. Magn. Reson. Med. 62, 1652–1657. doi: 10.1002/mrm.22156
Liu, C. (2010). Susceptibility tensor imaging. Magn. Reson. Med. 63, 1471–1477. doi: 10.1002/mrm.22482
MacKay, A., Laule, C., Vavasour, I., Bjarnason, T., Kolind, S., and Mädler, B. (2006). Insights into brain microstructure from the T2 distribution. Magn. Reson. Imaging 24, 515–525. doi: 10.1016/j.mri.2005.12.037
Magerkurth, J., Volz, S., Wagner, M., Jurcoane, A., Anti, S., Seiler, A., et al. (2011). Quantitative T*2-mapping based on multi-slice multiple gradient echo flash imaging: retrospective correction for subject motion effects. Magn. Reson. Med. 66, 989–997. doi: 10.1002/mrm.22878
Milotta, G., Corbin, N., Lambert, C., Lutti, A., Mohammadi, S., and Callaghan, M. F. (2023). Mitigating the impact of flip angle and orientation dependence in single compartment R2* estimates via 2-pool modeling. Magn. Reson. Med. 89, 128–143. doi: 10.1002/mrm.29428
Minassian, H., and Huang, S. (1979). Effect of sodium azide on the ultrastructural preservation of tissues. J. Microsc. 117, 243–253. doi: 10.1111/j.1365-2818.1979.tb01180.x
Mohammadi, S., Carey, D., Dick, F., Diedrichsen, J., Sereno, M. I., Reisert, M., et al. (2015). Whole-brain in-vivo measurements of the axonal G-ratio in a group of 37 healthy volunteers. Front. Neurosci. 9:441. doi: 10.3389/fnins.2015.00441
Oh, S.-H., Kim, Y.-B., Cho, Z.-H., and Lee, J. (2013). Origin of B0 orientation dependent R2* (=1/T2*) in white matter. NeuroImage 73, 71–79. doi: 10.1016/j.neuroimage.2013.01.051
Ordidge, R. J., Gorell, J. M., Deniau, J. C., Knight, R. A., and Helpern, J. A. (1994). Relative assessment of brain iron levels using MRI at 3 tesla. Magn. Reson. Mater. Phys. Biol. Med. 2, 449–450. doi: 10.1007/BF01705295
Pampel, A., Müller, D. K., Anwander, A., Marschner, H., and Möller, H. E. (2015). Orientation dependence of magnetization transfer parameters in human white matter. NeuroImage 114, 136–146. doi: 10.1016/j.neuroimage.2015.03.068
Papazoglou, S., Streubel, T., Ashtarayeh, M., Pine, K. J., Edwards, L. J., Brammerloh, M., et al. (2019). Biophysically motivated efficient estimation of the spatially isotropic component from a single gradient-recalled echo measurement. Magn. Reson. Med. 82, 1804–1811. doi: 10.1002/mrm.27863
Port, J. D., and Pomper, M. G. (2000). Quantification and minimization of magnetic susceptibility artifacts on GRE images. J. Comput. Assist. Tomogr. 24, 958–964. doi: 10.1097/00004728-200011000-00024
Roebroeck, A., Miller, K. L., and Aggarwal, M. (2018). Ex vivo diffusion MRI of the human brain: technical challenges and recent advances. NMR Biomed. 32:e3941. doi: 10.1002/nbm.3941
Rudko, D. A., Klassen, L. M., de Chickera, S. N., Gati, J. S., Dekaban, G. A., and Menon, R. S. (2014). Origins of <em>R</em><sub class="stack">2</sub><sup class="stack">∗</sup> orientation dependence in gray and white matter. Proc. Natl. Acad. Sci. 111, E159–E167. doi: 10.1073/pnas.1306516111
Schmahmann, J. D., Pandya, D. N., Wang, R., Dai, G., D’Arceuil, H. E., de Crespigny, A. J., et al. (2007). Association fibre pathways of the brain: parallel observations from diffusion spectrum imaging and autoradiography. Brain 130, 630–653. doi: 10.1093/brain/awl359
Schmahmann, J. D., Schmahmann, J., and Pandya, D., (2009). Fiber pathways of the brain. Oxford University Press, USA.
Schyboll, F., Jaekel, U., Petruccione, F., and Neeb, H. (2019). Fibre-orientation dependent R1(=1/T1) relaxation in the brain: the role of susceptibility induced spin-lattice relaxation in the myelin water compartment. J. Magn. Reson. 300, 135–141. doi: 10.1016/j.jmr.2019.01.013
Shin, H.-G., Oh, S.-H., Fukunaga, M., Nam, Y., Lee, D., Jung, W., et al. (2019). Advances in gradient echo myelin water imaging at 3T and 7T. NeuroImage 188, 835–844. doi: 10.1016/j.neuroimage.2018.11.040
Sra, S., and Karp, D. (2013). The multivariate Watson distribution: maximum-likelihood estimation and other aspects. J. Multivar. Anal. 114, 256–269. doi: 10.1016/j.jmva.2012.08.010
Stikov, N., Perry, L. M., Mezer, A., Rykhlevskaia, E., Wandell, B. A., Pauly, J. M., et al. (2011). Bound pool fractions complement diffusion measures to describe white matter micro and macrostructure. NeuroImage 54, 1112–1121. doi: 10.1016/j.neuroimage.2010.08.068
Tax, C. M. W., Kleban, E., Chamberland, M., Baraković, M., Rudrapatna, U., and Jones, D. K. (2021). Measuring compartmental T2-orientational dependence in human brain white matter using a tiltable RF coil and diffusion-T2 correlation MRI. NeuroImage 236:117967. doi: 10.1016/j.neuroimage.2021.117967
Tofts, P. S. (2004). “Concepts: measurement and MR” in Quantitative MRI of the brain. ed. Tofts, P. (Wiley, New Jersey, U.S.: John Wiley & Sons, Ltd), 1–15.
Uddin, M. N., Figley, T. D., Solar, K. G., Shatil, A. S., and Figley, C. R. (2019). Comparisons between multi-component myelin water fraction, T1w/T2w ratio, and diffusion tensor imaging measures in healthy human brain structures. Sci. Rep. 9:2500. doi: 10.1038/s41598-019-39199-x
van Gelderen, P., and Duyn, J. H. (2019). White matter intercompartmental water exchange rates determined from detailed modeling of the myelin sheath. Magn. Reson. Med. 81, 628–638. doi: 10.1002/mrm.27398
Vannesjo, S. J., Wilm, B. J., Duerst, Y., Gross, S., Brunner, D. O., Dietrich, B. E., et al. (2015). Retrospective correction of physiological field fluctuations in high-field brain MRI using concurrent field monitoring. Magn. Reson. Med. 73, 1833–1843. doi: 10.1002/mrm.25303
Veraart, J., Novikov, D. S., and Fieremans, E. (2018). TE dependent diffusion imaging (TEdDI) distinguishes between compartmental T2 relaxation times. NeuroImage 182, 360–369. doi: 10.1016/j.neuroimage.2017.09.030
Wang, N., Zhang, J., Cofer, G., Qi, Y., Anderson, R. J., White, L. E., et al. (2019). Neurite orientation dispersion and density imaging of mouse brain microstructure. Brain Struct. Funct. 224, 1797–1813. doi: 10.1007/s00429-019-01877-x
Weber, A. M., Zhang, Y., Kames, C., and Rauscher, A. (2020). Myelin water imaging and R2* mapping in neonates: investigating R2* dependence on myelin and fibre orientation in whole brain white matter. NMR Biomed. 33:e4222. doi: 10.1002/nbm.4222
Weiskopf, N., Edwards, L. J., Helms, G., Mohammadi, S., and Kirilina, E. (2021). Quantitative magnetic resonance imaging of brain anatomy and in vivo histology. Nat. Rev. Phys. 3, 570–588. doi: 10.1038/s42254-021-00326-1
Weiskopf, N., Suckling, J., Williams, G., Correia, M. M., Inkster, B., Tait, R., et al. (2013). Quantitative multi-parameter mapping of R1, PD(*), MT, and R2(*) at 3T: a multi-center validation. Front. Neurosci. 7:95. doi: 10.3389/fnins.2013.00095
Wharton, S., and Bowtell, R. (2013). Gradient Echo based Fiber orientation mapping using R2* and frequency difference measurements. NeuroImage 83, 1011–1023. doi: 10.1016/j.neuroimage.2013.07.054
Wharton, S., and Bowtell, R. (2012). Fiber orientation-dependent white matter contrast in gradient echo MRI. Proc. Natl. Acad. Sci. 109, 18559–18564. doi: 10.1073/pnas.1211075109
Xu, T., Foxley, S., Kleinnijenhuis, M., Chen, W. C., and Miller, K. L. (2018). The effect of realistic geometries on the susceptibility-weighted MR signal in white matter. Magn. Reson. Med. 79, 489–500. doi: 10.1002/mrm.26689
Yablonskiy, D. A., and Haacke, E. M. (1994). Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn. Reson. Med. 32, 749–763. doi: 10.1002/mrm.1910320610
Yao, B., Li, T. -Q., Gelderen, P. Van, Shmueli, K., de Zwart, J. A., and Duyn, J. H., (2009). Susceptibility contrast in high field MRI of human brain as a function of tissue iron content. NeuroImage 44, 1259–1266. doi: 10.1016/j.neuroimage.2008.10.029
Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., and Alexander, D. C. (2012). NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage 61, 1000–1016. doi: 10.1016/j.neuroimage.2012.03.072
Ziegler, G., Hauser, T. U., Moutoussis, M., Bullmore, E. T., Goodyer, I. M., Fonagy, P., et al. (2019). Compulsivity and impulsivity traits linked to attenuated developmental frontostriatal myelination trajectories. Nat. Neurosci. 22, 992–999. doi: 10.1038/s41593-019-0394-3
Glossary
Keywords: effective transverse relaxation rate, biophysical model, R2*, orientation-independent R2*, myelin water fraction, g-ratio, fibre dispersion, multi-echo gradient recalled echo
Citation: Fritz FJ, Mordhorst L, Ashtarayeh M, Periquito J, Pohlmann A, Morawski M, Jaeger C, Niendorf T, Pine KJ, Callaghan MF, Weiskopf N and Mohammadi S (2023) Fiber-orientation independent component of R2* obtained from single-orientation MRI measurements in simulations and a post-mortem human optic chiasm. Front. Neurosci. 17:1133086. doi: 10.3389/fnins.2023.1133086
Edited by:
Helene Ratiney, CREATIS, Unité CNRS UMR 5220 – INSERM U1294 – Université Lyon 1 – INSA Lyon, FranceReviewed by:
José P. Marques, Radboud University, NetherlandsChristoph Birkl, Innsbruck Medical University, Austria
Copyright © 2023 Fritz, Mordhorst, Ashtarayeh, Periquito, Pohlmann, Morawski, Jaeger, Niendorf, Pine, Callaghan, Weiskopf and Mohammadi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francisco J. Fritz, Zi5sYWdvc2ZyaXR6QHVrZS5kZQ==; Siawoosh Mohammadi, bW9oYW1tYWRpQG1waWItYmVybGluLm1wZy5kZQ==
 Francisco J. Fritz
Francisco J. Fritz Laurin Mordhorst1
Laurin Mordhorst1 Markus Morawski
Markus Morawski Carsten Jaeger
Carsten Jaeger Thoralf Niendorf
Thoralf Niendorf Kerrin J. Pine
Kerrin J. Pine Martina F. Callaghan
Martina F. Callaghan Nikolaus Weiskopf
Nikolaus Weiskopf Siawoosh Mohammadi
Siawoosh Mohammadi