Voltage–Time Transformation Model for Threshold Switching Spiking Neuron Based on Nucleation Theory

In this study, we constructed a voltage–time transformation model (V–t Model) to predict and simulate the spiking behavior of threshold-switching selector-based neurons (TS neurons). The V–t Model combines the physical nucleation theory and the resistor–capacitor (RC) equivalent circuit and successfully depicts the history-dependent threshold voltage of TS selectors, which has not yet been modeled in TS neurons. Moreover, based on our model, we analyzed the currently reported TS devices, including ovonic threshold switching (OTS), insulator-metal transition, and silver- (Ag-) based selectors, and compared the behaviors of the predicted neurons. The results suggest that the OTS neuron is the most promising and potentially achieves the highest spike frequency of GHz and the lowest operating voltage and area overhead. The proposed V–t Model provides an engineering pathway toward the future development of TS neurons for neuromorphic computing applications.

Introduction

With the increasing demand for massive data storage and processing, conventional computing systems based on the von-Neumann architecture have encountered their limitations. Frequent data transition between the separated processor and memory units makes conventional computation less efficient. Recently, emerging neuromorphic computing is regarded as the next-generation computing paradigm. Unlike the conventional von-Neumann-based computing system, brain-inspired neuromorphic computing not only provides energy-efficient computation with high parallelism but also shortens the latency of data transmission by realizing in-memory computing within crossbar memory arrays (Ielmini and Wong, 2018; Hua et al., 2019; Woo et al., 2019). In a neuromorphic computing system, an artificial synapse provides an adjustable and long-lasting weight value. In addition, an artificial neuron integrates and processes signals from synapses and then transmits the processed signals to the next neural layer as inputs. Both synapses and neurons have been extensively studied based on solid-state devices for neuromorphic hardware implementation (Lee et al., 2019a; Woo et al., 2019; Zhang et al., 2020). However, the conventional complementary metal-oxide semiconductor- (CMOS-)based neuron circuit occupies large chip areas because it requires a large number of transistors and capacitors for generating spike signals. In contrast, the neuron circuit area can be 10 times smaller by using novel devices, such as magnetoresistance memory (MRAM) (Wu et al., 2019, 2020; Liang et al., 2020), phase-change memory (PCM) (Tuma et al., 2016), and threshold switching (TS) selector (Park et al., 2016; Song et al., 2018; Grisafe et al., 2019; Hatem et al., 2019; Hua et al., 2019), which is beneficial for ultrahigh density neuromorphic computing applications (Liang et al., 2021).

Among several novel device-based neurons, threshold-switching selector-based neurons (TS neurons) are especially promising for ultra-high density neuromorphic architectures due to their simpler and smaller neuronal circuits (Liang et al., 2021). A circuit-level model solving Kirchhoff’s Law based on the resistor–capacitor (RC) equivalent circuit has been proposed to describe the behavior of TS neurons (RC Model) (Chen et al., 2016; Wang et al., 2020). However, the RC Model oversimplified the TS neuron by assuming constant switching behavior of the TS selector. Indeed, the switching dynamics of the real TS selector is affected by the external electric field, which can be explained using the nucleation theory (Karpov et al., 2008; Lee et al., 2020). Specifically, the way the external electric field is previously accumulated determines the device behavior, and we regard this time-dependent phenomenon as history dependence. Consequently, the TS voltage (V_th) in the TS selector is history dependent rather than constant. In this study, aiming for constructing a more comprehensive and accurate neuron model, we proposed an improved voltage–time transformation model (V–t Model) on top of the original RC Model by considering the TS behavior both experimentally and theoretically.

In the following sections, we will first verify the spiking behavior of the TS neuron according to different synaptic weights. A silver- (Ag-)based TS selector was chosen to observe the switching dynamics and the history-dependent V_th of the device. Additionally, based on the nucleation theory, we will introduce a V–t transformation (V–t) equation to describe the variant V_th of the TS selector, and a V–t Model will be constructed. Furthermore, several types of TS neurons based on the reported TS selectors, including ovonic threshold switching (OTS) (Song et al., 2018; Hatem et al., 2019), insulator–metal transition (IMT) (Park et al., 2016), and Ag-based selectors (Grisafe et al., 2019; Hua et al., 2019), will be evaluated. The results suggest that the OTS neuron has the fastest spike frequency and a lower history-dependent V_th. The V–t Model not only successfully depicts and predicts the characteristics of TS neurons, but it also provides a useful engineering guideline for future high-performance neuron circuits for neuromorphic computing applications.

Experimental Details and Measurement Setup

Ag-Based Threshold Switching Selector

In this study, an Ag/hafnium oxide (HfO_x)/Pt TS selector was fabricated and investigated. The schematic illustration of the Ag-based TS selector is shown in Figure 1A. The Pt bottom layer was first deposited on a Ti/Si substrate using electron beam evaporation, followed by the silicon dioxide (SiO₂) layer deposition using plasma-enhanced chemical vapor deposition. After the photolithography process, the reactive ion etching of SiO₂ was applied to form a via contact with a diameter of 1 μm, which defines the effective device area. Then, the 4.5-nm-insulating HfO_x layer was deposited using atomic layer deposition. After that, 2-nm-thick Ag was deposited on the HfO_x layer using electron beam evaporation followed by rapid thermal annealing (RTA) at 500°C for 5 min to form Ag nanoparticles (NPs) as the active electrode. Finally, a 60-nm-thick Ni capping layer was deposited using electron beam deposition to prevent the oxidation of Ag NPs. Electrical measurements were performed using an Agilent B1500A and B1530A waveform generation/fast measurement unit at room temperature. Figure 1B shows the scanning electron microscope (SEM) image of Ag NPs. The size distribution of NPs is shown in the inset. Figure 1C shows the DC current-voltage (I-V) characteristics of the Ag/HfO_x/Pt TS selector with 500 DC cycles of TS and a compliance current (I_cc) of 0.1 mA. The device provides an extremely high on/off ratio (∼10⁹) and small V_th and hold voltage (V_hold) for both positive and negative bias, showing typical behaviors of Ag-based TS selectors as reported in the literature (Yoo et al., 2017).

FIGURE 1

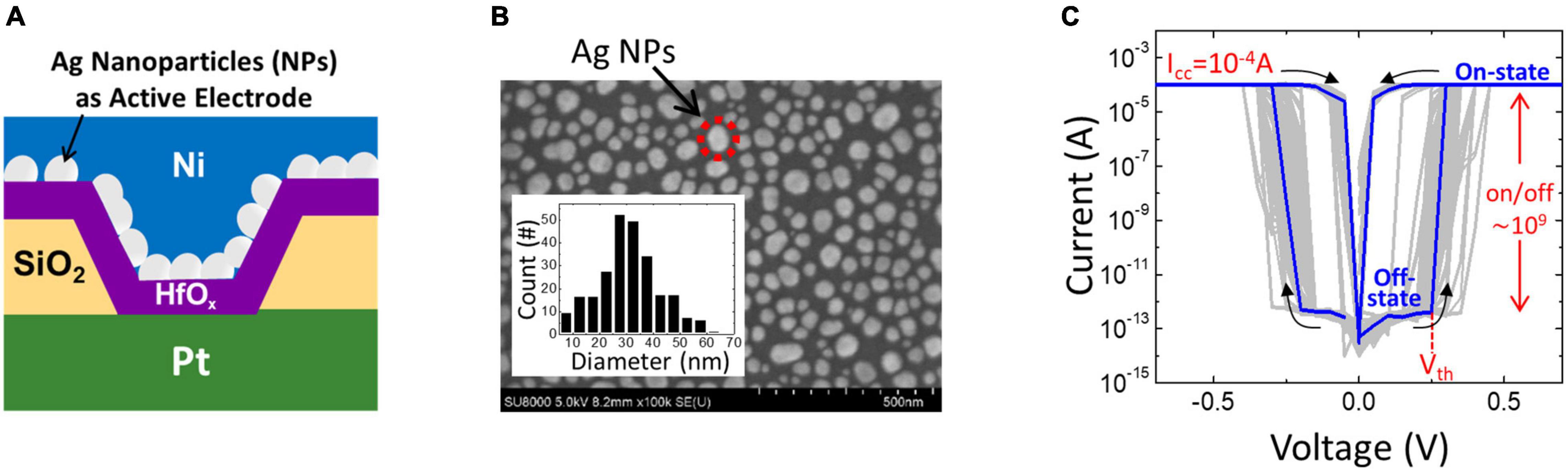
Figure 1. Silver- (Ag-) based threshold switching (TS) selector studied in this study. (A) The schematic structure showing the cross-section view of the Ag/hafnium oxide (HfO_x)/Pt device. (B) The top-view scanning electron microscope (SEM) image of Ag nanoparticles (NPs) with an average diameter of 30 nm formed by 500°C rapid thermal annealing (RTA) for 5 min. The inset shows the size distribution plot of the Ag NPs. (C) DC current–voltage (I–V) characteristics of the device with a current compliance of 0.1 mA, showing the success of TS for 500 DC cycles.

Threshold Switching Neuron Circuit

To emulate neuromorphic hardware in which synapses and neurons are connected in the neural network (Figure 2A), the measurement setup adopted in this study is illustrated in Figure 2B. The effective resistor connected in series (R_series) represents the total resistance of multiple synaptic devices in the synaptic array connecting in parallel to the same TS neuron. A parasitic capacitor (C_parasitic) of the TS selector is exploited; therefore, no extra capacitor is needed for signal integration. The evolution of the total current (I_total) flowing through R_series and the voltage across TS selector (V_selector) is described in Figure 2C: when a constant input voltage (V_input) is applied to the neuron circuit, most of the voltage initially drops across the TS selector in the off-state. Then, V_selector is gradually increased by charging C_parasitic. Once V_selector reaches V_th, the TS selector is switched to the on-state due to the formation of a volatile conducting filament, and an increase in I_total can be observed. However, V_selector drops right after the TS selector is switched to the on-state due to the discharge of C_parasitic, and I_total starts to decrease. The TS selector returns to the off-state when V_selector reduces to V_hold because of the rupture of the volatile conducting filament. t_on and t_off define the required period of time for the selector to be turned on (V_selector to increase from V_hold to V_th) and off (V_selector to decrease from V_th to V_hold) in the neuron circuit, respectively. When the circuit is biased, a series of continuous current and voltage spikes are generated, and the spike frequency can be calculated as the number of spikes per second (Hz) accordingly. To fulfill the requirement of neural network applications, artificial neurons should be capable of generating different spike frequencies according to the weights of connected synapses, i.e., R_series. In the RC Model (Chen et al., 2016; Wang et al., 2020), the t_on in the TS neuron circuit is obtained by

FIGURE 2

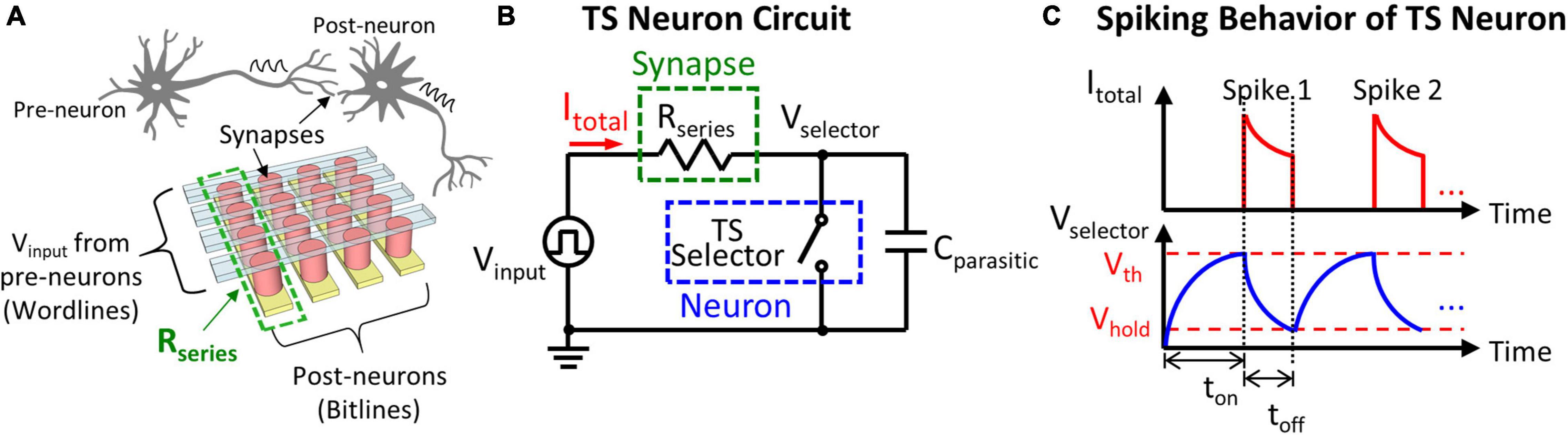
Figure 2. (A) Inspired by the biological neural network, neurons are connected with synapses through bit lines and word lines in the crossbar memory array. V_input received from the pre-neurons is applied on the word lines, and the post-neurons connected to bit lines generate output spikes according to the weight of synapses. (B) Equivalent circuit of the measurement setup where the synaptic devices along the same bit line (with a total resistance of R_series) are connected in series with a TS selector as a neuron. A parasitic capacitor C_parasitic is considered and is connected in parallel with the TS neuron. (C) The evolution of I_total and V_selector shows the spiking behavior of the TS neuron when V_input is applied due to the charging and discharging of C_parasitic. t_on and t_off define the required period of time for the TS selector to turned on and off in the neuron circuit, respectively.

$t_{\text{on}}=-R_{\text{series}}{C}_{\text{series}}\times \text{ln}\left(\left|\frac{V_{\text{input}}-V_{\text{th}}}{V_{\text{input}}-V_{\text{hold}}}\right|\right)(1)$

In this study, we assume that the IR voltage drop on R_series is negligible when the TS selector is at its off-state due to the low leakage current (below pA in our case). Figure 3A illustrates the statistically measured t_on of the TS neuron when connecting to different R_series, and the inset is an example of experimentally obtained current spikes (I_total) when R_series is 3,300 kΩ. Figure 3B presents the calculated spike frequency, as shown in Figure 3A. The results indicate that, with the decrease of R_series, t_on is decreased and the spike frequency is increased accordingly. However, the spike frequency cannot be further increased when R_series is < 100 kΩ. It is worth mentioning that R_series in the neuron circuit also acts as current compliance, where it controls the morphology and the size of conducting filaments in the TS selector (Chae et al., 2017). If R_series is too small, the filaments of extremely large size become non-volatile and cannot be ruptured even at V_hold = 0 V. Consequently, t_off increases and limits the spike frequency due to the difficult dissolution of large-size filaments in the TS selector. As a result, the resistance range of R_series requires careful adjustment (> 100 kΩ in our case) to prevent the dysfunction of neuron circuits. With a suitable range of R_series and with t_off being much smaller than t_on, the spike frequency is the inverse of t_on, thus proportional to the inverse of R_series, i.e., the effective total conductance of the synaptic array.

FIGURE 3

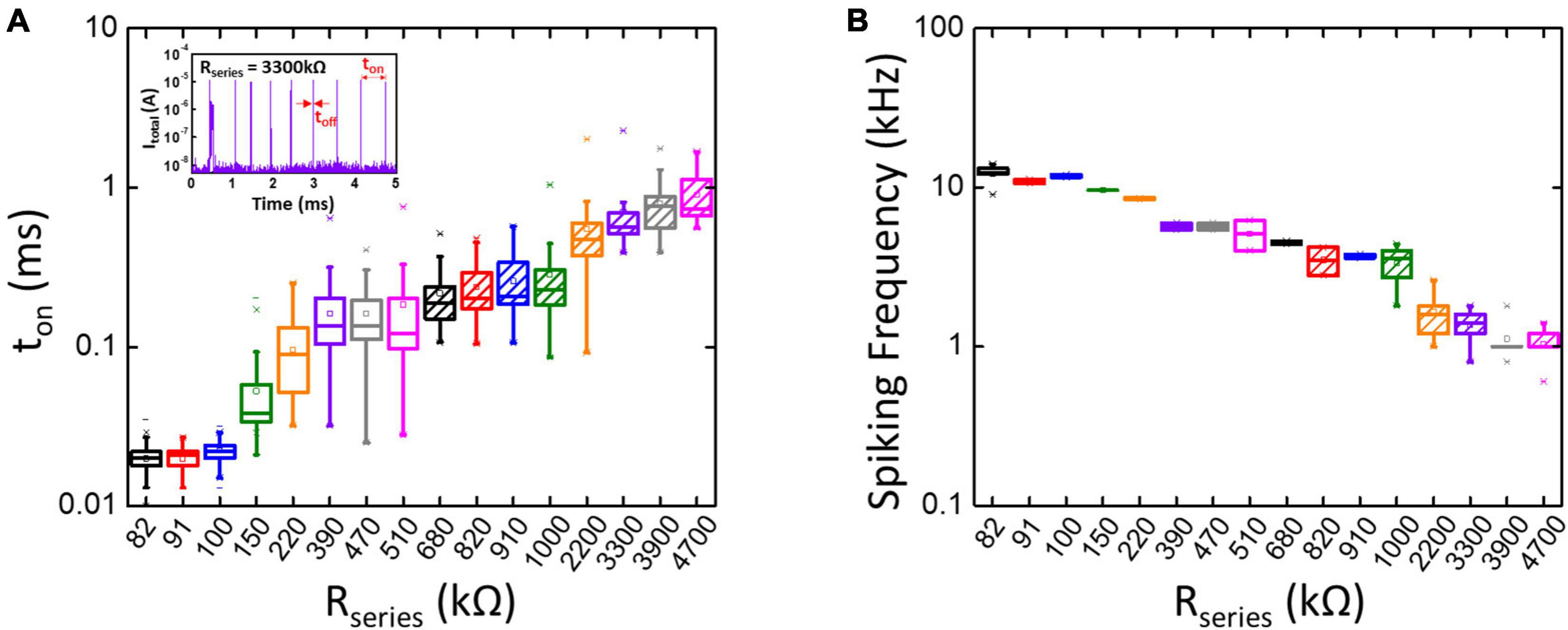
Figure 3. (A) The measured t_on increases with increasing R_series while the calculated spike frequency shown in panel (B) decreases with increasing R_series in the neuron circuit. The inset in panel (A) shows an example of the experimentally obtained spike current (I_total) when R_series is 3,300 kΩ. The spike frequency is defined by the number of spikes per second (Hz). The spike frequency is approximately equal to the inverse of t_on when R_series is greater than 100 kΩ and t_on is much larger than t_off.

Results and Discussion

History-Dependent V_th of the Threshold Switching Selector in Nueron Circuit

An important assumption of the RC Model in Equation 1 is that the V_th of the TS selector is constant. Figure 4A compares the measured V_th captured by an oscilloscope with R_series of 150 and 470 kΩ, and the statistical results are indicated in Figure 4B. Instead of remaining constant, the V_th of the TS selector varies with R_series. Different R_series modulate the charging rate of V_selector and give rise to the history-dependent V_th. The naïve RC model does not consider the history-dependent V_th of the TS selector, thus reducing the accuracy and prediction capability of the neuron model.

FIGURE 4

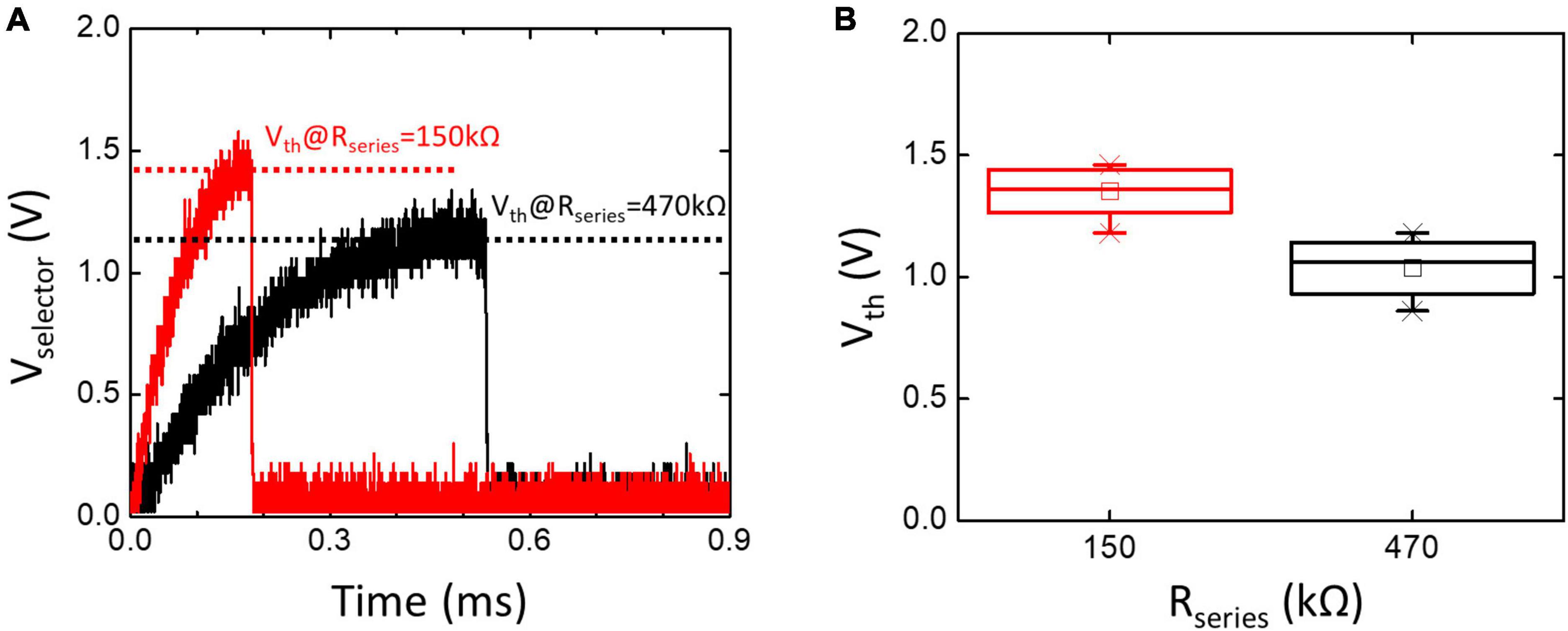
Figure 4. (A) The oscilloscope waveform of V_selector when the TS selector is connected with R_series of 150 and 470 kΩ and V_input = 2 V. Corresponding V_th is also indicated. (B) Statistically measured V_th increases with decreasing R_series. Instead of remaining constant, the history-dependent V_th needs to be carefully considered in the TS neuron model.

Voltage–Time Transformation Model

To include the characteristic of history-dependent V_th into the neuron model, the V–t Model is proposed. Starting from considering the switching dynamics of TS selectors when constant voltage stress (V_CVS) is applied directly on the device, i.e., V_selector equals to V_CVS. This is the case similar to Figure 2B but without the external R_series. The time delay before turning on the selector (t_{on_CVS}) is determined by the nucleation theory (Karpov et al., 2008; Lee et al., 2020):

$t_{\text{on\_CVS}}={\mathrm{\tau }}_0\exp \left(\frac{W_0{\mathrm{\alpha }}^{\frac{3}{2}}{E}_{0}d}{kT{V}_{\text{CVS}}}\right)(2)$

where τ₀ is the intrinsic time constant of the device, W₀ is the nucleation barrier energy without electric field, α is a geometric factor of a nucleus, E₀ is the voltage acceleration factor, d is the effective thickness of the insulating layer, k is Boltmann’s constant, and T is the ambient temperature. We define 𝔸 as a material-related constant at a fixed T, and (2) can be rewritten as

$𝔸=V_{\text{CVS}}\cdot \text{ln}\left(\frac{t_{\text{on\_CVS}}}{{\mathrm{\tau }}_0}\right)=\frac{W_0{\mathrm{\alpha }}^{\frac{3}{2}}{E}_{0}d}{kT}(3)$

where 𝔸 and τ₀ can be obtained from fitting the measured V_CVS and t_{on_CVS}. We assume 𝔸 remains constant when measuring the same device. Therefore, the V–t equation can be used to describe the transformation relation between any two arbitrary CVS voltages, V_CVS1 and V_CVS2, and their corresponding turn-on times, t_{on_CVS1} and t_{on_CVS2} as

$V_{\mathrm{CVS1}}\cdot \text{ln}\left(\frac{t_{\text{on}\mathrm{\_}\mathrm{CVS1}}}{{\mathrm{\tau }}_0}\right)=V_{\text{CVS}2}\cdot \text{ln}\left(\frac{t_{\text{on}\mathrm{\_}\mathrm{CVS2}}}{{\mathrm{\tau }}_0}\right)(4)$

When connecting the TS selector with R_series to form a complete TS neuron circuit, as shown in Figure 2B, V_selector becomes time-varying according to the RC equivalent circuit. The time-varying V_selector could be approximated using a finite number of CVS steps as depicted in Figure 5, which increase from (t₁, V₁) to (t₂, V₂) and eventually to (t_on, V_th) indicated by the blue line. ΔV and Δt are the voltage and time intervals, respectively. A similar conversion between CVS and ramp voltage stress has been reported and validated in resistive switching memory devices (Luo et al., 2013). As indicated in Figure 5, the stress effect of the (t₁, V₁) step indicated by the blue-filled rectangle on the device is transformed to that of an equivalent (t′₁, V₂) step indicated by the red dashed rectangle based on (4), t′₁ is therefore expressed as:

FIGURE 5

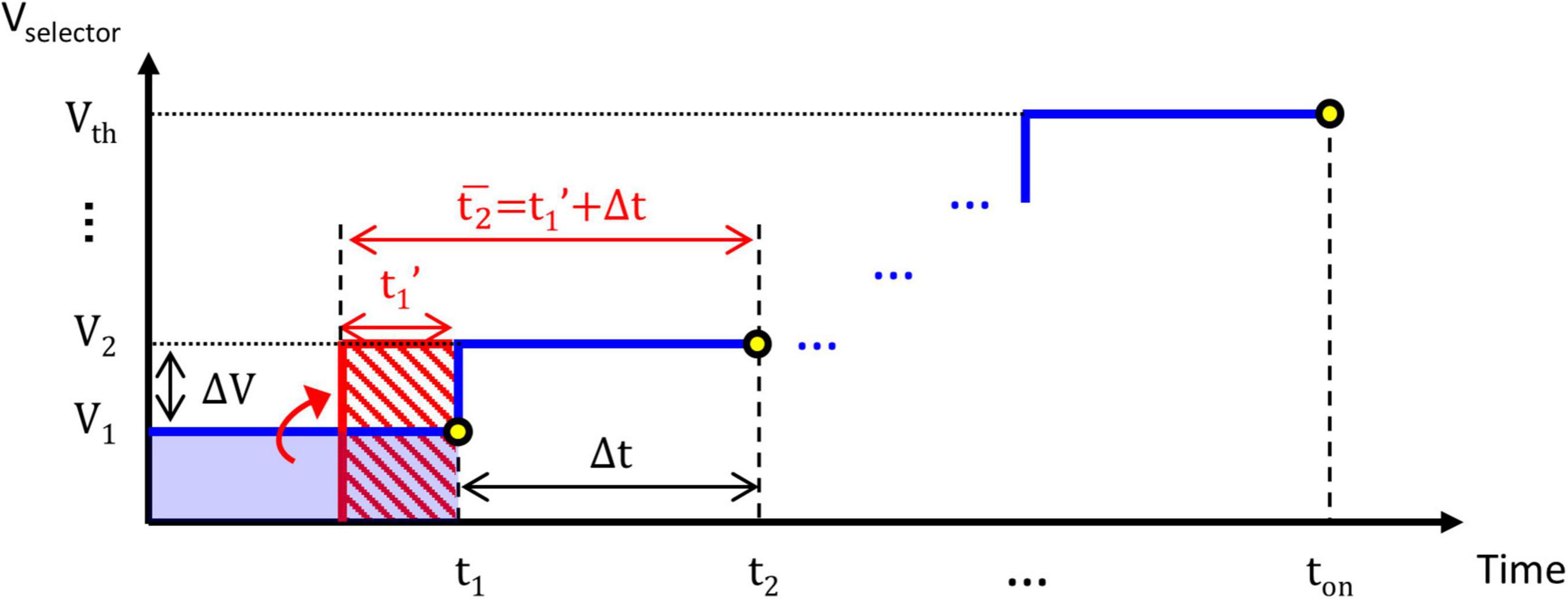
Figure 5. Time-varying V_selector in the neuron circuit is approximated using a finite number of constant voltage stress (CVS) steps from (t₁, V₁) to (t₂, V₂) and eventually to (t_on, V_th). ΔV and Δt determine the voltage and time intervals, respectively. Based on the proposed V–t Model, the transformed (t₁, V₂) step indicated by the red-dashed rectangle is equivalent to the (t₁, V₁) step indicated by the blue-filled rectangle. The new $\overline{{\mathbf{\text{t}}}_{\mathbf{2}}}$ of V₂ is now t′₁+Δt, which includes the history effect of the previously accumulated (t₁, V₁) step.

$t_1^{\prime }=\exp \left[\frac{V_1}{V_2}\cdot \text{ln}\left(\frac{t_1}{{\mathrm{\tau }}_0}\right)+\text{ln}\left({\mathrm{\tau }}_0\right)\right](5)$

A new equivalent CVS step of ($\overline{{\mathbf{\text{t}}}_{\mathbf{2}}}$, V₂) with an equivalent stress time of $\overline{{\mathbf{\text{t}}}_{\mathbf{2}}}$ = t′₁ + Δt at V₂ includes the history effect of the previous (V₁, t₁) step. This equivalent stress time is accumulated until it reaches the t_{on_CVS} at the stop voltage, i.e., V_th, which could be calculated by Equation 2. Under these circumstances, V_th becomes history-dependent and is affected by the RC charging process and R_series. The larger R_series, the lower V_th, and longer t_on.

To confirm the feasibility of the V–t Model on the prediction of the TS neuron behavior, the simulation results obtained from the RC Model (Chen et al., 2016; Wang et al., 2020) and the proposed V–t Model are compared in Figures 6A,B with the measurement. The RC Model only describes the RC behavior of the neuron circuit with a constant V_th of the TS selector, therefore it not only underestimates t_on but also fails to depict the history-dependent V_th of the TS selector. In contrast, the proposed V–t Model predicted well t_on and V_th of the TS selector under different R_series.

FIGURE 6

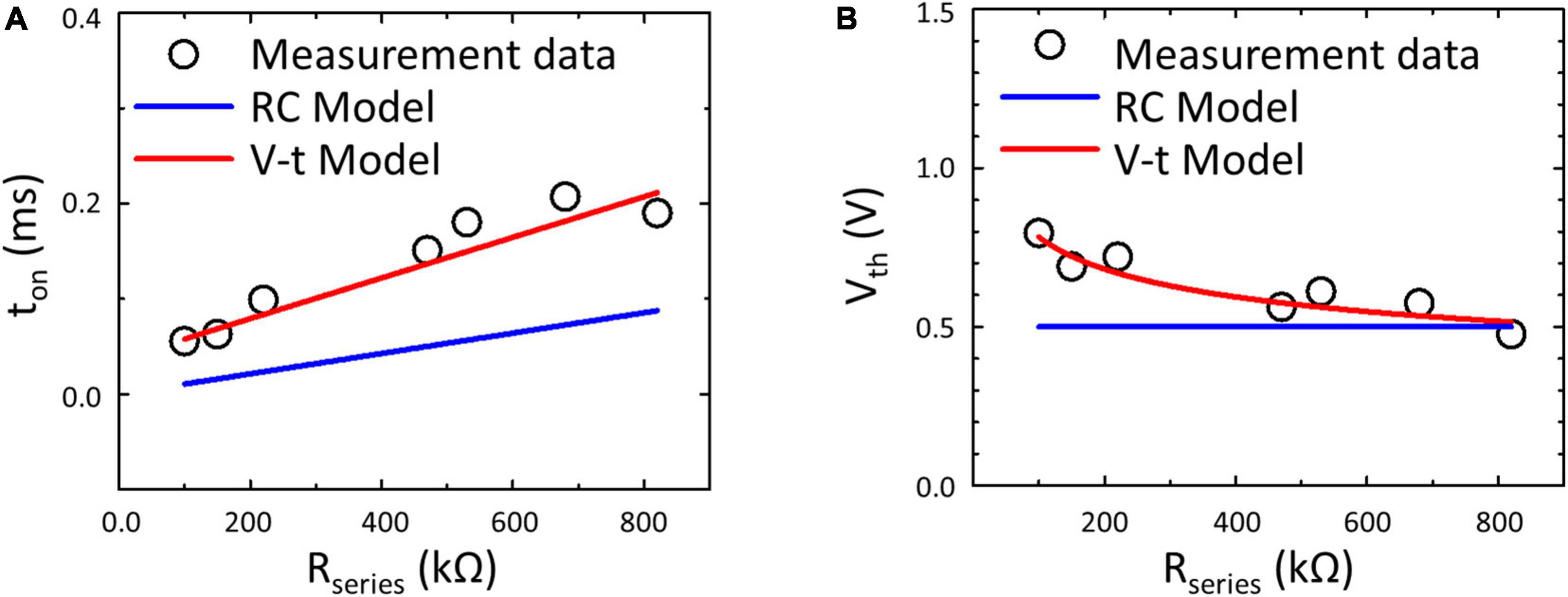
Figure 6. Measurement data and simulated results of (A) t_on and (B) V_th of the TS neuron with different R_series. The results suggest a more accurate prediction based on the V–t Model than the RC Model (Chen et al., 2016; Wang et al., 2020) by considering the history-dependent V_th of the TS selector.

Prediction of Threshold Switching Neuron Performance Based on V–t Model

In this section, we explored the impact of the TS selector on TS neurons, and the effect of t_on and 𝔸 on V_th can be predicted based on Equation 2. As shown in Figure 7, when t_on approaches τ₀, the voltage required for nucleation (V_th) approaches infinity. In addition, the TS selector with larger 𝔸 requires a higher V_th to be turned on. These results indicated that, under the same t_on, the TS selector with larger τ₀ and 𝔸 needs a higher applied voltage than the one with smaller τ₀ and 𝔸. However, the required high applied voltage is not favorable because it not only may result in an irreversible breakdown of the device but also may increase the difficulty of circuit integration. Therefore, the TS selector with larger τ₀ and 𝔸 may require an additional external integration capacitor to maintain a reasonable V_th, which on the other hand increases the circuit footprint and t_on and decreases the spike frequency. The energy consumption per spike of the neuron circuit could also increase due to slow spiking (Liang et al., 2021).

FIGURE 7

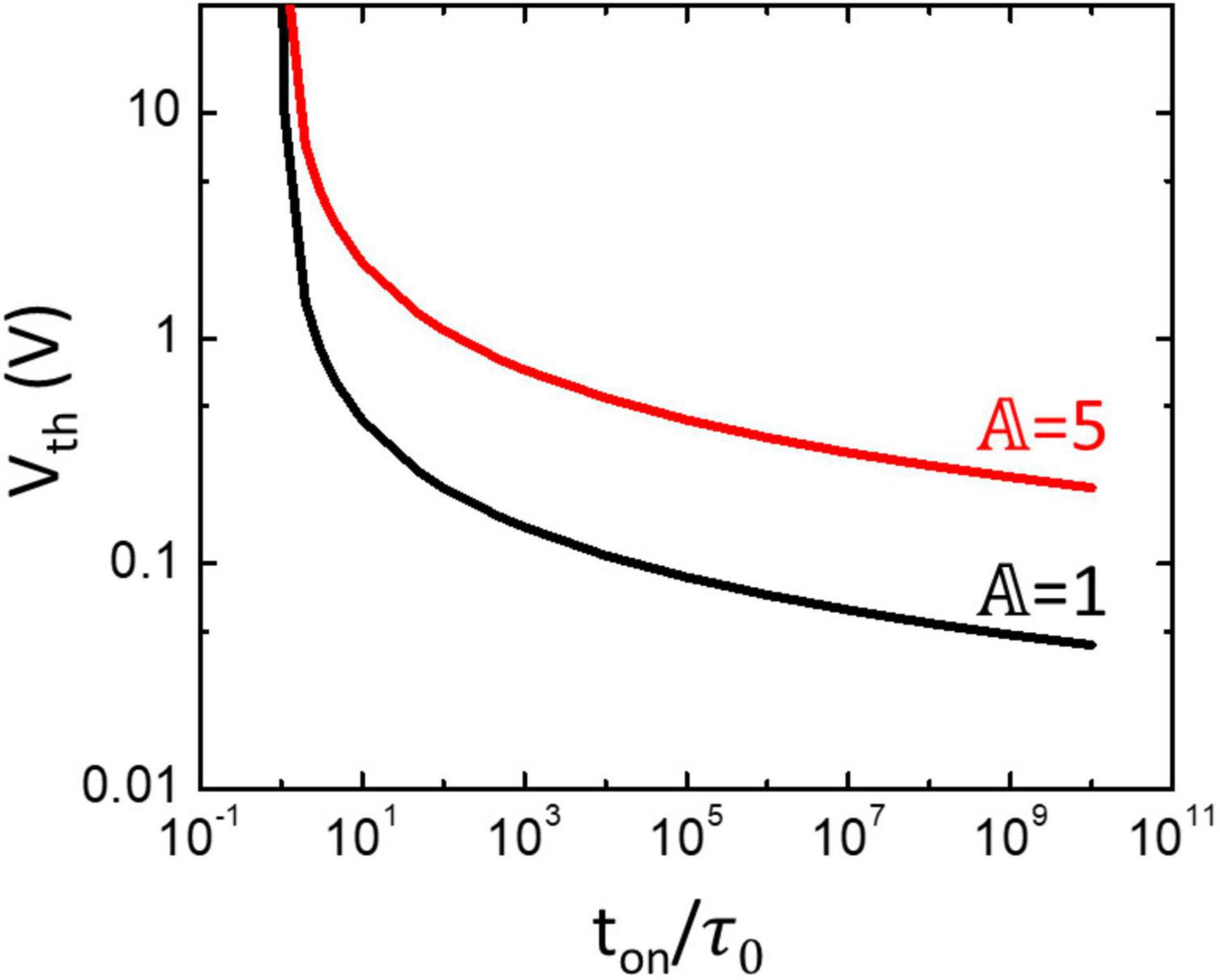
Figure 7. Relation between t_on, τ₀, 𝔸, and V_th of TS selectors based on the nucleation theory in Equation 2.

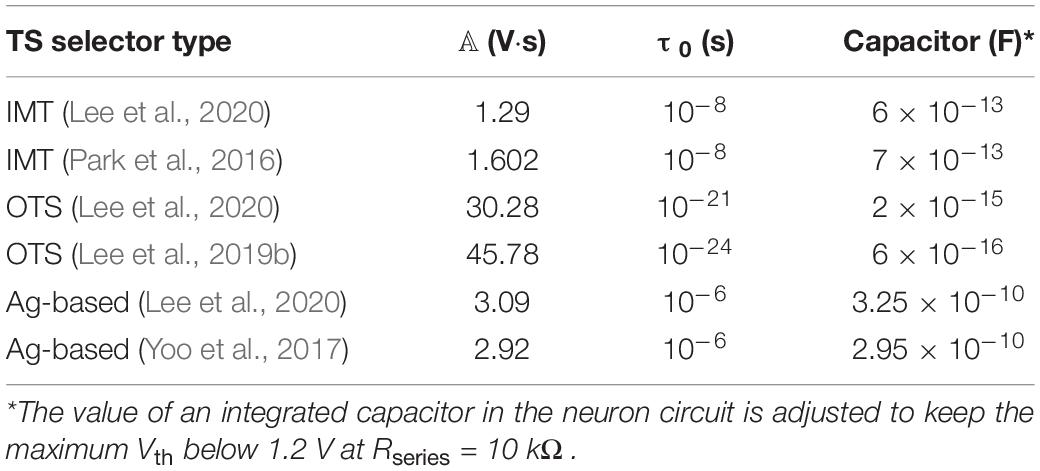
Table 1 lists the reported parameters of τ₀ and 𝔸 of different TS devices (Park et al., 2016; Yoo et al., 2017; Lee et al., 2019b,2020), and the simulated t_on and V_th of the neuron circuit based on the V–t Model are indicated in Figure 8. In this study, the R_series is given from 10 to 1,000 kΩ. The value of the integration capacitor in the neuron circuit is adjusted to keep the maximum V_th below 1.2 V at R_series = 10 kΩ, and the adopted capacitance corresponding to each TS device is also given. Among IMT, OTS, and Ag-based TS devices, the OTS neuron matched with the lowest capacitance is the most favorable for reducing the neuron circuit area. It is noted that the minimal integration capacitor is limited by the parasitic capacitor of the TS selector itself. As a result, the device area scaling would be necessary to achieve a low enough capacitance value. Moreover, the simulated t_on in Figure 8A shows that the OTS neuron is capable of achieving GHz-level spike frequency due to its extremely small τ₀ (10 ^{– 21}s), even though its 𝔸 is larger. Furthermore, in Figure 8B, the OTS selector with the smallest τ₀ results in a large t_on/τ₀; therefore, the V_th is less history dependent. The OTS selector shows promising potential not only in generating high spike frequency but also consuming less area and energy in the neuron circuit.

TABLE 1

Table 1. Key parameters extracted from the reported threshold switching (TS) selectors.

FIGURE 8

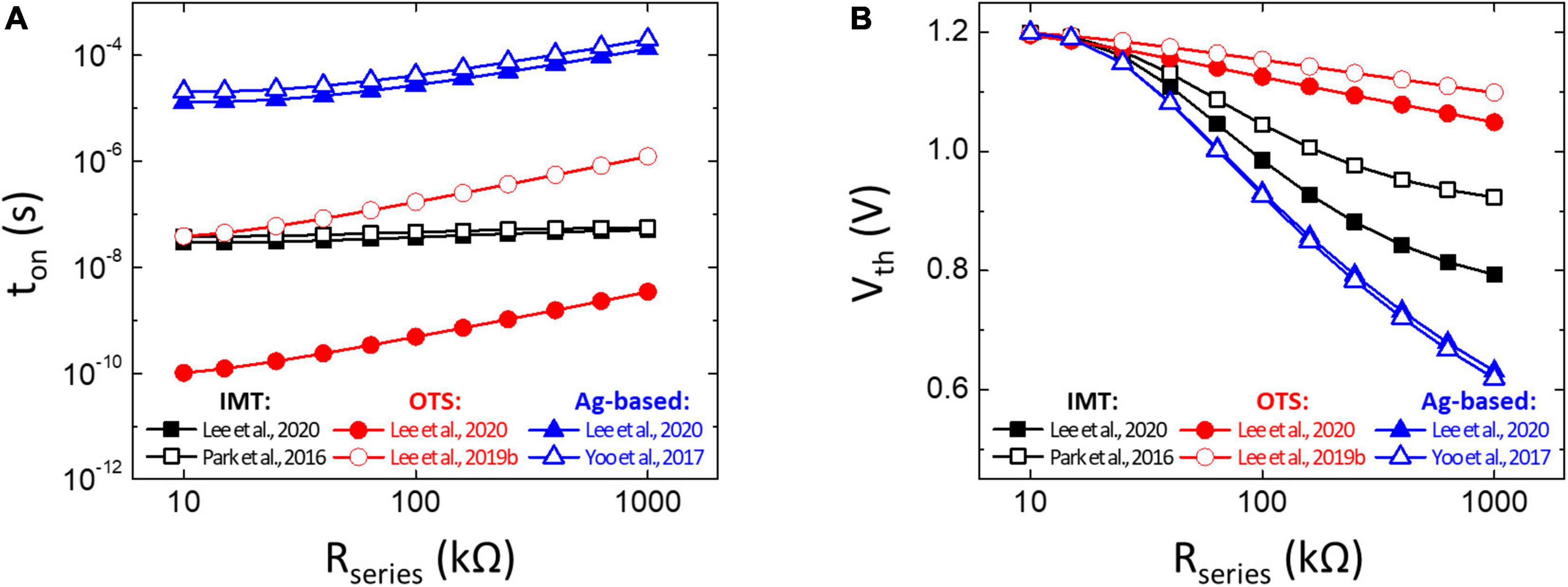
Figure 8. V–t Model prediction on (A) t_on and (B) V_th of the neuron circuit based on insulator–metal transition (IMT) (Park et al., 2016; Lee et al., 2020), ovonic threshold switching (OTS) (Lee et al., 2019b,2020), and Ag-based (Yoo et al., 2017; Lee et al., 2020) selectors. R_series is assumed to range from 10 kΩ to 1 MΩ. The value of an integrated capacitor in each condition is listed in Table 1.

Conclusion

In this study, a V–t Model is successfully constructed to simulate the spiking behavior of TS neurons according to the synaptic weight of connected synapses. By considering the history-dependent V_th of the TS selector based on the nucleation theory, the proposed V–t Model is in good agreement with the measurement results and provides more accurate prediction compared to the conventional RC Model. Moreover, the behavior of TS neurons based on different TS devices, including IMT, OTS, and Ag-based selectors, are simulated and compared using the proposed V–t Model. The results show that the OTS selector matched with the lowest capacitance that is the most favorable for reducing the circuit area overhead. Moreover, the OTS selector with the lowest τ₀ and t_on not only achieves less history-dependent V_th but also realizes a high-speed neuron with GHz-level spike frequency. The proposed V–t model provides a useful engineering pathway toward the future development of TS neurons.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

S-MY fabricated the device. S-MY and M-HW performed data analysis. S-MY, I-TW, M-HW, and T-HH contributed to the conception and discussion of the study. S-MY, I-TW, and T-HH drafted manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the Ministry of Science and Technology, Taiwan, under Grant Nos. 109-2221-E-009-020-MY3, 110-2221-E-A49-088-MY3, 110-2634-F-009-017, and 110-2622-8-009-018-SB.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chae, B.-G., Seol, J.-B., Song, J.-H., Baek, K., Oh, S.-H., Hwang, H., et al. (2017). Nanometer-scale phase transformation determins threshold and memory switching mechanism. Adv. Mater. 29:1701725. doi: 10.1002/adma.201701752

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, P.-Y., Seo, J.-S., Cao, Y., and Yu, S. (2016). “Compact oscillation neuron exploiting metal-insulator-transition for neuromorphic computing,” in Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), (Austin, TX: IEEE). doi: 10.1145/2966986.2967015

CrossRef Full Text | Google Scholar

Grisafe, B., Jerry, M., Smith, J. A., and Datta, S. (2019). Performance enhancement of Ag/HfO2 metal ion threshold switch cross-point selectors. IEEE Electron Device Lett. 40, 1602–1605. doi: 10.1109/LED.2019.2936104

CrossRef Full Text | Google Scholar

Hatem, F., Chai, Z., Zhang, W., Fantini, A., Degraeve, R., Clima, S., et al. (2019). “Endurance improvement of more than five orders in GexSe1-x OTS selectors by using a novel refreshing program scheme,” in Proceedings of the IEEE International Electron Devices Meeting (IEDM), (San Francisco, CA: IEEE), 827–830. doi: 10.1109/IEDM19573.2019.8993448

CrossRef Full Text | Google Scholar

Hua, Q., Wu, H., Gao, B., Zhao, M., Li, Y., Li, X., et al. (2019). A threshold switching selector based on highly ordered Ag nanodots for X-point memory applications. Adv. Sci. 6:1900024. doi: 10.1002/advs.201900024

PubMed Abstract | CrossRef Full Text | Google Scholar

Ielmini, D., and Wong, H.-S. P. (2018). In-memory computing with resistive switching devices. Nat. Electron. 1, 333–343. doi: 10.1038/s41928-018-0092-2

CrossRef Full Text | Google Scholar

Karpov, I. V., Mitra, M., Kau, D., Spadini, G., Kryukov, Y. A., and Karpov, V. G. (2008). Evidence of field induced nucleation in phase change memory. Appl. Phys. Lett. 92:173501. doi: 10.1063/1.2917583

CrossRef Full Text | Google Scholar

Lee, D., Kwak, M., Moon, K., Choi, W., Park, J., Yoo, J., et al. (2019a). Integrate and fire neuron based on various threshold switching devices with scalable device area and ultra-low power operation for neuromorphic system applications. Adv. Electron. Mater. 5:1800866. doi: 10.1002/aelm.201800866

CrossRef Full Text | Google Scholar

Lee, S., Yoo, J., Park, J., and Hwang, H. (2019b). Field-induced nucleation switching in binary ovonic threshold switches. Appl. Phys. Lett. 115:233503. doi: 10.1063/1.5126913

CrossRef Full Text | Google Scholar

Lee, S., Yoo, J., Park, J., and Hwang, H. (2020). Understanding of the abrupt resistive transition in different types of threshold switching devices from materials perspective. IEEE Trans. Electron Devices 67, 2878–2883. doi: 10.1109/TED.2020.2997670IEEE

CrossRef Full Text | Google Scholar

Liang, F.-X., Sahu, P., Wu, M.-H., Wei, J.-H., Sheu, S.-S., and Hou, T.-H. (2020). “Stochastic STT-MRAM spiking neuron circuit,” in Proceedings of International Symposium on VLSI Technology, Systems and Applications (VLSI-TSA), (Hsinchu: IEEE), 151–152. doi: 10.1109/VLSI-TSA48913.2020.9203701

CrossRef Full Text | Google Scholar

Liang, F.-X., Wang, I.-T., and Hou, T.-H. (2021). Progress and benchmark of spiking neuron devices and circuits. Adv. Intell. Syst. 3:2100007. doi: 10.1002/aisy.202100007

CrossRef Full Text | Google Scholar

Luo, W.-C., Liu, J.-C., Lin, Y.-C., Lo, C.-L., Huang, J.-J., Lin, K.-L., et al. (2013). Statistical model and rapid prediction of RRAM SET speed–disturb dilemma IEEE Trans. Electron Devices 60, 3760–3766. doi: 10.1109/TED.2013.2281991

CrossRef Full Text | Google Scholar

Park, J., Cha, E., Karpov, I., and Hwang, H. (2016). Dynamics of electroforming and electrically driven insulator-metal transition in NbOx selector. Appl. Phys. Lett. 108:232101. doi: 10.1063/1.4953323

CrossRef Full Text | Google Scholar

Song, B., Xu, H., Liu, S., Liu, H., and Li, Q. (2018). Threshold switching behavior of Ag-SiTe-based selector device and annealing effect on its characteristics. IEEE J. Electron Devices Soc. 6, 674–679. doi: 10.1109/JEDS.2018.2836400

CrossRef Full Text | Google Scholar

Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A., and Eleftheriou, E. (2016). Stochastic phase-change neurons. Nat. Nanotechnol. 11, 693–699. doi: 10.1038/nnano.2016.70

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Khan, A. I., and Yu, S. (2020). Cryogenic behavior of NbO2 based threshold switching devices as oscillation neurons. Appl. Phys. Lett. 116:162108. doi: 10.1063/5.0006467

CrossRef Full Text | Google Scholar

Woo, J., Wang, P., and Yu, S. (2019). Integrated crossbar array with resistive synapses and oscillation neurons. IEEE Electron Device Lett. 40, 1313–1316. doi: 10.1109/LED.2019.2921656

CrossRef Full Text | Google Scholar

Wu, M.-H., Hong, M.-C., Chang, C.-C., Sahu, P., Wei, J.-H., and Lee, H.-Y. (2019). “Extremely compact integrate-and-fire STT-MRAM neuron: a pathway toward all-spin artificial deep neural network,” in Proceedings of IEEE Symp. on VLSI Technol. (VLSI-T), T34-T35, (Kyoto: IEEE). doi: 10.23919/VLSIT.2019.8776569

CrossRef Full Text | Google Scholar

Wu, M.-H., Huang, M.-S., Zhu, Z., Liang, F.-X., Hong, M.-C., and Deng, J. (2020). “Compact probabilistic Poisson neuron based on back-hopping oscillation in STT-MRAM for all-spin deep spiking neural network,” in Proceedings of IEEE Symp. on VLSI Technol. (VLSI-T), JFS4.2.1-JFS4.2.2, (Honolulu, HI: IEEE). doi: 10.1109/VLSITechnology18217.2020.9265033

CrossRef Full Text | Google Scholar

Yoo, J., Park, J., Song, J., Lim, S., and Hwang, H. (2017). Field-induced nucleation in threshold switching characteristics of electrochemical metallization devices. Appl. Phys. Lett. 111:163109. doi: 10.1063/1.4985165

CrossRef Full Text | Google Scholar

Zhang, X., Wu, Z., Lu, J., Wei, J., Lu, J., Zhu, J., et al. (2020). “Fully memristive SNNs with temporal coding for fast and low-power edge computing,” in Proceedings of IEEE International Electron Devices Meeting (IEDM), (San Francisco, CA), 649–652. doi: 10.1109/IEDM13553.2020.9371937

CrossRef Full Text | Google Scholar