The Influence of Radio-Frequency Transmit Field Inhomogeneities on the Accuracy of G-ratio Weighted Imaging

G-ratio weighted imaging is a non-invasive, in-vivo MRI-based technique that aims at estimating an aggregated measure of relative myelination of axons across the entire brain white matter. The MR g-ratio and its constituents (axonal and myelin volume fraction) are more specific to the tissue microstructure than conventional MRI metrics targeting either the myelin or axonal compartment. To calculate the MR g-ratio, an MRI-based myelin-mapping technique is combined with an axon-sensitive MR technique (such as diffusion MRI). Correction for radio-frequency transmit (B1+) field inhomogeneities is crucial for myelin mapping techniques such as magnetization transfer saturation. Here we assessed the effect of B1+ correction on g-ratio weighted imaging. To this end, the B1+ field was measured and the B1+ corrected MR g-ratio was used as the reference in a Bland-Altman analysis. We found a substantial bias (≈-89%) and error (≈37%) relative to the dynamic range of g-ratio values in the white matter if the B1+ correction was not applied. Moreover, we tested the efficiency of a data-driven B1+ correction approach that was applied retrospectively without additional reference measurements. We found that it reduced the bias and error in the MR g-ratio by a factor of three. The data-driven correction is readily available in the open-source hMRI toolbox (www.hmri.info) which is embedded in the statistical parameter mapping (SPM) framework.

Introduction

The g-ratio [i.e., the ratio between the inner (r) and outer (R) radius of an axon with myelin sheath (g-ratio = r/R)] of a given axon quantifies the degree of relative myelination, ranging between 0 (no axon) and 1 (no myelin). The g-ratio captures both axonal and myelin damage by incorporating axonal and myelin volumes in one metric, making it potentially more specific to tissue integrity than focusing on one of these aspects only. For example, in multiple sclerosis, the g-ratio increases if the underlying disease mechanism is solely driven by demyelination (Yu et al., 2019), but is expected to remain unaffected if demyelination is accompanied by axonal degeneration. To differentiate such processes and understand their functional implications, neuroscience and clinical research would greatly benefit from in-vivo whole-brain measurements of MR g-ratio. Until recently, the g-ratio was measurable only by means of histology (Hildebrand and Hahn, 1978), which restricted the analyses to a small number of axons and a limited number of small brain regions or pathways. Stikov et al. (2011, 2015) introduced a methodology for an MRI-based whole-brain “aggregate” g-ratio mapping, to which we refer as “MR g-ratio” or “g-ratio weighted imaging.” In g-ratio weighted imaging, the MR g-ratio is computed on a voxel-by-voxel basis from the axonal (AVF) and myelin volume fraction (MVF) maps and reflects a weighted mean of g-ratio values within the voxel (West et al., 2016). Therefore, g-ratio weighted imaging requires the acquisition of separate sets of images that are sensitive to AVF and MVF, respectively (Campbell et al., 2018; Mohammadi and Callaghan, 2020). To generate MVF and AVF from the measured MR parameters, a calibration step is required that converts the measured MR-visible water signals into the respective volume fractions (Mohammadi and Callaghan, 2020).

Magnetization transfer saturation (MT_sat) has often been used as proxy for MVF (Mohammadi et al., 2015) as it is minimally affected by the longitudinal relaxation time (Helms et al., 2008) and is expected to show high correlation with macromolecular content (Sereno et al., 2013; Callaghan et al., 2015a; Campbell et al., 2018), making it a sensitive metric of MVF. One common approach to estimate AVF complements the parameters from neurite orientation and dispersion density imaging (NODDI Zhang et al., 2012) with a MVF-proxy, e.g., MT_sat (Ellerbrock and Mohammadi, 2018; Kamagata et al., 2019), to correct for the missing myelin water signal in diffusion MRI measurements (Stikov et al., 2015). Maps of MT_sat can be obtained, among others, from the multi-parameter mapping (MPM) protocol (Weiskopf et al., 2013) in combination with the hMRI toolbox¹ (Callaghan et al., 2019; Tabelow et al., 2019).

Although the MT_sat measure is largely insensitive to transmit field (B₁+) inhomogeneities (Helms et al., 2008), it still shows a residual dependence which introduces a bias and/or error in the MT_sat maps that can propagate into the MR g-ratio and lead to systematic bias. Such B₁+ inhomogeneities can be corrected based on an independently acquired B₁+ field map measurement (Helms, 2015; Helms et al., 2021). Residual B₁+ inhomogeneity effects on MT_sat have been shown to be not negligible when the B₁+ correction was omitted (Helms, 2015; Helms et al., 2021). However, the impact of B₁+ correction on MR g-ratio estimates is unknown. Additionally, it is unclear whether these residual B₁+ inhomogeneity in MT_sat and the MR g-ratio can retrospectively be corrected using a data-driven B₁+ field inhomogeneities estimation approach such as the “unified segmentation based correction of R1 maps for B₁+ inhomogeneities” (UNICORT, (Weiskopf et al., 2011)).

In this study, we investigate the effect of B₁+ inhomogeneities on MR g-ratio maps when omitting the B₁+ correction. As a reference, we use the B₁+ corrected MR g-ratio from a dataset of healthy controls. We compare the reference MR g-ratio values against (i) values obtained without B₁+ correction and (ii) values obtained with B₁+ correction using the data-driven UNICORT approach.

Materials and Methods

Subjects

This study included 25 healthy control subjects (12 females, age (mean ± standard deviation) of 25.4 ± 2.4 years). They were recruited at the University Medical Centre Hamburg-Eppendorf and screened for neurological or psychiatric illness. The study was in agreement with the Declaration of Helsinki and was approved by the local ethics committee (Ärztekammer Hamburg #PV5141).

Data Acquisition

Each subject was scanned twice within 1 week in a whole-body 3T Tim TRIO MR scanner (Siemens Healthcare, Erlangen, Germany) using the body RF-coil for transmission and a 32-channel radiofrequency (RF) head coil for signal reception, respectively. The MR acquisition on both scan days included a multi-parameter mapping (MPM) (Weiskopf et al., 2013; Callaghan et al., 2015b) and a diffusion-weighted imaging (DWI) protocol. The MPM protocol consists of three differently weighted 3D-multi-echo spoiled gradient echo sequences (Siemens FLASH). The echo train length and flip angle for the proton density (PD) weighted, T1-weighted, and magnetization transfer (MT) weighted sequences were 8/6, 8/21, and 6/6°, respectively. The MT-weighted sequence had a Gaussian RF pulse (2 kHz off resonance with 4 ms duration and a nominal flip angle of 220°). All other sequence parameters were the same for the three sequences: repetition time (TR) 25 ms, echo spacing, resolution 0.8 mm isotropic; field of view (FoV) 166 × 224 × 256 mm³, readout bandwidth 488 Hz/pixel, partially parallel imaging using the GRAPPA algorithm was employed in each phase-encoded direction (anterior-posterior and right-left) with 40 reference lines and a speed up factor of two, total acquisition time: ∼25 min. The B₁+ field reference map was acquired using the three-dimensional echo-planar imaging (3D EPI) method, including field maps for distortion correction (Lutti et al., 2010).

The DWI sequence was a twice-refocused single-shot spin-echo EPI scheme (Reese et al., 2003), consisting of 12 non-diffusion-weighted images (b₀ images), equidistantly distributed across the diffusion weighted images. The diffusion-weighted images were acquired at two b-values (1000$\frac{s}{m{m}^2}$ and 2000$\frac{s}{m{m}^2}$), sampled along 60 unique diffusion-gradient directions within each shell. The entire protocol was repeated with identical parameters but with reversed phase encoding direction (anterior-posterior) to correct for susceptibility-related image distortions (blip-up, blip-down correction). In total, 264 images were acquired per subject (120 diffusion-weighted images, 12 b₀ images, each acquired twice). Other acquisition parameters were: 86 slices with no gap, TR = 7.1 s, TE = 122 ms, an isotropic voxel size of (1.6 mm)³, FoV = 224 × 224 × 138 mm³, 7/8 partial Fourier imaging in phase encoding direction, readout bandwidth. To accelerate the data acquisition, GRAPPA (in-plane acceleration with factor two) and simultaneous multi-slice acquisitions (“multiband,” slice acceleration factor two) (Feinberg et al., 2010; Moeller et al., 2010; Xu et al., 2013) were used as described in Setsompop et al. (2012). The image reconstruction algorithm was provided by the University of Minnesota Centre for Magnetic Resonance Research. The total acquisition time was ∼37 min.

Data Processing

MT_sat maps were generated in the SPM-based hMRI toolbox (Tabelow et al., 2019). Note that the hMRI toolbox also generates additional maps of longitudinal (R₁) and effective transverse relaxation rates (${\text{R}}_2^{\star }$) and PD. Three MT_sat maps were generated: (i) ${\text{MT}}_{\text{sat}}^{\text{NO}}$ maps, without B₁+ correction; (ii) ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ map, using the reference B₁+ field map for correction (Lutti et al., 2010); and (iii) ${\text{MT}}_{\text{sat}}^{\text{UN}}$ maps, using the data-driven UNICORT approach for B₁+ estimation (Weiskopf et al., 2011; see Supplementary Figure 2). UNICORT is a probabilistic framework for unified-segmentation based correction of R₁ maps for B₁+ inhomogeneities. The framework incorporates a physically informed generative model of smooth B₁+ inhomogeneities and their multiplicative effect on R₁ estimates (Weiskopf et al., 2011). Parameters used in UNICORT such as the smoothness and regularization were optimized for R₁ B₁+ correction in a 3T scanner (i.e., Tim Trio scanner—Weiskopf et al., 2011).

For B₁+ correction, we used the following heuristic correction factor as detailed in Helms (2015), and Helms et al. (2021):

${\text{MT}}_{\text{sat}}^{\text{Corr}}={\text{MT}}_{\text{sat}}^{\text{NO}}\frac{1-C}{1-C{\text{B}}_1^{+}},(1)$

where C has been calibrated to be 0.4 for the MT pulse used in this paper. B₁+ can be either measured (${\text{MT}}_{\text{sat}}^{\text{Corr}}={\text{MT}}_{\text{sat}}^{\mathrm{B1}}$) or estimated with the UNICORT approach (${\text{MT}}_{\text{sat}}^{\text{Corr}}={\text{MT}}_{\text{sat}}^{\text{UN}}$).

The DWI data were processed based on the pipeline described in Ellerbrock and Mohammadi (2018) using the SPM-based ACID toolbox². It included several artifact corrections such as Rician signal bias correction (i.e., denoising) (André et al., 2014), correction for eddy current and motion artifacts (Mohammadi et al., 2010, 2014), and correction for image distortions due to susceptibility artifact using reversed phase encoding (Ruthotto et al., 2012, 2013; Macdonald and Ruthotto, 2018). The corrected images were fitted with the NODDI signal model (Zhang et al., 2012) to estimate the intra-cellular volume fraction (ν_icvf), the isotropic volume fraction (ν_iso), and the orientation dispersion index (ODI) in each voxel.

Spatial Alignment

Co-registration

The voxel-wise arithmetic between the MT_sat and ν_icvf maps, necessary for MR g-ratio computation, requires an accurate spatial alignment between the two maps (Mohammadi et al., 2015). To this end, we created two white matter (WM) tissue probability maps (TPMs) based on the ODI and ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ maps, respectively (Figure 1). To reduce the influence of contrast-specific artifacts (e.g., due to subject motion) on the registration quality, the WM TPM of the ODI map was co-registered to the WM TPM of the ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ map using rigid-body registration (spm_coreg algorithm, SPM toolbox). The estimated transformation parameters were applied to all other NODDI maps as well. Note that the segmentation quality of the second session was unsatisfactory for two subjects, and the ${\text{R}}_1^{{\text{B}}_1}$ map (R₁ with B₁+ inhomogeneities bias correction using the B₁+ reference measurements) was used to generate the WM TPM instead. In another subject, the ν_iso was segmented instead of the ODI to achieve satisfactory WM segments.

FIGURE 1

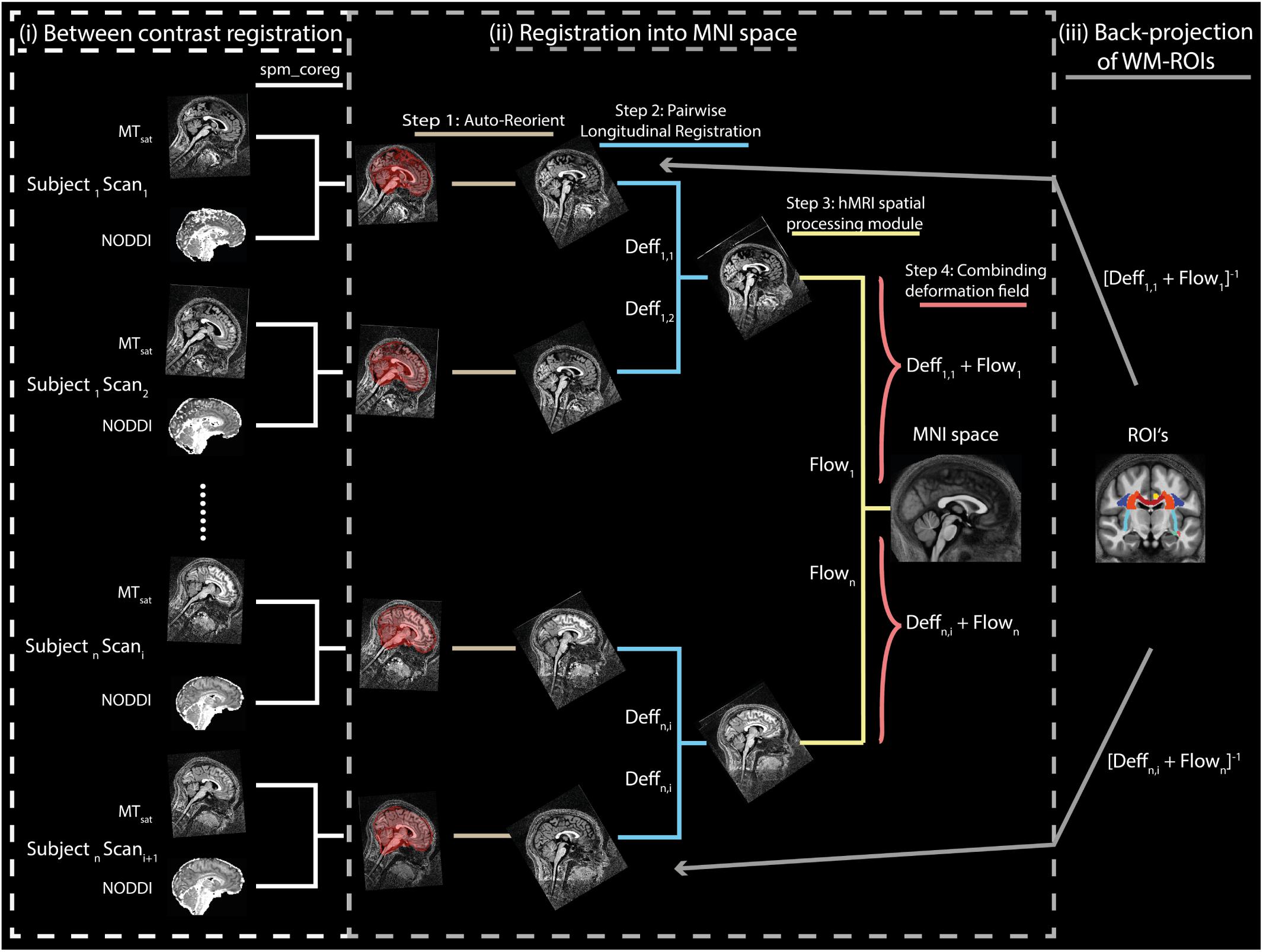
Figure 1. Illustration of the spatial alignment pipeline of the MT_sat and NODDI maps. The pipeline consists of (i) co-registration between MT_sat and NODDI maps (driven by ODI map), (ii) normalization into MNI space, and (iii) back-projection of ROIs into the native space. Note that each subject consists of two sets of images acquired in separate sessions. In the co-registration step (section “Co-registration”), the white matter (WM) tissue probability map (TPM) of the ODI was co-registered to the WM TMP of the MT_sat in each subject and session using rigid-body registration (spm_coreg algorithm, SPM12). The resulting transformation was applied to all other NODDI maps as well. In the normalization step (section “Normalization”), MT_sat maps were roughly aligned with the T1-weighted MNI template in each subject and session using the Auto-Reorient function. The realigned MT_sat maps from both sessions were then registered to their mid-point average using the Pairwise Longitudinal Registration (SPM12). In each subject, the mid-point average MT_sat map was normalized to the MNI space using the DARTEL-based (Ashburner, 2007) Spatial Processing module. Finally, all deformation fields were converted to a single deformation field and applied on the NODDI maps. In the last step (section “Region of Interest Selection”), the ROIs and the WM masks were back-projected into the native space using the inverse of the combined deformation field.

Normalization

Spatial normalization was performed in four steps. First, a rough alignment of the ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ maps with the T1-weighted MNI template image was achieved using the Auto-Reorient function (hMRI toolbox) and this was applied on the NODDI maps as well. Second, both ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ maps of each subject (corresponding to two sessions) were registered to the mid-point average using the Pairwise Longitudinal Registration (SPM12). Hereby, values below zero and above 10 were excluded to improve the registration. Third, the resulting mid-point average image was normalized to the MNI space using the DARTEL-based (Ashburner, 2007) Spatial Processing module (hMRI toolbox). Fourth, a combined deformation field was generated per subject and session, combining the deformation fields from steps 2 and 3.

Computation of MVF_MR, AVF_MR and g_MR

In this section, our approach to estimating MVF and AVF from the measured MR parameters is introduced. The MR-based MVF (MVF_MR) was assumed to be proportional to MT_sat without intercept, following (Mohammadi and Callaghan, 2020):

${\text{MVF}}_{\text{MR}}=\mathrm{\alpha }{\text{MT}}_{\text{sat}}(2)$

The proportionality constant α was estimated from Equation (2) in a region where the histological MVF (MVF_hist) was known. Due to the lack of own histological data, we used published histological data which contain the frequency distribution of inner-axon radius (r) and myelin sheath thickness (m) of 2,400 myelinated fibers in the medullary pyramids of a 71 years old human (see Table 1 in Graf von Keyserlingk and Schramm, 1984). The total volume (TV) of the sample is the sum of the total volume of myelinated axons (TAV_m), unmyelinated axons (TAV_u), myelin volume (TMV), and extra-cellular volume (TEV). TAV_m was calculated as ${\sum }_{i=1}^{{\text{N}}_{\text{m}}}\mathrm{\pi }{\text{r}}_i^2$ with i indexing the N_m myelinated axons only, and TMV was computed as ${\sum }_{i=1}^{{\text{N}}_{\text{m}}}\mathrm{\pi }{(r_i+{\text{m}}_i)}^2-{\text{TAV}}_{\text{m}}$. TAV_u, while not reported in Graf von Keyserlingk and Schramm (1984), was found to be approximately 43% of TAV_m for multiple mammals (Swadlow et al., 1980; LaMantia and Rakic, 1990; Olivares et al., 2001; Wang et al., 2008; Liewald et al., 2014). Note that the aforementioned papers typically reported the unmyelinated axons as 30% of the total volume of axons, which corresponds to 43% (= $\frac{0.3}{1-0.3}\cdot 100$) of TAV_m. EVF was estimated to be 25%, according to Lehmenkühler et al. (1993), Nicholson and Hrabìtová (2017), Tønnesen et al. (2018). Finally, MVF was calculated as

${\text{MVF}}_{\text{hist}}\approx \frac{1}{\text{TV}}\sum _{j=1}^{\text{N}}\mathrm{\pi }\left({\left({\text{r}}_j+{\text{m}}_j\right)}^2-{\text{r}}_j^2\right)(3)$

TABLE 1

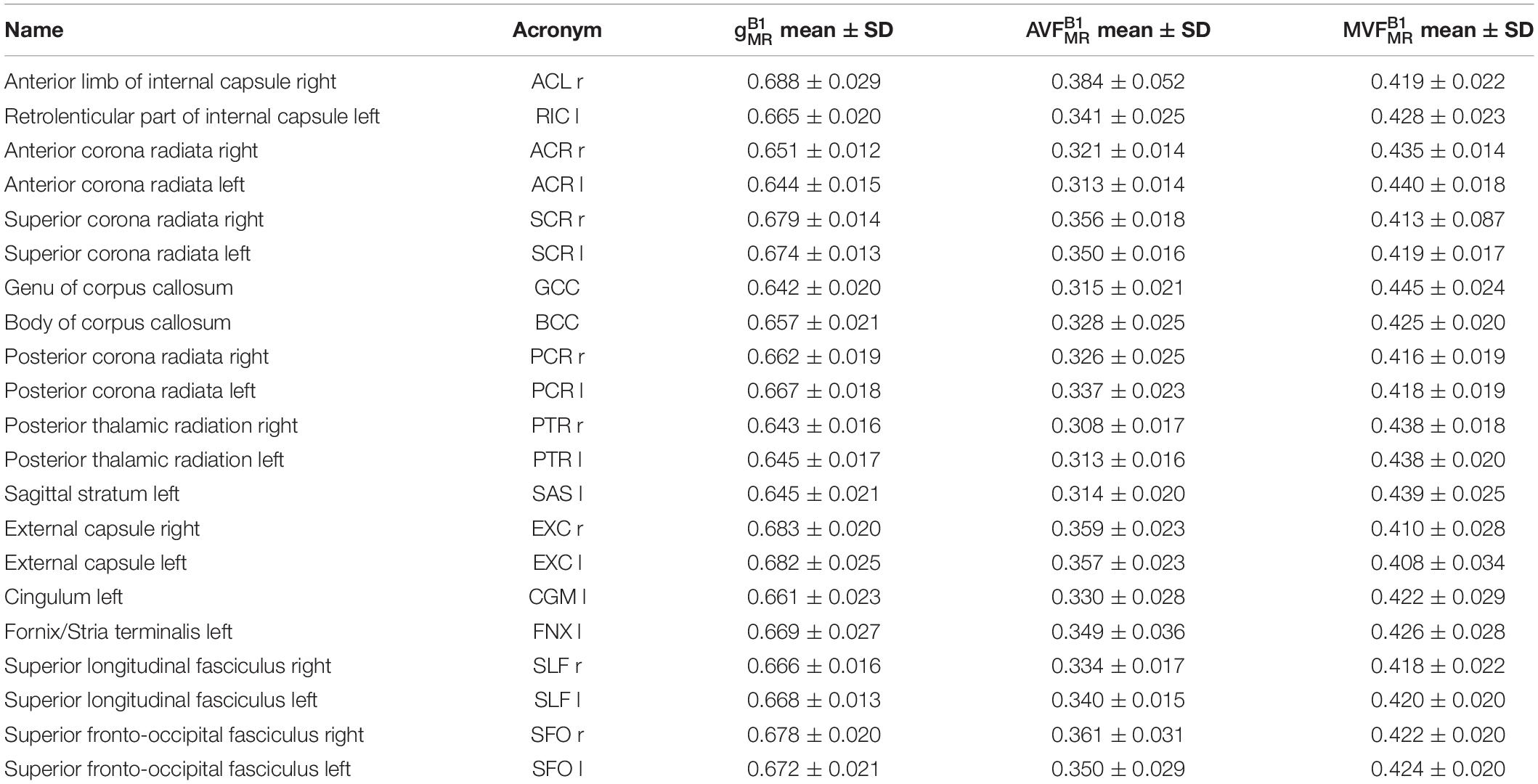
Table 1. Group-averaged mean and standard deviation (SD) of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ in 21 high-SNR ROIs.

with j indexing all N fibers, yielding MVF_hist ≈ 0.3623. Plugging this value into Equation (2) (assuming that MVF_MR ≈ MVF_hist) along with the group-average MT_sat within the medullary pyramids (see Figure 2 for ROI definition) yielded an α of 0.2496 for ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$, 0.2414 for ${\text{MT}}_{\text{sat}}^{\text{UN}}$, and 0.2884 for ${\text{MT}}_{\text{sat}}^{\text{NO}}$.

FIGURE 2

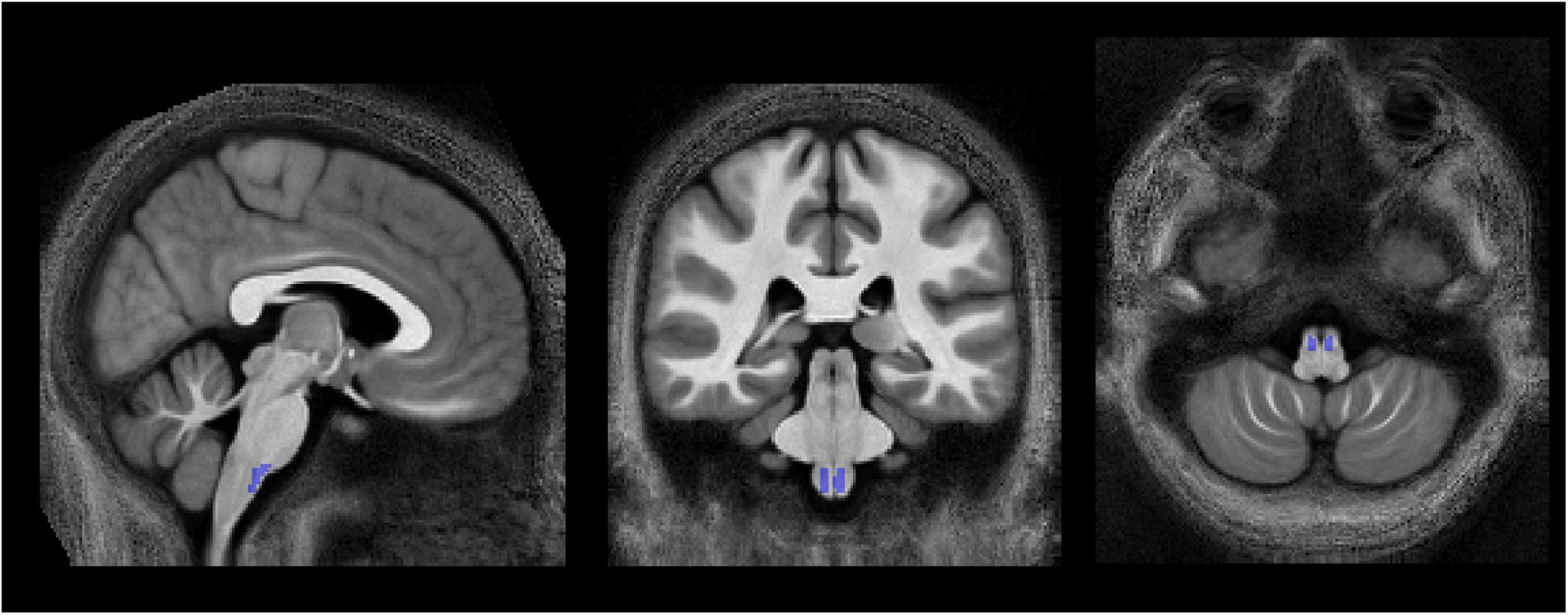
Figure 2. Location of the pyramidal tracts in the medulla oblongata ROI, overlaid on the group-averaged ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ map, that was used to determine the calibration constant, converting MT_sat into MVF_MR (section “Computation of MVF_MR, AVF_MR, and g_MR″). To create this ROI, the corticospinal tract ROI of the JHU-ICBM-DTI-81 atlas, which extends across the pons and medulla pyramids, was modified to cover only the medulla pyramids. Left-right position: X = 82; anterior-posterior position: Y = 77; superior-inferior position, Z = 30.

The MR-based AVF (AVF_MR = (1−MVF_MR)AWF_MR) was calculated as

${\text{AVF}}_{\text{MR}}=\left(1-\mathrm{\alpha }{\text{MT}}_{\text{sat}}\right)\left(1-{\mathrm{\nu }}_{\text{iso}}\right){\mathrm{\nu }}_{\text{icvf}}(4)$

where AWF = (1−ν_iso)ν_icvf is the axonal water fraction estimated from the NODDI parameters (Stikov et al., 2015) and MVF_MR = αMT_sat. The MR g-ratio was then computed according to Stikov et al. (2011, 2015)

${\text{g}}_{\text{MR}}=\sqrt{1-\frac{{\text{MVF}}_{\text{MR}}}{{\text{MVF}}_{\text{MR}}+{\text{AVF}}_{\text{MR}}}}(5)$

Note that three versions of MT_sat, AVF_MR, and g_MR were generated according to notation in section “Data Processing”: (i) ${\text{MVF}}_{\text{MR}}^{\text{NO}}$, ${\text{AVF}}_{\text{MR}}^{\text{NO}}$, ${\text{g}}_{\text{MR}}^{\text{NO}}$ for no correction, (ii) ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ for B₁+ reference measurement, and (iii) ${\text{MVF}}_{\text{MR}}^{\text{UN}}$, ${\text{AVF}}_{\text{MR}}^{\text{UN}}$, and ${\text{g}}_{\text{MR}}^{\text{UN}}$ for UNICORT B₁+ correction.

Definition of White Matter Masks

As g_MR and its constituents (MVF_MR, AVF_MR) are defined only in the WM, we restricted the analysis to the WM by creating binary WM masks (Mohammadi and Callaghan, 2020). WM tissue probability maps (WM-TPM) were created for each subject by segmenting AWF and ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ using the hMRI toolbox, and taking their intersection according to Mohammadi and Callaghan (2020). In two subjects, the ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ segmentation was of insufficient quality for segmentation and was replaced by the ${\text{R}}_1^{{\text{B}}_1}$ map. A group-specific binary WM mask (WM_group) was generated by averaging all individual WM-TPMs in the MNI space and thresholding it at 0.95.

A so-called high-SNR WM_group was also defined by taking the intersection of the WM_group and a binary signal-to-noise ratio (SNR) map. Hereby, the latter was used to reduce the number of voxels with unrealistically high values of ν_icvf (ν_icvf≥0.999). In 6 of 25 subjects, an SNR map was created by dividing the mean b₀ image by a single noise estimate in the native space and multiplied by the square root of the number of b₀ images per DWI dataset (n = 12). The noise was estimated within a noise ROI outside the brain in 72 images (6 subjects, both timepoints and 6 b0 images each) using the ACID toolbox, with the values averaged to obtain a single noise estimate. The threshold for SNR maps to create binary SNR map was chosen such that it minimizes the ratio between the number of artifactual voxels where ν_icvf≥0.999 and the total number of voxels in the SNR mask (Figure 3B), yielding a value of 39. This was motivated by the observation that unrealistically high ν_icvf values typically occur in low-SNR areas (Figures 3Aii,iii). This threshold selection represents a trade-off between removing unrealistic voxels while retaining as many voxels as possible.

FIGURE 3

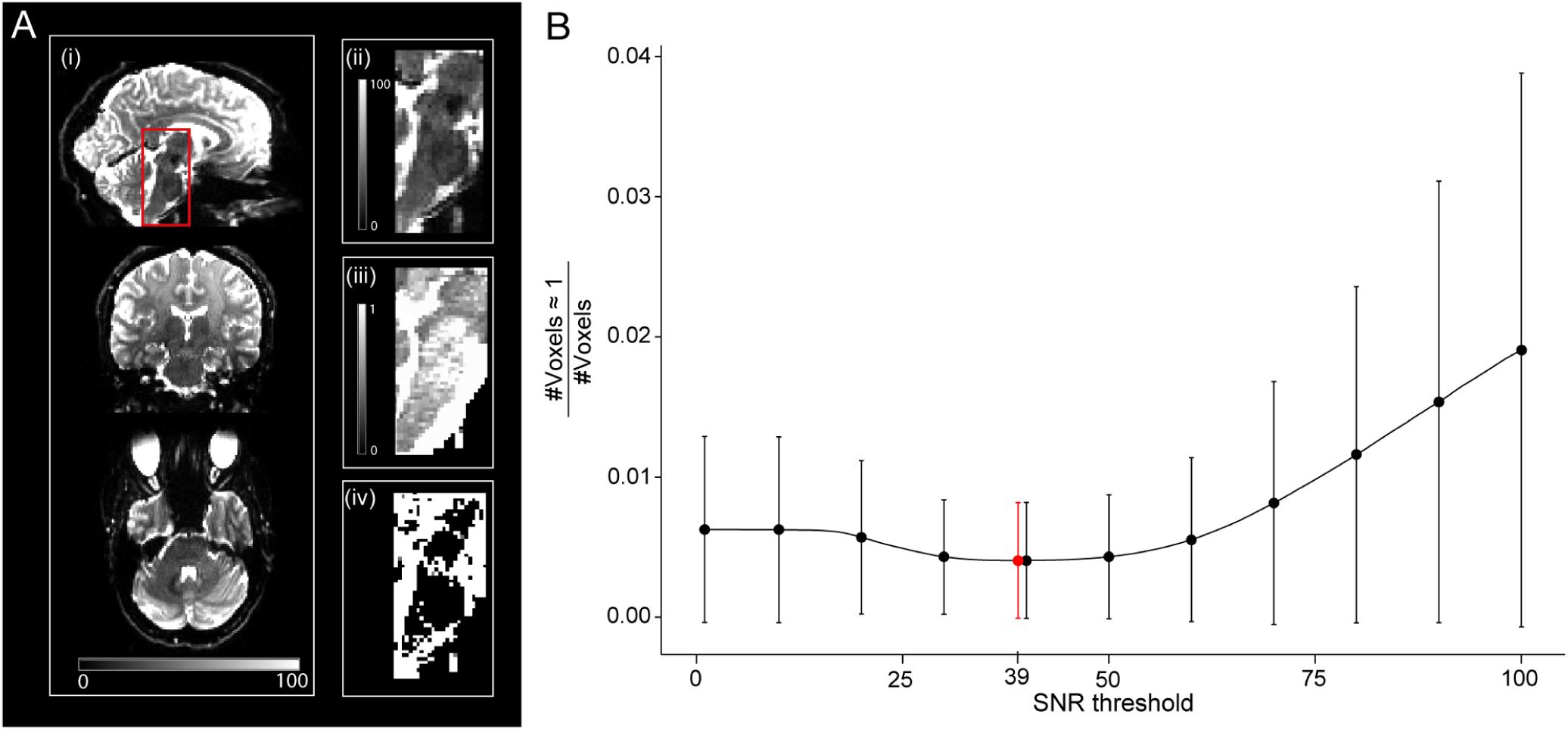
Figure 3. Relationship between signal-to-noise ratio (SNR) and unrealistically high ν_icvf values—here defined as ν_icvf ≥ 0.999. (A) Sagittal, coronal, and axial view of the whole-brain SNR map (i), with a zoom-in view of the brainstem (ii). The brainstem is characterized by low SNR due to the spatial characteristics of the receive coil array (ii) and high occurrence of unrealistically high ν_icvf (iii), also shown as a binary mask (iv). (B) Given the co-occurrence of low SNR and unrealistically high ν_icvf, a binary SNR mask was created to exclude low-SNR voxels. To determine the optimal threshold for the SNR mask, the ratio between the number of voxels with unrealistically high ν_icvf and the total number of voxels within the mask were plotted against the SNR threshold. The solid dots and error bars represent the group mean and group standard deviation of the ratio, respectively. The SNR value that yielded the minimum of this ratio was considered optimal (SNR = 39, shown in red).

Region of Interest Selection

For the region of interest (ROI) analysis, the JHU-ICBM-DTI-81 WM atlas (Hua et al., 2008) was transformed into the native space using the inverse of the combined deformation field. Two sets of ROIs were defined: (i) whole-WM ROIs and (ii) high-SNR ROIs, used for the main analysis. The whole-WM ROIs included those of the JHU-ICBM-DTI-81 WM atlas that were completely in WM_group defined in 2.6, yielding 43 ROIs (out of 48, leaving out the column and body of the fornix, the left and right cingulum part in the vicinity to the hippocampus, and the left and right uncinate fasciculus). The high-SNR ROIs included only those whole-WM ROIs that overlapped with the high-SNR WM_group to at least 95%, yielding 21 ROIs (Figure 4 and Table 2). For the analyses, group-averaged g_MR, AVF_MR, and MVF_MR were calculated within the WM_group. Note that averaging included both sessions of each subject for all analyses except for the analysis in section “Test-Retest Analysis of the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction.”

FIGURE 4

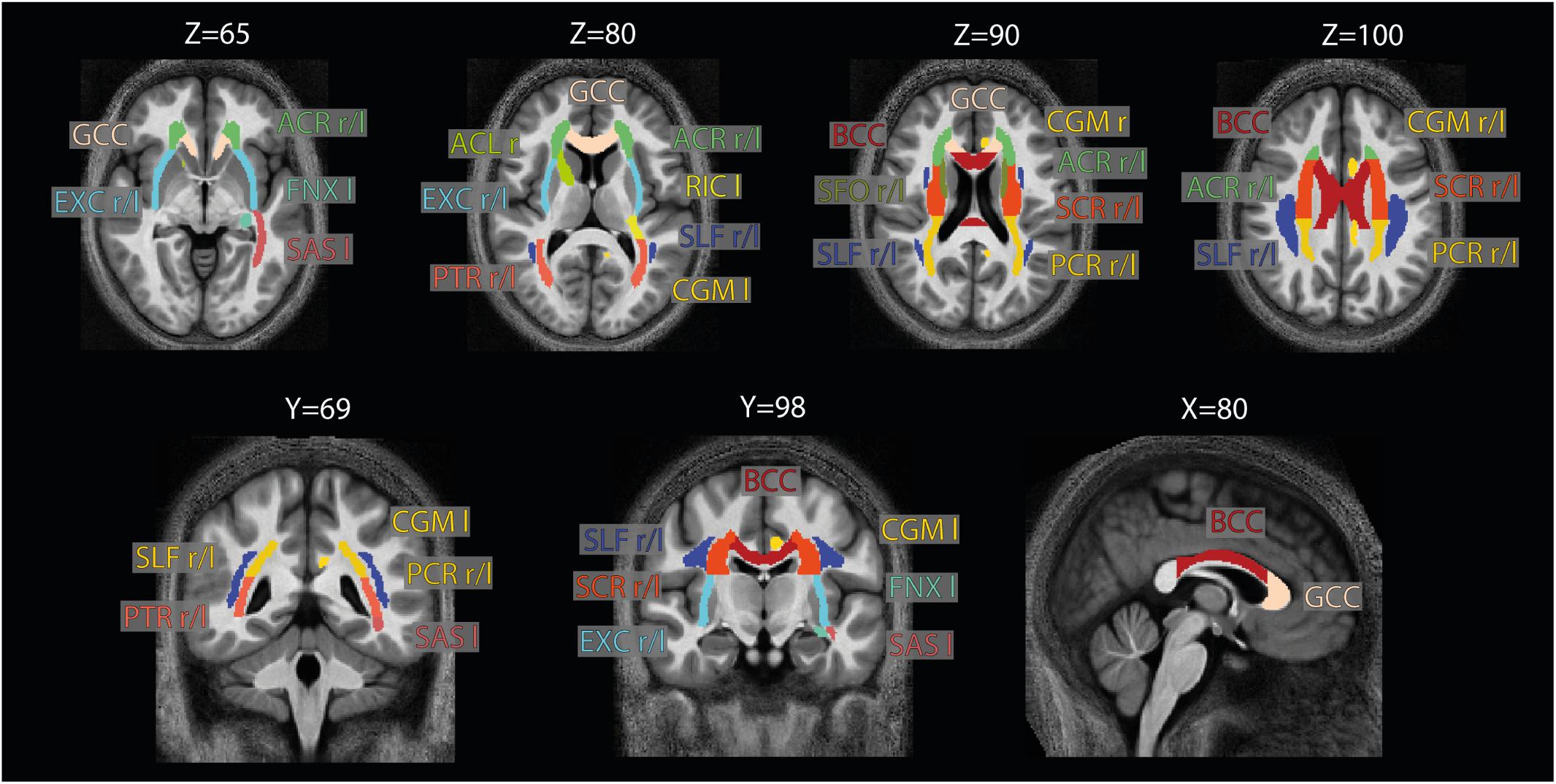
Figure 4. Location of the ROIs used for analysis. The 21 high-SNR ROIs (listed in Table 1) are part of the JHU-ICBM-DTI-81 WM atlas (Hua et al., 2008) and are displayed here on the group-averaged normalized ${\text{MT}}_{\text{sat}}^{\mathrm{B1}}$ image. Note that for ROI analysis, the ROIs were projected into the native space using the inverse of the combined deformation field.

TABLE 2

Table 2. Summary statistics of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$.

Test-Retest Analysis of the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction

The group-averaged ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ of the first and second session were compared within the previously mentioned 21 high-SNR ROIs using Bland-Altman plots (Bland and Altman, 1986). In the Bland-Altmann plots, the differences in ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ between the first (${\text{g}}_{{\text{MR}}_1}^{\mathrm{B1}}$) and second (${\text{g}}_{{\text{MR}}_2}^{\mathrm{B1}}$) session (${\mathrm{\delta }}_i^{\text{retest}}={({\text{g}}_{{\text{MR}}_1}^{\mathrm{B1}})}_i-{({\text{g}}_{{\text{MR}}_2}^{\mathrm{B1}})}_i$) were plotted against their means (${\text{mean}}_i^{\text{retest}}=\frac{{({\text{g}}_{{\text{MR}}_1}^{\mathrm{B1}})}_i+{({\text{g}}_{{\text{MR}}_2}^{\mathrm{B1}})}_i}{2}$), where i is the index of ROI i. Bias captures the offset (${\overline{\mathrm{\delta }}}^{\text{retest}}=\frac{1}{21}{\sum }_{i=1}^{21}{\mathrm{\delta }}_i^{\text{retest}}$), while error (${\mathrm{ϵ}}^{\text{retest}}=1.96\cdot \sqrt{\frac{1}{20}{\sum }_{i=1}^{21}({\mathrm{\delta }}_i^{\text{retest}}-{\overline{\mathrm{\delta }}}^{\text{retest}})}$) captures the variation between the first and second scan within the i^th ROI. The computed ${\overline{\mathrm{\delta }}}^{\text{retest}}$ and ϵ^retest were normalized by the dynamic range (△_DR) of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ within the high-SNR ROIs, defined as ${\mathrm{△}}_{\text{DR}}={max}_{\text{i}\in \text{ROI}}({\text{mean}}_{\text{i}}^{\text{retest}})-{min}_{\text{i}\in \text{ROI}}({\text{mean}}_{\text{i}}^{\text{retest}})$, yielding the relative error (${\mathrm{\delta }}_{\text{DR}\%}^{\text{retest}}=\frac{{\mathrm{ϵ}}^{\text{retest}}}{{\mathrm{△}}_{\text{DR}}}\cdot 100$) and relative bias (${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\text{retest}}=\frac{{\overline{\mathrm{\delta }}}^{\text{retest}}}{{\mathrm{△}}_{\text{DR}}}\cdot 100$). The same procedure was also applied to ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$.

The distinction between bias and error is important, because while a potential bias can be retrospectively corrected, the error in the MR g-ratio method defines its sensitivity to detect differences between individuals, groups, or time points. To reliably capture these differences, the error must be significantly lower than the expected effect size.

Influence of B₁+ Correction in the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction

Bland-Altman analysis was used to compare g_MR with and without B₁+ correction. In particular, the difference ${\mathrm{\delta }}_i^{\text{B}1}$ in g_MR between ${({\mathrm{g}}_{\text{MR}}^{\mathrm{B1}})}_i$, when using the reference method B₁+ correction, and ${({\mathrm{g}}_{\text{MR}}^{\text{k}})}_i$, when using no (k = NO) or UNICORT (k = UN) B₁+ correction: ${\mathrm{\delta }}_i^{\text{B}1}={({\mathrm{g}}_{\text{MR}}^{\mathrm{B1}})}_i-{({\mathrm{g}}_{\text{MR}}^{\text{k}})}_i$ was plotted against their mean: ${\text{mean}}_i^{\mathrm{B1}}=\frac{{({\mathrm{g}}_{\text{MR}}^{\mathrm{B1}})}_i+{\left({\text{g}}_{\text{MR}}^{\text{k}}\right)}_i}{2}$, with i being the index of the 21 high-SNR ROIs. The bias and error associated with the lack of (or UNICORT) B₁+ correction are defined as ${\overline{\mathrm{\delta }}}^{\mathrm{B1}}=\frac{1}{21}{\sum }_{i=1}^{21}{\mathrm{\delta }}_i^{\mathrm{B1}}$ and ${\mathrm{ϵ}}^{\mathrm{B1}}=1.96\cdot \sqrt{\frac{1}{20}{\sum }_{i=1}^{21}({\mathrm{\delta }}_i^{\mathrm{B1}}-{\overline{\mathrm{\delta }}}^{\mathrm{B1}})}$, respectively.

The computed ϵ^B1 and ${\overline{\mathrm{\delta }}}^{\mathrm{B1}}$were normalized by the dynamic range of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ within the high-SNR ROIs, yielding the relative error (${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}=\frac{{\mathrm{ϵ}}^{\mathrm{B1}}}{{\mathrm{△}}_{\text{DR}}}\cdot 100$) and relative bias (${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}=\frac{{\overline{\mathrm{\delta }}}^{\mathrm{B1}}}{{\mathrm{△}}_{\text{DR}}}\cdot 100$). The same procedure was also applied to AVF_MR and MVF_MR, comparing them to their respective reference method and dynamic range. For MVF_MR, the Bland-Altman analysis was additionally done using the whole-WM ROIs instead of the high-SNR ROIs (see section “Region of Interest Selection”) to assess the influence of including low-SNR voxels in the analysis.

Group Variability in MR G-ratio, Axon, and Myelin Volume Fraction

To assess group variability for each correction method, the coefficient-of-variation (CoV) across subjects and sessions was calculated for MVF_MR, AVF_MR, and g_MR in the MNI space after applying tissue-weighted smoothing (Tabelow et al., 2019), yielding: ${\text{CoV}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{CoV}}_{\text{MR}}^{\text{UN}}$, and ${\text{CoV}}_{\text{MR}}^{\text{NO}}$, where MR ∈ {g_MR,AVF_MR,andMVF_MR}. For tissue-weighted smoothing, a full width at half maximum Gaussian smoothing kernel of 6 mm was used. Bland-Altman analysis (see section “Test-Retest Analysis of the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction”) was used to compare ${\text{CoV}}_{\text{MR}}^{\text{UN}}$ and ${\text{CoV}}_{\text{MR}}^{\text{NO}}$ against ${\text{CoV}}_{\text{MR}}^{\mathrm{B1}}$ based on the reference method, yielding bias (${\overline{\mathrm{\delta }}}^{\text{CoV}}$) and error (ϵ^CoV) values. A higher variability across the brain is expected to increase ${\overline{\mathrm{\delta }}}^{\text{CoV}}$ whereas a higher local variability is expected to increase ϵ ^CoV.

Results

G-ratio, Myelin, and Axonal Volume Fraction Across the White Matter

Voxel-wise maps of group-averaged ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ in WM are shown in Figure 5. The group-averaged mean and standard deviation of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ in 21 high-SNR ROIs are reported in Table 1 and Figure 6. The dynamic range (△_DR), minimum and maximum values, and mean and standard deviation of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ across ROIs are listed in Table 2. The largest ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ were found in the right anterior limb of the internal capsule (0.688 and 0.384, respectively), while the largest ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ was in the genu of corpus callosum (0.445), where also the lowest ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ (0.642) can be found. The lowest ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ were found in the right posterior thalamic radiation (${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ = 0.308) and in the left external capsule (${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ = 0.408), respectively. The △_DR was the smallest for ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ (0.037), followed by ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ (0.046) and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ (0.076).

FIGURE 5

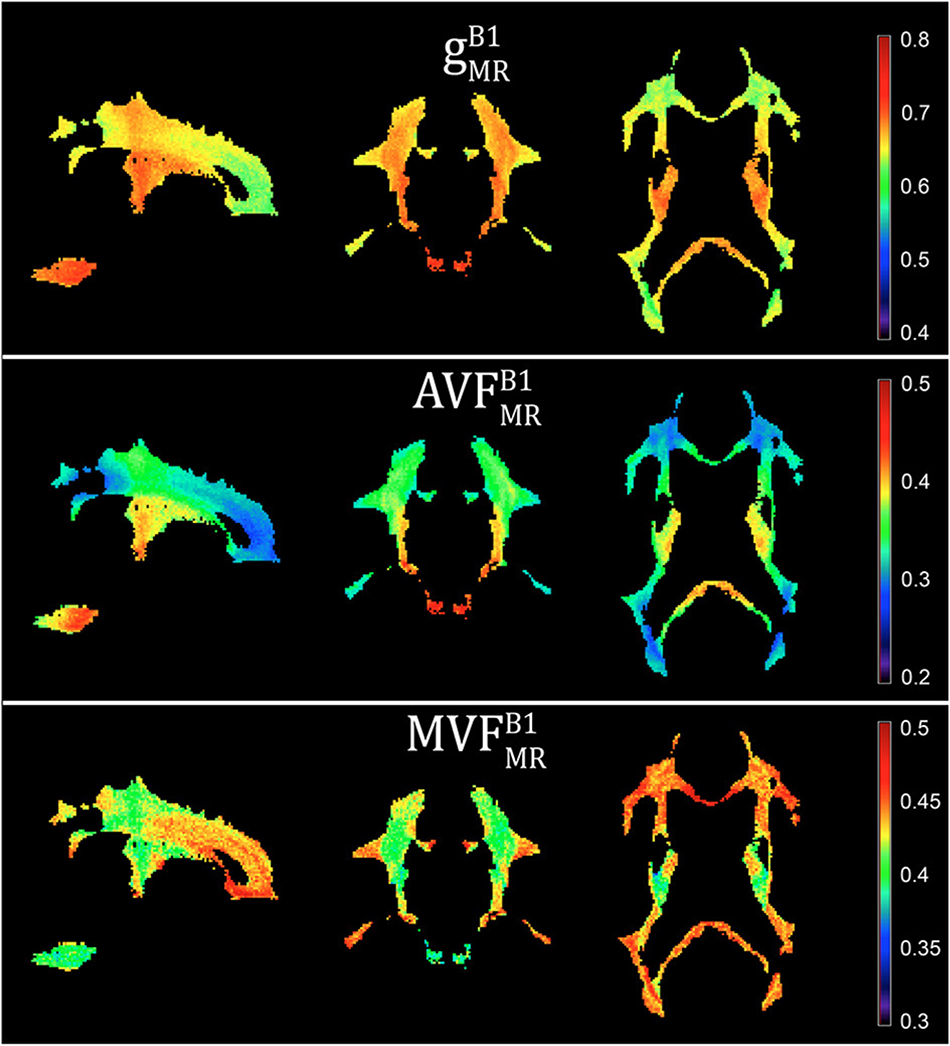
Figure 5. Voxel-wise maps of group-averaged g^B1_MR, AVF^B1_MR, and MVF^B1_MR, restricted to the group WM mask (cf. section “Definition of White Matter Masks”). Depicted are a single sagittal (x = 100), coronal (y = 91), and axial (z = 85) slice.

FIGURE 6

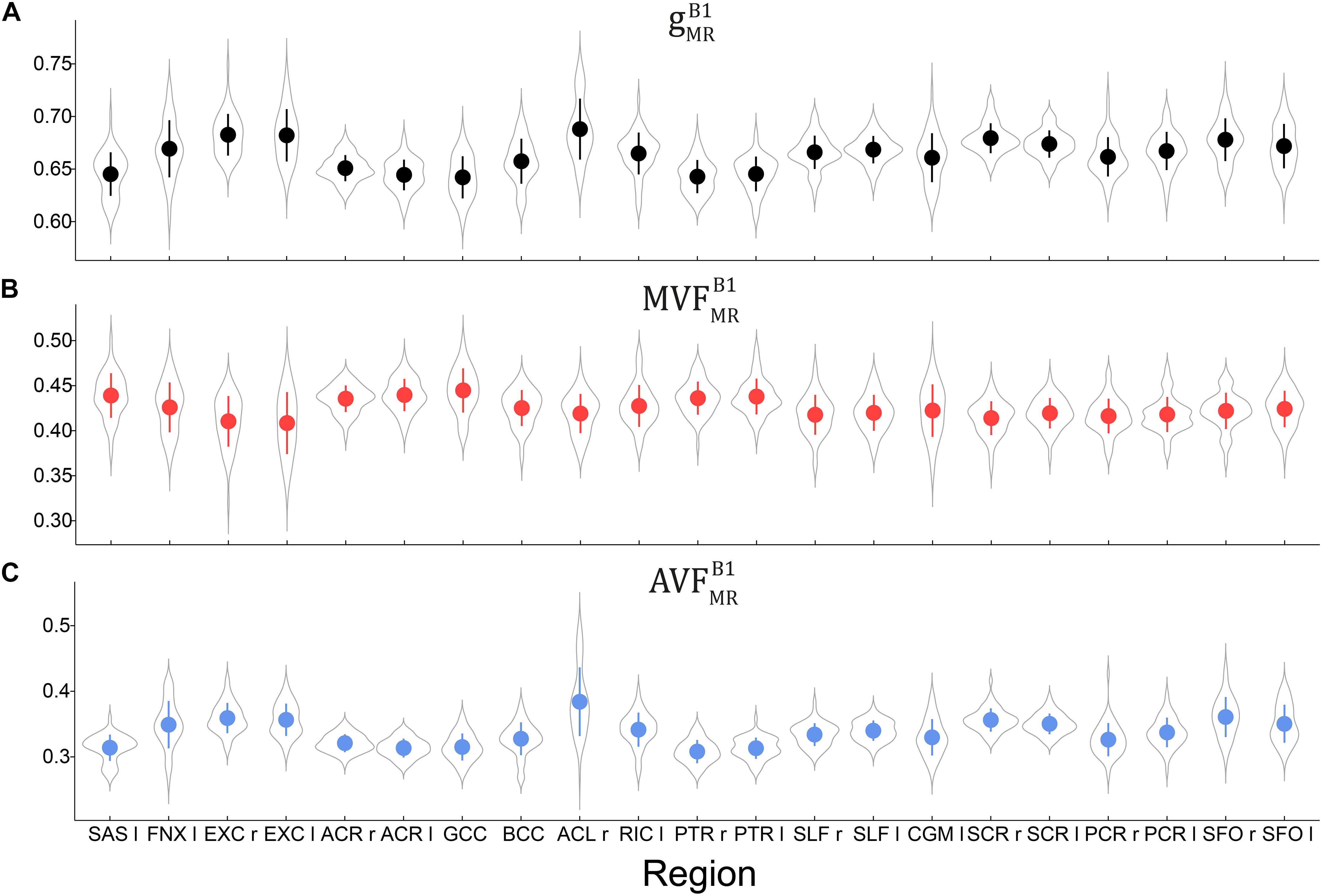
Figure 6. Violin plots representing the distribution of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ (A), ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ (B), and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ (C) across the group and in 21 high-SNR ROIs listed in Table 1. The mean and standard deviation of the distribution are indicated by solid dot and whiskers, respectively.

Test-Retest Analysis of the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction

The relative error (${\mathrm{ϵ}}_{\text{DR}\%}^{\text{retest}}$) and bias (${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\text{retest}}$) values of the test-retest analysis are summarized in Table 3 and shown as Bland-Altmann plots in Figure 7. The test-retest analysis revealed a ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\text{retest}}$ below an absolute value of 8.4% for each metric (${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$), where the ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ showed the lowest ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\text{retest}}$ with 0.79% (Figure 7 and Table 3). The ${\mathrm{ϵ}}_{\text{DR}\%}^{\text{retest}}$ was below 22.2% for each metric, where the ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ showed the lowest ${\mathrm{ϵ}}_{\text{DR}\%}^{\text{retest}}$ with 20.5% (Figure 7 and Table 3).

TABLE 3

Table 3. Bias and error between scans, in ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$, ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$, and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$.

FIGURE 7

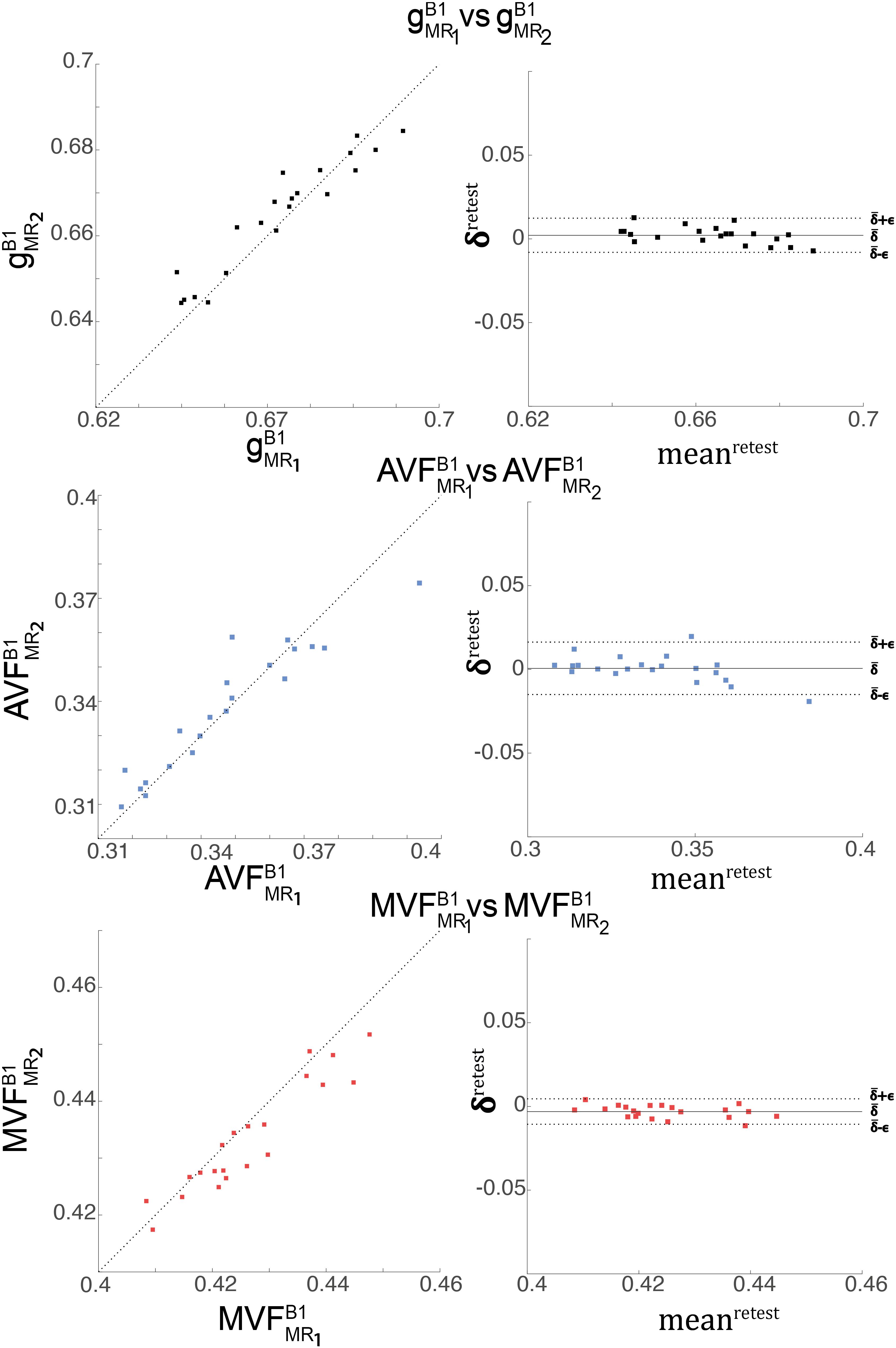
Figure 7. Depicted are scatter and Bland-Altman plots of ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ (first row), ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ (second row), and ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$(third row) from two session across 21 WM regions (denoted high-SNR ROIs, see Figure 4). The Bland-Altman plot illustrates the differences between values obtained from the two sessions (e.g., ${\text{g}}_{{\mathrm{MR}}_1}^{\mathrm{B1}}$ vs. ${\text{g}}_{\mathrm{MR2}}^{\mathrm{B1}}$; ${\mathrm{\delta }}_i^{\text{retest}}={\left({\text{g}}_{\mathrm{MR1}}^{\mathrm{B1}}\right)}_i-{({\text{g}}_{\mathrm{MR2}}^{\mathrm{B1}})}_i$) against their mean (e.g., ${\text{mean}}_i^{\text{retest}}=\frac{{({\text{g}}_{\mathrm{MR1}}^{\mathrm{B1}})}_i+{({\text{g}}_{\mathrm{MR2}}^{\mathrm{B1}})}_i}{2}$, with i indexing the i^th ROI). Each point in the scatter plot represents the group-averaged value in a single ROI. The bold black line represents the bias (${\overline{\mathrm{\delta }}}^{\text{retest}}=\frac{1}{21}{\sum }_{i=1}^{21}{\mathrm{\delta }}_i^{\text{retest}}$), while the dashed line shows error (${\mathrm{ϵ}}^{\text{retest}}=1.96\cdot \mathrm{SD}({\mathrm{\delta }}_i^{\text{retest}})$) between the two sessions.

Influence of B₁+ Correction on the Group-Averaged MR G-ratio, Axon, and Myelin Volume Fraction

The relative error (${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$) and bias (${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$) values of the B₁+ correction analysis are summarized in Table 4 and shown as Bland-Altmann plots in Figures 8, 9. For g_MR, compared to the no-correction case, UNICORT showed both lower ${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$ (UNICORT vs. no correction: 10.9% vs. 37.0%) and ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$ (30.4% vs. −89.1%). For both AVF_MR and MVF_MR, UNICORT yielded lower ${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$ (UNICORT vs. no correction; AVF_MR: 5.3% vs. 15.8%; 16.2% vs. 59.5%) and lower ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$ (AVF_MR: 14.5% vs. −40.8%; MVF_MR: 48.6% vs. 143.2%). Altogether, the UNICORT correction reduced the bias and error in the MR g-ratio and its constituents by roughly a factor of three. The lower ${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$ and ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$ associated with UNICORT was also reflected by the fact that values of ${\text{g}}_{\text{MR}}^{\text{UN}}$, ${\text{AVF}}_{\text{MR}}^{\text{UN}}$, and ${\text{MVF}}_{\text{MR}}^{\text{UN}}$ (Figure 8, lower panel) lie closer to the unit slope line than values of ${\text{g}}_{\text{MR}}^{\text{NO}}$, ${\text{AVF}}_{\text{MR}}^{\text{NO}}$, and ${\text{MVF}}_{\text{MR}}^{\text{NO}}$ (Figure 8, upper panel). When computing ${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$ and ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$ of g_MR in the whole-WM ROIs (see Supplementary Figure 1), ${\overline{\mathrm{\delta }}}_{\text{DR}\%}^{\mathrm{B1}}$ was consistently lower for both the no-correction case (whole-WM ROIs vs. high-SNR ROIs: 36.5% vs. 143.2%) and UNICORT (13.1% vs. 48.6%), whereas ${\mathrm{ϵ}}_{\text{DR}\%}^{\mathrm{B1}}$ was similar (no-correction: 52.8% vs. 59.5%; UNICORT: 24.0% vs. 16.2%).

TABLE 4

Table 4. Bias and error between methods, in g_MR, AVF_MR, and MVF_MR.

FIGURE 8

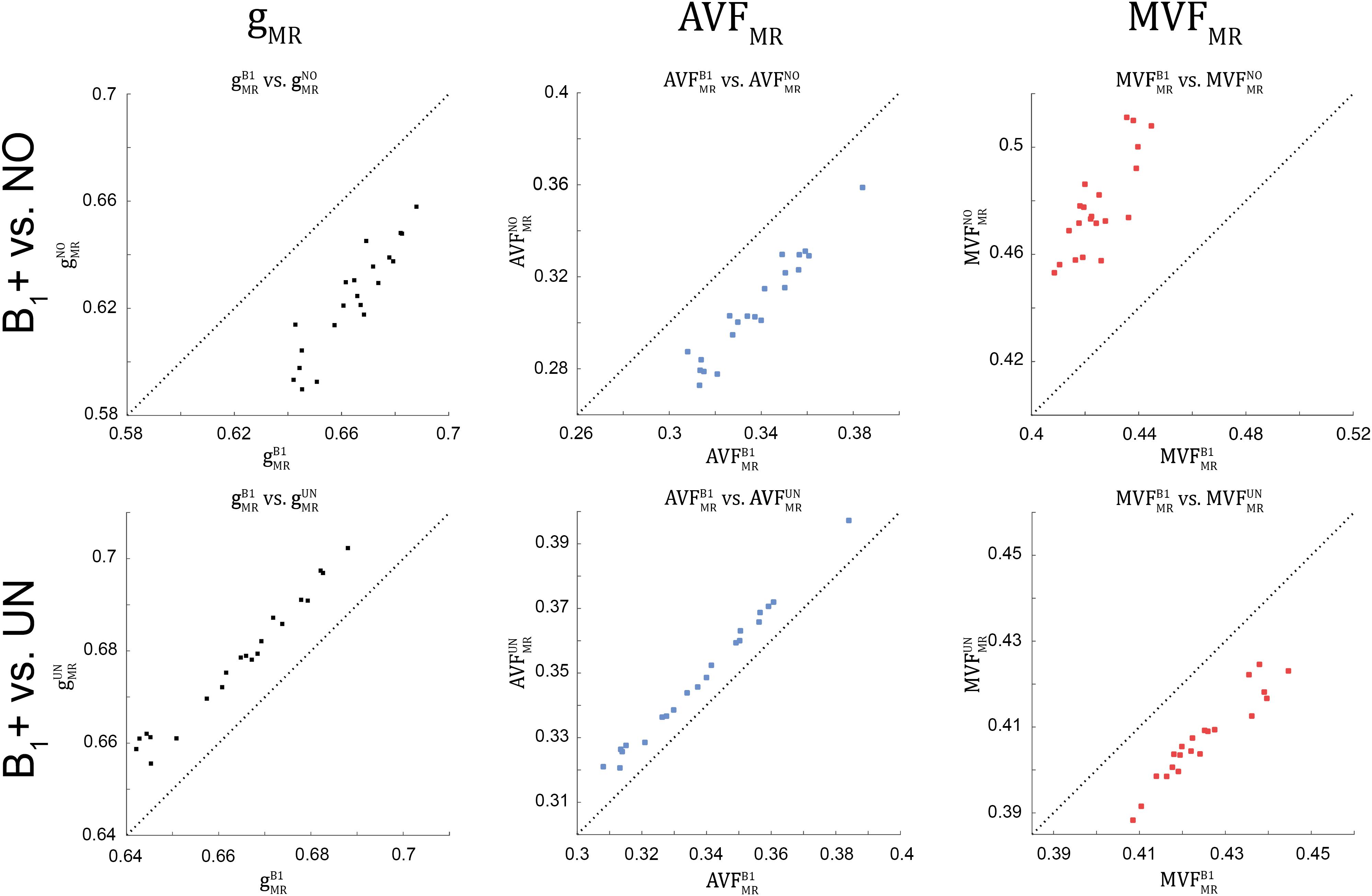
Figure 8. Scatter plots of g_MR, AVF_MR, and MVF_MR, plotting values obtained without B₁+ correction (superscript: NO, top row) and with UNICORT B₁+ correction (superscript: UN, bottom row) against values obtained with the reference method, i.e., B₁+ field map correction (superscript: B1). A dashed unit slope line is plotted for reference. Each point in the scatter plot represents the group-averaged value in a single ROI (see Figure 4 for the locations of the 21 high-SNR ROIs).

FIGURE 9

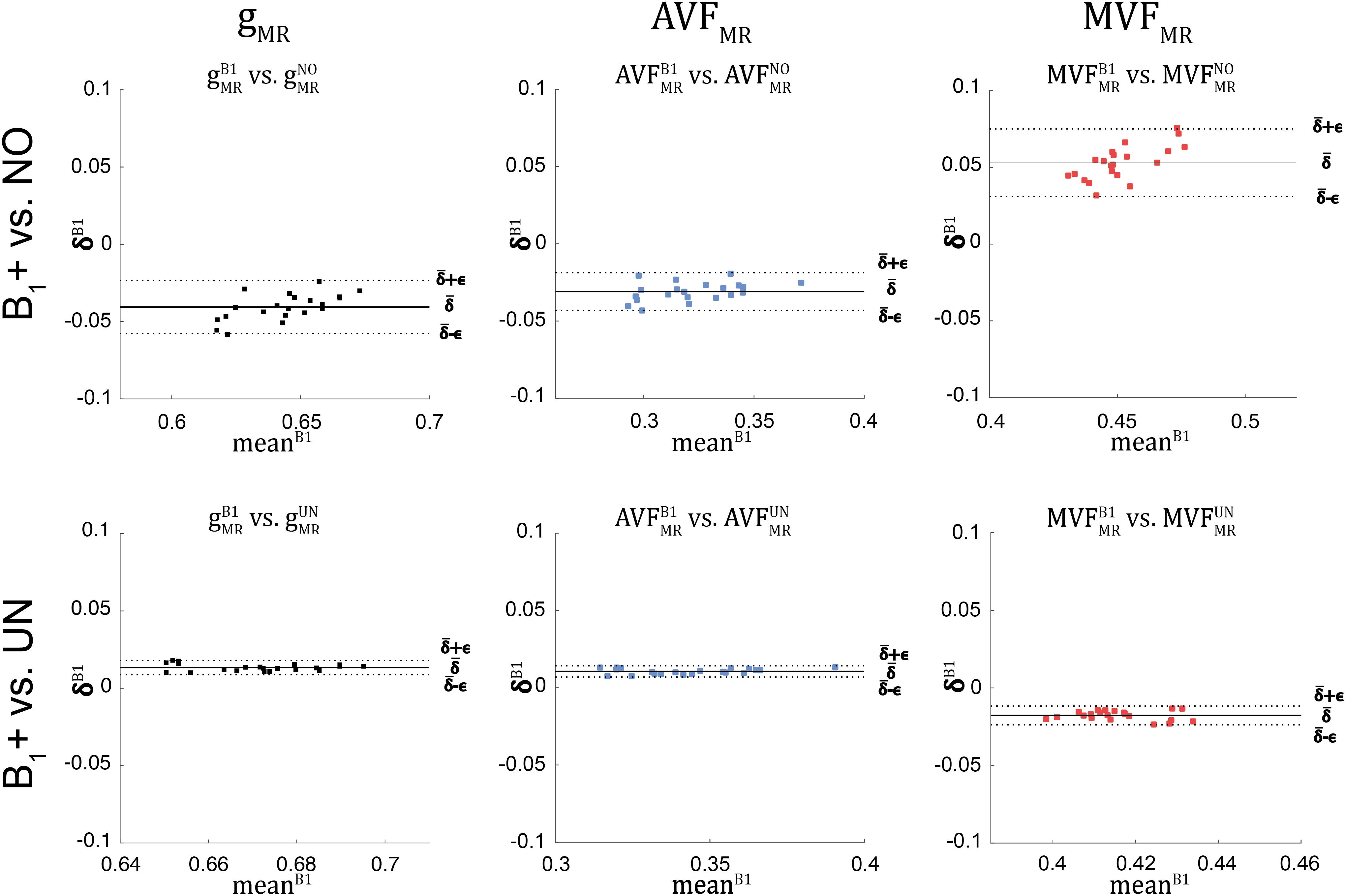
Figure 9. Bland-Altman plots of g_MR, AVF_MR, and MVF_MR, comparing values obtained without B₁+ correction (NO, top row) and with UNICORT B₁+ correction (UN, bottom row) against values obtained by B₁+ field map correction (superscript: B1). The Bland-Altman plot illustrates the differences between values obtained by two different methods (reference vs. tested method); e.g., ${\mathrm{\delta }}_i^{\mathrm{B1}}={({\mathrm{g}}_{\text{MR}}^{\mathrm{B1}})}_i-{({\mathrm{g}}_{\text{MR}}^{\text{k}})}_i$ against their mean (${\text{mean}}_i^{\mathrm{B1}}=\frac{{({\mathrm{g}}_{\text{MR}}^{\mathrm{B1}})}_i+{({\text{g}}_{\text{MR}}^{\text{k}})}_i}{2}$, with k = {UN, NO} and i indexing the i^th ROI). Each point in the scatter plot represents the group-averaged value in a single ROI (see Figure 4 for the locations of the 21 high-SNR ROIs). The bold black line represents the bias (${\overline{\mathrm{\delta }}}^{\mathrm{B1}}={\sum }_{i=1}^{21}{\mathrm{\delta }}_i^{\mathrm{B1}}$), while the dashed line shows error (${\mathrm{ϵ}}^{\mathrm{B1}}=1.96\cdot \mathrm{SD}({\mathrm{\delta }}_i^{\mathrm{B1}})$) between the reference and the tested method. Error and bias values averaged across all ROIs and subjects are listed in Table 5.

Group Variability in MR G-ratio, Axon, and Myelin Volume Fraction

g_MR showed on average smaller CoV than AVF_MR and MVF_MR (Figure 10). In all maps, the CoV was the highest in the deep brain areas. The relative error ($\frac{{\mathrm{ϵ}}^{\text{CoV}}}{{\text{CoV}}^{\mathrm{B1}}}\cdot 100$) and bias ($\frac{{\overline{\mathrm{\delta }}}^{\text{CoV}}}{{\text{CoV}}^{\mathrm{B1}}}\cdot 100$) values of CoV with respect to the B₁+ reference measurement are summarized in Table 5 and the error and bias are also displayed as Bland-Altman density plot in Figure 11. For g_MR, compared to the no correction case, UNICORT showed similar ϵ^CoV (UNICORT vs. no correction: 0.6% vs. 0.6%) but lower ${\overline{\mathrm{\delta }}}^{\text{CoV}}$ (−0.1% vs. −0.4%). UNICORT yielded higher ϵ^CoV (UNICORT vs. no correction; 1.0% vs. 0.8%) and lower ${\overline{\mathrm{\delta }}}^{\text{CoV}}$ (−0.2% vs. −0.4%) for AVF_MR, and higher ϵ^CoV (1.2% vs. 0.4%) and higher ${\overline{\mathrm{\delta }}}^{\text{CoV}}$(−0.5% vs. −0.1%) for MVF_MR. The lower ${\overline{\mathrm{\delta }}}^{\text{CoV}}$ of g_MR and AVF_MR associated with UNICORT reveals itself as a slight shift of the points toward the unit slope line in the scatter density plot (Figure 12).

FIGURE 10

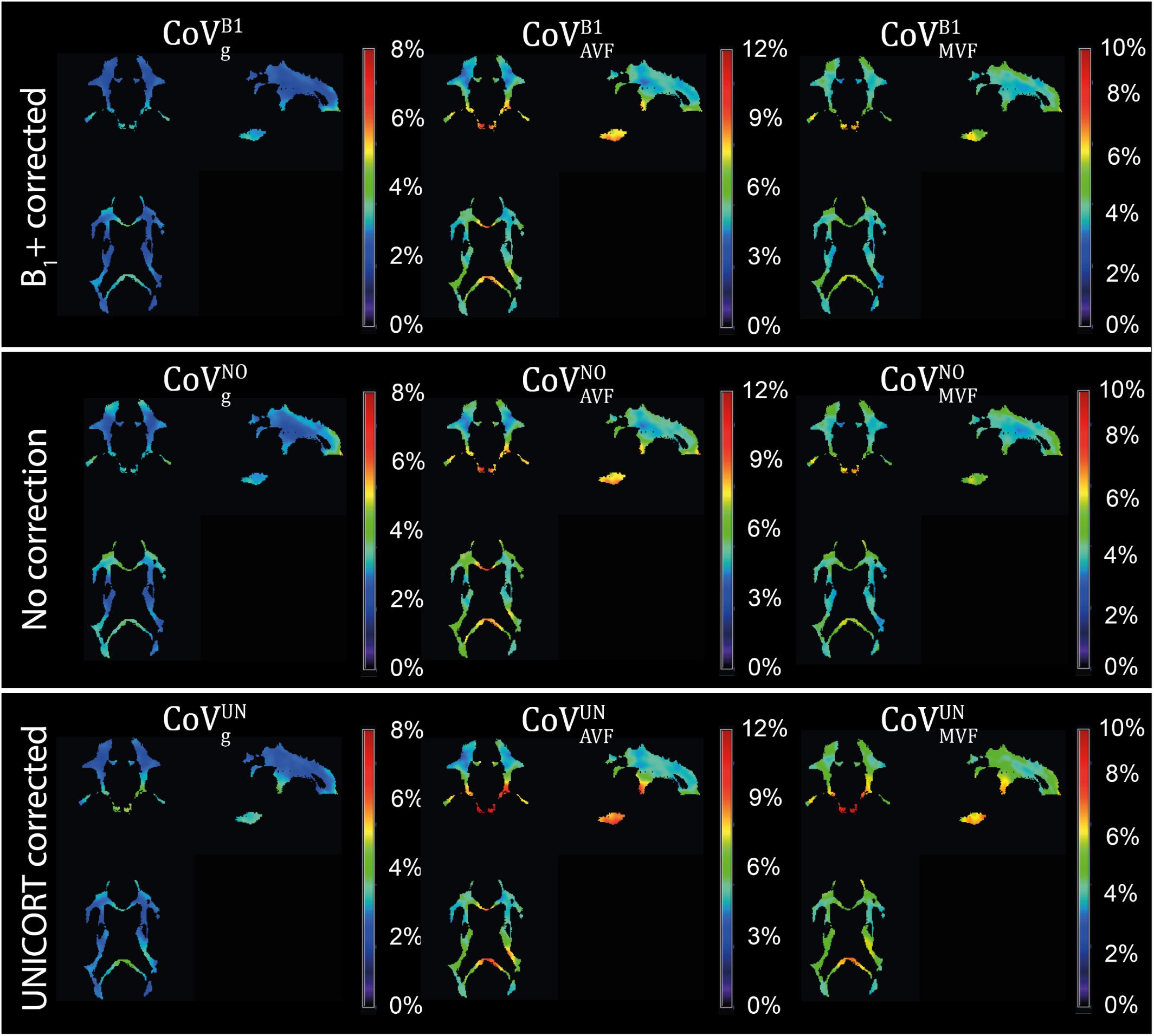
Figure 10. Coefficient of variation (CoV) maps of g_MR, AVF_MR, and MVF_MR with B₁+ correction (${\text{CoV}}_{\text{g}}^{\mathrm{B1}}$, ${\text{CoV}}_{\text{AVF}}^{\mathrm{B1}}$, and ${\text{CoV}}_{\text{MVF}}^{\mathrm{B1}}$), no correction (${\text{CoV}}_{\text{g}}^{\text{NO}}$, ${\text{CoV}}_{\text{AVF}}^{\text{NO}}$, and ${\text{CoV}}_{\text{MVF}}^{\text{NO}}$), and UNICORT B₁+ correction (${\text{CoV}}_{\text{g}}^{\text{UN}}$, ${\text{CoV}}_{\text{AVF}}^{\text{UN}}$, and ${\text{CoV}}_{\text{MVF}}^{\text{UN}}$). CoV maps, expressed in percentage, were computed as the voxel-wise ratio between the group mean and group standard deviation maps of the normalized g_MR, AVF_MR, or MVF_MR. The voxel-wise computation of CoV is restricted to the group WM mask (cf. section “Definition of White Matter Masks”). Shown are a single coronal (y = 91), sagittal (x = 100), and axial (z = 85) slice.

TABLE 5

Table 5. Bias and error between methods, in the CoV of g_MR, AVF_MR, and MVF_MR.

FIGURE 11

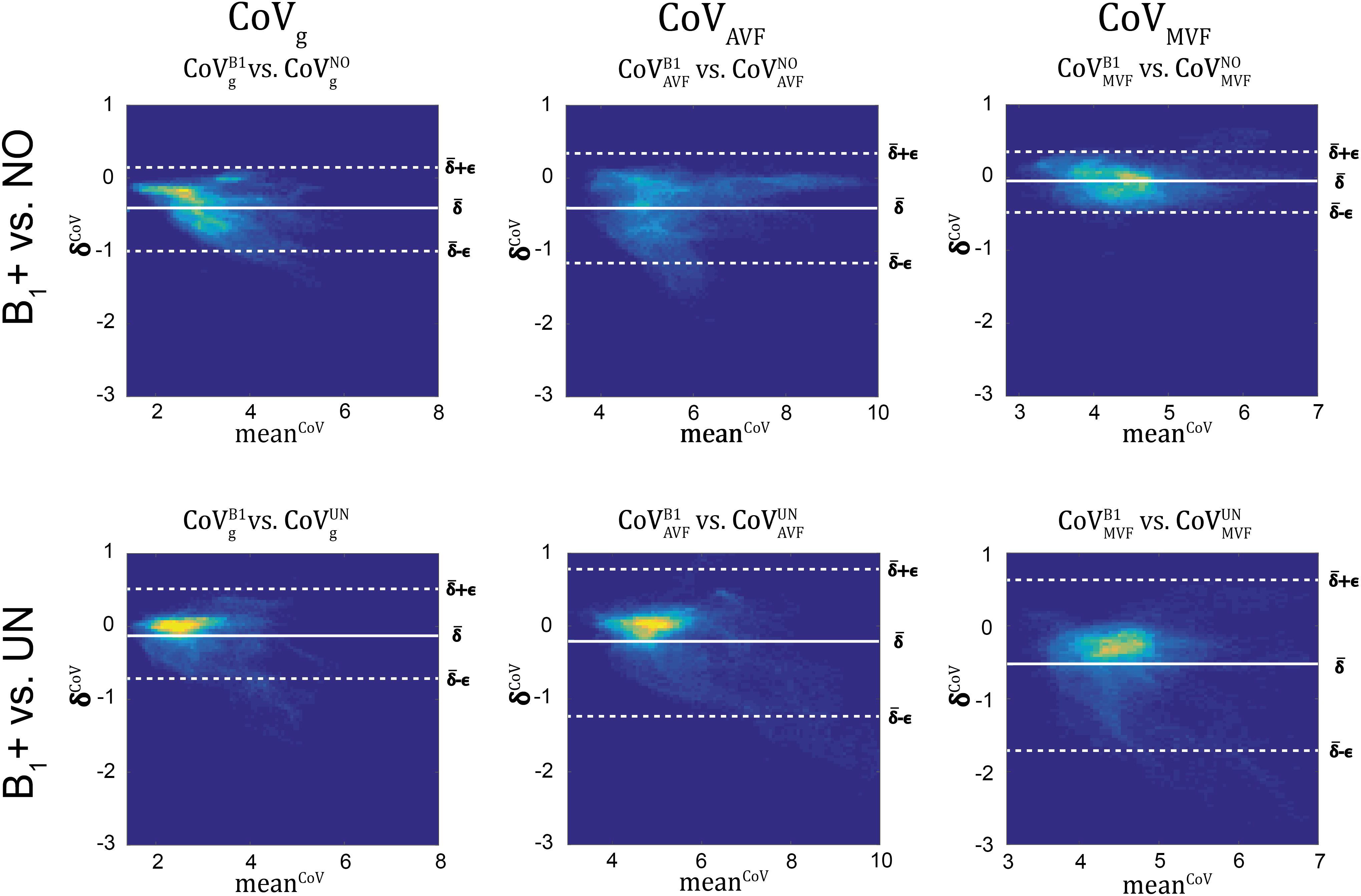
Figure 11. Bland-Altman density plots of CoV_g, CoV_AVF, and CoV_MVF for no correction (NO, top row) and UNICORT B₁+ correction (UN, bottom row) against the reference method (B₁+) (yellow indicates high density and blue low). The Bland-Altman plot depicts the differences between the tested parameter maps and the reference method (e.g., ${\mathrm{\delta }}_i^{\text{CoV}}={({\mathrm{CoV}}_{\text{g}}^{\mathrm{B1}})}_i-{({\mathrm{CoV}}_{\text{g}}^{\text{k}})}_i$) against their mean (e.g., ${\text{mean}}_i^{\text{CoV}}=\frac{{({\mathrm{CoV}}_{\text{g}}^{\mathrm{B1}})}_i+{\text{CoV}}_{\text{g}}^{\text{k}}){}_i}{2}$) with k = {UN,NO} and i being the index of the i^th region. The bold white line represents the bias (${\overline{\mathrm{\delta }}}^{\text{CoV}}={\sum }_{i=1}^{\text{N}}{}_i^{\text{CoV}}$; N = number of voxels) and the dashed lines represent ${\overline{\mathrm{\delta }}}^{\text{CoV}}$ the error (${\mathrm{ϵ}}^{\text{CoV}}=1.96\cdot \mathrm{SD}({\mathrm{\delta }}_{\text{i}}^{\text{CoV}})$]. The error and bias values are summarized in Table 5.

FIGURE 12

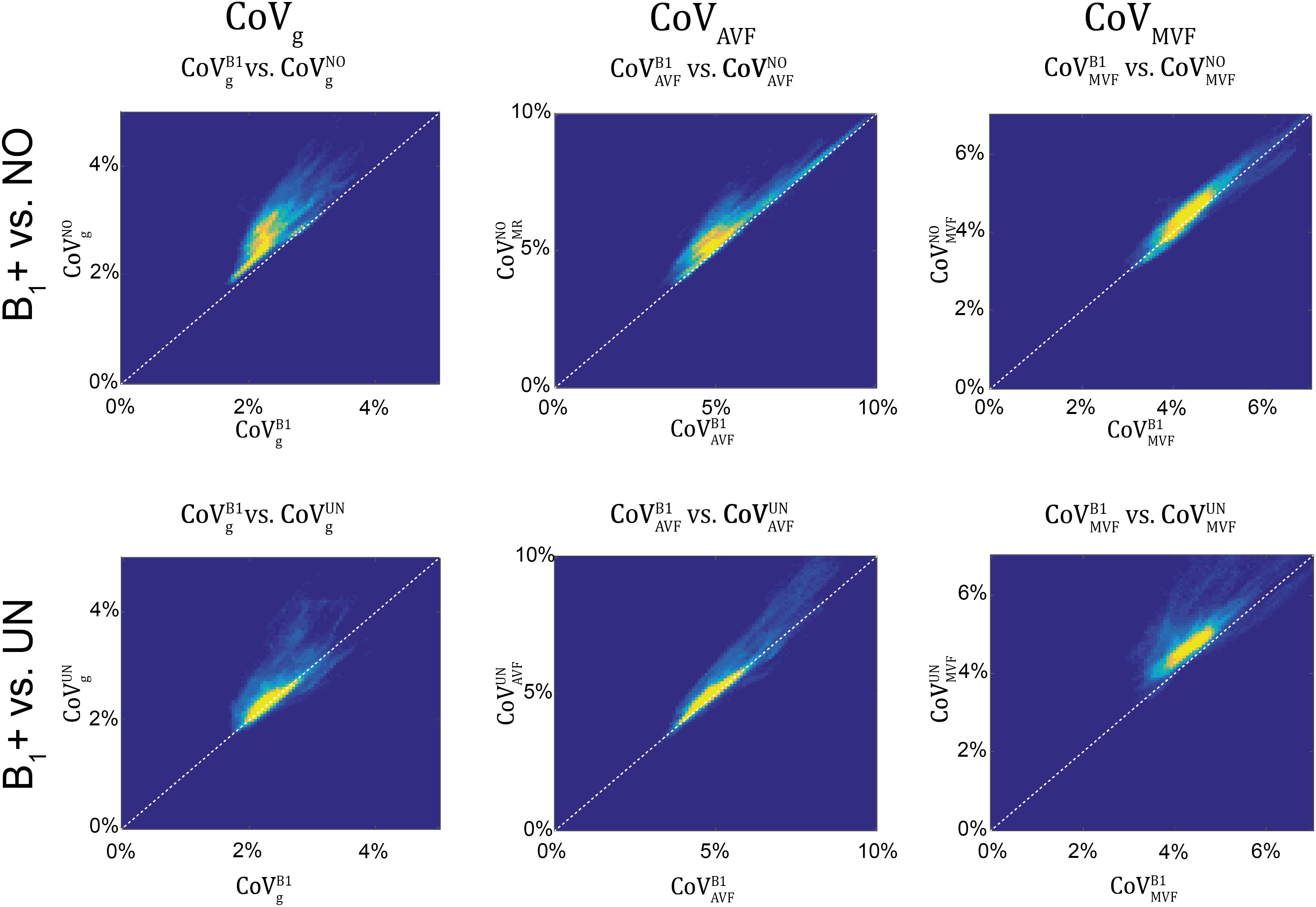
Figure 12. Scatter density plots of CoV_g (left column), CoV_AVF (middle column), and CoV_MVF (right column), plotting values obtained with no correction (superscript: NO, top row) and with UNICORT B₁+ correction (UN, bottom row) against values obtained by B₁+ field map correction (superscript: B1). The unit slope line is plotted for orientation (dotted line). The dots in the scatter plots represent the WM voxels in the CoV maps in Figure 10 (yellow indicates high voxel density).

Discussion

In this study, we showed that omitting the correction of the magnetization transfer saturation map (MT_sat) for residual B₁ + effects introduces large error and bias in the MR g-ratio and the constituents (myelin and axon volume fractions, or in short MVF_MR and AVF_MR). We also demonstrated that this error and bias can be reduced by roughly a factor of three using the data-driven UNICORT B₁+ correction (implemented in the hMRI toolbox, see text footnote 1) when a B₁+ field measurement is unavailable.

The Effect of Omitting the B₁+ Field Measurement

MT_sat have been often used as a proxy for the MVF_MR in g-ratio weighted imaging (Mohammadi et al., 2015; Campbell et al., 2018; Ellerbrock and Mohammadi, 2018; Hori et al., 2018; Kamagata et al., 2019), because they are directly linked to the macromolecular pool with an intrinsic correction for underlying longitudinal relaxation time and B₁+ field inhomogeneities effects (Helms et al., 2008). Despite the latter intrinsic correction for B₁+ field inhomogeneities, we found that the residual B₁+ effects on MT_sat map were still observable. In particular, the bias and error of the MR g-ratio (g_MR) was about −89 and 37% higher, respectively, when omitting the B₁+ correction. We found the same trend for MVF_MR and AVF_MR; while the error and bias were even larger for MVF_MR when B₁+ correction was omitted, it was smaller but still substantial for the AVF_MR. We found that omitting B₁ + leads to a substantially higher (more than 10-fold) bias in the MR g-ratio and its constituents when compared to a test-retest analysis of our data (Figure 7 and Table 3). Also, the error due to omitting the B1+ correction was twice as large as the error observed in the test retest analysis for the MR g-ratio and the MVF, whereas for AVF the errors were similar. We expect that the high error will be of particular relevance for group studies because it can be regarded as an error that evolves when replacing the reference method with the alternative method. For comparison, age-related changes assessed by g-ratio weighted imaging (Cercignani et al., 2017; Berman et al., 2018) have been reported to vary between 30 and 100% (in absolute values: g_MR0.02–0.04 (Figure 5 in Cercignani et al., 2017). Consequently, the reported effect size of age-related changes would have become potentially undetectable if the B₁+ field correction has been omitted in the study of Cercignani et al. (2017). The B₁+ effect is particularly relevant for the MR g-ratio method by Cercignani et al. (2017) that combined quantitative MT (Gloor et al., 2008) with NODDI, because the qMT method does not possess an intrinsic correction for B₁+ field inhomogeneities as opposed to the MT_sat methods used here. Note that we reported, for better intuition, the bias and error relative to the dynamic range of the parameters across the investigated white matter (WM) ROIs (the dynamic range of g_MR is △_DR = 0.046; the absolute bias and error can be found in Table 4).

To reduce this source of bias and error, we propose a data-driven approach to correct for B₁+ field inhomogeneities when no B₁+ field measurement is available. To this end, we used UNICORT to estimate the B₁+ field (Weiskopf et al., 2011). We found that using the UNICORT-estimated B₁+ field to correct residual B₁+ field inhomogeneities in MT_sat reduces at the group level the bias and error in the MR g-ratio and its constituents by roughly a factor of three. However, the UNICORT estimated B₁+ inhomogeneity can be erroneous with the error varying across subjects. To assess this variability, we estimated coefficient-of-variance (CoV) maps of g_MR, AVF_MR, and MVF_MR for all three methods. In general, an increased CoV can be found at tissue boundaries (e.g., cerebral spinal fluid to WM) due to slight misregistration between the maps of axonal and myelin markers and/or imperfect normalization (Figure 10). Additionally, we found a strong increase in the bias and error of the CoV of MVF maps (increase in bias: 11% and in error: 18%) when UNICORT B₁+ correction was used as compared to no correction. The CoV of g_MR and AVF_MR did not show a consistent trend: while the bias decreased, the error increased for both parameters. In other words, the UNICORT B₁+ correction leads to higher accuracy in the g-ratio and its constituents but comes at the cost of a lower precision in MVF.

G-ratio, Myelin, and Axonal Volume Fraction Across the White Matter

Our ${\text{g}}_{\text{MR}}^{\mathrm{B1}}$ and ${\text{AVF}}_{\text{MR}}^{\mathrm{B1}}$ across the white matter were within the range of the reported values of previous studies (g_MR: 0.64–0.76; AVF_MR: 0.26–0.43 in (Cercignani et al., 2017; Berman et al., 2018). The range of ${\text{MVF}}_{\text{MR}}^{\mathrm{B1}}$ was in the upper half of previously reported values (0.17–0.42 in Cercignani et al., 2017). Our slightly higher MVF_MR values might be due to differences in the calibration approach: while we calculated the reference MVF_REF from previously published ex-vivo histology data (Graf von Keyserlingk and Schramm, 1984), Cercignani et al. (2017), used a reference from previously published ex-vivo histology g-ratio data in the corpus callosum and Berman et al. (2018), did not perform any calibration assuming that macromolecular tissue volume and MVF_MR are equal. An error in the calibration constant can lead to a bias in the MVF estimates which in turn leads to an error and bias in the MR g-ratio (Campbell et al., 2018).

Confounding Factors

As this study calculates the in-vivo MR g-ratio, there is no histological data available from the participants of this study, which could be used for calibration or as a gold standard reference. For calibration of MT_sat to MVF_MR, we estimated the histological MVF (MVF_hist) from published ex-vivo data within the human medulla oblongata (Graf von Keyserlingk and Schramm, 1984). Since the reference MVF_hist and the calibrated MT_sat map were taken from different subjects, this might introduce a systematic bias in the MR g-ratio. However, since we found a relatively good agreement between our g_MR, AVF_MR, and MVF_MR values with previously reported values obtained by a different calibration approach (Cercignani et al., 2017; Berman et al., 2018), we expect that it had a small effect on the results. Moreover, we focused on the effect of omitting B₁+ correction, which will lead to additional inaccuracies in g-ratio weighted imaging, independent of the quality of the calibration.

Although, not reported in previous NODDI-based g-ratio mapping studies (Stikov et al., 2015; Cercignani et al., 2017; Jung et al., 2017; Mancini et al., 2017; Ellerbrock and Mohammadi, 2018; Hori et al., 2018), we found that the intra-cellular volume fraction (ν_icvf) determined with NODDI tends to be biased at small signal-to-noise ratios (SNR < 39), resulting in a ceiling effect, i.e., ν_icvf ≈ 1. To avoid a corresponding bias in g_MR (and AVF_MR), we restricted the analysis to regions with sufficiently high SNR (Figure 3). To investigate whether our findings generalize to low-SNR regions as well, we performed an additional Bland-Altman analysis of MVF_MR in whole-WM ROIs. To this end, a larger set of ROIs was used covering the entire white matter. Although the bias was smaller for the whole-WM as compared to the high-SNR ROI analysis, we found the same trend: the error and bias were reduced when using UNICORT B₁+ correction relative to no correction. Note that the smaller bias for the whole-WM analysis is most probably an artifact of the calibration procedure. Since the ROI used for calibration was not part of the high-SNR ROIs but was part of the whole-WM ROIs, we think it could have reduced the bias in the whole-WM ROI analysis as compared to the high-SNR analysis.

We note that the presented results were based on a customized B₁+ mapping method (Lutti et al., 2010). Using vendor specific protocols for B₁+ and MT_sat mapping may influence the results (Leutritz et al., 2020). Moreover, the calibration factor in Equation (1) may have to be recalibrated for different MT-pulses.

Future studies should investigate the effect of B₁+ correction on MR g-ratio mapping when using alternative biomarkers to estimate AVF_MR and MVF_MR (e.g., Ellerbrock and Mohammadi, 2018). Moreover, there are alternative B₁+ mapping approaches available which might vary in precision (Lutti et al., 2010) and therefore can affect the MR g-ratio values. However, the differences in the precision of these methods are in the order of few percentage and thus much smaller than the effect of omitting the B₁+ field or using the data-driven UNICORT B₁+ estimate (Weiskopf et al., 2011).

Conclusion

In this study, we assessed the effect of B₁+ correction on the accuracy of MR g-ratio as well as axonal and myelin volume fraction based on MT_sat and NODDI. Our results demonstrate that B₁+ correction via a measured B₁+ field map is the method of choice. If the B₁+ field map cannot be acquired, we propose the retrospective, data-driven UNICORT B₁+ correction to estimate and correct for B₁+ field inhomogeneities, which reduces the error and bias by a factor of three. UNICORT is implemented in the free and open-source hMRI toolbox (see text footnote 1).

Data Availability Statement

The datasets presented in this article are not readily available because the data that support the findings of this study are available on request from the corresponding author. The data have not been made freely available on the internet due to privacy or ethical restrictions. Requests to access the datasets should be directed to corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by the Ärztekammer Hamburg. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

SM and TE contributed to the conception and design of the study, performed statistical analysis and MRI processing, and wrote the first draft of the manuscript. All authors contributed substantially to revising the manuscript critically for intellectual content and have approved the submitted version.

Funding

This project was by the ERA-NET NEURON (hMRIofSCI), the Federal Ministry of Education and Research (BMBF; 01EW1711A and B), and the German Research Foundation (DFG Priority Program 2041 “Computational Connectomics,” (AL 1156/2-1;GE 2967/1-1; MO 2397/5-1; MO 2249/3–1), DFG Emmy Noether Stipend: MO 2397/4-1), and the Forschungszentrums Medizintechnik Hamburg (fmthh; grant 01fmthh2017). GH was supported by the Swedish Research Council (NT 2014-6193). PF was funded by a SNF Eccellenza Professorial Fellowship grant (PCEFP3_181362/1), and the European Union’s Horizon 2020 research, innovation programme (grant agreement no 634541). EB received funding from the European Structural and Investment Fund/European Regional Development Fund and the Belgian Walloon Government, project BIOMED-HUB (programme 2014–2020). Our gratitude extends also to Jürgen Finsterbusch for support on the MR side, to the University of Minnesota Centre for Magnetic Resonance Research for providing the image reconstruction algorithm for the simultaneous multislice acquisitions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2021.674719/full#supplementary-material

Footnotes

1. ^ www.hMRI.info
2. ^ http://www.diffusiontools.com

References

André, E. D., Grinberg, F., Farrher, E. I, Maximov, I., Shah, N. J., Meyer, C., et al. (2014). Influence of noise correction on intra- and inter-subject variability of quantitative metrics in diffusion kurtosis imaging. PLoS One 9:e94531. doi: 10.1371/journal.pone.0094531

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashburner, J. (2007). A fast diffeomorphic image registration algorithm. Neuroimage 38, 95–113. doi: 10.1016/j.neuroimage.2007.07.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Berman, S., West, K. L., Does, M. D., Yeatman, J. D., and Mezer, A. A. (2018). Evaluating g-ratio weighted changes in the corpus callosum as a function of age and sex. Neuroimage 182, 304–313. doi: 10.1016/j.neuroimage.2017.06.076

PubMed Abstract | CrossRef Full Text | Google Scholar

Bland, J. M., and Altman, D. G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1, 307–310. doi: 10.1128/AAC.00483-18

PubMed Abstract | CrossRef Full Text | Google Scholar

Callaghan, M. F., Helms, G., Lutti, A., Mohammadi, S., and Weiskopf, N. (2015a). A general linear relaxometry model of R1 using imaging data. Magn. Reson. Med. 73, 1309–1314. doi: 10.1002/mrm.25210

PubMed Abstract | CrossRef Full Text | Google Scholar

Callaghan, M. F., Josephs, O., Herbst, M., Zaitsev, M., Todd, N., and Weiskopf, N. (2015b). An evaluation of prospective motion correction (PMC) for high resolution quantitative MRI. Front. Neurosci. 9:97. doi: 10.3389/fnins.2015.00097

PubMed Abstract | CrossRef Full Text | Google Scholar

Callaghan, M. F., Lutti, A., Ashburner, J., Balteau, E., Corbin, N., Draganski, B., et al. (2019). Example dataset for the hMRI toolbox. Data Brief 25:104132. doi: 10.1016/j.dib.2019.104132

PubMed Abstract | CrossRef Full Text | Google Scholar

Campbell, J. S. W., Leppert, I. R., Boudreau, M., Narayanan, S., Duval, T., Cohen-Adad, J., et al. (2018). Promise and pitfalls of g-ratio estimation with MRI. Neuroimage 182, 80–96. doi: 10.1016/j.neuroimage.2017.08.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Cercignani, M., Giulietti, G., Dowell, N. G., Gabel, M., Broad, R., Leigh, P. N., et al. (2017). Characterizing axonal myelination within the healthy population: a tract-by-tract mapping of effects of age and gender on the fiber g-ratio. Neurobiol. Aging 49, 109–118. doi: 10.1016/j.neurobiolaging.2016.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellerbrock, I., and Mohammadi, S. (2018). Four in vivo g -ratio-weighted imaging methods: comparability and repeatability at the group level. Hum. Brain Mapp. 39, 24–41. doi: 10.1002/hbm.23858

PubMed Abstract | CrossRef Full Text | Google Scholar

Feinberg, D. A., Moeller, S., Smith, S. M., Auerbach, E., Ramanna, S., Glasser, M. F., et al. (2010). Multiplexed echo planar imaging for sub-second whole brain FMRI and Fast Diffusion Imaging. Edited by Pedro Antonio Valdes-Sosa. PLoS One 5:e15710. doi: 10.1371/journal.pone.0015710

PubMed Abstract | CrossRef Full Text | Google Scholar

Gloor, M., Scheffler, K., and Bieri, O. (2008). Quantitative magnetization transfer imaging using balanced SSFP. Magn. Reson. Med. 60, 691–700. doi: 10.1002/mrm.21705

PubMed Abstract | CrossRef Full Text | Google Scholar

Graf von Keyserlingk, D., and Schramm, U. (1984). Diameter of axons and thickness of myelin sheaths of the pyramidal tract fibres in the adult human medullary pyramid. Anat. Anz. 157, 97–111. doi: 10.1097/PSY.0000000000000183

PubMed Abstract | CrossRef Full Text | Google Scholar

Helms, G. (2015). “Correction for residual effects of B1+ inhomogeniety on MT saturation in FLASH-based multi-parameter mapping of the brain,” in Proceedings of the International Society for Magnetic Resonance in Medicine Annual Meeting 2015, (Toronto: International Society for Magnetic Resonance in Medicine), 3360.

Google Scholar

Helms, G., Dathe, H., Kallenberg, K., and Dechent, P. (2008). High–resolution maps of magnetization transfer with inherent correction for RF inhomogeneity and T 1 relaxation obtained from 3D FLASH MRI. Magn. Reson. Med. 60, 1396–1407. doi: 10.1002/mrm.21732

PubMed Abstract | CrossRef Full Text | Google Scholar

Helms, G., Weiskopf, N., and Lutti, A. (2021). Correction of FLASH-based MT saturation in human brain for residual bias of B1-inhomogeneity at 3T. arXiv [Preprint]. arXiv:210414878 [physics].

Google Scholar

Hildebrand, C., and Hahn, R. (1978). Relation between myelin sheath thickness and axon size in spinal cord white matter of some vertebrate species. J. Neurol. Sci. 38, 421–434. doi: 10.1016/0022-510X(78)90147-8

CrossRef Full Text | Google Scholar

Hori, M., Hagiwara, A., Fukunaga, I., Ueda, R., Kamiya, K., Suzuki, Y., et al. (2018). Application of quantitative microstructural MR imaging with atlas-based analysis for the spinal cord in cervical spondylotic myelopathy. Sci. Rep. 8, 1–8. doi: 10.1038/s41598-018-23527-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hua, K., Zhang, J., Wakana, S., Jiang, H., Li, X., Reich, D. S., et al. (2008). Tract probability maps in stereotaxic spaces: analyses of white matter anatomy and tract-specific quantification. Neuroimage 39, 336–347. doi: 10.1016/j.neuroimage.2007.07.053

PubMed Abstract | CrossRef Full Text | Google Scholar

Jung, W., Lee, J., Shin, H. G., Nam, Y., Zhang, H., Oh, S. H., et al. (2017). Whole brain g-ratio mapping using myelin water imaging (MWI) and neurite orientation dispersion and density imaging (NODDI). Neuroimage 19, 109–118. doi: 10.1016/j.neuroimage.2017.09.053

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamagata, K., Zalesky, A., Yokoyama, K., Andica, C., Hagiwara, A., Shimoji, K., et al. (2019). MR g-ratio-weighted connectome analysis in patients with multiple sclerosis. Sci. Rep. 9:13522. doi: 10.1038/s41598-019-50025-2

PubMed Abstract | CrossRef Full Text | Google Scholar

LaMantia, A.-S., and Rakic, P. (1990). Cytological and quantitative characteristics of four cerebral commissures in the rhesus monkey. J. Comp. Neurol. 291, 520–537. doi: 10.1002/cne.902910404

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmenkühler, A., Syková, E., Svoboda, J., Zilles, K., and Nicholson, C. (1993). Extracellular space parameters in the rat neocortex and subcortical white matter during postnatal development determined by diffusion analysis. Neuroscience 55, 339–351. doi: 10.1016/0306-4522(93)90503-8

CrossRef Full Text | Google Scholar

Leutritz, T., Seif, M., Helms, G., Samson, R. S., Curt, A., Freund, P., et al. (2020). Multiparameter mapping of relaxation (R1, R2^∗), proton density and magnetization transfer saturation at 3 T: a multicenter dual-vendor reproducibility and repeatability study. Hum. Brain Mapp. 41, 4232–4247. doi: 10.1002/hbm.25122

PubMed Abstract | CrossRef Full Text | Google Scholar

Liewald, D., Miller, R., Logothetis, N., Wagner, H.-J., and Schüz, A. (2014). Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque. Biol. Cybern. 108, 541–557. doi: 10.1007/s00422-014-0626-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Lutti, A., Hutton, C., Finsterbusch, J., Helms, G., and Weiskopf, N. (2010). Optimization and validation of methods for mapping of the radiofrequency transmit field at 3T. Magn. Reson. Med. 238, 229–238. doi: 10.1002/mrm.22421

PubMed Abstract | CrossRef Full Text | Google Scholar

Macdonald, J., and Ruthotto, L. (2018). Improved susceptibility artifact correction of echo-planar MRI using the alternating direction method of multipliers. J. Math. Imaging Vis. 60, 268–282. doi: 10.1007/s10851-017-0757-x

CrossRef Full Text | Google Scholar

Mancini, M., Giulietti, G., Dowell, N., Spanò, B., Harrison, N., Bozzali, M., et al. (2017). Introducing axonal myelination in connectomics: a preliminary analysis of g-ratio distribution in healthy subjects. Neuroimage 182, 351–359. doi: 10.1016/j.neuroimage.2017.09.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Moeller, S., Yacoub, E., Olman, C. A., Auerbach, E., Strupp, J., Harel, N., et al. (2010). Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain FMRI. Magn. Reson. Med. 63, 1144–1153. doi: 10.1002/mrm.22361

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, S., and Callaghan, M. F. (2020). Towards in vivo g-ratio mapping using MRI: unifying myelin and diffusion imaging. J. Neurosci. Methods 348:108990. doi: 10.1016/j.jneumeth.2020.108990

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, S., Carey, D., Dick, F., Diedrichsen, J., Sereno, M. I., Reisert, M., et al. (2015). Whole-brain in-vivo measurements of the axonal g-ratio in a group of 37 healthy volunteers. Front. Neurosci. 9:441. doi: 10.3389/fnins.2015.00441

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, S., Möller, H. E., Kugel, H., Müller, D. K., and Deppe, M. (2010). Correcting eddy current and motion effects by affine whole-brain registrations: evaluation of three-dimensional distortions and comparison with slicewise correction. Magn. Reson. Med. 64, 1047–1056. doi: 10.1002/mrm.22501

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, S., Tabelow, K., Ruthotto, L., Feiweier, T., Polzehl, J., and Weiskopf, N. (2014). High-resolution diffusion kurtosis imaging at 3t enabled by advanced post-processing. Front. Neurosci. 8:427. doi: 10.3389/fnins.2014.00427

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicholson, C., and Hrabìtová, S. (2017). Brain extracellular space: the final frontier of neuroscience. Biophys. J. 113, 2133–2142. doi: 10.1016/j.bpj.2017.06.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Olivares, R., Montiel, J., and Aboitiz, F. (2001). Species differences and similarities in the fine structure of the mammalian corpus callosum. Brain Behav. Evol. 57, 98–105. doi: 10.1159/000047229

PubMed Abstract | CrossRef Full Text | Google Scholar

Reese, T. G., Heid, O., Weisskoff, R. M., and Wedeen, V. J. (2003). Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn. Reson. Med. 49, 177–182. doi: 10.1002/mrm.10308

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruthotto, L., Kugel, H., Olesch, J., Fischer, B., Modersitzki, J., Burger, M., et al. (2012). Diffeomorphic susceptibility artifact correction of diffusion-weighted magnetic resonance images. Phys. Med. Biol. 57, 5715–5731. doi: 10.1088/0031-9155/57/18/5715

CrossRef Full Text | Google Scholar

Ruthotto, L., Mohammadi, S., Heck, C., Modersitzki, J., and Weiskopf, N. (2013). “Hyperelastic susceptibility artifact correction of DTI in SPM,” in Bildverarbeitung Für Die Medizin 2013, eds H. P. Meinzer, T. Deserno, H. Handels, and T. Tolxdorff (Berlin: Springer), 344–349. doi: 10.1007/978-3-642-36480-8_60

CrossRef Full Text | Google Scholar

Sereno, M. I., Lutti, A., Weiskopf, N., and Dick, F. (2013). Mapping the human cortical surface by combining quantitative T1 with retinotopy. Cereb. Cortex 23, 2261–2268. doi: 10.1093/cercor/bhs213

PubMed Abstract | CrossRef Full Text | Google Scholar

Setsompop, K., Gagoski, B. A., Polimeni, J. R., Witzel, T., Wedeen, V. J., and Wald, L. L. (2012). Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med. 67, 1210–1224. doi: 10.1002/mrm.23097

PubMed Abstract | CrossRef Full Text | Google Scholar

Stikov, N., Campbell, J. S., Stroh, T., Lavelée, M., Frey, S., Novek, J., et al. (2015). In vivo histology of the myelin g-ratio with magnetic resonance imaging. Neuroimage 118, 397–405. doi: 10.1016/j.neuroimage.2015.05.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Stikov, N., Perry, L. M., Mezer, A., Rykhlevskaia, E., Wandell, B. A., Pauly, J. M., et al. (2011). Bound pool fractions complement diffusion measures to describe white matter micro and macrostructure. Neuroimage 54, 1112–1121. doi: 10.1016/j.neuroimage.2010.08.068

PubMed Abstract | CrossRef Full Text | Google Scholar

Swadlow, H. A., Waxman, S. G., and Geschwind, N. (1980). Small-diameter nonmyelinated axons in the primate corpus callosum. Arch. Neurol. 37, 114–115. doi: 10.1001/archneur.1980.00500510072016

PubMed Abstract | CrossRef Full Text | Google Scholar

Tabelow, K., Balteau, E., Ashburner, J., Callaghan, M. F., Draganski, B., Helms, G., et al. (2019). hMRI – A toolbox for quantitative MRI in neuroscience and clinical research. Neuroimage 194, 191–210.

Google Scholar

Tønnesen, J., Inavalli, V. V. G. K., and Nägerl, U. V. (2018). Super-resolution imaging of the extracellular space in living brain tissue. Cell 172, 1108–1121. doi: 10.1016/j.cell.2018.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, S. S., Shultz, J. R., Burish, M. J., Harrison, K. H., Hof, P. R., Towns, L. C., et al. (2008). Functional trade-offs in white matter axonal scaling. J. Neurosci. 28, 4047–4056. doi: 10.1523/JNEUROSCI.5559-05.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiskopf, N., Lutti, A., Helms, G., Novak, M., Ashburner, J., and Hutton, C. (2011). Unified segmentation based correction of R1 brain maps for RF transmit field inhomogeneities (UNICORT). Neuroimage 54, 2116–2124. doi: 10.1016/j.neuroimage.2010.10.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiskopf, N., Suckling, J., Williams, G., Correia, M. M., Inkster, B., Tait, R., et al. (2013). Quantitative multi-parameter mapping of R1, PD(^∗), MT, and R2(^∗) at 3T: a multi-center validation. Front. Neurosci. 7:95. doi: 10.3389/fnins.2013.00095

PubMed Abstract | CrossRef Full Text | Google Scholar

West, K. L., Kelm, N. D., Carson, R. P., and Does, M. D. (2016). A revised model for estimating g-ratio from MRI. Neuroimage 125, 1155–1158. doi: 10.1016/j.neuroimage.2015.08.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, J., Moeller, S., Auerbach, E. J., Strupp, J., Smith, S. M., Feinberg, D. A., et al. (2013). Evaluation of slice accelerations using multiband echo planar imaging at 3T. Neuroimage 83, 991–1001. doi: 10.1016/j.neuroimage.2013.07.055

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, F., Fan, Q., Tian, Q., Ngamsombat, C., Machado, N., Bireley, J. D., et al. (2019). Imaging g-ratio in multiple sclerosis using high-gradient diffusion mri and macromolecular tissue volume. AJNR Am. J. Neuroradiol. 40, 1871–1877. doi: 10.3174/ajnr.A6283

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Schneider, T., Wheeler-Kingshott, C. A., and Alexander, D. C. (2012). NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61, 1000–1016. doi: 10.1016/j.neuroimage.2012.03.072

PubMed Abstract | CrossRef Full Text | Google Scholar