
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Neurosci. , 16 September 2020
Sec. Neuroprosthetics
Volume 14 - 2020 | https://doi.org/10.3389/fnins.2020.577937
This article is part of the Research Topic Advanced Deep-Transfer-Leveraged Studies on Brain-Computer Interfacing View all 23 articles
Magnetic Resonance Imaging (MRI) is an indispensable tool in the diagnosis of brain diseases due to painlessness and safety. Nevertheless, Rician noise is inevitably injected during the image acquisition process, which leads to poor observation and interferes with the treatment. Owing to the complexity of Rician noise, using the elimination method of Gaussian to remove it does not perform well. Therefore, the feature fusion and attention network (FFA-DMRI) is proposed to separate noise from observed MRI. Inspired by the attention-guided CNN network (ADNet) and Convolutional block attention module (CBAM), a spatial attention mechanism has been specially designed to obtain the area of interest in MRI. Furthermore, the feature fusion block concatenates local with global information, which makes full use of the multilevel structure and boosts the expressive ability of network. The comprehensive experiments on Alzheimer’s disease neuroimaging initiative dataset (ADNI) have demonstrated high effectiveness of FFA-DMRI with maintaining the crucial brain details. Moreover, in terms of visual inspections, the denoising results are also consistent with human perception.
Magnetic Resonance Imaging (MRI) of brains, with the superior features of non-radiation, non-invasiveness, and high resolution, is notable for diagnosis and treatment (Ikram et al., 2019; Jiang et al., 2019; Yu et al., 2019; Tripathi and Bag, 2020). In clinical practice, high-quality MRI can provide clear structural and functional information on brain tissues. However, noise is introduced into the raw image due to the circulation of magnetic fields and the interaction of magnets in MRI machines, which may hide the details of brain tissues and hinder the auto-computerized analysis (Jiang et al., 2017). Therefore, noise removal is a vital task to recover the clean MRI before the images are applied to diagnosis.
Previous research has established that the noise in MRI is governed by the Rician distribution, in which both real and imaginary parts are corrupted by Gaussian noise with equal variance (Bhadauria and Dewal, 2013; Li et al., 2020). The Rician distribution is signal-dependent as distinct from additive Gaussian noise. In other words, Rician noise is related to the image, and utilizing Gaussian denoising methods directly to remove it usually yields poor results. Thus, the right way to separate noise from the raw MRI without losing critical details is a huge challenge (Cai et al., 2020a).
With the increasing demand for image quality, a number of methods have been proposed for denoising. Existing methods can be mainly classified into two categories: transform domain methods and filtering methods (Mohan et al., 2014). The purpose of the transform domain method is to convert the original signal into a pattern that can remove noise more easily. For instance, a bilateral filtering scheme was proposed based on wavelets, in which the noise coefficient is expressed effectively by an undecimated wavelet transform (UDWT). There is a nice trade-off between the effect of noise removal and feature retention (Anand and Sahambi, 2010; Cai et al., 2020b). Based on wavelet shrinkage, the iterative scheme estimates the signal wavelet coefficients from the noisy images (Yu and Zhao, 2008). For signal high-dimensional singularities, wavelet transform does not perform well. Curvelet transform makes up for the shortcomings (Mohan et al., 2014). In this transform, edge directions are reproduced using the directivity and anisotropy of the curve (Do and Vetterli, 2005). However, the wavelet transform fails to resolve the curve with smooth edges. To overcome the drawback, a geometrical image transform was proposed, which greatly captures contours and details in MRI.
The filter methods, generally grouped into linear and non-linear parts, are adapted to remove noise in MRI. For linear filters, spatial filters and temporal filters are commonly employed (McVeigh et al., 1985; Mohan et al., 2014). Relatively, a spatial filter decreases the variance in MRI; however, it faces shortcomings in that it introduces the blurring of edges, which results in part of the required information that cannot be restored correctly (Soomro and Gao, 2016). Temporal filters are utilized only to spin-echo images. Furthermore, to prevent the aliasing artifacts, it is essential to select the appropriate filter to match filter sampling intervals. If the filters are too broad or too narrow, the performance is not satisfactory. For non-linear spatial filters, using a linear approach directly is not allowed. There are some typical examples in non-linear filters such as anisotropic diffusion filter (ADF) (Sijbers et al., 1999) and non-local means (NLM) (Coupé et al., 2006). The ADF approach obtains the denoising images efficiently with sharp edges. The filter of NLM employs redundant information to restore noise-free images. On the basis of the filter, unbiased NLM (Manjón et al., 2008) is exploited to improve the SNR in MRI; meanwhile, it does not influence the obvious structures. Nevertheless, the method has the shortcoming of high computational complexity.
Recently, methodologies based on deep learning are used to alleviate the above problem, such as deep plug-and-play super-resolution (DPSR) (Zhang K. et al., 2019), fast and flexible denoising convolutional neural network (FFDNet) (Zhang et al., 2018), and variance-stabilizing transformation inspired networks (VST-net) (Zhang M. et al., 2019). VST-net inherits the structures of traditional variance-stabilizing transformation and optimizes non-linear transformation through the design of a deep learning network. That shows the great potential of deep learning for denoising tasks. It is noted that the denoising convolutional neural network (DnCNN) (Zhang et al., 2017a) utilizes batch normalization and residual learning, which exhibits high effectiveness in JPEG image deblocking, single image super-resolution, and Gaussian denoising. Numerous deep learning methods for denoising have achieved outstanding performance. However, most research up to now has focused on the reduction of Gaussian noise, real noise, and blind noise. To our best knowledge, far too little attention has been paid to removing the Rician noise in MRI.
In this work, we propose a feature fusion and attention network (FFA-DMRI) for removing Rician noise in magnetic resonance (MR) images. Inspired by the structure of attention-guided CNN network (ADNet) (Tian et al., 2020), we have designed the FFA-DMRI network to restore noise-free images while maintaining critical brain tissues to the maximum extent possible. The main contributions of this paper are as follows:
(1) The proposed FFA-DMRI is dedicated to removing Rician noise in MR images. In contrast to other deep leaning methods for denoising, we specifically develop a spatial attention mechanism to focus on the area-of-interest of the brain.
(2) FFA-DMRI network is constructed with three blocks, including the feature extraction block, the feature fusion block, and the attention block. The feature extraction block utilizes the common convolution and the dilated convolution, which expands the receptive field and gains the details effectively. The feature fusion block is designed to combine the local and global features. Consequently, this block obtains more contextual information and promotes the reconstruction of pixels in MR images.
(3) The FFA-DMRI network is very superior for denoising on the ADNI dataset. In comparative experiments, it is competitive in quantitative metrics in terms of SSIM and PSNR. From the visual inspection, the denoising results are also in line with the human sense.
The raw image generated by magnetic resonance equipment is K-space, including the real channel Prand the imaginary channelPi. Both channels are governed by Gaussian noise with equal variance σ2 and a mean value of zero (Zhu et al., 2009), which can be given by
where R is the amplitude and α is the phase of raw signal. In addition, ℜ and ℑ denote the independent Gaussian noise which is injected into the real and the imaginary channel, respectively. An inverse discrete Fourier transform (Briggs and Henson, 1995) and the modular operation are exploited to reconstruct the MR images, which satisfies the human visual sense. The modular operation can be expressed as follows:
After the non-linear transformation, the noise distribution is converted from Gaussian to Rician (He and Greenshields, 2008). The probability distribution function (PDF) of Rician noise can be estimated as
where I0 stands for the zeroth-order modified Bessel function (Sijbers and den Dekker, 2004) when the discrete grid is utilized to define MRI. From the PDF, it can be inferred that Rician noise is associated with images. For images with different signal-to-noise ratios (SNR), the distributions of Rician noise are disparate. If the value of SNR is relatively high, Rician distribution degenerates into a Gaussian distribution. Conversely, it tends to the Rayleigh distribution in low SNR. Therefore, compared with Gaussian noise, Rician noise is more complicated.
Inspired by ADNet (Tian et al., 2020), the FFA-DMRI is proposed to eliminate noise in MRI. Figure 1 illustrates the overall architecture of FFA-DMRI. The network constructed by three sub-networks is as follows: a feature extraction block, a feature fusion block, and an attention block. These blocks correspond to the stages of denoising. Firstly, it employs common convolutions and dilated convolutions to expand the receptive field and acquires the features adequately. Furthermore, the operation of concatenation between global and local information enhances the expressive ability of network. Finally, the attention mechanism guides the network to extract useful information by assigning weights to different spatial positions and channels. The output of the network is the residual MR image and the potential clean image is obtained by subtracting the residual image from the input noisy image.
According to the structure of FFA-DMRI, the input of the network is noisy observed MRI, which is defined asS. The FFA-DMRI aims to learn the residual image N as an output rather than the potential clean imageC. Every block is assumed to be a function; hence the execution process of network is defined as
where gex, gfu, and gat denote the functions of the feature extraction, feature fusion, and attention block, respectively. The output N is the mapping of noise in MRI and the potential clean image can be reconstructed by subtracting N from S. The implementations can be expressed as
It is known that the crucial structural information in complex images is easily hidden, which leads to poor performance in practice. Therefore, extracting the representative features is notoriously hard but vital in deep learning. To overcome this problem, during the course of training, the network of FFA-DMRI is supposed to focus on the interest area of the brain and suppress the insignificant region. Motivated by that, we have designed the spatial attention mechanism inspired by CBAM (Woo et al., 2018), which is suitable for MR images specifically. Figure 2 depicts the spatial attention module with an additional layer of maximum pooling.
The attention module simulates the prioritization of visual information in human perception. In order to make the network pay more attention to the extraction of brain structure, an additional layer of maximum pooling is concatenated on the original architecture of CBAM. In this work, we consider another situation in which a spatial attention module is added with a layer of average pooling, as shown in Figure 3.
In terms of MR images, the pixels in the background are mostly black, and thus the values are zero. With respect to the brain regions, the pixel values are mostly greater than zero. For average pooling, the operation preserves background information and is suitable for the images where all pixels contribute to the prediction. Thus, average pooling is less applicable to MRI denoising. Relatively, maximum pooling is utilized to extract textures and assists the network in focusing on the brain regions, hence maximum pooling is selected in the module. To sum up, we take advantage of spatial attention to enhance the ability to extract brain features, which results in spending a lower amount of computing resources and achieving outstanding effects.
The batch normalization (BN) operation normalizes the input data; hence, it will destroy the original contrast of MR images. Besides, it has been pointed out that BN is more suitable to map data with regular distribution (Li et al., 2020). From the generation of Rician noise, it can be determined that the noise is non-linear. Thus, we do not employ the BN operation in the first two convolutions. Furthermore, the extraction of the context plays a crucial role in computer vision applications. For the denoising task, the construction of pixels is closely related to the context information (Yu and Koltun, 2016). In order to obtain more context, dilated convolution is utilized for the network, which enlarges the receptive field without reducing image resolution and losing details. Numerous works have been reported in the validity of dilated convolution (Yu and Koltun, 2016; Wei et al., 2018). For example, compared with a common convolution-based 3×3 kernel, a dilated convolution can serve a 5×5 or greater receptive field, but no increase in the number of parameters and computations. In FFA-DMRI, we integrate the common convolution and dilated convolution to take full advantage of information.
AlexNet (Krizhevsky et al., 2012), VGG-Net (Simonyan and Zisserman, 2014), and other deep learning models yield excellent results by increasing network layers. Nevertheless, on the one hand, the deeper network presents the phenomenon of gradient explosion and gradient disappearance. On the other hand, with continuous convolution, the effect of shallow features on a deep layer grows weak gradually. Thus, the way to extract high-quality features is pivotal for denoising tasks. To cope with the problem, we apply a lightweight and efficient feature-fusion module to combine low-level and high-level features. The module concatenates the intermediate feature map with the noisy observed MRI at the same scale, which makes full use of the structural information in the shallow network and boosts the network performance.
At the end of the feature fusion block, the two layers employ convolutions with the Rectified Linear Unit activation function (ReLU) and batch normalization. Compared with the sigmoid function, the ReLU function greatly reduces network computation and avoids the problem of gradient disappearance. Additionally, the ReLU function increases the non-linear relationship between the network layers, and thus it is appropriate to process the non-linear Rician noise. In this block, BN yields the distribution of images more stable, which greatly simplifies parameter adjustment and alleviates the problem of gradient disappearance.
In computer vision, the attention mechanism improves the efficiency and accuracy of network to a certain extent. It adjusts the weight of each channel through training in order to enhance the influence of useful channels and suppress the unnecessary channels. Exploring the relationship between channels is beneficial to extract more vital content for the results and improve the denoising performance. In this paper, we exploit the maximum pooling and average pooling to the input feature map first. Furthermore, the two pooling layers are convolved separately. Then a sum of the convolutional layers yields the channel weights (Woo et al., 2018). The structure of channel attention is shown in Figure 4.
The loss function guides the further training of the network, and thus the selection of a loss function is directly related to the effect of execution. Different from the existing denoising networks that predict potential clean images directly, FFA-DMRI is able to estimate the residual images. Then subtracting the residual image from the input original image can obtain the clean images. Therefore, we use the mean square error (MSE) (Ephraim and Malah, 1984) to calculate the gap between the residual images generated by FFA-DMRI and the desired residual images. The desired residual image is obtained by subtracting noise-free image from noisy observed image. The loss function is described as
Where S represents the noisy observed image and G stands for the noise-free image. θ denotes the parameter of FFA-DMRI training. M is the number of noisy-clean training image pairs.
Deep learning is a data-driven technology. In other words, it requires a large amount of data for training to achieve promising performance. The network of FFA-DMRI is evaluated on the public real brain database of the Alzheimer’s disease neuroimaging initiative (ADNI)1. In our experiments, it consists of 199 three-dimensional (3D) images of brain MRI. We slice each 3D image to get the axial plane and select the slices that range from 37 to 86 due to less information in the head and tail regions. Then Rician noise is injected into images with noise levels of 5, 10, 20, and 30 according to formula (2), respectively. All the images have a resolution of 145×121, and they are divided into three parts; the training set contains 7,800 images, the test set includes 975 images, and the validation set consists of 975 images.
The network is trained with the PyTorch framework in Python and employs the NVIDIA GeForce GTX 960. In some scenarios, adaptive moment estimation (Adam) has better performance than the stochastic gradient descent (SGD) (Zhang, 2018). Thus, the optimizer used in this experiment is Adam (Kingma and Ba, 2014). The initial learning rate is chosen as 0.0001, and it is reduced by 0.5, 0.25, and 0.125 in the following training. The batch size is set to four due to the trade-off between GPU memory and computational speed.
There are two popular qualitative metrics to evaluate denoising methods, including peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) (Kala and Deepa, 2018; Yu et al., 2019). PSNR calculates the distortion between recovered images q(x,y) and ground truthp(x,y). It can be defined as
where M×N is the size of MR images and higher PSNR means the less distortion in images.
The metrics of SSIM is based on three comparative measurements, including luminance, contrast, and structure. Itis more consistent with human visual perception (Wang et al., 2004), that can be obtained by
where up, uq is the average of p, q, respectively. And is the variance of p; denotes the variance of q, and σpq represents the covariance of p and q. To avoid instability, SSIM appends two constants including c1 and c2. The value range of SSIM is [0,1].
In order to verify the effectiveness of the proposed FFA-DMRI, comparative experiments are conducted under the same dataset and parameters to guarantee fairness. The results of different denoising schemes are evaluated in terms of quantitative and qualitative metrics. Collectively, we compare the proposed network FFA-DMRI with common denoising algorithms, including NLM (Buades et al., 2011), BM3D (Danielyan et al., 2011), MRF (Ji, 2019), Wiener filter (Jang and Kim, 2001), WNNM (Gu et al., 2014), IRCNN (Zhang et al., 2017b) and DnCNN (Zhang et al., 2017a).
Based on the above Settings, the average PNSR results of different denoising methods are presented in Table 1, and the average SSIM results are reported in Table 2.

Table 1. The average PSNR/dB results of different methods on the ADNI dataset at different noise levels.

Table 2. The average SSIM results of different methods on the ADNI dataset at different noise levels.
It is known that the Rician noise depends on the images, so removing it is more complicated than Gaussian additive noise. From Table 1, the best result of PSNR at each noise level is shown in bold. It can be observed that the proposed FFA-DMRI outperforms other methods tested. For BM3D and NLM methods, it is difficult to match similar regions at higher noise levels. Besides, searching and matching regions consume much time. Therefore, the traditional method does not perform well on the dataset. It is noted that deep learning methods achieve outstanding denoising results. In particular, among the listed deep learning methods, the proposed FFA-DMRI promotes the removing performance at each noise level. On the specifics, FFA-DMRI exceeds IRCNN 1.43 dB at the noise level of 20 and is superior to DnCNN at every noise level. Additionally, we measured the results of the above methods in terms of SSIM.
The metrics of SSIM indicates that the structural similarity between recovered images and ground truth. As described in Table 2, FFA-DMRI achieves the best performance. It brings an improvement of 2.66% than IRCNN at the noise level of 20. Note that when the noise level is 5, our method tends to the highest value (the highest value in SSIM is 1), which shows that recovered images perfectly restore noise-free images. Besides, the value of SSIM is over 90% at each noise level for FFA-DMRI. Consistent with the results of PSNR, the traditional methods are inferior to the deep learning methods in this dataset. In summary, there is a significant improvement in brain MRI denoising, which reconstructs the latent clean image with maintaining the vital structure information. Thus FFA-DMRI is a competitive denoising method in terms of quantitative analysis.
In practice, it is indispensable to evaluate image quality through the human senses. In some cases, the metrics of SSIM and PSNR are outstanding in computer vision tasks; however, the images that do not satisfy human perception are distorted. In this paper, we list the visual inspections of comparative experiments as illustrated in Figures 5, 6.

Figure 5. Visual inspections of brain MRI denoised by traditional methods. (A) MRI with noise of different levels. (B) The results of BM3D at different noise levels. (C) The results of NLM at different noise levels.
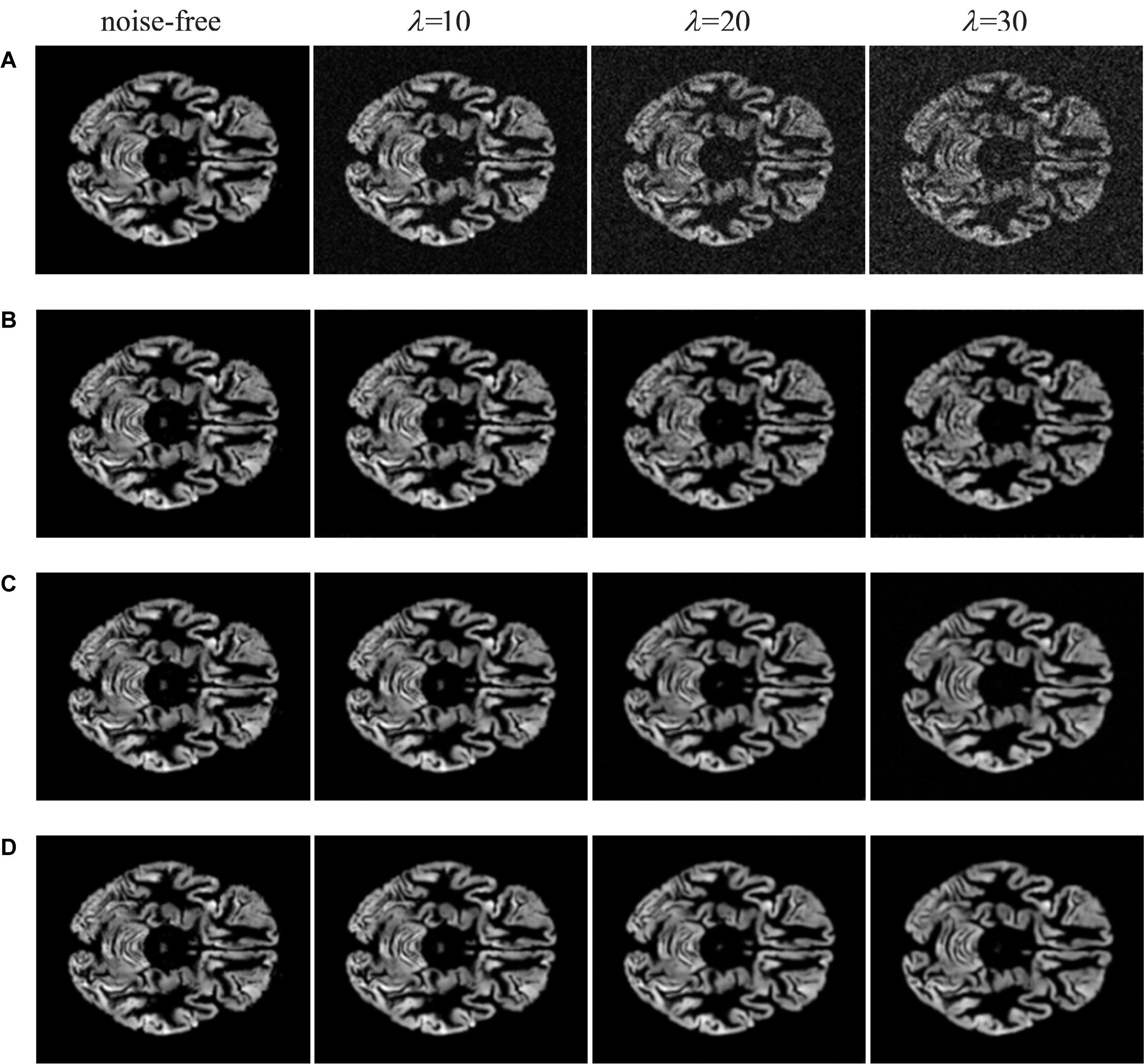
Figure 6. Visual inspections of brain MRI denoised by deep learning methods. (A) MRI with noise of different levels. (B) The results of IRCNN at different noise levels. (C) The results of DnCNN at different noise levels. (D) the results of FFA-DMRI at different noise levels.
From Figure 5, we illustrate traditional denoising methods for comparison. It is noticeable that the BM3D and NLM methods can remove a part of noise while generating the blurred structure of brain. Meanwhile, some crucial details in original images are lost. When the concentration of noise increases, the removal effect is worse on speediness with poor visual perception. In Figure 6, visual illustrations of deep learning methods are shown. It can be seen that the effect of deep learning methods is superior to traditional methods, which remove background noise and recover most of the complex brain structures.
In comparison with IRCNN, the proposed FFA-DMRI yields clearer brain tissues and sharper edges after noise removal. The method of DnCNN also achieves excellent results in the experiments; however, FFA-DMRI maintains more subtle features of the original image, and the contrast between brain regions and background is stronger than DnCNN. The obvious contrast contributes to enhancing the interpretation and recognition of images and satisfies the needs of clinical analysis. In general, FFA-DMRI we proposed performs well in the quantitative and qualitative analysis.
In this article, we propose a network to remove Rician noise from a brain MRI as well as FFA-DMRI. The network is composed of a feature extraction block, a feature fusion block, and an attention block. The feature extraction block exploits the spatial attention mechanism to obtain the area of interest emphatically. Moreover, we utilize dilated convolutions, which expand the receptive fields, and we fuse local and global information to boost the network performance. Then the channel attention mechanism is employed to enhance the influence of essential elements and suppress the useless channels. After the above steps are carried out, FFA-DMRI is trained on the ADNI dataset. In terms of quantitative evaluation, SSIM and PSNR are adopted. Experimental results show that FFA-DMRI can effectively remove Rician noise and maintain most of the crucial details. For quantitative evaluation, it can be seen from visual inspection that the recovered images are more consistent with human senses with obvious contrast, clear brain tissues, and sharp edges. Therefore, the proposed method FFA-DMRI is competitive in brain MRI denoising, which can assist clinicians in diagnosis and treatment.
Publicly available datasets were analyzed in this study. This data can be found here: http://adni.loni.usc.edu/.
DH was responsible for the work of writing the manuscript and doing experiments. CH, CY, JL, and YQ made the experiments. CC modified the English grammar of the article. All authors contributed to the article and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Anand, C. S., and Sahambi, J. S. (2010). Wavelet domain non-linear filtering for MRI denoising. Magn. Reson. Imaging 28, 842–861. doi: 10.1016/j.mri.2010.03.013
Bhadauria, H., and Dewal, M. L. (2013). Medical image denoising using adaptive fusion of curvelet transform and total variation. Comput. Electr. Eng. 39, 1451–1460. doi: 10.1016/j.compeleceng.2012.04.003
Briggs, W. L., and Henson, V. E. (1995). The DFT: An Owner’s Manual for the Discrete Fourier Transform. Philadelphia, PA: SIAM. doi: 10.1137/1.9781611971514
Buades, A., Coll, B., and Morel, J.-M. (2011). Non-local means denoising. Image Process. On Line 1, 208–212. doi: 10.5201/ipol.2011.bcm_nlm
Cai, C., Huang, C., Yang, C., Lu, H., Hong, X., Ren, F., et al. (2020a). Altered patterns of functional connectivity and causal connectivity in salience subnetwork of subjective cognitive decline and amnestic mild cognitive impairment. Front. Neurosci. 14:288. doi: 10.3389/fnins.2020.00288
Cai, C., Huang, C., Yang, C., Zhang, X., Peng, Y., Zhao, W., et al. (2020b). Altered patterns of phase position connectivity in default mode subnetwork of subjective cognitive decline and amnestic mild cognitive impairment. Front. Neurosci. 14:185. doi: 10.3389/fnins.2020.00185
Coupé, P., Yger, P., and Barillot, C. (2006). “Fast non local means denoising for 3D MR images,” in Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, (Berlin: Springer). doi: 10.1007/11866763_5
Danielyan, A., Katkovnik, V., and Egiazarian, K. (2011). BM3D frames and variational image deblurring. IEEE Trans. Image Process. 21, 1715–1728. doi: 10.1109/tip.2011.2176954
Do, M. N., and Vetterli, M. (2005). The contourlet transform: an efficient directional multiresolution image representation. IEEE Trans. Image Process. 14, 2091–2106. doi: 10.1109/tip.2005.859376
Ephraim, Y., and Malah, D. (1984). Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 32, 1109–1121. doi: 10.1109/tassp.1984.1164453
Gu, S., Zhang, L., Zuo, W., and Feng, X. (2014). “Weighted nuclear norm minimization with application to image denoising,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Piscataway, NJ: IEEE). doi: 10.1109/CVPR.2014.366
He, L., and Greenshields, I. R. (2008). A nonlocal maximum likelihood estimation method for Rician noise reduction in MR images. IEEE Trans. Med. Imaging 28, 165–172. doi: 10.1109/tmi.2008.927338
Ikram, S., Shah, J. A., Zubair, S. I, Qureshi, M., and Bilal, M. (2019). Improved reconstruction of MR scanned images by using a dictionary learning scheme. Sensors 19:1918. doi: 10.3390/s19081918
Jang, I.-H., and Kim, N.-C. (2001). Denoising of images using locally adaptive Wiener filter in wavelet domain. IEICE Trans. Inf. Syst. 84, 495–501.
Ji, Q. (2019). Probabilistic Graphical Models for Computer Vision. Cambridge: Academic Press. doi: 10.1016/B978-0-12-803467-5.00008-3
Jiang, Y., Wu, D., Deng, Z., Qian, P., Wang, J., Wang, G., et al. (2017). Seizure classification from EEG signals using transfer learning, semi-supervised learning and TSK fuzzy system. IEEE Trans. Neural Syst. Rehabil. Eng. 25, 2270–2284. doi: 10.1109/tnsre.2017.2748388
Jiang, Y., Zhao, K., Xia, K., Xue, J., Zhou, L., Ding, Y., et al. (2019). A novel distributed multitask fuzzy clustering algorithm for automatic MR brain image segmentation. J. Med. Syst. 43:118. doi: 10.1007/s10916-019-1245-1
Kala, R., and Deepa, P. (2018). Adaptive hexagonal fuzzy hybrid filter for Rician noise removal in MRI images. Neural Comput. Appl. 29, 237–249. doi: 10.1007/s00521-017-2953-4
Kingma, D. P., and Ba, J. L. (2014). “Adam: a method for stochastic optimization,” in Proceedings of the ICLR 2015: International Conference on Learning Representations 2015, San Diego, CA.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 25, 1097–1105.
Li, S., Zhou, J., Liang, D., and Liu, Q. (2020). MRI denoising using progressively distribution-based neural network. Magn. Reson. Imaging. 71, 55–68. doi: 10.1016/j.mri.2020.04.006
Manjón, J. V., Carbonell-Caballero, J., Lull, J. J., García-Martí, G., Martí-Bonmatí, L., and Robles, M. (2008). MRI denoising using non-local means. Med. Image Anal. 12, 514–523. doi: 10.1016/j.media.2008.02.004
McVeigh, E. R., Henkelman, R. M., and Bronskill, M. J. (1985). Noise and filtration in magnetic resonance imaging. Med. Phys. 12, 586–591. doi: 10.1118/1.595679
Mohan, J., Krishnaveni, V., and Guo, Y. (2014). A survey on the magnetic resonance image denoising methods. Biomed. Signal Process. Control 9, 56–69. doi: 10.1016/j.bspc.2013.10.007
Sijbers, J., and den Dekker, A. J. (2004). Maximum likelihood estimation of signal amplitude and noise variance from MR data. Magn. Reson. Med. 51, 586–594. doi: 10.1002/mrm.10728
Sijbers, J., den Dekker, A. J., Van der Linden, A., Verhoye, T. M., and Van Dyck, D. (1999). Adaptive anisotropic noise filtering for magnitude MR data. Magn. Reson. Imaging 17, 1533–1539. doi: 10.1016/s0730-725x(99)00088-0
Simonyan, K., and Zisserman, A. (2014). “Very deep convolutional networks for large-scale image recognition,” in Proceedings of the ICLR 2015: International Conference on Learning Representations 2015, San Diego, CA.
Soomro, T. A., and Gao, J. (2016). “Neural network based denoised methods for retinal fundus images and MRI brain images,” in Preoceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), (Piscataway, NJ: IEEE). doi: 10.1109/IJCNN.2016.7727327
Tian, C., Xu, Y., Li, Z., Zuo, W., Fei, L., and Liu, H. (2020). Attention-guided CNN for image denoising. Neural Netw. 124, 117–129. doi: 10.1016/j.neunet.2019.12.024
Tripathi, P. C., and Bag, S. (2020). CNN-DMRI: a convolutional neural network for denoising of magnetic resonance images. Pattern Recogn. Lett. 135, 57–63. doi: 10.1016/j.patrec.2020.03.036
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P. (2004). Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612. doi: 10.1109/tip.2003.819861
Wei, Y., Xiao, H., Shi, H., Jie, Z., Feng, J., and Huang, T. S. (2018). “Revisiting dilated convolution: A simple approach for weakly-and semi-supervised semantic segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Piscataway, NJ: IEEE). doi: 10.1109/CVPR.2018.00759
Woo, S., Park, J., Lee, J.-Y., and So Kweon, I. (2018). “Cbam: convolutional block attention module,” Proceedings of the European Conference on Computer Vision (ECCV). Glasgow: ECCV. doi: 10.1007/978-3-030-01234-2_1
Yu, F., and Koltun, V. (2016). “Multi-Scale Context Aggregation by Dilated Convolutions,” in Proceedings of the ICLR 2016: International Conference on Learning Representations 2016, San Juan.
Yu, H., Ding, M., and Zhang, X. (2019). Laplacian Eigenmaps Network-Based Nonlocal Means Method for MR Image Denoising. Sensors 19, 2918. doi: 10.3390/s19132918
Yu, H., and Zhao, L. (2008). “An efficient denoising procedure for magnetic resonance imaging,” in Preoceedings of the 2008 2nd International Conference on Bioinformatics and Biomedical Engineering, (Piscataway, NJ: IEEE). doi: 10.1109/ICBBE.2008.990
Zhang, K., Zuo, W., Chen, Y., Meng, D., and Zhang, L. (2017a). Beyond a gaussian denoiser: residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 26, 3142–3155. doi: 10.1109/tip.2017.2662206
Zhang, K., Zuo, W., Gu, S., and Zhang, L. (2017b). “Learning deep CNN denoiser prior for image restoration,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Piscataway, NJ: IEEE). doi: 10.1109/tip.2017.2662206
Zhang, K., Zuo, W., and Zhang, L. (2018). FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 27, 4608–4622. doi: 10.1109/tip.2018.2839891
Zhang, K., Zuo, W., and Zhang, L. (2019). “Deep plug-and-play super-resolution for arbitrary blur kernels,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (Piscataway, NJ: IEEE). doi: 10.1109/CVPR.2019.00177
Zhang, M., Zhang, F., Liu, Q., and Wang, S. (2019). VST-net: variance-stabilizing transformation inspired network for Poisson denoising. J. Vis. Commun. Image Represent. 62, 12–22. doi: 10.1016/j.jvcir.2019.04.011
Zhang, Z. (2018). “Improved adam optimizer for deep neural networks,” in Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), (Piscataway, NJ: IEEE). doi: 10.1109/IWQoS.2018.8624183
Keywords: magnetic resonance imaging, brain, denoising, feature fusion, attention mechanism
Citation: Hong D, Huang C, Yang C, Li J, Qian Y and Cai C (2020) FFA-DMRI: A Network Based on Feature Fusion and Attention Mechanism for Brain MRI Denoising. Front. Neurosci. 14:577937. doi: 10.3389/fnins.2020.577937
Received: 30 June 2020; Accepted: 13 August 2020;
Published: 16 September 2020.
Edited by:
Yizhang Jiang, Jiangnan University, ChinaCopyright © 2020 Hong, Huang, Yang, Li, Qian and Cai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chenxi Huang, Y2h5YW5nQHhtdS5lZHUuY24=; Chenhui Yang, eWNoOTg3QDEyNi5jb20=; Jianpeng Li, bGl3aXR0eUBvdXRsb29rLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.