
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Neurosci. , 17 April 2019
Sec. Autonomic Neuroscience
Volume 13 - 2019 | https://doi.org/10.3389/fnins.2019.00318
This article is part of the Research Topic Hybrid Intelligent Algorithms Based Learning, Optimization, and Application to Autonomic Control Systems View all 6 articles
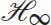 Filtering for T-S Fuzzy Discrete-Time Systems
Filtering for T-S Fuzzy Discrete-Time SystemsPeriodic event-triggered control (PETC) is a control strategy consisting of event-triggered control (ETC) and conventional periodic sampled-data control. By using event-triggering mechanisms (ETM) to periodically verify whether or not to transmit and compute the measured output, communication and computational datum are significantly reduced while still retaining a satisfactory performance. This paper investigates the PETC scheme of robust ∞ filtering for a class of uncertain discrete-time Takagi-Sugeno (T-S) fuzzy systems, where the sample time is assumed to be a constant. To analyze the filtering problems of the PETC strategy, we present two frameworks based on perturbed linear and piecewise linear systems, to model filtering error systems. Sufficient conditions for the existence of a robust ∞ filter are derived in the form of matrix inequalities (LMIs) under these two frameworks, respectively. Finally, a simulation example is used to testify to the effectiveness of the proposed approach.
T-S fuzzy models use a set of IF-THEN fuzzy rules to approximate complex nonlinear systems in terms of a set of local linear models that are connected smoothly by fuzzy membership functions at any preciseness (Sugeno, 1985; Tanaka and Wang, 2001). In other words, it can combine the merits of both the fuzzy logic theory and the linear system theory, and brings a 2-fold advantage: (i) any nonlinear systems can be approximately represented by the fuzzy dynamic models; (ii) the controller itself can be designed by utilizing the concept of parallel distributed compensation (PDC). Since a set of local linear models with T-S fuzzy rules can be used to represent a nonlinear system, it is a natural approach to design a local controller for each local model, respectively. In addition, digital fuzzy logic controllers (FLC) are successfully implemented in embedded microprocessors because of the availability of low-cost and high-speed computers, and are widely applied in a variety of engineering fields. Consequently, it becomes important to study problems of control for T-S fuzzy discrete-time systems, and there are some results on T-S fuzzy discrete-time systems in the open literature (Gao et al., 2005; Feng, 2006; Qiu et al., 2009; Wu et al., 2011; Zhong et al., 2013, 2019).
In many digital implementations of control systems, the embedded microprocessors forming the computational core of the control system are required to execute a variety of tasks, which consist of sampling the output of the plant, computing the input of the controller, and implementing the output of the controller. Under the execution of control tasks, two main schemes exist: time-triggered control and event-triggered control. The event-triggered control decides whether or not to execute the control task in terms of a given threshold, rather than a time-triggered control, in which the control task is carried out in a periodic manner. When compared to time-triggered control, the advantages of event-triggered control are 2-fold: a reduction in the data transmission and the computational cost of the controller. Over the past few years, there has been an increasing interest in event-triggered control, (see Hristu-Varsakelis and Kumar, 2002; Tabuada and Wang, 2006; Wang and Lemmon, 2011; Heemels and Donkers, 2013; Zhong and Zhu, 2017; Zhong, 2018, and references therein). The scheme of event-based control has appeared under several names, such as and periodic event-triggered control (PETC) (Heemels and Donkers, 2013; Zhong and Zhu, 2017), event-triggered feedback (Zhong, 2018), interrupt-based feedback Hristu-Varsakelis and Kumar (2002), self-triggered feedback Wang and Lemmon (2011), and state-triggered feedback Tabuada and Wang (2006).
Recently, an event-triggered scheme was studied for T-S fuzzy systems, and some results were reported in Guan et al. (2013); Jia et al. (2014), and He et al. (2013). It was noted that the controller designed in He et al. (2013) is based on the assumption that the premise variables between the fuzzy systems and the fuzzy controller are synchronous all the time. Alternatively, the condition that the premise variables between the fuzzy system and the controller are asynchronous is considered in Guan et al. (2013), Jia et al. (2014). In fact, it is worth pointing out that the premise variables of the controller decide whether or not to update, under the event-triggered strategy. In other words, if the difference between the current measured output and the most recently transmitted output value exceeds a specified threshold, then the premise variables of the controller are updated to the premise variables of the system. In this way, both the premise variables between the fuzzy system and the controller are synchronous. If the triggered condition is not satisfied, they are asynchronous. More recently, the premise variables with the PETC scheme was considered in Zhong and Zhu (2017, 2018), Zhong et al. (2018). More specifically, the work of Zhong et al. (2018) proposed a decentralized event-triggered mechanism for a class of large-scale networked fuzzy systems. The work in Zhong and Zhu (2018) introduced the asynchronous distributed event-triggered output-feedback controller to stabilize large-scale fuzzy systems. A distributed event-triggered controller was designed in Zhong and Zhu (2017) under a two-channel network.
On the other hand, the Kalman and ∞ filtering are the two main approaches among various filtering schemes. The ∞ filtering method minimizes the signal estimation error for the bounded disturbances and noise of the worst case, and does not require the exact knowledge of the statistics of the external noise signals. These two advantages render the ∞ filtering method very appropriate to practical applications. Most recently, some researchers have paid attention to state estimation/filtering problems for nonlinear systems (Yin et al., 2016, 2018; Lin et al., 2017; Yin and Liu, 2017; Zhu et al., 2018a,b). More specifically, the work of Yin and Liu (2017) focused on the distributed moving horizon estimation (DMHE) for a class of two-time-scale nonlinear systems described in the framework of singularly perturbed systems. The work in Yin et al. (2018) designed a distributed estimator for linear systems, deployed over sensor networks within a multiple communication channels (MCCs) framework. The HMM-based ∞ filtering problem for discrete-time markov jump LPV systems was studied via unreliable communication channels Zhu et al. (2018b). State and input simultaneous estimation for discrete-time switched singular delay systems were investigated under the missing measurements Lin et al. (2017). The ∞ estimation for a class of networked non-linear systems was considered in Yin et al. (2016). The problem of stability and stabilization for discrete-time switched PWA systems was studied by using a descriptor system approach in Zhu et al. (2018a).
Moreover, to the authors' best knowledge, few attempts have been researched on the ∞ filtering of T-S fuzzy systems under a PETC strategy, and the ∞ filtering of T-S fuzzy systems in the PETC strategy still remain open, which has motivated us to conduct this study.
In this paper, we will study the robust ∞ filtering design for a class of uncertain discrete-time T-S fuzzy systems under a PETC communication scheme, which is introduced to reduce the systematic resource, while preserving the desired performance. In this PETC scheme, the sample time is assumed to be a constant, and the measurement output and the premise variables of the filter are verified periodically on whether or not to update. Two frameworks based on perturbed linear and piecewise linear systems are presented to model the filtering error systems, respectively. By introducing a fuzzy-basis-dependent Lyapunov functional combined with Finsler lemma, sufficient conditions for the robust filtering PETC design of these two frameworks are derived, while satisfying a given ∞ performance index, and the filter gains can be obtained by solving a set of LMIs. Finally, an example is exploited in order to illustrate the effectiveness of the proposed results.
There are two main contributions in this paper. (i) Based on a PETC scheme, we study the robust ∞ filtering design for a class of uncertain discrete-time T-S fuzzy systems. To the best of our knowledge, relatively few theoretical results exist that study the PETC problem of robust ∞ filtering design for uncertain T-S fuzzy systems. (ii) In previous work on PETC approaches, the controller gains must be given a priori. In this paper, based on a fuzzy-basis-dependent Lyapunov functional and Finsler's lemma, the fuzzy ∞ filters for the filtering error systems, applying perturbed linear (PL) and the piecewise linear (PWL) system approaches, can be obtained by solving a set of linear matrix inequalities (LMIs).
Notations. The notations used throughout this paper are standard. ℝn and ℝn×m represent the n-dimensional Euclidean space and n × m real matrices. For a vector x ∈ ℝn, we denote by its 2-norm. The notation P > 0(≥ 0) means that the matrix P is positive (semi-positive) definite. For a matrix A ∈ ℝn×n, A−1 and AT are the inverse and transpose of the matrix A, respectively, and A−T denotes (A−1)T. Sym{A} is the shorthand notation for A+AT. In denotes an identity matrix with dimension n. The symbol “*” in a matrix stands for the transposed elements in the symmetric positions. l2[0, ∞) refers to the space of square-integrable vector functions over [0, ∞). If not explicitly stated, matrices are assumed to have compatible dimensions for algebraic operations.
Similar to Sugeno (1985), Tanaka and Wang (2001), Gao et al. (2005), Qiu et al. (2009), and Wu et al. (2011), a discrete-time T-S fuzzy dynamic model with parametric uncertainties can be described as follows:
Plant Rule Ri: IF ζ1(k) is and ζ2(k) is and … and ζg(k) is , THEN
where Ri denotes the ith fuzzy inference rule, r is the number of inference rules, (j = 1, 2, ···, g) are fuzzy sets, denotes the system state, is the bounded external disturbance, is the measurement output, is the signal to be regulated, ζ(k): = [ζ1(k), ζ2(k), ⋯ζg(k)] are some measurable variables of the system, (Ai, Bi, Ci, Di, Li, Fi) denotes the ith local model of the system, (ΔAi, ΔBi, ΔCi, ΔDi, ΔLi, ΔFi) denotes the uncertainty terms of the ith local model in the form of
where M1i, M2i, M3i, N1i, and N2i are known matrices, and denotes the unknown time-varying matrix satisfying
Let hi[ζ(k)] be the normalized fuzzy-basic-dependent function of the inferred fuzzy set i, where i:, and
where uiϕ(ζϕ(k)) is the grade of membership of ζϕ(k) in
By using a center-average defuzzifier, product fuzzy inference, and a singleton fuzzifier, the following global T-S fuzzy dynamic model can be obtained:
where
For the filtering design, the traditional approach continually executing the filtering task may be undesirable in many situations. It leads to a conservative design (over-provisioning of the system hardware). In order to reduce the unnecessary waste of resources, we consider the PETC strategy outlined below:
where ŷ(k) denotes the measurement output transmitting into the filtering system, δ ≥ 0 is a suitably chosen design parameter.
In practical implementations of the PETC strategy (7), we propose two different cases, see Figures 1, 2.
In Figure 1, two buffers located in the filtering system save the last measurement output transmitted to the filter and the last estimated signal, respectively. In every sample period, the event-triggering mechanism (ETM), based on the difference between the new measurement output and the last measurement output reserved in the buffer, determines whether or not to update ŷ(k). Both ŷ(k) and the fuzzy premise variables of the filter are updated when the difference exceeds a preselected threshold, and ŷ (k) will be executed by the filtering system. If not, the last estimated signal reserved in the other buffer is transmitted again and no date is executed in the filtering system. It should be noted that in this PETC strategy, the filter, the ETM, the buffers, and the fuzzy rule generator are designed in the filtering system, avoiding a long communication burden among them for the implementation of the filtering system. Thus, the PETC strategy is easy to implement in an inexpensive manner. However, it is impossible to reduce the transmitted datum. We will next present another PETC strategy which ensures a significant reduction in the number of transmission.
In this solution, a smart sensor system is proposed in Figure 2. The sensor system consists of a buffer stored at the last measurement output, and an ETM that determines whether or not to transmit the measurement output to the filtering system. The other buffer is to save the last estimated signal. Therefore, in every sample period the measurement output is transmitted to the filter and is executed only when the difference between the newly measurement output and the last measurement output transmitted to the filtering system exceeds a given threshold. Otherwise, the last estimated signal reserved in the other buffer will be transmitted again. In this way, this PETC strategy is capable of significantly reducing the number of filtering task transmission and executions, leading to a high cost and placing a long communication burden on the filter, the ETM, the buffers, and the fuzzy rule generator. This PETC strategy is also described by (7).
Now, given the fuzzy system (1) and the PETM strategy (7), a fuzzy filter for the estimation of z(k) with the structure described by
where xF (k) is the filter state, nf denotes the order of the fuzzy filter (nf = nx for the full-order filter and 1 ≤ nf < nx for the reduced-order filter), an estimation of z(k), and AFi, BFi, CFi, and DFi are appropriately dimensioned filter gains with the following form:
and
For convenience, define
Remark 1. It should be noted that the synchronous premise variables between T-S fuzzy systems and controllers are considered in He et al. (2013), and the asynchronous ones are considered in Guan et al. (2013), Jia et al. (2014). In fact, for the PECT strategy (7), the premise variables of the filter (8) are determined to decide whether or not to update by an ETM. In other words, the premise variables of the filter (8) are updated to the premise variables of the fuzzy system (5) when the newly measured output is transmitted to the filter. In this way, the premise variables between the filter (8) and the fuzzy system (5) are synchronous. Otherwise, they become asynchronous.
In order to apply a perturbed linear system approach proposed in Heemels et al. (2013), Zhong and Zhu (2017), we define
and based on (7), yields
where δ is a positive scalar.
By defining and augmenting the model (5) and the filter (8), together with the consideration of (12), we obtained the filtering error system:
where
By defining , and augmenting the model (5) and the filter (8), we obtain the following closed-loop system:
for ∥ y (k) − ŷ (k − 1) ∥ > δ ∥ y (k) ∥, and
for ∥ y (k) − ŷ (k − 1) ∥ > δ ∥ y (k) ∥, and
and
Then the robust ∞ filtering design problem with the PETC strategy (7) is stated as follows:
Given the fuzzy discrete-time system (5), a fuzzy PETC filter (8) is designed to satisfy the following two requirement simultaneously:
(a) The filtering error system (14) based on the PL system approach (the filtering error system (16) and (17) based on the PWL system approach) with ω(k) = 0 is asymptotically stable;
(b) The induced l2 norm of the operator from ω to the filtering error is less than γ under zero initial conditions
for any nonzero ω ∈ l2[0 ∞) and all admissible uncertainties.
Before ending this section, the following lemmas are introduced to prove our main results.
Lemma 1. Xie (1996) Given constant matrices X, Y, and Z with X = XT and 0 < Y = YT, then X + ZT Y−1 Z < 0 if and only if
Lemma 2. Xie (1996) Suppose that Δ(k) is given by (2) and (3), with matrices M = MT and S and N of appropriate dimensions; then, the inequality
holds if, and only if, for some positive scalar ϵ > 0
Lemma 3. de Oliveira and Skelton (2001) Let x ∈ ℝn, ℙ = ℙT ∈ ℝn×n, and ℍ ∈ ℝm×n such that rank (ℍ) = r < n. The following statements are equivalent:
1) 𝕏Tℙ𝕏 < 0 ∀ℍ𝕏 = 0, 𝕏 ≠ 0
2) (ℍ⊥)Tℙ(ℍ⊥) < 0,
3) ∃ℕ ∈ ℝn×m:ℙ+ Sym{ℕℍ} < 0,
4) ∃λ ∈ ℝ:ℙ−λℍTℍ < 0.
This section will carry out the filtering analysis and design with the PETC strategies by using the PL and PWL system approaches.
Theorem 1. Consider the fuzzy system (1) and the fuzzy filter (8) with the PETC strategy (7), the filtering error system (14) is robust asymptotically stabilization with ∞ performance γ if there exist sets of matrices , , , , , , , , and some positive scalars δ, εisj, (i, s, j) ∈ , such that for all j ∈ , the following LMIs hold
and
where
and Θil is defined in (36).
Moreover, the proposed fuzzy filter in the form of (8) is given by
Proof. Consider a fuzzy-basis-dependent Lyapunov functional (Zhong et al., 2015):
where
Define ΔV(k) = V(k+1)−V(k), and along the trajectory of the PL closed-loop system (14), yields
It is well known that under zero initial conditions for any nonzero ω∈l2[0 ∞) and all admissible uncertainties in the filtering error system in (14) is asymptotically stable with ∞ performance, if the following inequality satisfies
To facilitate the filtering design for the system (14), it has from (13) that
which implies (27).
Now, we directly specify the slack matrix variables with the following form:
In addition, it follows from (14) that
where
Then, based on Finsler's lemma (Lemma 3), substituting the matrix defined in (29) into (30), and together with (28), yields
where
By applying the Schur complement lemma (Lemmas 1), it is clear that the following inequality implies (32):
According to (6, 9, 11) and (15, 34) can be easily rewritten as
where
Since and so that the following inequalities imply (34):
and
On the other hand, using relations (2–3), one has
where Σisj, Wis, and Ei are defined in (22).
By introducing
and by applying the Schur complement and S-procedure (Lemmas 1 and 2) to (43), it is clear that (25) and (26) are obtained, respectively. The proof is therefore completed.
Based on the PWL closed-loop system given by (16, 17), we will present the filtering design as follows:
Theorem 2. Given the fuzzy system (1), and an admissible fuzzy filter (8) with the PETC strategy (7), the filtering error system given by (16) and (17) is robust asymptotically, stabilized with ∞ performance γ if there exist sets of matrices and some positive scalars δ, km, εisj, (m, i, s, j)∈, such that for all j ∈ , the following LMIs hold
for i ∈ , (n, m) = {1, 2}, and
for 1 ≤ i < s ≤ r, (n, m) = {1, 2}, and
and
and
Moreover, an admissible fuzzy filter in the form of (8) is given by
Proof. Consider a piecewise quadratic Lyapunov functional Zhong and Zhu (2018):
where
Along the trajectory of two subsystems given by (16, 17), yields
It follows from (7, 27), that
where ηm ≥ 0, and the inequality (49) implies
It is noted that the even-triggered information is particularly useful to reduce the conservatism of the systems with an event-triggered strategy. For the systems with parameter uncertainties involved in the matrices and , the terms yT(k)y(k) and [y(k) − ŷ(k − 1)]T(⋆) can be separated by applying the Schur complement and S-procedure lemma. However, it is easy to see that it will lead to a infeasible solution in (49). As a result, (49) is only suitable for the case of the matrices and without uncertainties. Otherwise, (50) should be used.
Based on (50), and similar to (29–31), the following results can be obtained
where (m, n) = {1, 2}, and
We directly specify the slack matrix variables:
According to (2, 6, 9) and (24), the following inequality implies (12):
where
and
and
The following proof is similar to the proof of Theorem 1 and is, therefore, omitted.
It is worth pointing out that for the case of the matrices and without uncertainties, the event-triggered information can be used to reduce the conservatism. The corresponding ∞ filtering design result can be readily obtained from Theorem 2 by including the event-triggered information. The result is summarized in the following corollary.
Corollary 3. Consider the fuzzy system (1) and the fuzzy filter (8) with the PETC strategy (7), the filtering error system given by (16, 17) is robust asymptotically stabilized with ∞ performance γ if there exist sets of matrices and some positive scalars δ, km, εisj, (m, i, s, j)∈, such that for all j∈, the following LMIs hold
for i∈, (n, m) = {1, 2}, and
for 1 ≤ i<s ≤ r, (n, m) = {1, 2}, and and Ẽi are defined in (42), and
Moreover, an admissible fuzzy filter in the form of (8) is given by
Note that the ∞ performance index γ described in Theorem 1, 2, and Corollary 3 can be optimized by the following algorithms:
Algorithm 1: min γ, subject to LMIs (21)-(22),
Algorithm 2: min γ, subject to LMIs (41)-(42),
Algorithm 3: min γ, subject to LMIs (58)-(59).
This section uses an example to illustrate the effectiveness of the proposed PETC filter design approach.
Consider a tunnel diode circuit, whose modeling was done in Assawinchaichote and Nguang (2003), that is
where x1(t) and x2(t) are the state variables, ω(t) is the disturbance noise input, y(t) is the measurement, z(t) is the controlled output, C, L, R, and S are the capacitance, the inductance, the resistance, and S the sensor matrix, respectively.
Given C = 20mF, L = 1000mH and R = 10Ω, consider the uncertainty ΔR = 0.1Ω. With a sampling time T = 0.02, the nonlinear system (62) can be approximated by the following discrete-time T-S model:
Plant Rule Ri: IF x1(k) is Fi, THEN
where
The uncertainty ΔA is assumed to satisfy the form of (2, 3), that is
where Δ(k) = sin(k), M =
Similar to Gao et al. (2009), the membership functions are given by
Firstly, the objective here is to design the PETC fuzzy filter (8) without A task delay, such that the filtering error system (13) is asymptotically stable with robust ∞ performance γmin. Given δ = 0.2, and applying Algorithm 1, the filter matrices and the minimum ∞ performance γmin are obtained as follows:

γmin = 0.4,
for the full-order case, and
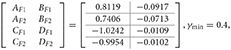
for the reduced-order (nf = 1) case.
Then, we are in a position to design the PETC fuzzy filter (14) with a task delay such that the filtering error system (18) is asymptotically stable with the ∞ performance γmin. Given δ = 0.2, and the task delay d(k) is assumed to satisfy (15) with 0 ≤ d(k) ≤ 5, and by applying Algorithm 2, the filter matrices and the minimum ∞ performance γmin are obtained as follows:

γmin = 0.86.
However, by applying Algorithm 3, the filter matrices and the minimum ∞ performance γmin are obtained as follows:

γmin = 0.90.
In this paper, we have investigated the filtering design for a class of uncertain discrete-time T-S fuzzy systems under a periodic event-triggered control (PETC) scheme, where the sample time was assumed to be a constant. These two frameworks, based on perturbed and piecewise linear systems, were presented to model the filtering error systems, respectively. Based on a fuzzy-basis-dependent Lyapunov functional combined with Finsler's lemma, sufficient conditions for the robust filtering PETC design of these two frameworks have been derived, respectively, and the filter gains were obtained by solving a set of LMIs. A simulation example was provided to demonstrate the effectiveness of the proposed method.
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
The work was supported in part by the Science and Technology Project of Fujian Province, China under Grants 2016H6019; the Fuzhou Municipal Science and Technology Project under Grant 2016-G-53, 2018-G-98; the National Natural Science Foundation of China (61772254), Fujian Provincial Leading Project (2017H0030), Key Project of College Youth Natural Science Foundation of Fujian Province (JZ160467); the Science and Research Project of Fujian Province, China (JAT160391).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors wish to thank the Editor-in-Chief, Guest Editor, and reviewers for their helpful comments which have improved the paper.
Assawinchaichote, W., and Nguang, S. K. (2003). ∞ filtering for fuzzy dynamic systems with D stability constraints. IEEE Trans. Circuits Syst. 50, 1503–1508. doi: 10.1109/TCSI.2003.818624
de Oliveira, M. C., and Skelton, R. E. (2001). Stability Tests for Constrained Linear Systems. New York, NY: Springer-Verlag, 241–257. doi: 10.1007/BFb0110624
Feng, G. (2006). A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 14, 676–697. doi: 10.1109/TFUZZ.2006.883415
Gao, H., Zhao, Y., Lam, J., and Chen, K. (2009). ∞ fuzzy filtering of nonlinear systems with intermittent measurements. IEEE Trans. Fuzzy Syst. 17, 291–300. doi: 10.1109/TFUZZ.2008.924206
Gao, H. J., Wang, Z. D., and Wang, C. H. (2005). Improved %∞ control of discrete-time fuzzy systems: a cone complementarity linearization approach. Inform. Sci. 175, 57–77. doi: 10.1016/j.ins.2004.10.004
Guan, Y. P., Han, Q. L., and Peng, C. (2013). “Event-triggered output feedback control for Takagi-Sugeno fuzzy systems,” in Proceedings of the 2013 IEEE Conference on Industrial Electronics Society, 5644-5649. doi: 10.1109/IECON.2013.6700059
He, D. Z., Jia, X. C., Chi, X. B., and Ma, W. W. (2013). “Fuzzy ∞ tracking control for a class of nonlinear networked control systems with a discrete event-triggered communication scheme,” in Proceedings of the 2013 IEEE Conference on Control and Decision, 2562–2567.
Heemels, W. P. M. H., and Donkers, M. C. F. (2013). Model-based periodic event-triggered control for linear systems. Automatica 49, 698–711. doi: 10.1016/j.automatica.2012.11.025
Heemels, W. P. M. H., Donkers, M. C. F., and Teel, A. R. (2013). Periodic event-triggered control for linear systems. IEEE Trans. Autom. Control 58, 847–861. doi: 10.1109/TAC.2012.2220443
Hristu-Varsakelis, D., and Kumar, P. (2002). “Interrupt-based feedback control over a shared communication medium,” in In Proceedings of the 2002 IEEE Conference on Decision Control (Las Vegas, NV), 3223–3228. doi: 10.1109/CDC.2002.1184368
Jia, X. C., Chi, X. B., Han, Q. L., and Zheng, N. N. (2014). Event-triggered fuzzy ∞ control for a class of nonlinear networked control systems using the deviation bounds of asynchronous normalized membership functions. Inform. Sci. 259, 100–117. doi: 10.1016/j.ins.2013.08.055
Lin, J., Jiang, G., Gao, Z., and Rong, L. (2017). State and input simultaneous estimation for discrete-time switched singular delay systems with missing measurements. Int. J. Robust Nonlin. Control 27, 2749–2772. doi: 10.1002/rnc.3709
Qiu, J., Feng, G., and Yang, J. (2009). A new design of delay-dependent robust ∞ filtering for discrete-time T-S fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 17, 1044–1058. doi: 10.1109/TFUZZ.2009.2017378
Tabuada, P., and Wang, X. (2006). “Preliminary results on state-triggered scheduling of stabilizing control tasks,” in In Proceedings of the 2006 IEEE Conference on Decision Control, 282–287.
Tanaka, T., and Wang, H. O. (2001). Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach. New York, NY: Wiley. doi: 10.1002/0471224596
Wang, X. F., and Lemmon, M. D. (2011). Event-triggering in distributed networked control systems. IEEE Trans. Autom. Control 56, 586–601. doi: 10.1109/TAC.2010.2057951
Wu, L. G., Su, X. J., Shi, P., and Qiu, J. B. (2011). A new approach to stability analysis and stabilization of discrete-time T-S fuzzy time-varying delay systems. IEEE Trans. Syst. Man Cyber. 41, 273–286. doi: 10.1109/TSMCB.2010.2051541
Xie, L. H. (1996). Output feedback ∞ control of systems with parameter uncertainty. Int. J. Control 63, 741–750. doi: 10.1080/00207179608921866
Yin, X., Li, Z., Zhang, L., and Han, M. (2018). Distributed state estimation of sensor-network systems subject to Markovian channel switching with application to a chemical process. IEEE Trans. Syst. Man Cybern. 48, 864–874. doi: 10.1109/TSMC.2016.2632155
Yin, X., Li, Z., Zhang, L., Ning, Z., Tian, D., Alsaedi, A., et al. (2016). State estimation via Markov switching-channel network and application to suspension systems. IET Control Theor. Applications 11, 411–419. doi: 10.1049/iet-cta.2016.1108
Yin, X., and Liu, J. (2017). Distributed moving horizon state estimation of two-time-scale nonlinear systems. Automatica 79, 152–161. doi: 10.1016/j.automatica.2017.01.023
Zhong, Z. (2018). Tracking synchronization for DC microgrid with multiple-photovoltaic arrays: an even-based fuzzy control scheme. IEEE Access 6, 24996–25006. doi: 10.1109/ACCESS.2018.2827363
Zhong, Z., Fu, S., Hayat, T., Alsaadi, F., and Sun, G. (2015). Decentralized piecewise H-infinity fuzzy filtering design for discrete-time large-scale nonlinear systems with time-varying delay. J. Franklin Inst. 352, 3782–3807. doi: 10.1016/j.jfranklin.2015.01.033
Zhong, Z., Lin, C., Shao, Z., and Xu, M. (2018). Decentralized event-triggered control for large-scale networked fuzzy systems. IEEE Trans. Fuzzy Syst. 26, 29–45. doi: 10.1109/TFUZZ.2016.2634090
Zhong, Z., and Zhu, Y. (2017). Observer-based output-feedback control of large-scale networked fuzzy systems with two-channel event-triggering. J. Franklin Inst. 354, 5398–5420. doi: 10.1016/j.jfranklin.2017.05.036
Zhong, Z., and Zhu, Y. (2018). Asynchronous piecewise output-feedback control for large-scale fuzzy systems via distributed event-triggering schemes. IEEE Trans. Fuzzy Syst. 26, 1688–1703. doi: 10.1109/TFUZZ.2017.2744599
Zhong, Z., Zhu, Y., Lin, C., and Huang, T. (2019). A fuzzy control framework for interconnected nonlinear power networks under TDS attack: Estimation and compensation. J. Franklin Inst. doi: 10.1016/j.jfranklin.2018.12.012
Zhong, Z. X., Sun, G. H., Karimi, H. R., and Qiu, J. B. (2013). Stability analysis and stabilization of T-S fuzzy delta operator systems with time-varying delay via an input-output approach. Math. Prob. Eng. 2013:913234. doi: 10.1155/2013/913234
Zhu, Y., Zhong, Z., Basin, M. V., and Zhou, D. (2018a). A descriptor system approach to stability and stabilization of discrete-time switched PWA systems. IEEE Trans. Autom. Control 63, 3456–3463. doi: 10.1109/TAC.2018.2797173
Keywords: discrete-time Takagi-Sugeno (T-S) fuzzy systems, ∞ filtering, periodic event-triggered, robust control, perturbed and piecewise linear system approach
Citation: Zhang Z, Lin D, Wang X, Shao Z and Lin W (2019) A Periodic Event-Triggered Design of Robust 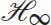 Filtering for T-S Fuzzy Discrete-Time Systems. Front. Neurosci. 13:318. doi: 10.3389/fnins.2019.00318
Filtering for T-S Fuzzy Discrete-Time Systems. Front. Neurosci. 13:318. doi: 10.3389/fnins.2019.00318
Received: 28 November 2018; Accepted: 20 March 2019;
Published: 17 April 2019.
Edited by:
Yanzheng Zhu, Western Sydney University, AustraliaReviewed by:
Ting Yang, Northwestern Polytechnical University, ChinaCopyright © 2019 Zhang, Lin, Wang, Shao and Lin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenzhong Lin, bHc4NTJuQDEyNi5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.