- 1Department of Neurosurgery, Hospital of the University of Pennsylvania, Philadelphia, PA, United States
- 2Department of Neuroscience, University of Pennsylvania, Philadelphia, PA, United States
- 3Department of Bioengineering, University of Pennsylvania, Philadelphia, PA, United States
- 4Department of Physics and Astronomy, University of Pennsylvania, Philadelphia, PA, United States
- 5Department of Neurology, University of Pennsylvania, Philadelphia, PA, United States
- 6Department of Electrical and Systems Engineering, University of Pennsylvania, Philadelphia, PA, United States
Brain computer interfaces (BCIs) have been applied to sensorimotor systems for many years. However, BCI technology has broad potential beyond sensorimotor systems. The emerging field of cognitive prosthetics, for example, promises to improve learning and memory for patients with cognitive impairment. Unfortunately, our understanding of the neural mechanisms underlying these cognitive processes remains limited in part due to the extensive individual variability in neural coding and circuit function. As a consequence, the development of methods to ascertain optimal control signals for cognitive decoding and restoration remains an active area of inquiry. To advance the field, robust tools are required to quantify time-varying and task-dependent brain states predictive of cognitive performance. Here, we suggest that network science is a natural language in which to formulate and apply such tools. In support of our argument, we offer a simple demonstration of the feasibility of a network approach to BCI control signals, which we refer to as network BCI (nBCI). Finally, in a single subject example, we show that nBCI can reliably predict online cognitive performance and is superior to certain common spectral approaches currently used in BCIs. Our review of the literature and preliminary findings support the notion that nBCI could provide a powerful approach for future applications in cognitive prosthetics.
Introduction
The Success of Sensorimotor BCI Technology
Brain computer interfaces (BCIs) utilize neural input functions to control task-oriented systems (Vidal, 1973). Motor BCIs highlight the translational success of this strategy. Motor or efferent BCIs transform neural signals from motor regions into command signals for external effectors such as robotic arms, or for internal effectors such as paralyzed forearm muscles. The success of translating motor BCIs, now in clinical trials, may be attributed to several contributing factors. First, motor decoding algorithms leverage decades of research characterizing the relationships between neural activity and movement behaviors in animal models (Sanes and Donoghue, 1993; Rizzolatti et al., 1996; Hatsopoulos et al., 1998; Kakei et al., 1999; Lu and Ashe, 2005; Li et al., 2015). Movement-related features may be extracted from a number of input sources, including single units, multi-units, and local field potentials (LFP) (Hochberg et al., 2006; Leuthardt et al., 2006). Input sources originate from brain regions with stable relationships to the desired output functions, including limb movements and muscle activations. Finally, movement-related features from neural signals may be extracted during passive observation of homologous movements – such as the movements of a robotic arm – just as they would during movement of an intact arm (Jeannerod, 1995; Decety, 1996; Pfurtscheller and Neuper, 1997; Lacourse et al., 2005; Hanakawa et al., 2008; Miller et al., 2010). Consequently, decoding algorithms may be calibrated from the motor regions of a paralyzed patient even though the patient lacks the ability to execute the movement him/herself.
The Challenges of Cognitive BCI Technology
BCI technology may be applied to other areas of unmet clinical need, such as restoring learning and memory for the cognitively impaired. Unfortunately, the fundamental physiology that underlies the development of sensorimotor BCIs is unlikely to be directly applicable to higher-order cognition. This is due, in part, to the fact that the processes underlying higher-order cognitive functions such as executive function depend upon the dynamic engagement and control of distributed neural circuits (Luna et al., 2001; Gläscher and Büchel, 2005; FitzGerald et al., 2012). Consequently, there is little agreement regarding the ideal brain target from which to derive neural input signals for a cognitive BCI. Nor is there agreement on the ideal input source itself, whether single- or multi-unit spiking, evoked potentials, or spectral profiles of sensor signals. Also, there is broad uncertainty concerning the stability of input signals as they relate to cognitive processes. These challenges are made even more acute by the substratal fact that animal models do not faithfully represent the complexities of human cognition.
Notably, these challenges have not prevented investigators from exploring putative cognitive prosthetic control signals. The best examples are those that attempt to define the neural signature of memory formation. Investigators have used changes in regional LFP oscillatory activity before (Guderian et al., 2009; Fell et al., 2011; Hanslmayr and Staudigl, 2014; Merkow et al., 2014) and during encoding (Klimesch et al., 1997; Fell et al., 2001; Sederberg et al., 2007), as well as temporally precise single unit hippocampal activity (Rutishauser et al., 2010), to predict subsequent recall. Utilizing multimodal analysis of event-related potentials and event-related desynchronization, a recent study was able to successfully predict depth of cognitive processing in memory, language, and visual imagination task domains (Nicolae et al., 2017). In other cognitive realms such as experiential learning, executive control, and dynamic online cognitive performance, less is known about local neural signatures. This may in part be due to the fact that critical regions involved in these higher-order functions are spatially distributed (Luna et al., 2001; Gläscher and Büchel, 2005; FitzGerald et al., 2012) and require coordinated activity (Friston, 1994; Tononi et al., 1994; Büchel et al., 1999; Salinas and Sejnowski, 2001; Kahana, 2006; Chennu et al., 2014; Voytek et al., 2015). Therefore, measuring local, regional, or global metrics of neural activity alone may not provide the ideal control signal for cognitive BCI technology. Rather, the addition of quantitative measures of coordinated activity – often referred to as functional connectivity – could improve the reliability and generalizability of the control signal.
Network Analysis in Cognitive Function
Network neuroscience is an emerging discipline that enables analysis of distributed, dynamical neural systems (Tononi et al., 1994; Sporns, 2002; Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Sporns, 2011) through a suite of flexible and generalizable mathematical tools borrowed from mathematics (graph theory), physics (statistical mechanics), computer science, and engineering. Networks are described in terms of neural elements (nodes) and the connections between them (edges). Notably, any edge between node i and node j can be assigned a continuous value of weight, which captures the strength of the connection between node i and node j. The pattern of weights across edges connecting nodes is frequently referred to as the network’s topology (Rubinov and Sporns, 2010). Network analysis tools can utilize structural (tractography) or functional (physiology) data sources to construct different sorts of networks. Networks composed of functional connections (or edges) are referred to as functional networks, and networks composed of structural connections (or edges) are referred to as structural networks. Functional networks can be constructed from data acquired either during the resting state or during the performance of a task.
During the performance of increasingly cognitively demanding tasks, oscillatory signals are thought to impart critical information regarding task-relevant neural activity in regions activated by the task (Friston, 1994; Rubinov and Sporns, 2010; Burke et al., 2015a). Functional connectivity (FC) can be measured through frequency-specific synchronization, or phase-locking (Luauté et al., 2015), of two oscillating neural sources (Bamdad et al., 2015; Luauté et al., 2015; Ezzyat et al., 2017; Jiang et al., 2017; Ezzyat et al., 2018). Two regions displaying phase synchrony, a statistical relation between the instantaneous phases of the signals in both areas, are often interpreted as being functionally connected. Ensemble synchrony is thought to be an important mechanism underlying cognitive processing (Salinas and Sejnowski, 2001; deBettencourt et al., 2015; Kucewicz et al., 2018), and the loss of synchrony is implicated in cognitive disease states such as dementia and schizophrenia (Burke et al., 2015b; Jacobs et al., 2016; Merkow et al., 2017; Ortner et al., 2017). More generally, functional connectivity reflects pairwise statistical relationships that can display complex patterns indicative of non-trivial network topologies. The features of the functional network can be quantified using numerous statistics commonly referred to as graph statistics, network measures, or connectomic metrics. The quantification of network architecture in patterns of FC can provide robust estimates of task-dependent interregional coordination, and its relation to multisensory processing, cognition, memory, and learning (Friston, 1997; Tononi, 1998; Sporns et al., 2004; Miller et al., 2007; Canolty et al., 2009; Bassett et al., 2015; McGregor and Gribble, 2017; Nicolae et al., 2017).
Here we propose that network approaches to distilling the topology of functional connectivity patterns could offer an improved framework for creating BCI control signals for the cognitive domain. Below we discuss the approach taken by current cognitive BCI systems and provide preliminary evidence for the utility, feasibility, and potential superiority of a network BCI (nBCI) approach.
Current Advances
Advances in Cognitive BCI
To date, experiments with cognitive BCIs have focused on improving memory, attention, and consciousness (Bamdad et al., 2015; Burke et al., 2015a; deBettencourt et al., 2015; Luauté et al., 2015; Ezzyat et al., 2017, 2018; Jiang et al., 2017; Ortner et al., 2017; Kucewicz et al., 2018). Burke et al. (2015a) attempted an initial memory BCI system using theta (4–8 Hz) and alpha (9–14 Hz) band spectral activity to trigger the optimal timing of object presentation during memory encoding. The authors found that features of theta and alpha band spectral activity did not constitute reliable control signals across sessions or across subjects (Burke et al., 2015a). Subsequent improvements in defining the control signal have employed supervised multivariate pattern analysis techniques to assess global spectral activity that correlates with superior and inferior encoding states within each subject (Ezzyat et al., 2017). Initial stimulation paradigms delivered during randomly assigned memory encoding epochs resulted in inconsistent behavioral effects (Jacobs et al., 2016; Ezzyat et al., 2017; Merkow et al., 2017). However, recent studies demonstrate that short bursts of lateral temporal cortex stimulation delivered only during poor encoding states are associated with a disruption of the innate spectral activity and an improvement in memory performance (Ezzyat et al., 2018; Kucewicz et al., 2018). In non-memory cognitive systems, control signals utilizing blood-oxygen-level dependent (BOLD), evoked potentials, or spectral analysis have been incorporated as biofeedback therapy for self-optimization of attentional networks (deBettencourt et al., 2015; Jiang et al., 2017) and as communicative tools for patients with altered levels of consciousness (Luauté et al., 2015; Ortner et al., 2017). These approaches have also been used to assess and predict the depth of cognitive processing, reflected by the level of task difficulty, in memory, language, and visual task domains (Nicolae et al., 2017).
Though current systems provide a foundation for cognitive BCI technology, there is difficulty extending these approaches to other realms of cognitive function such as experiential learning and executive control, or to adaptive contexts in which one wishes to optimize dynamic online cognitive performance in a singularly demanding task. This difficulty is due in part to a lack of spatiotemporally resolved BOLD, evoked, or oscillatory neural signals whose features reliably predict individual differences in these other areas of cognitive function. Furthermore, although a certain profile of spectral power, namely the spectral tilt phenomenon, is thought to reflect cortical activation (Miller et al., 2007; Burke et al., 2015b), analyzing multifocal spectral activity is not a quantitative measure of regional interactions. For dynamic cognitive tasks, precisely quantifying these interactions may be more task relevant than the collective regional pattern of activity (Varela, 1995; Friston, 1997; Tononi, 1998; Büchel et al., 1999; Sporns et al., 2004; Rypma et al., 2006; Canolty et al., 2009; Brancucci, 2012; Bassett et al., 2015; McGregor and Gribble, 2017).
Network Analysis Applied to Current BCI Systems
The concept of using phase-based FC as a putative control signal for BCI technology has been examined in a limited number of studies focused on motor imagery (Brunner et al., 2006; Carreiras et al., 2012; Billinger et al., 2013), motor execution (Billinger et al., 2015), and the visually evoked P300 speller response(Kabbara et al., 2016). All of these systems utilize non-invasive electroencephalography (EEG) as their neural input signal and phase-locking (Lachaux et al., 1999) as their FC metric; and all report improvement in BCI functionality with the incorporation of FC features. In a simple reach and saccade cognitive task Courellis et al. (2017), extract statistical dependencies of EEG region of interest time series data to demonstrate the plausibility of cognitive network detection using a non-invasive BCI. Using intracranial EEG, phase-based network analysis of high gamma (>70 Hz) synchrony has recently been shown to accurately distinguish wakeful versus sleep states (Mikulan et al., 2018). The potential to also incorporate complex network metrics has been examined in a simple finger-tapping task (Daly et al., 2012). This study assessed the discrimination ability between tap versus no-tap trials using the clustering coefficient, a graph metric of local network integration. The authors report a superior detection capability of tap versus no-tap trials when compared to traditional event-related EEG metrics of synchronization or desynchronization. However, this study was only a feasibility study of the analytical technique and did not actually utilize complex network metrics in a BCI system.
Future Directions
Proposing nBCI for the Cognitive Domain
Here we propose the incorporation of network analysis as a potential control signal for cognitive BCI systems. Global measures of network organization can provide insight into brain states during cognitive tasks (Palva et al., 2005; Besserve et al., 2008). One noted example of such a measure is network strength, which can be calculated by averaging the sum of edge weights from each node in a network. Furthermore, metrics quantifying the mesoscale integration or segregation states of functional circuits or networks include the clustering coefficient and the modularity. These two metrics have been shown to correlate with learning and cognitive performance over long time-scales (Husken et al., 2002; Bullmore and Sporns, 2009; Bassett et al., 2011; Hermundstad et al., 2011; Ellefsen et al., 2015). Anatomically, there is evidence for flexible hubs in dorsal and ventral frontoparietal networks and cingulo-opercular networks that have strong influence on saliency and cognitive control (Corbetta and Shulman, 2002; Cole et al., 2010, 2013; Power et al., 2011; Power and Petersen, 2013). Network metrics that account for the paths by which information can be transmitted in the network, such as betweenness centrality and communicability, may also provide meaningful insight regarding these types of regional influences on network information flow and brain state transitions (Borgatti, 2005; Newman, 2005; Estrada and Hatano, 2008; Crofts and Higham, 2009; Betzel et al., 2016). Therefore, these metrics may hold promise as a potential feature vector for predicting high performing brain states in otherwise difficult-to-decode neural data. For network metrics to constitute a plausible control signal, dynamic changes in network metrics must occur on short time-scales and must predict upcoming cognitive performance, allowing for real-time control of a neuromodulatory system.
Preliminary Results
Using single-trial phase locking statistics (Lachaux et al., 2000) we provide preliminary evidence in a single human subject on the use of dynamic changes in functional brain network statistics as a predictive signal for online cognitive performance. This subject was undergoing clinical monitoring for refractory epilepsy with stereotactically placed intracranial EEG (sEEG). A total of 122 electrode contacts located diffusely within bilateral frontal, temporal, and parietal cortical and subcortical regions, as well as deep limbic structures were used as individual nodes in our network analysis. We used a simple temporal expectancy reaction time (RT) task to assess online cognitive performance. Temporal expectancy engages several distinct cognitive processes such as those involved in saliency (Coull and Nobre, 1998), attention (Tecce, 1971, 1972; Colombo and Richman, 2002), temporal processing (Onoe et al., 2001; Mauk and Buonomano, 2004), and plasticity (Dallérac et al., 2017); with induced changes in regional electrophysiology (Walter et al., 1964; Funderud et al., 2012) and network-wide functional imaging (Onoe et al., 2001; Nagai et al., 2004). Trials consisted of a visual cue signal (a white box presented on a black screen), an instructed delay period (500 or 1500 ms randomly chosen with equal probability), and a go signal (a color change of box from white to yellow) after which the subject made a keypress to indicate the perception of the go signal. The RT was defined as the time between go and keypress. For the purposes of this report, only trials with a 1500-ms delay period were analyzed (n = 57 trials).
The phase-locking value (PLV) (Lachaux et al., 1999) for high gamma (70–100 Hz) activity between all pairs of electrodes was computed on each trial in sliding 500 ms time bins, using the Hilbert transform to extract instantaneous phase. For the network analysis, each sEEG electrode represented a network node and the edge weight between nodes was defined by the high gamma (70–100 Hz) PLV for that pair. Global network strength, a measure of ensemble synchrony, was computed by taking the average edge weight across all pairwise nodal interactions in the network. We divided trials based on ‘good’ (fast RT, n = 19) and ‘poor’ (slow RT, n = 19) performance such that the mean RT was significantly different in the two conditions (Figures 1A,B; one-sided Wilcoxon rank sum test, z = -5.2, p = 1.1 × 10-7). We compared global network strength across four 500-ms time bins between the two conditions: pre-cue (-500 to 0 ms relative to cue), early delay (0–500 ms), mid-delay (500–1000 ms), and late-delay (1000–1500 ms). We found that in the pre-cue period, fast-RT trials were characterized by significantly higher global network strength than slow-RT trials (Figure 1C; two-sided Wilcoxon rank sum test, z = 2.6, p = 0.008, multiple comparison threshold p = 0.0125). There was no significant difference in global network strength between performance conditions for the three delay time bins.
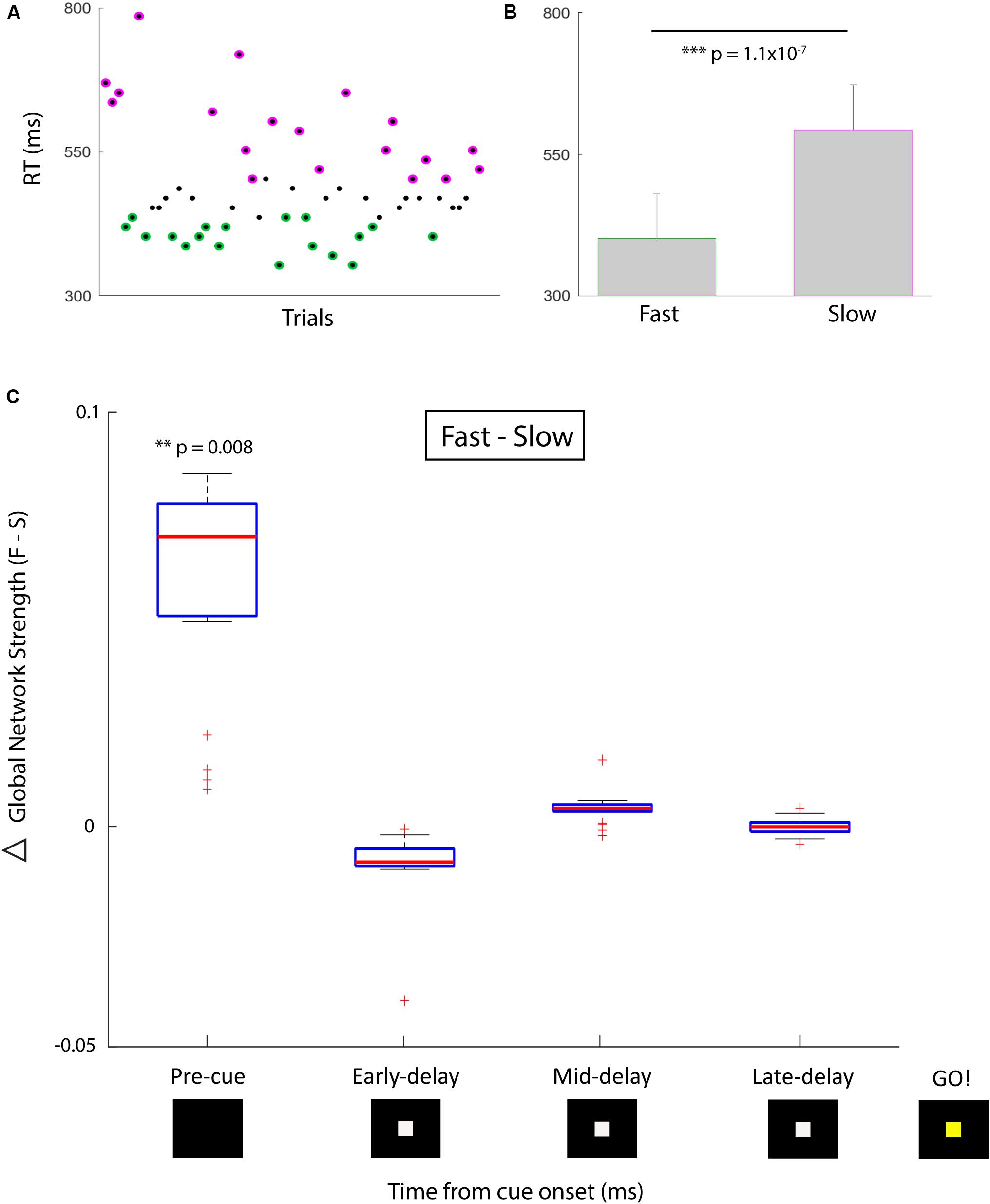
FIGURE 1. Behavioral performance and correlative network strength over time. (A) Simple temporal expectancy task reaction time (RT) per trial. Fastest third (green) and slowest third (magenta) of trials were determined. (B) Mean RTs for the fast versus slow trial groups were significantly different. (C) Global network strength (PLV) over time for fast (first plot) versus slow (second plot) trials. Box plots indicate median and interquartile range, whiskers indicate 95% data coverage. Timing is centered around cue presentation (0 ms). First time bin signifies pre-cue period (-500 to 0 ms), followed by three 500 ms delay period bins. After a 1500 ms delay, the cue changes color which designates the go signal. There was a significant difference in the pre-cue period for global network strength between the distribution of fast and slow trials. Asterisk denote degree of significance coinciding with p values.
Next, we compared the performance discrimination ability of nodal strength (network strength per node) to traditional spectral control signals for the pre-cue period: (i) high-frequency activity (HFA; 70–100 Hz power), and (ii) spectral tilt (70–100 Hz z score power minus 3–12 Hz z score power). We found that for nearly all sEEG channels, pre-cue nodal strength was significantly higher for fast-RT trials than for slow-RT trials (Figure 2A; t(35) = 3.83, p = 5.1 × 10-4 for the node with maximum difference). This predictive discriminatory ability of subsequent performance was not present for HFA or spectral tilt (Figures 2B,C). Trials were then separated into ‘early’ (first third of trials, n = 19) versus ‘late’ (last third of trials, n = 19) conditions. There was no significant difference in strength between these conditions at any node (Figure 2D; t(41) = 1.71, p = 0.09 for the node with maximum difference).
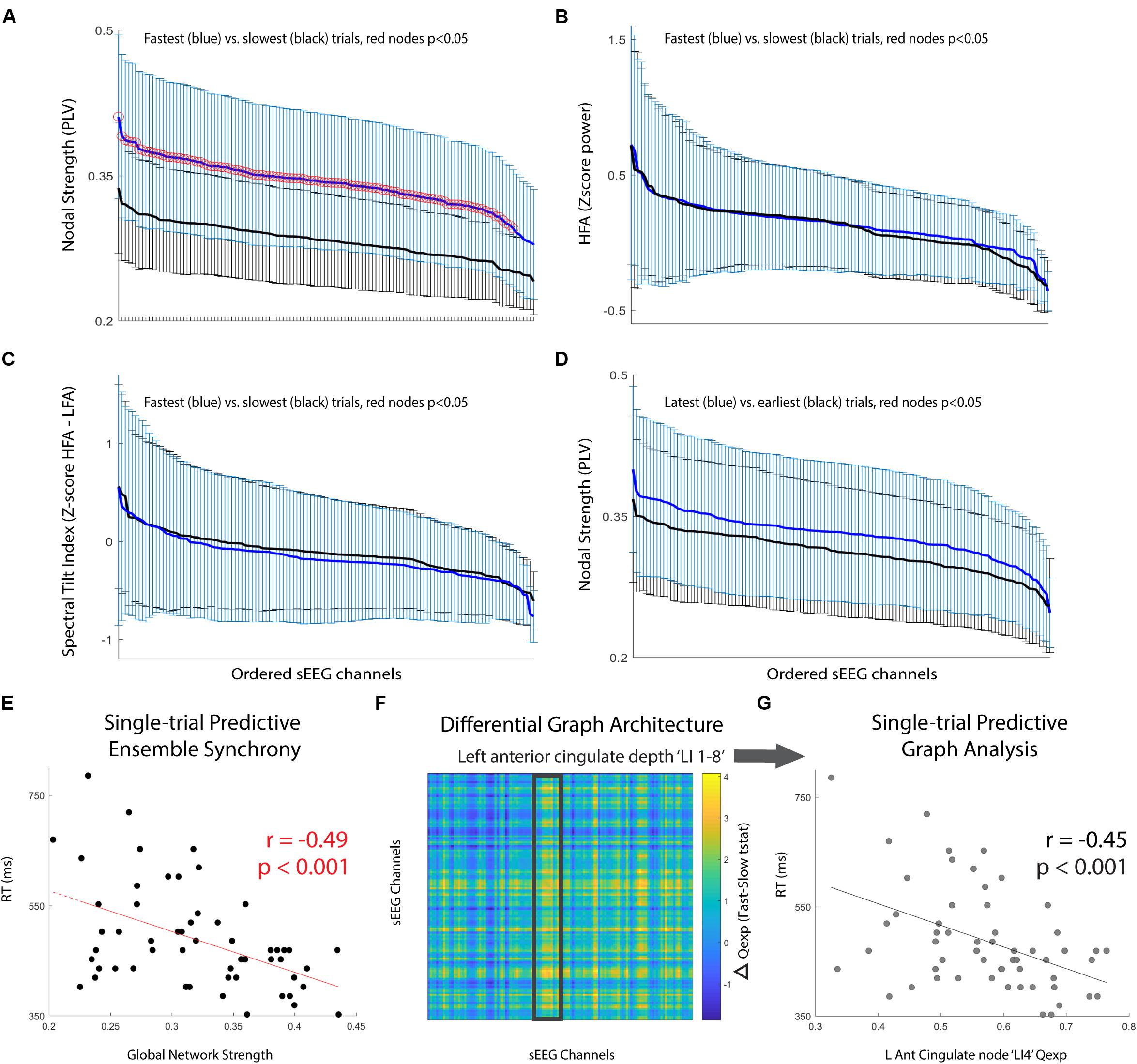
FIGURE 2. Pre-cue period network analysis. (A–C) Comparison of mean +/- std for fastest (blue) versus slowest (black) trials. Metrics used are (A) nodal strength, (B) high frequency (70–100 Hz) spectral power, and (C) spectral tilt (HFA-LFA), respectively. Nodal strength, a network statistical measure of average synchrony between that node and all others, shows significantly and globally increased pre-cue values in fast compared to slow trials. (D) Comparison of mean +/- std for latest (blue) versus earliest (black) trials using nodal strength. No significant difference for any particular node, however, there was a trend toward increasing mean nodal strength for latest compared to earliest trials (p = 0.08). (E) Global network strength in the pre-cue period corresponding to each upcoming trial and associated trial reaction time. There was a significant predictive correlation. (F) Difference in network communicability during the pre-cue period averaged across all fast-slow RT trials; the most significant increase was seen in the left anterior cingulate lead (highlighted box, max channel ‘LI4’ F-S difference t(35) = 2.50, p = 0.02). (G) Single-trial RT as a function of left anterior cingulate node ‘LI4’ single-trial communicability demonstrating independent predictive correlation.
Finally, we computed single-trial pre-cue global network strength and compared it to single-trial reaction time. There was a significant correlation between these two variables (Figure 2E; r = -0.49, p = 1.3 × 10-4). We then calculated the communicability (Qexp), a network metric given by the normalized matrix exponential of each single-trial weighted connectivity matrix (Estrada and Hatano, 2008; Crofts and Higham, 2009). Intuitively, communicability is the sum of all possible walks (and thus paths) between two nodes, exponentially down-weighted as length increases (accounting for the decreasing statistical relationship as length increases). The average communicability for a particular node k therefore quantifies the relative degree to which each node k contributes to walks (and thus paths) of different lengths (Estrada and Hatano, 2008; Crofts and Higham, 2009). We found that communicability was dynamic, and that high Qexp in the left anterior cingulate depth electrode during the pre-cue period was significantly correlated with the average difference in fast versus slow RT trials (Figure 2F, highlighted region ‘LI 1-8’, maximum nodal F-S difference ‘LI4’ t(35) = 2.50, p = 0.02). We then found that the single-trial communicability in the left anterior cingulate lead ‘LI4’ independently predicted RT (Figure 2G; r = -0.45, p = 4.6 × 10-4).
To assess the decoding ability of a feature space consisting of pre-cue high gamma global network strength and ‘LI4’ communicability, a support vector machine (SVM) was trained and cross-validated for binary classification of ‘Fast’ versus ‘Slow’ RT trials. Significance of 10-fold cross-validated classifier performance was assessed using a permutation test in which binary (‘Fast’ versus ‘Slow’) class labels were randomly generated, area under the curve (AUC) of classifier performance was calculated, and the randomization was repeated 1000 times to create a null distribution of AUCs. The SVM classifier for this single subject achieved reliable subsequent performance prediction (AUC = 0.72, p = 0.03).
These are the first data reporting single-trial ensemble synchrony and network metrics as predictive features for online cognitive performance; and they demonstrate superiority over certain common spectral approaches for quantifying behaviorally relevant neural activity. Interestingly, high gamma synchrony has been shown to be correlated with increased wakefulness (Mikulan et al., 2018), providing a possible mechanistic link for the enhanced performance predicted by high gamma ensemble synchrony in our subject. Further, we find dynamic communicability in the left anterior cingulate lead is also predictive of subsequent performance, perhaps consistent with previous evidence of a primary role for cingulo-opercular network influence on cognitive control (Corbetta and Shulman, 2002; Cole et al., 2010; Power and Petersen, 2013).
Conclusion
Though disorders of cognition are vast, network analyses of functional connectivity may provide meaningful quantifications and correlates of functional impairments as well as ready classifications of aberrant underlying neural processes (Voytek and Knight, 2015; Cohen and D’Esposito, 2016). We find that in this single human subject example of online cognitive performance, the network analysis approach (nBCI) outperforms certain traditional spectral approaches in antecedent, dynamic performance discrimination. Furthermore, using the Hilbert transformation-based PLV to create single-trial weighted networks provides a computationally lightweight methodology for potential real-time decoding and feature extraction. These data preliminarily support our proposed notion that network analysis could be applied as a control signal in cognitive BCI systems. As a rapidly quantifiable analysis of network interactions, nBCI may enable increased generalizability of BCI technology for cognitive rehabilitation.
Ethics Statement
This study was carried out in accordance with the recommendations of the Human Subjects Research guidelines by the University of Pennsylvania’s Office of Regulatory Affairs, Institutional Review Board. The protocol was approved by the University of Pennsylvania Institutional Review Board. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
Author Contributions
VB formulated the concept, performed the data analysis, and primarily wrote the paper. AR helped in the organization and writing of the paper and figures. CB was responsible for the data acquisition. JS guided the connectivity analysis. MK helped with the literature review. DB and TL provided their expertise to help frame the proposed idea as well as provided a detailed review of the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bamdad, M., Zarshenas, H., and Auais, M. A. (2015). Application of BCI systems in neurorehabilitation: a scoping review. Disabil. Rehabil. Assist. Technol. 00, 1–10. doi: 10.3109/17483107.2014.961569
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson, J. M., and Grafton, S. T. (2011). Dynamic reconfiguration of human brain networks during learning. Proc. Natl. Acad. Sci. U.S.A. 108, 7641–7646. doi: 10.1073/pnas.1018985108
Bassett, D. S., Yang, M., Wymbs, N. F., and Grafton, S. T. (2015). Learning-Induced autonomy of sensorimotor systems. Nat. Neurosci. 18, 744–751. doi: 10.1038/nn.3993
Besserve, M., Philippe, M., Florence, G., Laurent, F., Garnero, L., and Martinerie, J. (2008). Prediction of performance level during a cognitive task from ongoing EEG oscillatory activities. Clin. Neurophysiol. 119, 897–908. doi: 10.1016/j.clinph.2007.12.003
Betzel, R. F., Gu, S., Medaglia, J. D., Pasqualetti, F., and Bassett, D. S. (2016). Optimally controlling the human connectome: the role of network topology. Sci. Rep. 6:30770. doi: 10.1038/srep30770
Billinger, M., Brunner, C., and Gernot, R. M. (2013). Single-trial connectivity estimation for classification of motor imagery data. J. Neural Eng. 10:046006. doi: 10.1088/1741-2560/10/4/046006
Billinger, M., Brunner, C., and Müller-putz, G. R. (2015). Online visualization of brain connectivity. J. Neurosci. Methods 256, 106–116. doi: 10.1016/j.jneumeth.2015.08.031
Borgatti, S. P. (2005). Centrality and network flow. Soc. Netw. 27, 55–71. doi: 10.1016/j.socnet.2004.11.008
Brancucci, A. (2012). Neural correlates of cognitive ability. J. Neurosci. Res. 90, 1299–1309. doi: 10.1002/jnr.23045
Brunner, C., Scherer, R., Graimann, B., Supp, G., and Pfurtscheller, G. (2006). Online control of a brain-computer interface using phase synchronization. IEEE Trans. Biomed. Eng. 53, 2501–2506. doi: 10.1109/TBME.2006.881775
Büchel, C., Coull, J. T., and Friston, K. J. (1999). The predictive value of changes in effective connectivity for human learning. Science 283, 1538–1541. doi: 10.1126/science.283.5407.1538
Bullmore, E., and Sporns, O. (2009). Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198. doi: 10.1038/nrn2575
Burke, J. F., Merkow, M. B., Jacobs, J., Kahana, M. J., and Zaghloul, K. A. (2015a). Brain computer interface to enhance episodic memory in human participants. Front. Hum. Neurosci. 8:1055. doi: 10.3389/fnhum.2014.01055
Burke, J. F., Ramayya, A. G., and Kahana, M. J. (2015b). Human intracranial high-frequency activity during memory processing: neural oscillations or stochastic volatility? Curr. Opin. Neurobiol. 31, 104–110. doi: 10.1016/j.conb.2014.09.003
Canolty, R. T., Edwards, E., Dalal, S. S., Soltani, M., Nagarajan, S. S., Kirsch, H. E., et al. (2009). High gamma power is phase-locked to theta oscillations in human neocortex. Science 313, 1626–1628. doi: 10.1126/science.1128115
Carreiras, C., Borges De Almeida, L., and Sanches, J. M. (2012). “Phase-locking factor in a motor imagery brain-computer interface,” in Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, San Diego, CA, 2877–2880. doi: 10.1109/EMBC.2012.6346564
Chennu, S., Finoia, P., Kamau, E., Allanson, J., Williams, G. B., Monti, M. M., et al. (2014). Spectral signatures of reorganised brain networks in disorders of consciousness. PLoS Comput. Biol. 10:e1003887. doi: 10.1371/journal.pcbi.1003887
Cohen, J. R., and D’Esposito, M. (2016). The segregation and integration of distinct brain networks and their relationship to cognition. J. Neurosci. 36, 12083–12094. doi: 10.1523/JNEUROSCI.2965-15.2016
Cole, M. W., Pathak, S., and Schneider, W. (2010). Identifying the brain’s most globally connected regions. Neuroimage 49, 3132–3148. doi: 10.1016/j.neuroimage.2009.11.001
Cole, M. W., Reynolds, J. R., Power, J. D., Repovs, G., Anticevic, A., and Braver, T. S. (2013). Multi-task connectivity reveals flexible hubs for adaptive task control. Nat. Neurosci. 16, 1348–1355. doi: 10.1038/nn.3470
Colombo, J., and Richman, W. A. (2002). Infant timekeeping: attention and temporal estimation in 4-Month-olds. Psychol. Sci. 13, 475–479. doi: 10.1111/1467-9280.00484
Corbetta, M., and Shulman, G. L. (2002). Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 3, 201–215. doi: 10.1038/nrn755
Coull, J. T., and Nobre, A. C. (1998). Where and when to pay attention: the neural systems for directing attention to spatial locations and to time intervals as revealed by both PET and fMRI. J. Neurosci. 18, 7426–7435. doi: 10.1523/JNEUROSCI.18-18-07426.1998
Courellis, H., Mullen, T., Poizner, H., Cauwenberghs, G., and Iversen, J. R. (2017). EEG-based quantification of cortical current density and dynamic causal connectivity generalized across subjects performing BCI-monitored cognitive tasks. Front. Neurosci. 11:180. doi: 10.3389/fnins.2017.00180
Crofts, J. J., and Higham, D. J. (2009). A weighted communicability measure applied to complex brain networks. J. R. Soc. Interface 6, 411–414. doi: 10.1098/rsif.2008.0484
Dallérac, G., Graupner, M., Knippenberg, J., Martinez, R. C., Tavares, T. F., Tallot, L., et al. (2017). Updating temporal expectancy of an aversive event engages striatal plasticity under amygdala control. Nat. Commun. 8:13920. doi: 10.1038/ncomms13920
Daly, I., Nasuto, S. J., and Warwick, K. (2012). Brain computer interface control via functional connectivity dynamics. Pattern Recognit. 45, 2123–2136. doi: 10.1016/j.patcog.2011.04.034
deBettencourt, M., Cohen, J. D., Lee, R. F., Norman, K. A., and Turk-browne, N. B. (2015). Closed-loop training of attention with real-time brain imaging. Nat. Neurosci. 18, 470–475. doi: 10.1038/nn.3940
Decety, J. (1996). The neurophysiological basis of motor imagery. Behav. Brain Res. 77, 45–52. doi: 10.1016/0166-4328(95)00225-1
Ellefsen, K. O., Mouret, J. B., and Clune, J. (2015). Neural modularity helps organisms evolve to learn new skills without forgetting old skills. PLoS Comput. Biol. 11:e1004128. doi: 10.1371/journal.pcbi.1004128
Estrada, E., and Hatano, N. (2008). Communicability in complex networks. Phys. Rev. E 77:036111. doi: 10.1103/PhysRevE.77.036111
Ezzyat, Y., Kragel, J. E., Burke, J. F., Levy, D. F., Lyalenko, A., Wanda, P., et al. (2017). Direct brain stimulation modulates encoding states and memory performance in humans. Curr. Biol. 27, 1251–1258. doi: 10.1016/j.cub.2017.03.028
Ezzyat, Y., Wanda, P. A., Levy, D. F., Kadel, A., Aka, A., Pedisich, I., et al. (2018). Closed-loop stimulation of temporal cortex rescues functional networks and improves memory. Nat. Commun. 9:365. doi: 10.1038/s41467-017-02753-0
Fell, J., Klaver, P., Lehnertz, K., Grunwald, T., Schaller, C., Elger, C. E., et al. (2001). Human memory formation is accompanied by rhinal-hippocampal coupling and decoupling. Nat. Neurosci. 4, 1259–1264. doi: 10.1038/nn759
Fell, J., Ludowig, E., Staresina, B. P., Wagner, T., Kranz, T., Elger, C. E., et al. (2011). Medial temporal Theta/Alpha power enhancement precedes successful memory encoding: evidence based on intracranial EEG. J. Neurosci. 31, 5392–5397. doi: 10.1523/JNEUROSCI.3668-10.2011
FitzGerald, T. H. B., Friston, K. J., and Dolan, R. J. (2012). Action-specific value signals in reward-related regions of the human brain. J. Neurosci. 32, 16417–16423. doi: 10.1523/JNEUROSCI.3254-12.2012
Friston, K. J. (1994). Functional and effective connectivity in neuroimaging: a synthesis. Hum. Brain Mapp. 2, 56–78. doi: 10.1002/hbm.460020107
Funderud, I., Lindgren, M., Løvstad, M., Endestad, T., Voytek, B., Knight, R. T., et al. (2012). Differential Go/NoGo activity in both contingent negative variation and spectral power. PLoS One 7:e48504. doi: 10.1371/journal.pone.0048504
Gläscher, J., and Büchel, C. (2005). Formal learning theory dissociates brain regions with different temporal integration. Neuron 47, 295–306. doi: 10.1016/j.neuron.2005.06.008
Guderian, S., Schott, B. H., Richardson-Klavehn, A., and Duzel, E. (2009). Medial temporal theta state before an event predicts episodic encoding success in humans. Proc. Natl. Acad. Sci. U.S.A. 106, 5365–5370. doi: 10.1073/pnas.0900289106
Hanakawa, T., Dimyan, M. A., and Hallett, M. (2008). Motor planning, imagery, and execution in the distributed motor network: a time-course study with functional MRI. Cereb. Cortex 18, 2775–2788. doi: 10.1093/cercor/bhn036
Hanslmayr, S., and Staudigl, T. (2014). How brain oscillations form memories – A processing based perspective on oscillatory subsequent memory effects. Neuroimage 85, 648–655. doi: 10.1016/j.neuroimage.2013.05.121
Hatsopoulos, N. G., Ojakangas, C. L., Paninski, L., and Donoghue, J. P. (1998). Information about movement direction obtained from synchronous activity of motor cortical neurons. Proc. Natl. Acad. Sci. U.S.A. 95, 15706–15711. doi: 10.1073/pnas.95.26.15706
Hermundstad, A. M., Brown, K. S., Bassett, D. S., and Carlson, J. M. (2011). Learning, memory, and the role of neural network architecture. PLoS Comput. Biol. 7:e1002063. doi: 10.1371/journal.pcbi.1002063
Hochberg, L. R., Serruya, M. D., Friehs, G. M., Mukand, J. A., Saleh, M., Caplan, A. H., et al. (2006). Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature 442, 164–171. doi: 10.1038/nature04970
Husken, M., Igel, C., and Toussaint, M. (2002). Task-dependent evolution of modularity in neural networks. Connect. Sci. 14, 219–229. doi: 10.1080/09540090208559328
Jacobs, J., Miller, J., Lee, S. A., Coffey, T., Watrous, A. J., Sperling, M. R., et al. (2016). Direct electrical stimulation of the human entorhinal region and hippocampus impairs memory. Neuron 92, 983–990. doi: 10.1016/j.neuron.2016.10.062
Jeannerod, M. (1995). Mental imagery in the motor context. Neuropsychologia 33, 1419–1432. doi: 10.1016/0028-3932(95)00073-C
Jiang, Y., Abiri, R., and Zhao, X. (2017). Tuning up the old brain with new tricks: attention training via neurofeedback. Front. Aging Neurosci. 9:52. doi: 10.3389/fnagi.2017.00052
Kabbara, A., Khalil, M., El-Falou, W., Eid, H., and Hassan, M. (2016). Functional brain connectivity as a new feature for P300 speller. PLoS One 11:e0146282. doi: 10.1371/journal.pone.0146282
Kahana, M. J. (2006). The cognitive correlates of human brain oscillations. J. Neurosci. 26, 1669–1672. doi: 10.1523/JNEUROSCI.3737-05c.2006
Kakei, S., Hoffman, D. S., and Strick, P. L. (1999). Muscle and movement representations in the primary motor cortex. Science 285, 2136–2139. doi: 10.1126/science.285.5436.2136
Klimesch, W., Doppelmayr, M., Schimke, H., and Ripper, B. (1997). Theta synchronization and alpha desynchronization in a memory task. Psychophysiology 34, 169–176. doi: 10.1111/j.1469-8986.1997.tb02128.x
Kucewicz, M. T., Berry, B. M., Kremen, V., Miller, L. R., Khadjevand, F., Ezzyat, Y., et al. (2018). Electrical stimulation modulates high gamma activity and human memory performance. eNeuro 5:ENEURO.0369-17.2018. doi: 10.1523/ENEURO.0369-17.2018
Lachaux, J.-P., Rodriguez, E., Le Van Quyen, M., Lutz, A., Martinerie, J., Renault, B., et al. (2000). Studying single-trials of phase-synchronous activity in the brain. Int. J. Bifur. Chaos 10, 2429–2439. doi: 10.1142/S0218127400001560
Lachaux, J. P., Rodriguez, E., Martinerie, J., and Varela, F. J. (1999). Measuring phase synchrony in brain signals. Hum. Brain Mapp. 8, 194–208. doi: 10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C
Lacourse, M. G., Orr, E. L. R., Cramer, S. C., and Cohen, M. J. (2005). Brain activation during execution and motor imagery of novel and skilled sequential hand movements. Neuroimage 27, 505–519. doi: 10.1016/j.neuroimage.2005.04.025
Leuthardt, E. C., Miller, K. J., Schalk, G., Rao, R. P. N., and Ojemann, J. G. (2006). Electrocorticography-based brain computer interface – The seattle experience. IEEE Trans. Neural Syst. Rehabil. Eng. 14, 194–198. doi: 10.1109/TNSRE.2006.875536
Li, N., Chen, T. W., Guo, Z. V., Gerfen, C. R., and Svoboda, K. (2015). A motor cortex circuit for motor planning and movement. Nature 519, 51–56. doi: 10.1038/nature14178
Lu, X., and Ashe, J. (2005). Anticipatory activity in primary motor cortex codes memorized movement sequences. Neuron 45, 967–973. doi: 10.1016/j.neuron.2005.01.036
Luauté, J., Morlet, D., and Mattout, J. (2015). BCI in patients with disorders of consciousness: clinical perspectives. Ann. Phys. Rehabil. Med. 58, 29–34. doi: 10.1016/j.rehab.2014.09.015
Luna, B., Thulborn, K. R., Munoz, D. P., Merriam, E. P., Garver, K. E., Minshew, N. J., et al. (2001). Maturation of widely distributed brain function subserves cognitive development. Neuroimage 13, 786–793. doi: 10.1006/nimg.2000.0743
Mauk, M. D., and Buonomano, D. V. (2004). The neural basis of temporal processing. Annu. Rev. Neurosci. 27, 307–340. doi: 10.1146/annurev.neuro.27.070203.144247
McGregor, H. R., and Gribble, P. L. (2017). Functional connectivity between somatosensory and motor brain areas predicts individual differences in motor learning by observing. J. Neurophysiol. 118, 1235–1243. doi: 10.1152/jn.00275.2017
Merkow, M. B., Burke, J. F., Ramayya, A. G., Sharan, A. D., Sperling, M. R., and Kahana, M. J. (2017). Stimulation of the human medial temporal lobe between learning and recall selectively enhances forgetting. Brain Stimul. 10, 645–650. doi: 10.1016/j.brs.2016.12.011
Merkow, M. B., Burke, J. F., Stein, J. M., and Kahana, M. J. (2014). Prestimulus theta in the human hippocampus predicts subsequent recognition but not recall. Hippocampus 24, 1562–1569. doi: 10.1002/hipo.22335
Mikulan, E., Hesse, E., Sedeño, L., Bekinschtein, T., Sigman, M., García, M. D. C., et al. (2018). Intracranial high-γ connectivity distinguishes wakefulness from sleep. Neuroimage 169, 265–277. doi: 10.1016/j.neuroimage.2017.12.015
Miller, K. J., Leuthardt, E. C., Schalk, G., Rao, R. P., Anderson, N. R., Moran, D. W., et al. (2007). Spectral changes in cortical surface potentials during motor movement. J. Neurosci. 27, 2424–2432. doi: 10.1523/JNEUROSCI.3886-06.2007
Miller, K. J., Schalk, G., Fetz, E. E., den, Nijs M, Ojemann, J. G., and Rao, R. P. (2010). Cortical activity during motor execution, motor imagery, and imagery-based online feedback. Proc. Natl. Acad. Sci. U.S.A. 107, 4430–4435. doi: 10.1073/pnas.0913697107
Nagai, Y., Critchley, H. D., Featherstone, E., Fenwick, P. B., Trimble, M. R., and Dolan, R. J. (2004). Brain activity relating to the contingent negative variation: an fMRI investigation. Neuroimage 21, 1232–1241. doi: 10.1016/j.neuroimage.2003.10.036
Newman, M. E. J. (2005). A measure of betweenness centrality based on random walks. Soc. Netw. 27, 39–54. doi: 10.1016/j.socnet.2004.11.009
Nicolae, I.-E., Acqualagna, L., and Blankertz, B. (2017). Assessing the depth of cognitive processing as the basis for potential user-state adaptation. Front. Neurosci. 11:548. doi: 10.3389/fnins.2017.00548
Onoe, H., Komori, M., Onoe, K., Takechi, H., Tsukada, H., and Watanabe, Y. (2001). Cortical networks recruited for time perception: a monkey positron emission tomography (PET) study. Neuroimage 13, 37–45. doi: 10.1006/nimg.2000.0670
Ortner, R., Allison, B. Z., Pichler, G., Heilinger, A., Sabathiel, N., and Guger, C. (2017). Assessment and communication for people with disorders of consciousness. J. Vis. Exp. 126:53639. doi: 10.3791/53639
Palva, J. M., Palva, S., and Kaila, K. (2005). Phase synchrony among neuronal oscillations in the human cortex. J. Neurosci. 25, 3962–3972. doi: 10.1523/JNEUROSCI.4250-04.2005
Pfurtscheller, G., and Neuper, C. (1997). Motor imagery activates primary sensorimotor area in humans. Neurosci. Lett. 239, 65–68. doi: 10.1016/S0304-3940(97)00889-6
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A., Church, J. A., et al. (2011). Functional network organization of the human brain. Neuron 72, 665–678. doi: 10.1016/j.neuron.2011.09.006
Power, J. D., and Petersen, S. E. (2013). Control-related systems in the human brain. Curr. Opin. Neurobiol. 23, 223–228. doi: 10.1016/j.conb.2012.12.009
Rizzolatti, G., Fadiga, L., Gallese, V., and Fogassi, L. (1996). Premotor cortex and the recognition of motor actions. Cogn. Brain Res. 3, 131–141. doi: 10.1016/0926-6410(95)00038-0
Rubinov, M., and Sporns, O. (2010). Rubinov and sporns - 2010 - Complex network measures of brain connectivity. Neuroimage 52, 1059–1069. doi: 10.1016/j.neuroimage.2009.10.003
Rutishauser, U., Ross, I. B., Mamelak, A. N., and Schuman, E. M. (2010). Human memory strength is predicted by theta-frequency phase-locking of single neurons. Nature 464, 903–907. doi: 10.1038/nature08860
Rypma, B., Berger, J. S., Prabhakaran, V., Bly, B. M., Kimberg, D. Y., Biswal, B. B., et al. (2006). Neural correlates of cognitive efficiency. Neuroimage 33, 969–979. doi: 10.1016/j.neuroimage.2006.05.065
Salinas, E., and Sejnowski, T. J. (2001). Correlated neuronal activitiy and the flow of neural information. Nat. Rev. Neurosci. 2, 539–550. doi: 10.1038/35086012
Sanes, J. N., and Donoghue, J. P. (1993). Oscillations in local field potentials of the primate motor cortex during voluntary movement. Proc. Natl. Acad. Sci. U.S.A. 90, 4470–4474. doi: 10.1073/pnas.90.10.4470
Sederberg, P. B., Schulze-Bonhage, A., Madsen, J. R., Bromfield, E. B., McCarthy, D. C., Brandt, A., et al. (2007). Hippocampal and neocortical gamma oscillations predict memory formation in humans. Cereb. Cortex 17, 1190–1196. doi: 10.1093/cercor/bhl030
Sporns, O. (2002). Network analysis, complexity, and brain function. Complexity 8, 56–60. doi: 10.1002/cplx.10047
Sporns, O. (2011). The human connectome: a complex network. Ann. N. Y. Acad. Sci. 1224, 109–125. doi: 10.1111/j.1749-6632.2010.05888.x
Sporns, O., Chialvo, D. R., Kaiser, M., and Hilgetag, C. C. (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci. 8, 418–425. doi: 10.1016/j.tics.2004.07.008
Tecce, J. J. (1971). Contingent negative variation and individual differences a new approach in brain research. Arch. Gen. Psychiatry 24, 1–16. doi: 10.1001/archpsyc.1971.01750070003001
Tecce, J. J. (1972). Contingent negative variation (CNV) and psychological processes in man. Psychol. Bull. 77, 73–108. doi: 10.1037/h0032177
Tononi, G. (1998). Consciousness and complexity. Science 282, 1846–1851. doi: 10.1126/science.282.5395.1846
Tononi, G., Sporns, O., and Edelman, G. M. (1994). A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 91, 5033–5037. doi: 10.1073/pnas.91.11.5033
Varela, F. J. (1995). Resonant cell assemblies: a new approach to cognitive functions and neuronal synchrony. Biol. Res. Arch. 28, 81–95.
Vidal, J. J. (1973). Toward direct brain-computer communication. Annu. Rev. Biophys. Bioeng. 2, 157–180. doi: 10.1146/annurev.bb.02.060173.001105
Voytek, B., Kayser, A. S., Badre, D., Fegen, D., Chang, E. F., Crone, N. E., et al. (2015). Oscillatory dynamics coordinating human frontal networks in support of goal maintenance. Nat. Neurosci. 31, 1–10. doi: 10.1038/nn.4071
Voytek, B., and Knight, T. (2015). Dynamic network communication as a unifying neural basis for cognition, development, aging, and disease. Biol. Psychiatry 77, 1089–1097. doi: 10.1016/j.biopsych.2015.04.016
Keywords: network brain-computer interface, cognitive prosthetic, brain-computer interface (BCI), cognitive performance, connectivity, network science
Citation: Buch VP, Richardson AG, Brandon C, Stiso J, Khattak MN, Bassett DS and Lucas TH (2018) Network Brain-Computer Interface (nBCI): An Alternative Approach for Cognitive Prosthetics. Front. Neurosci. 12:790. doi: 10.3389/fnins.2018.00790
Received: 30 March 2018; Accepted: 12 October 2018;
Published: 01 November 2018.
Edited by:
Jonathan Miller, University Hospitals Cleveland Medical Center, United StatesCopyright © 2018 Buch, Richardson, Brandon, Stiso, Khattak, Bassett and Lucas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Vivek P. Buch, dml2ZWsuYnVjaEB1cGhzLnVwZW5uLmVkdQ==
 Vivek P. Buch
Vivek P. Buch Andrew G. Richardson
Andrew G. Richardson Cameron Brandon1
Cameron Brandon1 Jennifer Stiso
Jennifer Stiso Danielle S. Bassett
Danielle S. Bassett Timothy H. Lucas
Timothy H. Lucas