- Department of Psychology, Center for Studies in Behavioral Neurobiology, Concordia University, Montréal, QC, Canada
Almost 80 years ago, Lionel Robbins proposed a highly influential definition of the subject matter of economics: the allocation of scarce means that have alternative ends. Robbins confined his definition to human behavior, and he strove to separate economics from the natural sciences in general and from psychology in particular. Nonetheless, I extend his definition to the behavior of non-human animals, rooting my account in psychological processes and their neural underpinnings. Some historical developments are reviewed that render such a view more plausible today than would have been the case in Robbins’ time. To illustrate a neuroeconomic perspective on decision making in non-human animals, I discuss research on the rewarding effect of electrical brain stimulation. Central to this discussion is an empirically based, functional/computational model of how the subjective intensity of the electrical reward is computed and combined with subjective costs so as to determine the allocation of time to the pursuit of reward. Some successes achieved by applying the model are discussed, along with limitations, and evidence is presented regarding the roles played by several different neural populations in processes posited by the model. I present a rationale for marshaling convergent experimental methods to ground psychological and computational processes in the activity of identified neural populations, and I discuss the strengths, weaknesses, and complementarity of the individual approaches. I then sketch some recent developments that hold great promise for advancing our understanding of structure–function relationships in neuroscience in general and in the neuroeconomic study of decision making in particular.
Robbins’ Definition
In his landmark essay on the nature of economics, Lionel Robbins defined economics as
“the science which studies human behaviour as a relationship between ends and scarce means which have alternative uses” (Robbins, 1935, p. 16).
At first glance, this formulation seems a dry and inauspicious note on which to launch a discussion of the behavioral and neurobiological study of economic decision making in animals. Robbins’ definition confines economics to the study of human behavior, he sought to distinguish economics from the natural sciences, and he firmly opposed attempts to “vivisect the economic agent” (Maas, 2009).
Why then, use his definition as a starting point? I do so because deletion of a single word, “human,” frees the core idea underlying Robbins’ definition to apply as broadly and fundamentally in the domain of animal biology as in the originally envisaged domain of human economic behavior. Robbins opined:
“The material means of achieving ends are limited. We have been turned out of Paradise. We have neither eternal life nor unlimited means of gratification. Everywhere we turn, if we choose one thing we must relinquish others which, in different circumstances, we wish not to have relinquished. Scarcity of means to satisfy ends of varying importance is an almost ubiquitous condition of human behaviour” (Robbins, 1935, p. 15).
This statement is no less true of the behavior of non-human animals.
Robbins’ definition is highly general and is not restricted to exchanges such as barter or market transactions. To illustrate the point that even “isolated man” engages in economic behavior, Robbins (1935, pp. 34–35) describes a choice facing Robinson Crusoe, the castaway protagonist of the eponymous classic novel (Defoe, 1719/2010). Crusoe is marooned on a tropical island. A decision making challenge faced by this solitary individual is positioned by Robbins firmly within the economic realm:
“Let us consider, for instance, the behaviour of a Robinson Crusoe in regard to a stock of wood of strictly limited dimensions. Robinson has not sufficient wood for all the purposes to which he could put it. For the time being the stock is irreplaceable. […] if he wants the wood for more than one purpose – if, in addition to wanting it for a fire, he needs it for fencing the ground round the cabin and keeping the fence in good condition – then, inevitably, he is confronted by a […] problem – the problem of how much wood to use for fires and how much for fencing.”
Let us now ponder another example, one that illustrates both the boundary Robbins draws between non-economic and economic behavior and how readily his definition can be transposed to the behavior of non-human animals.
Scarce Means with Alternative Uses
Consider the case of a diving duck incubating eggs in a shoreline nest. In this terrestrial environment oxygen is abundant. Breathing can be performed at the same time as other activities, such as preening, incubating the eggs, and scanning for predators. The duck need not forgo engagement in other behaviors in order to devote time to the exchange of oxygen and carbon dioxide. If we extend Robbins’ definition to the circumstances of the nesting duck, we will see that no economic principles govern breathing in this environment and that no allocation decisions need be made to ensure the necessary gas exchange.
Now consider the same duck as it forages for fish. Entry into the aquatic environment renders oxygen a scarce good. According to my extension of Robbins’ definition, the duck’s quest for oxygen has moved into the economic realm. In the aquatic environment, oxygen, in a form exploitable by the duck, is available only at the surface whereas prey are found only in the depths. Two vital ends, gas exchange and energy balance, are now in conflict. The time available for attainment of each of these ends is scarce, and it has alternative uses. The duck can fish or breathe, but it cannot do both at the same time or in the same place. To maximize its rate of energy intake, the duck must draw down its precious supply of oxygen, traveling to the attainable locations where prey densities are highest and harvesting what it can while it is able to remain there. Maximization of net energy intake thus trades off against conservation of sufficient blood oxygen for a safe return to the surface. The duck must remain there long enough to at least partially replenish its oxygen supply. However, if it consistently lingers too long at the surface, it will starve, and if it tarries too long submerged, it will drown.
Many means of survival in the natural world are scarce or tend toward this condition. Consider a population that moves into a new environment where food is initially abundant. All else held equal, the population will grow, increasing demand for food while decreasing supply. Abundance will be fleeting and self-limiting.
The trade-off between breathing and feeding in aquatic animals has been modeled by behavioral ecologists using principles that are economic, in the spirit of Robbins’ definition, and that reflect the optimal allocation of scarce means with alternative uses (Kramer, 1988). In the case of the diving duck, such an optimal-foraging model predicts how variation in the depth and density of prey alter how the duck distributes its time between the surface and the underwater environment. More generally, such models predict how animals allocate their time in the pursuit of spatially constrained (“patchy”) resources. Time is the quintessentially scarce resource, a view Robbins expressed as follows:
“Here we are, sentient creatures with bundles of desires and aspirations, with masses of instinctive tendencies all urging us in different ways to action. But the time in which these tendencies can be expressed is limited. The external world does not offer full opportunities for their complete achievement. Life is short” (Robbins, 1935, pp. 12–13).
As the duck runs down its oxygen supply on a deep dive that has yet to yield any fish, the scarcity of time makes itself evident with particular force.
Later in this essay, I speculate about what Robbins meant by “sentient,” and I argue that sentience is not a necessary condition for economic behavior. I discuss the implications of extending Robbins’ definition into the biological realm, and I describe an experimental paradigm for the laboratory study of economic decision making in non-human animals that is based on the allocation of time as a scarce resource.
The Contribution of Psychophysics to Valuation
Allocation decision are based on information about the external world, such as distributions of predators and prey, and about the internal environment, such as the state of energy and oxygen stores. These exteroceptive and interoceptive data are acquired, processed, and stored by sensory, perceptual, and mnemonic mechanisms whose dynamic range, resolution, and bandwidth are limited by physics, anatomy, and physiology. Veridical representation of the external world is unfeasible.
Psychophysics describes how objective variables, such as luminance, are mapped into their subjective equivalents, such as brightness. Such mappings are typically non-linear and reference-dependent. Non-linearity is exemplified by the Weber–Fechner law (Weber, 1834/1965; Fechner, 1860, 1965), which posits that the smallest perceptual increment in a stimulus is a constant proportion of the starting value. Such logarithmic compression sacrifices accuracy as stimulus strength grows but makes efficient use of a finite dynamic range. Reference dependence is illustrated by demonstrations that the important information conveyed by the visual system does not concern luminance per se but rather relative differences in luminance with respect to the mean (i.e., contrast). This feature can be advantageous. Consider a checkerboard made of alternating dark-gray and light-gray squares. The objective property of the squares that causes them to look dark or light is called “reflectance,” and the corresponding subjective quality is called “lightness.” If perception were dependent only on the processing of local information according to the Weber–Fechner law, then increasing the intensity of the illumination impinging on the checkerboard would, in illusory fashion, drive the percept of the lighter squares toward white and the percept of the dark-gray squares toward a lighter gray. However, the contrast between adjoining squares remains constant as objective luminance increases. (By definition, contrast is normalized by the mean luminance.) Thus, we perceive the lightness of each kind of square as constant over a wide range of luminance.
In the example of the checkerboard, reference dependence helps the visual system recover a meaningful property of an object in the world, the relative reflectances of its components, factoring out the change in viewing conditions. However, reference dependence can also cause the subjective lightness of a region under constant illumination to vary as a function of changes in the illumination of the surrounding region (simultaneous lightness contrast). In that case, perhaps an unusual one in the natural environment, reference dependence leads to a perceptual error. Thus, a mechanism that normally serves to recover facts about the world can also produce illusions.
Whereas sensory systems provide information about the location, identity, and displacement of objects in the external world, valuation systems estimate what these objects are worth. Valuation systems provide the data for allocation decisions. The neural systems subserving valuation cannot put back information that has been filtered out by their sensory input, and these systems have information-processing constraints, rules, and objectives of their own. Thus, a realistic model of allocation decisions must take into account the psychophysical functions that map objective variables into subjective valuations. As we will see shortly, the mappings of variables involved in valuation also tend to be non-linear and reference-dependent. They, too, embody built-in rules of thumb that are usually beneficial but that can sometimes generate systematic errors.
Below, I describe a particular model in which psychophysical transformations contribute to the allocation of a scarce resource, and I illustrate how the form of these transformations can be used strategically to link stages in the processes of valuation and allocation to specific neural populations. But first, we must respond to Robbins’ objections to consideration of psychophysics in economic decision making.
Did Robbins Protest in Vain?
Prominent nineteenth century economists, such as Jevons (1871) and Edgeworth (1879), incorporated psychophysical concepts into their theories of valuation (Bruni and Sugden, 2007). For example, the Weber–Fechner law (Weber, 1834/1965; Fechner, 1860, 1965) was used to interpret the law of diminishing returns (Bernoulli, 1738, 1954), the notion that the subjective value of cumulative increments in wealth decreases progressively. Although the practice of incorporating psychophysics into economics was commonplace in the late nineteenth century, it was all but abandoned under the influence of a later generation of economists led by Pareto (1892–1893/1982, as cited in Bruni and Sugden, 2007) and Weber (1908), who sought to purge economics of psychological notions and to treat the principles of choice as axiomatic (Bruni and Sugden, 2007; Maas, 2009).
By the second edition of his landmark essay, Robbins had acknowledged that the foundations of valuation are “psychical,” but he treated such matters as beyond the scope of economics:
“Why the human animal attaches particular values […] to particular things, is a question which we do not discuss. That is quite properly a question for psychologists or perhaps even physiologists. All that we need to assume as economists is the obvious fact that different possibilities offer different incentives, and that these incentives can be arranged in order of their intensity” (Robbins, 1935, p. 86).
Robbins shared the firm opposition of Pareto and Weber to basing an economic theory of subjective value on psychophysics, and he also endorsed with their strong conviction that “the fundamental propositions of microeconomic theory are deductions from the assumption that individuals act on consistent preferences” (Sugden, 2009). He saw this assumption as self-evident and thus exempt from the need for experimental validation (Sugden, 2009).
Under Robbins’ influence and that of contemporary economic luminaries, such as Hicks and Allen (1934), and Samuelson (1938, 1948), the theory, and subject matter of psychology was all but banished from the economic mainstream by the middle of the twentieth century (Laibson and Zeckhauser, 1998; Bruni and Sugden, 2007; Angner and Loewenstein, in press). The psychophysical notions entertained by the nineteenth century economists came to be regarded as unnecessary to the economic enterprise because powerful, general theories could be derived without them based on assumptions that seemed irrefutable (Bruni and Sugden, 2007).
The exile of psychology from economics was not to last. At least a partial return has been driven by developments in the psychology of decision making and by the related emergence of behavioral economics as an important and influential sub-discipline (Camerer and Loewenstein, 2004; Angner and Loewenstein, in press). The behavioral economic program seeks to base models of the economic agent on realistic, empirically verified psychological principles. Crucial to this approach are challenges to notions that Robbins, Weber, and Pareto took to be self-evident (Bruni and Sugden, 2007; Sugden, 2009), such as the consistency and transitivity of preferences (Tversky, 1969; Tversky and Thaler, 1990; Hsee et al., 1999). The Homo psychologicus who emerges from behavioral economic research uses an array of cognitive and affective shortcuts to navigate an uncertain, fluid world in real time. These shortcuts generate systematic behavioral tendencies that are economically consequential. Homo psychologicus is more complex than the Homo economicus erected by the neoclassical economists, more challenging to model, but more recognizable among the people we know and observe.
Kahneman and Tversky’s work on heuristics and biases (Tversky and Kahneman, 1974), and on prospect theory (Kahneman and Tversky, 1979; Tversky and Kahneman, 1992), is seen to have brought behavioral economics into the economic mainstream (Laibson and Zeckhauser, 1998). Heuristics are simple rules of thumb that facilitate decision making by helping an economic agent avoid the paralysis of indecision and keep up with a rapidly evolving flow of events (Gigerenzer and Goldstein, 1996; Gilovich et al., 2002; Gigerenzer and Gaissmaier, 2011). One line of research on heuristics highlights the ways in which heuristics improve decision making (Gigerenzer and Goldstein, 1996; Gigerenzer and Gaissmaier, 2011). Another illustrates how shortcuts that ease the computational burden may sometimes do so at the cost of generating errors that Homo economicus would not make (Tversky and Kahneman, 1974; Kahneman and Tversky, 1996). Because these errors are not random, they lead to predictable biases in decision making.
Prospect theory (Kahneman and Tversky, 1979) provides a formal framework for integrating heuristics and mapping functions analogous to psychophysical transformations. Prospects, such as a pair of gambles, are first “framed” in terms of gains or losses. This imposes reference dependence at the outset by establishing the current asset position as the point of comparison. The position of this “anchor” can be displaced by verbal reformulations of a prospect that do not change its quantitative expectation, e.g., by casting a given prospect as a loss with respect to a higher reference point as opposed to a gain with respect to a lower one. Two mapping functions are proposed, one that transforms gains and losses into subjective values and a second that transforms objective probabilities into decision weights (which operate much like subjective probabilities). The outputs are multiplied so as to assign an overall value to a prospect. Like common psychophysical transformations, the mapping functions are non-linear. The shape of the value function not only captures the law of diminishing returns (Bernoulli, 1738, 1954), it is also asymmetric, departing more steeply from the origin in the realm of losses than in the realm of gains. This asymmetry makes predictions about changes in risk appetites when a prospect is framed as a loss rather than as a gain or vice-versa. The decision-weight function is bowed, capturing our tendency to overweight very low-probability outcomes, to assign an inordinately high weight to certain outcomes, and to underweight intermediate probabilities.
Prospect theory argues that the form and parameters of the non-linear functions mapping objective variables into subjective ones are consequential for decision making. On this view, the choices made by the economic agent can neither be predicted accurately nor understood without reference to such mappings. Thus, prospect theory and related proposals restore psychological principles of valuation to a central position in portrayals of the economic agent.
Below, I point out some analogies between prospect theory and a model that links time allocation by laboratory rats to benefits and costs (Arvanitogiannis and Shizgal, 2008; Hernandez et al., 2010). Although they advocate caution when drawing parallels between decision making in humans and non-human animals, Kalenscher and van Wingerden (2011) detail many cases in which departures from the axioms of rational choice, discovered by psychologists and behavioral economists in their studies of humans, are mirrored in the behavior of laboratory animals. Of particular relevance to this essay is their discussion of the work of Stephens (2008) showing how a rule that can generate optimal behavior in the natural environment can produce time-inconsistent preferences in laboratory testing paradigms. This is reminiscent of how simplifying rules that prove highly serviceable to our sensory systems in natural circumstances can generate perceptual illusions under laboratory conditions.
Vivisecting the Economic Agent
Since Robbins published his seminal essay almost 80 years ago, at least four intellectual, scientific, and technological revolutions have transformed the landscape in which battles about the nature of the economic agent are fought. The cognitive revolution, which erupted in force in the 1960s, overthrew the hegemony of the behaviorists (labeled a “queer cult” by Robbins), restored internal psychological states as legitimate objects of scientific study, and provided rigorous inferential tools for probing such states. A later revolt, propelled forward by Zajonc’s (1980) memorable essay on preferences, reinstated emotion as a major determinant of decisions and focused much subsequent work on the interaction of cognitive and affective processes (LeDoux, 1996; Metcalfe and Mischel, 1999; Slovic et al., 2002a,b). Meanwhile, progress in neuroscience has vastly expanded what we know about the properties of neurons and neural circuitry while generating an array of new tools for probing brain–behavior relationships at multiple levels of analysis. Finally, we now find ourselves surrounded by “intelligent machines” with capabilities that would likely have astounded Robbins. These computational devices have expanded common conceptions of what can be achieved in the absence of sentience.
Robbins strove to isolate economics from dependence on psychological theory. Thus, it is not surprising that his essay on the nature and significance of economics provides only a few indications of his views regarding the qualities of mind required of the economic agent. One of these is the ability to establish a consistent preference ordering. The use of such an ordering to direct purposive behavior is discussed as requiring time and attention, which suggests that he had in mind a deliberative process, the working of which the individual is aware. Robbins also refers to us as “sentient beings.” Webster’s II New Riverside University Dictionary (Soukhanov, 1984) defines “sentient” as “1. Capable of feeling: CONSCIOUS. 2. Experiencing sensation or feeling.” The definition of “purposive” provided by The Collins English Dictionary (Butterfield, 2003) includes the following: “1. relating to, having, or indicating conscious intention.” We cannot be sure exactly which meanings he intended, but Robbins’ text suggests to this reader that experienced feelings, deliberation and conscious intent were linked in his conception of what is required for the purposive pursuit of ends and the allocation of scarce means to achieve them.
Since Robbins wrote his essay, thinking about the role of experienced feelings, deliberation and conscious intent in decision making and purposive behavior has evolved considerably. A highly influential view (Fodor, 1983) links the enormous computational abilities of our brains to the parallel operation of multiple specialized modules that enable us to perform feats such as the extraction of stable percepts from the constantly changing flow of sensory information, construction of spatial maps of our environment, transformation of the babble of speech sounds into meaningful utterances, near-instantaneous recognition of thousands of faces, etc. Most of the processing subserving cognition, the workings of the specialized modules, is seen to occur below the waterline of awareness. The conscious processor is portrayed as serial in nature, narrowly limited in bandwidth by a very scarce cognitive resource: the capacity of working memory (Baddeley, 1992). Thus, conscious processing constitutes a formidable processing bottleneck, and it is reserved for applications of a special, integrative kind (Nisbett and Wilson, 1977; LeDoux, 1996; Baars, 1997; Metcalfe and Mischel, 1999).
The resurgence of interest in emotion has brought affective processing within the scope of phenomena addressed by a highly parallel, modularized computational architecture. In Zajonc’s (1980) view, evaluative responses such as liking or disliking emerge spontaneously and precede conscious recognition – they arise from fast processes operating in parallel to the machinery of cognition, as traditionally understood. Indeed, the cognitive apparatus often busies itself with the development of plausible after-the-fact rationalizations for unconscious affective responses of which it is eventually informed. Zajonc’s ideas have contributed to a dual view of decision making in which deliberative and emotional processes vie for control (Loewenstein, 1996; Metcalfe and Mischel, 1999; Slovic et al., 2002a,b). Deliberative processing entails reasoning, assessment of logic and evidence, and abstract encoding of information in symbols, words, and numbers; it operates slowly and is oriented toward actions that may lie far off in the future. In contrast, emotional processing operates more quickly and automatically; it is oriented toward imminent action. Under time pressure or when decisions are highly charged, the affective processor is at an advantage and is well equipped to gain the upper hand. Particularly important to the dual-process view is its emphasis on operations that take place outside the scope of consciousness thoughts and experienced feelings, i.e., beyond sentience. Unlike what I am guessing Robbins to have assumed, the dual-process view allows both cognitive and affective processing to influence decision making without necessarily breaching the threshold of awareness.
It has long been recognized that we share with non-human animals many of the rudiments of affective processing (Darwin, 1872). In parallel, much evidence has accumulated since Robbins’ time that non-human animals have impressive cognitive abilities, including the creation of novel tools (Whiten et al., 1999; Weir et al., 2002; Wimpenny et al., 2011) and the ability to plan for the future (Clayton et al., 2003; Correia et al., 2007). Thus, both the reintegration of emotion into cognitive science and new developments in the study of comparative cognition add force to the notion that basic processes underlying our economic decisions also operate in other animals. I leave aside the question of the degree to which sentience should be attributed to various animals, but I note that the continuing development of artificial computational agents has expanded our sense of what is possible in the absence of consciousness thoughts and experienced feelings. For example, reinforcement-learning algorithms equip machines with the ability to build models of the external world based on their interaction with it and to select and pursue goals with apparent purpose (Sutton and Barto, 1998; Dayan and Daw, 2008; Dayan, 2009).
Developments since Robbins’ time have not only lent momentum to the behavioral economic program, they have also motivated initiatives to further “vivisect the economic agent” by rooting it in neuroscience. Twenty-five years ago, a presentation on decision making would have evoked puzzlement and no small measure of disapproval at a neuroscientific conference; now, such conferences are far too short to allow participants to take in all the new findings on this topic of burgeoning interest. The emergence of computational neuroscience as an important sub-field has provided a mathematical lingua franca and a mutually accessible frame of reference for communication between scholars in neuroscience, decision science, computer science, and economics.
The neuroeconomic program (Glimcher, 2003; Camerer et al., 2005; Glimcher et al., 2008; Loewenstein et al., 2008) seeks to replace Homo psychologicus with Homo neuropsychologicus. This program offers the hope that internal states hidden to behavioral observation can be monitored by neuroscientific means and, particularly in laboratory animals, can be manipulated so as to support causal inferences. The spirit of the neuroeconomic initiative shares much with that of the behavioral economic program, which is also concerned with what is “going on inside” the economic agent. However, the neuroeconomist draws particular inspiration from the striking successes achieved in fields such as molecular biology, where our understanding of function has been expanded profoundly by discoveries about structure and mechanism.
An Experimental Paradigm for the Behavioral, Computational, and Neurobiological Study of Allocation under Scarcity
A neuroeconomic perspective has informed several different experimental paradigms for the study of decision making in non-human animals (Glimcher, 2003; Glimcher et al., 2005, 2008; Kalenscher and van Wingerden, 2011). One of these entails pursuit of rewarding electrical brain stimulation (Shizgal, 1997). In the following sections, I describe a variant of this paradigm (Breton et al., 2009; Hernandez et al., 2010), which I relate to Robbins’ definition of economics. At the end of this essay, I sketch a path from this particular way of studying animal decision making to broader issues in neuroeconomics.
Rats, and many other animals, will work vigorously to trigger electrical stimulation of brain sites arrayed along the neuraxis, from rostral regions of prefrontal cortex to the nucleus of the solitary tract in the caudal brainstem. The effect of the stimulation that the animal seeks, called “brain stimulation reward (BSR)”, can be strikingly powerful and can entice subjects to cross electrified grids, gallop an uphill course obstructed with hurdles, or forgo freely available food to the point of starvation. Although the stimulation makes no known contribution to the satisfaction of physiological needs, the animals act as if BSR were highly beneficial, and they will work to the point of exhaustion in order to procure the stimulation.
Adaptive allocation of scarce behavioral resources requires that benefits and costs be assessed and combined so as to provide a result that can serve as a proxy for enhancement of fitness. The electrical stimulation that is so ardently pursued appears to inject a meaningful signal into neural circuitry involved in computing the value of goal objects and activities. For example, the rewarding effect produced by electrical stimulation of the medial forebrain bundle (MFB) can compete with, summate with, and substitute for the rewarding effects produced by natural goal objects, such as sucrose and saline solutions (Green and Rachlin, 1991; Conover and Shizgal, 1994; Conover et al., 1994). This implies that the artificial stimulation and the gustatory stimuli share some common attribute that permits combinatorial operations and ultimate evaluation in a common currency.
My coworkers and I have likened the intensity dimension of BSR to the dimension along which the reward arising from a tastant varies as a function of its concentration (Conover and Shizgal, 1994; Hernandez et al., 2010). On this view, a rat that works harder for an intense electrical reward than for a weaker one is like a forager that pursues a fully ripe fruit more ardently than a partially ripe one. Both are relinquishing a goal they would have sought under other circumstances for a different goal that surpasses it in value. Viewed in this way, the subjective intensity dimension is fundamental to economic decision making, as defined in the broad manner advocated here.
In many experiments on intracranial self-stimulation (ICSS), the cost column of the ledger is manipulated by altering the contingency between delivery of the rewarding stimulation and a response, such as lever pressing. Conover and I have developed schedules of reinforcement that treat time as a scarce resource in the sense of Robbins’ definition (Conover and Shizgal, 2005; Breton et al., 2009). Like the human economic agents portrayed by Robbins, our rats have “masses of instinctive tendencies” urging them “in different ways to action.” Even in the barren confines of an operant test chamber, rats will engage in activities, such as exploration, grooming, and resting, that are incompatible with the actions required to harvest the electrical reward. One of our schedules imposes a well controlled opportunity cost on the electrical reward (Breton et al., 2009). (The opportunity cost is the value of the alternate activities that must be forgone to obtain the experimenter-controlled reward.) On this schedule, the rat must “punch a clock” so as to accumulate sufficient work time to “get paid.” This is accomplished by delivering the stimulation once the cumulative time the rat has held down a lever reaches the criterion we have set, which we dub the “price” of the reward. We use the term “cumulative handling-time” to label this schedule. (In behavioral ecology, handling-time refers to the period during which a prey item is first rendered edible, e.g., by opening a shell, and then consumed.) To paraphrase Robbins, the conditions of the cumulative handling-time schedule require that if the rat chooses to engage in one activity, such as holding down the lever, it must relinquish others, such as grooming, exploring, or resting, which, in different circumstances (e.g., in the absence of BSR), it would not have relinquished. Like stimulation strength, price acts as an economic variable, as defined in the broad manner advocated here.
The key to making time a scarce resource is to ensure the exclusivity of the different activities in which the rat might engage. An exception illustrates the rule. In an early test of our cumulative handling-time schedule, a rat was seen to turn its back to the lever, hold it down with its shoulder blades, and simultaneously groom its face. By repositioning the lever, we were able to dissuade this ingenious fellow from defeating our intentions, and none of our rats have been seen since to adopt such a sly means of rendering their time less scarce.
Traditional schedules of reinforcement (Ferster and Skinner, 1957) do not enforce stringent time allocation. Interval schedules control when rewards are available, but little time need be devoted to operant responding in order to harvest most of the rewards on offer; the subject can engage in considerable “leisure” activity without forgoing many rewards. Ratio schedules do control effort costs, but they leave open the option of trading off opportunity costs against the additional effort entailed in responding at a higher cadence. In contrast, the cumulative handling-time schedule enforces a strict partition of time between work and leisure.
Allocation of Time to the Pursuit of Rewarding Electrical Brain Simulation
Figure 1A illustrates how rats allocate their time while working for BSR on the cumulative handling-time schedule. We define an experimental trial as a time interval during which the price and strength of the electrical reward are held constant. The trial duration is made proportional to the price, and thus, a rat that works incessantly will accumulate a fixed number of rewards per trial. The ordinate of Figure 1A plots the proportion of trial time (“time allocation”) spent working for the electrical stimulation. When the price of BSR is low, the rat forgoes leisure activities and spends almost all its time holding down the lever to earn electrical rewards. As the price is increased, the rat re-allocates the scarce resource (its time), engaging more in leisure activities and less in work. Figure 1B illustrates what happens when the price of the electrical reward is held constant but its strength is varied. The stimulation consists of a train of current pulses; under the conditions in force when the data in Figure 1 were collected, each pulse is expected to have triggered an action potential in the directly activated neurons that give rise to the rewarding effect (Forgie and Shizgal, 1993; Simmons and Gallistel, 1994; Solomon et al., 2007). Thus, the higher the frequency at which pulses are delivered during a train, the more intense the neural response, and the more time is allocated to pursuit of BSR. Figures 1C,D are two views of the same data, which were obtained by varying both the pulse frequency and the price; the high-frequency stimulation trains were cheap whereas the low-frequency ones were expensive.
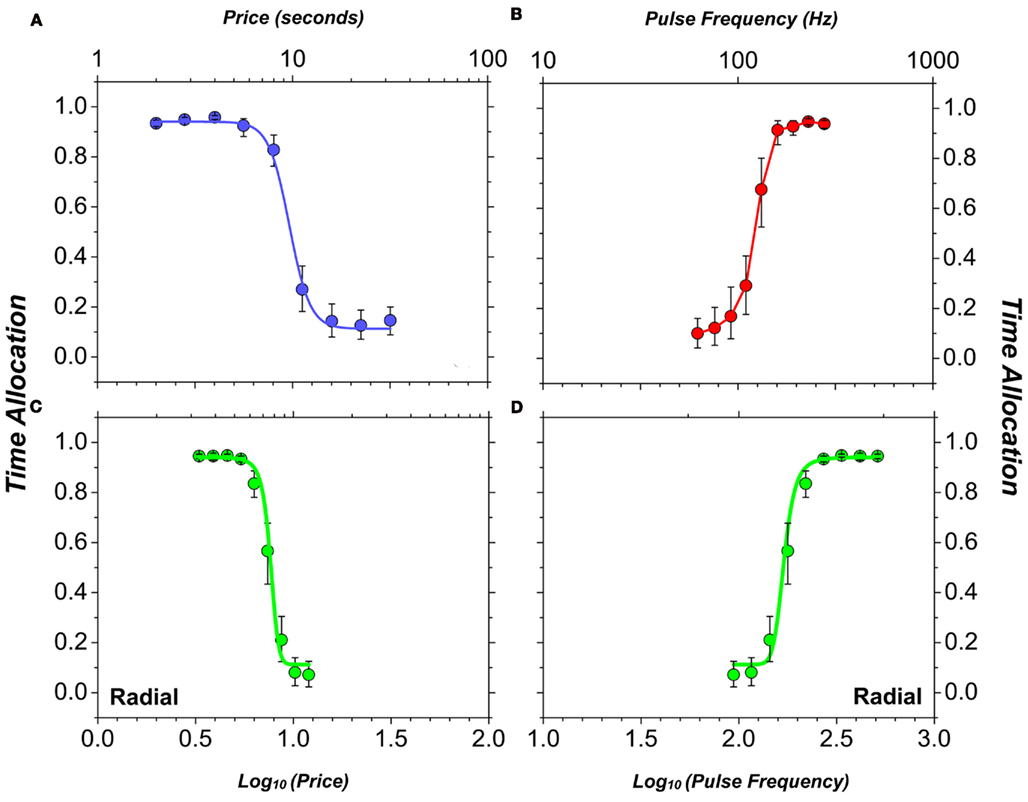
Figure 1. Sample data (Hernandez et al., 2010) showing how the strength (pulse frequency) and price (opportunity cost) of electrical stimulation trains influence the proportion of the rat’s time devoted to seeking out the electrical reward. (A) time allocation to pursuit of trains of different opportunity cost with reward strength held constant; (B) time allocation to pursuit of trains of different strength with opportunity cost held constant; (C) time allocation to pursuit of trains with inversely correlated strength and opportunity cost (strong trains are cheap, weak ones are expensive), plotted as function of opportunity cost; (D) time allocation to pursuit of trains with inversely correlated strength and opportunity cost (strong trains are cheap, weak ones are expensive), plotted as function of strength. Smooth curves are projections of the surface fitted to the data (shown in Figure 2A).
Figure 2A combines the data shown in Figure 1 in a three-dimensional (3D) depiction. We call the surface that was fit to the data points (depicted by the black mesh in Figure 2A and the colored curves in Figure 1) the “reward mountain.” Figure 2B summarizes the data in Figure 2A in a contour map. To obtain this map, the reward mountain is sectioned horizontally at regular intervals and the resulting profiles plotted as black lines; the gray level represents the altitude (time allocation). The shape of the reward mountain reflects the intuitive principle that the rat will allocate all or most of its time to pursuit of stimulation that is strong and cheap but will allocate less for stimulation that is weak and/or expensive.
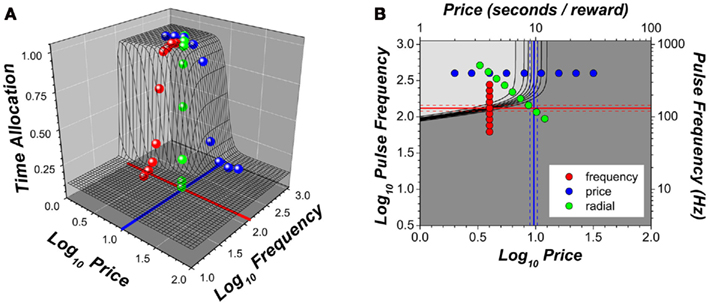
Figure 2. Three-dimensional views of the data in Figure 1. (A) Scatter plot of data means along the with surface fitted to the data; (B) contour plot of the fitted surface and the sampled pulse frequencies and prices. The solid red line represents the position parameter of the intensity-growth function: the pulse frequency that produces a reward of half-maximal intensity. This parameter determines the position of the three-dimensional structure along the pulse frequency axis. The solid blue line represents the price at which time allocated to pursuit of a maximal reward falls half-way between its minimal and maximal values; this parameter determines the position of the three-dimensional structure along the price axis. Dashed lines represent 95% confidence intervals.
A Functional/Computational Model
Figure 1 shows that the allocation of a scarce behavioral resource, the time available to obtain BSR, is tightly and systematically controlled by two objective economic variables: the strength (pulse frequency) and opportunity cost (price) of a stimulation train. Figure 3 depicts a empirically based model (Arvanitogiannis and Shizgal, 2008; Hernandez et al., 2010) of why the data in Figures 1 and 2 assume the form they do. Each component is assigned a specific role in processing the signal injected by the electrode and in translating it into an observable behavioral output. The mathematical form of each transformation is specified, and simulations can thus reveal whether the model can or cannot reproduce the dependence of the rat’s behavior on the strength and cost of the reward. The correspondence of the fitted surface to the data hints that it can. Insofar as the model specifies psychological processes involved in economic decisions, the model is positioned within the behavioral-economic tradition, and insofar as at least some of its components are couched in terms of neural activity, it is also has a neuroeconomic flavor.
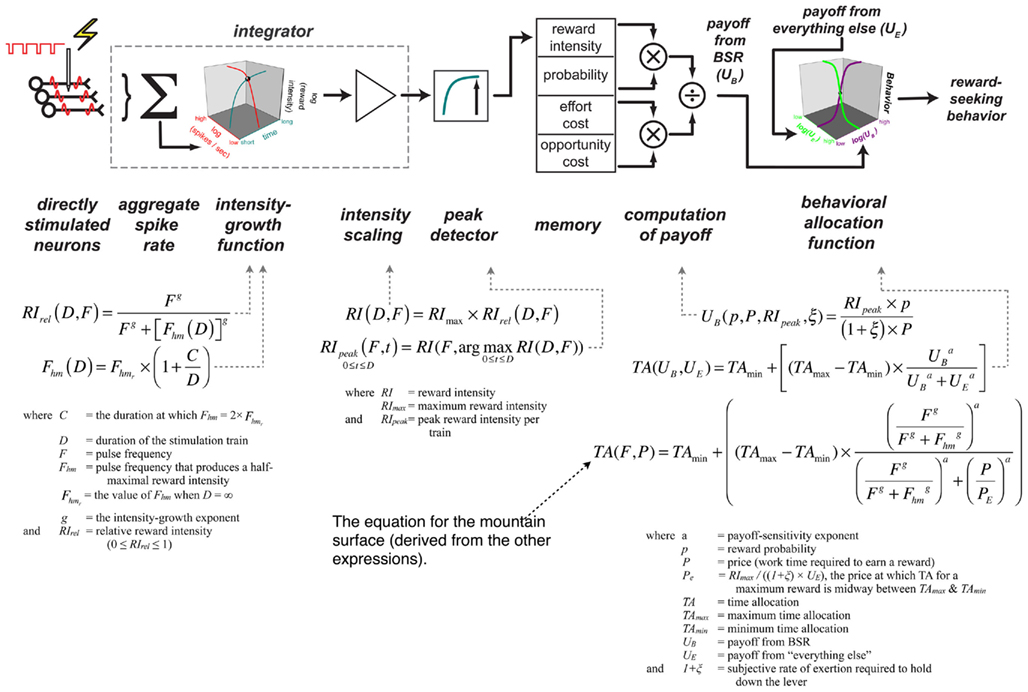
Figure 3. A functional/computational model of how time allocated to reward seeking is determined by the strength and cost the reward (Hernandez et al., 2010). The derivation of the expressions and their empirical basis is provided in the cited paper.
Let us consider first the core of the model, the memory vector in the center of the schema at the top of Figure 3. The elements of this vector are subjective values. Thus, the top and bottom elements are simply the subjective mapping of stimulation strength and opportunity cost. The remaining two elements represent the subjective estimate of the probability of receiving a reward upon satisfaction of the response requirement and the physical exertion required to hold down the lever. The values in the memory vector are combined in a manner consistent with generalizations (Baum and Rachlin, 1969; Killeen, 1972; Miller, 1976) of Herrnstein’s matching law (Herrnstein, 1970, 1974): The subjective reward intensity is scaled by the subjective probability and by the product of the subjective effort and opportunity costs. We refer to the result of this scalar combination as the “payoff” from pursuit of BSR.
Note the analogy between this model and prospect theory. In both cases, non-linear functions map objective economic variables into subjective ones, and the results are combined in scalar fashion. In both cases, the form and parameters of the mapping functions matter. Changing either can alter the ranking of a given option in the subject’s preference ordering.
To translate the payoffs obtained by scalar combination of the quantities in the memory vector into observable behavior, an adaptation (Hernandez et al., 2010) of McDowell’s (2005) single-operant version of the generalized matching law is employed. This expression relates the animal’s allocation of time to the relative payoffs from work and leisure. With the payoff from BSR held constant, time allocated to work decreases in sigmoidal fashion as the payoff from leisure activity grows (green curve in the 3D box at the right of Figure 3). Similarly, with the payoff from leisure activities fixed, time allocated to pursuit of a BSR train increases sigmoidally with the payoff from the stimulation (purple curve in the 3D box at the right of Figure 3).
The left portion of Figure 3 describes how the parameters of the pulse train are mapped into the subjective intensity of the rewarding effect. Several stages of processing are shown, including one of the four psychophysical functions that generate the values stored in the memory vector. The schema at the left represents the inference that over a wide range of frequencies, each pulse triggers a volley of action potentials in the directly stimulated neurons responsible for the rewarding effect (Gallistel, 1978; Gallistel et al., 1981; Forgie and Shizgal, 1993; Simmons and Gallistel, 1994; Solomon et al., 2007). The synaptic output of these neurons is integrated spatially and temporally and transformed by an intensity-growth function. In accord with experimental data (Leon and Gallistel, 1992; Simmons and Gallistel, 1994; Arvanitogiannis and Shizgal, 2008; Hernandez et al., 2010), the red curve in the 3D box on the left of Figure 3 shows that reward intensity grows as a logistic function of the aggregate firing rate produced by a stimulation train of fixed duration, and the cyan curve depicts the growth of reward intensity over time in response to a train of fixed strength (Sonnenschein et al., 2003). The scaled output of the intensity-growth function is passed through a peak detector en route to memory: it is the maximum intensity achieved that is recorded (Sonnenschein et al., 2003).
Not shown in Figure 3 are the three remaining psychophysical functions, the ones responsible for mapping reward probability, exertion of effort, and opportunity cost into their subjective equivalents. Figure 4 presents the prediction of Mazur’s hyperbolic temporal discounting model (Mazur, 1987) as applied to the psychophysical transformation of opportunity cost; the plotted curves are based on data from a study of delay discounting in ICSS (Mazur et al., 1987). Ongoing research (Solomon et al., 2007) is assessing the relative merits of the Mazur model and several alternatives as accounts of the impact of opportunity costs on performance for BSR. The subjective probability and effort–cost functions have yet to be described.
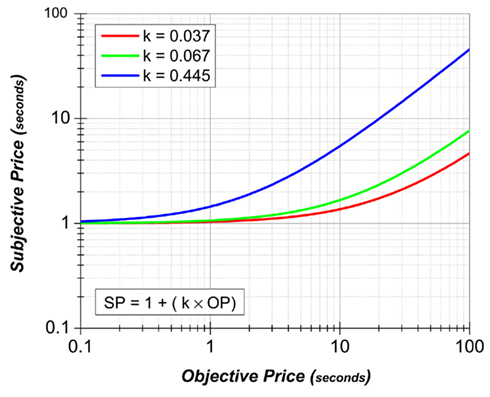
Figure 4. Mazur’s hyperbolic delay-discount function (Mazur, 1987), replotted as a subjective-price function. The price is the cumulative time the rat must hold down the lever in order to earn a reward. Thus, from the perspective of the Mazur model, the price is couched as a delay to reward receipt, and the subjective-price is inversely related to the discounted value. The value of the reward at zero delay has been set arbitrarily to one. The delay-discount constants (Mazur’s k) for the plotted curves are derived from a study by Mazur et al. (1987); the red curve represents the value for subject 1, the green curve for subject 2, and the blue curve for subject 3. Alternative models of the subjective-price function are under ongoing investigation (Solomon et al., 2007).
The contours in Figure 2B trace out the intensity-growth function (Hernandez et al., 2010). The non-linear form of this function makes it possible to discern in what direction the mountain surface described by these contours has been displaced by experimental manipulation of the reward circuitry. Figure 5 shows how the mountain is shifted by treatments acting at different stages of the model. Interventions in the early stages, prior to the output of the intensity-growth function, displace the mountain along the axis representing the strength of the rewarding stimulation (pink surface). In contrast, interventions in later stages displace the mountain along the axis representing the cost of the rewarding stimulation (blue surface). Consequently, the reward mountain can be used to narrow down the stages of processing at which manipulations such as drug administration, lesions, or physiological deprivation act to alter reward seeking. Conventional two-dimensional measurements are not up to this task: identical displacements of psychometric curves, such as the ones shown in Figure 1, can be produced by shifting the 3D reward mountain in orthogonal directions (Hernandez et al., 2010; Trujillo-Pisanty et al., 2011).
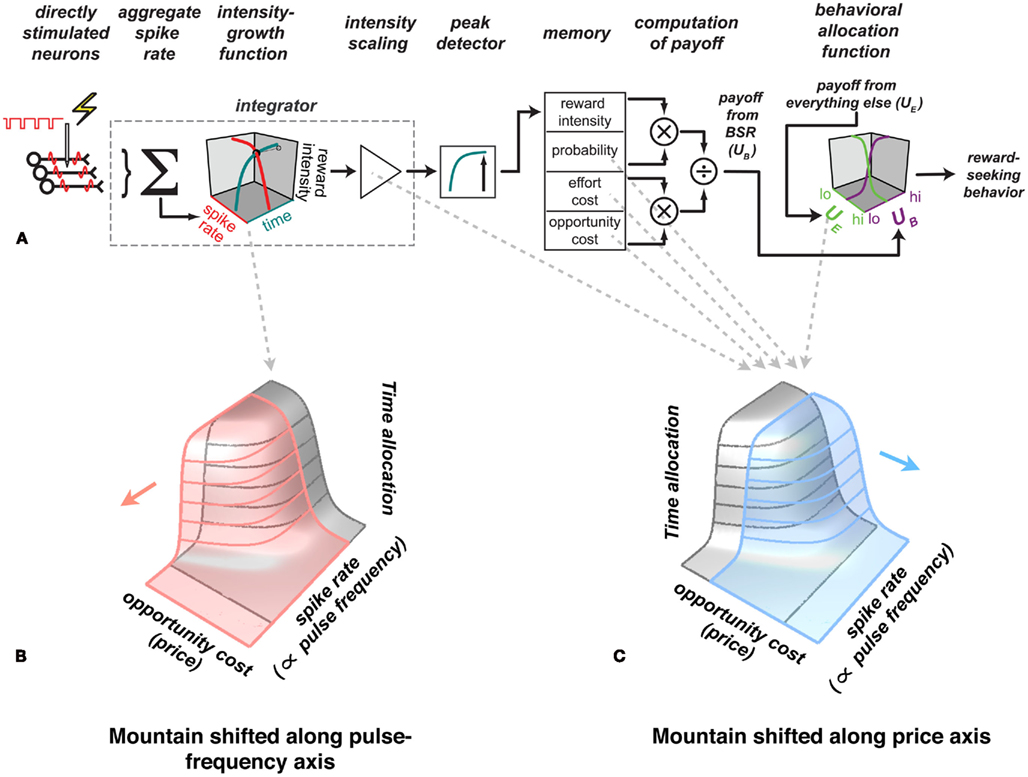
Figure 5. Inferring the stages of processes responsible for shifts of the mountain. (A) The mountain model. Experimental manipulations that act on the early stages of processing, prior to the output of the intensity-growth function, shift the three-dimensional structure along the pulse frequency axis (B) whereas manipulations that act on later stages produce shifts along the price axis (C). Thus, measuring the effects of such manipulations on the position of the three-dimensional structure constrains the stages of processing responsible for the behavioral effects of the manipulations. On this basis, the enhancement of reward seeking produced by cocaine (Hernandez et al., 2010) and the attenuation of reward seeking produced by blockade of cannabinoid CB-1 receptors (Trujillo-Pisanty et al., 2011) were shown to arise primarily from drug actions at stages of processing beyond the output of the intensity-growth function.
In early work on the role of dopamine neurons in BSR, the changes in reward pursuit produced by manipulation of dopaminergic neurotransmission were attributed to alterations in reward intensity (Crow, 1970; Esposito et al., 1978). However, cocaine, a drug that boosts dopaminergic neurotransmission, displaces the 3D reward mountain rightward along the price axis (Hernandez et al., 2010). This links the drug-induced change in dopamine signaling to a later stage of processing than was originally proposed, one beyond the output of the intensity-growth function. Among the actions of cocaine that are consistent with its effect on the position of the mountain are an upward rescaling of reward intensity (Hernandez et al., 2010) and a decrease in subjective effort costs (Salamone et al., 1997, 2005). Blockade of the CB-1 cannabinoid receptor also displaces the mountain along the price axis, but in the opposite direction to the shift produced by cocaine (Trujillo-Pisanty et al., 2011). These effects of perturbing dopamine and cannabinoid signaling illustrate why it is important to learn the form of psychophysical valuation functions, to measure them unambiguously, and to take into account multiple variables that contribute to valuation.
Limitations of the Model
The model in Figures 3 and 5 has fared well in initial validation experiments (Arvanitogiannis and Shizgal, 2008) and has also provided novel interpretations of the effects on pursuit of BSR produced by pharmacological treatments (Hernandez et al., 2010; Trujillo-Pisanty et al., 2011). That said, it important to acknowledge that the current instantiation is a mere way station en route to a challenging dual goal: a fully fleshed out description of the neural circuitry underlying reward-related decisions and a set of functional hypotheses about why the circuitry is configured as it is. The state of our current knowledge remains well removed from that objective, and the model presented here has numerous limitations. In later sections, I discuss a strategy for moving forward.
Let us consider various limitations as we traverse the schemata in Figures 3 and 5 from right to left. The first one encountered is the behavioral-allocation function, which has been borrowed from the matching literature. This application is an “off-label” usage of an expression developed to describe matching of response rates on variable-interval schedules to reinforcement rates. As is the case with ratio schedules, returns from the cumulative handling-time schedule are directly proportional to investment (of time, in this case). The predicted behavior is maximization, not matching. The justification for our off-label usage is empirical: the observed behavior corresponds closely to the predicted form. That said, other sigmoidal functions would likely do the job. We have not yet explored alternative functions in this class and have chosen instead to investigate behavioral-allocation decisions on a finer time scale.
Data from operant conditioning studies are commonly presented in aggregate form, as response and reinforcement totals accumulated during some time interval (i.e., as trial rates). This is reminiscent of the way behavior is modeled in economic theories of consumer choice (Kagel et al., 1995). What matters in such accounts is not the order and timing with which different goods are placed in the shopping basket but rather the kinds of goods that make up the final purchase and their relative proportions. This is unsatisfying to the neuroeconomist. The goods enter the shopping basket as a result of some real-time decision making process. What is the nature of that process, and what is its physical basis? To answer such questions, a moment-to-moment version of the behavioral-allocation function must be developed. Only then can the behavioral data be linked directly to real-time measurements such as electrophysiological or neurochemical recordings. A successful solution would generate accurate predictions both at the scale of individual behavioral acts and at the scale of aggregate accumulations. Such a solution should be functionally plausible in the sense that the behavioral strategies it generates not be dominated by alternatives available to competitors.
We have made an early attempt at real-time modeling (Conover et al., 2001) as well as at development of a behavioral-allocation model derived from first principles (Conover and Shizgal, 2005). Work on these initiatives is ongoing, but the formulation presented here appears adequate for its application in identifying circuitry underlying BSR, interpreting pharmacological data, and deriving psychophysical functions that contribute to reward-related decisions. For these purposes, we need the behavioral-allocation function to be only good enough to allow us to “see through it” (Gallistel et al., 1981) and draw inferences about earlier stages.
The computation of payoff is represented in Figures 3 and 5 immediately upstream of the behavioral-allocation function. “Benefits” (reward intensity) are combined in scalar fashion with costs, as is the case in matching law formulations (Baum and Rachlin, 1969; Killeen, 1972; Miller, 1976). This way of combining benefits and costs contrasts sharply with “shopkeeper’s logic,” which dictates that both be translated into a common currency and their difference computed (e.g., Niv et al., 2007). The scalar combination posited in the mountain model is why sections obtained at different levels of reward intensity are parallel when plotted against a logarithmic price axis. We have observed such parallelism using a different schedule of reinforcement (Arvanitogiannis and Shizgal, 2008), but additional work should be carried out to confirm whether strict parallelism holds when the cumulative handling-time schedule is employed.
As we move leftward through the model, we reach the stages most directly under the control of the stimulating electrode. An important limitation of the model as it now stands is that even these stages are described only computationally – the neural circuitry underlying them has yet to be pinned down definitively, either in the case of electrically induced reward or of the rewarding effects of natural stimuli. Candidate pathways subserving BSR are discussed in the following section. The key point to make here is that this crucial limitation is one that the ICSS paradigm would seem particularly well suited to overcome. The powerfully rewarding effect of the electrical stimulation arises from a stream of action potentials triggered in an identifiable set of neurons. This should make the ICSS phenomenon an attractive entry point for efforts to map the structure of brain reward circuitry and to account for its functional properties in terms of neural signaling between its components. Section “Linking Computational and Neural Models” provides some reasons why success has not yet been achieved and why newly developed techniques promise to surmount the obstacles that have impeded progress. These new methods should make it possible to associate the abstract boxes in Figures 3 and 5 with cells, spike trains and synaptic potentials in the underlying neural circuitry.
Candidate Neural Circuitry
In this section, I review some candidates for neural circuitry underlying BSR. This brief overview highlights some achievements of prior research as well as many challenges that have yet to be addressed in a satisfactory way.
The data in Figures 1 and 2 were generated by stimulation delivered at the lateral hypothalamic (LH) level of the MFB. Kate Bielajew and I have provided evidence that the volley of action potentials elicited by stimulation at this site must propagate caudally in order the reach the efferent stages of the circuit responsible for the rewarding effect (Bielajew and Shizgal, 1986). Figure 6 depicts some of the descending MFB components that course near the LH stimulation site as well as some of the circuitry connected to these neurons. Even this selective representation reveals a multiplicity of candidates for the directly stimulated neurons and spatio-temporal integrator in Figures 3 and 5.
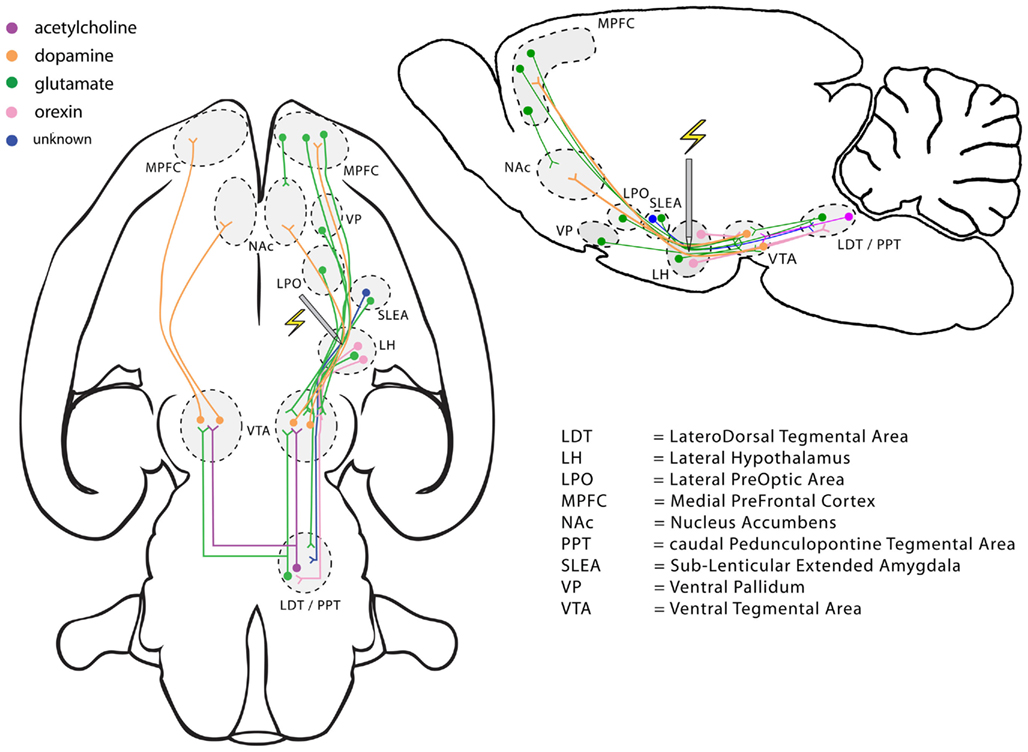
Figure 6. Selected descending pathways coursing through a lateral hypothalamic region of the medial forebrain bundle, where electrical stimulation is powerfully rewarding, and some associated neural circuitry. The lefthand view is in the horizontal plane and the righthand view in the sagittal plane.
Dopamine-containing neurons figure prominently in the literature on reward seeking in general (Wise and Rompré, 1989; Montague et al., 1996; Schultz et al., 1997; Ikemoto and Panksepp, 1999) and on BSR in particular (Wise and Rompré, 1989; Wise, 1996). Pursuit of BSR is attenuated by treatments that reduce dopaminergic neurotransmission (Fouriezos et al., 1978; Franklin, 1978; Gallistel and Karras, 1984) and is boosted by treatments that enhance such signaling (Crow, 1970; Gallistel and Karras, 1984; Colle and Wise, 1988; Bauco and Wise, 1997; Hernandez et al., 2010). Both long-lasting (“tonic”) and transient (“phasic”) release of dopamine are driven by rewarding MFB stimulation (Hernandez and Hoebel, 1988; You et al., 2001; Wightman and Robinson, 2002; Hernandez et al., 2006, 2007; Cheer et al., 2007). Figure 6 shows that the axons of midbrain dopamine neurons course through the MFB, passing close to the LH stimulation sites used in many studies of ICSS (Ungerstedt, 1971). Direct activation of dopaminergic fibers by rewarding stimulation was central to early accounts of ICSS (German and Bowden, 1974; Wise, 1978; Corbett and Wise, 1980). Nonetheless, these authors did express some reservations, which turn out to be well founded. The axons of dopamine neurons are fine, unmyelinated, and difficult to excite by means of extracellular stimulation (Yeomans et al., 1988; Anderson et al., 1996; Chuhma and Rayport, 2005). The mere proximity of these axons to the electrode tip does not guarantee that a large proportion of them are excited directly under the conditions of ICSS experiments. Indeed, the electrophysiological properties of these fibers provide a poor match to the properties inferred from behavioral studies of ICSS (Yeomans, 1975, 1979; Bielajew and Shizgal, 1982, 1986). These behavioral data suggest that non-dopaminergic neurons with descending, myelinated axons, more excitable than those of the dopamine-containing cells, compose an important part of the directly stimulated stage (Bielajew and Shizgal, 1986; Shizgal, 1997). Non-dopaminergic neurons driven by rewarding MFB stimulation, and with properties consistent with those inferred from the behavioral data, have indeed been observed by electrophysiological means (Rompré and Shizgal, 1986; Shizgal et al., 1989; Kiss and Shizgal, 1990; Murray and Shizgal, 1996).
Figure 6 provides several different ways to reconcile the dependence of ICSS on dopaminergic neurotransmission with the evidence implicating non-dopaminergic neurons in the directly stimulated stage of the circuit. Multiple components of the descending MFB provide monosynaptic input to dopamine cell bodies in the midbrain, and glutamatergic neurons are prominent among them (You et al., 2001; Geisler et al., 2007). Blockade of glutamatergic receptors on midbrain dopamine neurons decreases transient release of dopamine by rewarding electrical stimulation (Sombers et al., 2009). Cholinergic neurons in the pons constitute one limb of a disynaptic path that links MFB electrodes to activation of dopamine neurons (Oakman et al., 1995). These cholinergic neurons are implicated in the rewarding effect of MFB stimulation (Yeomans et al., 1993, 2000; Fletcher et al., 1995; Rada et al., 2000).
It has been proposed, in the case of posterior mesencephalic stimulation, that the spatio-temporal integration of the reward intensity signal arises prior to, or with the participation of, midbrain dopamine neurons (Moisan and Rompre, 1998). Application of this idea to self-stimulation of the MFB is consistent with the evidence that excitation driven by the rewarding stimulation arrives at the dopamine neurons via monosynaptic and/or disynaptic routes. Given the important roles ascribed to dopaminergic neurons in the allocation of effort and in reward-related learning, it is important to understand how information is processed in their afferent network. By driving inputs to the dopaminergic neurons directly, rewarding brain stimulation should play a useful role in this endeavor and should continue to contribute to the ongoing debate about the functional roles of phasic and tonic dopamine signaling (Wise and Rompré, 1989; Salamone et al., 1997, 2005; Schultz et al., 1997; Berridge and Robinson, 1998; Schultz, 2000; Wise, 2004; Niv et al., 2007; Berridge et al., 2009).
The preceding paragraphs attest to the fact that it has proved simple neither to identify the neurons composing the most accessible stage of the circuitry underlying ICSS, the directly activated stage, nor to determine the precise role played by the neural population most extensively studied in the context of BSR, midbrain dopamine neurons. In the following section, I discuss in more general terms the requirements for establishing such linkages, and I argue that new research techniques provide grounds for optimism that long-standing obstacles can be overcome.
Linking Computational and Neural Models
Multiple, converging, experimental approaches are required to link an identified neural population to a psychological process (Conover and Shizgal, 2005). Each approach tests the linkage hypothesis in a different way, by assessing correlation, necessity, modulation, sufficiency or computational adequacy. All of these approaches have been applied in the search for the directly stimulated neurons underlying BSR and in efforts to determine the role played by midbrain dopamine neurons. Nonetheless, the full promise of the convergent strategy has yet to be realized.
An example of a correlational test has already been mentioned. Inferences are drawn from behavioral data about physiological properties of a neural population, such as the directly stimulated neurons that give rise to BSR. A method such as single-unit electrophysiology is used to measure neural properties, which are then compared to those inferred from the behavioral data. For example, the experimenter can ascertain, by means of collision between spontaneous and electrically triggered antidromic spikes, that the axon of a neuron from which action potentials are recorded is directly activated by rewarding stimulation. Properties of the stimulated axon, such as its refractory period and conduction velocity, are then measured and compared to those inferred from the behavioral data (Shizgal et al., 1989; Murray and Shizgal, 1996). This approach can provide supporting evidence for a linkage hypothesis, but it cannot prove it. The portrait assembled on the basis of the behavioral data is unlikely to be unique, and the neuron under electrophysiological observation may resemble those responsible for the behavior in question but, in fact, subserve another function.
Tests of necessity entail silencing the activity of some population of neurons and then measuring any consequent changes in the behavior under study. Traditional methods include lesions, cooling, and injection of local anesthetics. Although this approach can also provide supporting evidence, it is fraught with difficulties. Many neurons in addition to the intended targets may be affected, and the silencing may alter the behavior under study in unintended ways, for example, by reducing the capacity of the subject to perform the behavioral task rather than the subjective value of the goal. The typically employed silencing methods have durations of action far longer than those of the neural signals of interest.
Tests of modulation are similar logically to tests of necessity but can entail either enhancement or suppression of neural signaling and are usually reversible. Drug administration is typically employed for this purpose. This approach often achieves greater specificity than is afforded by conventional silencing methods. Nonetheless, it is difficult to control the distribution of a drug injected locally in the brain, and the duration of drug action often exceeds that of the neural signal of interest by many orders of magnitude.
Tests of sufficiency entail exogenous activation of a neural population and determination of whether the artificially induced signal so produced affects the psychological process under study in the same way as a natural stimulus. The demonstration that the rewarding effect of electrical stimulation of the MFB competes and summates with the rewarding effect of gustatory stimuli (Conover and Shizgal, 1994; Conover et al., 1994) is an example of this approach. Traditional sufficiency tests, which often entail delivery of electrical brain stimulation, provide much better temporal control than local drug injection, but they too are plagued by major shortcomings: Many neurons in addition to the target population are typically activated, and the stimulation may produce undesirable behavioral side-effects.
Computational adequacy is another important criterion for establishing linkage. To carry out this test, a formal model is built, such as the one in Figures 3 and 5, and the role of the neural population under study is specified. Simulations are then performed to determine whether the model can reproduce the behavioral data using the parameters derived from neural measurement. This is a demanding test, but it too is not decisive. There is no guarantee that any given model is unique or sufficiently inclusive.
Although all its elements have shortcomings as well as virtues, the convergent strategy is nonetheless quite powerful. The virtues of some elements compensate for the shortcomings of others, and the likelihood of a false linkage decreases as more independent and complementary lines of evidence are brought to bear. That said, one may well wonder why, if the convergent approach is so powerful, has it not yet generated clear answers to straightforward questions such as the identity of the directly stimulated neurons subserving BSR or the role played by midbrain dopamine neurons? As I argue in the following section, many of the problems are technical in nature, and recent developments suggest that they are in the process of being surmounted.
The Promise of New Research Techniques
Ensemble recording
The example of the correlational approach described above entails recording from individual neurons, one at a time, in anesthetized subjects, after the collection of the behavioral data. Newer recording methods have now been developed that register the activity of dozens of neurons simultaneously while the behavior of interest is being performed. A lovely example of this substantial advance is a recent study carried out by a team led by David Redish (van der Meer et al., 2010). They recorded from ensembles of hippocampal neurons as rats learned to navigate a maze. As the rats paused at a choice point during a relatively early stage of learning, these neurons fired in patterns similar to those recorded previously as the animal was actually traversing the different paths. This demonstration supports Tolman’s (1948) idea that animals can plan by means of virtual navigation in stored maps of their environment. Tolman’s theory was criticized for leaving the rat “lost in thought.” The study by van der Meer et al. (2010) suggests that the rat is not lost at all but is instead exploring its stored spatial representation. This is a powerful demonstration of the potential of neuroscientific methods to open hidden states to direct observation.
The correlational approach adopted by van der Meer et al. (2010) was complemented by a test of computational adequacy: they determined the accuracy with which the population of neurons from which they recorded could represent position within the maze. Another aspect of their study dissociated the correlates of hippocampal activity from those of neurons in the ventral striatum, one of the terminal fields of the midbrain dopamine neurons. Unlike the activity of the hippocampal population, the activity of the ventral–striatal population accelerated as the rats approached locations where they had previously encountered rewards (van der Meer and Redish, 2009; van der Meer et al., 2010). This ramping activity was also seen at choice points leading to the locations in question. The authors point out that such a pattern of anticipatory firing, in conjunction with the predictive spatial information derived from hippocampal activity, could provide feedback to guide vicarious trial-and-error learning.
Once the neurons underlying BSR have been identified, it would be very interesting indeed to study them by means of ensemble recording methods. Such an approach could provide invaluable information about the function of the BSR substrate and might well explain how reward-related information is relayed to ventral–striatal neurons. In principle, ensemble recording from the appropriate neural populations could provide physical measurement of the subjective values of economic variables in real-time. This could go a long way toward putting to rest criticisms of models that incorporate states hidden to the outside observer, such as the one detailed in Figures 3 and 5. Ensemble recording coupled to appropriate computational methods promises to draw back the veil.
Chronic, in vivo voltammetry
Just as ensemble recording registers the activity of neural populations during behavior, in vivo voltammetry (Wightman and Robinson, 2002) can measure dopamine transients during performance of economic decision making tasks. In early studies, the measurements were obtained acutely over periods of an hour or so. However, Phillips and colleagues have now developed an electrode that can register dopamine transients over weeks and months (Clark et al., 2010), periods sufficiently long for the learning and execution of demanding behavioral tasks. Their method has already yielded dramatic results in neuroeconomic studies (Gan et al., 2010; Wanat et al., 2010; Nasrallah et al., 2011), and its application would provide a strong test of the hypothesis that phasic activity of midbrain dopamine neurons encodes the integrated reward intensity signal in ICSS.
Optogenetics
The recent development with the broadest likely impact is a family of “optogenetic” methods (Deisseroth, 2011; Yizhar et al., 2011). These circumvent the principal drawbacks of traditional silencing and stimulation techniques, achieving far greater temporal, spatial, and cell-type selectivity, while retaining all the principal advantages of the traditional tests for necessity and sufficiency. This technology is based on light-sensitive, microbial opsin proteins genetically targeted to restricted neuronal populations. Following expression, the introduced opsins are trafficked to the cell membrane, where they function as ion channels or pumps. By means of fiber-optic probes, which can be implanted and used chronically in behaving subjects, light is delivered to a circumscribed brain area, at a wavelength that activates the introduced opsin. Neural activity is thus silenced or induced for periods as short as milliseconds or as long as minutes.
The means for specific activation and silencing of dopaminergic (Tsai et al., 2009), cholinergic (Witten et al., 2010), glutamatergic (Zhao et al., 2011), and orexinergic (Adamantidis et al., 2007) neurons have already been demonstrated. Coupled with measurement methods such as the one that generated the data in Figures 1 and 2, application of optogenetic tools should reveal what role, if any, the different elements depicted in Figure 6 play in BSR. Indeed, it has already been shown by specific optogenetic means that activation of midbrain dopamine neurons is sufficient to support operant responding (Kim et al., 2010; Adamantidis et al., 2011; Witten et al., 2011). However, it remains unclear whether such activation fully recapitulates the rewarding effect of electrical stimulation or only a component thereof; the stage of processing at which the dopaminergic neurons intervene has not yet been established.
From Brain Stimulation Reward to Natural Rewards
Many decades have passed since BSR was discovered (Olds and Milner, 1954), but the neural circuitry underlying this striking phenomenon has yet to be worked out. Ensemble recordings, chronic in vivo voltammetry, and optogenetics promise to produce revolutionary change in the way this problem is approached and to circumvent critical technical obstacles that have blocked or impeded progress. Once components of the neural substrate for BSR have been identified, the convergent approaches described above can be brought to bear, with greatly increased precision and power, in the growing array of tasks for studying economic decision making in non-human animals. This will provide a natural bridge between the specialized study of BSR and the more general study of neural mechanisms of valuation and choice.
Kent Conover and I have developed a preparation (Conover and Shizgal, 1994) in which gustatory reward can be controlled with a precision similar to that afforded by BSR. The gustatory stimulus is introduced directly into the mouth, and a gastric cannula undercuts the development of satiety. Psychophysical data about the gustatory reward can be acquired from this preparation at rates approaching those typical of BSR studies. This method should make it possible to carry out a test, at the neural level, of the hypothesis that BSR and gustatory rewards are evaluated in a common currency. It can also render some fundamental questions about gustatory reward amenable to mechanistic investigation. For example, it has long been suspected that the thalamic projection of the pontine parabrachial area mediates discriminative aspects of gustation whereas the basal forebrain projections mediate the rewarding effects of gustatory stimuli (Pfaffmann et al., 1977; Spector and Travers, 2005; Norgren et al., 2006). Application of methodology developed for the study of BSR can put this notion to a strong test. Other basic questions that beg to be addressed concern the dependence of gustatory reward on energy stores. Within the framework of the model described in Figures 3 and 5, how do deprivation states act? Do they modulate early stages of processing, thus altering preference between different concentrations of a tastant of a particular type and/or do they act at later stages so as to alter preference between different classes of tastants, such as inputs to short- and long-term energy stores (Hernandez et al., 2010)?
Questions such as those posed in the preceding paragraph concern basic topics that economists have long abstained from addressing: the origin of preferences, their dependence on internal conditions, and the possibility that an important aspect of individual differences in valuation derives from constitutional factors. In Robbins’ account, the agent arrives on the economic stage already equipped with a set of “tastes” (i.e., preferences in general and not only gustatory ones). What is the physical basis of these tastes? What mechanisms change them? What determines when tastes serve biologically adaptive purposes or lead in harmful directions? Developments in the neurosciences may have rendered such questions addressable scientifically and may even be up to the challenge of providing some answers.
A Quadruple Heresy
I begin this essay within the canon of Robbins’ greatly influential definition of economics and then proceed to commit four heresies. First, I extend Robbins’ core concept of allocation under scarcity to non-human animals. Second, I make common cause with behavioral economists, who strive to base their theories of the economic agent on realistic psychological foundations, and I argue that psychophysics constitutes one of the fundamental building blocks of this structure. Third, I argue that sentience is not necessary for economic behavior. Fourth, I advocate grounding the theory of the economic agent in neuroscience, to the extent that our knowledge and methods allow. I predict that this initiative should lead to new insights, render otherwise hidden states amenable to direct observation, and provide a way to choose between models that appear equally successful when evaluated on the behavioral and computational levels alone.
Economic concepts have long played a central role in behavioral ecological studies of non-human animals (Stephens and Krebs, 1986; Commons et al., 1987; Stephens et al., 2007). It seems to me highly likely that machinery enabling other animals to make economic decisions has been conserved in humans and very unlikely indeed that this inheritance lies defunct and unused as we strive to navigate the choices confronting us.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The work of my research team is supported by a group grant from the “Fonds de la recherche en santé du Québec” to the “Groupe de Recherche en Neurobiologie Comportementale”/Center for Studies in Behavioural Neurobiology (Shimon Amir, principal investigator), a Discovery Grant from the Natural Science and Engineering Research Council of Canada (#308-2011), and a Concordia University Research Chair. The author is grateful to Marc-André Bacon, Yannick-André Breton, Brian J. Dunn, Rick Gurnsey, Aaron Johnson, Robert Leonard, Saleem Nicola, and Ivan Trujillo-Pisanty for their helpful comments and encouragement.
References
Adamantidis, A. R., Tsai, H.-C., Boutrel, B., Zhang, F., Stuber, G. D., Budygin, E. A., Touriño, C., Bonci, A., Deisseroth, K., and de Lecea, L. (2011). Optogenetic interrogation of dopaminergic modulation of the multiple phases of reward-seeking behavior. J. Neurosci. 31, 10829–10835.
Adamantidis, A. R., Zhang, F., Aravanis, A. M., Deisseroth, K., and de Lecea, L. (2007). Neural substrates of awakening probed with optogenetic control of hypocretin neurons. Nature 450, 420–424.
Anderson, R. M., Fatigati, M. D., and Rompre, P. P. (1996). Estimates of the axonal refractory period of midbrain dopamine neurons: their relevance to brain stimulation reward. Brain Res. 718, 83–88.
Angner, E., and Loewenstein, G. (in press). “Behavioral economics,” in Philosophy of Economics, ed. U. Mäki (Amsterdam: Elsevier).
Arvanitogiannis, A., and Shizgal, P. (2008). The reinforcement mountain: allocation of behavior as a function of the rate and intensity of rewarding brain stimulation. Behav. Neurosci. 122, 1126–1138.
Baars, B. J. (1997). In the Theater of Consciousness: The Workspace of the Mind. New York: Oxford University Press.
Bauco, P., and Wise, R. A. (1997). Synergistic effects of cocaine with lateral hypothalamic brain stimulation reward: lack of tolerance or sensitization. J. Pharmacol. Exp. Ther. 283, 1160–1167.
Baum, W. M., and Rachlin, H. C. (1969). Choice as time allocation. J. Exp. Anal. Behav. 12, 861–874.
Bernoulli, D. (1738, 1954). Exposition of a new theory on the measurement of risk. Econometrica 22, 23–36.
Berridge, K. C., and Robinson, T. E. (1998). What is the role of dopamine in reward: hedonic impact, reward learning, or incentive salience? Brain Res. Brain Res. Rev. 28, 309–369.
Berridge, K. C., Robinson, T. E., and Aldridge, J. W. (2009). Dissecting components of reward: “liking,” “wanting,” and learning. Curr. Opin. Pharmacol. 9, 65–73.
Bielajew, C., and Shizgal, P. (1982). Behaviorally derived measures of conduction velocity in the substrate for rewarding medial forebrain bundle stimulation. Brain Res. 237, 107–119.
Bielajew, C., and Shizgal, P. (1986). Evidence implicating descending fibers in self-stimulation of the medial forebrain bundle. J. Neurosci. 6, 919–929.
Breton, Y. A., Marcus, J. C., and Shizgal, P. (2009). Rattus psychologicus: construction of preferences by self-stimulating rats. Behav. Brain Res. 202, 77–91.
Bruni, L., and Sugden, R. (2007). The road not taken: how psychology was removed from economics, and how it might be brought back. Econ. J. 117, 146–173.
Butterfield, J. (2003). Collins English Dictionary – Complete and Unabridged. Glasgow: HarperCollins Publishers.
Camerer, C., Loewenstein, G., and Prelec, D. (2005). Neuroeconomics: how neuroscience can inform economics. J. Econ. Lit. 43, 9–64.
Camerer, C. F., and Loewenstein, G. (2004). “Behavioral economics: past, present, future,” in Advances in Behavioral Economics, eds C. F. Camerer, G. Loewenstein and M. Rabin (Princeton, NJ: Russell Sage Foundation, Princeton University Press), 3–51.
Cheer, J. F., Aragona, B. J., Heien, M. L., Seipel, A. T., Carelli, R. M., and Wightman, R. M. (2007). Coordinated accumbal dopamine release and neural activity drive goal-directed behavior. Neuron 54, 237–244.
Chuhma, N., and Rayport, S. (2005). Synaptic actions of mesoaccumbens dopamine neurons. Cellscience 2, #2.
Clark, J. J., Sandberg, S. G., Wanat, M. J., Gan, J. O., Horne, E. A., Hart, A. S., Akers, C. A., Parker, J. G., Willuhn, I., Martinez, V., Evans, S. B., Stella, N., and Phillips, P. E. M. (2010). Chronic microsensors for longitudinal, subsecond dopamine detection in behaving animals. Nat. Methods 7, 126–129.
Clayton, N. S., Bussey, T. J., and Dickinson, A. (2003). Can animals recall the past and plan for the future? Nat. Rev. Neurosci. 4, 685–691.
Colle, L. M., and Wise, R. A. (1988). Effects of nucleus accumbens amphetamine on lateral hyothalamic brain stimulation reward. Brain Res. 459, 361–368.
Commons, M. L., Kacelnik, A., and Shettleworth, S. J. (1987). Quantitative Analyses of Behavior: Foraging. Hillsdale: Lawrence Erlbaum.
Conover, K. L., Fulton, S., and Shizgal, P. (2001). Operant tempo varies with reinforcement rate: implications for measurement of reward efficacy. Behav. Process. 56, 85–101.
Conover, K. L., and Shizgal, P. (1994). Competition and summation between rewarding effects of sucrose and lateral hypothalamic stimulation in the rat. Behav. Neurosci. 108, 537–548.
Conover, K. L., and Shizgal, P. (2005). Employing labor supply theory to measure the reward value of electrical brain stimulation. Games Econ. Behav. 52, 283–304.
Conover, K. L., Woodside, B., and Shizgal, P. (1994). Effects of sodium depletion on competition and summation between rewarding effects of salt and lateral hypothalamic stimulation in the rat. Behav. Neurosci. 108, 549–558.
Corbett, D., and Wise, R. A. (1980). Intracranial self-stimulation in relation to the ascending dopaminergic systems of the midbrain: a moveable electrode mapping study. Brain Res. 185, 1–15.
Correia, S. P. C., Dickinson, A., and Clayton, N. S. (2007). Western scrub-jays anticipate future needs independently of their current motivational state. Curr. Biol. 17, 856–861.
Crow, T. J. (1970). Enhancement of coaine of intra-cranial self-stimulation in the rat. Life Sci. 9, 375–381.
Dayan, P., and Daw, N. D. (2008). Decision theory, reinforcement learning, and the brain. Cogn. Affect. Behav. Neurosci. 8, 429–453.
Esposito, R. U., Motola, A. H., and Kornetsky, C. (1978). Cocaine: acute effects on reinforcement thresholds for self-stimulation behavior to the medial forebrain bundle. Pharmacol. Biochem. Behav. 8, 437–439.
Fechner, G. T. (1860, 1965). “Gustav Theodor Fechner on Fechner’s law,” in A Source Book in the History of Psychology, eds R. J. Herrnstein and E. G. Boring (Cambridge, MA: Harvard University Press), 66–75.
Ferster, C. B., and Skinner, B. F. (1957). Schedules of Reinforcement. New York: Appleton-Century-Crofts.
Fletcher, P. J., Tampakeras, M., and Yeomans, J. S. (1995). Median raphe injections of 8-OH-DPAT lower frequency thresholds for lateral hypothalamic self-stimulation. Pharmacol. Biochem. Behav. 52, 65–71.
Fodor, J. A. (1983). The Modularity of Mind: An Essay on Faculty Psychology. Cambridge, MA: MIT Press.
Forgie, M. L., and Shizgal, P. (1993). Mapping the substrate for brain stimulation reward by means of current- number trade-off functions. Behav. Neurosci. 107, 506–524.
Fouriezos, G., Hansson, P., and Wise, R. A. (1978). Neuroleptic-induced attenuation of brain stimulation reward in rats. J. Comp. Physiol. Psychol. 92, 661–671.
Franklin, K. B. J. (1978). Catecholamines and self-stimulation: reward and performance effects dissociated. Pharmacol. Biochem. Behav. 9, 813–820.
Gallistel, C. R. (1978). Self-stimulation in the rat: quantitative characteristics of the reward pathway. J. Comp. Physiol. Psychol. 92, 977–998.
Gallistel, C. R., and Karras, D. (1984). Pimozide and amphetamine have opposing effects on the reward summation function. Pharmacol. Biochem. Behav. 20, 73–77.
Gallistel, C. R., Shizgal, P., and Yeomans, J. S. (1981). A portrait of the substrate for self-stimulation. Psychol. Rev. 88, 228–273.
Gan, J. O., Walton, M. E., and Phillips, P. E. M. (2010). Dissociable cost and benefit encoding of future rewards by mesolimbic dopamine. Nat. Neurosci. 13, 25–27.
Geisler, S., Derst, C., Veh, R. W., and Zahm, D. S. (2007). Glutamatergic afferents of the ventral tegmental area in the rat. J. Neurosci. 27, 5730–5743.
German, D. C., and Bowden, D. M. (1974). Catecholamine systems as the neural substrate for intracranial self-stimulation: a hypothesis. Brain Res. 73, 381–419.
Gigerenzer, G., and Gaissmaier, W. (2011). Heuristic decision making. Annu. Rev. Psychol. 62, 451–482.
Gigerenzer, G., and Goldstein, D. G. (1996). Reasoning the fast and frugal way: models of bounded rationality. Psychol. Rev. 103, 650–669.
Gilovich, T., Griffin, D., and Kahneman, D. (2002). Heuristics and Biases: The Psychology of Intuitive Judgment. Cambridge: Cambridge University Press.
Glimcher, P. W. (2003). Decisions, Uncertainty, and the Brain: The Science of Neuroeconomics. Cambridge, MA: MIT Press.
Glimcher, P. W., Camerer, C. F., Fehr, E., and Poldrack, R. A. (2008). Neuroeconomics: Decision Making and the Brain. London: Academic Press.
Glimcher, P. W., Dorris, M. C., and Bayer, H. M. (2005). Physiological utility theory and the neuroeconomics of choice. Games Econ. Behav. 52, 213–256.
Green, L., and Rachlin, H. (1991). Economic substitutablity of electrical brain stimulation, food, and water. J. Exp. Anal. Behav. 55, 133–143.
Hernandez, G., Breton, Y. A., Conover, K., and Shizgal, P. (2010). At what stage of neural processing does cocaine act to boost pursuit of rewards? PLoS ONE 5, e15081. doi:10.1371/journal.pone.0015081
Hernandez, G., Haines, E., Rajabi, H., Stewart, J., Arvanitogiannis, A., and Shizgal, P. (2007). Predictable and unpredictable rewards produce similar changes in dopamine tone. Behav. Neurosci. 121, 887–895.
Hernandez, G., Hamdani, S., Rajabi, H., Conover, K., Stewart, J., Arvanitogiannis, A., and Shizgal, P. (2006). Prolonged rewarding stimulation of the rat medial forebrain bundle: neurochemical and behavioral consequences. Behav. Neurosci. 120, 888–904.
Hernandez, L., and Hoebel, B. G. (1988). Feeding and hypothalamic stimulation increase dopamine turnover in the accumbens. Physiol. Behav. 44, 599–606.
Hicks, J. R., and Allen, R. G. D. (1934). A reconsideration of the theory of value. Part I. Economica 1, 52–76.
Hsee, C. K., Loewenstein, G. F., Blount, S., and Bazerman, M. H. (1999). Preference reversals between joint and separate evaluations of options: a review and theoretical analysis. Psychol. Bull. 125, 576–590.
Ikemoto, S., and Panksepp, J. (1999). The role of nucleus accumbens dopamine in motivated behavior: a unifying interpretation with special reference to reward-seeking. Brain Res. Brain Res. Rev. 31, 6–41.
Kagel, J. K., Battalio, R. C., and Green, L. (1995). Economic Choice Theory: An Experimental Model of Animal Behavior. Cambridge: Cambridge University Press.
Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291.
Kahneman, D., and Tversky, A. (1996). On the reality of cognitive illusions. Psychol. Rev. 103, 582–591; discusion 592–596.
Kalenscher, T., and van Wingerden, M. (2011). Why we should use animals to study economic decision making – a perspective. Front. Neurosci. 5:82. doi:10.3389/fnins.2011.00082
Kim, K., Baratta, M. V., Yang, A., Lee, D., Boyden, E. S., and Fiorillo, C. D. (2010). “Optical activation of dopamine neurons for 200 milliseconds is sufficient for operant reinforcement,” in Society for Neuroscience Annual Meeting, San Diego, CA.
Kiss, I., and Shizgal, P. (1990). Compound action potentials recorded in the ventral tegmental area, substantia nigra, and periaqueductal gray following rewarding stimulation of the lateral hypothalamus in the rat. Psychobiology 18, 205–214.
Kramer, D. L. (1988). The behavioral ecology of air breathing by aquatic animals. Can. J. Zool. 66, 89–94.
Laibson, D., and Zeckhauser, R. (1998). Amos Tversky and the ascent of behavioral economics. J. Risk Uncertain 16, 7–47.
LeDoux, J. E. (1996). The Emotional Brain: The Mysterious Underpinnings of Emotional Life. New York: Simon & Schuster.
Leon, M., and Gallistel, C. R. (1992). The function relating the subjective magnitude of brain stimulation reward to stimulation strength varies with site of stimulation. Behav. Brain Res. 52, 183–193.
Loewenstein, G. (1996). Out of control: visceral influences on behavior. Organ. Behav. Hum. Decis. Process. 65, 272–292.
Maas, H. (2009). Disciplining boundaries: Lionel Robbins, Max Weber, and the borderlands of economics, history, and psychology. J. Hist. Econ. Thought 31, 500–517.
Mazur, J. E. (1987). “An adjusting procedure for studying delayed reinforcement,” in Quantitative Analyses of Behavior, Vol. 5: The Effect of Delay and of Intervening Events on Reinforcement Value, eds M. L. Commons, J. E. Mazur, J. A. Nevin, and H. Rachlin (Hillsdale, NJ: Erlbaum), 55–73.
Mazur, J. E., Stellar, J. R., and Waraczynski, M. (1987). Self-control choice with electrical stimulation of the brain. Behav. Process. 151, 143–153.
McDowell, J. J. (2005). On the classic and modern theories of matching. J. Exp. Anal. Behav. 84, 111–127.
Metcalfe, J., and Mischel, W. (1999). A hot/cool-system analysis of delay of gratification: dynamics of willpower. Psychol. Rev. 106, 3–19.
Miller, H. L. (1976). Matching-based hedonic scaling in the pigeon. J. Exp. Anal. Behav. 26, 335–347.
Moisan, J., and Rompre, P. P. (1998). Electrophysiological evidence that a subset of midbrain dopamine neurons integrate the reward signal induced by electrical stimulation of the posterior mesencephalon. Brain Res. 786, 143–152.
Montague, P. R., Dayan, P., and Sejnowski, T. J. (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 16, 1936–1947.
Murray, B., and Shizgal, P. (1996). Physiological measures of conduction velocity and refractory period for putative reward-relevant MFB axons arising in the rostral MFB. Physiol. Behav. 59, 427–437.
Nasrallah, N. A., Clark, J. J., Collins, A. L., Akers, C. A., Phillips, P. E., and Bernstein, I. L. (2011). Risk preference following adolescent alcohol use is associated with corrupted encoding of costs but not rewards by mesolimbic dopamine. Proc. Natl. Acad. Sci. U.S.A. 108, 5466–5471.
Nisbett, R. E., and Wilson, T. D. (1977). Telling more than we can know: verbal reports on mental processes. Psychol. Rev. 84, 231–259.
Niv, Y., Daw, N. D., Joel, D., and Dayan, P. (2007). Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology (Berl.) 191, 507–520.
Norgren, R., Hajnal, A., and Mungarndee, S. S. (2006). Gustatory reward and the nucleus accumbens. Physiol. Behav. 89, 531–535.
Oakman, S. A., Faris, P. L., Kerr, P. E., Cozzari, C., and Hartman, B. K. (1995). Distribution of pontomesencephalic cholinergic neurons projecting to substantia nigra differs significantly from those projecting to ventral tegmental area. J. Neurosci. 15, 5859–5869.
Olds, J., and Milner, P. M. (1954). Positive reinforcement produced by electrical stimulation of septal area and other regions of rat brain. J. Comp. Physiol. Psychol. 47, 419–427.
Pareto, V. (1892–1893/1982). Considerazioni sui principi fondamentali dell’economia pura. Geneva: Droz. [Giornale degli Economisti, May, 390–420; June, 485–512; August, 119–57; Reprinted in Oeuvres Complètes of V. Pareto, Vol. 26, 1982].
Pfaffmann, C., Norgren, R., and Grill, H. J. (1977). “Sensory affect and motivation,” in Tonic Functions of Sensory Systems, eds B. Wenzel, and P. Zeigler (New York: New York Academy of Sciences), 18–34.
Rada, P. V., Mark, G. P., Yeomans, J. J., and Hoebel, B. G. (2000). Acetylcholine release in ventral tegmental area by hypothalamic self-stimulation, eating, and drinking. Pharmacol. Biochem. Behav. 65, 375–379.
Robbins, L. (1935). An Essay on the Nature and Significance of Economic Science. London: MacMillan and Co.
Rompré, P. P., and Shizgal, P. (1986). Electrophysiological characteristics of neurons in forebrain regions implicated in self-stimulation of the medial forebrain bundle in the rat. Brain Res. 364, 338–349.
Salamone, J. D., Correa, M., Mingote, S. M., and Weber, S. M. (2005). Beyond the reward hypothesis: alternative functions of nucleus accumbens dopamine. Curr. Opin. Pharmacol. 5, 34–41.
Salamone, J. D., Cousins, M. S., and Snyder, B. J. (1997). Behavioral functions of nucleus accumbens dopamine: empirical and conceptual problems with the anhedonia hypothesis. Neurosci. Biobehav. Rev. 21, 341–359.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Shizgal, P., Schindler, D., and Rompré, P. P. (1989). Forebrain neurons driven by rewarding stimulation of the medial forebrain bundle in the rat: comparison of psychophysical and electrophysiological estimates of refractory periods. Brain Res. 499, 234–248.
Simmons, J. M., and Gallistel, C. R. (1994). Saturation of subjective reward magnitude as a function of current and pulse frequency. Behav. Neurosci. 108, 151–160.
Slovic, P., Finucane, M., Peters, E., and MacGregor, D. G. (2002a). “The affect heuristic,” in Heuristics and Biases: The Psychology of Intuitive Judgment, ed. T. Gilovich (New York, NY: Cambridge University Press), 397–420.
Slovic, P., Finucane, M., Peters, E., and MacGregor, D. G. (2002b). Rational actors or rational fools: implications of the affect heuristic for behavioral economics. J. Socio Econ. 31, 329–342.
Solomon, R. B., Conover, K., and Shizgal, P. (2007). “Estimation of subjective opportunity cost in rats working for rewarding brain stimulation: further progress,” in Society for Neuroscience, San Diego.
Sombers, L. A., Beyene, M., Carelli, R. M., and Wightman, R. M. (2009). Synaptic overflow of dopamine in the nucleus accumbens arises from neuronal activity in the ventral tegmental area. J. Neurosci. 29, 1735–1742.
Sonnenschein, B., Conover, K., and Shizgal, P. (2003). Growth of brain stimulation reward as a function of duration and stimulation strength. Behav. Neurosci. 117, 978–994.
Soukhanov, A. H. (ed.). (1984). Webster’s II New Riverside University Dictionary. Boston: Houghton Mifflin.
Spector, A. C., and Travers, S. P. (2005). The representation of taste quality in the mammalian nervous system. Behav. Cogn. Neurosci. Rev. 4, 143–191.
Stephens, D. W. (2008). Decision ecology: foraging and the ecology of animal decision making. Cogn. Affect. Behav. Neurosci. 8, 475–484.
Stephens, D. W., Brown, J. S., and Ydenberg, R. C. (2007). Foraging: Behavior and Ecology. Chicago: University of Chicago Press.
Stephens, D. W., and Krebs, J. R. (1986). Foraging Theory. Princeton, NJ: Princeton University Press.
Sugden, R. (2009). Can economics be founded on “indisputable facts of experience?” Lionel Robbins and the pioneers of neoclassical economics. Economica 76, 857–872.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: MIT Press.
Trujillo-Pisanty, I., Hernandez, G., Moreau-Debord, I., Cossette, M. P., Conover, K., Cheer, J. F., and Shizgal, P. (2011). Cannabinoid receptor blockade reduces the opportunity cost at which rats maintain operant performance for rewarding brain stimulation. J. Neurosci. 31, 5426–5435.
Tsai, H., Zhang, F., Adamantidis, A., Stuber, G., Bonci, A., de Lecea, L., and Deisseroth, K. (2009). Phasic firing in dopaminergic neurons is sufficient for behavioral conditioning. Science 324, 1080–1084.
Tversky, A., and Kahneman, D. (1974). Judgment under uncertainty: heuristics and biases. Science 185, 1124–1131.
Tversky, A., and Kahneman, D. (1992). Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323.
Ungerstedt, U. (1971). Stereotaxic mapping of the monoamine pathways in the rat brain. Acta Physiol. Scand. Suppl. 367, 1–48.
van der Meer, M. A. A., Johnson, A., Schmitzer-Torbert, N. C., and Redish, A. D. (2010). Triple dissociation of information processing in dorsal striatum, ventral striatum, and hippocampus on a learned spatial decision task. Neuron 67, 25–32.
van der Meer, M. A. A., and Redish, A. D. (2009). Covert expectation-of-reward in rat ventral striatum at decision points. Front. Integr. Neurosci. 3:1. doi:10.3389/neuro.07.001.2009
Wanat, M. J., Kuhnen, C. M., and Phillips, P. E. M. (2010). Delays conferred by escalating costs modulate dopamine release to rewards but not their predictors. J. Neurosci. 30, 12020–12027.
Weber, M. (1908). Marginal utility theory and the “fundamental law of psychophysics.” Soc. Sci. Q. 56, 21–36.
Weber, E. H. (1834/1965). “Ernst Heinrich Weber on Weber’s law,” in A Source Book in the History of Psychology, eds R. J. Herrnstein and E. G. Boring (Cambridge, MA: Harvard University Press), 64–66.
Weir, A. A., Chappell, J., and Kacelnik, A. (2002). Shaping of hooks in New Caledonian crows. Science 297, 981.
Whiten, A., Goodall, J., McGrew, W. C., Nishida, T., Reynolds, V., Sugiyama, Y., Tutin, C. E., Wrangham, R. W., and Boesch, C. (1999). Cultures in chimpanzees. Nature 399, 682–685.
Wightman, R. M., and Robinson, D. L. (2002). Transient changes in mesolimbic dopamine and their association with “reward.” J. Neurochem. 82, 721–735.
Wimpenny, J. H., Weir, A. A. S., and Kacelnik, A. (2011). New Caledonian crows use tools for non-foraging activities. Anim. Cogn. 14, 459–464.
Witten, I. B., Lin, S.-C., Brodsky, M., Prakash, R., Diester, I., Anikeeva, P., Gradinaru, V., Ramakrishnan, C., and Deisseroth, K. (2010). Cholinergic interneurons control local circuit activity and cocaine conditioning. Science 330, 1677–1681.
Witten, I. B., Steinberg, E. E., Lee, S. Y., Davidson, T. J., Zalocusky, K. A., Brodsky, M., Yizhar, O., Cho, S. L., Gong, S., Ramakrishnan, C., Stuber, G. D., Tye, K. M., Janak, P. H., and Deisseroth, K. (2011). Recombinase-driver rat lines: tools, techniques, and optogenetic application to dopamine-mediated reinforcement. Neuron 72, 721–733.
Yeomans, J. S. (1975). Quantitative measurement of neural post-stimulation excitability with behavioral methods. Physiol. Behav. 15, 593–602.
Yeomans, J. S. (1979). The absolute refractory periods of self-stimulation neurons. Physiol. Behav. 22, 911–919.
Yeomans, J. S., Maidment, N. T., and Bunney, B. S. (1988). Excitability properties of medial forebrain bundle axons of A9 and A10 dopamine cells. Brain Res. 450, 86–93.
Yeomans, J. S., Mathur, A., and Tampakeras, M. (1993). Rewarding brain stimulation: role of tegmental cholinergic neurons that activate dopamine neurons. Behav. Neurosci. 107, 1077–1087.
Yeomans, J. S., Takeuchi, J., Baptista, M., Flynn, D. D., Lepik, K., Nobrega, J., Fulton, J., and Ralph, M. R. (2000). Brain-stimulation reward thresholds raised by an antisense oligonucleotide for the M5 muscarinic receptor infused near dopamine cells. J. Neurosci. 20, 8861–8867.
Yizhar, O., Fenno, L. E., Davidson, T. J., Mogri, M., and Deisseroth, K. (2011). Optogenetics in neural systems. Neuron 71, 9–34.
You, Z. B., Chen, Y. Q., and Wise, R. A. (2001). Dopamine and glutamate release in the nucleus accumbens and ventral tegmental area of rat following lateral hypothalamic self-stimulation. Neuroscience 107, 629–639.
Zajonc, R. B. (1980). Feeling and thinking: preferences need no inferences. Am. Psychol. 35, 151–175.
Keywords: behavioral economics, neuroeconomics, decision making, opportunity cost, psychophysics, reward, brain stimulation, dopamine
Citation: Shizgal P (2012) Scarce means with alternative uses: Robbins’ definition of economics and its extension to the behavioral and neurobiological study of animal decision making. Front. Neurosci. 6:20. doi: 10.3389/fnins.2012.00020
Received: 07 September 2011;
Paper pending published: 24 October 2011;
Accepted: 23 January 2012;
Published online: 09 February 2012.
Edited by:
Tobias Kalenscher, Heinrich-Heine University Duesseldorf, GermanyReviewed by:
Alex Kacelnik, University of Oxford, UKCharles Randy Gallistel, Rutgers University, USA
Copyright: © 2012 Shizgal. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Peter Shizgal, Center for Studies in Behavioral Neurobiology, Concordia University, SP-244, 7141 Sherbrooke Street West, Montréal, QC H4B 1R6, Canada. e-mail:cGV0ZXIuc2hpemdhbEBjb25jb3JkaWEuY2E=
