Brain inspired path planning algorithms for drones

Introduction: With the development of artificial intelligence and brain science, brain-inspired navigation and path planning has attracted widespread attention.

Methods: In this paper, we present a place cell based path planning algorithm that utilizes spiking neural network (SNN) to create efficient routes for drones. First, place cells are characterized by the leaky integrate-and-fire (LIF) neuron model. Then, the connection weights between neurons are trained by spike-timing-dependent plasticity (STDP) learning rules. Afterwards, a synaptic vector field is created to avoid obstacles and to find the shortest path.

Results: Finally, simulation experiments both in a Python simulation environment and in an Unreal Engine environment are conducted to evaluate the validity of the algorithms.

Discussion: Experiment results demonstrate the validity, its robustness and the computational speed of the proposed model.

1. Introduction

A drone, also called an unmanned aerial vehicle (UAV), is a vehicle capable to perform autonomous motion decisions or human like remote control. Due to the high mobility, flexibility, and low cost, drones have a wide range of military and civilian applications such as target detection, epidemic prevention, disaster relief and so on (Mohsan et al., 2022). Autonomous flight of a drone includes navigation, simultaneous localization and mapping as well as path planning. Path planning involves calculating an efficient route from a launch position to a target while avoiding obstacles, which plays an important role in the task execution of a drone (Aggarwal and Kumar, 2020). In practical applications, many flight tasks of UAV are in static environment, such as cargo transportation in a given environment, military attack driven by interest targets and so on. In these circumstances, it is particularly important to develop path planning algorithms for drones in static environments, and it also puts forward higher requirements for the intelligence, reliability and autonomy of path planning methods. Despite great progress in decades of drone research, there are still many open questions for path planners.

The conventional global path planning algorithms mainly include artificial potential field methods, A^* algorithm, ant colony algorithms, rapidly exploring random trees (RRT), and optimization and improvement algorithms of these algorithms (Noreen et al., 2016; Konatowski and Pawłowski, 2018; Cai et al., 2019; Mohammed et al., 2021). However, all these path planning algorithms need to model the environment in advance, which is not suitable for the problem of global path pre-planning of drones in complex environment. As neuroscience gradually reveals how the brain represents spatial information, the effort to construct biologically-inspired drone controllers that utilize these spatial representations has become feasible. Of particular interests in this context are place cells, which are assumed to be responsible for spatial representation (Leutgeb et al., 2005; Yartsev and Ulanovsky, 2013). Inspired by these advances, many neural models based on place cells have been proposed to enable an agent to find its way to a destination. Zannone et al. presented a reward-driven goal-directed method modeling place cells and action cells (Zannone et al., 2018). Koul et al. introduced a spiking neural network model and a neuromorphic implementation for path planning inspired by place cells that use spike latency in the pathfinding process (Koul and Horiuchi, 2019). Zennir proposed a robust path planning algorithm by propagating rhythmic spiking activity in a hippocampal network model (Zennir et al., 2017). Although all the above methods can guide an agent to a target and represent path planning algorithms in two-dimension (2D) environments. There is increasing interest on biologically-inspired path planning algorithms for drones in three- dimensional (3D) space. However, there are only a few reports addressing neural brain like approaches for 3D path planning.

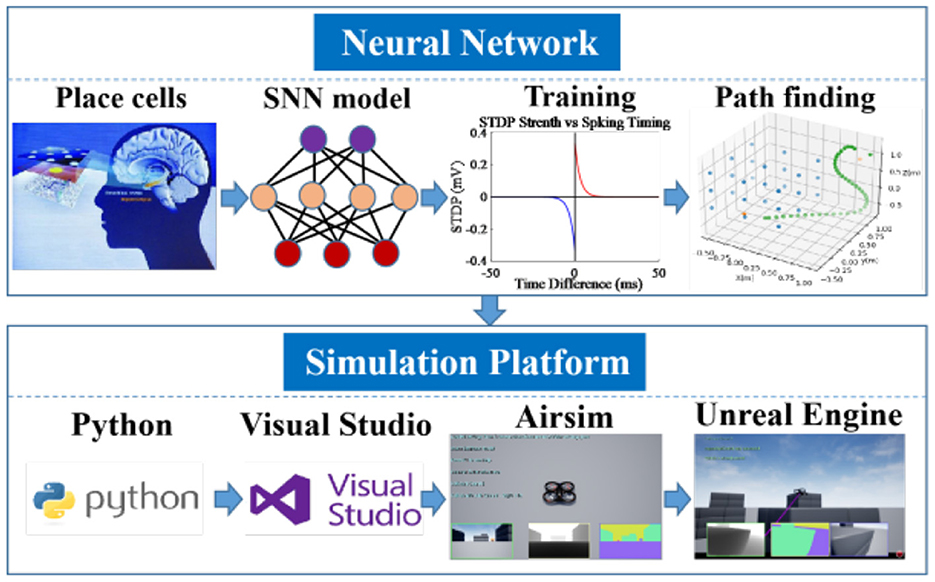
To bridge the major gap of existing studies, we propose a biologically plausible 3D model of a spiking neural network (SNN) that enables fast and reliable computation of a feasible pathway of a drone. The neural representation of place cells receives information about the initial position of the drone and performs position updates through neural plasticity. Obstacles are represented by inhibited neurons. When the network receives the coordinates of a target location, it is able to steer the drone toward a target based on a synaptic vector field. Finally, the feasibility of the model is to be verified by simulation experiments and Airsim. The rest of the paper is organized as follows: Section 2 describes the overall proposed framework, Section 3 depicts the implemented system and the proposed path planning algorithm, while Section 4 presents the experimental setup and simulation results, which are then summarized in Section 5.

2. Network architecture

The goal of this work is to design and implement a complete navigation system for drones in which most of the computation takes place in neural networks that use spatial representations similar to place cells in the brain of mammals. The drone should be able to compute feasible trajectories to targets in a complex environment with obstacles. In addition, the drone should be able to learn all necessary information about its environment by exploration. Finally, the algorithm is verified with the help of Airsim and the Unreal Engine. The overall architecture of the path planning system is shown in Figure 1.

FIGURE 1

Figure 1. The architecture of brain-inspired path planning.

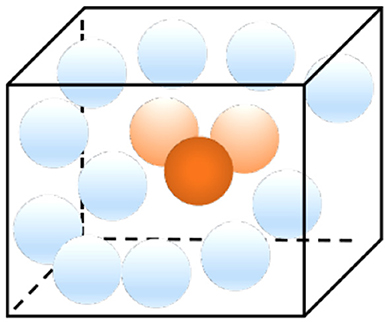
Place cells are a type of pyramidal neurons in the hippocampus that become active once an animal enters a specific location in its environment, called a place field. Place cells are assumed to form the basis of an internal representation of a particular position in space, known as a cognitive map (Burgess and O'Keefe, 1996). It is reported that the place cells in the hippocampus of the brain generate sequences that predict the future path when the animal explores the environment, which suggests that the hippocampus operates similarly to a GPS unit that shows not only where one currently is, but also how to reach the destination (Schmidt and Redish, 2013). 3D place cells in the mammalian hippocampal formation imply and support the existence of 3D cognitive maps. Figure 2 shows the firing representation of place cells to different regions (Soman et al., 2018). Place cells are filled throughout the spatial environment. The closer the cells are to the current position of the drone, the higher the firing rate of the place cells. In Figure 2, the red cell has the highest firing rate, while the lighter part has a lower firing rate. The cooperative firing of all place cells forms the basis of a spatial cognitive map.

FIGURE 2

Figure 2. The firing rate map of 3D place cells.

One promising approach to duplicate brain-inspired behavior is to mimic the underlying neural activity. Recent developments of large-scale neuromorphic hardware offering unprecedented asynchronous parallelism and energy efficiency such as the Intel Loihi, the IBM True North, and the SpiNNaker, have further advanced the development of SNN-based robotic controls (Xin et al., 2010; Lin et al., 2018; Löhr et al., 2020). However, despite the emerging interest in autonomous robot systems, research on SNN-controlled 3D drone navigation is still in its early exploratory stage. SNN-driven autonomous control systems for drones, capable of handling complex scenarios in a robust and natural way, are particularly needed. Spike-timing-dependent plasticity (STDP) occurs in synapses of hippocampal place cells. A classic STDP rule fits well with the synaptic information transfer mode. In this study, a SNN-based place cell model is applied to develop a biologically constrained brain- inspired navigation system. The connection weights between cells are trained with the help of STDP (Hao et al., 2020). On this basis we propose a neuromorphic navigation method for autonomous drones being capable to generate biologically plausible goal-directed behaviors.

A virtual drone platform is used to perform in simulation mode the required flight tests without damaging or harming a real drone, which allows improving training efficiency and saving training costs (Wang et al., 2017). Airsim is a widely popular virtual simulator due to its ability to interact with drones in simulation programs through languages such as Python, cross-platform flight control through flight controllers, and physically and visually realistic simulation environments.

3. Navigation with neural networks

To enable the drone to navigate to destinations that are not necessarily accessible by the shortest route from the current location, route planning is required. Here, a biologically plausible path planner is proposed for drones based on SNNs, where each neuron is modeled according the leaky integrate-and-fire model (LIF) and represents a place cell, as a basic unit of the discrete flying environment (Escamilla, 2006). The main processing steps are as follows: (1) A SNN is applied as a connected network of place cells which is producing a cognitive map and acts as a medium for a propagating wave that traverses the network with the successive activation of different neurons; (2) A control process supported by STDP, a temporally asymmetric learning rule induced by temporal correlations between the spikes of pre and post synaptic neurons, is introduced to change the synaptic connectivity within the network and to stabilize the place cell network; (3) A vector field converging on the target locations is generated by the updated synaptic connectivity weights, which enables the computation of a feasible path from the starting point to the target.

3.1. Neuron model

Each place cell is an excitatory neuron representing a part of the environment called the place cell field. The initial connections between neurons are modeled as synapses whose weights are inversely proportional to the distance between the current neuron and neighboring neurons. A probate method for modeling place cells is the Gaussian distribution, which can represent the firing of place cells but does not provide a basis for physiological message transmission. To better consider and rely on physiological phenomena, SNNs are introduced to model place cells in analogy to the physiology of cellular information transmission. SNNs are characterized by a spiking neuron model, and one widely used model is the LIF model (Rast et al., 2010; Zennir et al., 2015). Therefore, the LIF model is adapted to model the place cells. The membrane potential of place cells can be expressed as Ponulak and Hopfield (2013).

$\begin{array}{ll}{\tau }_m\frac{d{u}_m(t)}{dt}=-\left(u_m(t)-u_r\right)+R_m{I}_m& (1)\end{array}$

Where u_m(t) represents the membrane potential of the place cells; τ_m indicates the membrane time constant; u_ris the resting membrane potential; R_mdescribes the membrane resistance; I_mstands for the total synaptic current and can be written as,

$\begin{array}{ll}{I}_m=i_{sens}(t)+i_{syn}(t)+i_{ns}(t)-i_{inh}(t)-i_{Ca}(t)& (2)\end{array}$

Where i_sens(t) is the sensory input, i_syn(t) is a sum of the currents delivered by the individual excitatory synapses entering the given neuron, i_ns(t) is the non-specific background current modeled as a Gaussian process with mean zero and variance 5 nA, i_inh(t) is the global inhibitory current, i_Ca(t) represents a neuron- specific inhibitory current that could be activated by calcium-activated potassium channels in real neurons and can be calculated as,

$\begin{array}{ll}{\tau }_{Ca}\frac{d{i}_{Ca}(t)}{dt}=-i_{Ca}(t)& (3)\end{array}$

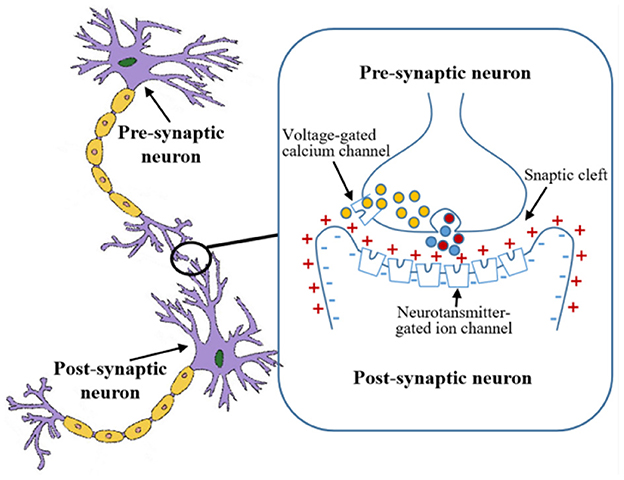
The ordinary differential equation describes a spiking neuron as a dynamic system in which the membrane potential is accumulated. When the membrane potential from the input signal reaches a certain threshold, the place cell emits a pulse, called a spike. The presence of spikes enables asynchronous communication between neurons. The LIF model of place cells is consistent with the biological neuronal synaptic information transmission mechanism. Namely, the pre-synaptic neuron releases neurotransmitters which open ion channels on the membrane of the post-synaptic neuron. The neuron model is shown in Figure 3.

FIGURE 3

Figure 3. Neuron model of place cells.

3.2. Neural plasticity-based weight update

Place cell model training plays a critical role for autonomous drone trajectory planning. STDP is a biological process related to SNNs that is thought to be responsible for learning and memorizing information in the brain (Izhikevich, 2007). This process provides a biologically plausible explanation for the activity-dependent development of nerves in terms of long-term potentiation and long-term depression, which is suitable for training the weights of the synaptic connections between place cell neurons. Suppose place cell x_i is connected to place cell x_j by a synapse running from x_i to, with weight w_ij. When x_i fires before x_j, STDP is assigned to increase the synaptic weight between the neurons, and when x_i fires after x_j, the synaptic weight between these two neurons decreases. The synaptic connections are changed according to the STDP model described by the following equation (Ponulak and Hopfield, 2013).

$\begin{array}{l}\frac{d{w}_{ji}(t)}{dt}=a+d\\ \left[S_i(t){\displaystyle \underset{0}{\overset{\infty }{\int }}}{a}_{ij}(s)S_i(t-s)ds+S_j(t-s){\displaystyle \underset{0}{\overset{\infty }{\int }}}{a}_{ji}(s)S_i(t-s)ds\right]& (4)\end{array}$

Where a < 0 denotes the activity-independent weight loss; S_i(t) and S_j(t) represent the presynaptic and postsynaptic spike trains, respectively. A spike train is defined as $S(t)={\sum }_f\delta (t^f-t)$, where t^f is the f-th firing time. The termsa_ij(s) and a_ji(s) are the integral kernels, where s is the delay between the presynaptic and postsynaptic firing times $s=t_i^f-t_j^f$.

The kernels a_ij(s) and a_ji(s) determine the shape of the STDP learning window and are defined as follows (Mahadevuni and Li, 2017).

$\begin{array}{ll}\{\begin{array}{l}{a}_{ji}(-s)=+A_{ji}·\exp (s/{\tau }_{ji})ifs\le 0\hfill \\ a_{ij}(-s)=+A_{ij}·\exp (-s/{\tau }_{ij})ifs>0\hfill \end{array}& (5)\end{array}$

Where A_ji, A_ij depict the amplitudes; τ_ji, τ_ij denote the time constants of the learning window and A_ji > A_ij > 0, τ_ji = τ_ij > 0. The STDP connection weights between place cells is shown in Figure 4.

FIGURE 4

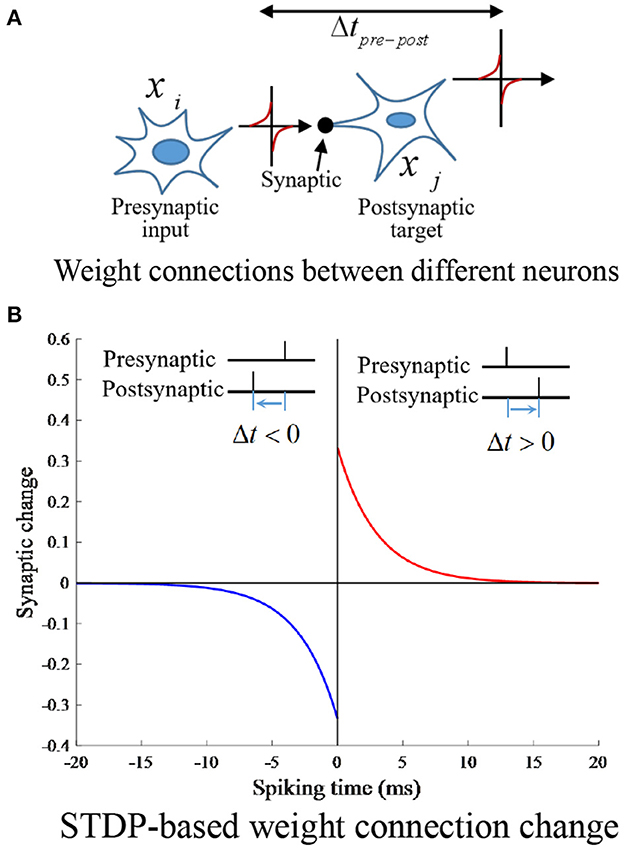
Figure 4. STDP connection weights between place cells. (A) Weight connections between different neurons. (B) STDP-based weight connection change.

3.3. Optimal path finding

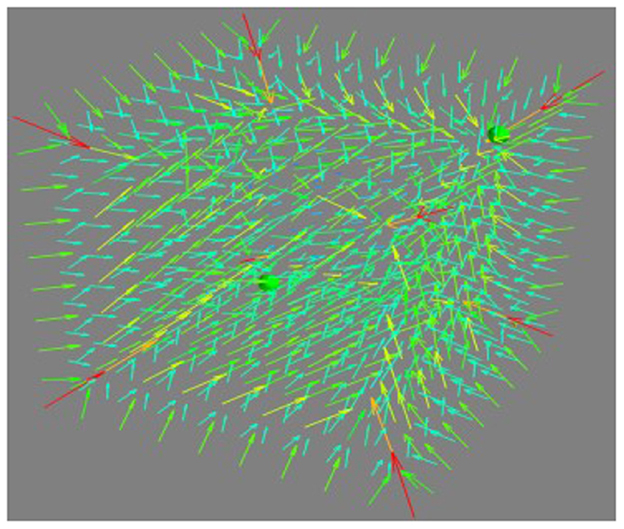
The SNN can be seen as an interconnected network of place cells that forms a cognitive map and is a medium for a propagating wave that traverses the network with the successive activation of different neurons. The propagating wave indirectly carries information about distance by generating a synaptic vector field. In the proposed model, obstacles and dangerous regions are considered as place cells that are inhibited by the prefrontal cortex. An inhibited neuron in the SNN cannot serve as a medium for the propagating wave. Consequently, all future paths will pass by the inhibited neurons (obstacles). For each place cell n_i in the network, we consider a set N_ji of all neurons n_j to which n_imakes direct synaptic projections. For the place cell n_i, the synaptic vector field r_i(t) is defined according to the connection weights of the place cell (Steffen et al., 2020).

$\begin{array}{ll}{r}_i(t)={\displaystyle \sum _j}{w}_{ji}(t)(x_j-x_i)/{\displaystyle \sum _j}{w}_{ji}(t)& (6)\end{array}$

Where x_i and x_j represent the current position of the drone and the center of the place cell field.

Suppose the vector r_i(t) starts at the current location x_i of place cell n_i and ends at a centroid of the center of the place cell field x_j of the neighboring place cells n_j∈N_ji, weighted by the corresponding connection weights w_ji(t). Then, the drone is driven by the synaptic vector field.

$\begin{array}{ll}{V}_{speed}(t+1)=V_{speed}(t)+{\left[V_{force}(t)+r_i(t)\right]}^{*}S& (7)\end{array}$

Where S is the smoothing factor in the range between zero and one. The synaptic vector field is shown in Figure 5.

FIGURE 5

Figure 5. The synaptic vector field.

At the same time, obstacles and dangerous locations are considered by place cells inhibited by the prefrontal cortex. An inhibited neuron in the SNN cannot transport the propagating wave. Consequently, all future paths will avoid the inhibited neurons. Finally, the current position of the drone can be updated as,

$\begin{array}{ll}P(t+1)=P(t)+V_{speed}(t+1)& (8)\end{array}$

Where P(t) and P(t+1) are the position of the drone at time t and time t+1, respectively; V_speed is the velocity vector. After training, the drone is able to find a feasible path to the target. The pseudocode for the brain-inspired path planning algorithm is shown in Algorithm 1.

ALGORITHM 1

Algorithm 1. Generating a feasible path.

4. Results

To investigate the effectiveness and the feasibility of the path planning method for drone operations, experiments have been conducted on simulation basis with a given environment supported by Airsim, which is based on a model of the flying engine.

4.1. Simulation experiments

In the first part of the experiments, the brain-inspired path planning algorithm is evaluated in simulation-only environments. The simulations were performed on a computer with a 1.60 GHz Core I5 processor and 16 GB RAM and implemented using the Python language and the Nengo package. The ranges of the environment along the axes OX, OY, and OZ are [0, 30], [0, 30], and [0, 30] m respectively. The start position and the target position are set to (0, 0, 0) and (26, 26, 26), respectively. Our goal is to enable the drone to find a short and collision-free path from the starting point to the target. The spiking neural network was trained using the STDP learning rule. The parameters for spiking neural network and STDP weight training were all determined empirically, as in Table 1. The parameters chosen are the same for all experiments.

TABLE 1

Table 1. Parameter setting.

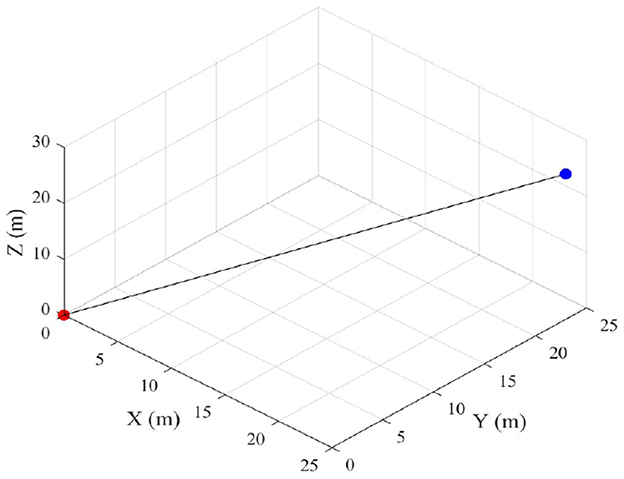
After training, a vector field is generated to guide the drone to the target. Finally, based on the proposed method, the most cost-effective path can be generated. Two types of environments were tested. First, a simple 3D environment without obstacles was considered. The simulation result is shown in Figure 6, in which a path is shown between the red starting point and the blue target position. The figure shows, that the drone is able to find a direct path between both points, using the proposed algorithm.

FIGURE 6

Figure 6. 3D path without obstacle.

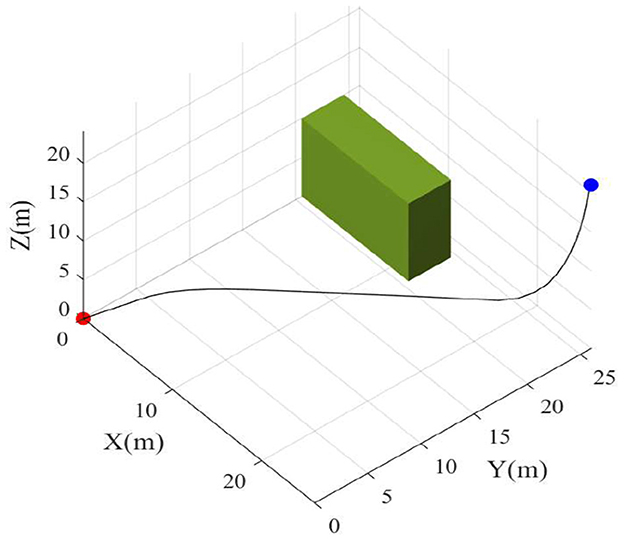
Second, an environment with an obstacle is utilized to verify the performance of the algorithm. As shown in Figure 7, the drone can avoid obstacles in its path and find a collision-free path.

FIGURE 7

Figure 7. 3D path with obstacle.

Both experiments in the Python simulation environment show that the proposed algorithm has good effect for intelligent path finding of drones. The execution time depends only on the length of the feasible path between the starting point and the target, not on the complexity of the environment.

4.2. Simulation in Airsim

To further verify the pathfinding capability of the proposed algorithm, the high-fidelity drone simulator Microsoft Airsim (https://microsoft.github.io/AirSim/; Shah et al., 2018) has been applied for this purpose. Microsoft Airsim acts as a plugin for the Unreal Engine, a 3D computer graphics game engine. The Unreal Engine can render photorealistic environments and provide features such as different flight conditions, realistic scenes, physical collision effects, etc. These features make the combination of Airsim and Unreal Engine a promising toolset for drones performing various flight tasks. Meanwhile, Visual Studio is applied to compile and launch Unreal Engine project files.

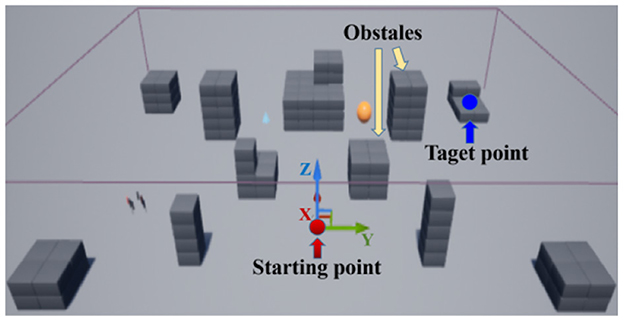
In Unreal Engine, there are many pre-built scenes in the application store that include blocks, landscapes, forests and so on. Airsim also provides users with rich interfaces that facilitate the control of the drone. In this research, the default environment “blocks” is utilized. The area of the map is 150^*230^*25 m. Since the Unreal Engine keeps track of all the objects displayed in the scene, it can easily retrieve the state of the drone and the pose of each object through APIs. The setting of the environment is shown in Figure 8. In the environment, the positions of the red dot and the blue dot are set as the starting point and the target point, respectively. The gray blocks of the considered as obstacles.

FIGURE 8

Figure 8. Flight environment settings in Airsim.

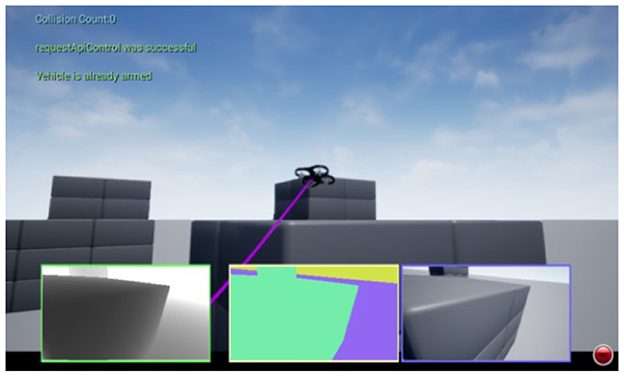
After setting the environment, the drone is trained using the method proposed in Section 3. Then a path can be generated. Figure 9 shows the realistic scenario of the flying drone with the help the Unreal Engine animation program. The three sub-windows in the lower part of Figure 9 present the depth image, segmentation view (Zhao et al., 2022), and RGB view (Xia et al., 2022) of the on-board camera during flight.

FIGURE 9

Figure 9. Real flight scene.

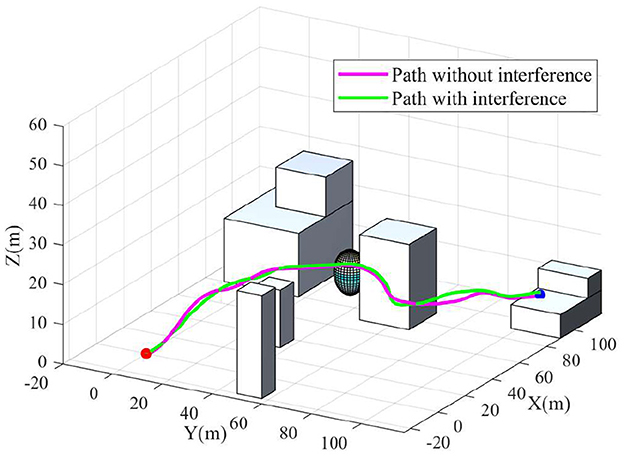
To get a better overview of the drone flight in Airsim, part of the environment and the flight path are extracted in a scaled sketch, as shown in Figure 10. In the figure, the red dot represents the starting position; the blue dot denotes the destination point; the purple line is the path generated by the proposed algorithm. The drone is capable to find a short path from the starting point to the target point without any collisions, which confirms the capability of the proposed algorithm. The STDP training process of the spiking neural network takes 2.59 min, and the whole path finding process takes 3.49 min. The simulation experiment with Airsim also shows that the algorithm has a great advantage in terms of path finding speed. In addition, the computationbal speed will be significantly improved if a GPU or neuromorphic hardware is to be applied. In order to further verify the robustness of the algorithme, wind speed interference is added in Airsim simulator. The green path in Figure 10 is the path generated when this interference is added. It can be seen that the drone can still find the target successfully after adding interference, and the path does not fluctuate sicnificantly, which underlines the robustness of the proposed method.

FIGURE 10

Figure 10. Scale map in Airsim and path comparison.

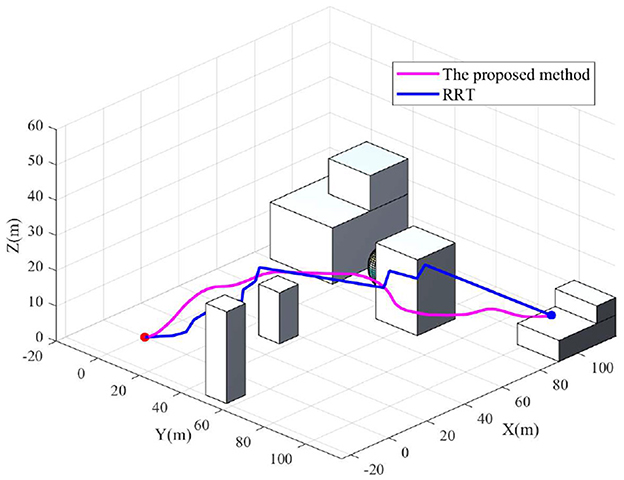
To further demonstrate the performance of the proposed method, comprehensive comparison with related algorithms is carried out. Among the most prominent path planning methods, RRT is one of the most promising and widely used methods. Therefore, the proposed method in this paper is compared with the RRT algorithm. The path comparison result is shown in Figure 11.

FIGURE 11

Figure 11. Path comparison between the proposed algorithm and RRT algorithm.

It can be seen from Figure 11 that the path generated by RRT does not conform to the optimal flight path of a drone. However, the path obtained by the proposed algorithm in this paper can generate a smooth path which is more suitable for the flight of a drone while ensuring the arrival of the target.

5. Discussion

A new approach for planning the trajectory of unmanned multicopter drones with obstacles based on SNN is described. The proposed method relies on the concept of propagating waves in a cognitive map to find a feasible and collision-free path. The computational complexity depends on the distance and resolution of the map. The unique feature of this method is that the considered neuron shows close analogy to the biological neurons. In our proposal, the wave is stabilized by exploiting the natural plasticity process of biological synapses, which regulates the synapse weight depending on the spiking time of the presynaptic and the postsynaptic neuron. The experimental results show that the proposed planning method can be used for routing a robust path of a drone flight in different environmental conditions.

Compared to related approaches, the described approach has the following proposing characteristics:

(1) A biologically plausible path planner that equips the drone with animal-like behavior, improving the decision-making intelligence of the drone.

(2) LIF is implemented to model the membrane potential of place cells to represent the spatial environment, which corresponds to the physiological mechanism of information transfer between neurons.

(3) A neuroplasticity based learning process, STDP, is applied to update the weights between neurons and select the optimal action that enables the synaptic vector field to steadily guide the drone to its target.

It is worth noting that the path generated by the proposed method is not the geometrically shortest path, but a smooth flight path that allows for the actual flight of the UAV while taking into account the shortest path.

In addition to relying on a physiological plausible basis, the proposed method has better robustness and allows higher computational speed compared with heuristic algorithms. And the designed algorithm in static and known environments does not need to equip a drone with model based sensors but with event cameras, which can greatly reduce the cost and speed up the path finding process.

However, the proposed algorithm also has some limitations. The drone starts flying only after the global path is generated. Therefore, the results are not real time but still robust, considering properties of the algorithm and the used processor. In addition, the main focus in this paper is to find collision-free paths for drones in static and known environment, without considering the perception and path planning in dynamic environment in some cases. Moreover, when the range of flight environment becomes larger, the computational cost increases exponentially and the path generation time becomes longer while keeping the resolution constant.

According to the above limitations, in future research, it is necessary to consider equipping Airsim with dynamic sensing sensors such as event cameras to capture the dynamic obstacles encountered in the flight environment and achieve dynamic obstacle avoidance in unknown environments. Moreover, the proposed algorithm needs to be combined with a dedicated brain-like chip to improve the computing performance through high- performance hardware and to be applied in practice.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported in part by the National Defense Basic Research Program under Grant JCKY2020605C009, in part by the Aeronautic Science Foundation of China under Grant ASFC-2020Z071052001, and supported by the China Scholarship Council under student Number 202106830082. Part of the work has been supported during a 1 year doctoral internship at FZI.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnbot.2023.1111861/full#supplementary-material

References

Aggarwal, S., and Kumar, N. (2020). Path planning techniques for unmanned aerial vehicles: a review, solutions, and challenges. Comput. Commun. 149, 270–299. doi: 10.1016/j.comcom.2019.10.014

CrossRef Full Text | Google Scholar

Burgess, N., and O'Keefe, J. (1996). Neuronal computations underlying the firing of place cells and their role in navigation. Hippocampus. 6, 749–762.

PubMed Abstract | Google Scholar

Cai, Y., Xi, Q., Xing, X., Gui, H., and Liu, Q. (2019). “Path planning for UAV tracking target based on improved A-star algorithm,” in 2019 1st International Conference on Industrial Artificial Intelligence (IAI) (Shenyang: IEEE), 1–6.

Google Scholar

Escamilla, J. E. A. (2006). A spiking neural network for self-organizing world representation. Honors Undergrad. Res. J. 18, 86.

Google Scholar

Hao, Y., Huang, X., Dong, M., and Xu, B. (2020). A biologically plausible supervised learning method for spiking neural networks using the symmetric STDP rule. Neural Net. 121, 387–395. doi: 10.1016/j.neunet.2019.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2007). Solving the distal reward problem through linkage of STDP and dopamine signaling. Cereb. Cortex. 17, 2443–2452. doi: 10.1093/cercor/bhl152

PubMed Abstract | CrossRef Full Text | Google Scholar

Konatowski, S., and Pawłowski, P. (2018). “Ant colony optimization algorithm for UAV path planning,” in 2018 14th International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET). IEEE. 177–182.

Google Scholar

Koul, S., and Horiuchi, T. K. (2019). Waypoint path planning with synaptic-dependent spike latency. IEEE Trans. Circ. Syst. 66, 1544–1557. doi: 10.1109/TCSI.2018.2882818

CrossRef Full Text | Google Scholar

Leutgeb, S., Leutgeb, J. K., Moser, M.-B., and Moser, E. I. (2005). Place cells, spatial maps and the population code for memory. Curr. Opin. Neurobiol. 15, 738–746. doi: 10.1016/j.conb.2005.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, C. K., Wild, A., Chinya, G., Davies, M., Srinivasa, N., and Lavery, D. (2018). Programming spiking neural networks on Intel's Loihi. Computer 51, 52–61. doi: 10.1109/MC.2018.157113521

CrossRef Full Text | Google Scholar

Löhr, M. P. R., Jarvers, C., and Neumann, H. (2020). “Complex neuron dynamics on the IBM TrueNorth neurosynaptic system,” in 2020 2nd IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS). IEEE, 113–117.

PubMed Abstract | Google Scholar

Mahadevuni, A., and Li, P. (2017). “Navigating mobile robots to target in near shortest time using reinforcement learning with spiking neural networks,” in 2017 International Joint Conference on Neural Networks (IJCNN). IEEE, 2243–2250.

Google Scholar

Mohammed, H., Romdhane, L., and Jaradat, M. A. (2021). RRT^* N: an efficient approach to path planning in 3D for static and dynamic environments. Adv. Robot. 35, 168–180. doi: 10.1080/01691864.2020.1850349

CrossRef Full Text | Google Scholar

Mohsan, S. A. H., Khan, M. A., Noor, F., Ullah, I., and Alsharif, M. H. (2022). Towards the unmanned aerial vehicles (UAVs): A comprehensive review. Drones 6, 147. doi: 10.3390/drones6060147

CrossRef Full Text | Google Scholar

Noreen, I., Khan, A., and Habib, Z. (2016). Optimal path planning using RRT^* based approaches: a survey and future directions. Int. J. Adv. Comput. Sci. Appl. 7, 97–107. doi: 10.14569/IJACSA.2016.071114

CrossRef Full Text | Google Scholar

Ponulak, F., and Hopfield, J. J. (2013). Rapid, parallel path planning by propagating wavefronts of spiking neural activity. Front. Comput. Neurosci. 7, 98. doi: 10.3389/fncom.2013.00098

PubMed Abstract | CrossRef Full Text | Google Scholar

Rast, A. D., Galluppi, F., Jin, X., and Furber, S. (2010). “The leaky integrate-and-fire neuron: a platform for synaptic model exploration on the SpiNNaker chip,” in The 2010 International Joint Conference on Neural Networks (IJCNN) (Barcelona: IEEE), 1–8. doi: 10.1109/IJCNN.2010.5596364

CrossRef Full Text | Google Scholar

Schmidt, B., and Redish, A. D. (2013). Navigation with a cognitive map. Nature. 497, 42–43. doi: 10.1038/nature12095

PubMed Abstract | CrossRef Full Text | Google Scholar

Shah, S., Dey, D., Lovett, C., and Kapoor, A. (2018). Airsim: High-fidelity visual and physical simulation for autonomous vehicles. Field Serv. Robotics 5, 621–635. doi: 10.1007/978-3-319-67361-5_40

CrossRef Full Text | Google Scholar

Soman, K., Chakravarthy, S., and Yartsev, M. M. (2018). A hierarchical anti-Hebbian network model for the formation of spatial cells in three-dimensional space. Nat. Commun. 9, 1–15. doi: 10.1038/s41467-018-06441-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Steffen, L., Silva, R., Ulbrich, S., Tieck, J., and Dillmann, R. (2020). “Networks of place cells for representing 3D environments and path planning,” in 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob) (IEEE), 1158–1165.

Google Scholar

Wang, S., Chen, J., Zhang, Z., Wang, G., Tan, Y., and Zheng, Y. (2017). “Construction of a virtual reality platform for UAV deep learning,” in 2017 Chinese Automation Congress (CAC). IEEE, 3912–3916. doi: 10.1109/CAC.2017.8243463

CrossRef Full Text | Google Scholar

Xia, L., Meng, D., Zhang, J., Zhang, D., and Hu, Z. (2022). Visual-inertial simultaneous localization and mapping: dynamically fused point-line feature extraction and engineered robotic applications. IEEE Trans. Instrum. Meas. 71, 1–11. doi: 10.1109/TIM.2022.3198724

CrossRef Full Text | Google Scholar

Xin, J., Lujan, M., Plana, L. A., Davies, S., Temple, S., and Furber, S. B. (2010). Modeling spiking neural networks on SpiNNaker. Comput. Sci. Eng. 12, 91–97. doi: 10.1109/MCSE.2010.112

CrossRef Full Text | Google Scholar

Yartsev, M. M., and Ulanovsky, N. (2013). Representation of three- dimensional space in the hippocampus of flying bats. Science 340, 367–372. doi: 10.1126/science.1235338

PubMed Abstract | CrossRef Full Text | Google Scholar

Zannone, S., Brzosko, Z., Paulsen, O., and Clopath, C. (2018). Acetylcholine -modulated plasticity in reward-driven navigation: a computational study. Sci. Rep. 8, 1–20. doi: 10.1038/s41598-018-27393-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Zennir, M. N., Benmohammed, M., and Boudjadja, R. (2015). Spike-time dependant plasticity in a spiking neural network for robot path planning. AIAI Workshops. 2–13.

Google Scholar

Zennir, M. N., Benmohammed, M., and Martinez, D. (2017). Robust path planning by propagating rhythmic spiking activity in a hippocampal network model. Biol. Inspired Cognit. Arch. 20, 47–58. doi: 10.1016/j.bica.2017.02.001

CrossRef Full Text | Google Scholar

Zhao, Y., Xiong, Z., Zhou, S., Peng, Z., Campoy, P., and Zhang, L. (2022). KSF-SLAM: a key segmentation frame based semantic SLAM in dynamic environments. J. Intell. Robot. Syst. 105, 1–13. doi: 10.1007/S10846-022-01613-4

CrossRef Full Text | Google Scholar