- 1School of Mechanical and Electrical Engineering, Guangzhou University, Guangzhou, China
- 2Department of Rehabilitation Medicine, Zhujiang Hospital, Southern Medical University, Guangzhou, China
Collaborative state recognition is a critical issue for physical human–robot collaboration (PHRC). This paper proposes a contact dynamics-based state recognition method to identify the human–robot collaborative grinding state. The main idea of the proposed approach is to distinguish between the human–robot contact and the robot–environment contact. To achieve this, dynamic models of both these contacts are first established to identify the difference in dynamics between the human–robot contact and the robot–environment contact. Considering the reaction speed required for human–robot collaborative state recognition, feature selections based on Spearman's correlation and random forest recursive feature elimination are conducted to reduce data redundancy and computational burden. Long short-term memory (LSTM) is then used to construct a collaborative state classifier. Experimental results illustrate that the proposed method can achieve a recognition accuracy of 97% in a period of 5 ms and 99% in a period of 40 ms.
Introduction
Human–robot collaboration has attracted the attention of researchers (Golz et al., 2015). Human–robot contact recognition is one of the critical issues for physical human–robot collaboration (PHRC) (Cherubini et al., 2016; Labrecque et al., 2017). Previous studies have mainly focused on the detection of a collision between humans and a robot (Billard and Kragic, 2019). Many types of observers have been proposed, including torque observer, energy observer, momentum observer, state observer based on electromyography (EMG) or touch, etc. (Haddadin et al., 2017; Losey et al., 2018). Different types of contact occur during human–robot collaboration (e.g., intentional interaction and accidental interaction), and early collision detection is not able to identify the different types of contact (Althoff et al., 2012). Intentional human interaction expects an active robot collaboration, while accidental collision calls for an immediate halt of the machine (Kang et al., 2019). In view of this, scholars attempt to identify the intention of physical human–robot interaction (PHRI) (Olivares-Alarcos et al., 2019). Many studies focused on identifying the occurrence, position, and direction of the interaction, without discussing the difference in dynamics between the human–robot interaction and the robot–environment contact. Without identifying the difference in dynamics between the human–robot contact and the robot–environment contact, it is difficult to precisely identify whether a robot is in contact with the environment or a human, especially when a robot is in contact with both the environment and a human in a similar direction.
This paper proposes a dynamics-based approach to identify the PHRC state. The main idea of the proposed approach is to analyze the dynamics of PHRC and find out an appropriate dynamic feature to classify the human–robot collaborative state. For this purpose, robotic grinding is selected as an example of PHRC and the corresponding dynamic model is established. The inputs of a classifier are generated in accordance with the dynamic model. A human–robot collaborative grinding state classifier is constructed based on long short-term memory (LSTM). To reduce data redundancy and increase reaction speed, feature selections based on Spearman's correlation and random forest recursive feature elimination are performed. The main contributions of this project are:
• Dynamic characteristics of the PHRC are used to generate features for PHRC grinding state recognition.
• Feature selections based on Spearman's correlation and random forest recursive feature elimination are performed to reduce data redundancy and increase reaction speed. LSTM is used to design a collaborative state classifier.
This paper is organized as follows. Section Related works presents related research. Section Human–robot collaborative grinding model presents models of PHRC grinding. Section Online collaborative state classifier presents an online human–robot collaborative grinding state classifier. Section Experimental validation illustrates experimental results. Section Conclusion presents conclusions to this paper.
Related works
Many approaches have been proposed to identify human intentions during human–robot collaboration, including vision-based classifiers, EMG-based classifiers, contact force-based classifiers, and multimodal fusion-based classifiers (Ajoudani et al., 2018). Some scholars attempted to design a state observer to detect the collision between a human and a robot (Zhou and Wachs, 2018; Zhang et al., 2021). These methods focused on identifying the occurrence and position of the human–robot contact. Cherubini et al. (2016) elucidated that the alternation of active and passive behaviors occurs frequently during human–robot collaboration, which requires a robot to actively collaborate with humans. The premise of active robot collaboration is the accurate and quick realization of human intentions (Villani et al., 2018; Veselic et al., 2021). In view of this, many scholars began to study the intention of a human–robot interaction (Veselic et al., 2021). Lanini et al. (2018) used the arm position and interaction force data during human–human collaboration to develop a multiclass classifier, enabling a robot to recognize human intentions during the collaborative task of carrying an object. Golz et al. (2015) acquired a set of human–robot contact features by analyzing the physical contact model and the real impact process. Using these data, an SVM-based classification system was constructed to identify intended and unintended human–robot contact. However, their contact model ignores damping, stiffness, and kinetic energy. Therefore, their classifier is only suitable for static or low-speed robotic tasks. Considering the difficulties in obtaining an accurate human–robot interaction model, Li and Ge (2014) used a neural network to construct an online intention estimation approach to estimate human motion intentions. Relying on human force and pose measurements, Cremer et al. (2020) proposed a neural network-based estimation method to predict human motion intentions. Yan et al. (2019) proposed an intentional classification model based on the radial basis function neural network, which can deduce human intentions, according to the dynamic behaviors of humans and robots within previous collaboration tasks.
Apart from the human–robot interaction, the robot–environment contact may occur during PHRC. It is difficult to recognize the human–robot contact when a robot is performing a contacting task. To address this, Lippi and Marino (2020) constructed a filter based on the robot–environment contact model to filter out the robot–environment contact force and to detect additional forces, e.g., human–robot contact force. The advantage of their method is that even if the robot is in contact with both the environment and humans in a similar direction, the human–robot contact can be recognized. However, this approach requires that the robot–environment contact force should be known in advance and the force fluctuation should be limited. Designing a human–robot collaboration dynamics-based classifier may be a viable way to obtain a universal human–robot collaborative state classifier.
Human collaborators always change their limb impedance or stiffness during human–robot collaboration. Upon this knowledge, Yu et al. (2020) used the least squares method to learn the impedance of the human body. Their study only focused on the adjustment of robot impedance control parameters to achieve collaboration compliance without discussing the value of human body dynamics for PHRI state recognition. Geravand et al. (2013) considered that an unexpected collision between a human and a machine can be defined as a hard contact between rigid bodies, while the human–robot contact can be defined as a soft contact. According to their analysis, a hard contact results in a high-frequency signal and a soft contact results in a low frequency signal. Based on this, Geravand designed a high-low pass filter to identify human–robot contact intention. Furthermore, Losey et al. (2018) clarified that human intentions during the human–robot contact are continuous and time-varying, which result in a non-linear contact force.
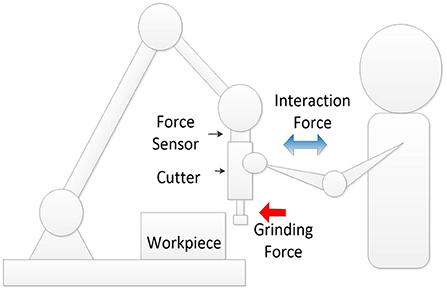
Up to now, only a few studies have focused on distinguishing between the human–robot and the robot–environment contact. The main issue is the impact of the fluctuation of contact force between the robot and the environment on the recognition of the human–robot contact. To address this problem, this paper proposed a dynamics-based approach for distinguishing the human–robot contact and the robot–environment contact. Experimental set-up is illustrated in Figure 1. The human–robot contact and the robot–environment contact occur at the same time in the similar direction.
Human–robot collaborative grinding model
Robot grinding dynamic model
Robot grinding dynamic model can be expressed as,
where Fc is the grinding force; M, C, and K are the system mass, damping and stiffness matrices; are the grinding depth and its first and second derivatives; u is motor voltage; is the contact force caused by motor voltage and grinding depth; Fr is external disturbance force; and Fris robotic grinding force, which can be expressed as (Chen et al., 2019).
where Fd is the deformation force caused by compression between a grinding tool and a workpiece; Fg is cutting force, which is affected by the grinding depth, feed rate, and rotation speed of a grinding tool. As frequent contacts between a grinding tool and a workpiece occur during robotic grinding, it is not efficient to construct a robot–environment contact model based on the additional contact constraint method. Therefore, the continuous contact force model based on the Hertz contact theory is used in this paper, which can be expressed as (Zhang et al., 2020).
where σ is normal embedding depth; α is exponential coefficient of deformation; and Ke is equivalent stiffness. Assuming that the main deformation is on a grinding tool. The grinding tool deformation has a relationship with the removal rate and feed rate, which can be expressed as,
where Ẋ is the feed rate and Ẋr is the removal rate. The cutting force produced by the revolution of a grinding tool can be regarded as a periodic force:
where is the cutting period of a blade, is the rotation period of a grinding tool, and vw is the rotation speed of a grinding tool. According to the traditional grinding force formula, grinding force is influenced by cutting depth, feed speed, tool rotation speed, and grinding area, which can be expressed as,
Combining Equations (1)–(6), the robotic grinding model can be expressed as,
A dynamic model of human–robot collaborative grinding
Human collaborators always adjust their muscles and change the stiffness or impedance of their body to control contact force, achieving a compliance collaboration. The human–robot collaborative grinding model can be expressed as,
where Fh is an external force exerted by humans. Considering the human arm as a spring-damping system and Fh can be calculated by,
where xd is the desired location expected by a human collaborator, Dh and Kh are the damper and stiffness matrices of the human arm and may vary or fluctuate during human–robot collaboration. Assuming that Dh and Kh non-linearly and continuously fluctuate within a bounded range, the fluctuation of Fh is also non-linear, continuous, and bounded. Therefore, ΔFh, ΔḞh, and are used to identify the human–robot interaction state.
where represents the force slope caused by ΔDhΔKh, which is non-linear and continuous and represents the mean value range of slope fluctuation.
Problem description
According to Equation (10) and the human–robot collaborative grinding process, five states can be defined, namely, tool idle state, cutting-in state, deformation release state, stable cutting state, and human–robot collaborative cutting state. These states are shown in Figures 2A,B.
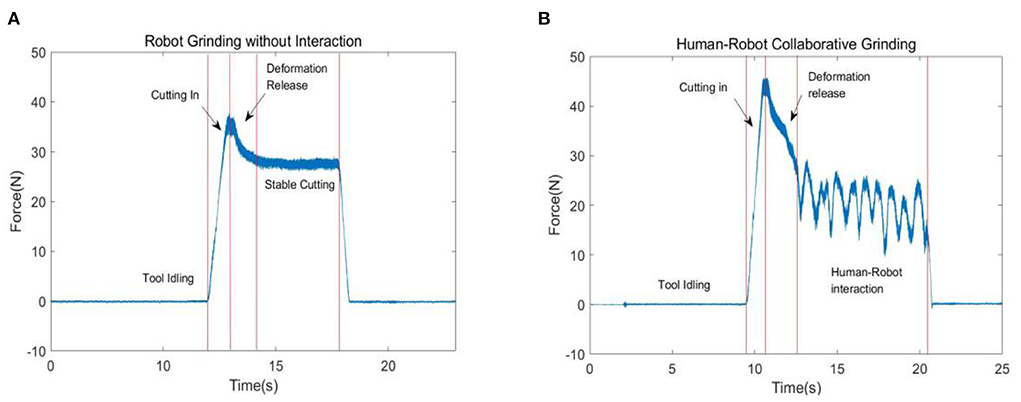
Figure 2. Collaborative state labeling. (A) Robotic grinding states and (B) human–robot collaborative grinding states.
To precisely identify the human–robot collaborative state, it is essential to analyze the characteristics of each state. The first step is to clearly describe the signal characteristics of each collaborative grinding state. According to the discussion above, the definition of a feature of each state is presented in Table 1.
According to the features of each state as presented in Table 1, the characteristics can be concluded.
After concluding the characteristics of each state, the next step is to construct a framework for collaborative state classification.
Online collaborative state classifier
Compared with offline classification, an online classifier is required to achieve quick and accurate classification with the least data and computation. More precisely, a collaborative robot requires a reaction at the millisecond level. Therefore, the issues need to be considered are classification accuracy, reacting speed, and data amount.
Overall process and feature acquisition
In this section, an overall structure of the human–robot collaborative grinding state classification is introduced. To develop this scheme, two kinds of grinding data are collected by the force sensor installed between the robot end effector and a grinding tool, including robotic grinding data and human–robotic collaborative grinding data.
Classification scheme
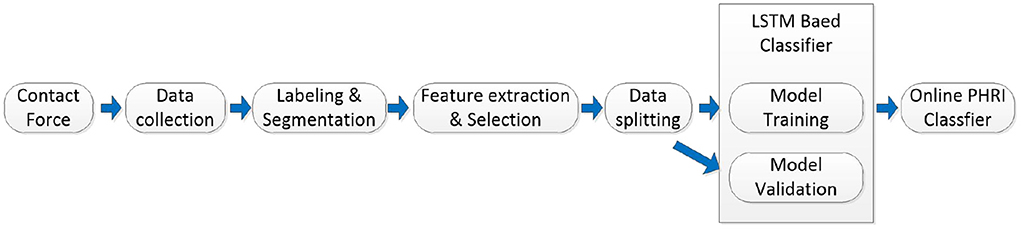
An overall structure of the proposed online human–robot collaborative grinding scheme is shown in Figure 3. Robotic grinding force and human–robot contacting force data are first collected, labeled, and divided into segments. The force data segments are then used to extract the features of different collaborative states. Feature selections are conducted after feature extraction to reduce data redundancy and increase reaction speed. The selected features are then put into an LSTM-based classifier to train the classifier model. Model parameters are later used to construct an online classifier of the PHRC grinding state.
Data collection
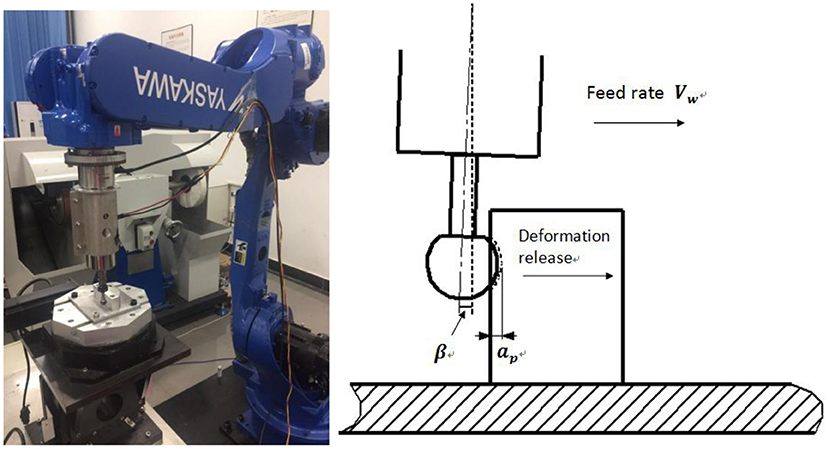
To construct a human–robot collaborative grinding data set, a six-degrees-of-freedom Yaskawa robot grinding system, as shown in Figure 4, is constructed. A six-degree force sensor is mounted between a grinding tool and the robot end effector to collect contact force data during human–robot collaborative grinding. The rotation speed of a grinding tool is 2,000 rpm. During robotic grinding, an experimenter exerts intentional contact on the clamping position of a grinding tool. Different PHRC states are conducted to obtain the data set.
Signal segmentation and sample labeling
After collecting human–robot collaborative grinding force signals, segmentation is performed to split force signals into segments with a fixed length l. The segment should be long enough to contain sufficient information to classify states and short enough to achieve a fast reaction. Therefore, the demand for reaction accuracy and speed influences the determination of l. The classification of experiments with different values of l is to explore the impact of l value on classification accuracy and speed. According to grinding tool rotation speed and the characteristics presented in Table 2, 11 values of l are set, which are 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 ms. In the segmentation process, invalid data caused due to the damage in the storage or an unrecognizable PHRI signal are eliminated. To avoid the deviation in results caused by uneven data distribution, the data were homogenized. Finally, 14,300 data are obtained and used for collaborative state classification experiments.
Feature extraction
Time-series signal features can be classified into time domain and frequency domain features. Time domain features include mean, variance, average amplitude, energy source, root mean square, root square amplitude, standard deviation (SD), peak coefficient, shape coefficient, skewness, pulse factor, margin factor, kurtosis, etc. Peak coefficient, shape coefficient, skewness, impulse factor, margin factor, and kurtosis are dimensionless time domain characteristics. Common frequency domain features include barycentric frequency, mean square frequency, root mean square frequency, frequency variance, frequency SD, etc. Considering the computing time required by frequency domain feature generation, only 12 time domain features are preselected for human–robot collaborative state classification, which are mean value, variance, average amplitude, energy source, root mean square, root amplitude, SD, shape parameter, skewness, pulse factor, margin factor, and kurtosis. Apart from these features, the contact force slope, slope fluctuation range, and force slope change speed are also considered.
Feature selection
To reduce feature redundancy and select the critical features for state classification, Spearman's correlation and recursive feature elimination based on random forest (RF-RFE) are used to evaluate the preselected features.
Spearman's correlation analysis can identify the dependency between any two features. It is not only suitable for linear correlation cases but also suitable for non-linear cases. Suppose there are two sums of eigenvalues:
where m is the data set size. Spearman's correlation coefficient can be calculated by,
where represents the mean value. ρX,Y is the coefficient describing the dependency of X on Y.
Random forest-based recursive feature elimination
Recursive feature elimination based on random forest is used to calculate the importance of features and selected features. The RF-RFE algorithm flow is shown in Figure 5 (Shang et al., 2021). Firstly, random forest model is established, and feature samples are randomly extracted based on the Bootstrap sampling technique. The impact of feature samples on classification accuracy is then evaluated to identify the importance of the selected feature to state classification. The least important features are removed, and the evaluation is reconducted by random forest with the remaining features. After that, the abovementioned steps are reconducted until the ranking of state features is obtained.
Deep learning-based classifier
LSTM-based classifier
The structure of an LSTM classifier used in this paper is shown in Figure 6 and is composed of one LSTM layer and two sense layers. The LSTM classifier is used to study the relationship between inputs and collaborative states. Therefore, the inputs of an LSTM classifier are the selected features mentioned above, and the output is a label of collaborative states.
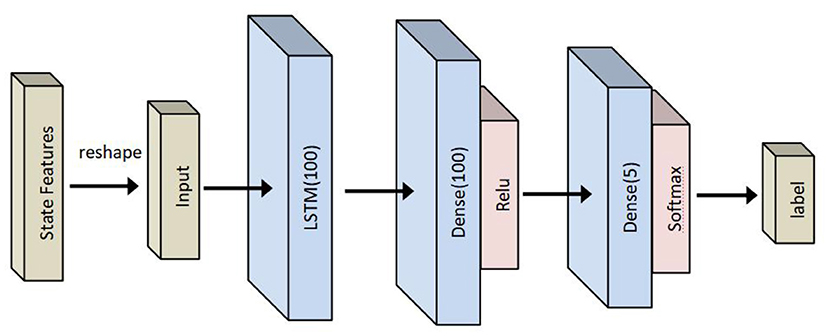
Figure 6. Long short-term memory- (LSTM-) based human–robot collaborative grinding state classifier.
LSTM fully convolutional network based classifier
For a comparison, long short-term memory FCN-based classifier is also evaluated. The performance of LSTM-FCN has been verified on public time series data sets (Karim et al., 2018). Its structure is shown in Figure 7, which is formed by paralleling LSTM and time convolution models. The selected features are first input to LSTM and CNN models. The LSTM model consists of a dimension transformation layer, an attention layer, a single-layer LSTM, and a dropout layer, while the CNN model consists of three time convolution networks with a filter size of 128, 256, and 128, respectively. Each convolution layer is normalized and followed by the Relu activation function. Finally, global pooling is carried out after the final convolution block.
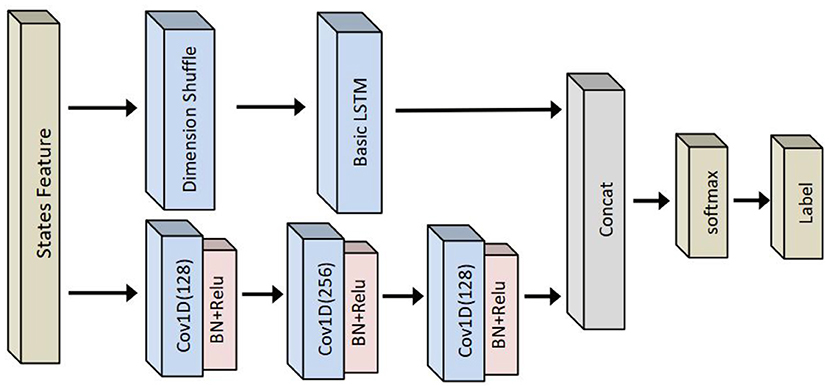
Figure 7. LSTM fully convolutional network (FCN-) based human–robot collaborative grinding state classifier.
Experimental validation
To verify the validity of the proposed approach, experiments of collaborative state classification are conducted. The first step is to extract 15 kinds of features. All the samples are randomly shuffled and split into a training set and a test set with the partition ratio 3:1. For classifier training, cross entropy is selected as loss function when the number of iterations is 2,000. The learning rate is set to 1e-2, and the reduction speed is 1e-4. To facilitate discussion, three groups of features are defined:
• Group 1 has domain features only, including contact force mean, variance, average amplitude, energy source, root mean square, root square amplitude, SD, peak coefficient, shape coefficient, skewness, pulse factor, margin factor, and kurtosis.
• Group 2 consists of the features in Group 1 and contact dynamic features ΔFh, ΔḞh, and .
• Group 3 consists of the features selected from Group 2.
Collaborative state classification based on time domain features
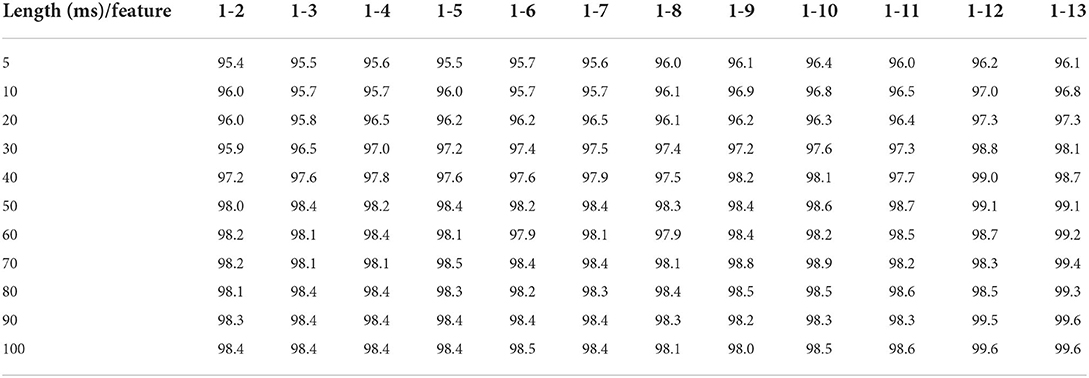
Time domain features included in Group 1 are used as inputs to classify the human–robot collaborative grinding state without considering the human–robot contact dynamics. The impact of segment length l and feature numbers on the performance of collaborative state recognition is explored. For a convenient discussion, time domain features are labeled with numbers 1–13 corresponding to contact force mean, variance, average amplitude, energy source, root mean square, root square amplitude, SD, peak coefficient, shape coefficient, skewness, pulse factor, margin factor, and kurtosis in the time domain features. Experimental results are presented in Table 3. The vertical axis of a table is segment length, while the horizontal axis is the time domain feature number.
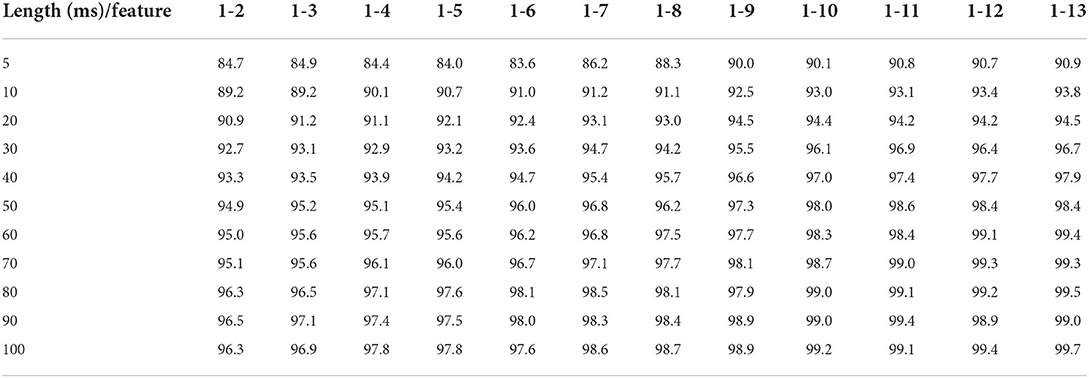
Table 3. Long short-term memory- (LSTM-) based physical human–robot collaboration (PHRC) state recognition (Group 1 features; %).
It can be observed from Table 3 that, while the segment length is 5 ms, the recognition accuracy of the collaborative state increases roughly as the number of features increases, from 84.7% at 1–2 to 90.9% at 1–13. It should be noticed that obvious improvements in accuracy occur at 1–7 and 1–9. Starting with 1–9, although the number of features increases, the accuracy does not change significantly, which means that features 9–13 may have a little impact on recognition accuracy. In other words, some features can be eliminated to reduce feature redundancy and computing burden. In general, recognition accuracy increases as the segment length and the feature number increase, and the earliest 99% occur at 60 ms and features 1–12.
Collaborative state classification based on time domain features and contact dynamics
Features contained in Group 2 are then used as classifier inputs for collaborative state recognition. It can be seen that the highest recognition accuracy at the 5-ms stage is 96.4%, which is 5% higher than the one presented in Table 4. The highest recognition accuracy is 99.6% appearing at 100 ms and features 1–13, which is almost the same as the one presented in Table 4. However, the earliest 99% appear at 40 ms and 1–12 features, which is 20 ms earlier than the one presented in Table 4. The contact dynamics features can increase the recognition accuracy of classifier in the early stage. In other words, contact dynamics-based classifier can achieve a quick and precise classification of the human–robot collaborative grinding state with little computational burden.
Collaborative state classification based on feature selection
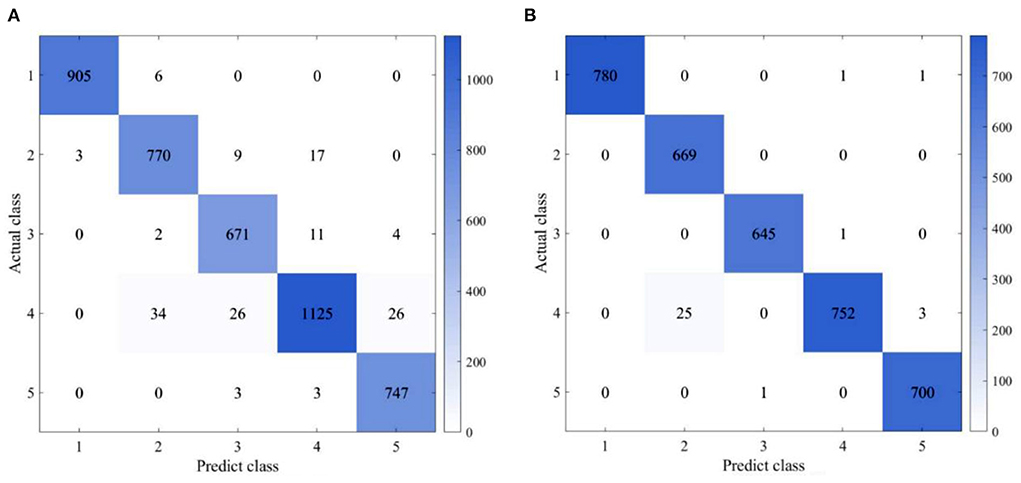
To further reduce computational burden, feature selections are then conducted based on the Spearman's correlation analysis and recursive feature elimination method. According to the Spearman's correlation analysis, the correlation coefficient between average amplitude and root square amplitude, root mean square, energy source, and peak coefficient is more than 0.9. Therefore, the root square amplitude, root mean square, energy source, and peak coefficient are represented by the average amplitude. The recursive feature elimination method based on random forest is also conducted. The remaining features include mean, variance, average amplitude, SD, and human–robot contact dynamics. Therefore, the selected features are mean value, variance, average amplitude, SD, and human–robot contact dynamic features ΔFh, ΔḞh, and . As presented in Table 5, although some features are removed, an LSTM-based state classifier can achieve a recognition accuracy of 97.0% in 5 ms and 99.4% in 100 ms. Compared with the ones presented in Table 5, there is no considerable decrease in recognition accuracy, which illustrates that feature selections can reduce computational burden while ensuring recognition accuracy. The confusion matrix, as shown in Figure 8, indicates that misclassifications occur in the distinction of cutting-in and human–robot contact states.
LSTM-FCN-based state recognition is also carried out to evaluate the performance of LSTM-based recognition. Compared with an LSTM-based classifier, the recognition accuracy obtained by an LSTM-FCN-based classifier is 2% lower on average from 5 to 60 ms. However, the structure of an LSTM-based classifier is simpler than one of the LSTM-FCN-based classifiers, which can be observed from Figures 6, 7. In other words, the number of parameters is less in an LSTM-based classifier than in LSTM-FCN-based classifiers. Therefore, while performing online recognition, an LSTM-based classifier can achieve lower computing time and cost compared with an LSTM-FCN-based classifier. Finally, LSTM-based state recognition experiments without feature extraction are conducted. As presented in Table 5, the highest recognition accuracy of the LSTM-based state without feature extraction is only 85%, which is 14% lower than one of the proposed approaches.
Conclusion
In this paper, a contact dynamics-based collaborative state recognition approach for human–robot collaborative grinding is proposed. Human–robot and robot–environment contact dynamics are analyzed. The result is used to extract human–robot collaborative grinding state features. Considering the computational burden and reaction speed required for online collaborative state recognition, feature selections based on the Spearman's correlation analysis and the recursive feature elimination method are performed. LSTM is finally used to construct a collaborative state classifier. Experimental results illustrate that the proposed approach can achieve a classification accuracy of 96.7% in 5 ms and 99.4% in 100 ms. The limitation of this paper is that the environment and a workpiece are assumed to be rigid. While a workpiece is flexible or soft, contact dynamics will be different and difficult to describe.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grants 51905115, 12172095, and 51775122.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ajoudani, A., Zanchettin, A. M., Ivaldi, S., Albu-Schaffer, A., Kosuge, K., and Khatib, O. (2018). Progress and prospects of the human-robot collaboration. Auton. Robots. 42, 957–975. doi: 10.1007/s10514-017-9677-2
Althoff, D., Kuffner, J., Wollherr, D., et al. (2012). Safety assessment of robot trajectories for navigation in uncertain and dynamic environments. Auton. Robots 32, 285–302. doi: 10.1007/s10514-011-9257-9
Billard, A., and Kragic, D. (2019). Trends and challenges in robot manipulation. Science. 364, 1–8. doi: 10.1126/science.aat8414
Chen, S. Y., Zhang, T., Zou, Y. B., and Xiao, M. (2019). Model predictive control of robotic grinding based on deep belief network. Complexity. 4, 1–16 doi: 10.1155/2019/1891365
Cherubini, A., Passama, R., Crosnier, A., Lasnier, A, and Fraisse, P. (2016). Collaborative manufacturing with physical human-robot interaction. Robot. Comput. Integr. Manuf. 40, 1–13. doi: 10.1016/j.rcim.2015.12.007
Cremer, S., Das, K., Wijayasinghe, I. B., Popa, D. O., and annd Lewis, F. L. (2020). Model-free online neuroadaptive controller with intent estimation for physical human-robot interaction. IEEE Trans. Robot. 36, 240–253. doi: 10.1109/TRO.2019.2946721
Geravand, M., Flacco, F., and Lucaet, A. D. (2013). “Human-robot physical interaction and collaboration using an industrial robot with a closed control architecture,” in IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe (Germany).
Golz, S., Osendorfer, C., and Haddadin, S. (2015). “Using tactile sensation for learning contact knowledge: discriminate collision from physical interaction,” in IEEE International Conference on Robotics and Automation (ICRA) (Seattle, WA).
Haddadin, S., Luca, A. D., and Albu-Schäffer, A. (2017). Robot collisions: a survey on detection, isolation, and identification. IEEE Trans. Robot. 33, 1292–1312. doi: 10.1109/TRO.2017.2723903
Kang, G., Oh, H. S., Seo, J. K., Kim, U., and Choi, H. R. (2019). Variable admittance control of robot manipulators based on human intention. IEEE-Asme Trans. Mechatron. 24, 1023–1032. doi: 10.1109/TMECH.2019.2910237
Karim, F., Majumdar, S., Darabi, H., and Chen, S. (2018). LSTM fully convolutional networks for time series classification. IEEE Access 6, 1662–1669. doi: 10.1109/ACCESS.2017.2779939
Labrecque, P. D., Haché, J. M, Abdallah, M., and Gosselin, C. (2017). Low-impedance physical human-robot interaction using an active–passive dynamics decoupling. IEEE Robot. Autom. Lett. 1, 938. doi: 10.1109/LRA.2016.2531124
Lanini, J., Hamed, R., Julen, U., and Auke, I. (2018). Human intention detection as a multiclass classification problem: application in physical human-robot interaction while walking. IEEE Robot. Autom. Lett. 3, 4171–4178. doi: 10.1109/LRA.2018.2864351
Li, Y. N., and Ge, S. S. (2014). Human-robot collaboration based on motion intention estimation. IEEE-Asme Trans. Mechatron. 19, 1007–1014. doi: 10.1109/TMECH.2013.2264533
Lippi, M., and Marino, A. (2020). “Enabling physical human-robot collaboration through contact classification and reaction,” in 29th IEEE International Conference on Robot and Human Interactive Communication (IEEE RO-MAN), Electr Network.
Losey, D., Craig, M., Edoardo, B., et al. (2018). A review of intent detection, arbitration, and communication aspects of shared control for physical human-robot interaction. Appl. Mech. Rev. 70, 1–19 doi: 10.1115/1.4039145
Olivares-Alarcos, A., Foix, S., and Alenyà, G. (2019). On inferring intentions in shared tasks for industrial collaborative robots. Electronics 8, 1306. doi: 10.3390/electronics8111306
Shang, Q., Feng, L., and Gao, S. (2021). A hybrid method for traffic incident detection using random forest-recursive feature elimination and long short-term memory network with bayesian optimization algorithm. IEEE Access 9, 140538–140559. doi: 10.1109/ACCESS.2021.3119085
Veselic, S., Zito, C., and Farina, D. (2021). Human-robot interaction with robust prediction of movement intention surpasses manual control. Front. Neurorobot. 15, 1–13. doi: 10.3389/fnbot.2021.695022
Villani, V., Pini, F., Leali, F., and Secchi, C. (2018). Survey on human-robot collaboration in industrial settings: safety, intuitive interfaces and applications. Mechatronics 55, 248–266. doi: 10.1016/j.mechatronics.2018.02.009
Yan, H., Ming, H., Yang, R. X., and Li, T. J. (2019). Research on intention recognition method based on radial basis function neural network. Inform. Technol. Control 48, 637–647. doi: 10.5755/j01.itc.48.4.23031
Yu, X. B., Li, Y. N., Zhang, S., Xue, C. Q., Wang, Y., et al. (2020). Estimation of human impedance and motion intention for constrained human-robot interaction. Neurocomputing 390, 268–279. doi: 10.1016/j.neucom.2019.07.104
Zhang, J., Li, W. H., Zhao, L., and He, G. P. (2020). A continuous contact force model for impact analysis in multibody dynamics. Mech. Mach. Theory 153, 103946. doi: 10.1016/j.mechmachtheory.2020.103946
Zhang, Z. J., Qian, K., Schuller, B. W., and Wollherr, D. (2021). An online robot collision detection and identification scheme by supervised learning and bayesian decision theory. IEEE Trans. Autom. Sci. Eng. 18, 1144–1156. doi: 10.1109/TASE.2020.2997094
Keywords: contact dynamics, online classification, collaborative grinding, physical human–robot collaboration, human intent classification
Citation: Chen S, Sun X, Zhao Z, Xiao M and Zou T (2022) An online human–robot collaborative grinding state recognition approach based on contact dynamics and LSTM. Front. Neurorobot. 16:971205. doi: 10.3389/fnbot.2022.971205
Received: 16 June 2022; Accepted: 06 July 2022;
Published: 02 September 2022.
Edited by:
Rui Huang, University of Electronic Science and Technology of China, ChinaReviewed by:
Yi Liu, Dalian Maritime University, ChinaHongjun Yang, Institute of Automation (CAS), China
Copyright © 2022 Chen, Sun, Zhao, Xiao and Zou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhijia Zhao, emhhb3pqQGd6aHUuZWR1LmNu; Meng Xiao, Y29keTEwQDE2My5jb20=
 Shouyan Chen
Shouyan Chen Xinqi Sun1
Xinqi Sun1