- 1School of Mechanical and Electrical Engineering, Guangzhou University, Guangzhou, China
- 2School of Computer and Information, Qiannan Normal University for Nationalities, Guizhou, China
In this paper, a prescribed performance adaptive event-triggered consensus control method is developed for a class of multiagent systems with the consideration of input dead zone and saturation. In practical engineering applications, systems are inevitably suffered from input saturation. In addition, input dead zone is widely existing. As the larger signal is limited and the smaller signal is difficult to effectively operate, system efficacious input encounters unknown magnitude limitations, which seriously impact system control performance and even lead to system instability. Furthermore, when constrained multiagent systems are required to converge quickly, the followers would achieve it with drastic and quick variation of states, which may violate the constraints and even cause security problems. To address those problems, an adaptive event-triggered consensus control is proposed. By constructing the transform function and the barrier Lyapunov function, while state constrained is guaranteed, multiagent systems quickly converge with prescribed performance. Finally, some examples are adopted to confirm the effectiveness of the proposed control method.
1. Introduction
With the rapid development of science and technology, multiagent systems are widely used in many fields, such as multirobot cooperation (Huang et al., 2018; Dai et al., 2021; Zhai et al., 2021), unmanned surface vehicles (Zhou et al., 2020; Gu et al., 2021; Huang et al., 2021), unmanned aerial vehicles (Gong et al., 2021; Tran et al., 2021; Zhou and Chen, 2021), and other fields. The multiagent system cooperative control mainly includes consensus, formation, and swarm, and the problem of consensus control, as the foundation of multiagent systems cooperative control, has received much attention from scholars (Cai et al., 2021; Ning et al., 2021; Su H. et al., 2021; Wang C. et al., 2021; Wei and Xiao, 2021). Cai et al. (2021) discussed the consensus problem of linear multiagent systems by constructing an adaptive coupling protocol. For second-order multiagent systems, a consensus algorithm was proposed based on sampled-data strategy by Su H. et al. (2021). Combined with the designed Nussbaum functions, the consensus problem of high-order nonlinear multiagent systems with unknown control directions was solved by an adaptive consensus tracking control scheme (Wang C. et al., 2021). It is noted that, while achieving systems consensus, taking the feature of convergence time into consideration is necessary.
Then, finite-time control was established. With faster convergence speed and robustness, it has received widespread attention (Li et al., 2020, 2021; Lu et al., 2021; Wang et al., 2022b). By finite-time control, it can be guaranteed that the systems converge within finite time. To achieve system convergence within predefined time for any initial states, the prescribed time control was extendedly proposed (Ren et al., 2020; Guo et al., 2021; Wang et al., 2021a; Chen et al., 2022; Gong et al., 2022). Focusing on first-order multiagent systems with single-integrator dynamics, a new control law with a scaling function was proposed (Chen et al., 2022). For the cluster lag consensus problem of multiagent systems, a distributed controller with time-varying gains was constructed by Ren et al. (2020). All of them achieved the aim that systems converge to preset states within predefined time, and the convergence time is independent of initial states. In addition, not only system convergence time but also transient performance and steady-state performance are important in practical engineering systems. It is a meaningful problem that how to develop a method to achieve multiagent system convergence with prescribed performance, especially while the system convergence time is settable.
Furthermore, many scholars have carried out a lot of research on nonlinear problems, such as input delay (Sun et al., 2022a), input hysteresis (Wang et al., 2021b), and time-varying mass (Sun et al., 2021). As the restriction of controller elements, input saturation is widely existing in systems. In prescribed time control, a large amount of energy is used to guarantee that the systems converge within a prescribed time. Especially when a short convergence time is prescribed, the input saturation problem becomes particularly acute. Therefore, input saturation is worth concerning when constructing a controller, many results were presented (Bai et al., 2020; Song et al., 2020; Cao et al., 2021; Min et al., 2021; Yang C. et al., 2021). Cao et al. (2021) used a smooth function and the mean-value theorem to approximate and transform the input saturation. Bai et al. (2020) constructed auxiliary systems to compensate for the influence of input saturation. On the contrary, due to the insensitivity of components to some small signals, input dead zone inevitably exists in systems. To reduce the impact of dead zone, some compensation methods were developed (Zhou et al., 2019; Ding et al., 2021; Lan et al., 2021; Jiang and Gao, 2022). For large-scale semi-Markovian jump interconnected systems with input dead zone, a local adaptive sliding mode control law was designed by Ding et al. (2021). For the output uncertainty problem caused by dead zone, a fuzzy algorithm was designed to deal with it by Lan et al. (2021). As the existence of input dead zone and saturation, many signals are difficult to perform effectively, control performance is seriously degraded, and it even affects system stability. To improve system reliability and practicability, it is significant to consider them when constructing control methods for multiagent systems.
With the improvement of safety performance requirements, the problem of state constraints has received more and more attention. Barrier Lyapunov functions, as a resultful way to constrain state, are used to solve various violation of constraints (Su W. et al., 2021; Zhao et al., 2021; Wang et al., 2022a; Wang N. et al., 2022). For a class of nonlinear systems, a new tracking control scheme was established based on barrier Lyapunov functions in Zhao et al. (2021). For high-order nonlinear multiagent systems, the barrier Lyapunov functions were used in the framework of the distributed adding-one-power-integrator control in Wang N. et al. (2022). Nevertheless, when systems required convergence in a short time, drastic variation of states is unavoidable, which may be against state constrained. How to balance state constraints and convergence time still needs to be further discussed.
Inspired by the above discussion, for constrained uncertain nonlinear multiagent systems with input dead zone and saturation, a prescribed time adaptive event-triggered consensus control with prescribed performance is developed. The main contributions are summarized as follows:
• To achieve the goal of system converging with prescribed performance within the prescribed time, the speed performance function is developed by incorporating the speed function into the performance function. By making blends and transformations, the transform function and the barrier Lyapunov function are constructed. Thus, prescribed time convergent processes of the systems satisfy prescribed performance, and the violation of state constrained is prevented.
• Both input dead zone and saturation exist in multiagent systems, which impact system control performance. As the model is non-smooth and the parameters are unknown, the design of the control method becomes difficult. Thus, the model is approximated by a non-affine smooth function and is further rewritten as the form of linear input and approximation error by the Mean Value Theorem. Moreover, an adaptive event-triggered control method is constructed to compensate them.
• To further improve the wide applicability and flexibility of the proposed method, the transform function and the barrier Lyapunov function are applied in each step, and all errors converge within the prescribed time.
The later sections are grouped as follows: Section 2 introduces the preliminary, Section 3 displays the control method design and stability analysis, Section 4 verifies the proposed control method through some simulation cases, and the conclusion is given in Section 5.
2. Preliminaries and problem description
2.1. System model
A class of multiagent systems included one virtual leader, and M(M > 2) followers are considered. The i-th (i = 1, 2, ⋯, M) follower is modeled as follows:
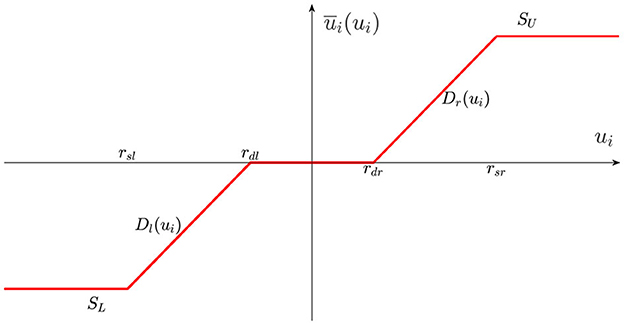
where xi,k(k = 1, 2, ⋯, m) and yi express the followers states and the output. fi,k(Xi,k) represents the bounded external disturbances, and . In addition, ui is input signal, ūi(ui) is system input with input dead zone and saturation as shown in Figure 1, and it can be described as follows:
where SU > 0 and SL < 0 are system input saturation parameters, and Dr(ui) and Dl(ui) are unknown nonlinear functions. Then, and rsr and rsl are the saturation breakpoints, rdr and rdl are the dead-zone breakpoints. They satisfy rsl < rdl < 0 < rdr < rsr.
Due to the nonlinear and non-smooth characteristics of ūi(ui), it is difficult to directly design control method. As a result, the ūi(ui) can be smoothly approximated as follows:
where εi(ui) = ūi(ui) − κi(ui) expresses the approximation error, and it satisfies . The smoothing function κi(ui) can be defined as follows:
where ιr, ιl, θ1, and θ2 are positive parameters.
According to the Mean Value Theorem, the function holds for , where is the derivative of smoothing function κi(uh), and l is a constant satisfies 0 < l < 1. Let , then κi(ui) is described as . Then, define , and the system input ūi(ui) can be rewritten as follows:
2.2. Graph theory
The communication topology of multiagent system which includes M(M > 2) followers can be described as a digraph G = (V, E), and each follower can be expressed as a node. Then, V = {1, ⋯, M} denotes the node set, and Vj × Vi ∈ E represents the edge set between note j and note i. A = [aij]M×M represents the adjacency matrix among notes, where aij is the information transmission coefficient between note j and note i. If note j can get information from note i, then aij > 0. Otherwise, aij = 0. In addition, the Laplacian matrix L is defined as L = D − A, where the diagonal matrix is with . For leader-follower multiagent systems, it can be represented by an augmented graph , where describes leader note 0 and followers note (1, ⋯, M), then .
Definition 1. The definition of i-th follower's synchronization error can be expressed as follows:
where y0 is the output signal of virtual leader, and bi denotes the information transmission coefficient between virtual leader and follower i. If the follower i can receive information from the leader, bi > 0. Otherwise, bi = 0.
2.3. Radial basis function neural networks
For any continuous function defined on a compact set Ω ∈ Rp, it can be modeled by radial basis function neural networks (RBFNNs). Radial basis function neural networks are expressed as follows Sun et al. (2022b):
where is input vector, and presents the approximation error, existing up bound satisfying . Then, expresses the basis function vector, and q > 1 is number of neural network node. can be selected by the Gaussian functions as follows:
where and πi are the center and width of the Gaussian function.
K* represents optimal weight value vector, and it can be described as follows:
where is the weight vector.
2.4. Transform function
To constrain the system error within a prescribed region, the prescribed performance function is introduced as follows:
where Z0 > 0 and Z∞ > 0 present the initial value and the final value of the prescribed performance function. Then, ϕ(t) is a decay function, which satisfies ϕ(0) = 1 and . Prescribed performance of the system error z(t) satisfies |z(t)| ≤ Z(t).
To enhance system convergence rate and achieve the final prescribed performance within a prescribed time, the following speed function is introduced:
where T is a prescribed time that can be designed.
Combining Equations (10), (11), the speed performance function can be obtained as follows:
Noting that the inequality Zv(t) ≤ Z(t) is keeping holds. Existing parameters λ and Q satisfy λ ≤ Z0 and λQ−1 ≤ Z∞, and such transform function is constructed as follows:
Remark 1. According to the aforementioned deduction and analysis, it is known that the prescribed time T is independent of the system initial states and design parameters. Noting that λg−1(t) ≤ Zv(t) is always holds, it is extremely significant for the later deduction and to prove.
2.5. Other preliminaries
Assumption 1. Zhang and Lewis (2012) the augmented graph Ḡ has a spanning tree, in which the root of the spanning tree is the virtual leader 0.
Assumption 2. The virtual leader output signal y0 is continuous function with up bound ȳ0 and has n-th order derivatives.
Assumption 3. Yang P. et al. (2021) define adjacency matrix as . At least existing one bi satisfies bi > 0, so that L + B is nonsingular.
Lemma 1. Liu et al. (2018) for any λ ∈ R and e ∈ R satisfy |e| ≤ λ, the following inequality holds
Lemma 2. Wang et al. (2022c) for variables m ∈ R and n ∈ R, existing constants a > 0, b > 0, and c > 0 satisfy
Lemma 3. Zhang and Lewis (2012) define , , and , satisfying
where ςmin is the minimum singular value of L + B, and YM − Yd is track error.
3. Controller design and ability analysis
3.1. Prescribed performance adaptive event-triggered control design
Define the following coordinate transformations:
where zi, 2, zi, 3, ⋯, zi,m represent error variables, and αi, 1, αi, 2, ⋯, αi,m−1 express virtual controllers.
Step 1: According to Equation (18), the derivative of ei, 1 can be obtained as follows:
where
The following modified barrier Lyapunov function Vi, 1 is constructed.
where λi, 1 is the design parameter with . It should be indicated that the inequality |ei, 1| ≤ λi, 1 holds when Vi, 1 is bounded. βi, 1 is a positive design parameter. is a parameter estimation error, is the estimation value of μi, 1, and μi, 1 will be defined later.
Remark 2. To multiagent system, prescribed time convergence progress meet prescribed performance while state constrained does not being violated, the transform function and barrier Lyapunov function are applied in Equations (18) and (20), and virtual controller and adaptive law will be developed to ensure Vi, 1 is bounded. Moreover, similar application will be shown in each step to further enhance system performance.
Taking the time derivation of Vi, 1 and combining with Equation (19), it can be obtained that
where is smoothing function and is defined as follows:
where .
According to RBFNNs, it can be estimated with any given
Remark 3. The unknown and uncertainty of the multiagent system will bring difficulties to the design of the control method. Neural networks are introduced to approximate any unknown functions, which is handled by Young's inequality. In addition, selecting an optimal weight value vector K* becomes difficult as the system gets more complex. Thus, the unknown parameter is estimated by an adaptive law .
By utilizing Lemma 2, the following inequalities can be obtained:
where ℓi,1 > 0 and are designed parameters.
Substituting into Equation (21), one has the following equation:
Define parameter , the following inequality can be obtained:
where .
To guarantee the Vi,1 bounded, constructing the virtual controller αi,1 and adaptive law as follows:
where γi,1 > 0 and δi,1 > 0 are design parameters.
Substituting Equations (28), (29) into Equation (26), one has the following equation
Step k (k = 2, 3, ⋯, m − 1) : According to the definition of error ei,k in Equation (18), the derivative of ei,k can be obtained as follows:
where .
The following barrier Lyapunov function Vi,k is constructed:
where λi,k is the design parameter with , βi,k is positive design parameter, is parameter estimation error, is the estimation value of μi,k, and μi,k will be defined later.
Taking the time derivation of Vi,k and substituting Equation (31), the following equation can be obtained:
where is smoothing function and is defined as follows:
where .
According to RBFNNs, the function can be estimated with any given
By utilizing Lemma 2, the following inequalities can be deduced:
where ℓi,k > 0 and are designed parameters.
Substituting the inequalities into Equation (33), hence
Define and , one has
To guarantee the Vi,k bounded, constructing the virtual controller αi,k and adaptive law as follows:
where γi,k > 0 and δi,k > 0 are design parameters.
Substituting Equations (40), (41) into Equation (39), it can be obtained as follows:
Step m: To relieve system communication pressure, an adaptive event-triggered strategy is constructed as follows:
where 0 < ζi < 1, σi > 0, and oi > 0 are design parameters. The intermediate signal is defined as follows:
where , and αi,m is virtual controller, which will be constructed later. Consider hi is unknown constant, by utilizing to estimate ηi,m, and is the estimation error. Then, can be rewritten as follows:
Remark 4. Consider the restricted communication resources, an event-triggered scheme (Equation 43) is established to reduce unnecessary communication transmission. At the same time, an intermediate signal with adaptive law is established in Equation (44) to compensate the impact of dead zone and saturation.
According to Equation (43), one has
where |vi,1| ≤ 1, |vi,2| ≤ 1.
For any constant x ∈ R and y > 0, the inequality holds. Then, it can be obtained as follows:
According to Equation (18), the derivative of ei,m can be obtained as follows:
where .
The following barrier Lyapunov function Vi,m is constructed:
where λi,m is the design parameter with , βi,m and ρi,m are positive design and positive parameter. is parameter estimation error, is the estimation value of μi,m, and μi,m will be defined later.
Taking the time derivation of Vi,m, it can be obtained as follows:
Combined with Equation (47), one has
Define the smoothing function as follows:
where .
By utilizing Lemma 2, the following inequalities can be deduced as follows:
According to the RBFNNs, the function can be estimated with any given
where .
According to Lemma 2, the following inequalities can be obtained:
where ℓi,m > 0 and are designed parameters.
Substituting the inequalities into Equation (51), one has
Define and , it can be deduced as follows:
To guarantee the Vi,m bounded, constructing the virtual controller αi,m and adaptive laws and as follows:
where γi,m > 0, δi,m > 0, and ξi,m > 0.
Remark 5. Because the input dead-zone and saturation nonlinearities are unknown, parameters of them are difficult to obtained. Thus, an intermediate signal with adaptive law is designed to compensate them, and the approximation error is simultaneously handled by RBFNNs and adaptive law. The design difficulties caused by unknown parameters are effectively avoided.
Substituting Equations (58)–(60) produces Equation (57):
According to Lemma 1 and Lemma 2, the following inequalities hold:
Based on Equations (61)–(64) can be converted as follows:
where , .
3.2. System stability analysis
Theorem 1. For uncertain nonlinear multiagent systems with input dead zone and saturation, by constructed virtual controllers (Equations 28, 40, and 58), adaptive laws (Equation 29, 41, 59, and 60), and event-triggered strategy (Equation 43), the following results can be achieved:
(1) All the signals of systems are bounded, and system error zi,j converges to prescribed regions within prescribed time T.
(2) System performance satisfies prescribed performance function Zi,j(t) and system states are fulfilling the constraints.
(3) There exits the minimum interval time between any twice triggering, so Zeno Behavior can be surely avoided.
Proof of Theorem 1 (1). The following total Lyapunov function is constructed:
According to Equation (65), the following equation is obtained:
where and Γ = min{Γi, i = 1, 2, ⋯, M}.
Integrating the Equation (67), one has
According to the definition of V, it can be included that ei,j, and all are bounded for j = 1, 2, ⋯, m, i = 1, 2, ⋯, M. Since μi,j and ηi,m are constant, then and , it can be deduced that and are bounded. In addition, based on the definition of αi,j, it can be deduced that αi,j is bounded, and existing up bound satisfies . Based on the definition of Vi,m, the following inequality holds:
Thus, the solution ei,j can be deduced as follows:
where
Then, combined with Equations (13), (18), one has
Thus, all the signals are bounded, and error zi,j converges to prescribed areas within the prescribed time T. □
Proof of Theorem 1 (2). From Equation (71), it is obvious that , according to the definition , inequality is holds. Combined with , it can be deduced that |zi,j| ≤ Zi,j(t) is always holds. Therefore, systems error zi,j satisfies prescribed performance function Zi,j(t).
Remark 6. According to the aforementioned deduction and analysis, it is obvious that both the final convergence area and convergence time T are prescribed. In addition system convergence progress satisfies prescribed performance function. From (70), it can be known that |zi,j| can become smaller, by increasing the design parameters γi,j, βi,j, and ρi,m and decreasing design parameters δi,j and ξi,m. However, both convergence time and convergence area are not affected by the adjustment of design parameters γi,j, δi,j, ξi,m, βi,j, and ρi,m.
In addition, according to Equation (71), it is obvious that . Applying Lemma 3, inequality is holds. As y0 satisfies y0 ≤ ȳ0, it can be obtained that . Define λi,1 ≤ Qςmin(Bi,1−ȳd), hence xi,1 ≤ Bi,1 is holds.
Similarly, it is obvious that holds from Equation (71). Due to zi,2 = xi,2 − αi,1, it can be obtained that . Consider the αi,1 satisfies , and . Define , hence xi,2 ≤ Bi,2 is holds. Similarly, existing xi,j ≤ Bi,j is holds for j = 3, ⋯, m
Remark 7. Most prescribed time control focuses on system convergence time but ignores the problem that, during rapid convergence progress, the system states may be out of safe ranges. To address the problem, by combining barrier Lyapunov function and transform function, achieving system quick convergence while ensuring state constraints. □
Proof of Theorem 1 (3). According to Equation (43), the derivative of Δi(t) satisfies the following:
Due to Δi(t) ≥ ϖi(t)−ui(t) and Δi(tω) = 0, the following equation is obtained:
Subsequently,
Thus, it can be concluded that interval time existing lower bound guarantees systems to avoid Zeno Behavior, and by increasing the design parameters σi, the minimum interval time can be longer. Then, more communication resources can be saved by increasing design parameters ζi.
The proof is completed. □
The proposed theorem has been proved. By the proposed adaptive event-triggered consensus control method, it can be achieved that system convergence with prescribed performance while suffering from input dead zone and saturation.
Remark 8. Based on the prescribed performance function, the transform function and the barrier Lyapunov function are constructed and applied in each step. Therefore, the developed control method not only makes the system quickly converge in the prescribed area but also avoids states violating constrained. By introducing RBFNNs and designing adaptive laws, achieve unknown input dead-zone and saturation compensation in the prescribed time.
4. Simulation
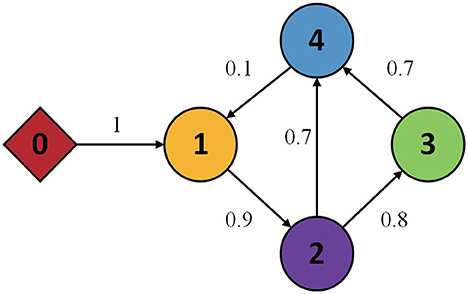
In this section, to prove the effectiveness of the control method developed in this study, some simulation experiments are presented. The MASs include four follower agents and one virtual leader is considered, and the topology of the communication graph is shown in Figure 2.
4.1. Example A
The model of i-th(i=1,2,3,4) follower is given as follows:
where unknown external disturbance expressed as fi,1(Xi,1) = 0.2 sin(2xi,1) and fi,2(Xi,2) = 0.2 sin(2xi,1xi,2). The dead-zone breakpoints are selected as rdl = −0.8 and rdr = 1, saturation breakpoints are selected as rsl = −20 and rsr = 25, and saturation values are SU = 25 and SL = −20. In addition, the unknown nonlinear functions are and .
The prescribed time is selected as T = 1.2, and then, prescribed performance functions are selected as and . Furthermore, transform function parameter is given as Q = 100. Define the values of state constraints as xi,1 < 2 and xi,2 < 5, then λi,1 = 5 and λi,2 = 10 are selected.
The developed adaptive event-triggered consensus control method is as follows:
The parameters of radial basis functions are selected as followers:
where the inputs of the RBFNNs are , , , , , , , and . Then . The parameters of event-triggered strategy are selected as ζi = 0.4, σi = 2.5, and oi = 0.3, and remaining parameters and initial states are given in Table 1.
The simulation results are shown in Figure 3. Figure 3A presents the follower output signal and leader output signal, and Figure 3B shows the states of each follower. From Figures 3A, B, it is obvious that followers track the leader quickiy, and state constraints are not violated at the same time. Figures 3C, D present the synchronization error and dynamics error of each follower. It can be seen that all errors converge in prescribed area within prescribed time (T = 1.2s), and convergence progress meet the prescribed performance. Figure 3E displays the systems input and event-triggered input, and it can be seen that the input is suffered from the input dead zone and saturation. And the triggered time intervals are presented in Figure 3F, it can be shown that the maximum interevent intervals from follower 1 to follower 4 are 0.15s, 0.22s, 0.20s, and 0.22s.
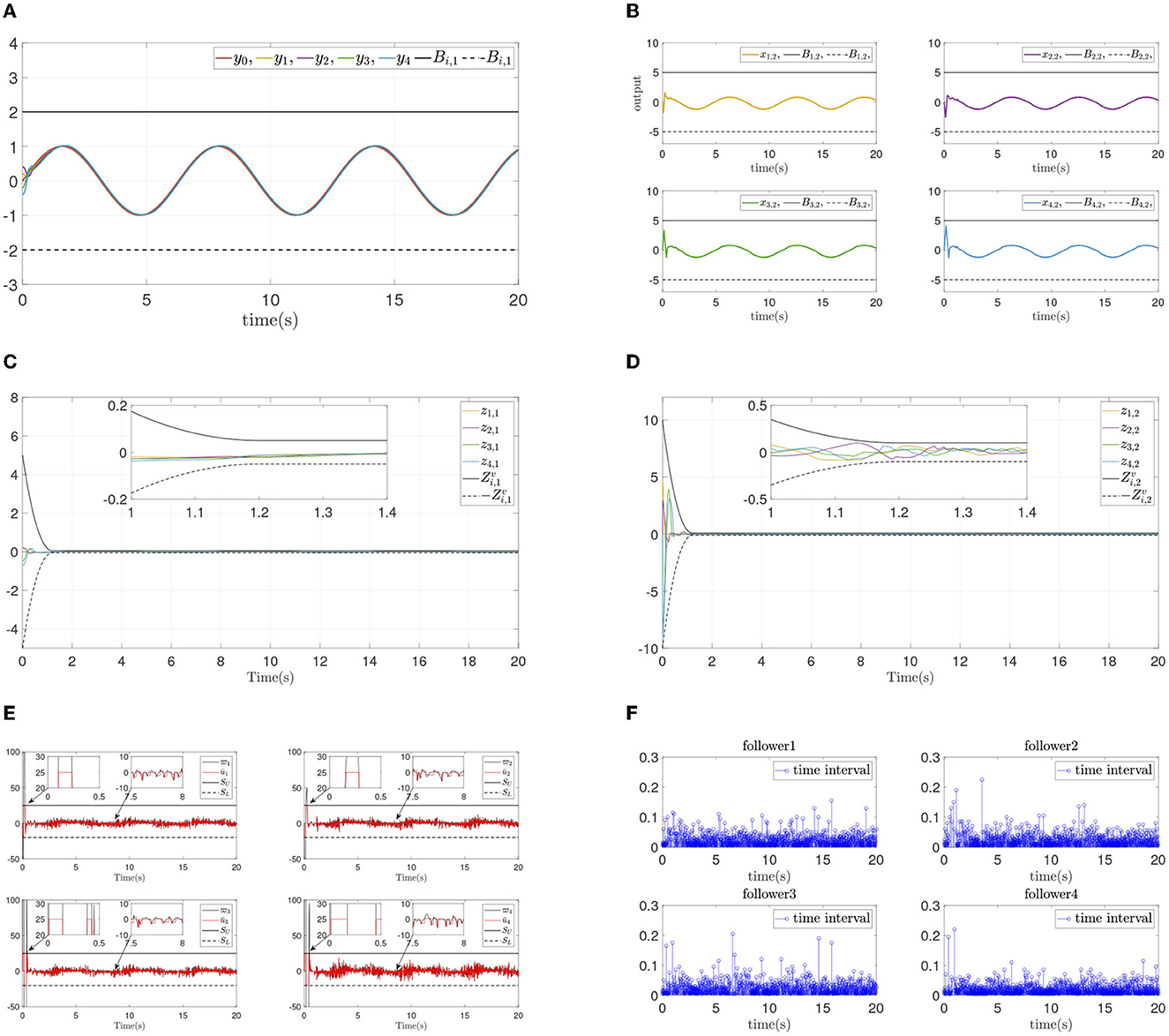
Figure 3. Simulations results of Example A case I. (A) Followers' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2. (E) systems input ūi and event-triggered input ϖi. (F) Time intervals.
To verify the convergence performance and time are not affected by systems initial states and control parameters, and ensure state constraints at the same time, two simulation experiments are done again for different design parameters and different initial states. The states and errors of two simulations are shown in Figures 4, 5. For different parameters or initial states, two similar results can be obtained: Each follower converge to the leader quickly while state constraints are not violated. All errors prescribed time convergence progress meet the prescribed performance. The simulation results verified the effectiveness of the developed control method.
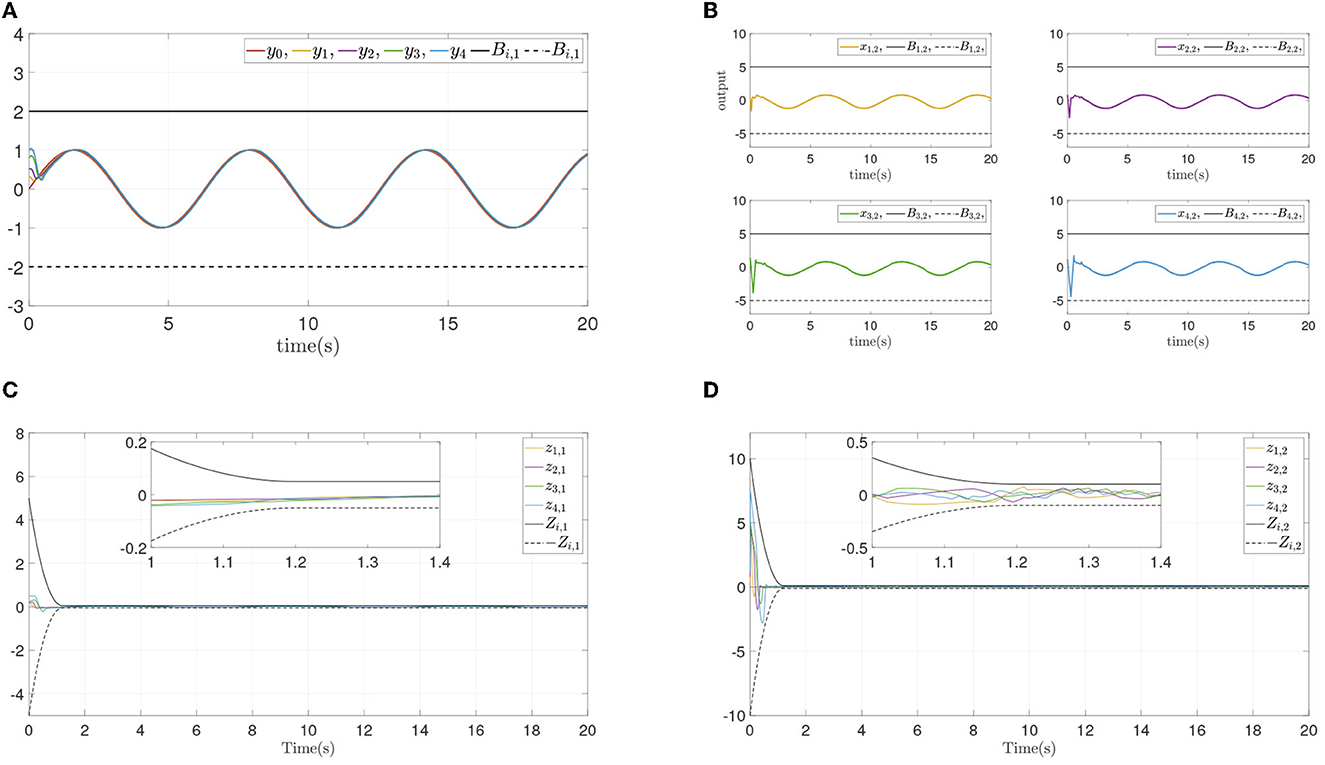
Figure 4. Simulation results of Example A case II. (A) Follower' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2.
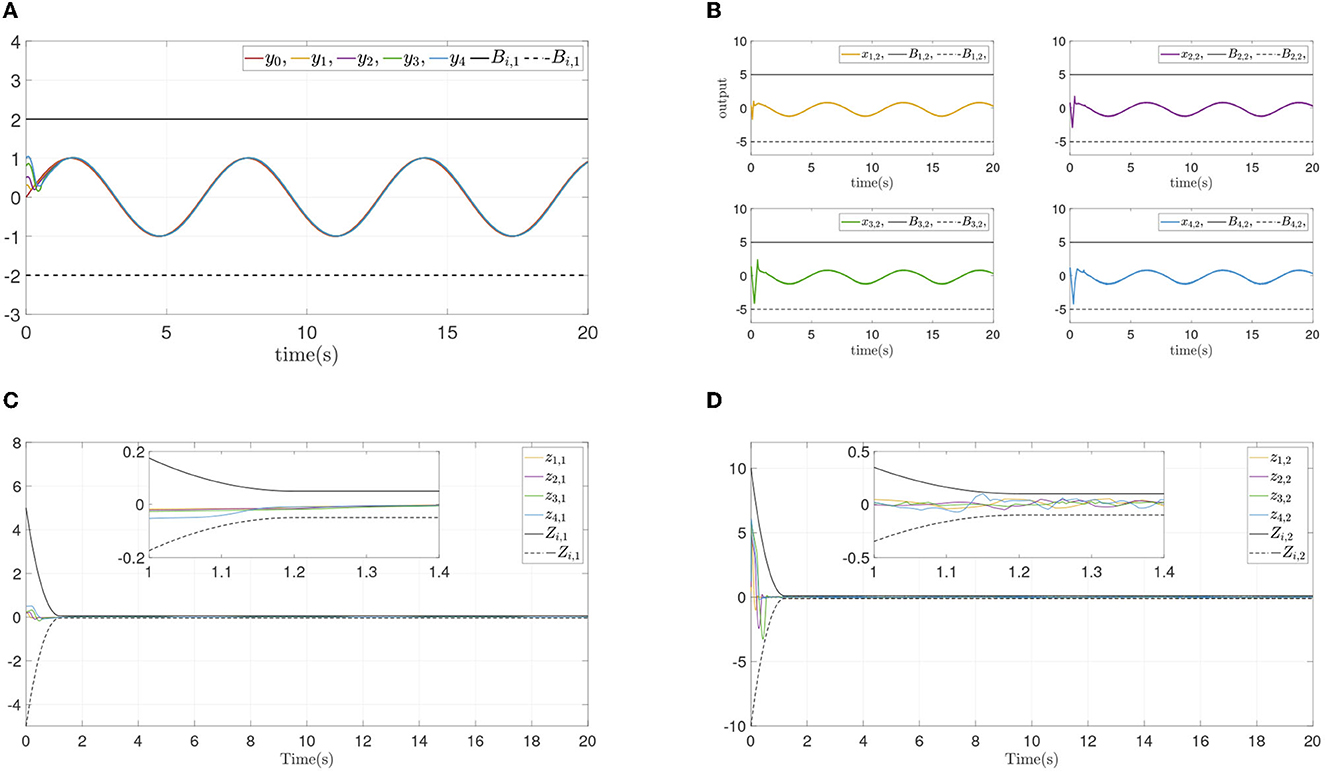
Figure 5. Simulation results of Example A case III. (A) Followers' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2.
4.2. Example B
To further verify the applicability of the constructed method, a class of constrained single-link robotic arm systems with input dead zone and saturation are adopted, and the models of i-th(i=1,2,3,4) arm are given as follows:
where xi,1 and xi,2, respectively, represent the i-th link angle and angular velocity. Then, Ji = 1 is the inertia moment. For fi(X) = (Bixi,2 + GiLisin(xi,1)), Bi = 1 is the viscous friction coefficient, Gi = 9.8 and li = 0.1 represent the mass and length of the i-th link, .
In Example B, a shorter prescribed time is selected as T = 1; then, prescribed performance functions are given as and . Furthermore, transform function parameter is given as Q = 75. Define the same state constraints values as xi,1 < 2 and xi,2 < 5, then λi,1 = 3.75 and λi,2 = 7.5 are chosen. The parameters of the event-triggered strategy are the same as in Example A. The remaining parameters and initial states are given in Table 2.
From the simulation result in Figure 6, it can be seen that similar control performance in Example A is shown. Considering different design parameters and different initial states in Table 2, two simulation experiments are done ulteriorly. The system states and error convergence progress are displayed in Figures 7, 8. According to the result from Figures 6–8, it is obvious that system quickly converges in the prescribed area with prescribed performance while affected by input dead zone and saturation, and state constraints are guaranteed. Therefore, the effectiveness of the proposed control method is confirmed.
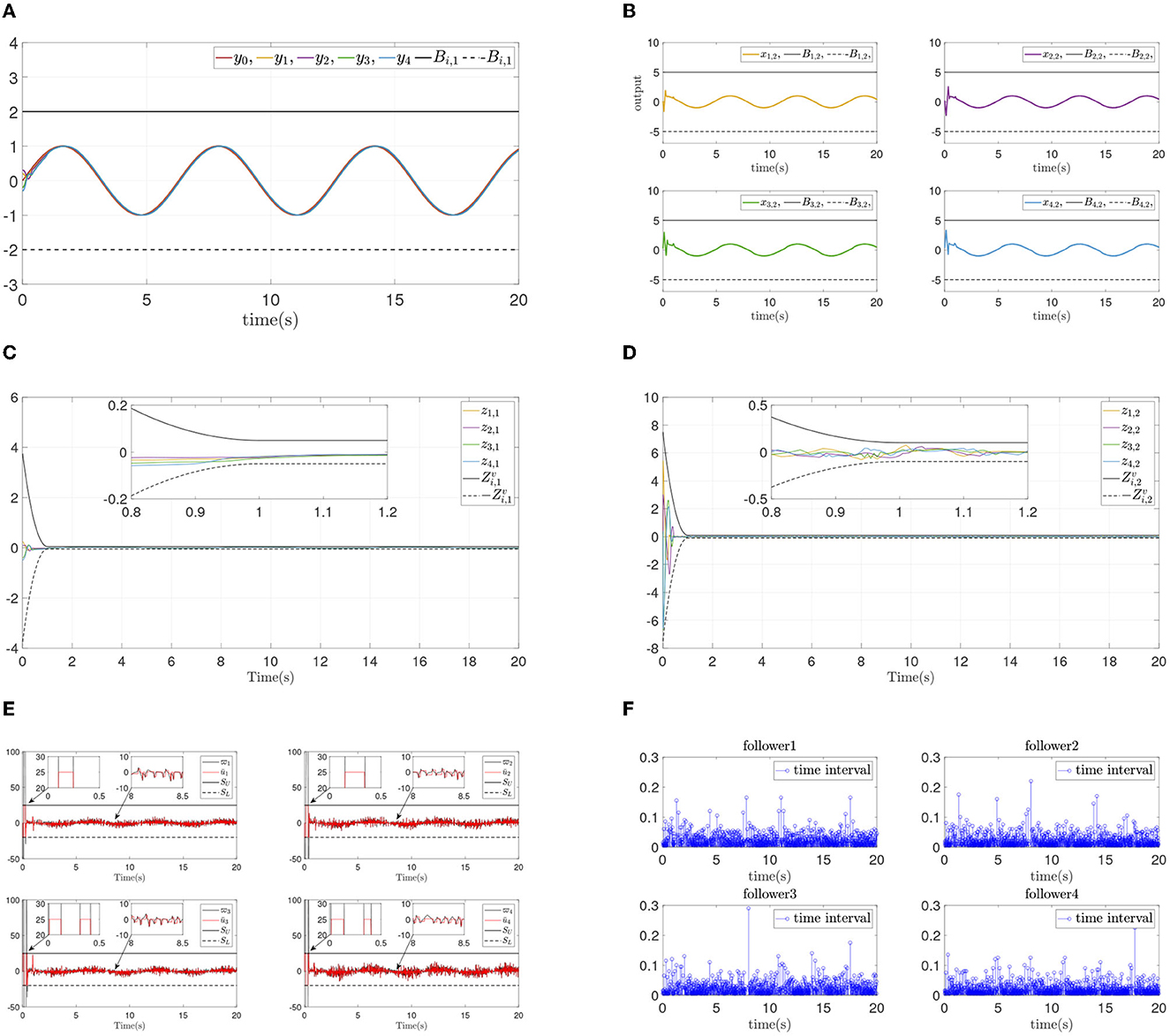
Figure 6. Simulation results of Example B case I. (A) Followers' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2. (E) systems input ūi and event-triggered input ϖi. (F) Time intervals.
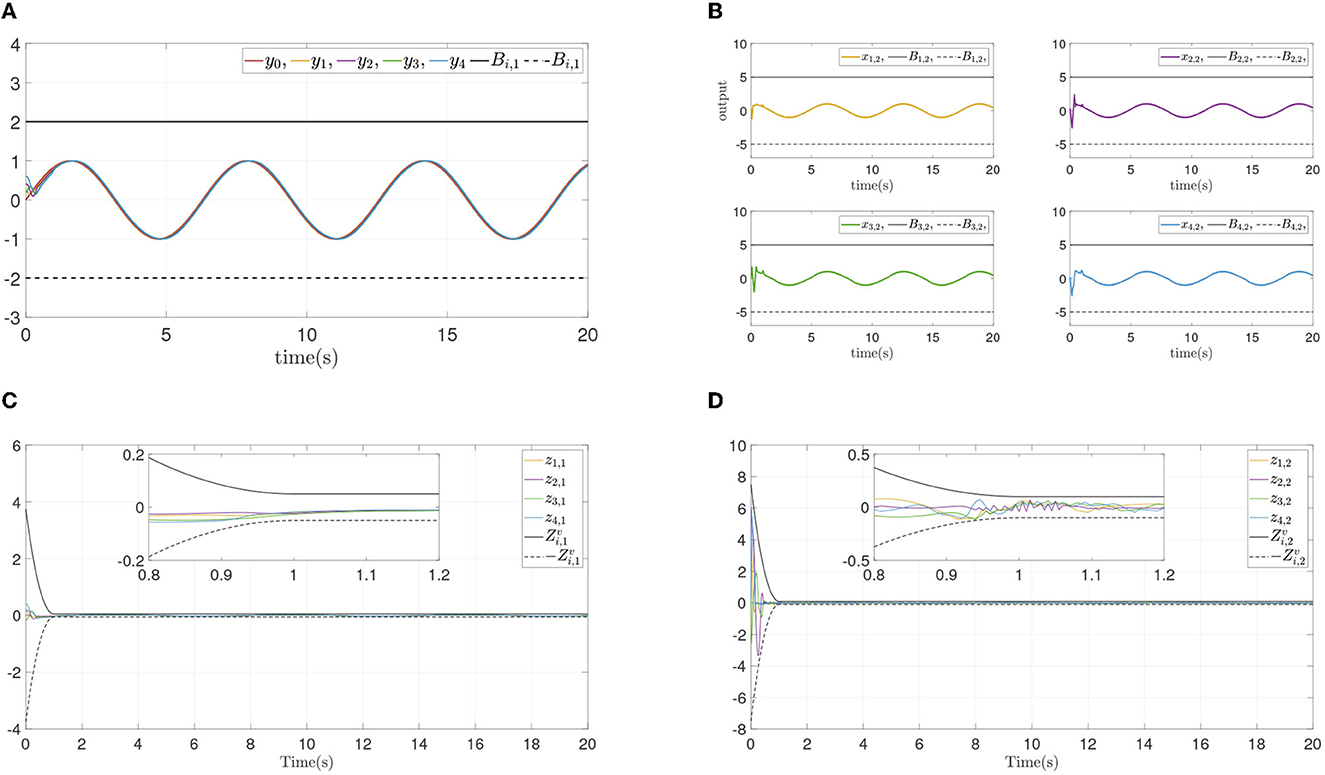
Figure 7. Simulation results of Example B case II. (A) Followers' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2.
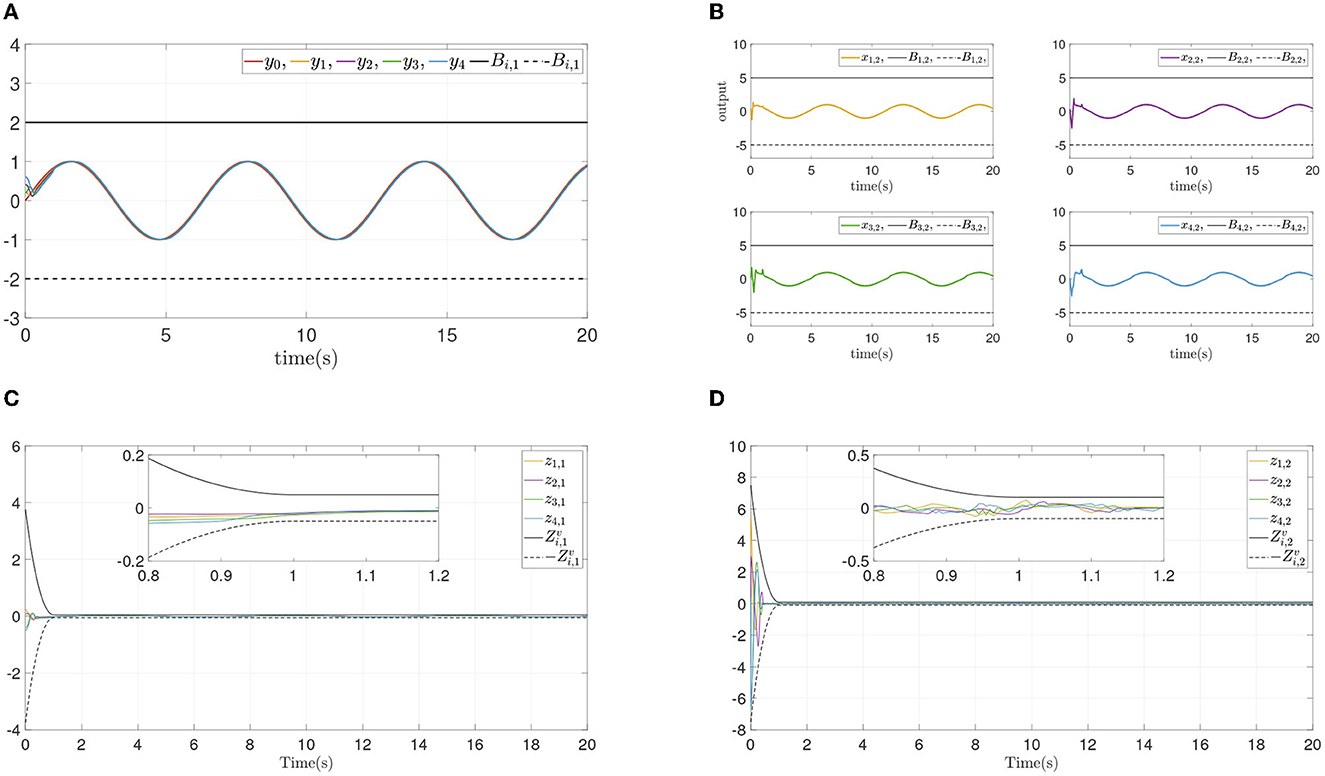
Figure 8. Simulation results of Example B case III. (A) Followers' outputs yi. (B) Followers' states xi,2. (C) Synchronization error zi,1. (D) Dynamics error zi,2.
5. Conclusion
This study has discussed the prescribed performance consensus problem of constrained multiagent systems with input dead zone and saturation. An adaptive event-triggered consensus control method is developed to address the problem. To compensate for the impact caused by unknown input dead zone and saturation, adaptive laws and RBFNNs are adopted to deal with them. Based on constructed transform function and barrier Lyapunov function, the control method is designed by backstepping technology, which guarantees the system convergence performance and prevents constraint violation. Under the proposed control method, all followers achieve prescribed time and preset precision synchronization, irrespective of the presence of limited bandwidth, input dead zone, and saturation. Some simulations show the feasibility of the proposed control method. In future studies, we tend to discuss the consensus problem when the parameters of input dead zone and saturation are unknown and time-varying. Moreover, how to compensate for actuator failures and the input time delay is also an interesting topic that merits research.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
XY and JL: conceptualization, writing—original draft preparation, data curation, writing—review and editing, and funding acquisition. XY, JL, and KC: methodology. KC: validation and supervision. YZ and ZH: formal analysis and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the National Natural Science Foundation of China under grant 62103115, the Natural Science Foundation of Guangdong Province under grant 2021A1515011636, the Science and Technology Research Program of Guangzhou under grant 202102020975, the Basic and Applied Basic Research Projects jointly funded by Guangzhou and schools (colleges) under grant 202201020233, the Guangzhou Yangcheng Scholars Research Project under grant 202235199, the Special Funds for the Cultivation of Guangdong College Students' Scientific and Technological Innovation (Climbing Program Special Funds.) under grant pdjh2022a0404, and the College Students' Innovative Entrepreneurial Training Plan Program under grant 202211078101.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bai, W., Zhou, Q., shan Li, T., and Li, H. (2020). Adaptive reinforcement learning neural network control for uncertain nonlinear system with input saturation. IEEE Trans. Cybern. 50, 3433–3443. doi: 10.1109/TCYB.2019.2921057
Cai, Y., Zhang, H., Duan, J., and Zhang, J. (2021). Distributed bipartite consensus of linear multiagent systems based on event-triggered output feedback control scheme. IEEE Trans. Syst. Man Cybern. Syst. 51, 6743–6756. doi: 10.1109/TSMC.2020.2964394
Cao, L., Li, H., Dong, G., and Lu, R. (2021). Event-triggered control for multiagent systems with sensor faults and input saturation. IEEE Trans. Syst. Man Cybern. Syst. 51, 3855–3866. doi: 10.1109/TSMC.2019.2938216
Chen, X., Yu, H., and Hao, F. (2022). Prescribed-time event-triggered bipartite consensus of multiagent systems. IEEE Trans. Cybern. 52, 2589–2598. doi: 10.1109/TCYB.2020.3004572
Dai, W., Liu, Y., Lu, H., Zhou, Z., and Zhen, Z. (2021). Shared control based on a brain-computer interface for human-multirobot cooperation. IEEE Rob. Autom. Lett. 6, 6123–6130. doi: 10.1109/LRA.2021.3091170
Ding, L., Li, S., Gao, H., Liu, Y., Huang, L., and Deng, Z. (2021). Adaptive neural network-based finite-time online optimal tracking control of the nonlinear system with dead zone. IEEE Trans. Cybern. 51, 382–392. doi: 10.1109/TCYB.2019.2939424
Gong, B., Wang, S., Hao, M., Guan, X., and Li, S. (2021). Range-based collaborative relative navigation for multiple unmanned aerial vehicles using consensus extended kalman filter. Aerospace Sci. Technol. 112, 106647. doi: 10.1016/j.ast.2021.106647
Gong, X., Cui, Y., Shen, J., Xiong, J., and Huang, T. (2022). Distributed optimization in prescribed-time: theory and experiment. IEEE Trans. Netw. Sci. Eng. 9, 564–576. doi: 10.1109/TNSE.2021.3126154
Gu, N., Wang, D., Peng, Z., and Liu, L. (2021). Observer-based finite-time control for distributed path maneuvering of underactuated unmanned surface vehicles with collision avoidance and connectivity preservation. IEEE Trans. Syst. Man Cybern. Syst. 51, 5105–5115. doi: 10.1109/TSMC.2019.2944521
Guo, G., Gao, Z., and Dong, K. (2021). Prescribed-time formation control of surface vessels with asymmetric constraints on los range and bearing angles. Nonlinear Dyn. 104, 3701–3712. doi: 10.1007/s11071-021-06462-8
Huang, B., Song, S., Zhu, C., Li, J., and Zhou, B. (2021). Finite-time distributed formation control for multiple unmanned surface vehicles with input saturation. Ocean Eng. 233, 109158. doi: 10.1016/j.oceaneng.2021.109158
Huang, B., Ye, M., Hu, Y., Vandini, A., Lee, S.-L., and Yang, G.-Z. (2018). A multirobot cooperation framework for sewing personalized stent grafts. IEEE Trans. Ind. Inform. 14, 1776–1785. doi: 10.1109/TII.2017.2773479
Jiang, B., and Gao, C. (2022). Decentralized adaptive sliding mode control of large-scale semi-markovian jump interconnected systems with dead-zone input. IEEE Trans. Automat. Contr. 67, 1521–1528. doi: 10.1109/TAC.2021.3065658
Lan, J., Liu, Y., Liu, L., and Tong, S. (2021). Adaptive output feedback tracking control for a class of nonlinear time-varying state constrained systems with fuzzy dead-zone input. IEEE Trans. Fuzzy Syst. 29, 1841–1852. doi: 10.1109/TFUZZ.2020.2986705
Li, Y., Qu, F., and Tong, S. (2021). Observer-based fuzzy adaptive finite-time containment control of nonlinear multiagent systems with input delay. IEEE Trans. Cybern. 51, 126–137. doi: 10.1109/TCYB.2020.2970454
Li, Y., Yang, T., and Tong, S. (2020). Adaptive neural networks finite-time optimal control for a class of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 31, 4451–4460. doi: 10.1109/TNNLS.2019.2955438
Liu, Y., Lu, S., Tong, S., Chen, X., Chen, C. L. P., and Li, D. (2018). Adaptive control-based barrier lyapunov functions for a class of stochastic nonlinear systems with full state constraints. Automatica 87, 83–93. doi: 10.1016/j.automatica.2017.07.028
Lu, J., Wang, Y., Shi, X., and Cao, J. (2021). Finite-time bipartite consensus for multiagent systems under detail-balanced antagonistic interactions. IEEE Trans. Syst. Man Cybern. Syst. 51, 3867–3875. doi: 10.1109/TSMC.2019.2938419
Min, H., Xu, S., and Zhang, Z. (2021). Adaptive finite-time stabilization of stochastic nonlinear systems subject to full-state constraints and input saturation. IEEE Trans. Automat. Contr. 66, 1306–1313. doi: 10.1109/TAC.2020.2990173
Ning, B., Han, Q., and Zuo, Z. (2021). Bipartite consensus tracking for second-order multiagent systems: a time-varying function-based preset-time approach. IEEE Trans. Automat. Contr. 66, 2739–2745. doi: 10.1109/TAC.2020.3008125
Ren, Y., Zhou, W., Li, Z., Liu, L., and Sun, Y. (2020). Prescribed-time cluster lag consensus control for second-order non-linear leader-following multiagent systems. ISA Trans. 109, 49–60. doi: 10.1016/j.isatra.2020.09.012
Song, S., Park, J. H., Zhang, B., and Song, X. (2020). Adaptive hybrid fuzzy output feedback control for fractional-order nonlinear systems with time-varying delays and input saturation. Appl. Math. Comput. 364. doi: 10.1016/j.amc.2019.124662
Su, H., Wang, X., Chen, X., and Zeng, Z. (2021). Second-order consensus of hybrid multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 51, 6503–6512. doi: 10.1109/TSMC.2019.2963089
Su, W., Niu, B., Wang, H., and Qi, W. (2021). Adaptive neural network asymptotic tracking control for a class of stochastic nonlinear systems with unknown control gains and full state constraints. Int. J. Adapt. Control Signal. Process. 35, 2007–2024. doi: 10.1002/acs.3304
Sun, Y., Xu, J., Chen, C., and Hu, W. (2022a). Reinforcement learning-based optimal tracking control for levitation system of maglev vehicle with input time delay. IEEE Trans. Instrum. Meas. 71, 1–13. doi: 10.1109/TIM.2022.3142059
Sun, Y., Xu, J., Lin, G., Ji, W., and Wang, L. (2022b). Rbf neural network-based supervisor control for maglev vehicles on an elastic track with network time delay. IEEE Trans. Ind. Inform. 18, 509–519. doi: 10.1109/TII.2020.3032235
Sun, Y., Xu, J., Lin, G., and Sun, N. (2021). Adaptive neural network control for maglev vehicle systems with time-varying mass and external disturbance. Neural Comput. Appl. 2021, 1–12. doi: 10.1007/s00521-021-05874-2
Tran, V. P., Santoso, F., Garratt, M. A., and Anavatti, S. G. (2021). Distributed artificial neural networks-based adaptive strictly negative imaginary formation controllers for unmanned aerial vehicles in time-varying environments. IEEE Trans. Ind. Inform. 17, 3910–3919. doi: 10.1109/TII.2020.3004600
Wang, C., Wen, C., and Guo, L. (2021). Adaptive consensus control for nonlinear multiagent systems with unknown control directions and time-varying actuator faults. IEEE Trans. Automat. Contr. 66, 4222–4229. doi: 10.1109/TAC.2020.3034209
Wang, J., Gong, Q., Huang, K.-C., Liu, Z., Chen, C. L. P., and Liu, J. (2021a). Event-triggered prescribed settling time consensus compensation control for a class of uncertain nonlinear systems with actuator failures. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–11. doi: 10.1109/TNNLS.2021.3129816
Wang, J., Wang, C., Chen, C. L. P., Liu, Z., and Zhang, C. (2022a). Fast finite-time event-triggered consensus control for uncertain nonlinear multiagent systems with full-state constraints. IEEE Trans. Circ. Syst. I Regular Pap. 2022, 1–10. doi: 10.1109/TCSI.2022.3225287
Wang, J., Yan, Y., Liu, Z., Chen, C. L. P., Zhang, C., and Chen, K. (2022b). Neural network-based event-triggered finite-time control of uncertain nonlinear systems with full-state constraints and actuator failures. Int. J. Robust Nonlinear Control. doi: 10.1002/rnc.6444
Wang, J., Yan, Y., Liu, Z., Chen, C. P., Zhang, C., and Chen, K. (2022c). Finite-time consensus control for multi-agent systems with full-state constraints and actuator failures. Neural Netw. 157, 350–363. doi: 10.1016/j.neunet.2022.10.028
Wang, J., Zhang, H., Ma, K., Liu, Z., and Chen, C. L. P. (2021b). Neural adaptive self-triggered control for uncertain nonlinear systems with input hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 33, 6206–6214. doi: 10.1109/TNNLS.2021.3072784
Wang, N., Wang, Y., Wen, G., Lv, M., and Zhang, F. (2022). Fuzzy adaptive constrained consensus tracking of high-order multi-agent networks: A new event-triggered mechanism. IEEE Trans. Syst. Man Cybern. Syst. 52, 5468–5480. doi: 10.1109/TSMC.2021.3127825
Wei, B., and Xiao, F. (2021). Distributed consensus control of linear multiagent systems with adaptive nonlinear couplings. IEEE Trans. Syst. Man Cybern. Syst. 51, 1365–1370. doi: 10.1109/TSMC.2019.2896915
Yang, C., Huang, D., He, W., and Cheng, L. (2021). Neural control of robot manipulators with trajectory tracking constraints and input saturation. IEEE Trans. Neural Netw. Learn. Syst. 32, 4231–4242. doi: 10.1109/TNNLS.2020.3017202
Yang, P., Zhang, A., and Zhou, D. (2021). Event-triggered finite-time formation control for multiple unmanned aerial vehicles with input saturation. Int. J. Control Autom. Syst. 19, 1760–1773. doi: 10.1007/s12555-019-0833-7
Zhai, Y., Ding, B., Zhang, P., and Luo, J. (2021). Cloudroid swarm: a qos-aware framework for multirobot cooperation offloading. Wireless Commun. Mobile Comput. 2021, 6631111. doi: 10.1155/2021/6631111
Zhang, H., and Lewis, F. L. (2012). Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica 48, 1432–1439. doi: 10.1016/j.automatica.2012.05.008
Zhao, L., Liu, G., and Yu, J. (2021). Finite-time adaptive fuzzy tracking control for a class of nonlinear systems with full-state constraints. IEEE Trans. Fuzzy Syst. 29, 2246–2255. doi: 10.1109/TFUZZ.2020.2996387
Zhou, P., and Chen, B. M. (2021). Semi-global leader-following consensus-based formation flight of unmanned aerial vehicles. Chin. J. Aeronaut. 35, 31–43. doi: 10.1016/j.cja.2021.02.013
Zhou, Q., Zhao, S., Li, H., Lu, R., and Wu, C. (2019). Adaptive neural network tracking control for robotic manipulators with dead zone. IEEE Tran. Neural Netw. Learn. Syst. 30, 3611–3620. doi: 10.1109/TNNLS.2018.2869375
Keywords: prescribed time, prescribed performance, event-triggered strategy, multiagent systems, input dead-zone, input saturation
Citation: Yue X, Liu J, Chen K, Zhang Y and Hu Z (2023) Prescribed performance adaptive event-triggered consensus control for multiagent systems with input saturation. Front. Neurorobot. 16:1103462. doi: 10.3389/fnbot.2022.1103462
Received: 20 November 2022; Accepted: 30 December 2022;
Published: 19 January 2023.
Edited by:
Ming-Feng Ge, China University of Geosciences Wuhan, ChinaCopyright © 2023 Yue, Liu, Chen, Zhang and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kairui Chen,  a3JheWNoZW5AMTM5LmNvbQ==
a3JheWNoZW5AMTM5LmNvbQ==
 Xia Yue1
Xia Yue1 Jiarui Liu
Jiarui Liu Kairui Chen
Kairui Chen