- 1Shandong Provincial Key Laboratory of Network Based Intelligent Computing, School of Information Science and Engineering, University of Jinan, Jinan, China
- 2College of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing, China
- 3State Key Laboratory of Networking and Switching Technology, Information Security Center, Beijing University of Posts and Telecommunications, Beijing, China
This paper investigates the fixed-time synchronization and the predefined-time synchronization of memristive complex-valued bidirectional associative memory neural networks (MCVBAMNNs) with leakage time-varying delay. First, the proposed neural networks are regarded as two dynamic real-valued systems. By designing a suitable feedback controller, combined with the Lyapunov method and inequality technology, a more accurate upper bound of stability time estimation is given. Then, a predefined-time stability theorem is proposed, which can easily establish a direct relationship between tuning gain and system stability time. Any predefined time can be set as controller parameters to ensure that the synchronization error converges within the predefined time. Finally, the developed chaotic MCVBAMNNs and predefined-time synchronization technology are applied to image encryption and decryption. The correctness of the theory and the security of the cryptographic system are verified by numerical simulation.
1. Introduction
After entering the twenty-first century, brain-like intelligence and neural network have developed rapidly. With the support of technologies such as artificial intelligence, deep learning, and cloud computing, corresponding achievements have emerged in an endless stream (Su et al., 2021; Wen and Su, 2022), which also poses greater challenges to the large-scale information processing capacity of computing systems. Many researchers have explored the direction of brain-like research (Rubinov and Sporns, 2010; Zhao H. et al., 2021), trying to get inspiration from the structure of the human brain and the way of information processing. Associative memory is one of the most active behaviors in the human brain, and it simulates the ability of the real nervous system to process information. In 1988, Kosko extended the traditional Hopfield neural networks and established bidirectional associative memory (BAM) neural networks (Kosko, 1988). The networks have a relatively complex structure, and their neurons are distributed in two layers. Each neuron in each layer is connected to all neurons in the other layer, while all neurons in the same layer are not connected to each other. At present, with the rapid development of artificial intelligence, the synchronous control and stability analysis of BAM neural networks has become the mainstream research direction. Researchers have invested a lot of time and energy to explore BAM neural networks, which provides a new research idea for the theoretical analysis of complex networks (Ke and Miao, 2013; Zhang et al., 2014; Qi et al., 2015; Zhang and Quan, 2015; Zhang and Yang, 2020; Zhao Y. et al., 2021; Liu et al., 2022).
In recent years, the development of many industrial products has involved complex signal problems. The introduction of complex signals extends the state variables of the controlled system from the real domain to the complex domain, which leads to an upsurge of research on complex-valued neural networks. The state variables, connection weights, and activation functions of complex-valued neural networks are complex numbers, which can solve problems that cannot be solved by real-valued neural networks, such as XOR and symmetry detection. The complex-valued neural networks have more advantages in network learning ability and self-organization. At present, some interesting results have been proposed (Liu et al., 2017; Zhang et al., 2018; Li and Mu, 2019; You et al., 2020).
The memristor was originally predicted by Chua (1971). HP laboratory first developed the memristor components of nanometer size in 2008 (Strukov et al., 2008). The resistance of the memristor will vary with the charge flow and can remain unchanged after power failure. In addition, the memristor is considered to be a perfect device for simulating synapses due to its advantages of nanometer size, low power consumption, and easy large-scale integration. There has been much interesting research on the dynamics of memristive neural networks (Li and Cao, 2016; Wang et al., 2017; Yang et al., 2020). Compared with traditional artificial neural networks, memristor neural networks can better simulate the structure and function of the human brain.
As one of the dynamic behaviors, synchronization behavior describes the cooperative consistency in a group, which is manifested in the network as the cooperative and consistent relationship after the interaction of node states. Fixed-time synchronization is a special kind of finite-time synchronization. The corresponding synchronization time has a certain upper bound, which is not dependent on the initial value of the system but only related to the system parameters and the controller. At present, there are some research results on fixed-time synchronization. Cao and Li (2017) studied a fixed-time synchronization control method based on memristor and recurrent neural networks with time delay and estimated the settling time of fixed-time synchronization. Chen et al. (2019) derived a new fixed-time stability theorem, and sufficient conditions were derived to guarantee the fixed-time synchronization of neural networks. Yang et al. (2019) investigated the fixed-time synchronization of memristor-based neural networks with time-delay and coupling. The research of fixed-time stability promotes the development of many practical applications. In some practical engineering applications, the system is required to reach the origin in the specified time, but the main disadvantage of fixed-time stability is that the relationship between the system parameters and the convergence time is not clear. Then, Sanchez-Torres et al. (2014) proposed the definition of predefined-time stability, which could be solved by adjusting the parameters in the process of controller design. Therefore, the system can achieve stability before the predefined-time Tc. Predefined-time stability is the result of fixed-time stability optimization. At present, there are some research results on predefined-time synchronization. Lin et al. (2020) proposed a predefined-time stability theorem based on a piecewise Lyapunov function, in which the Lyapunov function should satisfy the inequality: with α, c, p > 0, Gc is the minimum upper bound for fixed-time stability and Tc is a custom parameter. Aldana-Lopez et al. (2019) studied more relaxed predefined time stability conditions, where the Lyapunov function should satisfy the inequality with α, β > 0, p> 1 and 0 < q < 1. Anguiano-Gijon et al. (2019) introduced Gc into inequality in the form of with 0 < q < 1. The predefined-time stability theorem proposed in this paper is more general than (Aldana-Lopez et al., 2019; Anguiano-Gijon et al., 2019; Lin et al., 2020). Synchronization has important applications in many fields, such as secure communication, nonlinear control systems, pattern recognition, and information processing (Alimi et al., 2019; Ouyang et al., 2020). Synchronization also plays an important role in laser systems, superconducting materials, and conventional bus dispatching (Gkiotsalitis et al., 2020; Wang et al., 2021). In addition, Su et al. (2020) studied the manipulator control based on an improved recurrent neural network. The ultimate end-effector tracking error can reach asymptotic convergence, which is also a concrete manifestation of synchronous control.
This paper also studies the image encryption scheme based on MCVBAMNNs. As we all know, the research results of brain-like neural networks have shown great power in practical applications. Memristor-based neural networks, which are more similar to the structure of human synapses, also show unique functions and values in the application. The digital image is an important way to represent information, research on image data privacy protection based on a general memristor-based neural network learning mode has broad application prospects. However, there are still few studies on image data privacy protection using memristor-based artificial neural networks and their network behavior characteristics. As an ideal tool to simulate human neural networks, memristor-based neural networks can be used to maximize the ability of the human brain to recognize and classify, which shows the potential of memristor-based neural networks in pattern recognition. Recognition and classification of sensitive areas of digital images and proposing appropriate privacy protection solutions can give full play to the advantages of memory-based neural networks in recognition and classification and have a wide range of applications.
Motivated by the above discussions, we investigated the fixed-time synchronization and the predefined-time synchronization of MCVBAMNNs with leakage time-varying delay. The innovations of this paper are presented as follows: First, based on the appropriate fixed-time stability lemma, the feedback controller is designed, and the fixed-time synchronization problem of MCVBAMNNs is studied. By comparison, the results of this paper are less conservative. Second, a new predefined-time stability theorem is introduced, where the predefined time is set more flexibly and in a more general form. Thirdly, a more simple and effective discontinuous controller is designed, and sufficient conditions for MCVBAMNNs to achieve predefined-time synchronization are obtained. The synchronization time does not depend on the initial value and can be adjusted according to the controller parameters. Finally, an image encryption and decryption scheme based on predefined-time synchronization is presented, and the predefined time can be used as the secret key. Numerical simulation verifies the validity of the theoretical results and the feasibility of the encryption scheme.
Notations: In this study, ℝ, ℂ, ℝn, and ℂn represent the real field, complex field, n-dimensional real space, and n-dimensional complex space, respectively. u = R + Ii ∈ ℂ, where i meets .
2. Problem formulation and preliminaries
We consider the following MCVBAMNNs as the drive system, which is given as:
where i = 1, 2, ..., n, j = 1, 2, ...m; represent the voltage of the capacitor ith and jth nodes at time t. The initial values of the system (1) are and , s ∈ ℝ; and : ℂ → ℂ are complex-valued activation functions; τ(t) and σ(t) are the leakage time-varying delays satisfying 0 < τ(t) < σ(t) < C (C is a constant); and are the rates of neuron self-inhibition; , , , are the memristive connection weights.
The parameters signification and performance of MCVBAMNNs are described as:
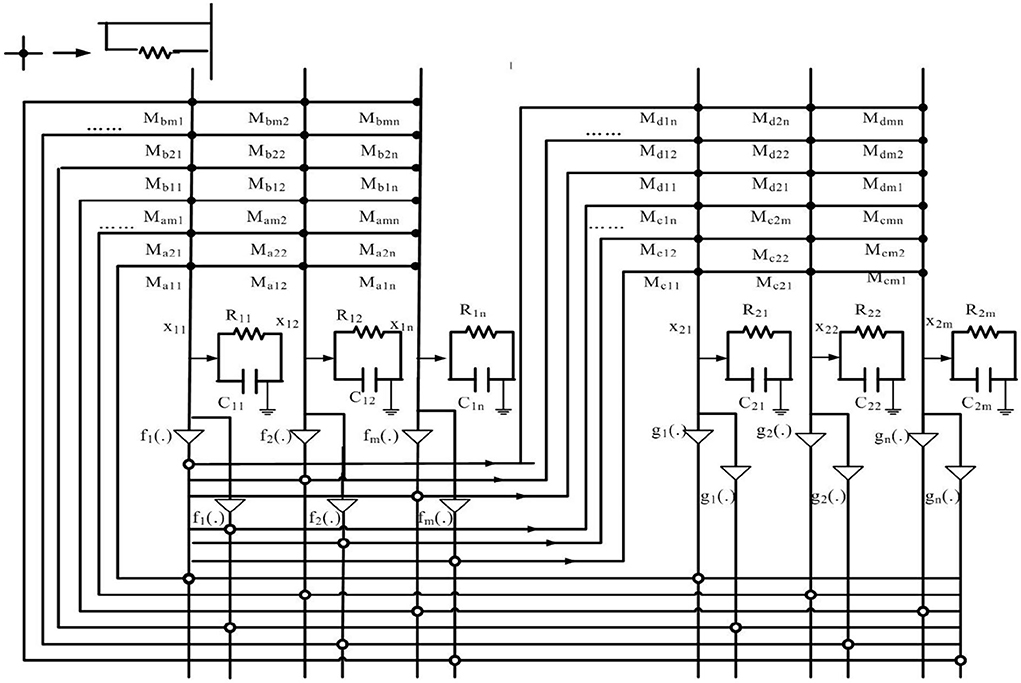
The memristor-based BAM neural networks model can be implemented by very large-scale integration (VLSI) circuits as shown in Figure 1. Taking a real-valued system as an example, where signij = signij = 1 if i ≠ j, otherwise signij = signij = −1, x1i(·) and x2j(·) represent the state of the subsystems, fj(·) and gi(·) are amplifiers, Maji is the connection memristor between the amplifier fj(x2j(t)) and state x1i(t), Mbji is the connection memristor between the amplifier fj(x2j(t−σ(t))) and state x1i(t), Mcij is the connection memristor between the amplifier gi(x1i(t)) and state x2j(t), Mdij is the connection memristor between the amplifier gi(x1i(t−τ(t))) and state x2j(t), Rij and Cij are the resistor and capacitor.
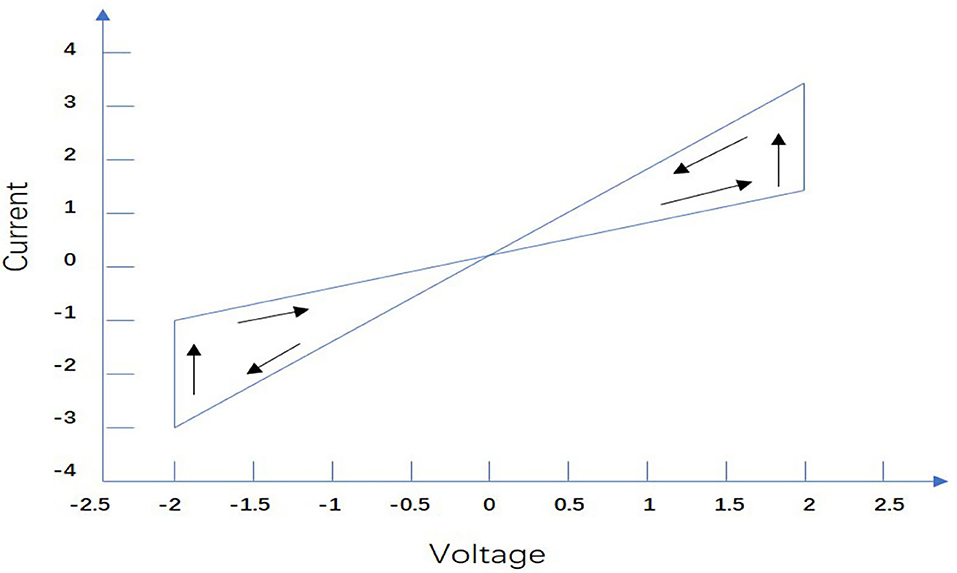
Figure 2 illustrates the simplified current- voltage characteristics of the memristor, we define the neuron self-inhibition and connection weight as the following state correlation functions:
where the switching jumps .
System (1) is called the drive system, the response system can be described as follows:
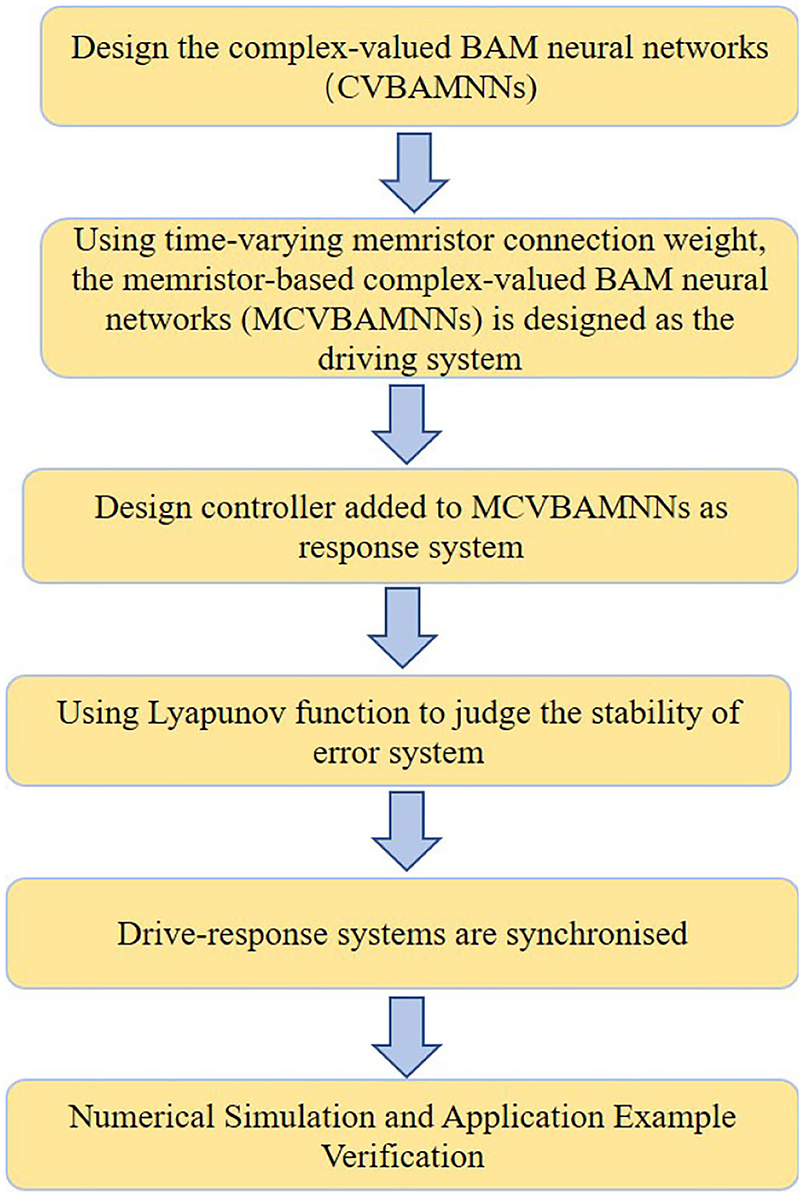
where i = 1, 2, ..., n, j = 1, 2, ...m; . The initial values of the system (2) are and . and are denoted as controllers. The remaining parameters are similar to those of the drive system. To better understand the following work, Figure 3 is the flow chart of the system.
Definition 1. Filippov (1999) consider dynamical systems with discontinuous right-hand side ẋ(t) = F(t, x), x(t) is a solution of the differential system on [0,T) in Filippov's sense, if x(t) is absolutely continuous and satisfies the differential inclusion of
where
where is the convex closure hull of a set, B(x, δ) = {y:∥y − x∥ ≤ δ} is the ball centered at x(t) with radius δ, and μ(N) is the Lebesgue measure of set N.
Definition 2. Hu et al. (2017) the MCVBAMNNs (1) and (2) are said to achieve fixed-time synchronization if there exists a fixed-time Tmax>0, which is independent of the initial values but may be relevant with some parameters of MCVBAMNNs and controller, and a settling time function T(e(0)) ≤ Tmax such that and ∥e(t)∥2 ≡ 0 for ∀t > T(e(0)).
Definition 3. Anguiano-Gijon et al. (2019) if the settling time T(e(0)) of fixed-time stability can be predicted by adjusting the constant Tc, it means that the drive-response systems can achieve globally predefined-time stability, where T(e(0)) ≤ Tc, ∀e(0) ∈ ℝn.
Remark 1. Predefined-time synchronization is a special kind of fixed-time synchronization. The problem of predefined-time synchronization of drive-response systems can be converted into the predefined-time stability of the error systems. The purpose of this paper is to design an appropriate controller to stabilize the error systems in the expected time by adjusting the controller parameter Tc.
Based on Definition 1 and the theory of differential inclusion, the drive system (1) can be written as
The response system (2) is represented as
To obtain the synchronization criteria by set-valued mapping, let
The synchronization errors are defined as , , we can conclude that
where i = 1, 2, ..., n, j = 1, 2, ..., m; the initial values of error system (5) are , , , . We define P(t), , H(t), Ĥ(t), , , , as follows:
Assumption 1. Suppose the activation functions satisfy , , , , for are positive constants, i = 1, 2, ..., n, j = 1, 2..., m.
Lemma 1. Guo et al. (2020) the following inequality holds: , , , for
Lemma 2. Hardy et al. (1952) if α1, α2, ..., αn ≥ 0, 0 < ρ ≤ 1, ζ > 1, then we have
Lemma 3. Chen et al. (2020) suppose the continuous and positive definite function V(t) satisfies the following two conditions:
(i) V(t) = 0 ⇔ t = 0;
(ii) Any solution t of system V(t) satisfies
for a, b, c > 0, 0 < ρ < 1, and ζ > 1. Then the origin of the system V(t) is fixed-time stable and the settling time is estimated by
Lemma 4. Polyakov (2012) suppose the continuous and positive definite function V(t) satisfies the following two conditions:
(i) V(t) = 0 ⇔ t = 0;
(ii) Any solution t of system V(t) satisfies
for a, b > 0, 0 < ρ < 1, and ζ > 1, where D+V(t) denotes the upper right-hand Dini derivative of V(t). Then the origin of the system V(t) is fixed-time stable and the settling time is estimated by
Lemma 5. Hu et al. (2017) suppose the continuous and positive definite function V(t) satisfies the following two conditions:
(i) V(t) = 0 ⇔ t = 0;
(ii) Any solution t of system V(t) satisfies
for a, b > 0, 0 < ρ < 1, and ζ > 1. Then the origin of the system V(t) is fixed-time stable and the settling time is estimated by
Lemma 6. Parsegov et al. (2013) suppose the continuous and positive definite function V(t) satisfies the following two conditions:
(i) V(t) = 0 ⇔ t = 0;
(ii) Any solution t of system V(t) satisfies
for , and , where d > 1. Then the origin of the system V(t) is fixed-time stable, and the settling time is estimated by
Remark 2. If m > 0, ln(1 + m) < m. Since ,, we have , , then . Therefore, Lemma 3 can give a more accurate Tmax than Lemma 4.
Remark 3. Most of the designed controllers are discontinuous. To ensure the solution existence of the error system, the Dini derivative is introduced to guarantee continuity at breakpoints.
3. Main results
3.1. Fixed-time synchronization analysis
We design the following controller:
where i = 1, 2, ..., n, j = 1, 2, ..., m, and the constants wi, , , ki, , , pj, , , qj, , should be determined later. Meanwhile, λ2i, λ3i, λ4i, k2j, k3j, k4j are any positive constants, and 0 < α < 1, β > 1.
Theorem 1. If , , , , , , , , , , , , i = 1, 2, ..., n, j = 1, 2, ..., m, then systems (1) and (2) can achieve the fixed-time synchronization under the controller (14). Additionally, the settling time is , where , , b = 2μ, , c = 2ω, , , .
Proof 1. To prove this theorem, we construct the Lyapunov function as follows:
where , , , .
We calculate the derivative of :
According to Assumption 1 and Lemma 1, we have
The proofs of , , and are similar with that of :
According to the analysis above, we can obtain that
Therefore, we get
According to the above results and referring to Lemma 3, it can be obtained that the systems (1) and (2) have achieved fixed-time synchronization under controller (14). Then the settling time , and , , b = 2μ, , c = 2ω, where , , .
Corollary 1. If , , , , , , , , , , , , i = 1, 2, ..., n, j = 1, 2, ..., m, then the systems (1) and (2) can achieve fixed-time synchronization under the controller (14). Furthermore, , where , , b = 2μ, .
Proof 2. Similarly, it can be proved that
where , b = 2μ, c = 2ω, , . Since the Lyapunov function Vu(t) is derivable, we have . Therefore,
According to Lemma 4, the origin of system (5) can achieve fixed-time stability.
Corollary 2. If , , , , , , , , , , , , i = 1, 2, ..., n, j = 1, 2, ..., m. According to Lemma 5, systems (1) and (2) can achieve fixed-time synchronization under the controller (14). Furthermore, . where , , b = 2μ, , , . The proof process is similar to Corollary 1, so it is omitted here.
Corollary 3. If , , , , , , , , , , , , i = 1, 2, ..., n, j = 1, 2, ..., m. According to Lemma 6, systems (1) and (2) can achieve fixed-time synchronization under the controller (14). Furthermore, where , b = 2μ, , . The proof process is similar to Corollary 1, so it is omitted here.
3.2. Predefined-time synchronization analysis
Theorem 2. For system (5), if there exists a continuous and positive definite function V(e(t)):ℂn → ℝ, Tc is a user-defined parameter, and the following conditions hold:
(i) V(e(t)) = 0 ⇔ e(t) = 0;
(ii) For any V(e(t)) > 0, there exist a, b, c > 0, 0 < p < 1, q > 1 satisfying
then the origin of system (5) is predefined-time stable within predefined time Tc, in which
Proof 3. For any V(e(t)) > 0, the corresponding analysis is shown as follows:
The setting time function is given as follows:
Then we have
Let W = V1−p, dW = (1−p)V−pdV, , then we have
Let Z = V1−q, dZ = (1−q)V−qdV, , then we have
Therefore, we have
In order to realize the predefined-time synchronization of systems (1) and (2), we designed the following controller:
Theorem 3. If , , , , , , , , , , , , i = 1, 2, ..., n, j = 1, 2, ..., m, , systems (1) and (2) can achieve the predefined-time synchronization within predefined time Tc and the controller (15), where , b = 2μ, c = 2ω, , , , , .
Proof 4. To prove this theorem, we construct the Lyapunov function as follows:
where , , , .
We calculate the derivative of as follows:
According to Assumption 1 and Lemma 1, we have
The proofs of , and are similar with that of . Additionally, we have
According to the analysis above, we can obtain that
Therefore,
where , , b = 2μ, , c = 2ω, , , .Under Theorem 2, the drive system (1) and the response system (2) can achieve predefined-time synchronization under the controller (15). The proof is completed.
Remark 4. In Theorems 2 and 3, the error system (5) can achieve predefined-time stability, in which Gc can be considered as the minimum upper bound Tmax of the stability time in fixed-time stability. In addition, the theorem also provides a tuning parameter Tc to adjust the stability time to the expected value.
4. Numerical examples
Three examples are shown in this section. Example 1 demonstrates the effects of Theorem 1, Example 2 verifies the validity of the predefined-time synchronization in Theorems 2 and 3, and Example 3 is an application of image encryption and decryption.
Example 1. The simulation model is a two-dimensional MCVBAMNNs with time-varying delays, and it is shown as follows:
The response system is
where i = 1, 2, j = 1, 2; , ; ; , ; τ(t) = t+0.1sin(t), σ(t) = t−0.1cos(t). The initial values of system (16) are φ1R(s) = (1, 2.1)T, φ1I(s) = (1.3, −1)T, φ2R(s) = (0.4, 1.2)T, φ2I(s) = (1, 0.25)T. The initial values of system (17) are ϕ1R(s) = (0.9, −1)T, ϕ1I(s) = (1.1, 0.75)T, ϕ2R(s) = (0.5, −0.8)T, ϕ2I(s) = (−0.6, 1.4)T. The memristor-based connection weights are listed as follows:
Some real and imaginary parts phase plots of the drive system (16) are shown in Figure 4. We choose wi = 1.5, ki = 1, pj = 1.3, qj = 1; ; λ2i = 12, k2j = 20; λ3i = λ4i = 0.4; k3j = k4j = 0.6. Errors of the drive system (16) and the response system (17) without and with feedback controller (14) are shown in Figures 5A,B, respectively.
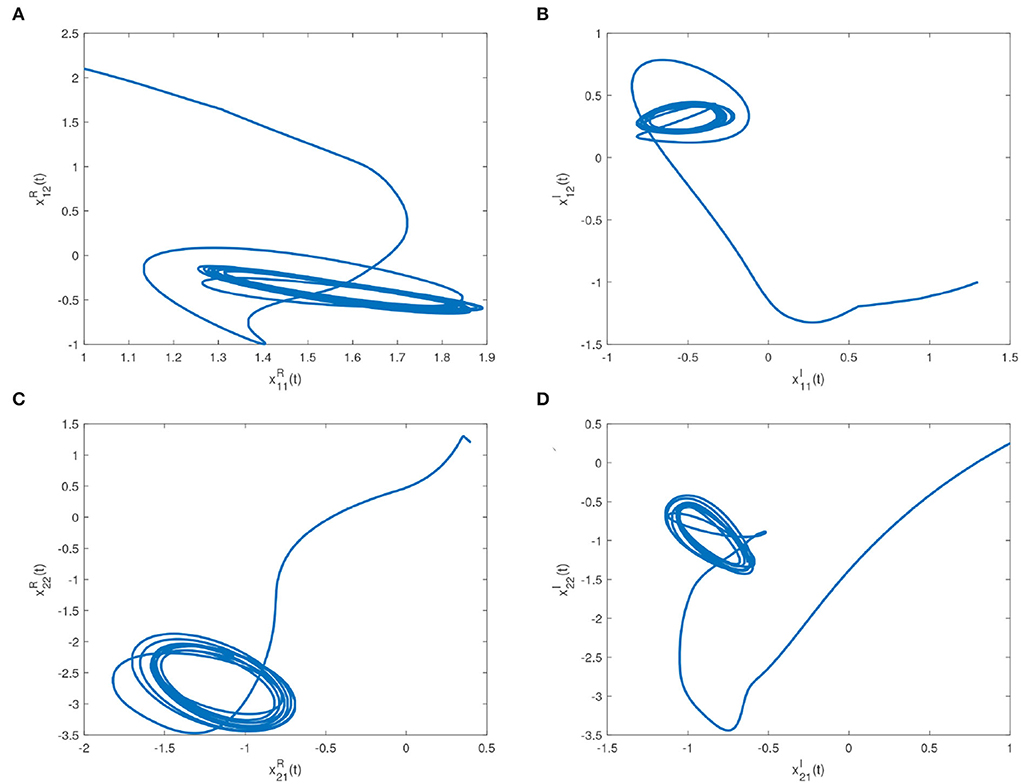
Figure 4. Real part and imaginary part phase plots of the drive system (16). (A) Phase plot of real part with initial conditions , . (B) Phase plot of imaginary part with initial conditions , . (C) Phase plot of real part with initial conditions , . (D) Phase plot of imaginary part with initial conditions , .
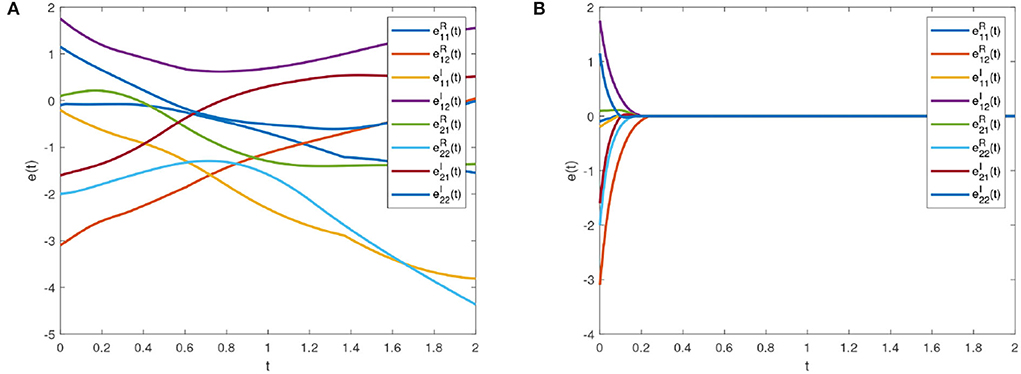
Figure 5. Error system trajectories of the drive system (16) and response system (17). (A) Synchronization errors without control. (B) Synchronization errors under control.
Table 1 shows that is much smaller than with the same controller parameters. In Table 1, is derived by Theorem 1 and Lemma 3, is derived by Corollary 1 and Lemma 4, is derived by Corollary 2 and Lemma 5, and is derived by Corollary 3 and Lemma 6. Therefore, compared with Corollaries 1-3, Theorem 1 provides a more strict upper bound estimation formula.
Example 2. According to Theorems 2-3, the settling time of the error system (5) can be adjusted by a tuning parameter Tc.
We set two initial values:
(1) Initial value 1: φ1R(s) = (1, 2.1)T, φ1I(s) = (1.3, −1)T, φ2R(s) = (0.4, 1.2)T, φ2I(s) = (1, 0.25)T. ϕ1R(s) = (0.9, −1)T, ϕ1I(s) = (1.1, 0.75)T, ϕ2R(s) = (0.5, −0.8)T, ϕ2I(s) = (−0.6, 1.4)T;
(2) Initial value 2: φ1R(s) = (0.5, 2.5)T, φ1I(s) = (1.3, −1.5)T, φ2R(s) = (2, 1.25)T, φ2I(s) = (1.5, 0.25)T. ϕ1R(s) = (0.9, −1.5)T, ϕ1I(s) = (1.1, −1.2)T, ϕ2R(s) = (0.5, −1.8)T, ϕ2I(s) = (−0.6, 1.4)T.
Figure 6 is the synchronization error diagram when Tc = 5. Figures 6A,B show that different initial values can achieve synchronization within a given time. Figure 7 is the synchronization error diagram when Tc = 0.5. From Figures 6, 7, it can be seen that the actual synchronization time is changed according to Tc. We can set the ideal synchronization time Tc in the controller, which is that the system can achieve predefined-time stability.
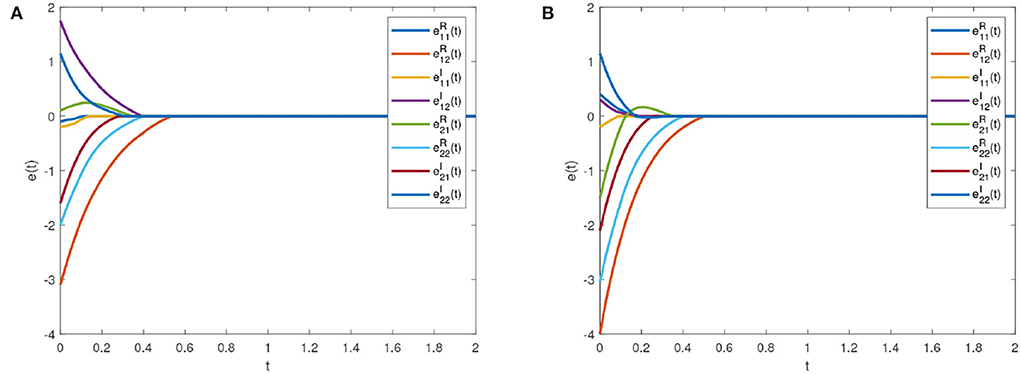
Figure 6. Synchronization errors with Tc = 5. (A) Synchronization errors with initial value 1. (B) Synchronization errors with initial value 2.
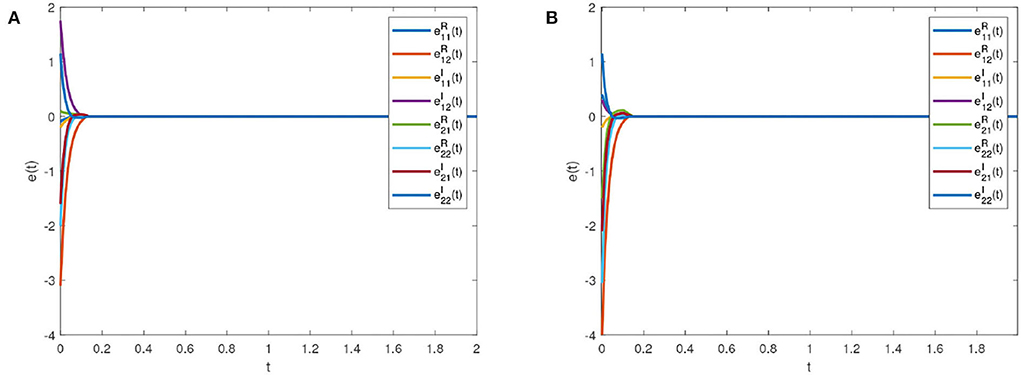
Figure 7. Synchronization errors with Tc = 0.5. (A) Synchronization errors with initial value 1. (B) Synchronization errors with initial value 2.
Example 3. We use the predefined-time stability and chaotic characters of the drive system (16) and response system (17) to achieve image encryption and decryption. The proposed image encryption algorithm consists of pixel scrambling and diffusion.
We choose Tc = 0.2, and the other parameters are the same as in Example 1. According to the drive system (16), our encryption algorithm is designed as follows.
Step 1. Enter the color original image “Lena” with the size of M × N × 3, where M = 256, N = 256.
Step 2. According to of the drive system (16), we can get the real part sequence and imaginary part sequence , . Based on the descending order of chaotic sequences and , the index of the sequences ϱ1 and ϱ2 is obtained.
ϱ1 is used to scramble half of the original image, and ϱ2 is used to scramble the other half of the original image.
Step 3. Scramble the pixels of R, G, B channels and compose new channels.
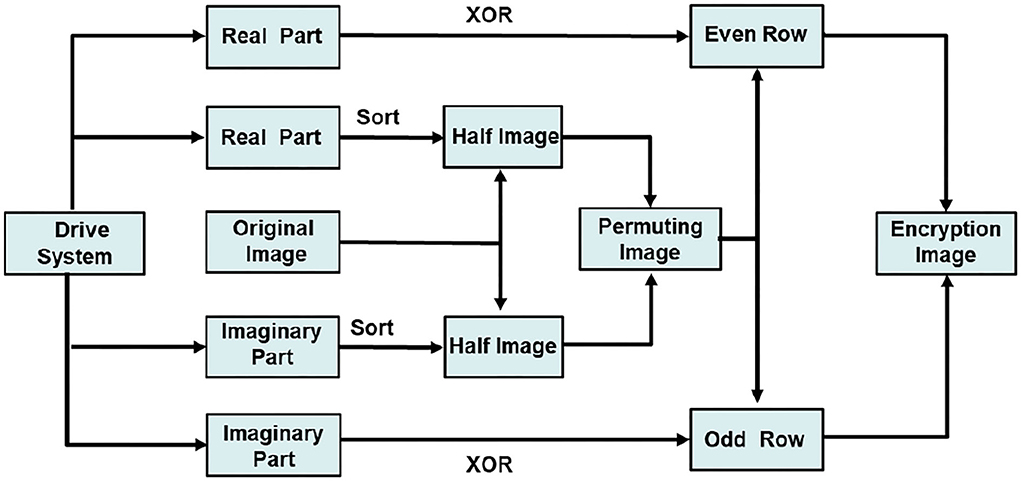
Step 4. Converts and of the drive system (16) into M×N dimension matrices z1(i, j) and z2(i, j). Encrypt the channel as follows. For even-row pixels,
for odd-row pixels,
use x21 and x22 to encrypt channels according to the above method, respectively.
The original picture is shown in Figure 8A. We use a chaotic sequence to scramble the pixels in the encrypted area, as shown in Figure 8B. The final encrypted image is shown in Figure 8C. When the drive system (16) and the response system (17) reach predefined-time synchronization, decryption is the opposite process of encryption, and the decrypted picture is shown in Figure 8D.

Figure 8. Original encryption and decryption pictures. (A) Original picture “Lena.” (B) Pixel scrambling picture. (C) The encrypted picture. (D) The decrypted picture (This image is taken from a public database).
According to MCVBAMNNs and predefined-time synchronization, the flow charts of image encryption and decryption are shown in Figures 9, 10. We use the controller (15) to flexibly set the parameter Tc, then the chaotic sequence can be selected in a controllable range, which ensures the effectiveness of the encryption and decryption algorithm. In this scheme, Tc = 0.2 is chosen as the secret key, and the wrong secret key will affect the decryption result.
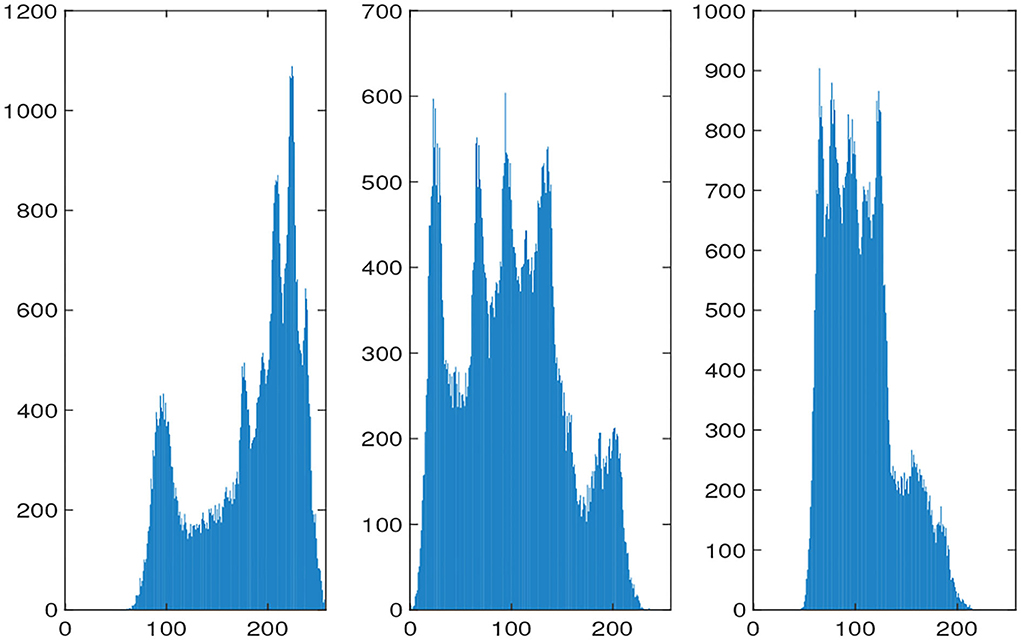
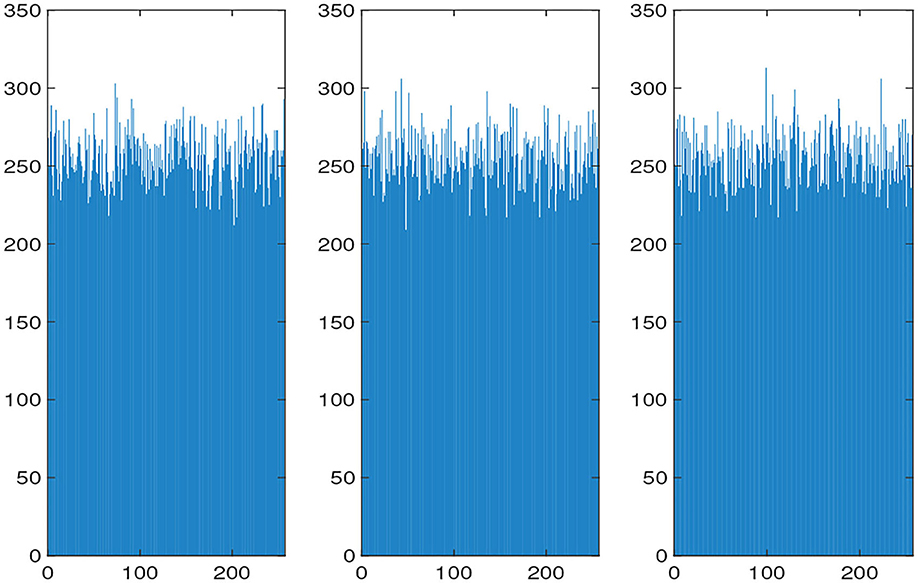
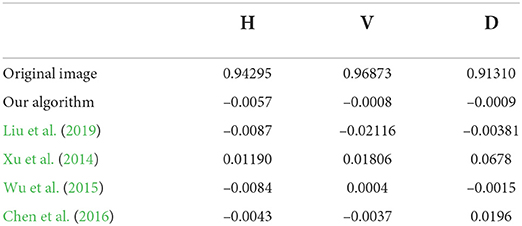
The histograms of the original and encrypted image are shown in Figures 11, 12, which shows that the histograms of the encryption image become highly disordered. In a digital image, there is a high correlation between each pixel. Therefore, the pixel adjacency correlation of encrypted images generated by a reasonable encryption algorithm should be close to zero. The horizontal correlation coefficients of the original and the encryption image in the R are shown in Figures 13, 14. The correlation coefficient of the encryption image becomes much lower. Table 2 lists the correlation coefficients of the encryption algorithm and the comparisons with others, which indicates our algorithm has good results1.
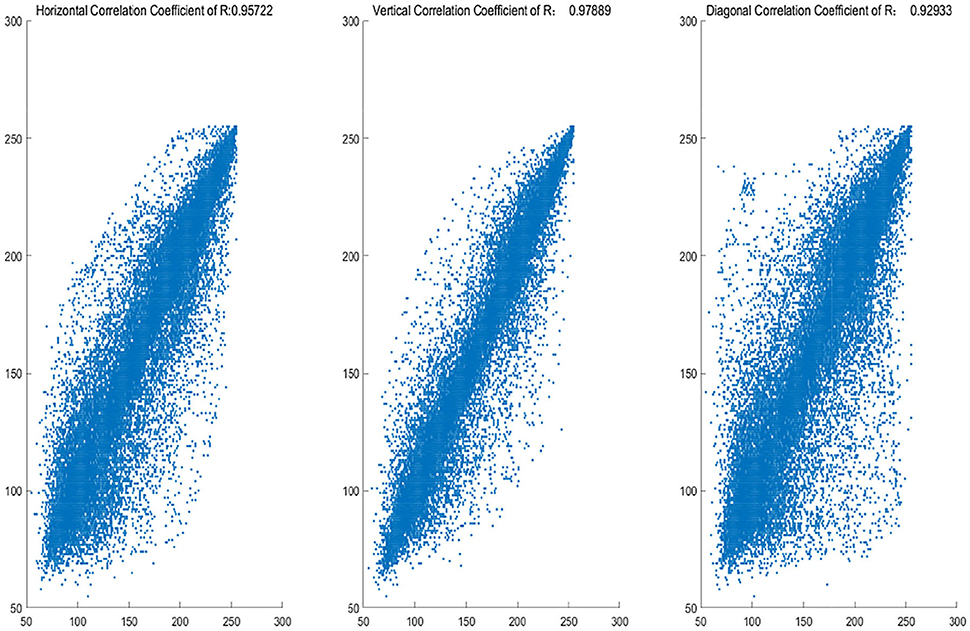
Figure 13. R-channel correlation coefficients of the original image (From left to right: Horizontal Correlation Coefficient of R: 0.95722; Vertical Correlation Coefficient of R: 0.9789; Diagonal Correlation Coefficient of R: 0.92933).
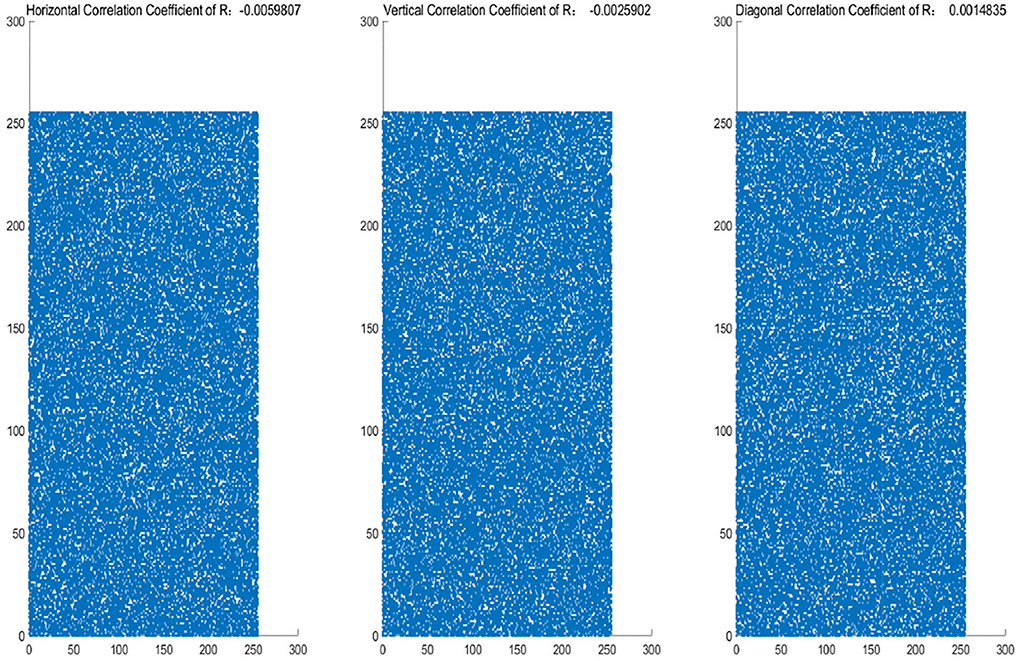
Figure 14. R-channel correlation coefficients of encryption image (from left to right:Horizontal Correlation Coefficient of R:-0.0059807; Vertical Correlation Coefficient of R: -0.0025902; Diagonal Correlation Coefficient of R: 0.0014835).
Remark 5. Digital images can convey information intuitively and effectively and are widely used. A considerable part of images in daily life and work contains sensitive data and belong to sensitive areas. If the sensitive block data is not protected, it may cause some losses to individuals or other objects. Therefore, the image encryption and decryption scheme based on the predefined-time synchronization of MCVBAMNNs in this paper has important application value for the privacy protection of image blocks with uncertain size without losing image availability. For example, Figure 15 is a picture containing employee information. In order to avoid privacy disclosure, important information such as ID numbers or mobile phone numbers can be encrypted.
Remark 6. At present, most of the neural network dynamics achievements are still in the theoretical stage, and the research on relevant practical applications is not extensive enough. But fortunately, researchers are aware of this problem and are trying to explore its future research direction, such as its application in human-computer interaction (Su et al., 2022).
5. Conclusion
In this paper, the fixed-time and predefined-time stability of MCVBAMNNs with leakage time-varying delay is studied. Based on differential inclusion and set-valued mapping theory, an effective discontinuous controller is designed, sufficient conditions for conservative smaller fixed-time synchronization are obtained, and a more general predefined-time stability theorem is proposed. By adjusting the controller parameters, the MCVBAMNNs can achieve synchronization within a predetermined time. On this basis, we design an effective image encryption scheme. Through comparative analysis, the algorithm proposed in this paper has good results. Inspired by Feng et al. (2020), in the future, we will consider the method of complex-valued nonseparation and propose more general predefined-time stability conditions, which will be an interesting and challenging job.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author contributions
AL: formal analysis, validation, and writing—original draft. HZ: data curation and funding acquisition. QW: data curation. SN: funding acquisition and supervision. XG, ZS, and LL: funding acquisition and supervision. All authors contributed to the article and approved the submitted version.
Funding
This study is supported by the National Natural Science Foundation of China (Grant Nos. 62103165, 62032002, 62101213, and 61902048), the Natural Science Foundation of Shandong Province (Grant No. ZR2020QF107), the Natural Science Foundation of Beijing Municipality (Grant No. M21034), the Chongqing High Tech Research Program (Grants No. cstc2018jcyjAX0279), and Development Program Project of Youth Innovation Team of Institutions of Higher Learning in Shandong Province.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^Code is available at: https://github.com/Liu-aidi/MCVBAMNNs.
References
Aldana-Lopez, R., Gomez-Gutierrez, D., Jimenez-Rodriguez, E., Sanchez-Torres, J., and Defoort, M. (2019). Enhancing the settling time estimation of a class of fixed-time stable systems. Int. J. Robust Nonlinear Control 29, 4135–4148. doi: 10.1002/rnc.4600
Alimi, A., Aouiti, C., and Assali, E. (2019). Finite-time and fixed-time synchronization of a class of inertial neural networks with multi-proportional delays and its application to secure communication. Neurocomputing 332, 29–43. doi: 10.1016/j.neucom.2018.11.020
Anguiano-Gijon, C., Munoz-Vazquez, A., Sanchez-Torres, J., Romero-Galvan, G., and Martinez-Reyes, F. (2019). On predefined-time synchronization of chaotic systems. Chaos Solitons Fractals 122, 172–178. doi: 10.1016/j.chaos.2019.03.015
Cao, J., and Li, R. (2017). Fixed-time synchronization of delayed memristor-based recurrent neural networks. Sci. China 60, 108–122. doi: 10.1007/s11432-016-0555-2
Chen, C., Li, L., Peng, H., Yang, Y., Mi, L., and Wang, L. (2019). A new fixed-time stability theorem and its application to the synchronization control of memristive neural networks. Neurocomputing 349, 290–300. doi: 10.1016/j.neucom.2019.03.040
Chen, C., Li, L., Peng, H., Yang, Y., Mi, L., and Zhao, H. (2020). A new fixed-time stability theorem and its application to the fixed-time synchronization of neural networks. Neural Netw. 123, 412–419. doi: 10.1016/j.neunet.2019.12.028
Chen, W., Luo, S., and Zheng, W. (2016). Impulsive synchronization of reactiondiffusion neural networks with mixed delays and its application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 27, 2696–2710. doi: 10.1109/TNNLS.2015.2512849
Chua, L. (1971). Memristor-the missing circuit element. IEEE Trans. Circ. Theory 18, 507–519. doi: 10.1109/TCT.1971.1083337
Feng, L., Yu, Y., Hu, C., Yang, C., and Jiang, H. (2020). Nonseparation methosd-based finite/fixed-time synchronization of fully complex-valued discontinuous neural networks. IEEE Trans. Cybern. 99, 1–12. doi: 10.1109/TCYB.2020.2980684
Filippov, A. (1999). Differential equations with diacontinuous right-hand side. J. Matemat. Anal. Appl. 154, 99–128.
Gkiotsalitis, K., Eikenbroek, O., and Cats, O. (2020). Robust network-wide bus scheduling with transfer synchronizations. IEEE Trans. Intell. Transport. Syst. 21, 4582–4592. doi: 10.1109/TITS.2019.2941847
Guo, Y., Luo, Y., Wang, W., and Luo, X. (2020). Fixed-time synchronization of complex-valued memristive bam neural network and applications in image encryption and decryption. Int. J. Control Autom. Syst. 18, 462–476. doi: 10.1007/s12555-018-0676-7
Hardy, G., Littlewood, J., and Polya, G. (1952). Inequalities. Cambridge: Cambridge University Press.
Hu, C., Yu, J., Chen, Z., Jiang, H., and Huang, T. (2017). Fixed-time stability of dynamical systems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw. 89, 74–83. doi: 10.1016/j.neunet.2017.02.001
Ke, Y., and Miao, C. (2013). Stability and existence of periodic solutions in inertial bam neural networks with time delay. Neural Comput. Appl. 23, 1089–1099. doi: 10.1007/s00521-012-1037-8
Kosko, B. (1988). Bidirectional associative memories. IEEE Trans. Syst. Man Cybern. 18, 49–60. doi: 10.1109/21.87054
Li, L., and Mu, G. (2019). Synchronization of coupled complex-valued impulsive neural networks with time delays. Neural Process. Lett. 50, 2515–2527. doi: 10.1007/s11063-019-10028-6
Li, N., and Cao, J. (2016). Lag synchronization of memristor-based coupled neural networks via ω-measure. IEEE Trans. Neural Netw. Learn. Syst. 27, 686–697. doi: 10.1109/TNNLS.2015.2480784
Lin, L., Wu, P., Chen, Y., and He, B. (2020). Enhancing the settling time estimation of fixed-time stability and applying it to the predefined-time synchronization of delayed memristive neural networks with external unknown disturbance. Chaos 30, 083110. doi: 10.1063/5.0010145
Liu, A., Zhao, H., aand, S., Niu, Q. W., Gao, X., Chen, C., et al. (2022). A new predefined-time stability theorem and its application in the synchronization of memristive complex-valued bam neural networks. Neural Netw. 153, 152–163. doi: 10.1016/j.neunet.2022.05.031
Liu, D., Zhu, S., and Ye, E. (2017). Synchronization stability of memristor-based complex-valued neural networks with time delays. Neural Netw. 96, 115–127. doi: 10.1016/j.neunet.2017.09.008
Liu, X., Song, Y., and Jiang, G. (2019). Hierarchical bit-level image encryption based on chaotic map and feistel network. Int. J. Bifurcat. Chaos 29, 1950016. doi: 10.1142/S0218127419500160
Ouyang, D., Shao, J., Jiang, H., Nguang, S., and Shen, H. (2020). Impulsive synchronization of coupled delayed neural networks with actuator saturation and its application to image encryption. Neural Netw. 128, 158–171. doi: 10.1016/j.neunet.2020.05.016
Parsegov, S., Polyakov, A., and Shcherbakov, P. (2013). Nonlinear fixed-time control protocol for uniform allocation of agents on a segment. Doklady Math. 87, 133–136. doi: 10.1134/S106456241301033X
Polyakov, A. (2012). Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Automat. Contr. 57, 2106–2110. doi: 10.1109/TAC.2011.2179869
Qi, J., Li, C., and Huang, T. (2015). Stability of inertial bam neural network with time varying delay via impulsive control. Neurocomputing 161, 162–167. doi: 10.1016/j.neucom.2015.02.052
Rubinov, M., and Sporns, O. (2010). Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069. doi: 10.1016/j.neuroimage.2009.10.003
Sanchez-Torres, J., Sanchez, E., and Loukianov, A. (2014). “A discontinuous recurrent neural network with predefined time convergence for solution of linear programming,” in 2014 IEEE Symposium on Swarm Intelligence (Orlando, FL: IEEE), 1–4.
Strukov, D., Snider, G., Stewart, D., and Williams, R. (2008). The missing memristor found. Nature 453, 80–83. doi: 10.1038/nature06932
Su, H., Hu, Y., Karimi, H., Knoll, A., Ferrigno, G., and Momi, E. (2020). Improved recurrent neural network-based manipulator control with remote center of motion constraints: experimental results. Neural Netw. 131, 291–299. doi: 10.1016/j.neunet.2020.07.033
Su, H., Qi, W., Li, Z., Chen, Z., Ferrigno, G., and Momi, E. (2021). Deep neural network approach in emg-based force estimation for human-robot interaction. IEEE Trans. Artif. Intell. 2, 404–412. doi: 10.1109/TAI.2021.3066565
Su, H., Qi, W., Schmirander, Y., Ovur, S., Cai, S., and Xiong, X. (2022). A human activity-aware shared control solution for medical human-robot interaction. Assembly Automat. 42, 388–394. doi: 10.1108/AA-12-2021-0174
Wang, H., Duan, S., Huang, T., Wang, L., and Li, C. (2017). Exponential stability of complex-valued memristive recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 28, 766–771. doi: 10.1109/TNNLS.2015.2513001
Wang, Z., Wu, W., Zhu, T., Hua, K., Chang, S., annd, F., et al. (2021). High-power synchronous multi-wavelength solitons from a multimode mode-locked fiber laser system. Opt. Lett. 46, 118–121. doi: 10.1364/OL.412739
Wen, Q., and Su, H. (2022). A cybertwin based multimodal network for ecg patterns monitoring using deep learning. IEEE Trans. Ind. Inform. 18, 6663–6670. doi: 10.1109/TII.2022.3159583
Wu, X., Kan, H., and Kurths, J. (2015). A new color image encryption scheme basedon dna sequences and multiple improved 1d chaotic maps. Appl. Soft. Comput. 37, 24–39. doi: 10.1016/j.asoc.2015.08.008
Xu, Y., Wang, H., Li, Y., and Pei, B. (2014). Image encryption based on synchronization of fractional chaotic systems. Commun. Nonlinear Sci. Num. Simulat. 19, 3735–3744. doi: 10.1016/j.cnsns.2014.02.029
Yang, C., Huang, L., and Cai, Z. (2019). Fixed-time synchronization of coupled memristor-based neural networks with time-varying delays. Neural Netw. 116, 101–109. doi: 10.1016/j.neunet.2019.04.008
Yang, N., Yu, Y., Zhong, S., Wang, X., Shi, K., and Cai, J. (2020). Exponential synchronization of stochastic delayed memristive neural networks via a novel hybrid control. Neural Netw. 131, 242–250. doi: 10.1016/j.neunet.2020.07.034
You, X., Song, Q., and Zhao, Z. (2020). Global mittag-leffler stability and synchronization of discrete-time fractional-order complex-valued neural networks with time delay. Neural Netw. 122, 382–394. doi: 10.1016/j.neunet.2019.11.004
Zhang, L., and Yang, Y. (2020). Finite time impulsive synchronization of fractional order memristive bam neural networks. Neurocomputing 384, 213–224. doi: 10.1016/j.neucom.2019.12.056
Zhang, W., Cao, J., Chen, D., and Alsaadi, F. (2018). Synchronization in fractional-order complex-valued delayed neural networks. Entropy 20, 54. doi: 10.3390/e20010054
Zhang, Z., Cao, J., and Zhou, D. (2014). Novel lmi-based condition on global asymptotic stability for a class of cohen-grossberg bam networks with extended activation functions. IEEE Trans. Neural Netw. Learn. Syst. 25, 1161–1172. doi: 10.1109/TNNLS.2013.2289855
Zhang, Z., and Quan, Z. (2015). Global exponential stability via inequality technique for inertial bam neural networks with time delays. Neurocomputing 151, 1316–1326. doi: 10.1016/j.neucom.2014.10.072
Zhao, H., Liu, A., Wang, Q., Zheng, M., Chen, C., Niu, S., et al. (2021). Predefined-time stability/synchronization of coupled memristive neural networks with multi-links and application in secure communication. Front. Neurorobot. 15, 783809. doi: 10.3389/fnbot.2021.783809
Keywords: fixed-time synchronization, predefined-time synchronization, bidirectional associative memory, image encryption and decryption, complex-valued neural networks
Citation: Liu A, Zhao H, Wang Q, Niu S, Gao X, Su Z and Li L (2022) Fixed/Predefined-time synchronization of memristor-based complex-valued BAM neural networks for image protection. Front. Neurorobot. 16:1000426. doi: 10.3389/fnbot.2022.1000426
Received: 22 July 2022; Accepted: 26 September 2022;
Published: 17 October 2022.
Edited by:
Hang Su, Fondazione Politecnico di Milano, ItalyReviewed by:
Zi-Ming Wang, Shandong Normal University, ChinaRobert W. Newcomb, University of Maryland, College Park, United States
Xiaotong He, Jilin University, China
Copyright © 2022 Liu, Zhao, Wang, Niu, Gao, Su and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hui Zhao, aHpfcGFwZXJAMTYzLmNvbQ==
†These authors have contributed equally to this work and share first authorship
 Aidi Liu1†
Aidi Liu1† Hui Zhao
Hui Zhao Qingjie Wang
Qingjie Wang Sijie Niu
Sijie Niu Zhen Su
Zhen Su Lixiang Li
Lixiang Li