
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Neurorobot. , 11 June 2019
Volume 13 - 2019 | https://doi.org/10.3389/fnbot.2019.00035
This article is part of the Research Topic Bioinspired Design and Control of Robots with Intrinsic Compliance View all 10 articles
Variable Stiffness Actuators (VSAs) have been introduced to develop new-generation compliant robots. However, the control of VSAs is still challenging because of model perturbations such as parametric uncertainties and external disturbances. This paper proposed a non-linear disturbance observer (NDOB)-based composite control approach to control both stiffness and position of VSAs under model perturbations. Compared with existing non-linear control approaches for VSAs, the distinctive features of the proposed approach include: (1) A novel modeling method is applied to analysis the VSA dynamics under complex perturbations produced by parameter uncertainties, external disturbances, and flexible deflection; (2) A novel composite controller integrated feedback linearization with NDOB is developed to increase tracking accuracy and robustness against uncertainties. Both simulations and experiments have verified the effectiveness of the proposed method on VSAs.
Recently, compliant robots have attracted increasing attention in the robotics community. Variable stiffness actuators (VSAs), a kind of compliant actuators, have been introduced to develop new-generation robots because of its abilities to increase safety in human-robot interaction, to satisfy dynamic requirements, and to provide adaptability in unknown environments (Vanderborght et al., 2013; Grioli et al., 2015; Guo et al., 2015; Wolf et al., 2016; Pan et al., 2017). VSAs are usually multi-input multi-output (MIMO) non-linear systems, where the stiffness and position of the VSAs can be adjusted simultaneously by decoupling control methods (Kim and Song, 2012). However, in these actuators, the stiffness variation brings physical modifications, which requires the controllers to transit among different working conditions quickly. The physical coupling between stiffness and position mechanisms also introduces undesired complexity to control systems (Jafari, 2014). Furthermore, the performances of these actuators are severely affected by parametric uncertainties and external load perturbations, especially during interacting with environments. Therefore, it is essential to develop advanced control strategies for VSAs used in robotic systems.
Different control approaches have been proposed to for VSAs. The PD-based control is a simple and easy method to regulate position and stiffness of VSAs simultaneously. However, PD parameters should be tuned manually to obtain good tracking accuracy in different stiffness condition. Recently, a feedback linearization technique was also exploited for the control of VSAs in Palli et al. (2008) and Buondonno and De Luca (2016). This technique requires significant efforts in system modeling as well as the identification of the system parameters. In addition, a control strategy with fixed gains can cause limited performance in the dynamic variations of the VSAs (Buondonno and De Luca, 2016). To improve the control performance, other advanced control approaches, such as backstepping control (Petit et al., 2015), gain-scheduling control (Sardellitti et al., 2013), non-linear model predictive control (Zhakatayev et al., 2015), adaptive neural network control (Guo et al., 2017), and prescribed performance control (Psomopoulou et al., 2015), have been proposed for VSAs. Although these control approaches have been proved to be effective to improve tracking performances of VSAs, they have a significant limitation that the performances heavily depend on exact models of VSAs (Palli and Melchiorri, 2011; Petit and Albu-Schaffer, 2011). In addition, the disturbance rejection ability of these controllers is achieved by sacrificing the nominal control performance. A novel approach has been proposed to the control of VSA actuated robots, aiming to preserve their dynamic behavior which has been obtained because of the elastic element in the robot structure (Della Santina et al., 2017; Keppler et al., 2018). Furthermore, a decentralized, iteratively learned feedforward approach, combined with a locally optimal feedback control has been introduced in (Angelini et al., 2018). The effectiveness of the method is experimentally verified on several robotic structures and working conditions.
Disturbance observer (DOB)-based control is promising to reject disturbances and to improve robustness against modeling uncertainties (Roozing et al., 2016). This approach has been adopted in the control of serial elastic actuators (SEAs). For instance, a linear DOB-based control method was used for the prismatic SEA to achieve high precision force control in Park et al. (2017). However, this method cannot be directly applied to control VSAs because of non-linearities and model uncertainties. This paper introduces a non-linear disturbance observer (NDOB)-based composite controller to improve the control performance and reject load disturbances for a new type of serial VSA (SVSA), in which stiffness and position can be separately controlled by two motors with a series configuration (Sun et al., 2017, 2018a,b). In the proposed control framework, a NDOB is applied to estimate disturbances so as to enhance the disturbance rejection ability. Based on feedback linearization, a composite control law is developed to stabilize the non-linear dynamics. It is proven that the proposed controller can eliminate external disturbances by a proper selection of the compensation gain. The major contributions of this study include: (i) Different from exising VSA models, the SVSA model in this study considers the composite disturbances produced by system uncertainties, flexible effects, and external disturbances; (ii) A novel disturbance compensation method is developed to attenuate model perturbations for the control of SVSAs; (iii) Experimental studies have been carried out to demonstarete effectivencess and robustness of the proposed controller for SVSAs. In our previous work (Guo et al., 2018), we introduced a NDOB-based control (NDOBC) method for SVSAs, and conducted basic experiments related to position and theoretical stiffness tracking. The current work extends our previous work in terms of dynamic modeling and real-time control of SVSAs. We conduct both simulations and experiments comparing our approach with a feedback linearization-based controller.
The remainder of this paper is organized as follows. Section Actuator Dynamics and Problem Formulation introduces the SVSA dynamics and formulates the control problem. Section Non-Linear Disturbance Observer-Based Control describes the proposed NDOBC design and the control system stability issue. Section Simulation Results shows simulation and experimental results of the proposed controller. Section Experimental Results draws the conclusion of this study.
In this section, the SVSA model is presented firstly. Subsequently, by considering parametric variations and external disturbances acted on the actuator, the control problem is formulated.
A novel SVSA based on an Archimedean spiral relocation mechanism (ASRM) was developed in Sun et al. (2017). As illustrated in Figure 1, this SVSA consists of a variable stiffness mechanism (VSM), a principal motor and a secondary motor, where the principal motor drives the output link motion through the spring transmission, and the secondary motor adjusts the actuator theoretical stiffness by the ASRM. Figure 1 shows the CAD model, prototype, and schematic model of the SVSA.
By considering gravity and external loads, the SVSA dynamics can be represented as follows:
where q is a position of the output link, θi with i = 1, 2 is the angle position of each motor, φ: = q − θ1 is a deflection angle of the elastic transmission, M is an inertia of the output link, Bi is a reflected inertia of each motor, D is a reflected damping of the link, Di is a reflected damping of each motor, τg(q) is a gravity torque, τr is a coupling reaction torque, τe is an elastic torque of the spring transmission, ui is a control input of each motor, and τext is an external torque. The general specifications are shown in Table 1.
The elastic torque across the transmission is given by
where Ks is a spring stiffness, R is a radius of the output link, and μ is a lever length ratio. The stiffness of this SVSA is the first order of elastic torque
The level length ratio μ can be written by the position of the secondary motor as follows:
where μ0 is an initial level length ratio. The coupled resistance torque, demonstrating the transmission deformation reacts on the stiffness motor, is given by
where β = arctan(−θ2/γ) is a tangent angle of the Archimedean Spiral gear, γ is a reduction gear ratio of the secondary motor, and a = μR = Rθ2/2π is a distance from the pivot point to the joint center.
Considering the parametric variations and modeling uncertainties in (1), we define the differences between the nominal and real variables as ΔM = M − Mn, ΔB1 = B1 − B1n, ΔB2 = B2 − B2n, ΔD = D − Dn, ΔD1 = D1 − D1n, ΔD2 = D2 − D2n, Δτe = τe − τen, Δτr = τr − τrn, where Mn is an equivalent inertia of the output link, Bin (i = 1, 2) is an equivalent reflected inertia of each motor, Dn is an equivalent damping of the link, Din (i = 1, 2) is an equivalent damping of each motor, τen and τrn are nominal elastic torque and resistance torque.
Substituting these variations into (1), we wet a nominal model
The model uncertainties, gravity, and external disturbances are regarded as equivalent disturbances of the system:
Substituting Equation (7) into (6), the dynamic equations can be obtained as follows:
The above dynamics can be rewritten in standard form
where a states vector, is the control input for each motor, y = [q, σ]T is the output position and stiffness of the actuator, and
The equilibrium point of the system (9) is x0 = 0. Let qd ∈ R and σd ∈ R be bounded desired outputs. Let be an equivalent disturbance.
This paper aims to design a NDOB-based composite control law to compensate for unknown disturbances, without knowing the exact SVSA model. The control inputs of the SVSA are from two motors, while the control outputs are the position and stiffness of the actuator.
A NDOB as follows is applied to compensate for the unknown disturbance in the non-linear system (9) (Chen et al., 2000; Yang et al., 2012):
where zw is internal state of the NDOB, and is the estimated vector of the unknown disturbance, λ(x)is an intermediate variable for the observer gain l(x), which is defined as
We define the disturbance error ew = w − ŵ. The estimated disturbance error of (10) is given by
Assumption 1: The first time derivative of the disturbance ėw is bounded, and satisfy limt → ∞ẇ(t) = 0. If the observer gain satisfies the differential equation
The estimated disturbance error (12) is locally input-to-state stable (ISS).
In order to make sure the observer error converges to 0, the observer gain is defined as
We define the intermediate variable λ(x) as
Thus, the state equation of the disturbance observer is given by
Definition: The vector relative degree of the system (9) is (r1, r2) at the equilibrium x0 if (1 ≤ j ≤ 2, 1 ≤ i ≤ 2) for all x in a neighborhood of x0 and all k < ri − 1, thus the matrix
is non-singular at x = x0. The input relative degree of (9) is calculated as r = [4, 2] with n = r1 + r2, so (9) can be linearized. Thus, A(x) can be rearranged as
A new coordinate transformation for feedback linearization is define as follows:
where
The system (9) can be represented as
We define
From (21), we can get
and ,
where
Substituting the disturbance w in system (22), a NDOB based composite control law is developed as
where ŵ is the estimated disturbance by (10), and
where parameters are selected such that the polynomials
are Hurwitz stable.
The schematic diagram of the proposed NDOB-based control design can be expressed in Figure 2. In order to prove that the control law is effective on disturbance, the disturbance estimation should be replaced by real disturbance.
Substituting (26) into (23), we can get
Combining (27) with (22), the error dynamic equation can be rewritten as
where
Equation (28) can be written as
in which
and
We can see that the disturbance has been compensated according to (31) and .
Theorem 1. If the following conditions are satisfied, the system (9) is locally ISS around x0:
(i) The parameters ci in the NDOBC law (24) are chosen such that the polynomials (25) are Hurwitz stable;
(ii) The disturbance gain is chosen to keep the function g(x)A−1(x)Γ(x) + p(x) continuously differentiable at x0;
(iii) The observer gain is chosen such that the system (13) is asymptotically stable.
Proof: Substituting the NDOBC law (24) into the dynamic system (9), we can get the closed-loop system:
where
and
Based on the new coordinate transformation , the closed-loop system (26) includes the system ẋ = f(x) + g(x)u and the control law u = A−1(x)(−b(x) + v) is represented by
where
It can be concluded that the system (34) is asymptotically stable at equilibrium x = 0.
Let , the system (34) is given by
where
Based on the theorem of the asymptotic stability (Khalil, 2002), the system is locally asymptotically stable at X = 0, according to the condition (ii), the system (34) is locally ISS.
To demonstrate the proposed NDOBC approach and point out its performance properties, a comparative simulation study with the control law has been conducted for the SVSA under external load disturbances as presented in Figure 3. The SVSA is first considered to verify and clarify the operation of the developed controller. The specifications of the SVSA given in Table 1 is used for simulation. We set the parameters for nominal model Mn = 0.0153kg ▪ m2, B1n = 0.0284kg ▪ m2, B2n = 0.019kg ▪ m2, Dn = 0.007N ▪ m ▪ s, D1n = 0.007N ▪ m ▪ s, D2n = 0.003N ▪ m ▪ s, and the initial variables are set as x(0) = [0 0 0 0 0 0]. To make a comparison, a feedback linearization-based (FL) controller is selected as a baseline controller, which is given by
The unknown external disturbances are given by
The results of the comparison between the baseline controller and the NDOB controller are illustrated.
Sinusoidal trajectory of the actuator position with frequency of 0.2 Hz and amplitude of 60° was taken. A 3 kg load disturbance is introduced at 5 s. The purpose of the simulation is to test the performance of the controller to track the trajectory at two different stiffness conditions, which is low stiffness (15 Nm/rad) and high stiffness (60 Nm/rad), respectively.
Figure 4 shows that the proposed NDOBC approach exhibits promising disturbance attenuation and reference tracking performance. It is also observed that the tracking trajectory under the NDOBC is overlapped with the baseline control method during the first 5 s when there is no disturbance acted on the system, but poor tracking performance after loading, which proves that the property of the NDOBC method. In addition, the stiffness has little effect on the tracking performance under constant stiffness condition.
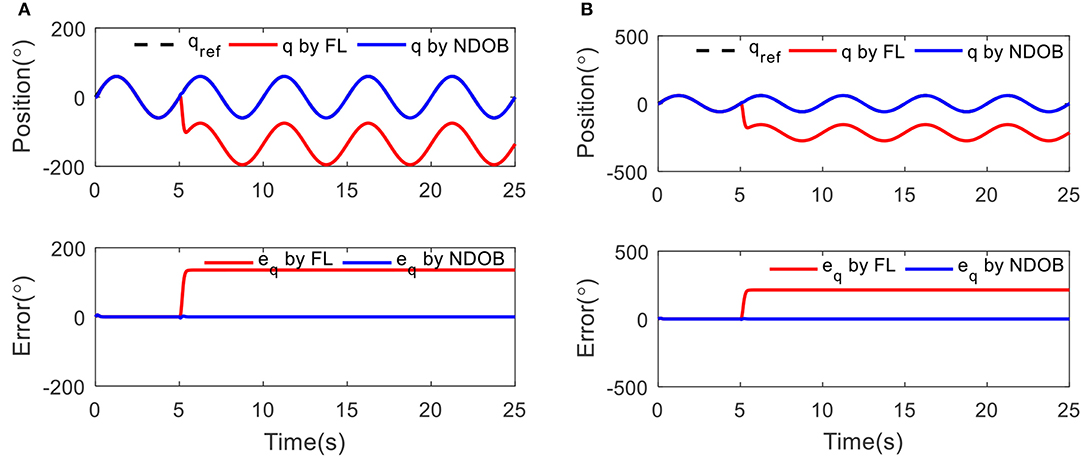
Figure 4. The position tracking results under 3 kg load disturbance at 5 s with different condition: (A) low stiffness (15 Nm/rad) and (B) high stiffness (60 Nm/rad).
Sinusoidal trajectory was taken under variable stiffness condition, where σ(t) = 35 + sin(2πft + 1.5π)with the frequency of 0.2 Hz. In Figure 5, it can be seen that both the position and stiffness tracking errors are small without external load for two controllers. After loading 3 kg at 5 s, position and stiffness tracking errors increase with FL control, but the NDOBC performance is better than the baseline. The tracking error is small, which means the disturbance can be compensated.
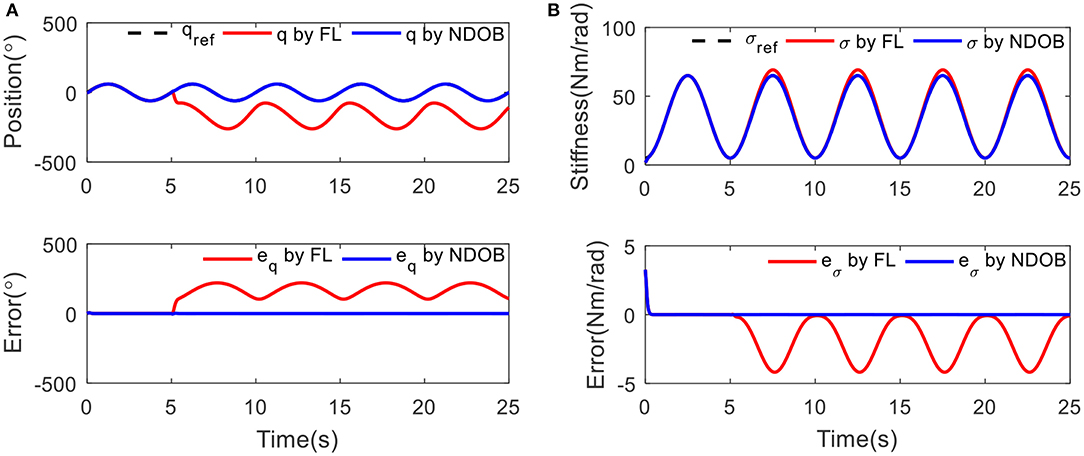
Figure 5. The tracking results under 3 kg load disturbance at 5 s: (A) position tracking and (B) stiffness tracking.
To further verify the robustness of the controller, an experimental procedure was carried out on the SVSA platform. Two DC motors (RE50, 60W and RE25, 20W, Maxon motor) were selected as the driving modules. Two motor drivers (RMDS-102, ShenZhen RoboModule Technology Co., China) were used to control the motors. Encoders with 500 pluses per revolution were installed to measure the motor position. An Omron encoder (E6B2-CWZ1X) was utilized to measure the deflection angle of the SVSA. A Simulink real-time control system was built based on MATLAB/RTW in xPC target environment using CAN-AC2-PCI board (as shown in Figure 3). The angles of the encoders were collected via a data acquisition card (PCI-6259, National Instruments Corp., TX) to MATLAB/RTW control system. The communication between the real-time system and the Plant is through CAN Bus.
Sinusoidal tracking experiments with frequency of 0.2 Hz and amplitude of 60° at two different conditions, low stiffness (15 Nm/rad) and high stiffness (60 Nm/rad), were conducted. Figure 6 shows the position tracking and output errors for both controllers in the presence of external load disturbance at 5 s. The robustness of the NDOB controller is obvious because the error continues to reduce despite the external load. The disturbance is also clearly shown in the output error. It shows that the NDOB control can achieve better position tracking results within the first 5 s. The baseline control performance is deteriorated when adding the 3 kg load. In addition, compared with the low stiffness condition, we can find that the tracking error is reduced in high stiffness, which means external disturbances have less impact on the position tracking error at high stiffness. This can be explained that the deflection angle in low stiffness is larger than that of the high stiffness condition. However, compared with the simulation results, the experimental data exhibit small oscillations during the tracking.
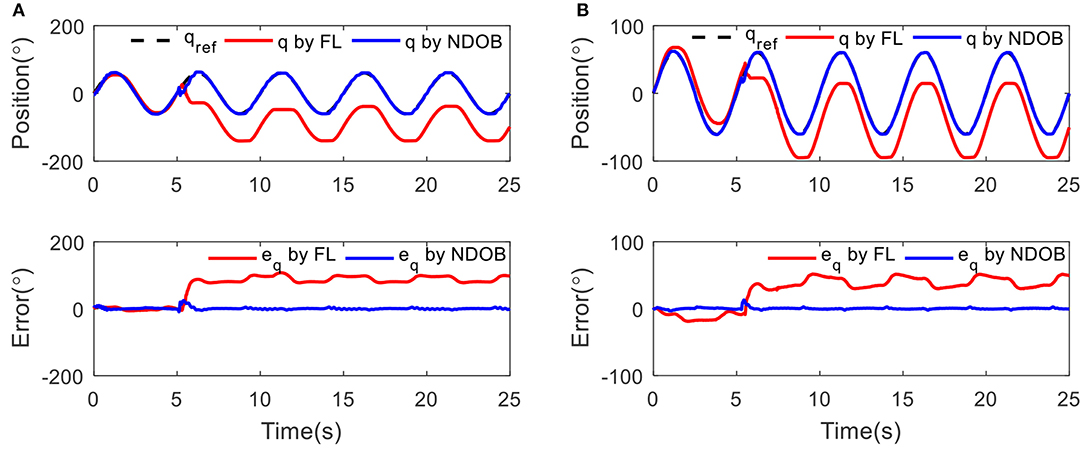
Figure 6. The position tracking results under 3 kg load disturbance at 5 s with different condition: (A) low stiffness (15 Nm/rad) and (B) high stiffness (60 Nm/rad).
Secondly, the controller performance has been tested while tracking a sine wave reference on continuous position and stiffness. Three kilograms load is applied at 5 s. The stiffness σ(t) = 35 + sin(2πft + 1.5π) has been adjusted with the frequency of 0.2 Hz. Figure 7 shows the position and stiffness tracking results with and without external load disturbance for two controllers. The NDOB control achieved better results than the FL controller. The position tracking error suddenly increases due to the external disturbances at 5 s. In stiffness tracking, there is no obvious change under the disturbance compensation algorithm while the error increases for FL control.
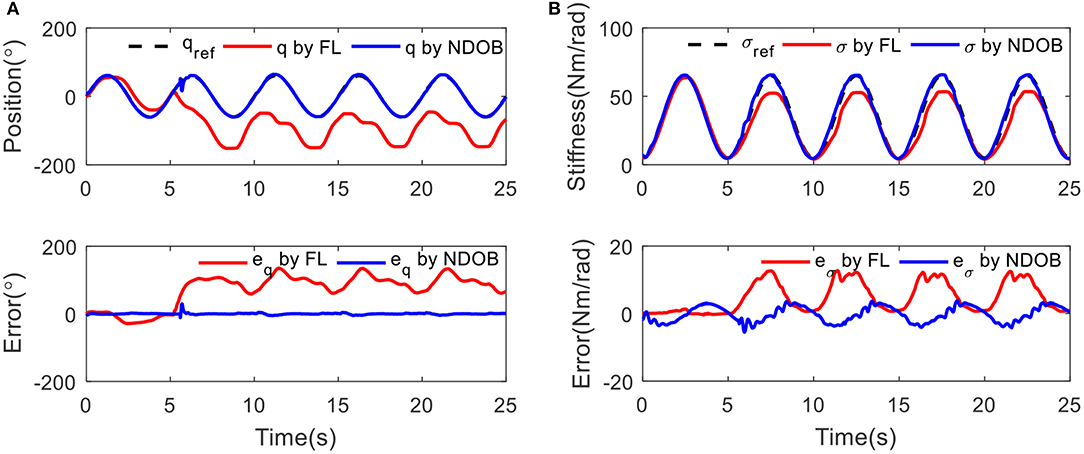
Figure 7. The tracking results under 3 kg load disturbance at 5 s: (A) position tracking and (B) stiffness tracking.
This paper proposed a NDOBC to attenuate the model uncertainties and external disturbances for a class of SVSA. Simulation and experimental results verify the ability of the proposed approach to cope with load disturbance by showing remarkable control performances for both position and stiffness tracking. The stability of the composite controller has been proved by the tracking results. Future work will focus on other non-linear composite adaptive control designs for the SVSA to solve the input saturation and unmodeled dynamics (Pan and Yu, 2016; Sun N. et al., 2018) and the application of this actuator to the design of variable stiffness robots in real-world applications.
The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.
ZG: theoretical analysis and writing paper. JS: VSA design. JL: guide doing experiment. YP: guide control plan. XX: guide writing paper.
This project was supported in part by the National Natural Science Foundation of China (Grant No. 51605339, 61703295), in part by the Fundamental Research Program of Jiangsu Province, China (Grant No. BK20181183), the Natural Science Foundation of Hubei Province, China (Grant No. 2017CFB496), the Wuhan Youth Science and Technology Plan (Grant No. 2017050304010304), and the Shenzhen Science and Technology Program (Grant No. JCYJ20180302153933318).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Angelini, F., Della Santina, C., Garabini, M., Bianchi, M., Gasparri, G. M., Grioli, G., et al. (2018). Decentralized trajectory tracking control for soft robots interacting with the environment. IEEE Trans. Robot. 34, 924–935. doi: 10.1109/TRO.2018.2830351
Buondonno, G., and De Luca, A. (2016). Efficient computation of inverse dynamics and feedback linearization for VSA-based robots. IEEE Robot. Autom. Lett. 1, 908–915. doi: 10.1109/LRA.2016.2526072
Chen, W.-H., Ballance, D. J., Gawthrop, P. J., and O'Reilly, J. (2000). A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 47, 932–938. doi: 10.1109/41.857974
Della Santina, C., Bianchi, M., Grioli, G., Angelini, F., Catalano, M., Garabini, M., et al. (2017). Controlling soft robots: balancing feedback and feedforward elements. IEEE Robot. Autom. Mag. 24, 75–83. doi: 10.1109/MRA.2016.2636360
Grioli, G., Wolf, S., Garabini, M., Catalano, M., Burdet, E., Caldwell, D., et al. (2015). Variable stiffness actuators: the user's point of view. Int. J. Robot. Res. 36, 727–743. doi: 10.1177/0278364914566515
Guo, Z., Pan, Y., Sun, T., Zhang, Y., and Xiao, X. (2017). Adaptive neural network control of serial variable stiffness actuators. Complexity 2017:5361246. doi: 10.1155/2017/5361246
Guo, Z., Pan, Y., Wee, L. B., and Yu, H. (2015). Design and control of a novel compliant differential shape memory alloy actuator. Sens. Actuators A Phys. 225, 71–80. doi: 10.1016/j.sna.2015.01.016
Guo, Z., Sun, J., Ling, J., Sun, T., Pan, Y., and Xiao, X. (2018). “Robust control of a serial variable stiffness actuator based on Nonlinear Disturbance Observer (NDOB),” in 2018 IEEE International Conference on Advanced Robotics and Mechatronics (ICARM) (Singapore), 1–6.
Jafari, A. (2014). Coupling between the output force and stiffness in different variable stiffness actuators. Actuators 3, 270–284. doi: 10.3390/act3030270
Keppler, M., Lakatos, D., Ott, C., and Albu-Schäffer, A. (2018). Elastic structure preserving (esp) control for compliantly actuated robots. IEEE Trans. Robot. 34, 317–335. doi: 10.1109/TRO.2017.2776314
Kim, B. S., and Song, J. B. (2012). Design and control of a variable stiffness actuator based on adjustable moment arm. IEEE Trans. Robot. 28, 1145–1151. doi: 10.1109/TRO.2012.2199649
Palli, G., and Melchiorri, C. (2011). Output-based control of robots with variable stiffness actuation. J. Robot. 2011:735407. doi: 10.1155/2011/735407
Palli, G., Melchiorri, C., and De Luca, A. (2008). “On the feedback linearization of robots with variable joint stiffness,” in Proceeding of the IEEE International Conference on Robotics and Automation (Pasadena, CA), 1753–1759.
Pan, Y., Guo, Z., Li, X., and Yu, H. (2017). Output-feedback adaptive neural control of a compliant differential SMA actuator. IEEE Trans. Control Syst. Technol. 25, 2202–2210. doi: 10.1109/TCST.2016.2638958
Pan, Y., and Yu, H. (2016). Composite learning from adaptive dynamic surface control. IEEE Trans. Autom. Control 61, 2603–2609. doi: 10.1109/TAC.2015.2495232
Park, Y., Paine, N., and Oh, S. (2017). Development of force observer in series elastic actuator for dynamic control. IEEE Trans. Ind. Electron. 65, 2398–2407. doi: 10.1109/TIE.2017.2745457
Petit, F., and Albu-Schaffer, A. (2011). “State feedback damping control for a multi DOF variable stiffness robot arm,” in Proceeding of the IEEE International Conference on Robotics and Automation (Shanghai), 5561–5567.
Petit, F., Daasch, A., and Albu-Schäffer, A. (2015). Backstepping control of variable stiffness robots. IEEE Trans. Control Syst. Technol. 23, 2195–2202. doi: 10.1109/TCST.2015.2404894
Psomopoulou, E., Theodorakopoulos, A., Doulgeri, Z., and Rovithakis, G. A. (2015). Prescribed performance tracking of a variable stiffness actuated robot. IEEE Trans. Control Syst. Technol. 23, 1914–1926. doi: 10.1109/TCST.2015.2394748
Roozing, W., Malzahn, J., Caldwell, D. G., and Tsagarakis, N. G. (2016). “Comparison of open-loop and closed-loop disturbance observers for series elastic actuators,” in 2016 IEEE/RSJ International Conference on In Intelligent Robots and Systems (IROS) (Daejeon), 3842–3847.
Sardellitti, I., Medrano-Cerda, G. A., Tsagarakis, N., Jafari, A., and Caldwell, D. G. (2013). Gain scheduling control for a class of variable stiffness actuators based on lever mechanisms. IEEE Trans. Robot. 29, 791–798. doi: 10.1109/TRO.2013.2244787
Sun, J., Guo, Z., Zhang, Y., Xiao, X., and Tan, J. (2018a). A novel design of a compact Serial Variable Stiffness Actuator (SVSA) based on an archimedean spiral relocation mechanism. IEEE ASME Trans. Mechatron. 23, 2121–2231. doi: 10.1109/TMECH.2018.2854742
Sun, J., Sun, D., He, S., Guo, Z., and Xiao, X. (2018b). Design, modeling and control of a novel compact, energy-efficient, and rotational Serial Variable Stiffness Actuator (SVSA-II). Mech. Mach. Theor. 130, 123–136. doi: 10.1016/j.mechmachtheory.2018.07.024
Sun, J., Zhang, Y., Zhang, C., Guo, Z., and Xiao, X. (2017). “Mechanical design of a compact serial variable stiffness actuator (SVSA) based on lever mechanism,” in Proceeding of the IEEE International Conference on Robotics and Automation (ICRA) (Singapore), 33–38.
Sun, N., Yang, T., Fang, Y., Wu, Y., and Chen, H. (2018). Transportation control of double-pendulum cranes with a nonlinear quasi-PID scheme: design and experiments. IEEE Trans. Syst. Man Cybern. 1–11. doi: 10.1109/TSMC.2018.2871627
Vanderborght, B., Albu-Schaeffer, A., Bicchi, A., Burdet, E., Caldwell, D. G., Catalano, M., et al. (2013). Variable impedance actuators: a review. Rob. Auton. Syst. 61, 1601–1614. doi: 10.1016/j.robot.2013.06.009
Wolf, S., Grioli, G., Eiberger, O., Friedel, W., Grebenstein, M., Höppner, H., et al. (2016). Variable stiffness actuators: review on design and components. IEEE ASME Trans. Mechatron. 21, 2418–2430. doi: 10.1109/TMECH.2015.2501019
Yang, J., Li, S., and Chen, W. H. (2012). Nonlinear disturbance observer-based control for multi-input multi-output nonlinear systems subject to mismatching condition. Int. J. Control 85, 1071–1082. doi: 10.1080/00207179.2012.675520
Keywords: variable stiffness actuator, nonlinear disturbance observer, compliant actuator, feedback linearization, composite control, model perturbations
Citation: Guo Z, Sun J, Ling J, Pan Y and Xiao X (2019) Robust Trajectory Tracking Control for Variable Stiffness Actuators With Model Perturbations. Front. Neurorobot. 13:35. doi: 10.3389/fnbot.2019.00035
Received: 13 March 2019; Accepted: 17 May 2019;
Published: 11 June 2019.
Edited by:
Hong Qiao, University of Chinese Academy of Sciences, ChinaCopyright © 2019 Guo, Sun, Ling, Pan and Xiao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jie Ling, amFtZXNsaW5nQHdodS5lZHUuY24=; Yongping Pan, cGFueXA2QG1haWwuc3lzdS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.