Justin Faber1*
Dolores Bozovic1,2*- 1Department of Physics and Astronomy, University of California, Los Angeles, Los Angeles, CA, United States
- 2California NanoSystems Institute, University of California, Los Angeles, Los Angeles, CA, United States
The remarkable signal-detection capabilities of the auditory and vestibular systems have been studied for decades. Much of the conceptual framework that arose from this research has suggested that these sensory systems rest on the verge of instability, near a Hopf bifurcation, in order to explain the detection specifications. However, this paradigm contains several unresolved issues. Critical systems are not robust to stochastic fluctuations or imprecise tuning of the system parameters. Further, a system poised at criticality exhibits a phenomenon known in dynamical systems theory as critical slowing down, where the response time diverges as the system approaches the critical point. An alternative description of these sensory systems is based on the notion of chaotic dynamics, where the instabilities inherent to the dynamics produce high temporal acuity and sensitivity to weak signals, even in the presence of noise. This alternative description resolves the issues that arise in the criticality picture. We review the conceptual framework and experimental evidence that supports the use of chaos for signal detection by these systems, and propose future validation experiments.
1 Introduction
The ability of the auditory system to respond to sound waves that elicit only angstroms of mechanical displacement in the sensory cells has been a subject of research for many decades (1–5). Experiments performed on many scales, from molecular studies to in vivo measurements, have revealed the presence of multiple energy-consuming mechanisms that amplify the responsiveness to weak signals, mediate adaptation on different timescales, maintain concentration gradients, and generally provide active feedback dynamics (6–9). While the specific biophysical mechanisms of amplification may vary across the species, the presence of some active process seems to be ubiquitous, and the resulting nanoscale sensitivity prevalent. A common feature of all auditory end organs is that the sensory cells are immersed in an aqueous environment, and hence their stereociliary bundles are subject to stochastic noise and the resulting viscous damping. Thus, the sensitivity of detection must be considered not only in terms of amplification of weak signals, but in the context of extracting signals from equal or higher levels of noise.
Nonlinear response has likewise been demonstrated in the dynamics of individual hair cells (10–12), semi-intact end organs, and otoacoustic emissions of live animals (13, 14). The nonlinearity is closely linked to and dependent upon the active process, as it vanishes with metabolic disruption. Further, it is dominant at weak signals, indicative of an essential nonlinearity. These empirical data have motivated theoretical models based on nonlinear dynamics, which have proposed that the hair cell can be described as an active oscillator positioned near a supercritical Hopf bifurcation (15–17). Proximity to a critical point has been shown to capture the nonlinearity, amplification, frequency selectivity, and ability to exhibit autonomous oscillation (18–21). In the vicinity of this bifurcation, the response of the system is generic, not dependent on the microscopic mechanisms governing the active oscillator. Thus, the behavior of complex numerical models near criticality can be captured by the normal form equation for the Hopf bifurcation (22). Consistent with a large body of experimental evidence, this theoretical framework provides a powerful paradigm for describing the dynamics of the auditory system, with the hair cell as the key element.
While criticality provides many advantages, several limitations arise in the full characterization of the response of this dynamical system. Firstly, criticality is only optimal in a noiseless, deterministic system. In this regime, the bifurcation point provides maximal amplification, and as the system crosses into the oscillatory, limit-cycle regime, its sensitivity is degraded. In the presence of noise, criticality is removed, in the sense that a singular point dividing the quiescent and oscillatory regimes is replaced by a gradual transition (23). The regime around the critical point still exhibits many features of criticality, such as amplification and nonlinear response. However, in the presence of noise, it was shown that a stable limit cycle, rather than proximity to bifurcation, provides maximal sensitivity (24).
Secondly, a noiseless system poised exactly at the supercritical Hopf bifurcation would exhibit a phenomenon known as critical slowing down (25), where infinitely long transient times of the response arrise from the loss of local stability. Thus, when the system is maximally sensitive, it is also maximally slow. For a model of the auditory system, this limitation is highly significant, as experimental studies have shown that many phenomena, such as localization of sound in space, require temporal acuity that reaches 10 microseconds (26, 27). In the presence of noise, critical slowing down is reduced, but so is the sensitivity. The inherent tradeoff between the sensitivity and speed of response persists, posing a highly undesirable tradeoff for auditory detection.
Nonlinear dynamics theory provides another class of systems, that does not rely on criticality to achieve sensitivity. Chaotic attractors have received much attention in mathematics and physics literature, as they provide intricate fractal patterns in their trajectories, exhibit universal phenomena, and model the behaviors of systems as far ranging as lasers, transistors, mercury films, and others (25). Of relevance to biology are several key features of chaotic systems. First, they require only three degrees of freedom to arise in a dynamical system. As biology typically involves a multiplicity of interacting active processes, one expects many more dimensions than three to characterize its dynamics, making the occurrence of chaos easily feasible. Secondly, chaos reconciles sensitivity of detection with temporal resolution. In fact, the very definition of chaos relies on this feature: the trajectories of a chaotic system diverge exponentially as a result of infinitesimally small perturbation. This divergence of trajectories thus reflects the sensitivity of response and imposes no tradeoff with its speed.
Furthermore, while chaotic dynamics can be obscured by the presence of noise, their key features are not removed. On the contrary, certain dynamical systems that show stable limit cycles when noiseless can be rendered chaotic by the introduction of stochastic fluctuations (28). Specifically, the theoretical model for the Hopf bifurcation, in its most general form, exhibits a chaotic regime in the presence of noise (29). This regime would enable the system to exhibit its requisite sensitivity as well as maintain rapid response, achieving these features in the presence of noise levels comparable to those expected in biological tissue.
2 Chaos in hair-bundle dynamics
Most theoretical and experimental studies of chaos in the auditory and vestibular systems have focused on the sensory elements - individual hair cells. As these sensory cells exhibit all of the key signatures of the active, nonlinear response that characterizes hearing, they provide a natural starting point for the analysis of underlying dynamics. However, defining features of chaos have traditionally been explored in theoretical models, mostly deterministic in nature, as they can be difficult to identify even in numerical simulations that introduce stochastic elements. Hence, proving the presence of chaos in experimental systems poses a challenge, due to the presence of thermal fluctuations and limitations in measurement precision and duration (30, 31). For instance, the standard metric for quantifying chaos in a numerical model is the Lyapunov exponent, which quantifies the divergence rate of neighboring trajectories and estimates how rapidly uncertainties in the present state of a system diverge. Extracting the Lyapunov exponent from experimental data can prove unreliable, as the presence of noise limits measurement precision, thereby obscuring the degree of separation of two phase-space trajectories.
Despite the challenges, time-series analysis techniques have been developed in applied mathematics, which can identify the presence of chaos in experimental recordings and even quantify its degree. Specifically, a fruitful approach for the analysis of experimental data is to identify a transition to the chaotic regime, usually through variation of an experimental parameter. Transitions to chaos tend to arise from one of several well-known routes. The period-doubling route has been identified in stimulated squid giant axons (32), while the quasiperiodic route has been shown to occur in the intervals between heartbeats, at the onset of cardiac fibrillation (33, 34).
Identifying these transitions involves taking “snapshots” of the system through the use of Poincaré maps. For example, in the case of heartbeats, one may capture the time interval between two subsequent heartbeats (In) and form a scatter plot against each interval that follows (In+1). Regular heartbeats would correspond to a single cluster of points in this plane. Multiple clusters of points would indicate occasional skipping of beats, or some form of mode-locking behavior. Alternatively, a ring-like structure in this Poincaré map would indicate the presence of two incommensurate frequencies (quasiperiodicity) in the dynamics. Quasiperiodic dynamics correspond to trajectories on the surface of a 2-torus, where the ringlike structure represents a cross-section of the torus. A common route to chaos in dynamical systems theory is torus breakdown, where the surface of the torus loses smoothness, giving rise to chaotic dynamics (35).
The approach of utilizing Poincaré maps was performed on spontaneously oscillating hair bundles of the bullfrog sacculus, in order to identify chaos in the dynamics of individual sensory hair cells (36). The calcium concentration and viscosity of the endolymph solution surrounding the hair bundles were varied, as these have been shown to influence the regularity of oscillations (37). In Figure 1A, we show traces of hair-bundle spontaneous oscillations for three choices of endolymph calcium concentration. For low values of the calcium concentration, the hair bundles exhibit regular oscillations and a tall, narrow peak in the power spectrum. However, as the calcium concentration is increased, the oscillations become more irregular and more chaotic (29).
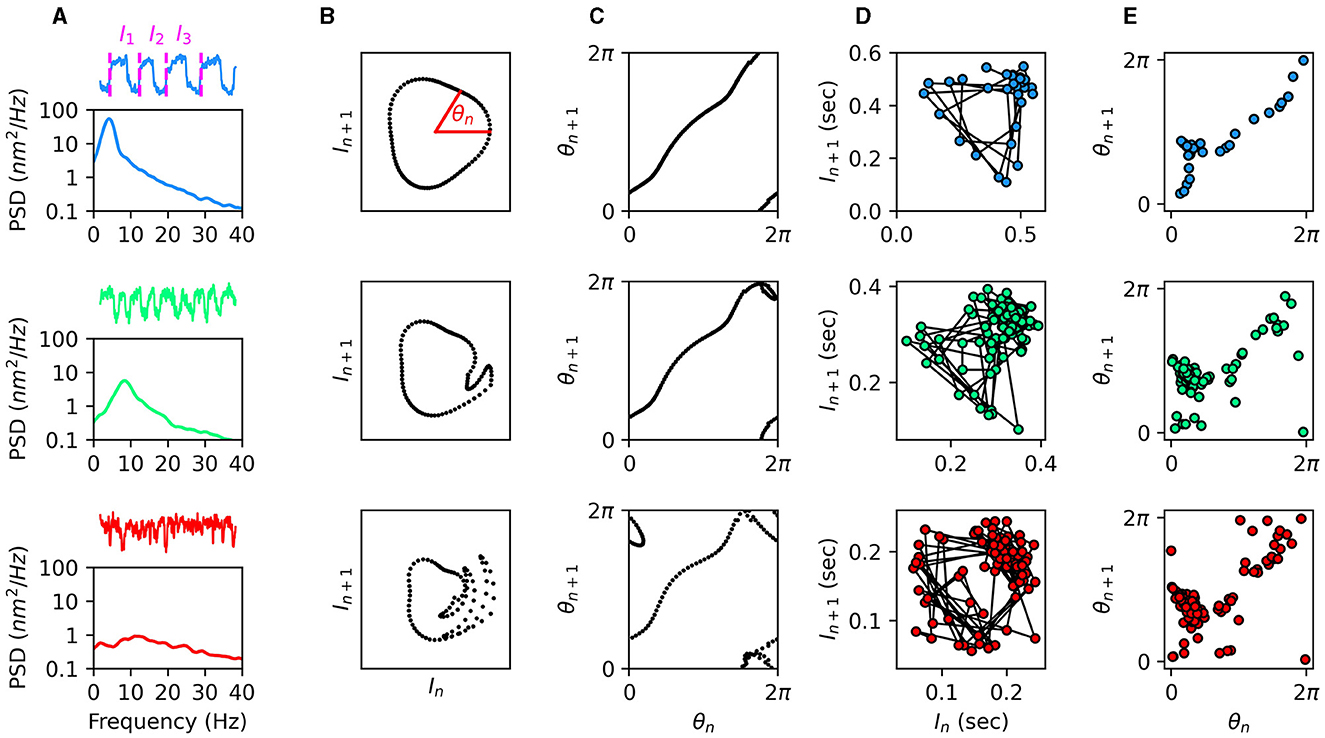
Figure 1. (A) Traces and power spectral density of spontaneous hair-bundle oscillations under various calcium concentrations of the endolymph. From top to bottom: 100 μM (low calcium), 250 μM (natural calcium), and 325 μM (high calcium). Oscillation intervals are illustrated in the top trace. (B) Illustrations of the torus-breakdown transition to chaos from top to bottom. (C) Circle maps corresponding to the Poincaré maps in (B). The 1-to-1 relationship in the top panel is indicative of non-chaotic dynamics, while the other two panels are indicative of chaos. (D) Experimental measurements of oscillation intervals from a hair bundle with the three calcium concentrations in (A) during an off-resonance stimulus. (E) Circle maps corresponding to the Poincaré maps in (D). The 1-to-1 relationship in the top panel (low calcium) is indicative of non-chaotic dynamics, while the other two panels are indicative of chaos. Data was reproduced from (29) with permission.
An external, sinusoidal stimulus was then introduced to the system. Variation in the amplitude of this stimulus was used to control the system, with large amplitudes causing entrainment of the hair bundle and resulting in limit-cycle dynamics. In Figure 1B, we illustrate the anticipated Poincaré maps for a quasiperiodic transition to chaos via torus breakdown. The smoothness of the torus can be tested using circle maps, where the angle each point makes with the In-axis is plotted against the angle of the point that follows. Smoothness can be identified if there is a 1-to-1 relationship in the circle map, such that the points follow an invertible, monotonic function (Figure 1C) (35). The experimental data shown in Figures 1D, E indicates that for low calcium concentrations, the hair bundle exhibits limit-cycle dynamics. However, for natural and high calcium concentrations, the system exhibits chaotic dynamics.
Though the Poincaré maps are useful for identifying chaos, they provide no information about the degree of chaoticity. The Kolmogorov entropy provides a useful metric for quantifying chaos, with larger values corresponding to more limited predictability (38, 39). Closely related to the Lyapunov exponents of a dynamical system, this information-theoretic metric quantifies how rapidly phase-space information is lost with time, due to the expansion of uncertainties (40). While Lyapunov exponents track the divergence of distances between neighboring trajectories, the Kolmogorov entropy tracks expansion rates of volumes confining local neighborhoods of the phase space. Though its algorithmic implementation is more complex than that of the Lyapunov exponent, measuring the Kolmogorov entropy of time-series data does not rely on extremely high measurement precision. Instead, the phase space is partitioned into discrete bins, and the flow of trajectories through these bins is used to calculate the rate at which the probability distribution of local trajectories spreads out. This metric was implemented to quantify the level of chaos in hair-bundle dynamics. As expected, increasing the calcium concentration of the endolymph increased the Kolmogorov entropy (29).
3 Signal detection by chaotic oscillators
Exploiting the instabilities of chaotic systems in the design of sensitive signal detectors was proposed decades ago (41, 42). This idea was likewise tested on a detailed biophysical model of hair-cell response, which was shown to be most sensitive to a step-like stimulus when the system was poised in the chaotic regime (28). Subsequent theoretical studies further demonstrated that a simple dynamical systems model of a hair cell, based on a generalized form of the Hopf bifurcation, greatly benefits from the chaotic regime, providing signal detection that is more robust to thermal noise than the equivalent system poised at criticality (23). To test these theoretical predictions on live and biologically functional hair cells, the level of chaos was first measured from long recordings of spontaneous hair-bundle oscillations. At the end of each recording, the hair bundle was stimulated with an external signal, and its responsiveness was measured. Thus, the level of chaos observed in the innate dynamics of a hair bundle could be directly related to its responsiveness to an external mechanical stimulus. The level of chaos was then adjusted though variation of the calcium concentration or viscosity of the endolymph, and the identical experimental protocol was repeated (29).
To characterize the hair-bundle sensitivity, several metrics were used. First, a pure tone was applied, and the amplitude gain was measured at the stimulus frequency (Figure 2A). This metric is appropriate for the frequency-selective detectors of the auditory system. Telegraphic noise (burst noise) was also applied to the bundle (Figure 2B). This allowed for calculation of the transfer entropy, a metric that quantifies how much information the receiver obtains about the stimulus (43). The advantage of this metric is that it makes no assumptions about what components of the signal are relevant, such as the amplitude, frequency, or phase. Instead it directly measures how much information about the stimulus is encoded in the response. Lastly, a step-function stimulus was repeatedly applied to the bundle (Figure 2C), and the mean displacement of the response was calculated. This metric is appropriate for characterizing broadband detection by vestibular systems, as step functions are transient and contain a broad range of frequencies in their Fourier representation. All three of these metrics showed enhanced responsiveness in the chaotic regime and exhibited a single peak as a function of the Kolmogorov entropy. These experimental results are consistent with theoretical predictions, which demonstrated that optimal signal detection occurs in the weakly chaotic regime (23, 29).
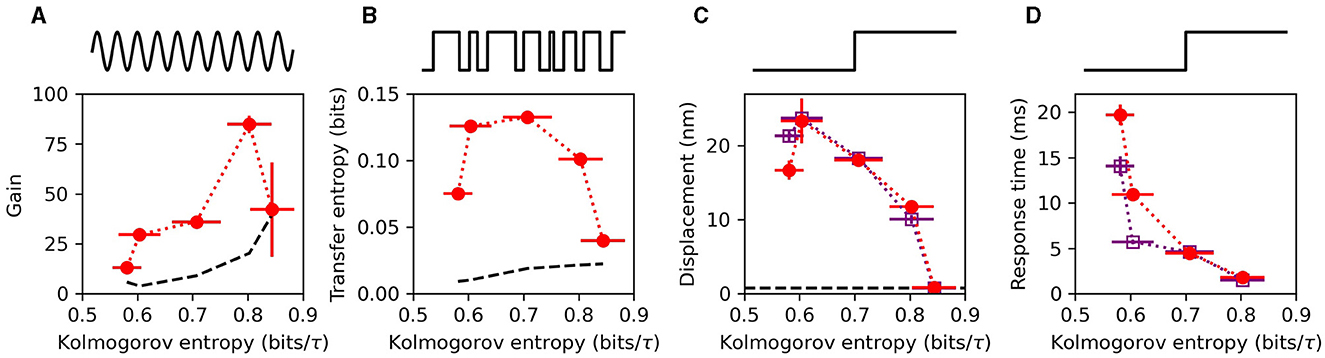
Figure 2. (A) Phase-locked amplitude gain for weak sinusoidal stimulus, presented at the characteristic frequency of the bundle. (B) Transfer entropy from burst-noise stimulus to the hair bundle response. (C) mean, steady-state displacement induced on the hair bundle from a step stimulus, averaged over ~200 steps. (D) Response time to the step stimulus, characterized by fitting the mean response to an exponential function and extracting the decay time. The black, dashed curves in (A–C) represent the noise floors associated with each metric. In (C, D), the red circles, and purple squares represent stimulus steps in the channel-opening and channel-closing direction, respectively. All measurements were performed on the same hair cell. Stimulus waveforms used for each metric are illustrated above each panel. Data was reproduced from (29) with permission.
The speed of response could also be extracted from these experimental recordings, providing a measure of the temporal acuity of individual hair bundles. Using multiple repetitions of a step-function stimulus, the responses were averaged to reveal an exponentially decaying function. The timescale obtained from exponential fits to the data yielded the response time (Figure 2D). For all of the hair cells measured, the speed of response increased monotonically with increasing levels of chaos. These results are consistent with analytic calculations of the phenomenological Hopf model for hair cells (44).
The monotonic increase in temporal acuity with increasing level of chaos, combined with the optimum observed in the sensitivity metrics, suggests that the preferred level of chaos for signal detection depends on the specific application and requirements for the detector. For example, a recent theoretical study, which considered many detection metrics, proposed that weakly chaotic oscillators perform best as auditory detectors, while strongly chaotic oscillators are best suited for vestibular detection (23).
4 Mechanically-coupled chaotic oscillators
According to a theoretical study, the only detection metric that is degraded by the presence of chaos is the frequency selectivity of the system, as quantified by the quality factor of the response (23). This is to be expected of chaotic oscillators, as they tend to exhibit broad ranges of frequencies in their Fourier representation and are susceptible to entrainment within this frequency range. While this poses no tradeoffs for the broadband detectors of vestibular systems, it raises the question of how auditory systems achieve their frequency selectivity if they are comprised of chaotic oscillators. One possible resolution to the issue of frequency selectivity was proposed in a recent study (45), which demonstrated that mechanically coupled, active oscillators are more likely to synchronize when they are individually chaotic. This study also confirmed that the increase in synchronization susceptibility was accompanied by an increase in frequency selectivity of the full, coupled system. Though the individual detectors were not frequency selective, when many synchronize their autonomous motion, they form a sharply-tuned, frequency-selective system. Mechanical coupling between hair cells is present in both auditory and vestibular systems, and the strength and extent of this coupling varies between species and depends on the function of the sensory system (46). This raises the possibility that chaotic dynamics can persist in large arrays of coupled hair cells, and that specific morphology of the overlying structures fine-tunes the level of chaos and the emergent detection characteristics of the full system.
5 Discussion
Our theoretical studies have prioritized the inclusion of stochastic noise in measurements of sensitivity, as it drastically affects the performance of signal detectors and can qualitatively alter the conclusions as to which regime in parameter space yields optimal detection. Furthermore, we propose that both theoretical and experimental studies can benefit from using information theoretic metrics to characterize the response of a hair bundle. These metrics allow one to assess how external stimuli impact the dynamics of a cell, beyond the effects on its mechanical compliance. For example, transfer entropy provides a particularly useful measure for characterizing the sensitivity of hair cells, as it caries no assumptions of which signal features are neurologically meaningful.
We note that the experimental measurements of chaotic dynamics have thus far been performed only on hair cells of the amphibian sacculus, a primarily vestibular end organ. Our theoretical studies, however, suggest that the benefits entailed in chaotic dynamics may be far more generic and hence applicable to other systems as well. Vertebrate species indeed exhibit a diverse range of sensory organs, specialized to perform both auditory and vestibular tasks. While the morphology of their macroscopic structures varies widely, these systems universally rely on active hair bundle motility, somatic electromotility, or a combination thereof (46). Prior work has demonstrated that nonlinear dynamic models of active hair cells are very versatile and can describe a broad range of sensory specializations (47, 48).
We hence propose that the auditory system exploits the instabilities inherent to chaotic dynamics in order to achieve its remarkable sensitivity, temporal acuity, and robustness to noise. Future experimental studies will aim to test these theoretical predictions by exploring whether chaotic dynamics can arise in auditory end organs under natural conditions. One experimental study found signatures of chaos in the spontaneous otoacoustic emissions of humans (49), raising the possibility that the auditory system exhibits chaoticity in vivo.
Author contributions
JF: Writing – original draft, Writing – review & editing. DB: Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The authors gratefully acknowledge the support of the National Science Foundation, Physics of Living Systems, under grant 2210316.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Dalhoff E, Turcanu D, Zenner HP, Gummer AW. Distortion product otoacoustic emissions measured as vibration on the eardrum of human subjects. Proc Nat Acad Sci. (2007) 104:1546–51. doi: 10.1073/pnas.0610185103
2. Narins PM, Lewis ER. The vertebrate ear as an exquisite seismic sensor. J Acoust Soc Am. (1984) 76:1384–7. doi: 10.1121/1.391455
3. Gold T, Pumphrey RJ. Hearing. I the cochlea as a frequency analyzer. Proc Royal Soc B. (1948) 135:462–91. doi: 10.1098/rspb.1948.0024
4. Gold T. Hearing. II the physical basis of the action of the Cochlea. Proc Royal Soc B. (1948) 135:492–8. doi: 10.1098/rspb.1948.0025
5. Reichenbach T, Hudspeth AJ. The physics of hearing: fluid mechanics and the active process of the inner ear. Rep Prog Phys. (2014) 77:076601. doi: 10.1088/0034-4885/77/7/076601
6. Eguíluz VM, Ospeck M, Choe Y, Hudspeth AJ, Magnasco MO. Essential nonlinearities in hearing. Phys Rev Lett. (2000) 84:5232–5. doi: 10.1103/PhysRevLett.84.5232
7. Martin P, Hudspeth AJ, Jülicher F. Comparison of a Hair Bundle's Spontaneous Oscillations with Its Response to Mechanical Stimulation Reveals the Underlying Active Process. Proc Nat Acad Sci. (2001) 98:14380–5. doi: 10.1073/pnas.251530598
8. Hudspeth AJ. Making an effort to listen: mechanical amplification in the ear. Neuron. (2008) 59:530–45. doi: 10.1016/j.neuron.2008.07.012
9. Hudspeth AJ. Integrating the active process of hair cells with cochlear function. Nat Rev Neurosci. (2014) 15:600–14. doi: 10.1038/nrn3786
10. Martin P, Hudspeth AJ. Compressive nonlinearity in the hair bundle's active response to mechanical stimulation. Proc Nat Acad Sci. (2001) 98:14386–91. doi: 10.1073/pnas.251530498
11. Jaramillo F, Markin VS, Hudspeth AJ. Auditory illusions and the single hair cell. Nature. (1993) 364:527–9. doi: 10.1038/364527a0
12. Barral J, Martin P. Phantom tones and suppressive masking by active nonlinear oscillation of the hair-cell bundle. Proc Nat Acad Sci. (2012) 109:E1344–51. doi: 10.1073/pnas.1202426109
13. Robles L, Ruggero MA. Mechanics of the mammalian cochlea. Physiol Rev. (2001) 81:1305–52. doi: 10.1152/physrev.2001.81.3.1305
14. Kemp DT. Stimulated acoustic emissions from within the human auditory system. J Acoust Soc Am. (1978) 64:1386–91. doi: 10.1121/1.382104
15. Choe Y, Magnasco MO, Hudspeth AJ. A model for amplification of hair-bundle motion by cyclical binding of Ca2+ to mechanoelectrical-transduction channels. Proc Nat Acad Sci. (1998) 95:15321–6. doi: 10.1073/pnas.95.26.15321
16. Ospeck M, Eguluz VM, Magnasco MO. Evidence of a Hopf bifurcation in frog hair cells. Biophys J. 80:2597–607. doi: 10.1016/S0006-3495(01)76230-3
17. Duke TAJ, Jülicher F. Critical oscillators as active elements in hearing. In: Active Processes and Otoacoustic Emissions in Hearing. New York, NY: Springer (2008). p. 63–92.
18. Martin P, Bozovic D, Choe Y, Hudspeth AJ. Spontaneous oscillation by hair bundles of the Bullfrog's sacculus. J Neurosci. (2003) 23:4533–48. doi: 10.1523/JNEUROSCI.23-11-04533.2003
19. Benser ME, Marquis RE, Hudspeth AJ. Rapid, active hair bundle movements in hair cells from the Bullfrog's sacculus. J Neurosci. (1996) 16:5629–43. doi: 10.1523/JNEUROSCI.16-18-05629.1996
20. Martin P, Hudspeth AJ. Active hair-bundle movements can amplify a hair cell's response to oscillatory mechanical stimuli. Proc Nat Acad Sci. (1999) 96:14306–11. doi: 10.1073/pnas.96.25.14306
21. Crawford AC, Fettiplace R. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J Physiol. (1985) 364:359–79. doi: 10.1113/jphysiol.1985.sp015750
22. Jülicher F, Andor D, Duke T. Physical basis of two-tone interference in hearing. Proc Nat Acad Sci. (2001) 98:9080–5. doi: 10.1073/pnas.151257898
23. Faber J, Bozovic D. Criticality and chaos in auditory and vestibular sensing. Sci Rep. (2024) 14:13073. doi: 10.1038/s41598-024-63696-3
24. Ó Maoiléidigh D, Hudspeth AJ. Sinusoidal-signal detection by active, noisy oscillators on the brink of self-oscillation. Physica D: Nonlinear Phenomena. (2018) 378–379:33–45. doi: 10.1016/j.physd.2018.05.001
26. Leshowitz B. Measurement of the two-click threshold. J Acoust Soc Am. (2005) 49:462–466. doi: 10.1121/1.1912374
27. Brughera A, Dunai L, Hartmann WM. Human interaural time difference thresholds for sine tones: the high-frequency limit. J Acoust Soc Am. (2013) 133:2839–55. doi: 10.1121/1.4795778
28. Neiman AB, Dierkes K, Lindner B, Han L, Shilnikov AL. Spontaneous voltage oscillations and response dynamics of a hodgkin-huxley type model of sensory hair cells. J Mathem Neurosci. (2011) 1:11. doi: 10.1186/2190-8567-1-11
29. Faber J, Bozovic D. Chaotic dynamics enhance the sensitivity of inner ear hair cells. Sci Rep. (2019) 9:18394. doi: 10.1038/s41598-019-54952-y
30. Abarbanel H. Analysis of Observed Chaotic Data. New York: Springer Science & Business Media. (1996).
31. Kantz H, Schreiber T. Nonlinear Time Series Analysis. Cambridge: Cambridge University Press. (1997).
32. Kaplan DT, Clay JR, Manning T, Glass L, Guevara MR, Shrier A. Subthreshold dynamics in periodically stimulated squid giant axons. Phys Rev Lett. (1996) 76:4074–7. doi: 10.1103/PhysRevLett.76.4074
33. Garfinkel A, Spano ML, Ditto WL, Weiss JN. Controlling cardiac chaos. Science. (1992) 257:1230–5. doi: 10.1126/science.1519060
34. Garfinkel A, Chen PS, Walter DO, Karagueuzian HS, Kogan B, Evans SJ, et al. Quasiperiodicity and chaos in cardiac fibrillation. J Clini Investigat. (1997) 99:305–14. doi: 10.1172/JCI119159
35. Shilnikov A, Shilnikov L, Turaev D. On some mathematical topics in classic synchronization. A tutorial. Int J Bifurc Chaos Appl Sci Eng. (2004) 14:2143–60. doi: 10.1142/S0218127404010539
36. Faber J, Bozovic D. Chaotic dynamics of inner ear hair cells. Sci Rep. (2018) 8:3366. doi: 10.1038/s41598-018-21538-z
37. Barral J, Jülicher F, Martin P. Friction from transduction channels' gating affects spontaneous hair-bundle oscillations. Biophys J. (2018) 114:425–36. doi: 10.1016/j.bpj.2017.11.019
38. Grassberger P, Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys Rev A. (1983) 28:2591–3. doi: 10.1103/PhysRevA.28.2591
39. Kim YH, Garfinkel A, Ikeda T, Wu TJ, Athill CA, Weiss JN, et al. Spatiotemporal complexity of ventricular fibrillation revealed by tissue mass reduction in isolated swine right ventricle: further evidence for the quasiperiodic route to chaos hypothesis. J Clini Investigat. (1997) 100:2486–500. doi: 10.1172/JCI119791
40. Eckmann JP, Ruelle D. Ergodic theory of chaos and strange attractors. Mod Rev Phys. (1985) 53:617. doi: 10.1103/RevModPhys.57.617
41. Wang G, Chen D, Lin J, Chen X. The application of chaotic oscillators to weak signal detection. IEEE. (1999) 46:440–4. doi: 10.1109/41.753783
42. Hu NQ, Wen XS. The application of duffing oscillator in characteristic signal detection of early fault. J Sound Vib. (2003) 268:917–31. doi: 10.1016/S0022-460X(03)00002-6
43. Schreiber T. Measuring information transfer. Phys Rev Lett. (2000) 85:461. doi: 10.1103/PhysRevLett.85.461
44. Faber J, Bozovic D. Noise-induced chaos and signal detection by the nonisochronous hopf oscillator. Chaos. (2019) 29:043132. doi: 10.1063/1.5091938
45. Faber J, Li H, Bozovic D. Synchronization and chaos in systems of coupled inner-ear hair cells. Phys Rev Res. (2021) 3:013266. doi: 10.1103/PhysRevResearch.3.013266
46. Ó Maoiléidigh D, Ricci AJ. A bundle of mechanisms: inner-ear hair-cell mechanotransduction. Trends Neurosci. (2019) 42:221–36. doi: 10.1016/j.tins.2018.12.006
47. Ó Maoiléidigh D, Nicola EM, Hudspeth AJ. The diverse effects of mechanical loading on active hair bundles. Proc Natl Acad Sci USA. (2012) 109:1943–8. doi: 10.1073/pnas.1120298109
48. Ó Maoiléidigh D, Jülicher F. The interplay between active hair bundle motility and electromotility in the cochlea. J Acoust Soc Am. (2010) 128:1175–90. doi: 10.1121/1.3463804
Keywords: chaos, hair cell, signal detection, hearing, vestibular system, nonlinear dynamics, information theory, Hopf bifurcation
Citation: Faber J and Bozovic D (2024) Review of chaos in hair-cell dynamics. Front. Neurol. 15:1444617. doi: 10.3389/fneur.2024.1444617
Received: 05 June 2024; Accepted: 26 June 2024;
Published: 10 July 2024.
Edited by:
Didier Dulon, Institut de lAudition, Institut Pasteur, FranceReviewed by:
Huaguang Gu, Tongji University, ChinaKuni Iwasa, National Institutes of Health (NIH), United States
Copyright © 2024 Faber and Bozovic. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Justin Faber, ZmFiZXImI3gwMDA0MDtwaHlzaWNzLnVjbGEuZWR1; Dolores Bozovic, Ym96b3ZpYyYjeDAwMDQwO3BoeXNpY3MudWNsYS5lZHU=