- 1VA Boston Healthcare System, Boston, MA, United States
- 2Departments of Medicine and Public Health, Boston University Chobanian and Avedisian School of Medicine, Boston, MA, United States
- 3Department of Neurology, Brigham and Women’s Hospital, Boston, MA, United States
- 4Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA, United States
- 5Channing Division for Network Medicine, Brigham and Women’s Hospital, Boston, MA, United States
- 6Harvard Medical School, Boston, MA, United States
Background and objectives: Crossover designs are frequently used to assess treatments for patients with Parkinson’s disease. Typically, two-period two-treatment trials include a washout period between the 2 periods and assume that the washout period is sufficiently long to eliminate carryover effects. A complementary strategy might be to jointly model carryover and treatment effects, though this has rarely been done in Parkinson’s disease crossover studies. The primary objective of this research is to demonstrate a modeling approach that assesses treatment and carryover effects in one unified mixed model analysis and to examine how it performs in a simulation study and a real data analysis example, as compared to other data analytic approaches used in Parkinson’s disease crossover studies.
Methods: We examined how three different methods of analysis (standard crossover t-test, mixed model with a carryover term included in model statement, and mixed model with no carryover term) performed in a simulation study and illustrated the methods in a real data example in Parkinson’s disease.
Results: The simulation study based on the presence of a carryover effect indicated that mixed models with a carryover term and an unstructured correlation matrix provided unbiased estimates of treatment effect and appropriate type I error. The methods are illustrated in a real data example involving Parkinson’s disease. Our literature review revealed that a majority of crossover studies included a washout period but did not assess whether the washout was sufficiently long to eliminate the possibility of carryover.
Discussion: We recommend using a mixed model with a carryover term and an unstructured correlation matrix to obtain unbiased estimates of treatment effect.
1. Introduction
In a crossover clinical trial, the effects of different treatments are administered on the same subject during different treatment periods (1, 2). A very common example of such a design is the two-period two-treatment design, often called the AB/BA design, where a subject is randomly assigned to either sequence AB or BA. A washout period may be included between the two periods to reduce carryover of the effect of treatment from one period to the next.
Crossover trials are being used more often and in a variety of clinical contexts. They are most appropriate for studies evaluating symptomatic treatment of diseases that are chronic or relatively stable (e.g., Parkinson’s disease [PD], rheumatoid arthritis), at least over the period under study (3). There continues to be debate on the analysis of treatment and carryover effects. We chose to examine methods of analysis being used in a defined clinical situation (PD) over the last 10 years.
The present paper considers several different methods to analyze crossover trials and examines their performance in a simulation study. The methods are illustrated in a PD crossover trial (4).
2. Methods
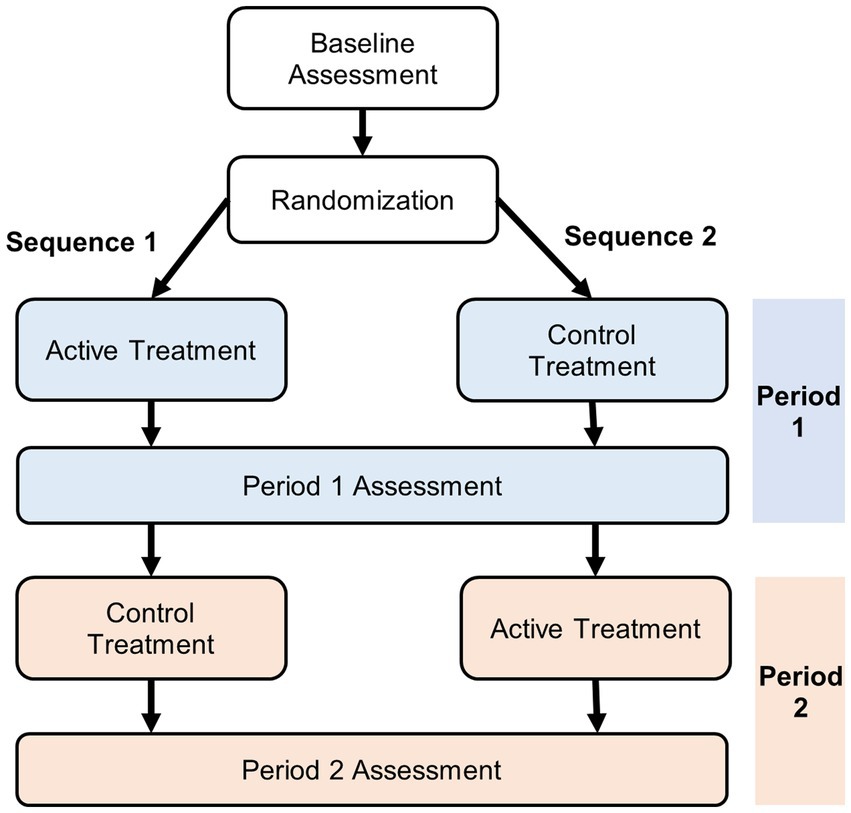
We will describe approaches for the analysis of AB/BA crossover trials with an active treatment and a control treatment (i.e., no treatment/placebo) as illustrated in Figure 1. In this design, study participants undergo a baseline assessment and are then randomized to receive one of the two treatments (active or control) during period 1. At the end of the period 1, an assessment is conducted followed by a switch to the other treatment to be received during period 2 (with or without a washout period). At the end of period 2, a second assessment is conducted.
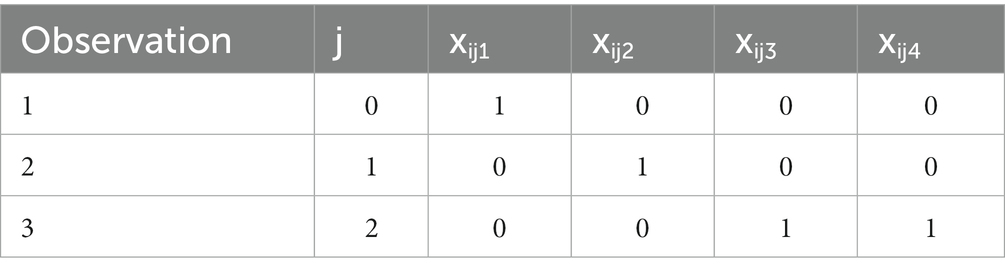
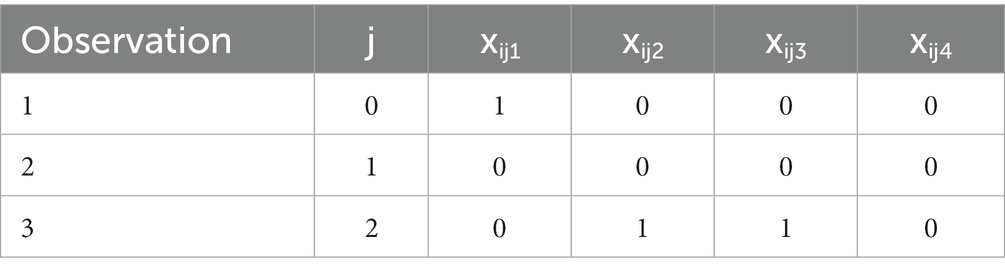
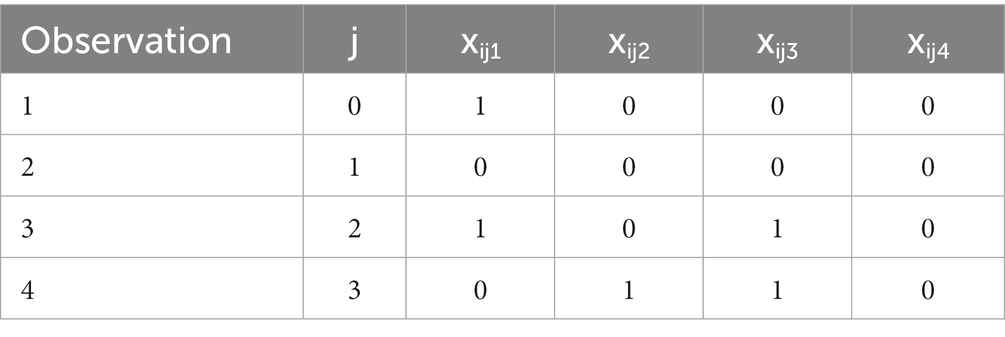
Some specific notation and definitions are used throughout this article. In general, let i = subject, j = assessment, where j = 0 if period 1 baseline, j = 1 if end of period 1, j = 2 if end of period 2. We will consider analytic strategies that assess effects of baseline, treatment, period, and carryover. Specifically, let:
yij = outcome value for the jth assessment of the ith subject (assumed continuous);
xij1 = 1 if baseline, = 0 else, referred to subsequently as BASELINE;
xij2 = 1 if active treatment (treatment 1), = 0 else, referred to subsequently as TREATMENT;
xij3 = 1 if period 2, = 0 if period 1, referred to subsequently as PERIOD2;
xij4 = 1 if carryover of treatment 1, = 0 else (1 − xij2) xij3, referred to subsequently as CARRYOVER;
Si = sequence for the ith subject, = 1,2.
We assume that n1 subjects are randomly assigned to sequence 1 and n2 subjects to sequence 2, where N = n1 + n2 with 3 observations per subject.
Sequence 1. For sequence 1, subjects’ 1st period = active, 2nd period = control and 3 observations per subject are given by:
Sequence 2. For sequence 2, subjects’ 1st period = control, 2nd period = active and 3 observations per subject are given by:
The goal of the analysis is to estimate the treatment effect.
2.1. Methods of analysis
We consider three different methods of analysis that can be used for AB/BA crossover trials.
2.1.1. Standard crossover t-test
For a standard crossover t-test, separate estimates of the mean of the within-subject differences between active and control are obtained for each sequence and separate variances of treatment effect are obtained in each sequence. The overall estimated treatment effect is an unweighted average of treatment effect estimates obtained in sequence 1 and 2 subjects and the variance is a weighted average of variance estimates obtained in sequence 1 and 2. Thus, the overall treatment effect is the unweighted average of the mean differences in outcome measurements between the active and control periods in sequence group 1 and sequence group 2, respectively. Specifically,
This procedure assumes that there is no carryover effect of active treatment in period 1 on outcome in period 2.
2.1.2. Mixed model with carryover term included in model statement
Because we have 3 repeated observations from each subject, which in general will be correlated with each other, we consider a mixed model approach to the analysis of the data. For this analysis, we use.
SAS PROC MIXED (Version 9.4, SAS Institute Inc., Cary, NC) with terms BASELINE (xij1), TREATMENT (xij2), PERIOD2 (xij3), and CARRYOVER (xij4) in the model statement. Specifically, we propose two different models:
a. Model 1: (mixed model with an unstructured covariance matrix)
where
β1 = BASELINE effect, β2 = TREATMENT effect, β3 = PERIOD2 effect, and β4 = CARRYOVER effect, all mutually adjusted for each other.
In this setting, we allow for a different correlation between outcomes for each pair of assessments ( and also a different variance at each assessment ( . Thus, the correlation between the baseline observation and the end of the first period ( ) is assumed to be different from the correlation between the baseline and the end of the second period ( ) as well as the correlation between outcomes at the end of the first period vs. the end of the second period ( ).
We implemented this analysis by using the REPEATED statement with TYPE = UNR (with an unstructured covariance matrix, which allows for different variance estimates at each observation and unequal correlations between outcomes at different pairs of observations).
b. Model 2: (mixed model with a compound symmetry covariance matrix)
where
In this setting, we assume that the within-subject variance ( ) is the same at each time point, and the correlation ( )) between outcomes for each pair of assessments are the same. This analysis was performed using the RANDOM statement (compound symmetry covariance matrix where the variances at each observation are forced to be the same and the correlation between outcomes at pairs of observations are also forced to be the same) with a random intercept.
The goal of the analysis is to estimate the TREATMENT effect (β2) and it’s variance (var(β2)) and to compare the variance when carryover is present (β4 ≠ 0) vs. when it is absent (β4 = 0), which we study in detail using simulation study analyses in Section 2.2.
2.1.3. Mixed model with no carryover term
If we assume there is no carryover effect, we can use similar modeling approaches as in Section 2.1.2 but removing the term for CARRYOVER (xij4). Therefore, equation 2 can be reduced to accommodate only BASELINE (xij1), TREATMENT (xij2), and PERIOD2 (xij3) effects as follows:
and, likewise, equation 3 can be reduced to the following:
where the same notation is used as in equations 2 and 3.
The correlated data were accommodated using either the REPEATED or the RANDOM statement of SAS PROC MIXED in a similar manner as in Section 2.1.2 (model 1 or model 2, respectively).
2.2. Simulation study design
The simulation study will focus on the performance of the three methods of analysis listed above with simulation settings from the real data example using Mini-BESTest data (see Section 3.2 of Results below). Four thousand simulations were run for different parameter combinations. The n = 4,000 was chosen because one can show that in order to test that type I error is 0.05 with a one sample binomial test, one would have 80% power to reject the null hypothesis if the true type I error is 0.04. In each simulated sample, the sample size was set to 32, which is the approximate median sample size used in actual PD crossover trials (see Section 3.3 of Results), where 16 subjects were assigned to sequence 1 (active treatment followed by control) and 16 were assigned to sequence 2 (control followed by active treatment). Three outcome values were generated for each subject in the sample corresponding to outcomes obtained during (i) period 1 baseline, (ii) end of period 1, and (iii) end of period 2. The model used to simulate the outcome data, Yit for the ith subject at time t, when a carryover effect was assumed to be present was:
i.e. β1 = 0.4, β2 = 2, β3 = −2, and β4 = 1, and eit is a random error term for the ith subject at time t. When no carryover effect was assumed, the term CARRYOVER was removed from equation 6 to simulate the data.
In the simulations, random errors were generated using SAS PROC SIMNORMAL with three different covariance structures as described in Sections 2.2.1 to 2.2.3.
2.2.1. Compound symmetry
We set the pairwise correlations ρ01 = ρ12 = ρ02 = ρ for 3 different values of ρ (intraclass correlation coefficient [ICC]) = 0.8, 0.5, and 0.2, respectively. The covariance matrix was constructed with a common variance σ02 = σ12 = σ22 = σ2 set to 13.4.
2.2.2. Unstructured correlation, equal variance
We set ρ01 = 0.8, ρ12 = 0.2, and ρ02 = 0.1, where correlations are much stronger for outcomes within the same period (period 1 baseline and end of period 1) than for outcomes assessed at different periods (period 1 baseline and end of period 2; end of period 1 and end of period 2). The covariance matrix was constructed with a common variance σ02 = σ12 = σ22 = σ2 set to 13.4.
2.2.3. Unstructured correlation, unequal variance
We set ρ01 = 0.8, ρ12 = 0.2, and ρ02 = 0.1, but allowed the variances to be heterogeneous as well (σ02 = 17, σ12 = σ22 = 11).
Several performance measures, including mean and variance of estimated treatment effect, bias, coverage, power, and type I error were obtained from the simulations.
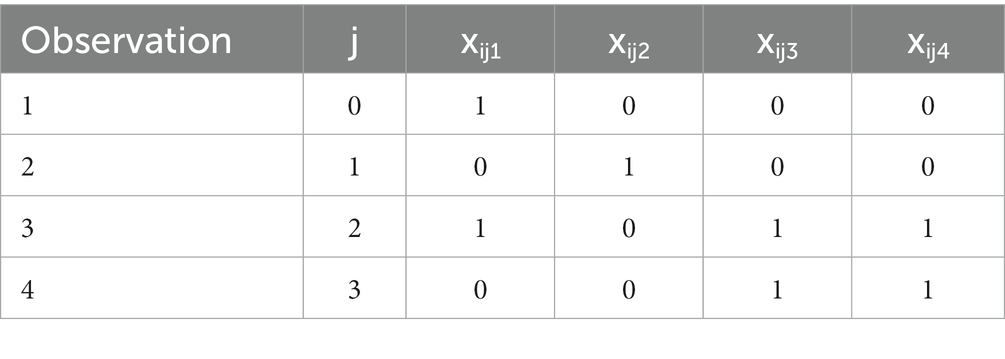
2.3. Crossover trials with 4 observations
The mixed model defined in equation 2 can be extended to allow for 4 observations with baseline measurements at the beginning of each of two periods. The design matrices for this situation are given below.
Sequence 1. For sequence 1, subjects’ 1st period = active, 2nd period = control and 4 observations per subject are given by:
Sequence 2. For sequence 2, subjects’ 1st period = control, 2nd period = active and 4 observations per subject are given by:
The mixed model based on 4 observations is given in equation 7.
where the are defined similarly to the 3-observation design in equation 2.
2.4. Systematic review
Crossover trials are being used more often and in a variety of clinical contexts, including PD. We searched PubMed, EMBASE, CINAHL, and Health & Medical Collection between 2012 and 2021 with the combination of the search terms “Parkinson disease” and “crossover.” The search strategy was adapted for multiple databases. A detailed description of the search procedure is provided in Supplementary Table S1, which may be found in the online version of this article at the publisher’s web-site.
3. Results
3.1. Simulation results
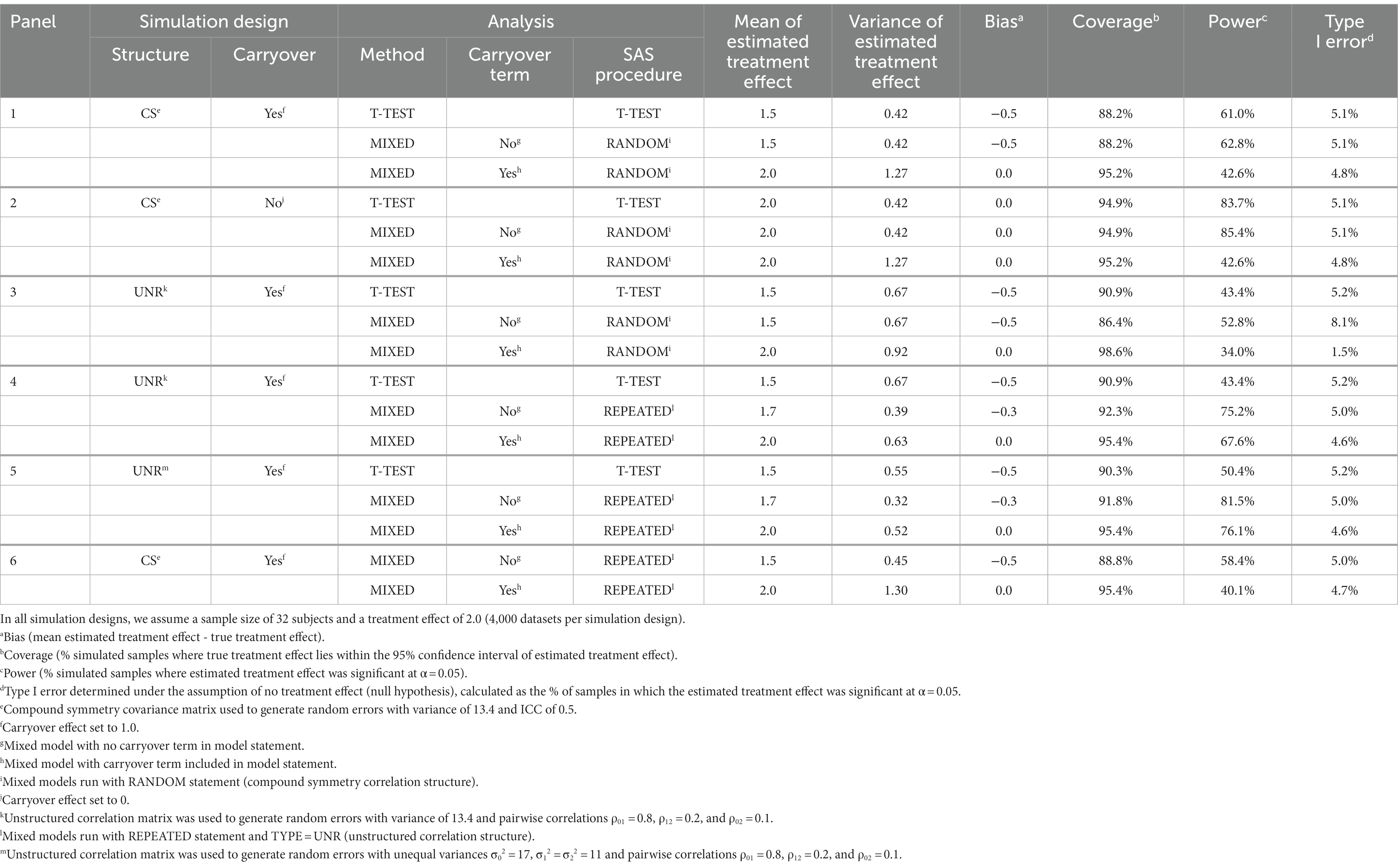
For designs with three observations, we considered several different methods for simulating the data presented in Panels 1–6 and for each Panel several different methods for analyzing the data (see Table 1).
3.1.1. Table 1, Panel 1
The three methods of analysis were performed on the first set of simulated data based on a compound symmetry correlation structure with an ICC of 0.5 and a carryover effect of 1. The standard crossover t-test provides a biased estimate of treatment effect and has coverage lower than the nominal 95% coverage. The type I error is appropriate. The results of the mixed model with no carryover term (equation 4) are virtually identical to those of the crossover t-test. The mixed model that includes a carryover term provides an unbiased treatment estimate, appropriate coverage probability, and appropriate type I error. In general, differences between the mixed model with a carryover term and the other two methods are greatest when the correlations between repeated measures is high. Similar conclusions are obtained for the other ICC values (0.2, 0.8; results not shown); hereafter, for ease of presentation, only the results for ICC = 0.5 are presented.
3.1.2. Table 1, Panel 2
With the carryover effect set to 0, the standard crossover t-test and the mixed model with no carryover term have no bias, appropriate coverage, and appropriate type I error. The mixed model with a term for carryover also has no bias, correct coverage, and correct type I error, but does suffer in terms of power compared to the mixed model with no carryover term and the standard crossover t-test.
3.1.3. Table 1, Panel 3
For the simulated data based on a more general unstructured (heterogeneous) correlation structure and a carryover effect, the standard crossover t-test has a correct type I error; however, the treatment estimate is biased and the coverage is too low. The mixed model with no carryover term and a covariance matrix constructed with common variance has an incorrect type I error, is biased, and has coverage probability too low. The mixed model with a carryover term has no bias but the type I error is too low and the coverage is too high. These mixed models were run using the RANDOM statement for repeated measures, which assumes a compound symmetry correlation structure, which differs from the actual correlation structure of the data (unstructured correlation structure). The results suggest the need for a modeling approach that assumes a different correlation structure.
3.1.4. Table 1, Panels 4 and 5
We repeated the mixed models (with and without a carryover term) with the use of the REPEATED statement with TYPE = UNR (unstructured correlation structure; Panel 4). This provided an appropriate type I error with the carryover term included. However, the model with no carryover term still has low coverage and is biased, whereas the model with a carryover term (equation 2) is unbiased with appropriate coverage. We repeated the simulation described in Panel 4 but generated the data so that the standard deviations were different for the three observations (σ02 = 17, σ12 = σ22 = 11). The modeling (with and without a carryover term) results (Panel 5) were comparable to those in Panel 4 in terms of bias, coverage, and type I error. Power for the mixed model with carryover term increased from 68 to 76%. This is probably because the unstructured correlation structure used to analyze the data allows for heterogeneous variances of the three repeated measures, which is more consistent with the simulation design in Panel 5 where the variances were allowed to be different than the simulation design in Panel 4 where they were forced to be the same.
3.1.5. Table 1, Panel 6
We repeated the mixed models in Table 1, Panel 1 replacing the RANDOM statement with a REPEATED statement with an unstructured correlation matrix. With the use of the REPEATED statement, there is still an appropriate type I error but a slight reduction in power (43% vs. 40% if carryover term is present and 63% vs. 58% if carryover term is absent). Also, the model with a carryover term present continues to provide an unbiased estimate of treatment effect and appropriate 95% coverage. The fact that modeling with use of the REPEATED statement with an unstructured correlation matrix can accommodate many different types of correlation structure that may be present in the data argues for using this method.
3.2. Real data example
Data from a real life two-period two-treatment crossover trial is used to illustrate our methods of analysis. The study evaluated the efficacy of 3 months of balance exercise training compared with usual care on the outcomes of dynamic balance (Mini-BESTest) and fear of falling (Falls Efficacy Scale-International [FES-I]) in patients with PD (4).
3.2.1. Mini-BESTest
Subjects in both sequences improved in dynamic balance (as assessed by Mini-BESTest) with exercise vs. usual care; however, there was more improvement in sequence 2 suggesting the possibility of a carryover effect (Table 2, Section A). We conducted a mixed model analysis with a carryover term and observed a significant treatment effect and a significant positive carryover effect (Table 2, Section Ba). Table 2, Section Bb indicates that there is greater variance at baseline than in periods 1 and 2 and that the correlation structure is mildly divergent from compound symmetry. The estimated treatment effect from the standard crossover t-test, which does not adjust for carryover, is substantially smaller than that of the mixed model with a carryover term (Table 2, Section C). Our results from Table 1, Panel 4 suggest that it is smaller because it is biased and, therefore, an underestimate of the treatment effect.
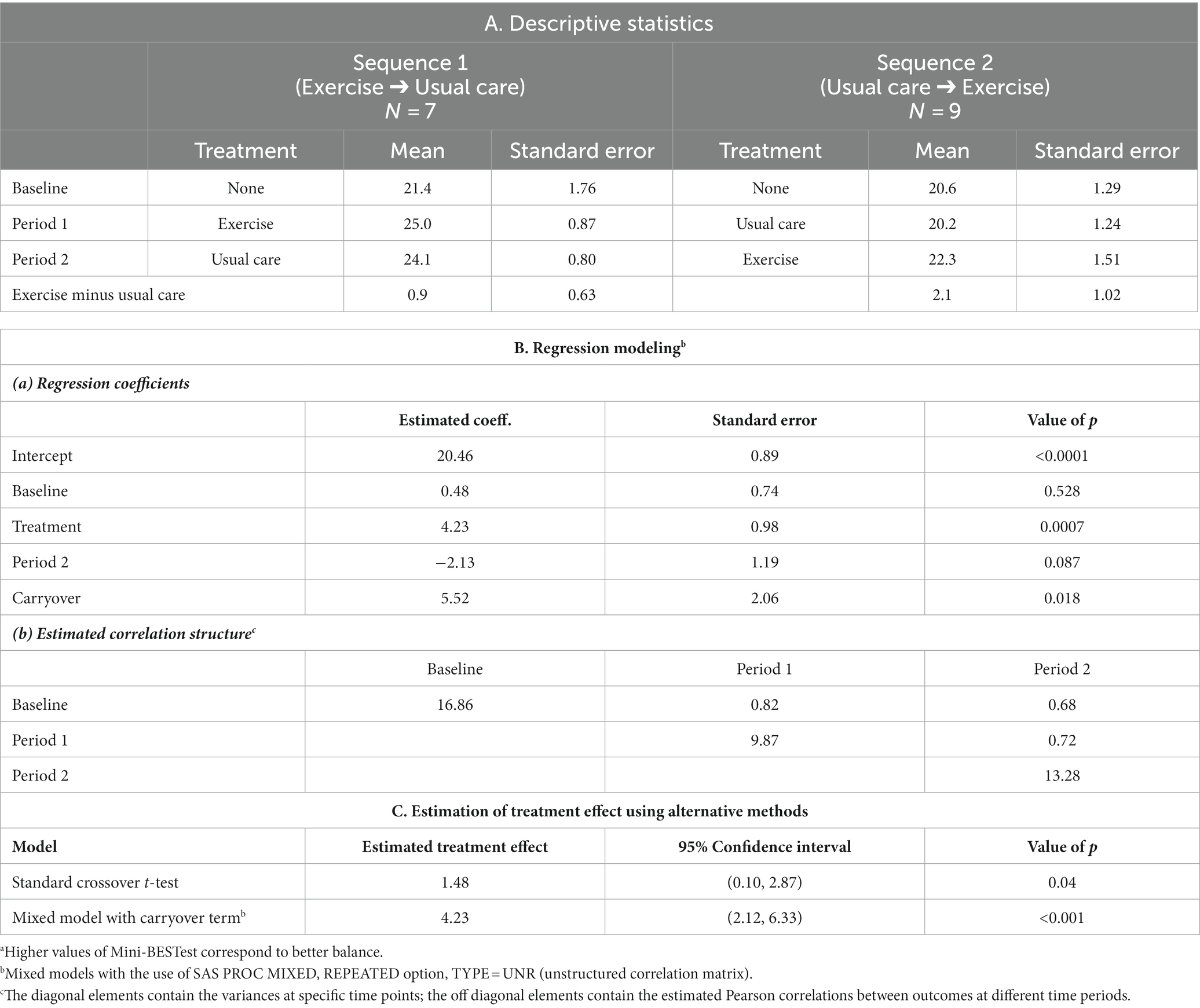
Table 2. Analysis of a balance exercise training intervention for PD patients: descriptive statistics and alternative methods of analysis for the Mini-BESTest.a
3.2.2. FES-I
Subjects in both sequences had less fear of falling (as assessed by FES-I) with exercise vs. usual care; however, there was less fear in sequence 2 again suggesting the possibility of a carryover effect (Table 3, Section A). We conducted a mixed model analysis with a carryover term and observed no significant carryover effect (Table 3, Section Ba). There is strong evidence of heterogenous variance over different periods with a higher variance for baseline measurements than during subsequent periods (Table 3, Section Bb). In addition, there is also strong evidence of heterogeneous correlation with higher within period 1 correlation (0.86) and lower between period 1 and 2 correlation (0.41 to 0.46). The estimated treatment effect from the standard crossover t-test is slightly smaller than that of the mixed model with a carryover term (Table 3, Section C).
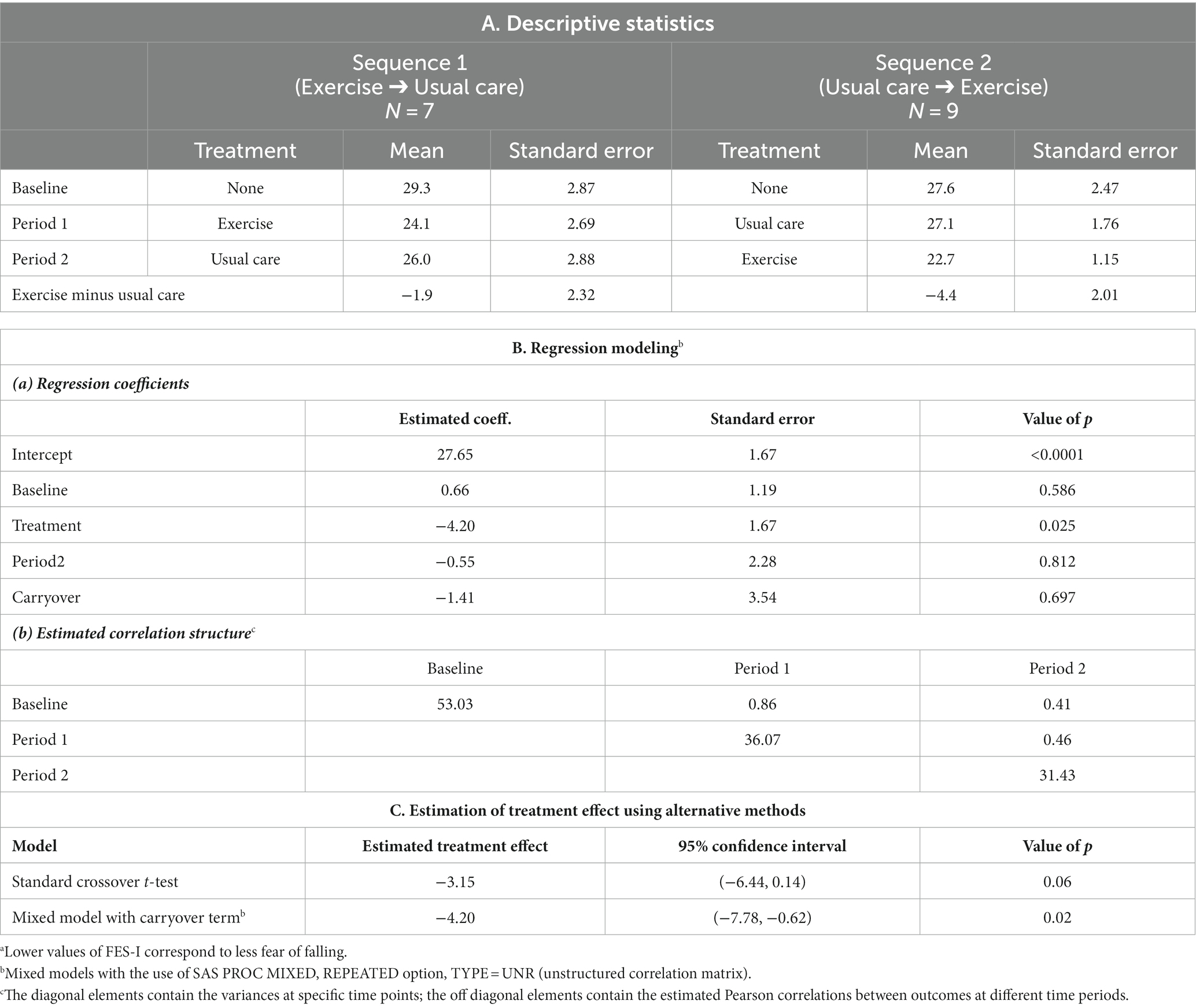
Table 3. Analysis of a balance exercise training intervention for PD patients: descriptive statistics and alternative methods of analysis for the FES-Ia.
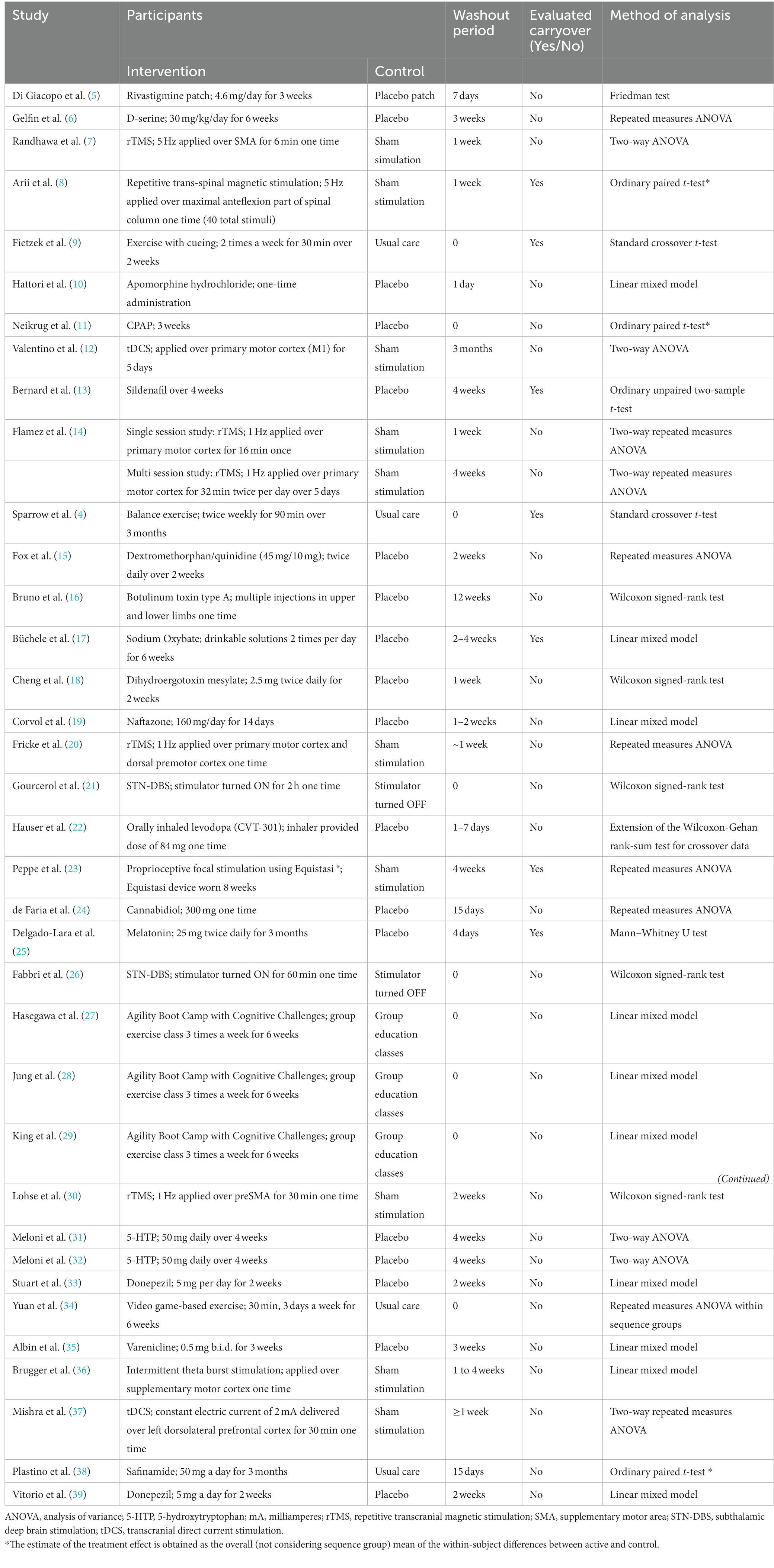
3.3. Results of the literature search
Our initial search retrieved 691 abstracts of potential interest. After full text review and consideration of inclusion criteria (Supplementary Table S1), 36 AB/BA crossover trials in PD with an active treatment and a control treatment were identified and evaluated (Table 4). There was no evidence that any of these studies controlled for carryover. Furthermore, only six provided some information to suggest that carryover was minimal: in two studies, the washout period was seemingly long enough based on pharmacokinetics (25, 33); in four other studies, a test for carryover was performed but not statistically significant (8, 9, 13, 17). However it’s well known that tests for carryover often have low statistical power (40).
Eighteen of the 36 AB/BA crossover trials evaluated a drug intervention (5, 6, 10, 13, 15–19, 22, 24, 25, 31–33, 35, 38, 39); all 18 included a washout period (range, 1 day to 12 weeks). Washout period duration can be based on estimates of drug half-life and the number of days to reach a steady state as in two of these trials (25, 33). The remaining 16 studies did not provide a justification for the washout period duration. Of these 16, only two investigated carryover effect and both of these studies found it nonsignificant; however, it is not clear how these investigations were done (13, 17). Despite these nonsignificant findings, a residual carryover effect may not be negligible and thus should be controlled (41, 42).
Eighteen of the 36 AB/BA crossover trials evaluated an intervention other than a drug (exercise, transcranial direct current stimulation [tDCS], repetitive transcranial magnetic stimulation [rTMS], proprioceptive focal stimulation, subthalamic deep brain stimulation [STN-DBS], theta burst stimulation, CPAP) (4, 7–9, 11, 12, 14, 20, 21, 23, 26–30, 34, 36, 37). Nine of these trials did not include a washout period and provided no justification whereas nine included a washout period but provided no justification for the length of the washout period.
4. Discussion
AB/BA crossover studies can produce results that are statistically and clinically valid, and the sample size required for a given power is typically much smaller, compared to that of a parallel-group design. The smaller sample size required in crossover studies is an important advantage because patient recruitment is often a problem in clinical research (43–45), particularly in PD. Evidence suggests that insufficient enrollment prevents completion of 30% of PD clinical trials and delays 85% of those eventually completed (46). In addition, research that is underpowered (due to small sample size) will have a higher probability of failing to detect true therapeutic benefits, potentially resulting in missed opportunities to utilize effective interventions (47). Furthermore, in our experience with treatment trials using a placebo as a comparator and a parallel group design, many subjects are put off by the chance that they may not receive the active treatment. In a crossover trial all patients will receive the active treatment, which helps many subjects to legitimize the time and effort that goes into being a study participant and enhances recruitment possibilities.
A problem particularly associated with crossover trials is a residual carryover effect (e.g., a drug carryover effect when traces of the period 1 drug persist). This is a particular concern in trials with no washout period, which in our review occurred in 25% of the trials. Although many crossover trials include a washout period as a means of reducing carryover, we found that a substantial number of trials lacked justification for the length of the washout period, which is also very concerning. Even when a washout of an active treatment is completely effective, physiological or psychological states induced by the treatment may linger into the subsequent period (41, 48). But the required length of a physiological/psychological washout period is usually unknown.
Some authors have argued that the use of the crossover design is effectively built on the assumption that there is minimal carryover of the effect of a treatment into the next period (49, 50). Following this philosophy, rather than addressing carryover, one should proceed as if there were no carryover. Therefore, it is not surprising that our literature review revealed no evidence that any of the 36 AB/BA crossover trials controlled for carryover effect, which is particularly problematic for studies without a washout period (4, 9, 11, 21, 26–29, 34). Fortunately, researchers are increasingly including a washout period.
This study aims at assessing different strategies for dealing with potential carryover in crossover trials. Crossover trials should be designed with a sufficiently long washout period. Prior trials can be used to provide information on designing an adequate washout period (1, 2). Additionally, for drug intervention studies, washout period duration can be based on estimates of drug half-life and the number of days to reach a steady state. On the other hand, having too long of a washout period could lead to significant loss of subjects. In addition, including a longer washout period could alter results due to disease progression or other lifestyle circumstances (i.e., unrelated illness, fatigue, change in social circumstances). In addition to carefully choosing a washout period, a complementary analytical strategy, which we advocate, is to jointly model carryover, period, and treatment effects in the interest of obtaining unbiased estimates of treatment effect, whether carryover effect is statistically significant or not.
With the use of a mixed model with carryover term we avoided such bias in each set of simulated data. Such modeling performed with the use of an unstructured correlation structure (equation 2) resulted in the most appropriate type I error and coverage probability. In contrast, modeling with the use of an incorrect correlation structure, specifically compound symmetry (Table 1, Panel 3), and including a carryover term, has a large effect on the type I error (i.e., an invalid test procedure), whether a true carryover effect is present or not. Conversely, if an unstructured correlation structure is used for modeling and compound symmetry was the true correlation structure, type I error and coverage probability are preserved and power is only slightly reduced.
Thus, it appears the most conservative approach is to use a mixed model with a carryover term and an unstructured correlation structure (equation 2). With this approach we obtain unbiased estimates of treatment effect both with and without carryover effect present and obtain appropriate coverage regardless of the actual correlation structure in the data. Therefore, we recommend that researchers apply this modeling approach in the analysis of all AB/BA crossover trials with an active treatment and a control treatment and a single baseline.
Although we have concentrated on bias arising from carryover effect in this paper, we would be remiss not to mention other sources of bias: bias arising from period effect (1, 51) or missing outcome data (2, 51). Bias due to period effect may occur when the disease changes systematically over time, or if there are changes over time in background factors such as underlying medical management strategies. However, potential bias arising from period effect can be overcome by using a statistical analysis that includes period effect, such as in our mixed model analyses featured in this article. Bias due to missing outcome data may occur because a participant drops out in the second treatment period because of a poorer experience than in the first period.
In this paper, we provide modeling strategies for crossover studies with either 3-observation or 4-observation designs and provide simulation results for alternative modeling strategies in the 3-observation setting. It is likely that unbiased estimates of treatment effect can be obtained with both 3-observation and 4-observation designs, but it would be expected that the standard errors of parameter estimates would be somewhat smaller with the 4-observation design. On the other hand, dropout is more likely with a 4-observation vs. a 3-observation design since patient burden is increased. A detailed simulation study comparing the efficiency of these 2 designs will be the subject of another paper.
In this paper, we have discussed several modeling options for crossover design and present detailed SAS code for implementing these modeling options (Supplementary Datasheet S1). Mixed model analyses are also available in Stata (using the mixed command), R (using the lmer command), and SPSS (using the mixed command), although specific options available may vary across different packages.
In summary, mixed model analyses offer the opportunity to realize the advantages of crossover designs in obtaining unbiased estimates of treatment effect by simultaneously modeling treatment, period, and carryover effects and providing for an appropriate correlation structure among the repeated measures. We recommend this analytic strategy to fully take advantage of the reduced sample size needed for crossover designs while still obtaining unbiased estimates of treatment effects.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
DS: research project: conception, execution, statistical analysis: review and critique, manuscript preparation: writing of the first draft, and review and critique. DD and BR: research project: organization, execution, statistical analysis: design, execution, review and critique, manuscript preparation: writing of the first draft, and review and critique. OD and RD: research project: organization, statistical analysis: review and critique, manuscript preparation: review and critique. All authors contributed to the article and approved the submitted version.
Funding
The work in this manuscript was supported by VA Rehabilitation Research and Development.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fneur.2023.1197281/full#supplementary-material
References
1. Senn, S . The AB/BA crossover: past, present and future? Stat Methods Med Res. (1994) 3:303–24. doi: 10.1177/096228029400300402
2. Louis, TA, Lavori, PW, Bailar, JC3rd, and Polansky, M. Crossover and self-controlled designs in clinical research. N Engl J Med. (1984) 310:24–31. doi: 10.1056/NEJM198401053100106
3. Mills, EJ, Chan, AW, Wu, P, Vail, A, Guyatt, GH, and Altman, DG. Design, analysis, and presentation of crossover trials. Trials. (2009) 10:27. doi: 10.1186/1745-6215-10-27
4. Sparrow, D, DeAngelis, TR, Hendron, K, Thomas, CA, Saint-Hilaire, M, and Ellis, T. Highly challenging balance program reduces fall rate in Parkinson disease. J Neurol Phys Ther. (2016) 40:24–30. doi: 10.1097/NPT.0000000000000111
5. Di Giacopo, R, Fasano, A, Quaranta, D, Della Marca, G, Bove, F, and Bentivoglio, AR. Rivastigmine as alternative treatment for refractory REM behavior disorder in Parkinson's disease. Mov Disord. (2012) 27:559–61. doi: 10.1002/mds.24909
6. Gelfin, E, Kaufman, Y, Korn-Lubetzki, I, Bloch, B, Kremer, I, Javitt, DC, et al. D-serine adjuvant treatment alleviates behavioural and motor symptoms in Parkinson's disease. Int J Neuropsychopharmacol. (2012) 15:543–9. doi: 10.1017/S1461145711001015
7. Randhawa, BK, Farley, BG, and Boyd, LA. Repetitive transcranial magnetic stimulation improves handwriting in Parkinson's disease. Parkinsons Dis. (2013) 2013:751925. doi: 10.1155/2013/751925
8. Arii, Y, Sawada, Y, Kawamura, K, Miyake, S, Taichi, Y, Izumi, Y, et al. Immediate effect of spinal magnetic stimulation on camptocormia in Parkinson's disease. J Neurol Neurosurg Psychiatry. (2014) 85:1221–6. doi: 10.1136/jnnp-2014-307651
9. Fietzek, UM, Schroeteler, FE, Ziegler, K, Zwosta, J, and Ceballos-Baumann, AO. Randomized crossover trial to investigate the efficacy of a two-week physiotherapy programme with repetitive exercises of cueing to reduce the severity of freezing of gait in patients with Parkinson's disease. Clin Rehabil. (2014) 28:902–11. doi: 10.1177/0269215514527299
10. Hattori, N, and Nomoto, M. 6500-004 study group, sustained efficacy of apomorphine in Japanese patients with advanced Parkinson's disease. Parkinsonism Relat Disord. (2014) 20:819–23. doi: 10.1016/j.parkreldis.2014.04.008
11. Neikrug, AB, Liu, L, Avanzino, JA, Maglione, JE, Natarajan, L, Bradley, L, et al. Continuous positive airway pressure improves sleep and daytime sleepiness in patients with Parkinson disease and sleep apnea. Sleep. (2014) 37:177–85. doi: 10.5665/sleep.3332
12. Valentino, F, Cosentino, G, Brighina, F, Pozzi, NG, Sandrini, G, Fierro, B, et al. Transcranial direct current stimulation for treatment of freezing of gait: a crossover study. Mov Disord. (2014) 29:1064–9. doi: 10.1002/mds.25897
13. Bernard, BA, Metman, LV, Levine, L, Ouyang, B, Leurgans, S, and Goetz, CG. Sildenafil in the treatment of erectile dysfunction in Parkinson's disease. Mov Disord Clin Pract. (2016) 4:412–5. doi: 10.1002/mdc3.12456
14. Flamez, A, Cordenier, A, De Raedt, S, Michiels, V, Smetcoren, S, Van Merhaegen-Wieleman, A, et al. Bilateral low frequency rTMS of the primary motor cortex may not be a suitable treatment for levodopa-induced dyskinesias in late stage Parkinson's disease. Parkinsonism Relat Disord. (2016) 22:62–7. doi: 10.1016/j.parkreldis.2015.11.009
15. Fox, SH, Metman, LV, Nutt, JG, Brodsky, M, Factor, SA, Lang, AE, et al. Trial of dextromethorphan/quinidine to treat levodopa-induced dyskinesia in Parkinson's disease. Mov Disord. (2017) 32:893–903. doi: 10.1002/mds.26976
16. Bruno, V, Freitas, ME, Mancini, D, Lui, JP, Miyasaki, J, and Fox, SH. Botulinum toxin type a for pain in advanced Parkinson's disease. Can J Neurol Sci. (2018) 45:23–9. doi: 10.1017/cjn.2017.245
17. Büchele, F, Hackius, M, Schreglmann, SR, Omlor, W, Werth, E, Maric, A, et al. Sodium Oxybate for excessive daytime sleepiness and sleep disturbance in Parkinson disease: a randomized clinical trial. JAMA Neurol. (2018) 75:114–8. doi: 10.1001/jamaneurol.2017.3171
18. Cheng, YQ, Ge, NN, Zhu, HH, Sha, ZT, Jiang, T, Zhang, YD, et al. Dihydroergotoxine mesylate for the treatment of sialorrhea in Parkinson's disease. Parkinsonism Relat Disord. (2019) 58:70–3. doi: 10.1016/j.parkreldis.2018.08.022
19. Corvol, JC, Durif, F, Meissner, WG, Azulay, JP, Haddad, R, Guimarães-Costa, R, et al. Naftazone in advanced Parkinson's disease: an acute L-DOPA challenge randomized controlled trial. Parkinsonism Relat Disord. (2019) 60:51–6. doi: 10.1016/j.parkreldis.2018.10.005
20. Fricke, C, Duesmann, C, Woost, TB, von Hofen-Hohloch, J, Rumpf, JJ, Weise, D, et al. Dual-site transcranial magnetic stimulation for the treatment of Parkinson's disease. Front Neurol. (2019) 10:174. doi: 10.3389/fneur.2019.00174
21. Gourcerol, G, Maltete, D, Chastan, N, Welter, ML, Leroi, AM, and Derrey, S. Does bilateral deep brain stimulation of the subthalamic nucleus modify Ano-rectal motility in Parkinson's disease? Results of a randomized cross-over study. Neuromodulation. (2019) 22:478–83. doi: 10.1111/ner.12947
22. Hauser, RA, Isaacson, SH, Ellenbogen, A, Safirstein, BE, Truong, DD, Komjathy, SF, et al. Orally inhaled levodopa (CVT-301) for early morning OFF periods in Parkinson's disease. Parkinsonism Relat Disord. (2019) 64:175–80. doi: 10.1016/j.parkreldis.2019.03.026
23. Peppe, A, Paravati, S, Baldassarre, MG, Bakdounes, L, Spolaor, F, Guiotto, A, et al. Proprioceptive focal stimulation (Equistasi®) may improve the quality of gait in middle-moderate Parkinson's disease patients. Double-blind, double-dummy, randomized, crossover, Italian multicentric study. Front Neurol. (2019) 10:998. doi: 10.3389/fneur.2019.00998
24. de Faria, SM, de Morais Fabrício, D, Tumas, V, Castro, PC, Ponti, MA, Hallak, JE, et al. Effects of acute cannabidiol administration on anxiety and tremors induced by a simulated public speaking test in patients with Parkinson's disease. J Psychopharmacol. (2020) 34:189–96. doi: 10.1177/0269881119895536
25. Delgado-Lara, DL, González-Enríquez, GV, Torres-Mendoza, BM, González-Usigli, H, Cárdenas-Bedoya, J, Macías-Islas, MA, et al. Effect of melatonin administration on the PER1 and BMAL1 clock genes in patients with Parkinson's disease. Biomed Pharmacother. (2020) 129:110485. doi: 10.1016/j.biopha.2020.110485
26. Fabbri, M, Zibetti, M, Rizzone, MG, Giannini, G, Borellini, L, Stefani, A, et al. Should we consider deep brain stimulation discontinuation in late-stage Parkinson's disease? Mov Disord. (2020) 35:1379–87. doi: 10.1002/mds.28091
27. Hasegawa, N, Shah, VV, Harker, G, Carlson-Kuhta, P, Nutt, JG, Lapidus, JA, et al. Responsiveness of objective vs. clinical balance domain outcomes for exercise intervention in Parkinson's disease. Front Neurol. (2020) 11:940. doi: 10.3389/fneur.2020.00940
28. Jung, SH, Hasegawa, N, Mancini, M, King, LA, Carlson-Kuhta, P, Smulders, K, et al. Effects of the agility boot camp with cognitive challenge (ABC-C) exercise program for Parkinson's disease. NPJ Parkinsons Dis. (2020) 6:31. doi: 10.1038/s41531-020-00132-z
29. King, LA, Mancini, M, Smulders, K, Harker, G, Lapidus, JA, Ramsey, K, et al. Cognitively challenging agility boot camp program for freezing of gait in Parkinson disease. Neurorehabil Neural Repair. (2020) 34:417–27. doi: 10.1177/1545968320909331
30. Lohse, A, Meder, D, Nielsen, S, Lund, AE, Herz, DM, Løkkegaard, A, et al. Low-frequency transcranial stimulation of pre-supplementary motor area alleviates levodopa-induced dyskinesia in Parkinson's disease: a randomized crossover trial. Brain Commun. (2020) 2:fcaa147. doi: 10.1093/braincomms/fcaa147
31. Meloni, M, Puligheddu, M, Carta, M, Cannas, A, Figorilli, M, and Defazio, G. Efficacy and safety of 5-hydroxytryptophan on depression and apathy in Parkinson's disease: a preliminary finding. Eur J Neurol. (2020) 27:779–86. doi: 10.1111/ene.14179
32. Meloni, M, Puligheddu, M, Sanna, F, Cannas, A, Farris, R, Tronci, E, et al. Efficacy and safety of 5-Hydroxytryptophan on levodopa-induced motor complications in Parkinson's disease: a preliminary finding. J Neurol Sci. (2020) 415:116869. doi: 10.1016/j.jns.2020.116869
33. Stuart, S, Morris, R, Giritharan, A, Quinn, J, Nutt, JG, and Mancini, M. Prefrontal cortex activity and gait in Parkinson's disease with cholinergic and dopaminergic therapy. Mov Disord. (2020) 35:2019–27. doi: 10.1002/mds.28214
34. Yuan, RY, Chen, SC, Peng, CW, Lin, YN, Chang, YT, and Lai, CH. Effects of interactive video-game-based exercise on balance in older adults with mild-to-moderate Parkinson's disease. J Neuroeng Rehabil. (2020) 17:91. doi: 10.1186/s12984-020-00725-y
35. Albin, RL, Müller, MLTM, Bohnen, NI, Spino, C, Sarter, M, Koeppe, RA, et al. α4β2* nicotinic cholinergic receptor target engagement in Parkinson disease gait-balance disorders. Ann Neurol. (2021) 90:130–42. doi: 10.1002/ana.26102
36. Brugger, F, Wegener, R, Baty, F, Walch, J, Krüger, MT, Hägele-Link, S, et al. Facilitatory rTMS over the supplementary motor cortex impedes gait performance in Parkinson patients with freezing of gait. Brain Sci. (2021) 11:321. doi: 10.3390/brainsci11030321
37. Mishra, RK, and Thrasher, AT. Transcranial direct current stimulation of dorsolateral prefrontal cortex improves dual-task gait performance in patients with Parkinson's disease: a double blind, sham-controlled study. Gait Posture. (2021) 84:11–6. doi: 10.1016/j.gaitpost.2020.11.012
38. Plastino, M, Gorgone, G, Fava, A, Ettore, M, Iannacchero, R, Scarfone, R, et al. Effects of safinamide on REM sleep behavior disorder in Parkinson disease: a randomized, longitudinal, crossover pilot study. J Clin Neurosci. (2021) 91:306–12. doi: 10.1016/j.jocn.2021.07.011
39. Vitorio, R, Stuart, S, Giritharan, A, Quinn, J, Nutt, JG, and Mancini, M. Changes in prefrontal cortical activity and turning in response to dopaminergic and cholinergic therapy in Parkinson's disease: a randomized crossover trial. Parkinsonism Relat Disord. (2021) 86:10–4. doi: 10.1016/j.parkreldis.2021.03.014
40. Brown, BWJr . The crossover experiment for clinical trials. Biometrics. (1980) 36:69–79. doi: 10.2307/2530496
41. Liang, Y, and Carriere, KC. On the role of baseline measurements for crossover designs under the self and mixed carryover effects model. Biometrics. (2010) 66:140–8. doi: 10.1111/j.1541-0420.2009.01229.x
42. Ozan, MO, and Stufken, J. Assessing the impact of carryover effects on the variances of estimators of treatment differences in crossover designs. Stat Med. (2010) 29:2480–5. doi: 10.1002/sim.4009
43. Huang, GD, Bull, J, Johnston McKee, K, Mahon, E, Harper, B, and Roberts, JN. Clinical trials recruitment planning: a proposed framework from the clinical trials transformation initiative. Contemp Clin Trials. (2018) 66:74–9. doi: 10.1016/j.cct.2018.01.003
44. Mathur, S, DeWitte, S, Robledo, I, Isaacs, T, and Stamford, J. Rising to the challenges of clinical trial improvement in Parkinson's disease. J Parkinsons Dis. (2015) 5:263–8. doi: 10.3233/JPD-150541
45. Carlisle, B, Kimmelman, J, Ramsay, T, and MacKinnon, N. Unsuccessful trial accrual and human subjects protections: an empirical analysis of recently closed trials. Clin Trials. (2015) 12:77–83. doi: 10.1177/1740774514558307
46. MJFF, The Michael J. Fox Foundation Launches “Parkinson’s Clinical Trial Companion,” Educational Suite Designed to Support Progress in Parkinson’s Research by Increasing Patient Participation in Clinical Studies. Available at: https://www.michaeljfox.org/publication/michael-j-fox-foundation-launches-parkinsons-clinical-trial-companion-educational-suite (Accessed December 15, 2022)
47. Berk, S, Greco, BL, Biglan, K, Kopil, CM, Holloway, RG, Meunier, C, et al. Increasing efficiency of recruitment in early Parkinson's disease trials: a case study examination of the STEADY-PD III trial. J Parkinsons Dis. (2017) 7:685–93. doi: 10.3233/JPD-171199
48. Hills, M, and Armitage, P. The two-period cross-over clinical trial. Br J Clin Pharmacol. (1979) 8:7–20. doi: 10.1111/j.1365-2125.1979.tb05903.x
50. Ho, WK, Matthews, JN, Henderson, R, Farewell, D, and Rodgers, LR. Dropouts in the AB/BA crossover design. Stat Med. (2012) 31:1675–87. doi: 10.1002/sim.4497
51. Higgins, J.P.T, Li, T., and Sterne, J., on behalf of the RoB 2 working group on crossover trials. (Eds) Revised Cochrane Risk of Bias Tool for Randomized Trials (RoB 2) Additional Considerations for Crossover Trials; (2021). Available at: https://www.riskofbias.info/welcome/rob-2-0-tool/rob-2-for-crossover-trials (Accessed July 17, 2023).
Keywords: Parkinson’s disease, crossover study design, clinical trials, mixed models, carryover effect
Citation: Sparrow D, DeMolles D, Dubaz O, Durso R and Rosner B (2023) Design issues in crossover trials involving patients with Parkinson’s disease. Front. Neurol. 14:1197281. doi: 10.3389/fneur.2023.1197281
Edited by:
Alexandre Gironell, Universitat Autònoma de Barcelona, SpainReviewed by:
Marian L. Dale, Oregon Health and Science University, United StatesSasivimol Virameteekul, Chulalongkorn University, Thailand
Copyright © 2023 Sparrow, DeMolles, Dubaz, Durso and Rosner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Sparrow, ZGF2aWQuc3BhcnJvd0B2YS5nb3Y=
 David Sparrow
David Sparrow Deborah DeMolles1
Deborah DeMolles1