
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Neurol., 29 June 2021
Sec. Epilepsy
Volume 12 - 2021 | https://doi.org/10.3389/fneur.2021.685814
This article is part of the Research TopicSeizure Forecasting and Detection: Computational Models, Machine Learning, and Translation into DevicesView all 19 articles
 Pawel Glaba1
Pawel Glaba1 Miroslaw Latka1*
Miroslaw Latka1* Małgorzata J. Krause2
Małgorzata J. Krause2 Sławomir Kroczka3
Sławomir Kroczka3 Marta Kuryło2
Marta Kuryło2 Magdalena Kaczorowska-Frontczak4
Magdalena Kaczorowska-Frontczak4 Wojciech Walas5
Wojciech Walas5 Wojciech Jernajczyk6
Wojciech Jernajczyk6 Tadeusz Sebzda7
Tadeusz Sebzda7 Bruce J. West8
Bruce J. West8Absence seizures are generalized nonmotor epileptic seizures with abrupt onset and termination. Transient impairment of consciousness and spike-slow wave discharges (SWDs) in EEG are their characteristic manifestations. This type of seizure is severe in two common pediatric syndromes: childhood (CAE) and juvenile (JAE) absence epilepsy. The appearance of low-cost, portable EEG devices has paved the way for long-term, remote monitoring of CAE and JAE patients. The potential benefits of this kind of monitoring include facilitating diagnosis, personalized drug titration, and determining the duration of pharmacotherapy. Herein, we present a novel absence detection algorithm based on the properties of the complex Morlet continuous wavelet transform of SWDs. We used a dataset containing EEGs from 64 patients (37 h of recordings with almost 400 seizures) and 30 age and sex-matched controls (9 h of recordings) for development and testing. For seizures lasting longer than 2 s, the detector, which analyzed two bipolar EEG channels (Fp1-T3 and Fp2-T4), achieved a sensitivity of 97.6% with 0.7/h detection rate. In the patients, all false detections were associated with epileptiform discharges, which did not yield clinical manifestations. When the duration threshold was raised to 3 s, the false detection rate fell to 0.5/h. The overlap of automatically detected seizures with the actual seizures was equal to ~96%. For EEG recordings sampled at 250 Hz, the one-channel processing speed for midrange smartphones running Android 10 (about 0.2 s per 1 min of EEG) was high enough for real-time seizure detection.
Typical absence seizures are brief (lasting seconds) generalized nonmotor epileptic seizures with an abrupt onset and termination (1, 2). Transient impairment of consciousness and spike-slow wave discharges (SWDs) in electroencephalogram (EEG) are their characteristic manifestations. Typical absence seizures are severe in childhood (CAE) and juvenile (JAE) absence epilepsies but mild or inconspicuous in other syndromes such as juvenile myoclonic epilepsy (JME). Typical absence seizures are predominantly spontaneous, but in about 90% of untreated patients, they may be provoked by hyperventilation. Sleep deprivation, photostimulation, specific geometric patterns, video games, and even thinking may also precipitate them. The pathophysiology of absence seizures is fundamentally different from other types of seizures, making their diagnosis and treatment unique.
CAE is the most common pediatric epileptic syndrome with an age of onset of around 6–8 years (3). It has a prevalence of 10–15% in childhood epilepsies. In children under the age of 16 years, the incidence rate is 1.3 to 6 per 100,000. The ictal EEG of a CAE seizure demonstrates rhythmic 3 Hz bilateral, synchronous, and symmetrical spike and wave discharges (SWDs) with a median duration of approximately 10 s, which on average appear several times per day. In pyknoleptic cases, hundreds of seizures may occur daily (4). The 2010 Childhood Absence Epilepsy Study showed that only 37% of all enrolled subjects were free from treatment failure on their first medication a year after diagnosis (5).
JAE typically begins between 10 and 16 years of age and is usually a life-long condition. JAE seizures tend to be longer than in CAE (lasting up to 45 s) and non-pyknoleptic (typically occurring less than daily).
While CAE and JAE are distinct epilepsy syndromes, there is considerable overlap between them, and the cut-off age remains controversial. During disease, patients with JAE or patients in the overlap group are more likely to develop generalized tonic-clonic seizures and myoclonic attacks. In the long-term follow-up (mean 26 years, range 3–69), only 58% of the patients with absence seizures were in remission (6).
The diagnosis of absence seizures is laborious since it requires analysis of long video-EEGs (on average around 30 minutes long) to detect seizures and their clinical manifestations (consciousness impairment, motor symptoms) and abnormal EEG background activity.
The appearance of low-cost, portable EEG devices (7) has paved the way for long-term, remote monitoring of patients with absence seizures. The potential benefits of this kind of monitoring include facilitation of diagnosis, personalized drug titration, and determining of duration of pharmacotherapy. The need for automatic and reliable detection of absence seizures has long been recognized (8). Diverse algorithms have been proposed so far to detect seizures in animal models of epilepsy (9–12) or in human EEG (13–21). Herein, we present a novel approach to absence seizure detection, which is applicable both to clinical EEGs and recordings made with portable EEG devices with a small number of channels. The algorithm's efficiency and robustness to motion artifacts enable its implementation on mobile devices.
Wroclaw Medical University's Ethics Committee approved a retrospective analysis of routine anonymized video-EEG recordings of patients (36 with CAE and 28 with JAE) as well as 30 EEGs of age-matched controls. Epilepsy syndrome was established based on history, age at onset, clinical EEG findings, and neuroimaging. EEGs were acquired with Elmiko Digitrack (BRAINTRONICS B.V. ISO-1032CE amplifier) or Grass Comet Plus EEG (AS40-PLUS amplifier) using 200 or 250 Hz sampling frequency. The international 10-20 standard was used to arrange 19 Ag/AgCl electrodes (impedance below 5k℧). Total EEG duration was equal to 37 and 9 h for the patients and controls, respectively.
We assigned patients' EEG to either training or testing datasets. In the first one, there were 34 recordings (22 CAE and 12 JAE) with 199 seizures (6 ± 4 per patient and averaged seizure duration equal to 12 ± 4 s). In the 30 recordings of the testing dataset (15 CAE and 15 JAE), there were 177 absence seizures (6 ± 5 per patient and averaged duration equal to 12 ± 6 s). An experienced neurologist carried out a visual EEG inspection and marked the seizures with a 1 s accuracy.
Figure 1 provides the rationale for using the longitudinal bipolar montage. The seizure detector was developed and tested for two channels: Fp1-T3 and Fp2-T4.
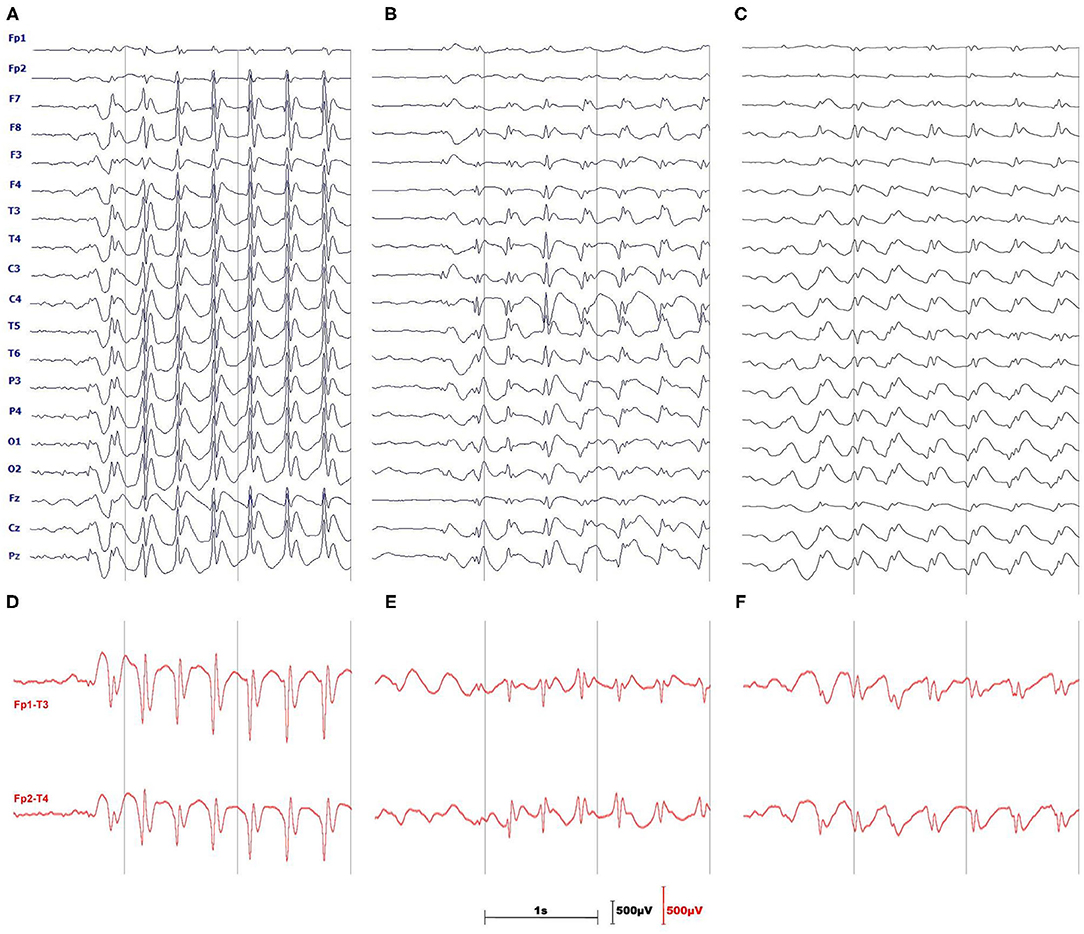
Figure 1. Three monopolar EEGs illustrate the difficulties of absence seizure detection in a single channel. (A) is a textbook example of prominent, generalized SWDs. The amplitude of spikes (B) or slow waves (C) may be small and SWDs may be pronounced only in a handful of channels. (D–F) show the advantages of using the longitudinal, bipolar montage which in most cases augments both spikes and slow waves of SWDs.
We used three filters for EEG preprocessing: a second-order infinite impulse response (IIR), 6th-order high-pass Butterworth with a cutoff frequency of 0.5 Hz, and 6th-order low-pass Butterworth with a cutoff frequency of 25 Hz. These filters remove 50 Hz power line noise, EEG baseline drift, and muscle artifacts, respectively.
The continuous wavelet transform (CWT) of a signal s(t) is an integral transform:
with the basis functions ψ(a, t0) = ψ(t−t0/a), known as wavelets, that are translated and scaled version of the mother function ψ(t) (22). Motivated by the results of the previous study (23), as a mother function, we use the complex Morlet wavelet (24, 25):
whose Fourier transform is given by
The real parameter fc is called the center frequency since it is equal to the maximum point of the wavelet's Fourier power spectrum. The scale a corresponds to the following pseudofrequency:
As we can see in Equations (2, 3), the wavelets are localized both in time and frequency domains. This dual localization makes CWT particularly applicable to the detection of transient events such as absence seizures.
Seizure detection is based on the properties of the instantaneous wavelet power normalized by signal's variance σ2:
If we apply the convolution theorem to Equation (1), then it is apparent that the Fourier transform of T[s](a, t0) is the pointwise product of the Fourier transforms of the signal and wavelet. Thus, it is possible to calculate CWT by taking the inverse Fourier transform of such a product. We used this approach in the MATLAB function, presented in Supplementary Materials, which calculates the complex Morlet CWT (25). We included the listing to facilitate the reproduction of the results and avoid confusion related to erroneous normalization of the most popular Python and MATLAB CWT implementations. We will discuss this problem in a forthcoming publication.
For the most commonly used wavelets, such as the complex Morlet, the analytical expression for their Fourier transform is known. Therefore, in the presented function, we calculate only the FFT of the signal and use Equation (3) to obtain the wavelet's FFT spectrum.
The complex Morlet CWT of the preprocessed Fp1-T3 and Fp2-T4 channels was calculated without signal partitioning.
The detection of an absence seizure (Figures 2A,E), defined as an SWD lasting for more than 2 s (26), proceeds in two steps. First, we locate the train of slow waves and then verify that there are epileptic spikes embedded in it. One can see in the scalogram Figure 2B that when the wavelet's pseudofrequency is close to that of an absence (~3 Hz), then the wavelet power forms a prominent ridge. We refer to the time interval during which the power exceeds the chosen threshold TE as the slow-wave envelope. This envelope is a unit boxcar function that takes on one whenever the power is greater than TE. As the frequency of SWDs is subject-dependent and may even slightly vary during a seizure (15), we construct two envelopes with wavelet frequencies flow and fhigh (Figure 2C) and merge them as shown in Figure 2D. The merging amounts to a pointwise application of a logical OR function to both envelopes.
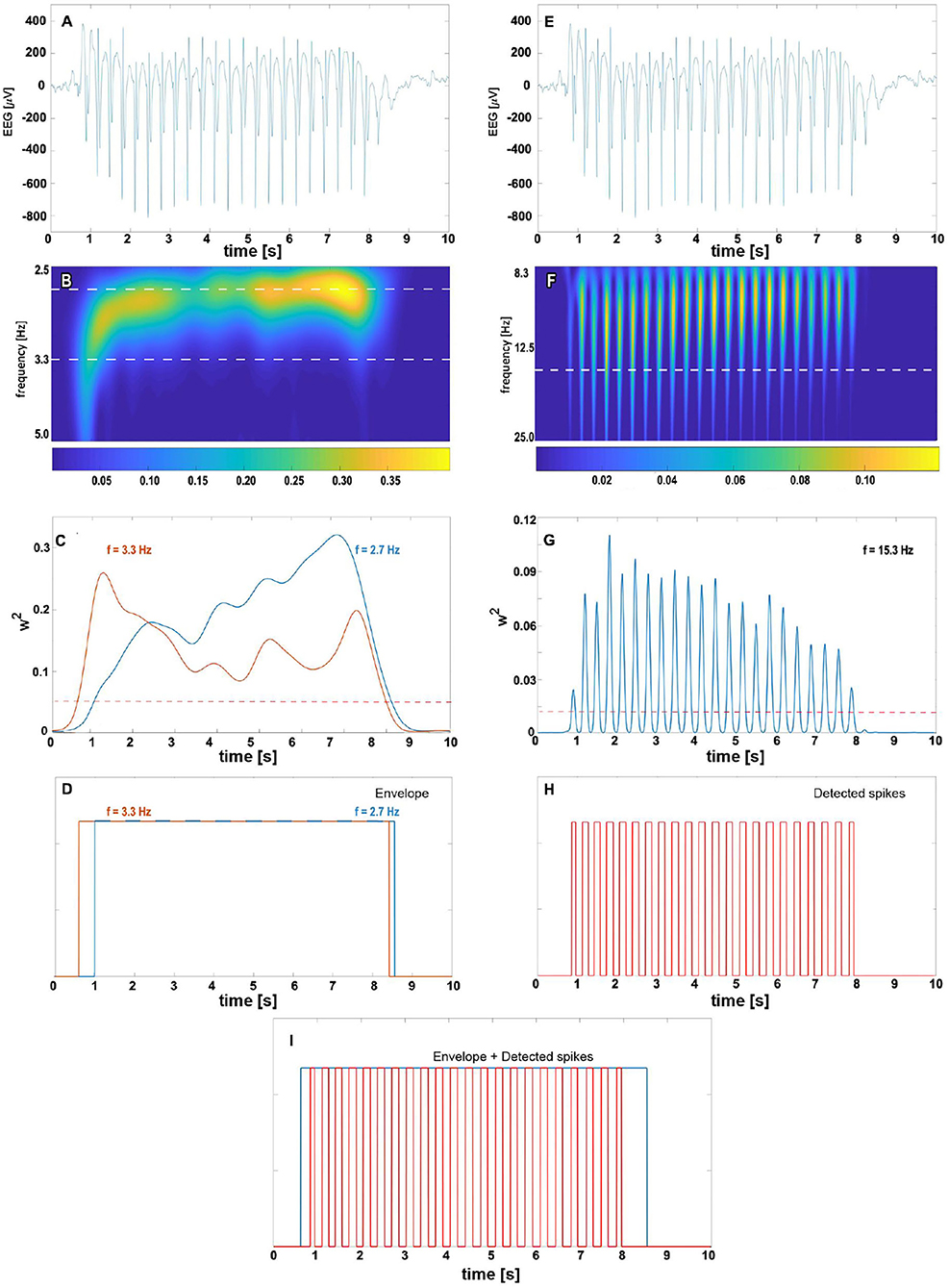
Figure 2. The complex Morlet wavelet analysis of absence slow wave (B–D) and spikes (F–H). For clarity, absence EEG is presented at the top of both columns (subplots A,E). The density map (B) shows the time evolution of normalized wavelet power for pseudo-frequencies in [2.5, 5] Hz range. The 2.7 and 3.3 Hz cuts (marked with the white horizontal dashed line) are plotted in subplot (C) with the blue and orange lines, respectively. We refer to time intervals during which the wavelet power for these frequencies exceeds the predetermined threshold (represented in (C) by the red dashed horizontal line) as the slow-wave envelopes. For a given seizure, the total envelope is obtained by merging 2.7 and 3.3 Hz envelopes as shown in (D). The right column shows the complex Morlet analysis with parameters tuned to spike detection. The prominent ridges in wavelet power density map (F) and peaks in 15.3 Hz cut (G) are manifestations of seizure's spikes. The white horizontal dashed line in (F) corresponds to the spike frequency 15.3 Hz obtained in the grid search. The train of unit pulses in (H) indicates time intervals during which wavelet power for 15.3 Hz is greater than the spike threshold value (marked in subplot (G) with the red dashed horizontal line). An absence is detected whenever the epileptic spikes are found in the slow-wave envelope (I).
For a suitably chosen pseudofrequency fspike, the wavelet power peaks around the position of epileptic spikes (Figure 2F). If the percentage of samples PT within the final envelope for which the wavelet power is greater than TS, we conclude that there are spikes (Figure 2H) within the envelope (Figure 2I). Such the envelope delineates the absence seizure.
In some cases, may also be elevated for high-amplitude artifacts. To reduce the number of false positives, we modified the original algorithm. We do the following amplitude check and disregard all envelopes for which:
• More than 10% of the samples have amplitudes outside the range [−500 μV, 500 μV] (in the differential montage epileptic spikes can have amplitudes of the order of hundreds μV).
• Any sample is outside the range [–1,000 μV, 1,000 μV].
For envelopes shorter than 5 s, we also calculate the variance of to detect the wavelet power pulsatility of absence (Figure 2G). If such variance is greater than TV, the detector flags the envelope as a seizure. We refer to such a comparison as the wavelet variance check.
Figure 3 shows the flowchart of the final absence seizure detection algorithm. The proposed algorithm may be used independently for channels Fp1-T3 and Fp2-T4. Alternatively, the seizure envelopes from these two channels may be superposed.
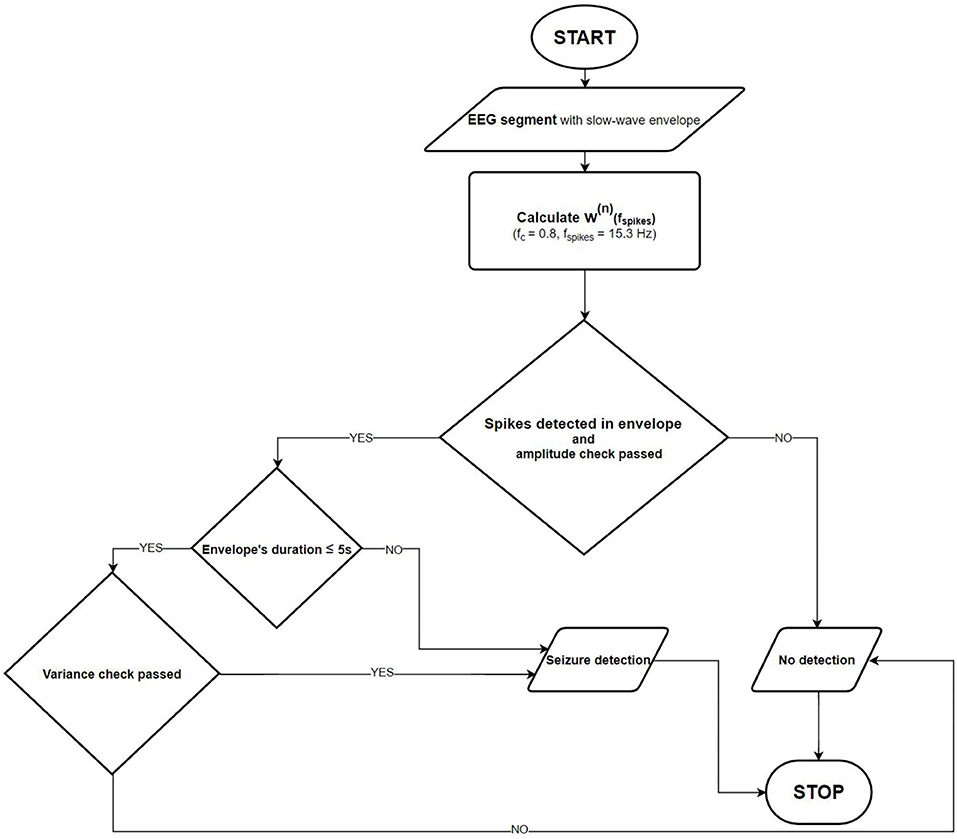
Figure 3. Absence seizure detection flowchart. Once the slow-wave envelope is present in an analyzed EEG segment, the detector checks whether there are epileptic spikes embedded in it. The amplitude and the normalized wavelet power variance checks are also performed to eliminate artifacts.
We determine flow, fhigh, and TE by maximizing the overlap of slow-wave envelopes with the absence seizures from a training dataset disregarding possible false detections.
Using these values, we search for the maximum of the following objective function:
to find fspike, TS, and PTS – spike detection parameters. In Eq (6), OVRf is the percentage overlap of slow-wave envelopes with seizures. PERR is the percentage of the number of false positive samples in a given EEG. FDET and FDETC are the number of false detections for the patients and controls, respectively.
The form of the objective function follows two requirements. The first is that we want to overlap the slow-wave envelope with the seizure as accurately as possible. The second is that in patients, false positives can be associated with epileptiform discharges with no clinical manifestations. Therefore, in Eq (6), the weight assigned to the patients' false detection penalty (FDET) is half of that given to the controls. We arbitrarily chose the 1:2 weight ratio.
TV can be determined in the following way. We calculate the variance of for the controls' EEGs. Then, we calculate the mean and standard deviation of the distribution. Finally, TV is set to the mean increased by three standard deviations (TV = 0.05).
We determined the slow-wave and spike detection parameters using the exhaustive grid search.
The seizure detection software was implemented both in MATLAB (R2018a) and Java. In the latter case, we wrote a desktop version (which can be run on any computer with Java virtual machine) and a mobile version for Android smartphones. In Java software, we used the class FastFourierTransformer from Apache Commons Math Library (version 3.6.1). Testing and performance benchmarking was performed on a desktop PC with AMD Ryzen 7 3700X 8-Core processor running Windows 10 and Samsung S9 mobile phone (4GB of RAM and 2.8 GHz Samsung Exynos 9810 8-Core processor) with Android 10.
Using two-step (slow-wave envelope and spike detection) optimization on the training dataset, we obtained the following model parameters flow = 2.7 Hz, fhigh = 3.3 Hz, TE = 0.05, fspike = 15.3 Hz, TS = 0.012, PTS = 12%. After the parameters were determined, we lowered the value of TV from 0.05 to 0.008. This change is explained in Discussion section.
The seizure detector had 98.5% and 96.6% sensitivity for the training and testing datasets, respectively (see Supplementary Tables 1, 2). The corresponding false detection rates were equal to 0.9/h and 0.4/h. The overlap OVR of the detected and actual seizures was good for both datasets (97% ± 6% and 95% ± 10%). The percentage error PERR that accounts for both false positives and erroneously extended slow-wave envelopes was equal to 0.9% ± 0.7% for both datasets.
Supplementary Table 3 shows that both the amplitude and wavelet variance checks contribute to the false detection reduction.
In Supplementary Table 4, we compare the execution times of three absence seizure detector implementations. The execution time is determined by the efficiency of an FFT function, which is used to calculate the continuous wavelet transform. Matlab is renowned for its FFT implementation. Thus, it is not surprising that for the longest segment (N = 218), the Matlab version of the detector ran almost 16 and 19 times faster than the Java software running on Windows 10 and Android 10 (0.18 s vs. 2.79 s and 3.41 s). Interestingly enough, for shorter segments, the detector ran faster on the mid-range Android device than on the PC. Nevertheless, the single-channel Android processing speed of 0.2 s per minute of EEG is adequate for real-time seizure detection.
It has long been recognized that long-term EEG monitoring is the most reliable method for absence detection (27). Parents notice only about 6% of daytime seizures, and very often, teachers are the ones who recognize the CAE/JEA beginning (28). The 2010 Childhood Absence Epilepsy Study (5) has provided a compelling rationale for using portable EEG devices in the management of CAE/JEA patients. This randomized controlled trial showed that only 37% of all enrolled subjects were free from treatment failure on their first medication a year after diagnosis.
In the last two decades, many researchers have investigated absence seizure detection (13–17, 20). The datasets in these studies were small–the analyzed SWDs came from nine patients (range 2–20). On average, there were 70 seizures longer than 2 s (range 2–158). In all but one algorithm (20), discrete wavelet transform was used for signal preprocessing. Machine learning was used in 3 of 4 detectors. On average, 11 features were extracted from 15 EEG channels.
Kjaer et al. (19) used an experimental EEG setup with 3 electrodes for 24-h EEG monitoring of 6 patients (593 seizures). Their support vector machine detected 98.4% SWD's with 0.23/h false detection rate using 10 features of five-level db4 wavelet EEG decomposition.
The absence seizure detection algorithm presented in this work is unique because it exploits the apparent traits of SWDs and EEG motion artifacts. Despite the simplicity, its 97.6% accuracy matches that of black-box machine learning classifiers.
Our experience indicates that frequent, albeit not excessively long, EEG home monitoring is feasible in pediatric patients as long as an EEG wearable is easy to put on and is comfortable. This study used the bipolar channels Fp1-T3 and Fp2-T4 for seizure detection because they approximately corresponded to the Muse headband electrode placement. On the one hand, this choice seems to be rational given absence seizures are usually well pronounced in the frontal regions (29) and the large spacing between the electrodes augments the characteristic features of SWDs as shown in Figure 1. On the other hand, Fp1 and Fp2 channels are prone to muscle and eyeblink artifacts. There were 26 and 8 false detections in the patients and controls, respectively. In the patients, all false detections were associated with epileptiform discharges, which did not yield clinical manifestations. Half of the errors in the control group were caused by the prominent SWDs. We show the examples of misclassified EEG segments in Figure 4. We used the stringent value TV = 0.05 for the determination of the model parameters. Once we realized that false detections are not caused by motion artifacts, for classification, we lowered this parameter to 0.008 to maximize the detection sensitivity (for TV = 0.05, the sensitivity was equal to 93% with the false detection rate 0.4/h). Some pediatricians agree that sensitivity of 90% and false detection rate of 1/h are clinically acceptable (19).
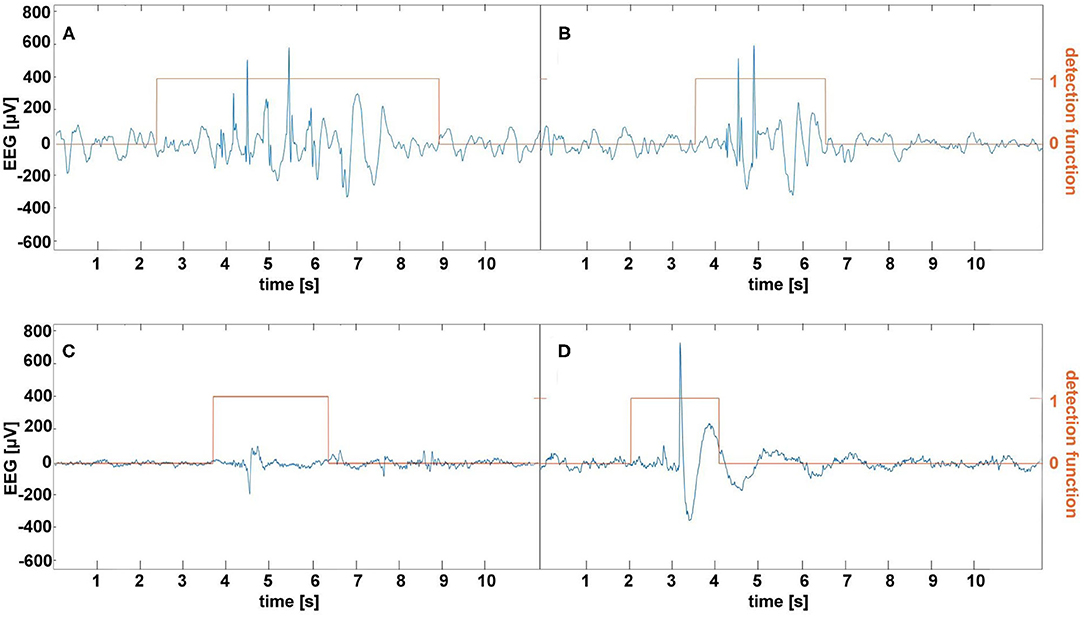
Figure 4. Examples of false absence seizure detection in the EEG of the patients (A,B) and controls (C,D). The epileptiform discharges in (A,B) were not accompanied by the clinical manifestations. (C) shows a rare example of a muscle artifact classified as an absence. A prominent spike-and-wave in (D) appeared in a healthy subject's EEG.
Unlike previous studies, the false detection rate was not determined by the motion artifacts. We would like to emphasize that the presented seizure detection was performed on clinical EEGs, which is the main limitation of this study. The question arises as to whether the amplitude and wavelet variance checks would be equally effective in eliminating motion artifacts in EEGs acquired with wearable devices in home settings. It is worth mentioning that the false detection rate can be reduced by using secondary electrodes for artifact cancellation (30) and employing different single-channel artifact detectors (31, 32). As most commercial EEG bands have MEMS accelerometers, one may also explore the possibility of incorporating head acceleration in the artifact removal algorithm. However, the connection between EEG artifacts and head movement is not always apparent (33).
In a recent study, Dan et al. presented an absence seizure detector based on a linear multichannel filter that was precomputed offline in a data-driven fashion based on the spatial-temporal signature of the seizure and peak interference statistics (21). The performance of this detector depends on the number of channels (from 3 to 18) used in the calculations. For the three channels, the accuracy was equal to 95% with a 0.4/h false detection rate. The authors set the minimum seizure length to 3 s (34). It is worth pointing out that for this absence duration threshold, the two-channel detector described in this work had the false detection rate equal to 0.5/h (18 and 6 false detections for the patients, and controls, respectively.
To the best of our knowledge, we used the most diverse set of CAE/JAE EEGs (37 h of recordings from 64 patients) for development and testing. The overlap of automatically detected seizures with the actual seizures was high (about 96%). The poor overlap in some patients is predominantly caused by a very small amplitude of the epileptic spikes. Consequently, the detector does not classify such SWD trains as absence seizures. At the end of the seizure, the frequency of SWDs can decrease far below the canonical value of 3 Hz. In this case, the slow-wave envelope is shorter than expected. The frequency drop during the seizure leads to its sfragmentation.
For EEG recordings sampled at 250 Hz, the one-channel processing speed for midrange smartphones running Android 10 was high enough (about 0.2 s per 1 min of EEG) for real-time seizure detection. We found that the detection accuracy was highest for a sliding 30 s EEG buffer, which was shifted by 10 s.
Absence seizure manifestations are mild compared to other epileptic syndromes. Consequently, the rationale for using seizure detectors in CAE/JAE patients is different. Emphasis may be shifted from detection alerts to the facilitation of drug titration and side effects elimination. Unobtrusiveness and ease of use are particularly important for pediatric patients, who may be more willing to tolerate regular EEG measurements if they are incorporated into daily routines such as watching cartoons, playing mobile games, or listening to music.
It is worth pointing out that remote seizure monitoring will be one of the elements of personalized CAE/JAE treatment. There is a growing interest in the development of biomarkers of treatment response and side effects (35). These problems are the subject of our research (36).
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
The studies involving human participants were reviewed and approved by Wroclaw Medical University's Ethics Committee. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
ML, PG, and MK: conceptualization and methodology. PG, ML and MJK: investigation original draft preparation. BW, WW, SK, TS, and WJ: review and editing. All authors contributed to formal analysis.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fneur.2021.685814/full#supplementary-material
1. Panayiotopoulos CP. The Epilepsies: Seizures, Syndromes and management. Oxfordshire (UK): Bladon Medical Publishing (2005).
2. Fisher RS, Cross JH, French JA, Higurashi N, Hirsch E, Jansen FE, et al. Operational classification of seizure types by the International league against epilepsy: position paper of the ILAE commission for classification and terminology. Epilepsia. (2017) 58:522–30. doi: 10.1111/epi.13670
3. Covanis A. Childhood Absence Epilepsy. Springer-Verlag: Atlas of epilepsies London (2010) p. 1013–23.
4. Schomer DL, da Silva FL. Niedermeyer's Electroencephalography: Basic Principles, Clinical Applications, and Related Fields. Oxford University Press (2018).
5. Glauser TA, Cnaan A, Shinnar S, Hirtz DG, Dlugos D, Masur D, et al. Ethosuximide, valproic acid, and lamotrigine in childhood absence epilepsy: initial monotherapy outcomes at 12 months. Epilepsia. (2013) 54:141–55. doi: 10.1111/epi.12028
6. Trinka E, Baumgartner S, Unterberger I, Unterrainer J, Luef G, Haberlandt E, et al. Long-term prognosis for childhood and juvenile absence epilepsy. J Neurol. (2004) 251:1235–41. doi: 10.1007/s00415-004-0521-1
7. Krigolson OE, Williams CC, Norton A, Hassall CD, Colino FL. Choosing MUSE: validation of a low-cost, portable EEG system for ERP research. Front Neurosci. (2017) 11:109. doi: 10.3389/fnins.2017.00109
8. Faust O, Acharya UR, Adeli H, Adeli A. Wavelet-based EEG processing for computer-aided seizure detection and epilepsy diagnosis. Seizure. (2015) 26:56–64. doi: 10.1016/j.seizure.2015.01.012
9. Sitnikova E, Hramov AE, Koronovsky AA, van Luijtelaar G. Sleep spindles and spike–wave discharges in EEG: their generic features, similarities and distinctions disclosed with Fourier transform and continuous wavelet analysis. J Neurosci Methods. (2009) 180:304–16. doi: 10.1016/j.jneumeth.2009.04.006
10. Ovchinnikov A, Lüttjohann A, Hramov A, Van Luijtelaar G. An algorithm for real-time detection of spike-wave discharges in rodents. J Neurosci Methods. (2010) 194:172–8. doi: 10.1016/j.jneumeth.2010.09.017
11. Bauquier SH, Lai A, Jiang JL, Sui Y, Cook MJ. Evaluation of an automated spike-and-wave complex detection algorithm in the EEG from a rat model of absence epilepsy. Neurosci Bull. (2015) 31:601–10. doi: 10.1007/s12264-015-1553-5
12. Grubov V, Sitnikova E, Pavlov A, Koronovskii A, Hramov A. Recognizing of stereotypic patterns in epileptic EEG using empirical modes and wavelets. Phys A Stat Mech Appl. (2017) 486:206–17. doi: 10.1016/j.physa.2017.05.091
13. Adeli H, Zhou Z, Dadmehr N. Analysis of EEG records in an epileptic patient using wavelet transform. J Neurosci Methods. (2003) 123:69–87. doi: 10.1016/S0165-0270(02)00340-0
14. Subasi A. Application of adaptive neuro-fuzzy inference system for epileptic seizure detection using wavelet feature extraction. Comput Biol Med. (2007) 37:227–44. doi: 10.1016/j.compbiomed.2005.12.003
15. Xanthopoulos P, Rebennack S, Liu CC, Zhang J, Holmes GL, Uthman BM, et al. A novel wavelet based algorithm for spike and wave detection in absence epilepsy. In: 2010 IEEE International Conference on BioInformatics and BioEngineering. (Washington, DC: IEEE) (2010). p. 14–19.
16. Petersen EB, Duun-Henriksen J, Mazzaretto A, Kjær TW, Thomsen CE, Sorensen HB. Generic single-channel detection of absence seizures. In: 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. (Boston, MA: IEEE) (2011). p. 4820–3.
17. Duun-Henriksen J, Madsen RE, Remvig LS, Thomsen CE, Sorensen HB, Kjaer TW. Automatic detection of childhood absence epilepsy seizures: toward a monitoring device. Pediatr Neurol. (2012) 46:287–92. doi: 10.1016/j.pediatrneurol.2012.02.018
18. Zeng K, Yan J, Wang Y, Sik A, Ouyang G, Li X. Automatic detection of absence seizures with compressive sensing EEG. Neurocomputing. (2016) 171:497–502. doi: 10.1016/j.neucom.2015.06.076
19. Kjaer TW, Sorensen HB, Groenborg S, Pedersen CR, Duun-Henriksen J. Detection of paroxysms in long-term, single-channel EEG-monitoring of patients with typical absence seizures. IEEE J Transl Eng Health Med. (2017) 5:1–8. doi: 10.1109/JTEHM.2017.2649491
20. Tenneti SV, Vaidyanathan P. Absence seizure detection using Ramanujan filter banks. In: 2018 52nd Asilomar Conference on Signals, Systems, and Computers. (Danvers, MA: IEEE) (2018). p. 1913–7.
21. Dan J, Vandendriessche B, Paesschen WV, Weckhuysen D, Bertrand A. Computationally-Efficient Algorithm for Real-Time Absence Seizure Detection in Wearable Electroencephalography. Int J Neural Syst. (2020) 30:2050035. doi: 10.1142/S0129065720500355
23. Latka M, Was Z, Kozik A, West BJ. Wavelet analysis of epileptic spikes. Phys Rev E. (2003) 67:052902. doi: 10.1103/PhysRevE.67.052902
24. Addison PS. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance. Boca Raton, FL; London; New York, NY: CRC Press (2017).
25. Addison PS. Introduction to redundancy rules: the continuous wavelet transform comes of age. Phil Trans R Soc A. (2018) 376:20170258. doi: 10.1098/rsta.2017.0258
26. Szaflarski JP, DiFrancesco M, Hirschauer T, Banks C, Privitera MD, Gotman J, et al. Cortical and subcortical contributions to absence seizure onset examined with EEG/fMRI. Epilepsy Behav. (2010) 18:404–13. doi: 10.1016/j.yebeh.2010.05.009
27. Browne TR, Dreifuss FE, Penry JK, Porter RJ, White BG. Clinical and EEG estimates of absence seizure frequency. Arch Neurol. (1983) 40:469–72. doi: 10.1001/archneur.1983.04210070009004
28. Keilson MJ, Hauser WA, Magrill JP, Tepperberg J. Ambulatory cassette EEG in absence epilepsy. Pediatr Neurol. (1987) 3:273–6. doi: 10.1016/0887-8994(87)90067-1
29. Jun YH, Eom TH, Kim YH, Chung SY, Lee IG, Kim JM. Source localization of epileptiform discharges in childhood absence epilepsy using a distributed source model: a standardized, low-resolution, brain electromagnetic tomography (sLORETA) study. Neurol Sci. (2019) 40:993–1000. doi: 10.1007/s10072-019-03751-4
30. Nordin AD, Hairston WD, Ferris DP. Dual-electrode motion artifact cancellation for mobile electroencephalography. J Neural Eng. (2018) 15:056024. doi: 10.1088/1741-2552/aad7d7
31. Chen X, Liu A, Chiang J, Wang ZJ, McKeown MJ, Ward RK. Removing muscle artifacts from EEG data: multichannel or single-channel techniques? IEEE Sensors J. (2015) 16:1986–97. doi: 10.1109/JSEN.2015.2506982
32. Dhindsa K. Filter-bank artifact rejection: high performance real-time single-channel artifact detection for EEG. Biomed Sig Proc Control. (2017) 38:224–35. doi: 10.1016/j.bspc.2017.06.012
33. Kline JE, Huang HJ, Snyder KL, Ferris DP. Isolating gait-related movement artifacts in electroencephalography during human walking. J Neural Eng. (2015) 12:046022. doi: 10.1088/1741-2560/12/4/046022
34. Tenney JR, Glauser TA. The current state of absence epilepsy: can we have your attention? the current state of absence epilepsy. Epilepsy Curr. (2013) 13:135–40. doi: 10.5698/1535-7511-13.3.135
35. Kessler SK, McGinnis E. A practical guide to treatment of childhood absence epilepsy. Pediatr Drugs. (2019) 21:15–24. doi: 10.1007/s40272-019-00325-x
Keywords: childhood absence epilepsy, EEG, wavelets, detector, portable device
Citation: Glaba P, Latka M, Krause MJ, Kroczka S, Kuryło M, Kaczorowska-Frontczak M, Walas W, Jernajczyk W, Sebzda T and West BJ (2021) Absence Seizure Detection Algorithm for Portable EEG Devices. Front. Neurol. 12:685814. doi: 10.3389/fneur.2021.685814
Received: 25 March 2021; Accepted: 03 June 2021;
Published: 29 June 2021.
Edited by:
Sharon Chiang, University of California, San Francisco, United StatesReviewed by:
Kais Gadhoumi, Duke University, United StatesCopyright © 2021 Glaba, Latka, Krause, Kroczka, Kuryło, Kaczorowska-Frontczak, Walas, Jernajczyk, Sebzda and West. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miroslaw Latka, bWlyb3NsYXcubGF0a2FAcHdyLmVkdS5wbA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.