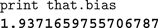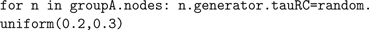Large-scale neural modeling requires software tools that not only support efficient simulation of hundreds of thousands of neurons, but also provide researchers with high-level organizational tools. Such neural models involve heterogeneous components with complex interconnections that may be either speculative in nature or constrained by existing neurobiological evidence. To effectively construct, modify, and investigate the behaviour of these models, researchers need to be able to specify the collective behavior of large groups of neurons as well as the low-level physiological details.
In order to support this style of research, we have developed a neural simulator package called Nengo. For high-level organization, Nengo makes use of the neural engineering framework (NEF;
Eliasmith and Anderson, 2003
), which provides methods for abstractly describing the representations and transformations involved in a neural model and how they relate to spiking behavior. To provide access to the broad range of functionality we require (from neural groups to individual synapses), we integrated a Python language scripting system into the simulator. This enables a variety of novel features, including the inspection and modification of running models, the ability to script common experimental tasks, and the integration of non-neural cognitive models. In this paper, we describe this system (see Introduction), discuss the features related to its use of Python (see Python and Nengo), and provide an extended example of ongoing research that has directly benefited from these abilities (see Integration with Other Libraries).
Nengo
Nengo is an open-source cross-platform software package for modeling neuronal circuits, and tested on Macintosh OS X, Linux, and Microsoft Windows. It is implemented in Java, and provides both a detailed Application Programming Interface and a Graphical User Interface (Figure
1
), so that it is suitable for both novice and expert modelers. As will be discussed, the Python scripting system forms a bridge between the easy-to-use graphical environment and the full power of the underlying programmatic interface. This ensures a smooth transition from novice to expert, as all aspects of the simulation are accessible at all times.
Figure 1. A neural model of the basal ganglia developed in Nengo.
A variety of spiking point-neuron models are provided with Nengo. This includes the standard LIF neuron and the Hodgkin-Huxley model, as well as an adapting LIF (
La Camera et al., 2004
) and the Izhikevich model (
Izhikevich, 2003
). Integration is performed with a variable-timestep integrator, using the Dormand-Prince 4th and 5th order Runge-Kutta formulae (
Dormand and Prince, 1980
). At the network level, interaction between neurons treats spikes as discrete events; Nengo is not meant for neural models where the detailed voltage profile of a specific spike affects the post-synaptic neurons.
These neuron models can be connected directly to form simple networks, and input can consist of current injection or voltage clamp. Spike times, membrane voltages, and current can be recorded from the neurons. This approach is suitable for situations where connectivity information is known, or where the dynamics of a particular configuration are being investigated. However, modeling of more sophisticated population-coding networks is greatly facilitated by using the NEF-related features of the simulator.
Neural Engineering Framework
For complex neural models, it is often useful to describe the system of interest at a higher level of abstraction, such as that shown in Figure
2
. For this reason, we define heterogeneous groups of neurons (where individual neurons vary in terms of their neural properties such as bias current and gain) and projections between these groups. We can then use the NEF (
Eliasmith and Anderson, 2003
) as a method for realizing this high-level description using neural models with adjustable degrees of accuracy. The NEF provides not only a method for encoding and decoding time-varying representations using spike trains, but also a method for deriving linearly optimal synaptic connection weights to transform and combine these representations. This approach combines work from a variety of researchers, most notably
Georgopoulos et al. (1986)
,
Rieke et al. (1999)
,
Salinas and Abbott (1994)
, and
Seung (1996)
.
Figure 2. A neural model of the mammalian vestibular system using the NEF. Boxes represent distinct neural populations and arrows represent projections between them. Inputs to the system are linear acceleration sensed by the left and right otoliths (
AL,
AR) and the angular velocity from the canals (Ω
L and Ω
R). From these, the system calculates inertial acceleration (
I) using the formula developed by
Angelaki et al. (1999)
. (For further details, see
Eliasmith et al., 2002
).
The NEF has been used to model the barn owl auditory system (
Fischer, 2005
), rodent navigation (
Conklin and Eliasmith, 2005
), escape and swimming control in zebrafish (
Kuo and Eliasmith, 2005
), working memory systems (
Singh and Eliasmith, 2006
), the translational vestibular ocular reflex in monkeys (
Eliasmith et al., 2002
), and the manipulation of symbolic representations to support high-level cognitive systems (
Stewart and Eliasmith, 2009
).
Within the NEF, a neural group forms a distributed representation of a time-varying vector
x(
t) of arbitrary length. Each neuron
i has an associated preferred direction vector
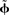
(the stimulus for which it most strongly fires), bias current
Jbias, and scaling factor α. For a given neuron, α and
Jbias can be experimentally determined from its maximum firing rate and the minimum value of
x for which it responds. If the nonlinearities of any given neural model (LIF, ALIF, etc.) are written as
G[·
] and the neural noise of variance σ
2 is η(σ), then the encoding of any given
x(
t) as the temporal spike pattern across the neural group is given as Eq. 1.
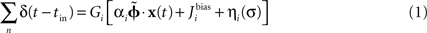
Given this spiking pattern, we can in turn estimate the original vector as
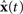
. In some approaches (e.g.
Georgopoulos et al., 1986
), this is done by weighting each encoding vector
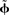
by the average firing rate of the corresponding neuron. In the NEF, however, we derive the linearly optimal decoding vectors
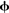
for each neuron (see
Eliasmith and Anderson, 2003
for details). This method has been shown to uniquely combine accuracy and neurobiological plausibility (e.g.
Salinas and Abbott, 1994
).
Since x(t) varies over time, we do not weight these decoding vectors by the average firing rate. Instead, we weight them with the post-synaptic current h(t) induced by each spike. The shape and time-constant of this current are determined from the physiological properties of the neural group:
The representational error between
x(
t) and
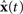
is dependent on the particular neural parameters and encoding vectors, but in general is inversely proportional to the number of neurons in the group. Given a sufficient number of neurons, an arbitrary level of accuracy can be reached. For a known number of neurons with known physiological properties, we can determine how well the values can be represented.
The derivation of the optimal decoding vector also allows us to determine the optimal connection weights to perform arbitrary transformations of these representations. For linear functions, consider two neural populations, X representing x(t) and Y representing y(t). If we want y(t) = M x(t), we can derive the following for the neurons in population Y:
This manipulation converts weighted post-synaptic currents caused by the spikes in neural group X into a spiking pattern for group Y that would cause Y to represent the value in X transformed by the linear operation M. Crucially, if we set the synaptic connection weights between the
ith neuron in X and the
jth neuron in Y to be
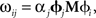
then the post-synaptic neurons will encode
M x(
t). This allows us to develop a model by defining the hypothesized computations and directly solving for the corresponding connection weights, rather than relying on a learning rule or manually setting the weights.
For nonlinear transformations, we can generalize the derivation of the decoding vector to estimate the desired function
f(
x). This provides a new set of decoding vectors
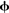 f(x)
f(x) which can be used in place of the previous
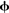
to provide an optimal linear estimate of this function. This allows arbitrary nonlinear functions to be computed, although more complex nonlinearities across multiple dimensions of
x will require more neurons with
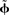
values that lie in those dimensions.

Treating neural groups as representing time-varying vectors and synaptic connections as performing arbitrary transformations allows us to organize a neural system using the powerful framework of control theory.
Eliasmith and Anderson (2003)
have shown how to translate any state-space model from modern control theory into an equivalent neural circuit. For example, an ideal integrator is shown in Figure
3
A, and its NEF counterpart, a neural integrator implemented with 300 LIF neurons, is shown in Figure
3
B. Importantly, the idealized version can be seen as an approximation of the actual neural behaviour. As is discussed in the next section, this feature can be used to create large-scale models where every component can potentially be simulated at the level of neurons, even though it may be too computationally expensive to do so for the whole system.
Figure 3. A classic control-theory integrator (A) and an NEF integrator (B). Both integrators are provided with the same sine wave input x(t). The NEF integrator uses 300 LIF neurons with maximum firing rates distributed uniformly between 100 and 200 Hz, post-synaptic current time constants of 20 ms, and refractory periods of 2 ms. The output value for the NEF integrator is determined from the individual spike times of each neuron using Eq. 3. Neuron spikes are shown as dots in panel (B), with neurons arranged along the y-axis.
The NEF provides a generic method for modeling any neural system where groups of neurons are taken to represent scalars, vectors, and functions, and where synaptic connections implement transformations on these representations. The system generalizes to higher dimensional vectors and has also been used as the basis of models of path integration (
Conklin and Eliasmith, 2005
) and working memory (
Singh and Eliasmith, 2006
). Arbitrary nonlinear encodings are supported by adjusting
G to be the output of any neural model. While the above derivation assumes linear dendrites, the approach generalizes to nonlinear dendritic behavior as well (see
Eliasmith and Anderson, 2003
).
Programming Interface
Nengo is a highly modular object-oriented Java program, making the underlying simulation system extensible and adaptable to novel modeling situations. The following features are directly exposed to the developer by the architecture:
Neuron models
Specialized neuron models can be written in Python or Java. These can extend existing models and/or use generic components, such as the built-in dynamical system solver. For example, a Nengo implementation of a dopamine-sensitive bistable striatal neuron (
Gruber et al., 2003
) was recently developed. The core of its implementation is shown later in this paper.
Neural plasticity
Arbitrary functions can be added for adjusting synaptic weights based on spike timing and modulatory signals.
Muscle models
For any neural models involving motor neurons, the dynamic behavior of the muscles form an important part of the model as well. Nengo supports multiple approaches to muscle modeling (e.g.
Keener and Sneyd, 1998
;
Winter, 1990
).
All of these components, along with other useful tools for modeling such as external inputs and probability distribution functions for various neural properties, can be implemented in either Java or Python. As discussed in further detail below, all of the features of Nengo are exposed in both languages, allowing developers the flexibility to choose the approach which is most suitable to them.
Since the software was developed for large-scale modeling, each component within a Nengo model has an adjustable simulation mode. For neural groups defined using the NEF approach, three modes are provided: spiking neurons, rate neurons, and a direct high-level abstraction of the overall neural behavior. This direct mode allows for fast approximate simulations where the individual neurons within the group are not simulated; instead the behavior is approximated in terms of the underlying represented values
x(
t). When neural groups simulated at a low level connect with groups simulated at a high level, Eqs 1 and 3 (above) are used to determine the corresponding spike trains and
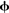
values. If sufficient time and computational resources are available, all parts of the model can be simulated in terms of spiking neurons. However, this capability of mixing levels of simulation means that a detailed neural model involving tens of thousands of neurons can be embedded within a high-level approximation of the millions of other neurons with which this system must interact. By switching modes of particular neural groups, the effect of different degrees of accuracy can be easily determined. Changing simulation models is also a useful exploratory tool, since approximate behavior can be determined quickly.
User Interface
Nengo also provides a graphical user interface for constructing and simulating models. Neural groups can be created and configured, projections and synaptic connection weights can be defined, and simulations can be run and analyzed, all through a point-and-click interface. This provides a direct method for visualizing the overall organization of a complex neural circuit at multiple levels of abstraction.
This interface is intended to be equally suitable for novice and expert users. In particular, we wanted to ensure that while common tasks are made easier by the interface, more experienced users have simultaneous access to the full capabilities of the programmatic interface. To achieve this, a Python scripting interface is embedded in the graphical user interface, complete with a full history and object-inspection based code completion tools. Usage examples of this combined graphical and scripting system are given in the next section.
To blend the graphical interface with the full power of the underlying programmatic interface, we embedded a Python scripting engine. This allows Python code and scripts to run in concert with the user interface. In this way, users can follow a graphical point-and-click approach for common modeling tasks, and turn to Python scripting for more complex or specialized tasks.
Since Nengo is implemented in Java, the scripting interface was implemented with Jython. This is a Java implementation of Python, which allows Python code to be compiled to the Java Virtual Machine, and provides seamless interaction between languages, including inheritance between languages and full access to the Java API using Python syntax. Importantly, no extra development effort (beyond embedding Jython within the Nengo graphical user interface) was required to allow Python access to the Nengo code; Jython automatically provides the Python syntax and interactive capabilities described here.
As an example, Figure
4
shows the Python scripting interface being used to duplicate an existing group of neurons (
groupA, created using the point-and-click interface). This duplication is performed using the standard Java
clone() method. The name of this new neural group is then changed to
groupB and it is added to the existing network. These tasks can also be performed via the graphical interface; this example is meant to show the direct relationship between the underlying Java entities, the graphically displayed objects, and the Python scripting.
Figure 4. Basic usage of the Python scripting interface to interact programmatically with a neural model.
Run-Time Inspection and Modification
The simplest use of the scripting system is to display and edit the values of variables within the simulation. The most recent object selected in the graphical display is always bound to the variable that in the scripting system. This allows us to quickly inspect and change objects. For example, to display the bias current (Jbias in Eq. 1) of a given neuron, we can click on it in the interface and type the following, with the output from Nengo shown in bold:
The command that.bias is automatically converted by Jython into the Java method invocation getBias() on the currently selected object, and the result is printed to the screen. This convenience functionality is built in to Jython and works with any Java code that conforms to the JavaBean properties standards.
For more complex situations, we use Python to extract relevant information and analyze and record it in the desired manner. For example, we can display all of the Jbias values across a group of neurons, find their average, and save the values in a comma-separated values (CSV) file.
This approach can also be used to set values within the simulation; the command that.bias = 0.3 is converted into the Java method setBias(0.3) by Jython. This allows model parameters to be set in a flexible manner. For example, to cause the RC time constant for a group of neurons that use an LIF spike generator to be uniformly distributed between 200 and 300 ms, we can do the following:
Programmatic Model Creation
Python can also be used to directly create models. This involves defining the various neural groups and specifying the projections between them. As this is done, Nengo automatically solves for the required synaptic weight matrices, based on the neural properties, preferred direction vectors, and the desired transformation.
To configure a NEF neural group, we define the various parameters based on the neurobiological properties of the particular types of neurons being modeled. This can include specifying probability distributions for those aspects that are heterogenous across the group.

Given this definition, we can now create neural groups of the desired size, encoding vectors of a given length. Terminations are defined by providing the linear transformation matrix (M in Eq. 4) and the post-synaptic time constant. Nonlinear functions are computed by creating a separate origin and providing the desired function. This separate origin does not imply a separate source of action potentials; it is implemented internally using the same spike timing as the standard projection origin (i.e. the neural group’s axons), but with a different set of decoding vectors, as per Eq. 5. For example, the following script will create a neural group which accepts five inputs and outputs the maximum value encoded by those five inputs, using the neural properties defined above.

We have found this approach to be flexible and highly useful for our ongoing research. In particular, this has allowed us to quickly explore the behaviors of complex cognitive models, including our ongoing work on neural implementation of Kalman filters for sensorimotor integration, language based reasoning, the role of basal ganglia in motor control, and other projects. While much of Nengo is devoted to supporting NEF-style models, similar commands are used for models that directly specify neural connections and plasticity, or that merge the two approaches.
Scripting of Common Tasks
Besides directly creating or modifying models, Python is also useful for defining stimuli, controlling simulations, and analyzing or recording results. Inputs to neural groups can be defined using arbitary Python code, allowing for anything from simply adding white noise to a baseline input value to providing dynamic inputs based on the current motor outputs of the model.
More generally, we can use the scripting system to evaluate neural models. That is, we can easily run multiple simulations, adjusting parameters, and recording the data. For example, the following code runs an existing simulation 10 times, adjusts the refractory period each time, and records the model output to a MATLAB® file. This allows us to quickly explore the behavioral effects of physiological parameters.
Defining Neuron Types
Given the wide range of existing neuron models, and the continual development of new ones, Nengo needs to allow the user to easily define and use new neuron models throughout the system. This is facilitated by a general-purpose dynamical system solver which creates spiking neuron models based on their dynamical description. Given the simplicity of the Python syntax, existing published neural models can be easily translated from their mathematical description into code.
For example, the following Python code defines the membrane dynamics for a dopamine-sensitive bistable striatal neuron developed by
Gruber et al. (2003)
. This model’s behaviour is affected by levels of dopamine, which are set using a separate modulatory input within Nengo, allowing it to be controlled by other neural groups.
Using this approach, any component of a neural system expressed in terms of its internal dynamics can be integrated into a Nengo model.
Integration with other Libraries
Since Nengo integrates a Python scripting system via Jython, Nengo models can also make use of other code libraries. This not only includes the standard built-in Python libraries for string processing, random number generation, asynchronous communication, and other common tasks, but also any other library written in Java or 100% Python. Unfortunately, Jython currently does not support direct integration with Python extension modules, such as NumPy or SciPy. To make use of such tools for data analysis, the output from Nengo can be exported to a file. However, for modules which can be directly integrated, Nengo allows for seamless communication between systems from within the graphical user interface.
ACT-R
As an example of this model integration, we have combined Nengo with a Python implementation of ACT-R, a high-level model of human cognition (
Anderson and Lebiere, 1998
). ACT-R divides human cognitive function into a variety of separate modules, which map on to particular brain areas (
Anderson et al., 2008
). Although no neural implementation of these modules exists as of yet, the underlying theory provides millisecond-level timing information for the behaviour of these modules which accords well with timing of overt behavior and of fMRI BOLD responses. ACT-R distills decades of cognitive science research into a form that provides a high-level model of many brain regions that can, in theory, interact with a lower-level neural model. In order to bring about this possibility, we connected the Python implementation of ACT-R (
Stewart and West, 2007
) to Nengo. This is freely available as part of CCMSuite.
The modules in ACT-R (see Figure
5
) were developed to explain human cognitive performance across a wide variety of tasks, including serial recall, visual search, mental arithmetic, task switching, and the use of graphical interfaces. Each cortical module maintains a
buffer which contains one
chunk of information. This chunk is a symbolic representation of the current working memory associated with that module. For example, the declarative memory module may retrieve the fact that
two plus two is four, storing that in its buffer as the chunk
quotidnvalue1:two value2:two operation:plus result:fourquotidn. The symbolic values within a chunk are organized into
slots, and a chunk of a given type always has the same set of slots.
Figure 5. The basic modules of ACT-R and their corresponding brain regions. The buffers are small-capacity working memories and represent the current cognitive state. The basal ganglia match this state against learned production rules, resulting in and output which can change the values stored in the different buffers. These changes in turn can cause other modules to perform various actions, including memory recall, motor commands, and visual search.
Communication between modules is controlled by a generalized action selection system associated with the basal ganglia. This contains a set of production rules: IF-THEN statements which identify which values should be placed in which buffers based on the current values in other buffers. To fit a wide range of behavioral data, a cycle of determining which productions match the current situation, selecting one of them, and sending its associated values is assumed to take the brain approximately 50 ms.
Representation Mapping
To integrate ACT-R and Nengo, we need to define a system of communication between them. That is, if we construct a neural model of a given brain region, we need to remove the corresponding component from the ACT-R model and connect the Nengo model in its place. This connection requires translating the symbolic representations used in ACT-R into spiking patterns and vice-versa, since communication in ACT-R is via chunks and communication in Nengo is via spikes.
Since Nengo provides access to the NEF, this mapping from symbols to population spike trains is facilitated by Eqs 1 and 3 described above for mapping vectors to population spike trains. We simply need to map the symbolic representation of a chunk into a vector and back again. In theory, this could be as simple as having a separate dimension in the vector for every possible chunk, or as sophisticated as using Vector Symbolic Architectures (
Gayler, 2006
). For example, the following code maps the chunk
quotidnstate:Aquotidn to [1,0,0], quotidnstate:Bquotidn to
[0,1,0], and
quotidnstate:Cquotidn to
[0,0,1] and vice-versa. Note that the mapping from vector to chunk must take into account the representational noise introduced by the spiking neurons.
Integrated Simulation
To demonstrate this integration, we can create a Nengo implementation of an ACT-R buffer and connect it to an ACT-R model. For simplicity, the ACT-R model is of a set of three production rules which causes the goal buffer to cycle through three possible values (from state:A to state:B to state:C and back to state:A and so on). This simplistic model is sufficient to demonstrate communication from the ACT-R portion of the model to the Nengo portion and back again.

Once this model is defined, it can be created within Nengo. This involves the helper function nengo.create which is provided by CCMSuite and ensures that time in the ACT-R model is synchronized with time in the Nengo simulation. Once the model is created, a Nengo origin and termination are defined that use the defined mapping between ACT-R symbols and Nengo spike trains given above. Once these origins and terminations are defined, they are treated exactly as any other in Nengo, allowing neural models to be built and connected to them via either the Nengo graphical user interface or through the scripting system.
For this case, we implement the buffer using a three-dimensional integrator of the same type as that shown in Figure
3
. This consists of 300 LIF neurons in a single neural group which integrates the value provided by ACT-R and outputs the current stored value back to ACT-R. These neurons are configured as per section “Programmatic Model Creation”
The behavior of this model is shown in Figure
6
. The neural group maintains the stored value over time, and then quickly changes this value when requested by the ACT-R production system. Importantly, the behavior of the model is robust over the time frame expected by ACT-R.
Figure 6. Spike pattern and vector decoding of a neural population implementing an ACT-R goal buffer. Dots indicate spike times for each neuron in the goal buffer, arranged along the y-axis. The three lines show the three-dimensional value decoded from the spikes using Eq. 3. The three dimensions correspond to the three possible values for the buffer, showing that the represented value cycles through the three states.
Nengo greatly facilitates the creation of complex neural circuits. The use of the NEF provides a general-purpose framework for representing information in spiking neurons that is flexible enough to support a wide variety of neuron models. The way in which the NEF systematically relates high-level information processing to electro-physiology facilitates modeling of complex circuits and validation against both behavioral and electro-physiological data. Finally, the integrated Python scripting language, with its emphasis on readability and rapid development, makes it ideal for quickly creating models and exploring model variations.
This system is also supported by a rich graphical user interface suitable for introducing new users in, for example, classroom situations. Common tasks are supported directly by the user interface, and Python scripting offers a highly readable syntax for more complex situations without extensive language-specific training. Nengo is currently being used in a graduate-level course on the NEF, and students without previous Python exposure are able to make use of it and the user interface to create complex models, including modeling sensorimotor control using Kalman filters and sequence recognition in birdsong. Importantly, having the Python scripting available means that both experienced researchers and new students can use Nengo effectively.
Nengo’s ability to integrate with other software libraries written in either Java or Python opens up many new research possibilities. For example, there are two key research benefits from integrating Nengo neural models with higher-level behavioral models such as ACT-R. First, it is of benefit to cognitive scientists, since the neural models provide a more detailed implementation of the components postulated by the overall cognitive theory. This may lead to more detailed and more accurate predictions, as well as a strong neurological grounding for these components. Second, it is of benefit to neuroscientists, since the cognitive theory provides realistic boundary conditions for the neural components. That is, the inputs to a neural model can be derived from a dynamic cognitive model, and the outputs from the neurons in turn affect the behaviour of that model. This provides a more realistic environment for simulating neural models.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Shu Wu for developing Nengo’s graphical user interface.
Anderson, J. R., Fincham, J. M., Qin, Y., and Stocco, A. (2008). A central circuit of the mind.
Trends Cogn. Sci. 12, 136–143.
Anderson, J. R., and Lebiere, C. (1998). The Atomic Components of Thought. Mahwah, Erlbaum.
Angelaki, D. E., McHenry, M. Q., Dickman, J. D., Newlands, S. D., and Hess, B. J. M. (1999). Computation of inertial motion: neural strategies to resolve ambiguous otolith information.
J. Neurosci. 19, 316–327.
Conklin, J., and Eliasmith, C. (2005). An attractor network model of path integration in the rat.
J. Comput. Neurosci. 18, 183–203.
Dormand, J. R., and Prince, P. J. (1980). A family of embedded Runge–Kutta formulae.
J. Comput. Appl. Math. 6, 19–26.
Eliasmith, C., and Anderson, C. (2003). Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems. Cambridge, MIT Press.
Eliasmith, C., Westover, M. B., and Anderson, C. H. (2002). A general framework for neurobiological modeling: an application to the vestibular system.
Neurocomputing 46, 1071–1076.
Fischer, B. (2005). A model of the computations leading to a representation of auditory space in the midbrain of the barn owl. PhD thesis. St Louis, Washington University in St Louis.
Gayler, R. W. (2006). Commentary: vector symbolic architectures are a viable alternative for Jackendoff’s challenges.
Behav. Brain. Sci. 29, 78–79.
Georgopoulos, A. P., Schwartz, A. B., and Kettner, R. E. (1986). Neuronal population coding of movement direction.
Science 233, 1416–1419.
Gruber, A. J., Solla, S. A., Surmeier, D. J., and Houk, J. C. (2003). Modulation of striatal single units by expected reward: a spiny neuron model displaying dopamine-induced bistability.
J. Neurophysiol. 90, 1095–1114.
Izhikevich, E. M. (2003). Simple model of spiking neurons.
IEEE Trans. Neural Netw. 14, 1569–1572.
Keener, J., and Sneyd, J. (1998). Mathematical Physiology. New York, Springer.
Kuo, D., and Eliasmith, C. (2005). Integrating behavioral and neural data in a model of zebrafish network interaction.
Biol. Cybern. 93, 178–187.
La Camera, G., Rauch, A., Lüscher, H.-R., Senn, W., and Fusi, S. (2004). Minimal models of adapted neuronal response to in vivo-like input currents.
Neural Comput. 16, 2101–2124.
Rieke, F., Warland, D., de Ruyter van Steveninck, R., and Bialek, W. (1999). Spikes: Exploring the Neural Code. Cambridge, MIT Press.
Salinas, E., and Abbott, L. F. (1994). Vector reconstruction from firing rates.
J. Comput. Neurosci. 1, 89–107.
Seung, H. S. (1996). How the brain keeps the eyes still.
Proc. Natl. Acad. Sci. U.S.A. 93, 13339–13344.
Singh, R., and Eliasmith, C. (2006). Higher-dimensional neurons explain the tuning and dynamics of working memory cells.
J. Neurosci. 26, 3667–3678.
Stewart, T. C., and Eliasmith, C. (2009). Compositionality and biologically plausible models. In Oxford Handbook of Compositionality, W. Hinzen, E. Machery and M. Werning, eds (Oxford University Press).
Stewart, T. C., and West, R. L. (2007). Deconstructing and reconstructing ACT-R: exploring the architectural space.
Cogn. Syst. Res. 8, 227–236.
Winter, D. A. (1990). Biomechanics and Motor Control of Human Movement. John Wiley & Sons, New Jersey.

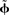 (the stimulus for which it most strongly fires), bias current Jbias, and scaling factor α. For a given neuron, α and Jbias can be experimentally determined from its maximum firing rate and the minimum value of x for which it responds. If the nonlinearities of any given neural model (LIF, ALIF, etc.) are written as G[·] and the neural noise of variance σ2 is η(σ), then the encoding of any given x(t) as the temporal spike pattern across the neural group is given as Eq. 1.
(the stimulus for which it most strongly fires), bias current Jbias, and scaling factor α. For a given neuron, α and Jbias can be experimentally determined from its maximum firing rate and the minimum value of x for which it responds. If the nonlinearities of any given neural model (LIF, ALIF, etc.) are written as G[·] and the neural noise of variance σ2 is η(σ), then the encoding of any given x(t) as the temporal spike pattern across the neural group is given as Eq. 1.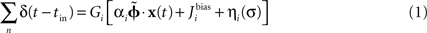
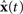 . In some approaches (e.g. Georgopoulos et al., 1986
), this is done by weighting each encoding vector
. In some approaches (e.g. Georgopoulos et al., 1986
), this is done by weighting each encoding vector 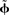 by the average firing rate of the corresponding neuron. In the NEF, however, we derive the linearly optimal decoding vectors
by the average firing rate of the corresponding neuron. In the NEF, however, we derive the linearly optimal decoding vectors 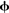 for each neuron (see Eliasmith and Anderson, 2003
for details). This method has been shown to uniquely combine accuracy and neurobiological plausibility (e.g. Salinas and Abbott, 1994
).
for each neuron (see Eliasmith and Anderson, 2003
for details). This method has been shown to uniquely combine accuracy and neurobiological plausibility (e.g. Salinas and Abbott, 1994
).
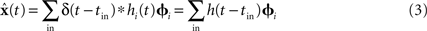
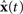 is dependent on the particular neural parameters and encoding vectors, but in general is inversely proportional to the number of neurons in the group. Given a sufficient number of neurons, an arbitrary level of accuracy can be reached. For a known number of neurons with known physiological properties, we can determine how well the values can be represented.
is dependent on the particular neural parameters and encoding vectors, but in general is inversely proportional to the number of neurons in the group. Given a sufficient number of neurons, an arbitrary level of accuracy can be reached. For a known number of neurons with known physiological properties, we can determine how well the values can be represented.
 then the post-synaptic neurons will encode M x(t). This allows us to develop a model by defining the hypothesized computations and directly solving for the corresponding connection weights, rather than relying on a learning rule or manually setting the weights.
then the post-synaptic neurons will encode M x(t). This allows us to develop a model by defining the hypothesized computations and directly solving for the corresponding connection weights, rather than relying on a learning rule or manually setting the weights. f(x) which can be used in place of the previous
f(x) which can be used in place of the previous  to provide an optimal linear estimate of this function. This allows arbitrary nonlinear functions to be computed, although more complex nonlinearities across multiple dimensions of x will require more neurons with
to provide an optimal linear estimate of this function. This allows arbitrary nonlinear functions to be computed, although more complex nonlinearities across multiple dimensions of x will require more neurons with 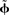 values that lie in those dimensions.
values that lie in those dimensions.
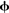 values. If sufficient time and computational resources are available, all parts of the model can be simulated in terms of spiking neurons. However, this capability of mixing levels of simulation means that a detailed neural model involving tens of thousands of neurons can be embedded within a high-level approximation of the millions of other neurons with which this system must interact. By switching modes of particular neural groups, the effect of different degrees of accuracy can be easily determined. Changing simulation models is also a useful exploratory tool, since approximate behavior can be determined quickly.
values. If sufficient time and computational resources are available, all parts of the model can be simulated in terms of spiking neurons. However, this capability of mixing levels of simulation means that a detailed neural model involving tens of thousands of neurons can be embedded within a high-level approximation of the millions of other neurons with which this system must interact. By switching modes of particular neural groups, the effect of different degrees of accuracy can be easily determined. Changing simulation models is also a useful exploratory tool, since approximate behavior can be determined quickly.