Adaptive proactive inhibitory control for embedded real-time applications

Psychologists have studied the inhibitory control of voluntary movement for many years. In particular, the countermanding of an impending action has been extensively studied. In this work, we propose a neural mechanism for adaptive inhibitory control in a firing-rate type model based on current findings in animal electrophysiological and human psychophysical experiments. We then implement this model on a field-programmable gate array (FPGA) prototyping system, using dedicated real-time hardware circuitry. Our results show that the FPGA-based implementation can run in real-time while achieving behavioral performance qualitatively suggestive of the animal experiments. Implementing such biological inhibitory control in an embedded device can lead to the development of control systems that may be used in more realistic cognitive robotics or in neural prosthetic systems aiding human movement control.

Introduction

Psychological research reveals that humans can adapt to dynamic environments using inhibitory control (Logan and Cowan, 1984; Logan and Gordon, 2001; Emeric et al., 2007). In cognitive models of behavior, proactive inhibition can be understood as the suppression of previously activated or planned cognitive processes. This type of inhibition is a vital part of human behavior because it allows flexible adaptation to changing environments or rules. Inhibitory control in countermanding tasks is studied in the motor system, since it requires the suppression of motor outputs. In humans, evidence of neural correlates of inhibitory control can be revealed from neuroimaging (e.g., functional magnetic resonance imaging; Curtis et al., 2005; Chikazoe et al., 2009). However, studies such as these often do not provide sufficient temporal or spatial information to reveal the possibly rapid neural mechanisms underlying inhibitory behavior such as stopping an impending (saccadic) eye movement. During the last decade, animal electrophysiologists have begun to employ behavioral task paradigms in psychology, such as the saccade countermanding tasks to search for the neuronal correlates of inhibitory control behavior (Hanes et al., 1998; Murthy et al., 2001; Sato and Schall, 2003; Schall, 2004; Schall et al., 2004, 2011; Cohen et al., 2007; Pouget et al., 2011).

This series of electrophysiological work on behaving non-human primates has shown that there are neurons in the frontal eye fields (FEFs) and superior colliculus that correlate with an impending saccadic eye movement (classified as “movement” neurons) or inhibition (classified as “fixation” neurons), while neurons in other brain regions (e.g., supplementary eye fields) seem to correlate with monitoring and/or controlling voluntary movements. These findings have inspired various computational neural models (Boucher et al., 2007; Lo et al., 2009; Wong-Lin et al., 2010), which provide good accounts of how the interaction between go and stop processes can be reconciled with the observation at the neuronal and behavioral levels. More recently, Pouget et al. (2011) interestingly shows that movement neurons can temporally shift their activation onset times based on whether the previous trials have a stop-signal or not, thus allowing longer term adaptation in the inhibitory control system. This phenomenon has not been accounted for in previous computational models.

Modern neural computational models can provide powerful ideas to be used in neural prosthetics and robotic development. Specifically, implementations of these models in hardware may give (especially transfemoral) prosthetics users or cognitive/mobile robots an enhanced capability of controlling their pre-movement acts related to the decision of whether to move, and also the possibility of adapting to dynamically changing environments (Farwell and Donchin, 1988; Schwartz, 2004; Chestek et al., 2009; Perrin et al., 2010). However, while many attempts to implement neuronal models in hardware have been made, neural computational models for a countermanding task are currently coded in software and used to account for experimental findings. They have not, as yet, been implemented in a real-time embedded field-programmable gate array (FPGA) system for more practical applications.

In this paper, we build on our previous computational inhibitory control model for countermanding saccadic eye movements and propose an adaptive inhibitory control mechanism inspired by Pouget et al. (2011). We then implement the proactive adaptive inhibitory control exploring a synthesizable HDL coding approach. The proposed framework has been evaluated on an FPGA (Xilinx Virtex-6 LX240) platform (Xilinx Inc., 2011a). The implementation in digital hardware provides the possibility of creating a realistic motor control system in embedded portable devices and is anticipated to integrate into existing neuronal prosthetics and robotic systems.

Materials and Methods

As a first step toward prototyping, we shall focus only on a firing-rate type model modified from Wong et al. (2007), Wong-Lin et al. (2010). The model was designed in a way similar to the saccade countermanding task in animal experiments to account for the experimental data (Hanes et al., 1998; Boucher et al., 2007).

Experimental Motivation

The countermanding stop-signal task is a common procedure for investigating the control of thought and action by probing the subjects’ ability to withhold a planned movement in response to an unanticipated countermanding signal (Logan, 1981; Logan and Cowan, 1984). This task has been used to study executive control and flexibility in behavior, since the performance of this task demonstrates an empirical model of self-control (Lappin and Eriksen, 1966; Logan, 1981; Akerfelt et al., 2005; Boucher et al., 2007; Bissett and Logan, 2011).

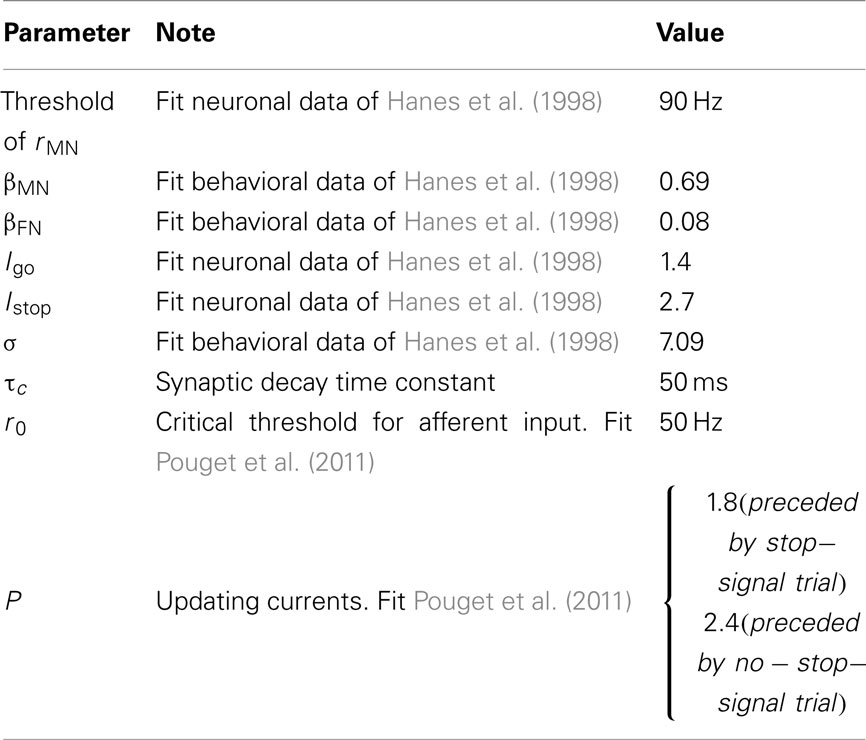
In the countermanding task experiment, two types of trials (no-stop-signal trial and stop-signal trial) were designed, as shown in Figures 1A,B. Trials with or without the stop signal are referred to as stop-signal trials or no-stop-signal trials, respectively. As shown in Figure 1A, in a typical experimental trial, the task started with a black screen. In Hanes et al. (1998) a fixation point (stop signal) was on after 1 s. Then the fixation point was then turned off while a peripheral target (go signal) was turned on at the same time after 500 ms. The subject is instructed to make a saccadic eye movement to this target. However, a fraction of the trials include a stop signal (e.g., in the form of a reappearance of the fixation point) shortly after target onset (Figure 1B). The subject is instructed to withhold their gaze at the fixation point whenever a stop signal appears. The ability of the subject to withhold his or her gaze at the fixation point depends on the delay between the go signal and stop signal onset times, termed the stop signal delay (SSD); the shorter the SSD, the easier to withhold the gaze. Thus, stop-signal trials can be further categorized into (successfully) canceled trials and non-canceled trials (also known as “signal inhibit” and “signal respond” respectively, in the literature; Logan and Cowan, 1984). A trial will end after another 700 ms has elapsed.

FIGURE 1

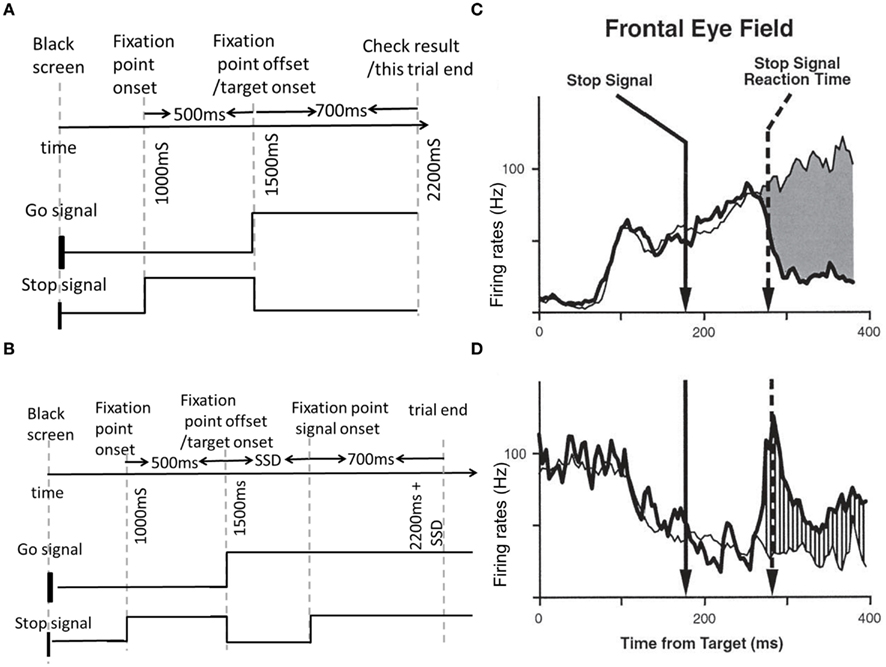
Figure 1. Schematic and neural activities in a saccade countermanding task. (A,B) Schematic representation of a no-stop-signal trial type (A), and a stop-signal trial type (B). These two trial types are randomly interleaved in a block of trials. In both trials, a central fixation signal (also the stop signal) is presented for a period of time, and then the peripheral target for a saccade (go signal) turns on. In a stop-signal trial, briefly after the go signal onset, a stop signal appears (i.e., fixation point reappears). This time interval is labeled as the stop-signal delay (SSD). (C,D) Neural firing rates of movement (C) and fixation (D) neurons in the frontal eye fields (FEFs) during the task. Saccades are correlated with the movement neuronal activities reaching a certain firing rate threshold level; successful cancelations correlated with simultaneous reactivation of fixation neuronal activities and suppression of movement neuronal activities (bold lines) before reaching some motor response threshold. (C,D) Adapted from Schall et al., 2002; with permission).

An inhibition function describes the probability of stopping across a range of SSD values can be easily gathered from the behavioral response. We would expect the probability of responding in a stop-signal trial to increase with SSD. The change in reaction time distribution with different SSDs can also be used to estimate the length of time needed to cancel the planned movement. This time length is also called the stop signal reaction time (SSRT). We would expect only the faster responses not to be inhibited when SSD is short. Therefore, a subject’s ability to inhibit the motor response will depend on the individual’s SSRT and the experimentally controlled SSD.

Previously, the inhibition function and the SSRT were the only means to deduce an individual’s responsiveness and cognitive control abilities. However, more recent neurophysiological experiments using implanted electrodes in non-human primates have allowed measurements with better spatial and temporal resolution, prior to a movement or no movement (Schall et al., 2002). The behavioral and neuronal data in the classic experiments of Hanes et al. (1998) were collected from monkeys, who were trained to allocate their gaze to spot on the screen. One of the most interesting findings in these experiments was that unlike previous cognitive models such as the race model (Logan, 1981; Logan and Cowan, 1984), the movement and stopping processes could interact. That is, neurons that encode the impeding movement ramp up their firing rates over time after a go signal onset and suppressed to baseline level during successful saccade or fixation cancelation. These movement neurons were anti-correlated with the drop and rise in firing rate of another group of neurons – the fixation neurons (as illustrated in Figures 1C,D).

Both response time and probability of responding can also be influenced by previous trials, depending upon whether the former have stop signals, and less so on whether the stop trials were successfully canceled (Emeric et al., 2007; Bissett and Logan, 2011; Pouget et al., 2011). Variations in the fraction of stop-signal trials can also influence the countermanding performance (Schall et al., 2002). Chikazoe et al. (2009) introduced a concept of prepared inhibition, in which inhibition is prepared in anticipation of an upcoming stop cue. A more recent research finding suggests that if the previous trials are (canceled) stop trials, the movement neurons show a delay in the onset time of their stereotypical ramping up activities (Pouget et al., 2011; Figure 5B). This is also correlated with behavioral performance changes. For example, Bissett and Logan, 2011 suggests that there is a small slowing after signal-inhibit (canceled stop trial) and signal-respond trials (non-canceled stop trial). Those results provide new insights into the adaptive mechanisms of inhibitory control.

Neural Network Model of the FEF

Our neural control circuit adopts the basic firing-rate type model of Wong-Lin et al. (2010) that can perform the countermanding task. The proposed neural network model includes two main units: a FEF network module, and an adaptive control module.

As shown in Figure 2A, the inhibitory dynamics of the interneurons is implicitly modeled by an effective direct mutual inhibition. This is justified if the excitatory timescale is much slower than its inhibitory counterpart (Wong and Wang, 2006; Wong-Lin et al., 2010). In a no-stop-signal trial or unsuccessfully canceled trial, the movement neurons successfully crossed a prescribed movement threshold in order to make a motor (saccadic eye) movement. However, in a stop-signal trial, the fixation neurons can be reactivated in time to suppress the movement neurons from crossing the movement threshold via a highly potent lateral inhibition, which can successfully prevent a motor movement.

FIGURE 2

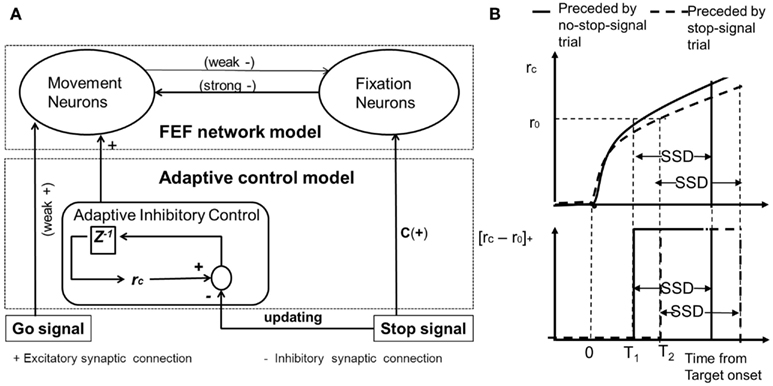
Figure 2. (A) The proposed neural network model of inhibitory control for the countermanding task. The schematic model architecture consists of a population of movement neurons, a population of fixation neurons, and a population of neurons for adaptive control. Z⁻¹ corresponds to the delay. C is a fixation stimulus input to set the fixation neurons to be at a high firing rate prior to the target onset. (B) The schematic mechanism of delaying the onset of control signal. Top: when a trial is preceded by a no-stop-signal trial (as compared to a stop-signal trial), it takes a shorter time to reach threshold (r0), due to a larger p value. T₁ denotes threshold-crossing time when the current trial is preceded by a no-stop-signal trial. T2 denotes the threshold-crossing time when the current trial is preceded by a stop-signal trial. Bottom: The corresponding afferent inputs into the movement neural population are delayed. Gain is turned off upon stop-signal onset at time T₁/T₂ plus SSD (for current stop-signal trial) or T₁/T₂ plus decision time (for current no-stop-signal trial; not shown), i.e., upon crossing saccadic/decision threshold.

The neural activity of movement neurons (r_MN) and the neural activity of fixation neurons (r_FN) can be described by Eqs 1 and 2, respectively.

$d{r}_{MN}=\left(-r_{MN}+{\left[{\beta }_{\text{MN}}{r}_{FN}+I_{go}\right]}_{+}\right)\frac{dt}{{\tau }_E}+\sigma \sqrt{\frac{dt}{{\tau }_E}}\gamma$    (1)

$d{r}_{\text{FN}}=\left(-r_{\text{FN}}+{\left[{\beta }_{\text{FN}}{r}_{\text{MN}}+I_{\text{stop}}\right]}_{+}\right)\frac{dt}{{\tau }_E}+\sigma \sqrt{\frac{dt}{{\tau }_E}}\gamma$    (2)

Here, r_MN and r_FN represent population firing rates of movement and fixation neurons respectively; β_MN and β_FN are the effective inhibitory synaptic strengths from fixation to movement neurons and from movement to fixation neurons; σ is the magnitude of additive noise and γ is a random Gaussian variable with zero mean and standard deviation of 1. [x]₊ denotes a threshold-linear function which is equal to x if x > 0, and 0 otherwise. I_go and I_stop are the input currents in the presence of the go and stop signals, respectively. During the appearance of the fixation point prior to target onset, an input current is applied to the fixation neural population to allow a high firing rate of about 80 Hz (Hanes et al., 1998).

A Neural Network Model of FEF with an Adaptive Control Model

Previous studies have demonstrated the presence of behavioral monitoring and control in the supplementary eye field and the anterior cingulate cortex of macaque monkeys and their possible influence on behavioral psychophysics over trials (Chen et al., 2010; Stuphorn et al., 2010). In particular, such studies have shown that the onset of movement neuronal activities upon a go signal onset can be delayed and the reaction times in the no-stop-signal trials can be slowed down, if the immediately preceding trials are stop-signal trials, thus, affecting the overall countermanding performance (Emeric et al., 2007; Pouget et al., 2011).

Compared to the neural network model of FEF (Wong-Lin et al., 2010), we have included an input-output/gating function of adaptive inhibitory control module to account for an excitatory control on the movement neurons. This control can be adjusted based on whether the previous history is a stop-signal trial or not. As the input from the control module to the movement neural population is a non-linear threshold function, it takes a longer time to activate the movement neurons when the control module has a lower activation level compared to when the previous trial is a no-stop-signal trial.

We propose a simple adaptive inhibitory control module to gate the flow of the control signal input into the movement neural population (Figure 2), depending on whether the previous trial is a stop-signal trial or not. The neural activity of fixation neurons (r_FN) can be described by Eq. 2. The neural activity of movement neurons (r_FN) can be described by Eq. 3.

$d{r}_{\text{MN}}=\left(-r_{\text{MN}}+{\left[{\beta }_{\text{MN}}{r}_{\text{FN}}+I_{\text{go}}+{\left[r_{\text{c}}-r_{\text{0}}\right]}_{+}\right]}_{+}\right)\frac{dt}{{\tau }_{\text{E}}}+\sigma \sqrt{\frac{dt}{{\tau }_{\text{E}}}}\gamma$    (3)

Where a threshold-linear function (denoted by []₊) gates an afferent input into the movement neural population. r_c is the control activity of the control neural population and is assumed to follow leaky integrating dynamics with a steady state value of P that depends on the previous trial (as described in Eq. 4). r₀ is the fixed threshold for gating the afferent input. The output from the control neural population sends a delayed excitatory input to the movement neurons upon receipt of a go signal onset. The specific temporal delay can be controlled by the value of P, related to heightened urgency to respond. The neural activity of the control neural population can be described by Eq. 4:

${\tau }_{\text{c}}\frac{d{r}_{\text{c}}}{dt}=-r_{\text{c}}+\text{P}$    (4)

P adopts a higher value if the previous trial is a no-stop-signal trial compared to a stop-signal trial (Table 1). Intuitively, the control activity can relate a higher sense of urgency signal (that increases over time) when the previous trial is a no-stop-signal trial. Thus a subject may anticipate the current trial to also be a no-stop-signal trial (Bissett and Logan (2011)). This urgency-gating signal can be related to previous work in response time tasks in perceptual decision-making (Cisek et al., 2009; Gao et al., 2009; Standage et al., 2011). However, when the previous trial is an occasional stop-signal trial, the urgency to respond is lowered, and the current trial is anticipated to be a stop-signal trial, and a more cautious response is required. The control (r_c) is turned off upon stop-signal onset during a current stop-signal trial or upon decision threshold (for saccadic eye movement) during a current no-stop-signal trial (Figure 2B). The dynamical time constant for the control neural population is assumed to be that of the NMDA-mediated synapses (which is prevalent in brain areas associated with higher-order cognition and cognitive control, e.g., prefrontal cortex; Wang, 2001).

TABLE 1

Table 1. Parameter values for the models.

As shown in Figure 2B, we can see that the control activity is generally higher if the previous trial is a no-stop-signal trial as compared to a stop-signal trial. In both cases, the control activity increases. As the input from the control module to the movement neural population is a threshold-linear function, it will take a longer time to activate the movement neurons when the control module has a lower activation level compared to when the previous trial is a stop-signal trial. Consequently, the onset of the movement neural activities due to the target signal is delayed, as observed in Pouget et al. (2011).

The model and related behavioral data parameters were selected to be consistent with experiment data of Hanes et al. (1998) and Boucher et al. (2007). For instance, we choose the time constant to be 50 ms (assumed mediated by slow receptors such as those mediated by NMDA). The FEF network model has asymmetrical mutual inhibitory couplings with β_MN is 0.69 « β_FN = 0.08, which fit the data of Hanes et al. (1998). White Gaussian noise is included in the model, which provides overall fluctuations in the network, and thus creating a distribution of reaction times, and also allows non-zero spontaneous firing rate in the network. Further details of the model parameters are given in Table 1. Following the neuronal activities in Hanes et al. (1998), movement neurons are assumed to respond to a go signal onset after a delay of 100 ms and fixation neurons respond 80 ms after the stop-signal appears. In this modeling simulation, the inter-trial interval of 1 s is assumed.

Results

In this experiment, we use a rapid prototyping flow on an FPGA-based embedded system. Parameterized electronic design entries are defined and used as inputs to the parameterized System Generator models (.mdl files; Xilinx Inc., 2011b). These models provide a library of pre-designed circuit blocks that can be converted into a hardware description language for seamless integration with the Xilinx FPGA design flow. After a successful synthesis process, an FPGA bit stream file is generated using the ISE synthesis tools. Following this, the simulation is executed in real-time using the FPGA resource, working in conjunction with a host PC. All simulation results can be imported into Matlab for visualization (Mathworks Inc., 2011). More FPGA implementation details are described in the Appendix.

In this section, we shall first reproduce the essential neural and behavioral data in the experiments. We then demonstrate that the model can also exhibit trial-history (sequential) effects on the movement neural activity and behavioral performance.

Behavior of the FEF Network Model

The observed neural activities from FPGA simulation are shown in Figure 3. When there is a stop-signal presented, this ramping activity may be suppressed in time to inhibit the impending saccade (as shown in Figure 3A). Neural activity of the fixation neural population ramps back up when there is a stop-signal (as shown in Figure 3B). This anti-correlation of activities between the two neural populations is a manifestation of the mutual inhibitory couplings in the FEF network.

FIGURE 3

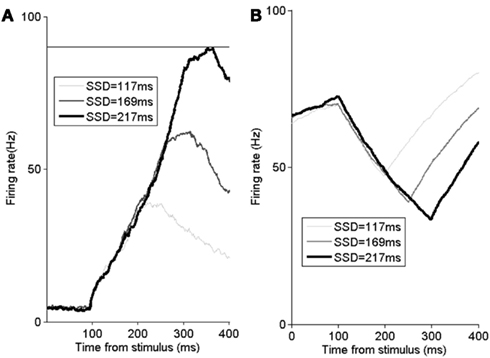
Figure 3. The FEF model’s neural activity time-course simulated with the FPGA platform. (A) Time course of trial-averaged activities of successfully canceled trials for movement neurons with various SSDs. All data are averaged over 5000 trials. Horizontal line: decision to saccade threshold (90 Hz). (B) Time course of trial-averaged activities of successfully canceled trials for fixation neurons with various SSDs. SSDs of 117 ms (light gray), 169 ms (dark gray), and 217 ms (thick black). To be compared with Boucher et al. (2007) and Wong-Lin et al. (2010). All data are averaged over 5000 trials.

As previously discussed, a subject’s ability to stop a pre-planned saccade can be evaluated through the inhibition function and reaction time distribution SSRT with various SSD. The proportion of canceled trials at each delay is referred to as the “inhibition function.” To investigate the efficiency of an inhibitory process, the probability of stop-signal trials with signal-response trials as a function of SSD is plotted. As SSD increases, the probability of non-canceled trials increases (Figure 4A). In Figure 4A, the model demonstrates that it can capture the inhibition function rather well (compared with Boucher et al., 2007). It should be noted that the probability of a canceled stop trial is very low when SSD is 69 ms (the data used in the study of Boucher et al., 2007) and is thus not included in this study. Figure 4B shows the signal-respond reaction time cumulative probability distribution from non-canceled stop-signal trials. We can see that when SSD is short (e.g., 117 ms), only the faster responses are not inhibited. The distribution is very similar to in the experiments in Boucher et al. (2007). These results confirm that our model implemented in hardware can replicate both the essential neurophysiological and behavioral findings in the experiments (Hanes et al., 1998).

FIGURE 4

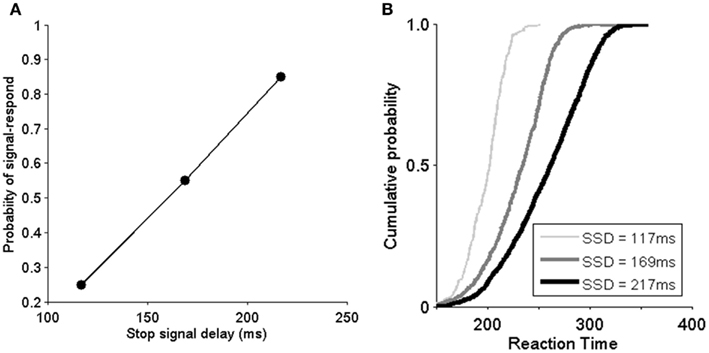
Figure 4. Model implemented in hardware replicates the behavioral data of the monkey experiments (Hanes et al., 1998; Boucher et al., 2007). (A) Inhibition function shows the probability of non-canceled (signal response) in stop-signal trials as a function of stop-signal delay (SSD). SSD: 117, 169, and 217 ms. (B) Cumulative distribution of reaction times from non-canceled stop-signal trials for different SSDs. To be compared with Boucher et al. (2007).

Neural Activity and Behavioral Modulation by the Adaptive Control System

An important part of this study is to implement the sequential effects due to adaptive adjustment based on the trial history. We have proposed a simple mechanism that depends on whether the previous trial is a stop-signal trial type. This modulation can affect the gating onset of incoming neural signal due to the no-stop-signal trial stimulus.

To study the effects on the dynamics of the adaptive control system and movement neural activity, we simulated 5000 trials randomly mixed with equal number of stop-signal trials and no-stop-signal trials. The simulation was carried out using FPGA-based embedded system platform (see Appendix for more details). The results are recorded in FPGA on-board SDRAM and read back into Matlab. We subsampled the activation of the fixation and movement neurons in a manner comparable to the sampling of neural activity in the physiology experiments via the following procedure. We simulated the model with 10–12 trials at each SSD to mimic the number of trials typically obtained in the physiology experiments. In this simulation, we mix 25% of stop-signal trials and 75% of no-stop-signal trials randomly.

In particular, Figure 5A shows that the model produces a rightward shift in the reaction time distribution for no-stop-signal trials if the previous trial is a stop-signal trial type, very similar to that as in the experimental data (Figure 5B).This rightward shift in the movement neural activity onset due to a previous stop-signal trial can result in longer reaction times, and allows a better chance of inhibiting a respond. Figure 6 confirms these predictions in our model.

FIGURE 5

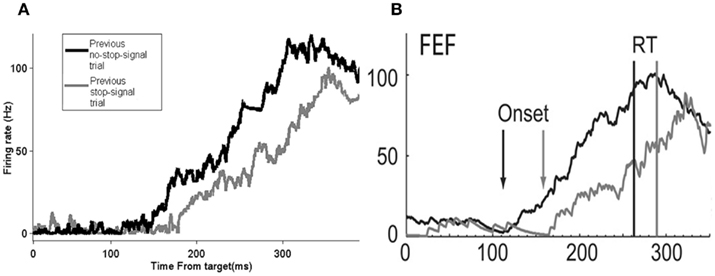
Figure 5. The model’s neural activity time course is similar to that of the experimental data. The time course of average firing rates activity of movement neurons response time for no-stop-signal trials preceded by either a no-stop-signal trial or a stop-signal trial for data collected in 25% stop-signal trials session experiment in the model with 5000 trials (A) and in the experiment (B). (B) Adapted from Pouget et al., 2011; with permission).

FIGURE 6

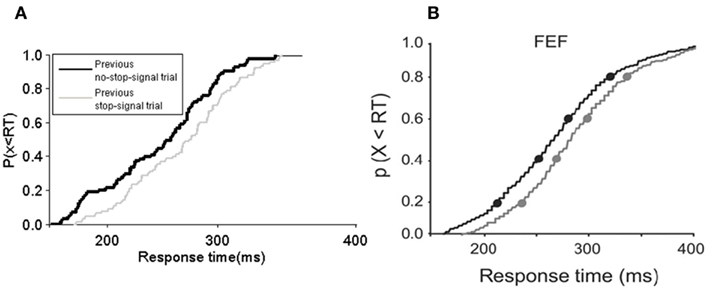
Figure 6. Cumulative frequency distribution of response time in the model and experiment. (A) The cumulative frequency distribution of response time in the model and (B) in the experiment of Pouget et al. (2011). (A,B) Both using a 25% stop-signal trials session experiment with SSD of 217 ms. Black: Preceded by no-stop-signal trial. Gray: stop-signal trial [canceled trial in (B)]. (B) Adapted from Pouget et al., 2011; with permission).

Intuitively, we can understand that the occurrence of a previous stop-signal trial triggers the need for subsequent caution, and resulting in prolonged response time. This adaptive adjustment has been regarded as the “goal priority hypothesis” in cognitive psychology (Bissett and Logan, 2011), which suggests that stimuli that occur on stop trials become associated with stopping. If the stimuli do not repeat, they do not retrieve associations with stopping to slow RT. Thus the memory hypothesis predicts greater post-stop-signal slowing when stimuli repeat after stop trials than when stimuli do not repeat.

Discussion

In this work, we have implemented in hardware a computational neural model of the FEF with proactive inhibitory control for the saccade countermanding task. Inspired by recent experimental findings (Emeric et al., 2007; Pouget et al., 2011), we have proposed a simple adaptive neural inhibitory control module to gate the flow of the go signal input into the movement neural population, depending on whether the previous trial is a stop-signal trial or not. Our hardware implementation is based on a FPGA prototyping system using dedicated real-time hardware circuitry.

Hardware Implementation of a Computational Model of Inhibitory Control

The main goal of this work is to implement an adaptive proactive inhibitory control model for voluntary movement on an FPGA platform. Emulating biological signal processing on an FPGA platform is an economical option for complex systems modeling, prior to proceeding to fully integrated circuit design and fabrication. This work is an important step toward the eventual goal of incorporating into hardware a sufficiently biologically realistic FEF model potentially for neural prosthetic or robotic devices. We have demonstrated that a hardware implementation is feasible using currently available technology.

Field-programmable gate arrays have been less commonly used in bionic creativity engineering, with several exceptions. Protein (Armstrong et al., 2007) and DNA sequencing search (Knodel et al., 2011) are using FPGAs to reduce processing time. Real-time processing, registration and fMRI image analyses are enabled by FPGAs (Koo et al., 2009). Most modeling applications on FPGAs have been limited to studying neural dynamics in low-level simulations. Recently we have made several implementation of spiking neural network models which include integrate-and-fire neuronal models and conductance-based neural models (Maguire et al., 2007; Glackin et al., 2009; Ghani et al., 2011; Yang and McGinnity, 2011). However, each of these designs consists of a relatively small number of neurons, and do not typically link to behavioral data. This paper extends previous work of firing-rate type neural models and cognitive neural models in countermanding impending actions by providing fast prototyping architecture for current software-based cognitive neural modeling into FPGA-based embedded system. Building on this work, we should be more confident that we will be able to build a fast inhibitory control system that deals with more realistic neuronal spike coding (Lo et al., 2009). In fact, we should expect the FPGA-based system to greatly enhance the computational speed of the model in Lo et al. (2009).

The research presented in this work has shown that our fast prototyping platform with hardware evaluation framework reproduced qualitatively the data from Pouget et al. (2011). The disadvantage of our FPGA model is that once the algorithm is synthesized and programmed into the FPGA the parameters cannot be changed without another synthesis. The design cycle is longer than software implementation, but much shorter than for a full-Application Specific Integrated Circuit (ASIC) design. For fabricating a chip to be used in neural prosthetic devices, more work for design optimization is necessary. Firstly, an efficient way to save power consumption could be achieved using a low frequency clock. Secondly, balancing between high precision and silicon area is a key issue for implementation in a small die area. Thirdly, the analog-to-digital converters should be integrated for sensor inputs/control outputs. Finally, as shown in Figures A1 and A2, in Appendix, the overall logic usage for the proactive control design is just over 4% of that available, which is very promising for future extensions, since it suggests that there is plenty of scope left to add new embedded features.

Adaptive Inhibitory Control Mechanism

In this work, we have proposed a mechanism for implementing an inhibitory control system that can adapt to previous trial type and performance. Specifically, we have implemented a neural transit delay mechanism of the inhibitory control unit that depends on whether the previous trial is a stop-signal trial or no-stop-signal trial type. This may allow the system to autonomously track the statistics in noisy, dynamic environments (e.g., there is a stop-signal in 25% of the time) better in order to respond more appropriately (Sugrue et al., 2004; Wong et al., 2007; Shenoy et al., 2010). This is an extension of our previous computational model; the results are qualitatively suggestive of the neural and behavioral data in Hanes et al. (1998), Boucher et al. (2007), and Pouget et al. (2011).

Our simple adaptive control mechanism has the interesting features of incorporating previous neural mechanisms in simple decision-making tasks; namely, the integration of the urgency-gating mechanism (Cisek et al., 2009; Niyogi and Wong-Lin, 2010; Standage et al., 2011) and sequential effects (Fecteau and Munoz, 2003; Gao et al., 2009). In the model, we have assumed that the memory of the previous trial affects the current trial differently, depending on the previous trial type. Bissett and Logan (2011) has shown that when the frequency of stop-signal trials increases, the post-stop-signal slowing is greater. This can be implemented easily in our model either by having the parameter P as a monotonically increasing function of the frequency of stop-signal trial or with slightly longer memory trace (e.g., memory of two trials back instead of one). This memory-based hypothesis may perhaps be tested by slightly modifying the present task. For example, by presenting a distractor stimulus during the inter-trial intervals, the memory of the previous trials may be reduced (i.e., the P values due to the two different previous trial types are closer). As a consequence, the difference of the movement neural activity accumulating onset times and reaction times between a previously stop-signal and no-stop-signal trial may also be reduced. In the future, it would also be interesting to study quantitatively how this history-dependent mechanism is related to more optimal performance in action countermanding in a dynamic environment, e.g., in the form of maximizing overall reward rates (Shenoy et al., 2010; Wong-Lin et al., 2010; Shenoy and Yu, 2011).

Although we have explored other control mechanisms which include more realistic transient activation of the control unit via inhibitory feedback mechanism, similar neural and behavioral results can be obtained (not shown).Our simple adaptive control mechanism with minimal biological features is sufficient to readily account for both neural and behavioral data from the experiments. Before we embark on a fully fledged biological implementation of the adaptive control mechanism, it may be worth identifying more extensive neuronal recording brain areas responsible for such adaptive control/adjustment and also performance monitoring. These regions may include the supplementary eye fields, the inferior frontal gyrus and the dorsal lateral prefrontal cortex, and the anterior cingulate cortical areas (Schall, 2004). Good temporal resolution will be needed since this control module may operate transiently within a timescale of tens of milliseconds. Thus, techniques such as fMRI may ultimately not be appropriate. However, in terms of its practical applications (e.g., in neural prosthetics), our simple autonomous history-based adjustment mechanism may be able to circumvent the need to search for sources of inhibitory controls or performance monitoring; our efficient artificial control system mimic the real biological system fairly well. This may also reduce the amount of extensive surgery to be performed on motor-impaired patients, e.g., one in FEF for eye movement (or supplementary motor area for finger movement) and another in the area(s) for monitoring, control, and adjustment (e.g., prefrontal cortex).

Generalizability

Although we have focused only on modeling the FEF, our model may be generalized to other brain areas that are part of the oculomotor system such as the superior colliculus (e.g., Paré and Hanes, 2003) as their organization is quite similar. We further speculate that our model may be useful in task-switching paradigms when to switch rapidly between different tasks (due to context or rule changes), subjects typically have to first inhibit the previous “task set” through active inhibitory control of the previous motor plan or action before implementing the new one (Stuphorn et al., 2010). However, there is a limit to generalizing our current model to inhibitory control for arm movement as there is evidence that shows distinctive differences between countermanding saccadic and arm movements (Mirabella et al., 2009, 2011). In the future, it would be interesting to compare among multiple modalities (e.g. finger and saccadic eye movement) and search for common brain regions for cognitive monitoring and control in the countermanding task paradigm.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akerfelt, A., Colonius, H., and Diederich, A. (2005). Visual-tactile saccadic inhibition. Exp. Brain Res. 169, 554–563.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Armstrong, N. B., Lopes, H. S., and Erig Lima, R. C. (2007). “Reconfigurable computing for accelerating protein folding simulations,” in Proceedings of the 3rd International Conference on Reconfigurable Computing: Architectures, Tools and Applications (ARC’07), Berlin, 314–325.

Pubmed Abstract | Pubmed Full Text

Bissett, P. G., and Logan, G. D. (2011). Balancing cognitive demands: control adjustments in the stop-signal paradigm. J. Exp. Psychol. Learn. Mem. Cogn. 37, 392–404.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Boucher, L., Palmeri, T. J., Logan, G. D., and Schall, J. D. (2007). Inhibitory control in mind and brain: an interactive race model of countermanding saccades. Psychol. Rev. 114, 376–397.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chen, X., Scangos, K. W., and Stuphorn, V. (2010). Supplementary motor area exerts proactive and reactive control of arm movements. J. Neurosci. 30, 14657–14675.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chestek, C. A., Gilja, V., Nuyujukian, P., Kier, R. J., Solzbacher, F., Ryu, S. I., Harrison, R. R., and Shenoy, K. V. (2009). HermesC: low-power wireless neural recording system for freely moving primates. IEEE Trans. Neural Syst. Rehabil. Eng. 17, 330–338.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Chikazoe, J., Jimura, K., Hirose, S., Yamashita, K., Miyashita, Y., and Konishi, S. (2009). Preparation to inhibit a response complements response inhibition during performance of a stopsignal task. J. Neurosci. 29, 15870–15877.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cisek, P., Puskas, G. A., and El-Murr, S. (2009). Decisions in changing conditions: the urgency-gating model. J. Neurosci. 29, 11560–11571.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cohen, J. Y., Pouget, P., Woodman, G. F., Subraveti, C. R., Schall, J. D., and Rossi, A. F. (2007). Difficulty of visual search modulates neuronal interactions and response variability in the frontal eye field. J. Neurophysiol. 98, 2580–2587.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Curtis, C. E., Cole, M. W., Rao, V. Y., and D’Esposito, M. (2005). Canceling planned action: an FMRI study of countermanding saccades. Cereb. Cortex 15, 1281–1289.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Emeric, E. E., Brown, J. W., Boucher, L., Carpenter, R. H., and Hanes, D. P. (2007). Influence of history on saccadecountermanding performance in humans and macaque monkeys. Vision Res. 47, 35–49.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Farwell, L. A., and Donchin, E. (1988). Talking off the top of your head: toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr. Clin. Neurophysiol. 70, 510–523.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fecteau, J. H., and Munoz, D. P. (2003). Exploring the consequences of the previous trial. Nat. Rev. Neurosci. 4, 435–443.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Gao, J., Wong-Lin, K., Holmes, P., Simen, P., and Cohen, J. D. (2009). Sequential effects in two-choice reaction time tasks: decomposition and synthesis of mechanisms. Neural. Comput. 21, 2407–2436.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ghani, A., McDaid, L., Belatreche, A., Kelly, P., Hall, S., Dowrick, T., Huang, H., Marsland, J., and Smith, A. (2011). “Evaluating the training dynamics of a CMOS based synapse,” in International Joint Conference on Neural Networks, San Jose, 1–7.

Glackin, B., Harkin, J., McGinnity, T. M., and Maguire, L. P. (2009). “A hardware accelerated simulation environment for spiking neural networks, ARC ‘09,” in Proceedings of the 5th International Workshop on Reconfigurable Computing: Architectures, Tools and Applications, Karlsruhe, 336–341.

Hanes, D. P., Patterson, W. F., and Schall, J. D. (1998). The role of frontal eye field in countermanding saccades: visual, movement and fixation activity. J. Neurophysiol. 79, 817–834.

Pubmed Abstract | Pubmed Full Text

Knodel, O., Preusser, T. B., and Spallek, R. G. (2011). “Next-generation massively parallel short-read mapping on FPGAs 2011,” in IEEE International Conference on Application-Specific Systems, Architectures and Processors (ASAP), Santa Monica, 195–201.

Koo, J. J., Evans, A. C., and Gross, W. J. (2009). 3-D Brain MRI tissue classification on FPGAs. IEEE Trans. Image Process 18, 2735–2746.

Pubmed Abstract | Pubmed Full Text

Lappin, J. S., and Eriksen, C. W. (1966). Use of a delayed signal to stop a visual reaction-time response. J. Exp. Psychol. 72, 803–811.

CrossRef Full Text

Lo, C. C., Boucher, L., Paré, M., Schall, J. D., and Wang, X. J. (2009). Proactive inhibitory control and attractor dynamics in countermanding action: a spiking neural circuit model. J. Neurosci. 29, 9059–9071.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Logan, G. D. (1981). “Attention, automaticity, and the ability to stop a speeded choice response,” in Attention and Performance IX, eds J. Long and A. Baddeley (Hillsdale, NJ: Erlbaum), 205–222.

Logan, G. D., and Cowan, W. B. (1984). On the ability to inhibit thought and action. A theory of an act of control. Psychol. Rev. 91, 295–327.

CrossRef Full Text

Logan, G. D., and Gordon, R. D. (2001). Executive control of visual attention in dual-task situations. Psychol. Rev. 108, 393–434.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Maguire, L. P., McGinnity, T. M., Glackin, B., Ghani, A., Belatreche, A., and Harkin, J. (2007). Challenges for large-scale implementations of spiking neural networks on FPGAs. Neurocomputing 71, 13–29.

CrossRef Full Text

Mathworks Inc. (2011). MATLAB Version 7.12.0. Natick, MA: The MathWorks Inc.

Mirabella, G., Pani, P., and Ferraina, S. (2009). The presence of visual gap affects the duration of stopping process. Exp. Brain Res. 192, 199–209.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mirabella, G., Pani, P., and Ferraina, S. (2011). Neural correlates of cognitive control of reaching movements in the dorsal premotor cortex of rhesus monkeys. J. Neurophysiol. 106, 1454–1466.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Murthy, A., Thompson, K. G., and Schall, J. D. (2001). Dynamic dissociation of visual selection from saccade programming in frontal eye field. J. Neurophysiol. 86, 2634–2637.

Pubmed Abstract | Pubmed Full Text

Niyogi, R., and Wong-Lin, K. F. (2010). “Time-varying gain modulation on neural circuit dynamics and performance in perceptual decisions, Abstract #246,” in Computational and Systems Neuroscience 2010, Salt Lake City, UT.

Paré, M., and Hanes, D. P. (2003). Controlled movement processing: superior colliculus activity associated with countermanded saccades. J. Neurosci. 23, 6480–6489.

Pubmed Abstract | Pubmed Full Text

Perrin, X., Chavarriaga, R., Colas, F., Siegwart, R., and Millán, J. R. (2010). Brain-coupled interaction for semi-autonomous navigation of an assistive robot. Rob. Auton. Syst. 58, 1246–1255.

CrossRef Full Text

Pouget, P., Logan, G. D., Palmeri, T. J., Boucher, L., Pare, M., and Schall, J. D. (2011). Neural basis of adaptive response time adjustment during saccade countermanding. J. Neurosci. 31, 12604–12612.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sato, T., and Schall, J. D. (2003). Effects of stimulus-response compatibility on neural selection in frontal eye field. Neuron 38, 637–648.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schall, J. D. (2004). On building a bridge between brain and behaviour. Annu. Rev. Psychol. 55, 23–50.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schall, J. D., Purcell, B. A., Heitz, R. P., Logan, G. D., and Palmeri, T. J. (2011). Neural mechanisms of saccade target selection: gated accumulator model of the visual–motor cascade. Eur. J. Neurosci. 33, 1991–2002.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schall, J. D., Sato, T. R., Thompson, K. G., Vaughn, A. A., and Juan, C. H. (2004). Effects of search efficiency on surround suppression during visual selection in frontal eye field. J. Neurophysiol. 91, 2765–2769.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schall, J. D., Stuphorn, V., and Brown, J. W. (2002). Monitoring and control of action by the frontal lobes. Neuron 36, 309–322.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Schwartz, A. B. (2004). Cortical neural prosthetics. Annu. Rev. Neurosci. 27, 487–507.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Shenoy, P., Rao, R., and Yu, A. J. (2010). “A rational decision making framework for inhibitory control,” in Advances in Neural Information Processing Systems, Vol. 23 (Cambridge: MIT Press), 2146–2154.

Shenoy, P., and Yu, A. J. (2011). Rational decision-making in inhibitory control. Front. Hum. Neurosci. 5:48. doi:10.3389/fnhum.2011.00048

CrossRef Full Text

Standage, D., You, H., Wang, D. H., and Dorris, M. C. (2011). Gain modulation by an urgency signal controls the speed-accuracy trade-off in a network model of a cortical decision circuit. Front. Comput. Neurosci. 5:7. doi:10.3389/fncom.2011.00007

CrossRef Full Text

Stuphorn, V., Brown, J. W., and Schall, J. D. (2010). Role of supplementary eye field in saccade initiation: executive, not direct, control. J. Neurophysiol. 103, 801–816.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sugrue, L. P., Corrado, G. S., and Newsome, W. T. (2004). Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wang, X.-J. (2001). Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 24, 455–463.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wong, K.-F., Eckhoff, P., Holmes, P., and Cohen, J. D. (2007). Analysis of a biologically realistic model for saccade-countermanding tasks. Soc. Neurosci., abstr. 719.

Wong, K.-F., and Wang, X.-J. (2006). A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci. 26, 1314–1328.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wong-Lin, K., Eckhoff, P., Holmes, P., and Cohen, J. D. (2010). Optimal performance in a countermanding saccade task. Brain Res. 1318, 178–187.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xilinx Inc. (2011a). Getting Started with the Xilinx Virtex-6 FPGA ML605 Evaluation Kit UG533 (V. 1.5), San Jose. Available at: http://www.Xilinx.com

Xilinx Inc. (2011b). System Generator for DSP User Guide UG640 (V. 13.1), San Jose. Available at: http://www.Xilinx.com

Xilinx Inc. (2011c). ML605 Reference Design User Guide UG535 (V. 1.0), San Jose. Available at: http://www.Xilinx.com

Yang, S., and McGinnity, T. M. (2011). “A biologically plausible real-time spiking neuron simulation environment based on a multiple-FPGA platform,” in ACM SIGARTH Computer Architecture News, London, 39, 78–81.

Appendix

The system generator diagrams for implementing the FEF module and the control module are shown in Figure A1.

The following describes our architecture using a Xilinx ML605 evaluation board equipped with an XC6VLX240T FPGA with speedgrade-1 and package FF1156 (Xilinx Inc., 2011c).

FIGURE A1

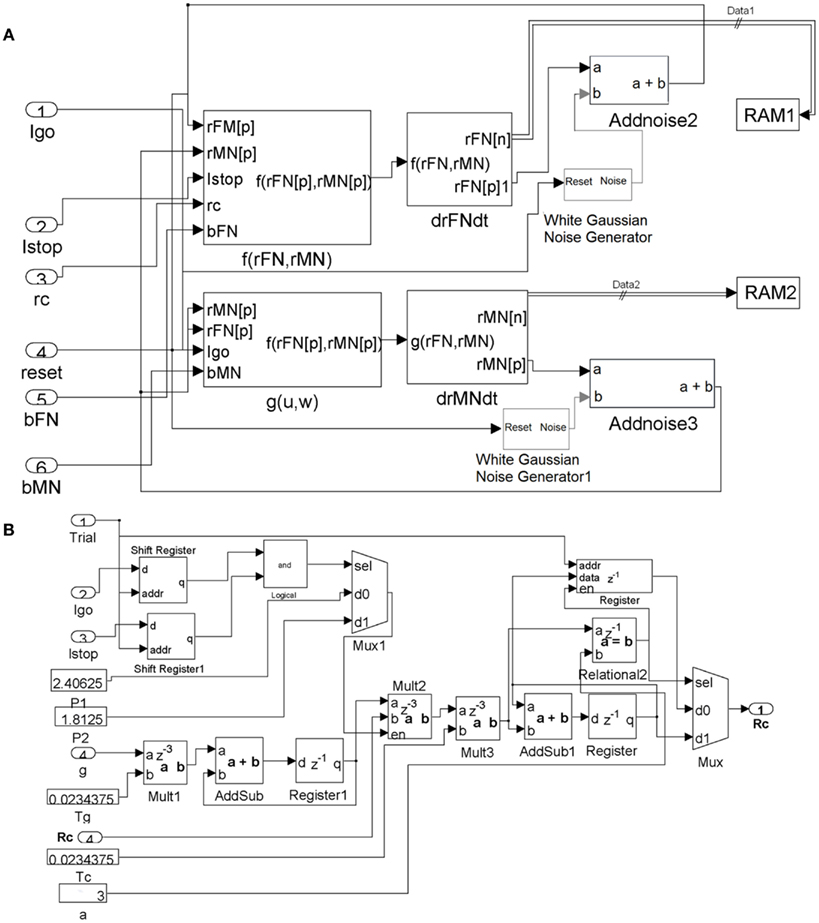
Figure A1. (A) System Generator diagram of the FEF module. Data ports for the subsystems are the numbered oval blocks. Delays through the system are expressed in the z domain where the superscript is the latency in cycles from output back to input. The resulting data (rFM and rMN) are continuously stored back in RAM, via the RAM1 and RAM2 connections. (B) System Generator diagram of the adaptive control module.

FIGURE A2

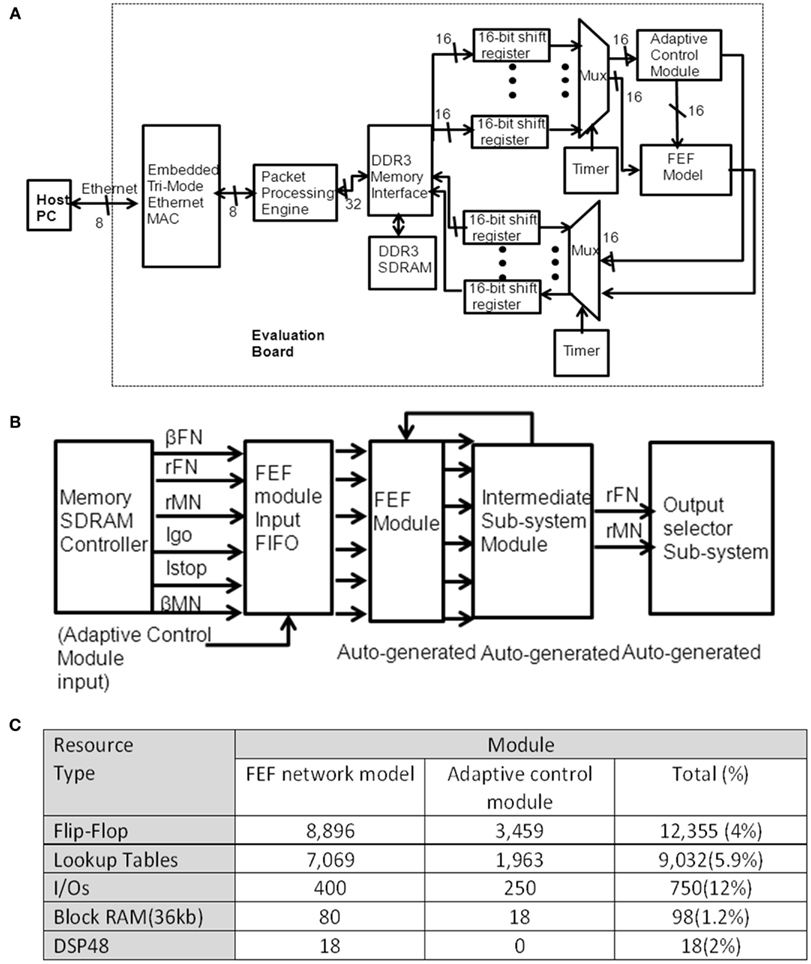
Figure A2. (A) illustrates a top-level structure of the inhibitory control prototyping system. Our prototype design includes common functions for Ethernet interface, external memory interface, adaptive control, and FEF module. The Ethernet interface includes an on-chip MAC module and a packet processing engine. Every packet is sent or received using the packet processing engine. A DDR3 memory block is used to store both the simulation setup (stimuli) and simulation results locally on a FPGA device. The stored stimuli are read from DDR3 SDRAM. The outputs are stored back into a DDR3 memory bank. The control activity (rc) is an input from the adaptive control subsystem module. With the programmable timer, all the tasks in a trial are guaranteed to complete before the next trial starts. (B) Illustrates a top-layer diagram of the FPGA design of the FEF module. After circuit reset, the data are read from SDRAM into the FEF module’s input FIFO. The design of movement and fixation neural populations in the FEF module is generated by System Generator. The circuitry to implement the adaptive control model includes the memory interface (using similar modules to the FEF module design) and the adaptive function (as descripted in Eqs 4 and 5). (C) Summarizes the resource usage for the whole design. We divided the design into two modules in order to analysis the adaptive control resource usage, which will be useful for considering a potential future Application Specific Integrated Circuit (ASIC) design. The first column shows the type of hardware resources. The second column shows the number of the specified logical resource used. The third column shows the total number of logical resource usage and utilization. The extra usage of DSP is due to the small amount of arithmetic logic utilized.