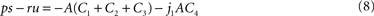Food availability is on the rise in many countries (
Popkin, 2006
). In parallel with this the epidemic of obesity and type 2 diabetes is spreading (
Caballero, 2007
;
Wild et al., 2004
). A few theoretical frameworks have been set up to derive the possible determinative cause of obesity. A first concept some experts agree upon is that “the current epidemic of obesity is caused largely by an environment that promotes excessive food intake” (
Hill and Peters, 1998
). According to this, an external environment offering abundant energy determines the energy uptake into the human organism, in other words, the energy appears to be “pushed” into the body. However, there is doubt about such a pure “push”-concept, because in the countries with food abundance there are still many people who are able to maintain their normal body weight.
A second widely held concept is that the human organism rather “pulls” food from the environment governed by signals reflecting its internal milieu. The “lipostatic theory” for example, established by
Kennedy (1953)
, describes the fat deposition feedback system. According to that theory, the hypothalamus regulates food intake by signals originating in the body in order to keep the fat depots constant. In the same year,
Mayer (1953)
presented the glucostatic theory which describes the blood glucose feedback system. According to that theory, the hypothalamus controls food intake via receptors that measure glucose concentrations in the blood in order to keep blood glucose concentrations constant. Interestingly, Mayer already made attempts to take the brain with its high energy consumption into consideration. However, he implicitly made the assumption that the body-to-brain energy flux was a passive process that was only determined by the available blood glucose. The lipostatic theory, which received a boost by the discovery of leptin in 1994, as well as the glucostatic theory and its moderate revisions remained the basis of obesity and diabetes research for more than 50 years (
Campfield and Smith, 2003
;
Flier and Maratos-Flier, 2005
). There are, however, still open questions with these pure “pull” concepts, since they cannot explain for example why all these people who carry the burden of their large fat depots and their high blood glucose eat at all.
The third and novel concept we would like to present in this paper might be quite surprising at first sight: A healthy organism maintaining its state of systemic energy homeostasis, i.e. that of balanced cerebral and peripheral metabolism, relies on properly functioning brain-pull mechanisms. In contrast, if the brain lets glucose enter muscle and adipose tissue too easily, it needs more effort to get glucose from the blood, and it tends to compensate for that deficit by increasing ingestive behaviour. A little further on we will describe the energy supply of the brain as a “supply chain”. According to this concept, it is a “competent brain-pull” that guarantees systemic energy homeostasis, and it is an “incompetent brain-pull”, i.e. the inability of the brain to properly demand glucose from the body, that causes obesity. In this supply chain, incompetent brain-pull leads to a disturbance of the glucose flux to the brain – resembling a “bottleneck” – and obesity and type 2 diabetes can be regarded as build-ups. This explanation might be less surprising, if one takes into account that recent experimental evidence suggests the pull principle to constitute a natural process in neurometabolism (
Pellerin and Magistretti, 1994
). The postulate of a brain-pull mechanism is directly derived from the “Selfish Brain” theory (
Peters et al., 2004
,
2007b
), which unifies research fields of cerebral and peripheral energy metabolism. After having obtained experimental key results supporting the axioms of this theory previously (
Oltmanns et al., 2008
;
Peters et al., 2007a
;
Schweiger et al., 2008
;
Steinkamp et al., 2007
), the current paper aims to expand the theory’s scope of validity with respect to the indispensability and susceptibility of brain-pull mechanisms for the maintenance of systemic energy homeostasis. Against this background, we hypothesize that under conditions of food abundance incompetent brain-pull is required for the development of obesity and type 2 diabetes.
In the current paper, we also aim to clarify whether such brain-pull mechanisms are necessary at all. Therefore, we analysed energy allocation within the human organism under conditions of food deficiency. The human brain consumes 20% of the total energy (or oxygen) that is available within the organism (
Kety, 1957
;
Kety and Schmidt, 1948
). Particularly, it consumes large amounts of glucose, i.e. more than 130 g per day (
Reinmuth et al., 1965
). Given a glucose ingestion of 200 g per day in a man of normal weight and height, the brain would take up approximately 65% of that total amount ingested. The central nervous system is separated by the blood–brain barrier (BBB) from the general circulation and thus constitutes a distinct entity. The amount of glucose that crosses the blood–brain barrier varies with the behavioural state, i.e. it decreases during deep sleep and increases with a mental challenge (
Boyle et al., 1994b
;
Madsen et al., 1995
). There is general agreement among clinicians and scientists that a continuous supply of brain fuel is mandatory for survival. Therefore, we also hypothesize that during food shortages a competent brain-pull mechanism is indispensable for maintaining cerebral homeostasis.
In order to work on both of these hypotheses, we firstly designed a brain-supply-chain model (Figure
1
). Because the brain has been shown to be the organ that consumes the largest share of glucose in the organism, we have regarded it as the final consumer in this model. Energy from the remote environment is brought to the immediate environment, it is then taken up by the body (into the blood stream), and from there approximately 2/3 of the circulating glucose enters in the brain. Supply chains in industrial production processes display striking similarities to the glucose pathway from the environment through the body towards the brain. In the field of logistics such supply chains have been extensively studied. Over the decades, a number of basic principles have been formulated and elaborated (
Slack et al., 2004
). The so-called “push”-principle operates according to the following rule: The supplier delivers material and in so doing determines the activity of a production step. In contrast, the so-called “pull”-principle works in the following manner: The material required for a production step is provided only when the receiver needs it (just-in-time). In comparison with the “push”-principle the “pull”-principle offers clear economic advantages; with the latter there are short set-up times and only small (economically optimized) storage sites. Many modern industrial branches have recognized that pull components are particularly efficient. While designing our brain-supply-chain model we referred to the basic principles of general supply chains.
Figure 1. General supply chain of the human brain. Energy from the remote environment is brought to the immediate environment, it is then taken up by the body, and from there a large part of it enters the brain. In a general supply chain, the flux of energy can principally be determined by the supplier (previous step) or by the receiver (proximate step). The share of the flux which is determined by the supplier is called the “push component” (blue arrows), the share which is determined by the receiver is called the “pull component” (black arrows). The glucostatic and lipostatic theory cover a particular section (gray area) within the extended supply chain of the brain. A principle is adherent to general supply chains: The flow of goods (energy) is directed antegrade (towards the final consumer), but in case of an interruption at some point, the disturbance propagates retrograde, in the opposite direction, i.e. away from the consumer. In this way, build-ups can develop in front of the “bottleneck.”
To test our hypotheses, we secondly took advantage of the experience of mathematicians who have refined their methods to describe and optimize supply chains and supply networks (including side buffers) (
Langemann, 2007
). We applied the mathematical methods used in supply-chain modelling to the energetic supply chain of the living organism. These tools allowed us to include both push and pull components at all levels of the supply chain of the brain, in contrast to the widely used aforementioned pure “push” and pure “pull” concepts.
Thirdly, we tested our hypotheses by comparing experimental data sets with the predictions of our brain-supply-chain model. From among the many experiments we and other researchers have performed on energy metabolism we particularly selected crucial data sets that we expected to challenge our and others’ theoretical concepts.
Fourthly, we carried out a hypothesis cross-check. In order to do this we derived the alternative hypotheses from the pure “push” and pure “pull” concepts and tested them by comparing the same experimental data sets with the predictions of these alternative models. In the frame of our investigation, we uncovered contradictions between the alternative hypotheses, e.g. those derived from the generally accepted lipostatic theory and the widely held but occasionally doubted glucostatic theory, and the experimental data obtained by our and other research groups. On the contrary, we can show that the tested data sets support our hypotheses that brain-pull mechanisms are vital, and if they do not function properly, cause peripheral metabolic disease.
Mathematical Model
The model deals with abstract energy contents in the compartments environment, blood, brain, and fat/muscle and with abstract activation degrees of allocative brain-pull and ingestive pull. These elements are linked by energy fluxes and signalling pathways. We focus on long-term developments so that the energy levels are mean levels without any diurnal rhythms. The energy occurs in various substantial forms in the respective compartments such as alimentary products and food in the environment, glucose in the blood, ATP in the brain, and lipids in the fat/muscle compartment. The abstract energy content denotes the total energy in the compartment, which is accessible for being metabolised. The fluxes follow the continuity equation and the law of energy conservation, respectively.
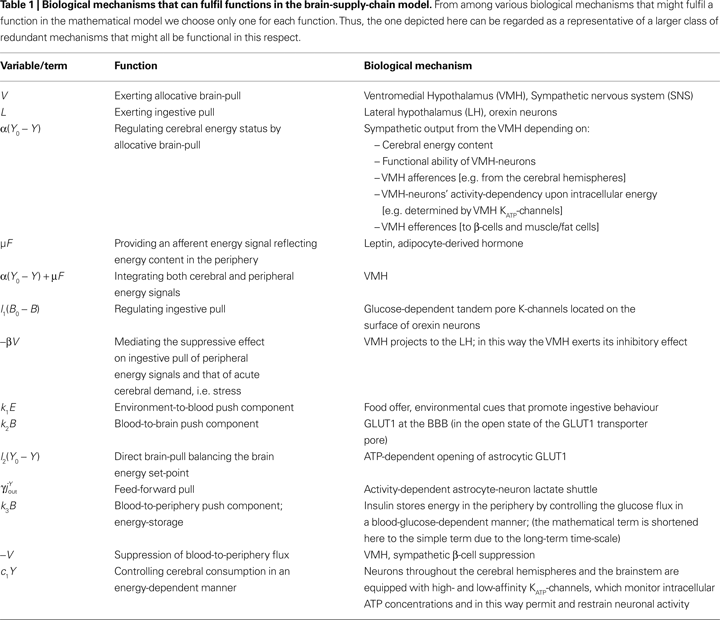
We focus on investigating the behaviour of the mathematical model. In particular, we are interested in those properties, which are independent of the specific choice of parameters. These general model properties will be conserved in any physiological reasonable parameter choice. They will generate the first steps into an integrative understanding of human metabolism. This is the reason for the restriction to those mechanisms regarded as the ones that will best fulfil the function in the model and which are selected as discussed in the chapter “biological correlates of pull mechanisms” (Discussion section). While describing the mathematical model, we denote each specific function in the model and assign to it one of the biological mechanisms, which have already been experimentally identified (Table
1
). Since we are looking for a qualitative understanding, we only use linear dependencies as small deviations from an equilibrium. Linear relations are the simplest representatives in the class of all relations with a given monotonicity behaviour, and they can be regarded as linearization of more detailed relations near the steady state.
The energy content in the environment is termed
E, the one in the blood
B, the one in the brain
Y, and the energy content in the fat/muscle compartment
F (Figure
2
). The energy content in the blood is proportional to the energy concentration in the blood, whereas the size of the fat/muscle compartment may vary. The flux from the environment into the blood is termed
jEB, the flux from the blood into the brain
jBY and the flux from the blood into the fat
jBF. Furthermore, we also assume that the nearby environment is supplied by an abundant remote environment via the flux
jin. The consumption of the brain is denoted
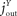
, and the consumption of the fat/muscle compartment
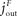
.
Figure 2. Flow-chart of the brain-supply-chain model. The graphical representation of the mathematical supply-chain model displays the branching of the energy flow between the brain and the side buffer, i.e. the fat/muscle compartment. In the “Discussion” section we will refer to experiments identifying distinct biological mechanisms that can fulfil specific pull-functions in the model. In short, the mechanisms are organized to satisfy the needs of the respective compartment: Firstly, upon the fall of astrocytic ATP concentrations, e.g. due to neuronal excitation, astrocytes use direct brain-pull mechanisms. Secondly, upon a fall of ATP concentrations in the brain, the allocative brain-pull mechanisms are activated (via red dotted arrow). The core of these mechanisms is represented by the ventromedial hypothalamus (VMH) and the sympatho-adrenal system (SNS), which inhibits peripheral glucose uptake in order to enhanced the supply of the brain. Thirdly, upon a fall of the blood glucose concentration, ingestive pull mechanisms in the lateral hypothalamus (LH) are initiated, i.e. food is taken up. Fourthly, upon energy deprivation in the peripheral buffers, the fall of leptin also promotes ingestive behaviour (via green dotted arrow) and prepares peripheral glucose uptake. When blood glucose concentrations rise after food intake, insulin functions as an energy-storage hormone and mediates a push-mechanism, which drives glucose in a glucose-dependent manner from blood to fat/muscle. Fifthly, upon recognition of food deprivation in the immediate vicinity, foraging pull mechanisms are initiated for locomotion and orientation.
The energy balance connects the time derivatives of energy levels with the sum of inflow and outflow in every compartment, and the continuity equation simply reads as

The fluxes at the interfaces of the model are determined by the following three assumptions. Firstly, the inflow
jin is assumed to be proportional to an energy deficit in the near environment, i.e. it acts compensatory with respect to an energy set-point
E0, the proportionality factor is called
lin. Different cases of food abundance are modelled by different proportionality factors describing different difficulties in food acquisition. That means, that an abundant food offer is modelled by a large factor
lin, and small deficits in the energy content of the near environment suffice to result in a large inflow. On the other hand, a small factor
lin produces the situation that a larger energy deficit in the environment only organizes the necessary energy inflow. Consequently, the environmental compartment is properly filled in the case of an abundant food offer, and it is emptied with a restricted food offer. Hence, the energy content
E shows the wealth of the food offer (cf Figures
3 and
4
). Secondly, the cerebral energy consumption
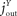
is essentially related to the degree of neuronal activity, which depends on the level of neuronal stimulation
c1 and the available cerebral energy
Y required for that process. Thus, the cerebral consumption is supposed to increase in an affine manner with the cerebral energy content (for biological mechanisms that fulfil the function of controlling neuronal consumption in an energy-dependent manner see Table
1
). As observed the energy content in the brain is nearly constant, and we will see that the model reproduces this property although the brain energy content is even not mathematically fixed. Thirdly, the energy consumption of the fat/muscle compartment is differentiated into a constant maintenance
j0 and a component proportional to its size. Hence, we find
Figure 3. The effect of brain-pull efficiency on the maintenance of cerebral homeostasis under the condition of food restriction in a “supply chain” simulation study. The model is non-dimensional; time is denoted as t. In model 1 (bold line), there is an efficient brain-pull component, in model 2 (thin line) the brain-pull component is inefficient. For both models, the nutritional availability in the environment is set to be restricted from a certain time point onwards. In model 1, the supply-chain model predicts a fall of the blood glucose concentration and a decrease of the energy content in the fat/muscle compartment. The energy content in the brain is only marginally reduced, i.e. energetic brain homeostasis is maintained. In model 2, however, the model predicts a considerable disturbance of the brain energy homeostasis. Besides, the energy uptake from the environment is smaller in model 1 than in model 2, indicating a more economic utilisation of the food offer.
Figure 4. The effect of brain-pull inefficiency on the development of obesity and diabetes under the condition of food abundance in a “supply chain” simulation study. In both cases, the food offer in the environment is set to be abundant. In case 1 (dashed line; large α) there is an efficient allocative brain-pull mechanism present, in case 2 (bold line; small α) this brain-pull mechanism is inefficient from a certain moment onwards (indicated by the arrow). In case 1, with normal allocative brain-pull, the model predicts stably normal energy content in blood, muscle, fat, and brain. In case 2, with a disrupted ATP-dependency of the allocative brain-pull mechanisms, the model predicts accumulation of energy in the fat and muscle stores and also an accumulation of energy in the blood vessels, i.e. hyperglycaemia. Despite all these changes in case 2, the model predicts the maintenance of cerebral homeostasis. Bottom left: Peripheral glucose uptake jBF/F decreases in the long-term – a phenomenon commonly referred to as “insulin resistance”. Bottom right: Increasing fat compartment with decreasing brain-pull efficiency (α).
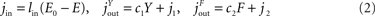
Here, linear and affine relations are used. They are the simplest representatives in the class of all relations with a given monotonicity behaviour, and they can be regarded as linearization of more detailed relations near the equilibrium point.
Signals from the compartments brain
Y, fat/muscle
F, and blood
B are integrated in order to regulate fluxes by allocation and ingestion. The allocative brain-pull mechanism is denoted
V (for biological mechanisms that fulfil allocative brain-pull function see Table
1
). The ingestive pull mechanism is termed
L (for mechanisms that fulfil ingestive pull function see Table
1
).
V is activated by an energy deficiency below a set-point
Y0 in the brain (α denotes the allocative brain-pull efficiency) and by an afferent energy signal reflecting energy content in fat/muscle (for cerebral and peripheral mechanisms that fulfil the function of regulating allocative brain-pull see Table
1
). Of note,
V integrates both cerebral and peripheral energy signals in order to exert allocative brain-pull function (for mechanisms that fulfil integrative function see Table
1
).
L is increased by a deficiency in blood glucose below a set-point
B0 and
L is diminished by
V (for mechanisms that fulfil the function of regulating ingestive pull see Table
1
). As such we have the activation equations
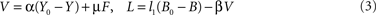
Again, the relations are linear due to the same argument as in Eq. 2, e.g. a non-linear relation V = V(Y, F), which contains possibly a detailed physiological relation, can be linearized to V(Y, F) = V(F1, Y1) + (F – F1) VF(F1, Y1) + (Y – Y1) VY(F1, Y1) with α = −VY and μ = VF, which leads to Eq. 3. Similarly, all linear relations can be assumed to be valid with suitable parameters in a near environment of a stationary solution.
The fluxes between the compartments are determined both by push and pull components. The flux from the environment into the blood is governed by a push component (mechanisms fulfilling environmental push function see Table
1
) depending on
E and by the ingestive pull component
L. Hence, we have
The flux from the blood into the brain consists of a push component from the blood (mechanism that fulfils the function of a blood-to-brain push component see Table
1
), a direct pull balancing the brain energy set-point (direct brain-pull see Table
1
) and a feed-forward pull (see Table
1
) that directs a proportion of the brain need
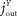
from the blood to the brain. Thus, we get
with γ < 1.
The flux from the blood into the fat/muscle compartment also depends on two components. Firstly, the blood-to-periphery flux is increased by a push component from the blood (for a mechanism that fulfils the function of a blood-to-periphery push component see Table
1
) and secondly the blood-to-periphery flux is diminished by
V (Table
1
). That yields

We resume that the Eqs 1–6 form a system of linear ordinary differential equations for the energy levels
E,
B,
Y,
F in the four compartments environment, blood, brain and muscle/fat. The model contains the most general description of the fluxes given in Figure
2
. We have the parameters
k1,
k2,
k3 of the push-components, the pull parameters
l1,
l2,
lin, the consumption parameters
c1,
c2,
j0 and the action of hormones and cerebral control centres α, β, μ as well as the proportion γ < 1, which is the only additional restriction, because all 13 parameters are arbitrarily non-negative. Thus, the model contains all functions discussed above and depicted in Figure
2
. In all, this is the complete model we used as a basis for the simulations, the hypothesis-testing, and the analytical proof reported in this paper.
We will present a consideration in the “Results” section, cf. analytical proof, that demonstrates the conservation of the qualitative model behaviour for all feasible parameter choices. The set of possible parameters is restricted by a few constraints, which excludes obviously non-physiological parameters. Nevertheless, in order to illustrate the behaviour of the model certain parameters are chosen for the example calculation. We choose the example parameter by starting from the relation of the fluxes to each other, e.g. the flux
jEB from the near environment to the blood is decomposed by the push component
k1E, the pull component
l1(
B0 −
B) and the inhibiting influence of the allocative brain-pull −β
V. In the equilibrium, we assume
k1E :
l1(
B0 −
B) : (−β
V) = 40 : 120 : (−40), so that the sum of the sub-fluxes is 100. The pull mechanism originated by the blood is assumed to be dominant in the model, i.e. the ingestive behaviour is mainly governed by a deficit in the blood glucose. Similarly, the flux
jBY is decomposed by
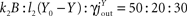
in the equilibrium. Next the flux
jBF is decomposed by
k3B : [−α(
Y0 −
Y)] : (−μ
F) = 120 : (−15) : (−5), where the second term and the third term are inhibitory. Here, the insulin-mediated influence of the blood is dominant. The inflow in the equilibrium is set to
jin = 200, and the outflow of the brain and the fat/muscle compartment is
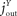
=
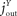
= 100, always in the equilibrium. All these values and relations are variable in the simulation of time-dependent developments. Furthermore, we set the values
E0 = 100,
B0 = 1000 and the stationary values
E* = 50,
B* = 90,
F* = 100 and
Y* = 100. The high set-point for the blood glucose codes the position that the blood is nearly always pulling, even in diabetic ketoacidosis or hyperglycaemic hyperosmolar state, when the blood glucose concentrations are extremely elevated. These choices result in the example parameters
lin = 4,
k1 = 1.6,
k2 = 0.556,
k3 = 1.333,
l1 = 0.264,
l2 = 20, μ = 0.05,
c1 = 1,
c2 = 1, α = 15, β = 6, γ = 0.3,
j1 = 0,
j2 = 50. Let us mention that we will prove the asserted qualitative behaviour for a wide range of parameters in the “Results” section, analytical proof. A scaling of parameter like e.g. a change of
c1 corresponds to a scaling of the measure units of the energy contents
Y. In all, we can regard the model as non-dimensional. Yet, some of the values might remind to realistic values like the blood glucose of 90 in the equilibrium could be imagined as 90 mg/dl, and the inflow of 200 can be interpreted as an daily intake of 200 g glucose, cf. above.
The differential equations in Eq. 1 with the constitutive equations in Eqs 2–6 are non-stiff equations with respect to the regarded time-scales without diurnal cycling. Thus, they can be integrated with standard explicit methods like the Dormand–Prince method with step-size control (
Hairer et al., 1993
) or comparable ones. The accuracy of the integration is tested by the estimation of the occurring errors and checking different error bounds and bounds of the step-sizes.
Hypothesis A: During Food Shortages, A “Competent Brain-Pull” is Required to Maintain Cerebral Energy Homeostasis
Data-based testing
To test “hypothesis A” we compared the predictions of a supply-chain model with medical observations. The pathological study of
Krieger (1921)
, scholar of one of the pioneers of pathology Robert Rössle, provides a valuable basis for analyzing chronic energy allocation within the human organism. She reported with her data set that in the state of inanition all the organs like the heart, the liver, the pancreas, and the kidney lost approximately 40% of their mass, while the brain mass hardly changed (less than 2%). Inanition in these cases was due to malnutrition, cancer, and chronic infection. The autopsy material was partly provided by the exceptional circumstances which went along with world war I, making this experiment difficult to reproduce. So far, her observation could consistently be confirmed by many researchers, who used state-of-the-art technologies and examined humans and animals in adult (
Goodman et al., 1984
;
Muhlau et al., 2007
) or in fetal life (
Gong et al., 1998
;
Kind et al., 2005
;
Miller et al., 2002
). Therefore, Marie Krieger’s experiment can be regarded to represent a larger class of crucial experiments, demonstrating the brain’s priority in energy metabolism.
To re-evaluate this data set we used our mathematical model of the brain-supply chain. We assume that there is an efficient brain-pull component present (Figure
3
; model 1). For the conditions of caloric restriction, we solved the differential equations and compared the solutions with the above-mentioned medical observations. The brain-supply-chain model predicted a considerable decline in the body energy content and a stable maintained brain energy content (Figure
3
). This prediction is in agreement with medical observations (
Krieger, 1921
).
For cross-checking, we derived the alternative hypothesis from the aforementioned concepts, the gluco- and lipostatic theory, which do not consider the brain as distinct. According to these previous concepts, a brain-pull mechanism is dispensable for the maintenance of cerebral energy homeostasis under conditions of food deprivation. This alternative hypothesis is the negation “hypothesis A”. To test this alternative hypothesis we used model 2, which is essentially identical to model 1, except that it differs in the one parameter (α), which determines the efficiency of the brain-pull. The assumption of an inefficient brain-pull component (model 2; small α) led to the prediction that parallel with the decline in body energy content there is a concomitant decrease in the brain energy content (Figure
3
). Since the prediction of the latter model failed to fit the medical data (
Krieger, 1921
), the alternative “hypothesis A” should be rejected. Strikingly, high neuronal energy consumption is not enough to maintain cerebral energy homeostasis, since model 2 assumes such high consumption, but still fails to fit Krieger’s data set.
Noteworthy, both models 1 and 2 appear to be in agreement with the majority of experimental data sets on energy metabolism that have been performed in animals and humans yet. The problem that one experimental data set can be in agreement with two distinct theoretical approaches has often prompted a scientific debate. In many instances, few crucial experimental data sets are available, which can be explained by either one or the other of two distinct theoretical approaches. This dilemma is referred to as the “inverse problem” (
Tarantola, 2005
). Therefore, we especially aimed at finding and generating crucial data sets like the one of Krieger, e.g. (
Boyle et al., 1994a
,
1995
;
Gong et al., 1998
;
Goodman et al., 1984
;
Kind et al., 2005
;
Miller et al., 2002
;
Muhlau et al., 2007
;
Oltmanns et al., 2008
), which are likely to be consistent with only one of the two models 1 and 2. Actually, these listed citations refer to data sets, which in addition to the one of Krieger turn out to be contradictory to model 2, which lacks a strong brain-pull mechanism. Our results demonstrate that the Krieger data set is consistent with model 1, but not with model 2. Thus, we regard the scope of validity of model 1 to be larger (at least by one study) than that of model 2. In conclusion, the comparison between theoretical predictions of our supply-chain model and the experimental data supports our “hypothesis A” stating that brain-pull is a necessary component for the maintenance of cerebral homeostasis.
Hypothesis B: During Food Abundance, An “Incompetent Brain-Pull” is Required for the Development of Obesity
Data-based testing
In order to test “hypothesis B” we begin with referring to two animal experiments from recent neurobiological obesity research. First, Barry E. Levin and co-workers investigated diet-resistant animals and compared them to animals prone to develop diet-induced obesity on a high energy diet (
Tkacs and Levin, 2004
). With this data set, the researchers showed that the diet-resistant animals were distinguished by their particularly efficient responses of the sympathetic nervous system. Secondly, Susumu Seino and co-workers showed the complete absence of both functional K
ATP-channels and glucose responsiveness in the neurons of the ventromedial hypothalamus (VMH) in
Kir6.2−/− mice (
Miki et al., 2001
). These knock-out animals exhibited inappropriate responses in plasma epinephrine and glucagon during insulin challenge tests.
Next we used our brain-supply-chain model to investigate two cases which we consider to correspond to the respective data sets. In case 1, we used a model-parameter (large α), which represents efficient allocative brain-pull mechanisms; in case 2 this parameter is decreased from a certain time point onwards (small α), representing an inefficient brain-pull mechanism (Figure
4
). In the “Discussion” section we will refer to experiments, which identify among others two biological mechanism: first the sympathetic response to a given energy cerebral state, which fulfils the function of the term α(
Y0 −
Y), (i.e. regulating cerebral energy status by allocative brain-pull), and second the K
ATP-channel coupling neuronal ATP status with neuronal activity, which fulfils the function of the model-parameter α (i.e. efficiency of generating allocative brain-pull; see also Table
1
). Therefore, we regard case 1 as the mathematical correspondence to the diet-resistant animals studied by Barry Levin’s group, which are characterized by their strong sympatho-adrenal response, and case 2 as that of the VMH knock-out animals studied by Seino’s group, which are characterized by a disruption between their sympatho-adrenal response and their cerebral ATP-concentrations.
The assumption of an
efficient allocative brain-pull mechanism (case 1) led to the prediction that the brain energy content, blood glucose concentrations, and body store content remain stably normal (Figure
4
). This prediction is consistent with the observation that diet-resistant animals, which characteristically displayed the properly functioning allocative brain-pull mechanism, maintained their normal body mass even if they had unrestricted access to a high fat diet (
Tkacs and Levin, 2004
).
With the assumption of an
inefficient allocative brain-pull due to a disruption of the ATP-dependency of the VMH (case 2), the model predicted a preserved stability of the brain energy content, but a perturbation in the body: a build-up in the supply chain, which arises from the accumulation of energy in the fat/muscle compartment. In fact, when the phenotype of these
Kir6.2−/− mice has been assessed in a subsequent large study, obesity was found (
Kanezaki et al., 2004
). The obesity observed in animals lacking K
ATP-channels in the VMH was not excessive, which is not surprising given that they also lacked K
ATP-channels in the pancreatic β-cells. Thus, the animals did not have a sensitive insulin push-component, which drives glucose in a concentration-dependent manner from blood to fat/muscle. This insulin push-component favours energy accumulation in the buffer stores, as is evidenced by further experiments in which
Kir6.2−/− mice were crossbred with mice that exhibited disruptions in the insulin-mediated metabolic pathways. Our model predicts that ATP-independency of VMH neurons alone leads to obesity, while ATP-independency of both VMH neurons and β-cells leads to a less severe form of obesity – as is shown in the experiments (
Kanezaki et al., 2004
).
Modelling of case 2 predicted an additional build-up in the supply chain, which arises from the accumulation of energy in the vascular system. Such an energy build-up manifests in form of elevated blood glucose concentrations, and depending on the severity of hyperglycaemia the emerging pathological condition is termed either pre-diabetes or diabetes (
American Diabetes Association, 2008
). Of note, modelling of case 2 also predicted a long-term suppression of peripheral glucose uptake as indicated by a reduced amount of glucose flowing into the fat/muscle compartment per time unit and per weight unit fat/muscle-tissue (Figure
4
, panel bottom left). Such a predicted suppression of peripheral glucose uptake due to an inefficient brain-pull, is phenotypically in accordance with what former concepts on the pathogenesis of diabetes called “insulin resistance”: the inability of the fat and muscle tissue to take up glucose, a phenomenon typically observed in obese subjects (
Swinburn et al., 1991
). In fact, these
Kir6.2−/− mice exhibited decreased whole-body glucose disposal in contrast to their wild-type littermates as well as glucose intolerance, i.e. pre-diabetes (
Kanezaki et al., 2004
). Thus, all predictions were in agreement with the observations from the selected studies.
For cross-checking, we derived the alternative hypothesis from the aforementioned pure “push” concept. According to that previous concept, the condition of food abundance is sufficient to cause obesity. This alternative hypothesis is the negation “hypothesis B”. Such a pure “push” model (α = 0) led to the prediction that even the diet-resistant animals would become obese – but this was contradictory to the experimental data (
Levin and Keesey, 1998
;
Tkacs and Levin, 2004
). Thus, the alternative “hypothesis B” – that food abundance is sufficient to cause obesity – should be rejected. In conclusion, the data-based testing supports hypothesis B.
Analytical proof
Now that we have demonstrated data-based support of hypothesis B, which describes the dependency of body mass regulation on brain-pull mechanisms, we will analyse the properties underlying this dependency by analytical means. We propose that the brain-supply chain described by Eqs 1–6 has the following general property: The energy content in the fat/muscle compartment F depends on brain-pull efficiency α in a strictly inverse manner.
Since E, B, Y, F occur linearly in the right-hand sides and the control centres VMH and LH depend algebraically on E, B, Y, F, we can write the system of ordinary differential equations in Eq. 1 as
with q = (E, B, Y, F)T, the 4 × 4-matrix J containing exclusively parameters and the absolute vector c composed of parameters and set-points. The Jacobian of the dynamical system in Eq. 7 is J = J1+ J2(α, β) with
We want to show, that the system Eq. 7 has exactly one stationary point which is stable for a wide range of parameters, i.e. we have to show that the real parts of the constant Jacobian J are negative. Since the matrix J is rather filled with non-trivial terms, the Hurwitz criterion as well as giving the eigenvalues explicitly lead to very long expressions. Therefore, we argue by hands of the perturbation theory.
If γ ≤ 1/2 +
l2/
c1 holds true, then the Gershgorin circles (
Varga, 2004
) of the columns of
J1 lie left of the imaginary axis in the complex plane and Re
spec (
J1) ≤ 0. Since all entries of
J1 are real, the Gershgorin circles are symmetric to the real axis and 0 ∈ Re
spec (
J1) would imply 0 ∈
spec (
J1). That is impossible because the determinant
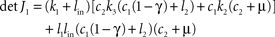
is positive for all positive parameter choices with γ ≤ 1 (see above) and
J1 is regular. This assures the existence and the uniqueness of the stationary point in Eq. 7. According to the perturbation theory of eigenvalues Re
spec (
J1 +
J2(α,β)) depends continuously on α and β. Due to
J1(0,0) = 0, the eigenvalues of the system’s Jacobian
J =
J1 +
J2(α,β) have negative real parts whenever α and β are not too large. In the present example with the parameters given above and in particular with α = 15 and β = 6, a numerical calculation gives
spec(
J) = {−23.392, −4.803, −0,652 ± 0.335
i} and
spec(
J1) = {−21.274, −5.699, −1.596, −0.934}, i.e. the only stationary point is asymptotically stable with the whole space as attraction domain. Therefore, stationary points are asymptotically stable, i.e. a stationary solution is preserved as long as exogenous parameters are constant. Furthermore, the any initial condition tends to a stationary point. Furthermore, the determinant of the Jacobian
J is not vanishing, and the stationary solution is unique. This stationary solution with
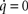
can be computed by solving the system
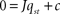
of linear equations. We get
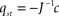
, which can be calculated by formula manipulation software like e.g. Mathematica.
The stationary fat compartment is the fourth component of the stationary solution, hence Fst = Fst(α) = qst,4. We find that the dependency of Fst on the brain-pull efficiency α is of the type
with real constants
p,
u,
r,
s which are independent of the parameter α. Consequently, the stationary energy content of the fat compartment falls with increasing brain-pull efficiency α if and only if
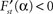
and thus
ps −
ru < 0 holds. Indeed, we find
where the abbreviations are
with Γ = 1 − γ > 0. We remark that A, C2, C4 > 0 holds true for all parameter choices. Since C1 and C3 can be negative for certain parameters, Eq. 8 contains the condition C1 + C2 + C3 > 0 which assures that ps − ru < 0 for all non-negative j1 and which describes that e.g. the push and pull parameter k1, l1 in the beginning of the supply chain as well the coupling β are not too strong. The given parameters for the examples provide C1 + C2 + C3 ≈ 18.4 > 0 If this condition holds, then the proposition of a decreasing fat compartment with increasing brain-pull efficiency and vice versa is proven for all parameter choices.
Hence, we have proved that a general property is inherent in the presented brain supply chain: the fat compartment increases with decreasing brain-pull efficiency and vice versa (Figure
4
, bottom right).
Biological Correlates of Pull Mechanisms
In this paper, we have provided evidence that brain-pull mechanisms are vital to preserve cerebral energy homeostasis in times of food deprivation. Which biological mechanisms can fulfil “pull”-function in a supply-chain model? When focussing on the proximal, final part of the supply chain, we find strong experimental evidence identifying two brain-pull mechanisms, a “direct” and an “allocative” one. Of note, these two components act synergistically to supply the brain.
Direct pull mechanisms have been found which enable astrocytes to actively take up glucose depending on three energetic conditions: firstly their need, secondly the available glucose supply from blood, and thirdly their adjacent neuron’s energy needs. Astrocytes are equipped with mechanisms that enable them to monitor changes in their own ATP concentrations. The glucose transporter 1 (GLUT1) has been found to mediate glucose transport in a manner that depends on cytoplasmic ATP (
Blodgett et al., 2007
). GLUT1, as a prototypic member of the facilitative glucose transporter family, contains 12 membrane-spanning alpha helices; six of those helices bind together in the membrane to create a polar pore in the center through which glucose can traverse. A recent study showed that ATP binding to GLUT1 causes the GLUT1 cytoplasmic carboxyl terminus to interact with the GLUT1 cytoplasmic loop 6–7 in a sequence-specific manner to inhibit glucose transport (
Blodgett et al., 2007
). GLUT1 are abundantly located on the luminal and abluminal side of endothelial cells forming the BBB (
Cornford and Hyman, 2005
) and on the end feet of the adjacent astrocytes which make contact to the endothelial cells (
Kacem et al., 1998
). It has further been shown that astrocytes enhance their GLUT1 mediated glucose uptake once they consume ATP, e.g. by activating their Na
+/K
+ ATPase (
Pellerin and Magistretti, 1997
). Thus, astrocytes feature mechanisms that fulfil pull functions serving to control their energy balance.
In addition, astrocytes can react to changes in glucose concentrations in the cerebral vasculature. GLUT1-mediated glucose transport has been shown to increase parallel to the extracellular glucose concentrations (
Cloherty et al., 1996
). Once the pore of the facilitative GLUT1 is opened up, glucose can traverse the BBB. Thus, it is conceivable that GLUT1 pores in the open state allow a push component to couple the level of glycemia to the astrocytic energy content. In hypoglycemia, a state characterized by its minor push component, an astrocytic ATP-dependent pull mechanism can be regarded as neuroprotective, as it can compensate for lacking blood-borne glucose by enhancing the astrocyte-driven glucose transport. Such a neuroprotective brain-pull mechanism is evident in subjects who are able to maintain their cerebral glucose uptake despite hypoglycaemia, when they have experienced hypoglycaemic episodes before (
Boyle et al., 1994a
).
In 1994,
Pellerin and Magistretti (1994)
discovered that astrocytes particularly respond to activity of their neighbouring neurons. The researchers found that astrocytes actively pull glucose from their vicinity, when their neighbouring neurons are at work, and termed this process “energy on demand” (
Magistretti et al., 1999
). The conception of such a “pull-mechanism” has come to be known as the astrocyte-neuron lactate shuttle hypothesis (ANLSH) (
Pellerin et al., 2007
). Upon neuronal excitation, glutamate released in the synaptic cleft is taken up by astrocytes to be recycled via the specific glutamate transporters. In this way, neurons send glutamergic signals to their astrocytes conveying that energy is needed in these neurons at this very moment. A large Na
+ influx caused by glutamate uptake takes place and activates the Na
+/K
+ ATPase (
Pellerin and Magistretti, 1997
). Since the astrocytic uptake and processing of glutamate molecules is in itself an energy consuming process, which requires a small amount of energy, the astrocytes are able to detect a small astrocytic ATP-need that reflects a larger energy need in the neighbouring neurons at work. Using their ATP-dependent GLUT1-mediated mechanisms, the astrocytes are capable to assess their energy needs, to take up glucose molecules when required, and to use glycolysis to cover their own astrocytic small need. Accordingly, glutamate uptake has been shown to activate astrocytic glucose uptake (
Loaiza et al., 2003
) and utilization (
Pellerin and Magistretti, 1994
). Then astrocytes pass on lactate molecules to the working neurons, which use oxidative phosphorylation to cover their large needs. The enhancement of aerobic glycolysis in astrocytes first causes a large increase in cytosolic NADH (
Kasischke et al., 2004
) that normalizes with the conversion of pyruvate into lactate and its release via monocarboxylate transporters expressed on astrocytes. Increased glucose uptake by astrocytes is not immediate but delayed compared to neuronal activation (
Kasischke et al., 2004
), a process for which consistent kinetics could be demonstrated recently (
Aubert and Costalat, 2005
;
Aubert et al., 2007
). Such a lactate release following glutamatergic activation corresponds to the increase in extracellular lactate levels measured
in vivo (
Demestre et al., 1997
;
Hu and Wilson, 1997
). Lactate produced by astrocytes during this later phase of activation not only replenishes the extracellular pool, but also could help sustain neuronal energy needs as activation persists. Astrocytes do not only function as single entities, but rather act in perivascular astroglial metabolic networks, allowing activity-dependent intercellular trafficking of energetic metabolites to sustain glutamatergic synaptic activity (
Rouach et al., 2008
). In all, astrocytic ATP fulfils the criterion of a key regulator in an active “energy on demand” pull process. In the current paper we took the view of integrative physiology and provide evidence for the necessity of brain-pull mechanisms for the maintenance of cerebral homeostasis. In this way, our work supports the contribution of theses recent findings from the field of neuroenergetics to the function of astrocytes.
Furthermore, mechanisms exerting “allocative brain-pull mechanisms” have been experimentally located (Figure
2
). Such mechanisms are capable of limiting peripheral energy storage in favour of the brain. Those experiments have sustained the “Selfish Brain” theory, whose foundations have been laid from 1998 to 2004 by Achim Peters, postulating the existence of such allocative mechanisms and implementing them as functional elements serving to maintain the brain’s high energy content at the expense of the body. According to that concept, the brain simultaneously represents the highest regulatory authority and the consumer with the highest priority – it looks after itself first. In this respect, a competition among all organs drives energy allocation. In the following, we take a closer look at the mechanisms that can fulfil the function of allocative brain-pull.
In the ventromedial hypothalamus (VMH), neurons have been found that sensitively respond to changes in cerebral intracellular ATP (
Miki et al., 2001
). In this brain area, ATP-sensitive potassium (K
ATP) channels have been shown to monitor ATP (
Spanswick et al., 1997
). When cerebral intracellular ATP levels fall, presynaptic K
ATP channels alter the release of GABA within the VMH, hereupon the postsynaptic VMH-neurons release glutamate, and in so doing act via the sympatho-adrenal system in order to inhibit insulin secretion and action (
Ahren, 2000
;
Chan et al., 2007
;
Mulder et al., 2005
;
Tong et al., 2007
). Because insulin is required for glucose uptake in the peripheral fat and muscle tissue via glucose transporter 4 (GLUT4), these postsynaptic VMH-neurons are able to limit glucose outflow from the blood into the peripheral buffers. In this way, these allocative mechanisms are able to preserve blood glucose as a source for the insulin-independent glucose uptake via GLUT1 into the brain. These hypothalamic neurons receive additional stimulatory input via the adipocyte-derived hormone leptin (
Dhillon et al., 2006
). When there is an energy overflow in the side buffers, leptin concentrations rise, leptin stimulates the VMH-neurons, and in so doing limits further energy uptake into the side buffers. These VMH-triggered mechanisms can be regarded as pull mechanisms because they safeguard blood glucose availability, a necessity for adequate brain supply. According to the literature, VMH neurons can meet the functions of allocative brain-pull mechanisms which guarantee the blood-to-brain energy flux.
When looking up at the more distal part of the supply chain, two further pull mechanisms can be identified: an ingestive and a foraging one. “Ingestive pull mechanisms” are initiated when blood glucose concentrations decline (Figure
2
). Recent experimental evidence suggests that orexigenic neurons in the lateral hypothalamus (LH) fulfil such a pull function. Glucose from the blood circulation crosses the endothelial cells of the blood-brain-barrier via glucose transporters 1 and enters the brain interstitial space. Glucose acts at an extracellular site on the orexin neurons. These LH neurons respond to changes in extracellular glucose concentrations by modulating their tandem-pore K
+ channels (
Burdakov et al., 2006
;
Gonzalez et al., 2008
). Upon a fall in extracellular glucose, these neurons depolarize. With activation of these neurons, appetite increases and ingestive behaviour is initiated. Upon the depletion of the peripheral buffers, the fall of leptin entails that the ingestive pull is enhanced and that the buffers can take up glucose. Both of these actions are coordinated by the VMH. This latter hypothalamic nucleus has been shown to be an indispensible part of the circuitry for the maintenance of systemic energy homeostasis (
Dhillon et al., 2006
). The VMH is known to inhibit LH-actions on the one hand (
Oomura et al., 1964
;
Sakurai et al., 2005
) and suppress insulin release and action on the other. According to the literature, the VMH can fulfil a function as a hypothalamic crosspoint centre, which integrates the competing demands from the brain and the periphery. The LH neurons can fulfil the functions of ingestive pull mechanisms that aim to replenish energy in blood and buffers.
“Foraging” pull mechanisms regulate the access of energy resources in the remote environment. When food availability decreases in the immediate environment, this is recognized by the brain and food-searching behaviour is started (Figure
2
). Foraging behaviour includes locomotion and orientation and is aimed at searching out food in the remote environment. The foraging pull appears to be a complex process in which the substantia nigra and ventral tegmental area amongst other brain areas appear to be involved (
Hommel et al., 2006
;
Swanson, 2000
). This latter pull component, however, is not included in the analyses of this paper but shall instead be a topic of an upcoming one.
We have in fact refrained from including a large number of biological mechanisms that might also fulfil functions in the supply-chain model (Table
1
). A list of various possible redundant signals was presented in earlier papers (
Peters et al., 2002
,
2004
). However, we decided to assign only a single functional mechanism and a single anatomical structure to a single signal pathway in the model. We are aware that there might be a better selection for such a substitute, and that in future hormones might be discovered that fulfil this function better and so have a greater biological relevance than the ones mentioned here. We are also aware that the assignments proposed here might be the subject of some debate, but we do feel that the specificities of the model presented are less important than the general basic principle proposed here for energy metabolism.
Correlates of Incompetent Brain-Pull
In the current paper, we have also provided evidence that an incompetent brain-pull is required for the development of obesity. Inefficiency of brain-pull mechanisms (small α) can occur at all levels of the autonomic-neuroendocrine motor system. In order to systematically explore such correlates, we looked at the entire system. The autonomic-neuroendocrine motor system is hierarchically organized among the cerebral hemispheres (including amygdala/hippocampus), the hypothalamus (including VMH), and peripheral autonomic-visceromotor and the neuroendocrine-secretomotor neurons (
Swanson, 2000
). The amygdala and hippocampus neurons project with axons to the VMH and the paraventricular nucleus. Here, the sympathetic nervous system is activated and neuropeptides are formed and released such as corticotropin-releasing-hormone and vasopressin. These releasing hormones stimulate adrenocorticotropin release into the general blood circulation within the pituitary. Adrenocorticotropin ultimately stimulates the release of cortisol from the adrenal cortex. In turn, cortisol feeds back to the pituitary, the hypothalamus, the amygdala and hippocampus. Particularly in amygdala and hippocampus, cortisol acts through mineralocorticoid receptors (MR) and glucocorticoid receptors (GR), in this way alters excitability and plasticity in the amygdala and the hippocampus. Taken together, the autonomic-neuroendocrine motor system fulfils brain-pull function within the organism and is a highly organized and adaptive homeostatic system (
Peters et al., 2007a
). In principle, all mechanisms within the system can be subject to malfunctioning or maladaptation and thus be the cause of incompetent brain-pull.
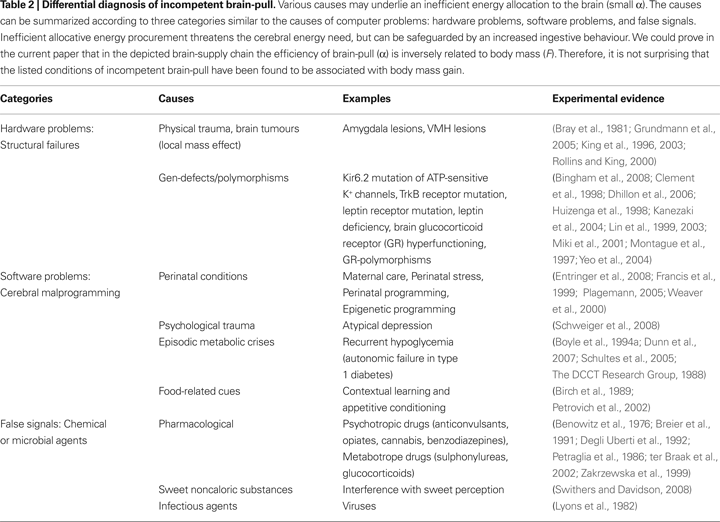
There is range of clinical and experimental evidence showing that malfunction of the VMH neurons plays a crucial role in the development of obesity (Table
2
). VMH leptin-receptor-knock-out mice are specific examples among many other possibilities of signalling disruptions in the VMH which are associated with obesity (
Bingham et al., 2008
;
Dhillon et al., 2006
). Another example is shown by studies on mice with a leptin receptor defect which have been shown to exhibit incompetent brain-pull. In the developmental phase of these animals their bodies’ mass largely grew, but their brains were 25% smaller than those of control mice (
Vannucci et al., 1997
). Furthermore, the VMH neurons can be destroyed by tumours e.g. craniopharyngioma leading to inefficiency of brain-pull mechanisms and obesity (
Muller et al., 2004
). Moreover, the VMH neurons receive massive excitatory input from the cerebral hemispheres, particularly from the amygdala (
Petrovich et al., 2001
;
Swanson, 2000
). Thus it is not surprising that bilateral lesions of the amygdala cause a severe obesity syndrome (
King et al., 2003
). It could also be that monogenetic defects like TrkB mutation lead to an inefficient brain-pull with obesity and cognitive dysfunction as became evident in the case of an 8-year-old boy who displayed extreme obesity (50 kg) and cognitive deficits (
Yeo et al., 2004
). In addition, environmental food-related cues have been shown in humans and rats to induce conditional learning in the amygdala and override satiety signals (
Birch et al., 1989
;
Petrovich et al., 2002
). Such external cues affect the information processing by amygdala neurons and their triple-descending pathways to the hypothalamus (
Petrovich et al., 2001
), and in so doing may induce a conditioned brain-pull hypofunction. Finally, the brain glucocorticoid feedback in the autonomic-neuroendocrine motor system may be affected. Cortisol, via its brain GR, exerts feedback inhibition in order to reset the system into a state of rest after a stressful event. If brain GR act too strongly, they dampen the autonomic-neuroendocrine motor system too much, and in so doing impair the allocative brain-pull. In fact, brain GR have been confirmed in a genetic mouse model to promote energy accumulation within the body via their effects on the hypothalamus-pituitary-adrenal system (
Kellendonk et al., 2002
). Human carriers of the GR-polymorphism N363S, which display higher GR-sensitivity to glucocorticoids (
Huizenga et al., 1998
), display signs of an inefficient brain-pull and are also prone to develop obesity (
Lin et al., 1999
). Early life events have be shown in pigs to increase GR function and body mass in the long-term (
Weaver et al., 2000
), a process referred to as “perinatal programming”. Michael J. Meaney and co-workers have found in rats that the epigenomic state of the hippocampal GR promoter can be established through behavioural programming, and that it is potentially reversible (
Weaver et al., 2004
). Epigenetic programming of neurons by psychosocial, dietary, and environmental factors opens a field for future obesity research. Thus, a variety of causes may underlie a malfunctioning and maladaptation of the autonomic-neuroendocrine motor system which may lead to an incompetent brain-pull.
Physiological Potential of Brain-Pull
Inanition can be regarded as a slow energy allocation towards the brain occurring after approximately 1 month (
Krieger, 1921
). Under normal nutritional conditions, energy allocation towards the brain can also take place very fast. Rapid energy allocation to the brain could be shown by recent magnetic resonance spectroscopy studies from our lab (
Oltmanns et al., 2008
). We examined short-term changes in high energy phosphates in the human brain and muscle after manipulating the energy supply in the blood circulation (by injection of either insulin or dextrose). Using
31phosphor magnetic resonance spectroscopy, we found that the high energy phosphates changed in favour of the brain cells and not in favour of muscle cells. Such a divergent energetic response of brain and muscle with a rise in cerebral and a drop in muscle high energy phosphate content could be observed already after 20–30 min.
At the million-year timescale, comparative studies on primate and non-primate vertebrates reveal that there is an evolutionary trend towards improved energy allocation to the brain (
Mink et al., 1981
). The advantage of a strong allocative brain-pull mechanisms may have become particularly evident in prolonged periods of food scarcity. As shown above in this paper, an efficient brain-pull mechanism (large α) is necessary to reduce body size in favour of maintained brain size. In fact, brains of
Homo sapiens not only use a larger proportion of the organism’s energy supply (20%) than do the brains of rats, cats, and dogs (4–6%) (
Mink et al., 1981
), brains of
Homo sapiens are also the largest compared to their body size, where humans exhibit a relatively gracile physique (
Aiello and Wheeler, 1995
;
Armstrong, 1983
). Better diet quality or sparing expensive body functions have been proposed to set the stage for enhanced brain consumption (
Aiello and Wheeler, 1995
;
Fish and Lockwood, 2003
;
Isler and van Schaik, 2006
). But how can a brain ensure that its needs are covered, once the cerebral needs have increased relative to the needs of the body? Is it conceivable that the “competence of brain-pull” drives the encephalization in human brain evolution?
By setting up a model of the brain’s supply chain and by comparing its predictions with medical and experimental data, we have demonstrated data-based support of our hypothesis, which states that a competent brain-pull is indispensable for cerebral energy homeostasis, especially at times of nutritional deficiency. The brain – since it actively controls its own energy procurement – behaves “selfishly” in this respect (
Peters et al., 2004
). In the same manner, we were also able to show support of the related hypothesis, which states that at times of caloric abundance an incompetent brain-pull is necessary to cause build-ups in the supply chain of the brain culminating in obesity and diabetes type 2. We have proved analytically that extent of the resultant obesity depends on brain-pull efficiency in a strictly inverse manner. Finally we put together what we have found by testing these two related hypotheses: In order to ensure both cerebral and peripheral energy homeostasis in a healthy subject, a supply chain ranging from the environment, through the body, towards the brain must feature a competent brain-pull mechanism – which was to be demonstrated. The logistic supply-chain approach may be a useful tool for a better targeting of the obesity problem: to improve the metabolic competence of the brain, i.e. the brain-pull.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was granted by the German Research Foundation (DFG): Clinical research group KFO 126.
Ahren, B. (2000). Autonomic regulation of islet hormone secretion – implications for health and disease.
Diabetologia 43, 393–410.
Aiello, L. C., and Wheeler, P. (1995). The expensive-tissue hypothesis: the brain and the digestive system in human and primate evolution.
Curr. Anthropol. 36, 199–221.
American Diabetes Association (2008). Standards of medical care in diabetes – 2008.
Diabetes Care 31(Suppl. 1), S12–S54.
Armstrong, E. (1983). Relative brain size and metabolism in mammals.
Science 220, 1302–1304.
Aubert, A., and Costalat, R. (2005). Interaction between astrocytes and neurons studied using a mathematical model of compartmentalized energy metabolism.
J. Cereb. Blood Flow Metab. 25, 1476–1490.
Aubert, A., Pellerin, L., Magistretti, P. J., and Costalat, R. (2007). A coherent neurobiological framework for functional neuroimaging provided by a model integrating compartmentalized energy metabolism.
Proc. Natl. Acad. Sci. U.S.A. 104, 4188–4193.
Benowitz, N. L., Jones, R. T., and Lerner, C. B. (1976). Depression of growth hormone and cortisol response to insulin-induced hypoglycemia after prolonged oral delta-9-tetrahydrocannabinol administration in man.
J. Clin. Endocrinol. Metab. 42, 938–941.
Bingham, N. C., Anderson, K. K., Reuter, A. L., Stallings, N. R., and Parker, K. L. (2008). Selective loss of leptin receptors in the ventromedial hypothalamic nucleus results in increased adiposity and a metabolic syndrome.
Endocrinology 149, 2138–2148.
Birch, L. L., McPhee, L., Sullivan, S., and Johnson, S. (1989). Conditioned meal initiation in young children.
Appetite 13, 105–113.
Blodgett, D. M., De Zutter, J. K., Levine, K. B., Karim, P., and Carruthers, A. (2007). Structural basis of GLUT1 inhibition by cytoplasmic ATP.
J. Gen. Physiol. 130, 157–168.
Boyle, P. J., Kempers, S. F., O’Connor, A. M., and Nagy, R. J. (1995). Brain glucose uptake and unawareness of hypoglycemia in patients with insulin-dependent diabetes mellitus.
N. Engl. J. Med. 333, 1726–1731.
Boyle, P. J., Nagy, R. J., O’Connor, A. M., Kempers, S. F., Yeo, R. A., and Qualls, C. (1994a). Adaptation in brain glucose uptake following recurrent hypoglycemia.
Proc. Natl. Acad. Sci. U.S.A. 91, 9352–9356.
Boyle, P. J., Scott, J. C., Krentz, A. J., Nagy, R. J., Comstock, E., and Hoffman, C. (1994b). Diminished brain glucose metabolism is a significant determinant for falling rates of systemic glucose utilization during sleep in normal humans.
J. Clin. Invest. 93, 529–535.
Bray, G. A., Inoue, S., and Nishizawa, Y. (1981). Hypothalamic obesity. The autonomic hypothesis and the lateral hypothalamus.
Diabetologia 20(Suppl.), 366–377.
Breier, A., Davis, O. R., and Buchanan, R. W. (1991). Alprazolam attenuates metabolic stress-induced neuroendocrine and behavioral effects in humans.
Psychopharmacology (Berl) 104, 479–484.
Burdakov, D., Jensen, L. T., Alexopoulos, H., Williams, R. H., Fearon, I. M., O’Kelly, I., Gerasimenko, O., Fugger, L., and Verkhratsky, A. (2006). Tandem-pore K+ channels mediate inhibition of orexin neurons by glucose.
Neuron 50, 711–722.
Caballero, B. (2007). The global epidemic of obesity: an overview.
Epidemiol. Rev. 29, 1–5.
Campfield, L. A., and Smith, F. J. (2003). Blood glucose dynamics and control of meal initiation: a pattern detection and recognition theory.
Physiol. Rev. 83, 25–58.
Chan, O., Lawson, M., Zhu, W., Beverly, J. L., and Sherwin, R. S. (2007). ATP-sensitive K(+) channels regulate the release of GABA in the ventromedial hypothalamus during hypoglycemia.
Diabetes 56, 1120–1126.
Clement, K., Vaisse, C., Lahlou, N., Cabrol, S., Pelloux, V., Cassuto, D., Gourmelen, M., Dina, C., Chambaz, J., Lacorte, J. M., Basdevant, A., Bougneres, P., Lebouc, Y., Froguel, P., and Guy-Grand, B. (1998). A mutation in the human leptin receptor gene causes obesity and pituitary dysfunction.
Nature 392, 398–401.
Cloherty, E. K., Heard, K. S., and Carruthers, A. (1996). Human erythrocyte sugar transport is incompatible with available carrier models.
Biochemistry 35, 10411–10421.
Cornford, E. M., and Hyman, S. (2005). Localization of brain endothelial luminal and abluminal transporters with immunogold electron microscopy.
NeuroRx 2, 27–43.
Degli Uberti, E. C., Salvadori, S., Trasforini, G., Margutti, A., Ambrosio, M. R., Rossi, R., Portaluppi, F., and Pansini, R. (1992). Effect of deltorphin on pituitary-adrenal response to insulin-induced hypoglycemia and ovine corticotropin-releasing hormone in healthy man.
J. Clin. Endocrinol. Metab. 75, 370–374.
Demestre, M., Boutelle, M., and Fillenz, M. (1997). Stimulated release of lactate in freely moving rats is dependent on the uptake of glutamate.
J. Physiol. 499(Pt 3), 825–832.
Dhillon, H., Zigman, J. M., Ye, C., Lee, C. E., McGovern, R. A., Tang, V., Kenny, C. D., Christiansen, L. M., White, R. D., and Edelstein, E. A. (2006). Leptin directly activates SF1 neurons in the VMH, and this action by leptin is required for normal body-weight homeostasis.
Neuron 49, 191–203.
Dunn, J. T., Cranston, I., Marsden, P. K., Amiel, S. A., and Reed, L. J. (2007). Attenuation of amydgala and frontal cortical responses to low blood glucose concentration in asymptomatic hypoglycemia in type 1 diabetes: a new player in hypoglycemia unawareness?
Diabetes 56, 2766–2773.
Entringer, S., Wust, S., Kumsta, R., Layes, I. M., Nelson, E. L., Hellhammer, D. H., and Wadhwa, P. D. (2008). Prenatal psychosocial stress exposure is associated with insulin resistance in young adults.
Am. J. Obstet. Gynecol. 199, 498.e1–498.e7
Fish, J. L., and Lockwood, C. A. (2003). Dietary constraints on encephalization in primates.
Am. J. Phys. Anthropol. 120, 171–181.
Flier, J. S., and Maratos-Flier, E. (2005). Obesity. In Harrison’s Principles of Internal Medicine, D. L. Kasper, E. Braunwald, A. S. Fauci, S. L. Hauser, D. L. Longo, and J. L. Jameson, eds. (New York, McGraw-Hill), pp. 422–429.
Francis, D., Diorio, J., Liu, D., and Meaney, M. J. (1999). Nongenomic transmission across generations of maternal behavior and stress responses in the rat.
Science 286, 1155–1158.
Gong, Q. Y., Roberts, N., Garden, A. S., and Whitehouse, G. H. (1998). Fetal and fetal brain volume estimation in the third trimester of human pregnancy using gradient echo MR imaging.
Magn. Reson. Imaging 16, 235–240.
Gonzalez, J. A., Jensen, L. T., Fugger, L., and Burdakov, D. (2008). Metabolism-independent sugar sensing in central orexin neurons.
Diabetes 57, 2569–2576.
Goodman, M. N., Lowell, B., Belur, E., and Ruderman, N. B. (1984). Sites of protein conservation and loss during starvation: influence of adiposity.
Am. J. Physiol. 246, E383–E390.
Grundmann, S. J., Pankey, E. A., Cook, M. M., Wood, A. L., Rollins, B. L., and King, B. M. (2005). Combination unilateral amygdaloid and ventromedial hypothalamic lesions: evidence for a feeding pathway.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 288, R702–R707.
Hairer, E., Nørsett, S. P., and Wanner, G. (1993). Solving Ordinary Differential Equations I. New York, Springer Verlag.
Hill, J. O., and Peters, J. C. (1998). Environmental contributions to the obesity epidemic.
Science 280, 1371–1374.
Hommel, J. D., Trinko, R., Sears, R. M., Georgescu, D., Liu, Z. W., Gao, X. B., Thurmon, J. J., Marinelli, M., and Dileone, R. J. (2006). Leptin receptor signaling in midbrain dopamine neurons regulates feeding.
Neuron 51, 801–810.
Hu, Y., and Wilson, G. S. (1997). A temporary local energy pool coupled to neuronal activity: fluctuations of extracellular lactate levels in rat brain monitored with rapid-response enzyme-based sensor.
J. Neurochem. 69, 1484–1490.
Huizenga, N. A., Koper, J. W., De Lange, P., Pols, H. A., Stolk, R. P., Burger, H., Grobbee, D. E., Brinkmann, A. O., de Jong, F. H., and Lamberts, S. W. (1998). A polymorphism in the glucocorticoid receptor gene may be associated with and increased sensitivity to glucocorticoids in vivo.
J. Clin. Endocrinol. Metab. 83, 144–151.
Isler, K., and van Schaik, C. (2006). Costs of encephalization: the energy trade-off hypothesis tested on birds.
J. Hum. Evol. 51, 228–243.
Kacem, K., Lacombe, P., Seylaz, J., and Bonvento, G. (1998). Structural organization of the perivascular astrocyte endfeet and their relationship with the endothelial glucose transporter: a confocal microscopy study.
Glia 23, 1–10.
Kanezaki, Y., Obata, T., Matsushima, R., Minami, A., Yuasa, T., Kishi, K., Bando, Y., Uehara, H., Izumi, K., Mitani, T., Matsumoto, M., Takeshita, Y., Nakaya, Y., Matsumoto, T., and Ebina, Y. (2004). K(ATP) channel knockout mice crossbred with transgenic mice expressing a dominant-negative form of human insulin receptor have glucose intolerance but not diabetes.
Endocr. J. 51, 133–144.
Kasischke, K. A., Vishwasrao, H. D., Fisher, P. J., Zipfel, W. R., and Webb, W. W. (2004). Neural activity triggers neuronal oxidative metabolism followed by astrocytic glycolysis.
Science 305, 99–103.
Kellendonk, C., Eiden, S., Kretz, O., Schutz, G., Schmidt, I., Tronche, F., and Simon, E. (2002). Inactivation of the GR in the nervous system affects energy accumulation.
Endocrinology 143, 2333–2340.
Kennedy, G. C. (1953). The role of depot fat in the hypothalamic control of food intake in the rat.
Proc. R. Soc. Lond. Ser. 140, 578–592.
Kety, S. S. (1957). The general metabolism of the brain in vivo. In Metabolism of the Nervous System, Richter, D. ed. (London, Pergamon Press), pp. 221–237.
Kety, S. S., and Schmidt, C. F. (1948). The nitrous oxide method for the quantitative determination of cerebral blood flow in man: theory, procedure and normal values.
J. Clin. Invest. 27, 476–483.
Kind, K. L., Roberts, C. T., Sohlstrom, A. I., Katsman, A., Clifton, P. M., Robinson, J. S., and Owens, J. A. (2005). Chronic maternal feed restriction impairs growth but increases adiposity of the fetal guinea pig.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 288, R119–R126.
King, B. M., Cook, J. T., and Dallman, M. F. (1996). Hyperinsulinemia in rats with obesity-inducing amygdaloid lesions.
Am. J. Physiol. 271, R1156–R1159.
King, B. M., Cook, J. T., Rossiter, K. N., and Rollins, B. L. (2003). Obesity-inducing amygdala lesions: examination of anterograde degeneration and retrograde transport.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 284, R965–R982.
Krieger, M. (1921). Über die Atrophie der menschlichen Organe bei Inanition.
Z. Angew. Anat. Konstitutionsl. 7, 87–134.
Langemann, D. (2007). Selfish-brain theory: mathematical challenges in the top-down analysis of metabolic supply chains.
CRPIT 83, 39–49.
Levin, B. E., and Keesey, R. E. (1998). Defense of differing body weight set points in diet-induced obese and resistant rats.
Am. J. Physiol. 274, R412–R419.
Lin, R. C., Wang, W. Y., and Morris, B. J. (1999). High penetrance, overweight, and glucocorticoid receptor variant: case-control study.
BMJ 319, 1337–1338.
Lin, R. C., Wang, X. L., Dalziel, B., Caterson, I. D., and Morris, B. J. (2003). Association of obesity, but not diabetes or hypertension, with glucocorticoid receptor N363S variant.
Obes. Res. 11, 802–808.
Loaiza, A., Porras, O. H., and Barros, L. F. (2003). Glutamate triggers rapid glucose transport stimulation in astrocytes as evidenced by real-time confocal microscopy.
J. Neurosci. 23, 7337–7342.
Lyons, M. J., Faust, I. M., Hemmes, R. B., Buskirk, D. R., Hirsch, J., and Zabriskie, J. B. (1982). A virally induced obesity syndrome in mice.
Science 216, 82–85.
Madsen, P. L., Hasselbalch, S. G., Hagemann, L. P., Olsen, K. S., Bulow, J., Holm, S., Wildschiodtz, G., Paulson, O. B., and Lassen, N. A. (1995). Persistent resetting of the cerebral oxygen/glucose uptake ratio by brain activation: evidence obtained with the Kety–Schmidt technique.
J. Cereb. Blood Flow Metab. 15, 485–491.
Magistretti, P. J., Pellerin, L., Rothman, D. L., and Shulman, R. G. (1999). Energy on demand.
Science 283, 496–497.
Mayer, J. (1953). Glucostatic mechanism of regulation of food intake.
N. Engl. J. Med. 249, 13–16.
Miki, T., Liss, B., Minami, K., Shiuchi, T., Saraya, A., Kashima, Y., Horiuchi, M., Ashcroft, F., Minokoshi, Y., Roeper, J., and Seino, S. (2001). ATP-sensitive K+ channels in the hypothalamus are essential for the maintenance of glucose homeostasis.
Nat. Neurosci. 4, 507–512.
Miller, S. L., Green, L. R., Peebles, D. M., Hanson, M. A., and Blanco, C. E. (2002). Effects of chronic hypoxia and protein malnutrition on growth in the developing chick.
Am. J. Obstet. Gynecol. 186, 261–267.
Mink, J. W., Blumenschine, R. J., and Adams, D. B. (1981). Ratio of central nervous system to body metabolism in vertebrates: its constancy and functional basis.
Am. J. Physiol. 241, R203–R212.
Montague, C. T., Farooqi, I. S., Whitehead, J. P., Soos, M. A., Rau, H., Wareham, N. J., Sewter, C. P., Digby, J. E., Mohammed, S. N., Hurst, J. A., Cheetham, C. H., Earley, A. R., Barnett, A. H., Prins, J. B., and O’Rahilly, S. (1997). Congenital leptin deficiency is associated with severe early-onset obesity in humans.
Nature 387, 903–908.
Muhlau, M., Gaser, C., Ilg, R., Conrad, B., Leibl, C., Cebulla, M. H., Backmund, H., Gerlinghoff, M., Lommer, P., Schnebel, A., Wohlschlager, A. M., Zimmer, C., and Nunnemann, S. (2007). Gray matter decrease of the anterior cingulate cortex in anorexia nervosa.
Am. J. Psychiatry 164, 1850–1857.
Mulder, A. H., Tack, C. J., Olthaar, A. J., Smits, P., Sweep, F. C., and Bosch, R. R. (2005). Adrenergic receptor stimulation attenuates insulin-stimulated glucose uptake in 3T3-L1 adipocytes by inhibiting GLUT4 translocation.
Am. J. Physiol. Endocrinol. Metab. 289, E627–E633.
Muller, H. L., Emser, A., Faldum, A., Bruhnken, G., Etavard-Gorris, N., Gebhardt, U., Oeverink, R., Kolb, R., and Sorensen, N. (2004). Longitudinal study on growth and body mass index before and after diagnosis of childhood craniopharyngioma.
J. Clin. Endocrinol. Metab. 89, 3298–3305.
Oltmanns, K. M., Melchert, U. H., Scholand-Engler, H. G., Howitz, M. C., Schultes, B., Schweiger, U., Hohagen, F., Born, J., Peters, A., and Pellerin, L. (2008). Differential energetic response of brain vs. skeletal muscle upon glycemic variations in healthy humans.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 294, R12–R16.
Oomura, Y., Kimura, K., Ooyama, H., Maeo, T., Iki, M., and Kuniyoshi, N. (1964). Reciprocal activities of the ventromedial and lateral hypothalamic area of cats.
Science 143, 484–485.
Pellerin, L., Bouzier-Sore, A. K., Aubert, A., Serres, S., Merle, M., Costalat, R., and Magistretti, P. J. (2007). Activity-dependent regulation of energy metabolism by astrocytes: an update.
Glia 55, 1251–1262.
Pellerin, L., and Magistretti, P. J. (1994). Glutamate uptake into astrocytes stimulates aerobic glycolysis: a mechanism coupling neuronal activity to glucose utilization.
Proc. Natl. Acad. Sci. U.S.A. 91, 10625–10629.
Pellerin, L., and Magistretti, P. J. (1997). Glutamate uptake stimulates Na+, K+-ATPase activity in astrocytes via activation of a distinct subunit highly sensitive to ouabain.
J. Neurochem. 69, 2132–2137.
Peters, A., Conrad, M., Hubold, C., Schweiger, U., Fischer, B., and Fehm, H. L. (2007a). The principle of homeostasis in the hypothalamus-pituitary-adrenal system: new insight from positive feedback.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 293, 83–98.
Peters, A., Pellerin, L., Dallman, M. F., Oltmanns, K. M., Schweiger, U., Born, J., and Fehm, H. L. (2007b). Causes of obesity: looking beyond the hypothalamus.
Prog. Neurobiol. 81, 61–88.
Peters, A., Schweiger, U., Fruhwald-Schultes, B., Born, J., and Fehm, H. L. (2002). The neuroendocrine control of glucose allocation.
Exp. Clin. Endocrinol. Diabetes 110, 199–211.
Peters, A., Schweiger, U., Pellerin, L., Hubold, C., Oltmanns, K. M., Conrad, M., Schultes, B., Born, J., and Fehm, H. L. (2004). The selfish brain: competition for energy resources.
Neurosci. Biobehav. Rev. 28, 143–180.
Petraglia, F., Bakalakis, S., Facchinetti, F., Volpe, A., Muller, E. E., and Genazzani, A. R. (1986). Effects of sodium valproate and diazepam on beta-endorphin, beta-lipotropin and cortisol secretion induced by hypoglycemic stress in humans.
Neuroendocrinology 44, 320–325.
Petrovich, G. D., Canteras, N. S., and Swanson, L. W. (2001). Combinatorial amygdalar inputs to hippocampal domains and hypothalamic behavior systems.
Brain Res. Brain Res. Rev. 38, 247–289.
Petrovich, G. D., Setlow, B., Holland, P. C., and Gallagher, M. (2002). Amygdalo-hypothalamic circuit allows learned cues to override satiety and promote eating.
J. Neurosci. 22, 8748–8753.
Plagemann, A. (2005). Perinatal programming and functional teratogenesis: impact on body weight regulation and obesity.
Physiol. Behav. 86, 661–668.
Popkin, B. M. (2006). Global nutrition dynamics: the world is shifting rapidly toward a diet linked with noncommunicable diseases.
Am. J. Clin. Nutr. 84, 289–298.
Reinmuth, O. M., Scheinberg, P., and Bourne, B. (1965). Total cerebral blood flow and metabolism.
Arch. Neurol. 12, 49–66.
Rollins, B. L., and King, B. M. (2000). Amygdala-lesion obesity: what is the role of the various amygdaloid nuclei?
Am. J. Physiol. Regul. Integr. Comp. Physiol. 279, R1348–R1356.
Rouach, N., Koulakoff, A., Abudara, V., Willecke, K., and Giaume, C. (2008). Astroglial metabolic networks sustain hippocampal synaptic transmission.
Science 322, 1551–1555.
Sakurai, T., Nagata, R., Yamanaka, A., Kawamura, H., Tsujino, N., Muraki, Y., Kageyama, H., Kunita, S., Takahashi, S., Goto, K., Koyama, Y., Shioda, S., and Yanagisawa, M. (2005). Input of orexin/hypocretin neurons revealed by a genetically encoded tracer in mice.
Neuron 46, 297–308.
Schultes, B., Kern, W., Oltmanns, K., Peters, A., Gais, S., Fehm, H. L., and Born, J. (2005). Differential adaptation of neurocognitive brain functions to recurrent hypoglycemia in healthy men.
Psychoneuroendocrinology 30, 149–161.
Schweiger, U., Greggersen, W., Rudolf, S., Pusch, M., Menzel, T., Winn, S., Hassfurth, J., Fassbinder, E., Kahl, K. G., Oltmanns, K. M., Hohagen, F., and Peters, A. (2008). Disturbed glucose disposal in patients with major depression; application of the glucose clamp technique.
Psychosom. Med. 70, 170–176.
Slack, N., Chambers, S., and Johnston, R. (2004). Operations Management. Harlow, FT Prentice Hall.
Spanswick, D., Smith, M. A., Groppi, V. E., Logan, S. D., and Ashford, M. L. (1997). Leptin inhibits hypothalamic neurons by activation of ATP-sensitive potassium channels.
Nature 390, 521–525.
Steinkamp, M., Li, T., Fuellgraf, H., and Moser, A. (2007). K(ATP)-dependent neurotransmitter release in the neuronal network of the rat caudate nucleus.
Neurochem. Int. 50, 159–163.
Swanson, L. W. (2000). Cerebral hemisphere regulation of motivated behavior.
Brain Res. 886, 113–164.
Swinburn, B. A., Nyomba, B. L., Saad, M. F., Zurlo, F., Raz, I., Knowler, W. C., Lillioja, S., Bogardus, C., and Ravussin, E. (1991). Insulin resistance associated with lower rates of weight gain in Pima Indians.
J. Clin. Invest. 88, 168–173.
Swithers, S. E., and Davidson, T. L. (2008). A role for sweet taste: calorie predictive relations in energy regulation by rats.
Behav. Neurosci. 122, 161–173.
Tarantola, A. (2005). Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, Society for Industrial and Applied Mathematics.
ter Braak, E. W., Appelman, A. M., van der Tweel, I., Erkelens, D. W., and Van Haeften, T. W. (2002). The sulfonylurea glyburide induces impairment of glucagon and growth hormone responses during mild insulin-induced hypoglycemia.
Diabetes Care 25, 107–112.
The DCCT Research Group (1988). Weight gain associated with intensive therapy in the diabetes control and complications trial.
Diabetes Care 11, 567–573.
Tkacs, N. C., and Levin, B. E. (2004). Obesity-prone rats have preexisting defects in their counterregulatory response to insulin-induced hypoglycemia.
Am. J. Physiol. Regul. Integr. Comp. Physiol. 287, R1110–R1115.
Tong, Q., Ye, C., McCrimmon, R. J., Dhillon, H., Choi, B., Kramer, M. D., Yu, J., Yang, Z., Christiansen, L. M., Lee, C. E., Choi, C. S., Zigman, J. M., Shulman, G. I., Sherwin, R. S., Elmquist, J. K., and Lowell, B. B. (2007). Synaptic glutamate release by ventromedial hypothalamic neurons is part of the neurocircuitry that prevents hypoglycemia.
Cell Metab. 5, 383–393.
Vannucci, S. J., Gibbs, E. M., and Simpson, I. A. (1997). Glucose utilization and glucose transporter proteins GLUT-1 and GLUT-3 in brains of diabetic (db/db) mice.
Am. J. Physiol. 272, E267–E274.
Varga, R. S. (2004). Gershgorin and His Circles. Berlin, Springer.
Weaver, I. C., Cervoni, N., Champagne, F. A., D’Alessio, A. C., Sharma, S., Seckl, J. R., Dymov, S., Szyf, M., and Meaney, M. J. (2004). Epigenetic programming by maternal behavior.
Nat. Neurosci. 7, 847–854.
Weaver, S. A., Aherne, F. X., Meaney, M. J., Schaefer, A. L., and Dixon, W. T. (2000). Neonatal handling permanently alters hypothalamic-pituitary-adrenal axis function, behaviour, and body weight in boars.
J. Endocrinol. 164, 349–359.
Wild, S., Roglic, G., Green, A., Sicree, R., and King, H. (2004). Global prevalence of diabetes: estimates for the year 2000 and projections for 2030.
Diabetes Care 27, 1047–1053.
Yeo, G. S., Connie Hung, C. C., Rochford, J., Keogh, J., Gray, J., Sivaramakrishnan, S., O’Rahilly, S., and Farooqi, I. S. (2004). A de novo mutation affecting human TrkB associated with severe obesity and developmental delay.
Nat. Neurosci. 7, 1187–1189.
Zakrzewska, K. E., Cusin, I., Stricker-Krongrad, A., Boss, O., Ricquier, D., Jeanrenaud, B., and Rohner-Jeanrenaud, F. (1999). Induction of obesity and hyperleptinemia by central glucocorticoid infusion in the rat.
Diabetes 48, 365–370.

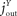 , and the consumption of the fat/muscle compartment
, and the consumption of the fat/muscle compartment 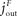 .
.
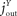 is essentially related to the degree of neuronal activity, which depends on the level of neuronal stimulation c1 and the available cerebral energy Y required for that process. Thus, the cerebral consumption is supposed to increase in an affine manner with the cerebral energy content (for biological mechanisms that fulfil the function of controlling neuronal consumption in an energy-dependent manner see Table 1
). As observed the energy content in the brain is nearly constant, and we will see that the model reproduces this property although the brain energy content is even not mathematically fixed. Thirdly, the energy consumption of the fat/muscle compartment is differentiated into a constant maintenance j0 and a component proportional to its size. Hence, we find
is essentially related to the degree of neuronal activity, which depends on the level of neuronal stimulation c1 and the available cerebral energy Y required for that process. Thus, the cerebral consumption is supposed to increase in an affine manner with the cerebral energy content (for biological mechanisms that fulfil the function of controlling neuronal consumption in an energy-dependent manner see Table 1
). As observed the energy content in the brain is nearly constant, and we will see that the model reproduces this property although the brain energy content is even not mathematically fixed. Thirdly, the energy consumption of the fat/muscle compartment is differentiated into a constant maintenance j0 and a component proportional to its size. Hence, we find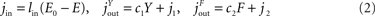
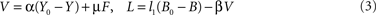

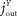 from the blood to the brain. Thus, we get
from the blood to the brain. Thus, we get

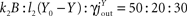 in the equilibrium. Next the flux jBF is decomposed by k3B : [−α(Y0 − Y)] : (−μF) = 120 : (−15) : (−5), where the second term and the third term are inhibitory. Here, the insulin-mediated influence of the blood is dominant. The inflow in the equilibrium is set to jin = 200, and the outflow of the brain and the fat/muscle compartment is
in the equilibrium. Next the flux jBF is decomposed by k3B : [−α(Y0 − Y)] : (−μF) = 120 : (−15) : (−5), where the second term and the third term are inhibitory. Here, the insulin-mediated influence of the blood is dominant. The inflow in the equilibrium is set to jin = 200, and the outflow of the brain and the fat/muscle compartment is  =
=  = 100, always in the equilibrium. All these values and relations are variable in the simulation of time-dependent developments. Furthermore, we set the values E0 = 100, B0 = 1000 and the stationary values E* = 50, B* = 90, F* = 100 and Y* = 100. The high set-point for the blood glucose codes the position that the blood is nearly always pulling, even in diabetic ketoacidosis or hyperglycaemic hyperosmolar state, when the blood glucose concentrations are extremely elevated. These choices result in the example parameters lin = 4, k1 = 1.6, k2 = 0.556, k3 = 1.333, l1 = 0.264, l2 = 20, μ = 0.05, c1 = 1, c2 = 1, α = 15, β = 6, γ = 0.3, j1 = 0, j2 = 50. Let us mention that we will prove the asserted qualitative behaviour for a wide range of parameters in the “Results” section, analytical proof. A scaling of parameter like e.g. a change of c1 corresponds to a scaling of the measure units of the energy contents Y. In all, we can regard the model as non-dimensional. Yet, some of the values might remind to realistic values like the blood glucose of 90 in the equilibrium could be imagined as 90 mg/dl, and the inflow of 200 can be interpreted as an daily intake of 200 g glucose, cf. above.
= 100, always in the equilibrium. All these values and relations are variable in the simulation of time-dependent developments. Furthermore, we set the values E0 = 100, B0 = 1000 and the stationary values E* = 50, B* = 90, F* = 100 and Y* = 100. The high set-point for the blood glucose codes the position that the blood is nearly always pulling, even in diabetic ketoacidosis or hyperglycaemic hyperosmolar state, when the blood glucose concentrations are extremely elevated. These choices result in the example parameters lin = 4, k1 = 1.6, k2 = 0.556, k3 = 1.333, l1 = 0.264, l2 = 20, μ = 0.05, c1 = 1, c2 = 1, α = 15, β = 6, γ = 0.3, j1 = 0, j2 = 50. Let us mention that we will prove the asserted qualitative behaviour for a wide range of parameters in the “Results” section, analytical proof. A scaling of parameter like e.g. a change of c1 corresponds to a scaling of the measure units of the energy contents Y. In all, we can regard the model as non-dimensional. Yet, some of the values might remind to realistic values like the blood glucose of 90 in the equilibrium could be imagined as 90 mg/dl, and the inflow of 200 can be interpreted as an daily intake of 200 g glucose, cf. above.
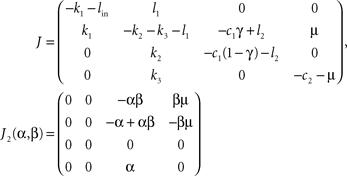
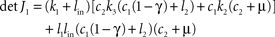
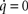 can be computed by solving the system
can be computed by solving the system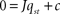
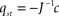 , which can be calculated by formula manipulation software like e.g. Mathematica.
, which can be calculated by formula manipulation software like e.g. Mathematica.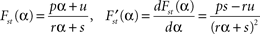
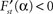 and thus ps − ru < 0 holds. Indeed, we find
and thus ps − ru < 0 holds. Indeed, we find