Smallest Chimeras Under Repulsive Interactions

We present an exemplary system of three identical oscillators in a ring interacting repulsively to show up chimera patterns. The dynamics of individual oscillators is governed by the superconducting Josephson junction. Surprisingly, the repulsive interactions can only establish a symmetry of complete synchrony in the ring, which is broken with increasing repulsive interactions when the junctions pass through serials of asynchronous states (periodic and chaotic) but finally emerge into chimera states. The chimera pattern first appears in chaotic rotational motion of the three junctions when two junctions evolve coherently, while the third junction is incoherent. For larger repulsive coupling, the junctions evolve into another chimera pattern in a periodic state when two junctions remain coherent in rotational motion and one junction transits to incoherent librational motion. This chimera pattern is sensitive to initial conditions in the sense that the chimera state flips to another pattern when two junctions switch to coherent librational motion and the third junction remains in rotational motion, but incoherent. The chimera patterns are detected by using partial and global error functions of the junctions, while the librational and rotational motions are identified by a libration index. All the collective states, complete synchrony, desynchronization, and two chimera patterns are delineated in a parameter plane of the ring of junctions, where the boundaries of complete synchrony are demarcated by using the master stability function.

1 Introduction

Chimera states (Abrams and Strogatz, 2004; Sethia et al., 2008; Laing, 2009; Hagerstrom et al., 2012; Martens et al., 2013; Omelchenko et al., 2013; Gopal et al., 2014; Schöll, 2016; Hart et al., 2019; Majhi et al., 2019; Parastesh et al., 2020; Wang and Liu, 2020) became a paradigm of collective phenomena in dynamical systems that started with the first report by Kuramoto and Battogtokh (2002) of two coexisting synchronous and asynchronous groups of phase oscillators arranged in a ring and coupled in a non-local fashion. The main question was how the symmetry in a completely synchronous ensemble of identical oscillators breaks into two clusters, one synchronous group and another asynchronous group. How stable is this chimera state? In the beginning, it was apprehended that the chimera state is a transient behavior; the transient time increases with the size of a network (Wolfrum and Omel’chenko, 2011; Rosin et al., 2014). Later, it has been established that chimera states are possible stable states (Pecora et al., 2014; Omel’chenko, 2018; Laing, 2019) in an ensemble of identical oscillators and with symmetry in the connectivity matrix or the topology of a network. By this time, this phenomenon has been widely explored in single-layer networks (Abrams and Strogatz, 2004; Sethia et al., 2008; Laing, 2009; Hagerstrom et al., 2012; Martens et al., 2013; Omelchenko et al., 2013; Gopal et al., 2014; Hart et al., 2019; Majhi et al., 2019; Parastesh et al., 2020; Wang and Liu, 2020), multilayer networks (Ghosh and Jalan, 2016; Maksimenko et al., 2016; Sawicki et al., 2018; Ruzzene et al., 2020), and 3D networks (Maistrenko et al., 2015; Kasimatis et al., 2018; Kundu et al., 2019) with different forms of chimeras such as traveling chimera (Bera et al., 2016a; Omel’chenko, 2019; Dudkowski et al., 2019; Alvarez-Socorro et al., 2021) and spiral chimera (Martens et al., 2010; Gu et al., 2013). Various dynamical models (Hizanidis et al., 2015; Banerjee et al., 2016; Bera et al., 2016b; Saha et al., 2019) with different coupling schemes (Meena et al., 2016; Bera et al., 2017) and global coupling (Sethia and Sen, 2014; Yeldesbay et al., 2014; Hens et al., 2015a; Mishra et al., 2015) have been used for observing chimera patterns. The concepts of amplitude chimera (Hens et al., 2015a; Anna et al., 2016; Banerjee et al., 2018) and amplitude death chimera (Zakharova et al., 2014; Banerjee, 2015; Dutta and Banerjee, 2015) have been introduced. All the examples of chimera states revolve around the symmetry breaking of a complete coherent state into coherent and incoherent groups. This perception has been extended further to the observation of two coexisting subgroups of in-phase and antiphase oscillators (Maistrenko et al., 2017), which was also referred to as a chimera state. The necessary requirement of a large set of oscillators for chimera states to observe has also been relaxed with a smaller size of the network: Chimera patterns emerge in a set of four oscillators (Hart et al., 2016; Meena et al., 2016; Senthilkumar and Chandrasekar, 2019) and even three oscillators (Wojewoda et al., 2016; Maistrenko et al., 2017). In a laser system, delay in coupling has been used (Hart et al., 2016) for the observation of chimera states in four oscillators. A modified Kuramoto phase oscillators with inertia (Maistrenko et al., 2017) were used to demonstrate both in-phase and antiphase chimeras in three oscillators and later confirmed in experiments with three attractively coupled pendula (Wojewoda et al., 2016). In almost all the reported studies, attractive coupling has been used for the observation of chimeras, while a few examples are found to use a combination of both attractive and repulsive coupling (Hens et al., 2015a; Mishra et al., 2015) to originate chimera states in globally coupled oscillators.

We focus here on the role of repulsive interactions in the origin of chimera patterns in a small ensemble of three identical dynamical units. As reported earlier (Mishra et al., 2017; Ray et al., 2020), chimera states may emerge in a large ensemble of globally coupled Josephson junctions under repulsive interactions. Indeed, the repulsive coupling can induce chimera states in a smallest set of three Josephson junctions arranged in a ring. Interestingly, a single Josephson junction shows typical neuron-like spiking and bursting behaviors (Hens et al., 2015b; Hongray et al., 2015; Dana et al., 2006; Mishra et al., 2021), which is one of the reasons that encourage us to investigate the role of repulsive interactions (inhibitory in the sense of neuronal interaction) in a ring of three junctions. A single Josephson junction is represented by a resistance–capacitance shunted junction (RCSJ) circuit (Dana et al., 2001; Dana et al., 2006; Mishra et al., 2021), which remains in an excitable state until an external bias current is applied across the junction. The junction shows spiking limit cycle oscillation for bias current above a critical value. The dynamics of the junction also depends upon a damping-like parameter that is related to the shunted resistance and capacitance of the junction. It shows a bistable region, in the parameter space, where the limit cycle coexists with a steady state for a range of low damping. The RCSJ model can be represented by a second-order phase dynamics of the junction that governs the voltage drop across it. The RCSJ model also represents the dynamics of the simple pendulum model and discrete sine-Gordon equation. The dynamics of the junction is rotational when the trajectory of the junction makes a complete rotation around a cylindrical surface like an inverted pendulum, thereby originating a large-amplitude spiking oscillation. On the other hand, the junction may show, for an appropriate choice of parameters, librational motion when the trajectory of the junction dynamics is restricted to a small region of the cylindrical phase space. This appears like the small-amplitude oscillation of a pendulum.

Three Josephson junctions with identical parameters and by our choice of parameters are kept in rotational motion in an uncoupled state but kept away from the bistable region to avoid further complexity. The ring of three identical oscillators represents an all-to-all (or globally) coupled network and hence perfect symmetry. The junctions in the ring show 2π/3 out-of-phase motion in a cyclic order in time but emerge into a state of complete synchrony (CS) for repulsive interactions above a critical value. When the repulsive interactions in the ring are increased further, the symmetry is broken with the emergence of a sequence of desynchronous states, followed by chimera patterns: 1) two junctions are in complete synchrony (CS) in a state of rotational motion and one junction in incoherent rotational motion when they are all in a chaotic state, 2) two junctions in CS in rotational motion and one junction in incoherent libration when the dynamics of the junctions is periodic; this chimera pattern flips to two coherent junctions in libration and one in incoherent rotation for a change in initial conditions. We numerically delineate the different collective states in a two-parameter plane of the junctions using coherence measures and a libration index and use the master stability function (MSF) to demarcate the stable region of CS in the parameter plane.

2 Three Josephson Junctions in a Ring

A schematic diagram of the ring of three junctions is shown in Figure 1A. The RCSJ circuit is shown at right that represents the dynamics of each node. The dynamics of the ring of junctions is represented by the phase dynamics θ_i and voltage v_i (i = 1, 2, 3) across the ith junction given as follows (Josephson, 1962; Mishra et al., 2017):

$\begin{array}{ccc}\hfill \dot{{\theta }_i}& =\hfill & v_i,\hfill \end{array}(1)$

$\begin{array}{ccc}\hfill \dot{v_i}& =\hfill & I-\mathit{sin}{\theta }_i-\alpha v_i+\epsilon (v_{i-1}-2v_i+v_{i+1}),\hfill \end{array}$

where v_i+1 = v₁, if (i + 1) > n and v_i−1 = v₃, if (i − 1) < 1. The initial conditions are randomly chosen from the range θ_i(0) ∈ [ − π, π] and v_i(0) ∈ [0.1, 1]. The damping parameter $\alpha ={[h/2\pi e{I}^{2}RC]}^{1/2}$, where h is Planck’s constant and e is the electronic charge, and R and C are the resistance and capacitance of a junction, respectively. I is the external bias current normalized by the critical current I_c = 1.0 at each junction. The interaction between the nodes is established through junction voltages with a coupling strength ɛ, which is considered repulsive (negative) to observe our targeted chimera patterns. Figure 1B shows a phase diagram in an α − I plane for a single junction. The single junction remains excitable (FP) for bias current I < I_c and transits to limit cycle oscillation via saddle-node-invariant circle (SNIC) bifurcation for I > I_c and α > 1.19. In a lower range of α < 1.19 and I < I_c, the junction shows bistability (BS) when the limit cycle coexists with a steady state. The bistable state transits to limit cycle oscillation via fold bifurcation when I > 1.0. The bistable region is bounded by fold bifurcation (dashed horizontal line) and homoclinic (HC) bifurcation (blue curve) in the α − I parameter plane. For our observation of chimeras, we make a choice of parameters I > I_c and α > 1.19 so as to obtain limit cycle oscillation (rotational motion) in all three junctions in uncoupled state and keep them away from the bistable region to avoid further complexity in dynamics.

FIGURE 1

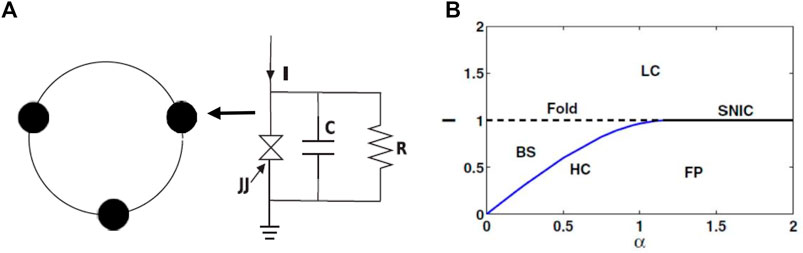
FIGURE 1. (A) Ring of three Josephson junctions (JJ). A schematic diagram of one RCSJ circuit shown at the right that represents the dynamics of each node in black circle. (B) Phase diagram of one RCSJ dynamics in an α − I parameter plane. Normalized critical current I_c = 1.0. The junction shows limit cycle (LC) oscillation for I > I_c = 1.0. The junction has a bistable (BS) region bounded by a fold bifurcation line (horizontal dashed line) and a homoclinic (HC) bifurcation curve (blue line). A stable fixed point (FP) coexists with a saddle for I < 1.0 in a region between the HC (blue line) and the saddle-node-invariant circle (SNIC) line. The junction transits to an LC state via SNIC bifurcation for I > 1.0.

3 Coherence and Libration Index

To check the CS state, we first calculate the error functions between all the pairs of nodes, separately, as follows:

$e_{12}=\sqrt{⟨{(v_1-v_2)}^2⟩};e_{13}=\sqrt{⟨{(v_1-v_3)}^3⟩};e_{23}=\sqrt{⟨{(v_2-v_3)}^2⟩},(2)$

where $⟨.⟩$ indicates time average. We check all the three error functions simultaneously and detect a chimera state when two of the partial error functions are zero (say, e₁₂ = 0 and e₁₃ = 0).

The global error variable is then calculated as follows:

$err=(e_{12}+e_{13}+e_{23})/3.(3)$

For CS in the network, err = 0 and err ≠ 0 indicate partial synchrony or incoherence. We use a libration index (Mishra et al., 2017) to distinguish librational and rotational motion of the junctions in different collective states:

$LI=\frac{1}{3}\sum _{j=1}^3{\mathrm{\Theta }}_j,(4)$

where Θ_j = Θ(δ − m_j). Θ(.) is the Heaviside step function, where δ is an arbitrarily chosen small threshold and $m_j=1-0.5*\left(\mathit{max}(\mathit{cos}[{\theta }_j(t)])-\mathit{min}(\mathit{cos}[{\theta }_j(t)])\right)$. The libration index becomes LI = 0 for oscillators in libration and LI = 1 when they are in rotational motion. A value of 0 < LI < 1 indicates the coexistence of librational and rotational motions in the ring of junctions.

For demarcation of the stable CS state in the parameter plane of the junctions in Figure 2, we numerically estimate the MSF (Pecora and Carroll, 1998) of identical junctions by using the variational equation of the ring of junctions. The dynamics of the ith node is ${\dot{\mathbf{x}}}_i=\mathbf{F}({\mathbf{x}}_{\mathbf{i}})+\epsilon {\sum }_j{G}_{ij}\mathbf{H}({\mathbf{x}}_{\mathbf{j}})$. Now, let x = (x₁, x₂, …, x_n), F(X) = [F(x₁), F(x₂), …, F(x_n)], H(X) = [H(x₁), H(x₂), …, H(x_n)] is the coupling matrix and G be the adjacency matrix {G_ij}, then

$\dot{\mathbf{x}}=\mathbf{F}(\mathbf{x})+\epsilon \mathbf{G}\otimes \mathbf{H}(\mathbf{x}),(5)$

where ⊗ denotes the direct product. The variational equation of Eq. 5 by assuming ξ_i as a small perturbation in the ith node when ξ = (ξ₁, ξ₂, …, ξ_n), (i = 1, 2, ..n) is given as follows:

$\dot{\xi }=[{\mathbf{1}}_{\mathbf{n}}\otimes D\mathbf{F}+\epsilon \mathbf{G}\otimes D\mathbf{H}]\xi ,(6)$

when H is the coupling matrix E = (0 0; 1 0), implying coupling in second variable and DH = E. By a block diagonalization of the variational equation, each block will be of the form as follows:

$\dot{{\xi }_k}=[D\mathbf{F}+\epsilon {\gamma }_{k}D\mathbf{H}]{\xi }_k,(7)$

where γ_k is the eigenvalue of G, k = 0, 1, 2, …, n − 1. For k = 0, we have the variational equation for the synchronization manifold γ₀ = 0. The Jacobian matrices DF and DH are the same for each block, since they are evaluated on the synchronized state. Thus, for each k, the form of each block [Eq. 7] is same with only the scalar multiplier ɛγ_k differing. This leads us to the following formulation of the master stability equation and the associated MSF: We calculate the maximum Lyapunov exponents λ_max for the generic variational equation as follows:

$\dot{\zeta }=[D\mathbf{F}+(\alpha +i\beta )D\mathbf{H}]\zeta ,(8)$

as a function of α and β. This yields the λ_max as a point on the real axis since we check the real part of the exponent, and G has only the real eigenvalues in our case. The sign of λ_max will reveal the stability of the eigenmodes, and hence, we have the MSF, which is used for delineating the boundary (blue dashed lines) of the CS region (A, yellow) as shown in Figure 2, where λ_max becomes negative.

FIGURE 2

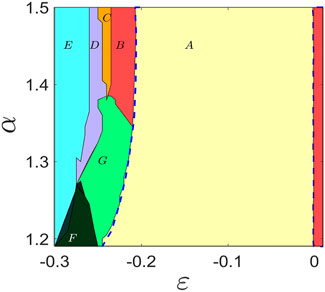
FIGURE 2. Phase diagram in an α − ɛ plane of a ring of three identical Josephson junctions. A large region of CS (region A, yellow) is demarcated within the boundaries of blue dashed lines, where λ_max is negative as estimated by using the MSF (8) for a range of repulsive coupling and α values. For larger repulsive coupling (beyond the blue dashed curve), CS becomes unstable, and there first emerges a state of asynchronous limit cycle dynamics (B, red), then asynchronous chaos (C, orange), followed by a reasonable range of rotational chimera (D, purple) in a chaotic state, and finally, a chimera state of mixed rotational and libration (E, cyan) in periodic motion for larger repulsive coupling and a broad range of α > 1.2. Stability of CS is also lost for attractive coupling (ɛ > 0, red region) as marked by a vertical dashed blue line. There are regions of mixed states F (black) and G (green) of coexisting chimera and desynchronization. Parameter I = 1.5.

4 Phase Diagram: Ring of Josephson Junctions

We draw a phase diagram to delineate the regions of a variety of collective states including the chimera patterns for the three junctions in the ring in an α − ɛ parameter plane in Figure 2. All the junctions are in out-of-phase for attractive coupling (ɛ > 0) when the junction voltages evolve in 2π/3 cyclic motion however become completely synchronized (CS) in the periodic state for a range of repulsive coupling (ɛ < 0). The boundaries of ɛ for CS are demarcated at two ends (by two blue dashed lines), which are indicated by a transition of λ_max to a negative value as estimated by using the MSF and perfectly matching with the numerically simulated boundaries of CS (region A, yellow) in the phase diagram. CS breaks down for attractive coupling at one end (red region) and larger repulsive coupling as well at the other end (regions B and G). CS transits to asynchronous periodic motion (B, red) of the junctions and a mixed state (G, green) for larger repulsive coupling. The chimera pattern (partial synchrony) coexists with complete asynchronous oscillation in region G (chaotic or higher periodic rotational motion). The ring of junctions becomes chaotic in region C (orange) and remains completely asynchronous. They form a chaotic chimera pattern with two coherent and one incoherent junctions in region D when all the junctions maintain rotational motion. Finally, a periodic state re-emerges in region E (cyan) with a chimera pattern. Two junctions become coherent in rotational periodic motion that coexists with a single junction in incoherent periodic libration. These chimera patterns flip with a new pattern when two junctions become coherent in libration and one in incoherent rotation; this flipping occurs due to sensitivity in initial conditions. Region F represents mixed states of coexisting chimera patterns and asynchronous states.

5 Smallest Chimeras in Three Junctions

Three identical junctions in the ring evolve out of phase in time in a cyclic order of 2π/3 phase lag for attractive coupling (ϵ > 0), and they evolve into a state of complete identical phase and amplitude for a repulsive coupling (ϵ < 0) above a threshold as decided by the MSF. The time evolution of the three junctions is plotted in Figures 3A,B when the junctions emerge in an out-of-phase state and CS state, for ɛ = 0.02 and ɛ = − 0.01, respectively. Both the out-of-phase and CS states are true for N > 3 number of junctions in the ring (results not shown here but checked for N = 4, 7, 8). For further illustration, the dynamics of three junction voltages v are demonstrated in Figure 4. We have already recognized two reasonably broad parameter regions of chimera patterns in the parameter planes (D and E). Now, we demonstrate their exemplary dynamics using the trajectories of the three junctions in a θ − v cylindrical plane and their corresponding spatiotemporal dynamics and how they evolve against varying repulsive coupling ɛ at a fixed α = 1.45. Figures 4A,B represent the CS state for repulsive interactions as confirmed by a plot of the trajectories (red) of three junctions in a θ − v cylindrical plane (left panel) and its corresponding spatiotemporal plot at the right panel. For stronger repulsive interaction, Figures 4C,D show that CS breaks down, although the junctions maintain rotational periodic motion; however, their trajectories are distinctly different (blue, red, and green) which is confirmed by their incoherent motion in the spatiotemporal plot (right panel). The junctions become chaotic for larger repulsive current yet continue with rotational incoherent motion as depicted by their trajectories and spatiotemporal evolution in Figures 4E,F. The first sign of the chimera pattern appears for further increase in repulsive coupling when all the junctions are in chaotic rotational motion, as shown in Figure 4G. However, two of the junctions (indices 1 and 2) are evolving in the coherence of amplitude and phase, while the third junction (index 3) is incoherent in rotational motion as depicted in the spatiotemporal plot in Figure 4H. The collective dynamics of three junctions then switches to periodic motion for a further increase in repulsive coupling. Interestingly, the junctions split into two groups when a pair of junctions remains in coherent rotation (blue), as shown in Figure 4I, and one junction 3) switches to librational motion (red) and incoherent to the other two junctions (1 and 2). This state of coexisting coherence and incoherence in two groups as typically defined as a chimera pattern is confirmed by their spatiotemporal evolution in Figure 4J.

FIGURE 3

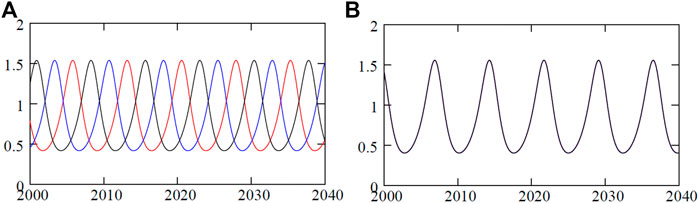
FIGURE 3. Time evolution of voltage in three junctions. Voltages v_i (i = 1, 2, 3) in three junctions evolve in (A) out-of-phase 2π/3 motion in a cyclic order in time (red, black, and blue lines) for ɛ = 0.02, (B) converge into complete synchrony of amplitude and phase (black lines) for ɛ = − 0.01. Parameters α = 1.45 and i = 1.5.

FIGURE 4

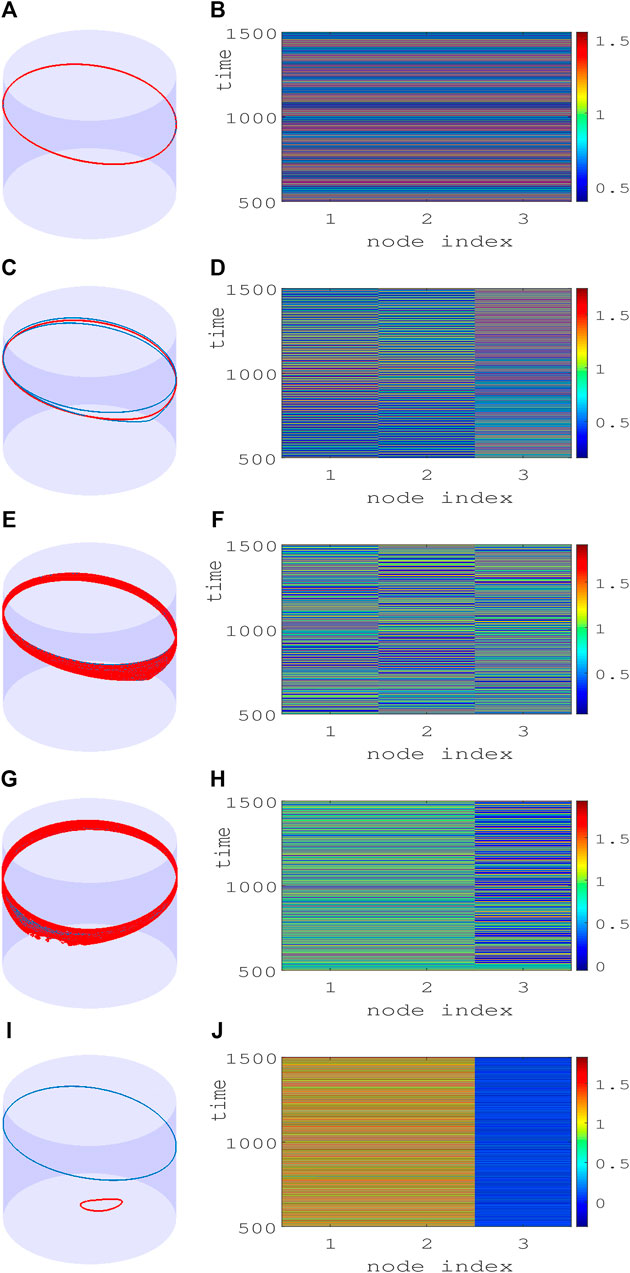
FIGURE 4. Smallest chimeras in a ring of three Josephson junctions (A,C,E,G,I). Trajectory of junctions (panels in left column) in a θ-v cylindrical plane and (B,D,F,H,J) spatiotemporal evolution (panels in right column) of junction voltage v in three junctions. Region (A): (A) One coherent periodic trajectory (red) is seen with (B) coherent evolution of all three junctions in time for α = 1.45, ɛ = − 0.02. Region (B): Three distinctly separate periodic rotational trajectories (C) are seen in incoherent motion in time (D) for α = 1.45, ɛ = − 0.23. Region (C): Three junctions are in chaotic rotational motion (E) with incoherent spatial evolution in time (F) for α = 1.45, ɛ = − 0.24. Region (D): Chimera pattern in chaotic motion (G) when two junctions are evolving in coherent motion in time (H) and one is incoherent for α = 1.45, ɛ = − 0.25. Region (E): Chimera pattern in dual motion. One coherent pair of junctions in rotational motion (I) and one junction in incoherent librational motion for α = 1.45, ɛ = − 0.265. Regions (A–E) are identified here as depicted in Figure 2. Color bars depict the amplitude limit of junction voltages.

6 Conclusion

The role of repulsive interactions in the origin of chimera patterns in a small set of three dynamical units in a ring has been explored here. A ring of three nodes with all-to-all coupling is quite often considered as a network motif (Milo et al., 2002). We used the exemplary model of the superconducting Josephson junction as dynamical units that basically represent a second-order phase dynamics under damping and external bias. Noteworthy that this model also represents the dynamics of a simple pendulum and the discrete sine-Gordon equation. For attractive coupling, three junctions maintain an out-of-phase in 2π/3 alternate rotational motion in a cyclic order, which is counterintuitive to the common notion of synchrony under attractive coupling. Interestingly, three junctions emerge into CS for repulsive coupling only. We are still working on this strange collective behavior but yet to find a complete explanation, although we make some inroads into why and when such a behavior may emerge that is to be reported in the future. However, we have checked this new paradigm of CS using the MSF that establishes its stability in a range of repulsive coupling independent of the number of junctions in the ring. Chimera patterns emerge in three junctions beyond the CS state when it breaks down for larger repulsive coupling. We define chimera states here as two coherent junctions and one junction incoherent to the other two that follow the standard definition of chimera states in the literature. We identified two different patterns of chimera states for repulsive interactions. Three junctions may remain in chaotic rotational motion, yet two of them evolve in coherence, while the third junction also evolves in rotational motion but incoherent to the other two junctions. In another kind of chimera pattern, for larger repulsive coupling, two junctions may evolve in coherent rotational motion, while the third junction switches to small-amplitude librational motion and becomes incoherent to the other two junctions. This chimera pattern is sensitive to initial conditions when the chimera pattern may flip to coherent oscillators in coherence, while the third is in incoherent rotational motion. We cannot designate the chimera patterns as strong chimera (Zhang and Motter, 2021). However, some recent reports consider this latter chimera pattern as a solitary state (Jaros et al., 2018; Semenova et al., 2018; Rybalova et al., 2021) since a single oscillator behaves differently, in the dynamical sense, from the other two coherent oscillators.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Files, and further inquiries can be directed to the corresponding author.

Author Contributions

SS and SD both worked on the simulations and wrote the manuscript. SS worked more on the rigors of numerical simulations, master stability functions, and drawing the two-parameter bifurcation diagram and others.

Conflict of Interest

The reviewer DG declared a past collaboration with one of the authors SKD to the handling editor.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abrams, D. M., and Strogatz, S. H. (2004). Chimera States for Coupled Oscillators. Phys. Rev. Lett. 93 (17), 174102. doi:10.1103/physrevlett.93.174102

PubMed Abstract | CrossRef Full Text | Google Scholar

Alvarez-Socorro, A. J., Clerc, M. G., and Verschueren, N. (2021). Traveling Chimera States in Continuous media. Commun. Nonlinear Sci. Numer. Simulation 94, 105559. doi:10.1016/j.cnsns.2020.105559

CrossRef Full Text | Google Scholar

Anna, Z., Kapeller, M., and Schöll, E. (2016). Amplitude Chimeras and Chimera Death in Dynamical Networks. J. Phys. Conf. Ser. 727, 012018. IOP Publishing. doi:10.1088/1742-6596/727/1/012018

CrossRef Full Text | Google Scholar

Banerjee, T., Dutta, P. S., Zakharova, A., and Schöll, E. (2016). Chimera Patterns Induced by Distance-dependent Power-Law Coupling in Ecological Networks. Phys. Rev. E 94 (3), 032206. doi:10.1103/PhysRevE.94.032206

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, T., Biswas, D., Ghosh, D., Schöll, E., and Zakharova, A. (2018). Networks of Coupled Oscillators: from Phase to Amplitude Chimeras. Chaos 28 (11), 113124. doi:10.1063/1.5054181

PubMed Abstract | CrossRef Full Text | Google Scholar

Banerjee, T. (2015). Mean-Field-Diffusion-Induced Chimera Death State. EPL 110 (6), 60003. doi:10.1209/0295-5075/110/60003

CrossRef Full Text | Google Scholar

Bera, B. K., Ghosh, D., and Banerjee, T. (2016). Imperfect Traveling Chimera States Induced by Local Synaptic Gradient Coupling. Phys. Rev. E 94 (1), 012215. doi:10.1103/PhysRevE.94.012215

PubMed Abstract | CrossRef Full Text | Google Scholar

Bera, B. K., Ghosh, D., and Lakshmanan, M. (2016). Chimera States in Bursting Neurons. Phys. Rev. E 93 (1), 012205. doi:10.1103/PhysRevE.93.012205

PubMed Abstract | CrossRef Full Text | Google Scholar

Bera, B. K., Majhi, S., Ghosh, D., and Perc, M. (2017). Chimera States: Effects of Different Coupling Topologies. EPL 118 (1), 10001. doi:10.1209/0295-5075/118/10001

CrossRef Full Text | Google Scholar

Dana, S. K., Sengupta, D. C., and EdohEdoh, K. D. (2001). Chaotic Dynamics in Josephson junction. IEEE Trans. Circuits Syst. 48 (8), 990–996. doi:10.1109/81.940189

CrossRef Full Text | Google Scholar

Dana, S. K., Sengupta, D. C., and Hu, C.-K. (2006). Spiking and Bursting in Josephson junction. IEEE Trans. Circuits Syst. 53 (10), 1031–1034. doi:10.1109/tcsii.2006.882183

CrossRef Full Text | Google Scholar

Dudkowski, D., Czołczyński, K., and Kapitaniak, T. (2019). Traveling Chimera States for Coupled Pendula. Nonlinear Dyn. 95 (3), 1859–1866. doi:10.1007/s11071-018-4664-5

CrossRef Full Text | Google Scholar

Dutta, P. S., and Banerjee, T. (2015). Spatial Coexistence of Synchronized Oscillation and Death: A Chimeralike State. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 92 (4), 042919. doi:10.1103/PhysRevE.92.042919

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghosh, S., and Jalan, S. (2016). Emergence of Chimera in Multiplex Network. Int. J. Bifurcation Chaos 26 (07), 1650120. doi:10.1142/s0218127416501200

CrossRef Full Text | Google Scholar

Gopal, R., Chandrasekar, V. K., Venkatesan, A., and Lakshmanan, M. (2014). Observation and Characterization of Chimera States in Coupled Dynamical Systems with Nonlocal Coupling. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 89 (5), 052914. doi:10.1103/PhysRevE.89.052914

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, C., St-Yves, G., and Davidsen, J. (2013). Spiral Wave Chimeras in Complex Oscillatory and Chaotic Systems. Phys. Rev. Lett. 111 (13), 134101. doi:10.1103/physrevlett.111.134101

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagerstrom, A. M., Murphy, T. E., Roy, R., Hövel, P., Omelchenko, I., and Schöll, E. (2012). Experimental Observation of Chimeras in Coupled-Map Lattices. Nat. Phys 8 (9), 658–661. doi:10.1038/nphys2372

CrossRef Full Text | Google Scholar

Hart, J. D., Bansal, K., Murphy, T. E., and Roy, R. (2016). Experimental Observation of Chimera and Cluster States in a Minimal Globally Coupled Network. Chaos 26 (9), 094801. doi:10.1063/1.4953662

PubMed Abstract | CrossRef Full Text | Google Scholar

Hart, J. D., Larger, L., Murphy, T. E., and Roy, R. (2019). Delayed Dynamical Systems: Networks, Chimeras and Reservoir Computing. Phil. Trans. R. Soc. A. 377 (2153), 20180123. doi:10.1098/rsta.2018.0123

PubMed Abstract | CrossRef Full Text | Google Scholar

Hens, C. R., Mishra, A., Roy, P. K., Sen, A., and Dana, S. K. (2015). Chimera States in a Population of Identical Oscillators under Planar Cross-Coupling. Pramana - J. Phys. 84 (2), 229–235. doi:10.1007/s12043-015-0941-8

CrossRef Full Text | Google Scholar

Hens, C., Pal, P., and Dana, S. K. (2015). Bursting Dynamics in a Population of Oscillatory and Excitable Josephson Junctions. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 92 (2), 022915. doi:10.1103/PhysRevE.92.022915

PubMed Abstract | CrossRef Full Text | Google Scholar

Hizanidis, J., Panagakou, E., Omelchenko, I., Schöll, E., Hövel, P., and Provata, A. (2015). Chimera States in Population Dynamics: Networks with Fragmented and Hierarchical Connectivities. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 92 (1), 012915. doi:10.1103/PhysRevE.92.012915

PubMed Abstract | CrossRef Full Text | Google Scholar

Hongray, T., Balakrishnan, J., and Dana, S. K. (2015). Bursting Behaviour in Coupled Josephson Junctions. Chaos 25 (12), 123104. doi:10.1063/1.4936675

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaros, P., Brezetsky, S., Levchenko, R., Dudkowski, D., Kapitaniak, T., and Maistrenko, Y. (2018). Solitary States for Coupled Oscillators with Inertia. Chaos 28 (1), 011103. doi:10.1063/1.5019792

PubMed Abstract | CrossRef Full Text | Google Scholar

Josephson, B. D. (1962). Possible New Effects in Superconductive Tunnelling. Phys. Lett. 1, 251–253. doi:10.1016/0031-9163(62)91369-0

CrossRef Full Text | Google Scholar

Kasimatis, T., Hizanidis, J., and Provata, A. (2018). Three-Dimensional Chimera Patterns in Networks of Spiking Neuron Oscillators. Phys. Rev. E 97 (5), 052213. doi:10.1103/PhysRevE.97.052213

PubMed Abstract | CrossRef Full Text | Google Scholar

Kundu, S., BeraBera, B. K., Ghosh, D., and Lakshmanan, M. (2019). Chimera Patterns in Three-Dimensional Locally Coupled Systems. Phys. Rev. E 99 (2), 022204. doi:10.1103/PhysRevE.99.022204

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuramoto, Y., and Battogtokh, D. (2002). Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators. arXiv preprint cond-mat/0210694.

Google Scholar

Laing, C. R. (2009). Chimera States in Heterogeneous Networks. Chaos 19 (1), 013113. doi:10.1063/1.3068353

PubMed Abstract | CrossRef Full Text | Google Scholar

Laing, C. R. (2019). Dynamics and Stability of Chimera States in Two Coupled Populations of Oscillators. Phys. Rev. E 100 (4), 042211. doi:10.1103/PhysRevE.100.042211

PubMed Abstract | CrossRef Full Text | Google Scholar

Maistrenko, Y., Sudakov, O., Osiv, O., and Maistrenko, V. (2015). Chimera States in Three Dimensions. New J. Phys. 17 (7), 073037. doi:10.1088/1367-2630/17/7/073037

CrossRef Full Text | Google Scholar

Maistrenko, Y., Brezetsky, S., Jaros, P., Levchenko, R., and Kapitaniak, T. (2017). Smallest Chimera States. Phys. Rev. E 95 (1), 010203. doi:10.1103/PhysRevE.95.010203

PubMed Abstract | CrossRef Full Text | Google Scholar

Majhi, S., BeraBera, B. K., Ghosh, D., and Perc, M. (2019). Chimera States in Neuronal Networks: a Review. Phys. Life Rev. 28, 100–121. doi:10.1016/j.plrev.2018.09.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Maksimenko, V. A., Makarov, V. V., Bera, B. K., Ghosh, D., Dana, S. K., Goremyko, M. V., et al. (2016). Excitation and Suppression of Chimera States by Multiplexing. Phys. Rev. E 94 (5), 052205. doi:10.1103/PhysRevE.94.052205

PubMed Abstract | CrossRef Full Text | Google Scholar

Martens, E. A., LaingLaing, C. R., and Strogatz, S. H. (2010). Solvable Model of Spiral Wave Chimeras. Phys. Rev. Lett. 104 (4), 044101. doi:10.1103/PhysRevLett.104.044101

PubMed Abstract | CrossRef Full Text | Google Scholar

Martens, E. A., Thutupalli, S., Fourrière, A., and Hallatschek, O. (2013). Chimera States in Mechanical Oscillator Networks. Proc. Natl. Acad. Sci. U S A. 110 (26), 10563–10567. doi:10.1073/pnas.1302880110

PubMed Abstract | CrossRef Full Text | Google Scholar

Meena, C., Murali, K., and Sinha, S. (2016). Chimera States in star Networks. Int. J. Bifurcation Chaos 26 (09), 1630023. doi:10.1142/s0218127416300238

CrossRef Full Text | Google Scholar

Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network Motifs: Simple Building Blocks of Complex Networks. Science 298 (5594), 824–827. doi:10.1126/science.298.5594.824

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishra, A., Hens, C., Bose, M., Roy, P. K., and Dana, S. K. (2015). Chimeralike States in a Network of Oscillators under Attractive and Repulsive Global Coupling. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 92 (6), 062920. doi:10.1103/PhysRevE.92.062920

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishra, A., Saha, S., Hens, C., Roy, P. K., Bose, M., Louodop, P., et al. (2017). Coherent Libration to Coherent Rotational Dynamics via Chimeralike States and Clustering in a Josephson Junction Array. Phys. Rev. E 95 (1), 010201. doi:10.1103/PhysRevE.95.010201

PubMed Abstract | CrossRef Full Text | Google Scholar

Mishra, A., Ghosh, S., Kumar Dana, S., Kapitaniak, T., and Hens, C. (2021). Neuron-Like Spiking and Bursting in Josephson Junctions: A Review. Chaos 31 (5), 052101. doi:10.1063/5.0050526

PubMed Abstract | CrossRef Full Text | Google Scholar

Omel’chenko, O. E. (2018). The Mathematics Behind Chimera States. Nonlinearity 31 (5), R121. doi:10.1088/1361-6544/aaaa07

CrossRef Full Text | Google Scholar

Omel’chenko, O. E. (2019). Traveling Chimera States. J. Phys. A: Math. Theor. 52 (10), 104001. doi:10.1088/1751-8121/ab0043

CrossRef Full Text | Google Scholar

Omelchenko, I., Omel’chenko, O. E., Hövel, P., and Schöll, E. (2013). When Nonlocal Coupling between Oscillators Becomes Stronger: Patched Synchrony or Multichimera States. Phys. Rev. Lett. 110 (22), 224101. doi:10.1103/physrevlett.110.224101

PubMed Abstract | CrossRef Full Text | Google Scholar

Parastesh, F., Jafari, S., Azarnoush, H., Shahriari, Z., Wang, Z., Boccaletti, S., et al. (2020). Chimeras. Phys. Rep. doi:10.1016/j.physrep.2020.10.003

CrossRef Full Text | Google Scholar

Pecora, L. M., and Carroll, T. L. (1998). Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 80 (10), 2109–2112. doi:10.1103/physrevlett.80.2109

CrossRef Full Text | Google Scholar

Pecora, L. M., Sorrentino, F., Hagerstrom, A. M., Murphy, T. E., and Roy, R. (2014). Cluster Synchronization and Isolated Desynchronization in Complex Networks with Symmetries. Nat. Commun. 5 (1), 4079. doi:10.1038/ncomms5079

PubMed Abstract | CrossRef Full Text | Google Scholar

Ray, A., Mishra, A., Ghosh, D., Kapitaniak, T., Dana, S. K., and Hens, C. (2020). Extreme Events in a Network of Heterogeneous Josephson Junctions. Phys. Rev. E 101 (3), 032209. doi:10.1103/PhysRevE.101.032209

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosin, D. P., Rontani, D., Haynes, N. D., Schöll, E., and Gauthier, D. J. (2014). Transient Scaling and Resurgence of Chimera States in Networks of Boolean Phase Oscillators. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 90 (3), 030902. doi:10.1103/PhysRevE.90.030902

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruzzene, G., Omelchenko, I., Sawicki, J., Zakharova, A., Schöll, E., and Andrzejak, R. G. (2020). Remote Pacemaker Control of Chimera States in Multilayer Networks of Neurons. Phys. Rev. E 102 (5), 052216. doi:10.1103/PhysRevE.102.052216

PubMed Abstract | CrossRef Full Text | Google Scholar

Rybalova, E. V., Zakharova, A., and Strelkova, G. I. (2021). Interplay between Solitary States and Chimeras in Multiplex Neural Networks. Chaos, Solitons & Fractals 148, 111011. doi:10.1016/j.chaos.2021.111011

CrossRef Full Text | Google Scholar

Saha, S., Bairagi, N., and Kumar Dana, S. (2019). Chimera States in Ecological Network under Weighted Mean-Field Dispersal of Species. Front. Appl. Maths. Stat. 5, 15. doi:10.3389/fams.2019.00015

CrossRef Full Text | Google Scholar

Sawicki, J., Omelchenko, I., Anna, Z., and Schöll, E. (2018). Synchronization Scenarios of Chimeras in Multiplex Networks. Eur. Phys. J. Spec. Top. 227 (10), 1161–1171. doi:10.1140/epjst/e2018-800039-y

CrossRef Full Text | Google Scholar

Schöll, E. (2016). Synchronization Patterns and Chimera States in Complex Networks: Interplay of Topology and Dynamics. Eur. Phys. J. Spec. Top. 225 (6), 891–919. doi:10.1140/epjst/e2016-02646-3

CrossRef Full Text | Google Scholar

Semenova, N., Vadivasova, T., and Anishchenko, V. (2018). Mechanism of Solitary State Appearance in an Ensemble of Nonlocally Coupled Lozi Maps. Eur. Phys. J. Spec. Top. 227 (10), 1173–1183. doi:10.1140/epjst/e2018-800035-y

CrossRef Full Text | Google Scholar

Senthilkumar, D. V., and Chandrasekar, V. K. (2019). Local and Global Chimera States in a Four-Oscillator System. Phys. Rev. E 100 (3), 032211. doi:10.1103/PhysRevE.100.032211

PubMed Abstract | CrossRef Full Text | Google Scholar

Sethia, G. C., and Sen, A. (2014). Chimera States: The Existence Criteria Revisited. Phys. Rev. Lett. 112 (14), 144101. doi:10.1103/physrevlett.112.144101

PubMed Abstract | CrossRef Full Text | Google Scholar

Sethia, G. C., Sen, A., and Atay, F. M. (2008). Clustered Chimera States in Delay-Coupled Oscillator Systems. Phys. Rev. Lett. 100 (14), 144102. doi:10.1103/physrevlett.100.144102

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., and Liu, Z. (2020). A Brief Review of Chimera State in Empirical Brain Networks. Front. Physiol. 11, 724. doi:10.3389/fphys.2020.00724

PubMed Abstract | CrossRef Full Text | Google Scholar

Wojewoda, J., Czolczynski, K., Maistrenko, Y., and Kapitaniak, T. (2016). The Smallest Chimera State for Coupled Pendula. Sci. Rep. 6 (1), 34329. doi:10.1038/srep34329

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolfrum, M., and Omel'chenko, O. E. (2011). Chimera States Are Chaotic Transients. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 84 (1), 015201. doi:10.1103/PhysRevE.84.015201

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeldesbay, A., Pikovsky, A., and Rosenblum, M. (2014). Chimeralike States in an Ensemble of Globally Coupled Oscillators. Phys. Rev. Lett. 112 (14), 144103. doi:10.1103/physrevlett.112.144103

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakharova, A., Kapeller, M., and Schöll, E. (2014). Chimera Death: Symmetry Breaking in Dynamical Networks. Phys. Rev. Lett. 112 (15), 154101. doi:10.1103/PhysRevLett.112.154101

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and Motter, A. E. (2021). Mechanism for strong Chimeras. Phys. Rev. Lett. 126 (9), 094101. doi:10.1103/PhysRevLett.126.094101

PubMed Abstract | CrossRef Full Text | Google Scholar