- Department of Physics and Astronomy and Center for Neurodynamics, University of Missouri at St. Louis, St. Louis, MO, United States
We model the dynamics of sleep states in two connected model brain hemispheres, using groups of coupled individual Hindmarsh-Rose neural oscillators. In a single isloated hemisphere, sleep-promoting neurons and wake-promoting neurons exhibit alternating levels of within-group mean field activity, as well as alternating levels of stochastic phase synchronization, as the system moves between simulated day and night. In a two-hemisphere model, we find differences in the behavior of the sleep-promototing or wake-promoting regions between hemispheres, indicative of chimera-like behavior. We observe phase-cluster states, in which different hemispheres exhibit different bursting dynamics, as well as differences in synchronization between hemispheres. This provides a basis for modeling unihemispheric sleep, which occurs naturally in cetaceans and some bird species, among others, as well as asymmetric sleep, which occurs in human subjects suffering from sleep apnea or experiencing the “first night effect” induced by sleeping in a novel environment.
Introduction
Sleep is a nearly ubiquitous phenomenon among living organisms. Even the jellyfish Cassiopea, which lacks a centralized nervous system, exhibits a sleep-like state (Nath et al., 2017). Yet the reason for the necessity of sleep, and the processes that control it, are far from well understood, despite a rapidly growing literature on the genetic regulation of sleep and other circadian rhythms in animals (Rijo-Ferreira and Takahashi, 2019) and plants (Oakenfull and Davis, 2017; Creux and Harmer, 2019), and extensive studies of the neural regions controlling sleep states in mammals (Scammell et al., 2017).
Sleep is an inherently dynamical phenomenon. In the mammalian brain, sleep is modulated by external drives such as the light-dark cycle, and also by an internal circadian rhythm generated within the suprachiasmatic nucleus (SCN) (Moore and Eichler, 1972), which receives input from external light stimuli (Moore and Lenn, 1972). In concert with external light stimuli, the SCN moderates a mammal’s daily and seasonal rhythms and behaviors (Aton and Herzog, 2005). Computational studies of sleep dynamics often use empirically-based models of the generated circadian rhythm, rather than simulating neural activity in the SCN. These include the model of Daan et al. (1984), who used a skewed sine wave as the circadian drive; a two-oscillator model developed by Strogatz (1987); a square array of SCN oscillators (Kunz and Achermann, 2003); and a light-based model with an additional non-photic input (St. Hilaire et al., 2007).
From a dynamical standpoint, sleep can be pictured as a phenomenon of neural synchronization modulated by internal pacemakers in the SCN and external drives such as the light-dark cycle. However, the situation is significantly complicated by the fact that various brain regions are involved in mutual excitatory and inhibitory interactions which regulate sleep processes, as will be discussed further below. Moreover, brains have two hemispheres, and sleep is not always symmetric.
Most mammals experience bihemispheric sleep (BHS), in which both hemispheres exhibit the same sleep state at the same time (Rattenborg et al., 2000; Corsi-Cabrera et al., 2006). Although not a very common occurrence, interhemispheric asymmetry has been observed in human sleep (Braun et al., 1997). Asymmetry can arise from separation of the hemispheres through surgery (Corsi-Cabrera et al., 2006), and also in humans with sleep apnea (Abeyratne et al., 2010; Rial et al., 2013), which has been found to correlate with the magnitude of hemispheric asymmetry (Abeyratne et al., 2010). During normal breathing in sleep, apneic patients exhibit asymmetry; at the onset of an apneic episode, the hemispheres resynchronize (Rial et al., 2013).
Asymmetry between hemispheres during sleep can also occur in healthy humans, as discovered by Tamaki et al. (2016). When humans fall asleep in a new, unfamiliar location, portions of one hemisphere do not sleep as deeply as the other hemisphere, maintaining a heightened awareness of the environment. During this time, unfamiliar sounds will arouse a person more frequently and with faster response time when detected by the more lightly sleeping hemisphere than when detected by the more deeply sleeping hemisphere. This phenomenon has only been observed during the first night in a novel environment and is thus called the “first night effect”.
Unlike humans, during normal sleep Cetaceans (whales, dolphins and porpoises) allow one hemisphere at a time to sleep while the other maintains vigilance, switching multiple times during a period of rest. This form of sleep is called unihemispheric sleep (UHS), characterized by one hemisphere exhibiting an electroencephalography (EEG) pattern congruent with non-rapid eye movement (NREM) sleep (characterized by high amplitude and low frequency, synchronized), while the other hemisphere shows an EEG pattern that indicates wakefulness (low amplitude and high frequency, desynchronized). The wakeful hemisphere can exhibit intermediate activity between NREM and wakefulness, without dipping so far into sleep that both hemispheres are considered in the same state (Rattenborg et al., 2000). An early EEG study by Mukhametov et al. (1977) found simultaneous, independent synchronization and desynchronization in the two hemispheres of the dolphin brain.
Even before the discovery of UHS, some birds’ ability to fly continuously for days at a time was a scientific puzzle. When did they sleep? Due to the size mismatch between tiny avian subjects and large experimental recording apparatus, studies have been limited (Rattenborg et al., 2000; Rattenborg, 2017). Scientists hypothesized, based on visual observations and indirect studies, that birds might fly either using only one hemisphere (UHS), or simply lock their wings and glide (BHS), supported by the evidence that birds are still capable of flight after the connections between the brain and the spinal cord had been severed (Rattenborg et al., 2000). Indeed, due to newer tracking capabilities, it has been found that great frigatebirds (Fregata minor) do utilize both UHS and BHS while they fly. However, the amount of time they spend sleeping during flight was surprisingly small, less than an hour per day (mostly UHS or asymmetric sleep), in contrast to nearly 13 h of sleep per day while nesting (Rattenborg, 2017).
In contrast to studies of birds in flight, birds exhibit UHS conditionally while resting on land. Rattenborg et al. (1999) studied Mallard ducks (Anas platyrhynchos) and showed that, when sleeping in groups, the ducks showed a predilection for sleeping unihemispherically when on the outer edge of the group, with the open eye facing away from the group, presumably to watch for predators. Ducks in the center showed no preference for which eye they held open during UHS, and also exhibited less UHS than those on the outer edge (Rattenborg et al., 1999). Some species adjust their behavior from UHS to BHS depending on circumstances. For example, eared seals experience UHS while in the water and BHS on land. In the water, they use their “awake” hemisphere to paddle and keep their face above water to breathe, occasionally switching sides (Rattenborg et al., 2000). Rapid eye movement (REM) sleep is not present during UHS; it has been suggested that REM has been lost in aquatic mammals due to natural selection in response to predators or other environmental pressures, the need to remain at or regularly return to the surface for air, and/or temperature maintenance (Madan and Jha, 2012). Consistent with this hypothesis, fur seals have been recently shown to suppress REM sleep for extended periods of time (up to 2 weeks) while in the water (Lyamin et al., 2018).
Many researchers have suggested an analogy between unihemispheric or asymmetric sleep and chimera states (Abrams et al., 2008; Tinsley et al., 2012; Panaggio and Abrams, 2015; Majhi et al., 2019; Wang and Liu, 2020). A chimera state is a dynamical state in which subsets of an ensemble of identical, interacting oscillators exhibit distinct dynamical states, such as one group of synchronized oscillators and one group of desynchronized oscillators (Abrams and Strogatz, 2004). Chimera states have been found in systems of different types of oscillators, including mechanical (Martens et al., 2013), optical (Hagerstrom et al., 2012), chemical (Tinsley et al., 2012; Nkomo et al., 2013; Wickramasinghe and Kiss, 2013), and of course neural (Omelchenko et al., 2013, Hizanidis et al., 2014; Glaze et al., 2016, and others; see Majhi et al., 2019 for review). Systems that generate chimera states can also exhibit phase-cluster states, in which different groups exhibit different synchronized oscillatory patterns (Tinsley et al., 2012). In the present paper, we develop a model of unihemispheric sleep incorporating individual neural oscillators. Unihemispheric sleep was modeled by Kedziora et al. (2012), who adapted a preexisting model to create two hemispheres, which alternately switched between sleep and wake states. We take inspiration from this approach, but develop a model based on coupled individual neurons, rather than single equations governing entire regions of the brain. This approach is novel in that it allows for the examination of interactions not only between regions, as can be done with neuronal mass models, but also within regions, using measures such as stochastic phase synchronization (Pikovsky et al., 2001). As we will show below, asymmetric sleep dynamics are observed in the model, in the form of chimera-like dynamical states, and alternations between levels of synchronization are observed within the sleep-promoting and wake-promoting neural regions throughout the simulated circadian cycle.
Model Background and Design
The simplest form of a sleep-wake model is a “flip-flop” switch based on the interaction between neurons that promote a sleep state (such as those in the ventrolateral preoptic area, or VLPO), and neurons that promote a wake state (such as neurons in the locus coeruleus, or LC). In such models, each state is stable on its own, but an external drive (such as homeostatic sleep pressure) and mutual inhibition between the two groups cause the overall system state to switch from wake to sleep or vice versa (Gallopin et al., 2000; McGinty and Szymusiak, 2000; Saper et al., 2001; Nakao et al., 2007; Rempe et al., 2010). Booth and Diniz Behn (2014) developed a flip-flop-like model that exhibited hysteresis as the external drive was tuned. They showed that their results were comparable to the two-process model developed by Daan et al. (1984), which incorporates two separate, interacting processes corresponding to the circadian drive or rhythm, and the sleep propensity, or the homeostatic drive. These approaches were used by Kedziora et al. (2012) in order to investigate unihemispheric sleep in a two-hemisphere neuronal mass model.
The model used in the present paper combines aspects of these approaches with dynamical models of individual neural oscillators. This allows for the comparison of neural synchronization within subpopulations of oscillators, rather than simply comparisons between brain regions, as in the neural mass models such as those developed by Kedziora et al. (2012). For each “hemisphere,” we consider a small group of neurons (typically four neurons, unless otherwise specified) that are active during the wake state (corresponding to AMIN neurons in the locus coeruleus), another group of neurons active during the sleep state (corresponding to the VLPO region), and a circadian pacemaker which drives the state-switching. The sleep and wake groups mutually inhibit each other, and the state of the system is determined by the (more) active group. A schematic diagram for one hemisphere is shown in Figure 1. This can be compared to the approach of Postnova et al. (2009), who modeled sleep-wake cycles based on feedback between two individual neurons.
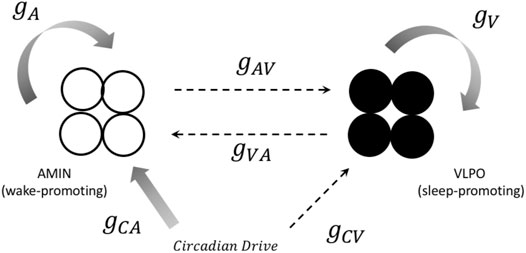
FIGURE 1. A representation of the connections between components in the one-hemisphere model. Both the sleep (black circles) and wake (open circles) regions consist of four neurons. Solid arrows represent excitatory projections, and dashed arrows represent inhibitory projections. The notation for the corresponding coupling constant is shown next to each arrow. See text for more details.
The role of the ventrolateral preoptic area (VLPO) in sleep regulation was first recognized with the demonstration of insomnia in rats whose hypothalamic preoptic area had been lesioned (Nauta, 1946). That the VLPO specifically contains sleep-promoting neurons was not discovered, however, until 1996 (Sherin et al., 1996). A reciprocal inhibitory relationship has been observed between the VLPO and the wake-promoting regions of the hypothalamus, leading to the use of the VLPO in flip-flop switch models (Gallopin et al., 2000; McGinty and Szymusiak, 2000; Saper et al., 2001; Saper and Lowell, 2014). VLPO activity has also been simulated in more complex models of sleep-wake dynamics, including that of Phillips and Robinson (2007), a model developed to replicate mouse sleep-wake behavior (Diniz Behn et al., 2007), the two-hemisphere sleep-wake model developed by Kedziora et al. (2012) to simulate unihemispheric sleep, and others. In the present work, we will associate the sleep-promoting neurons with the VLPO region.
Monoaminergic neurons (typically referred to as AMIN neurons) in the locus coeruleus have been shown to promote wakefulness (Diniz Behn et al., 2007). The LC and VLPO have reciprocal inhibitory connections (Saper et al., 2001; Saper et al., 2010), making AMIN neurons a prime choice to pair with the VLPO for flip-flop switch models. AMIN neurons from the LC are also frequently used in other sleep models to represent a group or region that promotes waking (Diniz Behn et al., 2007; Phillips and Robinson 2007). In the present model, we will associate the wake-promoting neurons with AMIN neurons in the locus coeruleus.
In the model used here, the circadian pacemaker is a skewed sine wave with its peak in the early day and the trough occurring in early night, as defined by Daan et al. (1984). The input from the pacemaker function is given as
It has a range from −1 to 1, with
Individual neurons are modeled using the three-dimensional version of the Hindmarsh-Rose model (Hindmarsh and Rose, 1984), which consists of three coupled nonlinear differential equations:
Here,
Wake-promoting region parameters are designated with the subscript A (for AMIN), and sleep-promoting region parameters are designated with the subscript V (for VLPO). Each neuron receives input from all other neurons as well as the circadian drive. These inputs are combined in the coupling term
where
with
where the second term in the brackets corresponds to the mean field of the VLPO region. Lastly, the coefficient
and summation in Eq. 7 over the VLPO neurons except the neuron of interest, and the summation in Eq. 8 over the AMIN neurons.
To make the wake neurons active during the day, at the peak of the circadian drive (CD), and inactive during the night, at the trough of CD, the projection from CD to the AMIN region is excitatory, and the projection from CD to the VLPO region is inhibitory. The time delay
Synchronization within and between groups is assessed using stochastic phase synchronization analysis. Briefly, two oscillators are considered synchronized if their phase difference
where neuron i spikes at time
where the brackets denote time averages. This corresponds to the intensity of the first Fourier mode of the distribution of phase differences. If
Results
The Hindmarsh-Rose model exhibits different bursting states as the parameter
For the case in which uncoupled neurons exhibit single spikies (
Synchronization within the AMIN and VLPO groups was assessed using phase synchronization analysis, as described in the previous section, with a sliding window 100 spikes wide and a step forward of one spike, allowing for the analysis of the synchronization index as a function of time. In the bursting regime, greater synchronization was observed in the AMIN neurons during the night, and greater synchronization in the VLPO neurons during the day. In other words, synchronization correlated inversely with overall activity, as shown in Figure 2A, for
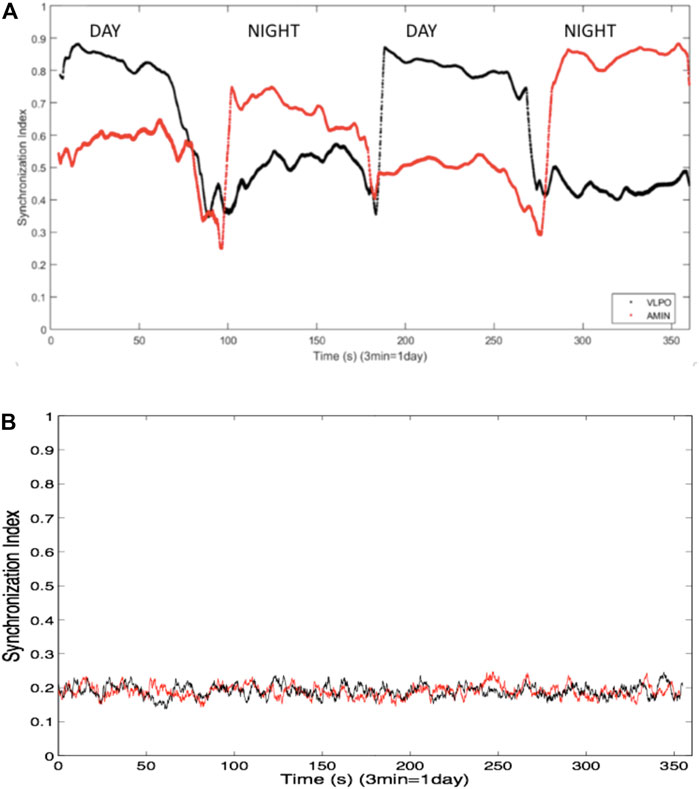
FIGURE 2. (A) Synchronization indices averaged over all non-identical pairs of neurons the VLPO region (black trace) and the AMIN region (red trace) in the single hemisphere model using a sliding window of 100 spikes, and over ten replicate data sets. Parameters are
In order to confirm that the ordering of the spike trains was responsible for the synchronization, the spike times were shuffled while retaining the distribution of interspike intervals. Figure 2B shows the averaged synchronization index, again using a 100-spike sliding window, between the shuffled spike trains from all non-identical neuron pairs for one of the ten data sets. The synchronization is markedly decreased in comparison to the indices shown in Figure 2A, and no difference is observed between the indices for the AMIN and VLPO neural pairs. Similar results are obtained upon shuffling the other data sets used to generate Figure 2A.
The single hemisphere model shown in Figure 1 can be extended to a two-hemisphere model, shown schematically in Figure 3. Each hemisphere has its own VLPO and AMIN regions, each consisting of a group of individual neurons. The circadian drive projects to each of the VLPO and AMIN regions in the same fashion as the single-hemisphere model. The hemispheres communicate via excitatory connections (solid arrows) between the VLPO regions. This form of the model was inspired by the two-hemisphere sleep-wake model designed by Kedziora et al. (2012). With the exception of the added excitatory coupling between VLPO regions, the parameters in the two-hemisphere model use the same naming scheme as in Figure 1. For the new cross-hemispheric VLPO connections, the coupling constants are given as
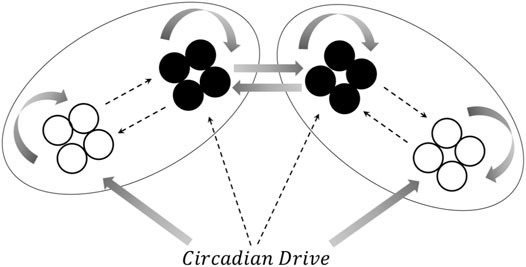
FIGURE 3. A schematic representation of the two-hemisphere version of the model. Connections within each hemisphere are identical those shown in Figure 1, though the circadian drive now projects to the AMIN and VLPO regions in each hemisphere. Additionally, excitatory connections are added between the right and left VLPO regions. See text for details.
The two-hemisphere model can generate chimera states in which the hemispheres exhibit significantly different dynamical behaviors. The mean field activity for each hemisphere, when the system is in the single-spiking regime (
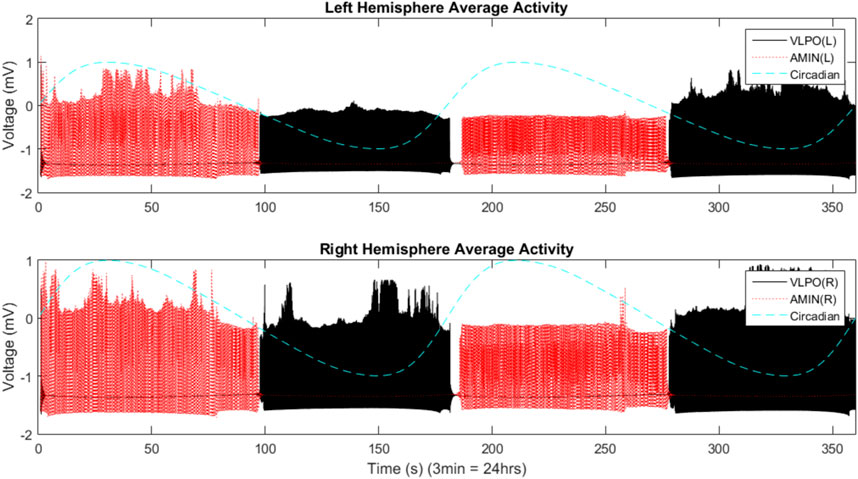
FIGURE 4. Mean field activity in the two-hemisphere model in the regime where uncoupled neurons fire single spikes. The mean field is calculated as the average value of the x variable over all neurons in any give group at each time point. The vertical axis is labeled with “voltage” in units of “mV” to reflect the fact that this variable is analogous to the transmembrane potential. The mean field activity of the “left” hemisphere is shown in the top panel, and that of the “right” hemisphere in the bottom panel. AMIN activity is shown in red, and VLPO is shown in black. The circadian oscillations given in Eq. 1 are shown with the blue dashed line. Parameters are
The mean field activity of the VLPO and AMIN for
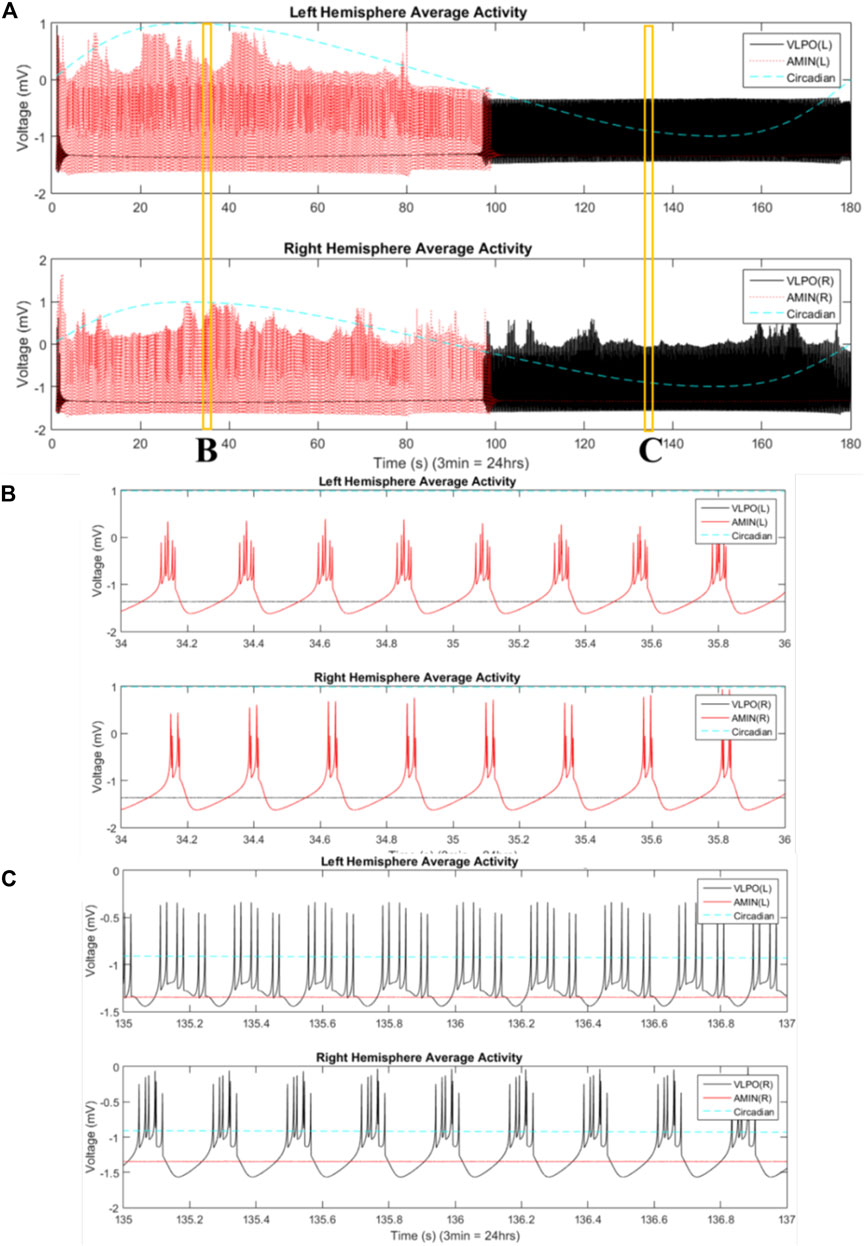
FIGURE 5. Phase-cluster chimera states are observed between hemispheres. (A) Mean field activity of the “left” hemisphere is shown in the top panel, and that of the “right” hemisphere in the bottom panel. AMIN activity is shown in red, and VLPO is shown in black. The circadian oscillations given in Eq. 1 are shown with the blue dashed line. Parameters are
Moving into the bursting regime, with
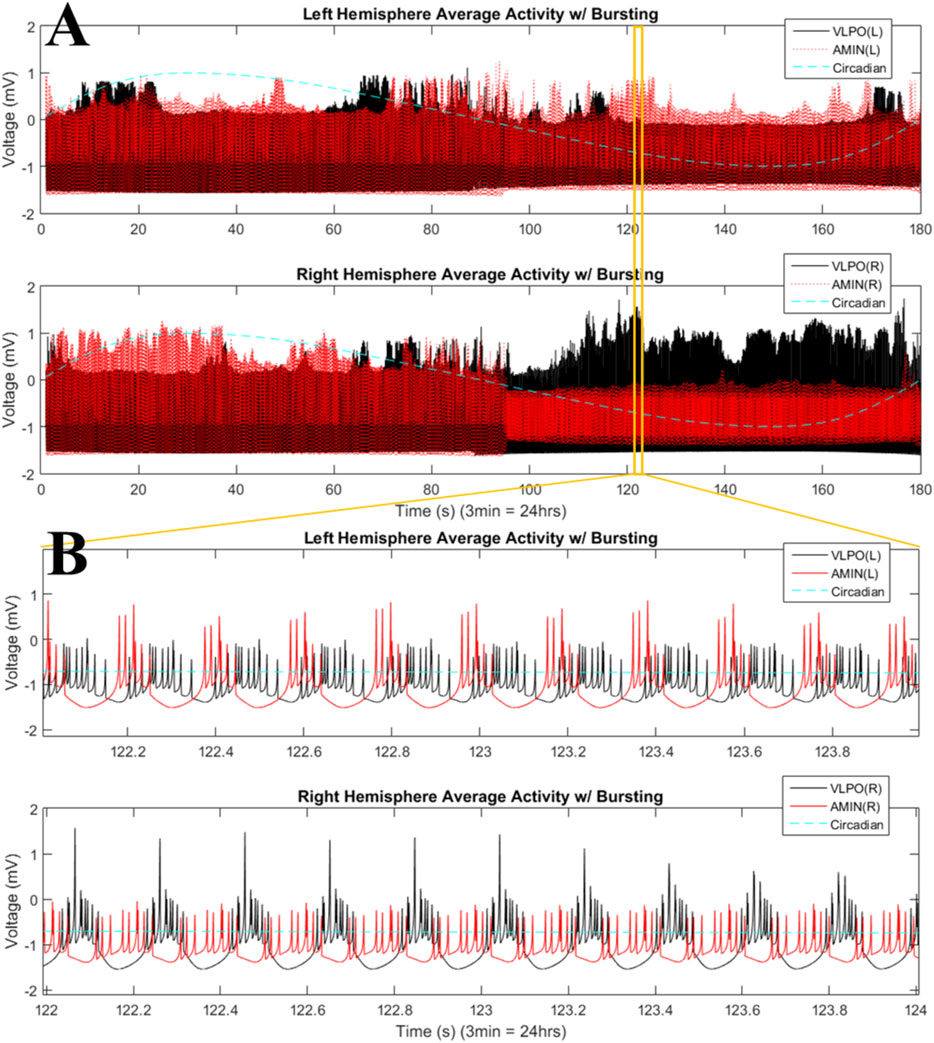
FIGURE 6. Phase-cluster states in the bursting regime for the two-hemisphere model. (A) Mean field activity is shown for the left (top panel) and right (bottom panel) hemispheres. AMIN activity is shown in red, and VLPO is shown in black. The circadian oscillations given in Eq. 1 are shown with the blue dashed line. (B) Magnification of a time interval from (A), 122–124s, with the top panel showing mean field activity from the left hemisphere and the lower panel showing mean field activity from the right hemisphere. Parameters are
The results shown in Figure 6 can be quantified using the synchronization index, which reveals significantly different levels of synchronization between the left and right hemispheres (Figure 7). Note that the VLPO regions have similar synchronization during the day, but the left hemisphere VLPO is significantly more synchronized at night. This implies that the VLPO regions, which can be classified as exhibiting a phase-cluster chimera state based on the bursting state differences shown in Figure 6B, could also be described as exhibiting a classical dynamical chimera state (in which one group is synchronized and the other is comparatively desynchronized) at night. Likewise, the right hemisphere AMIN region is significantly more synchronized than the left AMIN region during the day, again indicative of a classical chimera state. This can be illustrated more clearly, for example, for the VLPO region, by showing the synchronization indices of the right and left VLPO on the same plot (Figure 8).
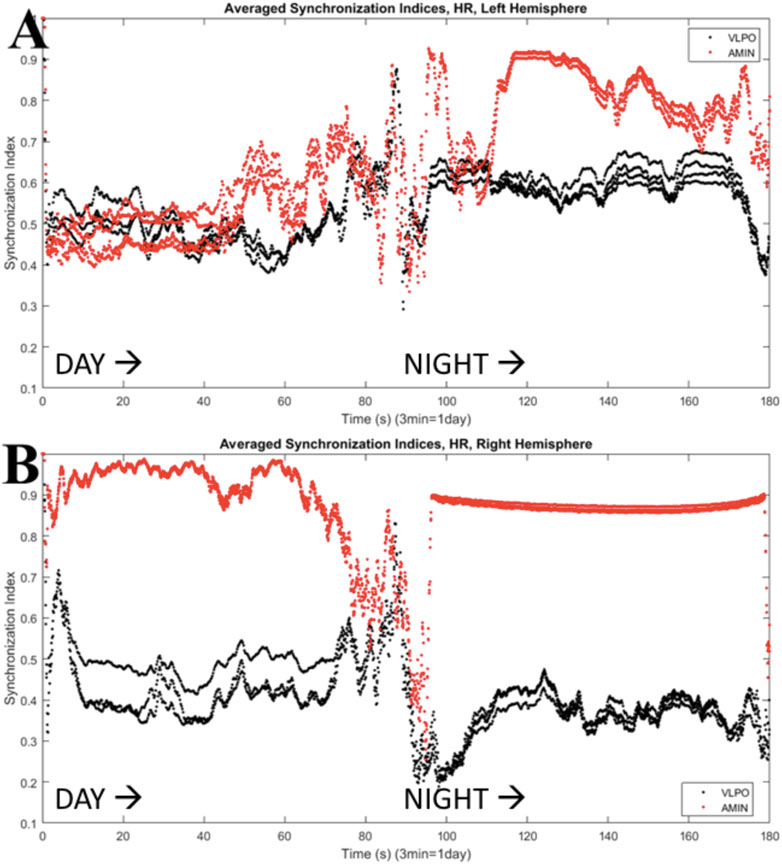
FIGURE 7. Synchronization indices calculated over a 10-spike sliding window for each hemisphere, with a one-spike step forward, from data shown in Figure 6. AMIN synchronization indices are shown in red, and VLPO is shown in black. (A) Left hemisphere synchronization. (B) Right hemisphere synchronization. Parameters are
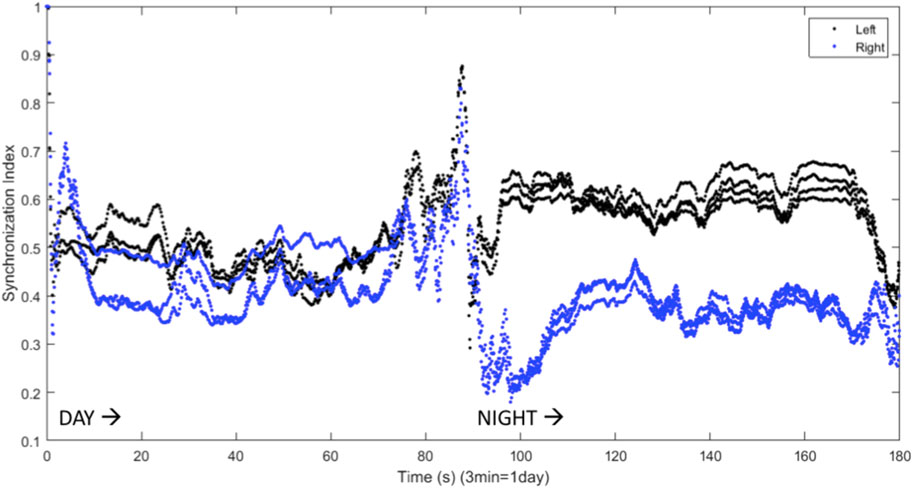
FIGURE 8. Synchronization indices calculated over a 10-spike sliding window for the left and right VLPO, with a one-spike step forward, from data shown in Figures 6, 7. This figure combines the VLPO synchronization indices from Figure 7 for ease of visual comparison. The left hemisphere VLPO is shown with the black trace, and the right with the blue trace. Parameters are
Kedziora et al. (2012) found that inhibitory connections were necessary for the production of UHS in a computational model. Inhibitory coupling is also more likely to produce chimera states, though excitatory coupling can produce chimeras as well (Tinsley et al., 2012; Glaze et al., 2016). The results shown above all involve symmetric excitatory coupling between the hemispheres (
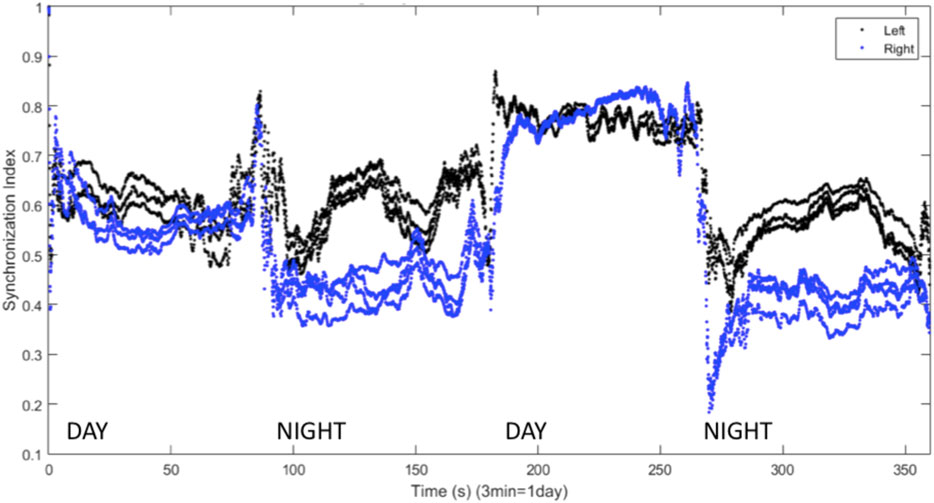
FIGURE 9. Synchronization indices calculated over a 10-spike window with a 1-spike step forward, for left (black line) and right (blue line) hemisphere VLPO, showing asymmetric sleep with inhibitory coupling between the hemispheres. Parameters are
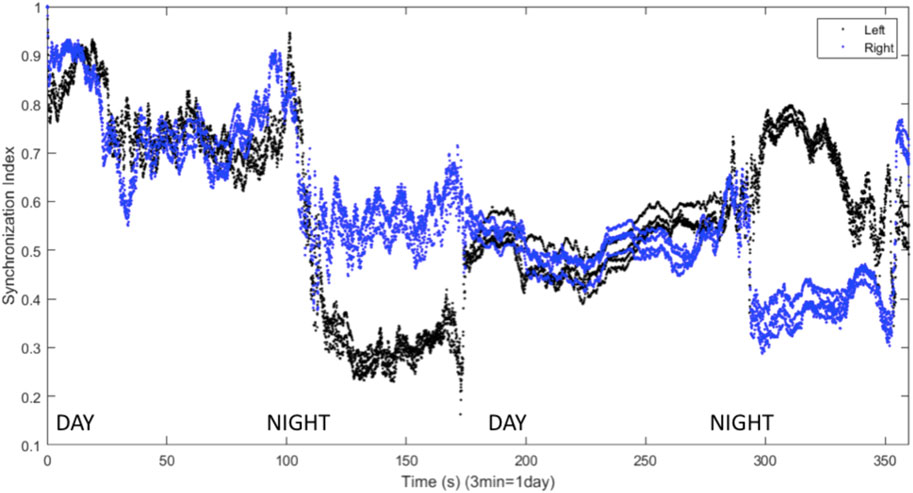
FIGURE 10. Synchronization indices calculated with a 10-spike sliding window and a 1-spike step forward for left (black line) and right (blue line) hemisphere VLPO, with inhibitory interhemispheric coupling. Note the interhemispheric switching: the right VLPO is more synchronized on the first night, and the left VLPO on the second. Parameters are
Discussion and Conclusions
We have presented a model of sleep dynamics based on coupled subgroups of individual Hindmarsh-Rose neurons and a circadian drive. In contrast to neuronal mass models such as that of Kedziora et al. (2012), this approach allows for the investigation of the synchronization within, as well as between, subgroups. We observe changes in synchronization within the sleep-promoting region and within the wake-promoting region as the system transitions from day to night (Figure 2). In a two-hemisphere version of the model, shown schematically in Figure 3, we find chimera-like and phase cluster states analogous to both asymmetric bihemispheric sleep (BHS), and unihemispheric sleep for both excitatory and inhibitory interhemispheric coupling (Figures 5–9). We also observe interhemispheric switching (Figure 10). These results indicate that chimera dynamics in coupled neural models can be used to model the unique dynamically asymmetric sleep states observed in a wide range of species, including human subjects suffering from pathological sleep conditions such as sleep apnea (Abeyratne et al., 2010; Rial et al., 2013) and the asymmetric sleep observed in the “first night effect” (Tamaki et al., 2016).
In Figure 2, the AMIN neurons are observed to have higher synchronization than the VLPO during the simulated night, while they are less synchronized than the VLPO during the simulated day. While this result is consistently observed in the model, the result should not be overinterpreted. A similarly structured model (Glaze, 2019) using a Hodgkin-Huxley-type neural model, the Huber-Braun model (Braun et al., 1998), shows more synchronization in AMIN than VLPO during the day and less at night, suggesting that there may be significant model-dependence in the dynamics. Single-unit recordings from sleep-promoting and wake-promoting neurons in situ would provide an experimental test of whether such synchronization differences exist, and studies using cultured cells on a chip could determine what neuronal properties lead to state-dependent differences in synchrony.
At the whole brain level, EEG recordings suggest that human brain activity is more synchronized during sleep (Krueger et al., 2008; de Andrés et al., 2011; Schwartz and Kilduff, 2015), but this data does not provide resolution at the level of small nuclei within the brain. The results in Figure 2 suggest the hypothesis that relative changes in neural synchrony may occur between sleep-promoting and wake-promoting nuclei during the circadian cycle. This could be investigated with single unit recordings in in vitro studies such as brain slice experiments, including cells from the SCN, VLPO, and locus coeruleus, as well as in vivo recordings. Reciprocally, further model development will be informed by experimental measurements of local synchronization dynamics in vitro and in the intact brain, for example single-unit recordings like those of Takahashi et al. (2010) in the locus coeruleus, and Sakai (2014) in the SCN.
Like other models of neural chimera states (Glaze et al., 2016; Santos et al., 2017; Majhi et al., 2019), the present model includes a Gaussian white noise term (Eq. 2a). While this produces instantaneous differences between the simulated hemispheres, these differences will average to zero, since the noise is applied using an identical algorithm to each neuron at each time step. The differences observed between the dynamical behavior of the two hemispheres, as shown in Figures 5, 6, moreover, are over a much greater time scale than these instantaneous fluctuations, which occur on the time scale of the integration time step. Chimera states have been found to be robust to the presence of noise (Laing, 2012; Panaggio and Abrams, 2015; Loos et al., 2016; Bukh et al., 2018); tuning the noise amplitude has been shown to affect the lifetime of chimera states (Zakharova et al., 2016), and a coherence resonance effect has been observed in which an intermediate amount of noise enhances the occurrence of chimera states (Semenova et al., 2016; Zakharova et al., 2017; Tang et al., 2019; Wang and Liu, 2020).
The model described here could be further developed with the addition of realistic features other than noise. For example, the circadian drive could be decoupled into an intrinsic SCN rhythm and an external drive, in order to examine the effects of circadian misalignment (Fischer et al., 2016), jet lag (Sack et al., 2007a; Sack et al., 2007b) and drugs such as caffeine (Puckeridge et al., 2011) or other non-photic stimuli (St. Hilaire et al., 2007).
An additional wake-promoting region, such as orexinergic (ORX) neurons from the lateral hypothalamic area (LHA) could shift the dynamics of the model. These neurons release the neurotransmitter orexin (also called hypocretin), a crucial element of sleep-wake regulation. Lack of orexin can cause narcolepsy (Sakurai, 2007; Schwartz and Kilduff, 2015). ORX is present in many models of sleep, including the UHS model developed by Kedziora et al. (2012) and the sleep/wake flip-flop model of Rempe et al. (2010). The ORX neurons of LHA interact with both VLPO and AMIN (Saper and Lowell, 2014), and could strengthen and stabilize the wake state, as well as provide additional factors regulating the emergence of chimera-like states.
In conjunction with the circadian drive, the homeostatic drive builds up sleep pressure as time spent awake accumulates, and decreases sleep pressure with time spent asleep. This relationship was put forward by Borbély (1982) and modeled by Daan et al. (1984). The homeostatic drive has been proposed to be regulated by neurons in the VLPO and median preoptic nucleus (MnPO) (Gvilia et al., 2006), as well as by ORX (Postnova et al., 2009). Addition of a homeostatic drive term to the present model would also allow the investigation of how processes such as sleep debt (Borbély et al., 2016) would affect sleep asymmetry.
The effects of other regions involved in sleep regulation such as the MnPO could also be investigated. Located in the hypothalamus, this region promotes the transition from wake to sleep (Gvilia et al., 2006). Firing ahead of the switch to sleep, MnPO may add to sleep pressure (Saper et al., 2010). It also inhibits the LHA, promoting the wake-to-sleep transition (Suntsova et al., 2007), in opposition to the effects of ORX. Another key region in sleep regulation is the extended ventrolateral preoptic nucleus (eVLPO). This region inhibits the REM-off regions in the brain, allowing the transition from NREM to REM sleep (Lu et al., 2006; Rempe et al., 2010). The eVLPO exists in a flip-flop switch with both AMIN neurons (which inhibit REM-on regions) and the VLPO (to regulate the switching between NREM and REM sleep) (Rempe et al., 2010). This region makes inhibitory projections onto the LC, where the AMIN neurons reside (Saper et al., 2010). However, note that REM sleep does not occur during UHS (Rattenborg et al., 2000), and REM is largely, if not entirely, absent in aquatic mammals (Madan and Jha 2012; Lyamin et al., 2018).
In the present model, the VLPO and AMIN regions have been modeled with identical Hindmarsh-Rose neurons. The difference between the two regions was implemented only via the differential input from the circadian drive. In a more realistic model, parameters could be used which would better reflect the firing patterns typical of these regions, as these become better understood from in vitro studies and single unit recordings; more realistic neural models, of course, could be used as well, though this would come with the inevitable tradeoffs of increased computational time and additional parameters. Size effects could also play a role as the number of neurons in each region is increased, though preliminary results suggest that size effects have minimal effect on AMIN and VLPO synchronization in a one-hemisphere model using Huber-Braun neurons (Glaze, 2019).
Another important direction for investigation is the use of connectivity between regions based on empirical data (Wang and Liu, 2020). A recent study by Ramlow et al. (2019) found partial synchronization in a network of FitzHugh-Nagumo oscillators with connections based on empirical data from healthy human subjects. They observed asymmetries in the synchronization dynamics analogous to unihemispheric sleep, but found that these were due to the structural asymmetry in the model rather than to a true chimera effect. Santos et al. (2017) took a similar approach in developing a network model of the cat cerebral cortex, using the Hindmarsh-Rose equations, based on an empirical connectivity matrix. Such studies drive home the importance of combining both fundamental dynamical studies and empirical data by introducing different time delays or asymmetric coupling matrices within and across hemispheres.
Given that real brains exhibit structural asymmetry, does the chimera-state approach provide a reasonable model for unihemispheric sleep? Structural asymmetry has been shown to be important in driving the dynamics of the default mode network, whch is active during a state of quiet (awake) resting (Saenger et al., 2012). Recent advances in understanding how the brain’s structure shapes its dynamics (Deco et al., 2011; Shen et al., 2015), as well as advances in the understanding of the neural connectome (Sporns et al., 2005; Kaiser, 2017; Betzel and Bassett, 2018) can provide the basis for models incorporating realistic structural asymmetries. This structural information could be combined with the modeling of individual neural oscillators, in order to investigate local synchronization changes, not only in bespoke code, but also in simulation platforms such as NEST (Kunkel and Schenck, 2017).
Incorporation of more realistic connectome data will be an important future step in determining the balance between dynamics and structural connectivity in driving sleep dynamics and other possible chimera-like states in the brain. Of particular interest in this regard will be studies such as Petkoski et al. (2018) and Petkoski and Jirsa (2019) which highlight the role of time delays and phase lags in large-scale brain network synchronization, because time delays are an important component of chimera dynamics (Tinsley et al., 2012).
Despite its obvious importance, structural asymmetry alone is unlikely to be the primary driver of sleep dynamics in species which exhibit hemispheric switching during unihemispheric sleep. Such switching must be, at its core, dynamically driven, since structural architecture is surely not rewired multiple times each night. Expanded versions of the chimera-generating model described here, with an emphasis on local synchronization within neural clusters, will, in combination with experimental data, be essential for decoupling dynamically-driven sleep asymmetries from those determined by functional architecture.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
TG and SB developed the model; TG performed the simulations; SB and TG wrote the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abeyratne, U. R., Swarnkar, V., Hukins, C., and Duce, B. (2010). Interhemispheric Asynchrony Correlates with Severity of Respiratory Disturbance Index in Patients with Sleep Apnea. IEEE Trans. Biomed. Eng. 57 (12), 2947–2955. doi:10.1109/tbme.2010.2060197
Abrams, D. M., Mirollo, R., Strogatz, S. H., and Wiley, D. A. (2008). Solvable Model for Chimera States of Coupled Oscillators. Phys. Rev. Lett. 101, 084103. doi:10.1103/PhysRevLett.101.084103
Abrams, D. M., and Strogatz, S. H. (2004). Chimera States for Coupled Oscillators. Phys. Rev. Lett. 93 (17), 174102. doi:10.1103/physrevlett.93.174102
Aton, S. J., and Herzog, E. D. (2005). Come Together, Right…Now: Synchronization of Rhythms in a Mammalian Circadian Clock. Neuron 48 (4), 531–534. doi:10.1016/j.neuron.2005.11.001
Behn, C. G. D., Brown, E. N., Scammell, T. E., and Kopell, N. J. (2007). Mathematical Model of Network Dynamics Governing Mouse Sleep-Wake Behavior. J. Neurophysiol. 97, 3828–3840. doi:10.1152/jn.01184.2006
Behrens, T. E., and Sporns, O. (2012). Human Connectomics. Curr. Opin. Neurobiol. 22 (1), 144–153. doi:10.1016/j.conb.2011.08.005
Betzel, R. F., and Bassett, D. S. (2018). Specificity and Robustness of Long-Distance Connections in Weighted, Interareal Connectomes. Proc. Natl. Acad. Sci. U.S.A. 115 (21), E4880–E4889. doi:10.1073/pnas.1720186115
Booth, V., and Diniz Behn, C. G. (2014). Physiologically-based Modeling of Sleep-Wake Regulatory Networks. Math. Biosciences 250, 54–68. doi:10.1016/j.mbs.2014.01.012
Borbély, A. A., Daan, S., Wirz-Justice, A., and Deboer, T. (2016). The Two-Process Model of Sleep Regulation: a Reappraisal. J. Sleep Res. 25 (2), 131–143. doi:10.1111/jsr.12371
Braun, A. R., Balkin, T. J., Wesenten, N. J., Carson, R. E., Varga, M., Baldwin, P., et al. (1997). Regional Cerebral Blood Flow throughout the Sleep-Wake Cycle. An H2(15)O PET Study. Brain 120 (Pt 7), 1173–1197. doi:10.1093/brain/120.7.1173
Braun, H. A., Huber, M. T., Dewald, M., Schafer, K., and Voigt, K. (1998). Computer Simulations of Neuronal Signal Transduction: the Role of Nonlinear Dynamics and Noise. Intl. J. Bif. Chaos 8 (5), 881–889. doi:10.1142/s0218127498000681
Bukh, A. V., Slepnev, A. V., Anishschenko, V. S., and Vadivasova, T. E. (2018). Stability and Noise-Induced Transitions in an Ensemble of Nonlocally Coupled Chaotic Maps. Reg. Chaotic Dyn. 23 (3), 326–339. doi:10.1134/s1560354718030073
Corsi-Cabrera, M., Ondarza, R., Martínez-Gutiérrez, V., Río-Portilla, Y. d., Guevara, M. A., and Ramos-Loyo, J. (2006). Role of Corpus Callosum in Interhemispheric Coherent Activity during Sleep. Clin. Neurophysiol. 117 (8), 1826–1835. doi:10.1016/j.clinph.2006.05.008
Creux, N., and Harmer, S. (2019). Circadian Rhythms in Plants. Cold Spring Harb. Perspect. Biol. 11, a034611. doi:10.1101/cshperspect.a034611
Daan, S., Beersma, D. G., and Borbély, A. A. (1984). Timing of Human Sleep: Recovery Process Gated by a Circadian Pacemaker. Am. J. Physiol. 246 (2 Pt 2), R161–R183. doi:10.1152/ajpregu.1984.246.2.R161
de Andrés, I., Garzón, M., and Reinoso-Suárez, F. (2011). Functional Anatomy of Non-REM Sleep. Front. Neur. 2, 70. doi:10.3389/fneur.2011.00070
Deco, G., Jirsa, V. K., and McIntosh, A. R. (2011). Emerging Concepts for the Dynamical Organization of Resting-State Activity in the Brain. Nat. Rev. Neurosci. 12 (1), 43–56. doi:10.1038/nrn2961
Fischer, D., Vetter, C., and Roenneberg, T. (2016). A Novel Method to Visualise and Quantify Circadian Misalignment. Sci. Rep. 6, 38601. doi:10.1038/srep38601
Fox, R. F., Gatland, I. R., Roy, R., and Vemuri, G. (1988). Fast, Accurate Algorithm for Numerical Simulation of Exponentially Correlated Colored Noise. Phys. Rev. A 38 (11), 5938–5940. doi:10.1103/physreva.38.5938
Gallopin, T., Fort, P., Eggermann, E., Cauli, B., Luppi, P.-H., Rossier, J., et al. (2000). Identification of Sleep-Promoting Neurons In Vitro. Nature 404 (6781), 992–995. doi:10.1038/35010109
Glaze, T. A. (2019). A Computational Study of Sleep and the Hemispheres of the Brain. St. Louis: Doctoral Dissertation, University of Missouri at St. Louis.
Glaze, T. A., Lewis, S., and Bahar, S. (2016). Chimera States in a Hodgkin-Huxley Model of Thermally Sensitive Neurons. Chaos 26 (8), 083119. doi:10.1063/1.4961122
González-Miranda, J. M. (2007). Complex Bifurcation Structures in the Hindmarsh-Rose Neural Model. Intl. J. Bif. Chaos 17 (9), 3071–3083. doi:10.1142/S0218127407018877
Gvilia, I., Xu, F., McGinty, D., and Szymusiak, R. (2006). Homeostatic Regulation of Sleep: a Role for Preoptic Area Neurons. J. Neurosci. 26 (37), 9426–9433. doi:10.1523/jneurosci.2012-06.2006
Hagerstrom, A. M., Murphy, T. E., Roy, R., Hövel, P., Omelchenko, I., and Schöll, E. (2012). Experimental Observation of Chimeras in Coupled-Map Lattices. Nat. Phys. 8, 658–661. doi:10.1038/nphys2372
Hindmarsh, J. L., and Rose, R. M. (1984). A Model of Neuronal Bursting Using Three Coupled First Order Differential Equations. Proc. R. Soc. Lond. B 221 (1222), 87–102. doi:10.1098/rspb.1984.0024
Hizanidis, J., Kanas, V. G., Bezerianos, A., and Bountis, T. (2014). Chimera States in Networks of Nonlocally Coupled Hindmarsh-Rose Neuron Models. Int. J. Bif. Chaos 24, 1450030. doi:10.1142/s0218127414500308
Kaiser, M. (2017). Mechanisms of Connectome Development. Trends Cogn. Sci. 21 (9), 703–717. doi:10.1016/j.tics.2017.05.010
Kedziora, D. J., Abeysuriya, R. G., Phillips, A. J. K., and Robinson, P. A. (2012). Physiologically Based Quantitative Modeling of Unihemispheric Sleep. J. Theor. Biol. 314, 109–119. doi:10.1016/j.jtbi.2012.08.031
Krueger, J. M., Rector, D. M., Roy, S., Van Dongen, H. P. A., Belenky, G., and Panksepp, J. (2008). Sleep as a Fundamental Property of Neuronal Assemblies. Nat. Rev. Neurosci. 9 (12), 910–919. doi:10.1038/nrn2521
Kunkel, S., and Schenck, W. (2017). The NEST Dry-Run Mode: Efficient Dynamic Analysis of Neuronal Network Simulation Code. Front. Neuroinform. 11, 40. doi:10.3389/fninf.2017.00040
Kunz, H., and Achermann, P. (2003). Simulation of Circadian Rhythm Generation in the Suprachiasmatic Nucleus with Locally Coupled Self-Sustained Oscillators. J. Theor. Biol. 224 (1), 63–78. doi:10.1016/s0022-5193(03)00141-3
Laing, C. R. (2012). Disorder-induced Dynamics in a Pair of Coupled Heterogeneous Phase Oscillator Networks. Chaos 22, 043104. doi:10.1063/1.4758814
Loos, S. A., Claussen, J. C., Schöll, E., and Zakharova, A. (2016). Chimera Patterns under the Impact of Noise. Phys. Rev. E 93, 012209. doi:10.1103/PhysRevE.93.012209
Lu, J., Sherman, D., Devor, M., and Saper, C. B. (2006). A Putative Flip-Flop Switch for Control of REM Sleep. Nature 441 (7093), 589–594. doi:10.1038/nature04767
Lyamin, O. I., Kosenko, P. O., Korneva, S. M., Vyssotski, A. L., Mukhametov, L. M., and Siegel, J. M. (2018). Fur Seals Suppress REM Sleep for Very Long Periods without Subsequent Rebound. Curr. Biol. 28 (12), 2000–2005. doi:10.1016/j.cub.2018.05.022
Madan, V., and Jha, S. K. (2012). Sleep Alterations in Mammals: Did Aquatic Conditions Inhibit Rapid Eye Movement Sleep? Neurosci. Bull. 28 (6), 746–758. doi:10.1007/s12264-012-1285-8
Majhi, S., Bera, B. K., Ghosh, D., and Perc, M. (2019). Chimera States in Neuronal Networks: a Review. Phys. Life Rev. 28, 100–121. doi:10.1016/j.plrev.2018.09.003
Martens, E. A., Thutupalli, S., Fourrière, A., and Hallatschek, O. (2013). Chimera States in Mechanical Oscillator Networks. Proc. Natl. Acad. Sci. U.S.A. 110 (26), 10563–10567. doi:10.1073/pnas.1302880110
McGinty, D., and Szymusiak, R. (2000). The Sleep-Wake Switch: a Neuronal Alarm Clock. Nat. Med. 6 (5), 510–511. doi:10.1038/74988
Moore, R. Y., and Eichler, V. B. (1972). Loss of a Circadian Adrenal Corticosterone Rhythm Following Suprachiasmatic Lesions in the Rat. Brain Res. 42 (1), 201–206. doi:10.1016/0006-8993(72)90054-6
Moore, R. Y., and Lenn, N. J. (1972). A Retinohypothalamic Projection in the Rat. J. Comp. Neurol. 146 (1), 1–14. doi:10.1002/cne.901460102
Mukhametov, L. M., Supin, A. Y., and Polyakova, I. G. (1977). Interhemispheric Asymmetry of the Electroencephalographic Sleep Patterns in Dolphins. Brain Res. 134, 581–584. doi:10.1016/0006-8993(77)90835-6
Nakao, M., Karashima, A., and Katayama, N. (2007). Mathematical Models of Regulatory Mechanisms of Sleep-Wake Rhythms. Cell. Mol. Life Sci. 64, 1236–1243. doi:10.1007/s00018-007-6534-z
Nath, R. D., Bedbrook, C. N., Abrams, M. J., Basinger, T., Bois, J. S., Prober, D. A., et al. (2017). The Jellyfish Cassiopea Exhibits a Sleep-like State. Curr. Biol. 27 (19), 2984–2990. doi:10.1016/j.cub.2017.08.014
Nauta, W. J. H. (1946). Hypothalamic Regulation of Sleep in Rats. An Experimental Study. J. Neurophysiol. 9, 285–316. doi:10.1152/jn.1946.9.4.285
Nkomo, S., Tinsley, M. R., and Showalter, K. (2013). Chimera States in Populations of Nonlocally Coupled Chemical Oscillators. Phys. Rev. Lett. 110 (24), 244102. doi:10.1103/physrevlett.110.244102
Oakenfull, R. J., and Davis, S. J. (2017). Shining a Light on the Arabidopsis Circadian Clock. Plant Cel Environ. 40, 2571–2585. doi:10.1111/pce.13033
Omelchenko, I., Omel’chenko, O. E., Hövel, P., and Schöll, E. (2013). When Nonlocal Coupling between Oscillators Becomes Stronger: Patched Synchrony or Multichimera States. Phys. Rev. Lett. 110 (22), 224101. doi:10.1103/physrevlett.110.224101
Panaggio, M. J., and Abrams, D. M. (2015). Chimera States: Coexistence of Coherence and Incoherence in Networks of Coupled Oscillators. Nonlinearity 28, R67–R87. doi:10.1088/0951-7715/28/3/r67
Petkoski, S., Iatsekno, D., Basnarkov, L., and Stefanovska, A. (2013). Mean-field and Mean-Ensemble Frequencies of a System of Coupled Oscillators. Phys. Rev. E 87, 032908. doi:10.1103/physreve.87.032908
Petkoski, S., and Jirsa, V. K. (2019). Transmission Time Delays Organize the Brain Network Synchronization. Phil. Trans. R. Soc. A 377 (2153), 20180132. doi:10.1098/rsta.2018.0132
Petkoski, S., Palva, J. M., and Jirsa, V. K. (2018). Phase-lags in Large Scale Brain Synchronization: Methodological Considerations and In-Silico Analysis. Plos Comput. Biol. 14 (7), e1006160. doi:10.1371/journal.pcbi.1006160
Phillips, A. J. K., and Robinson, P. A. (2007). A Quantitative Model of Sleep-Wake Dynamics Based on the Physiology of the Brainstem Ascending Arousal System. J. Biol. Rhythms 22 (2), 167–179. doi:10.1177/0748730406297512
Pikovsky, A., Rosenblum, M., and Kurths, J. (2001). Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press.
Postnova, S., Voigt, K., and Braun, H. A. (2009). A Mathematical Model of Homeostatic Regulation of Sleep-Wake Cycles by Hypocretin/orexin. J. Biol. Rhythms 24 (6), 523–535. doi:10.1177/0748730409346655
Puckeridge, M., Fulcher, B. D., Phillips, A. J. K., and Robinson, P. A. (2011). Incorporation of Caffeine into a Quantitative Model of Fatigue and Sleep. J. Theor. Biol. 273 (1), 44–54. doi:10.1016/j.jtbi.2010.12.018
Ramlow, L., Sawicki, J., Zakharova, A., Hlinka, J., Claussen, J. C., and Schöll, E. (2019). Partial Synchronization in Empirical Brain Networks as a Model for Unihemispheric Sleep. Europhys. Lett. 126, 50007. doi:10.1209/0295-5075/126/50007
Rattenborg, N. C., Amlaner, C. J., and Lima, S. L. (2000). Behavioral, Neurophysiological and Evolutionary Perspectives on Unihemispheric Sleep. Neurosci. Biobehavioral Rev. 24 (8), 817–842. doi:10.1016/s0149-7634(00)00039-7
Rattenborg, N. C., Lima, S. L., and Amlaner, C. J. (1999). Half-awake to the Risk of Predation. Nature 397 (6718), 397–398. doi:10.1038/17037
Rattenborg, N. C. (2017). Sleeping on the wing. Interf. Focus. 7 (1), 20160082. doi:10.1098/rsfs.2016.0082
Rempe, M. J., Best, J., and Terman, D. (2010). A Mathematical Model of the Sleep/wake Cycle. J. Math. Biol. 60, 615–644. doi:10.1007/s00285-009-0276-5
Rial, R., González, J., Gené, L., Akaârir, M., Esteban, S., Gamundí, A., et al. (2013). Asymmetric Sleep in Apneic Human Patients. Am. J. Physiology-Regulatory, Integr. Comp. Physiol. 304 (3), R232–R237. doi:10.1152/ajpregu.00302.2011
Rijo-Ferreira, F., and Takahashi, J. S. (2019). Genomics of Circadian Rhythms in Health and Disease. Genome Med. 11, 82. doi:10.1186/s13073-019-0704-0
Sack, R. L., Auckley, D., Auger, R. R., Carskadon, M. A., Wright, K. P., Vitiello, M. V., et al. (2007a). Circadian Rhythm Sleep Disorders: Part I, Basic Principles, Shift Work and Jet Lag Disorders. Sleep 30 (11), 1460–1483. doi:10.1093/sleep/30.11.1460
Sack, R. L., Auckley, D., Auger, R. R., Carskadon, M. A., Wright, K. P., Vitiello, M. V., et al. (2007b). Circadian Rhythm Sleep Disorders: Part II, Advanced Sleep Phase Disorder, Delayed Sleep Phase Disorder, Free-Running Disorder, and Irregular Sleep-Wake Rhythm. Sleep 30 (11), 1484–1501. doi:10.1093/sleep/30.11.1484
Saenger, V. M., Barrios, F. A., Martínez-Gudiño, M. L., and Alcauter, S. (2012). Hemispheric Asymmetries of Functional Connectivity and Grey Matter Volume in the Default Mode Network. Neuropsychologia 50 (7), 1308–1315. doi:10.1016/j.neuropsychologia.2012.02.014
Sakai, K. (2014). Single Unit Activity of the Suprachiasmatic Nucleus and Surrounding Neurons during the Wake-Sleep Cycle in Mice. Neuroscience 260, 249–264. doi:10.1016/j.neuroscience.2013.12.020
Sakurai, T. (2007). The Neural Circuit of Orexin (Hypocretin): Maintaining Sleep and Wakefulness. Nat. Rev. Neurosci. 8 (3), 171–181. doi:10.1038/nrn2092
Santos, M. S., Szezech, J. D., Borges, F. S., Iarosz, K. C., Caldas, I. L., Batista, A. M., et al. (2017). Chimera-like States in a Neuronal Network Model of the Cat Brain. Chaos, Solitons & Fractals 101, 86–91. doi:10.1016/j.chaos.2017.05.028
Saper, C. B., Chou, T. C., and Scammell, T. E. (2001). The Sleep Switch: Hypothalamic Control of Sleep and Wakefulness. Trends Neurosciences 24 (12), 726–731. doi:10.1016/s0166-2236(00)02002-6
Saper, C. B., Fuller, P. M., Pedersen, N. P., Lu, J., and Scammell, T. E. (2010). Sleep State Switching. Neuron 68 (6), 1023–1042. doi:10.1016/j.neuron.2010.11.032
Saper, C. B., and Lowell, B. B. (2014). The Hypothalamus. Curr. Biol. 24 (23), R1111–R1116. doi:10.1016/j.cub.2014.10.023
Scammell, T. E., Arrigoni, E., and Lipton, J. O. (2017). Neural Circuitry of Wakefulness and Sleep. Neuron 93, 747–765. doi:10.1016/j.neuron.2017.01.014
Schwartz, M. D., and Kilduff, T. S. (2015). The Neurobiology of Sleep and Wakefulness. Psychiatr. Clin. North America 38 (4), 615–644. doi:10.1016/j.psc.2015.07.002
Semenova, N., Zakharova, A., Anishchenko, V., and Schöll, E. (2016). Coherence Resonance Chimeras in a Network of Excitable Elements. Phys. Rev. Lett. 117, 014102. doi:10.1103/physrevlett.117.014102
Shen, K., Hutchison, R. M., Bezgin, G., Everling, S., and McIntosh, A. R. (2015). Network Structure Shapes Spontaneous Functional Connectivity Dynamics. J. Neurosci. 35 (14), 5579–5588. doi:10.1523/jneurosci.4903-14.2015
Sherin, J. E., Shiromani, P. J., McCarley, R. W., and Saper, C. B. (1996). Activation of Ventrolateral Preoptic Neurons during Sleep. Science 271 (5246), 216–219. doi:10.1126/science.271.5246.216
Sporns, O., Tononi, G., and Kötter, R. (2005). The Human Connectome: a Structural Description of the Human Brain. Plos Comp. Biol. 1 (4), e42. doi:10.1371/journal.pcbi.0010042
St. Hilaire, M. A., Khalsa, S. B. S., Wright, K. P., Czeisler, C. A., Kronauer, R. E., et al. (2007). Addition of a Non-photic Component to a Light-Based Mathematical Model of the Human Circadian Pacemaker. J. Theor. Biol. 247 (4), 583–599. doi:10.1016/j.jtbi.2007.04.001
Strogatz, S. H. (1987). Human Sleep and Circadian Rhythms: a Simple Model Based on Two Coupled Oscillators. J. Math. Biol. 25, 327–347. doi:10.1007/bf00276440
Suntsova, N., Guzman-Marin, R., Kumar, S., Alam, M. N., Szymusiak, R., and McGinty, D. (2007). The Median Preoptic Nucleus Reciprocally Modulates Activity of Arousal-Related and Sleep-Related Neurons in the Perifornical Lateral Hypothalamus. J. Neurosci. 27 (7), 1616–1630. doi:10.1523/jneurosci.3498-06.2007
Takahashi, K., Kayama, Y., Lin, J. S., and Sakai, K. (2010). Locus Coeruleus Neuronal Activity during the Sleep-Waking Cycle in Mice. Neuroscience 169 (3), 1115–1126. doi:10.1016/j.neuroscience.2010.06.009
Tamaki, M., Bang, J. W., Watanabe, T., and Sasaki, Y. (2016). Night Watch in One Brain Hemisphere during Sleep Associated with the First-Night Effect in Humans. Curr. Biol. 26 (9), 1190–1194. doi:10.1016/j.cub.2016.02.063
Tang, J., Zhang, J., Ma, J., and Luo, J. (2019). Noise and Delay Sustained Chimera State in Small World Neuronal Network. Sci. China Technol. Sci. 62, 1134–1140. doi:10.1007/s11431-017-9282-x
Tinsley, M. R., Nkomo, S., and Showalter, K. (2012). Chimera and Phase-Cluster States in Populations of Coupled Chemical Oscillators. Nat. Phys. 8, 662–665. doi:10.1038/nphys2371
Wang, Z., and Liu, Z. (2020). A Brief Review of Chimera State in Empirical Brain Networks. Front. Physiol. 11, 724. doi:10.3389/fphys.2020.00724
Wickramasinghe, M., and Kiss, I. Z. (2013). Spatially Organized Dynamical States in Chemical Oscillator Networks: Synchronization, Dynamical Differentiation, and Chimera Patterns. PLoS One 8 (11), e80586. doi:10.1371/journal.pone.0080586
Wolfrum, M., and Omel'chenko, O. E. (2011). Chimera States are Chaotic Transients. Phys. Rev. E 84, 015201. doi:10.1103/PhysRevE.84.015201
Zakharova, A., Loos, S. A. M., Siebert, J., Gjurchinovski, A., Claussen, J. C., and Schöll, E. (2016). “Controlling Chimera Patterns in Networks: Interplay of Structure, Noise and Delay,” in Control of Self-Organizing Linear Systems. Editors E. Schöll (Switzerland: Springer International Publishing). doi:10.1007/978-3-319-28028-8_1
Keywords: chimera states, neural synchronization, sleep dynamics, unihemispheric sleep, asymmetric sleep
Citation: Glaze TA and Bahar S (2021) Neural Synchronization, Chimera States and Sleep Asymmetry. Front. Netw. Physiol. 1:734332. doi: 10.3389/fnetp.2021.734332
Received: 01 July 2021; Accepted: 27 September 2021;
Published: 12 October 2021.
Edited by:
Olga Sosnovtseva, University of Copenhagen, DenmarkReviewed by:
Spase Petkoski, INSERM U1106 Institut de Neurosciences des Systèmes, FranceArcady A. Putilov, Independent researcher, Novosibirsk, Russia
Copyright © 2021 Glaze and Bahar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sonya Bahar, YmFoYXJzQHVtc2wuZWR1
 Tera A. Glaze
Tera A. Glaze Sonya Bahar
Sonya Bahar