Are we still chasing molecules that were never there? The role of quantum chemical simulations of NMR parameters in structural reassignment of natural products

Covering: 2019 to 2023. Even with the advent of modern and complementary spectroscopy techniques, comprehensive characterization of natural product continues to represent an onerous and time-consuming task, being far away to become rather “routine”. Mainly due to their highly complex structures and small amount of isolated sample, in milligram or sub-milligram quantities, structural misassignment of natural products are still a recurrence theme in the modern literature. Since the seminal paper from Nicolau and Snider, in 2005, evaluating the various cases of reassignment of natural products, from the present era, in which NMR parameters calculations play such an important role in the structural elucidation of natural products, helping to uncover and ultimately revise the structure of previously reported compounds, a pertinent question arises: are we still chasing molecules that were never there? In this minireview, we intent to discuss the current state of computational NMR parameter calculations, with a particular focus on their application in the structural determination of natural products. Additionally, we have conducted a comprehensive survey of the literature spanning the years 2019–2023, in order to select and discuss recent noteworthy cases of incorrectly assigned structures that were revised through NMR calculations. Therefore, our main goal is to show what can be done through computational simulations of NMR parameters, currently user-friendly and easily implemented by non-expert users with basic skills in computational chemistry, before venturing into complex and time-consuming total synthesis projects. In conclusion, we anticipate a promising future for NMR parameter calculations, fueled by the ongoing development of user-friendly tools and the integration of artificial intelligence. The emergence of these advancements is poised to broaden the applications of NMR simulations, offering a more accessible and reliable means to address the persistent challenge of structural misassignments in natural product chemistry.

Introduction

Over the years, the structural characterization of natural products has continually remained a subject of significant interest. Since the early decades of the 20th century, in which degradation and derivatization reactions were employed for structure determination, up to the contemporary application of modern analytical methodologies, instances of reevaluation and reassignment of natural product structures have consistently surfaced (Nicolaou and Snyder, 2005; Chhetri et al., 2018).

The reassignment cases arise mainly due to the complex nature inherent in various natural product structures, thereby imposing a difficult challenge in the assignment and interpretation of experimental spectra (Nicolaou and Snyder, 2005). Advances in analytical techniques, such as Nuclear Magnetic Resonance (NMR) spectroscopy, Mass Spectrometry (MS), Electronic and Vibrational Circular Dichroism (ECD and VCD), have been developed to overcome these issues (Bross-Walch et al., 2005; Petrovic et al., 2010; Pescitelli and Bruhn, 2016). Nevertheless, notwithstanding these advancements, the comprehensive characterization of natural product structures continues to represent an onerous and time-consuming task (Nicolaou and Snyder, 2005; Chhetri et al., 2018).

In this context, quantum mechanical (QM) simulations of NMR parameters assume a pivotal role. These computational predictions offer a clear correspondence between NMR parameters and the nuclei that generate them. Consequently, they significantly enhance the precision and simplicity of spectral assignment and interpretation (Lodewyk et al., 2012; Marcarino et al., 2020; Costa et al., 2021; Rusakova, 2022).

The case of hexacyclinol (Figure 1), a natural product isolated from the fungus Panus rudis, stands as the seminal and, simultaneously, one of the most notable instances of applying NMR parameters calculations for structural revisions. In 2006, following its isolation and initial structural proposal, La Clair et al. proposed a total synthesis of hexacyclinol (Schlegel et al., 2002; La Clair, 2006). However, the NMR spectra of the synthetic product did not match with the originally posited structure, giving rise to a controversy in the literature. Resolution came when Rychnovysky proposed a revised structure, based on ¹³C NMR chemical shifts calculations (Rychnovsky, 2006). Subsequently, in the same year, this latter structure was confirmed through both total synthesis and X-ray crystallography (Porco et al., 2006). This case demonstrates that NMR parameters calculations can be successfully employed to avoid the misassignment of natural product structures, thus saving valuable time and resources that might otherwise have been expended on the pursuit of total synthesis for structural elucidation (Saielli and Bagno, 2009; Cortés et al., 2023).

FIGURE 1

FIGURE 1. Originally proposed (left) and revised (right) structure of hexacyclinol.

Much like the case of hexacyclinol, numerous misassigned natural product structures have continued to be identified over the last decades. In 2005, Nicolaou and Snyder published a comprehensive review paper, in which they discussed modern methodologies for structure elucidation and delineated several cases of natural product structure revisions, with a particular emphasis on the role played by total synthesis (Nicolaou and Snyder, 2005). However, it is worth noting that misassignments in the structural elucidation process are often identified subsequent to attempts at total synthesis of the presumed structure. This results in the spending of significant time and financial resources. This whole issue can be prevented with the aid of a computer-guided structural elucidation process. Through computer simulations, errors in the structural determination of natural products can be anticipated, and in certain cases, the total synthesis process can be directed toward the correct structure in the first place (Cortés et al., 2023).

Therefore, in the present era, in which NMR parameters calculations play such an important role in the structural elucidation, a pertinent question arises: are we still chasing molecules that were never there?

The primary aim of this review paper is to discuss the current state of computational NMR parameter calculations, with a particular focus on their application in the structural determination of natural products. Additionally, we have conducted a comprehensive survey of the literature spanning the years 2019–2023, in order to select and discuss recent noteworthy cases of incorrectly assigned structures that were revised through NMR calculations. Therefore, our main goal is to show what can be done through computational simulations of NMR parameters, currently user-friendly and easily implemented by non-expert users with basic skills in computational chemistry, before venturing into complex and time-consuming total synthesis projects.

The current state of computational calculation of NMR parameters

Dealing with multiple conformations: conformational analysis

As the timescale of a conformational change is too fast to be detected in NMR experiments, the resultant NMR spectrum typically portrays an ensemble average of the most energetically favorable conformers, according to the Boltzmann distribution analysis. However, it is important to note that QM computations often rely on a single, static molecular structure. Consequently, such calculations fail to account for dynamic conformational changes. Therefore, it is recommended to precede computational determination of NMR parameters with a comprehensive conformation analysis (Lodewyk et al., 2012; Costa et al., 2021).

Conformational analysis is commonly carried out using one of two methods, and the choice of the method depends on molecular flexibility. When the molecule presents few rotatable bonds, a systematic conformational search becomes a feasible choice. This approach involves a regular and predictable alteration of all bond lengths, angles, and/or dihedrals angles, followed by geometry optimization at a QM level of theory for each resulting structure. A notable advantage of this method is its ability to thoroughly explore the entire Potential Energy Surface (PES). On the other hand, at the same time, the computational cost increases with molecular flexibility. Consequently, when a molecule features multiple rotatable bonds, a systematic conformational search may become computationally prohibitive. In such instances, a stochastic conformational search is employed, often performed using Molecular Dyamics (MD) simulations (Lei and Duan, 2007; Malloci et al., 2016) or the Metropolis Monte Carlo (MC) algorithm (Metropolis and Ulam, 1949). In a stochastic conformational search, modifications in Cartesian coordinates or torsional angles of rotational bonds occur randomly, generating structures subsequently subjected to geometry optimization calculations (Lodewyk et al., 2012; Bagno and Saielli, 2015; Costa et al., 2021).

Given that most natural product structures are complex, flexible and, consequently, present multiple rotatable bonds, stochastic conformational searches typically emerge as the preferred method of choice. This approach enables the advantageous combination of reduced computational cost with a comprehensive exploration of the PES (Bagno and Saielli, 2015; Fabio L.P.; Costa et al., 2021). However, it is important to recognize that the complete replication of stochastic conformational searches is not feasible. As such, the set of conformers utilized for computing the final NMR parameters should be provided as Cartesian coordinates and included as supporting documentation in published papers to enable reproducibility of the computational work.

Refining structural geometries: geometry optimization calculations

Given that NMR parameters are extremely sensitive to molecular geometry, it is necessary to perform calculations based on reasonable geometries to accurately reproduce experimental NMR data. It is possible to obtain an appropriate geometry directly through experimental data, such as extracting coordinates from a crystalline structure. Alternatively, snapshots from MD simulations can also be used for generating molecular geometries. Nevertheless, the most common approach is to perform a geometry optimization calculation, commencing from an initial structure. However, it is worth emphasizing that geometry optimization computations yield the closest local energy minimum, as determined by energy analyses, and do not encompass different conformations. Consequently, each conformation generated through a previous conformational analysis must be submitted to subsequent geometry optimization (Willoughby et al., 2014; Casabianca, 2020; Rusakova, 2022).

QM methods stands as the preferred choice for conducting geometry optimizations, owing to their capacity to reproduce the geometries with superior accuracy when compared to semi-empirical and molecular mechanics (MM) approaches. Usually, Density Functional Theory (DFT) and post-Hartree-Fock (HF) methods are the most commonly employed approaches, with the latter being predominantly applied to smaller systems due to its higher computational demands (Bursch et al., 2022).

Several works have established a benchmark for evaluating various density functionals to calculate geometry optimizations for NMR parameters. Overall, most papers indicate that the popular B3LYP, coupled with a consistent basis set of at least double-ζ quality, emerges as the preferred choice for obtaining an appropriate molecular geometry. Minnesota density functionals, including M06 and M06-2X, represent viable alternatives to B3LYP for this purpose (Mardirossian and Head-Gordon, 2017).

To ensure that the optimized geometry does not correspond a local saddle point on the PES, or in simpler terms, to confirm that it is not a transition structure, it is advisable to conduct a frequency calculation. Usually, this calculation is performed at the same level of theory as the geometry optimization. If the optimized geometry indeed corresponds to a local saddle point, it will exhibit an imaginary (negative) frequency. Otherwise, the absence of such an imaginary frequency confirms that the optimized geometry corresponds to a true energy minimum (Willoughby et al., 2014).

Within the frequency calculations, the net free energy associated with the optimized geometry is computed. These values can subsequently be used to conduct a Boltzmann distribution analysis. This analysis serves the purpose of enhancing the conformer selection, from a QM level of theory (Costa et al., 2021).

Calculating NMR parameters

After selecting the most energetically favorable conformers and optimizing their molecular geometries, it is possible to compute NMR parameters.

There are basically two types of parameters that can be computationally simulated: spin-spin coupling constants (SSCC) and chemical shifts (δ) (Lodewyk et al., 2012; Costa et al., 2021). One approach to simulating these parameters is through the utilization of empirical methods, which rely on databases of parameters derived from known molecules, enabling the estimation of parameters for novel molecules (Jonas et al., 2022). In recent years, machine learning algorithms have been implemented to predict NMR parameters using sets of parameters for established molecules (Gerrard et al., 2020; Guan et al., 2021). However, the pools of molecules used in these databases for NMR predictions can often be limited, restricting the chemical diversity of molecules that can be used in these methods. As an alternative, one can rely on QM computations of SSCC and δ parameters (Jonas et al., 2022).

Concerning the computation of δ, it is important to highlight that this parameter is not directly simulated within the calculations. Instead, nuclear magnetic shieldings (σ) are computed and subsequently converted into δ values through the application of a reference compound (σ_ref), as delineated in Equation 1. The reference compound should be calculated under identical conditions as the molecule of interest and, ideally, should correspond to the same reference compound utilized during the acquisition of the experimental spectrum. Consequently, for natural products, the commonly employed reference compound is tetramethylsilane (TMS) (Lodewyk et al., 2012; Chhetri et al., 2018).

$\mathrm{\delta }={\mathrm{\sigma }}_{\text{ref}}-\mathrm{\sigma }(1)$

Just like in the geometry optimization calculations, in most cases, both SSCC and σ are most commonly computed employing DFT or post-HF level of theory. Both parameters are very sensitive to electron correlation effects, and DFT and post-HF approaches take into account these effects (Rzepiela et al., 2022). Several benchmark studies have been conducted to compare different levels of theory in the reproduction of experimental data (Bally and Rablen, 2011; Flaig et al., 2014; Oliveira et al., 2021; Schattenberg and Kaupp, 2021). Density functionals like B3LYP, mPW1PW91, PBE0, and PBE1 are frequently preferred due to their commendable performance in reproducing experimental data within organic molecules, all while maintaining computational efficiency. Furthermore, the assessment of long-range corrected functionals has indicated that, in certain instances, these functionals can offer superior reproduction of the experimental data (Iron, 2017).

Keal and Tozer have introduced a family of GGA functionals denoted as KT-n (where n = 1, 2, or 3), explicitly developed for the computation of σ and SSCC. In evaluations of these functionals, KT-1 and KT-2 exhibited enhanced accuracy in simulating σ values for a set of molecules when compared to commonly utilized density functionals. However, when applied to SSCC calculations, these functionals did not yield substantial improvements over conventional functionals (Keal and Tozer, 2004; Keal and Tozer, 2003; Allen et al., 2003; Keal et al., 2004). It is noteworthy that regarding natural products chemistry, this particular set of density functionals has not found widespread application in calculating natural product structures.

WC04 and WP04 represent two density functionals derived from the widely employed B3LYP, with parameterization for the computation of ¹³C and ¹H σ, respectively. A comparative analysis of these functionals and other commonly used for σ calculations, encompassing 40 organic molecules, revealed that WC04 and WP04 exhibited an ability to yield calculated δ values that were closely aligned with experimental data (Wiitala et al., 2006). Nevertheless, similar to KT-n functionals, WC04 and WP04 are not commonly employed in calculations for natural product structures.

The computation of NMR parameters requires dealing with the so-called “gauge problem”. This issue arises with the use of finite basis sets, which is the standard approach for the calculations, resulting in a dependence of the origin of the magnetic field vector. There is a great variety of approaches to mitigate the gauge problem, but the most commonly employed ones are the Gauge-Including Atomic Orbital (GIAO) (Ditchfield, 1974) and the Continuous Set of Gauge Transformations (CSGT) (Keith and Bader, 1993a; Keith and Bader, 1993b).

Simulating solvation effects

To achieve the best reproduction possible of the experimental NMR parameters, it is recommendable to replicate certain experimental conditions within the computational calculations. Among these conditions, solvation effects warrant particular attention. It is a well-established fact that the chemical environment of the nuclei is highly sensitive to solvation effects. Consequently, the interaction of nuclei with solvents can exert a significant impact on NMR spectra (Mari et al., 2019; Casabianca, 2020).

Solvation can be simulated at the atomistic level, a method commonly referred to as discrete solvation, wherein solvent molecules are explicitly incorporated into the calculations. This approach is especially valuable when simulating systems characterized by specific interactions between solute and solvent, such as hydrogen bonding and van der Waals interaction. Nevertheless, it is important to note that the explicit inclusion of all solvent molecules in the calculations can result in a dramatic increase in the computational cost due to the QM treatment of an extensive number of additional atoms. This can often make the calculations unfeasible, even with the use of substantial computational resources (Kaupp et al., 2004).

An alternative approach for simulating solvation effects involves the use of the so-called implicit methods, including the Generalized Born (GB) approximations, the density-based solvation model (SMD) and the popular Polarizable Continuum Model (PCM) (Marenich et al., 2009; Mennucci, 2012; Zhang et al., 2017). In this coarse-grained approach, the solvent medium is assumed as an infinitely continuum medium, characterized by its dielectric and interfacial properties. This method can accurately account for nonspecific solvation effects, including polarization and orientation of multipole moments. Notably, the absence of explicit inclusion of additional particles in the QM treatment of the system enables implicit solvation approaches to be less computationally expensive than explicit methods. Consequently, an implicit simulation of the solvents as a dielectric continuum permits the application of a purely quantum treatment to solute-solvent interactions (Cramer and Truhlar, 1999).

Usually, the inclusion of implicit models for calculations of natural product structures is generally adequate for providing accurate calculated NMR parameters in comparison to experimental data (Pierens, 2014). As a result, implicit models, particularly the integral equation formalism variant within the PCM (IEFPCM), are the preferred method for computing NMR parameters of natural product structures (Lodewyk et al., 2012; Willoughby et al., 2014; Costa et al., 2021).

Reducing sources of errors in calculations

While QM methods for computing NMR parameters have experienced significant advancement in the last decades, various approximations are still employed in the treatment of multielectronic systems, so that these calculations do not become prohibitive in the computational cost. However, the incorporation of these approximations into the calculations introduces errors in the computed parameters. Indeed, it is observable that without employing error-reduction techniques, calculated chemical shifts can exhibit average deviations up to 0.4 ppm or greater for ¹H nuclei and 10 ppm or greater for ¹³C nuclei (Lodewyk et al., 2012).

A significant proportion of errors associated with computed NMR parameters are systematic and, as such, can be empirically cancelled (Hehre et al., 2019). A commonly employed method for mitigating the systematic errors inherent in calculated chemical shifts involves the application of scaling factors, obtained through linear regression analyses between calculated chemical shifts versus experimental values for a carefully selected set of molecules. These linear regressions yield linear equations, and the slope (a) and intercept (b) values can be used to correct computed chemical shifts, resulting in values that closely approximate the experimental data (Costa et al., 2010; de Albuquerque et al., 2016).

Usually, molecules selected for generating scaling factors are chosen with the aim of ensuring significant structural diversity, thus enabling the applicability to a wide range of different structures. Alternatively, a smaller set of molecules with structural resemblance to the molecule of interest may be chosen. A third approach involves the creation of an internal scaling factor, in which the experimental and theoretical data sets used for scaling factor generation are obtained directly from the molecule of interest itself (Lodewyk et al., 2012).

In recent years, several works have focused on the development of scaling factors for ¹H and ¹³C NMR chemical shifts, along with their application to various natural product structures (Barone et al., 2002; Costa et al., 2015; Kovács et al., 2023). Typically, the systematic error reduction achieved by scaling factors is sufficient to yield accurate results, obviating the necessity for more expensive computational methods. The CHESHIRE CCAT database, developed by Tantillo and coworkers and accessible at http://www.cheshirenmr.info, serves as a valuable resource for guiding the selection and implementation of these scaling factors.

Recently, Li and coworkers developed a novel protocol for the computation of ¹³C NMR chemical shifts based on linear regressions. This methodology, known as Sorted Training Sets (STS), involves the categorization of carbon nuclei into distinct training sets based on three primary parameters: hybridization type, solvation cavity radii, and interactions with solvent molecules. Subsequently, the carbon shielding tensors for each training set are calculated and utilized in a linear regression analysis with experimental data separately. The resulting specialized linear scaling equations are then applied to transform the shielding tensors into calculated chemical shifts. Notably, this protocol has demonstrated the potential to reduce Mean Absolute Error (MAE) and Root Mean Square (RMS) values by approximately 50% when compared to conventional linear scaling protocols, particularly for nuclei that are challenging to reproduce, such as sp² nuclei (Li et al., 2020).

Systematic errors in SSCC can be empirically cancelled through the application of parametric corrections. This methodology, originally pioneered by Kutateladze’s research group, is based on the predominance of the Fermi contact (FC) term over the SSCC parameters (Kutateladze and Mukhina, 2014; Kutateladze and Mukhina, 2015b; Kutateladze and Reddy, 2017). The first parametric correction, known as DU4, was specifically developed for calculating ¹H–¹H SSCC values and was formulated by categorizing SSCC classes based on nuclear connectivity and hybridization. In this approach, hydrogen atoms are computed employing a novel DU4 basis set, while carbon atoms are computed using the 4-31G basis set (Kutateladze and Mukhina, 2014). After the publication of this first parametric correction term, additional methodologies have been further developed and refined.

DU8 represents another parametric correction term that uses Natural Bond Orbitals (NBO) as an aid for the scaling of ¹H–¹H SSCC values. Subsequently, the DU8c approach was introduced to extend the empirical scaling to encompass ¹³C-¹H SSCCs in additional to the ¹H–¹H SSCCs, already present in the past approaches. More recently, the DU8+ term was developed, combining computed SSCC values with theoretical ¹³C NMR chemical shifts data, with the primary aim of elucidating the structures of compounds containing heavy atoms. This methodology was applied to a set of 16 structures comprising halogenated natural products with misassignments, leading to successful structural revisions (Kutateladze and Mukhina, 2015a; Kutateladze and Mukhina, 2015b).

Correlating calculated and experimental data: the use of statistical tools

Establishing a correlation between sets of computed and experimental NMR parameters is a non-trivial task. Naturally, a set of simulated parameters is expected to exhibit closer agreement with the corresponding set of experimental parameters when the molecular structure is correct, as opposed to when it is erroneous. However, there are instances where two stereoisomers of a natural product structure yield two sets of data very similar to each other. In such cases, conventional statistical parameters, such as R², MAE, and RMSD may prove insufficient for distinguishing between data from such closely analogous structures (Costa et al., 2021).

To address this particular issue, in 2009, Smith and Goodman introduced a novel suite of statistical procedures, known as CPn methods (Smith and Goodman, 2009). This seminal work marked the inception of a more sophisticated category of statistical tools design to establish a more precise correlation between computed and experimental NMR data. Specifically, CPn methods were formulated for application in scenarios involving two sets of experimental δ correlated to two sets of calculated δ.

In the formulation of CPn methods, the authors took into account that, because of a cancellation of systematic errors, the difference between two sets of NMR δ derived from similar nuclei is calculated greater precision than the individual NMR δ values themselves. Consequently, when dealing with two sets of experimental data denoted as A and B, along with two corresponding sets of computed data represented as a and b, the correlation A = a/B = b will exhibit a markedly distinct outcome in comparison to the correlation A = b/B = a, even when the nuclei yield NMR δ values that are significantly similar. Therefore, the correct assignment (A = a/B = b) should be accurately reproduced in the calculations, while the incorrect assignment (A = b/B = a) in anticipated to result in a substantially inferior level of agreement.

Within the CPn methods, Smith and Goodman introduced three statistical parameters, namely CP1, CP2, and CP3. Among these, CP3 demonstrated a significantly superior performance in establishing correlations between sets of calculated and experimental data when compared with CP1 and CP2. Furthermore, CP3 provides a heightened level of confidence compared to conventional statistical metrics such as R², MAE and RMSD (Smith and Goodman, 2009).

Despite its extensive application in the structural analysis of numerous organic molecules (Smith et al., 2010; Hwang et al., 2015; Junior et al., 2015), the CP3 method exhibited a limitation: it did not take into account situations where only one set of experimental NMR δ was available alongside multiple sets of calculated NMR δ values. Such scenarios frequently arise in natural product chemistry when a sole stereoisomer is isolated, and its relative stereochemistry should be determined. In such cases, often, all potential stereoisomers are calculated, and their simulated data must be compared to the experimental data. Consequently, in response to this need, Smith and Goodman devised the widely popular DP4 parameter (Smith and Goodman, 2010).

Within the DP4 method, the calculated δ are presented in a scaled form, δ_scal, which is derived through linear regression analysis between the calculated and experimental δ (δ_exp). Subsequently, the errors between δ_exp and δ_scal are computed. Based on these discrepancies, assuming a t-distribution, and employing Bayes’s theorem, DP4 yields the probability of each candidate structure to be correct. Various parameters in the formulation of DP4 were extracted from a dataset consisting of calculated δ values for 117 organic molecules, employing the B3LYP/6-31G(d,p)//MMFF level of theory. DP4 has been consistently employed in the structural analysis of several natural products compounds (Cen-Pacheco et al., 2014; Cairns et al., 2015; Challinor et al., 2015).

Despite DP4’s extensive application in the context of natural product structure elucidation and correction, there have been instances of unsuccessful application of this method, wherein DP4 yielded unreliable outcomes or even misidentified the correct stereoisomer. Grimblat and coworkers postulated two hypotheses to account for these issues in the DP4 formulation: (1) the application of a relatively poor level of theory, particularly during geometry optimizations (MMFF), for the obtention of the calculated δ values; and (2) the exclusive utilization of scaled δ values (Grimblat et al., 2015).

Both of these issues were effectively addressed through the development of the DP4+ methodology by Grimblat and coworkers (Grimblat et al., 2015). Particularly, with regard to the level of theory adopted in the method, the B3LYP/6-31G(d) level of theory was employed for the geometry optimization step. The use of DFT, as opposed to a molecular mechanics approach such as MMFF, ensures a more precise depiction of the molecular geometry, a factor that can significantly impact the calculated NMR data. In terms of NMR δ calculation, 24 different levels of theory were employed, encompassing two density functionals (B3LYP and mPW1PW91) and six Pople basis sets, with computations conducted both in the gas phase and solution, using PCM to implicitly simulate the solvation effects. Concerning the exclusive use of scaled δ values, Grimblat and coworkers introduced a dual-component formulation within the DP4+ framework: one component corresponding to the probabilities computed using scaled δ values and another component corresponding to the probabilities computed using unscaled δ values. The application of DP4+ methodology to a dataset of 48 organic compounds demonstrated its capacity to provide more accurate results than the original DP4 formulation. Subsequent to its development, DP4+ has been extensively employed to the elucidation and correction of natural products structures (Batista et al., 2019; Martorano et al., 2020; Marcarino et al., 2022; Silva et al., 2022; Santos et al., 2022).

Another advancement over the original DP4 methodology was proposed by Grimblat and coworkers, leading to the development of a refine approach known as J-DP4 (Grimblat et al., 2019). This method incorporated vicinal couplings (³J_HH) into the DP4 formulation. Two distinct approaches were devised for integrating ³J_HH into the original DP4 framework: one method was termed direct J-DP4 (dJ-DP4), while the other was referred to as indirect J-DP4 (iJ-DP4). In the dJ-DP4 approach, ³J_HH values are computed at a DFT level of theory, in addition to the conventional calculation of δ values. These calculated ³J_HH values are then incorporated into a modified DP4 equation, resulting in new probabilities for the candidate structures. Alternatively, in the iJ-DP4 approach, experimental ³J_HH values are used to impose constraints on the molecular geometries during the conformational analysis process. This approach facilitates a more accurate depiction of molecular geometries, as only conformations that align with the observed ³J_HH values are selected for the subsequent NMR δ calculations.

A comparative evaluation between the dJ-DP4 approach and the original DP4 formulation, performed on a set comprising 69 organic compounds, revealed that the DP4 method achieved an accuracy of 75%, while the dJ-DP4 approach exhibited a substantially higher accuracy rate of 96%. Notably, in instances where the DP4 method resulted in an incorrect assignment, the dJ-DP4 approach was capable of predicting the correct assignment. Additionally, the analysis of the iJ-DP4 approach demonstrated its potential to yield superior results compared to the original DP4 method, particularly when two ³J_HH values are employed. This improvement was achieved with a significantly reduced computational cost relative to the dJ-DP4 approach, as it does not necessitate any additional calculations beyond the original DP4 method, except for the inclusion of experimental ³J_HH values (Grimblat et al., 2019).

In 2018, Zanardi and coworkers introduced a novel statistical tool, derived from DP4+ formulation, known as DP4+ Integrated Probability (DIP) (Zanardi et al., 2018). This method was purposefully designed for scenarios involving the determination of absolute configurations through double derivatization techniques employing chiral derivatization agents, such as Mosher’s agent. In such instances, two distinct DP4+ probabilities are generated, leading to two potential outcomes based on their results: either the most probable candidate in both cases shares the same absolute configuration as the substrate (referred to as “matched”), or they do not (referred to as “mismatched”). Within the matched case, two possibilities exist: (1) DP4+ correctly identifies both configurations; or (2) DP4+ fails to identify both configurations. Studies have indicated that this latter scenario is highly improbable. Therefore, if two DP4+ results match, it is likely that the assignments are accurate. Conversely, the mismatched case presents a scenario where one of the DP4+ outcomes must be correct while the other is incorrect. To address this challenge, DIP was developed as a means to consolidate both independent DP4+ predictions into a unified parameter. This approach was applied to a dataset consisting of 114 chiral alcohols and amines, resulting in a correct assignment of absolute configuration in 96% of the cases (Zanardi et al., 2018).

Misassignment case studies

In this section, we present four new carefully selected examples (2019-2023) in which, through NMR parameter simulations combined with the latest available tools, revisions to the original structures are proposed. We hope both newcomers and experienced researchers will gain valuable insights from these regular state-of-the-art reviews, which highlight recent advances in the research field.

Isoserrins A, B, and D: DU8+

The first example discussed a misassignment of compounds isolated from Isodon serra by Xing et al., in 2020. This article was selected because it applies a combination of statistical parameters with DU8+ calculations of ¹³C NMR chemical shifts to recognize a possible reassignment. Furthermore, a computationally driven structure revisions are presented in this communication led by Novitskiy et al. (2021) in 2021.

In 2020, Xing et al. successfully isolated several ent-kauranoids derived from the aerial components of Isodon serra. These ent-kauranoids compounds, isoserrin A-J, characterized by tetrahydropyran and oxirane moieties, were assigned through rigorous and comprehensive spectroscopic studies based on 1D and 2D NMR methods, such as ¹H, ¹³C{¹H}, COSY, HMBC and NOESY (Novitskiy et al., 2021).

Due to the frequent misinterpretation of experimental NMR data regarding oxygenated natural products, Novitskiy’s research group directed their focus toward four highly oxidized compounds isolated by Xing et al, namely isoserrins A, B, D, and E (see Figure 2).

FIGURE 2

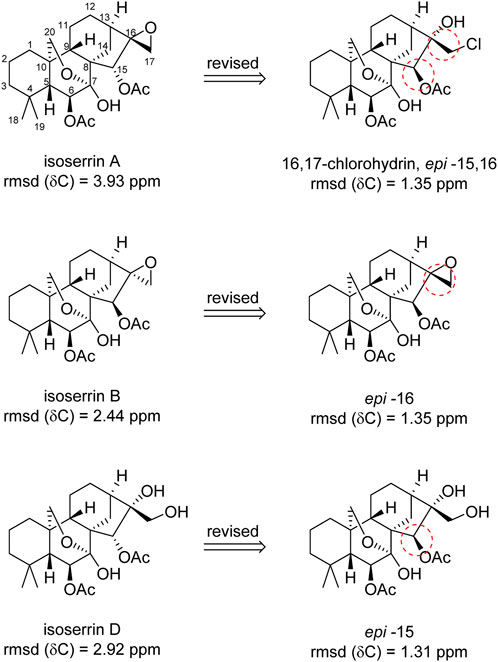
FIGURE 2. Structures of oxygenated isoserrins; originally proposed and revised by DU8+ calculations.

The group led by Kutateladze developed a fast and accurate method, called DU8+, which has already been widely used by the aforementioned group in the validation and structural revision of several natural products. In previews studies, the accuracy of DU8+ was verified by the authors in a comprehensive dataset containing thousands of reliable experimental chemical shifts (Novitskiy et al., 2021). Based on these calculations, the authors demonstrated that obtained RMSD (δC) values ranging from 1.0 to 1.8 ppm can be used as structural validation. On the other hand, obtained RMSD (δC) values greater than this range suggests the putative structure may require revision (Novitskiy et al., 2021).

Based on that, Novitskiy et al. (2021) identified only the original structure of isoserrin E yielded a good match between the experimental and simulated data, resulting in a RMSD value of (δC) = 1.30 ppm, and did not require revision. However, three isoserrins (A, B, and D) exhibited RMSD (δC) over 2.44 ppm, revealing a possible misassignment in the originally proposed structure.

In the case of isoserrin A, the highest deviation between experimental and computed spectra was obtained, yielding a RMSD (δC) of 3.93 ppm. A notable discrepancy was observed in C16, the oxirane carbon. The simulated obtained value was 70.27 ppm, which differs 13.93 ppm when compared to the experimental value. These discrepancies suggest the absence of the epoxide group in the isolated natural product, prompting the authors to propose a modification from oxirane to a chlorohydrin structure, along with an inversion of C15. It is important to highlight that the proposed structure revision by the authors was acquired by examination based on trial and error. This adjustment proposal markedly enhanced the alignment with the original data, reducing the RMSD value from 3.93 to 1.35 ppm and MAE of 0.97 ppm, see Figure 2 (Novitskiy et al., 2021). However, it is noteworthy that this revised proposed structure challenges the original mass spectrometry findings. Nevertheless, the authors postulated a potential misinterpretation of the ion molecular peak [M–HCl] in the original study. Additionally, Novitskiy et al. reported another evidence that isoserrin A is unlikely to present an oxirane moiety, the obtained retention time (t_R = 38 min) diverges from the characteristic profile of othef oxirane compound of the class (t_R = 29 min), and is more aligned with the t_R values for diols compounds, with t_R around 35–39 min.

Finally, the relative configuration of carbons C15 and C16 in isoserrin A was originally proposed based on NOESY interactions as 15R*,16R*. The NOESY are in accordance with the proposed revised structure with the exception of data for H15 which, according to the authors, is challenging due to overlapping NOE signals. However, after close examination of the reported data, it was suggested that the strong interaction ‘H15∙∙∙H9’ (δH = 2.00 ppm) must be revised to H15∙∙∙OAc-6 (δH = 2.01 ppm). A cross-peak attributed to ‘H15∙∙∙H5’ is dispersed and dubious; however, significant NOE enhancement is observed for H15∙∙∙H14β. Nevertheless, based on that analysis (also the change in atom priorities around C16 for chlorohydrin and oxirane), the relative configuration of the proposed revised structure should be (15S*,16S*) (see Figure 2) (Novitskiy et al., 2021).

Regarding the isoserrins B and D, the significant discrepancies between the computed and experimental data were lower when compared to isoserrins A, but still significant: RMSD (δC) of 2.44 and 2.92 ppm, respectively. In the instance of isoserrin B, the disparities observed in C16 and C17 were around ΔδC 7–8 ppm, showing the potential misassignment point. Based on that, the authors suggested that C16 epimer provided a better agreement with the original experimental NMR data resulting in a RMSD (δC) of 1.35 ppm and MAE of 1.00 ppm, aligning with the authors’ confidence range (RMSD) of 1.0–1.8 ppm (Figure 2) (Novitskiy et al., 2021).

Regarding isoserrin D, the most significant disparity was in C9 (ΔδC 9 ppm downfield), which can be explained due to a shielding effect of the acetyl group. Therefore, a inversion of C15 was proposed. Doing that, C15 would brought into proximity C9 and OAc-15, resulting in a reduction of RMSD from 2.92 to 1.31 ppm and MAE of 0.97 ppm, as shown in Figure 2 (Novitskiy et al., 2021). However, it is important to emphasize that Novitskiy et al. (2021) were unable to verify the stereochemical reassignment of isoserrin B and D, as the original paper only provides the NOESY spectrum for isoserrin A.

In conclusion, based on DU8+ calculations, the authors identified a possible misassignment in the structure and stereochemistry of isoserrins, a highly-oxygenated ent-kaurane diterpenoids, and a computationally driven structure revisions are proposed. However, it is important to highlight that the correct structure of isoserrins still needs confirmation by any independent evidence. This can be unequivocally achieved by reisolation of the natural product, followed by an accurate comprehensive spectroscopic study or through total synthesis, which as far as we know, has not yet been carried out.

Diphenazine-based natural Products: DP4+ and ECD

The second example of application discuss a protocol for structure elucidation and revision of members of diphenazine class, a challenging compound containing three bridged stereocenters, several conformations, ring fusions and multiple spatially isolated OH groups. The selection of this article is grounded to the application of NMR and ECD simulations, along with the implementation of the DP4+ methodology. Based on their findings, the authors isolated and characterized the structure of two new diphenazines, baraphenazine H and izumiphenazine E. In addition, the structure of three diphenazine compounds, namely phenazinolin D, izumiphenazine A, and baraphenazine G was reassigned (Zhuang et al., 2023).

Recently, Zhuang and coworkers through the application of a catalytic enzyme-linked click chemistry assay (cat-ELCCA) tool carried out the screening of the full length of protein−protein interactions, including the eukaryotic translation initiation factor 4E (eIF4E) and its regulators. eIF4E is an important RNA-binding protein which the availability regulates the Cap-dependent mRNA translation initiation (CDT). As CDT is crucial for encoding oncoproteins, growth and survival factors, the overexpression of eIF4E has been shown to induce tumorigenesis in several cancer types. Thus, deploying an elegant high-throughput screening protocol to identify natural product-based inhibitors of eIF4E, the authors isolated monophenazine- and diphenazine-based natural products as inhibitors of eIF4E from an active bacterial strain, Streptomyces sp. 06282-1I.

Diphenazine compounds presents inherent characteristics, such as the presence three bridged stereocenters, numerous conformations, and ring fusions which makes their complete structure characterization a challenging task. Therefore, often the application of empirical NMR and spatial analyzes using ROESY/NOESY techniques become unsuccessful. Another difficulty is the determination of the position of the OH groups, which sometimes are even neglected due to the lack of NMR correlations between the OH groups and the rest of the molecules. Although in theory this can be done through ¹H−¹⁵N HMBC experiments, it requires a large amount of compound, impractical for low-yielding molecules such as diphenazine class. In this scenario, quantum chemical simulations of spectroscopy parameters become extremely useful and have been widely used for the structure characterization of complex natural products. Therefore, using this pipeline, Zhuang and colleagues accomplish the isolation and structure elucidation of 8 compounds, belonging to the monophenazine and diphenazine classes, namely: 1,6-phenazinediol (1), baraphenazine F (2), baraphenazine H (3), phenazinolin D (4), izumiphenazine A (5), izumiphenazine E (6), baraphenazine G (7), and baraphenazine I (8), from Streptomyces sp. 06282-1I. Among these compounds, 3 and 6 are new diphenazines, and 4, 5 and 7 had their structure revised, see Figure 3.

FIGURE 3

FIGURE 3. Structures of isolated molecules.

For compound 2, the LC-MS and NMR data matched with the known baraphenazine F (Wang et al., 2019). Based on the bicyclic rings geometry and the ¹H NMR chemical shifts of H10 (3.82 ppm) and H21 (5.74 ppm), the authors conclude that both hydrogens points to the same direction, resulting in only four stereoisomers for the three chiral centers (see Figure 4): 2a (10S,11S,21S), 2b (10S,11R,21S), and their enantiomers. After a non-conclusive ROESY correlations to determine the C11 configuration, the authors establish the 10S,11S, 21S configuration through correlation of small vicinal coupling constant observed between H11 (4.79 ppm) and OH11 (6.20 ppm, J = 3.7 Hz) with a dihedral angle of 50.9° in H11−C11−O11−OH11 for 2a in contrast to 171.0° for 2b, corresponding to the original proposed relative configurations. On the other hand, the absolute configuration and the position of the OH groups of baraphenazine F were not established in the original article (Zhuang et al., 2023). As mentioned, the sample amount requirement for application of ¹H−¹⁵N HMBC precluded its use to determine the position of the OH groups. Therefore, the authors employed ECD calculations to determine the absolute configuration and NMR/DP4+ analyses to confirm the relative configuration and the OH groups position.

FIGURE 4

FIGURE 4. Possible isomers of 2, 3, 4, 5 and 6.

For the ECD calculations, the authors considered 2a and 2b configurations as the starting point and simulated the ECD for the eight possible isomers (see Figure 4). This first analysis was sufficient to determine that isomers 2a−2d (OH group at C1 in ring G) produced a better agreement with the ECD curve when compared to 2e-2f (OH group at C4 in ring G). However, it was not possible to differentiate 2a and 2b, due to the distance from the chromophores to C11 in compound 2. To solve this problem, the ¹H and ¹³C NMR chemical shifts of 2a−2d were simulated and compared with the original data through DP4+ protocol. However, during the calculations, the authors realized that small differences (<0.5 ppm) were obtained between the calculated and the experimental chemical shifts for most carbon-bound hydrogens, in addition to the larger differences (OH1: ∼3 ppm; OH11: ∼4.5 ppm; OH18: ∼2 ppm) observed in exchangeable protons (especially OHs). Any improvement was obtained even with different DFT functionals. This issue was successfully solved by the use of unscaled and scaled DP4+ analyses, resulting in an overall DP4+ probability score of 95.95% (all data) for 2a compared to 0.09% for 2b, 3.94% for 2c, and 0.03% for 2d. These findings were in accordance with the first analysis using coupling constant and dihedral angle carried out by the authors. It is crucial to emphasize two points. First, including the chemical shift of the OH protons in a DP4+ analyses is not ideal, due to the fact these chemical shifts strongly depend on experimental conditions (pH, concentration, temperature) that cannot be reproduced by using the continuous solvent model. Therefore, large errors can be obtained between the calculated and the experimental chemical shifts (as discussed by the authors on the paper). These large errors can jeopardize the quality of the assignment of DP4+. Thus, the ideal scenario would be to evaluate whether the DP4+ results are the same after removing the OH chemical shifts. Second, as mentioned in both this manuscript and the original DP4+ paper (Marcarino et al., 2020), the importance of using (when possible) all NMR data into the DP4+ tool. A pertinent exemplification of this principle is evident in this paper of Zhuang and colleagues, where they reported that the DP4+ tool yielded 59.50% (H data) and 36.32% (C data) for 2a, and 1.41% (H data) and 63.08% (C data) for 2c. In other words, while the carbon NMR data favored 2c as the correct candidate, the combination of H and C DP4+ probability (all data) correctly identify the isomer 2a as the most probable, thereby confirming the reported structure of baraphenazine F.

Compound 3 was elucidated through HRESIMS and NMR analysis. Based on the NMR spectra, the authors propose that this compound exhibits the same A−E rings as compound 2, as well as the identical 10S,11S, 21S relative configuration of 2 in rings C and D. This configuration was supported through the observation of small vicinal coupling constants between H11 (4.74 ppm) and OH11 (6.06 ppm, J = 3.1 Hz), with the observed dihedral angle of 50.7° in H11−C11−O11−OH11 for (10S,11S,21S)-3 in contrast to 171.8° for (10S,11R,21S)-3. Nevertheless, the NMR spectrum of 3 presented some differences when compared to 2. The absence of the proton peak for OH1 (12.03 ppm) in ring G, a more deshielded chemical shift for H2 (6.15 ppm), and HMBC indicated the presence of a carbonyl at C1 in ring G due to the weak correlation between H3 (8.15 ppm) and a carbon with a δC of 177.5 ppm. Furthermore, the proton of the NH5 group in ring F was not observed in ¹H NMR spectrum, hindering the determination of its position.

To overcome these problems, the authors employed the same methodology as was applied to compound 2, involving ECD calculations and NMR analysis, along with the application of the DP4+ tool, to determine the absolute configuration and the positions of the carboxylic acid and OH groups in 3. Considering only candidates 3a-3d in ECD calculations, the absolute configuration of 3 was confirmed as 10S,11S, 21S (see Figure 4). However, the authors were unable to ascertain which simulated ECD curves correlated better with the experimental data. Therefore, NMR calculations were applied to all four candidates to determine the position of the NH5 proton, the carboxylic acid, and OH groups in 3. Nevertheless, the authors did not incorporate the chemical shifts of C4, C24, and NH5 due to their absence in the NMR spectra. Applying the DP4+ tool, 3a exhibited the highest probability of 83.77% (all data), while 3b obtained 16.23%. Interestingly, when the DP4+ results were analyzed independently, into the H and C DP4+ form, the results were conflicting, yielding 97.52% (H data) and 10.64% (C data) for 3a and 2.25% (H data) and 89.36% (C data) for 3b, showing the importance of use as much information as possible in DP4+ tool. Despite a relatively not excellent probability of 83.77%, the authors assert that the structure 3a is the most likely configuration for compound 3, named baraphenazine H, based on its structural similarities to 2. The proposed structure of 3 was also corroborated by observing the tautomerization of 3 to 2 after long-term storage at −20°C.

Compound 4 exhibited substantial alignment of LC-MS and NMR data with known molecule phenazinoline D (Ding et al., 2011). Interestingly, the original paper relied solely on NMR data and optical rotation calculations to determine the absolute configuration. Regarding the relative configuration of H11 (R) in rings C and D, it was determined by the observed small vicinal coupling constant (3.3 Hz) between H10 and H11. However, Zhuang and colleagues reported that the analysis conducted in the original article is insufficient for precisely determining the relative configuration of H11. After evaluate the two possible stereoisomers 10S,11S, 21S (4a) and 10S,11R, 21S (4b), the authors showed that the dihedral angles H10−C10−C11−H11 were almost identical, 62.2° for 4a and 61.5° for 4b, precluding an unequivocal differentiation. In fact, Zhuang’s analyses suggested that 4a was favored over 4b. Several facts indicated this suggestion. First, a weak ROESY was observed between OH11 (6.20 ppm) and H12_ax (3.87 ppm), showing better correlation with the distance OH11/H12_ax in 4a (3.5 Å) in contrast to 4b (4.6 Å). Furthermore, Mosher analysis unambiguously indicate the configuration of C11 as S. Additionally, the combined application of ECD and NMR calculations further supported the proposed configuration as 10S,11S, 21S configuration, obtained from ROESY and Mosher’s analyses. The DP4+ indicate isomer 4a as the correct one with a 100% (all data). Therefore, the authors revise the absolute configuration of phenazinolin D as 10S,11S, 21S from that previously proposed in the original article (Ding et al., 2011).

Compound 5 also exhibited a strong correlation between the LC-MS and NMR data and known molecule izumiphenazine A (Abdelfattah et al., 2010). In the original article, the relative configuration 10R,11R, 21S was determined based on NOE correlation, which was proven to be insufficient for the diphenazine class of molecules by Zhuang and collegues. In addition, the original article did not provide any evidence for the proposed OH groups position in 5.

Different from the previously discussed cases, this time compound 5 yields a relatively flexible planar bicyclic moiety, see Figure 3, which makes with H10 (5.59 ppm) and H21 (4.84 ppm) in rings C and D could face either the same or opposite directions. Therefore, eight stereoisomers are possible: 5a (10S,11R,21S), 5b (10S,11S,21S), 5c (10R,11R,21S), 5d (10R,11S,21S), and their respective enantiomers (see Figure 4). Upon observing strong ROESY correlations between H10/H21 (5.59/4.84 ppm) and H11/H20_eq (5.35/3.69 ppm) in rings C and D, 5c and 5d were favored due to the observed smaller atomic distances. In addition, the correlation of the observed coupling constants between H10 (5.59 ppm)/H11 (5.35 ppm, J = 5.6 Hz) are in accordance with the dihedral angle of 59.9° in H10−C10−C11−H11 for 5d, which not occur for 5c, with a correspondent dihedral angle of 161.6°. This fact contradicts the previously reported 10R,11R, 21S configuration for izumiphenazine A.

The observed ¹H−¹⁵N HMBC correlations between H17/N18 (7.40/321.9 ppm) and H20_ax,H20_eq/N18 (4.19,3.69/321.9 ppm) were used to determine the OH groups position in ring A at C14. However, due to insufficient NMR data to determine the OH groups position in ring G, the authors simulated ECD curves for all possible isomers 5a−5h. The candidates that exhibited the best correlations, 5d and 5h, had their NMR chemical shifts calculated and were subjected to analysis using the DP4+ tool. Isomer 5d yielded 100% probability for all data, and also a 100% for the independent H and C data, in accordance with the previously proposed OH group at C1. Consequently, the authors propose that the previously reported absolute configuration of izumiphenazine A should be revised to 10R,11S, 21S (Zhuang et al., 2023).

For compound 6, its structure elucidation relied on LC-MS and NMR data. Due to similarities in the NMR data between compounds 5 and 6, it was suggested the same skeleton and rings C and D connecting the two phenazine units. However, the main distinction were a singlet aromatic proton in 6 (7.05 ppm) in contrast to a more deshielded H8 (8.15 ppm) in 5 and C22 (116.6 ppm) in 6, in contrast to 124.9 ppm for 5. In combination with the HMBC correlations between this singlet aromatic proton (7.05 ppm) and C22 (116.6 ppm) in rings D/E, the authors suggest that 6 contains a flipped hydroxyphenazine-carboxylic acid unit when compared to 5, see Figure 3. However, this information was not enough to determine whether the proton is located at C23 or C24.

To address the (7.05 ppm) proton’s position and the absolute configuration, ECD calculations and NMR/DP4+ were employed for the eight possible stereoisomers (6a-6h), see Figure 4. Nevertheless, to reduce computational cost and based on the OH groups position in 2-5, the authors conducted a preliminary analysis where they tentatively assign the two OH groups at C14 and C6. The simulated ECD curves of 6e and 6g, both with the same configuration 10S,11R,21R, best aligned with the experimental data and were selected for NMR/DP4+ calculations. Despite the lack of experimental NMR peaks for C8, C24, and 25COOH, which were not included in the DP4+ analysis, the tool indicated 91.83% (all data) for 6e (97.36% H data and 23.39% C data) and 8.17% (all data) for 6g (2.64% H data and 76.61% C data), establishing the proton at C23.

Returning to the issue of the OH groups position, the authors once again conducted ECD calculations for isomers 6e and 6i−6k, which yielded indiscernible ECD curves. Interestingly, the authors determined the structure through NMR/DP4+ calculations of these four isomers, which indicated DP4+ probability (all data) of 65.64% (66.72% for H data and 0.01% for C data) for isomer 6j, in contrast to 30.66% (0% for H data and 93.18% for C data) for 6k. Despite the DP4+ obtained low probability, biosynthetic pathway consideration suggested all diphenazines should share the same ring G, which aligns with DP4+ results, where the correct OH group position is C6 (6j) instead of C3 in (6k).

The last compound, 7, the LC-MS and NMR data were similar to the know molecule baraphenazine G. Interestingly, the original paper did not provide any proof for the proposed absolute configurations and OH groups position (Wang et al., 2019). However, through ¹H−¹⁵N HMBC correlations of OH14/N12 (10.23/302.8 ppm), OH10/N12 (8.30/302.8 ppm), H8/N5 (7.92/298.1 ppm), and H4/N5 (7.73/298.1 ppm), the authors suggest the positions of the OH groups, OH1 (10.67 ppm) in rings G and OH14 (10.23 ppm) in ring A, were different from the previously reported structure of baraphenazine G. Therefore, a structure revision is proposed, in which the OH groups position should be corrected to C4 from C1 in ring G. Nevertheless, based on ECD calculations, the reported absolute configuration of 10R, 21R were confirmed.

In conclusion, Zhuang and coworkers developed a powerful pipeline for structure elucidation of diphenazines using ECD and GIAO NMR calculations coupled with a DP4+ probability tool, leading to several structure revisions, including the resolution of the absolute configuration of C11 of 4 and 5 from R to S. In addition, based on ¹H−¹⁵N HMBC experiments, the position of the OH groups from C4 to C1 in 7 was also corrected. Moreover, it was elucidated the structures of two new diphenazines 5 and 6 using this pipeline protocol.

(+)-Diplopyrone: DP4/J-DP4/ECD/DP4+/DIP

The third example is an elegant and extensive theoretical work carried out by Ariel Sarotti in 2020. Due to inconsistencies found between the synthesis and the isolated natural product, through quantum NMR calculations combined with the DP4/J-DP4/DP4+/DIP tools and ECD calculations, the structural revision of natural (+)-diplopyrone was proposed.

In 2003, Evidente and collaborators successfully isolated the phytotoxic tetrahydropyranpyran-2-one from Diplodia mutila, denominated as (+)-diplopyrone. The structure and relative configuration were assigned via extensive NMR analysis, including J coupling constants, COSY, TOCSY, NOESY, HSQC, and HMBC experiments. In addition, the author also determined the absolute configuration by means of Mosher analysis, after derivatization of the C9 secondary alcohol with the two enantiomers of MTPA-Cl (Evidente et al., 2003). Subsequently in 2005, in another publication by the same researchers, the absolute configuration 4a(S),8a(S),6(R),9(S) of 1 (see Figure 5) was reinforced through ECD and optical rotation methods, supported by TDDFT calculations (Giorgio et al., 2005; Sarotti, 2020).

FIGURE 5

FIGURE 5. Structures of compounds 1-8.

However, in 2017, Mohapatra and co-workers, achieved the first total synthesis of (+)-diplopyrone and highlighted irreconcilable differences in the ¹H and ¹³C NMR data with the original article, suggesting a possible revision of the original proposed structure (Maity et al., 2017). Moreover, in 2019, Giuliano and collaborators succeed in another total synthesis of (−)-diplopyrone from D-galactose and confirm the error in the putative original structure through X-ray of the enantiomer of 1 (ent-1) corresponding acetate (Lazzara et al., 2019).

Due to these discrepancies, Sarotti decided to apply the modern computational toolboxes available to assist in the determination of the real structure of the natural (+)-diplopyrone and also endorse the synthetic structure.

Upon comparison of NMR chemical shifts of the isolated natural product with the corresponding data of synthetic 1, the author suggest that the inconsistency should be of stereochemistry nature. As the molecule presents four stereocenters, there are 16 possible stereoisomers. However, due to the reliance on Mosher’s analysis which established the absolute configuration at C9 as S, only the eight resulted stereoisomers were considered into theoretical analysis carried out by Sarotti, see Figure 5.

Initially, after simulation of the 1-8 candidates NMR chemical shifts at the preliminary B3LYP/6-31G**//MMFF level and using the reported synthetic data of diplopyrone, as expected, the best match was shown for stereoisomer 1. It was obtained the lowest values of ¹H and ¹³C CMAE (1.6 and 0.11, respectively) for 1, in contrast to the poor agreement obtained for the remaining candidates (2.3–3.4 and 0.13–0.32 ppm, respectively). Additionally, applying the DP4 methodology also indicated stereoisomer 1 with a high level of confidence (exceeding 99%) as the correct structure of synthetic diplopyrone. Thus, corroborating the assignment made by both papers from Mohapatra and Giuliano. Interestingly, when using the data from the isolated diplopyrone, stereoisomer 1 (the initially proposed structure) yielded a low probability of less than 1% in contrast to 2, 3, and 4, which emerges as the highest probabilities of 25%, 62%, and 13%, respectively, where the stereoisomer 3 stands out as the most probable one. On the other hand, candidates 5-8, featuring trans-fusion (see Figure 5), presented a low probability consistent with the reported J_4a-8a value of the isolated diplopyrone of 2.8 Hz. Due to these inconsistent results, Sarotti turned to the J-DP4 tool, using the iJ/dJ approach. First, it was only considered in the conformational analysis step the subset of candidates compatible with the experimental ³J_HH values of 4a-8a and 6-9, removing the unsuitable conformations. After that, the calculations of the Fermi contact term of J was carried out at the B3LYP/6-31G** level for the remaining selected conformations. Once again, the J-DP4 indicates candidates 3 (73%) as the most probable one, followed by candidate 4 (27%). It is interesting to highlight that both structures present the same syn/syn configuration at C6/C4a/C8a stereotriad but with opposite configuration (see Figure 5). It is important to mention that both DP4 and J-DP4 methods share the same molecular mechanics level (MMFF) at the optimization step. Although it provides good results in calculating the NMR shifts with a low computational cost, it would sometimes generate modest performance of the method. Therefore, after this preliminary evaluation, through a more robust methodology, the NMR chemical shifts of 1-8 were recomputed at a higher PCM/mPW1PW91/6-31+G**//B3LYP/6-31G* level for DP4+. Similarly, candidates 3 and 4 yielded the higher probability of 62% and 38%, respectively, when compared to the experimental data of the isolated diplopyrone. The obtained ¹³C CMAE statistical values for 3 and 4 were 1.0 and 0.9 ppm, respectively, and ¹H CMAE were 0.10 and 0.11 ppm, respectively. This results clearly indicated a better agreement with the isolated diplopyrone data when compared to the other candidates (¹³C CMAE of 1.3–4.1 ppm and ¹H CMAE of 0.14–0.20 ppm).

Since these results are conflicting, favoring 3 but not dismissing 4, and take into consideration that 3 and 4 exhibit an opposing configuration in the bicyclic core (see Figure 5), they should present a pseudo-enantiomeric relationship in the simulated ECD spectra. However, as the Evidente paper (2005) only reported the experimental CD spectrum of the isolated diplopyrone along with the simulated spectra of 1 and 2 (which features the opposite configuration at the bicyclic core), Sarotti carried out the ECD calculations of all stereoisomers (1–8) using TDDFT at the B3LYP/6-31G* level and compared these with the experimental spectrum presented in the 2005 article by Evidente. While stereoisomer 4 yielded a good correlation with the experimental spectrum, stereoisomer 3 displayed a opposite correlation, suggesting that the original structure would be represented by structure 4, in disagreement with DP4/J-DP4/DP4+ (Sarotti, 2020). However, this would only be right if C9 configuration were S, as initially proposed through Mosher method. Otherwise, if C9 configuration were R, the enantiomer of 3 (ent-3) should be the real structure of the isolated diplopyrone.

As a conclusive measure, it was calculated the NMR chemical shifts of the (R)- and (S)-MTPA esters of 4 and ent-3 at the PCM/mPW1PW91/6-31+G**//B3LYP/6-31G* level and subsequently, the simulated Δδ_RS values were compared with the corresponding experimental Δδ_RS values of the isolated MTPA-diplopyrone. As a result, for MTPA-4, only H9 was in accordance with the experimental Δδ_RS signs. On the other hand, for MTPA-ent-3, the predicted Δδ_SR signs perfectly fits the reported values. This clearly shows that C9 configuration might be R and not S, as originally proposed. To confirm that, DP4+ was applied.

When the NMR chemical shifts simulated for (R)-MTPA-ent-3 and (S)-MPTA-ent-3 were correlated with the ¹H NMR experimental data of the (R)-MPTA ester of the isolated diplopyrone, a higher probability of 82.8% was obtained for (R)-MTPA-ent-3, confirming that the absolute configuration at C9 should be R. Likewise, when the experimental NMR data of (S)-MTPA ester of isolated diplopyrone was used, a probability over 99.9% was obtained for the (S)-MPTA-ent-3 candidate, also confirming the absolute configuration at C9.

In a final attempt, the author applied DIP, which is the combination of two independent DP4+ results into a unique probability. As expected, the obtained DIP probability was over 99.9% for C9 configuration as R. Additionally, DIP determined the relative and absolute configurations of the molecule simultaneously and accurately with a confidence of 91.9%, showing that a correct identification was possible even in the absence of ECD data, see Figure 6. Interestingly, at the same year, Evidente and Barone groups achieved the same conclusion using VCD and IR calculations (Fusè et al., 2019).

FIGURE 6

FIGURE 6. Structure of (+)-diplopyrone; originally proposed and revised.

In conclusion, in this work, Sarotti demonstrated through a comprehensive quantum chemical calculation of NMR parameters, the relative and absolute configuration of a challenging natural product can be safely determined. By the combined application of DP4/J-DP4/ECD/DP4+/DIP methods, both the relative and absolute configuration of the (+)-diplopyrone natural product were unquestionable revised.

d) 5,5′-dioxo-2,2′-bifurans (DOBFs): CASE, DP4+ and statistical parameters

The last example of misassignment cases was chosen because it uses the combination of CASE algorithm, DP4+ and statistical parameters to propose the structural review of 5,5′-dioxo-2,2′-bifurans (DOBFs) as Phthalic Acid Esters (PAEs). In fact, it is important to highlight that the correct nomenclature for 5,5′-dioxo-2,2′-bifurans should be 5,5′-dialkoxy-2,2′-bifurans, as there are no OXO group at position 5 and 5’.

DOBFs are a class of natural symmetrical bifurans originally isolated in 2008 from Chrysanthemum coronarium L. To date, three novel natural products from this class (Dobf A, B and C) have been found, where some of them presented potential pharmacological properties. On the other hand, PAEs is a widely used plasticizers in packaging, drug carrier and medical polymer materials. Usually, PAEs are frequently involved as external contamination (Lv et al., 2020).

Strikingly, DOBFs and PAEs presents perfectly equivalent NMR data, which is recurrent reported in the literature. As an example of that, is precisely the Lv and coworkers article, which observed a close similarity between the ¹³C NMR data of a compound isolated from Ailanthus altissima with the reported data of Dobf A and also for a type of PAE, called DBP. However, the authors highlighted major discrepancies indicating the structure inference as Dobf A might be questionable. The primary disparity between Dobf A and DBP is expected to in the 2D NMR data, on the HMBC cross peak between 7.54 and 167.7, which was J₄ correlation (H1/C4) in DBP, while it should be observed a J₂ correlation (H4/C5) in Dobf A. In addition, certain coupling constants of Dobf A (J_H3/H4) exhibited significant differences when compared to similar compounds. The usual J coupling constant of symmetrical furans were presented as singlets or doublets for H3/H4, on the other hand, Dobf A yielded a doublet of doublets between H3/H4 (dd, 1H, J = 5.6, 3.3 Hz). Regardless, the authors are not convinced that sufficient evidence to prove error inference existed in Dobf A structure (Lv et al., 2020).

Therefore, to unequivocally determine the isolated compound, the authors applied CASE algorithms and GIAO ¹³C NMR calculations (Lv et al., 2020). For the NMR calculations, the authors employed the PCM/B3LYP/6-311+G(d,p)//B3LYP/6-31G(d,p) level of theory in chloroform solvent. Regarding the use of CASE algorithms, to interpret the results, the researchers utilized two primary metrics: the Multi Spec (MF) value, quantifying the alignment between the ¹³C spectrum data and the structure derived through the empirical CASE algorithm; and the d_N (¹³C+¹H) value, representing the average of the max unsigned deviation between theoretical and calculated chemical shift values for ¹³C and ¹H nuclei. Additionally, they carried out statistical parameter analyses by comparing the calculated and experimental data and also the DP4+ tool (Lv et al., 2020).

Based on the CASE results, the ACD/¹³C NMR workbook assessment demonstrated a poor match for Dobf A, with MF values of 0.05, in comparison with 0.95 obtained for DBP, alongside with a d_N (¹³C+¹H) values of 16.975 for Dobf A while 1.258 for DBP. Additionally, statical parameters were in accordance with CASE results. For Dobf A, a poor metrics were obtained: RMSD (δC) of 18.65 and R² of 0.9531. On the contrary, as expected, DBP yielded satisfactory agreement with the experimental data: RMSD (δC) of 2.76 and R² of 0.9997. This result was supported by the DP4+ tool, indicating 100% in favor of DBP. In conclusion, the authors unequivocally determine the structure of the compound isolated from Ailanthus altissima as DBP. On top of that, the author conducted a structural revision of Dobf A as DBP (Lv et al., 2020).

With the reassignment of Dobf A, Tian-Ming Lv and colleagues turned their attention to Dobf B and Dobf C. However, due to the lack of the original spectra for these DOBFs, the use of CASE algorithm was precluded. Therefore, the authors relied solely on GIAO ¹³C NMR calculations. The obtained results showed that the structure of Dobf B and Dobf C might be questionable. By respectively comparison of the simulated NMR data of Dobf B and C with different types of PAEs, called DIBP and DEHP, similarly statistical results as Dobf A were obtained. A deficient RMSD (δC) and R² values for Dobf B were 18.37 and 0.9528, respectively, in contrast with the good agreement for DIBP were 2.30 and 0.9996. Likewise, Dobf C presented a poor RMSD (δC) and R² values of 9.28 and 0.966, in contrast for DEHP, with 1.27 and 0.9994, respectively. Besides, DP4+ of 100% were obtained for PAEs compounds, supporting the undeniable structural revision of DOBFs as PAEs, see Figure 7 (Lv et al., 2020).

FIGURE 7

FIGURE 7. Structures of DOBFs and PAEs.

Conclusion

The case studies discussed here underscore the recurrent issue of structural misassignments in natural product chemistry. Despite the progress made in analytical methods and the application of computer simulations to facilitate structural elucidation, it becomes evident that, even 18 years after the question raised by Nicolaou and Snyder in their review paper (Nicolau and Snyder, 2005), we are still chasing molecules that were never there.

The increasing number of papers addressing the correction of natural product structures through NMR parameter calculations are evidence of the utility of these computational simulations in complex structural determinations. The development of novel user-friendly statistical methodologies, such as DP4+ and J-DP4, significantly enhances the reliability of structural assignments for closely related compounds. We believe that the synergistic combination of experiment and theoretical calculations offers an accessible and reliable means to avoid structural misassignments and, importantly, to initially direct experimental endeavors toward the putative structure.

Nevertheless, the topic of NMR simulations is still an effervescent and on-growing field. Besides the significant development of novel tools in the last few years to assist in the NMR elucidation process, the application of artificial intelligence into these simulations are emerging. There is a growing trend in the creation of machine learning algorithms that facilitate the prediction of NMR parameters and their correlation with experimental data (Zanardi and Sarotti, 2015; Gerrard et al., 2020; Guan et al., 2021; Tsai et al., 2022; Cortés et al., 2023). We believe that these emerging tools are about to broaden the applications of NMR parameter calculations and make them more accessible for the use by non-experts. All these recent updates significantly broadening the research activity in the NMR simulation area, to the point that nowadays such studies are routinely found in the high impact literature.

Author contributions

AA: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. LM: Conceptualization, Investigation, Writing–original draft, Writing–review and editing. FS: Conceptualization, Funding acquisition, Project administration, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The authors are thankful to National Council for Scientific and Technological Development - CNPq and to the Coordination of Improvement of Higher Education Personnel - CAPES (Financial Code 001) and Rio de Janeiro Research Foundation - FAPERJ (Grants 211.319-2019; E-26/201.295/2022 JCNE; E-26/210.313/2022 PROGRAMA DE APOIO AO JOVEM PESQUISADOR FLUMINENSE) for funding.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelfattah, M. S., Kazufumi, T., and Ishibashi, M. (2010). Izumiphenazines A−C: isolation and structure elucidation of phenazine derivatives from Streptomyces sp. IFM 11204. J. Nat. Prod. 73, 1999–2002. doi:10.1021/np100400t

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, M. J., Keal, T. W., and Tozer, D. J. (2003). Improved NMR chemical shifts in density functional theory. Chem. Phys. Lett. 380, 70–77. doi:10.1016/j.cplett.2003.08.101

CrossRef Full Text | Google Scholar

Bagno, A., and Saielli, G. (2015). Addressing the stereochemistry of complex organic molecules by density functional theory-NMR. Wiley Interdiscip. Rev. Comput. Mol. Sci. 5, 228–240. doi:10.1002/wcms.1214

CrossRef Full Text | Google Scholar

Bally, T., and Rablen, P. R. (2011). Quantum-chemical simulation of ¹H NMR spectra. 2. † Comparison of DFT-based procedures for computing proton-proton coupling constants in organic molecules. J. Org. Chem. 76, 4818–4830. doi:10.1021/jo200513q

PubMed Abstract | CrossRef Full Text | Google Scholar

Barone, G., Gomez-Paloma, L., Duca, D., Silvestri, A., Riccio, R., and Bifulco, G. (2002). Structure validation of natural products by quantum-mechanical GIAO calculations of ¹³C NMR chemical shifts. Chem. Eur. J. 8, 3233–3239. doi:10.1002/1521-3765(20020715)8:14<3233::AID-CHEM3233>3.0.CO;2-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Batista, A. N. L., Dos Santos, F. M., Valverde, A. L., and Batista, J. M. (2019). Stereochemistry of spongosoritins: beyond optical rotation. Org. Biomol. Chem. 17, 9772–9777. doi:10.1039/c9ob02010a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bross-Walch, N., Kühn, T., Moskau, D., and Zerbe, O. (2005). Strategies and tools for structure determination of natural products using modern methods of NMR spectroscopy. Chem. Biodivers. 2, 147–177. doi:10.1002/cbdv.200590000

PubMed Abstract | CrossRef Full Text | Google Scholar

Bursch, M., Mewes, J. M., Hansen, A., and Grimme, S. (2022). Best-practice DFT protocols for basic molecular computational chemistry. Angew. Chem. - Int. Ed. 61, e202205735. doi:10.1002/anie.202205735

PubMed Abstract | CrossRef Full Text | Google Scholar

Cairns, E., Hashmi, M. A., Singh, A. J., Eakins, G., Lein, M., and Keyzers, R. (2015). Structure of Echivulgarine, a Pyrrolizidine alkaloid isolated from the pollen of Echium vulgare. J. Agric. Food Chem. 63, 7421–7427. doi:10.1021/acs.jafc.5b02402

PubMed Abstract | CrossRef Full Text | Google Scholar

Casabianca, L. B. (2020). Calculating nuclear magnetic resonance chemical shifts in solvated systems. Magn. Reson. Chem. 58, 611–624. doi:10.1002/mrc.4994

PubMed Abstract | CrossRef Full Text | Google Scholar

Cen-Pacheco, F., Norte, M., Fernández, J. J., and Daranas, A. H. (2014). Zoaramine, a zoanthamine-like alkaloid with a new skeleton. Org. Lett. 16, 2880–2883. doi:10.1021/ol500860v

PubMed Abstract | CrossRef Full Text | Google Scholar

Challinor, V. L., Johnston, R. C., Bernhardt, P. V., Lehmann, R. P., Krenske, E. H., and De Voss, J. J. (2015). Biosynthetic insights provided by unusual sesterterpenes from the medicinal herb Aletris farinosa. Chem. Sci. 6, 5740–5745. doi:10.1039/c5sc02056e

PubMed Abstract | CrossRef Full Text | Google Scholar

Chhetri, B. K., Lavoie, S., Sweeney-Jones, A. M., and Kubanek, J. (2018). Recent trends in the structural revision of natural products. Nat. Prod. Rep. 35, 514–531. doi:10.1039/c8np00011e

PubMed Abstract | CrossRef Full Text | Google Scholar

Cortés, I., Cuadrado, C., Daranas, A. H., and Sarotti, A. M. (2023). Machine learning in computational NMR-aided structural elucidation. Front. Nat. Prod. 2, 1–11. doi:10.3389/fntpr.2023.1122426

CrossRef Full Text | Google Scholar

Costa, F. L. P., Da Silva Mota, G. V., De Albuquerque, A. C. F., Dos Santos Junior, F. M., and De Amorim, M. B. (2015). A comparative quantum chemical study of a novel synthetic prenylated chalcone: high accuracy of NMR 13C GIAO-DFT scaling factor calculations at the mPW91PW91/6-31G(d) Level of Theory. J. Comput. Theor. Nanosci. 12, 2202–2207. doi:10.1166/jctn.2015.4008

CrossRef Full Text | Google Scholar

Costa, F. L. P., De Albuquerque, A. C. F., Fiorot, R. G., Lião, L. M., Martorano, L. H., Mota, G. V. S., et al. (2021). Structural characterisation of natural products by means of quantum chemical calculations of NMR parameters: new insights. Org. Chem. Front. 8, 2019–2058. doi:10.1039/d1qo00034a

CrossRef Full Text | Google Scholar

Costa, F. L. P., De Albuquerque, A. C. F., Martins Dos Santos, F., and De Amorim, M. B. (2010). GIAO-HDFT scaling factor for ¹³C NMR chemical shifts calculation. J. Phys. Org. Chem. 23 (10), 972–977. doi:10.1002/poc.1749

CrossRef Full Text | Google Scholar

Cramer, C. J., and Truhlar, D. G. (1999). Implicit solvation models: equilibria, structure, spectra, and dynamics. Chem. Rev. 99, 2161–2200. doi:10.1021/cr960149m

PubMed Abstract | CrossRef Full Text | Google Scholar

de Albuquerque, A. C. F., Ribeiro, D. J., and de Amorim, M. B. (2016). Structural determination of complex natural products by quantum mechanical calculations of ¹³C NMR chemical shifts: development of a parameterized protocol for terpenes. J. Mol. Model. 22, 183. doi:10.1007/s00894-016-3045-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Z. G., Li, M. G., Ren, J., Zhao, J. Y., Huang, R., Wang, Q. Z., et al. (2011). Phenazinolins A–E: novel diphenazines from a tin mine tailings-derived Streptomyces species. Org. Biomol. Chem. 9, 2771–2776. doi:10.1039/C1OB05044C

PubMed Abstract | CrossRef Full Text | Google Scholar

Ditchfield, R. (1974). Self-consistent perturbation theory of diamagnetism I. A gauge-invariant LCAO method for N.M.R. Chemical shifts. Mol. Phys. 27, 789–807. doi:10.1080/00268977400100711

CrossRef Full Text | Google Scholar

Evidente, A., Maddau, L., Spanu, E., Franceschini, A., Lazzaroni, S., and Motta, A. (2003). Diplopyrone, a new phytotoxic tetrahydropyranpyran-2-one produced by Diplodia mutila, a fungus pathogen of cork oak. J. Nat. Prod. 66, 313–315. doi:10.1021/np020367c

PubMed Abstract | CrossRef Full Text | Google Scholar

Flaig, D., Maurer, M., Hanni, M., Braunger, K., Kick, L., Thubauville, M., et al. (2014). Benchmarking hydrogen and carbon NMR chemical shifts at HF, DFT, and MP2 levels. J. Chem. Theory Comput. 10 (2), 572–578. doi:10.1021/ct400780f

PubMed Abstract | CrossRef Full Text | Google Scholar

Fusè, M., Mazzeo, G., Longhi, G., Abbate, S., Masi, M., Evidente, A., et al. (2019). Unbiased determination of absolute configurations by vis-à-vis comparison of experimental and simulated spectra: the challenging case of diplopyrone. J. Phys. Chem. B 123, 9230–9237. doi:10.1021/acs.jpcb.9b08375

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerrard, W., Bratholm, L. A., Packer, M. J., Mulholland, A. J., Glowacki, D. R., and Butts, C. P. (2020). IMPRESSION-prediction of NMR parameters for 3-dimensional chemical structures using machine learning with near quantum chemical accuracy. Chem. Sci. 11, 508–515. doi:10.1039/c9sc03854j

PubMed Abstract | CrossRef Full Text | Google Scholar

Giorgio, E., Maddau, L., Spanu, E., Evidente, A., and Rosini, C. (2005). Assignment of the absolute configuration of (+)-diplopyrone, the main phytotoxin produced by Diplodia mutila, the pathogen of the cork oak decline, by a nonempirical analysis of its chiroptical properties. J. Org. Chem. 70, 7–13. doi:10.1021/jo0488255

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimblat, N., Gavín, J. A., Hernández Daranas, A., and Sarotti, A. M. (2019). Combining the power of J coupling and DP4 analysis on stereochemical assignments: the J-DP4 methods. Org. Lett. 21 (11), 4003–4007. doi:10.1021/acs.orglett.9b01193

PubMed Abstract | CrossRef Full Text | Google Scholar

Grimblat, N., Zanardi, M. M., and Sarotti, A. M. (2015). Beyond DP4: an improved probability for the stereochemical assignment of isomeric compounds using quantum chemical calculations of NMR shifts. J. Org. Chem. 80 (24), 12526–12534. doi:10.1021/acs.joc.5b02396

PubMed Abstract | CrossRef Full Text | Google Scholar

Guan, Y., Shree Sowndarya, S. V., Gallegos, L. C., St. John, P. C., and Paton, R. S. (2021). Real-time prediction of ¹H and ¹³C chemical shifts with DFT accuracy using a 3D graph neural network. Chem. Sci. 12, 12012–12026. doi:10.1039/d1sc03343c

PubMed Abstract | CrossRef Full Text | Google Scholar

Hehre, W., Klunzinger, P., Deppmeier, B., Driessen, A., Uchida, N., Hashimoto, M., et al. (2019). Efficient protocol for accurately calculating ¹³C chemical shifts of conformationally flexible natural products: scope, assessment, and limitations. J. Nat. Prod. 82 (8), 2299–2306. doi:10.1021/acs.jnatprod.9b00603

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, I. H., Oh, J., Zhou, W., Park, S., Kim, J. H., Chittiboyina, A. G., et al. (2015). Cytotoxic activity of rearranged drimane meroterpenoids against colon cancer cells via down-regulation of β-catenin expression. J. Nat. Prod. 78 (3), 453–461. doi:10.1021/np500843m

PubMed Abstract | CrossRef Full Text | Google Scholar

Iron, M. A. (2017). Evaluation of the factors impacting the accuracy of ¹³C NMR chemical shift predictions using density functional theory - the advantage of long-range corrected functionals. J. Chem. Theory Comput. 13, 5798–5819. doi:10.1021/acs.jctc.7b00772

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonas, E., Kuhn, S., and Schlörer, N. (2022). Prediction of chemical shift in NMR: a review. Magn. Reson. Chem. 60, 1021–1031. doi:10.1002/mrc.5234

PubMed Abstract | CrossRef Full Text | Google Scholar

Junior, F. M. S., Covington, C. L., De Albuquerque, A. C. F., Lobo, J. F. R., Borges, R. M., De Amorim, M. B., et al. (2015). Absolute configuration of (-)-Centratherin, a sesquiterpenoid lactone, defined by means of chiroptical spectroscopy. J. Nat. Prod. 78, 2617–2623. doi:10.1021/acs.jnatprod.5b00546

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaupp, M., Bühl, M., and Malkin, V. G. (2004). Calculation of NMR and EPR parameters: theory and applications. Wiley-VCH Verlag GmbH & Co. KGaA. doi:10.1002/3527601678

CrossRef Full Text | Google Scholar

Keal, T. W., and Tozer, D. J. (2003). The exchange-correlation potential in Kohn-Sham nuclear magnetic resonance shielding calculations. J. Chem. Phys. 119, 3015–3024. doi:10.1063/1.1590634

CrossRef Full Text | Google Scholar

Keal, T. W., and Tozer, D. J. (2004). A semiempirical generalized gradient approximation exchange-correlation functional. J. Chem. Phys. 121, 5654–5660. doi:10.1063/1.1784777

PubMed Abstract | CrossRef Full Text | Google Scholar

Keal, T. W., Tozer, D. J., and Helgaker, T. (2004). GIAO shielding constants and indirect spin-spin coupling constants: performance of density functional methods. Chem. Phys. Lett. 391, 374–379. doi:10.1016/j.cplett.2004.04.108

CrossRef Full Text | Google Scholar

Keith, T. A., and Bader, R. F. W. (1993a). Topological analysis of magnetically induced molecular current distributions. J. Chem. Phys. 99, 3669–3682. doi:10.1063/1.466165

CrossRef Full Text | Google Scholar

Keith, T. A., and Bader, R. F. W. (1993b). Calculation of magnetic response properties using a continuous set of gauge transformations. Chem. Phys. Lett. 210, 223–231. doi:10.1016/0009-2614(93)89127-4

CrossRef Full Text | Google Scholar

Kovács, T., Lajter, I., Kúsz, N., Schelz, Z., Bózsity-Faragó, N., Borbás, A., et al. (2023). Isolation and NMR scaling factors for the structure determination of lobatolide H, a flexible sesquiterpene from neurolaena lobata. Int. J. Mol. Sci. 24 (6), 5841. doi:10.3390/ijms24065841

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutateladze, A. G., and Mukhina, O. A. (2014). Relativistic force field: parametric computations of proton-proton coupling constants in ¹H NMR spectra. J. Org. Chem. 79 (17), 8397–8406. doi:10.1021/jo501781b

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutateladze, A. G., and Mukhina, O. A. (2015a). Minimalist relativistic force field: prediction of proton-proton coupling constants in ¹H NMR spectra is perfected with NBO hybridization parameters. J. Org. Chem. 80 (10), 5218–5225. doi:10.1021/acs.joc.5b00619

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutateladze, A. G., and Mukhina, O. A. (2015b). Relativistic force field: parametrization of ¹³C-¹H nuclear spin-spin coupling constants. J. Org. Chem. 80 (21), 10838–10848. doi:10.1021/acs.joc.5b02001

PubMed Abstract | CrossRef Full Text | Google Scholar

Kutateladze, A. G., and Reddy, D. S. (2017). High-throughput in silico structure validation and revision of halogenated natural products is enabled by parametric corrections to DFT-computed ¹³C NMR chemical shifts and spin-spin coupling constants. J. Org. Chem. 82 (7), 3368–3381. doi:10.1021/acs.joc.7b00188

PubMed Abstract | CrossRef Full Text | Google Scholar

La Clair, J. J. (2006). Total syntheses of hexacyclinol, 5-epi-hexacyclinol, and desoxohexacyclinol unveil an antimalarial prodrug motif. Angew. Chem. Int. Ed. Engl. 45 (17), 2769–2773. doi:10.1002/anie.200504033

PubMed Abstract | CrossRef Full Text | Google Scholar

Lazzara, N. C., Rosano, R. J., Vagadia, P. P., Giovine, M. T., Bezpalko, M. W., Piro, N. A., et al. (2019). Synthesis and biological evaluation of 6-[(1r)-1-hydroxyethyl]-2,4a(R),6(S),8a(R)-tetrahydropyrano-[3,2-b]-pyran-2-one and structural analogues of the putative structure of diplopyrone. J. Org. Chem. 84 (2), 666–678. doi:10.1021/acs.joc.8b02490

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, H., and Duan, Y. (2007). Improved sampling methods for molecular simulation. Curr. Opin. Struct. Biol. 17, 187–191. doi:10.1016/j.sbi.2007.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Liu, J. K., and Wang, W. X. (2020). GIAO ¹³C NMR calculation with sorted training sets improves accuracy and reliability for structural assignation. J. Org. Chem. 85, 11350–11358. doi:10.1021/acs.joc.0c01451

PubMed Abstract | CrossRef Full Text | Google Scholar

Lodewyk, M. W., Siebert, M. R., and Tantillo, D. J. (2012). Computational prediction of ¹H and ¹³C chemical shifts: a useful tool for natural product, mechanistic, and synthetic organic chemistry. Chem. Rev. 112 (3), 1839–1862. doi:10.1021/cr200106v

PubMed Abstract | CrossRef Full Text | Google Scholar

Lv, T. M., Song, G. S., Yang, P. Y., Lin, B., and Huang, X. X. (2020). Reassignments of the structure DOBFs directed by CASE algorithms and GIAO ¹³C NMR computations. J. Mol. Struct. 1219, 128602. doi:10.1016/j.molstruc.2020.128602

CrossRef Full Text | Google Scholar

Maity, S., Kanikarapu, S., Marumudi, K., Kunwar, A. C., Yadav, J. S., and Mohapatra, D. K. (2017). Asymmetric total synthesis of the putative structure of diplopyrone. J. Org. Chem. 82, 4561–4568. doi:10.1021/acs.joc.7b00086

PubMed Abstract | CrossRef Full Text | Google Scholar

Malloci, G., Serra, G., Bosin, A., and Vargiu, A. V. (2016). Extracting conformational ensembles of small molecules from molecular dynamics simulations: ampicillin as a test case. Computation 4, 5. doi:10.3390/computation4010005

CrossRef Full Text | Google Scholar

Marcarino, M. O., Cicetti, S., Zanardi, M. M., and Sarotti, A. M. (2022). A critical review on the use of DP4+ in the structural elucidation of natural products: the good, the bad and the ugly. A practical guide. Nat. Prod. Rep. 39, 58–76. doi:10.1039/d1np00030f

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcarino, M. O., Zanardi, M. M., Cicetti, S., and Sarotti, A. M. (2020). NMR calculations with quantum methods: development of new tools for structural elucidation and beyond. Acc. Chem. Res. 53 (9), 1922–1932. doi:10.1021/acs.accounts.0c00365

PubMed Abstract | CrossRef Full Text | Google Scholar

Mardirossian, N., and Head-Gordon, M. (2017). Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals. Mol. Phys. 115 (19), 2315–2372. doi:10.1080/00268976.2017.1333644

CrossRef Full Text | Google Scholar

Marenich, A. V., Cramer, C. J., and Truhlar, D. G. (2009). Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 113, 6378–6396. doi:10.1021/jp810292n

PubMed Abstract | CrossRef Full Text | Google Scholar

Mari, S. H., Varras, P. C., Atia-Tul-Wahab, , Choudhary, I. M., Siskos, M. G., and Gerothanassis, I. P. (2019). Solvent-dependent structures of natural products based on the combined use of DFT calculations and ¹H-NMR chemical shifts. Molecules 24 (12), 2290. doi:10.3390/molecules24122290

PubMed Abstract | CrossRef Full Text | Google Scholar

Martorano, L. H., Valverde, A. L., Ribeiro, C. M. R., De Albuquerque, A. C. F., Carneiro, J. W. D. M., Fiorot, R. G., et al. (2020). Unraveling the helianane family: a complementary quantum mechanical study. New J. Chem. 44, 8055–8060. doi:10.1039/d0nj01396j

CrossRef Full Text | Google Scholar

Mennucci, B. (2012). Polarizable continuum model. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2 (3), 386–404. doi:10.1002/wcms.1086

CrossRef Full Text | Google Scholar

Metropolis, N., and Ulam, S. (1949). The Monte Carlo method. JASA 44 (247), 335–341. doi:10.1080/01621459.1949.10483310

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicolaou, K. C., and Snyder, S. A. (2005). Chasing molecules that were never there: misassigned natural products and the role of chemical synthesis in modern structure elucidation. Angew. Chem. - Int. Ed. 44 (7), 1012–1044. doi:10.1002/anie.200460864

PubMed Abstract | CrossRef Full Text | Google Scholar

Novitskiy, I. M., Holt, T. A., and Kutateladze, A. G. (2021). Structure revision of ent-kaurane diterpenoids, isoserrins A, B, and D, enabled by DU8+ computation of their NMR spectral data. Mendeleev Commun. 31 (3), 300–301. doi:10.1016/j.mencom.2021.04.007

CrossRef Full Text | Google Scholar

Oliveira, M. T., Alves, J. M. A., Braga, A. A. C., Wilson, D. J. D., and Barboza, C. A. (2021). Do double-hybrid exchange-correlation functionals provide accurate chemical shifts? A benchmark assessment for proton NMR. J. Chem. Theory Comput. 17 (11), 6876–6885. doi:10.1021/acs.jctc.1c00604

PubMed Abstract | CrossRef Full Text | Google Scholar

Pescitelli, G., and Bruhn, T. (2016). Good computational practice in the assignment of absolute configurations by TDDFT calculations of ECD spectra. Chirality 28 (6), 466–474. doi:10.1002/chir.22600

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrovic, A. G., Navarro-Vazquez, A., and Lorenzo Alonso-Gomez, J. (2010). From relative to absolute configuration of complex natural products: interplay between NMR, ECD, VCD, and ORD assisted by ab initio calculations. Curr. Org. Chem. 14 (15), 1612–1628. doi:10.2174/138527210793563215

CrossRef Full Text | Google Scholar

Pierens, G. K. (2014). ¹H and ¹³C NMR scaling factors for the calculation of chemical shifts in commonly used solvents using density functional theory. J. Comput. Chem. 25, 1388–1394. doi:10.1002/jcc.23638

PubMed Abstract | CrossRef Full Text | Google Scholar

Porco, J. A., Su, S., Lei, X., Bardhan, S., and Rychnovsky, S. D. (2006). Total synthesis and structure assignment of (+)-hexacyclinol. Angew. Chem. - Int. Ed. 45 (35), 5790–5792. doi:10.1002/anie.200602854

PubMed Abstract | CrossRef Full Text | Google Scholar

Rusakova, I. L. (2022). Quantum chemical approaches to the calculation of NMR parameters: from fundamentals to recent advances. Magnetochemistry 8 (5), 50. doi:10.3390/magnetochemistry8050050

CrossRef Full Text | Google Scholar

Rychnovsky, S. D. (2006). Predicting NMR spectra by computational methods: structure revision of hexacyclinol. Org. Lett. 8 (13), 2895–2898. doi:10.1021/ol0611346

PubMed Abstract | CrossRef Full Text | Google Scholar

Rzepiela, K., Kaminský, J., Buczek, A., Broda, M. A., and Kupka, T. (2022). Electron correlation or basis set quality: how to obtain converged and accurate NMR shieldings for the third-row elements? Molecules 27 (23), 8230. doi:10.3390/molecules27238230

PubMed Abstract | CrossRef Full Text | Google Scholar

Saielli, G., and Bagno, A. (2009). Can two molecules have the same NMR spectrum? Hexacyclinol revisited. Org. Lett. 11 (6), 1409–1412. doi:10.1021/ol900164a

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, F. M., Mota, G. V. S., Martorano, L. H., de Albuquerque, A. C. F., Silva, C. A., Silva, A. M., et al. (2022). Combined application of DP4+ and ANN-PRA to determine the relative configuration of natural products: the alpha-bisabol case study. Magn. Reson. Chem. 60, 533–540. doi:10.1002/mrc.5261

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarotti, A. M. (2020). In silico reassignment of (+)-Diplopyrone by NMR calculations: use of a DP4/J-DP4/dp4+/DIP tandem to revise both relative and absolute configuration. J. Org. Chem. 85 (17), 11566–11570. doi:10.1021/acs.joc.0c01563

PubMed Abstract | CrossRef Full Text | Google Scholar

Schattenberg, C. J., and Kaupp, M. (2021). Extended benchmark set of main-group nuclear shielding constants and NMR chemical shifts and its use to evaluate modern DFT methods. J. Chem. Theory Comput. 17, 7602–7621. doi:10.1021/acs.jctc.1c00919

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlegel, B., Härtl, A., Dahse, H. M., Gollmick, F. A., Gräfe, U., Dörfelt, H., et al. (2002). Hexacylinol, a new antiproliferative metabolite of Panus rudis HKI 0254. J. Antibiot. 55, 814–817. doi:10.7164/antibiotics.55.814

PubMed Abstract | CrossRef Full Text | Google Scholar

Silva, J. P. R., Pereira, L. C. O., Abreu, L. S., Lins, F. S. V., De Souza, T. A., Do Espírito-Santo, R. F., et al. (2022). Targeted isolation of anti-inflammatory lignans from Justicia aequilabris by molecular networking approach. J. Nat. Prod. 85, 2184–2191. doi:10.1021/acs.jnatprod.2c00478

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, S. G., Channon, J. A., Paterson, I., and Goodman, J. M. (2010). The stereochemical assignment of acyclic polyols: a computational study of the NMR data of a library of stereopentad sequences from polyketide natural products. Tetrahedron 66 (33), 6437–6444. doi:10.1016/j.tet.2010.06.022

CrossRef Full Text | Google Scholar

Smith, S. G., and Goodman, J. M. (2009). Assigning the stereochemistry of pairs of diastereoisomers using GIAO NMR shift calculation. J. Org. Chem. 74 (12), 4597–4607. doi:10.1021/jo900408d

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, S. G., and Goodman, J. M. (2010). Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: the DP4 probability. J. Am. Chem. Soc. 132 (37), 12946–12959. doi:10.1021/ja105035r

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, Y. H., Amichetti, M., Zanardi, M. M., Grimson, R., Daranas, A. H., and Sarotti, A. M. (2022). ML-J-DP4: an integrated quantum mechanics-machine learning approach for ultrafast NMR structural elucidation. Org. Lett. 24, 7487–7491. doi:10.1021/acs.orglett.2c01251

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Abbas, M., Zhang, Y., Elshahawi, S. I., Ponomareva, L. V., Cui, Z., et al. (2019). Baraphenazines A–G, divergent fused phenazine-based metabolites from a himalayan Streptomyces. J. Nat. Prod. 82, 1686–1693. doi:10.1021/acs.jnatprod.9b00289

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiitala, K. W., Hoye, T. R., and Cramer, C. J. (2006). Hybrid density functional methods empirically optimized for the computation of ¹³C and ¹H chemical shifts in chloroform solution. J. Chem. Theory Comput. 2 (4), 1085–1092. doi:10.1021/ct6001016

PubMed Abstract | CrossRef Full Text | Google Scholar

Willoughby, P. H., Jansma, M. J., and Hoye, T. R. (2014). A guide to small-molecule structure assignment through computation of (¹H and ¹³C) NMR chemical shifts. Nat. Protoc. 9, 643–660. doi:10.1038/nprot.2014.042

PubMed Abstract | CrossRef Full Text | Google Scholar

Zanardi, M. M., Biglione, F. A., Sortino, M. A., and Sarotti, A. M. (2018). General quantum-based NMR method for the assignment of absolute configuration by single or double derivatization: scope and limitations. J. Org. Chem. 83, 11839–11849. doi:10.1021/acs.joc.8b01749

PubMed Abstract | CrossRef Full Text | Google Scholar

Zanardi, M. M., and Sarotti, A. M. (2015). GIAO C-H COSY simulations merged with artificial neural networks pattern recognition analysis. Pushing the structural validation a step forward. J. Org. Chem. 80, 9371–9378. doi:10.1021/acs.joc.5b01663

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Zhang, H., Wu, T., Wang, Q., and Van Der Spoel, D. (2017). Comparison of implicit and explicit solvent models for the calculation of solvation free energy in organic solvents. J. Chem. Theory Comput. 13, 1034–1043. doi:10.1021/acs.jctc.7b00169

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuang, Y., Yang, F., Menon, A., Song, J. M., Espinoza, R. V., Schultz, P. J., et al. (2023). An ECD and NMR/DP4+ computational pipeline for structure revision and elucidation of diphenazine-based natural products. J. Nat. Prod. 86, 1801–1814. doi:10.1021/acs.jnatprod.3c00306

PubMed Abstract | CrossRef Full Text | Google Scholar