Plasmonic slot waveguides: a quantum leap in nonlinear nanophotonics

Interest and excitement in nanophotonics—the study and control of light-matter interactions at the nanoscale—are driven by the ability to confine light to volumes well below a cubic wavelength, and, thereby, achieve extremely high intensities. This leads to light-matter interactions of unprecedented localization and strength. Such extreme behavior—both in terms of field enhancement and localization—can be achieved using plasmonic nanostructures, which concentrate light in regions much smaller than the wavelength of light, reducing the excitation power and, under certain conditions, removing phase-matching requirements in the nonlinear regime. In this study, we theoretically show that metal–dielectric–metal (MDM) slot waveguides (WGs), consisting of a thin dielectric layer sandwiched between metal films, provide the strongest confinement. We also demonstrate that integrating epsilon-near-zero (ENZ) materials within the MDM slot significantly improves the nonlinear conversion efficiency of these structures. The results show that the degenerate four-wave mixing conversion efficiency of these ENZ-MDM structures surpasses that of regular plasmonic structures and their dielectric counterparts, even under low pump power conditions, and remains robust despite higher losses in the ENZ material.

1 Introduction

As photonic technologies progress, there is a growing need for faster, more compact integrated photonic circuits that deliver ultrafast response times, broad bandwidth, and reduced driving power (Tuniz, 2021; Yue et al., 2024; Garmire, 2013).

Photonic integrated circuits (PICs), which have waveguides (WGs) as their fundamental building block, were developed in the 1960s (Miller, 1969) and are currently an established and successful platform for transporting and processing light on-chip. PICs are nowadays ubiquitous, from telecommunications (Doerr, 2015) to sensing (Subramanian et al., 2015), machine learning (Bogaerts et al., 2020), potential neuromorphic intelligence (Prucnal and Shastri, 2017), and quantum optical technologies (O'Brien, 2007; Kim et al., 2020; Madsen et al., 2022; Bartolucci et al., 2023). Quantum computing advancements, for instance, have been greatly enhanced by PICs, where effects such as spontaneous four-wave mixing (SFWM) and non-classical light states like squeezed light are crucial for achieving advantages in quantum optical computation, as exemplified by advanced photonic systems like the Jiuzhang quantum computer and Xanadu’s Borealis processor (Madsen et al., 2022; Zhong et al., 2020).

PICs have tremendous advantages over their electronic counterparts, like repeatability, robustness to electromagnetic noise, room temperature operation, and the capability to modulate and transport information directly via photons—hence, at the speed of light. However, all optical processing that requires photon–photon interactions, like coherent light generation, all-optical switching, quantum optical squeezing, and terahertz photonics, is impaired because photons do not interact with each other. For this to occur, photon interactions must be mediated by a medium and are essentially photon-electron nonlinear interactions. These interactions are extremely weak and, consequently, require both high light intensities and materials with large intrinsic nonlinearities (Boyd, 2003).

One of the many “nonlinear effects” produced by light-matter interactions is the change in the refractive index $n$, which defines the speed of light through a material, i.e., how the light is refracted and reflected. This change is a function of the light intensity and the intrinsic nonlinear optical properties of the material. The inspiring work of the last few years has focused on materials for which, at a specific frequency of light, $n=\sqrt{\epsilon }\approx 0$, where $\epsilon$ is the dielectric function. These materials, called epsilon-near-zero (ENZ), have been at the heart of unique discoveries and demonstrations that are pushing the limits of what was thought possible in photonics (Liberal and Engheta, 2017; Alam et al., 2016; Reshef et al., 2017). ENZ materials, like indium–tin oxide (ITO), used in modern touch screen devices, are a category of materials that have garnered attention for enabling high-fidelity transmission and enhancing the electric field at material interfaces, which significantly boosts nonlinear optical responses like Kerr nonlinearities (Wu et al., 2021; Li et al., 2024). Although these materials are still substantially unexplored (Peleckis et al., 2006; Jood et al., 2011; Sachet et al., 2015), their nonlinear optical properties are arguably profoundly interesting, as they can be enhanced by several orders of magnitude in the $n=\sqrt{\epsilon }\approx 0$ regime (Alam et al., 2016; Caspani et al., 2016; Ciattoni et al., 2010; Vincenti et al., 2011). For example, in ITO, the refractive index change can be as high as 170% due to the strong field enhancement effect (Wu et al., 2021). Additionally, they enable supercoupling and tunneling (Li et al., 2024), which allows for efficient transmission through sharp bends and obstacles in waveguides. The supercoupling properties of ENZ materials, particularly when assisted by transmission-type doping, enable high transmission efficiency with zero-phase advance, minimizing losses (Li et al., 2024). These materials also support the design of flexible waveguides that maintain high transmission efficiency with low insertion losses (Li et al., 2024). However, devices made from ENZ materials need to be as small as possible due to their high optical losses.

Nonlinear photonic devices are attractive for signal generation and processing in classical and quantum regimes and for applications in sensing and imaging (Wabnitz and Eggleton, 2015; Hendrickson et al., 2014; Garmire, 2013). However, small, efficient, nonlinear nanophotonic devices require huge optical intensities to be confined in nanoscale volumes. PICs are not suitable for this due to their intrinsic limitation caused by the diffraction of light, which constrains waveguides to dimensions larger than $\sim 200\times 300$ nm in the telecom. Moreover, using conventional dielectric materials for such waveguides demands high power levels to achieve the necessary nonlinear effects and cannot be integrated into microscale devices (Tuniz, 2021; Cherchi et al., 2013). Plasmonic waveguides address these challenges (Suchowski et al., 2013; Palomba et al., 2009), more specifically metal–dielectric–metal slot waveguides—which consist of a nanoscale dielectric layer sandwiched between metal films—providing a platform for efficient nonlinear devices (Yue et al., 2024). These provide the strongest confinement without being limited by diffraction, with a lower driving power (Li et al., 2018a). Calculations show that for plasmonic waveguides, the nonlinear coefficient (γ) can be orders of magnitude larger than in fully dielectric waveguides, thus proving the proficiency of nonlinear plasmonics (Hossain et al., 2011). Nonetheless, the performance of nonlinear plasmonic waveguides is restricted by significant losses. Hence, plasmonic devices must remain confined to the nanoscale to be effective, with waveguide lengths not exceeding a few microns.

In the work done by Li et al. (2018a), the authors explored the nonlinear performance of plasmonic waveguides by comparing different plasmonic waveguide configurations. In their investigation of the Kerr nonlinear performance of plasmonic waveguides, Li et al. (2018a) focused on the maximum achievable nonlinear effects in waveguides while accounting for optical damage by ensuring that the local field intensity remains below the damage threshold of the nonlinear materials. They highlighted that the best nonlinear plasmonic structure is the MDM. Its enhancement originates from the slow-light effect due to the forward propagation of energy in a nonlinear dielectric and backward propagation in the metal due to its negative permittivity. As a result, this provides a significant increase in the effective interaction length within a nonlinear medium and gives rise to a larger nonlinear response. MDM structures also maintain strong and uniform energy confinement even as the thickness of the central layer approaches 0 (Maradudin et al., 2014). The authors also showed that the maximum nonlinear conversion efficiency is inversely proportional to the linear refractive index of the nonlinear medium to the power of α, which is an integer determined by the structure’s configuration. This relationship suggests significant potential for enhancing performance by selecting materials with lower refractive indices, such as ENZ materials.

Still, ENZ materials alone, like ITO, reach a limit as they suffer from relatively high optical losses that are intrinsically linked to their nonlinear behavior (Tuniz, 2021; Wu et al., 2021). These losses are caused by free carrier scattering, arising from energy dissipation due to ohmic losses (Tuniz, 2021) and making it essential for ENZ materials to be as compact as possible when integrated into plasmonic devices (Li et al., 2024). This constitutes one of the major challenges in the development of nonlinear nanophotonic devices, requiring extreme optical intensities to be confined within nanoscale volumes. As previously mentioned, MDM slot waveguides provide the strongest confinement with the least amount of driving power compared to other waveguide geometries and, therefore, serve as an ideal platform for exploiting the extreme nonlinear effects of ENZ materials.

Multiple works have reported that ENZ films in nano-antenna plasmonic structures result in larger nonlinear responses, achieving high field confinement, tunable second-harmonic generation (SHG), and ultrafast refractive index changes (Schulz et al., 2020; Alam et al., 2018; Dass et al., 2020; Xu et al., 2023). Dass et al. (2020) reported that ENZ-modified metal–insulator–metal (MIM) patch nano-antennas coupled with ITO films showed SHG enhancements up to 50,000 times compared to off-device setups and achieved near-perfect absorption (>98%) across a 245 nm range at a wavelength of 1,150 nm, enabling tunable SHG with high enhancement factors.

In this work, we show that integrating ENZ materials with MDM slot waveguides would boost the nonlinear conversion efficiency, even if the losses of the ENZ are higher than those of the metal. We conduct simulations on MDM slot waveguides integrated with ENZ media, which exhibit unprecedented nonlinear optical conversion efficiency in an ultra-compact device. We first demonstrate that the degenerate four-wave mixing (DFWM) conversion efficiency of MDM slot waveguides integrated with the DDMEBT polymer as the nonlinear medium is significantly higher than that of any dielectric counterpart; furthermore, the device is extremely compact and exhibits a pump power consumption of orders of magnitude lower than any dielectric counterpart. We then theoretically demonstrate that changing the nonlinear polymer with an ENZ material effectively supplies an additional benefit to the nonlinear conversation efficiency.

2 Methods

2.1 Theoretical model

The nonlinear effect of interest in this proposal is the Kerr effect. In conventional treatment, it leads, amongst other things, to a variation $∆n$ in the refractive index $n$ with light intensity $I$, i.e., $n=n_0+∆n;∆n\approx n_{2}I$, where $n_0$ and $n_2$ are, respectively, the linear and nonlinear refractive indices of the material. In turn, this leads to an intensity-dependent nonlinear phase shift, which expresses the strength of the nonlinear effects ${∆\varphi }_{NL}=\left(n_2{P}_0/A\right)k_0{L}_{\text{eff}}$, where $k_0=2\pi /\lambda$, $n_2$ is the nonlinear refractive index of the material, $\lambda$ is the wavelength, $P_0$ is the input power, $A$ is the area of the beam, and $L_{\text{eff}}$ is the effective length, i.e., the length over which the light can propagate before it is mostly absorbed. In conventional nonlinear optics, ${∆\varphi }_{NL}$ effects are weak and require phase matching to prevent destructive interference of the generated fields, along with high optical field excitations. Hence, it is crucial to use materials with the strongest possible nonlinearity and geometries that maximize these effects in small volumes.

Comparing different classes of devices typically requires an appropriate figure of merit (FOM). FOMs for waveguides that have been used include $\mathrm{\gamma }$, which is related to the nonlinear phase shift (${∆\varphi }_{NL}=\gamma P_0{L}_{\text{eff}}$, where $\gamma =k_0{n}_2/A_0$). For example, compared to bulk optics, an optical WG’s nonlinear phase shift per unit length (${∆\varphi }_{NL}/L$) is more pronounced as it reaches its maximum at much lower driving power (Stegeman and Stolen, 1989). This is illustrated in Figure 1, where, initially, both bulk and optical waveguides’ nonlinear materials exhibit similar behavior for a plane wave; however, due to the slow-light effect and field confinement present in waveguides (Li et al., 2018a), their low-power slope, which is given by $\gamma =k_0{n}_2/A_{eff}$, is larger than that of bulk materials. High values of $\gamma$ were demonstrated in structures such as chalcogenide tapers with $\gamma =90{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ (Yeom et al., 2008) and silicon-organic slot waveguides with $\gamma ={10}^3{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ (Koos et al., 2009).

Figure 1

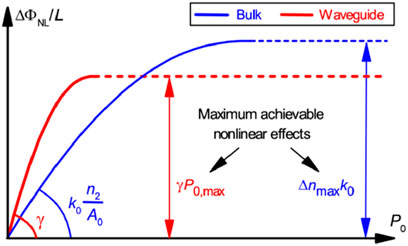
Figure 1. Nonlinear phase shift per unit length ${∆\mathit{\varphi }}_{\mathit{N}\mathit{L}}/\mathit{L}$ versus driving power ${\mathit{P}}_{\mathbf{0}}$ for bulk material (blue) and a waveguide (red). Both show an initial linear increase with slope ${\mathit{k}}_{\mathbf{0}}{\mathit{n}}_{\mathbf{2}}/{\mathit{A}}_{\mathbf{0}}$ and $\mathit{\gamma }$, respectively. The maximum achievable nonlinear effect is limited by optical damage (dashed) (Li et al., 2018a).

For many years, metal-based waveguide devices have promised to overcome many challenges in nonlinear optics (Palomba et al., 2009; Palomba et al., 2010; Kauranen and Zayats, 2012). Compared to dielectric slot waveguides, MDM plasmonic waveguides have demonstrated higher nonlinear conversion efficiency.

On one hand, metals can strongly compress light, leading to high intensities. On the other hand, losses reduce the power $P_0$ during propagation, thus limiting the maximum achievable ${∆\varphi }_{NL}$. Although the literature on nonlinear plasmonic devices is vast (Sederberg and Elezzabi, 2015; Palomba and Novotny, 2008; Palomba et al., 2010; Kauranen and Zayats, 2012), most papers describe the numerical investigation and optimization of a particular plasmonic structure. For example, it was recently proposed to combine dielectric materials and metals in so-called hybrid-plasmonic waveguides, which maintain high field confinement with mitigated losses (Oulton et al., 2008), thus enhancing light-matter interactions and reaching $\gamma ={10}^4{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$, which is two orders of magnitude larger than that of typical silicon waveguides (Pitilakis et al., 2014; Pitilakis and Kriezis, 2013; Diaz et al., 2016). More general parameter combinations have been proposed but without presenting a rigorous justification or systematic optimization (Hossain et al., 2011). While such reports typically identify the optimal thickness of a certain layer in a particular device based on numerical simulations, there are few studies that address general trends. It is, therefore, not clear whether a chosen optimized device represents a local or a global maximum.

A subtle deficiency of using γ as a FOM is the implicit assumption that nonlinear effects are independent of power. This cannot be true since, at very high power levels, the material sustains damage and ultimately disintegrates. There must be a power level, $P_{th}$, at which the maximum nonlinear refractive index change is reached before damaging the material. For this reason, we introduced a comprehensive FOM, $\mathcal{F}=\gamma P_{th}{L}_{ATT}$, where $L_{ATT}=1/\alpha$ with $\alpha$ being the absorption coefficient (Li et al., 2016). Rigorous calculations showed that the optimal nonlinear interaction length of lossy waveguides is $L_{OPT}=\mathit{ln}3\cdot L_{ATT}$. At $L_{OPT}$, the nonlinear phase shift is ${∆\varphi }_{NL,OPT}=2\mathcal{F}/3$ and the maximum DFWM conversion efficiency is ${\eta }_{\mathit{max}}={4\mathcal{F}}^2/27$ (Li et al., 2016). In MDM structures, $1\le \beta \le 3$ depending on device geometry, where $∆n_{\mathit{max}}\propto \gamma P_{th}$ is the maximum nonlinear index change sustainable by the dielectric material and $n$ is the refractive index of the nonlinear medium (Li et al., 2018a; Li et al., 2018b). Since $\mathcal{F}$ becomes significantly large as $n\approx 0$, it is highly advantageous to use ENZ materials in MDM structures.

$\mathcal{F}\propto \frac{∆n_{\mathit{max}}}{n^{\beta }}.(1)$

ENZ materials were largely overlooked in nonlinear optics until 2016, when their unusually large nonlinear properties were first reported by Alam et al. (2016) and by Caspani et al. (2016), who conducted free-space, intensity-dependent reflection and transmission measurements on a 310-nm-thick ITO sample. They reported unprecedented changes in the ITO refractive index $∆n\sim 0.72$ and a nonlinear response time of , which is compatible with ultrafast nonlinear signal processing. Caspani et al. additionally reported free-space, pump-probe measurements on a 900-nm-thick aluminum-doped zinc oxide (AZO), which also exhibited an immense intensity-dependent change in the refractive index $∆n\sim 0.45$.

This large change in the refractive index can be qualitatively understood from the relation $∆n\approx ∆\epsilon /\left(2\sqrt{\epsilon }\right)=∆\epsilon /\left(2n\right)$. When $n\ll 1$, $∆n$ can be very large, even for modest $∆\epsilon$, which is consistent with the experiments conducted by Alam et al. (2016) and Caspani et al. (2016). However, in materials with low $n$ like ENZ materials, the implicit assumption in traditional nonlinear optics—that $∆n$ is a small perturbation—is no longer valid, meaning that the conventional nonlinear optics theory needs to be reviewed. A first step was taken by Reshef et al. (2017), who derived a more general equation for the intensity-dependent refractive index that remains valid in low-index materials by accounting for significant higher-order nonlinearities. In addition to this, ENZ materials also support high field intensities: the continuity of the normal component of the displacement field $\mathit{D}=\epsilon \mathit{E}$ causes this electric field component to become very large as $\epsilon \approx 0$ (Liberal and Engheta, 2017). Phase matching is also not required since ENZ materials do not exhibit phase accumulation (Suchowski et al., 2013).

In summary, thus far, only free-space nonlinear optical experiments with ENZ materials have been reported. These experiments show enormous nonlinear effects, orders of magnitude larger than those in conventional materials. Transferring these experiments to waveguide geometries such as MDMs will enhance the nonlinear effects of such structures.

2.2 Computational details

Following the method reported by Li et al. (2016) and Li et al. (2018a), the DFWM conversion efficiency, ${\eta }_{DFWM}$, at a length $L$ driven by a power $P_0$, can be calculated by Equation 2 as follows:

${\eta }_{DFWM}\approx e^{-\alpha L}{\left(\gamma P_0{L}_{eff}\right)}^2,(2)$

where the attenuation and nonlinear coefficients, respectively, $\alpha$ and $\gamma$, were calculated from the electromagnetic field, using the mode analysis outlined by Equation 3 in the following manner:

$\gamma =k_0\left(\frac{{\epsilon }_0}{{\mu }_0}\right)\int n_{\mathrm{m}}^2\left(x,y\right)n_2\left(x,y\right)\left[\frac{\rho \frac{\left.2\right|\mathbf{e}{|}^4+\left(\mathbf{e}\cdot \mathbf{e}\right)\left({\mathbf{e}}^{*}\cdot {\mathbf{e}}^{*}\right)}{3}+\left(1-\rho \right){\displaystyle \sum _{j=x,y,z}}{\left|e_j\right|}^4]\mathrm{d}A}{{\left|\int \left(\mathbf{e}\times {\mathbf{h}}^{*}\right)\cdot \widehat{z}\mathrm{d}A\right|}^2}\right].(3)$

Here, ${\epsilon }_0$, ${\mu }_0$, and $k_0$ are the permittivity, permeability, and wave vector in vacuum, respectively; $n_m$ and $n_2$ are the linear and nonlinear refractive indices, respectively; $\rho =1$ for isotropic materials, while $\rho =1.27$ if silicon is used when the wavelength is in the telecom band; and both $\mathbf{e}$ and $\mathbf{h}$ were given by the eigenmode, found through mode analysis; and the effective length $L_{eff}$ was defined as $L_{eff}=\left(1-e^{-\alpha L}\right)/\alpha$. This expression is in agreement with the one reported by Li et al. (2020) for lossy waveguides.

We have considered that the linear refractive index ($n_m$) for silver, at a wavelength $\lambda =1550nm$, is $n_m=0.144+11.366i$, while at $\lambda =1425nm$ (ENZ wavelength of ITO), it is $n_m=0.133+10.358i$. At the telecom frequency, $n_m$ of the nonlinear polymer DDMEBT and silicon is $1.8$ and $3.5$, respectively. For the ENZ materials, ITO has a refractive index of $n_m=\sqrt{0+0.5i}$ and AZO has a refractive index of $n_m=\sqrt{0+0.2i}$. The nonlinear refractive index ($n_2$) is $n_2=2.5\times {10}^{-18}{m}^2{W}^{-1}$ for silicon, $n_2=1.7\times {10}^{-17}{m}^2{W}^{-1}$ for DDMEBT, $n_2=5.2\times {10}^{-16}{m}^2{W}^{-1}$ for AZO (Reshef et al., 2019), and $n_2=0.11{cm}^{2}G{W}^{-1}$ for ITO (Alam et al., 2016). Finally, the damage power threshold for different structures can be calculated following the work of Li et al. (2018a).

3 Results and discussion

In this section, we have applied the outlined theory to simulate the DFWM conversion efficiency of a plasmonic MDM slot waveguide, where the dielectric “D” is composed of a highly nonlinear medium, like the DDMEBT polymer. We compared the results with those of the most efficient photonic platform to generate nonlinear signals like DFWM, i.e., a fully dielectric Si-slot waveguide. We have run two simulations: one where the pump power is set to the maximum power threshold ($P_{th}$) allowed for each structure and another where $P_{th}$ is fixed based on the plasmonic slot waveguide with the smallest slot since it exhibits the lowest power threshold. We then swapped the nonlinear polymer with an ENZ material, observing a further boost in the nonlinear conversion efficiency for DFWM generation in plasmonic slot waveguides. This enhancement is due to the inverse proportionality of the nonlinear figure of merit $\mathcal{F}$ (Equation 1), which is directly related to the nonlinear conversion efficiency. The increase in ${\eta }_{DFWM}$ is due to the low, close to 0, refractive index of the nonlinear material, which maintains its high intrinsic nonlinearities.

3.1 MDM with DDMEBT material

The first set of simulations is performed with a highly nonlinear medium, like DDMEBT, inserted within the gap of an MDM slot waveguide. These are shown in Figure 2, where the DFWM conversion efficiency of MDM slot waveguides, with the DDMEBT polymer embedded in the small gap as the nonlinear medium, is higher than its dielectric counterpart, i.e., the Si-slot waveguides.

Figure 2

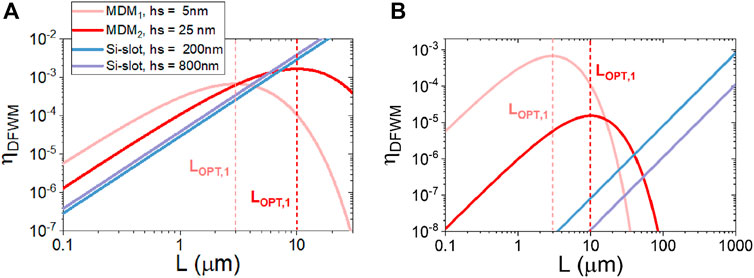
Figure 2. DFWM conversion efficiency of MDM and Si-slot waveguides for two different spacer thicknesses $\left(t_c\right)$ when each structure is driven at (A) its own pump power threshold ($P_{0,th}$ $=1.8\times 10⁻²$ for $\text{MD}{\mathrm{M}}_1$, $P_{0,th}$ $=1.7\times 10⁻³$ for $\text{MD}{\mathrm{M}}_2$, $P_{0,th}=1$ for Si-${\text{slot}}_1$, and $P_{0,th}=0.32$ for Si-${\text{slot}}_2$) and (B) the same pump power threshold where $P_{0,th}$ was set to the maximum achievable pump power of $\text{MD}{\mathrm{M}}_1$, which is limited by optical damage. Based on the respective $L_{OPT}$ values, which refers to the optimal length, (A) MDM waveguides are shown to have a superior footprint when $L\le 6\mu m$ and (B) MDMs outperform Si-slots for footprints of $L\le 30\mu m$. The simulations were performed at the telecom wavelength, i.e., $\lambda =1,550nm.$

When the MDM and the Si-slot waveguides are driven at their respective power thresholds (Figure 2A), both plasmonic structures exhibit a nonlinear conversion efficiency at least an order of magnitude higher than their dielectric counterparts at a device length smaller than the optimal length ($L_{OPT}$). When the waveguides are longer than this $L_{OPT}$, plasmonic structures no longer perform effectively due to metal losses, which deplete the confined electromagnetic field propagating within their gaps. This shows that the photonic slot waveguides are superior only at large footprints, whereas the plasmonic slot waveguides are superior for footprints smaller than $6\mu m$ and gaps smaller than $25nm$.

Moreover, in terms of nonlinear effectiveness ${\text{EFF}}_{\text{NL}}$ (Li et al., 2018a), which is defined as the ratio between the nonlinear phase shift change in the mode and that of a plane wave in bulk—thus quantifying a mode’s ability to convert a material’s nonlinear index change into a nonlinear phase shift—the results we have obtained are summarized in Table 1. ${\text{EFF}}_{\text{NL}}<1$ for a dielectric Si-slot waveguide, whereas ${\text{EFF}}_{\text{NL}}>1$ for an MDM slot waveguide with a gap smaller than $25nm$. This implies that an MDM slot waveguide harvests more nonlinearity than in the bulk. This superiority is explained by the fact that the MDM slot waveguide has substantial slow-light effects for small values of the gap ($h_s$), leading to a longer effective path length through the nonlinear material, thus increasing nonlinearities. The slow-light effects in MDM structures arise because the energy in the metal propagates backward as a result of the metal’s negative permittivity (Li et al., 2018a). Since the permittivity of the dielectric and the metal have opposite signs for a broad wavelength range, the slow-light effect and, thus, the nonlinear effectiveness of MDM are intrinsically broadband. This phenomenon is similar to slow-light effects observed in photonic crystals; however, unlike photonic crystals, it does not rely on resonance, making it extremely broadband.

Table 1

Table 1. Nonlinear effectiveness at each structure’s pump power threshold.

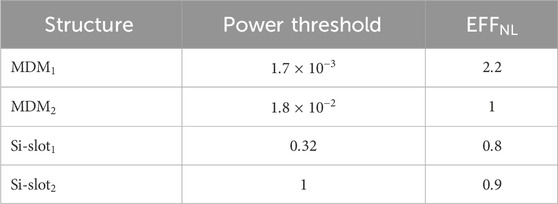
Table 1 shows that the plasmonic slot waveguide with the smallest gap, i.e., ${\text{MDM}}_1$, ($h_s=5nm$) requires a maximum pump power that is 1,000 times smaller than that of the respective photonic slot waveguide. Hence, the plasmonic slot waveguide not only achieves significantly higher nonlinear conversion efficiency but also does so while consuming three orders of magnitude less power than a conventional photonic slot waveguide with the same footprint. Furthermore, its nonlinear effectiveness is twice that of bulk material, which implies that plasmonic slot waveguides with small gaps have a higher capability of harnessing a nonlinear phase shift change than bulk materials. However, when operated at the same pump power, MDM’s superiority is even more evident (Figure 2B). The nonlinear conversion efficiency of ${\text{MDM}}_1$ is approximately five orders of magnitude higher than that of the best respective photonic counterpart. Therefore, when pumped with the same power, plasmonic slot waveguides outperform their photonic counterparts, particularly in compact footprints up to .

3.2 MDM with ENZ materials

In the previous section, we have demonstrated that plasmonic slot waveguides outperform their photonic counterparts for small footprints, i.e., length up to when using the same pump power and up to when using their respective pump thresholds. In this study, we show that by combining the high nonlinearity from ENZ materials, such as ITO, with high field enhancements from MIM waveguides and the additional boost provided by the inverse proportionality of the conversion efficiency with the linear refractive index, ENZ-MDM slot waveguides prove to be the best-performing architecture at small footprints. This performance gain is attributed to the low refractive index of ENZ materials and its relationship, as described by Equation 1 with the nonlinear conversion efficiency, i.e., the lower the linear refractive index, the higher the expected nonlinear conversion efficiency.

The major issue with ENZ materials is their significant losses, which are higher than those of metals. Therefore, although it may initially appear that the addition of ENZ materials to slot waveguides would not notably enhance plasmonic structures the results shown in Figure 3 demonstrate the opposite. M–ITO–M slot waveguides exhibit a conversion efficiency that is two orders of magnitude higher than that of the most efficient MDM slot waveguide, even considering the substantial loss of the ENZ material at a wavelength where the dielectric function crosses 0. $\text{In\hspace{0.17em}this\hspace{0.17em}case},L_{OPT}$ of the M–ITO–M slot waveguide is very low, $\sim 100nm$, which makes it difficult to classify as a waveguide. Regardless of this terminology, the key advantage is that the ENZ-MDM slot waveguides are the highest-performing nonlinear devices, showing superior nonlinear conversion efficiency within ultra-compact footprints.

Figure 3

Figure 3. Comparison of DFWM conversion efficiency of M–ENZ–M and MDM for two different spacer thicknesses $\left(t_c\right)$ when each structure is driven at the same maximum threshold intensity ${\mathit{P}}_{\mathbf{0}}=0.32$ (from MDM,$t_c=5$ nm) for fairness.

4 Conclusion

The results of our investigation highlight the significant advances achieved through MDM-ENZ slot waveguide architecture. Building on the foundational work by Li et al. (2018a), which identified MDMs as the most effective nonlinear plasmonic waveguides, we compared these structures with Si-slot waveguides and demonstrated the clear superiority of MDMs. This distinction becomes even more pronounced when all waveguides operate under the same pump power, set to the lowest power threshold. Under this condition, MDMs exhibit a nonlinear conversion efficiency approximately five orders of magnitude higher than their photonic counterparts. The unprecedented results, however, were observed when ENZ materials, such as ITO, were incorporated into the MDM structures. These M–ITO–M configurations leveraged the unique properties of ENZ materials to enhance nonlinear interactions while harnessing the strong, uniform field confinement and slow-light effects inherent to plasmonic slot waveguides. This integration resulted in an additional two orders of magnitude improvement in nonlinear conversion efficiency, surpassing even the top-performing MDM slot waveguides. Our findings demonstrate ENZ-MDM waveguide’s ability to contribute to nonlinear plasmonic structure development while also paving the way for their integration into cutting-edge on-chip applications.

Although the performance of ENZ-MDM structures is remarkable, their optimal propagation length (∼100 nm) challenges the conventional definition of waveguides. Despite this, the nonlinear conversion efficiency shown by M–ITO–M slot waveguides underscores their value, especially in applications where compactness and efficiency at a nanoscale outweigh propagation constraints. Potential applications can be sought in the field of quantum optical applications where extreme compactness and high efficiency in harnessing pure and strong nonlinearities become crucial, such as in squeezed light or photon pairs. Overall, this work underscores the untapped potential of ENZ materials in nonlinear optics, suggesting exciting directions for future experimental validation and material optimization.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors upon request, without undue reservation.

Author contributions

LY: writing–original draft and writing–review and editing. HH: data curation, software, validation, and writing–review and editing. CC: supervision, validation, and writing–review and editing. SP: conceptualization, supervision, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to acknowledge the insightful discussions on this subject with Prof. Martijn de Sterke (University of Sydney) and Assoc/Prof Guangyuan Li (Shenzhen Institute of Advanced Technology), which resulted to be essential for the preparation of this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam, M. Z., De Leon, I., and Boyd, R. W. (2016). Large optical nonlinearity of indium tin oxide in its epsilon-near-zero region. Science 352, 795–797. doi:10.1126/science.aae0330

PubMed Abstract | CrossRef Full Text | Google Scholar

Alam, M. Z., Schulz, S. A., Upham, J., De Leon, I., and Boyd, R. W. (2018). Large optical nonlinearity of nanoantennas coupled to an epsilon-near-zero material. Nat. Photonics 12, 79–83. doi:10.1038/s41566-017-0089-9

CrossRef Full Text | Google Scholar

Bartolucci, S., Birchall, P., Bombín, H., Cable, H., Dawson, C., Gimeno-Segovia, M., et al. (2023). Fusion-based quantum computation. Nat. Commun. 14, 912. doi:10.1038/s41467-023-36493-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bogaerts, W., Pérez, D., Capmany, J., Miller, D. A. B., Poon, J., Englund, D., et al. (2020). Programmable photonic circuits. Nature 586, 207–216. doi:10.1038/s41586-020-2764-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Boyd, R. W. (2003). Nonlinear optics. Academic Press.

Google Scholar

Caspani, L., Kaipurath, R. P. M., Clerici, M., Ferrera, M., Roger, T., Kim, J., et al. (2016). Enhanced nonlinear refractive index in epsilon-near-zero materials. Phys. Rev. Lett. 116, 233901. doi:10.1103/physrevlett.116.233901

PubMed Abstract | CrossRef Full Text | Google Scholar

Cherchi, M., Ylinen, S., Harjanne, M., Kapulainen, M., and Aalto, T. (2013). Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform. Opt. Express 21, 17814–17823. doi:10.1364/oe.21.017814

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciattoni, A., Rizza, C., and Palange, E. (2010). Extreme nonlinear electrodynamics in metamaterials with very small linear dielectric permittivity. Phys. Rev. A 81, 043839. doi:10.1103/physreva.81.043839

CrossRef Full Text | Google Scholar

Dass, C. K., Kwon, H., Vangala, S., Smith, E. M., Cleary, J. W., Guo, J., et al. (2020). Gap-Plasmon-enhanced second-harmonic generation in epsilon-near-zero nanolayers. ACS Photonics 7, 174–179. doi:10.1021/acsphotonics.9b01350

CrossRef Full Text | Google Scholar

Diaz, F. J., Li, G., De Sterke, C. M., Kuhlmey, B. T., and Palomba, S. (2016). Kerr effect in hybrid plasmonic waveguides. J. Opt. Soc. Am. B 33, 957–962. doi:10.1364/josab.33.000957

CrossRef Full Text | Google Scholar

Doerr, C. (2015). Silicon photonic integration in telecommunications. Front. Phys. 3. doi:10.3389/fphy.2015.00037

CrossRef Full Text | Google Scholar

Garmire, E. (2013). Nonlinear optics in daily life. Opt. Express 21, 30532–30544. doi:10.1364/oe.21.030532

PubMed Abstract | CrossRef Full Text | Google Scholar

Hendrickson, S. M., Foster, A. C., Camacho, R. M., and Clader, B. D. (2014). Integrated nonlinear photonics: emerging applications and ongoing challenges [Invited]. J. Opt. Soc. Am. B 31, 3193–3203. doi:10.1364/josab.31.003193

CrossRef Full Text | Google Scholar

Hossain, M. M., Turner, M. D., and Gu, M. (2011). Ultrahigh nonlinear nanoshell plasmonic waveguide with total energy confinement. Opt. Express 19, 23800–23808. doi:10.1364/oe.19.023800

PubMed Abstract | CrossRef Full Text | Google Scholar

Jood, P., Mehta, R. J., Zhang, Y., Peleckis, G., Wang, X., Siegel, R. W., et al. (2011). Al-doped Zinc oxide nanocomposites with enhanced thermoelectric properties. Nano Lett. 11, 4337–4342. doi:10.1021/nl202439h

PubMed Abstract | CrossRef Full Text | Google Scholar

Kauranen, M., and Zayats, A. V. (2012). Nonlinear plasmonics. Nat. Photonics 6, 737–748. doi:10.1038/nphoton.2012.244

CrossRef Full Text | Google Scholar

Kim, J.-H., Aghaeimeibodi, S., Carolan, J., Englund, D., and Waks, E. (2020). Hybrid integration methods for on-chip quantum photonics. Optica 7, 291–308. doi:10.1364/optica.384118

CrossRef Full Text | Google Scholar

Koos, C., Vorreau, P., Vallaitis, T., Dumon, P., Bogaerts, W., Baets, R., et al. (2009). All-optical high-speed signal processing with silicon-organic hybrid slot waveguides. Nat. Photonics 3, 216–219. doi:10.1038/nphoton.2009.25

CrossRef Full Text | Google Scholar

Li, G. H. Y., De Sterke, C. M., and Tuniz, A. (2020). Omnidirectional field enhancements drive giant nonlinearities in epsilon-near-zero waveguides. Opt. Lett. 45, 6514–6517. doi:10.1364/ol.412761

PubMed Abstract | CrossRef Full Text | Google Scholar

Liberal, I., and Engheta, N. (2017). Near-zero refractive index photonics. Nat. Photonics 11, 149–158. doi:10.1038/nphoton.2017.13

CrossRef Full Text | Google Scholar

Li, G., De Sterke, C. M., and Palomba, S. (2016). Figure of merit for Kerr nonlinear plasmonic waveguides. Laser and Photonics Rev. 10, 639–646. doi:10.1002/lpor.201600020

CrossRef Full Text | Google Scholar

Li, G., De Sterke, C. M., and Palomba, S. (2018a). Fundamental limitations to the ultimate Kerr nonlinear performance of plasmonic waveguides. ACS Photonics 5, 1034–1040. doi:10.1021/acsphotonics.7b01331

CrossRef Full Text | Google Scholar

Li, G., Palomba, S., and De Sterke, C. M. (2018b). A theory of waveguide design for plasmonic nanolasers. Nanoscale 10, 21434–21440. doi:10.1039/c8nr04898c

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P., Yan, W., Wang, S., Fu, P., Zhang, Y., and Li, Y. (2024). Engineering epsilon-near-zero media with waveguides. Adv. Phys. Res. 3, 2400070. doi:10.1002/apxr.202400070

CrossRef Full Text | Google Scholar

Madsen, L. S., Laudenbach, F., Askarani, M. F., Rortais, F., Vincent, T., Bulmer, J. F. F., et al. (2022). Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81. doi:10.1038/s41586-022-04725-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Maradudin, A. A., Sambles, J. R., and Barnes, W. L. (2014). Modern plasmonics. Burlington: Elsevier Science.

Google Scholar

Miller, S. E. (1969). Integrated optics: an introduction. Bell Syst. Tech. J. 48, 2059–2069. doi:10.1002/j.1538-7305.1969.tb01165.x

CrossRef Full Text | Google Scholar

O'Brien, J. L. (2007). Optical quantum computing. Science 318, 1567–1570. doi:10.1126/science.1142892

PubMed Abstract | CrossRef Full Text | Google Scholar

Oulton, R. F., Soreger, V. J., Genov, D. A., Pile, D. F. P., and Zhang, X. (2008). A hybrid plasmonic waveguide for subwavelength confinement and long range propagation. Nat. Photonics 2, 496–500. doi:10.1038/nphoton.2008.131

CrossRef Full Text | Google Scholar

Palomba, S., Danckwerts, M., and Novotny, L. (2009). Nonlinear plasmonics with gold nanoparticle antennas. J. Opt. A Pure Appl. Opt. 11, 114030. doi:10.1088/1464-4258/11/11/114030

CrossRef Full Text | Google Scholar

Palomba, S., Harutyunyan, H., Renger, J., Quidant, R., Hulst, N. F. V., and Novotny, L. (2010). Nonlinear plasmonics at planar metal surfaces. Philosophical Trans. R. Soc. A 369, 3497–3509. doi:10.1098/rsta.2011.0100

PubMed Abstract | CrossRef Full Text | Google Scholar

Palomba, S., and Novotny, L. (2008). Nonlinear excitation of surface plasmon polaritons by four-wave mixing. Phys. Rev. Lett. 101, 056802. doi:10.1103/physrevlett.101.056802

PubMed Abstract | CrossRef Full Text | Google Scholar

Peleckis, G., Wang, X., and Dou, S. X. (2006). High temperature ferromagnetism in Ni-doped In2O3 and indium-tin oxide. Appl. Phys. Lett. 89, 022501. doi:10.1063/1.2220529

CrossRef Full Text | Google Scholar

Pitilakis, A., and Kriezis, E. E. (2013). Highly nonlinear hybrid silicon-plasmonic waveguides: analysis and optimization. J. Opt. Soc. Am. B 30, 1954–1965. doi:10.1364/josab.30.001954

CrossRef Full Text | Google Scholar

Pitilakis, A., Tsilipakos, O., and Kriezis, E. E. (2014). Optimizing silicon-plasmonic waveguides for $$\chi ^{(3)}$$ χ (3) nonlinear applications. Appl. Phys. a-Materials Sci. and Process. 115, 475–479. doi:10.1007/s00339-013-8055-y

CrossRef Full Text | Google Scholar

Prucnal, P. R., and Shastri, B. J. (2017). Neuromorphic photonics. Boca Raton: CRC Press, Taylor and Francis Group.

Google Scholar

Reshef, O., De Leon, I., Alam, M. Z., and Boyd, R. W. (2019). Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 4, 535–551. doi:10.1038/s41578-019-0120-5

CrossRef Full Text | Google Scholar

Reshef, O., Giese, E., Zahirul Alam, M., De Leon, I., Upham, J., and Boyd, R. W. (2017). Beyond the perturbative description of the nonlinear optical response of low-index materials. Opt. Lett. 42, 3225–3228. doi:10.1364/ol.42.003225

PubMed Abstract | CrossRef Full Text | Google Scholar

Sachet, E., Shelton, C. T., Harris, J. S., Gaddy, B. E., Irving, D. L., Curtarolo, S., et al. (2015). Dysprosium-doped cadmium oxide as a gateway material for mid-infrared plasmonics. Nat. Mater. 14, 414–420. doi:10.1038/nmat4203

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulz, S. A., Wynne, L. C., and Falco, A. D. (2020). “Optical metasurfaces based on epsilon-near-zero materials: towards low power nonlinear optics,” in 2020 22nd International Conference on Transparent Optical Networks (ICTON), USA, 19-23 July 2020, 1–4. doi:10.1109/icton51198.2020.9203047

CrossRef Full Text | Google Scholar

Sederberg, S., and Elezzabi, A. Y. (2015). Coherent visible-light-generation enhancement in silicon-based nanoplasmonic waveguides via third-harmonic conversion. Phys. Rev. Lett. 114, 227401. doi:10.1103/physrevlett.114.227401

PubMed Abstract | CrossRef Full Text | Google Scholar

Stegeman, G. I., and Stolen, R. H. (1989). Waveguides and fibers for nonlinear optics. J. Opt. Soc. Am. B 6, 652–662. doi:10.1364/josab.6.000652

CrossRef Full Text | Google Scholar

Subramanian, A. Z., Ryckeboer, E., Dhakal, A., Peyskens, F., Malik, A., Kuyken, B., et al. (2015). Silicon and silicon nitride photonic circuits for spectroscopic sensing on-a-chip [Invited]. Photonics Res. 3, B47–B59. doi:10.1364/prj.3.000b47

CrossRef Full Text | Google Scholar

Suchowski, H., O’Brien, K., Wong, Z. J., Salandrino, A., Yin, X., and Zhang, X. (2013). Phase mismatch–free nonlinear propagation in optical zero-index materials. Science 342, 1223–1226. doi:10.1126/science.1244303

PubMed Abstract | CrossRef Full Text | Google Scholar

Tuniz, A. (2021). Nanoscale nonlinear plasmonics in photonic waveguides and circuits. La Riv. del Nuovo Cimento 44, 193–249. doi:10.1007/s40766-021-00018-7

CrossRef Full Text | Google Scholar

Vincenti, M. A., De Ceglia, D., Ciattoni, A., and Scalora, M. (2011). Singularity-driven second- and third-harmonic generation at ε-near-zero crossing points. Phys. Rev. A 84, 063826. doi:10.1103/physreva.84.063826

CrossRef Full Text | Google Scholar

Wabnitz, S., and Eggleton, B. J. (2015). All-optical signal processing: data communication and storage applications. Springer Cham.

Google Scholar

Wu, J., Xie, Z. T., Sha, Y., Fu, H. Y., and Li, Q. (2021). Epsilon-near-zero photonics: infinite potentials. Photonics Res. 9, 1616–1644. doi:10.1364/prj.427246

CrossRef Full Text | Google Scholar

Xu, Y., Zhao, L., Chen, G., Bai, Z., and Miao, L. (2023). Enhanced nonlinear optical response by strong coupling between plasmonic antenna arrays and epsilon-near-zero film. Appl. Phys. Express 16, 075002. doi:10.35848/1882-0786/ace025

CrossRef Full Text | Google Scholar

Yeom, D.-I., Mägi, E. C., Lamont, M. R. E., Roelens, M. A. F., Fu, L., and Eggleton, B. J. (2008). Low-threshold supercontinuum generation in highly nonlinear chalcogenide nanowires. Opt. Lett. 33, 660–662. doi:10.1364/ol.33.000660

PubMed Abstract | CrossRef Full Text | Google Scholar

Yue, Y., Fang, Y., Geng, W., and Bao, C. (2024). “Conclusions and perspectives,” in Integrated optical supercontinuum generation: physics, advances, and applications. Editors Y. YUE, Y. FANG, W. GENG, and C. BAO (Singapore: Springer Nature Singapore).

Google Scholar

Zhong, H.-S., Wang, H., Deng, Y.-H., Chen, M.-C., Peng, L.-C., Luo, Y.-H., et al. (2020). Quantum computational advantage using photons. Science 370, 1460–1463. doi:10.1126/science.abe8770

PubMed Abstract | CrossRef Full Text | Google Scholar