Estimation of extreme temperatures in direct solar methane pyrolysis within a porous medium

Porous media have wide application in renewable energy conversion processes, such as solar-thermal fuels production and decarbonization. Heat transport mechanisms within porous media can be highly complex, particularly under extreme conditions encountered in concentrated solar thermal reactors in which direct measurement of temperature is challenging. Here, we implement and report an inverse heat conduction model to estimate the temperature distribution throughout a porous substrate domain in a direct solar methane pyrolysis process. By solving a two-dimensional heat transfer problem and applying an inverse optimization algorithm, we estimate the quasi-steady state spatial temperature distribution in a fibrous porous carbon substrate. The results are validated indirectly by experimentally measured graphite deposition and a simplified reaction kinetic model.

1 Introduction

Sustainable energy processes are gaining increasing importance in climate risk mitigation (Chu and Majumdar, 2012), and solar energy is widely utilized in many different forms around the world (Kannan and Vakeesan, 2016). In addition to direct generation of electricity, solar energy can convert conventional fossil fuels into alternative low-carbon, carbon-neutral or even potentially carbon-negative fuels (Muradov and Veziroğlu, 2008). Methane comprises major proportions of biogas and natural gas supplies with broad applications, but it is also the second-largest contributor to greenhouse gas emissions (Al-Ghussain, 2019). Additionally, location incongruity of methane generation and consumption makes methane storage and long-distance transportation necessary, typically requiring energy-intensive processes such as liquefaction (Song et al., 2019; Sun et al., 2020). As such, conversion of methane into higher-value chemicals enabled by renewable energy sources is regarded as a potential means of utilizing this abundant resource in a sustainable manner (Song et al., 2019).

Common methane conversion processes, however, burden the environment as they involve excessive carbon dioxide emission. Direct solar methane pyrolysis is an attractive approach to produce valuable chemicals in a carbon neutral or negative manner. A recent study reported a direct catalysis-free solar methane pyrolysis process that produces hydrogen while at the same time exhibiting exceptionally fast deposition of high-quality graphitic carbon on a porous substrate (Abuseada et al., 2022b; Abuseada et al., 2023). In this process, methane infiltrates a fibrous porous carbon substrate that is located near the focal plane of a solar concentrator. Detailed understanding of the thermochemical mechanisms involved is necessary to optimize field-scale utility, and accurate estimation of the temperature in the reaction zone of the fibrous porous substrate is therefore essential and the subject of the present work.

Fibrous porous media (FPM) are employed in a wide variety of applications, such as fuel cells (Farzaneh et al., 2021), thermal insulation (Lakatos, 2020), phase change heat transfer and energy storage (Ren et al., 2021; Li et al., 2013), fluid filtration and separation (Knapik and Stopa, 2018), sound absorption and reduction (Tang and Yan, 2017), bio-medicine (Chen et al., 2022), and high-temperature solar receivers with reticulated porous ceramics (Patil et al., 2021). Heat transfer analysis of such fibrous porous media is necessary to understand critical transport processes in many of these applications (Kaviany, 2012). Efforts have been made to model FPM transport properties including permeability (Xiao et al., 2019), tortuosity (Vallabh et al., 2010), and effective thermal conductivity $(k)$ (Hager and Steere, 1967; Tong and Tien, 1980; Lee and Cunnington, 1998; Lee and Cunnington, 2000; Daryabeigi et al., 2011; Daryabeigi et al., 2013; Lian et al., 2024), and the present work incorporates various approaches that have been reported to date as applied to very high temperature processes.

In the past several decades, the theory and application of inverse problems have been important in many branches of science and engineering. For example, the development of solution techniques for inverse heat transfer problems in space applications has been particularly useful due to the need to conduct complex experiments with complicated materials and limited direct experimental data (Alifanov, 2012). Typical solution logic, which is also implemented in this work, for such problems usually starts with constructing a verified numerical solution to a forward problem including unknown parameters and then estimating these unknown parameters by assimilating limited experimental data with numerical optimization techniques (Ozisik, 2018).

This paper reports the application of an inverse method in estimating the temperature distribution of a FPM in a direct solar methane pyrolysis process (Abuseada et al., 2022b; Abuseada et al., 2023). Finite-difference heat transfer methods are constructed to solve the heat diffusion equation with temperature-dependent $k$ in the computational domain. An inverse optimization algorithm is then applied to determine the parameterized $k$. The substrate is located in the solar-thermal experimental system such that its back-side (the side without direct solar irradiation) temperature is experimentally measured using an infrared (IR) camera. This back-side temperature distribution is then applied as an input to the inverse problem. The Nelder-Mead method (Gao and Han, 2012) is implemented to identify the minimum of an objective function and to solve for the 2D domain’s temperature distribution. The analysis includes the decomposition reaction that occurs as methane flows through the FPM. The results are validated indirectly through a simplified kinetics model and experimentally observed graphite deposition rates.

2 Methodology

2.1 Experimental setup

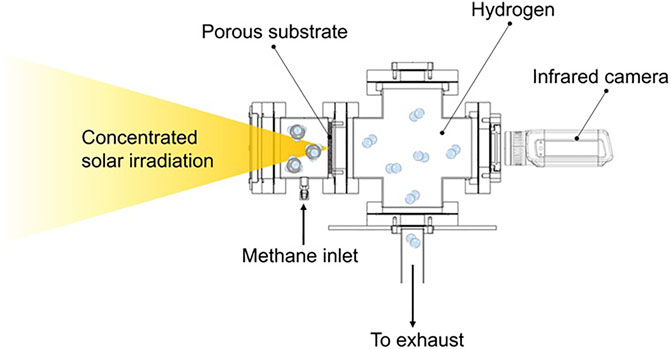
The solar-thermal experimental system is schematically illustrated in Figure 1. Concentrated solar irradiation is generated from a custom-made high flux solar simulator, which consists of a 10 kWe xenon short arc bulb (Superior Quartz, SQP-SX100003) and a silver coated aluminum ellipsoidal reflector (Optiforms, E1023F). The power output from the solar simulator is controllable by a power supply. The heat flux distribution at the focal plane inside the reactor is characterized to be Gaussian-Lorentzian (Abuseada et al., 2022a):

$q_s\prime \prime \left(r,I\right)=A_s\left(I\right)\left[\frac{1-{\alpha }_L}{{\sigma }_G\sqrt{2\pi }}\exp \left(-\frac{r^2}{2{\sigma }_G^2}\right)+\frac{{\alpha }_L}{\pi }\left(\frac{{\sigma }_L}{r^2+{\sigma }_L^2}\right)\right](1)$

Figure 1

Figure 1. Schematic of the main section of solar-thermal methane pyrolysis system.

In the Equation 1, $A_s(I)=0.683I-28.52$kW/m is the amplitude parameter, $I$ the power supply input current, and $r$ the radius from the geometric center of the substrate. The weighting factor for balancing the contribution between the Gaussian and Lorentzian distribution is ${\alpha }_L=0.595$. The Gaussian parameter ${\sigma }_G$ and Lorentzian parameter ${\sigma }_L$ are 0.00684 m and 0.0222 m, respectively.

The solar-thermal reactor is made of stainless steel and consists of three major sections. The reactant gas with controlled flow rate is supplied into the first section, a full nipple, which is 9.7 cm in inner diameter. Then the reactant flows through a fibrous porous carbon substrate (FuelCellEarth, C100) attached to the second major section, a reducing flange with an inner diameter of 6.86 cm. After passing through the porous reaction zone, the remaining reactant and product mixture flow into the third section, a 4-way cross. An infrared camera (FLIR, A655sc) is mounted on one of the ports of the cross, pointing toward the backside (the side without direct illumination) of the substrate, and the reactant and product gaseous mixture is passed into downstream in-situ laser diagnostics and mass spectrometry systems for species analysis and eventually into the exhaust through the bottom port.

2.2 Inverse heat transfer modeling

Inverse methods have been widely applied in solving heat transfer problem in various branches of engineering (Alifanov, 2012). We implement an inverse approach for FPM temperature estimation employing the Nelder-Mead method (Gao and Han, 2012). A schematic of the computational domain with thermal and geometric conditions is depicted in Figure 2. The back-side temperature of the substrate is measured using an infrared (IR) camera. The 2D temperature matrix is azimuthally averaged and used as an input to the inverse problem.

Figure 2

Figure 2. Thermal conditions and geometric information of porous substrate domain.

2.2.1 Computational approach

The steady-state heat diffusion equation in cylindrical coordinates is solved to estimate the unknown effective thermal conductivity (Faghri et al., 2010). Because of geometric symmetry, a 2D governing equation suffices to describe the problem:

$\frac{1}{r}\frac{\partial }{\partial r}\left(kr\frac{\partial T}{\partial r}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+Q_v=0(2)$

where $k$ is the effective thermal conductivity, and $Q_v$ is an internal volumetric heat source/sink intensity in Equation 12.

The surrounding is treated as a blackbody with an estimated average temperature $T_{\mathit{surr}}=550$ K (Abuseada et al., 2022a). The boundary conditions are represented as:

${\left.-k\left(T\right)\frac{\partial T}{\partial r}\right|}_{r=R}=q_R\prime \prime (3)$

${\left.-k\left(T\right)\frac{\partial T}{\partial z}\right|}_{z=0}={\alpha }_{sqs}\prime \prime +{\alpha }_{\mathit{surr}}\sigma T_{\mathit{surr}}^4-\epsilon \sigma T^4(4)$

${\left.-k\left(T\right)\frac{\partial T}{\partial z}\right|}_{z=Z}=-{\alpha }_{\mathit{surr}}\sigma T_{\mathit{surr}}^4+\epsilon \sigma T^4(5)$

where $q_R\prime \prime$ is the heat flux at the outer radius $R$ of the substrate estimated via finite differencing of the IR camera readings near $r=R$, ${\alpha }_s$ and ${\alpha }_{\mathit{surr}}$ are the porous substrate absorptivity to the simulated solar irradiation and the surrounding irradiation respectively. $\epsilon$ is the substrate emissivity, $R$ and $Z$ are the radius and thickness of the cylindrical computational domain in Equations 3–5.

The porous substrate’s emissivity in the mid-infrared band was measured to be $\epsilon =0.9$ (Abuseada, 2022), and this value is assumed to be extendable to the near-infrared here (Neuer, 1992; Li et al., 2024). Moreover, the substrate’s directional emissivity is expected to be relatively constant (Balat-Pichelin et al., 2006). From the experimental results, the front central substrate up to a radius of around 14.5 mm is deposited with graphite, exhibiting an approximated emissivity of $\epsilon =0.85$ (Neuer, 1992; Li et al., 2024). The substrate’s absorptivities to both solar and surrounding irradiation are assumed to be ${\alpha }_s={\alpha }_{\mathit{surr}}=0.9$.

The governing equation and boundary conditions are discretized to numerically solve for the substrate temperature distribution via finite-differencing scheme. The elements in the substrate domain can be categorized into nine different types. Mesh independence analysis and detailed derivations of finite difference equations are provided in the supporting information (SI).

2.2.2 Effective thermal conductivity models

The effective thermal conductivity $(k)$ of the porous substrate with graphitic carbon deposition is highly temperature-dependent. In this work, it is approximated to include primary contributions of conduction and radiation (Daryabeigi et al., 2011). We model $k$ in a parametrized form to account for 1) the multi-modal heat transfer process and 2) albeit indirectly, the temperature-dependent growth of graphitic carbon layers around the fibers of the porous substrate, which have high thermal conductivity:

$k\left(T\right)=C_0{T}^3+C_1{T}^{-1}(6)$

Here, $C_0$ to $C_1$ are unknown parameters to be determined by applying the inverse method. The exponent of temperature in the first term is set to 3 from theoretical effective thermal conductivity models (Hager and Steere, 1967; Daryabeigi et al., 2011) to represent radiation transport within the porous medium. In the second term, the temperature exponent is set to −1 to represent the conduction component (Fisher, 2013).

Additionally, the porous medium substrate can possibly exhibit anisotropy in $k$, especially after pyrolytic graphite deposition. Thus, an anisotropic $k$ model is also considered to assess its influence on the estimated temperature distribution. The simplified 2D anisotropic $k$ tensor takes the form:

$\mathit{k}=\left[\begin{array}{cc}\hfill k_{rr}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill k_{zz}\hfill \end{array}\right](7)$

The steady-state heat diffusion equation with anisotropic $k$ in the absence of the chemical reaction is (Chang and Tsou, 1977):

$\frac{1}{r}\frac{\partial }{\partial r}\left(k_{rr}r\frac{\partial T}{\partial r}\right)+\frac{\partial }{\partial z}\left(k_{zz}\frac{\partial T}{\partial z}\right)=0(8)$

where $k_{rr}$ and $k_{zz}$ are modeled using similar expressions as used for isotropic $k$, taking both radiation and conduction into account for consistency and comparison:

$k_{rr}\left(T\right)=C_{r,0}{T}^3+C_{r,1}{T}^{-1}(9)$

$k_{zz}\left(T\right)=C_{z,0}{T}^3+C_{z,1}{T}^{-1}(10)$

2.2.3 Reaction-induced internal heat sink and temperature change

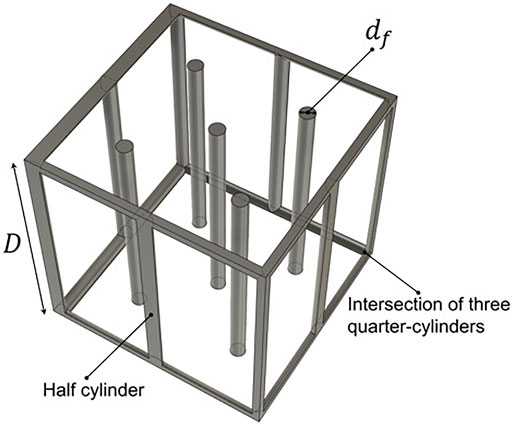
To assess the heat sink terms associated with the methane pyrolysis reaction, we construct a model to incorporate the chemical reaction. To facilitate the estimation of the magnitude of internal heat sink terms, we employ a highly simplified geometric model of the porous substrate using a periodic unit cell shown in Figure 3. The diameter of the fiber is $d_f$, and the length of the elemental cube is approxi.$D=121.1\mu$m. Before any graphitic carbon deposition, the fibrous porous substrate has an approximate fiber diameter of 9.6 $\mu$m and a porosity of 0.952.

Figure 3

Figure 3. Schematic of a single element of fibrous porous substrate.

The porosity of the unit cell and therefore the porous substrate can be expressed as Zeng et al. (1995):

$\varphi =1-\frac{1}{D^3}\left(\frac{5}{2}\pi D{d}_f^2-\left(\sqrt{2}+\frac{4}{3}\right)d_f^3\right)(11)$

The time-averaged fiber diameter change rate is:

$\dot{d_f}=\frac{d_f\left(t_e\right)-d_f\left(t_0\right)}{\mathrm{\Delta }t}(12)$

where the experiment duration $\mathrm{\Delta }t=t_e-t_0$ is 20 $\text{min}$. The porosity change rate can be obtained as:

$\frac{d\varphi \left(d_f\right)}{dt}=-\frac{\dot{d_f}}{D^3}\left[5\pi D{d}_f-3\left(\sqrt{2}+\frac{4}{3}\right)d_f^2\right](13)$

The reaction-induced internal heat sink is next calculated as:

$Q_v=-{\rho }_g\frac{\mathrm{\Delta }H}{M_c}\frac{d\varphi \left(d_f\right)}{dt}(14)$

Here, ${\rho }_g$ is graphite density, $M_c$ is the molecular weight of carbon, and $\mathrm{\Delta }H$ is the temperature-dependent enthalpy of the global thermal methane decomposition reaction as evaluated using the CoolProp package (Bell et al., 2014).

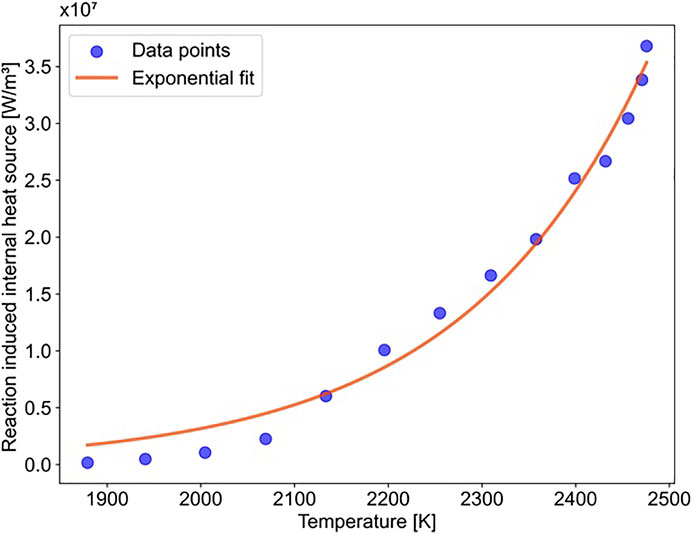
The calculated internal heat sink term is a function of the reaction temperature as shown in Figure 4. The symbols are calculated values from Equation 14; the red curve is an exponential fit as follows:

$Q_v=f_1{e}^{f_{2}T}(15)$

Figure 4

Figure 4. Temperature induced internal heat sink term $Q_v$: original data points and exponential fit.

2.2.4 Penetration depth

Considering the intrinsic porosity of the substrate employed in this study, the actual solar irradiation into the substrate may not be well-described by a surface heat flux owing to the finite penetration depth into the porous substrate. To capture the influence of this consideration, the surface heat flux is converted into a shallow volumetric heat source. The actual penetration depth will depend on the incident wavelength as well as various fiber composite morphologies, and the radiative flow into the substrate follows an exponential-decay in the incident direction (Gusarov et al., 2019). In this work, the surface incident heat flux is treated as a simplified uniform heat source and calculated as:

$Q_v\left(r\right)=q_s\prime \prime \left(r\right)/\delta (16)$

where $q_s\prime \prime (r)$ is the surface incident heat flux, and $\delta$ is the penetration thickness, with a value chosen to be 98 $\mu$m that corresponding to the first two layers of elements in the thickness direction.

2.2.5 Other assumptions

In addition to the assumptions discussed in the foregoing sections, other major assumptions include:

$•$ Thermally quasi-steady behavior in the experimental duration of interest.

$•$ The gas phase is in local thermal equilibrium with the substrate.

$•$ Negligible convection in analyzing the heat transfer and effective thermal conductivity owing to the small flow rate and low pressure.

2.3 Fiber diameter measurements

A ZEISS Supra 40VP field emission scanning electron microscope (SEM) with a secondary electrons (SE) detector was used to obtain SEM images of graphitic carbon deposition followed by the local fiber diameter measurements. These values are applied for calculating the deposition rate and chemical reaction-induced internal heat sink.

2.4 Kinetic model for activation energy approximation

After the inverse problem is solved, we use the results to estimate reaction kinetics. The global methane decomposition reaction is usually considered to be a first order reaction (Abanades and Flamant, 2007; Holmen et al., 1995; Trommer et al., 2004), noting that such a treatment is simplified without considering the complex subreactions network and minor intermediate species. The net rate of the decomposition can thus be expressed as:

$\frac{d{n}_{C{H}_4}}{dt}=-A\text{exp}\left(-E_a/RT\right)n_{C{H}_4}(17)$

where $A$ is the pre-exponential factor, $E_a$ is the activation energy, $R$ is universal gas constant, and $n_{C{H}_4}$ is the methane amount in moles. The mass deposition rate per unit length can be calculated as:

$\frac{{\dot{m}}_C\left(T\right)}{L}=\frac{{\rho }_g\pi \left(r_f^2-r_i^2\right)}{\mathrm{\Delta }t}(18)$

where ${\rho }_g=1650$ kg/m³, $r_i=4.8$ $\mu$ m and $\mathrm{\Delta }t=20$ min.

Incorporating all the information and equations above, the activation energy can be estimated from a linear-fit of the following Arrhenius expression:

$\text{ln}\left(\frac{{\dot{m}}_C\left(T\right)}{L}\right)=\text{ln}\left(\frac{A{M}_C{n}_{C{H}_4}}{L}\right)-\frac{E_a}{RT}(19)$

3 Results and discussion

Knowledge of the reaction zone temperature is crucial for understanding and elucidating the chemical reaction kinetics, especially when the reaction is under direct light exposure. While the direct measurements and thermophysical mechanisms are extremely complex, the inverse heat transfer analysis plays an effective role in estimating the spatial temperature distribution and can provide helpful thermochemical information of the solar methane pyrolysis process under extreme conditions. In this work, we conduct inverse-estimation analyses on four cases of model differing assumptions:

1. A standard case based only on isotropic heat conduction (see section 2.2.2; Equation 6, and assumptions made in section 2.2.5 that treats the porous carbon substrate as isotropic, neglects heat absorbed by chemical reactions, and regards heat flux as a surface boundary condition).

2. An anisotropic $k$ case compared with the standard case. This case treats the porous carbon substrate as anisotropic (see section 2.2.3; Equations 7–10).

3. A chemical reaction case (see section 2.2.3; Equations 15, 17–19). This case, in comparison with the standard case, considers the heat absorbed by methane pyrolysis by incorporating reaction enthalpy.

4. A penetration depth case (see section 2.2.4; Equation 16). In contrast to the standard case, this case considers the finite penetration depth of the solar irradiation into the porous substrate.

3.1 Reaction zone temperature distribution and activation energy approximation

The solar methane pyrolysis experiment is conducted at a total solar power of 1.86 kW, system pressure of 3.33 kPa, methane flow of 100 sccm and experimental duration of 20 min. Substrate back-side temperature is measured using an IR camera as shown in Figure 5A. The temperature distribution is clearly symmetric about the substrate’s geometric center. As such, the two-dimensional temperature contour is azimuthally averaged without losing accuracy. The reaction-zone (front-side) temperature without considering chemical reaction, penetration depth, anisotropic effective thermal conductivity, is estimated inversely by matching the experimentally measured back-side and numerically-estimated back-side temperatures. These temperature profiles are summarized in Figure 5B. The backside temperature estimated from the inverse heat transfer model falls into the measurement uncertainty range, showing good agreement with the measured back-side temperature.

Figure 5

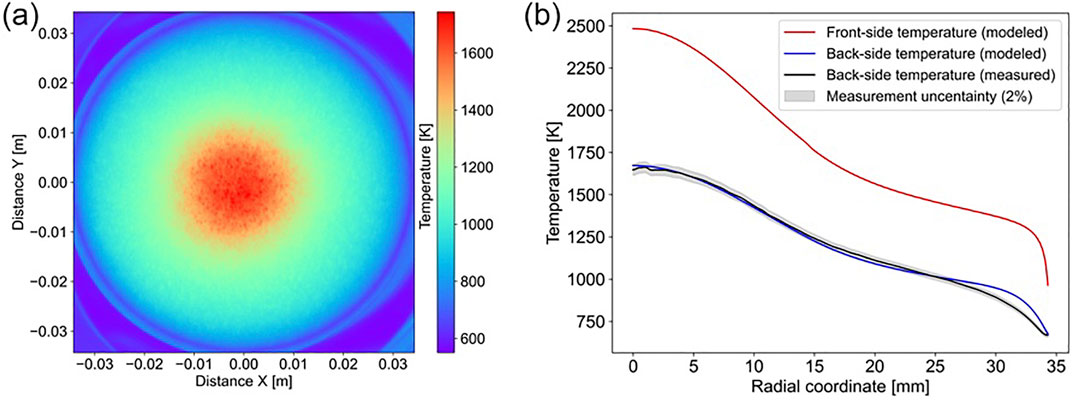
Figure 5. Temperature distributions (A) IR camera temperature contours of the back side of the porous substrate at solar power 1.86 kW, pressure 3.33 kPa, and methane flow rate 100 sccm. (B) Summary of standard case inverse-estimated front-side, back-side and experimentally measured back-side temperatures.

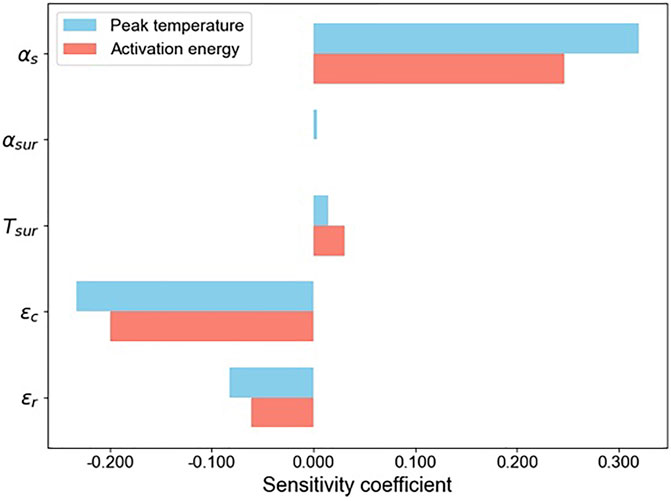
In the inverse heat transfer model, several thermal and optical parameters can influence the estimated temperature. A sensitivity analysis is conducted to quantify the effects of these parameters on the inversely-determined peak front-side temperature, $T_f$, and activation energy, $E_a$, as described by sensitivity coefficients $S_{T_f}$ and $S_{E_a}$, respectively. These two coefficient are obtained from $\pm 10\%$ perturbations around the nominal parameters values using a central difference approach:

$S_{T_f}=\frac{\partial T_f}{\partial P}\frac{P_o}{T_{f,o}}=\frac{T_f\left(P_0+\mathrm{\Delta }P\right)-T_f\left(P_0-\mathrm{\Delta }P\right)}{2\mathrm{\Delta }P}\frac{P_0}{T_{f,o}}(20)$

$S_{E_a}=\frac{\partial E_a}{\partial P}\frac{P_o}{E_{a,o}}=\frac{E_a\left(P_0+\mathrm{\Delta }P\right)-E_a\left(P_0-\mathrm{\Delta }P\right)}{2\mathrm{\Delta }P}\frac{P_0}{E_{a,o}}(21)$

where $P$ is the parameter to be analyzed including emissivity, absorptivity to solar and surrounding irradiation, and the temperature of the surroundings. $P_o$, $T_{f,o}$ and $E_{a,o}$ are the nominal value of these parameters in Equations 20, 21.

Based on the results summarized in Figure 6, the model is most sensitive to the absorptivity of solar irradiation ${\alpha }_s$, which directly determines the most dominant input energy captured by the substrate. Approximately 8$\%$ deviation in peak temperature and 6$\%$ in activation energy are observed with $\pm 10\%$ perturbation in ${\alpha }_s$. The second most sensitive parameter is the central region emissivity ${\epsilon }_c$, which quantifies the rate of energy the substrate can release into the surroundings from the central part of the substrate. Additionally, the estimated results exhibit weak sensitivities to the emissivity of the rest region ${\epsilon }_r$, surrounding temperature $T_{\mathit{surr}}$, and absorptivity to the surroundings ${\alpha }_{\mathit{surr}}$.

Figure 6

Figure 6. Sensitivity analysis of various parameters in inverse estimation.

To evaluate the influence of finite penetration depth, anisotropic $k$ and chemical reactions. Each of these factors is considered and incorporated into the code to quantify their effects on the temperature profiles. The temperature profiles and differences relative to the standard case are summarized in Figure 7.

Figure 7

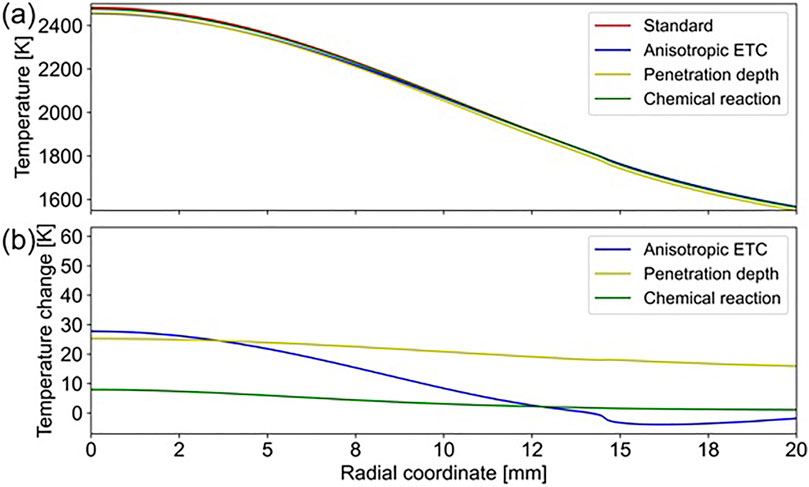
Figure 7. Temperature profiles (A) and differences (B) considering penetration depth, anisotropic $k$ and chemical reaction.

These factors clearly have limited influence on predicted temperatures. The most influential consideration is the anisotropic $k$, at least potentially due to a slightly improved fitting owing to more floating parameters in $k$. As for the penetration depth, this study considers only a simplified case with uniform heat distribution, which can be refined with detailed material characterization and optical analysis in future work. Considering the thin penetration depth applied in this work, its effect on predicted temperature is negligible. The chemical reaction-induced temperature difference is the least significant in part due to the low solar-to-chemical efficiency, which is less than 1% for the conditions considered here (Abuseada, 2022). The approximated parameters in $k$ and peak front-side temperature of the four foregoing cases are summarized in Table 1 below.

Table 1

Table 1. Summary of front-center temperature and inversely-estimated parameters in $k$.

Spatial reaction-zone temperature of the standard case and fiber diameters measured using SEM at different substrate radii are shown in Figure 8A. The deposition rates derived from fiber diameters are further employed to approximate the activation energy of the global direct solar methane pyrolysis experiment through a linear fit (see Figure 8B) (Xu et al., 2024). The resulting activation energy of $E_a=325$ kJ/mol lies in the typical range for thermal methane decomposition (Holmen et al., 1995). The activation energy corresponding to inclusion of more detailed processes in the model as discussed above produce very similar predictions for activation energy: 327 kJ/mol when considering chemical reaction effects, 322 kJ/mol when incorporating penetration depth effects, and 336 kJ/mol when including anisotropic thermal conductivity. Clearly, these more detailed considerations have limited influence on the estimated temperature profile and activation energy.

Figure 8

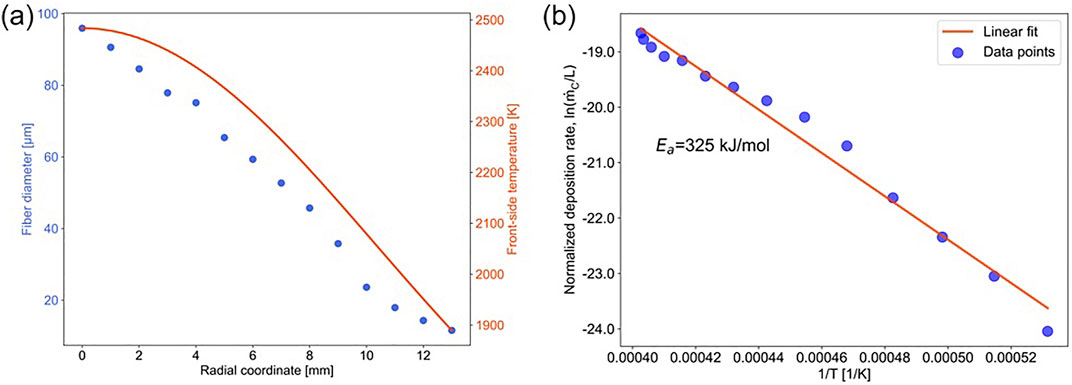
Figure 8. Standard case data and analysis (A) Fiber diameter measurements and estimated spatial reaction-zone temperature. (B) Arrhenius plot and activation energy approximation.

4 Conclusion

In conclusion, we substantiate the application of the inverse method in a fibrous porous medium (FPM) temperature estimation and activation energy approximation of a direct solar-methane pyrolysis reaction. Finite-difference equations are built to solve the heat diffusion equation with assumed isotropic temperature-dependent $k$, and the temperature of the whole FPM domain is obtained. The potential influences of chemical reactions, $k$ anisotropy, and finite penetration depth of the irradiation on the front-side temperature are also considered and quantified to show that these influences are not significant. The activation energy of the global methane pyrolysis reaction is approximated to be 325 kJ/mol based on an simple Arrhenius analysis. Further effort should focus on the direct measurement of the front-side temperature, which is a difficult challenge at such high temperatures with limited optical access, to provide direct validation or potential refinement of the current model.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HX: Conceptualization, Methodology, Writing–original draft, Writing–review and editing, Data curation, Formal Analysis, Investigation, Software, Validation, Visualization. MA: Conceptualization, Investigation, Methodology, Validation, Visualization, Writing–original draft. YJ: Investigation, Methodology, Validation, Formal Analysis, Funding acquisition, Project administration, Supervision, Writing–review and editing. RS: Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Writing–review and editing, Conceptualization, Resources. TF: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–review and editing, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by California Energy Commission (PIR-21-004), the US Department of Energy National Energy Technology Laboratory (DE-FE0032354) and Basic Energy Sciences division (DE-SC0023962). The authors thank the California NanoSystems Institute at UCLA and its Elman Family Foundation Innovation Fund for facilities and initial support.

Acknowledgments

The authors thank Jeff D. Eldredge, Abdalla Alghfeli, Yijun Ge, Indronil Ghosh and Barathan Jeevaretanam of UCLA for their helpful discussions in the process of finishing this work.

Conflict of interest

TF and RS are co-founders of SolGrapH Inc., a company specializing in solar-thermal material synthesis. This submitted work is an independent academic study and is not associated with commercial endeavors or intended as a promotion.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnano.2024.1502539/full#supplementary-material

References

Abanades, S., and Flamant, G. (2007). Experimental study and modeling of a high-temperature solar chemical reactor for hydrogen production from methane cracking. Int. J. Hydrogen Energy 32, 1508–1515. doi:10.1016/j.ijhydene.2006.10.038

CrossRef Full Text | Google Scholar

Abuseada, M., Alghfeli, A., and Fisher, T. S. (2022a). Indirect inverse flux mapping of a concentrated solar source using infrared imaging. Rev. Sci. Instrum. 93, 073101. doi:10.1063/5.0090855

PubMed Abstract | CrossRef Full Text | Google Scholar

Abuseada, M., Spearrin, R. M., and Fisher, T. S. (2023). Influence of process parameters on direct solar-thermal hydrogen and graphite production via methane pyrolysis. Int. J. Hydrogen Energy 48, 30323–30338. doi:10.1016/j.ijhydene.2023.04.198

CrossRef Full Text | Google Scholar

Abuseada, M., Wei, C., Spearrin, R. M., and Fisher, T. S. (2022b). Solar–thermal production of graphitic carbon and hydrogen via methane decomposition. Energy and Fuels 36, 3920–3928. doi:10.1021/acs.energyfuels.1c04405

CrossRef Full Text | Google Scholar

Abuseada, M. M. (2022). Solar-thermal production of hydrogen and graphitic carbon via methane decomposition. Ph.D. thesis. Los Angeles: University of California.

Google Scholar

Al-Ghussain, L. (2019). Global warming: review on driving forces and mitigation. Environ. Prog. and Sustain. Energy 38, 13–21. doi:10.1002/ep.13041

CrossRef Full Text | Google Scholar

Alifanov, O. M. (2012). Inverse heat transfer problems. Germany: Springer Science and Business Media.

Google Scholar

Balat-Pichelin, M., Robert, J., and Sans, J. (2006). Emissivity measurements on carbon–carbon composites at high temperature under high vacuum. Appl. Surf. Sci. 253, 778–783. doi:10.1016/j.apsusc.2006.01.007

CrossRef Full Text | Google Scholar

Bell, I. H., Wronski, J., Quoilin, S., and Lemort, V. (2014). Pure and pseudo-pure fluid thermophysical property evaluation and the open-source thermophysical property library coolprop. Industrial and Eng. Chem. Res. 53, 2498–2508. doi:10.1021/ie4033999

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, Y., and Tsou, R. (1977). Heat conduction in an anisotropic medium homogeneous in cylindrical regions—unsteady state. J. Heat Transf. 99, 41–46. doi:10.1115/1.3450652

CrossRef Full Text | Google Scholar

Chen, Y., Hao, Y., Mensah, A., Lv, P., and Wei, Q. (2022). Bio-inspired hydrogels with fibrous structure: a review on design and biomedical applications. Biomater. Adv. 136, 212799. doi:10.1016/j.bioadv.2022.212799

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, S., and Majumdar, A. (2012). Opportunities and challenges for a sustainable energy future. Nature 488, 294–303. doi:10.1038/nature11475

PubMed Abstract | CrossRef Full Text | Google Scholar

Daryabeigi, K., Cunnington, G. R., and Knutson, J. R. (2011). Combined heat transfer in high-porosity high-temperature fibrous insulation: theory and experimental validation. J. Thermophys. Heat Transf. 25, 536–546. doi:10.2514/1.55989

CrossRef Full Text | Google Scholar

Daryabeigi, K., Cunnington, G. R., and Knutson, J. R. (2013). Heat transfer modeling for rigid high-temperature fibrous insulation. J. Thermophys. Heat Transf. 27, 414–421. doi:10.2514/1.t3998

CrossRef Full Text | Google Scholar

Faghri, A., Zhang, Y., and Howell, J. R. (2010). Advanced heat and mass transfer. Columbia, MO USA: Global Digital Press.

Google Scholar

Farzaneh, M., Ström, H., Zanini, F., Carmignato, S., Sasic, S., and Maggiolo, D. (2021). Pore-scale transport and two-phase fluid structures in fibrous porous layers: application to fuel cells and beyond. Transp. Porous Media 136, 245–270. doi:10.1007/s11242-020-01509-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisher, T. S. (2013). Thermal energy at the nanoscale. Singapore: World Scientific Publishing Co.

Google Scholar

Gao, F., and Han, L. (2012). Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 51, 259–277. doi:10.1007/s10589-010-9329-3

CrossRef Full Text | Google Scholar

Gusarov, A. V., Poloni, E., Shklover, V., Sologubenko, A., Leuthold, J., White, S., et al. (2019). Radiative transfer in porous carbon-fiber materials for thermal protection systems. Int. J. Heat Mass Transf. 144, 118582. doi:10.1016/j.ijheatmasstransfer.2019.118582

CrossRef Full Text | Google Scholar

Hager, N. E., and Steere, R. C. (1967). Radiant heat transfer in fibrous thermal insulation. J. Appl. Phys. 38, 4663–4668. doi:10.1063/1.1709200

CrossRef Full Text | Google Scholar

Holmen, A., Olsvik, O., and Rokstad, O. (1995). Pyrolysis of natural gas: chemistry and process concepts. Fuel Process. Technol. 42, 249–267. doi:10.1016/0378-3820(94)00109-7

CrossRef Full Text | Google Scholar

Kannan, N., and Vakeesan, D. (2016). Solar energy for future world:-a review. Renew. Sustain. Energy Rev. 62, 1092–1105. doi:10.1016/j.rser.2016.05.022

CrossRef Full Text | Google Scholar

Kaviany, M. (2012). Principles of heat transfer in porous media. Germany: Springer Science and Business Media.

Google Scholar

Knapik, E., and Stopa, J. (2018). Fibrous deep-bed filtration for oil/water separation using sunflower pith as filter media. Ecol. Eng. 121, 44–52. doi:10.1016/j.ecoleng.2017.07.021

CrossRef Full Text | Google Scholar

Lakatos, Á. (2020). Investigation of the thermal insulation performance of fibrous aerogel samples under various hygrothermal environment: Laboratory tests completed with calculations and theory. Energy Build. 214, 109902. doi:10.1016/j.enbuild.2020.109902

CrossRef Full Text | Google Scholar

Lee, S., and Cunnington, G. (1998). Heat transfer in fibrous insulations: comparison of theory and experiment. J. Thermophys. Heat Transf. 12, 297–303. doi:10.2514/2.6356

CrossRef Full Text | Google Scholar

Lee, S.-C., and Cunnington, G. R. (2000). Conduction and radiation heat transfer in high-porosity fiber thermal insulation. J. Thermophys. Heat Transf. 14, 121–136. doi:10.2514/2.6508

CrossRef Full Text | Google Scholar

Li, J.-Q., Xia, X.-L., Sun, C., Chen, X., and Wang, Q.-Y. (2024). A multispectral radiometry method for measuring the normal spectral emissivity and temperature. Infrared Phys. and Technol. 136, 105060. doi:10.1016/j.infrared.2023.105060

CrossRef Full Text | Google Scholar

Li, W., Qu, Z., Zhang, B., Zhao, K., and Tao, W. (2013). Thermal behavior of porous stainless-steel fiber felt saturated with phase change material. Energy 55, 846–852. doi:10.1016/j.energy.2013.02.064

CrossRef Full Text | Google Scholar

Lian, X., Tian, L., Li, Z., and Zhao, X. (2024). Thermal conductivity analysis of natural fiber-derived porous thermal insulation materials. Int. J. Heat Mass Transf. 220, 124941. doi:10.1016/j.ijheatmasstransfer.2023.124941

CrossRef Full Text | Google Scholar

Muradov, N. Z., and Veziroğlu, T. N. (2008). “Green” path from fossil-based to hydrogen economy: an overview of carbon-neutral technologies. Int. J. Hydrogen Energy 33, 6804–6839. doi:10.1016/j.ijhydene.2008.08.054

CrossRef Full Text | Google Scholar

Neuer, G. (1992). Emissivity measurements on graphite and composite materials in the visible and infrared spectral range. Paris: QIRT, 92.

Google Scholar

Ozisik, M. N. (2018). Inverse heat transfer: fundamentals and applications. New York: Routledge.

Google Scholar

Patil, V. R., Kiener, F., Grylka, A., and Steinfeld, A. (2021). Experimental testing of a solar air cavity-receiver with reticulated porous ceramic absorbers for thermal processing at above 1000 °C. Sol. Energy 214, 72–85. doi:10.1016/J.SOLENER.2020.11.045

CrossRef Full Text | Google Scholar

Ren, Q., Wang, Z., Lai, T., Zhang, J., and Qu, Z. (2021). Conjugate heat transfer in anisotropic woven metal fiber-phase change material composite. Appl. Therm. Eng. 189, 116618. doi:10.1016/j.applthermaleng.2021.116618

CrossRef Full Text | Google Scholar

Song, H., Meng, X., Wang, Z.-j., Liu, H., and Ye, J. (2019). Solar-energy-mediated methane conversion. Joule 3, 1606–1636. doi:10.1016/j.joule.2019.06.023

CrossRef Full Text | Google Scholar

Sun, L., Wang, Y., Guan, N., and Li, L. (2020). Methane activation and utilization: current status and future challenges. Energy Technol. 8, 1900826. doi:10.1002/ente.201900826

CrossRef Full Text | Google Scholar

Tang, X., and Yan, X. (2017). Acoustic energy absorption properties of fibrous materials: a review. Compos. Part A Appl. Sci. Manuf. 101, 360–380. doi:10.1016/j.compositesa.2017.07.002

CrossRef Full Text | Google Scholar

Tong, T., and Tien, C. (1980). Analytical models for thermal radiation in fibrous insulations. J. Therm. Insulation 4, 27–44. doi:10.1177/109719638000400102

CrossRef Full Text | Google Scholar

Trommer, D., Hirsch, D., and Steinfeld, A. (2004). Kinetic investigation of the thermal decomposition of CH₄ by direct irradiation of a vortex-flow laden with carbon particles. Int. J. Hydrogen Energy 29, 627–633. doi:10.1016/j.ijhydene.2003.07.001

CrossRef Full Text | Google Scholar

Vallabh, R., Banks-Lee, P., and Seyam, A.-F. (2010). New approach for determining tortuosity in fibrous porous media. J. Eng. Fibers Fabr. 5, 155892501000500302. doi:10.1177/155892501000500302

CrossRef Full Text | Google Scholar

Xiao, B., Wang, W., Zhang, X., Long, G., Fan, J., Chen, H., et al. (2019). A novel fractal solution for permeability and kozeny-carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 349, 92–98. doi:10.1016/j.powtec.2019.03.028

CrossRef Full Text | Google Scholar

Xu, H., Abuseada, M., Ju, Y. S., Spearrin, R. M., and Fisher, T. S. (2024). Local thermochemical mechanisms in direct solar graphite synthesis from methane. Energy and Fuels 38, 18087–18089. doi:10.1021/acs.energyfuels.4c03327

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, S., Hunt, A., and Greif, R. (1995). Geometric structure and thermal conductivity of porous medium silica aerogel. J. Heat Transf. 117, 1055–1058. doi:10.1115/1.2836281

CrossRef Full Text | Google Scholar