Dynamic in situ control of heat rectification in graphene nano-ribbons using voltage-controlled strain

An increasing number of papers propose routes to implement thermal counterparts of electronic rectification. These schemes are mainly based on combinations of crystal anharmonicity and broken mirror symmetry. With respect to graphene, proposals pivot around shape asymmetry induced by using hetero-structures of nano-patterned or defected sections of pristine graphene. Using Molecular Dynamics (MD) we show that it suffices to split a graphene nano-ribbon into two unequal strained sections using external force which leads to large asymmetry in the forward and reverse heat fluxes. We find that the corresponding rectification ratio is enhanced by up to 60%. Also, and more importantly, the polarity is controllable on-the-fly i.e., by changing the position where the force is applied. Based upon our results we propose a thermo-electric device which obviates the complex nano-patterning and lithography required to pattern graphene every time a new rectification value or sign is sought for, opening a route to simpler fabrication and characterization of phononic phenomena in 2D materials.

1 Introduction

Graphene is currently a prime candidate material for micro-scale and nano-scale heat management applications Cahill et al. (2014) due to its exceptional thermal conductivity Huang et al. (2021); Chen et al. (2020); Pop et al. (2012); Nika and Balandin (2012); Balandin (2011); Li and Zhang (2013). By nanoscale patterning or shaping, the material properties can be tailored to suit particular demands. In the context of thermal transport, this pattering is done to locally modify the phonon dispersion relation Hu et al. (2016) and the corresponding research area, phononics, is sharply on the rise Maldovan (2013); Li et al. (2012). Phononics aims at engineering devices to control transport and detect phonons (heat carriers) in the same way electrons carry information in electronics. Just as the semiconductor diode paved the way for integrated electric circuitry, efforts to construct efficient acoustic and thermal diodes aim at a similar revolution in phononics Maldovan (2013); Zhu et al. (2018); Zhang et al. (2022).

In a thermal diode, or rectifier, the magnitude of the heat flux resulting from a temperature difference applied at the two terminals differ depending on which terminal is the hotter Li et al. (2012); Shih et al. (2015). An important figure of merit is the rectification ratio, $RR$, defined as the relative difference between these two heat fluxes (currents) or $RR=(J^{+}-J^{-})/J^{-}$ in which $J^{+}$ and $J^{-}$ are left to right (forward) and right to left (reverse) heat fluxes, respectively. However, in contrast to acoustic diode proposals, which mostly rely on single-mode phononic analogs of photonic crystals, the implementation of thermal diodes is not as straightforward. This is because heat is carried by a wide spectrum of phonon modes.

The necessary conditions for a device to display rectification are nonlinearity of the inter-atomic potential and broken mirror symmetry. If this leads to a temperature dependent mismatch of the vibrational density of states (vDOS) between the left and right regions, thermal rectification may ensue. Achieving this condition is easy by attaching two pieces of bulk solid materials with different dependence of their thermal conductivity to the temperature. An example is a junction of bulk pristine crystal to an alloyed or amorphous variant of that in Kobayashi et al. (2009). However, inducing asymmetry and difference in vDOS in the same material needs extra measures. Most proposals relating to carbon nanotubes Wu and Li (2007); Ni et al. (2011), graphene, and other 2D materials have thus so far focused on asymmetry in (a) the number of layers, (b) internal geometry, (c) external or edge shape, (d) material (hetero structure), and (e) asymmetry due to defect i.e., pristine-defective junctions. Implementing heat rectifying devices using the above methods may be very hard to realize, even if it shows promising $RR$ in theory. For a few examples of the above-mentioned devices see Yang et al. (2009); Hu et al. (2017); Hu et al., (2009); Xu et al. (2014); Wang et al. (2014).

Here we show that simply using two weakly connected graphene ribbon segments of unequal length can provide sufficient mismatch of vDOS for significant thermal rectification to emerge. We attribute this to the temperature dependency of the vDOS which emanates from the non-linearity of atomic potentials as well as the length difference which leads to different amount of mechanical strain applied to each section. This will result in different vDOS overlaps for thermal bias in the forward and the backwards directions, which in turn leads to a highly asymmetric flow of heat. Chief among our results is that the rectification ratio and its sign can be adjusted by changing the length of the short and long nano-ribbon sections on-the-fly using electric field-induced strain. An array of electrodes patterned under the free standing graphene controls the point of force application. The point of applying force (strain) acts as the third terminal of the device and causes breaking the symmetry of heat flow. Our proposed principle is akin to applying a normal magnetic field to a two-terminal two-dimensional electron gas (2DEG) device and breaking the time-reversal symmetry and causing non-reciprocity in electric current. The value of $RR$ can reach up to 60% which is comparable or better than some of the proposals based on more elaborate nano-patterning of graphene by defects [See Malik and Fobelets (2022); Zhao et al. (2022)].

The reported values of $RR$ vary among different works. For example, in graphene-based devices this changes from 6% Yousefi et al. (2020a) to 2,580% Yang et al. (2018). Partly, this depends on how the rectification ratio is defined, what is the base temperature, and how much is the applied temperature gradient or bias across the junction. Also some definition of $RR$ are based on the difference of thermal conductivity $\mathrm{\Delta }\kappa ={\kappa }^{+}-{\kappa }^{-}$ rather than the heat flux difference $(\mathrm{\Delta }J=J^{+}-J^{-})$. Roberts and Walker (2011), Malik and Fobelets (2022), and Zhao et al. (2022) have reviewed the theoretical and experimental works on heat rectification in solid and 2D materials and listed the achieved $RR$ in detailed tables. While some numbers in these tables show very promising values, it must be remembered, that these predictions assume nano-fabrication with high tolerances, and may thus be sensitive to structural changes on the nanometer scale. Also the reported $RR$ values are not adjustable after the fabrication of the device. Furthermore, we here prefer to use a more conservative definition of $RR$ defined as $|J^{+}-J^{-}|/\mathrm{m}\mathrm{a}\mathrm{x}(J^{+},J^{-})$. This makes $RR$ insensitive to direction and confines it to an interval between zero and unity, where $RR=0$ means no rectifying behavior and $RR=1$ implies completely unidirectional transport.

The remainder of this paper is organized as follows. In the next section the molecular dynamics calculations using LAMMPS package and post-processing steps are explained. To demonstrate that thermal rectification can be achieved without detailed nano-patterning, we consider a simple thermal junction composed of a short and a long graphene nano-ribbon connected via a thermal weak link, and review the basic physical explanation of the origin of this effect in terms of temperature dependent vDOS-overlap. Although we can attribute the effect to the behavior of the overlap of the vDOS, we show that the conventional measure of the overlap is here too simple to quantitatively explain the large observed rectification. Thereafter, we present a simplified system made adjustable using an external force due to applied DC voltage. This showcase the role of the third terminal and the mechanical strain which causes symmetry breaking in analogy to the normal magnetic field applied to 2DEG layer. The success of every proposed scheme to achieve heat rectification depends on how much strain is induced in each section of the heat diode. We proved that strain enhances the Umklapp process or down-conversion of phonons and this modifies the low-frequency portion of the vDOS Shiri and Isacsson (2019).

2 Methods

The molecular dynamics simulation is performed using LAMMPS package Plimpton (1995). The graphene nano ribbons are of rectangular shape in zigzag direction and their widths and lengths are (22 nm and 22 nm) and (10 nm and 100 nm), respectively along $x$ and $y$ directions. The size of the simulation box along the $z$ direction is $\pm$50 Å to avoid interaction of the graphene ribbon with its periodic replica along the $z$ direction. The ribbon is built with ATOMSK code Hirel (2015) starting from a unit cell made of four carbon atoms cut from the upper half of a carbon hexagonal ring. The metal unit is chosen. The molecular dynamics simulation flow is divided into the following sequential steps.

$•$ energy minimization The energy of the ribbon is minimized under periodic boundary conditions in all directions using Conjugate Gradient (CG) algorithm with box/relax command. The Tersoff three-body potential by Lindsay and Broido (2010) which is modified for heat transport in graphene is used. The integration time step is 0.5 fs.

$•$ NPT To achieve the equilibration temperature with zero pressure, the NPT ensemble is used together with Nosé-Hoover thermostat and barostat for time duration of 500 ps or 1 million steps. The time constants, $\tau$, for temperature and pressure settling are 0.05 and 0.5, respectively.

$•$ NVT Another round of NVT ensemble i.e., constant volume and temperature is used for 500 ps −1 ns while both ends of graphene nano ribbons are fixed using zero force and velocity at all time steps. The fixed edges are 10 Å wide stripes of atoms and are called Hot and Cold for which non equilibrium method is applied to sustain a temperature gradient along the ribbon. Both ending edges of the nanoribbon are fixed by fixing their atoms in their equilibrium positions as shown in Figure 1B by brightly-colored atoms. After the fixed layers, there are two 10 Å stipes in which the atoms are placed in Nosé–Hoover thermostat. These so-called Hot and Cold regions are to apply the temperature gradient along the nanoribbon by keeping their temperature fixed at $T_H$ and $T_C$, respectively. To apply the temperature bias, the velocity (momentum) of these atoms is updated according to Equation 1 of Hu et al. (2010).

$•$ BC At this stage the boundary conditions (BC) is changed to fixed the boundary along $x$ direction while keeping the boundary along $y$ to be periodic to avoid the edge effects.

$•$ NVE The NVE (constant energy and volume) ensemble is used for 10 ns for the Middle section which is the nano ribbon excluding fixed, Hot and Cold sections. The temperature of Hot and Cold sections are controlled by Nosé-Hoover thermostats. After the initial 10 ns, heat flux, velocity auto correlation function (VACF), and temperature will be window averaged for every 10,000 steps and the results are recorded for 20 nsec or more depending how good the average of the flux is stabilized around a fixed value.

Figure 1

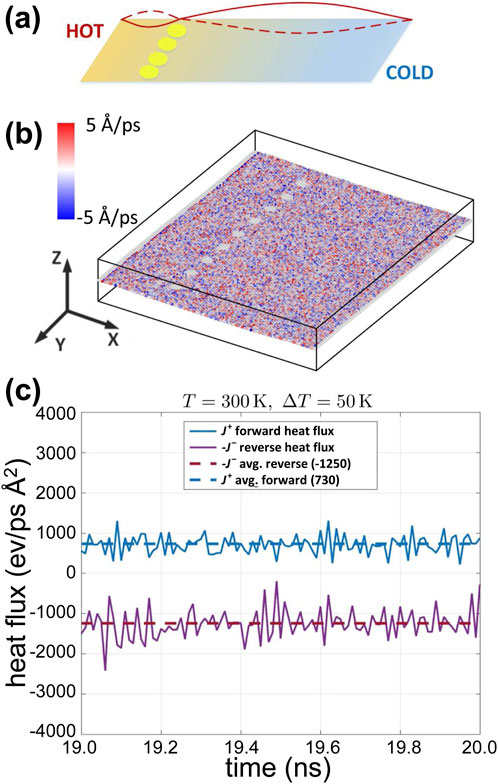
Figure 1. (A) Thermal rectification in an asymmetric graphene junction composed of a short and a long section. (B) Asymmetric junction made from a $22\mathrm{n}\mathrm{m}\times 22\mathrm{n}\mathrm{m}$ graphene sheet clamped at two ends. A phononic junction is formed by an equidistantly spaced array of pinned circular regions having diameter $d=10$ Å. The brightly colored areas are clamped sections, i.e., sections with zero velocity and zero force. (C) Forward $(J^{+})$ and reverse (-$J^{-}$) heat fluxes when biased with ($T_{\mathrm{L}}$, $T_{\mathrm{R}}$) = (350 K, 250 K) and (250 K, 350 K), respectively. A clear rectification behavior is observed i.e., $J^{-}>J^{+}$.

For visualizing purposes e.g., viewing the output geometry at each time step, The OVITO package provided by Stukowski (2010) is used. The vibrational density of states of atoms within a region is calculated from velocity auto correlation function (VACF) which is implemented in LAMMPS. The VACF for each region is recorded in the output file for each time step (e.g., $dt=0.5$ fs). For each component of the atomic velocity there is one column of VACF data which is accessible using [1], [2] and [3] suffixes and [4] is used for the total value of VACF i.e., $⟨v(t)v(0)⟩=⟨v_x(t)v_x(0)⟩+⟨v_y(t)v_y(0)⟩+⟨v_z(t)v_z(0)⟩$. Fourier transforming the VACF in MATLAB returns the vibrational DOS spanning from zero to frequencies around 60 THz for the left and the right side respectively. Finally, the overlap $S$ is defined by Lan and Li (2006) as

$S=\frac{\int DO{S}_{\mathrm{L}}\left(\omega \right)DO{S}_{\mathrm{R}}\left(\omega \right)\mathrm{d}\omega }{\int DO{S}_{\mathrm{L}}\left(\omega \right)\mathrm{d}\omega \int DO{S}_{\mathrm{R}}\left(\omega \right)\mathrm{d}\omega }(1)$

where $\omega$ is phonon frequency and L and R correspond to Left and Right sections of the thermal junction, respectively. To simulate the effect of force it is possible to apply the force (max 0.05 eV/Å) every few time steps to the chosen area using addforce command and this divides the 10 nm$\times$100 nm nano ribbon into long and short sections. Alternatively it is possible to add electric charge of one electron to the atoms of the chosen area and apply electric field along $z$ direction using efield command with a value between 0.01–0.05 V/Å.

3 Junction thermal rectification

We consider first a simple junction geometry as shown in Figures 1A, B, consisting of a 22 nm × 22 nm graphene sheet clamped at two ends, interrupted by a thermal weak link made from an equidistantly-spaced array of pinned circular regions. Using molecular dynamics (MD), the average heat flux flowing through the structure when the two clamped ends are at different temperatures was recorded.

Prior to imposing pinned sections on the graphene nano-ribbon, the thermal conductivity of the graphene sheet is calculated using Non-Equilibrium Molecular Dynamics (NEMD) Hu et al. (2016) for calibration purposes. Immediately after and before the left and right clamped ends, hot and cold regions are kept at 320 K and 280 K, respectively. Calculating the heatflux $J$, the thermal conductivity $\kappa$ is determined from

$J_i=-{\kappa }_{ij}\frac{\partial T}{\partial x_j},$

where $i$ and $j$ are coordinate indices as the heat conductivity is in general a tensor.

Values of ${\kappa }_{xx}=570$ W/m K and ${\kappa }_{xx}=360$ W/m K are obtained using modified Tersoff Lindsay and Broido (2010) and CH-AIREBO Stuart et al. (2000) potentials, respectively. These values are in close agreement with those obtained using MD for graphene nano-ribbons of similar sizes Hu et al. (2010); Guo et al. (2015). As the length of the ribbon is smaller than the intrinsic phonon mean free path (MFP) in graphene, $l_{\mathrm{M}\mathrm{F}\mathrm{P}}=600$ nm Pop et al. (2012), a difference between thermal conductivity of a 22 nm × 22 nm in our model and a 20 nm × 20 nm nano ribbon in Hu et al. (2010) and Guo et al. (2015) is expected. The higher thermal conductivity calculated by using the Tersoff potential is attributed to the stiffer Carbon-Carbon bonding in the Tersoff potential as opposed to the AIREBO potential. Stiffer bonds gives a higher group velocity for acoustic phonons and, consequently, a larger thermal conductivity (Chen et al. (2020)) since

$k=\frac{1}{3}{c}_V{v}_{\mathrm{g}}{l}_{\mathrm{M}\mathrm{F}\mathrm{P}},$

where $c_V$, $v_{\mathrm{g}}$, and $l_{\mathrm{M}\mathrm{F}\mathrm{P}}$ are specific heat, group velocity, and mean free path of phonons in a bulk isotropic solid. Finally, it should be pointed out that classical MD neglects quantum corrections, which can be rather large for graphene due to its large Debye temperature Tewary and Yang (2009); Jiang et al. (2010). However, we are here interested in demonstrating a qualitative phenomenon and derive a ratio between heat-fluxes. Hence, for our purposes, classical MD suffices.

Note that the absolute value of thermal conductivity does not matter for study of heat rectification. What matters is the stress-strain relation and how soon or late the applied force leads to asymmetry in the heat flux. Therefore, we speculate that using CH-AIREBO (soft) potential instead of Tersoff (hard) potential leads to down-shift of frequency contents in VDOS, and it should not change the results qualitatively.

Figure 1C shows the result of simulating the phononic junction of Figures 1A, B where the terminals where kept at temperatures $T_{\mathrm{L}}=350$ K, $T_{\mathrm{R}}=250$ K and vice versa. A clear rectifying behavior with heat fluxes $J^{\pm }$ obeying $J^{-}>J^{+}$ and a rectification ratio of $\approx 41$ % is observed. This rectification ratio corresponds to the 160% ratio of reverse to forward heat fluxes, i.e., $J^{-}/J^{+}=1.6$. Changing the pinning diameters to 20 Å gives similar results. Results for similar simulations at other base temperatures are shown in Table 1. Interestingly, we find values which are strongly temperature dependent and non-monotonic with increasing temperature.

Table 1

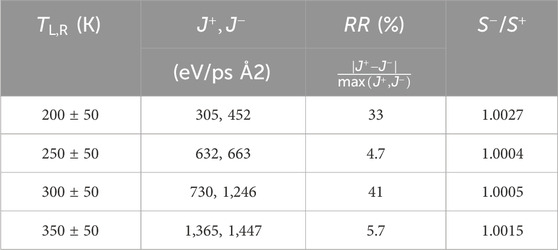
Table 1. Heat fluxes $J^{\pm }$, rectification ratios $RR$ and vDOS overlap ratios [see Equation 1] at different thermal biases and base temperatures for the simple junction system in Figure 1.

To understand the mechanism of rectification in this system, it is instructive to first recall the well studied model of a nonlinear one dimensional chain of oscillators connected by an interface layer (or interface bond) Li et al. (2004); Terraneo et al. (2002); Lepri et al. (1997); Yang et al. (2007) which is shown in Figure 2A. If the elastic properties on the two sides of the junction differ, by using for instance different spring constants and different strength of nonlinear potential, as a result the corresponding density of vibrational modes will differ. In the absence of inelastic scattering, the vDOS must have an overlap for phonons to cross the junction. Following the discussion of Benenti et al. (2016) and Li et al. (2004) we consider a system which is composed of two sections modeled as atoms connected by springs, and a Hamiltonian $H=H_{\mathrm{L}}+H_{\mathrm{R}}$. The left and right sections are weakly linearly coupled with a single link $k_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k}}$ yielding a total Hamiltonian $H=H_{\mathrm{L}}+H_{\mathrm{R}}+H_{\mathrm{i}\mathrm{n}\mathrm{t}}$. The necessary nonlinearity is introduced through adding a Frenkel-Kontorova (FK) co-sinusoidal potential to each section as shown by Li et al. (2004) which results in

$\begin{array}{ccc}\hfill H_{\mathrm{L},\mathrm{R}}& =\hfill & {\displaystyle \sum _i}\left[\frac{P_i^2}{2m_i}+\frac{1}{2}{k}_{\mathrm{L},\mathrm{R}}{\left(x_i-x_{i+1}-a\right)}^2\right.\hfill \\ \hfill & \hfill & -\left.\frac{V_{L,R}}{{\left(2\pi \right)}^2}\cos \left(2\pi x_i\right)\right].\hfill \end{array}$

Figure 2

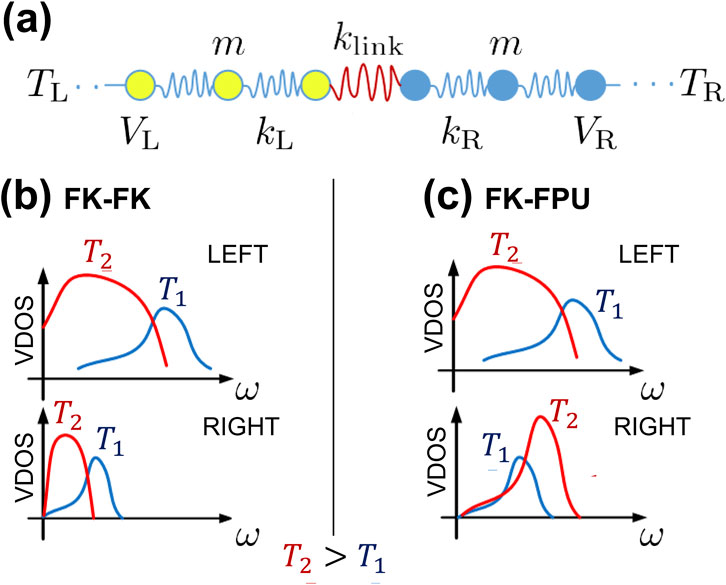
Figure 2. (A) One dimensional model of a thermal junction composed of lattices with different potentials joined by a weak link modelled as a spring with stiffness $k_{\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k}}$. (B) When both potentials are of Frenkel-Kontorova (FK) type, stiffer springs and deeper potential for the left section lead to different spectrum for the left section compared to the right. Although for both sections the spectra are red-shifted with increasing temperature, they do so at different rates and in frequency ranges. This leads to asymmetry in the overlap of the vDOS. For example, if $T_{\mathrm{L}}=T_2>T_{\mathrm{R}}=T_1$, there is a larger overlap hence $J^{+}>J^{-}$. (C) When the right hand lattice is modelled by Fermi-Pasta-Ulam (FPU) potential. Since the temperature behavior of the FPU is opposite to that of the FK potential, frequency shifts are in opposite directions with temperature, thereby enhancing further the rectification ratio $RR$.

Here $V_{\mathrm{L},\mathrm{R}}$ are the depths of the FK potential, $x_i$ and $a$ are atom positions and the lattice constant, respectively.

Rectifying behavior requires a combination of nonlinearity and broken symmetry. Symmetry breaking is obtained by setting $V_{\mathrm{L}}>V_{\mathrm{R}}$ and $k_{\mathrm{L}}>k_{\mathrm{R}}$. This means that the atoms in the left section are connected by stiffer springs and are exposed to a deeper FK potential as opposed to the right section. The FK-potential is a softening potential, i.e., high amplitude vibrations have lower frequencies than low amplitude ones. Hence, at low temperatures they oscillate with higher frequencies than at high temperatures. With increased temperatures the vDOS moves toward lower frequencies [see Figure 2B]. The same trend exists for the right section of the junction however with different rate as well as different frequency. As springs on the right are softer than those on the left, the vDOS on the left is predominantly covering lower frequencies. This explains why for $T_R>T_L$ the vDOS overlap is smaller than when $T_{\mathrm{R}}<T_{\mathrm{L}}$ [see Figure 2B].

To enhance the rectification, it is favorable to use hardening and softening potentials on either sides. An example is to replace the FK-potential in the right with a Fermi-Pasta-Ulam (FPU) type system. The nonlinearity in the FPU-$\beta$ model is an extra anharmonic term like $\beta x^4$ in the Hamiltonian with $\beta >0$. Due to this term, the behavior of the vDOS with temperature is opposite on the right and left sides. Hence, for an FPU-$\beta$ potential Lan and Li (2006) the increase of temperature shifts the spectrum to higher frequencies according to $\omega \propto {(\beta T)}^{1/4}$. This means that vDOS of the left and right sections of the thermal junction move in opposite directions with increasing temperatures and, consequently, enhance the thermal rectification [see Figure 2C].

We now return to the 2D-system of Figure 1. We consider the area with pinned circles as the weak link between the left and right sections creating the symmetry breaking. To test if the rectification mechanism is similar to the 1D-systems we have studied the vDOS $D_{\mathrm{L},\mathrm{R}}(\omega )$ corresponding to the left and right sections of the nano ribbon at different temperatures (Figure 3).

Figure 3

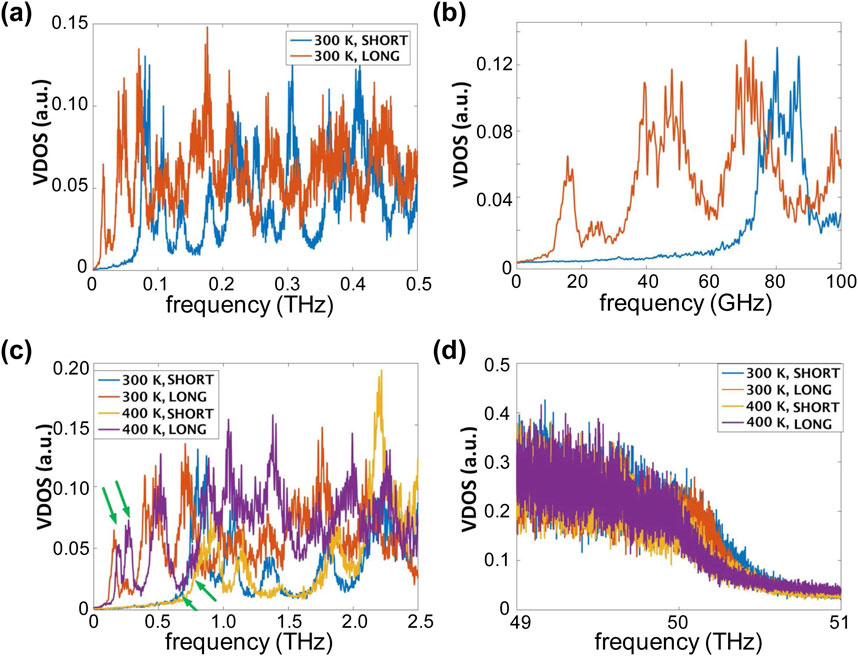
Figure 3. Low frequency density of vibrational states for temperatures of 300 K and 400 K. (A) Spectra for long and short sections of device at 300 K, (B) Magnified section of the spectra shown at (A) for 0–100 GHz frequency range. (C) Spectra for both sections at 300 K and 400 K revealing stiffening of the sections by increasing the temperature which is manifested as frequency up shift (marked by arrows), and (D) the high frequency section of the spectra from 49 THz to 51 THz shows softening of the optical phonon modes, hence a frequency down shift is observed for both sections by increasing the temperature.

First we inspect the low-frequency part of $D(\omega )$, as shown in Figure 3 for the two sections at $T=300$ K in panels (a) and (b). As anticipated, and in contrast to the case of spring-mass models where the spring constant determines the bottom of the band, here the lateral confinement will determine the band bottom. Indeed, regardless of temperature, the left section (short) is gapped from 0 GHz to 58 GHz, while the right (long) section supports pronounced low frequency modes from 10 GHz and upwards. Hence, we can identify the longer (right) side with the soft-spring part and the short side (left) with the stiff-spring part.

Figure 3C shows how the acoustic parts of the spectra shifts with changing temperature for both sides. For these low frequency portions of the spectra, increasing the temperature causes blue-shift to higher frequencies, which resembles the way in which FPU-$\beta$ model behaves Lan and Li (2006). The nonlinearities responsible for this comes partly from non-linearity of the Tersoff many-body potential Lindsay and Broido (2010) itself. Partly, it can be attributed to the negative thermal contraction of graphene which stiffens the acoustic ZA-modes. This leads to a situation akin to the FK-FK situation in Figure 2B where both spectra shift in the same direction but by unequal amounts. Qualitatively we indeed find agreement that $J^{-}>J^{+}$ for all investigated cases listed in Table 1.

Although giving little contribution to the thermal transport, the high-frequency part of $D_{\mathrm{L},\mathrm{R}}(\omega )$, corresponding to the optical phonon branches, is shown in Figure 3D. Here the short section supports high frequency modes up to 50.7 THz even at 50 K. However, by increasing the temperature from 300 K to 400 K we observe a gradual shift to lower frequencies e.g., 50 THz. The same trend is true for the long (right) section of the ribbon although the modes have generally lower frequency spanning from 50 THz to 50.4 THz. This is consistent with the observed red shift of the G-peak in Raman measurements, and suggests that increased temperature causes softening of the optical modes and reduction of group velocity due to tensile strain build-up Hong et al. (2016); Wei et al. (2011).

As a measure of the degree of overlap, Li et al. (2005) defined a phenomenological quantity $S$ as the vDOS overlap which was shown in Equation 1 and relates to the rectification ratio by comparing $J^{-}/J^{+}$ to $S^{-}/S^{+}$. To quantitatively support the above mentioned arguments we have calculated the ratio $S^{-}/S^{+}$ according to Equation 1 for the simulations presented in Table 1. We obtain $D_{\mathrm{L},\mathrm{R}}$ from using the velocity auto correlation function (see section 2). Qualitatively we find, in agreement with the simulated heat fluxes, that the overlap is always larger when $T_{\mathrm{R}}>T_{\mathrm{L}}$. This is reflected in Table 1 as $S^{-}/S^{+}>1$. However, we find no other quantitative correlations between $S^{-}/S^{+}$ and $RR$. This is hardly surprising, considering the inclusion and thermal shift of optical modes in the calculation as well as the presence of localized modes in the spectra which may contribute to $S$ but not to $J$. Hence, we conclude that the overlap $S$ alone is not sufficient to quantify the rectifying behavior.

4 Adjustable heat rectification

Based on the above method of dividing a nano-ribbon into a short and long section, we here propose a simpler design with two distinct advantages to other proposals. Instead of partitioning the ribbon in two sections by pinning, we consider applying a force to the nano-ribbon in an asymmetric fashion. The applied force could emanate from sources like mechanical actuation [e.g., piezoelectricity, Atomic Force Microscopy (AFM) tip Hod and Scuseria (2009), Scanning Tunneling Microscopy (STM) tip Neek-Amal et al. (2014)] or electrical force due to an electric field from a local back-gate. The first advantage is that no explicit nano-patterning is needed. The second, and more important advantage, is that changing the position and magnitude of the applied force allow for in situ reconfiguration and control of the rectification.

Specifically we envision a setup here as shown in Figure 4 which is similar to the experimental setup already used to modulate the electron transport properties in carbon nanotubes by Benyamini et al. (2013). Applying electric field to the selected electrode can divide the nano-ribbon into a short and long section. Here a proof of concept molecular dynamics simulation is performed to demonstrate the rectification as a result of force-induced asymmetry.

Figure 4

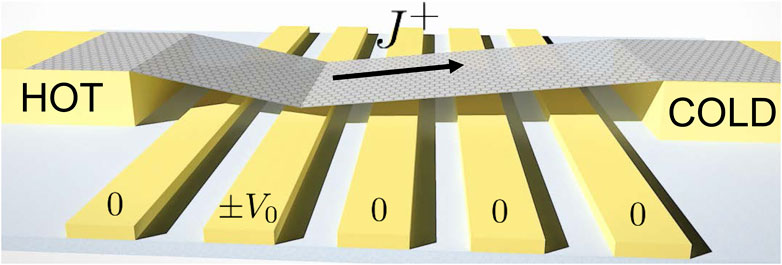
Figure 4. Proposal for a tunable thermal diode where the sign and value of rectification ratio is controlled by applying electric field to the chosen gate electrode underneath a thermally biased graphene nano-ribbon.

Figure 5A, shows a simulation set-up of a 10 nm × 100 nm nano-ribbon, in which a force is locally applied along the $z$-direction to a narrow strip causing deflection. The asymmetric application of the force divides the strip into a long and short section with unequal tensile stresses. The magnitude of forces used in the simulations are of the order nN (nano Newton), characteristic for nano-electromechanical devices. The diode sign in Figure 5 shows the heat rectification direction.

Figure 5

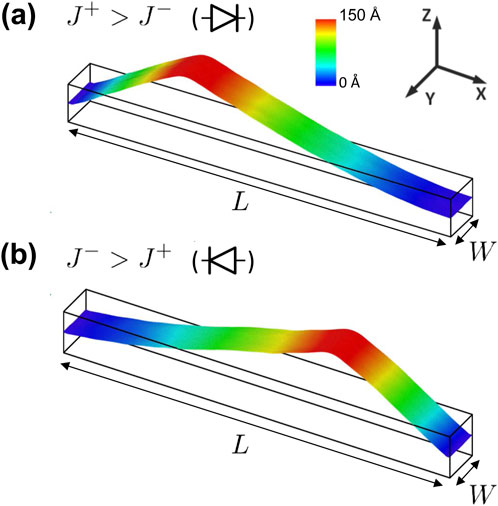
Figure 5. Adjustable heat rectification by asymmetric application of electric field-induced force to a graphene nano ribbon of dimensions $L=100$ nm and $W=10$ nm. (A) Schematic shows the rectification direction of the heat diode when the force is applied to the left section. (B) When the force is applied to the right section, rectification direction is reversed. With the proposed setup in Figure 4 it is thus possible to realize an in situ re-configurable thermal rectifier.

The recorded values of average heat fluxes are shown in Table 2 and they suggest rectification ratios of 35% and 42% for temperature/gradient values of $300\mathrm{K}\pm 100\mathrm{K}$ and $300\mathrm{K}\pm 50\mathrm{K}$, respectively. If the position of force is changed and it is moved to the right side as in Figure 5B, the same values as above are obtained for the rectification ratios however, with the reversed sign. As for the junction rectifier, we also changed the base temperature to 200 K and 400 K respectively. As can be seen from Table 2, the value of the rectification ratio changes. In case of $T_{\mathrm{L},\mathrm{R}}=400\mathrm{K}\pm 50\mathrm{K}$ and $T_{\mathrm{L},\mathrm{R}}=200\mathrm{K}\pm 50\mathrm{K}$, the $RR$ values are 60% and 22%, respectively. The enhanced $RR$ at higher temperature is due to stiffening of acoustic phonon branches which leads to more strain and more VACF asymmetry.

Table 2

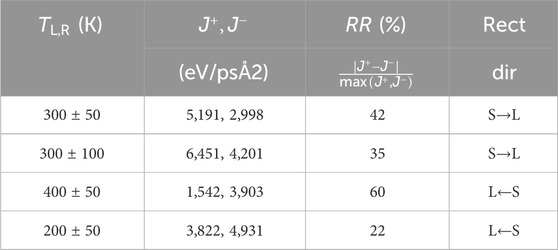
Table 2. Heat fluxes $J^{\pm }$, rectification ratios $RR$ and rectification direction (Short$\to$ Long) for the tunable configuration in Figure 5. The top two rows correspond to configuration in panel (a), while the bottom two correspond to panel (b).

To verify that the rectification is indeed induced from asymmetric length of the nanoribbon section, we also applied the force symmetrically, dividing the ribbon into two equal partitions. The resulting flux differences for the imposed temperature differences of $\mathrm{\Delta }T=50\mathrm{K}$ and $\mathrm{\Delta }T=100\mathrm{K}$ corresponded to $RR=6$ % and $RR=1$ %, respectively. This corroborates that the large asymmetry in the values of heat flux indeed stems from the strain-induced asymmetry in the nanoribbon. The significance of this work lies in its flexibility in changing the value and sign of heat rectification without resorting to a newly nano-patterned and/or functionalized graphene. It is also possible to generalize the proposed principle to other two-dimensional materials using not only the electric field but also the magnetic field with proper electrode design e.g., electrodes shaped as current loops under the free standing 2D material.

In the simulation setup the graphene nanoribbon is periodic along the width direction, which means that changing the width of the nanoribbon does not affect the results. In a real device, the change of width leads to a change of thermal conductivity because phonon branches contribute more to heat conduction. However, in this study, the focus is on effect of asymmetry to rectification, and the absolute value of the thermal conductivity does not matter. However, the change of length needs careful study. For a short nanoribbon, the applied force (stress) leads to larger strain value as both asymmetric parts suffer more length change. For a longer nanoribbon, the same force leads to less deflection and less strain as a result. This means that the same rectification ratio requires more applied force (voltage). With respect to the edge type, it was shown that the zigzag edge along the length of the nanoribbon has more stretchability than the armchair edge. For strain values under 20% the stress-strain plot of graphene is the same for both types of edges, and the difference appears for strain values above 30% in which zigzag shows more robustness. Thus, for a device proposed in our work, if the strain is below 20% both edge types perform equally in terms of heat rectification.

5 Conclusion

Based on molecular dynamics studies of non equilibrium heat transport in graphene nano-ribbons we showed that the thermal rectification ratio can be simply adjusted both in value and sign using a force to divide the graphene into strained long and short sections. Starting from a simple structure in which long and short sections are weakly linked by pinned areas, we showed how this partition lead to the necessary temperature dependent asymmetric vibrational density of states required for thermal rectification.

The importance of this observation and the proposal of Figure 4 is reflected in the simplicity in implementing an in situ tunable heat diode, as exemplified by using an array of local back gates which can selectively induce asymmetric stress in a suspended graphene membrane. Our findings show that the values of heat flux and the rectification ratio can be controlled on-the-fly while the device is operating. Consequently, to achieve rectification it is not necessary to fabricate elaborate asymmetric shapes, i.e., patterning arrays of holes, defects, inducing grain boundaries or the requirement of making a hetero-structure Hong et al. (2016) of pristine graphene with other kinds of graphene [multi-layer Zhang and Zhang (2011); Xu et al. (2014), defected Wang et al. (2012), patterned Yang et al. (2009); Hu et al. (2009); Hu et al., (2017); Wang et al. (2014)], etc. Thus, the combination of simplicity of implementation, and tunability of rectification ratio and sign, opens up for more controlled experiments and developments in the field of 2D-phononics.

Fabricating of gate arrays is a standard process for study of spin-based qubits in semiconducting nanowires and it is CMOS-compatible and is scalable to two dimensions. It was also used to study electron transport in quantum dots formed in a long carbon nanotube [See Benyamini et al. (2013)]. This process is much simpler than creating sophisticated patterns in graphene e.g., arrays of hexagonal holes, tapering the graphene with atom precision, or making graphene multilayer using CNT pillars as proposed in other theoretical works [See Yousefi et al. (2020b); Malik and Fobelets (2022); Zhao et al. (2022)].

In our study the applied voltage (force) is static although the place of the electrode can be changed in situ, however after the things are settled the same static mechanism explained here is valid. We did not study the role of dynamic (time-dependent) forces for example, applied sinusoidal voltage (force) on the heart rectification. As graphene is a nonlinear system, application of an external tone leads to mixing of different phonon modes and generation of different harmonics in VDOS. De Alba et al. (2016) et al. have shown that by applying sinusoidal force using back gate to a graphene disk, it is possible to parametrically amplify or de-amplify a vibrational mode. A recent theoretical study was brought to our attention in which the rectification ratio of 120% is achieved by application of strain gradient to a graphene nanoribbon Sai Kavuri and Sathian (2024).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DS: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Visualization, Writing–original draft, Writing–review and editing. AI: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Resources, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors greatly acknowledge access to the Swedish National Infrastructure for Computing (SNIC) and the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725. The computations were also enabled by resources provided by Chalmers e-Commons at Chalmers.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Balandin, A. A. (2011). Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 10, 569–581. doi:10.1038/nmat3064

PubMed Abstract | CrossRef Full Text | Google Scholar

Benenti, G., Casati, G., Mejía-Monasterio, C., and Peyrard, M. (2016). From thermal rectifiers to thermoelectric devices. Switzerland: Springer International Publishing, 365–407. doi:10.1007/978-3-319-29261-8_10

CrossRef Full Text | Google Scholar

Benyamini, A., Hamo, A., Kusminskiy, S. V., von Oppen, F., and Ilani, S. (2013). Real-space tailoring of the electron-phonon coupling in ultraclean nanotube mechanical resonators. Nat. Phys. 10, 151–156. doi:10.1038/nphys2842

CrossRef Full Text | Google Scholar

Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Fan, S., Goodson, K. E., et al. (2014). Nanoscale thermal transport. ii. 2003–2012. Appl. Phys. Rev. 1, 011305. doi:10.1063/1.4832615

CrossRef Full Text | Google Scholar

Chen, X.-K., Zeng, Y.-J., and Chen, K.-Q. (2020). Thermal transport in two-dimensional heterostructures. Front. Mater. 7. doi:10.3389/fmats.2020.578791

CrossRef Full Text | Google Scholar

De Alba, R., Massel, F., Storch, I. R., Abhilash, T. S., Hui, A., McEuen, P. L., et al. (2016). Tunable phonon-cavity coupling in graphene membranes. Nat. Nanotechnol. 11, 741–746. doi:10.1038/NNANO.2016.86

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, T., Sha, Z.-D., Liu, X., Zhang, G., Guo, T., Pei, Q.-X., et al. (2015). Tuning the thermal conductivity of multi-layer graphene with interlayer bonding and tensile strain. Appl. Phys. A 120, 1275–1281. doi:10.1007/s00339-015-9373-z

CrossRef Full Text | Google Scholar

Hirel, P. (2015). Atomsk: a tool for manipulating and converting atomic data files. Comput. Phys. Commun. 197, 212–219. doi:10.1016/j.cpc.2015.07.012

CrossRef Full Text | Google Scholar

Hod, O., and Scuseria, G. E. (2009). Electromechanical properties of suspended graphene nanoribbons. Nano Lett. 9, 2619–2622. doi:10.1021/nl900913c

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, Y., Zhang, J., and Zeng, X. C. (2016). Thermal contact resistance across a linear heterojunction within a hybrid graphene/hexagonal boron nitride sheet. Phys. Chem. Chem. Phys. 18, 24164–24170. doi:10.1039/C6CP03933B

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J., Ruan, X., and Chen, Y. P. (2009). Thermal conductivity and thermal rectification in graphene nanoribbons: a molecular dynamics study. Nano Lett. 9, 2730–2735. doi:10.1021/nl901231s

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J., Schiffli, S., Vallabhaneni, A., Ruan, X., and Chen, Y. P. (2010). Tuning the thermal conductivity of graphene nanoribbons by edge passivation and isotope engineering: a molecular dynamics study. Appl. Phys. Lett. 97, 133107. doi:10.1063/1.3491267

CrossRef Full Text | Google Scholar

Hu, S., An, M., Yang, N., and Li, B. (2016). Manipulating the temperature dependence of the thermal conductivity of graphene phononic crystal. Nanotechnology 27, 265702. doi:10.1088/0957-4484/27/26/265702

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., An, M., Yang, N., and Li, B. (2017). A series circuit of thermal rectifiers: an effective way to enhance rectification ratio. Small 13, 1602726. doi:10.1002/smll.201602726

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, P., Li, Y., Yang, G., Li, Z.-X., Li, Y.-Q., Hu, N., et al. (2021). Graphene film for thermal management: a review. Nano Mater. Sci. 3, 1–16. doi:10.1016/j.nanoms.2020.09.001

CrossRef Full Text | Google Scholar

Jiang, J.-W., Lan, J., Wang, J.-S., and Li, B. (2010). Isotopic effects on the thermal conductivity of graphene nanoribbons: localization mechanism. J. Appl. Phys. 107, 054314. doi:10.1063/1.3329541

CrossRef Full Text | Google Scholar

Kobayashi, W., Teraoka, Y., and Terasaki, I. (2009). An oxide thermal rectifier. Appl. Phys. Lett. 95, 171905. doi:10.1063/1.3253712

CrossRef Full Text | Google Scholar

Lan, J., and Li, B. (2006). Thermal rectifying effect in two-dimensional anharmonic lattices. Phys. Rev. B 74, 214305. doi:10.1103/PhysRevB.74.214305

CrossRef Full Text | Google Scholar

Lepri, S., Livi, R., and Politi, A. (1997). Heat conduction in chains of nonlinear oscillators. Phys. Rev. Lett. 78, 1896–1899. doi:10.1103/PhysRevLett.78.1896

CrossRef Full Text | Google Scholar

Li, B., Lan, J., and Wang, L. (2005). Interface thermal resistance between dissimilar anharmonic lattices. Phys. Rev. Lett. 95, 104302. doi:10.1103/PhysRevLett.95.104302

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Wang, L., and Casati, G. (2004). Thermal diode: rectification of heat flux. Phys. Rev. Lett. 93, 184301. doi:10.1103/PhysRevLett.93.184301

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., Ren, J., Wang, L., Zhang, G., Hänggi, P., and Li, B. (2012). Colloquium: phononics: Manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045–1066. doi:10.1103/RevModPhys.84.1045

CrossRef Full Text | Google Scholar

Li, X., and Zhang, G. (2013). Enhancing the extremely high thermal conduction of graphene nanoribbons. Front. Phys. 1. doi:10.3389/fphy.2013.00019

CrossRef Full Text | Google Scholar

Lindsay, L., and Broido, D. A. (2010). Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 81, 205441. doi:10.1103/PhysRevB.81.205441

CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Sound and heat revolutions in phononics. Nature 503, 209–217. doi:10.1038/nature12608

PubMed Abstract | CrossRef Full Text | Google Scholar

Malik, F. K., and Fobelets, K. (2022). A review of thermal rectification in solid-state devices. J. Semicond. 43, 103101. doi:10.1088/1674-4926/43/10/103101

CrossRef Full Text | Google Scholar

Neek-Amal, M., Xu, P., Schoelz, J. K., Ackerman, M. L., Barber, S. D., Thibado, P. M., et al. (2014). Thermal mirror buckling in freestanding graphene locally controlled by scanning tunnelling microscopy. Nat. Commun. 5, 4962. doi:10.1038/ncomms5962

PubMed Abstract | CrossRef Full Text | Google Scholar

Ni, X., Zhang, G., and Li, B. (2011). Thermal conductivity and thermal rectification in unzipped carbon nanotubes. J. Phys. Condens. Matter 23, 215301. doi:10.1088/0953-8984/23/21/215301

PubMed Abstract | CrossRef Full Text | Google Scholar

Nika, D. L., and Balandin, A. A. (2012). Two-dimensional phonon transport in graphene. J. Phys. Condens. Matter 24, 233203. doi:10.1088/0953-8984/24/23/233203

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Pop, E., Varshney, V., and Roy, A. K. (2012). Thermal properties of graphene: fundamentals and applications. MRS Bull. 37, 1273–1281. doi:10.1557/mrs.2012.203

CrossRef Full Text | Google Scholar

Roberts, N., and Walker, D. (2011). A review of thermal rectification observations and models in solid materials. Int. J. Therm. Sci. 50, 648–662. doi:10.1016/j.ijthermalsci.2010.12.004

CrossRef Full Text | Google Scholar

Sai Kavuri, D. V., and Sathian, S. P. (2024). Strain gradient induced thermal rectification in graphene. J. Appl. Phys. 136, 194301. doi:10.1063/5.0203328

CrossRef Full Text | Google Scholar

Shih, T.-M., Gao, Z., Guo, Z., Merlitz, H., Pagni, P. J., and Chen, Z. (2015). Maximal rectification ratios for idealized bi-segment thermal rectifiers. Sci. Rep. 5, 12677. doi:10.1038/srep12677

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiri, D., and Isacsson, A. (2019). Heat-to-mechanical energy conversion in graphene: manifestation of Umklapp enhancement with strain. J. Appl. Phys. 125, 125101. doi:10.1063/1.5081902

CrossRef Full Text | Google Scholar

Stuart, S. J., Tutein, A. B., and Harrison, J. A. (2000). A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112, 6472–6486. doi:10.1063/1.481208

CrossRef Full Text | Google Scholar

Stukowski, A. (2010). Visualization and analysis of atomistic simulation data with OVITO - the open visualization tool. Model. Simul. Mat. Sci. Eng. 18, 015012. doi:10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

Terraneo, M., Peyrard, M., and Casati, G. (2002). Controlling the energy flow in nonlinear lattices: a model for a thermal rectifier. Phys. Rev. Lett. 88, 094302. doi:10.1103/PhysRevLett.88.094302

PubMed Abstract | CrossRef Full Text | Google Scholar

Tewary, V. K., and Yang, B. (2009). Singular behavior of the Debye-Waller factor of graphene. Phys. Rev. B 79, 125416. doi:10.1103/PhysRevB.79.125416

CrossRef Full Text | Google Scholar

Wang, Y., Chen, S., and Ruan, X. (2012). Tunable thermal rectification in graphene nanoribbons through defect engineering: a molecular dynamics study. Appl. Phys. Lett. 100, 163101. doi:10.1063/1.3703756

CrossRef Full Text | Google Scholar

Wang, Y., Vallabhaneni, A., Hu, J., Qiu, B., Chen, Y. P., and Ruan, X. (2014). Phonon lateral confinement enables thermal rectification in asymmetric single-material nanostructures. Nano Lett. 14, 592–596. doi:10.1021/nl403773f

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, N., Xu, L., Wang, H.-Q., and Zheng, J.-C. (2011). Strain engineering of thermal conductivity in graphene sheets and nanoribbons: a demonstration of magic flexibility. Nanotechnology 22, 105705. doi:10.1088/0957-4484/22/10/105705

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, G., and Li, B. (2007). Thermal rectification in carbon nanotube intramolecular junctions: molecular dynamics calculations. Phys. Rev. B 76, 085424. doi:10.1103/PhysRevB.76.085424

CrossRef Full Text | Google Scholar

Xu, W., Zhang, G., and Li, B. (2014). Interfacial thermal resistance and thermal rectification between suspended and encased single layer graphene. J. Appl. Phys. 116, 134303. doi:10.1063/1.4896733

CrossRef Full Text | Google Scholar

Yang, N., Li, N., Wang, L., and Li, B. (2007). Thermal rectification and negative differential thermal resistance in lattices with mass gradient. Phys. Rev. B 76, 020301. doi:10.1103/PhysRevB.76.020301

CrossRef Full Text | Google Scholar

Yang, N., Zhang, G., and Li, B. (2009). Thermal rectification in asymmetric graphene ribbons. Appl. Phys. Lett. 95, 033107. doi:10.1063/1.3183587

CrossRef Full Text | Google Scholar

Yang, X., Wu, S., Xu, J., Yu, D., and Cao, B. (2018). Enhancing thermal rectification in graphene-carbon nanotube junctions by tuning the chirality of pillar. Europhys. Lett. 123, 44004. doi:10.1209/0295-5075/123/44004

CrossRef Full Text | Google Scholar

Yousefi, F., Khoeini, F., and Rajabpour, A. (2020a). Thermal conductivity and thermal rectification of nanoporous graphene: a molecular dynamics simulation. Int. J. Heat Mass Transf. 146, 118884. doi:10.1016/j.ijheatmasstransfer.2019.118884

CrossRef Full Text | Google Scholar

Yousefi, F., Khoeini, F., and Rajabpour, A. (2020b). Thermal rectification and interfacial thermal resistance in hybrid pillared-graphene and graphene: a molecular dynamics and continuum approach. Nanotechnology 31, 285707. doi:10.1088/1361-6528/ab8420

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, G., and Zhang, H. (2011). Thermal conduction and rectification in few-layer graphene Y junctions. Nanoscale 3, 4604–4607. doi:10.1039/C1NR10945F

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Lv, Q., Wang, H., Zhao, S., Xiong, Q., Lv, R., et al. (2022). Simultaneous electrical and thermal rectification in a monolayer lateral heterojunction. Science 378, 169–175. doi:10.1126/science.abq0883

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, S., Zhou, Y., and Wang, H. (2022). Review of thermal rectification experiments and theoretical calculations in 2D materials. Int. J. Heat Mass Transf. 195, 123218. doi:10.1016/j.ijheatmasstransfer.2022.123218

CrossRef Full Text | Google Scholar

Zhu, W., Wu, G., Chen, H., and Ren, J. (2018). Nonlinear heat radiation induces thermal rectifier in asymmetric holey composites. Front. Energy Res. 6. doi:10.3389/fenrg.2018.00009

CrossRef Full Text | Google Scholar