Low-temperature electron transport in [110] and [100] silicon nanowires: a DFT-Monte Carlo study

The effects of very low temperature on the electron transport in a [110] and [100] axially aligned unstrained silicon nanowires (SiNWs) are investigated. A combination of semi-empirical 10-orbital tight-binding method, density functional theory and Ensemble Monte Carlo (EMC) methods are used. Both acoustic and optical phonons are included in the electron-phonon scattering rate calculations covering both intra-subband and inter-subband events. A comparison with room temperature (300 K) characteristics shows that for both nanowires, the average electron steady-state drift velocity increases at least 2 times at relatively moderate electric fields and lower temperatures. Furthermore, the average drift velocity in [110] nanowires is 50 percent more than that of [100] nanowires, explained by the difference in their conduction subband effective mass. Transient average electron velocity suggests that there is a pronounced streaming electron motion at low temperature which is attributed to the reduced electron-phonon scattering rates.

1 Introduction

Since the first implementation of top-down Singh et al. (2008) and bottom-up Ma et al. (2003) approaches to fabricate Silicon nanowires (SiNWs), they have constantly shown promising applications in different areas of technology. These are all fueled by the compatibility of their fabrication with the mainstream silicon technology and enhanced quantum mechanical effects as a result of size reduction, e.g., direct bandgap. Tunability of the optical absorption and direct nature of the bandgap bring SiNWs into the photonic realm, for example, photo-detectors, resolving photon polarization Park and Crozier (2015); Zhao et al. (2017), and photovoltaic Gonchar et al. (2019). The surface effects in SiNWs lead to more sensitivity for chemical sensors Kashyap et al. (2022). Breaking the centro-symmetry of the crystal in SiNWs due to strain or surface effects enhances the nonlinear optical effects, e.g., second harmonic generation Wiecha et al. (2015) and third order nonlinear effects Park et al. (2023).

SiNWs have also shown promising benefits in enhancing the coherence of spin-based quantum bits (qubits) as opposed to III-V nanowires in which the coherence of the qubits is limited due to hyperfine magnetic interaction with nuclei. Implementing spin-based qubit chips based on CMOS-compatible SiNW systems are on the rise Zwanenburg et al. (2009); Maurand et al. (2016); Hu et al. (2012); Piot et al. (2022).

Low temperature effects on the charge carrier transport in silicon nanowires also open up new horizons in understandings and possible low-temperature (cryogenic) applications, e.g., CMOS-compatible cryogenic sensors, switches, and deep-space electronics Jones et al. (2020); Rohrbacher et al. (2023). For the latter, the traditionally large bandgap III-V semiconductors are of use despite the high price of their wafer fabrication and processing. SiNWs with direct and controllable bandgap promise a low-cost alternative for III-V counterparts. Different electronic applications of SiNWs are also rising Arjmand et al. (2022); Schmidt et al. (2009), thanks to the developments of CMOS-compatible top-down fabrication methods Singh et al. (2008); Pott et al. (2008). In this article we have studied the effect of low temperature on the transport of electrons at both steady-state and transient conditions under the influence of electron-phonon scattering. The scattering events include both intra- and inter-subband transition processes due to longitudinal acoustic (LA) and longitudinal optical (LO) phonons. Two SiNWs of different crystallographic directions were chosen for the study: a 1.3 nm [110] and a 1.1 nm [100] SiNW, terminated with hydrogen atoms. The band structure data (conduction subbands for electrons) and scattering rates are used by an ensemble Monte Carlo (EMC) code for calculation of electron transport under the influence of applied electric field. The EMC method is a very useful tool to investigate steady-state and transient phenomena in semiconducting nano-devices Tomizawa (1993).

It must be emphasized that in our study, we do not use phenomenological scattering rates or effective mass approximation, rather we calculate the scattering rates ab initio from the band structure information and feed the EMC code with these scattering rates. Reproducing the same experimental observations in SiNWFET Rohrbacher et al. (2023) and CNT Jovanovic and Leburton (1992); Ahmadi et al. (2008), showcase the strength of our model in predicting interesting effects for low-temperature applications. Our method also allows us to monitor how the population of electron is evolving within BZ in response to the applied field. That is a way of designing interesting devices by looking at BZ and determining how to scatter electrons to low mobility subbands and initiate, for example, Gunn effect.

In the next section, we discuss the computational methods including the calculation of band structures, electron-phonon scattering rates and EMC methods. In section 3 we discuss the results. We show that at low temperatures the average drift velocity is enhanced by at least a factor of two due to mitigation of scattering events involving phonon absorption. The difference in the effective mass of [110] and [100] SiNWs leads to better transport (higher electron velocity) in [110] SiNWs. Finally, we show that the initial back-and-forth displacement of electron population in the momentum space, within the first Brillouin zone (BZ), causes streaming motion at moderate bias electric fields. This is supported through transient EMC snapshots of the electron population at different time scales. This effect as well as saturation of drift velocity at higher fields corroborates with previous studies in carbon nanotubes (CNTs) Jovanovic and Leburton (1992); Ahmadi et al. (2008).

2 Computational methods

2.1 Energy minimization and band structure

Two silicon nanowires of different crystallographic directions are investigated here: [110] and [100]. The average diameters for these nanowires are 1.3 nm and 1.1 nm, respectively. The nanowires are considered freestanding, with the surface silicon dangling bonds passivated with hydrogen atoms. Terminating the dangling Si atoms on SiNW is a model for a nanowire surrounded by ideal vacuum or a large-bandgap material or a perfect oxide cladding free of dangling bonds or dislocations. The structural energy of the nanowires is minimized using the density functional theory code in SIESTA. This process allows for the most energetically favorable unit cell to take form and the formation of dangling $\mathrm{S}\mathrm{i}\mathrm{H}$ and ${\mathrm{S}\mathrm{i}\mathrm{H}}_2$ groups on the SiNW edge are finalized Soler et al. (2002).

The exchange-correlation functional which was used is the Generalized Gradient Approximation (GGA) type with Perdew–Burke–Ernzerhof (PBE) pseudopotentials. The number of $k$-points to sample the Brillouin Zone (BZ) are 1$\times$ 1$\times$ 40 based on Monkhorst-Pack algorithm with many number of points along the periodical axis of the nanowire (z-axis). The minimum distance of adjacent unit cells is more than 0.6 nm to avoid any possible wavefunction overlapping. The energy cut-off, split norm, and force tolerance are 680 eV, 0.15, and 0.01 eV/A°, respectively. The energy of the unit cell of nanowires is minimized using the conjugate gradient (CG) algorithm with a variable unit cell option. This option allows the volume of the unit cell to grow or shrink depending on the movement of Si-Si and Si-H bonds, particularly the canting of the silicon dihydride groups $({\mathrm{S}\mathrm{i}\mathrm{H}}_2)$ on the surface of SiNW. Figures 1A, B show the band structure and $xy$ cross sections of hydrogen-passivated SiNWs in [110], and [100] directions, respectively. After the minimization step, the coordinates of the atoms and new unit cell length are used to build the Hamiltonian of the unit cell with a semi-empirical $s{p}^3{d}^5{s}^{*}$ tight-binding (TB) scheme using parameters given by Jancu et al. (1998). This central Hamiltonian and the interaction Hamiltonians with the two neighboring unit cells (before and after) are filled to form the total Hamiltonian using Bloch’s theorem. Diagonalizing this Hamiltonian at each $k_z$ point and plotting the eigenenergies gives the band structure. The position-dependency in our tight-binding model is based on Harrison’s law in which the overlapping of orbitals (hopping parameter) is proportional with distance as $1/d^2$, where $d$ is the atom-atom bond length or distance. See Equation (40) in Jancu et al. (1998).

Figure 1

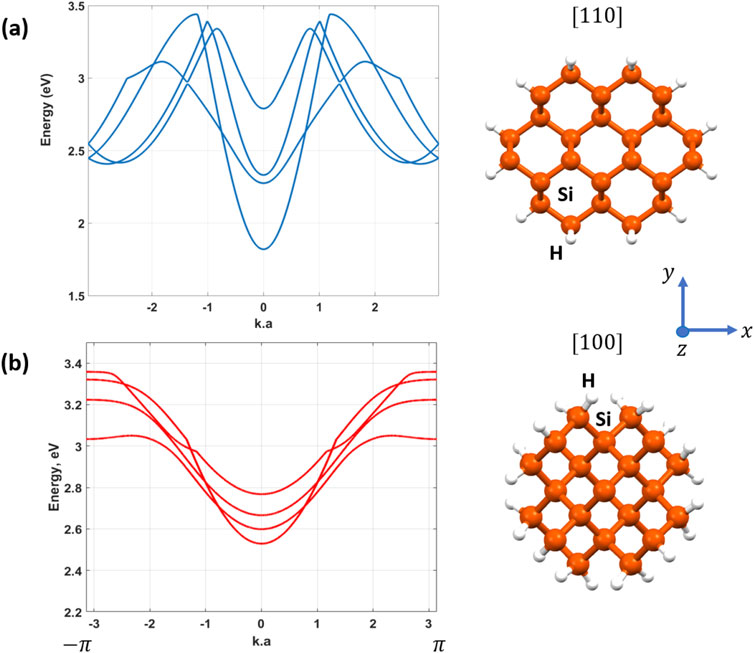
Figure 1. (A) The band structure of 1.3 nm [110] SiNW showing the first four conduction subbands used in the electron-phonon scattering calculation. (B) The band structure showing the first four conduction subbands for 1.1 nm [100] SiNW. The $xy$ cross sections of the SiNWs are shown on the right side. The orange and white atoms are Si and H, respectively.

It was shown that the TB method can faithfully reproduce the experimental data of photoluminescence in silicon nanowires under strain as reported in Walavalkar et al. (2010); Demichel et al. (2011); Bae et al. (2018). As can be seen in Figure 1A, both nanowires are of direct bandgap type. In the [110] SiNW the minimum conduction subband energy is $E_{\mathit{cmin}}=1.81\text{\hspace{0.17em}eV}$. In the [100] SiNW the minimum of the conduction band is at $E_{\mathit{cmin}}=2.528\text{\hspace{0.17em}eV}$. The effect of quantum confinement is more pronounced for the [100] SiNW, i.e., as it is narrower it has a higher energy level. The effective mass of [100] subbands is four times that of [110] (e.g., $m^{*}=0.16$ for [110] and $m^{*}=0.63$ for [100] for the first subband). As we will see later this leads to a less average drift velocity for [100] SiNWs.

2.2 Phonon scattering rates and EMC

For the calculation of electron-phonon scattering rates, four first subbands are chosen. The reason for this is to ensure that the energy difference between the minimum conduction energy and the highest one is more than $5k_{B}T$ which is $130\text{\hspace{0.17em}meV}$ at room temperature, i.e., $T=300\text{\hspace{0.17em}K}$. The fourth subband minimum is at $E_{c4}=2.8\text{\hspace{0.17em}eV}$ and $E_{c4}=2.76\text{\hspace{0.17em}eV}$ for [110] and [100] SiNWs, respectively. These four subbands are included in the EMC calculations. For the electron-phonon scattering rate calculation, the first Brillouin Zone (BZ) is divided into 8000 grid points along $k$ direction. For each $k$ point, the subband energies and eigenstates (TB wave functions) are calculated and tabulated. The electron-phonon scattering rates are numerically evaluated using the first order perturbation theory and deformation potential approximation, for different temperatures. Both types of phonons, i.e., longitudinal acoustic (LA) and optical (LO) phonons are included. The electron scattering includes both intra-subband and inter-subband scattering events. For acoustic phonons, we used the Debye approximation, i.e., it is assumed that the acoustic phonons have linear dispersion and their energy $(E_P=\hslash \omega )$ and wave vector $(|k|)$ are linearly proportional. Therefore, $E_P=\hslash \omega =c|k|$, where $\hslash$ is Planck’s constant and $c$ is the velocity of sound in silicon, and $\omega$ is the acoustic phonon frequency. For LO phonons, the dispersion is almost flat and as a result, all optical phonons can be considered to have the same energy which for silicon is $E_P=E_{LO}=54\text{\hspace{0.17em}meV}$. The scattering rates and the indices of the possible final (secondary) states in the BZ (after scattering) are sorted in a table depending on if they are phonon-absorption or phonon-emission type and if they are intra- or inter-subband. Indices of the secondary states to which electron scatters by absorption or emission of a phonon is used by the EMC algorithm to decide how an electron injected into the nanowire propagates as a result of applied electric field. Details of the scattering rates calculations are presented in Buin et al. (2008); Shiri et al. (2018).

The total scattering rates from the first subband to other bands (the first one included), due to LO and LA phonons for different nanowires and different temperatures are compared in Figure 2. Figure 2A shows the total scattering rates due to LO and LA phonons at room temperature calculated for [100] and [110] nanowires. As can be seen the scattering rates in [100] SiNW are overall higher by a factor of two compared to the [110] SiNW which can be attributed to the effective mass difference of these two nanowire directions as it was shown in Figure 1.

Figure 2

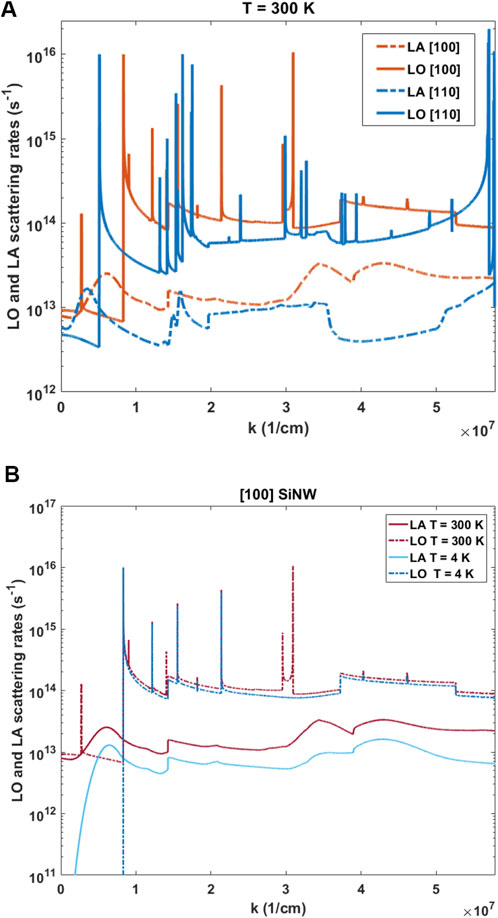
Figure 2. (A) The electron-phonon scattering rates for LA and LO phonons at $T=300\text{\hspace{0.17em}K}$. The [110] nanowire (blue plots) has lower scattering rates compared to [100] (red plots).(B) The comparison of LO and LA scattering rates for [100] SiNW at $T=4\text{\hspace{0.17em}K}$ and $T=300\text{\hspace{0.17em}K}$ temperatures. The scattering rates are enhanced by increasing the temperature as shown by crimson plots.

This is because the scattering rate depends on the availability of the secondary states quantified by the density of states (DOS). In a 1D solid like nanowire, DOS is proportional to the square root of the effective mass i.e., $DOS(E)\propto \sqrt{m^{*}}$. The scattering rates from the first subband to other subbands at two extreme temperatures of $T=4\text{\hspace{0.17em}K}$ and $T=300\text{\hspace{0.17em}K}$ are compared in Figure 2B for [100] nanowire. This is similar to the observations for [110] SiNWs as reported in Verma et al. (2023). The higher scattering rate at higher temperatures is due to higher phonon absorption scattering. The peaks in the LO scattering rates emanate from the van Hove singularities. They correspond to electron transitions to the bottom of different subbands once the electron energy reaches the $E_{LO}=54\text{\hspace{0.17em}meV}$ which is onset for a LO phonon emission event to occur. On the contrary, the peaks of LA scattering events are smooth as in the calculation of scattering rates a continuum of secondary states is available for every energy of electron due to linear dispersion of the acoustic phonons. At low temperatures, the dominant scattering event is due to the emission of LO phonons as well as acoustic phonons. The observed LO phonon peaks have significant effect on the electron transport under both steady-state and transient conditions, as will be seen shortly. The SiNWs are defect-free, infinitely long, and undoped. The temperature is assumed to be uniform. The applied electric field is along the nanowire axis ($z$ axis) and is uniform. For the steady-state analysis, the electrons are injected at $t=0\text{\hspace{0.17em}s}$ at the bottom of the lowest conduction band. For the transient results, the simulation is first run for 50,000 iterations at an electric field of $E_{\mathit{field}}=0\text{\hspace{0.17em}kV/cm}$ to achieve a near equilibrium distribution. We use the standard EMC algorithm and methodology as presented by Jacoboni and Lugli (1989) in our simulations.

A promising method to scale up the number of superconducting and spin-based qubits, is to co-integrate cryoCMOS control circuits on the same chip instead of relying on many microwave cables from room temperature to the 10 mK stage of dilution refrigerators. The cryoCMOS community is intensively researching on how to model nano-FETs at 4K and below. Therefore we chose 4K as the lower extreme of temperature in this study.

3 Results and discussions

Figure 3 shows the average electron drift velocity as a function of the applied electric field along the length of the nanowires ($z$ axis) for $T=4\text{\hspace{0.17em}K}$ and $T=300\text{\hspace{0.17em}K}$. As expected, the drift velocity is significantly higher for the lower temperatures due to reduced scattering rates which were shown in Figure 2. At an electric field of $E_{\mathit{field}}=15\text{\hspace{0.17em}kV/cm}$, the drift velocity at [100] drops approximately by one-fifth and for [110] it drops by a half as the temperature is increased to 300 K. This is attributed to the higher total scattering rates at higher temperatures. The enhancement of transport at $T=4\text{\hspace{0.17em}K}$ is also observed in the IV characteristics of cryogenic gate-all-around SiNW FETs reported by Rohrbacher et al. (2023). The electron-phonon scattering rate is proportional to $n(E_P)+1$ and $n(E_P)$ for phonon emission and absorption events, respectively. The population of phonons, $n(E_P)$, is determined by the Bose-Einstein factor and is given as:

$n\left(E_P\right)=\frac{1}{e^{E_P/k_{B}T}-1}$

where the phonon energy is $E_P$ and $k_B=1.3807\times 10^{-23}\text{\hspace{0.17em}J/K}$ is Boltzmann constant. As the temperature is lowered, the predominant scattering event becomes phonon emission because $n(E_P)\to 0$. As can be seen in Figure 3, the average drift velocity saturates at high electric fields. This is because velocity saturation occurs primarily through phonon emission scattering and is nearly temperature-independent threshold process Verma et al. (2009).The enhancement of saturation current by reducing the temperature is nonlinear as it is determined by the Boltzmann factor in the electron-LO phonon scattering term. We observed preciously Verma et al. (2023) that below 70 K the rate of drain-source current enhancement saturates and there is not much difference between the values of 70 K and 4 K.

Figure 3

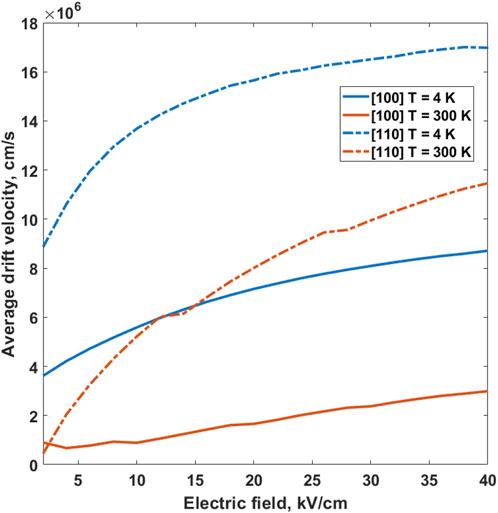
Figure 3. The average drift velocity of electron as a function of applied longitudinal electric field for [110] (dashed line) and [100] (solid line) SiNWs at $T=4\text{\hspace{0.17em}K}$ (blue) and $T=300\text{\hspace{0.17em}K}$ (red). Higher velocity (less scattering) is visible for [110] SiNW (dashed plots).

It is also important to look at the transient distribution function in conjunction with the scattering rates in Figure 2. Figure 4 (left panel) depicts the evolving (time-dependent) electron distribution function at $T=4\text{\hspace{0.17em}K}$ for the applied electric field of $30\text{\hspace{0.17em}kV/cm}$. As can be seen, the distribution function appears to stop moving beyond a wave vector $k$ value that roughly corresponds to a peak in the scattering rates at approximately $k=2\times 10^{6}1\text{/cm}$ for [110] and $k=6\times 10^{6}1\text{/cm}$ for [100] (see red plots in the left panel of Figure 4). These $k$ values correspond to blue and red peaks in LO data of Figure 2 and prove that the LO-phonon emission scattering peak impedes electrons from gaining relatively large crystal momentum with an increase in the electric field.

Figure 4

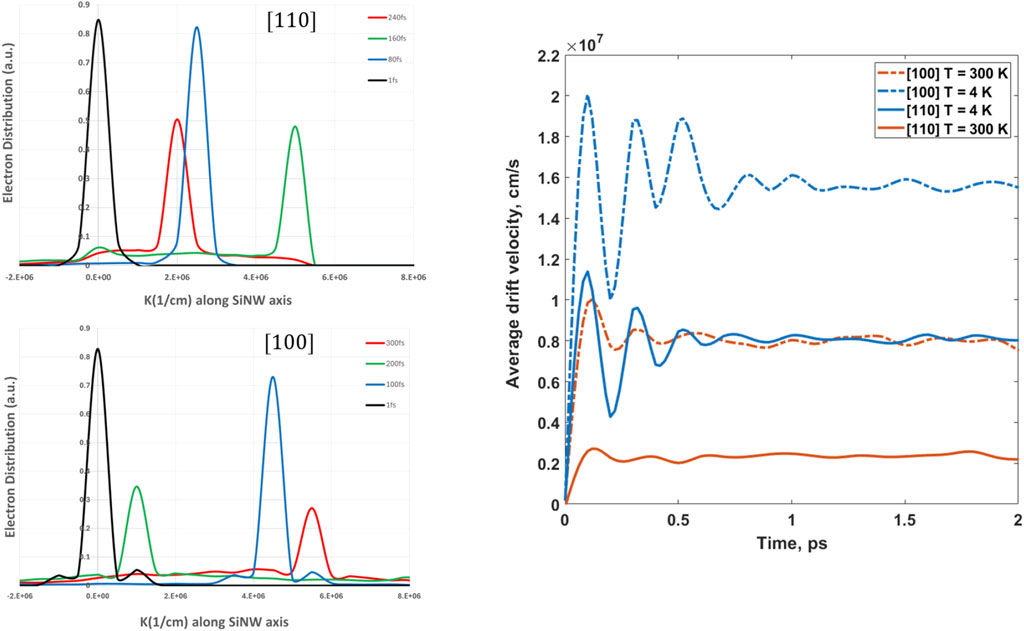
Figure 4. (Left panel, top) Oscillation of electron distribution within the first BZ at a constant electric field $(E_{\mathit{field}}=30\text{\hspace{0.17em}kV/cm})$ at $T=4\text{\hspace{0.17em}K}$ for [110] SiNW. (left panel, bottom) The same data for [100] SiNW at $T=4\text{\hspace{0.17em}K}$. The red plots show that as time passes the distribution is mostly centered around the $k$-points which correspond to LO peaks in Figure 2. (Right panel) Time evolution of electron average drift velocity for [110] and [100] SiNWs at low and high temperatures. The oscillation of velocity is more pronounced at the low temperature. The steady state velocity is higher for [110] nanowires as explained in the text.

The initial back and forth displacement of electron population in the BZ can be appreciated if we plot the time evolution of average drift velocity which reveals a wealth of information about the scattering mechanism and shows the importance of the peaks in scattering rates through phonon emission. Figure 4 (righ panel) shows the transient average electron drift velocity for the temperatures considered at an electric field of $E_{\mathit{field}}=20\text{\hspace{0.17em}kV/cm}$.

First, it shows that the velocity is enhanced by decreasing the temperature which is again due to lower scattering rates through phonon absorption at lower temperatures. Second, the streaming motion of electrons, i.e., the ringing of the velocity at initial times becomes more pronounced at lower temperatures, which is also predicted by Jovanovic and Leburton (1992). The streaming motion can be understood through the transient evolution of the electron distribution function (left panel of Figure 4) and scattering rates as shown in Figure 2. The reason for the velocity oscillation in Figure 4 (e.g., from 0 to 600 fs) can be understood if we look at electron distribution inside the first BZ versus time as it was shown in the left panel of Figure 4. The distribution function is seen to ‘bounce’ back and forth. In short, once the electric field is applied, electrons quickly gain crystal momentum and reach the first phonon emission scattering peak. This is where electrons are $E_{LO}=54\mathrm{m}\mathrm{e}\mathrm{V}$ above the minimum of the first conduction subband (approximately $k=2\times 10^{6}1\text{/cm}$ for [110] and $k=6\times 10^{6}1\text{/cm}$ for [100]). At this point, a significant number of electrons lose momentum and fall back to near the $k=0$ or BZ center, where they accelerate again. The process continues until phonon absorption scattering events cause the electrons to reach an average steady-state drift velocity. Saturation of the velocity at higher electric fields also corroborates with the electron transport under electric fields in narrow CNTs in Ahmadi et al. (2008). Recall that the scattering rates for emission and absorption of phonon are proportional to $n(E_P)+1$ and $n(E_P)$, respectively. Hence, at very low temperatures the emission term is dominant as the absorption term approaches to zero, i.e., $n(E_P)\to 0$. At high temperatures, however, the difference between the phonon populations becomes very small, i.e., $n(E_P)+1\approx n(E_p)$, which means both emission and absorption rates are dominant and the average of drift velocity settles to a lower but stable value relatively faster.

It is instructive at this point to discuss the relation between drift velocity and mobility. EMC is an outstanding modeling tool for moderate to high electric fields. At those electric fields, the linear relationship between drift velocity and electric field (the low-field mobility regime or $v_{\mathit{drift}}=\mu E$) is most often absent. Classic examples are average drift velocity saturation in bulk silicon, leading to a decrease in mobility with increase in field, or a decrease in drift velocity in bulk GaAs, leading to a negative differential mobility that is the basis for Gunn diodes. Unfortunately, there is no closed form expression that links drift velocity at high electric fields to scattering rates, which is where tools such as EMC come in. While EMC is used for relatively moderate to high electric fields, there are tools to compute low-field mobility from computed scattering rates–the linear region where average drift velocity is proportional to the applied electric field. One such is the momentum relaxation time approximation (MRTA), given by the following formulae Buin et al. (2008). This relates the mobility in subband $i$ to momentum relaxation rate $W_i(k_z)$ for a given state at $k_z$ within the first BZ.

${\mu }_i=\frac{e}{k_{B}T}\frac{{\int }_{\mathit{1st}\mathit{BZ}}{v}_i^2\left(k_z\right)W_i{\left(k_z\right)}^{-1}{f}_o\left(k_z\right)d{k}_z}{{\int }_{\mathit{1st}\mathit{BZ}}{f}_o\left(k_z\right)d{k}_z}$

$f_o(k_z)=e^{-E_i/k_{B}T}$ is the Boltzmann factor, $v_i(k_z)$ is the group velocity of subband $i$. Note that the momentum relaxation rate $W_i(k_z)$ is proportional to the momentum difference between the initial $k_z$ and the final state which in the case of LO phonon it is $W_i(k_z)\propto \frac{\mathrm{\Delta }{k}_z}{k_z}=\frac{q_{LO}}{k_z}$. Therefore, the mobility is related to the relaxation rate $1/W_i(k_z)$ which in turn is related to the drift velocity through momentum of the $k_z$ state i.e., $k_z=p_z/\hslash =m{v}_{\mathit{drift}}/\hslash$.

To manage the required computational resources, we used reasonably small nanowires in this work. However, from a practical point of view, fabrication of small-diameter nanowires i.e., 3 nm diameter, is possible using the top-down CMOS compatible methods Singh et al. (2008). Effect of diameter on the transport depends on the crystallographic direction. We observed previously in Shiri et al. (2018), that for a 3.3 nm [110] SiNW, the direct-indirect energy subband difference is 130 meV (as opposed to 700 meV in Figure 1A for 1.3 nm). As a result of this, at moderate electric fields higher population of electrons ends up in indirect subband with higher effective mass. This leads to lower mobility (current reduction) from which negative differential resistance or Gunn effect results.

4 Conclusion

Using DFT and Ensemble Monte Carlo methods we demonstrated that low temperature has significant effects on electron drift velocity in [110] and [100] silicon nanowires. It was shown that the velocity is enhanced at $T=4\text{\hspace{0.17em}K}$ in both nanowires as a result of diminished electron-phonon absorption scattering. For both nanowires, the velocity saturates at high electric fields showcasing the dominance of scattering events due to LO-phonons. This was examined by looking into the time-dependent bounce of electron population within the first BZ which also explained the observed streaming motion of electrons particularly at lower temperatures. Also we demonstrated that [110] SiNWs have better transport properties than [100] SiNWs. This is due to higher effective mass in [100] SiNWs which manifests itself in higher DOS for electron secondary states and, as a result, increased electron-phonon scattering rate. These observations promise potential applications of SiNWs at low temperatures, e.g., cryogenic devices and circuits. Silicon nanowires can host both nano-FET devices as well as spin-based qubits, therefore help in solving the scaling-up problem from both ends. That means (a) cryoCMOS circuits lead to co-integration of control/signal generation circuits with qubits, and (b) qubit devices are made of the same silicon nanowires. Hence, any effort in understanding the low temperature transport especially 4K and lower, will benefit both aspects, i.e., control circuits design and qubits themselves. See Camenzind et al. (2022).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DS: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. RN: Conceptualization, Data curation, Investigation, Resources, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. AV: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors sincerely acknowledge the access to the Stampede2 Supercomputing machine provided by the Texas Advanced Computing Center (TACC) at Austin, United States.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, M. T., Ismail, R., Tan, M. L. P., and Arora, V. K. (2008). The ultimate ballistic drift velocity in carbon nanotubes. J. Nanomater. 2008, 769250. doi:10.1155/2008/769250

CrossRef Full Text | Google Scholar

Arjmand, T., Legallais, M., Nguyen, T. T. T., Serre, P., Vallejo-Perez, M., Morisot, F., et al. (2022). Functional devices from bottom-up silicon nanowires: a review. Nanomaterials 12, 1043. doi:10.3390/nano12071043

PubMed Abstract | CrossRef Full Text | Google Scholar

Bae, G., Bae, D.-I., Kang, M., Hwang, S., Kim, S., Seo, B., et al. (2018). “3nm GAA technology featuring multi-bridge-channel FET for low power and high performance applications,” in 2018 IEEE international electron devices meeting (IEDM). doi:10.1109/IEDM.2018.8614629

CrossRef Full Text | Google Scholar

Buin, A. K., Verma, A., Svizhenko, A., and Anantram, M. P. (2008). Significant enhancement of hole mobility in [110] silicon nanowires compared to electrons and bulk silicon. Nano Lett. 8, 760–765. PMID: 18205425. doi:10.1021/nl0727314

PubMed Abstract | CrossRef Full Text | Google Scholar

Camenzind, L. C., Geyer, S., Fuhrer, A., Warburton, R. J., Zumbühl, D. M., and Kuhlmann, A. V. (2022). A hole spin qubit in a FIN field-effect transistor above 4 kelvin. Nat. Electron. 5, 178–183. doi:10.1038/s41928-022-00722-0

CrossRef Full Text | Google Scholar

Demichel, O., Calvo, V., Noé, P., Salem, B., Fazzini, P.-F., Pauc, N., et al. (2011). Quantum confinement effects and strain-induced band-gap energy shifts in core-shell Si-Si nanowires. Phys. Rev. B 83, 245443. doi:10.1103/PhysRevB.83.245443

CrossRef Full Text | Google Scholar

Gonchar, K. A., Kitaeva, V. Y., Zharik, G. A., Eliseev, A. A., and Osminkina, L. A. (2019). Structural and optical properties of silicon nanowire arrays fabricated by metal assisted chemical etching with ammonium fluoride. Front. Chem. 6, 653. doi:10.3389/fchem.2018.00653

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Kuemmeth, F., Lieber, C. M., and Marcus, C. M. (2012). Hole spin relaxation in Ge–Si core–shell nanowire qubits. Nat. Nanotechnol. 7, 47–50. doi:10.1038/nnano.2011.234

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacoboni, C., and Lugli, P. (1989). The Monte Carlo method for semiconductor device simulation. Wien: Springer. doi:10.1007/978-3-7091-6963-6

CrossRef Full Text | Google Scholar

Jancu, J.-M., Scholz, R., Beltram, F., and Bassani, F. (1998). Empirical tight-binding calculation for cubic semiconductors: general method and material parameters. Phys. Rev. B 57, 6493–6507. doi:10.1103/PhysRevB.57.6493

CrossRef Full Text | Google Scholar

Jones, A. T., Scheller, C. P., Prance, J. R., Kalyoncu, Y. B., Zumbühl, D. M., and Haley, R. P. (2020). Progress in cooling nanoelectronic devices to Ultra-Low temperatures. J. Low Temp. Phys. 201, 772–802. doi:10.1007/s10909-020-02472-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Jovanovic, D., and Leburton, J. (1992). Electron-phonon interaction and velocity oscillations in quantum wire structures. Superlattices Microstruct. 11, 141–143. doi:10.1016/0749-6036(92)90238-Z

CrossRef Full Text | Google Scholar

Kashyap, V., Pawar, H., Kumar, C., Chaudhary, N., and Saxena, K. (2022). Analysis of synthesized doped vertical silicon nanowire arrays for effective sensing of nitrogen dioxide: as gas sensors. Front. Mater. 9. doi:10.3389/fmats.2022.1022317

CrossRef Full Text | Google Scholar

Ma, D. D. D., Lee, C. S., Au, F. C. K., Tong, S. Y., and Lee, S. T. (2003). Small-diameter silicon nanowire surfaces. Science 299, 1874–1877. doi:10.1126/science.1080313

PubMed Abstract | CrossRef Full Text | Google Scholar

Maurand, R., Jehl, X., Kotekar-Patil, D., Corna, A., Bohuslavskyi, H., Laviéville, R., et al. (2016). A CMOS silicon spin qubit. Nat. Commun. 7, 13575. doi:10.1038/ncomms13575

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, H., and Crozier, K. B. (2015). Vertically stacked photodetector devices containing silicon nanowires with engineered absorption spectra. ACS Photonics 2, 544–549. doi:10.1021/ph500463r

CrossRef Full Text | Google Scholar

Park, J.-S., Li, C., Kim, K.-H., Tang, Y., Murphey, C. G. E., Teitsworth, T. S., et al. (2023). Optical nonlinearity in silicon nanowires enabled by bound states in the continuum. ACS Nano 17, 11729–11738. doi:10.1021/acsnano.3c02558

PubMed Abstract | CrossRef Full Text | Google Scholar

Piot, N., Brun, B., Schmitt, V., Zihlmann, S., Michal, V. P., Apra, A., et al. (2022). A single hole spin with enhanced coherence in natural silicon. Nat. Nanotechnol. 17, 1072–1077. doi:10.1038/s41565-022-01196-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Pott, V., Moselund, K., Bouvet, D., De Michielis, L., and Ionescu, A. (2008). Fabrication and characterization of gate-all-around silicon nanowires on bulk silicon. IEEE Trans. Nanotechnol. 7, 733–744. doi:10.1109/TNANO.2008.2007215

CrossRef Full Text | Google Scholar

Rohrbacher, C., Rivard, J., Ritzenthaler, R., Bureau, B., Lupien, C., Mertens, H., et al. (2023). Dual operation of gate-all-around silicon nanowires at cryogenic temperatures: FET and quantum dot. arXiv:2312. doi:10.48550/arXiv.2312.00903

CrossRef Full Text | Google Scholar

Schmidt, V., Wittemann, J. V., Senz, S., and Gösele, U. (2009). Silicon nanowires: a review on aspects of their growth and their electrical properties. Adv. Mater. 21, 2681–2702. doi:10.1002/adma.200803754

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiri, D., Verma, A., Nekovei, R., Isacsson, A., Selvakumar, C. R., and Anantram, M. P. (2018). Gunn-Hilsum effect in mechanically strained silicon nanowires: tunable negative differential resistance. Sci. Rep. 8, 6273. doi:10.1038/s41598-018-24387-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, N., Buddharaju, K. D., Manhas, S. K., Agarwal, A., Rustagi, S. C., Lo, G. Q., et al. (2008). Si, SiGe nanowire devices by top–down technology and their applications. IEEE Trans. Electron Devices 55, 3107–3118. doi:10.1109/TED.2008.2005154

CrossRef Full Text | Google Scholar

Soler, J. M., Artacho, E., Gale, J. D., García, A., Junquera, J., Ordejón, P., et al. (2002). The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 14, 2745–2779. doi:10.1088/0953-8984/14/11/302

CrossRef Full Text | Google Scholar

Tomizawa, K. (1993). Numerical simulation of submicron semiconductor devices. London: Artech House.

Google Scholar

Verma, A., Buin, A. K., and Anantram, M. P. (2009). High-field hole transport in silicon nanowires. J. Appl. Phys. 106, 113713. doi:10.1063/1.3264629

CrossRef Full Text | Google Scholar

Verma, A., Shiri, D., and Nekovei, R. (2023). “Low-temperature effects on electron transport in small-diameter silicon nanowire,” in 2023 IEEE nanotechnology materials and devices conference (NMDC), 31–34. doi:10.1109/NMDC57951.2023.10343599

CrossRef Full Text | Google Scholar

Walavalkar, S. S., Hofmann, C. E., Homyk, A. P., Henry, M. D., Atwater, H. A., and Scherer, A. (2010). Tunable visible and near-IR emission from sub-10 nm etched single-crystal Si nanopillars. Nano Lett. 10, 4423–4428. PMID: 20919695. doi:10.1021/nl102140k

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiecha, P. R., Arbouet, A., Kallel, H., Periwal, P., Baron, T., and Paillard, V. (2015). Enhanced nonlinear optical response from individual silicon nanowires. Phys. Rev. B 91, 121416. doi:10.1103/PhysRevB.91.121416

CrossRef Full Text | Google Scholar

Zhao, X., Alizadeh, M. H., and Reinhard, B. M. (2017). Generating optical birefringence and chirality in silicon nanowire dimers. ACS Photonics 4, 2265–2273. doi:10.1021/acsphotonics.7b00501

CrossRef Full Text | Google Scholar

Zwanenburg, F. A., van Rijmenam, C. E. W. M., Fang, Y., Lieber, C. M., and Kouwenhoven, L. P. (2009). Spin states of the first four holes in a silicon nanowire quantum dot. Nano Lett. 9, 1071–1079. doi:10.1021/nl803440s

PubMed Abstract | CrossRef Full Text | Google Scholar