- Department of Applied Science and Technology, Politecnico di Torino, Torino, Italy
Photochromic materials are of great interest because they enable the fabrication of photo-activated switches. In this study, an experiment is proposed in which two chromene-based photochromic layers were inserted into the arms of a Mach–Zehnder interferometer. The chromene was studied from the perspective of optical absorption to determine the wavelength-dependent complex refractive index. Impinging ultraviolet light on one of the chromene layers induces a transition from the closed to the open form of the chromene, resulting in different phase shifts in the two arms of the interferometer. This results in a change in the probability of detecting a photon by the two detectors after the second mirror of the Mach–Zehnder interferometer. The experiment may be of interest to researchers working in the fields of quantum information and quantum communications.
Introduction
Interest in photochromic materials is growing in the scientific community because of their use in devices that respond to light, such as rewritable displays, dynamic optical filters, optical memories, and neural surrogates in chemical artificial intelligence (Torres-Pierna et al., 2020; Barachevsky, 2018; Naren et al., 2019; Castaing et al., 2021; Gentili, 2022). The photochromism of different molecules and polymers has been recently reviewed by Xu and Feringa (2023). In the phenomenon of photochromism, there is a reversible transformation from a thermodynamically more stable A isomer to a metastable B isomer induced by electromagnetic radiation, especially in the ultraviolet range (Boelke and Hecht, 2019). Of particular interest are recent studies in which neuronal photostimulation has been demonstrated with an azobenzene-based photo-interrupter (DiFrancesco et al., 2020; Paternò et al., 2020). Chromene (C9H8O), also known as benzopyran, is a promising photochromic molecule due to the variety of its derivatives that can be synthesized (Hepworth and Heron, 2006; Perevozchikova et al., 2021). An interesting derivative of chromene, 3,3-diphenylbenzo[f]chromene forms two colored species in the photochromic reaction: transoid-cis and transoid-trans (Gierczyk et al., 2022). Photochromic materials have been employed in Mach–Zehnder interferometers in order to build all-optical modulators (Kang et al., 2002). Mach–Zehnder interferometers, consisting of two beam splitters, two mirrors, and two detectors, are very powerful and versatile tools for quantum optics experiments (Hajdušek and Van Meter, 2023; Rioux, 2019). Although it is true that electro-optic modulators, especially those based on lithium niobate, are the workhorse for integrated quantum optics (Palacios-Berraquero et al., 2017; Renaud et al., 2023), other solutions that require low-cost materials and fabrication techniques, such as photochromic molecules, can be an excellent alternative to conventional devices for quantum optics.
In this study, two chromene-based photochromic layers have been placed in the arms of a Mach–Zehnder interferometer. The optical properties of the closed and open forms of chromene have been simulated with the Hueckel theory (Guy and Troy, 2024; Solomon et al., 2011). The wavelength-dependent complex refractive index of the molecule has been determined from the simulations. A switch from the closed form to the open form of chromene is induced by impinging ultraviolet light on one of the chromene layers, leading to different phase shifts in the two arms of the interferometers. This results in a change in the probability of detecting a photon by the two detectors after the second mirror of the Mach–Zehnder interferometer.
Methods
The Hueckel theory has been employed to simulate the light absorption of chromene in its closed and open forms. The Heckel theory is a well-known molecular orbital theory in which the molecular orbitals are written as linear combinations of atomic orbitals (LCAO). The approximations employed in the theory are: i) the Born–Oppenheimer approximation, with fixed nuclei positions; ii) the molecular orbitals are linear combinations of pz orbitals, neglecting electron-electron interactions (Guy and Troy, 2024). In the Hueckel method, the time-independent Schrödinger equation is given by Equation 1
In this study, the Hulis package (Huckel Theory and HuLiS, 2013) has been used to define the Hamiltonian for open and closed forms of chromene (reported in the Appendix). Subsequently, eigenvalues and eigenvectors have been determined. The on-site energy α is set to 0 eV, and the nearest neighbor element β is set to −3 eV, in agreement with Solomon et al. (2011).
The Fermi golden rule has been used to find the transition probabilities (Equation 2):
The transition probabilities have been calculated between the highest occupied molecular orbital (HOMO) and the unoccupied orbitals. Gaussian peaks have been employed to simulate the absorption spectra, with a linewidth c of the peaks of 0.1 eV. Considering the transitions from the ground state ith to the different jth excited states, the absorption coefficient can be written as follows (Equation 3):
To extract the imaginary part of the complex refractive index, the following expression has been used, modifying the one reported by Kohandani and Saini (2022) (Equation 4):
where A is a parameter (its value is
The Kramers–Kronig relations are actually Hilbert transforms (Ogilvie and Fee, 2013). A constant offset of 1.5 has been used for the real part of the refractive index, as in Wiebeler et al. (2014) and Scotognella (2020). Thus, it is possible to derive the complex refractive index of chromene in the open (nco) and closed (ncc) forms (Equation 6):
Results and discussion
Figure 1 shows the closed form (top) and the open form (bottom) of chromene (carbon atoms are in gray, hydrogen atoms are in light gray, and oxygen atoms are in red).
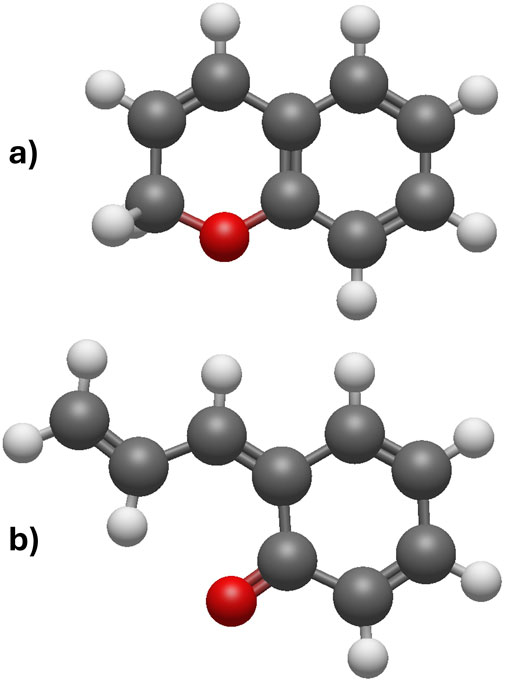
Figure 1. (A) Chromene in the closed form and (B) chromene in the open form (carbon atoms in gray, hydrogen atoms in light gray, and oxygen atoms in red).
The complex refractive index of chromene in its closed and open forms has been derived by employing the Hueckel method, and its dependence upon the energy is reported in Figure 2, where black curves correspond to the real part of the refractive index, and red curves correspond to the imaginary part of the refractive index. In the imaginary part of the refractive index, the open form shows resonances at 1.95 eV, 5.17 eV, and 8.31 eV. The closed form shows resonances at 2.54 eV, 2.67 eV, 4.19 eV, and 6.06 eV. The resonances are due to the electronic transitions of the molecule in the two different forms calculated by Hueckel’s method. At the resonances mentioned above, there are significant changes in the real part of the refractive index.
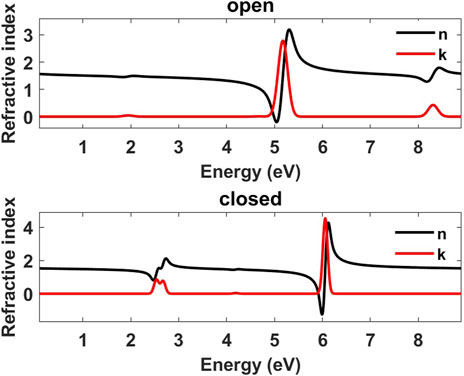
Figure 2. Real part n (black curve) and imaginary part k (red curve) of the refractive index for chromene in the open form (nco, top) and for chromene in the closed form (ncc, bottom).
A sketch of the Mach–Zehnder interferometer designed in this study is depicted in Figure 3. The interferometer consists of a photon source, two 50/50 beam splitters, BS1 and BS2, two mirrors M, and two detectors D1 and D2. The two layers of chromene are indicated with PCx (along the x direction after the beam splitter BS1) and PCy (along the y direction after the beam splitter BS1).
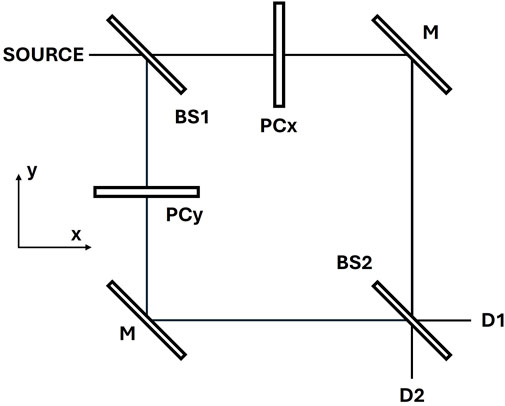
Figure 3. Sketch of the Mach–Zehnder interferometer with the photon source and the two detectors D1 and D2, the two mirrors M, the two 50/50 beam splitters BS1 and BS2, and the two photochromic layers PCx (along the x direction transmitted by BS1) and PCy (along the y direction reflected by BS1).
The state vectors and operators are adopted in agreement with Rioux (2019). The photon moving along the x-axis is represented by the state vector (Equation 7):
The photon moving on the y-axis is represented by the state vector (Equation 8):
The two mirrors are represented by the operator (Equation 9):
The two beam splitters are represented by the operator (Equation 10):
A 90-degree phase shift is assigned to the reflection. The chromene-based photochromic (PC) layer is represented by the operator (Equation 11):
where d is the thickness of the layer, and
Without the chromene-based photochromic layers in the Mach–Zehnder interferometer, the probability of measuring the photon with the detector D1 is (Equation 12)
Meanwhile, the probability of measuring the photon with the detector D2 is (Equation 13):
With the chromene-based photochromic layers in the Mach–Zehnder interferometer, the probability of measuring the photon with the detectors D1 is (Equation 14):
Meanwhile, the probability of measuring the photon with the detectors D2 is (Equation 15)
With both the chromene layers having the molecule in the closed form or open form, the probabilities at the two detectors are again
By impinging the chromene layer PCy with ultraviolet light, the chromene switches to the open form with a consequent change of its refractive index (nco, Figure 2 top), while chromene in PCx remains in its closed form (with refractive index ncc, Figure 2 bottom). Because of the different refractive indexes of the two layers PCx and PCy, the phase shifts will be different in the two arms of the Mach–Zehnder interferometer. In the case of a photon at a wavelength of 454 nm, the probabilities at the two detectors are
Conclusion
In this work, two chromene-based photochromic layers were inserted into the arms of a Mach–Zehnder interferometer. The absorption of light by chromene was studied by using Hueckel theory to determine the complex, wavelength-dependent refractive index. Impacting ultraviolet light on one of the chromene layers induces a transition from the closed to the open form of the chromene, resulting in different phase shifts in the two arms of the interferometer. This results in a change in the probability of detecting a photon by the two detectors after the second mirror of the Mach–Zehnder interferometer. Such an experiment may be of interest to the scientific community working in quantum information and quantum communications. Usually, modulators for Mach–Zehnder interferometers are based on the electro-optic effect (Palacios-Berraquero et al., 2017; Renaud et al., 2023). Obviously, this strategy needs electrical contacts to control the modulator. Should one wish to avoid using electrical contacts, other stimuli that do not require electrical contacts could be used. An example is the thermo-optical effect, with the change in refraction due to temperature change. In particular, the phase transition of some materials, such as the insulator-to-metal phase transition of vanadium oxide, can be exploited (Briggs et al., 2010). The photochromic effect of a polymer doped with molecules, was also used for a Mach–Zehnder interferometer. In this study, a small molecule was used to create a single-photon Mach–Zehnder interferometer in order to engineer a quantum communication simulation.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
FS: writing–review and editing, writing–original draft, methodology, funding acquisition, and conceptualization.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme [grant agreement No. (816313)].
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Barachevsky, V. A. (2018). Advances in photonics of organic photochromism. J. Photochem. Photobiol. A Chem. 354, 61–69. doi:10.1016/j.jphotochem.2017.06.034
Boelke, J., and Hecht, S. (2019). Designing molecular photoswitches for soft materials applications. Adv. Opt. Mater. 7, 1900404. doi:10.1002/adom.201900404
Briggs, R. M., Pryce, I. M., and Atwater, H. A. (2010). Compact silicon photonic waveguide modulator based on the vanadium dioxide metal-insulator phase transition. Opt. Express 18, 11192–11201. doi:10.1364/OE.18.011192
Castaing, V., Giordano, L., Richard, C., Gourier, D., Allix, M., and Viana, B. (2021). Photochromism and persistent luminescence in Ni-doped ZnGa2O4 transparent glass-ceramics: toward optical memory applications. J. Phys. Chem. C 125, 10110–10120. doi:10.1021/acs.jpcc.1c01900
DiFrancesco, M. L., Lodola, F., Colombo, E., Maragliano, L., Bramini, M., Paternò, G. M., et al. (2020). Neuronal firing modulation by a membrane-targeted photoswitch. Nat. Nanotechnol. 15, 296–306. doi:10.1038/s41565-019-0632-6
Gentili, P. L. (2022). Photochromic and luminescent materials for the development of chemical artificial intelligence. Dyes Pigments 205, 110547. doi:10.1016/j.dyepig.2022.110547
Gierczyk, B., Rode, M. F., and Burdzinski, G. (2022). Mechanistic insights into photochromic 3H-naphthopyran showing strong photocoloration. Sci. Rep. 12, 10781. doi:10.1038/s41598-022-14679-9
Guy, G. R., and Troy, V. V. (2024). Physical Chemistry. MIT OpenCourseWare. Available at: https://ocw.mit.edu/courses/chemistry/5-61-physical-chemistry-fall-2007/(Accessed February 5, 2022).
Hepworth, J. D., and Heron, B. M. (2006). “Photochromic naphthopyrans,” in Functional dyes (Elsevier), 85–135. doi:10.1016/B978-044452176-7/50004-8
Huckel Theory and HuLiS: a calculator that also describes mesomerism. (2013) Available at: http://www.hulis.free.fr/[Accessed June 8, 2020]
Kang, J.-W., Kim, J.-J., and Kim, E. (2002). All-optical Mach–Zehnder modulator using a photochromic dye-doped polymer. Appl. Phys. Lett. 80, 1710–1712. doi:10.1063/1.1459111
Kohandani, R., and Saini, S. S. (2022). Extracting optical absorption characteristics from semiconductor nanowire arrays. Nanotechnology 33, 395204. doi:10.1088/1361-6528/ac74cc
Naren, G., Hsu, C.-W., Li, S., Morimoto, M., Tang, S., Hernando, J., et al. (2019). An all-photonic full color RGB system based on molecular photoswitches. Nat. Commun. 10, 3996. doi:10.1038/s41467-019-11885-4
Ogilvie, J. F., and Fee, G. J. (2013). Equivalence of kramers-kronig and fourier transforms to convert between optical dispersion and optical spectra. MATCH 69, 249–262.
Palacios-Berraquero, C., Kara, D. M., Montblanch, A. R. P., Barbone, M., Latawiec, P., Yoon, D., et al. (2017). Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093–15096. doi:10.1038/ncomms15093
Pankove, J. I. (1975). Optical processes in semiconductors. Unabridged republication, with slight corrections. New York: Dover Publications, Inc.
Paternò, G. M., Colombo, E., Vurro, V., Lodola, F., Cimò, S., Sesti, V., et al. (2020). Membrane environment enables ultrafast isomerization of amphiphilic azobenzene. Adv. Sci. 7, 1903241. doi:10.1002/advs.201903241
Perevozchikova, P. S., Aliev, T. M., Nikitina, P. A., and Shepel, N. E. (2021). Synthesis and photochromic properties of a novel chromene derivative. INEOS OPEN. doi:10.32931/io2102a
Renaud, D., Assumpcao, D. R., Joe, G., Shams-Ansari, A., Zhu, D., Hu, Y., et al. (2023). Sub-1 Volt and high-bandwidth visible to near-infrared electro-optic modulators. Nat. Commun. 14, 1496. doi:10.1038/s41467-023-36870-w
Rioux, F. (2019). 8.86: simulating a quantum computer with a Mach-Zehnder interferometer. Chem. Libr. Available at: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Tutorials_(Rioux)/08%3A_Quantum_Teleportation/8.86%3A_Simulating_a_Quantum_Computer_with_a_Mach-Zehnder_Interferometer (Accessed February 27, 2024).
Scotognella, F. (2020). Multilayer plasmonic photonic structures embedding photochromic molecules or optical gain molecules. Phys. E Low-dimensional Syst. Nanostructures 120, 114081. doi:10.1016/j.physe.2020.114081
Solomon, G. C., Bergfield, J. P., Stafford, C. A., and Ratner, M. A. (2011). When “small” terms matter: coupled interference features in the transport properties of cross-conjugated molecules. Beilstein J. Nanotechnol. 2, 862–871. doi:10.3762/bjnano.2.95
Torres-Pierna, H., Ruiz-Molina, D., and Roscini, C. (2020). Highly transparent photochromic films with a tunable and fast solution-like response. Mater Horiz. 7, 2749–2759. doi:10.1039/D0MH01073A
Wiebeler, C., Bader, C. A., Meier, C., and Schumacher, S. (2014). Optical spectrum, perceived color, refractive index, and non-adiabatic dynamics of the photochromic diarylethene CMTE. Phys. Chem. Chem. Phys. 16, 14531–14538. doi:10.1039/C3CP55490B
Xu, F., and Feringa, B. L. (2023). Photoresponsive supramolecular polymers: from light-controlled small molecules to smart materials. Adv. Mater. 35, 2204413. doi:10.1002/adma.202204413
Appendix
Hamiltonian of chromene in its closed form:
Hamiltonian of chromene in its open form:
Keywords: photochromic materials, Mach–Zehnder interferometer, complex refractive index, Hueckel method, quantum communication
Citation: Scotognella F (2024) Quantum computation with photochromic films in a Mach–Zehnder interferometer. Front. Nanotechnol. 6:1422573. doi: 10.3389/fnano.2024.1422573
Received: 24 April 2024; Accepted: 15 October 2024;
Published: 11 November 2024.
Edited by:
Luca De Stefano, National Research Council (CNR), ItalyReviewed by:
Pier Luigi Gentili, Università degli Studi di Perugia, ItalyAtul Thakre, VIT University, India
Copyright © 2024 Scotognella. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Scotognella, ZnJhbmNlc2NvLnNjb3RvZ25lbGxhQHBvbGl0by5pdA==
 Francesco Scotognella
Francesco Scotognella
