
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
TECHNOLOGY AND CODE article
Front. Nanotechnol., 20 April 2022
Sec. Nanodevices
Volume 4 - 2022 | https://doi.org/10.3389/fnano.2022.851856
This article is part of the Research TopicBeyond CMOS Devices: From Novel Materials to Emerging ApplicationsView all 5 articles
Emerging two-terminal nanoscale memory devices, known as memristors, have demonstrated great potential for implementing energy-efficient neuro-inspired computing architectures over the past decade. As a result, a wide range of technologies have been developed that, in turn, are described via distinct empirical models. This diversity of technologies requires the establishment of versatile tools that can enable designers to translate memristors’ attributes in novel neuro-inspired topologies. In this study, we present NeuroPack, a modular, algorithm-level Python-based simulation platform that can support studies of memristor neuro-inspired architectures for performing online learning or offline classification. The NeuroPack environment is designed with versatility being central, allowing the user to choose from a variety of neuron models, learning rules, and memristor models. Its hierarchical structure empowers NeuroPack to predict any memristor state changes and the corresponding neural network behavior across a variety of design decisions and user parameter options. The use of NeuroPack is demonstrated herein via an application example of performing handwritten digit classification with the MNIST dataset and an existing empirical model for metal-oxide memristors.
Over the last decade, neuro-inspired computing (NIC) has experienced an immense growth, manifesting itself in a range of advances across theory, hardware, and infrastructure. Theoretical NIC has proposed a very wide range of artificial neural network (ANN) configurations, such as convolutional neural networks (LeCun et al., 1999) and LSTMs (Hochreiter and Schmidhuber, 1997), that may operate at various levels of weight and signal quantization (Dundar and Rose, 1995) and spanning across both spiking (Wu and Feng, 2018) and non-spiking (Sengupta et al., 2019) approaches. Evidently, this design process comprises multiple decision points that overall renders a very substantial and complex design space.
Simultaneously, research on novel hardware technologies has developed along multiple strands including fully digital architectures (Painkras et al., 2013; Akopyan et al., 2015; Davies et al., 2018), supra-threshold (Schmitt et al., 2017), and sub-threshold (Benjamin et al., 2014) analog architectures, with some more recent contenders (Burr et al., 2016) utilizing post-CMOS electronic components called “memristors” (Chua, 1971). This latter category is the focus of this work. Fundamentally, memristive devices are electrically tuneable (non-linear) resistors which have shown great promise in efficiently implementing the most numerous components found in neural networks: the synapses and mapping of their weights. Memristors feature the potential for extreme downscaling (Khiat et al., 2016), back-end-of-line (BEOL) integrability (Xia et al., 2009), sub-ns switching capability (Choi et al., 2016), and very low switching energy (Goux et al., 2012). Multiple families of memristive devices have been developed exploiting different electrochemical effects ranging from atomic-level effects in metal-oxides (Prodromakis et al., 2010) and atomic switches (Aono and Hasegawa, 2010) to bulk crystallisation/amorphisation effects in phase-change memory devices (Bedeschi et al., 2009) and magneto-resistive effects in spin-transfer torque (STT) devices (Vincent et al., 2015), to name a few. Each of these families features its own idiosyncrasies in terms of electrical behavior and is correspondingly described via distinct empirical models.
The broad interest in employing memristors within neuro-inspired hardware mainly stems from their multi-bit storage (Stathopoulos et al., 2017) capability and their simple architecture that can be tessellated in large arrays (Sivan et al., 2019). Those excellent features make memristors good candidates for multiply–accumulate operations (Serb et al., 2017) required in in-memory computing (IMC) applications. Moreover, the intrinsic properties of memristors are similar to those of biological synapses (Serrano-Gotarredona et al., 2013). Inspired by this fact, designs such as Serb et al. (2016) and Covi et al. (2016) successfully applied memristors as synapses in online learning with spike-timing-dependent plasticity (Markram et al., 1997), which is a learning rule inspired from biological NNs. Memristors have also been employed as components for NIC from offline classification (Yao et al., 2020) to online learning (Payvand et al., 2020). Along these lines, software-based simulation platforms designed for memristor-based neuomorphic systems become significant for fast validation of design ideas and predicting device behavior.
Current simulators (e.g., MNSIM (Xia et al., 2018) and NeuroSim (Chen et al., 2018)) focus more on circuit-level designs, serving as tools either to simulate the behavior of different hardware modules, or to estimate the performance of memristor-based neuromorphic hardware in integrated circuit designs. Sitting at a higher level of abstraction would be an “algorithm-level device-model-in-the-loop” simulator (or “algo-simulator” for short) designed to test functionally defined (as opposed to explicitly designed) circuits with memristive device models at algorithm level, for example, performing specific online or offline learning tasks with memristors as synapses in spike-based NNs. Such tools would allow fast verification of design concepts before serious hardware design effort is committed, in essence answering the question: Is my design likely to function given the knowledge on my memristive devices, assuming the rest of the circuit functions flawlessly? If yes, work can proceed to the next stage.
In this study, we present NeuroPack: a simulator for memristor-based neuro-inspired computing at algorithm level. NeuroPack is a complete, hierarchical framework for simulating spiking-based neural networks, supporting various neuron models, learning rules, memristor models, memristor devices, neural networks, and different applications. Written in Python, it can be easily extended and customized by users, as will be shown. NeuroPack also integrates an empirical memristor model proposed by Messaris Y. et al. (2017). Between processing algorithms and setting and monitoring memristor states, there is the significant step of applying a pulse of specific voltage and duration to trigger a memristor state change corresponding to some desired weight change calculated from learning rules. NeuroPack integrates a module to convert desired weight changes to estimated stimulation pulse parameters for bridging this gap. In addition, NeuroPack is also able to connect with commercially available instruments such as ArC 1 (Berdan et al., 2015) to use parameters extracted from real devices. In terms of applications, we use NeuroPack to demonstrate image classification on MNIST dataset in our ‘Results’ section. We also give result analysis for systems with different R tolerance, a parameter used in weight updating, and two biasing methods as examples to showcase that NeuroPack assists users to investigate how key design, device, and architectural factors affect memristor-based neuromorphic computing systems. Finally, NeuroPack includes a built-in analysis tool with a user-friendly graphic user interface (GUI) for visualizing and processing classification results. The main contributions of this work include:
1. Developing an algo-simulator for memristor-powered neuro-inspired computing with selectable neuron and device models, as well as learning rules
2. Modeling memristor state changes in neuro-inspired computing tasks given user-defined memristor parameters
3. Converting expected weight changes prescribed by learning rules into parameters of bias pulses used for triggering memristor state changes in weight updating
The rest of the article is organized as follows: In Section 2, we compared NeuroPack with related work. Section 3 introduces the architecture of NeuroPack with core parts and the workflow. Section 4 demonstrates an example application of handwritten digit recognition in MNIST dataset performed in NeuroPack, and Section 5 summarizes the article.
In this section, we compare NeuroPack with related neural network simulators with or without memristor models. Results are summarized in Table 1. We can broadly group these tools into three categories: 1) general algorithm-level SNN simulators, 2) hardware performance prediction (circuit level), and 3) more bespoke tools.

TABLE 1. Comparison of NeuroPack with other related work (Lammie et al., 2022).
First group tools focus on simulating spiking neural networks. Brian (Goodman and Brette, 2008) and snnTorch (Eshraghian et al., 2021) are such simulators. Brian targets the rapid prototyping of spiking neural network connectivity architectures, uses single-compartment neurons, and operates fully in Python. However, it does not integrate learning rules. snnTorch is designed to extend Pytorch, a mature tensor-based deep learning framework, to SNNs. It provides functions for backpropagation with surrogate gradient, spike generation, data conversion, and data visualization. It also supports CUDA implementation (i.e., the ability to run the model on NVidia’s “CUDA cores”), although it is not designed to provide information on hardware efficiency per se. To our knowledge, no such tool exists for memristor-based designs. The closest equivalent is memTorch (Lammie et al., 2020), which effectively extends Pytorch by introducing models of memristive devices, but does not include SNN support; it covers exclusively ANNs. It supports the “linear memristor” and VTEAM memristor models (Kvatinsky et al., 2015), and estimates non-ideal variation by generating random numbers given a predefined distribution. It is open source, and supports CUDA running. memTorch focuses on inference only, and does not include learning rule support.
Second group tools seek to predict the hardware performance of memristor-based microchip designs before they are fully developed and laid out. These have been progressively refined to take into account more and more parameters from basic ones such as technology node and array size to increasingly detailed ones such as line resistances. NeuroSim (Chen et al., 2018) and MNSIM (Xia et al., 2018) are such tools for parametrized designs of memristor-based neuromorphic integrated circuits. They receive parameters such as crossbar array size, memristive device ON and OFF resistances, technological node, and choice of read-out circuit module, and produce a prediction of layout area, dynamic power dissipation, latency, leakage power, and other such performance indicators. NeuroSim supports not only emerging non-volatile devices such as memristors but also mainstream memory devices. Similarly, MNSIM operates on the basis of a hierarchical, memristor-based neuromorphic computing system structure. Both NeuroSim and MNSIM allow simulation for both inference and training. Finally, TxSim (Roy et al., 2020) represents a further refinement over that mentioned above and evaluates training on memristor crossbars with DACs, memristor crossbars, and ADC non-linearity taken into consideration.
In the third group, we find work such as Demirag et al. (2021), which reported an online training task for spiking recurrent neural networks with phase-change memory models using the e-prop learning rule (Bellec et al., 2020). It developed an algorithm-level, fully Python-based, open-source simulator to perform online training. However, it is a more architecture-specific design focusing on spiking recurrent neural networks using the e-prop learning rule only.
Neuropack seeks to cover the area of general-purpose simulation sitting at algorithm level for memristor-based SNNs. Neuropack exhibits an unconventional combination of features: 1) it is oriented toward SNNs, 2) supports both inference and training operations, 3) is designed for extreme flexibility when it comes to neurons, memristive devices, and plasticity models, and 4) features an intimate connection to hardware by directly interfacing a memristive device characterization tool that can extract reasonably accurate models of physical devices.
NeuroPack is designed for predicting the outcomes of online learning or offline classification tasks under selectable neuron, plasticity and memristive device models, as well as for triggering and monitoring memristor state changes. To achieve those two tasks, NeuroPack’s workflow (see Figure 1) is divided into five parts: input file handling, virtual memristor array, neuron core, plasticity core, and analysis tool.
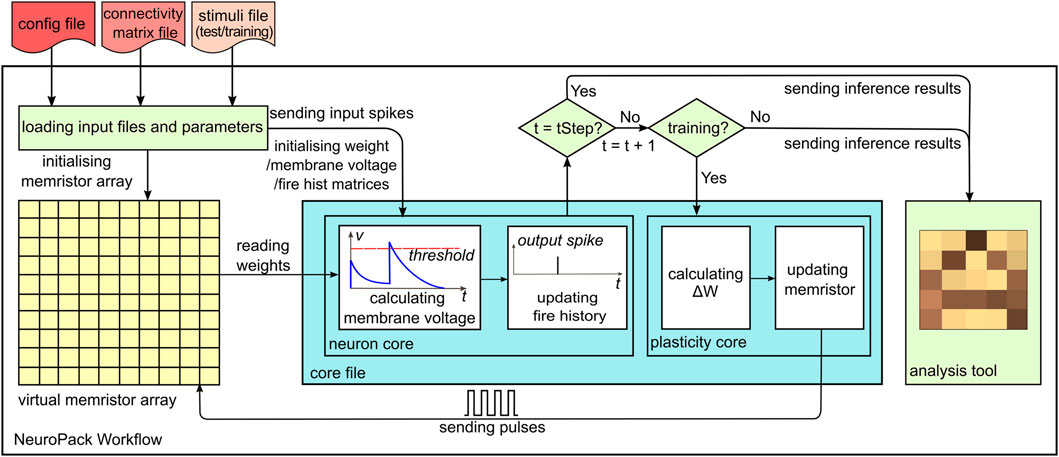
FIGURE 1. NeuroPack workflow. The system reads three configuration files: connectivity matrix, (neural) stimuli, and config. The memristor model is embedded within the virtual memristor array, which initializes a number of memristor devices according to instructions in the configuration and connectivity matrix files. Neuron models and learning rules are placed in the core file. In “updating fire history” stage, there are three separate steps: calculating fire states assuming neurons fire ‘freely’; adding network-level constraints; and updating the fire history matrix. “Calculating ΔW” is supported by most learning rules except STDP. By replacing the core file, users can apply different neuron models and learning rules.
For input data handling, there are three input files that need to be generated from users: configuration file, connectivity matrix file, and stimuli file. The configuration file contains the main parameters for building up NNs (e.g., network size, NN depth, number of neurons for each layer, etc.), setting up neuron models (e.g., leakage, noise scale, etc.), and initializing memristor devices (e.g., up and bottom boundaries for memristor resistance). The connectivity matrix file is used to define neuron connectivity and to map synapses to virtual memristors. The stimuli file stores both input signals and output labels. When loaded in the NeuroPack main panel, input signals and output labels are split by checking if the neuron is an output neuron using the information provided by the configuration file. Note: NeuroPack is designed to receive spike trains as an input. The specific encoding from raw (e.g., sensor) input to spikes should be performed independently before feeding the input to the simulator. All input files are loaded via the NeuroPack main panel. For more details on loading input files, please see Supplementary Material.
We now walk through the procedure for carrying out a classification task in a spiking network. First, the input signals to the neuron model are converted to spikes and saved in the stimuli file. Training and test datasets are loaded separately. Since NeuroPack uses a framework of consecutive, non-overlapping abstract time intervals, at each time step, an input neuron can either be spiking 1) or silent (0) lasting for exactly one time step. Next, the neuron core reads out the resistive states (RSs) from a virtual memristor array, and calculates internal variables, such as membrane voltages, according to the selected neuron model. The new fire states are then calculated in two steps: first, considering whether neurons are supposed to fire by checking if the membrane voltages surpass the threshold, and second, adding network-level constraints (e.g., winner-take-all networks). When the current input stimuli belong to a training dataset, inference results are sent to the plasticity core to trigger weight update as per selected learning rule. When the test dataset is processed, plasticity updates are skipped.
Weight updates happen during the plasticity phase. For STDP, long-term potentiation (LTP) or long-term depression (LTD) “events” are directly applied to memristor devices based on a calculation taking nothing into account except for spike-timing information. For other learning rules, other types of information may be necessary. These can be made available to the system configuration file. Importantly, there are two main conceptual ways of specifying plasticity events. The simpler way is to create a function that maps plasticity-relevant variables directly to pulsing parameters. Thereafter, the physics of the memristor (correspondingly the response of the memristor model) will determine the actual resistive state change, which in turn will be reflected into a weight change via a resistance-to-weight mapping function. The more complex route involves mapping plasticity-relevant variable configurations to a requested weight change, and then searching the device model (a model is necessary for this approach) for a solution, predicting that some set of pulse parameters will result in the required change. The same process will be repeated for the given number of samples. Inference results as well as internal variables and parameters, including membrane voltages, fire history, and weights, can be sent to the built-in analysis tool for further visualization and analysis.
Neuron models and learning rules are placed in “neuron core” and “plasticity core”, respectively, in Figure 1. For some learning rules, such as backpropagation which requires calculation of error gradients, the equations depend on the neuron model. Therefore, neuron models must be treated as first-class objects (in the “programming language” context of the term). However, a simpler solution implemented in this tool is to ensure that each learning rule is paired with one neuron core and placed together in the same “core” document because of the hefty interdependences between neuron and plasticity rule models. NeuroPack provides four example core files: leaky-integrate-and-fire neuron (LIF) (Abbott, 1999) with STDP, leaky-integrate-and-fire neuron with backpropagation (BP) (Rumelhart et al., 1986), Tempotron (Gütig and Sompolinsky, 2006), Izhikevich neuron (Izhikevich, 2003), and direct random target projection (DRTP) (Frenkel et al., 2021). Other neuron and plasticity rules can be customized according to users’ needs by simply using existing example cores as standard templates and introducing user-defined cores. In this section, we provide one specific example, where we use a LIF neuron model and BP to implement a fully connected multi-layer spiking neural network with winner-take-all functionality (Oster et al., 2009).
Leaky-integrate-and-fire (LIF) is a simple and relatively computationally friendly neuron model. Most neuromorphic accelerators, with (Guo et al. (2019)) or without memristors (Merolla et al. (2011); Yin et al. (2017a)), use LIF neurons. LIF has been implemented in NeuroPack using the following equations adapted from the differential form (Gerstner et al., 2014) by assuming discretised time steps:
where Vt represents membrane voltage at time t, W is the weight, xt is incoming spike to the neuron (considered 1 or 0), α ∈ [0, 1] is a leakage term, yt is the output spike, h(x) is the step function, and Vth is the neuron threshold. The equations describe that the neuron membrane voltage at any time step is determined by two parts: the weighted sum of incoming spikes at this time step and the membrane voltage at the last time step. If the membrane voltage surpasses the threshold, a spike is generated and the membrane voltage is reset. The cost function E at time step t is then given by
where N is the number of output neurons, i is the output neuron index, and
where η is the learning rate, k is the layer index, and K is the number of layers. Wk gives the weight matrix between layer k− 1 and k. ⊙ means element-wise multiplication. δ gives the error backpropagated from output neurons. Notably, gradient descent on SNNs is problematic because the step function h (Vt − Vth) is discontinuous. The common solution to address this issue is to use surrogate gradient descent (O’Connor et al., 2013) with straight through estimators (STEs) (Hinton, 2012; Bengio et al., 2013). In this work, we use a surrogate derivative proposed by Yin et al. (2017b). For the full derivation with the surrogate derivative, please refer to the supplementary material. We note that the only potentially problematic variable is
We now introduce winner-take-all (WTA) functionality, which constrains the output layer to have at most one firing neuron at each time step. This is performed by adding one softmax layer and making the neuron that has the largest softmax result fire:
The cost function correspondingly needs to be adjusted by taking a cross-entropy form:
where j is the index of the output neuron that should fire. Based on new cost function, weight changes are calculated as
Before application of WTA, all variables are accounted for; the freshly introduced softmax can be computed entirely within the same core file by simply adding network-level constraints. For the full derivation, please refer to the supplementary material.
In summary, to configure a multi-layer spiking neural network with WTA using LIF neurons with BP in NeuroPack, parameters including learning rate, noise scale, threshold, and leakage are loaded from the configuration file. Input spikes encoded from stimuli files are fed to the “neuron core” in the core file. The “neuron core” reads the memristor states from the device array, calculates membrane voltages, and updates fire history during the inference phase. If training is enabled, inference results, ground truth information as well as internal variables are loaded into the “plasticity core”, which then adjusts the memristive weights according to calculated weight changes, precisely as summarized in Figure 1.
When using virtual memristive devices, as is the case in Figure 1, a memristive model has to be used for predicting memristor RS as a function of read-out voltage and RS changes in response to plasticity events. Here, we use an empirical memristor model proposed by Messaris Y. et al. (2017), but other user-defined models are also compatible with NeuroPack. With different values of parameters, this model has shown flexibility to model large ranges of memristor devices. The model expresses RS switching rate
where An and Ap are scaling factors. The
While models may take different forms (e.g., charge-flux models (Shin et al., 2010)), the fundamental condition that is observed is that the device model is always fed a series of time-wise discretised voltages, and then must be able to calculate current and change in resistive state. Models that by default take current inputs are presently not supported. dt is treated as a predefined, fixed parameter and remains constant throughout the simulation in the current implementation. NeuroPack organizes memristor model instances in a virtual array with user-defined parameters as inputs by using a class ParametricDevice(*args) to create a device object and methods initialise(R) and step_dt(V, dt) in the same class to set the current resistance, and send a pulse with a magnitude of V and a pulse width of dt to the memristor device correspondingly. “Virtual memristor array” also provides methods, such as read (w,b) and pulse (w, b, v, pw), to read the RS of the device at a given wordline w and bitline b address within the virtual array and apply a pulse with magnitude of v and pulse width pw to the device at said address correspondingly. When we apply a ‘write’ operation, the pulse (w, b, v, pw) method is called. This takes pw and slices it into quanta of duration dt, and then applies the resulting group of ‘sub-pulses’ in succession. dt is a user-defined parameter stored in the configuration file. For a ‘read’ operation, we open an option for users to decide whether to consider the effect read-out voltages bring on memristor RSs, though it is ignored as default to save simulation time. It is these functions that neuron models and learning rules in the core files use to access memristor RS and trigger RS change. Using model parameter sets from different types of devices (different stacks or even devices with different underlying electrochemical mechanisms), as well as varying the parameters of the model in an exploratory fashion, are great tools to gain an understanding of how different memristive devices can influence the outcome of basic machine learning algorithms.
Most memristor-based neuromorphic designs (Hu et al., 2018); Li et al., 2018) store weights as memristor conductance and apply incoming inputs as voltages across memristors, so that the multiplication results can be easily attained by measuring the current according to Ohm’s law. Therefore, weights are mapped linearly to memristor conductance by default in NeuroPack, but users are allowed to define other mapping methods if needed. However, memristors being non-linear devices, obtaining well-controlled weight changes is challenging because the resistive state after application of a triggering pulse depends both on the current resistance state and biasing parameters (typ. pulse voltage and duration). To deal with this issue, NeuroPack includes a module for calculating biasing parameters, which is expected to produce the desired weight changes. In this module, inputs are memristor model parameters for initializing a memristor device, current state, target state, dt, and a list of tuples, each of which contains magnitude and pulse width to represent a pulse.
Inside the module, a ParametericDevice object is created by passing memristor model parameters. Resulting resistance for each set of pulse parameters is calculated by calling step_dt (V, dt) method. After all resulting resistance values are attained, distance to the resistance expected to be written to memristors is calculated, and the set of parameters that lead to the shortest distance will be selected. The pseudo code of this module has been included in the supplementary material.
The weight update scheme using the pulse parameter selection module is as follows: to begin with, user-defined R-tolerance, which is defined as the maximum
With Python as programming language, NeuroPack can be flexibly customized at both algorithm level and device level, and is able to encourage community-led engagement in the further development of this tool. At algorithm level, NeuroPack can apply user-defined neuron models and learning rules. As it is shown in Figure 1, neuron core and plasticity core are placed in the same core file. In NeuroPack, there are four example core files, which will be explained in detail in the next section. By writing and selecting user-defined core files, users can apply any customized neuron models and plasticity rules. At the device level, users can easily set and change memristor parameters to describe different device characteristics.
There are two main usage scenarios for NeuroPack. One is as a supporting tool to explore how different parameter values and settings affect classification performance in NIC tasks (Figure 2A). In this scenario, users can load parameters in the configuration file with different values to monitor how memristor devices behave differently, or to investigate how classification accuracy or error rate is affected. Another usage scenario is to use NeuroPack to test and validate NN algorithms, including neuron models and learning rules (Figure 2B). In this scenario, a user-defined core file or an example template is loaded to perform NN simulations. Users can then quickly test the algorithm and validate the idea by visualizing and displaying memristor device state and other NN key variables (such as membrane voltage).
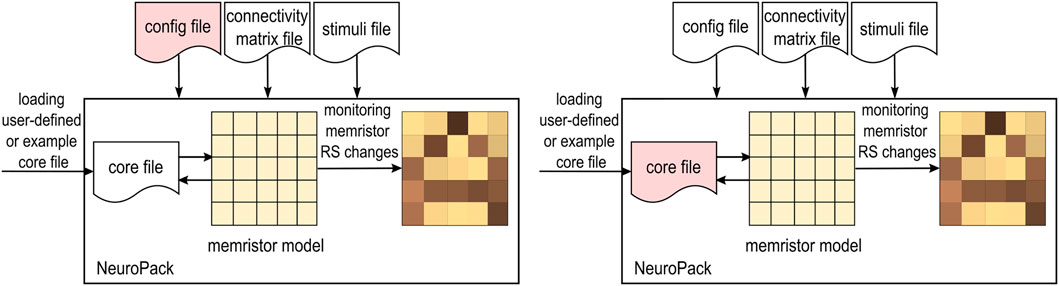
FIGURE 2. Usage scenarios for NeuroPack. Pink icons show the argeted part of design for exploration in different scenarios.
The visualization and analysis tool in NeuroPack provides a user-friendly GUI to display inference results. This tool is separated from the main panel of NeuroPack. When executing a classification task, NeuroPack saves variables for every sample including membrane voltages, input stimuli, fire history, output errors, and weights as measured from the memristors in a Numpy (.npz) file. Array-related variables such as weights are displayed in a color map, and neuron-related variables, for example, membrane voltages and fire history, are visualized in curves to show the changing tendencies.
We use an MNIST handwritten digit recognition task as an example application to validate NeuroPack. Original images with 28 × 28 pixels from the MNIST dataset have been cropped to 22 × 22 and binarised (see input images for 10 digits in Figure 3A). Background pixels and digit pixels are represented as 0 and 1, respectively. A single image is unrolled to a 484-dimensional vector with 0 and 1 only to be sent to input neurons in parallel. The spike encoding scheme sends a spike when the input bit is 1, and no spike for 0. The neural network used in this task is a 484-input 10-output two-layer feedforward winner-take-all spiking neural network with leaky-integrate-and-fire neuron model and gradient descent learning rule (see Figure 3E for neural network architecture for this task). To map all 484 × 10 synapses, a 100 × 100 array of memristors is used. The network was trained using 10,000 samples, and to evaluate the training effect quickly, we used a balanced 2000 subset from MNIST’s full 10,000 test image set. Please see supplementary section 6 for more details. In simulation, we use a “sample index”-based x-axis for performing an inference as opposed to having a real-time step. We acknowledge that this will have an impact in scenarios where the memristive devices used have volatile characteristics (and so real-time dynamics come into play), but due to the difficulties in controlling timing via a non–real-time operating system, adding this functionality currently remains a planned upgrade. Parameters used in NeuroPack for MNIST handwritten digit classification task can be found in Table 2. Memristor parameters listed in the table are based on the extraction method from Messaris I. et al. (2017) and devices presented in the work of Stathopoulos et al. (2017), given voltage range from 0.9 to 1.2 V for positive bias and from −0.9 V to −1.2 V for negative bias with 11 kΩ as initialized resistance. Therefore, pulse options used to update memristors are all within those ranges. The model yielded an estimated memristor operating range between 2.23 and 12.8 kΩ given a bias voltage of ±1.2V and 12.5–18.9 kΩ given a bias voltage of ±0.9 V. The resulting conductance caused by the bias voltages of ±0.9 V- ± 1.2 V is 5.3 × 10−5−4.48 × 10−4 S. To make sure the weights can be mapped to range (0, 1), the linear mapping between memristor conductance and weights is given by the equation below:
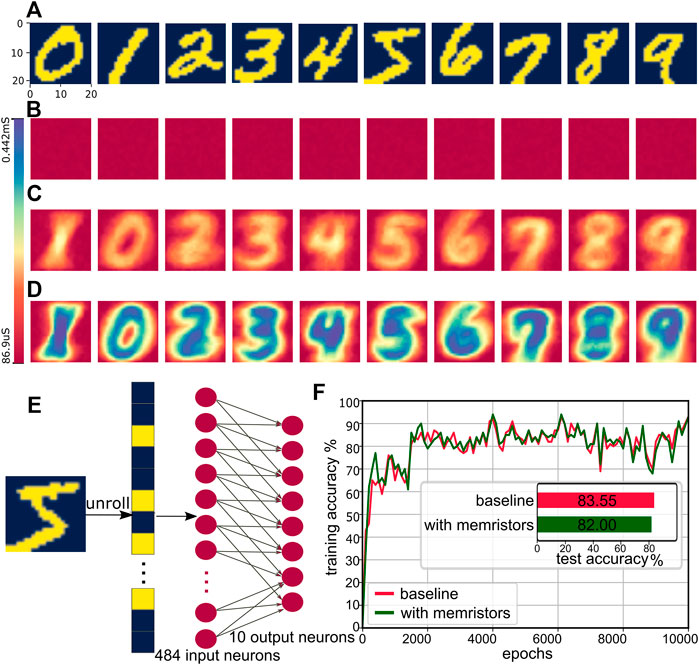
FIGURE 3. Image recognition task with TiOx memristor-based neural network simulation in NeuroPack. (A) Binary handwritten digits from MNIST dataset cropped to 22 × 22. Dark blue and yellow represent weights 0 and 1, respectively. (B)–(D) Conductance sets before training (B), after 2000 samples (C), and after 10,000 samples (D). Conductance spans from 86.9 uS to 0.442 mS, indicating final memristor RSs ranging from around 2.26–11.5 kohms (E) Concept diagram of spiking neural network used in this image recognition task. In practice, the network is fully connected. 22 × 22 -pixel images are unrolled to 484-bit input sending to 484 input neurons correspondingly as input spikes. In this task, a two-layer network with 484 input neurons and 10 output neurons is applied. (F) Accuracy curves over the training process for both memristor version and non-memristor version. We calculate and plot every 100 samples for clarity. Provided 2000 images from a separated test set, the memristor version and non-memristor version achieved an accuracy of 82.00 and 83.55%, respectively.
Before training, memristor RSs are initialized to 11 kΩ with a maximum variation of ±500 Ω. Memristor initial RSs are mapped to small weights close to the bottom boundary of the operating range, given conductance as the linear mapping of synaptic weights. Conductance maps before training, after training 2000 samples, and after training 10,000 samples can be found in Figures 3B,C,E. During training, conductance associated with digit pixels and labeled output neurons will be increased gradually, while other conductances stay small; therefore, targeted digits show up in the conductance sets along the training process. The weight sets show the same tendency as the mapping is linear. Figure 3F shows the accuracy evolution curve plotted for every 100 samples. 2000 images from a separated test set were fed to the network after training, and 1,640 out of 2000 got classified correctly, giving a general inference accuracy of 82.00%. The baseline given by the version storing weights directly without using memristor models achieved a test accuracy of 83.55%, which indicates that the accuracy bottleneck is not the memristor model. Further exploration regarding improving the accuracy can be found in supplementary section 7.
We now use NeuroPack to illustrate how the intimate device and programming protocol-related issue of selecting an appropriate R-tolerance affects recognition accuracy. Figures 4A,B show the training accuracy curves and test set accuracy results for different R-tolerance values. When R-tolerance is small (within 1%), the accuracy is not affected significantly. With a larger R-tolerance, training accuracy increases initially, but then starts to drop. This is also reflected in the corresponding test set accuracy. To investigate the causes, we look into the resistance changes in both stimulated and non-stimulated synapses with different R-tolerance values, as displayed in Figure 4C. The red line shows the baseline virtual resistance values calculated according to the weight mapping scheme for a stimulated synapse (specifically the one between input neuron 250 and output neuron 6) as yielded by a non-memristor, software synapse. The baseline shows a gradual decrease tendency throughout the whole training using 10,000 samples. In contrast, resistance update with different R-tolerance values cuts off increasingly early as R-tolerance increases: for 0.1, 1, 2, and 3%, saturation occurs roughly after training ∼ 9,000, 7,000, 1,000, and 100 samples, respectively. Intuitively speaking, if we use a smooth, continuous curve to fit the baseline trace, we find that its gradient progressively decreases. This can be explained by the decreasing gradient of the cost function during the training process. This indicates that the required resistance changes between successive time steps reduce as training continues. Meanwhile, R-tolerance is defined as
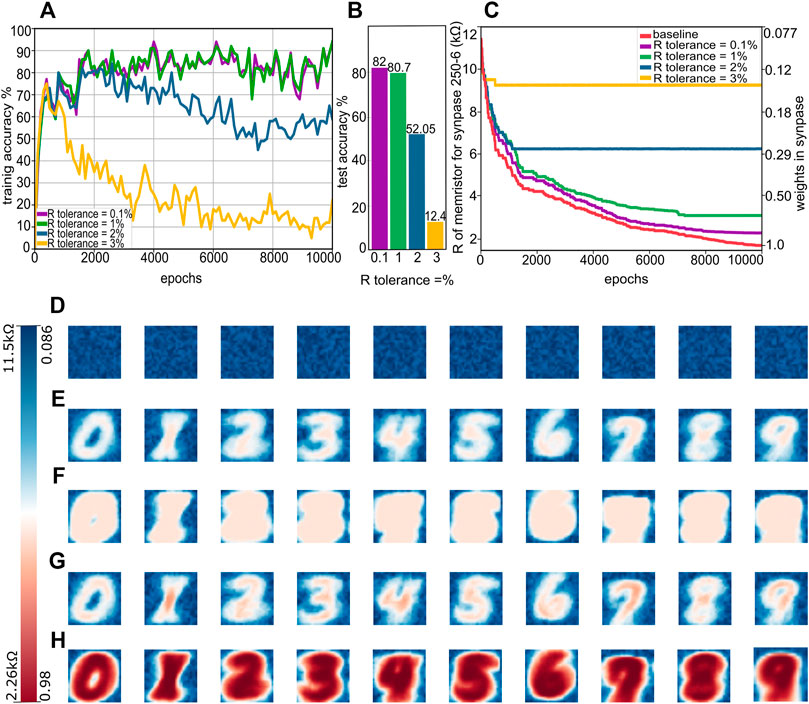
FIGURE 4. Classification accuracy affected by R tolerance. (A),(B) Accuracy in training and test phases with different R tolerance, respectively. (C) Resistance changes in a memristor representing a stimulated synapse (between input neuron 250 and output neuron 6) in training process with different R tolerance. Notice that we use virtual resistance values for the baseline (D)–(H). Memristor resistive states before training (D), after 1,000 samples for R tolerance of 2% (E) or 0.1% (F), and after 10,000 samples for R tolerance of 2%(G) or 0.1%(H). The total range of memristor RSs is from 2.26 to 11.5kΩ, which gives the range of weights as 0.98 to 0.086 correspondingly.
Finally, we present a comparison between two biasing schemes: 1) bias voltages are only applied to selected device (corresponding selector-based crossbar array) scenarios, and 2) half-bias voltages are also applied to unselected devices in the same bitlines and wordlines (as in selectorless crossbars). Figure 5A shows the accuracy of both versions. In the training accuracy curves, both versions show the same tendency with a noticeable gap in between. The test accuracy bar chart further displays the ∼20% gap. In order to explore the cause of the accuracy gap, we look into the resistance change curves of memristors representing a stimulated synapse (between input neuron 250 and output neuron 6) and a non-stimulated synapse (between input neuron 10 and output neuron 6). The baseline curves (red) are given by virtual resistance values of the baseline which stores weights directly without using memristor models. The resistance change for the stimulated synapse in the selector-based version (dark blue trace) shows the same decreasing tendency as the baseline (red), while the resistance in the selectorless version (orange) displays an increasing tendency. Zooming into samples 0 to 200, we observe unexpected resistance increases when no resistance update should happen for the selectorless scenario. This is because some memristors representing synapses connected to the neurons that are not supposed to fire have been applied pulses to increase the weights according to the learning rule, and they shared the same wordlines or bitlines with those whose resistance are supposed to decrease. A cycle of half-voltage bias only caused a trivial resistance increment, but there were many cycles of unexpected resistance drop happening in the same time step as there were many devices in the same wordlines/bitlines; therefore, the resistance increment accumulated and caused a large gap to the baseline. For the non-stimulated synapse, both the selector-based (purple) and the baseline (green) traces stay around their initial values throughout the whole training phase, while unexpected resistance increases occur in the selectorless version. However, the resistance in memristors representing the stimulated synapse is still slightly smaller than that of the non-stimulated synapse in the given examples in the selectorless scenario. Because of this slight resistance difference, the NN based on selectorless array is still able to learn images and classify correctly in some cases. We present the memristor resistive states before and after training for both versions in Figures 5C–E. Due to the half-voltage bias, the new memeristor operation range changes to 2.23 k-28kΩ, giving the new conductance range from 3.57 × 10−5 S to 4.48 × 10−4 S. Therefore, the linear mapping from conductance to weights now is changed to the following equation:
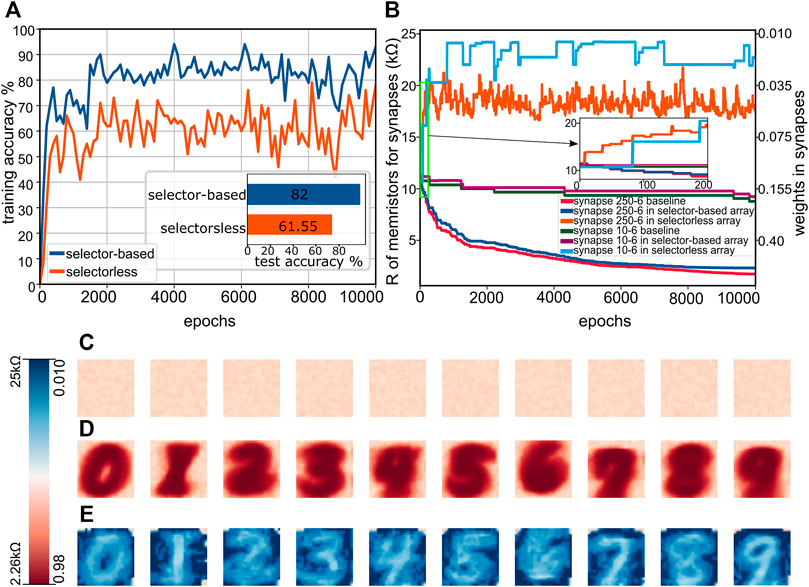
FIGURE 5. Classification with versions using selector-based and selectorless memristor arrays. (A) Accuracy in selector-based and selectorless arrays. (B) Resistance changes in memristors representing a stimulated (between input neuron 250 and output 6) and a non-stimulated (between input neuron 10 and output neuron 6) synapse (C)–(E) give memristor resistive states before training (C) and after training for both selector-based (D) and selectorless (E) versions. The color bar shows the memristor states from 2.26 k to 25kOmega, which give weights in range 0.98 to 0.01 correspondingly.
Memristor RSs are initialized as ∼11 kΩ before the training. After 10,000 samples, the resistive states of stimulated memristors in selector-based array (Figure 5D) decrease to a low resistive range (∼2.26 kΩ), while the non-stimulated stay in a high resistive range (∼11 kΩ). In the selectorless version, stimulated memristor RSs increase to a very high resistive range (∼18 kΩ), with non-stimulated ones increasing even higher to (∼22 kΩ). Thus, NeuroPack has helped us uncover the perhaps surprising result that even in the presence of invasive unexpected weight update, the NN is still capable of distinguishing the MNIST digits substantially better than chance, albeit with a very different weight distribution than the selector-based network.
In this study, we presented NeuroPack, a versatile algorithm-level software emulator for memristor-based neuro-inspired computing systems. NeuroPack allows users to customize the simulator at both system level and device level. This platform can work as a standalone tool to emulate neuro-inspired computing with different neuron models, learning rules, memristor models, different types and numbers of memristor devices, different neural network architectures, and different applications. We further showcased an application example using NeuroPack to simulate a two-layer SNN for handwritten digit recognition with the MNIST dataset. We explored how different factors such as R-tolerance in weight updating and biasing methods in different array structures affect system classification accuracy and quickly reached two conclusions: 1) Even a surprisingly lax 1% tolerance in resistive state (an engineering parameter) allows for sufficient training efficiency to closely match the performance of an ideal model for this architecture and dataset. This indicates that memristor-based systems may be able to achieve competitive performance without requiring expensive precision circuits at least in some scenarios. 2) Even in a scenario with unexpected weight updates due to the half-voltage biasing method in selectorless arrays, it may be possible to decode useful information from the state of the system after training. These investigations illustrate the role NeuroPack can play in assisting users to design and validate neuro-inspired concepts and improve system performance involving emerging nanoscale memory technologies. We envisage that by varying datasets, biasing and other experimental parameters, and device technology and connectivity patterns, users from across the community will be able to use this tool to generate the results that suit their needs quickly and efficiently.
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at https://github.com/hjq310/NeuroPack.
JH, AS, and TP wrote the manuscript. JH and SS developed the software design. JH delivered the experiments.
The authors acknowledge the support of the EPSRC FORTE Programme Grant (EP/R024642/1) and the RAEng Chair in Emerging Technologies (CiET 1819/2/93), as well as the EU projects SYNCH (824162) and CHIST-ERA net SMALL.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnano.2022.851856/full#supplementary-material
Abbott, L. F. (1999). Lapicque's Introduction of the Integrate-And-Fire Model Neuron (1907). Brain Res. Bull. 50, 303–304. doi:10.1016/S0361-9230(99)00161-6
Akopyan, F., Sawada, J., Cassidy, A., Alvarez-Icaza, R., Arthur, J., Merolla, P., et al. (2015). Truenorth: Design and Tool Flow of a 65 Mw 1 Million Neuron Programmable Neurosynaptic Chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 34, 1537–1557. doi:10.1109/TCAD.2015.2474396
Aono, M., and Hasegawa, T. (2010). The Atomic Switch. Proc. IEEE 98, 2228–2236. doi:10.1109/jproc.2010.2061830
Bedeschi, F., Fackenthal, R., Resta, C., Donze, E. M., Jagasivamani, M., Buda, E. C., et al. (2009). A Bipolar-Selected Phase Change Memory Featuring Multi-Level Cell Storage. IEEE J. Solid-state Circuits 44, 217–227. doi:10.1109/jssc.2008.2006439
Bellec, G., Scherr, F., Subramoney, A., Hajek, E., Salaj, D., Legenstein, R., et al. (2020). A Solution to the Learning Dilemma for Recurrent Networks of Spiking Neurons. Nat. Commun. 11. doi:10.1038/s41467-020-17236-y
Bengio, Y., Léonard, N., and Courville, A. C. (2013). Estimating or Propagating Gradients through Stochastic Neurons for Conditional Computation. CoRR abs/1308.3432.
Benjamin, B. V., Gao, P., McQuinn, E., Choudhary, S., Chandrasekaran, A. R., Bussat, J.-M., et al. (2014). Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 102, 699–716. doi:10.1109/JPROC.2014.2313565
Berdan, R., Serb, A., Khiat, A., Regoutz, A., Papavassiliou, C., and Prodromakis, T. (2015). A $\mu $ -Controller-Based System for Interfacing Selectorless RRAM Crossbar Arrays. IEEE Trans. Electron. Devices 62, 2190–2196. doi:10.1109/TED.2015.2433676
Burr, G. W., Brightsky, M. J., Sebastian, A., Cheng, H.-Y., Wu, J.-Y., Kim, S., et al. (2016). Recent Progress in Phase-Change_newline Memory Technology. IEEE J. Emerg. Sel. Top. Circuits Syst. 6, 146–162. doi:10.1109/JETCAS.2016.2547718
Chen, P.-Y., Peng, X., and Yu, S. (2018). Neurosim: A Circuit-Level Macro Model for Benchmarking Neuro-Inspired Architectures in Online Learning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 3067–3080. doi:10.1109/TCAD.2018.2789723
Choi, B. J., Torrezan, A. C., Strachan, J. P., Kotula, P. G., Lohn, A. J., Marinella, M. J., et al. (2016). High‐Speed and Low‐Energy Nitride Memristors. Adv. Funct. Mater. 26, 5290–5296. doi:10.1002/adfm.201600680
Chua, L. (1971). Memristor-the Missing Circuit Element. IEEE Trans. Circuit Theor. 18, 507–519. doi:10.1109/tct.1971.1083337
Covi, E., Brivio, S., Serb, A., Prodromakis, T., Fanciulli, M., and Spiga, S. (2016). Analog Memristive Synapse in Spiking Networks Implementing Unsupervised Learning. Front. Neurosci. 10, 482. doi:10.3389/fnins.2016.00482
Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y., Choday, S. H., et al. (2018). Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 38, 82–99. doi:10.1109/MM.2018.112130359
Demirag, Y., Frenkel, C., Payvand, M., and Indiveri, G. (2021). Online Training of Spiking Recurrent Neural Networks with Phase-Change Memory Synapses. CoRR abs/2108.01804.
Dundar, G., and Rose, K. (1995). The Effects of Quantization on Multilayer Neural Networks. IEEE Trans. Neural Netw. 6, 1446–1451. doi:10.1109/72.471364
Eshraghian, J. K., Ward, M., Neftci, E., Wang, X., Lenz, G., Dwivedi, G., et al. (2021). Training Spiking Neural Networks Using Lessons from Deep Learning. CoRR abs/2109.12894.
Frenkel, C., Lefebvre, M., and Bol, D. (2021). Learning without Feedback: Fixed Random Learning Signals Allow for Feedforward Training of Deep Neural Networks. Front. Neurosci. 15, 20. doi:10.3389/fnins.2021.629892
Gerstner, W., Kistler, W. M., Naud, R., and Paninski, L. (2014). Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition.
Goodman, D., and Brette, R. (2008). Brian: a Simulator for Spiking Neural Networks in python. Front. Neuroinform. 2. doi:10.3389/neuro.11.005.2008
Goux, L., Fantini, A., Kar, G., Chen, Y.-Y., Jossart, N., Degraeve, R., et al. (2012). “Ultralow sub-500nA Operating Current High-Performance TiN\Al2O3\HfO2\Hf\TiN Bipolar RRAM Achieved through Understanding-Based Stack-Engineering,” in 2012 Symposium on VLSI Technology (VLSIT), 159–160. doi:10.1109/VLSIT.2012.6242510
Guo, Y., Wu, H., Gao, B., and Qian, H. (2019). Unsupervised Learning on Resistive Memory Array Based Spiking Neural Networks. Front. Neurosci. 13, 1–16. doi:10.3389/fnins.2019.00812
Gütig, R., and Sompolinsky, H. (2006). The Tempotron: a Neuron that Learns Spike Timing–Based Decisions. Nat. Neurosci. 9, 420–428.
Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Hu, M., Graves, C. E., Li, C., Li, Y., Ge, N., Montgomery, E., et al. (2018). Memristor-based Analog Computation and Neural Network Classification with a Dot Product Engine. Adv. Mater. 30, 1705914. doi:10.1002/adma.201705914
Izhikevich, E. M. (2003). Simple Model of Spiking Neurons. IEEE Trans. Neural Netw. 14, 1569–1572. doi:10.1109/TNN.2003.820440
Khiat, A., Ayliffe, P., and Prodromakis, T. (2016). High Density Crossbar Arrays with Sub- 15 Nm Single Cells via Liftoff Process Only. Sci. Rep. 6, 32614–32618. doi:10.1038/srep32614
Kvatinsky, S., Ramadan, M., Friedman, E. G., and Kolodny, A. (2015). Vteam: A General Model for Voltage-Controlled Memristors. IEEE Trans. Circuits Syst. 62, 786–790. doi:10.1109/TCSII.2015.2433536
Lammie, C., Xiang, W., Linares-Barranco, B., and Azghadi, M. R. (2020). Memtorch: An Open-Source Simulation Framework for Memristive Deep Learning Systems. CoRR abs/2004.10971.
Lammie, C., Xiang, W., and Rahimi Azghadi, M. (2022). Modeling and Simulating In-Memory Memristive Deep Learning Systems: An Overview of Current Efforts. Array 13, 100116. doi:10.1016/j.array.2021.100116
LeCun, Y., Haffner, P., Bottou, L., and Bengio, Y. (1999). “Object Recognition with Gradient-Based Learning,” in Shape, Contour and Grouping in Computer Vision (Berlin, Heidelberg: Springer). doi:10.1007/3-540-46805-6_19
Li, C., Belkin, D., Li, Y., Yan, P., Hu, M., Ge, N., et al. (2018). Efficient and Self-Adaptive In-Situ Learning in Multilayer Memristor Neural Networks.
Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of Synaptic Efficacy by Coincidence of Postsynaptic Aps and Epsps. Science 275, 213–215. doi:10.1126/science.275.5297.213
Merolla, P., Arthur, J., Akopyan, F., Imam, N., Manohar, R., and Modha, D. S. (2011). “A Digital Neurosynaptic Core Using Embedded Crossbar Memory with 45pj Per Spike in 45nm,” in 2011 IEEE Custom Integrated Circuits Conference (CICC), 1–4. doi:10.1109/CICC.2011.6055294
Messaris, I., Nikolaidis, S., Serb, A., Stathopoulos, S., Gupta, I., Khiat, A., et al. (2017a). “A Tio2 Reram Parameter Extraction Method,” in 2017 IEEE International Symposium on Circuits and Systems (ISCAS), 1–4. doi:10.1109/ISCAS.2017.8050789
Messaris, Y., Serb, A., Khiat, A., Nikolaidis, S., and Prodromakis, T. (2017b). A Compact Verilog-A Reram Switching Model.
O'Connor, P., Neil, D., Liu, S.-C., Delbruck, T., and Pfeiffer, M. (2013). Real-time Classification and Sensor Fusion with a Spiking Deep Belief Network. Front. Neurosci. 7. doi:10.3389/fnins.2013.00178
Oster, M., Douglas, R., and Liu, S.-C. (2009). Computation with Spikes in a winner-take-all Network. Neural Comput. 21, 2437–2465. doi:10.1162/neco.2009.07-08-829
Painkras, E., Plana, L. A., Garside, J., Temple, S., Galluppi, F., Patterson, C., et al. (2013). Spinnaker: A 1-w 18-core System-On-Chip for Massively-Parallel Neural Network Simulation. IEEE J. Solid-state Circuits 48, 1943–1953. doi:10.1109/JSSC.2013.2259038
Payvand, M., Fouda, M. E., Kurdahi, F., Eltawil, A. M., Neftci, E. O., and Neftci, E. O. (2020). On-Chip Error-Triggered Learning of Multi-Layer Memristive Spiking Neural Networks. IEEE J. Emerg. Sel. Top. Circuits Syst. 10, 522–535. doi:10.1109/jetcas.2020.3040248
Prodromakis, T., Michelakis, K., and Toumazou, C. (2010). Switching Mechanisms in Microscale Memristors. Electron. Lett. 46, 63–65. doi:10.1049/el.2010.2716
Roy, S., Sridharan, S., Jain, S., and Raghunathan, A. (2020). Txsim: Modeling Training of Deep Neural Networks on Resistive Crossbar Systems. CoRR abs/2002.11151.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. Nature 323, 533–536. doi:10.1038/323533a0
Schmitt, S., Klahn, J., Bellec, G., Grubl, A., Guttler, M., Hartel, A., et al. (2017). “Neuromorphic Hardware in the Loop: Training a Deep Spiking Network on the Brainscales Wafer-Scale System,” in 2017 International Joint Conference on Neural Networks (IJCNN). doi:10.1109/ijcnn.2017.7966125
Sengupta, A., Ye, Y., Wang, R., Liu, C., and Roy, K. (2019). Going Deeper in Spiking Neural Networks: Vgg and Residual Architectures. Front. Neurosci. 13, 95. doi:10.3389/fnins.2019.00095
Serb, A., Bill, J., Khiat, A., Berdan, R., Legenstein, R., and Prodromakis, T. (2016). Unsupervised Learning in Probabilistic Neural Networks with Multi-State Metal-Oxide Memristive Synapses. Nat. Commun. 7. doi:10.1038/ncomms12611
Serb, A., Manino, E., Messaris, I., Tran-Thanh, L., and Prodromakis, T. (2017). “Hardware-level Bayesian Inference,” in Neural Information Processing Systems.
Serrano-Gotarredona, T., Masquelier, T., Prodromakis, T., Indiveri, G., and Linares-Barranco, B. (2013). STDP and STDP Variations with Memristors for Spiking Neuromorphic Learning Systems. Front. Neurosci. 7, 2–15. doi:10.3389/fnins.2013.00002
Shin, S., Kim, K., and Kang, S.-M. (2010). Compact Models for Memristors Based on Charge-Flux Constitutive Relationships. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 29, 590–598. doi:10.1109/tcad.2010.2042891
Sivan, M., Li, Y., Veluri, H., Zhao, Y., Tang, B., Wang, X., et al. (2019). All Wse2 1t1r Resistive Ram Cell for Future Monolithic 3d Embedded Memory Integration. Nat. Commun. 10. doi:10.1038/s41467-019-13176-4
Stathopoulos, S., Khiat, A., Trapatseli, M., Cortese, S., Serb, A., Valov, I., et al. (2017). Multibit Memory Operation of Metal-Oxide Bi-layer Memristors. Sci. Rep. 7. doi:10.1038/s41598-017-17785-1
Vincent, A. F., Larroque, J., Locatelli, N., Ben Romdhane, N., Bichler, O., Gamrat, C., et al. (2015). Spin-transfer Torque Magnetic Memory as a Stochastic Memristive Synapse for Neuromorphic Systems. IEEE Trans. Biomed. Circuits Syst. 9, 166–174. doi:10.1109/TBCAS.2015.2414423
Wu, Y.-c., and Feng, J.-w. (2018). Development and Application of Artificial Neural Network. Wireless Pers Commun. 102, 1645–1656. doi:10.1007/s11277-017-5224-x
Xia, L., Li, B., Tang, T., Gu, P., Chen, P.-Y., Yu, S., et al. (2017). Mnsim: Simulation Platform for Memristor-Based Neuromorphic Computing System. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 37, 1. doi:10.1109/TCAD.2017.2729466
Xia, Q., Robinett, W., Cumbie, M. W., Banerjee, N., Cardinali, T. J., Yang, J. J., et al. (2009). Memristor−CMOS Hybrid Integrated Circuits for Reconfigurable Logic. Nano Lett. 9, 3640–3645. doi:10.1021/nl901874j
Yao, P., Wu, H., Gao, B., Tang, J., Zhang, Q., Zhang, W., et al. (2020). Fully Hardware-Implemented Memristor Convolutional Neural Network. Nature 577, 641–646. doi:10.1038/s41586-020-1942-4
Yin, S., Venkataramanaiah, S. K., Chen, G. K., Krishnamurthy, R., Cao, Y., Chakrabarti, C., et al. (2017a). Algorithm and Hardware Design of Discrete-Time Spiking Neural Networks Based on Back Propagation with Binary Activations. CoRR abs/1709.06206. doi:10.1109/biocas.2017.8325230
Yin, S., Venkataramanaiah, S. K., Chen, G. K., Krishnamurthy, R., Cao, Y., Chakrabarti, C., et al. (2017b). “Algorithm and Hardware Design of Discrete-Time Spiking Neural Networks Based on Back Propagation with Binary Activations,” in 2017 IEEE Biomedical Circuits and Systems Conference (BioCAS), 1–5. doi:10.1109/BIOCAS.2017.8325230
Keywords: memristor, neuro-inspired computing, neuromorphic computing, neural networks, online learning, offline classification
Citation: Huang J, Stathopoulos S, Serb A and Prodromakis T (2022) NeuroPack: An Algorithm-Level Python-Based Simulator for Memristor-Empowered Neuro-Inspired Computing. Front. Nanotechnol. 4:851856. doi: 10.3389/fnano.2022.851856
Received: 10 January 2022; Accepted: 03 March 2022;
Published: 20 April 2022.
Edited by:
M. P. Anantram, University of Washington Tacoma, United StatesReviewed by:
Jason Eshraghian, University of Michigan, United StatesCopyright © 2022 Huang, Stathopoulos, Serb and Prodromakis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jinqi Huang, Si5IdWFuZ0Bzb3Rvbi5hYy51aw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.