
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mol. Biosci., 09 June 2023
Sec. Structural Biology
Volume 10 - 2023 | https://doi.org/10.3389/fmolb.2023.1159603
This article is part of the Research TopicFunctions, Working Mechanisms, and Regulation of Rotary ATPases and Ductin ProteinsView all 9 articles
We aim to develop a theory based on a concept other than the chemo-mechanical coupling (transduction of chemical free energy of ATP to mechanical work) for an ATP-driven protein complex. Experimental results conflicting with the chemo-mechanical coupling have recently emerged. We claim that the system comprises not only the protein complex but also the aqueous solution in which the protein complex is immersed and the system performs essentially no mechanical work. We perform statistical-mechanical analyses on V1-ATPase (the A3B3DF complex) for which crystal structures in more different states are experimentally known than for F1-ATPase (the α3β3γ complex). Molecular and atomistic models are employed for water and the structure of V1-ATPase, respectively. The entropy originating from the translational displacement of water molecules in the system is treated as a pivotal factor. We find that the packing structure of the catalytic dwell state of V1-ATPase is constructed by the interplay of ATP bindings to two of the A subunits and incorporation of the DF subunit. The packing structure represents the nonuniformity with respect to the closeness of packing of the atoms in constituent proteins and protein interfaces. The physical picture of rotation mechanism of F1-ATPase recently constructed by Kinoshita is examined, and common points and differences between F1- and V1-ATPases are revealed. An ATP hydrolysis cycle comprises binding of ATP to the protein complex, hydrolysis of ATP into ADP and Pi in it, and dissociation of ADP and Pi from it. During each cycle, the chemical compounds bound to the three A or β subunits and the packing structure of the A3B3 or α3β3 complex are sequentially changed, which induces the unidirectional rotation of the central shaft for retaining the packing structure of the A3B3DF or α3β3γ complex stabilized for almost maximizing the water entropy. The torque driving the rotation is generated by water with no input of chemical free energy. The presence of ATP is indispensable as a trigger of the torque generation. The ATP hydrolysis or synthesis reaction is tightly coupled to the rotation of the central shaft in the normal or inverse direction through the water-entropy effect.
Unveiling the mechanism of functional expression of an ATP-driven protein or protein complex is a most challenging subject in bioscience (Suzuki, 2018). It functions through the ATP hydrolysis cycle composed of binding of ATP to it, hydrolysis of ATP into ADP and Pi in it, and dissociation of ADP and Pi from it. Paradigmatic examples are myosin, a linear molecular motor, and F1- and V1-ATPases, rotary molecular motors (Suzuki, 2018; Kinoshita, 2021a). In this study, we deal primarily with F1- and V1-ATPases. F1-ATPase comprises three β subunits, three α subunits, and a γ subunit. The ATP hydrolysis cycle occurs in the β subunits, and the γ subunit rotates in the counterclockwise direction when F1-ATPase is viewed from the Fo side (Yoshidome et al., 2011; Kinoshita, 2021a). The B, A, and DF subunits in V1-ATPase correspond to the α, β, and γ subunits in F1-ATPase, respectively (Singharoy et al., 2019). That is, the ATP hydrolysis cycle occurs in the A subunits, and the DF subunit rotates in the counterclockwise direction when V1-ATPase is viewed from the Vo side. The central shaft, the γ subunit in F1-ATPase (α3β3γ complex) or the DF subunit in V1-ATPase (A3B3DF complex), performs unidirectional rotation.
Many experimental and theoretical efforts were devoted to the investigation of rotation mechanism of the rotary molecular motors, in particular, F1-ATPase. Typical examples of the theoretical studies are molecular dynamics (MD) simulations with coarse-grained (Koga and Takada, 2006; Kubo et al., 2020) or atomistic (Okazaki and Hummer, 2013; Czub and Grubmüller, 2014) models and analyses based on phenomenological or thermodynamic models (Nam and Karplus, 2019). These studies were conducted to explore specific subjects related to the mechanism or acquire microscopic information on the structure and properties of the α3β3γ complex. The elucidation of high efficiency suggested for the chemo-mechanical coupling (Toyabe et al., 2011; Toyabe and Muneyuki, 2015) has caught much attention. It was claimed that the chemo-mechanical coupling (transduction of chemical free energy of ATP to mechanical work) could be understood by a coarse-grained model (Vicatos et al., 2014) because the torque for rotating the γ subunit was generated only when an input of chemical free energy of ATP was incorporated, and the electrostatics played a dominant role (Mukherjee and Warshel, 2011; Mukherjee and Warshel, 2015). Despite the experimental and theoretical efforts mentioned above, the mechanism remains rather controversial. In our opinion, the problem in the previously reported studies is that the roles of water are unduly underestimated and a statistical-mechanical approach using a molecular model for water and treating the structure of the protein complex at the atomic level is missing.
According to the chemo-mechanical coupling, F1-ATPase transduces chemical free energy of ATP to mechanical work. F1-ATPase performs the mechanical work against the viscous resistance force by water for attaining the unidirectional rotation (Noji et al., 1997). In this case, F1-ATPase is regarded as the system and the aqueous solution in which F1-ATPase is immersed is regarded as the surroundings. The unidirectional movement of myosin along F-actin as well as the unidirectional rotation of the central shaft in F1-ATPase has been investigated extensively. Iwaki et al. (Iwaki et al., 2018) experimentally studied the effect of sucrose addition on the movement of myosin V. At a sucrose concentration of 1.25 mol/L, the viscosity of aqueous solution became ∼10 times higher but the movement velocity of the trailing head reduced only by a factor of ∼1/1.8: The viscous resistance force became ∼5.6 times stronger. Nevertheless, the head could move the same distance (∼77 nm) and perform ∼5.6 times more mechanical work. This result is not consistent with the chemo-mechanical coupling suggesting that the chemical free energy of ATP is transduced to mechanical work. By a novel experimental technique using high-speed atomic force microscopy (Kodera et al., 2010), for myosin V, Kodera et al. showed the following: The force responsible for the forward movement can be generated without transitioning through a state with ADP-Pi bound, meaning that no input of chemical free energy of ATP is required for the force generation; and even in the absence of ATP, when the trailing head is artificially detached from F-actin, it makes the forward movement (Kodera and Ando, 2014; Ngo et al., 2016). These observations conflict with the chemo-mechanical coupling.
Kinoshita and coworkers (Yoshidome et al., 2011; Yoshidome et al., 2012) have been developing a physical picture of rotation mechanism of F1-ATPase from a different point of view. Their approach is based on a statistical-mechanical theory wherein a molecular model is adopted for water, the structure of F1-ATPase is treated at the atomic level, and the effect of translational, configurational entropy of water in the system is highlighted. Recently, Kinoshita (Kinoshita, 2021a; Kinoshita, 2021b) constructed a more detailed physical picture where it is claimed that the system comprises not only F1-ATPase but also the aqueous solution in which F1-ATPase is immersed (i.e., the aqueous solution coexisting with F1-ATPase) and the system performs essentially no mechanical work during the rotation of the γ subunit. Strikingly, the torque driving the unidirectional rotation of the γ subunit is generated by water with no input of chemical free energy of ATP: A torque field acts on the γ subunit when it is accommodated within the α3β3 complex (such a torque field is absent for the γ subunit isolated). The mechanism of the torque generation becomes clearer as the argument proceeds; see Section 7.3.1 for the highlight. Though some of the basal concepts hypothesized in this physical picture need to be examined in further studies, such further examinations are difficult to achieve for F1-ATPase because crystal structures are experimentally available only for a limited number of different states. For V1-ATPase, on the other hand, crystal structures were experimentally solved by Murata and coworkers (Arai et al., 2013; Suzuki et al., 2016) for considerably more different states. Therefore, we have decided to perform a series of investigations based on statistical thermodynamics for V1-ATPase. Many of the results of theoretical analyses for V1-ATPase should be applicable to F1-ATPase as well. Our goal is to complete the physical pictures of rotation mechanisms of F1- and V1-ATPases the basal concepts of which are also applicable to the other ATP-driven proteins or protein complexes. This article provides an important first step in this direction.
Murata and coworkers (Arai et al., 2013; Singharoy et al., 2019; Arai et al., 2020) discussed how the unidirectional rotation of the DF subunit in V1-ATPase is induced by inferring the variations of chemical compounds bound to the three A subunits and the changes in structural properties of the three A-B subunit pairs during each ATP hydrolysis cycle. However, no physical rationalization was given from a statistical-thermodynamics viewpoint. In this study, we argue how the ATP hydrolysis cycle, variations of chemical compounds bound to the three A subunits, changes in the structural properties of the A3B3 complex, and unidirectional rotation of the DF subunit are correlated with one another using our statistical-thermodynamics analyses focused on the water-entropy effect.
As detailed in Supplementary Section S1, it was shown that many of the biological self-assembly processes in aqueous environment are driven by a gain of translational, configuration entropy of water. However, it is also essential to achieve and maintain the charge complementarity (see Section 2.2) in the structure formed. In F1- and V1-ATPases, the electrostatics should play important roles in the sense that the charge complementarity must not be broken during the rotation of the central shaft. Using all-atom MD simulations with explicit water for V1-ATPase, Singharoy and coworkers (Singharoy et al., 2017; Shekhar et al., 2022) showed that the electrostatic interactions at a specific residue-residue level and between a binding pocket and ATP, ADP+Pi, or ADP play important roles in the control of unidirectionality and rate of the rotation. The break of charge complementarity for a residue-residue pair must be compensated with the formation of charge complementarity for another residue-residue pair, and this is a significant factor in the rotation mechanism. In this study, we show that many of the fundamental characteristics of the rotation mechanisms of F1- and V1-ATPases can be elucidated by a model focused on the water-entropy effect and develop a theory based on a concept other than the chemo-mechanical coupling. Incorporation of the physical factors other than the water-entropy effect such as the electrostatics for making the theory more complete is a task for the future.
In the biological self-assembly, a gain of the translational, configurational entropy of water ascribed mainly to the mitigation of water crowding (i.e., entropic correlations among water molecules) in the system plays imperative roles (Kinoshita, 2013; Oshima and Kinoshita, 2015; Kinoshita, 2016) (Supplementary Section S1). The most fundamental self-assembly is protein folding (Figure 1). The presence of the backbone or a side chain of a protein generates an excluded volume (EV) to which the centers of water molecules are inaccessible (Harano and Kinoshita, 2005; Yoshidome et al., 2008; Yasuda et al., 2010; Hayashi et al., 2017; Hayashi et al., 2018). The formation of α-helix or β-sheet is accompanied by a reduction of the total EV generated by the backbone and an increase in the total volume available for the translational displacement of water molecules in the entire system, leading to a water-entropy gain. The formation undergoes an energy increase arising from the loss of protein-water hydrogen bonds. However, this energy increase is compensated with an energy decrease by the ensuring of protein intramolecular hydrogen bonds. Therefore, α-helix and β-sheet are very advantageous structural units from both entropic and energetic viewpoints (Hayashi et al., 2017; Hayashi et al., 2018). The close packing of side chains also leads to a reduction of the total EV followed by a water-entropy gain. The geometric properties of side chains play essential roles in the close packing. It was experimentally and theoretically shown that the water-entropy gain upon folding of apoplastocyanin (a protein with 99 residues) is as large as ∼670kB (kB is the Boltzmann constant) (Yoshidome et al., 2008). A protein folds so that its backbone and side chains can closely be packed with the formation of as much α-helix and β-sheet as possible (Hayashi et al., 2017; Hayashi et al., 2018). It is often, however, that the overall, sufficiently close packing cannot be achieved, in which case only the portions amenable to close packing are preferentially packed: In a protein, some portions are closely packed whereas the other portions are not. This nonuniform packing is more favorable than the overall uniform packing in terms of the water entropy (Yoshidome et al., 2011; Kinoshita, 2021a).
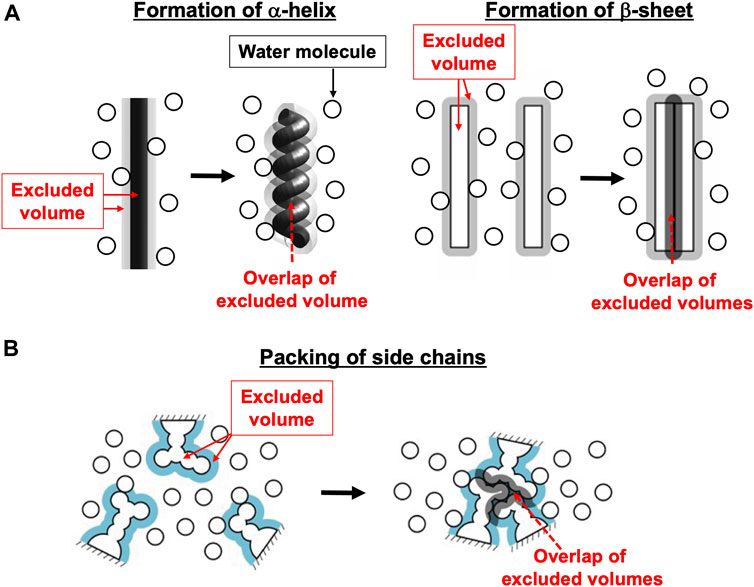
FIGURE 1. Basal processes in protein folding. (A) Formation of α-helix or β-sheet. (B) Close packing of side chains.
As rationalized in Supplementary Section S1, the translational, configurational entropy of water is a crucially important factor in the functional expression of F1-ATPase (Kinoshita, 2021a; Kinoshita, 2021b). Moreover, the nonuniform packing in F1-ATPase plays an essential role in its rotation mechanism. Hereafter, we use the terms, “packing efficiency (PE)” and “packing structure.” For a protein complex, from a viewpoint of the water entropy, it is required that not only the backbone and side chains of each protein in the complex but also the atoms in the protein interfaces be packed as closely as possible. However, it is often impossible to meet this requirement through uniform packing. The water entropy can become higher for nonuniform packing than for the uniform packing. The nonuniform packing means that only the portions of each protein and protein interfaces amenable to close packing are preferentially packed (Yoshidome et al., 2011; Kinoshita, 2021a). The PE signifies how close the packing is: When a protein in a complex or a protein interface is more closely packed, we state that its PE is higher. The physical meaning of the PE of a subunit or a subcomplex is made more definite in Section 4.1. The packing structure represents the differences in the PE among proteins and protein interfaces in a complex.
In determining which physical factors are more important than the others, it is absolutely necessary to employ an accurate model accounting for all the physical factors and compare their relative magnitudes quantitatively. By meeting this requirement for protein folding/denaturation problems (Inoue et al., 2020a; Inoue et al., 2020b) and protein-ligand binding processes (Yamada et al., 2019), we drew the conclusion that in aqueous environment the EV effect is a pivotal physical factor. Here, the EV effect works for increasing the translational, configurational entropy of water primarily by reducing the total EV. Matubayasi and coworkers (Kamo et al., 2016; Togunaga et al., 2018), using their all-atom MD simulation with explicit water based on a new solution theory in energy representation, showed that a useful modeling of protein folding is possible on the basis of not the electrostatics but the EV effect. (Graziano and coworkers (Merlino et al., 2017) also suggested that the EV effect is a principal driving force of protein folding.) This is because, for example, the decrease in protein intramolecular electrostatic interaction energy upon folding or transition to a more compact structure is accompanied by the penalty of electrostatic component of the energetic dehydration (i.e., the energy increase): The former is quite large but almost cancelled out by the latter that is equally large (Kinoshita, 2016; Kinoshita, 2021a), which can never be reproduced by a dielectric continuum model for water. In general, for a solute in aqueous solution, the EV effect becomes stronger as its size increases.
The intramolecular and intermolecular electrostatic attractive interactions of biomolecules do not work as a driving force of the biological self-assembly. However, the electrostatics is important in the following respect. When charged groups are buried upon protein folding or protein-ligand binding, the contact of oppositely charged groups (i.e., gain of electrostatic attractive interaction between groups with positive and negative charges) are essential for compensating for the electrostatic energetic dehydration penalty, namely, the loss of electrostatic attractive interactions between the group with a positive charge and water oxygens and between the group with a negative charge and water hydrogens. (Water oxygens and hydrogens carry negative and positive partial charges, respectively.) Thus, it is important to insure the charge complementarity in the biological self-assembly. The charge complementarity achieved in the stabilization of the structure of F1- or V1-ATPase is to be maintained during the rotation of the central shaft.
The ATP hydrolysis reaction is extremely slow in bulk aqueous solution in the absence of a catalyst. Since an ATP-driven protein or protein complex works as the catalyst for accelerating the reaction, it is involved in the reaction through the ATP hydrolysis cycle composed of binding of ATP to it, hydrolysis of ATP into ADP and Pi in it, and dissociation of ADP and Pi from it (Kinoshita, 2021a).
In F1-ATPase, a β subunit works as the catalyst. Let CX (mol/L) be the concentration of X. Unless otherwise specified, we consider the following aqueous-solution condition: CATP is sufficiently higher than CADP and CPi such that the reaction of ATP+H2O→ADP+Pi (ATP hydrolysis) occurs much more frequently than that of ATP+H2O←ADP+Pi (ATP synthesis) and the overall reaction is unidirectional and not ATP synthesis but ATP hydrolysis (Supplementary Section S3); and CATP is sufficiently high and CADP and CPi are sufficiently low such that on the whole, binding of ATP to and dissociation of ADP and Pi from a β subunit take place (Supplementary Section S4). It follows that the ATP hydrolysis cycle occurs spontaneously for lowering the system free energy.
Kinoshita’s physical picture (Kinoshita, 2021a; Kinoshita, 2021b) is distinguished from the others in the following respects.
(1) We must consider that the system comprises not only F1-ATPase but also the aqueous solution of ATP, ADP, and Pi in which F1-ATPase is immersed when we refer to the decrease in system free energy upon a state change of the system. The system exchanges energy with the surroundings (i.e., the heat bath) through heat and work. For the system comprising F1-ATPase and the aqueous solution such as the one employed in a single-molecule experiment, the pressure-volume work performed by the system against the pressure of the surroundings P, PΔV (ΔV is the change in system volume), is the only mechanical work. Since PΔV is negligibly small, the system performs essentially no mechanical work (for ΔV<0, the work is performed by the pressure of the surroundings). This argument is based on the fact that a structural change of a protein (Yoshidome et al., 2008; Inoue et al., 2020a) or protein-ligand binding (Yamada et al., 2019) is accompanied by only small ΔV and P|ΔV|<<kBT (the absolute temperature T is set at 298 K in this article) at P = 1 atm (Supplementary Section S1.1).
(2) It is suggested that the γ subunit is rotated by an entropic torque generated by water. The translational, configurational entropy of water is justifiably a pivotal component of the system free energy. A packing structure of F1-ATPase is stabilized so that this component can be almost maximized. During the ATP hydrolysis cycle which spontaneously occurs, however, the packing structure of the α3β3 complex is sequentially changed. The orientation of the γ subunit featuring its asymmetrical structure is also changed in accordance with the packing structure of the α3β3 complex for avoiding a water-entropy loss (the water entropy is strongly dependent on the orientation). The rotation of the γ subunit is thus induced.
The PE and packing structure related to the water entropy can be analyzed only by a statistical-mechanical approach using a molecular model for water and accounting for the complex structure at the atomic level. The measure of the PE of a subunit or subcomplex with nothing bound, η, is defined as
Here, S1 is the loss of water entropy (its major component is the translational, configurational entropy) upon the creation of a cavity, which geometrically matches the polyatomic structure of the subunit or subcomplex, in a fixed position within water, and S1∼S where S is the hydration entropy (Supplementary Section S1.1) (Hikiri et al., 2019). Smaller | η | implies higher PE. The measure of the PE of a subunit or subcomplex with chemical compound Y bound, ηY, is defined as
Smaller | ηY | implies higher PE. For the comparison between a subunit or subcomplex with nothing bound and that with Y bound in terms of the PE, Eqs 1a, 1b can be replaced by Eqs 2a, 2b, respectively:
It is unequivocal that the following equation holds:
Figure 2 illustrates the state stabilized in aqueous solution of nucleotides, which was experimentally observed (Bowler et al., 2007). Two nucleotides are bound to two of the three β subunits, respectively. AMP-PNP is an analogue of ATP and not hydrolyzed. AMP-PNP, which can thus be regarded as ATP whose hydrolysis does not occur, is used when the solution of a crystal structure is undertaken. States where the number of nucleotides bound to the three β subunits is zero, one, and three should be less stable (Supplementary Section S5), which is also the case for V1-ATPase. (Hereafter, unless otherwise mentioned, ATP and AMP-PNP are not distinguished.) It was observed that βDP, βTP, and βE take closed, closed, and open structures, respectively (Bowler et al., 2007). Namely, the backbone and side chains in a β subunit with a nucleotide bound is more closely packed than those in a β subunit with no nucleotides bound. Let β(Y) denote the PE of a β subunit to which chemical compound Y is bound and β denote the PE of a β subunit with nothing bound. It is experimentally definite that the following inequalities hold:
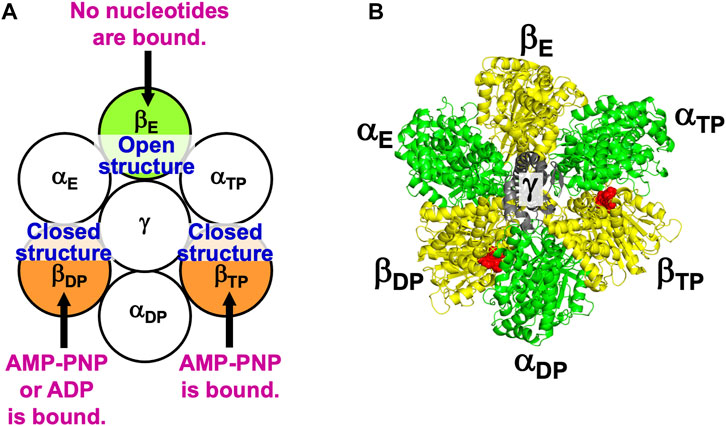
FIGURE 2. (A) State of F1-ATPase, α3β3γ complex, in which two nucleotides are bound to two of the three β subunits, respectively. “Nucleotides” signifies ATP, ADP, and related chemical compounds. Following the works of Walker and coworkers (Bowler et al., 2007), the three β subunits are named βDP, βTP, and βE, respectively, and the three α subunits are named αDP, αTP, and αE, respectively. In aqueous solution of AMP-PNP and ADP, the nucleotides bound to βDP and βTP are AMP-PNP and AMP-PNP, respectively. In aqueous solution of AMP-PNP, ADP, and azide, the nucleotides bound to βDP and βTP are ADP and AMP-PNP, respectively. Azide stabilizes the β subunit with ADP bound (Bowler et al., 2007). The structure of a β subunit with a nucleotide bound is closed whereas that without a nucleotide bound is open. (B) Top view of ribbon representation of α3β3γ-complex structure stabilized in aqueous solution of AMP-PNP and ADP (the Protein Data Bank (PDB) Code is 2JDI) (Bowler et al., 2007). The β subunits, α subunits, and γ subunit are colored yellow, green, and gray, respectively. AMP-PNP is represented by the red fused spheres. (AMP-PNP bound to each of the three α subunits is not shown.)
The state illustrated in Figure 2A is stabilized so that the water entropy can be almost maximized.
In aqueous solution of ATP, ADP, and Pi, even without the γ subunit, the structural rotation in the counterclockwise direction, “β[open]-β[closed]-β[closed] shown in Figure 2A” → “β[closed]-β[open]-β[closed] after 120° rotation” → “β[closed]-β[closed]-β[open] after 240° rotation” → ⋅⋅⋅, occurs in the α3β3 complex (Uchihashi et al., 2011). Here, β[open], for instance, denotes a β subunit possessing open structure. This experimental result indicates that the rotation mechanism is programmed in the α3β3 complex.
For F1-ATPase, we then define three subcomplexes regardless of the presence of the γ subunit as follows (Figure 3A):
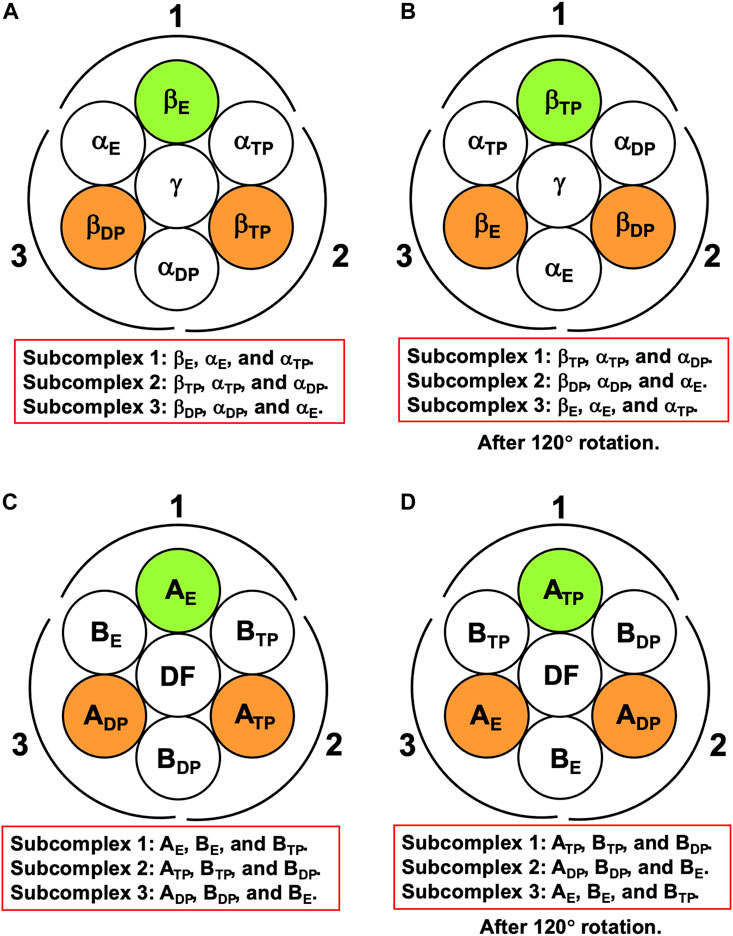
FIGURE 3. (A) Definition of subcomplexes 1, 2, and 3 for F1-ATPase. The three subcomplexes are named in respect of their positions. Two nucleotides are bound to βDP and βTP, respectively. (B) Subcomplexes 1, 2, and 3 after 120° rotation of γ subunit. (C) Definition of subcomplexes 1, 2, and 3 for V1-ATPase. The three subcomplexes are named in respect of their positions. Two nucleotides are bound to ADP and ATP, respectively. (D) Subcomplexes 1, 2, and 3 after 120° rotation of DF subunit.
The three subcomplexes are named in respect of their positions. Hence, after the γ subunit rotates by 120° (Figure 3B), subcomplex 3, for instance, now comprises βE, αE, and αTP. βDP, βTP, and βE take closed, closed, and open structures, respectively: The backbone and side chains are more closely packed in βDP or βTP than in βE.
It is the best to define the three subcomplexes for V1-ATPase here. They are defined as follows regardless of the presence of the DF subunit (Figure 3C):
The three subcomplexes are named in respect of their positions. Hence, after the DF subunit rotates by 120° (Figure 3D), subcomplex 3, for instance, now comprises AE, BE, and BTP. In this study, V1-ATPase is viewed from the Vo side and the central shaft, the DF subunit, rotates in the counterclockwise direction. The structure of the A3B3DF complex stabilized in aqueous solution of AMP-PNP and ADP is depicted in Figure 4. The naming for the six subunits of V1-ATPase adopted is the same as that for the six subunits of F1-ATPase. Hence, a detailed comparison between these two rotary molecular motors can be made. (In Supplementary Table S1, we summarize the differences between previous studies by Murata and coworkers (Arai et al., 2013; Suzuki et al., 2016) and this study in naming the A-B subunit pairs.) The subscript “DP” or “TP” for “A” in the naming does not necessarily imply that ADP or ATP is bound to the A subunit.
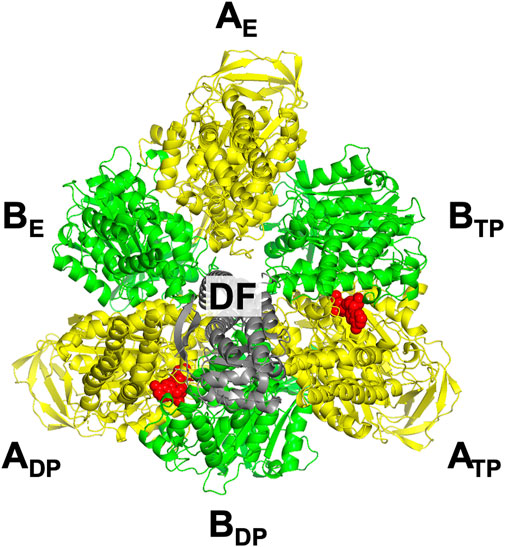
FIGURE 4. Top view of ribbon representation of A3B3DF-complex structure stabilized in aqueous solution of AMP-PNP and ADP. The A subunits, B subunits, and DF subunit are colored yellow, green, and gray, respectively. AMP-PNP is represented by the red fused spheres. (Unlike in the case of F1-ATPase, AMP-PNP bindings to the three B subunits do not occur.)
Kinoshita’s physical picture was constructed on the basis of observations in single-molecule experiments by Noji and coworkers (Yasuda et al., 1998; Yasuda et al., 2001; Adachi et al., 2007; Watanabe et al., 2010), those by Yoshida and coworkers (Shimabukuro et al., 2003), and theoretical analyses performed by Kinoshita and coworkers (Yoshidome et al., 2011; Yoshidome et al., 2012). The basal concepts hypothesized in this physical picture can be summarized as follows.
(1) Irrespective of the presence of nucleotides bound and the incorporation of the γ subunit, the PE of each subcomplex is determined by that of the β subunit in it. For instance, when the PE for a β subunit follows the order, “β subunit in subcomplex 3”>“β subunit in subcomplex 2”>“β subunit in subcomplex 1”, the PE for a subcomplex follows the order, “subcomplex 3”>“subcomplex 2”>“subcomplex 1”.
(2) The PE of a β subunit is variable depending on the chemical compound bound to it: ATP, ATP(ATP-H2O), ATP-H2O, ADP+Pi, or Pi. Here, ATP-H2O denotes ATP just before the ATP hydrolysis reaction and ATP(ATP-H2O) is an intermediate between ATP and ATP-H2O. (ATP(ATP-H2O) and ATP-H2O are the activated complexes.) The following inequality is justified as an extension of Order (4):
where “Nucleotide” signifies ATP, ATP(ATP-H2O), ATP-H2O, ADP+Pi, or ADP. We showed that β>β(Pi) in Order (6) holds as explained in what follows. Crystal structures of yeast F1-ATPase were solved for the following two states: a state which can be regarded as the catalytic dwell state where Pi was bound to βE and AMP-PNPs were bound to βDP and βTP, respectively; and the state after 16° rotation of the γ subunit (the first one is the state before the 16° rotation) (Kabaleeswaran et al., 2006). Since the ATP hydrolysis does not occur in βDP, the rotation is triggered by the dissociation of Pi from βE. We analyzed the packing structures of the two states by statistical-thermodynamics theory (Yoshidome et al., 2012) and all-atom MD simulation (Ito et al., 2013), and a significant result obtained was β>β(Pi). This result and the discussion in Section 7.1.2 lead to the following inequalities:
In the construction of the physical picture detailed in Section 7.1.2, it was assumed that the following inequality holds:
Comparing Order (7) with Orders (5) and (6), we notice that the inequality, β(ATP-H2O)>β(ATP(ATP-H2O))>β(ATP), is to be corroborated in further studies.
(3) The chemical compound bound to each β subunit is sequentially changed by the ATP binding to it, progress of ATP hydrolysis into ADP and Pi in it, and dissociation of ADP and Pi from it. As a result, the PEs of each β subunit and the subcomplex in which it is incorporated are also sequentially changed, which leads to sequential changes in packing structure of the α3β3 complex.
(4) The orientation of the γ subunit, on which the water entropy is strongly dependent, is changed in response to the change in packing structure of the α3β3 complex. That is, the sequential change in packing structure of the α3β3 complex induces the rotation of the γ subunit for retaining the water entropy.
(5) During each ATP hydrolysis cycle, the stabilized state of F1-ATPase, the state where two nucleotides are bound to two of the three β subunits, respectively, is maintained. In each cycle, one ATP molecule is hydrolyzed in bulk aqueous solution.
Some of the basal concepts described above are to be examined in further studies, and they are outlined in Table 1 (the others have already been justified). For F1-ATPase, however, crystal structures are experimentally known only for the α3β3γ complexes with no nucleotides bound and with two AMP-PNPs bound (Kinoshita, 2021a). A crystal structure of the α3β3γ complex with one AMP-PNP and one ADP bound was also solved, but the ADP binding was made by a bound azide ion (Bowler et al., 2007). There is not a crystal structure where ADP is bound to a β subunit without the azide ion. Hence, the difference in the PE between two β subunits to which ATP or AMP-PNP and ADP are bound, respectively, cannot be examined. Since crystal structures without the γ subunit (i.e., the α3β3 complex) are not found in the literature, effects due to the incorporation of the γ subunit cannot be analyzed. These problems can be solved by treating V1-ATPase instead.
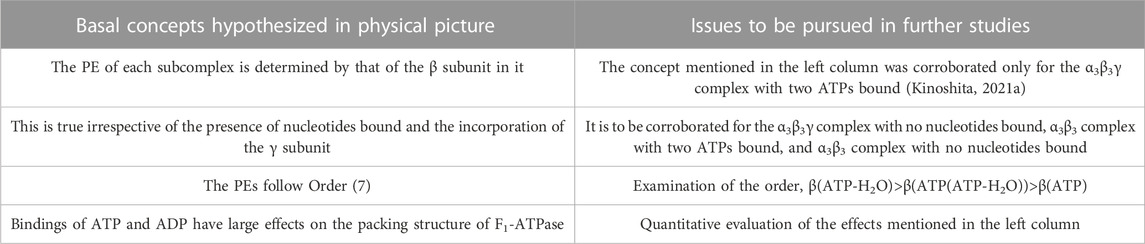
TABLE 1. Basal concepts to be examined in further studies for physical picture of rotation mechanism of F1-ATPase. β(Y) denotes the packing efficiency (PE) of a β subunit in F1-ATPase to which chemical compound Y is bound. “Nucleotides” signifies ATP, ADP, and related chemical compounds. ATP-H2O denotes ATP just before the ATP hydrolysis reaction, and ATP(ATP-H2O) is an intermediate between ATP and ATP-H2O (ATP(ATP-H2O) and ATP-H2O are the activated complexes).
Crystal structures were solved for the A3B3 complexes with no nucleotides bound (the PDB Code is 3VR2 and the resolution R is 2.8 Å) and two AMP-PNPs bound (3VR3 and R = 3.4 Å) and for the A3B3DF complexes with no nucleotides bound (3VR4 and R = 2.2 Å) and two AMP-PNPs bound (3VR6 and R = 2.7 Å) (Arai et al., 2013). A crystal structure is also available for the A3B3DF complex with two ADPs bound (5KNB and R = 3.3 Å): It is a state stabilized in aqueous solution of ADP in the absence of azide ions (Suzuki et al., 2016). Unlike for F1-ATPase, we can analyze not only the separate effects due to the binding of nucleotides and the incorporation of the DF subunit in the A3B3 complex but also the difference between two A subunits to which ATP and ADP are bound, respectively, in the PE. See Supplementary Section S6 for more information.
In this study, the hydration entropy is calculated by adopting fixed structures. We believe, however, that the basal aspects of our conclusions are not likely to be altered by accounting for the structural fluctuation.
For calculating the hydration entropy S1 (S1∼S: S1 can be referred to as the hydration entropy) of a solute (i.e., a chemical compound, protein, or protein complex) with a fixed structure, we employ our hybrid (Hikiri et al., 2019) of the angle-dependent integral equation theory (ADIET) combined with a multipolar model for water (Kusalik and Patey, 1988a; Kusalik and Patey, 1988b; Kinoshita, 2008) and the morphometric approach (MA) (Roth et al., 2006; Oshima and Kinoshita, 2015; Hayashi et al., 2018), the ADIET-MA method. Since the ADIET is employed, not only the translational contribution but also the orientational one is included in S1 though the latter is much smaller (Supplementary Section S1.1). More detailed descriptions of the ADIET and the MA are given in Supplementary Section S7. The high accuracy of the ADIET-MA method was corroborated in our earlier works (Hikiri et al., 2019; Yamada et al., 2019).
We analyze the PEs of ADP, ATP, and AE and those of the three subcomplexes. The key quantity is S1, and smaller | S1 | implies that the protein or subcomplex is more closely packed and its PE is higher. We use the crystal structures of the A3B3 complexes with no nucleotides bound and two AMP-PNPs bound (A3B3⋅2AMP-PNP) and those of the A3B3DF complexes with no nucleotides bound, two AMP-PNPs bound (A3B3DF⋅2AMP-PNP), and two ADPs bound (A3B3DF⋅2ADP). In A3B3⋅2AMP-PNP and A3B3DF⋅2AMP-PNP, AMP-PNP and Mg2+ are bound to ADP and ATP but nothing is bound to AE. In the calculation of S1, AMP-PNP is replaced by ATP. Since AE has fewer atoms than the other two A subunits, S1 of ATP-Mg2+ is added to S1 of any protein, protein pair, or protein complex including AE for impartial comparison among their PEs (i.e., Eqs 2a, 2b are adopted). A similar treatment is made for A3B3DF⋅2ADP. For all the crystal structures, the slight overlaps of the protein atoms are removed using a standard energy-minimization technique (Yoshidome et al., 2011).
The water-entropy gain upon contact of subunits I and J, ΔSIJ, is given by
Subunit pair I-J is taken from a complex, and subunits I and J are obtained by simply separating the pair. A-B, A-DF, and B-DF are considered as the subunit pairs. Larger ΔSIJ represents that the interface between subunits I and J are more closely packed, i.e., the PE of the interface is higher. For the interface between an A subunit with ATP bound and a B subunit, ΔSIJ is calculated for A⋅ATP+B→A⋅ATP-B (I = A⋅ATP and J = B where A⋅ATP is an A subunit with ATP bound).
We calculate the water-entropy gain ΔS1 (∼ΔS) upon association of ADP and BDP or ATP and BTP for the three cases where nothing, ATP, and ADP bind to ADP or ATP, respectively. ΔS1 upon ADP+ATP+BDP→ADP⋅ATP-BDP, for example, is “S1 of ADP⋅ATP-BDP”−(“S1 of ADP”+“S1 of ATP”+“S1 of BDP”). ADP, ATP, and BDP are obtained by simply separating ADP⋅ATP-BDP in the calculation. Larger ΔS1 implies higher affinity between the A and B subunits and closer packing of their interface.
The packing structure of A3B3DF⋅2ATP, one of the most stable states, is illustrated in Figure 5A. The hydration entropies of subcomplexes 1, 2, and 3 in this complex, which provide information on their PEs, are given in Table 2. (See Supplementary Section S9 emphasizing that the calculation results are reliable.) We find the following:
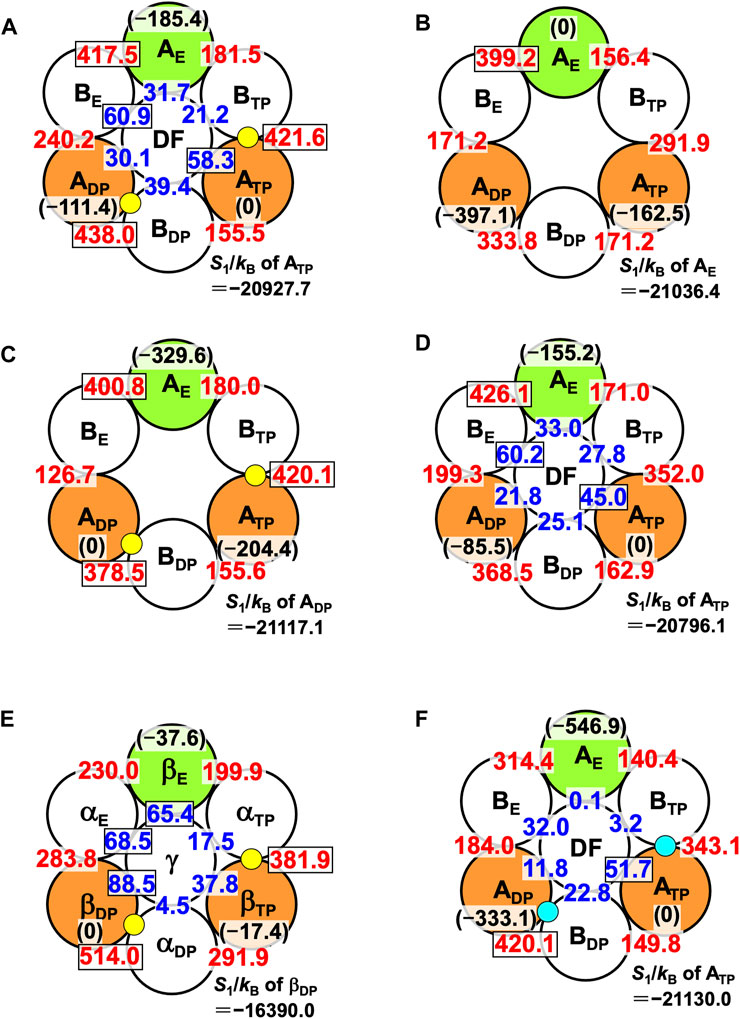
FIGURE 5. Packing structures of (A) A3B3DF⋅2ATP, (B) A3B3, (C) A3B3⋅2ATP, and (D) A3B3DF. A yellow circle denotes ATP. A number colored red quantifies ΔSIJ/kB (subunit I is an A subunit and subunit J is a B subunit; see Eq. 8). For example, ΔSIJ/kB in (A) for which subunits I and J denote ADP and BDP, respectively, is 438.0. A number colored blue quantifies ΔSIJ/kB (subunit I is an A subunit or a B subunit and subunit J is the DF subunit). For example, ΔSIJ/kB in (A) for which subunits I and J denote BE and the DF subunit, respectively, is 60.9. Larger ΔSIJ/kB implies closer packing of the interface of subunit pair I-J. In (A), for example, a number colored in black within parentheses denotes S1/kB (S1/kB<0) of an A subunit relative to S1/kB of ATP. For example, “S1/kB of AE”−“S1/kB of ATP” is −185.4. Smaller | S1/kB | implies closer packing or higher PE of an A subunit. The PE follows the order, ATP>ADP>AE. Relatively large numbers are surrounded by rectangles. (In (B), a number colored in black within parentheses denotes S1/kB (S1/kB<0) of an A subunit relative to S1/kB of AE. For example, “S1/kB of ATP”−“S1/kB of AE” is −162.5.) S1/kB of the A subunit which is the most closely packed among the three A subunits is also given. (E) Packing structures of catalytic dwell states for F1-ATPase (α3β3γ complex with two ATPs bound). S1/kB of the A or β subunit which is the most closely packed among the three A or β subunits is also given. (F) Packing structure of A3B3DF⋅2ADP. A right-blue circle denotes ADP. S1/kB of the A subunit which is the most closely packed among the three A subunits is also given.
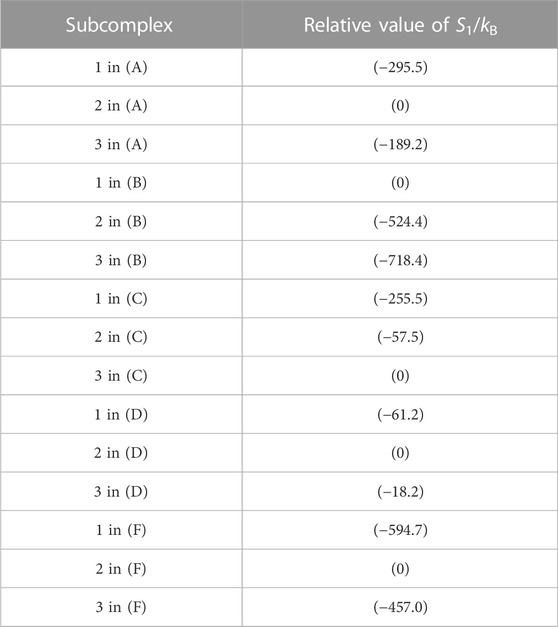
TABLE 2. Hydration entropies of subcomplexes 1, 2, and 3 in (A) A3B3DF⋅2ATP, (B) A3B3, (C) A3B3⋅2ATP, (D) A3B3DF, and (F) A3B3DF⋅2ADP. Subcomplexes 1, 2, and 3 are defined in Figure 7A. “1 in (A)”, for example, denotes subcomplex 1 in the A3B3DF complex with two ATPs bound (A3B3DF⋅2ATP). The “relative value of S1/kB” signifies S1/kB (S1/kB<0) of a subcomplex relative to S1/kB of the subcomplex with the smallest value of | S1/kB |. For example, “S1/kB of subcomplex 2 in (B)”−“S1/kB of subcomplex 1 in (B)” = −524.4. Smaller | S1/kB | implies closer packing or higher packing efficiency (PE) of the subcomplex. In (B), for example, the PE follows the order, subcomplex 1> subcomplex 2> subcomplex 3.
Thus, the PE of each subcomplex is determined by that of the A subunit in it, as in the case of α3β3γ⋅2ATP. Among the six A-B interfaces, ADP-BDP, ATP-BTP, and AE-BE are relatively more closely packed (ADP-BDP is the most closely packed). Among the six A-DF and B-DF interfaces, BE-DF and ATP-DF are relatively more closely packed (BE-DF is the most closely packed).
The packing structure of V1-ATPase (A3B3DF⋅2ATP) (Figure 5A) can be compared with that of F1-ATPase (α3β3γ⋅2ATP) (Figure 5E). The packing structure of F1-ATPase was unveiled in Ref. (Yoshidome et al., 2011). In F1-ATPase, “PE of subcomplex 3”>“PE of subcomplex 2”>“PE of subcomplex 1” and “PE of βDP”>“PE of βTP”>“PE of βE”.
We now discuss the values of ΔSIJ/kB for the DF-A and DF-B interfaces. ΔSIJ/kB is largest (60.9) for the DF-BE interface and smallest (21.2) for the DF-BTP interface (Figure 5A), and the difference between these two values, ∼40, is significantly large. The orientation of the DF subunit is determined so that the sum of the six values of ΔSIJ/kB can be maximized. The sum is ∼242. If the DF subunit took an unfavorable orientation and, for example, ΔSIJ/kB became 21.2 for all the six interfaces, the sum would be ∼127, giving rise to quite a large water-entropy loss of ∼115kB. Thus, the water entropy is strongly dependent on the orientation of the DF subunit for a packing structure of the A3B3DF complex given.
The packing structure of A3B3 is illustrated in Figure 5B. The hydration entropies of subcomplexes 1, 2, and 3 in this complex are included in Table 2. We find the following:
The PE of each subcomplex is determined by that of the A subunit in it. However, Orders (11) and (12) are different from Orders (9) and (10), respectively. Unlike in A3B3DF⋅2ATP, AE-BE is the most closely packed among the six A-B interfaces.
Even the structure of A3B3, the complex with no nucleotides bound and without the DF subunit, is asymmetric in the sense that the structures of the three A subunits (and the three B subunits) are different from one another. This result is in line with the feature of the crystal structure solved by Murata and coworkers (Arai et al., 2013). For F1-ATPase, on the other hand, it was observed using the high-speed atomic force microscopy that the structure of the α3β3 complex with no nucleotides bound and without the γ subunit is symmetric (Uchihashi et al., 2011).
Figure 5C illustrates the packing structure of A3B3⋅2ATP. The hydration entropies of subcomplexes 1, 2, and 3 in this complex are included in Table 2. We find the following:
The PE of each subcomplex is determined by that of the A subunit in it. Comparing the packing structures in Figures 5B, C, we notice that by the ATP binding to ADP and ATP, ADP-BDP and ATP-BTP become much more closely packed and AE, which was the most closely packed among the three A subunits, becomes the least closely packed (in other words, ADP and ATP become considerably more closely packed than AE). Among the six A-B interfaces, ADP-BDP, ATP-BTP, and AE-BE are relatively more closely packed as in the case of A3B3DF⋅2ATP (compare Figures 5A, C). The ATP binding to an A subunit results in not only higher PE of this A subunit but also closer packing of the interface between this A subunit and one of its adjacent B subunits.
The packing structure of A3B3DF is illustrated in Figure 5D. The hydration entropies of subcomplexes 1, 2, and 3 in this complex are included in Table 2. We find the following:
The PE of each subcomplex is determined by that of the A subunit in it. Among the six A-B interfaces, AE-BE is the most closely packed. Among the six A-DF and B-DF interfaces, BE-DF and ATP-DF are relatively more closely packed. Comparing the packing structures in Figures 5B, D, we notice that by the incorporation of the DF subunit, ADP-BDP and ATP-BTP become more closely packed and AE, which was the most closely packed among the three A subunits, becomes the least closely packed.
Comparison among Figures 5B–D leads us to the conclusion that the change in packing structure caused by the incorporation of the DF subunit is similar to that caused by the ATP bindings to ADP and ATP. Namely, the basal characteristics of packing structure shown in Figure 5A are constructed by the interplay of the two factors, the ATP bindings to two of the A subunits (factor 1) and the incorporation of the DF subunit (factor 2). The feature that all of ADP-BDP, ATP-BTP, and AE-BE are quite closely packed, which is found only in Figures 5A, C, originates primarily from factor 1. Factor 2 makes a larger contribution to the establishment of Orders (9) and (10) than factor 1. ADP-BDP becomes the most closely packed by factors 1 and 2. Another significant finding is that | S1/kB | of the A3B3 complex decreases by ∼1,670 upon the incorporation of the DF subunit, indicating that the DF subunit largely stabilizes the A3B3 complex.
The packing structure and the hydration entropies of subcomplexes 1, 2, and 3 of A3B3DF⋅2ADP can be compared to those of A3B3DF⋅2ATP in Figures 5A, F and in Table 2. Orders (9) and (10) hold in both of the two complexes. However, the packing structure of A3B3DF⋅2ADP possesses the following characteristics in comparison with that of A3B3DF⋅2ATP: The interfaces of the ATP-BTP and ADP-BDP pairs are looser; and the PEs of the three A subunits and the complex are considerably lower. It is important to look at the values of ΔSIJ/kB for the DF-A and DF-B interfaces. The sum of the six values of ΔSIJ/kB in A3B3DF⋅2ATP is ∼242 whereas that in A3B3DF⋅2ADP is only ∼122. This result is indicative that the A3B3 complex is much more stabilized in terms of the water entropy by the incorporation of the DF subunit in the presence of two ATPs bound than in that of two ADPs. On the basis of these results and the discussion on Figure 2A given above, the stability of the A3B3DF complex follows the order, A3B3DF⋅2ATP>A3B3DF⋅ATP⋅ADP>A3B3DF⋅2ADP, and the stability difference is quite large.
Table 3 presents the water-entropy gains upon association of ADP and BDP or ATP and BTP for the three cases where nothing, ATP, and ADP bind to ADP or ATP, respectively. In the Table, ADP, ADP-BDP, and ADP⋅ATP-BDP, for example, denote isolated ADP, complex of ADP and BDP, and complex of ADP with ATP bound and BDP, respectively. We find that the participation of ATP or ADP in the association increases the affinity between the A and B subunits. The increase is larger for ATP than for ADP.
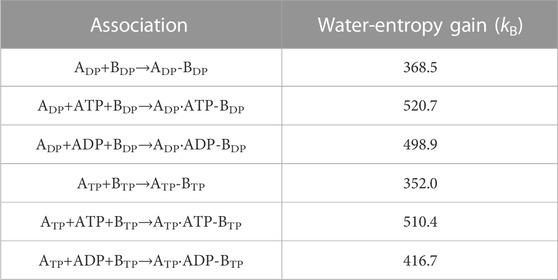
TABLE 3. Water-entropy gain upon association of B subunit and A subunit. Three cases where nothing, ATP, and ADP bind to ADP or ATP, respectively, are considered.
Significant results are as follows: Upon binding of a nucleotide, the PE of an A subunit becomes higher. A single-molecule experiment for V1-ATPase suggested that after ATP is hydrolyzed into ADP and Pi, Pi dissociates first (Iida et al., 2019). Therefore, the chemical compounds of interest are ATP, ADP+Pi, ADP, ATP-H2O, and ATP(ATP-H2O). As for the PE of an A subunit to which a chemical compound is bound, “A(ATP)>A(ADP)>A” is shown in this study (“β(ATP)>β(ADP)>β” should be applicable to F1-ATPase as well). We assume that the order for V1-ATPase corresponding to Order (7) for F1-ATPase is the following:
Here, A(Y) denotes the PE of an A subunit to which chemical compound Y is bound, and A denotes the PE of an A subunit with nothing bound. When the chemical compound binding to an A subunit changes from ATP to ADP, for example, the PE of this A subunit becomes lower (i.e., its packing becomes looser).
In Supplementary Section S10, we briefly discuss a case where protein side chains within the protein-ligand or protein-protein binding interface are significantly flexible (Rosenzweig and Kay, 2014; Wand and Sharp, 2018), possibly more flexible than those in an isolated protein, leading to an increase in the total conformational entropy upon binding (such a case is not applicable to F1- and V1-ATPases).
First, we review the physical picture recently developed by Kinoshita (Kinoshita, 2021a; Kinoshita, 2021b).
Noji and coworkers (Watanabe et al., 2010) reported that after the ATP hydrolysis into ADP and Pi within a β subunit, ADP dissociates from it first and Pi remains in it. The structures of states where any two of the nucleotides are bound to βDP and βTP, respectively, are similar. These states are collectively referred to as the “catalytic dwell state” (Abrahams et al., 1994; Bowler et al., 2007; Masaike et al., 2008; Okuno et al., 2008; Sieladd et al., 2008). In the catalytic dwell state considered here, the initial state in the ATP hydrolysis cycle, ATP-H2O and ATP are bound to βDP and βTP, respectively, and Pi remains in βE: It is one of the most stable states. The characteristics of its packing structure unveiled in our earlier work (Yoshidome, et al., 2011) are illustrated in Figure 6A. For comparison, the packing structure of the initial state in the ATP hydrolysis cycle, the catalytic dwell state, for V1-ATPase is illustrated in Figure 6B which is discussed in Section 7.2.1.
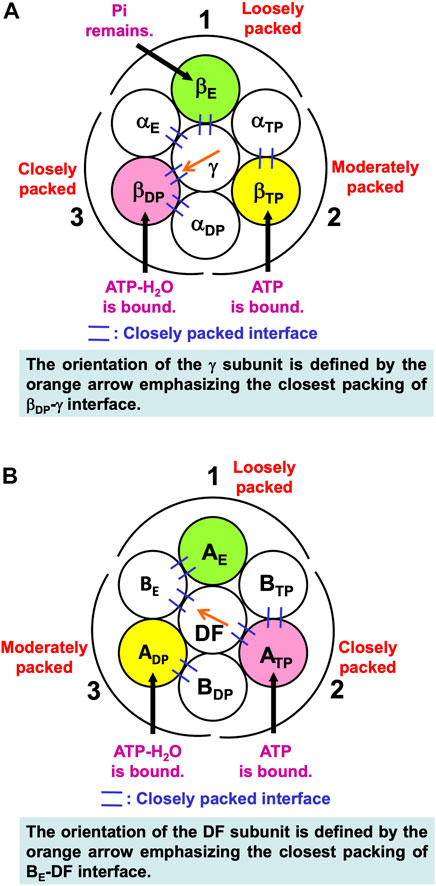
FIGURE 6. (A) Packing structure of catalytic dwell state of α3β3γ complex (F1-ATPase) stabilized in aqueous solution of ATP, ADP, and Pi. ATP-H2O and ATP are bound to βDP and βTP, respectively, and Pi remains in βE. ATP-H2O denotes ATP just before the ATP hydrolysis reaction (ATP-H2O is an activated complex). The packings of backbones and side chains in subcomplexes 1, 2, and 3 are relatively loose, moderate, and close, respectively: The packing efficiencies (PEs) of subcomplexes 1, 2, and 3 are relatively low, moderate, and high, respectively. (B) Packing structure of catalytic dwell state of A3B3DF complex (V1-ATPase) stabilized in aqueous solution of ATP, ADP, and Pi. ATP-H2O and ATP are bound to ADP and ATP, respectively, and nothing is bound to AE. The packings of backbones and side chains in subcomplexes 1, 2, and 3 are relatively loose, close, and moderate, respectively.
In Figure 6A, among the six β-α interfaces, βDP-αDP and βTP-αTP are relatively more closely packed (βDP-αDP is the most closely packed). βDP-αDP, for example, denotes the interface between βDP and αDP. Among the six β-γ and α-γ interfaces, βDP-γ, αE-γ, and βE-γ are relatively more closely packed (βDP-γ is the most closely packed). The same conclusion was drawn from a study using all-atom MD simulation (Ito and Ikeguchi, 2010) where the number of stable contacts within each of β-α, β-γ, and α-γ interfaces were analyzed. Here, the stable contact is defined as an inter-subunit residue pair maintaining its inter-atomic distance less than 4.5 Å for 98% of the snap shots along the MD trajectory.
Kinoshita’s physical picture can be recapitulated as follows (Figure 7). (Recall that under the aqueous-solution condition assumed, the ATP hydrolysis cycle occurs spontaneously as the dominant process.)
(1) The α3β3γ complex is in state (A), the catalytic dwell state shown in Figure 2A, where ATP-H2O, ATP, and Pi are bound to βDP, βTP, and βE, respectively. It was experimentally observed that βDP, βTP, and βE take closed, closed, and open structures, respectively (i.e., β(Nucleotide)>β(Pi) in Order (6) holds). The state changes as follows. The ATP hydrolysis (ATP-H2O→ADP+Pi), change of ATP to ATP(ATP-H2O), and Pi dissociation spontaneously occur in βDP, βTP, and βE, respectively. It was experimentally observed that the structure of βDP becomes half-open (Watanabe et al., 2010) (i.e., β(ATP-H2O)>β(ADP+Pi) in Orders (6) and (7) holds): The PE of βDP is lowered by the ATP hydrolysis. We denote the β subunit with this half-open structure by βDPHO. The PE of subcomplex 3 also becomes lower. ATP in βTP changes to ATP(ATP-H2O) with the result that the PE of βTP becomes higher (β(ATP(ATP-H2O))>β(ATP) in Order (7)). The β subunit with ATP(ATP-H2O) bound is denoted by β′TP. The PE of subcomplex 2 also becomes higher. Pi dissociates from βE, and the PE of βE becomes higher (β>β(Pi) in Order (7)). The PE of subcomplex 1 also becomes higher. The β subunit with nothing bound is denoted by β′E. The γ subunit rotates by 40° during state change (A)→(B) (Yasuda et al., 1998; Shimabukuro et al., 2003; Adachi et al., 2007; Watanabe et al., 2010) in response to the change in packing structure of the α3β3 complex.
(2) The α3β3γ complex is in state (B) where ADP+Pi, ATP(ATP-H2O), and nothing are bound to βDPHO, β′TP, and β′E, respectively. The state changes as follows. The ADP dissociation, change of ATP(ATP-H2O) to ATP-H2O, and ATP binding spontaneously occur in βDPHO, β′TP, and β′E, respectively. It was experimentally observed that the half-open structure of βDPHO becomes open (i.e., the packing of βDPHO becomes looser) upon dissociation of ADP from βDPHO (β(ADP+Pi)>β(Pi) in Orders (6) and (7) holds). The packing of subcomplex 3 also becomes looser. ATP(ATP-H2O)→ATP-H2O occurs in β′TP with the result of its higher PE (β(ATP-H2O)>β(ATP(ATP-H2O)) in Order (7)). The packing of β′TP and that of subcomplex 2 become closer. ATP binds to β′E, leading to its higher PE (β(ATP)>β in Order (7)). The packing of β′E and that of subcomplex 1 become closer. The γ subunit rotates by 80° during (B)→(C) (Yasuda et al., 1998; Shimabukuro et al., 2003; Adachi et al., 2007; Watanabe et al., 2010) by responding to the change in packing structure of the α3β3 complex.
(3) The α3β3γ complex is now in state (C) where ATP-H2O, ATP, and Pi are bound to βDP, βTP, and βE, respectively. Changes of βDP→βDPHO→βE, βTP→β′TP→βDP, and βE→β′E→βTP have occurred in subcomplexes 3, 2, and 1, respectively. The change in packing structure of the α3β3 complex has been followed by a rotation of 120° of the γ subunit in the counterclockwise direction, recovering the closely packed γ-βDP, γ-αE, and γ-βE interfaces.
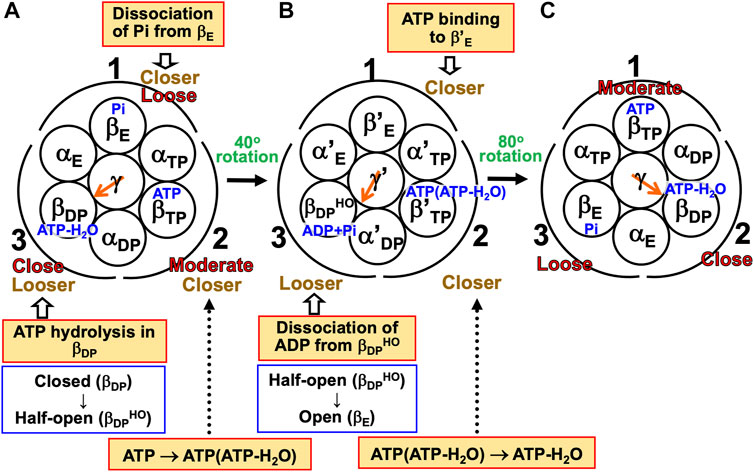
FIGURE 7. Physical picture of unidirectional rotation of γ subunit in F1-ATPase during one ATP hydrolysis cycle. In state (A), Pi, ATP, and ATP-H2O are bound to βE, βTP, and βDP, respectively. In (B), ATP(ATP-H2O) and ADP+Pi are bound to β′TP and βDPHO, respectively. The packings of βE and subcomplex 1 are loose in state (A) but they become closer in state change (A)→(B). Those of β′E and subcomplex 1 become further closer in (B)→(C). Those of βTP and subcomplex 1 are moderate in (C). Those of βTP and subcomplex 2 are moderate in (A) but they become closer in (A)→(B). Those of β′TP and subcomplex 2 become further closer in (B)→(C). Those of βDP and subcomplex 2 are close in (C). Those of βDP and subcomplex 3 are close in (A) but they become looser in (A)→(B). Those of βDPHO and subcomplex 3 become further looser in (B)→(C). Those of βE and subcomplex 3 are loose in (C). As mentioned in Section 4.3, even without the γ subunit, the α3β3 complex exhibits the structural rotation (Uchihashi et al., 2011; Yoshidome et al., 2011) illustrated in this figure.
For (A)→(B), it was experimentally and theoretically shown that the dissociation of Pi from βE as well as the ATP hydrolysis in βDP induces a rotation of the γ subunit in the counterclockwise direction (Kabaleeswaran et al., 2006; Yoshidome et al., 2012). The state where only two of ATP-H2O, ATP(ATP-H2O), ATP, and ADP+Pi are bound to two of the β subunits, respectively, is one of the most stable states. Nothing is bound to one of the β subunits (β′E) in state (B), allowing the binding of ATP to it, which is followed by the dissociation of ADP from an adjacent β subunit (βDPHO): (B)→(C) is induced. The packing structure stabilized as state (A) is maintained during each ATP hydrolysis cycle for avoiding a water-entropy loss.
The 120° rotation splits into the two substep rotations in (A)→(B) and (B)→(C). The rotation angle in (B)→(C) is larger than that in (A)→(B), because (B)→(C) includes the ATP binding by which a relatively larger state change is caused. It is desired that the structure of state (B) be solved experimentally for elucidating why the angles of the two substep rotations are 40° and 80°, respectively (Supplementary Section S17).
During one ATP hydrolysis cycle, the dissociation of Pi, dissociation of ADP, binding of ATP, and ATP hydrolysis within a β subunit leads to decreases in the system free energy of ΔG1<0, ΔG2<0, ΔG3<0, and ΔG4<0, respectively. The free-energy change due to the structural reorganization of the α3β3γ complex is kept quite small for the following reasons: When the PE of one of the subcomplexes is lowered, for example, the PEs of the other two subcomplexes are heightened so that the hydration entropy of the α3β3γ complex can be kept almost constant (i.e., the loss of water entropy can be avoided) together by the reorientation of the γ subunit. Though the overall structures of F1-ATPase before and after the 120° rotation are the same, one ATP molecule has been hydrolyzed in bulk aqueous solution, accompanying a decrease in system free energy of ΔG1+ΔG2+ΔG3+ΔG4 = ΔG∼−20kBT∼−12 kcal/mol at T = 298 K (Supplementary Section S3), the free-energy change upon the ATP hydrolysis in bulk aqueous solution. | ΔG4 | is much smaller than | ΔG | (Supplementary Section S11).
The packing structure of the initial state in the ATP hydrolysis cycle, the catalytic dwell state, is illustrated in Figure 6B. This state in which ATP and ATP-H2O are bound to two of the three A subunits, respectively, is one of the most stable states. The PEs of subcomplexes 1, 2, and 3 are relatively low, high, and moderate, respectively. Among the six A-B interfaces, ADP-BDP, ATP-BTP, and AE-BE are relatively more closely packed (ADP-BDP is the most closely packed). Among the six A-DF and B-DF interfaces, BE-DF and ATP-DF are relatively more closely packed (BE-DF is the most closely packed).
A single-molecule experiment for V1-ATPase showed that the 120° rotation of the DF subunit comprises 40° and 80° substeps (Iida et al., 2019). It also suggested the emergence of a stabilized state with three nucleotides bound, but we do not follow this suggestion for the reason mentioned above. On the basis of the calculation results described above, we can suggest the following rotation mechanism for V1-ATPase (Figure 8).
(1) The A3B3DF complex is in state (A) where ATP-H2O, ATP, and nothing are bound to ADP, ATP, and AE, respectively, the catalytic dwell state shown in Figure 6B. The state changes as follows. The ATP hydrolysis and the change of ATP to ATP(ATP-H2O) spontaneously occur in ADP and ATP, respectively. The PE of ADP is lowered by the ATP hydrolysis, ATP-H2O→ADP+Pi, due to A(ATP-H2O)>A(ADP+Pi) in Order (17). The A subunit with ADP+Pi bound is denoted by A’DP. The PE of subcomplex 3 also becomes lower. ATP in ATP changes to ATP(ATP-H2O) with the result that the PE of ATP becomes lower due to A(ATP)>A(ATP(ATP-H2O)) in Order (17). The A subunit with ATP(ATP-H2O) bound is denoted by A’TP. The PE of subcomplex 2 also becomes lower. The lowering of the PEs of ADP and ATP induces the heightening of the PE of AE. The PE of subcomplex 1 also becomes higher. AE changes to A’E. The DF subunit rotates by 40° during state change (A)→(B) by responding to the change in packing structure of the A3B3 complex.
(2) The A3B3DF complex is in state (B) where ADP+Pi, ATP(ATP-H2O), and nothing are bound to A’DP, A’TP, and A’E, respectively. The state changes as follows. Pi and ADP dissociate from A’DP with the result of its lower PE due to A(ADP+Pi)>A(ADP)>A in Order (17) (the PE becomes lower upon Pi dissociation and it becomes further lower upon ADP dissociation). The packing of A’DP and that of subcomplex 3 become looser. The change, ATP(ATP-H2O)→ATP-H2O, occurs in A’TP with the result of its lower PE (A(ATP(ATP-H2O))>A(ATP-H2O) in Order (17)). The packing of A’TP and that of subcomplex 2 become looser. ATP binds to A’E, leading to its higher PE (A(ATP)>A in Order (17)). The packing of A’E and that of subcomplex 1 become closer. The DF subunit rotates by 80° during (B)→(C) in response to the change in packing structure of the A3B3 complex.
(3) The A3B3DF complex is now in state (C) where ATP-H2O, ATP, and nothing bound to ADP, ATP, and AE, respectively. Changes of ADP→A’DP→AE, ATP→A’TP→ADP, and AE→A’E→ATP have occurred in subcomplexes 3, 2, and 1, respectively. The change in packing structure of the A3B3 complex has been followed by a rotation of 120° of the DF subunit in the counterclockwise direction, recovering the closely packed DF-ATP and DF-BE interfaces.
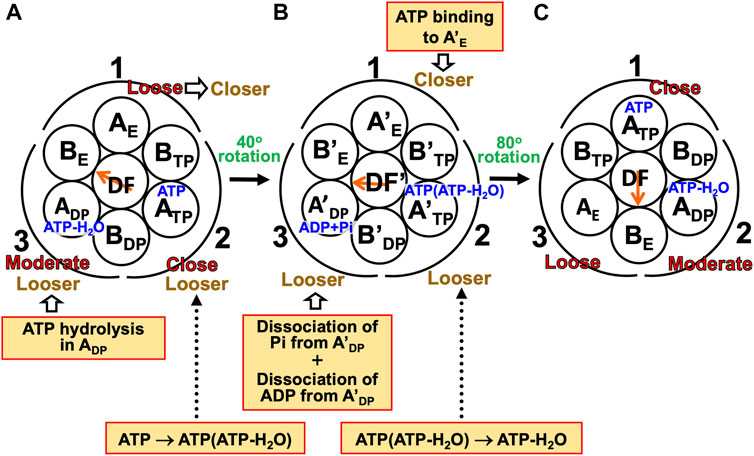
FIGURE 8. Physical picture of unidirectional rotation of DF subunit in V1-ATPase during one ATP hydrolysis cycle. In state (A), ATP and ATP-H2O are bound to ATP and ADP, respectively. In (B), ATP(ATP-H2O) and ADP+Pi are bound to A’TP and A’DP, respectively. ATP-H2O denotes ATP just before the ATP hydrolysis reaction, and ATP(ATP-H2O) is an intermediate between ATP and ATP-H2O (ATP(ATP-H2O) and ATP-H2O are the activated complexes). The packings of AE and subcomplex 1 are loose in state (A) but they become closer in state change (A)→(B). Those of A’E and subcomplex 1 become further closer in (B)→(C). Those of ATP and subcomplex 1 are close in (C). Those of ATP and subcomplex 2 are close in (A) but they become looser in (A)→(B). Those of A’TP and subcomplex 2 become further looser in (B)→(C). Those of ADP and subcomplex 2 are moderate in (C). Those of ADP and subcomplex 3 are moderate in (A) but they become looser in (A)→(B). Those of A’DP and subcomplex 3 become further looser in (B)→(C). Those of AE and subcomplex 3 are loose in (C).
During each ATP hydrolysis cycle, the stabilized state of V1-ATPase, the state where only two of ATP-H2O, ATP(ATP-H2O), ATP, and ADP+Pi are bound to two of the three A subunits, respectively, is maintained. If one of the two chemical compounds bound is replaced by ADP, the stability becomes considerably lower.
Here, we assume, unlike in the case of state (A) shown in Figure 8, that ATP, ATP-H2O, and nothing are bound to ADP, ATP, and AE, respectively, and the ATP hydrolysis reaction occurs in ATP in (A)→(B). If the packings of backbones and side chains in subcomplexes 2 and 3 are relatively close and moderate, respectively, the PE of ATP should be higher than that of ADP [i.e., A(ATP-H2O)>A(ATP)]. Hence, we assume that Order (7) where “β” is replaced by “A” holds. The DF subunit would then rotate in the inverse (i.e., clockwise) direction as illustrated in Supplementary Figure S2. On the other hand, with the assumption that the packings of backbones and side chains in subcomplexes 2 and 3 are relatively moderate and close, respectively, and Order (17) holds, the DF subunit would again rotate in the inverse direction as illustrated in Supplementary Figure S3. These results can readily be understood, because if the ATP hydrolysis reaction occurs in ATP, ATP with ATP-H2O bound changes to AE with nothing bound upon the 120° rotation, indicating the inverse rotation. Thus, the occurrence of ATP hydrolysis reaction in ADP as well as the packing structure of the A3B3DF complex is highly relevant to the rotation of central shaft in the normal (i.e., counterclockwise) direction observed in a single-molecule experiment (Suzuki et al., 2016).
We then discuss why the ATP hydrolysis reaction occurs in not ATP but ADP. For A3B3⋅2ATP and A3B3DF⋅2ATP, we calculate the values of the distance between E261 and ATP, L, in ADP and ATP. E261 is essential in the ATP hydrolysis reaction as shown in previous works (Liu et al., 1997; Dittrich et al., 2003). L is closely related to the PE of the A-B interface. The calculation result is given in Table 4. that Comparing the packing structures shown in Figures 5A, C, we notice that ATP-BTP is more closely packed than ADP-BDP and L in ATP is shorter in A3B3⋅2ATP, whereas the opposite is true in A3B3DF⋅2ATP. In A3B3⋅2ATP, since L’s in ADP and ATP are almost the same, the ATP hydrolysis reaction can occur either in ADP or ATP with almost equal probability. However, the incorporation of the DF subunit makes L in ADP shorter but L in ATP longer, which can lead to the preferential occurrence of the hydrolysis reaction in ADP. As for the packing structure of the α3β3γ complex (F1-ATPase), since βDP-αDP is more closely packed than βTP-αTP as observed in Figures 5A, E, it should be the case that L in βDP is shorter. Hence, the ATP hydrolysis reaction occurs in βDP, which is commensurate with the discussion made by Walker and coworkers (Bowler et al., 2007).
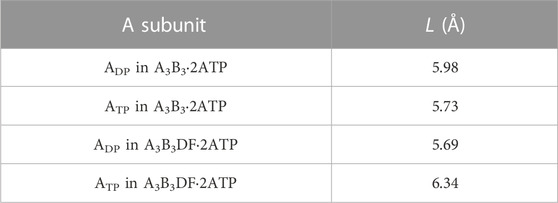
TABLE 4. Distance between E261 and ATP, L. L is defined as the distance between centers of the phosphorus atom (P) in the γ-phosphate of ATP and the carbon atom (C) in the carboxyl group of the side chain of E261. Shorter L implies higher probability of occurrence of the ATP hydrolysis reaction in the A subunit.
On the basis of the above discussion, we hypothesize for V1-ATPase that the incorporation of the central shaft in the A3B3 complex plays an essential role in the occurrence of ATP hydrolysis reaction in ADP. Without the central shaft, the ATP hydrolysis reaction occurs either in ADP or ATP with almost equal probability, giving rise to unattainability of the unidirectional rotation. Unlike in the case of the α3β3 complex (without the central shaft) for F1-ATPase, there is a possibility that the structural rotation of the A3B3 complex may not occur.
Kinoshita (Kinoshita, 2021a; Kinoshita, 2021b) claimed that water plays leading roles in the functional expression of F1-ATPase. In what follows, we refine his claim and describe it in detail. The statements are applicable to V1-ATPase when “α”, “β”, and “γ” are replaced by “B”, “A”, and “DF”, respectively.
First, we consider F-actin and a myosin head [e.g., myosin subfragment 1 (S1) (Kitamura et al., 1999)]. We assume that the position and structure of F-actin are fixed. Water (the aqueous solution is referred to simply as water when the water roles are emphasized) is included in the system. The free energy of the system is denoted by GSystem. (Since a structural change of a protein and a protein-ligand binding occur with the system volume being almost unchanged even under the isobaric condition (Yoshidome et al., 2008; Yamada et al., 2019; Inoue et al., 2020a), we use “free energy” instead of “Gibbs free energy” or “Helmholtz free energy.”) The structure and position of the myosin head change in the direction of lowering GSystem. For a prescribed structure of the myosin head, GSystem is variable depending on the position of the myosin head, and GSystem can be represented as a function of the Cartesian coordinates of the center of gravity of the myosin head, (x, y, z). The origin of the coordinate system (0, 0, 0) is chosen to be, for example, the left edge of F-actin. The x-axis is taken to be in the direction of forward movement of the myosin head along F-actin. Φ(x, y, z) defined as
represents the spatial distribution of the potential of mean force, the water-mediated potential, between F-actin and the myosin head (Kinoshita, 2021a; Kinoshita, 2021b). The mean force acting on the myosin head, f, is expressed as
where i, j, and k denote the direction unit vectors. f(x0, y0, z0) represents the force induced between F-actin and the myosin head averaged over all the possible configurations of water molecules in the entire system with (x, y, z) being fixed at (x0, y0, z0). Thus, a potential or force field acts on the myosin head due to the presence of F-actin near it. The myosin head makes a Brownian motion in the absence of F-actin whereas its motion is influenced by the potential or force field in the presence of F-actin.
The potential or force field is strongly dependent on the structure of the myosin head which is variable depending on the chemical compound (nothing, ATP, ADP+Pi, or ADP) bound to the myosin head. Upon a structural change of the myosin head, Φ(x, y, z) and f(x, y, z) also exhibit significantly large changes. That is, the potential or force field acting on myosin exhibits sequential changes during the ATP hydrolysis cycle (binding of ATP to the myosin head, hydrolysis of ATP into ADP and Pi in it, release of Pi from it, and release of ADP from it) which can lead to the unidirectional movement of the myosin head along F-actin as explained in Supplementary Section S13.
We then consider F1-ATPase. The system free energy is denoted by GSystem. For a structure of the α3β3 complex given, GSystem is a function of the rotation angle θ defined for the γ subunit in the counterclockwise direction with the origin suitably chosen. The structure of the γ subunit is also variable depending on θ. Denoting the mean torque acting on the γ subunit by τ(θ), we can express it as
τ(θ0) represents the torque acting on the γ subunit, which is averaged over all the possible translational configurations of water molecules in the entire system with θ being fixed at θ0. Since the dependence of GSystem on θ is strong, τ(θ) is also strong. GSystem sharply becomes minimum at θ = θmin and τ(θmin) = 0. During the ATP hydrolysis cycle, the chemical compounds bound to the three β subunits, the structure of the α3β3 complex, and τ(θ) and θmin exhibit sequential changes. This leads to the unidirectional rotation of the γ subunit (see the discussions in Section 7.1.2, Section 7.3.3, and Section 7.3.4).
As detailed in Supplementary Section S13, when we discuss ΔGSystem, the water entropy SWater can be regarded as a principal component of GSystem:
Here, ΔX signifies the change in X caused by structural and positional changes of the myosin head or by structural changes of the α3β3 complex and the γ subunit and an orientational change of the γ subunit. We can take the view that the structure and position of the myosin head or the structure of the α3β3 complex and the structure and orientation of the γ subunit are determined so that the water entropy can be increased. Thus, GSystem in Eqs 18, 20 can be replaced by −TΔSWater. τ(θ) can be referred to as the “entropic torque”.
Taken together, the force moving the myosin head and the torque rotating the central shaft are generated by water. No input of chemical free energy of ATP is required for the force or torque generation. It is just that in an ATP hydrolysis cycle the system free energy decreases by the free-energy change upon the ATP hydrolysis in bulk aqueous solution. We note, however, that this never means that ATP plays no significant roles. In the absence of ATP, the unidirectionality of the movement or rotation is not achievable: Once the myosin head with a prescribed structure, for example, is stabilized in the position where GSystem is minimized, its movement is stopped unless it can overcome the free-energy barrier because the potential or force field is not changed. The presence of ATP is certainly indispensable as a trigger of the force or torque generation. For actomyosin, the extension of the physical picture to the unidirectional movement of myosin V, a double-headed myosin, along F-actin is to be considered in future studies. In any case, the conformation of actomyosin (i.e., structures, orientations, and positions of myosin and F-actin) or that of F1-ATPase is perturbed by the ATP hydrolysis cycle (Section 3.1) but adjusted so that the system free energy can be lowered, which leads to the unidirectional movement or rotation.
When CATP is sufficiently higher than CADP and CPi, the overall reaction is unidirectional: It is not ATP synthesis but ATP hydrolysis. F1-ATPase is involved in the ATP hydrolysis reaction through a cycle comprising ATP binding to it, hydrolysis of ATP into ADP and Pi in it, and dissociation of ADP and Pi from it, with the result that the structure of the α3β3 complex undergoes sequential changes during the cycle. It is not the chemical free energy of ATP but the effect of translational, configurational entropy of water that generates the torque for rotating the γ subunit. ATP just triggers the structural change of the α3β3 complex. The ATP hydrolysis cycle and the maintenance of the stabilized state of F1-ATPase, where only two of ATP-H2O, ATP(ATP-H2O), ATP, and ADP+Pi are bound to two of the β subunits, respectively, are in concert with each other (Figure 7). The ATP binding can occur when the nucleotide-binding site of one of the three β subunits (β′E in state (B)) is vacant. Upon the ATP binding, ADP in one of the other two β subunits (βDPHO in state (B)) needs to dissociate from it.
Here, we discuss the following two cases: Even in the absence of ATP, when the trailing head of myosin V is artificially detached from F-actin, it makes the forward (unidirectional) movement (case 1) (Kodera and Ando, 2014; Ngo et al., 2016); and in the absence of ATP, the rotation of the central shaft in F1-ATPase does not occur (case 2) (Noji et al., 1997). These two cases can be explained as follows.
Case 1: A myosin head or the trailing head of myosin V is detached from F-actin when its structure is changed upon ATP binding to it (Supplementary Section S13). In the absence of ATP, the detachment does not occur, and it keeps binding to F-actin. Even in the absence of ATP, when the myosin head is artificially detached, the potential or force field acting on it is changed, which moves it in the forward direction (Supplementary Section S13). When the trailing head is artificially detached, the conformation of actomyosin is perturbed and adjusted so that the system free energy can be lowered, leading to the forward movement.
Case 2: In the absence of ATP, the sequential changes in chemical compounds bound to the three β subunits are also absent. None of the structure of the α3β3 complex, τ(θ), and θmin exhibits the sequential changes. Therefore, the rotation of the central shaft does not occur.
Kinoshita showed for F1-ATPase that the following four rotation modes, modes (i) through (iv), can be elucidated within the same theoretical framework (Kinoshita, 2021a). Three of them are (i) rotation in the normal (counterclockwise) direction; (ii) rotation in the inverse (clockwise) direction; and (iii) rotations in random directions where the normal and inverse directions take place with the same frequency. Modes (i), (ii), and (iii) are induced under the aqueous-solution conditions that the overall reaction is ATP hydrolysis, it is ATP synthesis, and ATP hydrolysis and synthesis reactions are in equilibrium, respectively. The last mode is (iv) rotation in the inverse direction even under the aqueous-solution condition that the overall reaction should be ATP hydrolysis, which is driven by sufficiently strong external torque imposed on the γ subunit, leading to the occurrence of ATP synthesis as the overall reaction.
As described in Supplementary Section S3, even under the aqueous-solution condition that the overall reaction is ATP hydrolysis, the frequency of ATP synthesis reaction is not zero. In fact, it was experimentally observed in mode (i) that rotation in the inverse direction accompanying ATP synthesis takes place with low frequency (Yasuda et al., 1998). Mode (ii) is useful as a thought experiment. In mode (iv) the overall reaction becomes ATP synthesis even under the aqueous-solution condition that the overall reaction should be ATP hydrolysis. Kinoshita’s physical pictures (Kinoshita, 2021a) for modes (ii) and (iv) are revisited in Section 7.3.3 and Section 7.3.4, respectively. Taken together, the ATP hydrolysis or synthesis reaction is tightly coupled to the rotation in the normal or inverse direction through the water-entropy effect.
The mechanism of inverse, unidirectional rotation of the γ subunit accompanying ATP synthesis can be outlined as follows (Figure 9) (Kinoshita, 2021a). Under the aqueous-solution condition assumed, ΔG defined in Supplementary Section S3 is positive, and the free-energy change becomes negative for ATP synthesis. The ATP synthesis cycle composed of binding of ADP and Pi to, synthesis of ADP and Pi into ATP in, and dissociation of ATP from the α3β3γ complex occurs spontaneously for lowering the system free energy.
(1) The α3β3γ complex is in state (A) where ATP-H2O, ATP, and Pi are bound to βDP, βTP, and βE, respectively (i.e., the catalytic dwell state shown in Figure 6A). The state changes as follows. The change of ATP-H2O to ATP(ATP-H2O), ATP dissociation, and ADP binding spontaneously occur in βDP, βTP, and βE, respectively. The PE of βDP is lowered by the change due to β(ATP-H2O)>β(ATP(ATP-H2O)) in Order (7). The PE of subcomplex 3 also becomes lower. ATP dissociates from βTP with the result that the PE of βTP becomes lower due to β(ATP)>β in Order (7). The PE of subcomplex 2 also becomes lower. ADP binds to βE, and the PE of βE becomes higher (β(ADP+Pi)>β(Pi) in Order (7)). The β subunits to which ADP+Pi, nothing, and ATP(ATP-H2O) are bound are denoted by β′E, β′TP, and β′DP, respectively. The γ subunit rotates by 80° in the inverse direction during state change (A)→(B) in response to the change in packing structure of the α3β3 complex.
(2) The α3β3γ complex is in state (B). The state changes as follows. The change of ATP(ATP-H2O) to ATP, Pi binding, and ATP synthesis (ADP+Pi→ATP-H2O) spontaneously occur in β′DP, β′TP, and β′E, respectively. ATP(ATP-H2O)→ATP occurs in β′DP with the result of its lower PE due to β(ATP(ATP-H2O))>β(ATP) in Order (7). The packing of β′DP and that of subcomplex 3 become looser. Pi binds to β′TP with the result of its lower PE (β>β(Pi) in Order (7)). The packing of β′TP and that of subcomplex 2 become looser. The ATP synthesis occurs in β′E, leading to its higher PE (β(ATP-H2O)>β(ADP+Pi) in Order (7)). The packings of β′E and subcomplex 1 become closer. The γ subunit rotates by 40° in the inverse direction during (B)→(C) by responding to the change in packing structure of the α3β3 complex.
(3) The α3β3γ complex is now in state (C) where ATP-H2O, ATP, and Pi are bound to βDP, βTP, and βE, respectively. Changes of βDP→β′DP→βTP, βTP→β′TP→βE, and βE→β′E→βDP have occurred in subcomplexes 3, 2, and 1, respectively. The change in packing structure of the α3β3 complex has been followed by a rotation of 120° of the γ subunit in the clockwise direction, recovering the closely packed γ-βDP, γ-αE, and γ-βE interfaces. Upon the 120° rotation, one ATP molecule is synthesized in bulk aqueous solution, accompanying a decrease in system free energy.
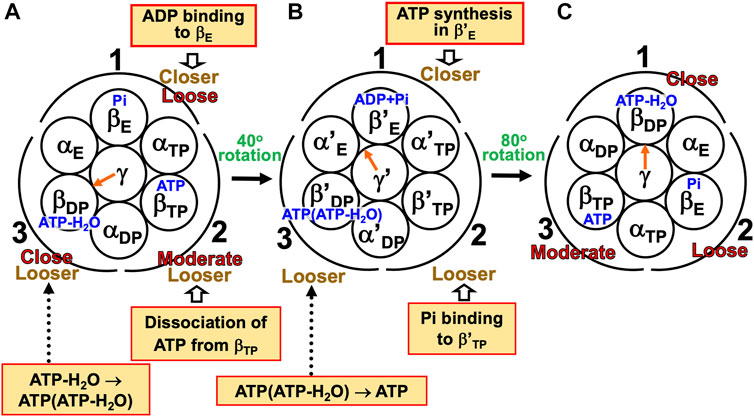
FIGURE 9. Physical picture of unidirectional rotation of γ subunit in F1-ATPase during one ATP synthesis cycle. In state (A), Pi, ATP, and ATP-H2O are bound to βE, βTP, and βDP, respectively. In (B), ADP+Pi and ATP(ATP-H2O) are bound to β′E and β′DP, respectively. The packings of βE and subcomplex 1 are loose in state (A) but they become closer in state change (A)→(B). Those of β′E and subcomplex 1 become further closer in (B)→(C). Those of βDP and subcomplex 1 are close in (C). Those of βTP and subcomplex 2 are moderate in (A) but they become looser in (A)→(B). Those of β′TP and subcomplex 2 become further looser in (B)→(C). Those of βE and subcomplex 2 are loose in (C). Those of βDP and subcomplex 3 are close in (A) but they become looser in (A)→(B). Those of β′DP and subcomplex 3 become further looser in (B)→(C). Those of βTP and subcomplex 3 are moderate in (C).
We discuss mode (iv) (Toyabe et al., 2011; Toyabe and Muneyuki, 2015). The system is under the aqueous-solution condition that the overall reaction should be ATP hydrolysis: ΔG defined as Eq. (S10) is negative. As the external torque increases from zero, the frequency of the inverse rotation accompanying the ATP synthesis becomes higher. When the external torque multiplied by 2π/3 (120°) is −ΔG > 0, F1-ATPase is in the stalled state where the frequency of the normal rotation accompanying the ATP hydrolysis becomes equal to that of the inverse rotation (Toyabe and Muneyuki, 2015). As it becomes further stronger, the frequency of the normal rotation accompanying the ATP hydrolysis becomes lower. Eventually, the inverse rotation occurs exclusively.
The packing structure of the α3β3 complex prescribed, the water entropy is strongly dependent on the orientation of the γ subunit. In mode (i), the orientation of the γ subunit is changed in accordance with the change in packing structure of the α3β3 complex induced by the ATP hydrolysis cycle. In mode (iv), on the other hand, the packing structure of α3β3 complex is changed in accordance with the orientational change of the γ-subunit. It is important to note that the change in packing structure is controlled by the variation of chemical compounds bound to the three β subunits.
We consider three different state changes per cycle, (A)→(B), (A)→(C), and (A)→(D) as illustrated in Figure 10. In states (C) and (D), since the γ subunit is not orientated toward βDP, the close packings of βDP-γ, αE-γ, and βE-γ are lost. State change (A)→(B), during which chemical compounds bound to the three β subunits vary as in Figure 9 and the ATP synthesis reaction occurs, does not cause a water-entropy loss. Since the system is under the aqueous-solution condition that the overall reaction should be ATP hydrolysis, the ATP synthesis cycle composed of binding of ADP and Pi to, synthesis of ADP and Pi into ATP in, and dissociation of ATP from the α3β3γ complex, which occurs as the overall process, gives rise to an increase in the system free energy. This is not thermodynamically inconsistent because there is an energy input per cycle through the external torque. During (A)→(C), chemical compounds bound to the three β subunits vary as in Figure 7 and the ATP hydrolysis occurs. ATP binding to, ATP hydrolysis in, and ADP and Pi dissociation from the α3β3γ complex leads to a decrease in the system free energy. During (A)→(D), chemical compounds bound to the three β subunits remain unchanged. Neither of the ATP hydrolysis and synthesis reactions occurs, which does not contribute to a change in system free energy. Upon (A)→(C) or (A)→(D), an acceptably large loss of water entropy is unavoidably caused. The free-energy increase arising from this water-entropy loss is much larger than the free-energy change due to the ATP hydrolysis or synthesis reaction (Section 6.1). Therefore, (A)→(C) and (A)→(D) are prohibitive, and (A)→(B) occurs exclusively in mode (iv). See Supplementary Section S14 as well.
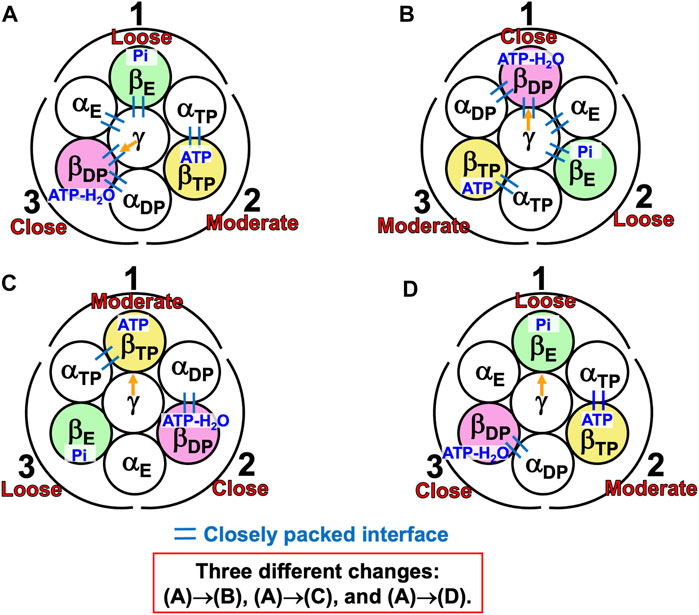
FIGURE 10. Three different state changes per cycle, (A)→(B), (A)→(C), and (A)→(D). The aqueous solution is under the condition that the ATP hydrolysis reaction should occur. However, the γ subunit is forcibly rotated it in the inverse direction by a sufficiently strong external torque imposed on it. The α3β3γ complex in state (B) corresponds to that in state (C) shown in Figure 9. The α3β3 complex in state (C) corresponds to that in state (C) shown in Figure 7.
Muneyuki and coworkers (Toyabe and Muneyuki, 2015; Tanaka et al., 2020) performed intriguing experiments for a mutant of F1-ATPase where a mutation of E190D is made for every β subunit. They observed that even by a weak external torque, the γ subunit often rotates in the inverse direction without the occurrence of ATP synthesis reaction (i.e., state change (A)→(D) in Figure 10 takes place). For the wild type, the catalytic dwell state is sufficiently stable, this stability is accomplished by the nonuniformity of PEs of the three β subunits, the PE of each β subunit is intimately correlated with the chemical compound bound, and the orientation of the γ subunit strongly influences the state stability. Hence, when the orientation of the γ subunit is forcibly changed, the PEs of the three β subunits need to be changed, and to this end the chemical compounds bound to them are also changed. These features are lost for the mutant. The water-entropy loss accompanying (A)→(D) is much smaller than for the wild type, and the increase in system free energy due to this loss can be comparable in magnitude to the energy received by the system. The tight coupling between ATP hydrolysis or synthesis reaction and the rotation in the normal or inverse direction is no more attainable for the mutant.
The theoretical analyses performed for V1-ATPase have enabled us to obtain the following results.
(1) The packing structure of the catalytic dwell state illustrated in Figure 6B is constructed by the interplay of ATP bindings to two of the A subunits (ATP and ADP) (more strictly, ATP-H2O is bound to ADP) and incorporation of the DF subunit. Replacing the two ATPs by two ADPs, respectively, lowers the packing efficiencies (PEs) of the three A subunits and markedly reduces the stability of the A3B3DF complex.
(2) The A3B3 complex is largely stabilized by the incorporation of the DF subunit. We can take the view that the orientation of the DF subunit follows the packing structure of the A3B3 complex thus largely stabilized (Section 7.2.2). There is the optimum orientation of the DF subunit for a packing structure of the A3B3 complex given, and even a slight shift from it gives rise to a significantly large loss of water entropy.
(3) Irrespective of the presence of nucleotides bound and the incorporation of the DF subunit, the PE of each subcomplex in V1-ATPase (Figure 5A) is determined by that of the A subunit. That is, Orders (9) and (10), (11) and (12), (13) and (14), and (15) and (16) hold for A3B3DF⋅2ATP, A3B3, A3B3⋅2ATP, and A3B3DF, respectively.
(4) The binding of ATP or ADP to an A subunit increases the affinity between this subunit and one of its neighbor B subunits, and thereby the ATP or ADP binding contributes to the formation of closer packing of the aforementioned A-B interface. The degree of the increase is much higher for the ATP binding. These results are in accord with the experimental observations reported by Murata and coworkers (Arai et al., 2020).
(5) Not only the packing structure of the A3B3DF complex but also the occurrence of ATP hydrolysis reaction in not ATP but ADP is highly relevant to the rotation of central shaft in the normal (i.e., counterclockwise) direction (Section 7.2.3).
(6) The packing efficiency (PE) of an A subunit (and that of the subcomplex in which it is included) is variable depending on the chemical compound bound to it. The packing structure where two nucleotides are bound to V1-ATPase is the most stable in terms of the water entropy. The most stable packing structure is characterized by the nonuniformity that the three A subunits are closely, moderately, and loosely packed, respectively, and the optimized orientation of the DF subunit. During each ATP hydrolysis cycle, when the chemical compound bound to one of the three A subunits changes in a direction that the PE of this A subunit becomes lower, the chemical compounds bound to the other two A subunits change in directions that their PEs become higher, thus maintaining the most stable packing structure (this view is supported by an experimental evidence (Kabaleeswaran et al., 2006): see Supplementary Section S15 for more details). Presumably, thanks to this maintenance, a significantly large free-energy barrier for the rotation of the DF subunit can be avoided. The ATP hydrolysis cycle and the maintenance of the most stable packing structure are in concert with each other (Section 7.3.1), accompanying a smooth rotation.
(7) It is possible that the incorporation of the central shaft in the A3B3 complex plays an essential role in the occurrence of ATP hydrolysis reaction in ADP.
The qualitative aspects of statements (1)−(6) should be applicable to F1-ATPase as well when “B”, “A”, and “DF” are replaced by “α”, “β”, and “γ”, respectively. [Statement (7) is not applicable to F1-ATPase as described below.] There are similarities and differences between F1-ATPase and V1-ATPase. The differences revealed in this study are summarized in Table 5. There can be another difference between the two rotary molecular motors. For F1-ATPase, since it was experimentally observed that the α3β3 complex fulfills its structural rotation in the normal direction (Uchihashi et al., 2011; Kinoshita, 2021a), the ATP hydrolysis should occur in βDP even without the central shaft. For V1-ATPase to which statement (7) is applicable, on the other hand, it is possible that the rotation mechanism is programmed in not the A3B3 complex but the A3B3DF complex. Hence, the structural rotation of the A3B3 complex may not occur, pending experimental studies. As understood in statements (2), (5), and (7), the effect of incorporation of the central shaft on the structure and properties is considerably large in V1-ATPase, presumably larger than in F1-ATPase. Once the central shaft is incorporated, however, the two rotary molecular motors share essentially the same rotation mechanism despite the differences revealed (Figures 7, 8).
The system, which comprises not only F1-ATPase or V1-ATPase but also the aqueous solution of ATP, ADP, and Pi in which it is immersed, performs essentially no mechanical work during one ATP hydrolysis cycle. The central shaft is rotated by the torque generated by water with no input of chemical free energy of ATP. Even under the aqueous-solution condition that the overall reaction should be ATP hydrolysis, the central shaft rotates in the inverse direction when sufficiently strong external torque is imposed on it, performing the ATP synthesis (Toyabe et al., 2011; Toyabe and Muneyuki, 2015). This experimental evidence can also be explained as described in Section 7.3.4, which is an appealing point of our concept. The ATP hydrolysis or synthesis reaction is tightly coupled to the rotation in the normal or inverse direction through the water-entropy effect. Our proposal is in line with the recent experimental results observed for actomyosin (Section 1) and the theoretical efforts (Amano et al., 2010; Suzuki et al., 2017; Kinoshita, 2018) showing that the force for moving myosin unidirectionally along F-actin is generated through the effect of hydration of actomyosin (see Supplementary Section S16 and Section 2.9 in the recently published book (Kinoshita, 2021a)). In one of the theoretical efforts (Suzuki et al., 2017), the force acting on S1 was estimated to be several piconewtons, as strong as the experimentally observed force. The free energy of the system is variable depending on the conformation of actomyosin (i.e., structures, orientations, and positions of myosin and F-actin) or F1-ATPase. The conformation is perturbed by the ATP hydrolysis cycle but adjusted so that the system free energy can be lowered, which leads to the unidirectional movement or rotation.
There are two more reasons for which we request that the chemo-mechanical coupling be reconsidered:
Reason 1. Though the overall structures of F1-ATPase before and after the 120° rotation are the same, one ATP molecule has been hydrolyzed in bulk aqueous solution, accompanying a decrease in system free energy of ΔG1+ΔG2+ΔG3+ΔG4 = ΔG∼−12 kcal/mol (see Section 7.1.3 for the physical meanings of ΔG1 through ΔG4). Importantly, |ΔG4| is much smaller than | ΔG | (| ΔG1 | and | ΔG3 | can be relatively larger). In actomyosin, the free energy change upon the ATP hydrolysis in myosin (not in bulk aqueous solution), M⋅ATP+H2O→M⋅ADP-Pi (M denotes the myosin head), which corresponds to ΔG4<0, is only ∼−1 kcal/mol (Kodama, 1985). In the proposition that actomyosin is the system and the aqueous solution is the surroundings, the decrease in system free energy which can be transduced to mechanical work (the input of chemical free energy of ATP utilized by myosin) is neither ΔG∼−12 kcal/mol nor ΔG°∼−7 kcal/mol (Supplementary Section S3): It should be ∼ −1 kcal/mol which seems to be too small to perform the mechanical work for moving myosin unidirectionally. (In a study on F1-ATPase (Mukherjee and Warshel, 2015), the input of chemical free energy was unreasonably set at −8 kcal/mol though the aqueous solution was regarded as the surroundings.).
Reason 2. In the view based on the chemo-mechanical coupling, the chemical free energy of ATP needs to be input for the unidirectional movement or rotation. It is often necessitated to assume that the free energy is stored in actomyosin or F1-ATPase and utilized for the so-called mechanical event or mechanical events occurring afterwards. However, this assumption is not justifiable for the following reason. The state of actomyosin or F1-ATPase is driven to change so that the free energy of the system including the aqueous solution can become lowest. It was theoretically and experimentally shown that the relaxation of vibrational energy in a protein occurs on a time scale of picoseconds to nanoseconds at room temperature (Xie et al., 2001; Fujisaki and Straub, 2005). Likewise, it should be improbable that only actomyosin or F1-ATPase remains being in a state with higher free energy for a time scale of milliseconds on which the step movement or rotation takes place (Kitamura et al., 1999; Iwaki et al., 2018; Iida et al., 2019).
In the concept of chemo-mechanical coupling, the force or torque field generated by water acting on myosin or the central shaft (Section 7.3.1) is overlooked with the result that the chemical free energy of ATP is considered to be the only source of the force or torque generation.
Last, the subjects to be theoretically investigated in further studies are summarized in Supplementary Section S17.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Conceptualization, MK; methodology, MK; investigation, SY; software, MK, TH, and SY; validation, MK, TM, SY, and TH; visualization, SY and MK; data curation, TM and MK; formal analysis, MK, SY, TM, and TH; writing − original draft preparation, MK; writing − review and editing, MK, SY, TM, and TH; resources, TM; supervision, MK and TM. All authors contributed to the article and approved the submitted version.
This work was supported by Grant-in-Aid for Scientific Research (Nos 17K15099 and 21K06108 to SY, No. 22K03547 to TH, and Nos 18H05425 and 21H02409 to TM) from Japan Society for the Promotion of Science (JSPS), by Platform Project and Research Support Project for Supporting Drug Discovery and Life Science Research [Basis for Supporting Innovative Drug Discovery and Life Science Research (BINDS)] from AMED under Grant Numbers JP19am0101083 and JP22ama121013 (to TM), and by IAAR Research Support Program, Chiba University, Japan.
One of the authors (MK) expresses his deep gratitude to Eiro Muneyuki and Mitsuhiro Iwaki who kindly answered a number of questions on F1-ATPase from him. Useful comments on the crystal structures of V1-ATPase from Kano Suzuki are gratefully acknowledged.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2023.1159603/full#supplementary-material
Abrahams, J. P., Leslie, A. G., Lutter, R., and Walker, J. E. (1994). Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature 370, 621–628. doi:10.1038/370621a0
Adachi, K., Oiwa, K., Nishizaka, T., Furuike, S., Noji, H., Itoh, H., et al. (2007). Coupling of rotation and catalysis in F1-ATPase revealed by single-molecule imaging and manipulation. Cell 130, 309–321. doi:10.1016/j.cell.2007.05.020
Amano, K., Yoshidome, T., Iwaki, M., Suzuki, M., and Kinoshita, M. (2010). Entropic potential field formed for a linear-motor protein near a filament: Statistical-mechanical analyses using simple models. J. Chem. Phys. 133, 045103. doi:10.1063/1.3462279
Arai, S., Maruyama, S., Shiroishi, M., Yamato, I., and Murata, T. (2020). An affinity change model to elucidate the rotation mechanism of V1-ATPase. Biochem. Biophys. Res. Commun. 533, 1413–1418. doi:10.1016/j.bbrc.2020.10.033
Arai, S., Saijo, S., Suzuki, K., Mizutani, K., Kakinuma, Y., Ishizuka-Katsura, Y., et al. (2013). Rotation mechanism of Enterococcus hirae V1-ATPase based on asymmetric crystal structures. Nature 493, 703–707. doi:10.1038/nature11778
Bowler, M. W., Montgomery, M. G., Leslie, A. G. W., and Walker, J. E. (2007). Ground state structure of F1-ATPase from bovine heart mitochondria at 1.9 Å resolution. J. Biol. Chem. 282, 14238–14242. doi:10.1074/jbc.M700203200
Czub, J., and Grubmüller, H. J. (2014). Rotation triggers nucleotide-independent conformational transition of the empty β subunit of F1-ATPase. J. Am. Chem. Soc. 136, 6960–6968. doi:10.1021/ja500120m
Dittrich, M., Hayashi, S., and Schulten, K. (2003). On the mechanism of ATP hydrolysis in F1-ATPase. Biophys. J. 85, 2253–2266. doi:10.1016/S0006-3495(03)74650-5
Fujisaki, H., and Straub, J. E. (2005). Vibrational energy relaxation in proteins. Proc. Natl. Acad. Sci. U. S. A. 102, 6726–6731. doi:10.1073/pnas.0409083102
Harano, Y., and Kinoshita, M. (2005). Translational-entropy gain of solvent upon protein folding. Biophys. J. 89, 2701–2710. doi:10.1529/biophysj.104.057604
Hayashi, T., Inoue, M., Yasuda, S., Petretto, E., Škrbić, T., Giacometti, A., et al. (2018). Universal effects of solvent species on the stabilized structure of a protein. J. Chem. Phys. 149, 045105. doi:10.1063/1.5042111
Hayashi, T., Yasuda, S., Škrbić, T., Giacometti, A., and Kinoshita, M. (2017). Unraveling protein folding mechanism by analyzing the hierarchy of models with increasing level of detail. J. Chem. Phys. 147, 125102. doi:10.1063/1.4999376
Hikiri, S., Hayashi, T., Inoue, M., Ekimoto, T., Ikeguchi, M., and Kinoshita, M. (2019). An accurate and rapid method for calculating hydration free energies of a variety of solutes including proteins. J. Chem. Phys. 150, 175101. doi:10.1063/1.5093110
Iida, T., Minagawa, Y., Ueno, H., Kawai, F., Murata, T., and Iino, R. (2019). Single-molecule analysis reveals rotational substeps and chemo-mechanical coupling scheme of Enterococcus hirae V1-ATPase. J. Biol. Chem. 294, 17017–17030. doi:10.1074/jbc.RA119.008947
Inoue, M., Hayashi, T., Hikiri, S., Ikeguchi, M., and Kinoshita, M. (2020a). Comparison based on statistical thermodynamics between globule-to-coil transition of poly(N-isopropylacrylamide) and cold denaturation of a protein. J. Mol. Liq. 317, 114129. doi:10.1016/j.molliq.2020.114129
Inoue, M., Hayashi, T., Hikiri, S., Ikeguchi, M., and Kinoshita, M. (2020b). Hydration properties of a protein at low and high pressures: Physics of pressure denaturation. J. Chem. Phys. 152, 065103. doi:10.1063/1.5140499
Ito, Y., and Ikeguchi, M. (2010). Structural fluctuation and concerted motions in F1-ATPase: A molecular dynamics study. J. Comput. Chem. 31, 2175–2185. doi:10.1002/jcc.21508
Ito, Y., Yoshidome, T., Matubayasi, N., Kinoshita, M., and Ikeguchi, M. (2013). Molecular dynamics simulations of yeast F1-ATPase before and after 16° rotation of the γ subunit. J. Phys. Chem. B 117, 3298–3307. doi:10.1021/jp312499u
Iwaki, M., Ito, K., and Fujita, K. (2018). “Single-molecule analysis of actomyosin in the presence of osmolyte,” in The role of water in ATP hydrolysis energy transduction by protein machinery. Part III. Editor M. Suzuki (Berlin, Germany: Springer Briefs in Molecular Science), 245–256. Chap 15.
Kabaleeswaran, V., Puri, N., Walker, J. E., Leslie, A. G. W., and Mueller, D. M. (2006). Novel features of the rotary catalytic mechanism revealed in the structure of yeast F1 ATPase. EMBO. J. 25, 5433–5442. doi:10.1038/sj.emboj.7601410
Kamo, F., Ishizuka, R., and Matubayasi, N. (2016). Correlation analysis for heat denaturation of Trp-cage miniprotein with explicit solvent. Protein Sci. 25, 56–66. doi:10.1002/pro.2754
Kinoshita, M. (2013). A new theoretical approach to biological self-assembly. Biophys. Rev. 5, 283–293. doi:10.1007/s12551-013-0100-8
Kinoshita, M. (2018). “Functioning mechanism of ATP-driven proteins inferred on the basis of water-entropy effect,” in The role of water in ATP hydrolysis energy transduction by protein machinery. Part III. Editor M. Suzuki (Berlin, Germany: Springer Briefs in Molecular Science), 303–323. Chap 18.
Kinoshita, M. (2021a). Mechanism of functional expression of F1-ATPase. Berlin, Germany: Springer Briefs in Molecular Science.
Kinoshita, M. (2016). Mechanism of functional expression of the molecular machines. Berlin, Germany: Springer Briefs in Molecular Science.
Kinoshita, M. (2008). Molecular origin of the hydrophobic effect: Analysis using the angle-dependent integral equation theory. J. Chem. Phys. 128, 024507. doi:10.1063/1.2823733
Kinoshita, M. (2021b). On the functioning mechanism of an ATP-driven molecular motor. Biophys. Physicobiol. 18, 60–66. doi:10.2142/biophysico.bppb-v18.007
Kitamura, K., Tokunaga, M., Iwane, A. H., and Yanagida, T. (1999). A single myosin head moves along an actin filament with regular steps of 5.3 nanometres. Nature 397, 129–134. doi:10.1038/16403
Kodama, T. (1985). Thermodynamic analysis of muscle ATPase mechanisms. Physiol. Rev. 65, 467–551. doi:10.1152/physrev.1985.65.2.467
Kodera, N., and Ando, T. (2014). The path to visualization of walking myosin V by high-speed atomic force microscopy. Biophys. Rev. 6, 237–260. doi:10.1007/s12551-014-0141-7
Kodera, N., Yamamoto, D., Ishikawa, R., and Ando, T. (2010). Video imaging of walking myosin V by high-speed atomic force microscopy. Nature 468, 72–76. doi:10.1038/nature09450
Koga, N., and Takada, S. (2006). Folding-based molecular simulations reveal mechanisms of the rotary motor F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 103, 5367–5372. doi:10.1073/pnas.0509642103
Kubo, S., Niina, T., and Takada, S. (2020). Molecular dynamics simulation of proton-transfer coupled rotations in ATP synthase Fo motor. Sci. Rep. 10, 8225. doi:10.1038/s41598-020-65004-1
Kusalik, P. G., and Patey, G. N. (1988a). On the molecular theory of aqueous electrolyte solutions. I. The solution of the RHNC approximation for models at finite concentration. J. Chem. Phys. 88, 7715–7738. doi:10.1063/1.454286
Kusalik, P. G., and Patey, G. N. (1988b). The solution of the reference hypernetted-chain approximation for water-like models. Mol. Phys. 65, 1105–1119. doi:10.1080/00268978800101631
Liu, Q., Leng, X-H., Newman, P. R., Vasilyeva, E., Kane, P. M., and Forgac, M. (1997). Site-directed mutagenesis of the yeast V-ATPase A subunit. J. Biol. Chem. 272, 11750–11756. doi:10.1074/jbc.272.18.11750
Masaike, T., Koyama-Horibe, F., Oiwa, K., Yoshida, M., and Nishizaka, T. (2008). Cooperative three-step motions in catalytic subunits of F1-ATPase correlate with 80° and 40° substep rotations. Nat. Struct. Mol. Biol. 15, 1326–1333. doi:10.1038/nsmb.1510
Merlino, A., Pontillo, N., and Graziano, G. (2017). A driving force for polypeptide and protein collapse. Phys. Chem. Chem. Phys. 19, 751–756. doi:10.1039/C6CP07397B
Mukherjee, S., and Warshel, A. (2015). Dissecting the role of the γ-subunit in the rotary-chemical coupling and torque generation of F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 112, 2746–2751. doi:10.1073/pnas.1500979112
Mukherjee, S., and Warshel, A. (2011). Electrostatic origin of the mechanochemical rotary mechanism and the catalytic dwell of F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 108, 20550–20555. doi:10.1073/pnas.1117024108
Nam, K., and Karplus, M. (2019). Insights into the origin of the high energy-conversion efficiency of F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 32, 15924–15929. doi:10.1073/pnas.1906816116
Ngo, K. X., Umeki, N., Kijima, S. T., Kodera, N., Ueno, H., Furutani-Umezu, N., et al. (2016). Allosteric regulation by cooperative conformational changes of actin filaments drives mutually exclusive binding with cofilin and myosin. Sci. Rep. 6, 35449. doi:10.1038/srep35449
Noji, H., Yasuda, R., Yoshida, M., and Kinosita, K. (1997). Direct observation of the rotation of F1-ATPase. Nature 386, 299–302. doi:10.1038/386299a0
Okazaki, K., and Hummer, G. (2013). Phosphate release coupled to rotary motion of F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 110, 16468–16473. doi:10.1073/pnas.1305497110
Okuno, D., Fujisawa, R., Iino, R., Hirono-Hara, Y., Imamura, H., and Noji, H. (2008). Correlation between the conformational states of F1-ATPase as determined from its crystal structure and single-molecule rotation. Proc. Natl. Acad. Sci. U. S. A. 105, 20722–20727. doi:10.1073/pnas.0805828106
Oshima, H., and Kinoshita, M. (2015). Essential roles of protein-solvent many-body correlation in solvent-entropy effect on protein folding and denaturation: Comparison between hard-sphere solvent and water. J. Chem. Phys. 142, 145103. doi:10.1063/1.4917075
Rosenzweig, R., and Kay, L. E. (2014). Bringing dynamic molecular machines into focus by methyl-TROSY NMR. Annu. Rev. Biochem. 83, 291–315. doi:10.1146/annurev-biochem-060713-035829
Roth, R., Harano, Y., and Kinoshita, M. (2006). Morphometric approach to the solvation free energy of complex molecules. Phys. Rev. Lett. 97, 078101. doi:10.1103/PhysRevLett.97.078101
Shekhar, M., Gupta, C., Suzuki, K., Chan, C. K., Murata, T., and Singharoy, A. (2022). Revealing a hidden intermediate of rotatory catalysis with X-ray crystallography and molecular simulations. ACS Cent. Sci. 8, 915–925. doi:10.1021/acscentsci.1c01599
Shimabukuro, K., Yasuda, R., Muneyuki, E., Hara, K. Y., Kinosita, K., and Yoshida, M. (2003). Catalysis and rotation of F1 motor: Cleavage of ATP at the catalytic site occurs in 1 ms before 40° substep rotation. Proc. Natl. Acad. Sci. U. S. A. 100, 14731–14736. doi:10.1073/pnas.2434983100
Sieladd, H., Rennekamp, H., Engelbrecht, S., and Junge, W. (2008). Functional halt positions of rotary FoF1-ATPase correlated with crystal structures. Biophys. J. 95, 4979–4987. doi:10.1529/biophysj.108.139782
Singharoy, A., Chipot, C., Ekimoto, T., Suzuki, K., Ikeguchi, M., Yamato, I., et al. (2019). Rotational mechanism model of the bacterial V1 motor based on structural and computational analyses. Front. Physiol. 10, 46. doi:10.3389/fphys.2019.00046
Singharoy, A., Chipot, C., Moradi, M., and Schulten, K. (2017). Chemomechanical coupling in hexameric protein−protein interfaces harnesses energy within V-type ATPases. J. Am. Chem. Soc. 139, 293–310. doi:10.1021/jacs.6b10744
Suzuki, K., Mizutani, K., Maruyama, S., Shimono, K., Imai, F., L., Muneyuki, E., et al. (2016). Crystal structures of the ATP-binding and ADP-release dwells of the V1 rotary motor. Nat. Commun. 7, 13235. doi:10.1038/ncomms13235
M. Suzuki (Editor) (2018). The role of water in ATP hydrolysis energy transduction by protein machinery (Berlin, Germany: Springer Briefs in Molecular Science).
Suzuki, M., Mogami, G., Ohsugi, H., Watanabe, T., and Matubayasi, N. (2017). Physical driving force of actomyosin motility based on the hydration effect. Cytoskeleton 74, 512–527. doi:10.1002/cm.21417
Tanaka, M., Kawakami, T., Okaniwa, T., Nakayama, Y., Toyabe, S., Ueno, H., et al. (2020). Tight chemomechanical coupling of the F1 motor relies on structural stability. Biophys. J. 119, 48–54. doi:10.1016/j.bpj.2020.04.039
Togunaga, Y., Yamamori, Y., and Matubayasi, N. (2018). Probabilistic analysis for identifying the driving force of protein folding. J. Chem. Phys. 148, 125101. doi:10.1063/1.5019410
Toyabe, S., and Muneyuki, E. (2015). Single molecule thermodynamics of ATP synthesis by F1-ATPase. New J. Phys. 17, 015008. doi:10.1088/1367-2630/17/1/015008
Toyabe, S., Watanabe-Nakayama, T., Okamoto, T., Kudo, S., and Muneyuki, E. (2011). Thermodynamic efficiency and mechanochemical coupling of F1-ATPase. Proc. Natl. Acad. Sci. U. S. A. 108, 17951–17956. doi:10.1073/pnas.1106787108
Uchihashi, T., Iino, R., Ando, T., and Noji, H. (2011). High-speed atomic force microscopy reveals rotary catalysis of rotorless F1-ATPase. Science 333, 755–758. doi:10.1126/science.1205510
Vicatos, S., Rychkova, A., Mukherjee, S., and Warshel, A. (2014). An effective coarse-grained model for biological simulations: Recent refinements and validations. Proteins 82, 1168–1185. doi:10.1002/prot.24482
Wand, A. J., and Sharp, K. A. (2018). Measuring entropy in molecular recognition by proteins. Annu. Rev. Biophys. 47, 41–61. doi:10.1146/annurev-biophys-060414-034042
Watanabe, R., Iino, R., and Noji, H. (2010). Phosphate release in F1-ATPase catalytic cycle follows ADP release. Nat. Chem. Biol. 6, 814–820. doi:10.1038/nchembio.443
Xie, A., van der Meer, A. F. G., and Austin, R. H. (2001). Excited-state lifetimes of far-infrared collective modes in proteins. Phys. Rev. Lett. 88, 018102. doi:10.1103/PhysRevLett.88.018102
Yamada, T., Hayashi, T., Hikiri, S., Kobayashi, N., Yanagawa, H., Ikeguchi, M., et al. (2019). How does the recently discovered peptide MIP exhibit much higher binding affinity than an anticancer protein p53 for an oncoprotein MDM2? J. Chem. Inf. Model. 59, 3533–3544. doi:10.1021/acs.jcim.9b00226
Yasuda, R., Noji, H., Kinosita, K., and Yoshida, M. (1998). F1-ATPase is a highly efficient molecular motor that rotates with discrete 120 degree steps. Cell 93, 1117–1124. doi:10.1016/s0092-8674(00)81456-7
Yasuda, R., Noji, H., Yoshida, M., Kinosita, K., and Itoh, H. (2001). Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature 410, 898–904. doi:10.1038/35073513
Yasuda, S., Yoshidome, T., Oshima, H., Kodama, R., Harano, Y., and Kinoshita, M. (2010). Effects of side-chain packing on the formation of secondary structures in protein folding. J. Chem. Phys. 132, 065105. doi:10.1063/1.3319509
Yoshidome, T., Ito, Y., Ikeguchi, M., and Kinoshita, M. (2011). Rotation mechanism of F1-ATPase: Crucial importance of the water entropy effect. J. Am. Chem. Soc. 133, 4030–4039. doi:10.1021/ja109594y
Yoshidome, T., Ito, Y., Matubayasi, N., Ikeguchi, M., and Kinoshita, M. (2012). Structural characteristics of yeast F1-ATPase before and after 16-degree rotation of the γ subunit: Theoretical analysis focused on the water-entropy effect. J. Chem. Phys. 137, 035102. doi:10.1063/1.4734298
Keywords: ATP-driven protein, linear molecular motor, rotary molecular motor, ATP hydrolysis, ATP synthesis, statistical mechanics, protein structure, water entropy
Citation: Yasuda S, Hayashi T, Murata T and Kinoshita M (2023) Physical pictures of rotation mechanisms of F1- and V1-ATPases: Leading roles of translational, configurational entropy of water. Front. Mol. Biosci. 10:1159603. doi: 10.3389/fmolb.2023.1159603
Received: 06 February 2023; Accepted: 25 May 2023;
Published: 09 June 2023.
Edited by:
Stephan Wilkens, Upstate Medical University, United StatesReviewed by:
Abhishek Singharoy, Arizona State University, United StatesCopyright © 2023 Yasuda, Hayashi, Murata and Kinoshita. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Takeshi Murata, dC5tdXJhdGFAZmFjdWx0eS5jaGliYS11Lmpw; Masahiro Kinoshita, cXE4ZDlmZTlAd29uZGVyLm9jbi5uZS5qcA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.