Shan Sun
David J. Huggins- 1Tri-Institutional Therapeutics Discovery Institute, New York, NY, United States
- 2Department of Physiology and Biophysics, Weill Cornell Medical College of Cornell University, New York, NY, United States
Software for accurate prediction of protein-ligand binding affinity can be a key enabling tool for small molecule drug discovery. Free energy perturbation (FEP) is a computational technique that can be used to compute binding affinity differences between molecules in a congeneric series. It has shown promise in reliably generating accurate predictions and is now widely used in the pharmaceutical industry. However, the high computational cost and use of commercial software, together with the technical challenges to setup, run, and analyze the simulations, limits the usage of FEP. Here, we use an automated FEP workflow which uses the open-source OpenMM package. To enable effective application of FEP, we compared the performance of different water models, partial charge assignments, and AMBER protein forcefields in eight benchmark test cases previously assembled for FEP validation studies.
Introduction
Accurate prediction of protein-ligand binding affinity can play an important role in hit-to-lead and lead optimization (Steinbrecher, 2012). It can accelerate drug discovery programs and improve the cost-efficiency when used to prioritize compounds for synthesis (Steinbrecher, 2012; Homeyer et al., 2014). Alchemical free energy calculations are a class of rigorous methods that can be used for binding affinity prediction (Christ et al., 2010; Chodera et al., 2011). They can compute both the absolute binding free energy (Boyce et al., 2009), (Mobley et al., 2007), (Irwin and Huggins, 2018) and, more commonly used in the pharmaceutical industry, the relative binding free energy (RBFE) between structurally related compounds (Christ et al., 2010; Steinbrecher and Labahn, 2010; Steinbrecher, 2012). RBFE calculations involve the transformation of one chemical species into another via an “alchemical” pathway. The alchemical transformation from the initial state to the final state is usually characterized by a non-physical coupling parameter λ. The free energy difference is calculated as the summation of alchemical transformation between fixed-λ states. Free energy perturbation (FEP) (Zwanzig, 1954; Bennett, 1976) and thermodynamic integration (TI) (Kirkwood, 1933), (Kirkwood, 1934), (Kirkwood, 1935) are both rigorous approaches that predict differences in protein-ligand binding affinities between congeneric molecules using molecular dynamics simulations. They are currently the most widely used approaches for RBFE calculations. (Abel et al., 2017a).
In particular, FEP is increasingly used in the pharmaceutical industry, typically in the lead optimization stage which involves synthesis of hundreds of close analogs with small structural modifications (Wade and Huggins, 2019). However, historically there have been numerous challenges limiting the success of FEP (Chodera et al., 2011). This includes inadequate sampling of relevant configurations, limited force field accuracy and technical hurdles to setup, run and analyze the calculations. (Mobley and Gilson, 2017). For example, when there are large structural reorganizations in the protein or ligand upon the alchemical transformation, large energy barriers can exist between different conformations. This can cause the protein or ligand to be trapped in a configuration during the simulation. (Gallicchio and Levy, 2011). The methods of Hamiltonian replica exchange and solute tempering (Liu et al., 2005) were developed to enhance sampling and address this issue. (Jiang and Roux, 2010).
Commercial software, such as Schrödinger’s FEP+ (Wang et al., 2015; Abel et al., 2017b), provides accurate force field parameters (Harder et al., 2016), (Lu et al., 2021) and an intuitive GUI for setting up and analyzing simulations. The FEP + protocol using replica exchange with solute tempering (REST) (Liu et al., 2005) and OPLS2.1 force field yielded an accurate free energy prediction with edgewise mean unsigned errors (MUEs) around 0.90 kcal/mol with respect to experiments on eight test cases (330 edges). (Wang et al., 2015). An orthogonal approach to free energy calculations called thermodynamic integration (TI) (Kirkwood, 1935) was also validated on the same dataset using AMBER (Salomon-Ferrer et al., 2013), (Cheatham et al., 2005) with a slightly larger overall edgewise MUE of 1.17 kcal/mol based on the cycle closure ddG. (Song et al., 2019). The FEP+ and AMBER TI validations both focus on edgewise MUEs: the MUE between experimental and predicted difference in binding affinity for all edges in the perturbation map. In this study we focus on the MUE of the compound binding affinities: the MUE between experimental and predicted binding affinity for all compounds. This provides a more direct comparison with experimental measurements, and we term it the MUE in binding affinity. For reference, we calculated the MUE in binding affinity for all 199 ligands from the FEP+ and TI studies: 0.77 kcal/mol and 1.01 kcal/mol respectively (Table 2).
Assessment of open-source MD packages for FEP and benchmarking of widely available force fields is of general interest to the community (Huggins, 2022). To explore applications of FEP calculations, we implemented an automated tool Alchaware, which performs FEP calculations using the open-source OpenMM code (Eastman and Pande, 2010a), (Eastman and Pande, 2010b), (Eastman et al., 2017), (Eastman and Pande, 2015). The performance and validity of a set of commonly used force field 26parameters were assessed with Alchaware on the eight test cases often referred as the JACS set for benchmarking free energy calculations. (Wang et al., 2015).
In this study, we validated FEP calculations with the widely used AMBER/GAFF forcefields (AMBER ff14SB (Maier et al., 2015)/GAFF2.1128) on the large dataset of eight test cases (330 edges). We selected water models that are available “out of the box” in the OpenMM package. The three-site water models are computationally efficient, therefore we chose the widely used three-site models SPC/E (Berendsen et al., 1987) and TIP3P (William et al., 1983). We also included a four-site model TIP4P-Ewald (Horn et al., 2004), which is optimized for PME calculations. We assessed the effect of these different water models on prediction accuracy. The AMBER ff15ipq protein force field, a second-generation force field developed using the Implicitly polarized charge model (IPolQ) for deriving implicitly polarized charges in the presence of explicit solvent, (Debiec et al., 2016), was compared with the AMBER ff14SB force field. Additionally, two partial charge models (AM1-BCC (Jakalian et al., 2002) and RESP (Christopher et al., 1993)) were evaluated in the FEP calculations. The five parameter sets tested are listed in Table 1.
TABLE 1. The five forcefield parameter sets tested.
Materials and methods
Test set selection
The existing JACS benchmark set (Wang et al., 2015) of BACE, CDK2, JNK1, MCL1, P38, PTP1B, Thrombin and TYK2 was used for validation.
Protein preparation
Protein structures were taken from the JACS benchmark set paper. (Wang et al., 2015). Protein N-termini were converted to a protonated amine and protein C-termini were converted to a charged carboxylate. For CDK2 (PDBID 1H1Q (Davies et al., 2002)), JNK1 (PDBID 2GMX (Szczepankiewicz et al., 2006)), MCL1 (PDBID 4HW3 (Friberg et al., 2013)), P38 (PDBID 3FLY (Goldstein et al., 2011)) and TYK2 (PDBID 4GIH (Liang et al., 2013)) there are no water molecules at these active sites. For BACE (PDBID 4DJW (Cumming et al., 2012)), PTP1B (PDBID 2QBS (Wilson et al., 2007)) and Thrombin (PDBID 2ZFF (Baum et al., 2009)), active site water molecules were retained. Ligands were aligned to a common core using the maximum common substructure. Input scripts and test set structure files are available on Github (https://github.com/shansun7994/Alchaware_v5.0).
Forcefields
The GAFF 2.11 forcefield (Wang et al., 2004) was used for ligand parameters. Three water models, two protein forcefields, and two charge models were tested. AM1-BCC charges (Jakalian et al., 2002) were calculated using the Antechamber package (Wang et al., 2001). RESP charges (Christopher et al., 1993) were calculated with Jaguar (Bochevarov et al., 2013) using the DFT/B3LYP method (Lee et al., 1988), (Becke, 1993) (Becke, 1993)with a Poisson-Boltzmann solver and water as the solvent. The crystallographic binding modes of the ligands were first subjected to minimization at the 3–21G* level and then charges were fit at the 6–31G** level.
FEP calculations
FEP calculations were performed using OpenMM 7.2 (Eastman et al., 2017) with the OpenMMTools toolkit for Hamiltonian replica exchange. All systems in all states were minimized with the OpenMM local energy minimizer. The equilibration was conducted in the NPT ensemble for 500ps at 300 K and 1 atm using a Monte Carlo Barostat. Production simulations for 5ns were performed with a Langevin integrator in the NPT ensemble with a timestep of 4.0 fs using hydrogen mass repartitioning and a hydrogen mass of 4 AMU (Hopkins et al., 2015), (Jung et al., 2021). The RBFEs were calculated using the MBAR estimator (Bennett, 1976; Shirts and Chodera, 2008) with 12 equally-spaced lambda windows. Two calculations were performed to estimate each relative binding free energy: conversion of molecule A to B in complex and conversion of molecule A to B in solvent. Solvent systems were generated with a 9.0 Å buffer between the solute and the edge of the cubic periodic box. Complex systems were generated with a 5.0 Å buffer between the solute and the edge of the cubic periodic box. Systems were neutralized and the ionic strength was set to 150 mM with Na+ and Cl-ions. Electrostatics were modelled using particle mesh Ewald method (Darden et al., 1993) and van der Waals were modelled using a nonbonded cutoff of 10.0 Å. Bonds to hydrogen were constrained, and water molecules were modeled as rigid. To avoid the numerical instabilities referred to as end point catastrophes that occur when ligands approach the fully decoupled state, OpenMMTools employs a softcore function. (Pham and Shirts, 2011). Default parameters were used for softcore_alpha (0.5), softcore_a (1), softcore_b (1), softcore_c (6), softcore_beta (0.0), softcore_d (1), softcore_e (1), and softcore_f (2). For transformations from molecule A to molecule B, hybrid molecules with dual topology were generated by identifying atoms shared between A and B that make a common core and atoms unique to A and B that appear and disappear. The sterics of A and B were first entirely coupled before switching the electrostatics. The predicted binding affinities are calculated using the Arsenic GitHub package (https://github.com/OpenFreeEnergy/arsenic). Perturbation networks are included in the Supported Information (Supplementary Figure S1).
Results and discussion
We studied the effect of the simulation parameters on Schrödinger’s JACS benchmark set, which includes eight protein targets, 199 ligands and 330 perturbations. It is worth noting that experimental uncertainties can be on the order of 0.64 kcal/mol. (Hahn et al., 2021). Starting with a parameter set using the GAFF 2.11 ligand force field, the AMBER ff14SB protein forcefield, the SPC/E water and AM1-BCC charges, the overall mean unsigned error (MUE) and root mean square error (RMSE) of 199 ligands were 0.89 kcal/mol and 1.15 kcal/mol, respectively (Table 2). With a simulation time of 5 ns per lambda window and a frequency of replica exchange at 4 ps, we examined the convergence of the representative edges in each test case (Table 3). The representative edges were chosen in each case by the lowest similarity score (Liu et al., 2013) reported in the Schrödinger FEP + panel. In general, the lower the similarity score, the higher the difficulty of the perturbation is likely to be. The total binding free energies estimated for these representative edges in each set are shown in Figure 1A. In all cases, predictions show reasonably good convergence after 2.5 ns. A repeat run of these perturbations was carried out using a different initial configuration by minimizing the protein structures. The ddG difference between the two configurations is within 1.0 kcal/mol for all test cases except BACE where the ddG difference between the two configurations is within 2.0 kcal/mol (Supplementary Figure S2). The overall accuracy of the prediction (MUE 0.89 kcal/mol, RMSE 1.15 kcal/mol) is better than the validation reported using TI (MUE 1.01 kcal/mol, RMSE 1.3 kcal/mol), and comparable to the commercial software FEP + using the OPLS2.1 force field and SPC/E water model (MUE 0.77 kcal/mol, RMSE 0.93 kcal/mol), though errors are a little larger (Table 2). Notably better performance was seen in the case of JNK1 with an improvement of 0.22 kcal/mol in MUE (Figure 2; Table 4). However, concerns were raised with the quality of the JNK1 structure (2GMX) used for benchmarking. (Hahn et al., 2021). The high R-free value (0.351), as well as the large difference between R-value and R-free for this JNK1 structure, indicates a possible overfit of the atomic model to the experimental diffraction pattern when solving the crystal structure. The coordinate error which assesses the precision of the model is 0.77. This does not fulfill the high-quality structure criteria (<0.7). (Hahn et al., 2021).
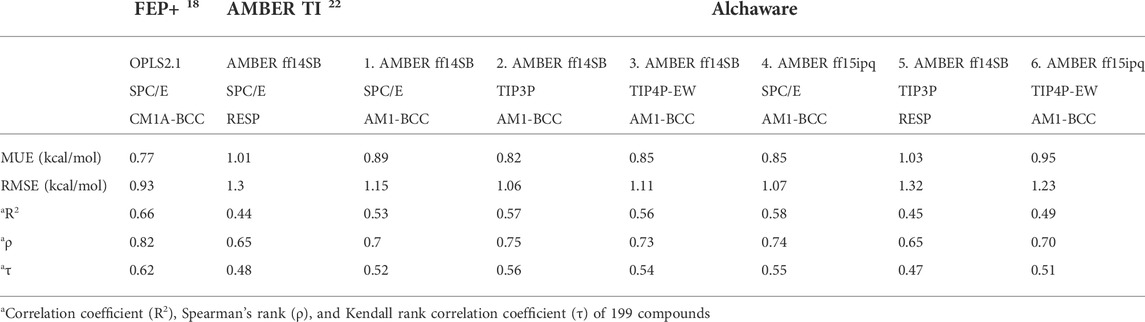
TABLE 2. Summary of accuracy and correlation statistic results of the five parameter sets tested here alongside two published datasets.
TABLE 3. The representative perturbations used to explore convergence for the eight test cases.
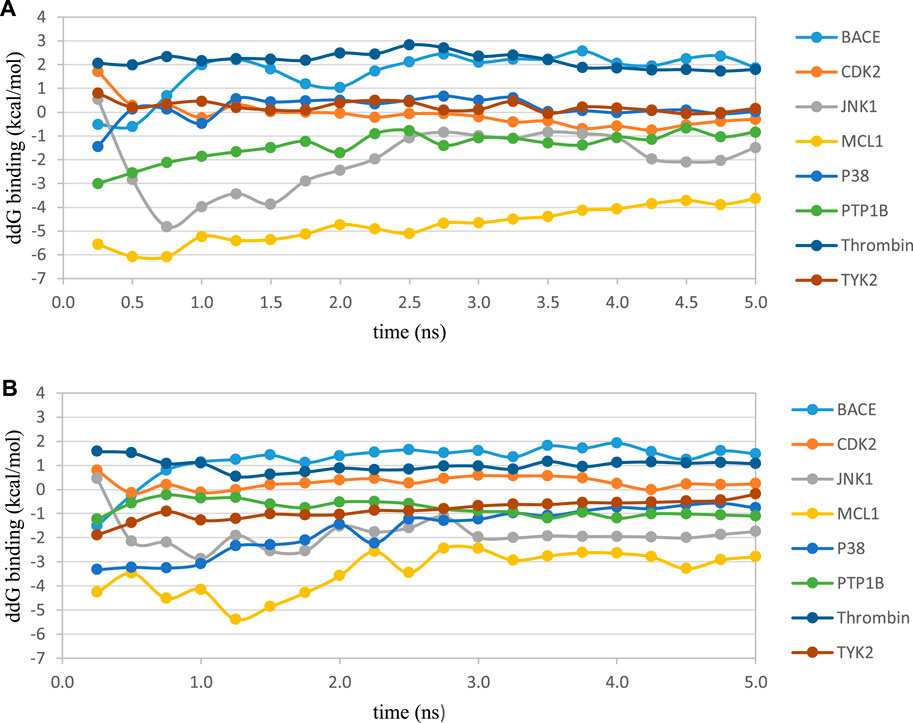
FIGURE 1. Convergence of the RBFE for the representative perturbation in each test case using the AMBER ff14SB force field with AM1-BCC charges and (A) SPC/E water model or (B) TIP3P water model. In each test case, the perturbation with the lowest similarity score (Liu et al., 2013) obtained from the Schrödinger FEP+ panel was chosen as the representative perturbation in this plot. Free energies were estimated every 0.25 ns.
FIGURE 2. Plots of MUE and R2 for each target separately.
TABLE 4. Summary of MUE, RMSE and R2 of 8 test cases and parameters.
We then used the same ligand and protein force fields to test whether the three-point TIP3P and four-point TIP4P-Ewald water models would improve the prediction accuracy. Both the TIP3P and TIP4P-Ewald water models slightly improve the overall performance with lower error and higher correlation coefficient compared to SPC/E water model (Table 2, parameter set 1, 2 and 3). This better performance could be due to the improvement of the convergence (Figure 1).
Using the GAFF 2.11 ligand force field, SPC/E water model and AM1-BCC charge, we found the AMBER ff15ipq force field (Table 2, parameter set 4), which better models the polarization effect, has a small improvement in the overall accuracy of ddG predictions (MUE 0.85 kcal/mol, RMSE 1.07 kcal/mol). This improvement is more notable in the MCL1 case, where the carboxylic acid group of all the ligands forms a critical salt bridge with the ARG263 residue. In this case, the AMBER ff15ipq force field improved the MUE by 0.44 kcal/mol compared to AMBER ff14SB (Figure 2, parameter set 1, 4). However, the four-point TIP4P-EW water model does not improve the accuracy on AMBER ff15ipq (Table 2, parameter set 6). A recent benchmark by Huai et al. evaluated AMBER protein force fields using a small test set has found that AMBER ff14SB and AMBER ff19SB (Tian et al., 2020) both perform well in alchemical calculation (Huai et al., 2021). There are problems with using the AMBER ff19SB force field in OpenMM due to the use of CMAP terms, but it should be explored in future work. In addition, the widely used CHARMM36 (Huang and MacKerell, 2013) and CHARMM36m (Huang et al., 2017) protein forcefield are also worth exploring.
The restrained electrostatic potential (RESP) approach is a commonly-used method of assigning partial charges to organic compounds (Christopher et al., 1993; Wang et al., 2000). Surprisingly, using RESP charges instead of the AM1-BCC charge does not tend to improve prediction accuracy or correlation (MUE 1.03 kcal/mol, RMSE 1.32 kcal/mol, R2 0.45). Song et al. (Song et al., 2019) validated the performance of similar force field parameters (AMBER ff14SB/GAFF1.8 force field, SPC/E, and RESP charges) using thermodynamic integration (TI) free energy calculation approach on the same benchmark set gave similar results (MUE 1.01 kcal/mol, RMSE 1.30 kcal/mol, R2 0.44) (Table 2, TI and parameter set 5). This suggested the differences in performance arise largely from the charge model employed.
Together, the parameter set 2 (AMBER ff14SB, TIP3P, AM1-BCC) has the best performance in the JACS benchmark set (Figure 3). For the 199 ligands, the majority of the binding free energy values are within 2.0 kcal/mol except for 17 ligands. Notably, these ligands are for BACE (3 ligands), MCL1 (9 ligands) and PTP1B (2 ligands) where the ligands are charged. The accuracy and correlation between the parameter sets are generally aligned, such that a high accuracy model also does better in ranking compounds. In cases where salt-bridges are formed between protein and ligand, the AMBER ff15ipq protein force field tends to increase the prediction accuracy.
FIGURE 3. Correlation between predicted binding free energies and experimental data with 6 parameter sets. Error bars indicate the cycle closure error.
Conclusion
We developed a workflow for calculating FEP RBFEs with an automated tool Alchaware using OpenMM. Validations of the FEP calculations with open-source force field parameters were carried out on the JACS benchmark set of eight test cases.
TIP3P and TIP4P-Ewald water models slightly improved the overall performance relative to SPC/E, with lower error and higher correlation coefficient with AMBER ff14SB protein force field and AM1-BCC charge. The AMBER ff15ipq protein force field (which was built to better model polarization effects) also improves the accuracy and correlation, particularly in cases where charged ligands form salt bridge interactions. This is particularly true in the case of MCL1, where the ligand forms a critical salt bridge with the charged residue (ARG263). Unfortunately, there is no improvement when using RESP charges relative to AM1-BCC charges. However, alternative protocols to generate the RESP charges should be explored in future work.
In summary, this work reports the predictive accuracy with 6 parameter sets in calculating RBFEs using FEP. Among those, set 2 (AMBER ff14SB/GAFF2.1 force field, TIP3P water model, and AM1-BCC changes) yields the best accuracy in 199 ligands (overall MUE 0.82 kcal/mol, RMSE 1.06 kcal/mol). Although the overall accuracy is not quite as good as the commercial FEP + results, in some cases (such as P38, PTP1B, and Thrombin) the accuracy is comparable. Although the better performance was seen in the case of JNK1, the protein structure used (2GMX) does not fulfill the high-quality structure criteria. This issue flags the importance of adopting best practices in constructing, preparing, and evaluating FEP calculations (Mey et al., 2020; Hahn et al., 2021). Finally, most of the poorly predicted compounds (MUE >2.0 kcal/mol) fall into three cases (BACE, MCL1 and PTP1B), where the ligands are charged. This suggests that better accuracy may be achieved by better models of charge and/or polarization and future work should be focused in this area.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, DH. Formal analysis, SS. Writing—original draft, SS. Writing—review and editing, DH.
Acknowledgments
The authors thank Alex Wade, Andrea Rizzi, Hannah Bruce McDonald, and Peter Eastman for useful discussions. The authors acknowledge the MSKCC supercomputing resources (https://www.mskcc.org/research/ski/core-facilities/high-performance-computing-group) made available for conducting the research reported in this paper.” The authors gratefully acknowledge the generous support to this project provided by the Tri-Institutional Therapeutics Discovery Institute (TDI), a 501(c) (3) organization. TDI receives financial support from Takeda Pharmaceutical Company, TDI’s parent institutes (Memorial Sloan Kettering Cancer Center, The Rockefeller University and Weill Cornell Medicine) and from a generous contribution from Lewis Sanders and other philanthropic sources.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2022.972162/full#supplementary-material
References
Abel, R., Wang, L., Harder, E. D., Berne, B. J., and Friesner, R. A. (2017). Advancing drug discovery through enhanced free energy calculations. Acc. Chem. Res. 50 (7), 1625–1632. doi:10.1021/acs.accounts.7b00083
Abel, R., Wang, L., Mobley, D. L., and Friesner, R. A. (2017). A critical review of validation, blind testing, and real- world use of alchemical protein-ligand binding free energy calculations. Curr. Top. Med. Chem. 17 (23), 2577–2585. doi:10.2174/1568026617666170414142131
Baum, B., Mohamed, M., Zayed, M., Gerlach, C., Heine, A., Hangauer, D., et al. (2009). More than a simple lipophilic contact: A detailed thermodynamic analysis of nonbasic residues in the s1 pocket of thrombin. J. Mol. Biol. 390 (1), 56–69. doi:10.1016/j.jmb.2009.04.051
Becke, A. D. (1993). Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98 (7), 5648–5652. doi:10.1063/1.464913
Berendsen, H. J. C., Grigera, J. R., and Straatsma, T. P. (1987). The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271. doi:10.1021/j100308a038
Bochevarov, A. D., Harder, E., Hughes, T. F., Greenwood, J. R., Braden, D. A., Philipp, D. M., et al. (2013). Jaguar: A high-performance quantum chemistry software program with strengths in life and materials sciences. Int. J. Quantum Chem. 113 (18), 2110–2142. doi:10.1002/qua.24481
Boyce, S. E., Mobley, D. L., Rocklin, G. J., Graves, A. P., Dill, K. A., and Shoichet, B. K. (2009). Predicting ligand binding affinity with alchemical free energy methods in a polar model binding site. J. Mol. Biol. 394 (4), 747–763. doi:10.1016/j.jmb.2009.09.049
Cheatham, T. E., Darden, T., Gohlke, H., Luo, R., Merz, K. M., Onufriev, A., et al. (2005). The Amber biomolecular simulation programs. J. Comput. Chem. 26 (16), 1668–1688. doi:10.1002/jcc.20290
Chodera, J. D., Mobley, D. L., Shirts, M. R., Dixon, R. W., Branson, K., and Pande, V. S. (2011). Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 21 (2), 150–160. doi:10.1016/j.sbi.2011.01.011
Christ, C. D., Mark, A. E., and van Gunsteren, W. F. (2010). Basic ingredients of free energy calculations: A review. J. Comput. Chem. 31 (8), 1569–1582. doi:10.1002/jcc.21450
Christopher, I., Bayly, P. C., Cornell, W., and Kollman, P. A. (1993). A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 97 (40), 10269–10280. doi:10.1021/j100142a004
Cumming, J. N., Smith, E. M., Wang, L., Misiaszek, J., Durkin, J., Pan, J., et al. (2012). Structure based design of iminohydantoin BACE1 inhibitors: Identification of an orally available, centrally active BACE1 inhibitor. Bioorg. Med. Chem. Lett. 22 (7), 2444–2449. doi:10.1016/j.bmcl.2012.02.013
Darden, T. Y., Darrin, Y., and Pedersen, L. (1993). Particle mesh Ewald: An Nṡlog(N) method for Ewald sums in large systems. J. Chem. Phys. 98 (12), 10089–10092. doi:10.1063/1.464397
Davies, T. G., Bentley, J., Arris, C. E., Boyle, F. T., Curtin, N. J., Endicott, J. A., et al. (2002). Structure-based design of a potent purine-based cyclin-dependent kinase inhibitor. Nat. Struct. Biol. 9 (10), 745–749. doi:10.1038/nsb842
Debiec, K. T., Cerutti, D. S., Baker, L. R., Gronenborn, A. M., Case, D. A., and Chong, L. T. (2016). Further along the road less traveled: AMBER ff15ipq, an original protein force field built on a self-consistent physical model. J. Chem. Theory Comput. 12 (8), 3926–3947. doi:10.1021/acs.jctc.6b00567
Eastman, P., and Pande, V. S. (2010). Efficient nonbonded interactions for molecular dynamics on a graphics processing unit. J. Comput. Chem. 31 (6), 1268–1272. doi:10.1002/jcc.21413
Eastman, P., and Pande, V. S. (2010). Constant constraint matrix approximation: A robust, parallelizable constraint method for molecular simulations. J. Chem. Theory Comput. 6 (2), 434–437. doi:10.1021/ct900463w
Eastman, P., and Pande, V. S. (2015). OpenMM: A hardware independent framework for molecular simulations. Comput. Sci. Eng. 12 (4), 34–39. doi:10.1109/MCSE.2010.27
Eastman, P., Swails, J., Chodera, J. D., McGibbon, R. T., Zhao, Y., Beauchamp, K. A., et al. (2017). OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol. 13 (7), e1005659. doi:10.1371/journal.pcbi.1005659
Friberg, A., Vigil, D., Zhao, B., Daniels, R. N., Burke, J. P., Garcia-Barrantes, P. M., et al. (2013). Discovery of potent myeloid cell leukemia 1 (Mcl-1) inhibitors using fragment-based methods and structure-based design. J. Med. Chem. 56 (1), 15–30. doi:10.1021/jm301448p
Gallicchio, E., and Levy, R. M. (2011). Advances in all atom sampling methods for modeling protein-ligand binding affinities. Curr. Opin. Struct. Biol. 21 (2), 161–166. doi:10.1016/j.sbi.2011.01.010
Goldstein, D. M., Soth, M., Gabriel, T., Dewdney, N., Kuglstatter, A., Arzeno, H., et al. (2011). Discovery of 6-(2, 4-difluorophenoxy)-2-[3-hydroxy-1-(2-hydroxyethyl)propylamino]-8-methyl-8H-pyrido[2, 3-d]pyrimidin-7-one (pamapimod) and 6-(2, 4-difluorophenoxy)-8-methyl-2-(tetrahydro-2H-pyran-4-ylamino)pyrido[2, 3-d]pyrimidin-7(8H)-one (R1487) as orally bioavailable and highly selective inhibitors of p38α mitogen-activated protein kinase. J. Med. Chem. 54 (7), 2255–2265. doi:10.1021/jm101423y
Hahn, D. F., Bayly, C. I., Macdonald, H. E. B., Chodera, J. D., Gapsys, V., Mey, A. S. J. S., et al. (2021). Best practices for constructing, preparing, and evaluating protein-ligand binding affinity benchmarks. San Francisco: arXiv:2105.06222 [q-bio.BM]. doi:10.48550/arXiv.2105.06222
Harder, E., Damm, W., Maple, J., Wu, C., Reboul, M., Xiang, J. Y., et al. (2016). OPLS4: Improving force field accuracy on challenging regimes of chemical space. J. Chem. Theory Comput. 12 (1), 281–296. doi:10.1021/acs.jctc.5b00864
Bennett, C. H. (1976). Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 22 (2), 245–268. doi:10.1016/0021-9991(76)90078-4
Homeyer, N., Stoll, F., Hillisch, A., and Gohlke, H. (2014). Binding free energy calculations for lead optimization: Assessment of their accuracy in an industrial drug design context. J. Chem. Theory Comput. 10 (8), 3331–3344. doi:10.1021/ct5000296
Hopkins, C. W., Le Grand, S., Walker, R. C., and Roitberg, A. E. (2015). Optimized hydrogen mass repartitioning scheme combined with accurate temperature/pressure evaluations for thermodynamic and kinetic properties of biological systems. J. Chem. Theory Comput. 11 (4), 1864–1874. doi:10.1021/ct5010406
Horn, H. W., Swope, W. C., Pitera, J. W., Madura, J. D., Dick, T. J., Hura, G. L., et al. (2004). Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 120 (20), 9665–9678. doi:10.1063/1.1683075
Huai, Z., Shen, Z., and Sun, Z. (2021). Binding thermodynamics and interaction patterns of inhibitor-major urinary protein-I binding from extensive free-energy calculations: Benchmarking AMBER force fields. J. Chem. Inf. Model. 61 (1), 284–297. doi:10.1021/acs.jcim.0c01217
Huang, J., and MacKerell, A. D. (2013). CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 34 (25), 2135–2145. doi:10.1002/jcc.23354
Huang, J., Rauscher, S., Nawrocki, G., Ran, T., Feig, M., de Groot, B. L., et al. (2017). CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 14 (1), 71–73. doi:10.1038/nmeth.4067
Huggins, D. J. (2022). Comparing the performance of different AMBER protein forcefields, partial charge assignments, and water models for absolute binding free energy calculations. J. Chem. Theory Comput. 18 (4), 2616–2630. doi:10.1021/acs.jctc.1c01208
Irwin, B. W. J., and Huggins, D. J. (2018). Estimating atomic contributions to hydration and binding using free energy perturbation. J. Chem. Theory Comput. 14 (6), 3218–3227. doi:10.1021/acs.jctc.8b00027
Jakalian, A., Jack, D. B., and Bayly, C. I. (2002). Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 23 (16), 1623–1641. doi:10.1002/jcc.10128
Jiang, W., and Roux, B. (2010). Free energy perturbation Hamiltonian replica-exchange molecular dynamics (FEP/H-remd) for absolute ligand binding free energy calculations. J. Chem. Theory Comput. 6 (9), 2559–2565. doi:10.1021/ct1001768
Jung, J., Kasahara, K., Kobayashi, C., Oshima, H., Mori, T., and Sugita, Y. (2021). Optimized hydrogen mass repartitioning scheme combined with accurate temperature/pressure evaluations for thermodynamic and kinetic properties of biological systems. J. Chem. Theory Comput. 17 (8), 5312–5321. doi:10.1021/acs.jctc.1c00185
Kirkwood, J. G. (1933). Quantum statistics of almost classical assemblies. Phys. Rev.Physical Rev. 44 (1), 31–37. doi:10.1103/PhysRev.44.31
Kirkwood, J. G. (1934). Quantum statistics of almost classical assemblies. Phys. Rev. 45 (2), 116–117. doi:10.1103/PhysRev.45.116
Kirkwood, J. G. (1935). Statistical mechanics of fluid mixtures. J. Chem. Phys. 3 (5), 300–313. doi:10.1063/1.1749657
Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B Condens. Matter 37 (2), 785–789. doi:10.1103/PhysRevB.37.785
Liang, J., Tsui, V., Van Abbema, A., Bao, L., Barrett, K., Beresini, M., et al. (2013). Lead identification of novel and selective TYK2 inhibitors. Eur. J. Med. Chem. 67, 175–187. doi:10.1016/j.ejmech.2013.03.070
Liu, P., Kim, B., Friesner, R. A., and Berne, B. J. (2005). Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. U. S. A. 102 (39), 13749–13754. doi:10.1073/pnas.0506346102
Liu, S., Wu, Y., Lin, T., Abel, R., Redmann, J. P., Summa, C. M., et al. (2013). Lead optimization mapper: Automating free energy calculations for lead optimization. J. Comput. Aided. Mol. Des. 27 (9), 755–770. doi:10.1007/s10822-013-9678-y
Lu, C., Wu, C., Ghoreishi, D., Chen, W., Wang, L., Damm, W., et al. (2021). OPLS4: Improving force field accuracy on challenging regimes of chemical space. J. Chem. Theory Comput. 17 (7), 4291–4300. doi:10.1021/acs.jctc.1c00302
Maier, J. A., Martinez, C., Kasavajhala, K., Wickstrom, L., Hauser, K. E., and Simmerling, C. (2015). ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 11 (8), 3696–3713. doi:10.1021/acs.jctc.5b00255
Mey, A. S. J. S., Allen, B. K., Bruce McDonald, H. E., Chodera, J. D., Hahn, D. F., Kuhn, M., et al. (2020). Best practices for alchemical free energy calculations [article v1.0]. Living J. comput. Mol. Sci. 2 (1), 18378. doi:10.33011/livecoms.2.1.18378
Mobley, D. L., and Gilson, M. K. (2017). Predicting binding free energies: Frontiers and benchmarks. Annu. Rev. Biophys. 46, 531–558. doi:10.1146/annurev-biophys-070816-033654
Mobley, D. L., Graves, A. P., Chodera, J. D., McReynolds, A. C., Shoichet, B. K., and Dill, K. A. (2007). Predicting absolute ligand binding free energies to a simple model site. J. Mol. Biol. 371 (4), 1118–1134. doi:10.1016/j.jmb.2007.06.002
Pham, T. T., and Shirts, M. R. (2011). Identifying low variance pathways for free energy calculations of molecular transformations in solution phase. J. Chem. Phys. 135 (3), 034114. doi:10.1063/1.3607597
Salomon-Ferrer, R., Case, D. A., and Walker, R. C. (2013). An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 3 (2), 198–210. doi:10.1002/wcms.1121
Shirts, M. R., and Chodera, J. D. (2008). Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 129 (12), 124105. doi:10.1063/1.2978177
Song, L. F., Lee, T.-S., Chun-Zhu, D, York, D. M., and Jr, K. M. M. (2019). Using AMBER18 for relative free energy calculations. J. Chem. Inf. Model. 59 (7), 3128–3135. doi:10.1021/acs.jcim.9b00105
Steinbrecher, T. (2012). “Free energy calculations in drug lead optimization,” in Protein-ligand interactions (Springer), 207–236.
Steinbrecher, T., and Labahn, A. (2010). Towards accurate free energy calculations in ligand protein-binding studies. Curr. Med. Chem. 17 (8), 767–785. doi:10.2174/092986710790514453
Szczepankiewicz, B. G., Kosogof, C., Nelson, L. T., Liu, G., Liu, B., Zhao, H., et al. (2006). Aminopyridine-based c-Jun N-terminal kinase inhibitors with cellular activity and minimal cross-kinase activity. J. Med. Chem. 49 (12), 3563–3580. doi:10.1021/jm060199b
Tian, C., Kasavajhala, K., Belfon, K. A. A., Raguette, L., Huang, H., Migues, A. N., et al. (2020). ff19SB: Amino-Acid-Specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J. Chem. Theory Comput. 16 (1), 528–552. doi:10.1021/acs.jctc.9b00591
Wade, A. D., and Huggins, D. J. (2019). Optimization of protein–ligand electrostatic interactions using an alchemical free-energy method. J. Chem. Theory Comput. 15 (11), 6504–6512. doi:10.1021/acs.jctc.9b00976
Wang, J., Cieplak, P., and Kollman, P. A. (2000). How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 21 (12), 1049–1074. doi:10.1002/1096-987x(200009)21:12<1049:aid-jcc3>3.0.co;2-f
Wang, J., Wang, W., Kollman, P. A., and Case, D. A. (2001). Antechamber: An accessory software package for molecular mechanical calculations. J. Am. Chem. Soc. 222 (U403), 1.
Wang, J., Wolf, R. M., Caldwell, J. W., Kollman, P. A., and Case, D. A. (2004). Development and testing of a general amber force field. J. Comput. Chem. 25 (9), 1157–1174. doi:10.1002/jcc.20035
Wang, L., Wu, Y., Deng, Y., Kim, B., Pierce, L., Krilov, G., et al. (2015). Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 137 (7), 2695–2703. doi:10.1021/ja512751q
William, L., Jorgensen, J. C., Madura, J. D., Impey, R. W., and Klein, M. L. (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79 (926), 935. doi:10.1063/1.445869
Wilson, D. P., Wan, Z. K., Xu, W. X., Kirincich, S. J., Follows, B. C., Joseph-McCarthy, D., et al. (2007). Structure-based optimization of protein tyrosine phosphatase 1B inhibitors: From the active site to the second phosphotyrosine binding site. J. Med. Chem. 50 (19), 4681–4698. doi:10.1021/jm0702478
Keywords: forcefield, relative binding free energy, free energy perturbation (FEP), OpenMM, validation
Citation: Sun S and Huggins DJ (2022) Assessing the effect of forcefield parameter sets on the accuracy of relative binding free energy calculations. Front. Mol. Biosci. 9:972162. doi: 10.3389/fmolb.2022.972162
Received: 17 June 2022; Accepted: 10 August 2022;
Published: 12 September 2022.
Edited by:
Germano Heinzelmann, Federal University of Santa Catarina, BrazilCopyright © 2022 Sun and Huggins. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David J. Huggins, dhuggins@tritdi.org