Membrane-Mediated Interactions Between Protein Inclusions

Integral or peripheral membrane proteins, or protein oligomers often get close to each other on cell membranes and carry out biological tasks in a collective manner. In addition to electrostatic and van der Waals interactions, those proteins also experience membrane-mediated interactions, which may be necessary for their functionality. The membrane-mediated interactions originate from perturbation of lipid membranes by the presence of protein inclusions, and have been the subject of intensive research in membrane biophysics. Here we review both theoretical and numerical studies of such interactions for membrane proteins and for nanoparticles bound to lipid membranes.

1 Introduction

The cell membrane is a fluid bilayer made up of lipids and proteins. The proteins are associated with the bilayer either via insertion of hydrophobic domains into one or two monolayers, or via covalent linkage or reversible adsorption to the lipids (Alberts et al., 2015). These proteins perform various biological tasks often in a collective manner. For example, two gramicidin molecules (linear peptides) each embedded in one leaflet of the bilayer dimerize in a head-to-head fashion to form a membrane-spanning ion channel with the dimerization rate dependent on the bilayer tension. In clathrin-mediated endocytosis, a multitude of proteins assemble on the cell membrane to form the clatherin-coated endocytic vesicle of size around 100 nm (Kaksonen and Roux, 2018). In addition to electrostatic and van der Waals interactions, those proteins that are spatially close on the membrane also experience membrane-mediated interactions, which may play an important part in membrane-associated processes.

In this review we present an overview of both theoretical and numerical studies on membrane-mediated interactions between protein inclusions. Protein inclusion is used here as a general term that refers to integral and peripheral membrane proteins or protein oligomers, and nanosized colloidal particles adhering to lipid membranes. The direct protein-lipid interactions lead to indirect, membrane-mediated interactions between the proteins. These interactions consist of short- and long-range parts. The former arises from local perturbation of bilayer structure by the protein inclusions, which decays over a length of around the protein size or bilayer thickness. The latter is ascribed to both modification of membrane fluctuations and perturbation of membrane equilibrium shape due to the presence of protein inclusions. The long-range interaction is treated on length scales larger than the protein size or membrane thickness. In Section 2, we discuss theoretical investigations that have shed lights on how different physical factors contribute to the short- and long-range interactions, and briefly describe the continuum approaches for deriving the interactions based on bilayer elasticity models. In Section 3, we focus on numerical studies that have quantified the short- or long-range interactions, with emphasis on different coarse-grained models for the fluid membranes. We also make qualitative comparison between numerical results and theoretical predictions. In this mini-review we do not discuss the experimental studies. Interested readers are referred to Refs (Bitbol et al., 2018; Idema and Kraft, 2019).

2 Theory

2.1 Short-Range Interaction

Insertion of protein molecules into a lipid bilayer perturbs the packing of nearby lipid chains, since the protein-lipid and lipid-lipid interactions are generically different. Such local perturbation leads to entropy loss of the lipid chains and induces a short-range interaction between the proteins. By defining an order parameter for lipid chain orientation, Marčelja (1976) constructed a mean-field Hamiltonian for a model system of two hexagonal proteins embedded in a flat lipid bilayer and predicted a pure attraction between the proteins. By taking the same assumption that fluctuations of lipid orientation are suppressed in the protein vicinity, Schröder (1977) derived an expression for the attraction. The attraction arising from lipid orientational entropy was first verified by coarse-grained Monte Carlo simulations (Sintes and Baumgärtner, 1997), as will be discussed in Section 3.1. May and Ben-Shaul (2000) applied detailed molecular chain packing theory to calculate the interaction between two protein walls in a bilayer and found that the interaction is attractive at small separations and repulsive at intermediate separations. This interaction starts to level off at separation around the hydrophobic thickness of the proteins or bilayer. Nonmonotonic lipid-mediated interaction potentials between protein inclusions were also reported by Lagüe et al. (2001) based on integral equation theory for liquids.

Protein inclusions generally exhibit different hydrophobic thickness from the embedding lipid bilayer. Lipid chains surrounding the inclusions will stretch or compress in order to avoid or alleviate the exposure of hydrophobic regions of the proteins or lipids. This deformation represents another source of free energy cost that contributes to the bilayer-mediated short-range interaction. Owicki and McConnell (1979) presented a Landau-de Gennes free energy to account for lipid chain deformation and bilayer area change caused by hydrophobically mismatched inclusions, and obtained a short-range attraction between such two inclusions. Huang (1986) formulated a continuum theory to describe the bilayer deformations around a rigid inclusion by considering the free energies associated with monolayer bending, lipid chain compression and surface tension, and reported a nonmonotonic bilayer thickness profile around single inclusions. Dan et al. (1993) and Aranda-Espinoza et al. (1996) adopted this continuum theory to calculate the membrane-mediated interaction between two cylindrical inclusions with hydrophobic mismatch. The interaction looks qualitatively similar, in the case of vanishing spontaneous curvature of the monolayers, to that obtained in Ref (May and Ben-Shaul, 2000), and has a range of about two to three times of the bilayer thickness.

The continuum approach (Huang, 1986; Dan et al., 1993; Aranda-Espinoza et al., 1996) based on membrane elasticity has been widely used to investigate the role of membrane-mediated interactions in such membrane protein processes as formation of gramicidin ion channels (Huang, 1986; Bitbol et al., 2012; Bories et al., 2018), cooperative gating of mechanosensitive channel of large conductance (Ursell et al., 2007; Haselwandter and Phillips, 2013; Kahraman et al., 2016a) and assembly of chemoreceptor trimers (Haselwandter and Wingreen, 2014). Extensions of the membrane elasticity model have been made by including lipid tilt (Fournier, 1999; Bohinc et al., 2003), Gaussian curvature (Brannigan and Brown, 2007), gradient of bilayer thickness (Bitbol et al., 2012), and asymmetry in two monolayers due to noncylindrical shape of the inclusions (Argudo et al., 2017). We briefly describe this approach for a up-down symmetric and single-component lipid bilayer. As shown in Figures 1A,B, the thickness deformations of the lipid bilayer around a hydrophobically mismatched protein inclusion are characterized by the relative displacement u(x, y) of the upper monolayer with respect to the horizontal midplane. By a Taylor-expansion around the unperturbed flat state of the bilayer with thickness 2u₀ and area per lipid Σ₀, the monolayer free energy can be expressed in terms of u, gradient of u (i.e., ∇u), mean curvature H ≈ ∇²u/2, and Gaussian curvature K ≈ det(∇∇u). The free energy of monolayer compression or stretching per projected area is $f_{\text{c}}=K_{\text{A}}{(u/u_0)}^2/4$ with K_A the bilayer’s area compression modulus. The corresponding surface-tension term is f_t = σ[u/u₀ + (∇u)²/2]/2 (Huang, 1986; Haselwandter and Phillips, 2013; Kahraman et al., 2016b) with σ the bilayer tension. The bending energy density assumes $f_{\text{b}}=[\kappa {({\nabla }^{2}u)}^2/2+\kappa c_0{\nabla }^{2}u+\kappa (c_0-c_0^{\prime }{\mathrm{\Sigma }}_0)(u/u_0){\nabla }^{2}u+\bar{\kappa }\text{det}(\nabla \nabla u)]/2$ (Dan et al., 1993; Aranda-Espinoza et al., 1996; Brannigan and Brown, 2007), where κ is the bilayer bending rigidity, c₀ the monolayer spontaneous curvature, $c_0^{\prime }={(\partial c_0/\partial \mathrm{\Sigma })}_{{\mathrm{\Sigma }}_0}$ the change of c₀ due to lipid area variation, and $\bar{\kappa }$ the bilayer Gaussian modulus. The total free energy of the perturbed monolayer per inclusion is then given by the functional $\mathcal{F}[u]=\int \int \text{d}x\text{d}y(f_{\text{c}}+f_{\text{t}}+f_{\text{b}})$. Minimization of $\mathcal{F}[u]$ under appropriate boundary conditions (Nielsen et al., 1998; Nielsen and Andersen, 2000; Brannigan and Brown, 2006) determines the bilayer deformations around the inclusions.

FIGURE 1

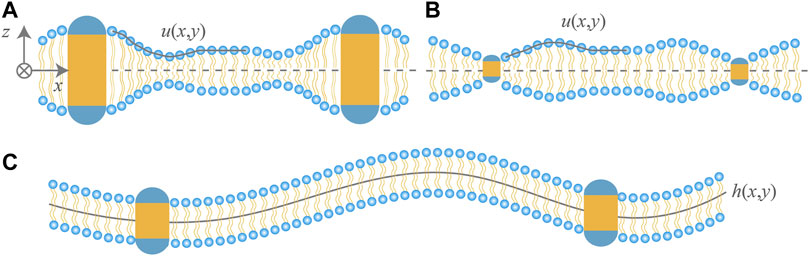
FIGURE 1. Cartoon of lipid bilayers containing two rigid cylindrical proteins. Hydrophilic regions of the proteins are shown in blue and hydrophobic in yellow. Hydrophobic thickness of the proteins in (A,B) is, respectively, greater and less than that of the bilayer in the unperturbed state. For up-down symmetric bilayers, the thickness deformations due to hydrophobic mismatch are described by the profile u(x, y) of the upper monolayer. The protein inclusions in (C) have the same hydrophobic thickness as the bilayer and modify the shape fluctuations of the bilayer as can be characterized by the midplane profile h(x, y). The bilayer midplane in (A,B) is drawn to be horizontal for simplicity, since thickness deformations decouple from midplane deformations.

2.2 Long-Range Interaction

There exist two types of long-range interactions between protein inclusions mediated by the embedding fluid membranes: fluctuation-induced interactions and curvature-induced elastic interactions. As the name suggests, they originate, respectively, from modification of membrane fluctuations and from perturbation of the equilibrium membrane shape by the presence of protein inclusions. In theoretical considerations, the fluid membrane, on length scales larger than its thickness, is coarse-grained into a two-dimensional (2D) elastic surface governed by the Helfrich Hamiltonian (Helfrich, 1973) ${\mathcal{H}}_{\text{el}}=\int [\kappa {(2H-c_0)}^2/2+\bar{\kappa }K+\sigma ]\text{d}A$, where H is the membrane’s mean curvature, K the Gaussian curvature, c₀ the spontaneous curvature due to bilayer asymmetry, κ the bending rigidity, $\bar{\kappa }$ the Gaussian modulus, and σ the lateral tension conjugate to the membrane area. Typical values for the physical properties of synthetic and biological membranes are κ ∼ 10k_BT ≈ 4 × 10⁻²⁰J, $-\kappa \le \bar{\kappa }\le -0.7\kappa$ (Deserno, 2015), and σ ∼ 1 μN/m (Simson et al., 1998). $\ell \equiv \sqrt{\kappa /\sigma }\sim 200\text{nm}$ is the characteristic length scale over which the surface tension dominates over the bending energy. A membrane surface that exhibits small deformations is parameterized by using a displacement field with respect to a planar, spherical, or cylindrical reference surface; see Figure 1C. The Helfrich Hamiltonian is then a function of the displacement field. Proteins that are embedded in or attached to the membrane are treated by applying boundary conditions to the displacement field or via extra energy terms that enter the Hamiltonian of the system. The fluctuation-induced interaction can be estimated from cumulant expansion, whereas the curvature-induced elastic interaction is often derived by finding the minimum-energy shape of the membrane under appropriate boundary conditions and additional requirements that the inclusions are in mechanical equilibrium, i.e., force- and torque-free. In all the following, we will use the notations ${\mathcal{F}}_{\text{fl}}$ and ${\mathcal{F}}_{\text{el}}$ in energy units to distinguish the two types of long-range interactions, and cite the leading-order expressions for ${\mathcal{F}}_{\text{fl}}$ and ${\mathcal{F}}_{\text{el}}$ as derived in literature unless specified otherwise.

2.2.1 Protein Inclusions in Quasiplanar Membranes

Theoretical account of membrane-mediated long-range interactions between protein inclusions was pioneered by Goulian et al. (1993), who considered two proteins of circular cross section embedded in a tensionless fluid membrane, and discovered that thermal fluctuations of the membrane induce a long-range interaction between the inclusions. This fluctuation-induced interaction ${\mathcal{F}}_{\text{fl}}$ decays as 1/R⁴ for interprotein separation R much larger than the protein radius or membrane thickness a, given that the bending rigidity κ_p and Gaussian modulus ${\bar{\kappa }}_{\text{p}}$ of the proteins differ from those of the membrane. More specifically, for infinitely rigid proteins (${\kappa }_{\text{p}}=-{\bar{\kappa }}_{\text{p}}=\infty$), ${\mathcal{F}}_{\text{fl}}\approx -6k_{\text{B}}T{(a/R)}^4$ (Goulian et al., 1993; Park and Lubensky, 1996) is purely attractive with magnitude set by the thermal energy k_BT and independent of the membrane rigidities κ or $\bar{\kappa }$. Very similarly, ${\mathcal{F}}_{\text{fl}}\approx -k_{\text{B}}Tco{s}^2(2{\theta }_1+2{\theta }_2)/128{(\sqrt{l_1{l}_2}/R)}^4$ when the rigid inclusions are two thin rods of length l_i and orientational angle θ_i (i = 1, 2) relative to the vector joining their centers (Golestanian et al., 1996). The membrane-mediated, fluctuation-induced attraction is of entropic origin and arises from the fact that the number of allowed modes in the membrane is suppressed by the presence of rigid inclusions. Helfrich and Weikl (2001) indeed rederived the expression ${\mathcal{F}}_{\text{fl}}\approx -6k_{\text{B}}T{(a/R)}^4$ for two rigid discoidal inclusions from fluctuation mode entropies of the membrane. For soft protein inclusions that have rigidities close to the membrane, i.e., κ_p = κ + Δκ and ${\bar{\kappa }}_{\text{p}}=\bar{\kappa }+\mathrm{\Delta }\bar{\kappa }$ with |Δκ/κ|≪ 1 and $|\mathrm{\Delta }\bar{\kappa }/\bar{\kappa }|\ll 1$, ${\mathcal{F}}_{\text{fl}}\approx \mathrm{\Delta }\kappa \mathrm{\Delta }\bar{\kappa }/(2{\kappa }^2)k_{\text{B}}T{(a/R)}^4$ (Goulian et al., 1993; Park and Lubensky, 1996), where the relative sign of Δκ and $\mathrm{\Delta }\bar{\kappa }$ dictates whether the interaction is attractive or repulsive. When $\mathrm{\Delta }\kappa \mathrm{\Delta }\bar{\kappa }<0$, the soft inclusions experience a fluctuation-induced attraction, consistent with the limiting case of infinitely rigid proteins. Lin et al. (2011) developed a method to deal with two discs of arbitrary rigidities in a membrane under tension, and obtained in the bending-dominated regime ($a\ll R\ll \ell \equiv \sqrt{\kappa /\sigma }$) the fluctuation-induced interaction ${\mathcal{F}}_{\text{fl}}\approx -k_{\text{B}}T{(a/R)}^{4}f(\kappa ,\mathrm{\Delta }\kappa ,\mathrm{\Delta }\bar{\kappa })$ with the dimensionless coefficient $f(\kappa ,\mathrm{\Delta }\kappa ,\mathrm{\Delta }\bar{\kappa })=2\mathrm{\Delta }\bar{\kappa }(3\mathrm{\Delta }{\bar{\kappa }}^2+6\mathrm{\Delta }\kappa \mathrm{\Delta }\bar{\kappa }-8\kappa \mathrm{\Delta }\kappa )/[{(4\kappa -\mathrm{\Delta }\bar{\kappa })}^2(2\kappa +2\mathrm{\Delta }\kappa +\mathrm{\Delta }\bar{\kappa })]$. This formula for ${\mathcal{F}}_{\text{fl}}$ applies to protein inclusions of circular cross section, and successfully reproduces the previous two expressions obtained in the case of tensionless membranes (σ = 0), since $f(\kappa ,\mathrm{\Delta }\kappa ,\mathrm{\Delta }\bar{\kappa })=6$ in the rigid-inclusion limit ($\mathrm{\Delta }\kappa =-\mathrm{\Delta }\bar{\kappa }=\infty$), and $f(\kappa ,\mathrm{\Delta }\kappa ,\mathrm{\Delta }\bar{\kappa })\approx -\mathrm{\Delta }\kappa \mathrm{\Delta }\bar{\kappa }/(2{\kappa }^2)$ for soft inclusions with |Δκ/κ|≪ 1 and $|\mathrm{\Delta }\bar{\kappa }/\bar{\kappa }|\ll 1$. In the tension-dominated regime (ℓ ≪ a ≪ R), ${\mathcal{F}}_{\text{fl}}\approx -9k_{\text{B}}T{(a/R)}^8$ for rigid proteins as also obtained in Ref (Yolcu et al., 2011) by using a different approach based on effective field theory, whereas ${\mathcal{F}}_{\text{fl}}\approx -k_{\text{B}}T{[\mathrm{\Delta }\bar{\kappa }/(a^2\sigma )]}^2{(a/R)}^8$ for soft inclusions. This 1/R⁸ attraction is different from the 1/R⁴ attraction for two thin rods embedded in a tension-controlled fluctuating film without curvature-energy term (Golestanian et al., 1996), possibly due to the different shapes. It is remarkable that in both the bending- and tension-dominated regimes, the fluctuation-induced interaction vanishes at $\mathrm{\Delta }\bar{\kappa }=0$, namely, for protein inclusions of the same Gaussian modulus as the membrane. The importance of Gaussian curvature to the fluctuation-induced interactions has been already appreciated in the simulation study of aggregation of rigid membrane inclusions (Weikl, 2001), as will be discussed later in Section 3.

Protein inclusions of shapes that break the bilayer’s up-down symmetry, e.g., cone shape, bend the membrane. Perturbation of the equilibrium membrane shape induces long-range interactions between such inclusions and has been taken into account by imposing either a contact angle (Goulian et al., 1993; Park and Lubensky, 1996; Weikl et al., 1998; Kim et al., 1998) or a curvature tensor (Dommersnes and Fournier, 1999a; Yolcu and Deserno, 2012) at the protein-membrane boundary. For rigid conical inclusions in a tensionless membrane (Goulian et al., 1993; Park and Lubensky, 1996; Weikl et al., 1998; Kim et al., 1998; Dommersnes and Fournier, 1999a,b; Yolcu and Deserno, 2012), the curvature-induced elastic interaction ${\mathcal{F}}_{\text{el}}\approx 4\pi \kappa ({\alpha }_1^2+{\alpha }_2^2){(a/R)}^4$ is repulsive and depends on the contact angle α_i=1,2 defined by the protein’s axis of rotational symmetry and the normal of the membrane at the boundary as shown in Figure 2A. For rigid conical inclusions in a membrane under tension, the elastic interaction obtained at a < ℓ takes the form ${\mathcal{F}}_{\text{el}}\approx 2\pi \kappa {\alpha }_1{\alpha }_2{(a/\ell )}^2{K}_0(R/\ell )+\pi \kappa ({\alpha }_1^2+{\alpha }_2^2){(a/\ell )}^4{K}_2^2(R/\ell )$ (Weikl et al., 1998) with K_n=0,2(x) the modified Bessel function of the second kind. This expression recovers the previous one for the case of vanishing membrane tension by approaching the limit ℓ → ∞, and implies that the presence of membrane tension can render the elastic interaction between two conical inclusions of opposite orientations (α₁α₂ < 0) attractive at separation R > R^∗. R^∗ is the separation for the minimum of ${\mathcal{F}}_{\text{el}}$ and assumes R^∗ ≈ 6.6a for a reasonable choice of parameters a/ℓ = 0.1 and α₁ = − α₂ ≠ 0. See Figure 2B for the elastic interaction between two conical inclusions.

FIGURE 2

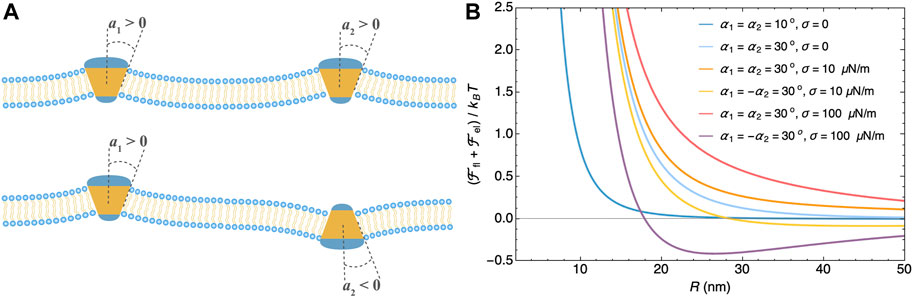
FIGURE 2. Membrane-mediated interaction between two conical inclusions. (A) Cartoon of membranes with two conical inclusions that have contact angles α₁ and α₂. (B) Membrane-mediated interaction as a function of the inter-inclusion distance R at different contact angles and membrane tensions calculated from ${\mathcal{F}}_{\text{fl}}\approx -6k_{\text{B}}T{(a/R)}^4$ and ${\mathcal{F}}_{\text{el}}\approx 2\pi \kappa {\alpha }_1{\alpha }_2{(a/\ell )}^2{K}_0(R/\ell )+\pi \kappa ({\alpha }_1^2+{\alpha }_2^2){(a/\ell )}^4{K}_2^2(R/\ell )$ (Weikl et al., 1998) with a = 5 nm and membrane bending rigidity κ = 25 k_BT. These two equations are explained in the main text.

Shape anisotropy of the protein inclusions (Park and Lubensky, 1996; Dommersnes and Fournier, 1999a, 2002; Chou et al., 2001; Yolcu and Deserno, 2012), external torques on the inclusions (Dommersnes and Fournier, 1999b), and forces exerted on the membranes by the inclusions (Evans et al., 2003) can alter the membrane-mediated interactions. Park and Lubensky (1996) characterized protein inclusions of noncircular cross section by using symmetric-traceless tensor order parameters, and found that 1) the fluctuation-induced interaction ${\mathcal{F}}_{\text{fl}}$ is anisotropic and can be attractive or repulsive depending on the relative orientations of the inclusions to their center-to-center vector and that 2) up-down asymmetry of the inclusion shape changes the distance dependence of ${\mathcal{F}}_{\text{fl}}$ from 1/R⁴ to 1/R². Chou et al. (2001) reported that the elastic interaction ${\mathcal{F}}_{\text{el}}$ between two inclusions of elliptic cross section averaged over their orientations changes from repulsive to attractive with increasing ellipticity. Dommersnes and Fournier (1999a, 2002), Yolcu and Deserno (2012), and Noguchi and Fournier (2017) showed that, for wedge-shaped, saddle-like, or arc-shaped protein inclusions that impose anisotropic curvature on a tensionless membrane, the leading term of the curvature-induced elastic interaction ${\mathcal{F}}_{\text{el}}$ is of 1/R²-order and can be attractive or repulsive depending on the imposed curvatures and orientations of the inclusions. Dommersnes and Fournier (1999b) investigated the membrane-mediated interactions between two protein inclusions with orientations restricted by external torques, and revealed that the presence of external torques strongly increases the range of both the fluctuation-induced attraction ${\mathcal{F}}_{\text{fl}}$ and curvature-induced repulsion ${\mathcal{F}}_{\text{el}}$. Specifically, ${\mathcal{F}}_{\text{fl}}$ is found to be a function of ln R, whereas ${\mathcal{F}}_{\text{el}}$ decays as 1/R² for the two inclusions with parallel orientations, or approximately as   ln(1/R) otherwise. Evans et al. (2003) calculated the elastic interaction between two cylindrical inclusions that apply normal forces to the membrane under tension and cause a variation in the membrane profile, and obtained the relation ${\mathcal{F}}_{\text{el}}\propto K_0(R/\ell )/(2\pi \sigma )$ with the omitted coefficient of proportionality measuring the strength of membrane-inclusion coupling due to the forces. This curvature-induced elastic interaction is repulsive and decays slower than 1/R⁴.

In addition to the aforementioned two-body interactions, there exist many-body interactions between the protein inclusions mediated by the membrane, which can not be simply accounted for by a sum of two-body interactions. Dommersnes and Fournier (2002) showed that the elastic interaction between three identical rigid conical inclusions in an equilateral-triangle arrangement is ${\mathcal{F}}_{\text{el}}\approx 12\pi \kappa {\alpha }^2{(a/R)}^4$, 50% less than the estimation of 24πκα²(a/R)⁴ by assuming pairwise additivity. Yolcu and Deserno (2012) obtained general expressions for three- and four-body interactions between rigid conical inclusions in the case of vanishing membrane tension. For instance, the three-body fluctuation-induced interaction ${\mathcal{F}}_{\text{fl}}\approx 4k_{\text{B}}T{(a_1{a}_2{a}_3)}^2/{(R_{12}{R}_{23}{R}_{31})}^2{\sum }_{(i,j,k)}cos(2{\vartheta }_{ijk}-2{\vartheta }_{jki})$, where a_i is the cross-sectional radius of protein i, $R_{ij}\equiv |{\vec{R}}_{ij}|$ the interprotein distance, ϑ_ijk the angle between the distance vectors ${\vec{R}}_{ij}$ and ${\vec{R}}_{jk}$, and the summation is over three cyclic permutations (i, j, k) = (1, 2, 3), (2, 3, 1), (3, 1, 2); the three-body elastic interaction ${\mathcal{F}}_{\text{el}}\approx 8\pi \kappa {\sum }_{(i,j,k)}{a}_i^2{a}_j{a}_k{\alpha }_j{\alpha }_k/{(R_{ij}{R}_{ki})}^{2}cos2{\vartheta }_{kij}$ with α_i the contact angle for protein i. The angular part in the above expression for ${\mathcal{F}}_{\text{el}}$ suggests that this interaction can be attractive and might stabilize aggregates of protein inclusions. Dommersnes and Fournier (1999a) derived the three-body elastic interaction for inclusions that induce anisotropic curvatures onto a tensionless membrane. Weitz and Destainville (2013) followed the approach in Ref (Dommersnes and Fournier, 1999a) to calculate the three-body interactions for rigid conical inclusions in the case of nonvanishing membrane tension. These studies demonstrated that the three- and four-body interactions are of the same order of magnitude as the two-body counterparts and depend on the spatial arrangement of the proteins. Nevertheless, the two-body interactions may serve as good approximations at low concentrations of protein inclusions.

2.2.2 Non-transmembrane Proteins Attached to Quasiplanar Membranes

In biological or biomimetic systems, the proteins can also be attached to lipid membranes in such a way that their center-of-mass positions are not at the center of the membrane bilayer. Park and Lubensky (1996) calculated the curvature-induced elastic interactions between non-transmembrane proteins that are bound to a membrane and have preferred center-of-mass positions off the bilayer midplane, and found that the three- and four-body interactions have a similar magnitude as the two-body interaction, and that all these interactions decrease with the distance as 1/R⁴; see Eqs. 5.11–5.13 in Ref (Park and Lubensky, 1996). Weikl (Weikl, 2003) considered the elastic interactions between two infinitely long and parallel cylinders of radius a adhering to a membrane under tension. For cylinders bound to the same membrane side, ${\mathcal{F}}_{\text{el}}\approx -{(\kappa +2a^2{u}_{\text{ad}})}^2/(4\kappa a/\ell )\{1+tanh[R/(2\ell )]\}$ is repulsive; for cylinders adhering at opposite membrane sides, ${\mathcal{F}}_{\text{el}}\approx -{(\kappa +2a^2{u}_{\text{ad}})}^2/(4\kappa a/\ell )\{1+cosh[R/(2\ell )]\}$ becomes attractive. u_ad < 0 is the adhesion energy per area. Müller et al. (2005) reproduced these results by calculating the membrane-mediated elastic forces via line integral of stress tensor. Mkrtchyan et al. (2010) revisited the elastic interactions between two membrane-bound cylinders, and also observed attractions between cylinders strongly adhering to the opposite side of the membrane from numerical calculations.

2.2.3 Protein Inclusions in Vesicular or Tubular Membranes

The previously discussed studies focused on quasiplanar membranes with small deviations from the reference flat state. For proteins embedded in vesicle or tubular membranes, the membrane size that characterizes the background curvature of the shape appears to be a relevant length scale. Dommersnes et al. (1998) calculated the elastic interaction between two identical conical inclusions in a spherical vesicle with fixed surface area, and found the interaction is always repulsive and proportional to the square of the contact angle. They recovered, at small separations, the 1/R⁴ repulsion as reported in Ref (Goulian et al., 1993), and observed a much stronger repulsion that decays as 1/R^0.33 for separations larger than the crossover length $R_{\text{c}}\approx 1.1a{(\mathcal{R}/a)}^{0.45}\ll \mathcal{R}$ with $\mathcal{R}$ the radius of the unperturbed spherical vesicle. Vahid and Idema (2016) predicted that two identical conical inclusions would attract each other when placed at the same longitudinal coordinates on a membrane tubule, in contrast to the repulsion in the case of quasiplanar membranes. When the conical inclusions are situated on the same transversal coordinates, the elastic interaction induced by the tubular membrane is repulsive at small separations and attractive at large separations.

3 Numerical Studies

As stated above, theoretical studies of membrane-mediated interactions are often restricted to small deformations of the membranes and do not take into account specific lipid-protein interactions. Numerical simulations can overcome those limitations, e.g., specific lipid-protein interactions can be dealt with atomistic molecular dynamics simulations. Figure 3 shows a variety of fluid membrane models used in coarse-grained simulations.

FIGURE 3

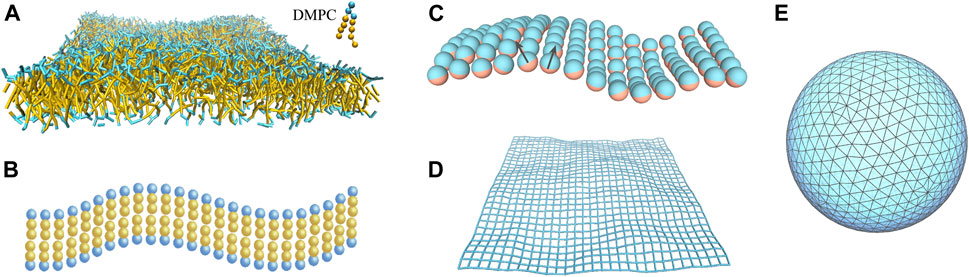
FIGURE 3. Computational models for fluid membranes at different levels of resolution. (A) Coarse-grained DMPC bilayer used in dissipative particle dynamics simulations. Water molecules are not shown here for clarity. (B) Cooke-Deserno model (Cooke and Deserno, 2005) with each lipid consisting of a hydrophilic head bead (in blue) and two hydrophobic tail beads (in yellow). Stable fluid bilayer can be simulated with a proper choice of tail-tail attraction without explicit solvent. (C) One-particle thick model (Yuan et al., 2010; Shiba and Noguchi, 2011). Any two particles experience short-range repulsion and long-range attraction. The particle-particle interaction depends on their orientations as specified by the normal vectors (black arrows). (D) Discretized elastic sheet model for a quasi-planar fluid membrane (Weikl, 2001; Dommersnes and Fournier, 2002). The membrane configuration is described by the displacement field h_i with respect to the horizontal reference plane at each discrete site i. (E) Triangulated surface model for vesicular membranes (Kroll and Gompper, 1992; Sunil Kumar et al., 2001; Hu et al., 2011). The angle between the normal vectors of each two neighboring triangles determines the local curvature of the membrane.

3.1 Short-Range Interaction

Monte Carlo (MC) (Sintes and Baumgärtner, 1997; West et al., 2009) and molecular dynamics (MD) (Venturoli et al., 2005; de Meyer et al., 2008; Schmidt et al., 2008; West et al., 2009) simulations based on coarse-grained models of lipids and proteins have been used to investigate membrane-mediated short-range interactions between two cylindrical protein inclusions with emphasis on the generic feature of the interactions. Simulation study of proteins without hydrophobic mismatch was first done by Sintes and Baumgärtner (1997), who considered two rigid cylinders (of diameter two to four times of lipid width σ) embedded in a lipid bilayer whose bending deformation was strongly suppressed. They found a depletion-induced attraction for inclusion separation R < σ and an oscillating interaction for σ < R < 6σ attributed to inhomogeneous distribution and orientational fluctuations of lipid chains around inclusions. In simulation studies with hydrophobic mismatch between the bilayer and protein inclusions, the bilayer thickness profile around single inclusions was found to exhibit similar nonmonotonic behavior (Venturoli et al., 2005; de Meyer et al., 2008; Schmidt et al., 2008; West et al., 2009), consistent with the elastic theory. The potential of mean force (PMF) between two rigid inclusions depends on inclusion size (de Meyer et al., 2008) and lipid-protein interaction (West et al., 2009). For protein inclusions that have no or weak affinity to lipid chains, the PMF is attractive at smaller separations and repulsive at intermediate separations (de Meyer et al., 2008; Schmidt et al., 2008), also in accordance with the elastic theory. For protein inclusions strongly attracting lipid chains, the PMF is highly oscillatory with a repulsion at close separations (West et al., 2009). Protein inclusions with hydrophobic thickness larger than that of the bilayer can be tilted (Venturoli et al., 2005; Klingelhoefer et al., 2009) or even bent (Venturoli et al., 2005) in the membrane in order to avoid exposure of their hydrophobic domains.

All-atom simulations can provide atomistic details of the bilayer deformation around single protein inclusions. Kim et al. (2012) performed all-atom MD simulations to measure the thickness profile of different bilayers embedding a Gramicidin A channel, and found qualitative discrepancy from theoretical predictions, probably due to specific protein-lipid interactions that are not addressed in the simplified membrane elasticity model. Mondal et al. (2011) studied the energetics of lipid bilayer deformations around a noncylindrical protein inclusion like G-protein coupled receptors by taking the continuum theory where the membrane-protein boundary conditions were extracted from atomistic MD simulations. Argudo et al. (2017) revisited the atomistic MD simulations of a Gramicidin A channel embedded in a POPC bilayer and showed that the membrane deformations and tilt of the ionic channel can be quantitatively captured by a refined bilayer model that incorporates the chemistry and geometry of the protein inclusions. However, due to the computational cost, it remains challenging to measure the membrane-mediated short-range interactions between two protein inclusions from all-atom MD simulations.

3.2 Long-Range Interaction

To directly measure the fluctuation-induced interactions remains a computationally difficult task, since they are weak and often coupled with the curvature-induced elastic interactions. Weikl (2001) studied the fluctuation-induced aggregation of protein inclusions much more rigid than the fluid membrane via MC simulations, where the membrane was represented by a discretized 2D elastic sheet and protein inclusions occupy single vacant sites on the membrane surface. The systems with inclusions of κ_p and ${\bar{\kappa }}_{\text{p}}$ two order-of-magnitude larger than those of the membrane were found to separate into inclusion-rich and inclusion-poor phases even in the absence of any direct protein-protein attraction, whereas the systems with no contrast in the Gaussian moduli (${\bar{\kappa }}_{\text{p}}=\bar{\kappa }$) exhibit the same critical point as if the membrane were completely flat without shape fluctuations. This finding points out that a difference in Gaussian moduli is necessary for a fluctuation-induced interaction between membrane inclusions, as mentioned in Section 2.2.1. Pezeshkian et al. (2016) reported from MD simulations the clustering of rigid pentagon shaped nanoparticles, coarse-grained model of bacterial Shiga toxin, on lipid membranes driven by the fluctuation-induced attraction. Very recently, Sadeghi and Noé (2021) extracted from MD simulations the membrane-mediated effective interactions between protein particles embedded in a fluid membrane modeled by particle-based elastic sheet. The interaction varies non-monotonically with interparticle separation and has a depth of about k_BT for different values of protein stiffness, which can not be accounted for by the sum of the two-body interactions ${\mathcal{F}}_{\text{fl}}+{\mathcal{F}}_{\text{el}}\approx -6k_{\text{B}}T{(a/R)}^4+4\pi \kappa ({\alpha }_1^2+{\alpha }_2^2){(a/R)}^4$. It is not clear whether the discrepancy is model specific.

MD simulations with coarse-grained models of lipid membranes at different levels of resolution (Reynwar et al., 2007; Olinger et al., 2016; Xiong et al., 2017; Spangler et al., 2018; Noguchi, 2016; Noguchi and Fournier, 2017), MC simulations (Bahrami et al., 2012; Šarić and Cacciuto, 2012b,a; Vahid et al., 2017; Bahrami and Weikl, 2018; Bonazzi and Weikl, 2019) and numerical minimizations (Reynwar and Deserno, 2011; Schweitzer and Kozlov, 2015) based on mesoscopic elastic surface models showed that proteins or particles adhering to membranes experience curvature-induced interactions, which are strongly attractive in many cases and can drive particle assembly on the membranes. We first review the studies of spherical particles. Reynwar et al. (2007) computed directly from coarse-grained MD simulations the force between two capsids adhering strongly to a lipid bilayer, and obtained repulsive forces at small capsid separations followed by attractive ones at large separations as shown in Figure 4A, seemingly contradictory to the theoretical prediction of pure elastic repulsion for conical inclusions in Section 2.2.1. By using the Surface Evolver package (Brakke, 1992) to numerically minimize the energy of a membrane adhering to two spherical particles, Reynwar and Deserno (2011) confirmed later that the curvature-induced force is indeed repulsive for small contact angles (i.e., weak adhesion), whereas for contact angles larger than 90° (i.e., strong adhesion), the force changes from repulsive to attractive with increasing separation, consistent with their MD results in Ref (Reynwar et al., 2007).

FIGURE 4

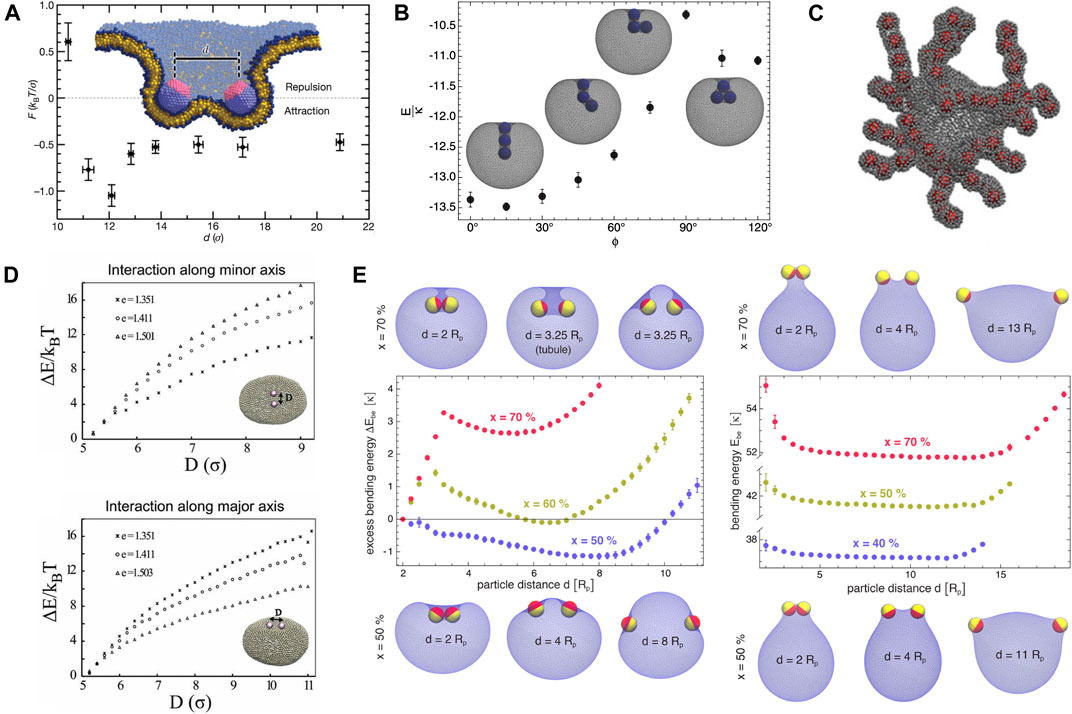
FIGURE 4. Membrane-mediated interactions between quasi-spherical or spherical particles adsorbed on fluid membranes obtained from coarse-grained MD or MC simulations. (A) Force F versus center-to-center distance d between two capsids (diameter of 8 nm) strongly bound to a fluid bilayer. Reprinted by permission from Springer Nature Customer Service Centre GmbH: Reynwar et al. (2007), Copyright (2007). The minimal attraction at d ≈ 12 σ = 12 nm is about k_BT/σ ∼ 4 pN. (B) Rescaled total energy E/κ of a vesicle with three adsorbed particles wrapped by membrane tubes as a function of the angle ϕ between the particles (Bahrami et al., 2012), copyright (2012) by the American Physical Society. Insets are energy-minimum configurations for ϕ = 0°, 45°, 90°, and 120°. The most stable configuration corresponds to linear aggregation of the three particles inside the membrane tube, reflecting membrane-mediated strong attraction between the particles. The vesicle membrane has a fixed area of $\mathcal{A}$ and a fixed enclosed volume of $\mathcal{V}=0.88\times (4\pi /3){[\mathcal{A}/(4\pi )]}^{3/2}$. The particle-membrane adhesion energy per area is $U=2\kappa /R_{\text{p}}^2$ with κ membrane bending rigidity and R_p particle radius. (C) Snapshot of aggregates of spherical particles adsorbed to vesicular membranes from MC simulations at constant temperature (Šarić and Cacciuto, 2012b), copyright (2012) by the American Physical Society. (D) Interaction energy ΔE versus distance D of two spheres bound to an ellipsoidal vesicle with eccentricity e (Vahid et al., 2017), with permission of The Royal Society of Chemistry. (E) Excess bending energy ΔE_be of a vesicle versus distance R of two Janus spherical particles adhered to the outside (left panel) or inside (right panel) of the membrane, reprinted with permission from Bahrami and Weikl (2018), copyright 2018 American Chemical Society. The adhesive cap in yellow is fully covered by the membrane and has an area fraction of x. For x = 60% and 70%, the increase of ΔE_be at small values of d corresponds to curvature-induced elastic attraction between the particles. The decrease of ΔE_be at intermediate values of d corresponds to curvature-induced repulsion between the particles.

Using a triangulated surface model for vesicle membranes, Bahrami et al. (2012) determined from simulated annealing MC simulations the minimum-energy shape of vesicle membranes interacting with adhesive spherical particles, and discovered stable membrane tubules that wrap one row of two or three particles; see Figure 4B. As shown in Figure 4C, similar membrane tubular structures were observed in constant-temperature MC simulations by Šarić and Cacciuto (2012b), who also reported linear aggregation of spherical particles adsorbed on vesicle membranes (Šarić and Cacciuto, 2012a). MD simulations (Reynwar et al., 2007; Xiong et al., 2017; Spangler et al., 2018) with molecular models for flat lipid bilayers showed that linear aggregation of adsorbed spherical particles induces membrane tubulation and vesiculation. These studies point towards curvature-induced strong attractions between spherical particles adhering to fluid membranes. Vahid et al. (2017) further demonstrated that, in the case of quasi-spherical vesicles, the curvature-induced attraction between two adsorbed spherical particles becomes weaker as the vesicle gets bigger. In the case of quasi-ellipsoidal vesicles, the attraction for two particles placed along the major axis is different from that along the minor axis, and their relative magnitude depends on the ellipticity of the vesicles; see Figure 4D. This MC simulation result suggests that the background curvature of closed membranes affects the curvature-mediated attraction. In the extension of their previous study (Bahrami et al., 2012), Bahrami and Weikl (2018) reported that two spherical Janus particles with one side strongly adhering to vesicle membranes can attract or repel each other, depending on the area fraction of the adhesive side and on the shape (i.e., concave or convex) of the adhering membrane segments; see Figure 4E. In all these simulated systems (Reynwar et al., 2007; Olinger et al., 2016; Xiong et al., 2017; Spangler et al., 2018; Noguchi, 2016; Noguchi and Fournier, 2017; Bahrami et al., 2012; Šarić and Cacciuto, 2012b,a; Vahid et al., 2017; Bahrami and Weikl, 2018; Bonazzi and Weikl, 2019; Reynwar and Deserno, 2011; Schweitzer and Kozlov, 2015), particle-membrane adhesion energy, membrane bending energy, and possible constraint due to conservation of the volume enclosed by membranes determine together the optimal membrane shape and thus how the curvature-induced interaction varies with inter-particle distance.

Numerical studies of anisotropic protein inclusions or scaffolds interacting with fluid membranes have also revealed that the membrane-mediated attractions are important for the protein to assemble and to remodel the membranes. Using Surface Evolver to find the minimum-energy shape of membranes interacting with two rigid protein scaffolds, Schweitzer and Kozlov (2015) showed that for circular scaffolds with anisotropic curvature (saddle-like or ellipsoidal shape), or isotropically curved scaffolds of elongated shapes (noncircular footprint on the membrane), the curvature-induced interaction is repulsive at small inter-scaffold separations and attractive at large separations. Specifically, the curvature-mediated attraction between two BAR-domain-like scaffolds was found to be very strong; see Figure 5A. Using a coarse-grained molecular model of N-BAR domain, Simunovic et al. (2013) showed from MD simulations that the proteins assemble on flat or vesicle membranes at low concentrations and form a mesh of linear aggregates as shown in Figure 5B. Noguchi (2016), and Noguchi and Fournier (2017) studied the assembly of arc-shaped proteins on flat membranes with coarse-grained MD simulations, and found side-by-side alignment of the proteins around membrane tubules; see Figure 5C. The membrane-mediated side-by-side arrangement was also reported by Bonazzi and Weikl (2019) in MC simulations of arc-shaped particles remodeling an initially spherical vesicle modeled by a triangulated surface; see Figure 5D, where the rather loose arrangement of particles has been experimentally reported for N-BAR proteins interacting with membrane tubules (Daum et al., 2016). We note that, in addition to the membrane-mediated indirect interactions, direct protein-protein interactions may also play a part in the assembly of anisotropic proteins on membranes. For instance, the helical arrangement of N-BAR proteins around membrane nanotubes found in coarse-grained MD simulations (Simunovic et al., 2016) is very likely due to the direct attraction between the proteins. Using the same discrete model as in Ref (Weikl, 2001) and treating saddle-like inclusions as point-like constraints that impinge anisotropic curvature on the membrane, Dommersnes and Fournier (2002) simulated the assembly of those inclusions, assisted by the curvature-induced attraction, into regular arrays that shape the membrane into the experimentally observed egg-carton pattern as shown in Figure 5E.

FIGURE 5

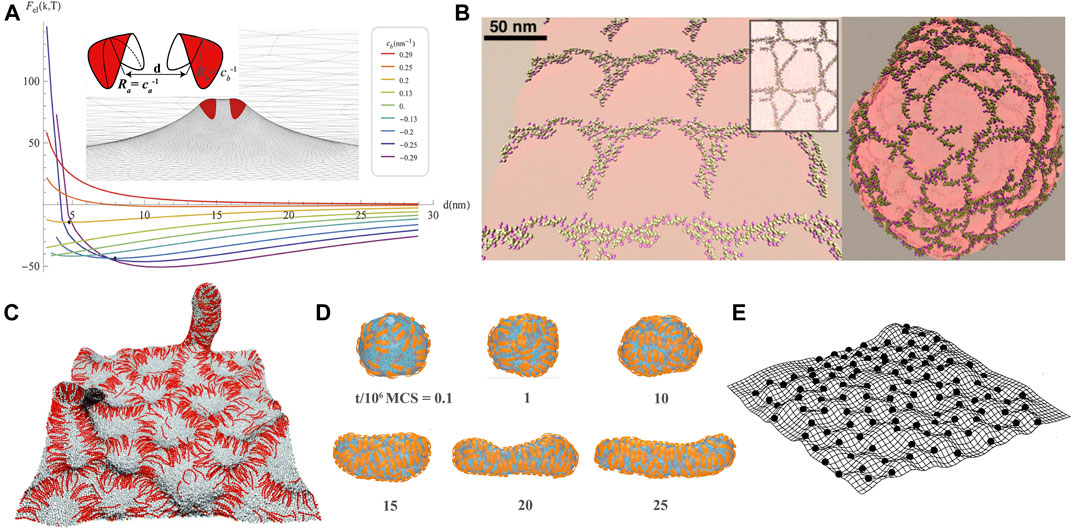
FIGURE 5. Membrane-mediated interactions between anisotropic protein inclusions (A) and assembly of anisotropic proteins on membranes (B–E). (A) Curvature-induced elastic energy F_el versus distance d of two BAR-like membrane scaffolds for different values of scaffold curvature c_b (Schweitzer and Kozlov, 2015)(CC BY 4.0). The BAR-like scaffold has principle curvatures c_a and c_b as illustrated in the inset. When projected to initial membrane plane, the scaffold has an elliptical shape with semi-axes of 6.5 and 1.5 nm. The membrane bending rigidity κ = 20 k_BT. (B) Linear aggregation of N-BARs on flat and vesicular membranes observed in coarse-grained MD simulations (Simunovic et al., 2013). Copyright (2013) National Academy of Sciences. (C) Side-by-side alignment of BAR-like particles on membrane bulges and tubes (Noguchi, 2016; Noguchi and Fournier, 2017), with permission of The Royal Society of Chemistry. (D) MC sequence of configurations of an initially spherical vesicle remodeled by arc-shaped scaffold. Reprinted from Bonazzi and Weikl (2019), copyright (2019), with permission from Elsevier. Free scaffolds unbound to the membrane are not shown here for clarity. (E) Assembly of saddle-shaped protein inclusions (modeled by point-like particles that locally impose two opposite eigenvalues of the membrane’s curvature tensor) into regular pattern on the membrane. Reprinted from Dommersnes and Fournier (2002), copyright (2002), with permission from Elsevier.

It is worthy to mention the membrane-mediated interactions in the systems of cell adhesion that is mediated by the specific binding of membrane-anchored receptors and ligands. The receptor-ligand complexes constrain the local separations of the two adhering membranes and thus experience fluctuation-induced attractions (Bruinsma and Pincus, 1996; Krobath et al., 2009; Weikl, 2018). An important biological consequence of these membrane-mediated attractions is the cooperative binding of cell adhesion proteins, as corroborated by MD simulations (Hu et al., 2013; Hu et al., 2015; Xu et al., 2015) and experiments (Steinkühler et al., 2018).

4 Summary and Outlook

We have reviewed both theoretical and numerical studies on membrane-mediated interactions between protein inclusions. The continuum theories for the short- and long-range interactions are based on membrane elasticity models at different length scales. A natural question to ask is whether these theories can be cast into a unified framework. Agrawal et al. (2016) introduced in the Helfrich Hamiltonian additional terms for the jump of displacement and rotation angles that account for the hydrophobic mismatch and structural rearrangement of lipids around the protein inclusions, and showed that the curvature-induced repulsion between conical protein inclusions can be reduced by orders of magnitude. This prediction shall be tested by large scale simulations with coarse-grained molecular models or even atomistic models for proteins and lipid bilayers.

Despite the physical insights provided by numerous simulation studies, quantitative comparison between simulations and existing theories is still very limited. Such comparison would be invaluable for checking the validity of the assumptions involved in the theories. Moreover, simulations on membrane remodeling by isotropic or anisotropic proteins or particles stimulate the necessity of developing theories for membrane-mediated interactions between protein inclusions under large membrane deformations. Theoretical approach based on line integral of stress tensor in Refs (Müller et al., 2005, 2007) represents a possible choice.

Finally, we would like to point out that the real cell environment is much more complicated than the model systems considered in the theories and simulations. Cell membranes are linked to cytoskeleton that undergoes active deformations. The membrane proteins or nanoparticles adhering to the membranes may also be associated with active processes (Ramaswamy et al., 2000). It is interesting to ask how such nonequilibrium factors contribute to or even change the membrane-mediated interactions between protein inclusions.

Author Contributions

JH conceived the project; JG, RH, LL, and JH wrote the manuscript.

Funding

JH and LL acknowledge support from the National Natural Science Foundation of China (Grants Nos. 21 973 040, 21 504 038, and 11 902 327) and Youth Innovation Promotion Association CAS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Agrawal, H., Liu, L., and Sharma, P. (2016). Revisiting the Curvature-Mediated Interactions Between Proteins in Biological Membranes. Soft Matter 12, 8907–8918. doi:10.1039/c6sm01572g

PubMed Abstract | CrossRef Full Text | Google Scholar

Alberts, B., Johnson, A., Lewis, J., Morgan, D., Raff, M., Roberts, K., et al. (2015). Molecular Biology of the Cell. 6th Edn. New York, NY: Garland Science, Taylor and Francis Group.

Google Scholar

Aranda-Espinoza, H., Berman, A., Dan, N., Pincus, P., and Safran, S. (1996). Interaction Between Inclusions Embedded in Membranes. Biophysical J. 71, 648–656. doi:10.1016/s0006-3495(96)79265-2

CrossRef Full Text | Google Scholar

Argudo, D., Bethel, N. P., Marcoline, F. V., Wolgemuth, C. W., and Grabe, M. (2017). New Continuum Approaches for Determining Protein-Induced Membrane Deformations. Biophysical J. 112, 2159–2172. doi:10.1016/j.bpj.2017.03.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahrami, A. H., Lipowsky, R., and Weikl, T. R. (2012). Tubulation and Aggregation of Spherical Nanoparticles Adsorbed on Vesicles. Phys. Rev. Lett. 109, 188102. doi:10.1103/physrevlett.109.188102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bahrami, A. H., and Weikl, T. R. (2018). Curvature-mediated Assembly of Janus Nanoparticles on Membrane Vesicles. Nano Lett. 18, 1259–1263. doi:10.1021/acs.nanolett.7b04855

PubMed Abstract | CrossRef Full Text | Google Scholar

Bitbol, A.-F., Constantin, D., and Fournier, J.-B. (2012). Bilayer Elasticity at the Nanoscale: The Need for New Terms. PLoS ONE 7, e48306. doi:10.1371/journal.pone.0048306

PubMed Abstract | CrossRef Full Text | Google Scholar

Bitbol, A.-F., Constantin, D., and Fournier, J.-B. (2018). Membrane-Mediated Interactions. Berlin: Springer International Publishing, 311–350. doi:10.1007/978-3-030-00630-3_13

CrossRef Full Text | Google Scholar

Bohinc, K., Kralj-Iglič, V., and May, S. (2003). Interaction Between Two Cylindrical Inclusions in a Symmetric Lipid Bilayer. J. Chem. Phys. 119, 7435–7444. doi:10.1063/1.1607305

CrossRef Full Text | Google Scholar

Bonazzi, F., and Weikl, T. R. (2019). Membrane Morphologies Induced by Arc-Shaped Scaffolds Are Determined by Arc Angle and Coverage. Biophysical J. 116, 1239–1247. doi:10.1016/j.bpj.2019.02.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Bories, F., Constantin, D., Galatola, P., and Fournier, J.-B. (2018). Coupling Between Inclusions and Membranes at the Nanoscale. Phys. Rev. Lett. 120. doi:10.1103/physrevlett.120.128104

PubMed Abstract | CrossRef Full Text | Google Scholar

Brakke, K. A. (1992). The Surface Evolver. Exp. Maths. 1, 141–165. doi:10.1080/10586458.1992.10504253

CrossRef Full Text | Google Scholar

Brannigan, G., and Brown, F. L. H. (2006). A Consistent Model for Thermal Fluctuations and Protein-Induced Deformations in Lipid Bilayers. Biophysical J. 90, 1501–1520. doi:10.1529/biophysj.105.075838

PubMed Abstract | CrossRef Full Text | Google Scholar

Brannigan, G., and Brown, F. L. H. (2007). Contributions of Gaussian Curvature and Nonconstant Lipid Volume to Protein Deformation of Lipid Bilayers. Biophysical J. 92, 864–876. doi:10.1529/biophysj.106.094953

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruinsma, R., and Pincus, P. (1996). Protein Aggregation in Membranes. Curr. Opin. Solid State. Mater. Sci. 1, 401–406. doi:10.1016/s1359-0286(96)80032-5

CrossRef Full Text | Google Scholar

Chou, T., Kim, K. S., and Oster, G. (2001). Statistical Thermodynamics of Membrane Bending-Mediated Protein-Protein Attractions. Biophysical J. 80, 1075–1087. doi:10.1016/s0006-3495(01)76086-9

CrossRef Full Text | Google Scholar

Cooke, I. R., and Deserno, M. (2005). Solvent-free Model for Self-Assembling Fluid Bilayer Membranes: Stabilization of the Fluid Phase Based on Broad Attractive Tail Potentials. J. Chem. Phys. 123, 224710. doi:10.1063/1.2135785

CrossRef Full Text | Google Scholar

Dan, N., Pincus, P., and Safran, S. A. (1993). Membrane-induced Interactions Between Inclusions. Langmuir 9, 2768–2771. doi:10.1021/la00035a005

CrossRef Full Text | Google Scholar

Daum, B., Auerswald, A., Gruber, T., Hause, G., Balbach, J., Kühlbrandt, W., et al. (2016). Supramolecular Organization of the Human N-Bar Domain in Shaping the Sarcolemma Membrane. J. Struct. Biol. 194, 375–382. doi:10.1016/j.jsb.2016.03.017

CrossRef Full Text | Google Scholar

de Meyer, F. J.-M., Venturoli, M., and Smit, B. (2008). Molecular Simulations of Lipid-Mediated Protein-Protein Interactions. Biophysical J. 95, 1851–1865. doi:10.1529/biophysj.107.124164

CrossRef Full Text | Google Scholar

Deserno, M. (2015). Fluid Lipid Membranes: From Differential Geometry to Curvature Stresses. Chem. Phys. Lipids 185, 11–45. doi:10.1016/j.chemphyslip.2014.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Dommersnes, P. G., and Fournier, J.-B. (1999b). Casimir and Mean-Field Interactions Between Membrane Inclusions Subject to External Torques. Europhys. Lett. 46, 256–261. doi:10.1209/epl/i1999-00253-5

CrossRef Full Text | Google Scholar

Dommersnes, P. G., and Fournier, J.-B. (1999a). N-body Study of Anisotropic Membrane Inclusions: Membrane Mediated Interactions and Ordered Aggregation. Eur. Phys. J. B 12, 9–12. doi:10.1007/s100510050968

CrossRef Full Text | Google Scholar

Dommersnes, P. G., and Fournier, J.-B. (2002). The Many-Body Problem for Anisotropic Membrane Inclusions and the Self-Assembly of "Saddle" Defects into an "Egg Carton". Biophysical J. 83, 2898–2905. doi:10.1016/s0006-3495(02)75299-5

CrossRef Full Text | Google Scholar

Dommersnes, P. G., Fournier, J. B., and Galatola, P. (1998). Long-range Elastic Forces Between Membrane Inclusions in Spherical Vesicles. Europhys. Lett. 42, 233–238. doi:10.1209/epl/i1998-00235-7

CrossRef Full Text | Google Scholar

Evans, A. R., Turner, M. S., and Sens, P. (2003). Interactions Between Proteins Bound to Biomembranes. Phys. Rev. E 67, 041907. doi:10.1103/physreve.67.041907

PubMed Abstract | CrossRef Full Text | Google Scholar

Fournier, J.-B. (1999). Microscopic Membrane Elasticity and Interactions Among Membrane Inclusions: Interplay between the Shape, Dilation, Tilt and Tilt-Difference Modes. Eur. Phys. J. B 11, 261–272. doi:10.1007/bf03219168

CrossRef Full Text | Google Scholar

Golestanian, R., Goulian, M., and Kardar, M. (1996). Fluctuation-induced Interactions Between Rods on Membranes and Interfaces. Europhys. Lett. 33, 241–246. doi:10.1209/epl/i1996-00327-4

CrossRef Full Text | Google Scholar

Goulian, M., Bruinsma, R., and Pincus, P. (1993). Long-range Forces in Heterogeneous Fluid Membranes. Europhys. Lett. 22, 145–150. doi:10.1209/0295-5075/22/2/012

CrossRef Full Text | Google Scholar

Haselwandter, C. A., and Phillips, R. (2013). Directional Interactions and Cooperativity Between Mechanosensitive Membrane Proteins. Europhys Lett. 101, 68002. doi:10.1209/0295-5075/101/68002

PubMed Abstract | CrossRef Full Text | Google Scholar

Haselwandter, C. A., and Wingreen, N. S. (2014). The Role of Membrane-Mediated Interactions in the Assembly and Architecture of Chemoreceptor Lattices. Plos Comput. Biol. 10, e1003932. doi:10.1371/journal.pcbi.1003932

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. für Naturforschung C 28, 693–703. doi:10.1515/znc-1973-11-1209

CrossRef Full Text | Google Scholar

Helfrich, W., and Weikl, T. R. (2001). Two Direct Methods to Calculate Fluctuation Forces Between Rigid Objects Embedded in Fluid Membranes. The Eur. Phys. J. E 5, 423–439. doi:10.1007/s101890170049

CrossRef Full Text | Google Scholar

Hu, J., Lipowsky, R., and Weikl, T. R. (2013). Binding Constants of Membrane-Anchored Receptors and Ligands Depend Strongly on the Nanoscale Roughness of Membranes. Proc. Natl. Acad. Sci. 110, 15283–15288. doi:10.1073/pnas.1305766110

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J., Weikl, T., and Lipowsky, R. (2011). Vesicles with Multiple Membrane Domains. Soft Matter 7, 6092–6102. doi:10.1039/c0sm01500h

CrossRef Full Text | Google Scholar

Hu, J., Xu, G.-K., Lipowsky, R., and Weikl, T. R. (2015). Binding Kinetics of Membrane-Anchored Receptors and Ligands: Molecular Dynamics Simulations and Theory. J. Chem. Phys. 143, 243137. doi:10.1063/1.4936135

CrossRef Full Text | Google Scholar

Huang, H. W. (1986). Deformation Free Energy of Bilayer Membrane and its Effect on Gramicidin Channel Lifetime. Biophysical J. 50, 1061–1070. doi:10.1016/s0006-3495(86)83550-0

CrossRef Full Text | Google Scholar

Idema, T., and Kraft, D. J. (2019). Interactions Between Model Inclusions on Closed Lipid Bilayer Membranes. Curr. Opin. Colloid Interf. Sci. 40, 58–69. doi:10.1016/j.cocis.2019.01.006

CrossRef Full Text | Google Scholar

Kahraman, O., Koch, P. D., Klug, W. S., and Haselwandter, C. A. (2016a). Architecture and Function of Mechanosensitive Membrane Protein Lattices. Sci. Rep. 6, 19214. doi:10.1038/srep19214

PubMed Abstract | CrossRef Full Text | Google Scholar

Kahraman, O., Koch, P. D., Klug, W. S., and Haselwandter, C. A. (2016b). Bilayer-thickness-mediated Interactions Between Integral Membrane Proteins. Phys. Rev. E 93, 042410. doi:10.1103/physreve.93.042410

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaksonen, M., and Roux, A. (2018). Mechanisms of Clathrin-Mediated Endocytosis. Nat. Rev. Mol. Cel Biol 19, 313–326. doi:10.1038/nrm.2017.132

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, K. S., Neu, J., and Oster, G. (1998). Curvature-mediated Interactions Between Membrane Proteins. Biophysical J. 75, 2274–2291. doi:10.1016/s0006-3495(98)77672-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, T., Lee, K. I., Morris, P., Pastor, R. W., Andersen, O. S., and Im, W. (2012). Influence of Hydrophobic Mismatch on Structures and Dynamics of Gramicidin a and Lipid Bilayers. Biophysical J. 102, 1551–1560. doi:10.1016/j.bpj.2012.03.014

CrossRef Full Text | Google Scholar

Klingelhoefer, J. W., Carpenter, T., and Sansom, M. S. P. (2009). Peptide Nanopores and Lipid Bilayers: Interactions by Coarse-Grained Molecular-Dynamics Simulations. Biophysical J. 96, 3519–3528. doi:10.1016/j.bpj.2009.01.046

CrossRef Full Text | Google Scholar

Krobath, H., Różycki, B., Lipowsky, R., and Weikl, T. R. (2009). Binding Cooperativity of Membrane Adhesion Receptors. Soft Matter 5, 3354–3361. doi:10.1039/b902036e

CrossRef Full Text | Google Scholar

Kroll, D. M., and Gompper, G. (1992). The Conformation of Fluid Membranes: Monte Carlo Simulations. Science 255, 968–971. doi:10.1126/science.1546294

PubMed Abstract | CrossRef Full Text | Google Scholar

Lagüe, P., Zuckermann, M. J., and Roux, B. (2001). Lipid-mediated Interactions Between Intrinsic Membrane Proteins: Dependence on Protein Size and Lipid Composition. Biophysical J. 81, 276–284. doi:10.1016/s0006-3495(01)75698-6

CrossRef Full Text | Google Scholar

Lin, H.-K., Zandi, R., Mohideen, U., and Pryadko, L. P. (2011). Fluctuation-induced Forces Between Inclusions in a Fluid Membrane Under Tension. Phys. Rev. Lett. 107, 228104. doi:10.1103/physrevlett.107.228104

PubMed Abstract | CrossRef Full Text | Google Scholar

Marčelja, S. (1976). Lipid-mediated Protein Interaction in Membranes. Biochim. Biophys. Acta 455, 1–7. doi:10.1016/0005-2736(76)90149-8

PubMed Abstract | CrossRef Full Text | Google Scholar

May, S., and Ben-Shaul, A. (2000). A Molecular Model for Lipid-Mediated Interaction Between Proteins in Membranes. Phys. Chem. Chem. Phys. 2, 4494–4502. doi:10.1039/b003570j

CrossRef Full Text | Google Scholar

Mkrtchyan, S., Ing, C., and Chen, J. Z. (2010). Adhesion of Cylindrical Colloids to the Surface of a Membrane. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 81, 011904. doi:10.1103/PhysRevE.81.011904

PubMed Abstract | CrossRef Full Text | Google Scholar

Mondal, S., Khelashvili, G., Shan, J., Andersen, O. S., and Weinstein, H. (2011). Quantitative Modeling of Membrane Deformations by Multihelical Membrane Proteins: Application to G-Protein Coupled Receptors. Biophysical J. 101, 2092–2101. doi:10.1016/j.bpj.2011.09.037

CrossRef Full Text | Google Scholar

Müller, M. M., Deserno, M., and Guven, J. (2007). Balancing Torques in Membrane-Mediated Interactions: Exact Results and Numerical Illustrations. Phys. Rev. E 76, 011921. doi:10.1103/physreve.76.011921

CrossRef Full Text | Google Scholar

Müller, M. M., Deserno, M., and Guven, J. (2005). Interface-mediated Interactions Between Particles: A Geometrical Approach. Phys. Rev. E 72, 061407. doi:10.1103/PhysRevE.72.061407

CrossRef Full Text | Google Scholar

Nielsen, C., and Andersen, O. S. (2000). Inclusion-induced Bilayer Deformations: Effects of Monolayer Equilibrium Curvature. Biophysical J. 79, 2583–2604. doi:10.1016/s0006-3495(00)76498-8

CrossRef Full Text | Google Scholar

Nielsen, C., Goulian, M., and Andersen, O. S. (1998). Energetics of Inclusion-Induced Bilayer Deformations. Biophysical J. 74, 1966–1983. doi:10.1016/s0006-3495(98)77904-4

CrossRef Full Text | Google Scholar

Noguchi, H., and Fournier, J.-B. (2017). Membrane Structure Formation Induced by Two Types of Banana-Shaped Proteins. Soft Matter 13, 4099–4111. doi:10.1039/c7sm00305f

PubMed Abstract | CrossRef Full Text | Google Scholar

Noguchi, H. (2016). Membrane Tubule Formation by Banana-Shaped Proteins with or without Transient Network Structure. Sci. Rep. 6, 20935. doi:10.1038/srep20935

PubMed Abstract | CrossRef Full Text | Google Scholar

Olinger, A. D., Spangler, E. J., Kumar, P. B. S., and Laradji, M. (2016). Membrane-mediated Aggregation of Anisotropically Curved Nanoparticles. Faraday Discuss. 186, 265–275. doi:10.1039/c5fd00144g

PubMed Abstract | CrossRef Full Text | Google Scholar

Owicki, J. C., and McConnell, H. M. (1979). Theory of Protein-Lipid and Protein-Protein Interactions in Bilayer Membranes. Proc. Natl. Acad. Sci. 76, 4750–4754. doi:10.1073/pnas.76.10.4750

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J.-M., and Lubensky, T. C. (1996). Interactions Between Membrane Inclusions on Fluctuating Membranes. J. Phys. France 6, 1217–1235. doi:10.1051/jp1:1996125

CrossRef Full Text | Google Scholar

Pezeshkian, W., Gao, H., Arumugam, S., Becken, U., Bassereau, P., Florent, J.-C., et al. (2016). Mechanism of Shiga Toxin Clustering on Membranes. ACS Nano 11, 314–324. doi:10.1021/acsnano.6b05706

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramaswamy, S., Toner, J., and Prost, J. (2000). Nonequilibrium Fluctuations, Traveling Waves, and Instabilities in Active Membranes. Phys. Rev. Lett. 84, 3494–3497. doi:10.1103/physrevlett.84.3494

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynwar, B. J., and Deserno, M. (2011). Membrane-mediated Interactions Between Circular Particles in the Strongly Curved Regime. Soft Matter 7, 8567. doi:10.1039/c1sm05358b

CrossRef Full Text | Google Scholar

Reynwar, B. J., Illya, G., Harmandaris, V. A., Müller, M. M., Kremer, K., and Deserno, M. (2007). Aggregation and Vesiculation of Membrane Proteins by Curvature-Mediated Interactions. Nature 447, 461–464. doi:10.1038/nature05840

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadeghi, M., and Noé, F. (2021). Quantitative Analysis of Membrane-Mediated Interactions and Aggregation of Flexible Peripheral Proteins Orchestrating Large-Scale Membrane Remodeling. bioRxiv 2021, 1–15.

Google Scholar

Šarić, A., and Cacciuto, A. (2012b). Mechanism of Membrane Tube Formation Induced by Adhesive Nanocomponents. Phys. Rev. Lett. 109, 188101. doi:10.1103/PhysRevLett.109.188101

PubMed Abstract | CrossRef Full Text | Google Scholar

Šarić, A., and Cacciuto, A. (2012a). Fluid Membranes Can Drive Linear Aggregation of Adsorbed Spherical Nanoparticles. Phys. Rev. Lett. 108, 118101.

Google Scholar

Schmidt, U., Guigas, G., and Weiss, M. (2008). Cluster Formation of Transmembrane Proteins Due to Hydrophobic Mismatching. Phys. Rev. Lett. 101, 128104. doi:10.1103/physrevlett.101.128104

PubMed Abstract | CrossRef Full Text | Google Scholar

Schröder, H. (1977). Aggregation of Proteins in Membranes. An Example of Fluctuation‐induced Interactions in Liquid Crystals. J. Chem. Phys. 67, 1617–1619. doi:10.1063/1.434993

CrossRef Full Text | Google Scholar

Schweitzer, Y., and Kozlov, M. M. (2015). Membrane-mediated Interaction Between Strongly Anisotropic Protein Scaffolds. Plos Comput. Biol. 11, e1004054. doi:10.1371/journal.pcbi.1004054

PubMed Abstract | CrossRef Full Text | Google Scholar

Shiba, H., and Noguchi, H. (2011). Estimation of the Bending Rigidity and Spontaneous Curvature of Fluid Membranes in Simulations. Phys. Rev. E 84, 031926. doi:10.1103/physreve.84.031926

PubMed Abstract | CrossRef Full Text | Google Scholar

Simson, R., Wallraff, E., Faix, J., Niewöhner, J., Gerisch, G., and Sackmann, E. (1998). Membrane Bending Modulus and Adhesion Energy of Wild-type and Mutant Cells of dictyostelium Lacking Talin or Cortexillins. Biophysical J. 74, 514–522. doi:10.1016/s0006-3495(98)77808-7

CrossRef Full Text | Google Scholar

Simunovic, M., Evergren, E., Golushko, I., Prévost, C., Renard, H.-F., Johannes, L., et al. (2016). How Curvature-Generating Proteins Build Scaffolds on Membrane Nanotubes. Proc. Natl. Acad. Sci. USA 113, 11226–11231. doi:10.1073/pnas.1606943113

PubMed Abstract | CrossRef Full Text | Google Scholar

Simunovic, M., Srivastava, A., and Voth, G. A. (2013). Linear Aggregation of Proteins on the Membrane as a Prelude to Membrane Remodeling. Proc. Natl. Acad. Sci. 110, 20396–20401. doi:10.1073/pnas.1309819110

PubMed Abstract | CrossRef Full Text | Google Scholar

Sintes, T., and Baumgärtner, A. (1997). Protein Attraction in Membranes Induced by Lipid Fluctuations. Biophysical J. 73, 2251–2259. doi:10.1016/s0006-3495(97)78257-2

CrossRef Full Text | Google Scholar

Spangler, E. J., Kumar, P. B. S., and Laradji, M. (2018). Stability of Membrane-Induced Self-Assemblies of Spherical Nanoparticles. Soft Matter 14, 5019–5030. doi:10.1039/c8sm00537k

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinkühler, J., Różycki, B., Alvey, C., Lipowsky, R., Weikl, T. R., Dimova, R., et al. (2018). Membrane Fluctuations and Acidosis Regulate Cooperative Binding of "marker of Self" CD47 with Macrophage Checkpoint Receptor SIRPα. J. Cel Sci. 132, jcs216770. doi:10.1242/jcs.216770

CrossRef Full Text | Google Scholar

Sunil Kumar, P. B., Gompper, G., and Lipowsky, R. (2001). Budding Dynamics of Multicomponent Membranes. Phys. Rev. Lett. 86, 3911–3914. doi:10.1103/physrevlett.86.3911

PubMed Abstract | CrossRef Full Text | Google Scholar

Ursell, T., Huang, K. C., Peterson, E., and Phillips, R. (2007). Cooperative Gating and Spatial Organization of Membrane Proteins Through Elastic Interactions. Plos Comput. Biol. 3, e81. doi:10.1371/journal.pcbi.0030081

PubMed Abstract | CrossRef Full Text | Google Scholar

Vahid, A., and Idema, T. (2016). Pointlike Inclusion Interactions in Tubular Membranes. Phys. Rev. Lett. 117, 138102. doi:10.1103/physrevlett.117.138102

PubMed Abstract | CrossRef Full Text | Google Scholar

Vahid, A., Šarić, A., and Idema, T. (2017). Curvature Variation Controls Particle Aggregation on Fluid Vesicles. Soft Matter 13, 4924–4930. doi:10.1039/c7sm00433h

PubMed Abstract | CrossRef Full Text | Google Scholar

Venturoli, M., Smit, B., and Sperotto, M. M. (2005). Simulation Studies of Protein-Induced Bilayer Deformations, and Lipid-Induced Protein Tilting, on a Mesoscopic Model for Lipid Bilayers with Embedded Proteins. Biophysical J. 88, 1778–1798. doi:10.1529/biophysj.104.050849

CrossRef Full Text | Google Scholar

Weikl, T. R. (2001). Fluctuation-induced Aggregation of Rigid Membrane Inclusions. Europhys. Lett. 54, 547–553. doi:10.1209/epl/i2001-00281-7

CrossRef Full Text | Google Scholar

Weikl, T. R. (2003). Indirect Interactions of Membrane-Adsorbed Cylinders. Eur. Phys. J. E 12, 265–273. doi:10.1140/epje/i2003-10058-x

CrossRef Full Text | Google Scholar

Weikl, T. R., Kozlov, M. M., and Helfrich, W. (1998). Interaction of Conical Membrane Inclusions: Effect of Lateral Tension. Phys. Rev. E 57, 6988–6995. doi:10.1103/physreve.57.6988

CrossRef Full Text | Google Scholar

Weikl, T. R. (2018). Membrane-mediated Cooperativity of Proteins. Annu. Rev. Phys. Chem. 69, 521–539. doi:10.1146/annurev-physchem-052516-050637

PubMed Abstract | CrossRef Full Text | Google Scholar

Weitz, S., and Destainville, N. (2013). Attractive Asymmetric Inclusions in Elastic Membranes Under Tension: Cluster Phases and Membrane Invaginations. Soft Matter 9, 7804. doi:10.1039/c3sm50954k

CrossRef Full Text | Google Scholar

West, B., Brown, F. L. H., and Schmid, F. (2009). Membrane-protein Interactions in a Generic Coarse-Grained Model for Lipid Bilayers. Biophysical J. 96, 101–115. doi:10.1529/biophysj.108.138677

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, K., Zhao, J., Yang, D., Cheng, Q., Wang, J., and Ji, H. (2017). Cooperative Wrapping of Nanoparticles of Various Sizes and Shapes by Lipid Membranes. Soft Matter 13, 4644–4652. doi:10.1039/c7sm00345e

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, G.-K., Hu, J., Lipowsky, R., and Weikl, T. R. (2015). Binding Constants of Membrane-Anchored Receptors and Ligands: A General Theory Corroborated by Monte Carlo Simulations. J. Chem. Phys. 143, 243136. doi:10.1063/1.4936134

CrossRef Full Text | Google Scholar

Yolcu, C., and Deserno, M. (2012). Membrane-mediated Interactions Between Rigid Inclusions: An Effective Field Theory. Phys. Rev. E 86, 031906. doi:10.1103/physreve.86.031906

PubMed Abstract | CrossRef Full Text | Google Scholar

Yolcu, C., Rothstein, I. Z., and Deserno, M. (2011). Effective Field Theory Approach to Casimir Interactions on Soft Matter Surfaces. Europhys Lett. 96, 20003. doi:10.1209/0295-5075/96/20003

CrossRef Full Text | Google Scholar

Yuan, H., Huang, C., Li, J., Lykotrafitis, G., and Zhang, S. (2010). One-particle-thick, Solvent-free, Coarse-Grained Model for Biological and Biomimetic Fluid Membranes. Phys. Rev. E 82, 011905. doi:10.1103/physreve.82.011905

PubMed Abstract | CrossRef Full Text | Google Scholar