- 1Department of Biology and Biochemistry, University of Bath, Bath, United Kingdom
- 2Biometrology, Chemical and Biological Sciences Department, National Physical Laboratory, London, United Kingdom
- 3UCB, Slough, United Kingdom
- 4School of Biochemistry, University of Bristol, Bristol, United Kingdom
- 5School of Science, Faculty of Science and Engineering, University of Waikato, Hamilton, New Zealand
- 6BLOC Laboratories Limited, Bath, United Kingdom
It is now over 30 years since Demchenko and Ladokhin first posited the potential of the tryptophan red edge excitation shift (REES) effect to capture information on protein molecular dynamics. While there have been many key efforts in the intervening years, a biophysical thermodynamic model to quantify the relationship between the REES effect and protein flexibility has been lacking. Without such a model the full potential of the REES effect cannot be realized. Here, we present a thermodynamic model of the tryptophan REES effect that captures information on protein conformational flexibility, even with proteins containing multiple tryptophan residues. Our study incorporates exemplars at every scale, from tryptophan in solution, single tryptophan peptides, to multitryptophan proteins, with examples including a structurally disordered peptide, de novo designed enzyme, human regulatory protein, therapeutic monoclonal antibodies in active commercial development, and a mesophilic and hyperthermophilic enzyme. Combined, our model and data suggest a route forward for the experimental measurement of the protein REES effect and point to the potential for integrating biomolecular simulation with experimental data to yield novel insights.
Introduction
Tracking protein conformational change and, even more subtly, changes in the equilibrium of available conformational states is central to molecular biosciences. Protein stability is intimately linked with the distribution of conformational states (Karshikoff et al., 2015) and, as a good generalization, increased stability tracks with a decrease in the distribution of conformational states (increasing rigidity, decreasing conformational entropy). (Vihinen, 1987). While engineering protein stability has advanced enormously, the tools to sensitively and quantitatively track these changes are lacking. There are a broad range of potential analytical tools, but only a few that can be applied routinely to the vast majority of proteins without unreasonable requirements regarding solvent, protein concentrations, and thermal stability, or without the requirement of surface attachment or labeling. (Magliery et al., 2011). Moreover, the vast majority of protein conformational changes are subtle, described as “breathing” motions, where most structural orders (primary to quaternary) of the protein are not altered, but it is the equilibrium of conformational states (protein flexibility) that changes (Kossiakoff, 1986).
The red edge excitation shift (REES) phenomenon is a sensitive reporter of a fluorophore’s environment, and the mechanism is shown in Figure 1A. (Azumi and Itoh, 1973; Itoh and Azumi, 1975; Azumi et al., 1976; Demchenko, 2002). Briefly, the REES effect is sensitive to shifts in the distribution of environments a fluorophore can sample. As this distribution of environments gets smaller, the REES effect becomes “smaller” (we discuss this in depth below) and vice versa. In proteins, such shifts in the distribution of states are how we conceptualize protein motions. Potentially then, the REES effect could be a powerful tool, both to study protein flexibility/motion but also (as above) stability.
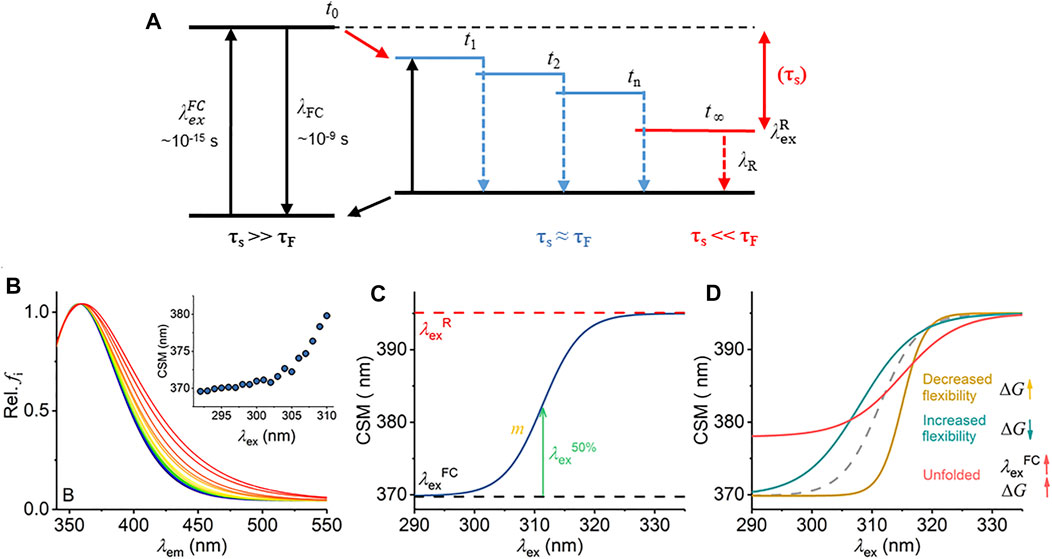
FIGURE 1. Mechanism of the REES effect, predicted experimental observables, and graphical description of Eq. (7). (A) Jablonski diagram illustrating the REES effect. (B) Example model Trp REES data showing the normalized emission spectrum with increasing excitation wavelength and inset as the change in CSM versus excitation wavelength. (C) Graphical depiction of Eq. (7). (D) Predicted spectral changes resulting from variations in Eq. (7) from shifts in protein flexibility and conformational state (folding).
Radiative fluorescence takes place after light absorption alongside non-radiative processes, which include vibrational relaxation and solvent relaxation (dipolar re-organization). Vibrational relaxation is typically fast (∼10−12 s) relative to the lifetime of fluorescence emission (τF ∼ 10−10–10−9 s) and so causes a complete relaxation of the system to its lowest energy level prior to emission. This gives rise to the familiar red shift of fluorescence emission compared to absorption (Stokes shift). The Lippert–Mataga equation [Eq. (1)] illustrates that the greater the polarity of solvent, the larger the anticipated Stokes shift (Mataga et al., 1956; Lippert Von, 1957).
where the Stokes shift (difference between wavenumber of absorption and emission),
Equation (1) assumes that the solvent relaxation is complete prior to emission. However, solvent relaxation is not necessarily always fast relative to fluorescence emission and under a range of solvent or environmental conditions can approach τF [∼10−10 –10−9 s]. The longer solvent relaxation lifetime (τS) can therefore affect the level from which emission occurs and so the emission wavelength, in which case it also contributes to the Stokes shift (Azumi and Itoh, 1973; Itoh and Azumi, 1975; Azumi et al., 1976; Demchenko, 2002). Specifically, one expects that an ensemble of energetic substates is formed related to the distribution of solvent relaxation lifetimes, i.e., the available distribution of solvent–fluorophore interaction energies. The additive contribution of these states to the steady-state emission spectrum gives rise to broad-band emission, which is observed as inhomogeneous broadening of the spectra. This broadening is then dependent on the excitation energy used, since as one decreases the excitation energy, there is an increasing photoselection of states (Figure 1A). Experimentally, one then observes a red shift in the emission spectra with respect to increasing excitation wavelength, i.e., decreasing excitation energy (Figure 1B). The inhomogeneous broadening will be dependent on a range of physical conditions that affect τS, including temperature, viscosity, and solvent dipole moment (and therefore the solvent dielectric constant) (Azumi and Itoh, 1973; Itoh and Azumi, 1975; Azumi et al., 1976; Demchenko, 2002).
The sensitivity of the REES effect to changes in the equilibrium of solvent–fluorophore interaction energies suggests potential for using the approach to track changes in protein conformational state using the intrinsic fluorescence of the aromatic amino acids (Demchenko, 2002; Chattopadhyay and Haldar, 2014). Indeed, tryptophan (Trp) has been shown to give a large REES effect in numerous proteins, and we point to excellent reviews that illustrate key examples (Demchenko and Ladokhin, 1988; Raghuraman et al., 2005; Chattopadhyay and Haldar, 2014; Brahama and Raghuraman, 2021). Demchenko and Ladokhin (1988) suggest that the selection between 1La and 1Lb electronic excited states of Trp acts to increase the magnitude of the red edge excitation shift. Trp has the advantage that its emission can be separated from tyrosine (Tyr) and phenylalanine (Phe) by excitation at wavelengths >∼292 nm (Adman and Jensen, 1981). Trp REES is therefore a potentially excellent probe of protein conformational change, intrinsic disorder, and possibly even of changes in the equilibrium of conformational states.
We have previously applied and validated an empirical model for describing protein REES data as a function of the equilibrium of conformational states, which we call QUBES (quantitative understanding of biomolecular edge shift) (Catici et al., 2016; Jones et al., 2017; Knight et al., 2020). Herein, we refer to changes in the equilibrium of conformational states as changes in flexibility, with a more flexible protein having a broader equilibrium of conformational states. We track the changes in inhomogeneous broadening as the change in the center of spectral mass (CSM; Eq. (2)) of steady-state emission spectra (example shown in Figure 1B).
where fi is fluorescence intensity, and
where
While Eq. (3) performs well at tracking shifts in protein rigidity/flexibility (also for multi-Trp containing proteins) (Catici et al., 2016; Jones et al., 2017; Knight et al., 2020; Hindson et al., 2021), it does not relate to a specific thermodynamic parameter and neglects the fact that protein Trp emission will have a finite maximum observable spectral red shift at
Herein, we describe a thermodynamic model for interpreting protein REES data, which builds on our early work. Using a range of model systems from Trp/solvent studies, single Trp-containing proteins and multi-Trp proteins, we find that the new model accurately tracks with independent metrics of changes in the equilibrium of protein conformational states and more gross metrics of protein folding. Moreover, our model points to the need for new experimental approaches to monitor the protein REES effect.
Results and Discussion
As described by Demchenko and Ladokhin (1988), we posit a two-state model and assume
where ∆G is the difference in free energy between the [FC] (Frank–Condon) and [R] (relaxed) states, noting that the RT term is gas constant temperature. We then assume that ∆G will change linearly with excitation wavelength:
with a gradient, m. Thus, we anticipate a two-state transition between FC and R states due to photoselection by excitation wavelength with baselines
Equations (6) and (7) establish three key parameters,
The combination of
ΔG arises from Eq. (4), calculated from the extracted
Inspection of Figure 1A yields two ready predictions for the information content of the parameters in Eq. (7), and we show how these are predicted to affect the resulting experimental data in Figure 1D:
i) A decrease in the gap between
ii) In a more rigid molecule, we expect to observe fewer intermediate states. Fewer energetically discrete solvent–fluorophore environments would reflect a larger energy gap between adjacent states (t1, t2, etc., Figure 1A). A smaller distribution of solvent–solute interaction energies would manifest as reduced inhomogeneous broadening of the emission spectra (Figure 1C). Experimentally, one then expects a steeper transition between
Changes in both
We acknowledge that it is not possible to experimentally reach saturation of the Trp REES effect
Tryptophan in Solution
Given that Eq. (7) is a new thermodynamic model for the REES effect, we first explore the sensitivity of the Trp REES effect to variation in the physical properties of the solvent. Solvent studies have been used to probe the sensitivity of the REES effect using viscous matrices such as ethylene glycol and glycerol and temperature variation, by monitoring Trp or indole emission. (Azumi et al., 1976; Demchenko and Ladokhin, 1988). One expects the REES effect to be sensitive to changes in the dielectric constant and viscosity of the solvent and the temperature owing to the effect on the lifetime of solvent relaxation as described above. We are not aware of a method to independently vary dielectric constant, viscosity, and temperature, so we have employed a matrix effect experiment, where we monitor the Trp REES effect as a function of methanol (MeOH) concentration (0%–70% v/v with buffered Tris–HCl, pH 8.0 as in Figure 2) and temperature (20°–50°C). Supplementary Figure S1 shows the variation in viscosity and dielectric constant for the conditions we used. Using this approach, we are able to explore the REES effect, which is quantified using Eq. (6) across a range of conditions. Figures 2A–D show the REES data as a function of the variation in MeOH concentration at each temperature studied. These data are then fit to Eq. (7), and the resulting parameters are shown in Figures 2E–G.
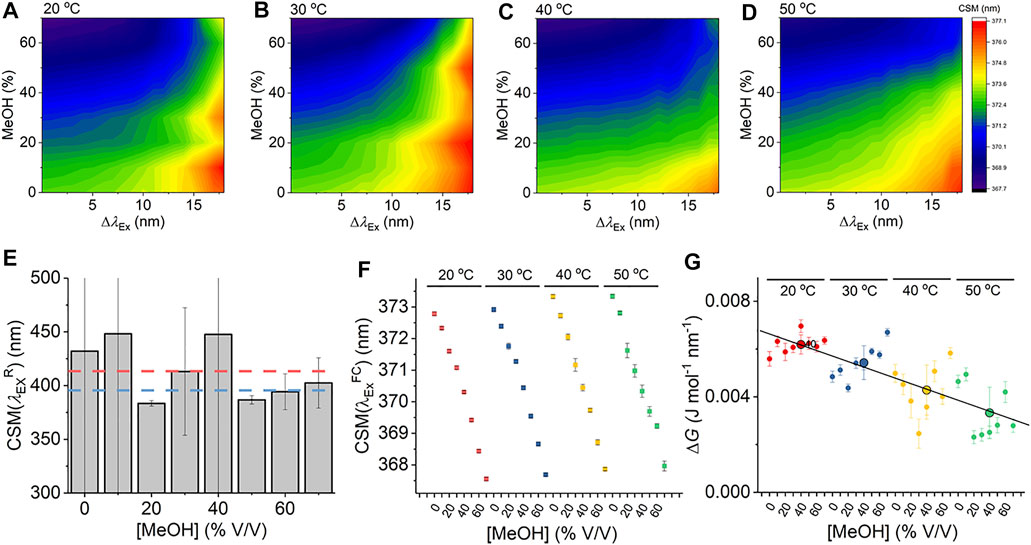
FIGURE 2. Solvent and temperature studies of the Trp REES effect. (A–D) Variation in CSM for L-Trp with varying percentages of MeOH and versus temperature. (E) Variation in the
As we describe above, accessing the limiting value of
Figure 2F shows the variation in
From Figure 2G, we do not observe a consistent trend in the magnitude of ΔG with respect to [MeOH]. It is not possible to independently vary viscosity, dielectric constant, and temperature, with viscosity having a strong dependence on both temperature and [MeOH]. In contrast to
Our data using free Trp in solution provides a detailed baseline for the sensitivity of Eq. (7) to track the protein Trp REES effect, most notably establishing realistic ranges for the magnitude of
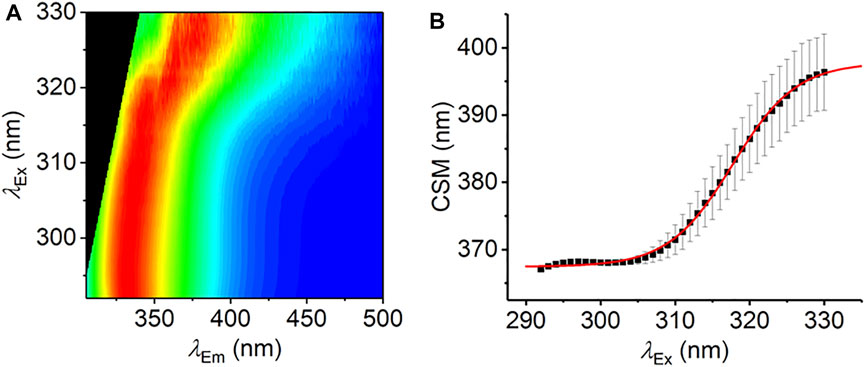
FIGURE 3. The REES effect monitored over extended λEx range. (A) Averaged, normalized raw emission spectra. (B) CSM data extracted from λEm = 340–500 nm. The solid red line is the fit to Eq. (7). Data collected in triplicate; error bars are the standard deviation. Conditions: 1.25 mM L-Trp, MeOH, 25°C.
Single Trp Proteins
With the characterization of the REES effect for free Trp in solution in hand, we now turn to single Trp-containing proteins to establish how the REES effect (quantified with Eq. (7)) changes when the Trp is part of a complex polymer (protein). We have selected a large, monomeric (48 kDa; 419 aa) human regulatory protein, which natively has a single Trp [NF-κB essential modulator (NEMO)] (Barczewski et al., 2019), and a natively unstructured protein (α-synuclein, 140 aa) (Meade et al., 2019) that lacks native Trp residues but where we have engineered them into specific sites. These model systems allow us to explore a broad range of conditions and physical environments for single Trp proteins. It also enables us both to explore the sensitivity of ΔG and, similar to our Trp in solution studies, define the range of
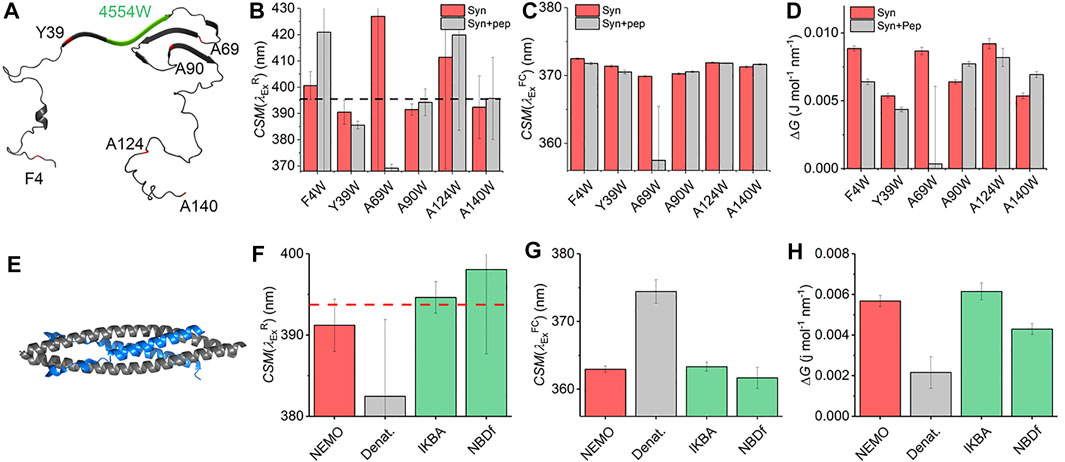
FIGURE 4. Single Trp protein REES. (A) Structural model of α-synuclein (PDB 2n0A24). (B–D) Variation in
Figure 4C shows the extracted
The finding of a decrease in both ΔG and
NF-κB essential modulator (NEMO) is a 48 kDa human regulatory protein involved in the mediation of the NF-κB signaling pathway. A range of studies suggest that NEMO is a flexible protein and can undergo ligand-specific conformational change (Catici et al., 2015; Catici et al., 2016). NEMO has a single native Trp residue (W6), which is conveniently located close to the residues that bind to the kinase regulated by NEMO (Figure 4E), IκB kinase-β (IKK-β) (Barczewski et al., 2019). Moreover, there is evidence that the IKK-β substrate, IκBα, is also able to interact with NEMO (Vieille and Zeikus, 2001). We have previously reported the binding of peptide mimics of these proteins to NEMO. We note that the peptides lack Trp residues either natively (IKBα) or by design [NBD-Phe, where the native Trp of the NEMO biding domain (NBD) of IKK-β is replaced by Phe] (Catici et al., 2016). Figures 4F–H show the results of fitting Eq. (7) to NEMO REES data in native and denatured forms and in the presence of these two ligands.
From Figure 4F we find that the extracted magnitude of
From Figure 4G, we find that the magnitude of
Combined, our data provide a means to interpret the physical meaning of the magnitude of ΔG. In the case of the denatured NEMO, the increase in
NEMO and α-synuclein give similar
These data therefore provide a “baseline” range for
Multi-Trp Protein
Having established a limiting value of
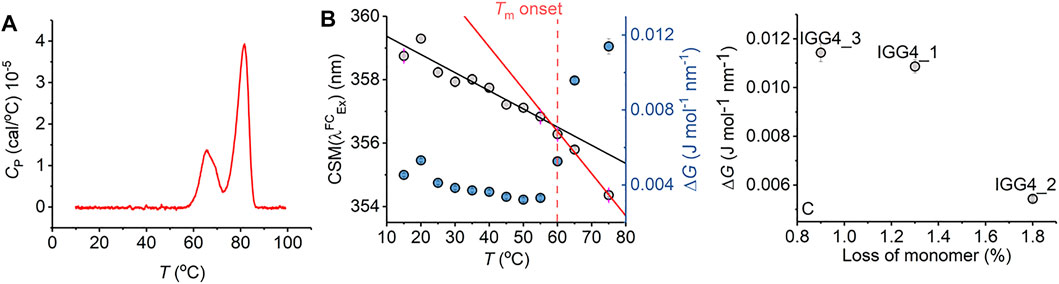
FIGURE 5. Antibody stability prediction and the effect of temperature. (A) Differential scanning calorimetry data for mAb1. (B) Temperature dependence of parameters extracted from fitting the IgG1 REES data to Eq. (7). (C) Percentage loss of monomer for mAb1-3 after 6 months incubation at room temperature versus ΔG extracted from fitting REEs data to Eq. (7) at t = 0. Raw REES data from panel (C) as reported previously in Ref. 14.
Notionally, changes in the equilibrium of conformational states should track with protein stability. That is, as the free energy landscape flattens, more discrete conformational states become accessible (i.e., a broader equilibrium of conformational states), including those corresponding to non-native conformations. For highly structurally similar proteins, we therefore anticipate that a decrease in the magnitude of ΔG will correlate with a less thermodynamically stable protein. Figure 5C shows the magnitude of ΔG for three monoclonal antibodies, in active development and all based on a common scaffold (IgG4), in relation with the fractional loss of monomer over 6 months at room temperature (reported recently; Ref. 16). From Figure 5C, we find that a decrease in the magnitude of ΔG correlates with a decrease in protein stability (as predicted). These data, therefore, suggest that the magnitude of ΔG is sensitive not only to the very earliest stages of protein unfolding but also to differences in thermodynamic stability.
We have explored a similar temperature relationship with the hyperthermophilic, tetrameric, glucose dehydrogenase from Sulfolobus solfataricus (ssGDH). The natural operating temperature of the S. solfataricus is ∼77°C; ssGDH is extremely thermally stable even at elevated temperatures and shows very high rigidity relative to a comparable mesophilic protein. (Vieille and Zeikus, 2001). Figure 6A shows the far-UV circular dichroism data for ssGDH at a range of different temperatures. From this figure, there is some change in helical content with respect to temperature, most noticeable from the spectra at >85°C. Figure 6B shows the change in ellipticity at 222 nm (Φ222nm) with respect to temperature. The solid red line in Figure 6B shows the fit to
where
where a and b are the slope and intercept of the folded (f) and unfolded (u) baseline, respectively. Tm is the melting temperature, and ΔH is the van’t Hoff enthalpy of unfolding at Tm. From Figure 6B, there is no evident complete unfolding transition, and so we have restrained the parameters in Eq. (8) to give a sense of where the unfolding transition would occur and an indicative Tm. That is, we fixed the ellipticity and gradient of the “unfolded” limb of the slope to zero, which is a reasonable approximation. Fitting the data using Eq. (8) gave Tm = 105.5 ± 5.5°C. That is, the data fits to an unfolding transition that is at an experimentally inaccessible temperature. We note the significant linear slope of the “folded” limb of Figure 6B. This linear phase of the thermal melt does not reflect unfolding, and there is no clear consistent interpretation of the magnitude of af; it is essentially always removed from analysis (Fenner et al., 2010) Potentially, it reflects changes in solvent dynamics with respect to temperature or more trivial effects. The transition from this linear phase to the apparent unfolding transition is at ∼ 80°C.
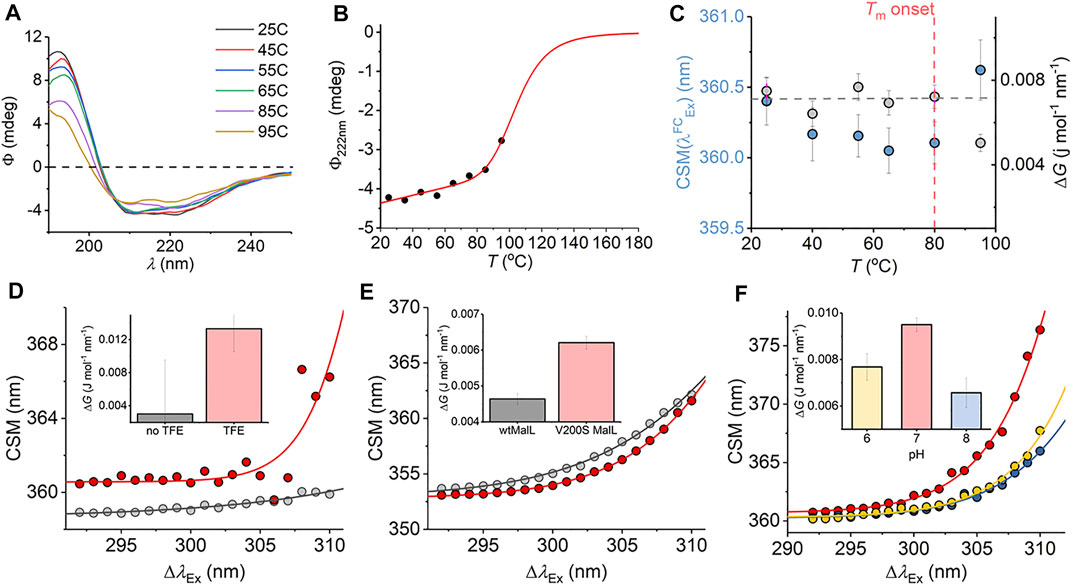
FIGURE 6. (A–C) Temperature dependence of the ssGDH REES effect and correlation with unfolding. (A) Temperature dependence of far-UV CD spectra. (B) Temperature dependence of Φ222nm. Solid line is the fit to Eq. (8) as described in the main text. (C) Temperature dependence of parameters extracted from fitting the ssGDH REES data to Eq. (7) (D–F) REES effect of C45 in the presence and absence of TFE, raw data as Ref. 17 (D); wtMalL and V200S MalL, raw data as Ref. 16 (E); and ssGDH at different pH values (F). The inset bar charts (D–F) show the magnitude of ΔG extract from fitting to Eq. (7).
From Figure 6C, we find that the magnitude of ΔG is essentially invariant with respect to temperature (within the error of the extracted value) up to 80°C. As with mAb1,
We were able to more directly explore the trend in ΔG on changes in molecular flexibility by correlating with evidence from NMR, simulation, and pH variation. We have recently demonstrated that a de novo heme peroxidase (C45; four α-helix bundle; 3 Trp residues) can be rigidified (and stabilized) in the presence of 2,2,2-trifluoroethanol (TFE) (Hindson et al., 2021). The NMR spectra (1H-15N TROSY-HSQC) show an increase in the number and sharpness of peaks in the presence of TFE, which is indicative of a more rigid protein (Hindson et al., 2021). This rigidification also tracks with an increase in thermal stability (Hindson et al., 2021). Fitting the REES data to Eq. (7) (shown in Figure 6D) gives a ΔG value that is measurably larger outside of error in the presence of TFE, ΔG = 0.003 ± 0.001 and 0.013 ± 0.004 J mol−1 nm−1 in the absence and presence of TFE, respectively.
For our multi-Trp examples above, we were not able to rule out conformational change convolved with changes in rigidity/flexibility. Maltose-inducible α-glucosidase (MalL) has become a paradigmatic enzyme for studying the temperature dependence of enzyme activity. (Hobbs et al., 2013). A single amino acid variant (V200S) is sufficient to increase the optimum temperature of reaction (Topt) from 58°C to 75°C, having an unfolding transition at a higher temperature (Hobbs et al., 2013). Molecular dynamics simulation show that V200S is globally more rigid than the wild-type (wt) enzyme, despite the X-ray crystal structures being essentially identical (Hobbs et al., 2013). Therefore, by using MalL we are able to explore the effect of changes in protein rigidity alone on the REES effect. Fitting the extracted REES data to Eq. (7) (shown in Figure 6E) gives a ΔG value that is measurably larger outside of error for V200S MalL, ΔG = 0.006 ± 0.0002, than for wtMalL, 0.004 ± 0.0002 J mol−1 nm−1.
Finally, we have explored pH variation with ssGDH. From our temperature studies (Figures 6A–C), we find that ssGDH is extremely structurally stable. In an effort to perturb the stability of ssGDH we have explored pH variation. Figure 6F shows the resulting REES data fit to Eq. (7) for ssGDH incubated at pH 6, 7, and 8. From Figure 6F inset, we find that the magnitude of ΔG is largest at pH 7, with a rather lower values at pH 6 and lowest at pH 8. From our data with the mAb1, C45, and MalL, we find that a larger magnitude of ΔG suggests a less flexible protein. Supplementary Figure S5 shows the pH dependence of the dynamic light scattering (DLS) profile. From these data, we cannot identify any oligomeric change associated with pH variation. However, the DLS profiles show some variation in width, which might suggest a shift in the distribution of conformational states. These data do not obviously correlate with our REES data (Figure 6F), but potentially highlight the sensitivity of the REES data to capture changes in the equilibrium of conformational states, which would not otherwise be obvious.
In summary, our combined data with multi-Trp proteins (mAb1, ssGDH, C45, and MalL) are consistent with the finding that a decrease in the magnitude of ΔG is associated with an increase in flexibility. Moreover, and as expected, reductions in molecular flexibility are correlated with increased stability. Finally, via the change in the
Conclusion
The REES effect is a drastically underutilized analytical tool, given its potential to sensitively track changes in protein microstates. Developing the theoretical models used to understand the effect has high potential to enable the REES effect to be used for unique applications in protein and biomolecular analysis. For example, Kabir et al. have recently posited a model for tracking the REES effect of a fluorescent ligand, potentially enabling the dissection of “hidden” ligand bound states of proteins (Kabir et al., 2021). Furthermore, we have demonstrated that quantifying the REES effect with Eq. (7) potentially allows for prediction of mAb stability, and this has potential for increasing the speed of drug development (Knight et al., 2020).
Our data suggests that the model presented here (Eq. (7)) represents a practically applicable, sensitive framework for quantifying the protein REES effect, based on fundamental thermodynamic theory. Specifically, we find that the magnitude of ΔG is sensitive to changes in molecular dynamics without structural change of the protein and specifically appears to be sensitive to changes in protein conformational sampling. Moreover, via the additional information provided by the
Our model defines a maximum red shift for a given system,
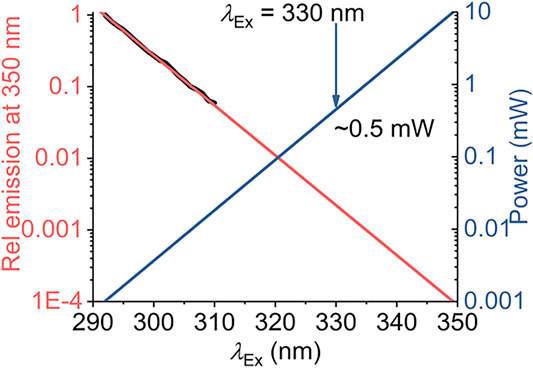
FIGURE 7. Calculated excitation power requirements to extend protein REES measurements to λEx > 310 nm. The black line is the experimentally extracted (natural logarithm) excitation spectrum of protein Trp (single Trp of NEMO as Ref. 15). The red line is the fit to a linear function. The blue line is the calculated power required to achieve an equivalent emission intensity at increasing values of λEx.
Methods
Red Edge Excitation Shift Data Collection
All fluorescence measurements were performed using a Perkin Elmer LS50B Luminescence Spectrometer (Perkin Elmer, Waltham, MA, United States), an Agilent Cary Eclipse fluorescence spectrometer (Agilent, Santa Clara, CA, United States), or an Edinburgh Instruments FS5 fluorescence spectrometer (data in Figure 3; Edinburgh Instrument, Livingstone, United Kingdom) connected to a circulating water bath for temperature regulation (1°C). Samples were thermally equilibrated by incubation for 5 min at the given conditions prior to recording measurements. Emission spectra were collected for increasing increments of excitation wavelength from 292 nm upwards with increments of 1 nm. The emission spectra were typically collected and analyzed across the range of 325–500 nm to prevent first- and second-order artifacts. Typical slit widths were 5 nm in each case (1.5 nm in the case of the data in Figure 3). For all samples, the corresponding buffer control was subtracted from the spectra for each experimental condition. REES data were collected as described previously (Knight et al., 2020). Data were processed as described in the text by first extracting the CSM values (Eq. (2)) and then fitting with Eq. (6). Data were composed of three to five replicates.
CD and Dynamic Light Scattering Data Collection
CD data were collected on an Applied Photophysics circular dichroism spectrometer. Corresponding buffer baselines were subtracted for each measurement. DLS data were collected on a Malvern Panalytical Zetasizer using a 50 μl quartz cuvette, thermostated to 25°C.
Protein Preparation
α-Synuclein, ssGDH, and mAb1 were expressed and purified as described previously in Refs. 28, 18, and 16, respectively.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
ARJ thanks the National Measurement System of the Department for Business, Energy and Industrial Strategy for funding. CRP acknowledges the Engineering and Physical Sciences Research Council (EPSRC) for funding (EP/V026917/1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2021.778244/full#supplementary-material
References
Adman, E. T., and Jensen, L. H. (1981). Structural Features of Azurin at 2.7 Å Resolution. Isr. J. Chem. 21, 8–12. doi:10.1002/ijch.198100003
Azumi, T., and Itoh, K-i. (1973). Shift of Emission Band upon Excitation at the Long Wavelength Absorption Edge. 1. A Preliminary Survey for Quinine and Related Compounds. Chem. Phys. Lett. 22, 395–399.
Azumi, T., Itoh, K. i., and Shiraishi, H. (1976). Shift of Emission Band upon the Excitation at the Long Wavelength Absorption Edge. III. Temperature Dependence of the Shift and Correlation with the Time Dependent Spectral Shift. J. Chem. Phys. 65, 2550–2555. doi:10.1063/1.433440
Barczewski, A. H., Ragusa, M. J., Mierke, D. F., and Pellegrini, M. (2019). The IKK-Binding Domain of NEMO Is an Irregular Coiled Coil with a Dynamic Binding Interface. Sci. Rep. 9, 2950. doi:10.1038/s41598-019-39588-2
Brahama, R., and Raghuraman, H. (2021). Novel Insights in Linking Solvent Relaxation Dynamics and Protein Conformations Utilizing Red Edge Excitation Shift Approach. Emerg. Top. Life Sci. 5, 89–101.
Catici, D. A. M., Amos, H. E., Yang, Y., van den Elsen, J. M. H., and Christopher, Roland Pudney (2016). The Red Edge Excitation Shift Phenomenon Can Be Used to Unmask Protein Structural Ensembles: Implications for NEMO-Ubiquitin Interactions. FEBS J. 283, 2272–2284. doi:10.1111/febs.13724
Catici, D. A. M., Horne, J. E., Cooper, G. E., and Pudney, C. R. (2015). Polyubiquitin Drives the Molecular Interactions of the NF-Κb Essential Modulator (NEMO) by Allosteric Regulation. J. Biol. Chem. 290, 14130–14139. doi:10.1074/jbc.m115.640417
Chattopadhyay, A., and Haldar, S. (2014). Dynamic Insight into Protein Structure Utilizing Red Edge Excitation Shift. Acc. Chem. Res. 47, 12–19. doi:10.1021/ar400006z
Demchenko, A. P., and Ladokhin, A. S. (1988). Red-edge-excitation Fluorescence Spectroscopy of Indole and Tryptophan. Eur. Biophys. J. 15, 369–379. doi:10.1007/BF00254724
Demchenko, A. P. (2002). The Red-Edge Effects: 30 Years of Exploration. Luminescence 17, 19–42. doi:10.1002/bio.671
Fenner, B. J., Scannell, M., and Prehn, J. H. M. (2010). Expanding the Substantial Interactome of NEMO Using Protein Microarrays. PLoS One 5, e8799. doi:10.1371/journal.pone.0008799
Greenfield, N. J. (2006). Using Circular Dichroism Collected as a Function of Temperature to Determine the Thermodynamics of Protein Unfolding and Binding Interactions. Nat. Protoc. 1, 2527–2535. doi:10.1038/nprot.2006.204
Gulácsy, C. E., Meade, R., Catici, D. A. M., Soeller, C., Pantos, G. D., Jones, D. D., et al. (2019). Excitation-Energy-Dependent Molecular Beacon Detects Early Stage Neurotoxic Aβ Aggregates in the Presence of Cortical Neurons. ACS Chem. Neurosci. 10, 1240–1250. doi:10.1021/acschemneuro.8b00322
Hammond, G. S. (1955). A Correlation of Reaction Rates. J. Am. Chem. Soc. 77, 334–338. doi:10.1021/ja01607a027
Hindson, S. A., Bunzel, H. A., Frank, B., Svistunenko, D. A., Williams, C., van der Kamp, M. W., et al. (2021). Rigidifying a De Novo Enzyme Increases Activity and Induces a Negative Activation Heat Capacity. ACS Catal. 11, 11532–11541. doi:10.1021/acscatal.1c01776
Hobbs, J. K., Jiao, W., Easter, A. D., Parker, E. J., Schipper, L. A., and Arcus, V. L. (2013). Change in Heat Capacity for Enzyme Catalysis Determines Temperature Dependence of Enzyme Catalyzed Rates. ACS Chem. Biol. 8, 2388–2393. doi:10.1021/cb4005029
Itoh, K.-i., and Azumi, T. (1975). Shift of the Emission Band upon Excitation at the Long Wavelength Absorption Edge. II. Importance of the Solute-Solvent Interaction and the Solvent Reorientation Relaxation Process. J. Chem. Phys. 62, 3431. doi:10.1063/1.430977
Jain, N., Bhasne, K., Hemaswasthi, M., and Mukhopadhyay, S. (2013). Structural and Dynamical Insights into the Membrane-Bound α-Synuclein. PLOS One 8, e83752. doi:10.1371/journal.pone.0083752
Jones, H. B. L., Wells, S. A., Prentice, E. J., Kwok, A., Liang, L. L., Arcus, V. L., et al. (2017). A Complete Thermodynamic Analysis of Enzyme Turnover Links the Free Energy Landscape to Enzyme Catalysis. FEBS J. 284, 2829–2842. doi:10.1111/febs.14152
Kabir, M. L., Wang, F., and Clayton, A. H. A. (2021). Red-Edge Excitation Shift Spectroscopy (REES): Application to Hidden Bound States of Ligands in Protein-Ligand Complexes. Ijms 22, 2582. doi:10.3390/ijms22052582
Karshikoff, A., Nilsson, L., and Ladenstein, R. (2015). Rigidity versus Flexibility: the Dilemma of Understanding Protein thermal Stability. FEBS. J. 282, 3899–3917. doi:10.1111/febs.13343
Knight, M. J., Woolley, R. E., Kwok, A., Parsons, S., Jones, H. B. L., Gulácsy, C. E., et al. (2020). Monoclonal Antibody Stability Can Be Usefully Monitored Using the Excitation-energy-dependent Fluorescence Edge-Shift. Biochem. J. 477, 3599–3612. doi:10.1042/bcj20200580
Kossiakoff, A. A. (1986). [20]Protein Dynamics Investigated by Neutron Diffraction. Methods Enzymol. 131, 433–447. doi:10.1016/0076-6879(86)31051-6
Lippert Von, E. (1957). Spektroskopische bistimmung des dipolmomentes aromatischer verbindungen im ersten angeregten singulettzustand. Z. Electrochem. 61, 962–975.
Magliery, T. J. M., Lavinder, J. J. L., and Sullivan, B. J. S. (2011). Protein Stability by Number: High-Throughput and Statistical Approaches to One of Protein Science's Most Difficult Problems. Curr. Opin. Chem. Biol. 15, 443–451. doi:10.1016/j.cbpa.2011.03.015
Mataga, N., Kaifu, Y., and Koizumi, M. (1956). Solvent Effects upon Fluorescence Spectra and the Dipolemoments of Excited Molecules. Bcsj 29, 465–470. doi:10.1246/bcsj.29.465
Meade, R. M., Fairlie, D. P., and Mason, J. M. (2019). Alpha-synuclein Structure and Parkinson's Disease - Lessons and Emerging Principles. Mol. Neurodegeneration 14, 29. doi:10.1186/s13024-019-0329-1
Meade, R. M., Morris, K. J., Watt, K. J. C., Williams, R. J., and Mason, J. M. (2020). The Library Derived 4554W Peptide Inhibits Primary Nucleation of α-Synuclein. J. Mol. Biol. 432, 166706. doi:10.1016/j.jmb.2020.11.005
Raghuraman, H., Kelkar, D. A., and Chattopadhyay, A. (2005). Novel Insights into Protein Structure and Dynamics Utilizing the Red Edge Excitation Shift Approach. Rev. Fluorescence, 199–214.
Reshetnyak, Y. K., Koshevnik, Y., and Burstein, E. A. (2001). Decomposition of Protein Tryptophan Fluorescence Spectra into Log-Normal Components. III. Correlation between Fluorescence and Microenvironment Parameters of Individual Tryptophan Residues. Biophysical J. 81, 1735–1758. doi:10.1016/s0006-3495(01)75825-0
Tuttle, M. D., Comellas, G., Nieuwkoop, A. J., Covell, D. J., Berthold, D. A., Kloepper, K. D., et al. (2016). Solid-state NMR Structure of a Pathogenic Fibril of Full-Length Human α-synuclein. Nat. Struct. Mol. Biol. 23, 409–415. doi:10.1038/nsmb.3194
Vieille, C., and Zeikus, G. J. (2001). Hyperthermophilic Enzymes: Sources, Uses, and Molecular Mechanisms for Thermostability. Microbiol. Mol. Biol. Rev. 65, 1–43. doi:10.1128/mmbr.65.1.1-43.2001
Keywords: protein stability, red edge excitation shift, fluorescence, tryptophan, conformational sampling
Citation: Kwok A, Camacho I, Winter S, Knight M, Meade R, Van der Kamp M, Turner A, O’Hara J, Mason J, Jones A, Arcus V and Pudney C (2021) A Thermodynamic Model for Interpreting Tryptophan Excitation-Energy-Dependent Fluorescence Spectra Provides Insight Into Protein Conformational Sampling and Stability. Front. Mol. Biosci. 8:778244. doi: 10.3389/fmolb.2021.778244
Received: 16 September 2021; Accepted: 27 October 2021;
Published: 03 December 2021.
Edited by:
Robert Stephen Phillips, University of Georgia, United StatesReviewed by:
Vladimir N. Uversky, University of South Florida, United StatesAndrew Harry Albert Clayton, Swinburne University of Technology, Australia
Kate Stafford, Atomwise Inc., United States
Copyright © 2021 Kwok, Camacho, Winter, Knight, Meade, Van der Kamp, Turner, O’Hara, Mason, Jones, Arcus and Pudney. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: AR Jones, YWxleC5qb25lc0BucGwuY28udWs=; VL Arcus, dmFyY3VzQHdhaWthdG8uYWMubno=; CR Pudney, Yy5yLnB1ZG5leUBiYXRoLmFjLnVr
†These authors have contributed equally to this work
 A Kwok1†
A Kwok1† IS Camacho
IS Camacho M Knight
M Knight RM Meade
RM Meade JM Mason
JM Mason AR Jones
AR Jones VL Arcus
VL Arcus CR Pudney
CR Pudney