
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mol. Biosci., 16 November 2021
Sec. Structural Biology
Volume 8 - 2021 | https://doi.org/10.3389/fmolb.2021.756701
This article is part of the Research TopicNuclear Magnetic Resonance and Molecular Modeling in the Field of GlycobiologyView all 5 articles
 Thomas Eckert1,2,3*
Thomas Eckert1,2,3* Jan von Cosel1
Jan von Cosel1 Benedict Kamps1,3
Benedict Kamps1,3 Hans-Christian Siebert4
Hans-Christian Siebert4 Ruiyan Zhang4,5
Ruiyan Zhang4,5 Ning Zhang4,5
Ning Zhang4,5 Konstantinos Gousias6
Konstantinos Gousias6 Athanasios K. Petridis7
Athanasios K. Petridis7 Dimitrios Kanakis8
Dimitrios Kanakis8 Konstantin Falahati1*
Konstantin Falahati1*The collagen-integrin interactions are mediated by the doubly charged Mg2+ cation. In nature this cation seems to have the optimal binding strength to stabilize this complex. It is essential that the binding is not too weak so that the complex becomes unstable, however, it is also of importance that the ligand-receptor binding is still labile enough so that the ligand can separate from the receptor in a suited environment. In the case of crystal growing for experimentally useful integrin-collagen fragment complexes it turned out that Co2+ cations are ideal mediators to form stable complexes for such experiments. Although, one can argue that Co2+ is in this context an artificial cation, however, it is now of special interest to test the impact of this cation in cell-culture experiments focusing on integrin-ligand interactions. In order to examine, in particular, the role cobalt ions we have studied a Co2+ based model system using quantum chemical calculations. Thereby, we have shown that hybrid and long-range corrected functional, which are approximations provide already a sufficient level of accuracy. It is of interest to study a potential impact of cations on the binding of collagen-fragments including collagens from various species because different integrins have numerous biological functions (e.g. Integrin – NCAM (Neural cell adhesion molecule) interactions) and are triggered by intact and degraded collagen fragments. Since integrin–carbohydrate interactions play a key role when bio-medical problems such as tumor cell adhesion and virus-host cell infections have to be addressed on a sub-molecular level it is essential to understand the interactions with heavy-metal ions also at the sub-atomic level. Our findings open new routes, especially, in the fields of tissue repair and neuro-oncology for example for cell-culture experiments with different ions. Since Co2+ ions seem to bind stronger to integrin than Mg2+ ions it should be feasible to exchange these cations in suited tumor tissues although different cations are present in other metalloproteins which are active in such tissues. Various staining methods can be applied to document the interactions of integrins with carbohydrate chains and other target structures. Thereby, it is possible to study a potential impact of these interactions on biological functions. It was therefore necessary to figure out first which histological–glycobiological experimental settings of tumor cells are suited for our purpose. Since the interactions of several metalloproteins (integrin, ADAM12) with polysialic acid and the HNK-1 epitope play a crucial role in tumor tissues selected staining methods are proper tools to obtain essential information about the impact of the metal ions under study.
A detailed understanding of integrin–ligand interactions requires that the impact of ligand structures is considered (Racine-Samson et al., 1997; Gabius et al., 2004; Petridis et al., 2011; Glinskii et al., 2014; Hussein et al., 2015; Cornelissen and Van Vliet, 2016; Marsico et al., 2018; Sharma et al., 2020; Eckert et al., 2021). The corresponding data are necessary to understand cellular mechanisms in neuroblastoma and in glioblastoma cells (Hemler, 1990; André et al., 2005; Bhunia et al., 2010; Petridis et al., 2011; Stötzel et al., 2012; Tsvetkov et al., 2012; Kanakis et al., 2013; Zhang et al., 2016a; Malric et al., 2017; Martinez-Olivera et al., 2018; McCarthy et al., 2018; Van Agthoven et al., 2019). This is possible on a sub-molecular size-level, however, as well as outlined in this article also on a sub-atomic scale where orbital-structures play an essential role. In this context it is important to analyze the influence of the heavy metal ion, which is involved in the binding process. Integrin-ligand interactions are mediated by Mg2+.It has been shown that the Mn2+ions stabilize integrin-ligand complexes [5FFO (Dong et al., 2017) and 6MSU (Van Agthoven et al., 2019)]. This leads to deeper insights in the structure function relationship of integrin–ligand model structures (Racine-Samson et al., 1997; Van Agthoven et al., 2019). Especially, when the heavy metal ion Co2+ is taken into account one can expect interesting results on a fundamental level regarding integrin-ligand interactions. The α1β1, α2β1, α10β1 and
One has observed Mg2+-dependent binding of the α1 I domain to the peptides in the following rank order: III-7 (GLOGEN), II-28 (GFOGER), II-7 and II-8 (GLOGER), II-18 (GAOGER), III-4 (GROGER) (Hamaia et al., 2012). It is important to note that special peptide sequences of collagen are able to influence the differentiation of cells in various ways. Our findings obtained by SPR measurements in combination with NMR and in silico calculations (Siebert et al., 2010) provide valuable hints to influence to such differentiation processes just by the choice of various suited cations. In order to understand the related biophysical processes on a deeper level quantum chemical calculations with different ions have to be carried out. We can show that the magnesium and cobalt cations are the most promising and interesting ones in this case (Jahn et al., 1937).
The structural-functional correlations between these ligand-receptor interactions are influencing cell growth and cell differentiation in a characteristic way. The sequence GVOGEA bound weakly to PC12 cells and strongly to activated Rugli cells or to an activated α1 I domain, but not to the α2 I domain or to C2C12 cells expressing α2β1 or α11β1. Thus, GVOGEA is specific for α1β1. Although, recognized by both binding sites α2β1 and α11β1, GLOGEN is a better ligand for binding site α1β1 compared with GFOGER. Finally, using biosensor assays, one can show that although GLOGEN is able to compete for the α1 I domain from collagen IV, GFOGER is much less potent, as shown previously. These data confirm the selectivity of GFOGER for binding site α2β1 and establish GLOGEN as a high affinity for binding site α1β1 for this peptide sequence (Hamaia et al., 2012).
Collagen contains specific cell adhesion domains, including the arginine- glycine-aspartic acid (RGD) motif. After the integrin receptor on the cell surface binds to the RGD motif on the collagen molecule, cell adhesion is actively induced. This interaction contributes to the promotion of cell growth as well as to the differentiation and the regulation of various other cell functions. In the fields of nanomedicine and nanopharmacology the structural–function relationship of biomolecules are described on a sub-molecular level in a clinical context. However, this is also the field of classical structure biology. However, the fields of nanomedicine and nanopharmacology are reaching much far. In the case it is necessary also the sub-atomic size level is included. The theoretical results are of highest importance for clinical research because no pathologist would start with such sophisticated and time-consuming experiments on human brain tissues without expecting diagnostic and therapeutic relevant results after heavy metal ion replacements.
All geometries considered in this study have been optimized at the long- range corrected CAM-B3LYP (Yanai et al., 2004) and the standard hybrid B3LYP (Becke, 1993) functional level of theory in combination with Ahlrichs SVP (Schäfer et al., 1992) and Pople 6-31G* (Hehre et al., 1972) basis set qualities as implemented in the Gaussian16 program package (Frisch et al., 2016). The B3LYP functional is well-established and tested in the field of transition metal computational chemistry, especially in the context of cobalt-containing systems of different multiplicity (Vargas et al., 2006). All minimum structures have been verified by analysis of the Hessian. Based on the crystal structure (PDB code 1DZI (Emsley et al., 2000) the model systems have been constructed using Hyperchem 8.0 (Hypercube (2007). Hyperch, 2007) to mimic the electronic environment of the cobalt and magnesium complexes respectively. All amino acid residues except the ones indicated in Figure 1A have been cleaved and the ends have been capped with methyl groups. The amino acids (Asp A151, Glu A152, Ser A153, Asn A154, Ser A155, Thr A221, Asp A254, Gly A255, Glu A256, Ser A257, His A258, Arg B12 und Glu C11) and two water molecules were used for the model. All residues are completely free to move during the calculations. Solvation effects have been addressed by means of the PCM (Miertuš et al., 1981; Miertus̃ and Tomasi, 1982) solvation model. In line with literature findings our benchmark calculations have indicated satisfying overall performance of the chosen hybrid and long-range corrected functional quality regarding geometric and electronic features of the metal complexes under consideration.
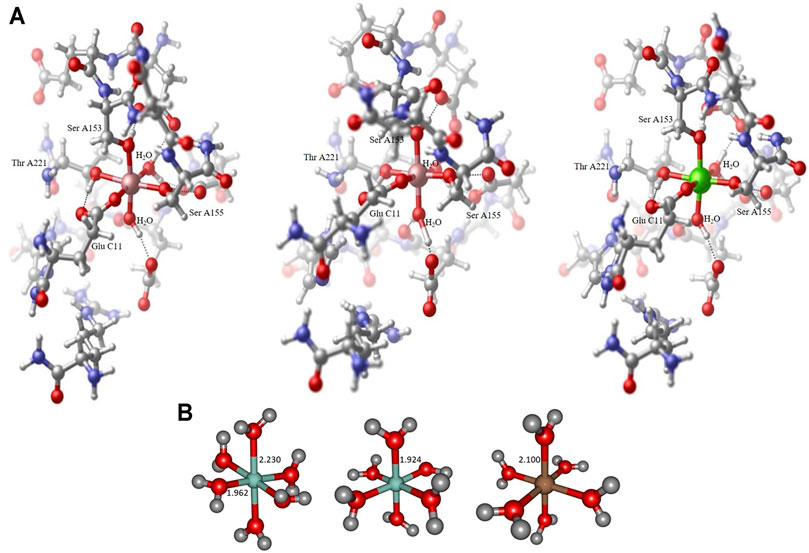
FIGURE 1. Collagen-integrin model complex containing a Co2+ center in a Jahn-Teller distorted octahedral ligand sphere (left), model complex containing a Co3+ center in an almost perfect octahedral ligand sphere (center) and model complex containing a Mg2+ center in an almost perfect octahedral ligand sphere (right). All structures obtained at the B3LYP/6-31G* level of theory, hydrogen bond interactions to adjacent amino acid residues indicated by dotted lines. The Collagen-integrin model complex contains the amino acids Asp A151, Glu A152, Ser A153, Asn A154, Ser A155, Thr A221, Asp A254, Gly A255, Glu A256, Ser A257, His A258, Arg B12 und Glu C11 and two water molecules of the structure 1DZI (37). The direct ligands on the divalent metal ions are Ser A153, Ser A155, Thr A221, Glu C11 and two water molecules (A). Hexaaqua model complex containing a Co2+ center in a Jahn-Teller distorted octahedral ligand sphere of water molecules, axial RCo−O distance 2.230 Å, equatorial RCo−O distances 1.962−1.967 Å (left), hexaaqua model complex containing a Co3+ center in an almost perfect octahedral ligand sphere of water molecules, all RCo−O distances 1.924 Å (center) and hexaaqua model complex containing a Mg2+ center in an almost perfect octahedral ligand sphere of water molecules, all RMg−O distances 1.924 Å (right). All structures obtained at the B3LYP/6-31G* level of theory (B).
The protein-complex 1DZI (Emsley et al., 2000) MD-simulation was run with YASARA 20.10.14 (Krieger and Vriend, 2014). The setup included an optimization of the hydrogen bonding network (Krieger et al., 2012) to increase the solute stability, and a pKa prediction to fine-tune the protonation states of protein residues at the chosen pH of 7.4 (Krieger et al., 2006). Na+ and Cl− ions were added with a physiological concentration of 0.9%, with an excess of either Na+ or Cl− to neutralize the cell. After steepest descent and simulated annealing minimizations to remove clashes, the simulation was run for 100 nanoseconds using the AMBER14 force field (Maier et al., 2015) for the solute, GAFF2 (Wang et al., 2004) and AM1BCC (Jakalian et al., 2002) for ligands, spezial amino acids (hydroxyprolin) and ions (Mg2+, Co2+, and Co3+) and TIP3P for water. The cutoff was set to 8 Å for Van der Waals forces (the default used by AMBER (Hornak et al., 2006), no cutoff was applied to electrostatic forces (using the Particle Mesh Ewald algorithm (Essmann et al., 1995). The equations of motion were integrated with a multiple timestep of 1.25 fs for bonded interactions and 2.5 fs for non-bonded interactions at a temperature of 310 K, 0,993,249 g/ml density and a pressure of 1 atm (NPT ensemble) using algorithms described in detail previously (Krieger and Vriend, 2015). After inspection of the solute RMSD as a function of simulation time, the first 10 ns were considered equilibration time and excluded from further analysis.
Graphical representation of the molecular geometries has been produced with the aid of CylView 1.0b (Legault, 2009) and Chemcraft (Zhurko, 2005).
The Methods of the Cell assay part are described in the Materials and Methods section of reference (Petridis et al., 2011).
Seven days old mice were sacrificed by decapitation under hypothermic anesthesia. The brains were removed and transferred into serum-free DMEM/F-12 medium supplemented with 1% penicillin/streptomycin (GIBCO-BRL; Carlsbad, CA), and 400 μm thick sagital slices were cut with a vibratome. Circular pieces (about 1 mm2) of the subventricular zone region l were extracted and put in DMEM/F-12 medium supplemented 1% penicillin/streptomycin. The cultures were treated with 6 U/ml of a polysialic acid (PSA)-specific endoneuraminidase (endo N). This amount of endo N is sufficient to completely remove PSA from the tissue. Armenian hamster monoclonal anti-β1 (10 μg/ml; BD Biosciences) was added together with endo N to the cultures to assess the role of β1-integrin in endo N-induced neuritogenesis. Untreated cultures were used as controls. All animal care and experimentation were carried out according to MSKCC (Memorial Sloan Kettering Cancer Center) institutional guidelines.
The cell line used in this study was the human neuroblastoma SH-SY5Y. The cell line was cultured in Dulbecco`s modified medium DMEM/F12 supplemented with 15% heat inactivated fetal calf serum (FCS) and 1% penicillin/streptomycin and Zeocin.
Cells were fixed in 4% paraformaldehyde at RT for 10 min, washed in PBS, then incubated with primary antibodies at 37°C for 2 h. After washing with PBS and incubation for 1 h at 37°C with the secondary antibodies, the cells were mounted in mowiol (Calbiochem; San Diego, CA). Primary antibodies used: mouse monoclonal anti-PSA (5A5, 1:1,000), armenian hamster monoclonal anti-β1 Integrin (1:200 BD Biosciences), mouse monoclonal anti-NF-M (145k) antibody for neurofilament staining (Chemicon), mouse monoclonal anti-NCAM (123C3; 1:150; Santa Cruz, Santa Cruz, CA). Secondary antibodies were FITC and Cy3 conjugated (Jackson Laboratories; West Groove, PA). Immunostaining with secondary antibodies alone was used as negative control. Cells were observed under a Zeiss 510LSM confocal microscope.
The PSA-positive neuroblastoma cell line SH-SY5Y (ATCC; Rockville, MD) was plated on glass coverslips and cultivated in Dulbecco’s modified medium DMEM/F12 supplemented with 15% heat inactivated fetal calf serum (FCS) and 1% penicillin/streptomycin. After cells reached a confluency of 60%, all-trans-retinoic acid (RA) (10 μM) was added. Retinoic acid treated and completely untreated cells were used as controls. Four days after addition of retinoic acid, 20 U/ml endo N was added together with serum and antibiotic free DMEM: F12 medium with or without blocking antibodies for 24 h. Antibodies used for blocking were, armenian hamster monoclonal anti-β1 (10 μg/ml; BD Biosciences) and rabbit polyclonal anti-NCAM Fab’-antibody 10 μg/ml (R004).
All experiments were repeated at least four times in triplicate. Statistical significance was assessed using analysis of variance (ANOVA).
The Methods of the AFM are described in the Materials and Methods section of reference (Stötzel et al., 2012).
As far as the immunohistochemistry experiments with the antibodies against ADAM12 and GFAP in the oligoastrocytoma tissues are concerned, these are described in every detail in the study published by Kanakis et al. (2013). In particular, regarding the quantification of the two antibodies (i.e ADAM12, GFAP) in the two different cell populations (i.e. neoplastic astrocytes, neoplastic oligodendrocytes) this was performed by estimating the number of immunostained cells for each antibody separately, which was then presented as a percentage value in a scale from 0 (no immunostained neoplastic cells) to ++++ (>75 positive neoplastic cells).
In this study we show how to correlate experimental results obtained from SPR, NMR and X-ray crystallographic analysis with quantum chemical DFT data regarding the transition metal compounds involved. In detail, the occupation of metal-centered orbitals related to the positively charged ions provide the essential key information regarding a direct impact on the structure-function relationship of this important bio-medical ligand-receptor complex. Experimentally obtained results on the impact of different ions on the stability of collagen-fragment-integrin complexes have been derived by Surface Plasmon Resonance (SPR) experiments by some of us (Siebert et al., 2010). However, as outlined in a review article (Zhang et al., 2016b) and in three original research articles (Siebert et al., 2001; Lenthe et al., 2004; Eckert et al., 2012) it is necessary to include ab initio or DFT calculations when an influence of the sub-atomic size level, especially, the impact of orbital shapes has to be analyzed in detail. The cation requirements of integrins (Xiong et al., 2002; Sen et al., 2018) are here studied on such a sub-atomic level and contributes in a significant way to an understanding of the binding processes in such complexes.
The amount of geometric distortion of the metal complex can be typically assigned to the structural strain that is imposed on the central cation by the respective ligand sphere, i.e. in the vicinity of a rather rigid peptide chain backbone the hexacoordinate Co2+ tends to depart from the assumed Jahn-Teller distortion where a clear distinction of axial and equatorial ligands is abandoned in favor of the overall complexation (cf. e.g. PDB codes 2GRU (Nango et al., 2008) and (Dowling et al., 2010). This is in sharp contrast to whenever geometric flexibility is increased, e.g. via the incorporation of water molecules as ligands at the complex center, in these cases the skeletal strain is relieved considerably allowing for more appropriate structural parameters for the metal complexation spheres (Chen et al., 2018).
Although the target systems are readily investigated and addressed experimentally, there is no thorough survey of the electronic structure properties documented in literature to date. Therefore, in this work, we aim to determine the electronic structure and geometric properties of selected Co2+, Co3+, and Mg2+ complexes that are chemically sufficiently close to experimentally addressable system at the center of the integrin-collagen complex.
By means of standard DFT methodology, we compare octahedral ligand spheres and Jahn-Teller distortions to indicate the oxidation states of the central cobalt ion thus clarifying the active species in the experimentally crystallized structures. We further characterize the most relevant interaction patterns favoring the complex stability incorporating cobalt and magnesium cations.
The structural analysis of the organometallic core complex is investigated as hexacoordinate model systems that are assumed to sufficiently mimic the experimental conditions. The main electronic influence is expected to arise from the most adjacent substituents that constitute the essentially octahedral ligand sphere of the cobalt and magnesium complexes respectively. As displayed in Figures 1A,B hexaaqua complex as well as a more realistic environment is employed in order to address the electronic structure of the investigated systems. For all cases, the triad of Co2+, Co3+, and Mg2+ central ion is considered constituting a set of 6 target complexes that are evaluated. In our investigation, the hexaaqua complexes serve as natural benchmark systems for the actual system. The structural and electronic properties are evaluated at several levels of theory to ensure best possible and efficient methodology in terms of computational demand and desired chemical accuracy. The influences of hybrid and long-range functionals in particular are crucial for a reliable description of the transition metal center and its nearest surroundings. Furthermore, the basis set dependability of geometric the relevant parameters at the metal center is evaluated.
As expected, the Co3+ and Mg2+ hexaaqua complexes are characterized by essentially symmetric octahedral ligand fields according to their electronic configurations while the Co2+ exhibits pronounced Jahn-Teller distortion due to its
As opposed to the cobalt based systems, the magnesium hexaaqua complex is largely stabilized by ion-dipole interactions indicated by the straight geometric orientation of the surrounding water molecules, cf. Figure 1B as opposed to the essentially covalent interactions that dominate the [Co(OH2)6]2+ and [Co(OH2)6]3+ geometries which exhibit bent orientations of the hydrogen atoms in the ligand water molecules with respect to the metal center.
Regarding the relevant electronic configurations for the [Co(OH2)6]2+ and [Co(OH2)6]3+ complexes respectively, the typical scheme is obtained in terms of the five d-orbitals of the central cobalt ion that are intermixed with the ligand orbitals as outlined in panels A and B of Figure 2. The resulting orbital occupations patterns can be rationalized as
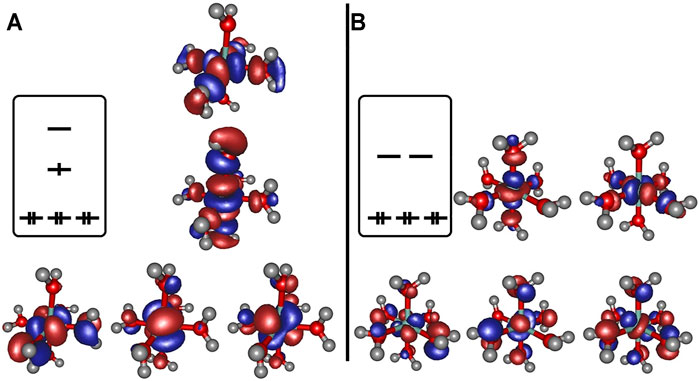
FIGURE 2. Frontier orbitals obtained at the B3LYP/6-31G* level of theory for [Co(OH2)6]2+ (panel A) and [Co(OH2)6]3+ (panel B), orbital occupation sketched for clarity.
The depiction of the net spin density (cf. panel A of Figure 3) emphasizes the notion of the singly occupied
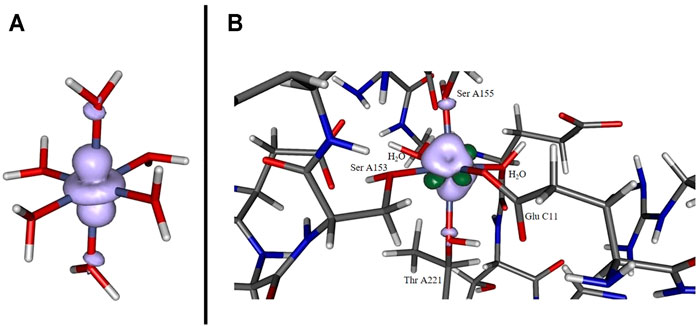
FIGURE 3. Spin density for [Co(OH2)6]2+ (panel A) and for the cobaltous model system (panel B) computed at the B3LYP/6-31G* level of theory. In the former case, a pronounced localization at the metal site originating from the singly occupied dz2 orbital. In the latter case the distribution is more diffuse and additionally features significant spin polarization contributions (dark green lobes).
Potential energy surface scans reveal distinct energetic differences in bond dissociation curves for axial and equatorial ligand cleavage from the [Co(OH2)6]2+ complex (Figure 4). Due to the elongated bond distances at the axial positions the net dissociation energy is expected to be considerably lowered by approximately 12 kcal/mol indicative of possible biological relevance in the Co2+-mediated processes in the full protein environment.
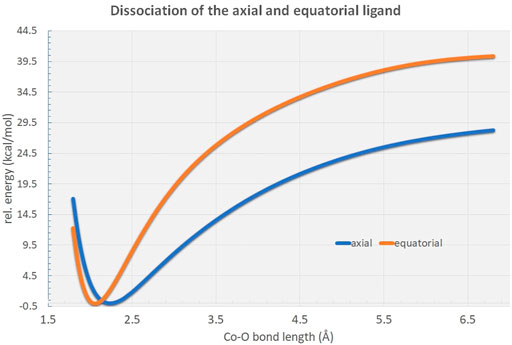
FIGURE 4. Rigid potential energy surface scans along the RCo−O distance in the [Co(OH2)6]2+ hexaaqua complex at the B3LYP/6-31G* level of theory. As can be figured from the curves, the axial ligand dissociation is energetically highly favored in comparison to the equatorial ligands by approximately 12 kcal/mol.
Our integrin-collagen model system consists of an inner layer of electronic interaction patterns inspired by the original chemical site at the crystal structure from the PDB code 1DZI by Emsley et al. (2000). As can be deduced only two coordinating water molecules are directly surrounding the central ion while the side chain residues of the protein chain occupy the four remaining positions in the hexacoordinate ligand sphere. The incorporation of the metal cation in the ligand sphere of the protein background affects the geometric arrangement of the complex and slightly alters the electronic interactions. Most prominently, the complex symmetry is lowered to certain degrees as the various bond lengths are determined by the nature and electronic properties of the respective ligand that is either a water substituent or an amino acid type residue. Table 2 displays the relevant bond lengths for the three investigated collagen-integrin model complexes. While the
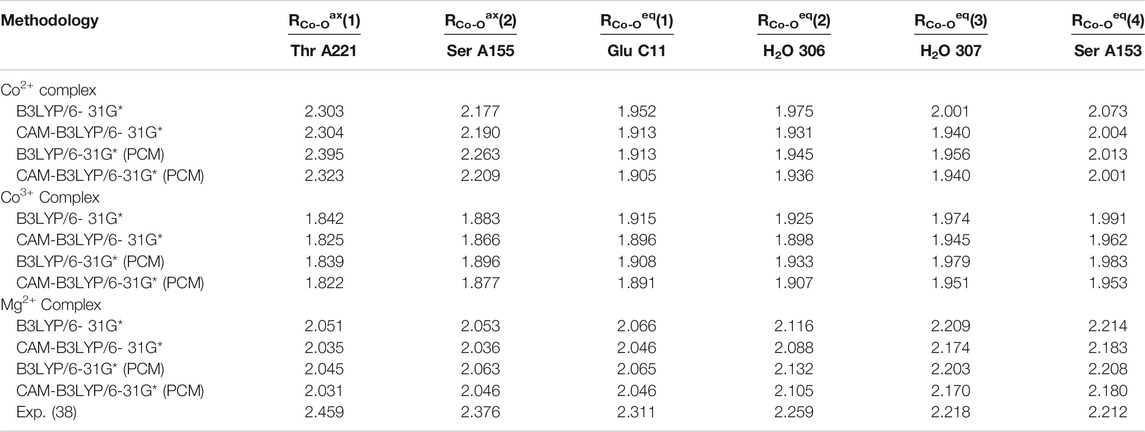
TABLE 2. Axial and equatorial bond lengths in Å for the collagen-integrin model complexes discussed in this study.
Analysis of the three model cases does, however, demonstrates the general tendency to asymmetrize the complex from its either perfect octahedral or Jahn-Teller distorted shape into somewhat tilted hybrid structures that qualitatively feature two subsets of bond lengths. This finding raises the doubt for a distinct cobaltous character of the central ion in the embedding of the experimental system. In Figure 5 the frontier orbital occupation (with significant Co contribution) are depicted for the cobaltous system. As can be deduced, the orbital shape and orientation is clearly affected by the asymmetric electronic environment due to the amino acid residues in direct proximity of the metal center. Thus, the tilting and bending of orbital character is apparent to optimize the interactions upon protein embedding of the cation unlike in the hexaaqua system where orbital deformation is less distinct (cf. panel A of Figure 2).
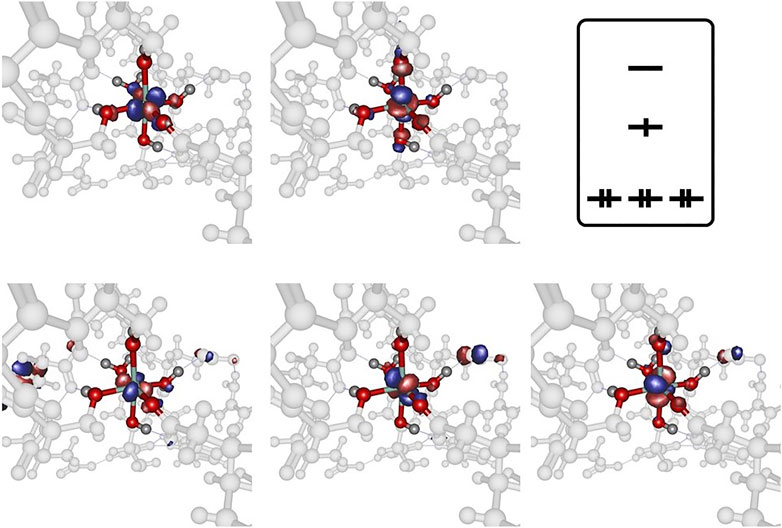
FIGURE 5. Frontier orbitals for the Co2+ model complex obtained at the B3LYP/6-31G* level of theory and sketched population scheme. Only orbitals with significant Co contribution are displayed. While the essential shape of the five Co d-orbitals is conserved, substantial deformation and bending of the respective orbital orientation is apparent. The amino acid residues are shaded collectively in gray color for the sake of clarity.
The spin density distribution in the Co2+ model complex (cf. panel B of Figure 3) is likewise altered in comparison to the hexaaqua ligand sphere: while the spin delocalization seems to dominate the situation in a coordination sphere of six water molecules as stated above, the asymmetric surroundings as well as the bond elongation with respect to the paramagnetic center induce a more complex spin density distribution. For instance, the additional dark green lobes are indicative of substantial spin polarization phenomena in the vicinity of the Co center. Given the more involved interaction patterns the Mulliken spin density of the cobalt center decreases ever so slightly from approximately 0.966 in the hexaaqua system to 0.961 in the model system based on our computations at the B3LYP/6-31G* level of theory. This trend, however, depends crucially on the quality of the long-range interaction description as provided by the CAM-B3LYP functional. In the latter case the numbers change from 0.962 to 0.971 thus showing a reversed picture with a more isolated spin density accumulated at the metal center. The effect of PCM solvation further intensifies the spin density aggregation at the Co center. The numbers are inferred from Table 3. As the computation of the spin density is, in general, less sensitive with respect to the employed level of theory and basis set quality (Cano et al., 1998; Ruiz et al., 2005; Giner and Angeli, 2016; Philips et al., 2010) the overall method dependency is, however, comparably negligible.

TABLE 3. Mulliken spin densities at the cobaltous center of the hexaaqua and the model complex at different levels of theory.
Further inspection reveals the marked deviations from the predicted structural arrangement: as Figure 6 suggests, the experimental cobalt complex extracted from the PDB file provided by Emsley et al. (2000) lacks the intrinsic symmetric properties that are characteristic for the [Co(OH2)6]2+ system in several ways. Firstly, the pseudo-equatorial ligand atom positions lead to a substantial cobalt out-of-plane relocation (featuring a dihedral angle of approx. 6° with respect the plane) in contrast to the hexaaqua complex. Secondly, the angle of the axial ligands (denoted as
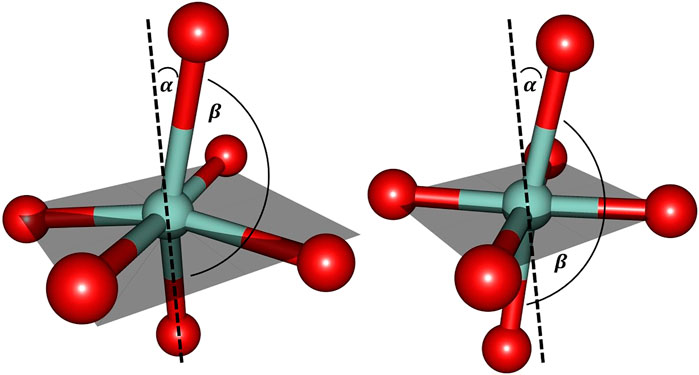
FIGURE 6. Cobalt coordination sphere extracted from the crystal structure data by Emsley et al. (2000) (left) and the ligand sphere for the freely optimized [Co(OH2)6]2+ complex (right) using the B3LYP/6-31G* level of theory. For the sake of clarity only the directly bound oxygen atoms are displayed. The gray shaded plane indicates the arrangement of equatorial ligands: in the optimized hexaaqua complex, the equatorial oxygen atoms essentially span a plane with minimal Co out-of-plane deviation while the experimental system features pronounced deformations. α denotes the deviation relative to the plane normal and βO−Co−O depicts the axial angle of the complex. The values for the angles are approximately given as: α = 15° and βO−Co−O = 165° (left) and α = 10° and βO−Co−O = 173° (right).
Comparison to the biological magnesium complex is reasonably reflected in the cobalt complex since it similarly allows for geometric rearrangements that are present in the more flexible embedding of the metal ion in an augmented hexacoordinate ligand sphere with elongated bonds as compared to the hexaaqua situation.
The MD simulation of 1DZI (Emsley et al., 2000) has been carried out to assess the structural stability of the protein complex complementary to our DFT analysis of the transition metal center. Our findings are in line with similar MD studies by (Siebert et al., 2010; Zheng et al., 2018) The explicitly mapped coordination sphere of the cobalt ion in our fully quantum mechanical structure turns out to be well-behaved during our optimization and no expansion or compression of our model system is observed indicative of unbalanced estimation of interaction patterns induced by the chemical environment in the native complex. To analyze the MD simulation, the RMSD was determined as a function of 100 ns runtime (Figure 7A). Figure 7A shows an average RMSD of about 2 Å. Higher RMSD values are only present within the range of 27 and 79 ns. In order to determine whether higher RMSD values affect the environment of the Co2+ ion, the Co-ligand bond distances have been included for these times in Table 4, displaying overall good agreement with the other evaluated bond distances. To analyze where the structural fluctuations come from, the RMSF values for the individual residuals were calculated (Figure 7B). In particular, the ends of the proteins are shown to be very flexible, with the exception of the N-terminal end of the integrin, which is well stabilized by two neighboring beta sheet structures. In particular, the ends of the proteins are shown to be very flexible, with the exception of the N-terminal end of the integrin (Mol A magenta), which is well stabilized by two neighboring β-sheet structures. The amino acids Ser A153, Ser A155, Thr A221, and Glu C11 exhibit a significantly reduced flexibility as integral parts of the transition metals coordination sphere. During the simulation over 100 ns, the bond distances of the above-mentioned amino acids and two water molecules fluctuated by approx. 0.1 Å and the bond angles by approx. 10 degrees around their equilibrium position (Figures 8A,B). The average bond distances extracted from our MD simulations (up to 100 ns) the complex based on the 1DZI code from the PDB displays satisfactory agreement with our findings based on the density functional treatment of the model system for all levels of theory employed. Incidentally, the asymmetrical coordination sphere of the metal center featuring six gradually different interatomic distances rather than a perfect (Jahn-Teller-based) octahedral geometry is reproduced in both computational approaches. Our integrin-collagen model system consists of an inner layer of electronic interaction patterns inspired by the original chemical site at the crystal structure from the PDB code 1DZI by Emsley et al. (2000).
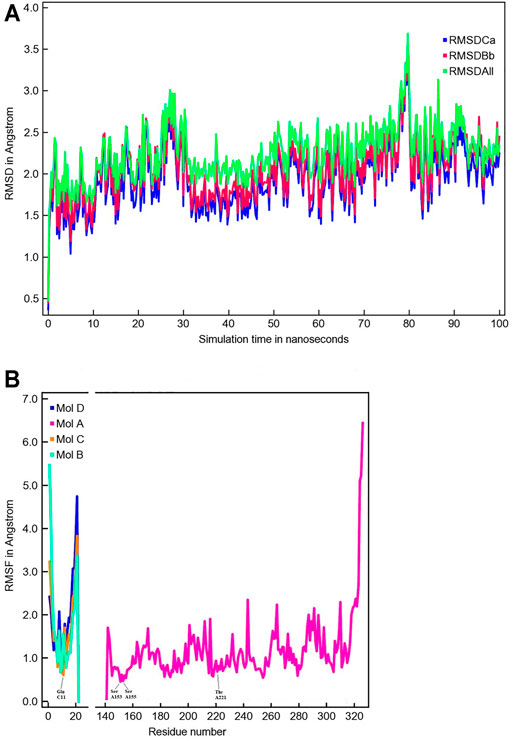
FIGURE 7. The time evolution of the root mean square deviation (RMSD) measured from the corresponding starting structure 1DZI (Emsley et al., 2000). The different RMSD plots have the following meaning: RMSDCa (blue) is the RMSD for C-alpha, RMSDBb (red) is the RMSD for the backbone and RMSDAll (green) is the RMSD plot for all-heavy atoms (A). The root mean square fluctuation (RMSF) in Angstrom per solute protein residue calculated from the average RMSF of the atoms constituting the residue: integrin Mol A (magenta), collagen Mol B (cyan), collagen Mol C (orange) and collagen Mol D (blue). A RMSF of exactly zero means that that residue number is not present in the Molecule (B).
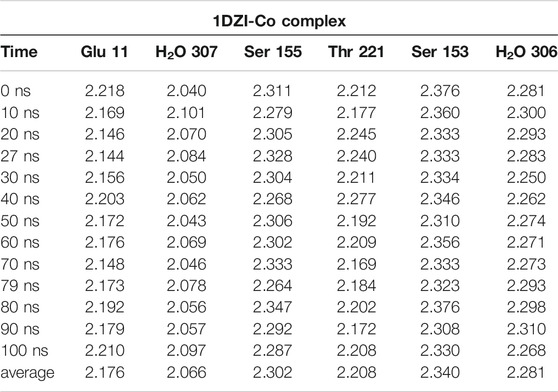
TABLE 4. MD-Simulation of 1DZI (Emsley et al., 2000) with cobalt-complex in Å.
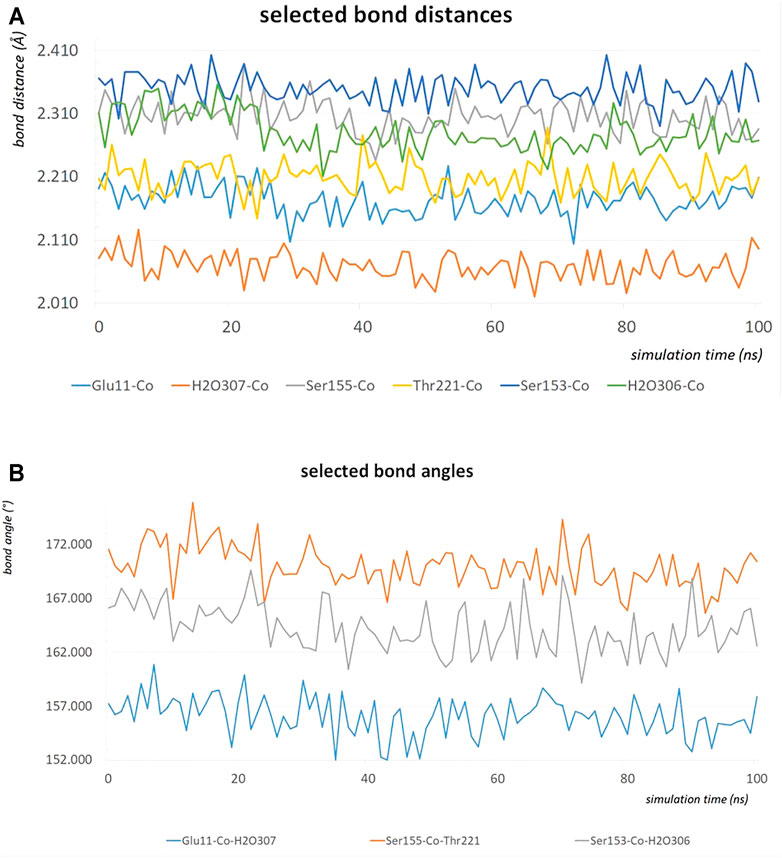
FIGURE 8. The bond distances in Å of the amino acids Ser A153, Ser A155, Thr A221, Glu C11, water 306 and water307 around the Co2+ during an MD simulation of 100 ns (A). The bond angles in degrees of Glu C11-Co2+-water 307, Ser A155-Co2+-Thr A221 and Ser A153-Co2+-water 306 during an MD simulation of 100 ns (B).
When SH-SY5Y neuroblastoma cells were treated with endo N, which specifically cleaves polysialic acid (PSA) from NCAM, neuritogenesis of these cells occurred (Figure 9A). Induction of neuronal processes, which were neurofilament M (NF-M)-positive (Figures 9B,C), was significantly inhibited by the use of an NCAM-blocking antibody (Figure 9A). Surprisingly, β1-integrin blocking antibody significantly inhibited the endo N induced effect on neuritogenesis (Figure 9A), but not at the same scale as anti-NCAM. Inhibition of endo N-induced neuritogenesis by β1-integrin blockage were not only applied in neuroblastoma cells but also in subventricular zone (SVZ) progenitor cells. Figure 9D shows that neurite outgrowth in SVZ explant cultures is induced by endo N and that addition of β1-integrin blocking antibody reduces the effect of endo N.
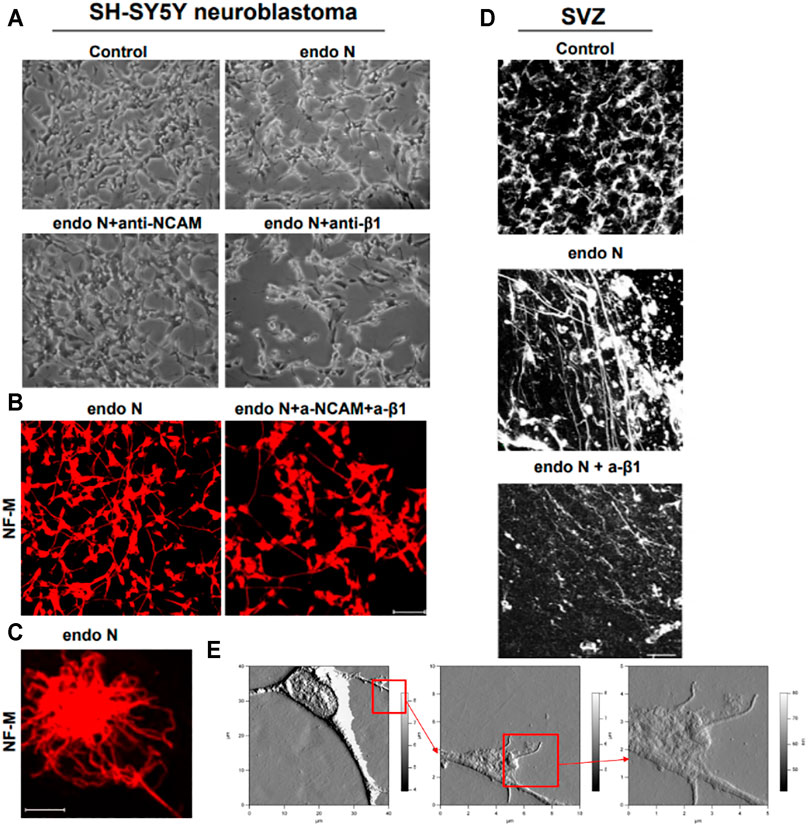
FIGURE 9. Neuroblastoma cells of a SH-SY5Y cell-line treated with endo N, which specifically cleaves polysialic acid (PSA) from NCAM. Neuritogenesis of these cells occurred (A). Induction of neurofilament M (NF-M)-positive neuronal processes (B,C) is clearly inhibited by the use of an NCAM-blocking antibody (A). β1-Integrinblocking antibody significantly inhibited the endo N induced effect on neuritogenesis (A). Inhibition of endo N-induced neuritogenesis by β1-integrinblockage is not only applied in neuroblastoma cells but also in sub ventricular zone (SVZ) progenitor cells. 9D shows that neurite outgrowth in SVZ explant cultures is induced by endo N. Addition of β1-integrin blocking antibody reduces the effect of endo N. Beside polysialic acid (PSA) a sulfated oligosaccharide (the HNK1 epitope) plays an important role as marker on neuroblastoma cells. Therefore, AFM (Atomic Force Microscopy) presentations of a HNK-1 positive neuroblastoma cell are shown (E) in different enlargements.
Our first approach for evaluating the relation between NCAM and β1-integrin in neuroblastoma cells was to immunostain cells for both molecules. We found that in the absence and presence of endo N, some NCAM colocalized with β1-integrin (Figure 10A). This colocalization was present at points where there was cell–cell contact and was independent of the presence of endo N (Figure 10B). β1-integrin was not expressed in isolated cells, whereas NCAM was expressed and was present on cell surface. In the case of cell–cell contact, NCAM was localized on the cell surface and β1-integrin was expressed in contact areas between the cells (Figures 9A, 10B).
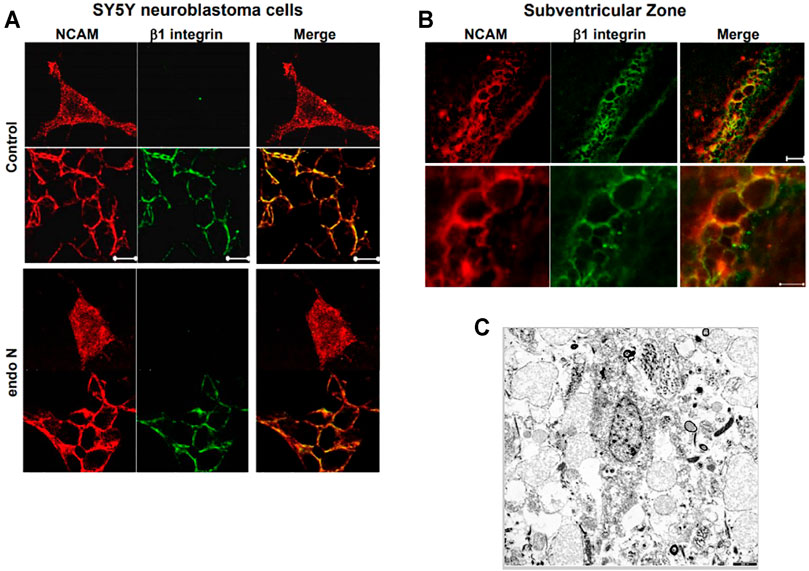
FIGURE 10. The relation between NCAM and β1-integrinin neuroblastoma cells was performed by an immune staining for both molecules. In the absence and presence of endo N, NCAM colocalized with β1-integrin (A). This colocalization was present at regions where no cell–cell contact occurred and was independent of the presence of endo N (B). β1-integrin was not expressed in isolated cells, whereas NCAM was expressed, but was present all over the cell. In the case of cell–cell contacts, NCAM was localized on the cell surface and β1-integrinwas expressed in contact areas between the cells, as indicated in (B) for the sub ventricular zone (SVZ). (C) shows cells of a glioblastoma multiform WHO grade 4 (9). In these kind of tumors specific integrin-interactions are also of highest importance.
For such cell systems it makes sense to carry out experiments with Co2+, Mg2+ and Mn2+ as well as Co3+ ions in order to identify the bio-medical role of heavy metal cations on a cell-tissue level.
The cell biological/histological data presented in this study avenues for further experimental settings in which the theoretical molecular modeling results are tested on tumor tissues obtained from neuroblastomas, oligodendrogliomas (WHO grade II-III), glioblastomas (WHO grade IV) and various metastatic cells.
It is known that cell differentiation and migration as well as tissue repair processes strongly depend on the occurrence of polysialic acids and the HNK-1 epitope which are contact-structures of the corresponding cell surfaces. The concentration of the HNK-1 epitope and the length of the polysialic acid chain on a tumor cell surface are suitable prognostic markers to determine the malignancy of such cells. Integrins which are glycoproteins and major players in cell differentiation as well as cell migration processes interact in various ways with the HNK-1 epitope and polysialic acids, thereby, influencing the fate of the cell. A number of questions are still unanswered in respect to this glycobiological processes. Especially, concerning the interaction processes on a sub-molecular level it is essential to evaluate potential tumor cell experiments in relation to the new insights provided by our DFT results. As shown already with SPR experiments it is possible to replace the Mg2+ cations of integrin by Co2+ cations. In the same way this can be performed for the integrins in tumor cell tissues. According to our molecular modeling studies in which parts of the metalloprotein integrin are analyzed even on sub-atomic size scale it has now tested by staining techniques whether there is an impact on the cells and tissues. This is of particular interest because potential therapeutic options with cobalt salts in cancer research could be a promising option and provide at least new insight in the structure–function relationship of tumor spread and migration. The answer why nature has chosen Mg2+ instead of Co2+ could then even be answered.
In histology, the glial fibrillary acidic protein (GFAP stain) is carried out to determine whether cells contain the glial fibrillary acidic protein, a protein found in glial cells (Kanakis et al., 2013). The GFAP staining is useful for determining whether a tumor of glial origin. ADAM (A Disintegrin And metalloprotease) 12 has also been implicated in the development of pathogen various forms of cancer, hypertension, liver fibrogenesis, and asthma (Estrella et al., 2009). Since collagen–integrin (Siebert et al., 2010) and collagen–ADAM interactions (Eckert et al., 2021) play a dominant role in cell experiments (Petridis et al., 2011; Martinez-Olivera et al., 2018) where Mg2+ is replaced by Co2+ we have already discussed their feasibility here.
Replacing the Mg2+ by a Co2+ cation in an integrin it is less complicated than the replacement of such cation in a complete tumor cell tissue probe which is necessary to study a potential impact on cell differentiation and migration processes. Special staining methods which are introduced in Figures 11A,B as well as in Figures 9, 10 can also be used to document the effects of these cation replacements. Nevertheless, one has to keep in mind that in a tumor cell tissue also other proteins with cations are triggering cellular processes (Kanakis et al., 2013). Figure 11A show cells of a previously diagnosed oligoastrocytoma WHO grade II. A vast majority of cells mainly from the oligodendroglioma component expresses the metalloprotease ADAM 12 which interacts with integrins in a specific way (Estrella et al., 2009; Kanakis et al., 2013). The results of our molecular model calculations clearly show that, especially, with integrins, a clear effect can be expected through the replacement of the Mg2+ ions by the Co2+ ions.
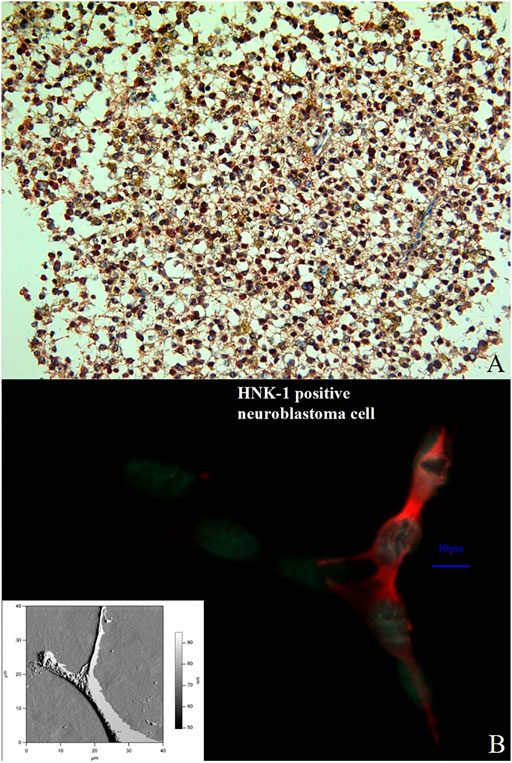
FIGURE 11. Double immunostaining with the antibodies against ADAM12 (red color) and GFAP (brownish color) in a previously diagnosed oligoastrocytoma WHO grade II. Immuno-histochemistry for these markers identifies and labels two distinct though intermixed tumor-cell populations; the oligodendroglioma cells stain positive for ADAM12 whereas the astrocytoma cells for GFAP. (Magnification × 200) (A). Comparison between an immune stained neuroblastoma cell (the HNK-1 epitope is stained in red) and an AFM presentation of a neuroblatoma cell of the same cell line (lower left corner). The relation between NCAM and β1-integrinin neuroblastoma cells was performed by an immune staining for both molecules (B).
In this study we analyzed the fundamental electronic structure of a Co2+ containing integrin-collagen-fragment complex. This complex served as appropriate model system for biologically relevant integrin-collagen structures featuring Mg2+ cations at their center. Based on our computational benchmark at the hexaaqua complexes of Co2+, Co3+ and Mg2+ we identify the combination of hybrid and long-range corrected density functional theory with standard basis set sizes of Pople and Ahlrichs quality to be a useful tool for geometry and electronic structure determination in these hexacoordinate transition metal ligand spheres.
In light of our investigations we determined a pronounced Jahn-Teller distortion of the [Co(OH2)6]2+ hexaaqua complex as well as a comparable distortion in our Co2+ model system that features the biologically relevant amino acid residues in the ligand sphere of the metal center. This is in line with the general picture of orbital energetic rearrangement due to the singly occupied
Our model system that mimics the electronic environment of the collagen-integrin complex has proven to be suited for the evaluation of the effective interaction patterns that are induced by the surrounding amino acid side chains that shape the ligand sphere of the respective central cation, i.e. Co2+, Co3+ and Mg2+. Unlike in the flexible hexaaqua ligand field, the Co2+ center in the model system is pinched in a considerably distorted electronic environment that significantly affects the geometric conditions compared to a typical Jahn-Teller-distorted arrangement for d7 metals. The clear distinction between elongated axial and considerably shorter equatorial bond distances is partly relieved in favor of a more erratic distribution of geometric parameters such as bond lengths and angles. In our MD simulation, bond lengths and bond angles were also found to be very stable (Figures 8A,B). In view of our MD simulations, we do confidently assume that given the overall structural conservation of the protein complex during our simulations, the transition metal center is crucial to the skeletal integrity of the protein and is therefore adequately described by our model system at the DFT level of theory. Upcoming research aims to combine the theoretical findings in this study in terms of hybrid quantum-classical QM/MM approaches to assess quantitative treatment of the system.
We conclude that consideration of quantum chemical effects for the transition metal complexes discussed in this study is crucial in order to adequately describe the geometry and electronic environments of the structures that are a sensitive function of the electronic configuration of the central cation. In particular, we emphasize the fact that the short interatomic ligand-metal distances in the cobalt based systems indicate a partial covalent bond character in contrast to the magnesium-based complex. It is therefore likely, that the former might be prone to sensitive changes in their biochemical functionality with respect to the oxidation state of the cobalt center due to elongation and compression of axial ligand distances from the center associated with Jahn-Teller type distortions. A clear biological application has not yet been found, but one can imagine that a change in the oxidation state or a change in the spatial direction of the Jahn-Teller distortion results in a change in the bond strength at the cobalt cation in a certain direction and so on perhaps a previously absorbed ligand can be released again at a later point in time. It could be some kind of biological switch.
The studied integrin-collagen complex is stabilized by a Co2+ cation which exhibits substantial Jahn-Teller distortion in its crystal structure (Emsley et al., 2000) as well as in our computational calculations discussed here. Depending on the orientation of the axial bond, ligands bind weaker or stronger to the central metal ion. Our analysis shows that bond cleavage of axial and equatorial ligands can vary within a few kcal/mol in binding energy. The quantum chemical DFT data may contribute to a better understanding of the function relationship of integrin ligand complexes including the role of integrins in tissue repair, glycobiology and neurooncology (Racine-Samson et al., 1997; Gabius et al., 2004; André et al., 2005; Bhunia et al., 2010; Petridis et al., 2011; Stötzel et al., 2012; Tsvetkov et al., 2012; Kanakis et al., 2013; Glinskii et al., 2014; Hussein et al., 2015; Zhang et al., 2016a; Cornelissen and Van Vliet, 2016; Malric et al., 2017; Marsico et al., 2018; Martinez-Olivera et al., 2018; McCarthy et al., 2018; Sharma et al., 2020; Eckert et al., 2021). The polysialylated neural cell adhesion molecule (NCAM) as well as the sulfated HNK-1 epitope are together with β1-integrin involved in cell differentiation processes. This includes with changes in the expression of these molecules correlated with changes in the malignancy of tumor cells. Functional correlation between NCAM, HNK-1, collagen, ADAM12 and β1-integrin adhesion and also neurite outgrowth in brain-tumor cells are key interactions in various tissues and can in principle be triggered by the use of certain heavy metal ions. Possible follow-up studies will focus on identification of related three-dimensional structures that exhibit similar Jahn-Teller distortion patterns in order to further elucidate the evidence concerning the relevance of quantum chemical effects in the characteristic mechanism of ions in protein complexes. Thereby, considering these insights in the corresponding cell-tissue experiments. A deeper insight in the correlation between quantum theory and bio-macromolecular systems has a tremendous impact on the understanding of numerous processes in live. In this publication we have provided introduced beside our DFT results also a suited cellular test system where these theoretical data can be tested on a cellular level.
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author/s.
The studies involving human participants were reviewed and approved by The study was approved by the Ethic Committees of the Westfaelische Wilhelms University of Münster (ethics committee vote2020-063-f-S). The patients/participants provided their written informed consent to participate in this study.
TE and KF planned the study. TE, KF, JvC, and BK conducted the MD-simulations and the DFT calculations. KG, AP and DK have contributed the cell assay part. TE, KF, RZ, and H-CS wrote the first version of the manuscript., TE, NZ, KG, AP, DK, and KF edited and approved the final version of the manuscript.
We thank for funding: National Natural Science Foundation of China (No. 82001286), Natural Science Foundation of Shandong province (No. ZR2020QH112) and Open Project of Liaocheng Universtiy Animal Husbandry Discipline, No. 319312101-25.
The Authors TE, BK, JC, and KF are employed by RISCC UG.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank Martin Bergmann (Institute of Veterinary Anatomy, -Histology, and -Embryology) for his support and helpful assistance about the handling of data sets obtained from electron microscopy.
André, S., Kaltner, H., Lensch, M., Russwurm, R., Siebert, H.-C., Fallsehr, C., et al. (2005). Determination of Structural and Functional Overlap/divergence of Five Proto-type Galectins by Analysis of the Growth-Regulatory Interaction with Ganglioside GM1in Silicoandin Vitroon Human Neuroblastoma Cells. Int. J. Cancer 114, 46–57. doi:10.1002/ijc.20699
Becke, A. D. (1993). Density‐functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 98 (7), 5648–5652. doi:10.1063/1.464913
Bhunia, A., Vivekanandan, S., Eckert, T., Burg-Roderfeld, M., Wechselberger, R., Romanuka, J., et al. (2010). Why Structurally Different Cyclic Peptides Can Be Glycomimetics of the HNK-1 Carbohydrate Antigen. J. Am. Chem. Soc. 132, 96–105. doi:10.1021/ja904334s
Cano, J., Ruiz, E., Alvarez, S., and Verdaguer, M. (1998). Spin Density Distribution in Transition Metal Complexes: Some Thoughts and Hints. Comments Inorg. Chem. 20 (1), 27–56. doi:10.1080/02603599808032749
Zhurko, G. A. (2005). Chemcraft - Graphical Program for Visualization of Quantum Chemistry Computations. Ivanovo, Russia. Available at: https://www.chemcraftprog.com/.
Chen, Y. W., Satange, R., Wu, P. C., Jhan, C. R., Chang, C. K., Chung, K. R., et al. (2018). CoII(Chromomycin)₂ Complex Induces a Conformational Change of CCG Repeats from I-Motif to Base-Extruded DNA Duplex. Int. J. Mol. Sci. 19 (9). doi:10.3390/ijms19092796
Cornelissen, L., and Van Vliet, S. (2016). A Bitter Sweet Symphony: Immune Responses to Altered O-Glycan Epitopes in Cancer. Biomolecules 6 (26), 26–19. doi:10.3390/biom6020026
Dong, X., Zhao, B., Iacob, R. E., Zhu, J., Koksal, A. C., Lu, C., et al. (2017). Force Interacts with Macromolecular Structure in Activation of TGF-β. Nature 542 (7639), 55–59. doi:10.1038/nature21035
Dowling, D. P., Gattis, S. G., Fierke, C. A., and Christianson, D. W. (2010). Structures of Metal-Substituted Human Histone Deacetylase 8 Provide Mechanistic Inferences on Biological Function,. Biochemistry 49 (24), 5048–5056. doi:10.1021/bi1005046
Eckert, T., Jährling-Butkus, M., Louton, H., Burg-Roderfeld, M., Zhang, R., Zhang, N., et al. (2021). Efficacy of Chondroprotective Food Supplements Based on Collagen Hydrolysate and Compounds Isolated from marine Organisms. Mar. Drugs 19 (542), 1–30. doi:10.3390/md19100542
Eckert, T., Stötzel, S., Burg-Roderfeld, M., Sewing, J., Lütteke, T., Nifantiev, N. E., et al. (2012). In Silico Study on Sulfated and Non-sulfated Carbohydrate Chains from Proteoglycans in Cnidaria and Their Interaction with Collagen. Open J. Phys. Chem. 2 (2), 123–133. doi:10.4236/ojpc.2012.22017
Emsley, J., Knight, C. G., Farndale, R. W., Barnes, M. J., and Liddington, R. C. (2000). Structural Basis of Collagen Recognition by Integrin α2β1. Cell 101 (1), 47–56. doi:10.1016/s0092-8674(00)80622-4
Essmann, U., Perera, L., Berkowitz, M. L., Darden, T., Lee, H., and Pedersen, L. G. (1995). A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 103, 8577–8593. doi:10.1063/1.470117
Estrella, C., Rocks, N., Paulissen, G., Quesada-Calvo, F., Noël, A., Vilain, E., et al. (2009). Role of A Disintegrin and Metalloprotease-12 in Neutrophil Recruitment Induced by Airway Epithelium. Am. J. Respir. Cel Mol. Biol. 41 (4), 449–458. doi:10.1165/rcmb.2008-0124OC
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2016). Gaussian 16, Revision B.01. Wallingford CT: Gaussian Inc.
Gabius, H.-J., Siebert, H.-C., André, S., Jiménez-Barbero, J., and Rüdiger, H. (2004). Chemical Biology of the Sugar Code. ChemBioChem 5, 740–764. doi:10.1002/cbic.200300753
Gailit, J., Xu, J., Bueller, H., and Clark, R. A. F. (1996). Platelet-derived Growth Factor and Inflammatory Cytokines Have Differential Effects on the Expression of Integrins α1β1 and α5β1 by Human Dermal Fibroblasts In Vitro. J. Cel. Physiol. 169 (2), 281–289. doi:10.1002/(sici)1097-4652(199611)169:2<281:aid-jcp7>3.0.co;2-k
Giner, E., and Angeli, C. (2016). Spin Density and Orbital Optimization in Open Shell Systems: A Rational and Computationally Efficient Proposal. J. Chem. Phys. 144 (10), 104104. doi:10.1063/1.4943187
Glinskii, O. V., Li, F., Wilson, L. S., Barnes, S., Rittenhouse-Olson, K., Barchi, J. J., et al. (2014). Endothelial Integrin α3β1 Stabilizes Carbohydrate-Mediated Tumor/endothelial Cell Adhesion and Induces Macromolecular Signaling Complex Formation at the Endothelial Cell Membrane. Oncotarget 5 (5), 1382–1389. doi:10.18632/oncotarget.1837
Hamaia, S. W., Pugh, N., Raynal, N., Némoz, B., Stone, R., Gullberg, D., et al. (2012). Mapping of Potent and Specific Binding Motifs, GLOGEN and GVOGEA, for Integrin α1β1 Using Collagen Toolkits II and III. J. Biol. Chem. 287 (31), 26019–26028. doi:10.1074/jbc.m112.353144
Hehre, W. J., Ditchfield, R., and Pople, J. A. (1972). Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 56 (5), 2257–2261. doi:10.1063/1.1677527
Heino, J., and Massagué, J. (1989). Transforming Growth Factor-β Switches the Pattern of Integrins Expressed in MG-63 Human Osteosarcoma Cells and Causes a Selective Loss of Cell Adhesion to Laminin. J. Biol. Chem. 264 (36), 21806–21811. doi:10.1016/s0021-9258(20)88255-6
Hemler, M. E. (1990). VLA Proteins in the Integrin Family: Structures, Functions, and Their Role on Leukocytes. Annu. Rev. Immunol. 8 (1), 365–400. doi:10.1146/annurev.iy.08.040190.002053
Hornak, V., Abel, R., Okur, A., Strockbine, B., Roitberg, A., and Simmerling, C. (2006). Comparison of Multiple Amber Force fields and Development of Improved Protein Backbone Parameters. Proteins 65, 712–725. doi:10.1002/prot.21123
Hoyer, B., Bernhardt, A., Lode, A., Heinemann, S., Sewing, J., Klinger, M., et al. (2014). Jellyfish Collagen Scaffolds for Cartilage Tissue Engineering. Acta Biomater. 10 (2), 883–892. doi:10.1016/j.actbio.2013.10.022
Hussein, H. A. M., Walker, L. R., Abdel-Raouf, U. M., Desouky, S. A., Montasser, A. K. M., Akula, S. M., et al. (2015). Beyond RGD: Virus Interactions with Integrins. Arch. Virol. 160, 2669–2681. doi:10.1007/s00705-015-2579-8
Jahn, H. A., Teller, E., and Donnan, F. G. (1937). Stability of Polyatomic Molecules in Degenerate Electronic States - I. Orbital Degeneracy. Proc. R. Soc. Lond. Ser. A - Math. Phys. Sci. 161 (905), 220–235.
Jakalian, A., Jack, D. B., and Bayly, C. I. (2002). Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: II. Parameterization and Validation. J. Comput. Chem. 23, 1623–1641. doi:10.1002/jcc.10128
Kanakis, D., Lendeckel, U., Theodosiou, P., Dobrowolny, H., Mawrin, C., Keilhoff, G., et al. (2013). ADAM 12: a Putative Marker of Oligodendrogliomas. Dis. Markers 34 (2), 81–91. doi:10.3233/DMA-120953
Krieger, E., Dunbrack, R. L., Hooft, R. W. W., and Krieger, B. (2012). Assignment of Protonation States in Proteins and Ligands: Combining pKa Prediction with Hydrogen Bonding Network Optimization. Methods Mol. Biol. 819, 405–421. doi:10.1007/978-1-61779-465-0_25
Krieger, E., Nielsen, J. E., Spronk, C. A. E. M., and Vriend, G. (2006). Fast Empirical pKa Prediction by Ewald Summation. J. Mol. Graphics Model. 25, 481–486. doi:10.1016/j.jmgm.2006.02.009
Krieger, E., and Vriend, G. (2015). New Ways to Boost Molecular Dynamics Simulations. J. Comput. Chem. 36, 996–1007. doi:10.1002/jcc.23899
Krieger, E., and Vriend, G. (2014). YASARA View-Molecular Graphics for All Devices-From Smartphones to Workstations. Bioinformatics 30, 2981–2982. doi:10.1093/bioinformatics/btu426
Lee, J. L., and Streuli, C. H. (2014). Integrins and Epithelial Cell Polarity. J. Cel Sci 127 (15), 3217–3225. doi:10.1242/jcs.146142
Legault, C. Y. (2009). CYLview Visualization and Analysis Software for Computational Chemistry. Sherbrooke, Canada: Université de Sherbrooke. Available at: https://www.cylview.org/.
Lenthe, J. H., den Boer, D. H. W., Havenith, R. W. A., Schauer, R., and Siebert, H.-C. (2004). Ab Initio calculations on Various Sialic Acids Provide Valuable Information about Sialic Acid-specific Enzymes. J. Mol. Struct. THEOCHEM 677 (1), 29–37. doi:10.1016/j.theochem.2004.01.013
Maier, J. A., Martinez, C., Kasavajhala, K., Wickstrom, L., Hauser, K. E., and Simmerling, C. (2015). ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theor. Comput. 11, 3696–3713. doi:10.1021/acs.jctc.5b00255
Malric, L., Monferran, S., Gilhodes, J., Boyrie, S., Dahan, P., Skuli, N., et al. (2017). Interest of Integrins Targeting in Glioblastoma According to Tumor Heterogeneity and Cancer Stem Cell Paradigm: an Update. Oncotarget 8 (49), 86947–86968. doi:10.18632/oncotarget.20372
Marsico, G., Russo, L., Quondamatteo, F., and Pandit, A. (2018). Glycosylation and Integrin Regulation in Cancer. Trends Cancer 4, 537–552. doi:10.1016/j.trecan.2018.05.009S
Martinez-Olivera, R., Datsi, A., Stallkamp, M., Köller, M., Kohtz, I., Pintea, B., et al. (2018). Silencing of the Nucleocytoplasmic Shuttling Protein Karyopherin A2 Promotes Cell-Cycle Arrest and Apoptosis in Glioblastoma Multiforme. Oncotarget 9 (71), 33471–33481. doi:10.18632/oncotarget.26033
McCarthy, E. M., Floyd, H., Addison, O., Zhang, Z. J., Oppenheimer, P. G., and Grover, L. M. (2018). Influence of Cobalt Ions on Collagen Gel Formation and Their Interaction with Osteoblasts. ACS Omega 3, 10129–10138. doi:10.1021/acsomega.8b01048
Miertuš, S., Scrocco, E., and Tomasi, J. (1981). Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of Ab Initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 55 (1), 117–129.
Miertus̃, S., and Tomasi, J. (1982). Approximate Evaluations of the Electrostatic Free Energy and Internal Energy Changes in Solution Processes. Chem. Phys. 65 (2), 239–245. doi:10.1016/0301-0104(82)85072-6
Nango, E., Kumasaka, T., Hirayama, T., Tanaka, N., and Eguchi, T. (2008). Structure of 2-Deoxy-Scyllo-Inosose Synthase, a Key Enzyme in the Biosynthesis of 2-Deoxystreptamine-Containing Aminoglycoside Antibiotics, in Complex with a Mechanism-Based Inhibitor and NAD+. Proteins 70 (2), 517–527. doi:10.1002/prot.21526
Petridis, A. K., Nikolopoulos, S. N., and El-Maarouf, A. (2011). Physical and Functional Cooperation of Neural Cell Adhesion Molecule and β1-integrin in Neurite Outgrowth Induction. J. Clin. Neurosci. 18, 1109–1113. doi:10.1016/j.jocn.2010.12.047
Philips, J. J., Hudspeth, M. A., Browne, P. M., and Peralta, J. E. (2010). Basis Set Dependence of Atomic Spin Populations. Chem. Phys. Lett. 495 (1-3), 146–150. doi:10.1016/j.cplett.2010.06.046
Pirilä, L., and Heino, J. (1996). Altered Integrin Expression in Rheumatoid Synovial Lining Type B Cells: In Vitro Cytokine Regulation of α1β1, α6β1, and αVβ5 Integrins. J. Rheumatol. 23, 1691–1698.
Racine-Samson, L., Rockey, D. C., and Bissell, D. M. (1997). The Role of α1β1 Integrin in Wound Contraction. J. Biol. Chem. 272 (49), 30911–30917. doi:10.1074/jbc.272.49.30911
Ruiz, E., Cirera, J., and Alvarez, S. (2005). Spin Density Distribution in Transition Metal Complexes. Coord. Chem. Rev. 249 (23), 2649–2660. doi:10.1016/j.ccr.2005.04.010
Schäfer, A., Horn, H., and Ahlrichs, R. (1992). Fully Optimized Contracted Gaussian Basis Sets for Atoms Li to Kr. J. Chem. Phys. 97 (4), 2571–2577. doi:10.1063/1.463096
Sen, M., Koksal, A. C., Yuki, K., Wang, J., and Springer, T. A. (2018). Ligand- and Cation-Induced Structural Alterations of the Leukocyte Integrin LFA-1. J. Biol. Chem. 293 (17), 6565–6577. doi:10.1074/jbc.ra117.000710
Sharma, S., Shekhar, S., Sharma, B., and Jain, P. (2020). Decoding Glycans: Deciphering the Sugary Secrets to Be Coherent on the Implication. RSC Adv. 10, 34099–34113. doi:10.1039/D0RA04471G
Siebert, H.-C., Burg-Roderfeld, M., Eckert, T., Stötzel, S., Kirch, U., Diercks, T., et al. (2010). Interaction of the α2A Domain of Integrin with Small Collagen Fragments. Protein Cell 1 (4), 393–405. doi:10.1007/s13238-010-0038-6
Siebert, H.-C., Tajkhorshid, E., and Dabrowski, J. (2001). Barrier to Rotation Around the Csp2-Csp2 Bond of the Ketoaldehyde Enol Ether MeC(O)CHCH−OEt as Determined by 13C NMR and Ab Initio Calculations. J. Phys. Chem. A. 105 (37), 8488–8494. doi:10.1021/jp004476g
Stötzel, S., Schurink, M., Wienk, H., Siebler, U., Burg-Roderfeld, M., Eckert, T., et al. (2012). Molecular Organization of Various Collagen Fragments as Revealed by Atomic Force Microscopy and Diffusion-Ordered NMR Spectroscopy. ChemPhysChem 13, 3117–3125. doi:10.1002/cphc.201200284
Tsvetkov, Y. E., Burg-Roderfeld, M., Loers, G., Ardá, A., Sukhova, E. V., Khatuntseva, E. A., et al. (2012). Synthesis and Molecular Recognition Studies of the HNK-1 Trisaccharide and Related Oligosaccharides. The Specificity of Monoclonal Anti-HNK-1 Antibodies as Assessed by Surface Plasmon Resonance and STD NMR. J. Am. Chem. Soc. 134, 426–435. doi:10.1021/ja2083015
Van Agthoven, J. F., Shams, H., Cochran, F. V., Alonso, J. L., Kintzing, J. R., Garakani, K., et al. (2019). Structural Basis of the Differential Binding of Engineered Knottins to Integrins αVβ3 and α5β1. Structure 27 (9), 1443–1451. doi:10.1016/j.str.2019.06.011
Vargas, A., Zerara, M., Krausz, E., Hauser, A., and Lawson Daku, L. M. (2006). Density-Functional Theory Investigation of the Geometric, Energetic, and Optical Properties of the Cobalt(II)tris(2,2'-bipyridine) Complex in the High-Spin and the Jahn−Teller Active Low-Spin States. J. Chem. Theor. Comput. 2 (5), 1342–1359. doi:10.1021/ct6001384
Wang, J., Wolf, R. M., Caldwell, J. W., Kollman, P. A., and Case, D. A. (2004). Development and Testing of a General Amber Force Field. J. Comput. Chem. 25, 1157–1174. doi:10.1002/jcc.20035
Xiong, J.-P., Stehle, T., Zhang, R., Joachimiak, A., Frech, M., Goodman, S. L., et al. (2002). Crystal Structure of the Extracellular Segment of Integrin αVβ3 in Complex with an Arg-Gly-Asp Ligand. Science 296 (5565), 151–155. doi:10.1126/science.1069040
Yanai, T., Tew, D. P., and Handy, N. C. (2004). A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3lyp). Chem. Phys. Lett. 393 (1), 51–57. doi:10.1016/j.cplett.2004.06.011
Zhang, R., Eckert, T., Lütteke, T., Hanstein, S., Scheidig, A., Bonvin, A. M., et al. (2016). Structure-Function Relationships of Antimicrobial Peptides and Proteins with Respect to Contact Molecules on Pathogen Surfaces. Curr. Top. Med. Chem. 16 (1), 89–98. doi:10.2174/1568026615666150703120753
Zhang, R., Jin, L., Zhang, N., Petridis, A. K., Eckert, T., Scheiner-Bobis, G., et al. (2019). The Sialic Acid-dependent Nematocyst Discharge Process in Relation to its Physical-Chemical Properties Is a Role Model for Nanomedical Diagnostic and Therapeutic Tools. Mar. Drugs 17 (8), 469. doi:10.3390/md17080469
Zhang, R., Loers, G., Schachner, M., Boelens, R., Wienk, H., Siebert, S., et al. (2016). Molecular Basis of the Receptor Interactions of Polysialic Acid (polySia), polySia Mimetics, and Sulfated Polysaccharides. ChemMedChem 11 (9), 990–1002. doi:10.1002/cmdc.201500609
Keywords: computational chemistry, computational biophysics, receptor-ligand binding, electronic structure, transition metal chemistry, Jahn-Teller-distortion, neuroblastoma cells, NCAM-beta1 integrin interactions
Citation: Eckert T, von Cosel J, Kamps B, Siebert H-C, Zhang R, Zhang N, Gousias K, Petridis AK, Kanakis D and Falahati K (2021) Evidence for Quantum Chemical Effects in Receptor-Ligand Binding Between Integrin and Collagen Fragments — A Computational Investigation With an Impact on Tissue Repair, Neurooncolgy and Glycobiology. Front. Mol. Biosci. 8:756701. doi: 10.3389/fmolb.2021.756701
Received: 10 August 2021; Accepted: 22 October 2021;
Published: 16 November 2021.
Edited by:
Vladimir I. Polshakov, Lomonosov Moscow State University, RussiaReviewed by:
Andrey Golovin, Lomonosov Moscow State University, RussiaCopyright © 2021 Eckert, von Cosel, Kamps, Siebert, Zhang, Zhang, Gousias, Petridis, Kanakis and Falahati. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas Eckert, VGhvbWFzLkVja2VydEB2ZXRtZWQudW5pLWdpZXNzZW4uZGU=; Konstantin Falahati, RmFsYWhhdGlAcmlzY2MuZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.