Nascent Folding of Proteins Across the Three Domains of Life

We study the nascent behavior of three model coarse-grained proteins in six rigid all-atom structures representing ribosomes that come from three domains of life. The synthesis of the proteins is implemented as a growth process. The geometry of the exit tunnel is quantified and shown to differ between the domains of life: both in volume and the size of constriction sites. This results in different characteristic times of capture within the tunnel and various probabilities of the escape. One of the proteins studied is the bacterial YibK which is knotted in its native state. A fraction of the trajectories results in knotting and the probability of doing so is largest for the bacterial ribosomes. Relaxing the condition of the rigidness of the ribosomes should result in a better avoidance of trapping and better proper folding.

Introduction

Ribosome is a biomolecular nanomachine that performs protein synthesis at its peptidyl-transferase center (PTC) as directed by an mRNA template. The schematic picture of the protein being created by the ribosome is presented in Figure 1. In terms of the evolution, the PTC has been recognized as the earliest part of the ribosome (Prosdocimi et al., 2020). Ribosome itself is an aggregate made of 2–6 RNA chains and around 50 proteins comprising altogether between 100,000 and 220,000 atoms. Six examples of the ribosomal structures, together with some parameters of their description, are listed in Table 1. Ribosomes are involved in the regulation of translation and they influence the folding process (Kaiser et al., 2011). The synthesis takes place at the rate that depends on the domain of life. For prokaryotes, it is about 20 amino acids (Young and Bremer, 1976) and for eukaryotes four amino acids (Boström et al., 1986; Ingolia et al., 2011). The PTC secretes the nascent protein into the exit tunnel that ends with a “mouth” that opens into the surrounding solvent. After the detachment from the center, the protein escapes the ribosome in less than 1 ms (Bui and Hoang, 2020; Nissley et al., 2020). The movement of the protein toward the solvent gets started at the PTC and then it is influenced mostly by diffusion, interactions with the walls of the tunnel, and the gain in the entropy associated with the escape. The walls of the tunnel are rough and its diameter varies between 10 and 20 Å (Voss et al., 2006; Cabrita et al., 2010; Frank and Gonzalez, 2010). It has been established (Melnikov et al., 2012; Dao Duc et al., 2019; Liutkute et al., 2020) that the very geometry of the tunnel depends on the domain of life. In particular, we find that the diameter in the bacterial ribosomes can reach even 30 Å. This happens at the branching points in the tunnel.

FIGURE 1

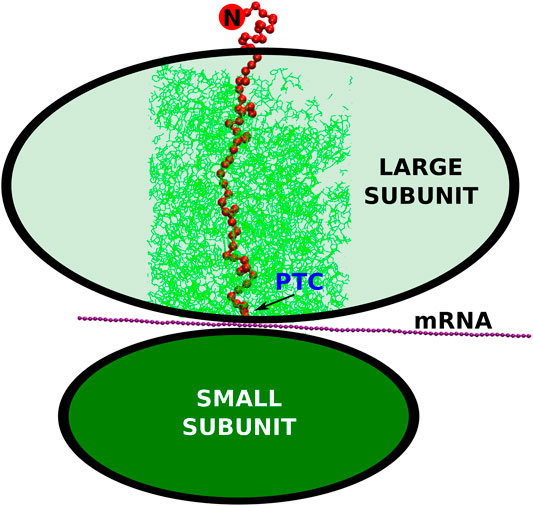
FIGURE 1. The schematic representation of the small and large ribosomal subunits (the green ovals). The arrow points to the peptidyl-transferase center where the conversion of the nucleic acid genetic information (mRNA) into the polypeptide (the red string) takes place. The cylindrical cut-out, considered in our simulations, is marked by the thin, green lines. The N-terminus of the synthesized protein is marked by the red circle with the letter “N”.

TABLE 1

TABLE 1. Six ribosomal structures considered in our analysis.

Here, we present results of a theoretical study in which we probe the impact of the nature of the ribosome on protein folding in a coarse-grained model. Specifically, we consider six ribosomes from three domains of life, bacteria, archea and eukarya, and elucidate the difference in behavior of three model bacterial proteins in the six ribosomal tunnels. The bacterial ribosomes considered correspond to structures PDB:5NJT (Beckert et al., 2017) and PDB:5AFI (Fischer et al., 2015) that originate from B. subtilis and E. coli respectively. The remaining structures and their origins are listed in Table 1. The first protein selected is the streptococcal protein G (Gronenborn et al., 1991) (PDB:1GB1) of 56 residues that is a common object of simulational studies. The second is YibK (Lim et al., 2003) (PDB:1J85) derived from Haemophilus influenze. YibK consists of 156 residues. The reason to consider it is that its native structure contains the deep trefoil knot between sites 75 and 119. It means that the backbone of the protein entangles themselves in to a knot. In the case of deeply knotted proteins, the transient state during the knotting process is often a slipknot. It is a conformation in which one of the protein termini adopts a hairpin-like conformation that threads a loop formed by the remainder of the chain (Faísca, 2015). The ribosomal action has been proposed (Chwastyk and Cieplak, 2015) to solve the puzzle of how the deeply knotted proteins form. An additional mechanism that may enhance knotting still further involves confinement generated by post-translational action of chaperonins (Takagi et al., 2003; Mallam and Jackson, 2011; Soler et al., 2016; Zhao et al., 2017; Especial et al., 2019; Chwastyk et al., 2021). It should be noted that the ribosome itself also provides a confining space that may favor formation of secondary structures (Elcock, 2006). The last protein we consider is Trp-Cage miniprotein (PDB:1L2Y) (Neidigh et al., 2002). It is composed of 20 amino acids and its small size allows it to fold near the PTC.

Theoretical studies of cotranslational folding, especially when knotting is involved, should start by considering simple coarse-grained structure-based models (see, e.g., ref (Sikora et al., 2009)) as they introduce a bias toward the native state. In our previous paper (Chwastyk and Cieplak, 2015), the mouth of the ribosome has been represented as an infinite repulsive plate which grows proteins by starting from the N-terminus. The plate has turned out to be positioning the planar knot loop of YibK (between sites 75–95) in a way that allows for formation of a C-terminal slipknot and then threading of the C-terminus through the loop on detachment. The effectiveness of this mechanism depends on the scheme to derive the contact map and it increases with time separation between the successive events of the emergence of new residues, t_w. The longest used was 5,000 τ where τ is of order 1 ns—the characteristic time scale of the CG simulation (Sikora et al., 2009). A better approach is to implement a steady growth at the PTC (Hoang and Cieplak, 2000; Krobath et al., 2013; Bui and Hoang, 2020).

Another simple model (Dabrowski-Tumanski et al., 2018) represents the exit tunnel as a smooth funnel-like potential. It is combined with an axial force that acts on the fully formed sequence placed near the PTC and pushes it toward the mouth. Necessarily, this force must induce an acceleration which is likely spurious. This approach was used for a large deeply knotted protein Tp0624 of 421 residues. The crucial ingredient in achieving high effectiveness in knotted folding was adding attractive centers at the mouth of the exit tunnel. However, we find that such centers generate trapping at the mouth.

Making comparisons between the domains of life, however, cannot be based on the ribosome models that are just generic. Here, we consider a coarse-grained model (Chwastyk et al., 2021) in which the growth takes place at the PTC and the tunnel has the shape that is determined by the structure file of the ribosome so that it is sensitive to the species (In ref. (Chwastyk et al., 2021), we have discussed the bacterial structure PDB:4V4J from Thermus thermophilus.). We first compare the geometries of the tunnels arising in the six ribosomes of Table 1 and show how they differ across the domains of life. We then compare the folding processes and show that the bacterial ribosomes enhance the folding and knotting processes stronger than the other ribosomes. The relatively small average diameters of the archaea and eukarya ribosomal exit tunnels make the protein growing process difficult. The most efficient folding process happens within the ribosomal structure which is natural for a given protein.

The Geometry of the Ribosomal Exit Tunnels

The complexity of the full ribosomal structure makes it hard to include all of the atoms in the simulations. Thus we limit the number of relevant atoms to a cylindrical cut-out of radius R_R = 70 Å around the ribosomal exit tunnel as illustrated in Figures 2, 3. The cylinder originates at the plane that goes through the PTC. It is oriented towards the mouth of the ribosome as shown in Figure 2 against the background of the full ribosome. The structures around the ribosomal exit tunnel incorporated in our simulations are presented in Figure 4. Each cylinder is composed of rRNA and ribosomal proteins atoms. The specific number of nucleic acid and protein chains are listed in Table 1. Here, we consider these atoms to be fixed rigidly during the dynamics but an improved model should allow for their flexibility.

FIGURE 2

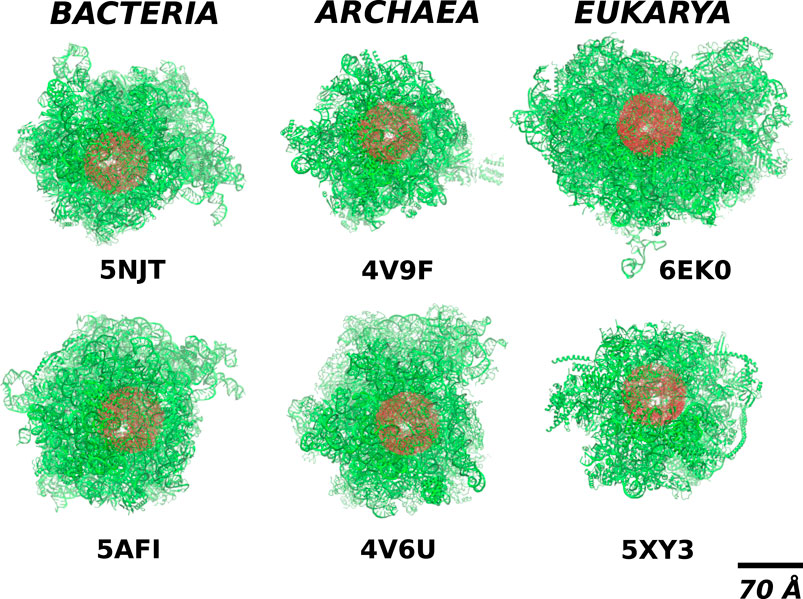
FIGURE 2. The location of the cylindrical cut-out (the red shadow) of radius R_R = 70Å within the full structure of ribosomes (the green colour) from different domains of life. The white spot within the red blob shows the position of the exit tunnel.

FIGURE 3

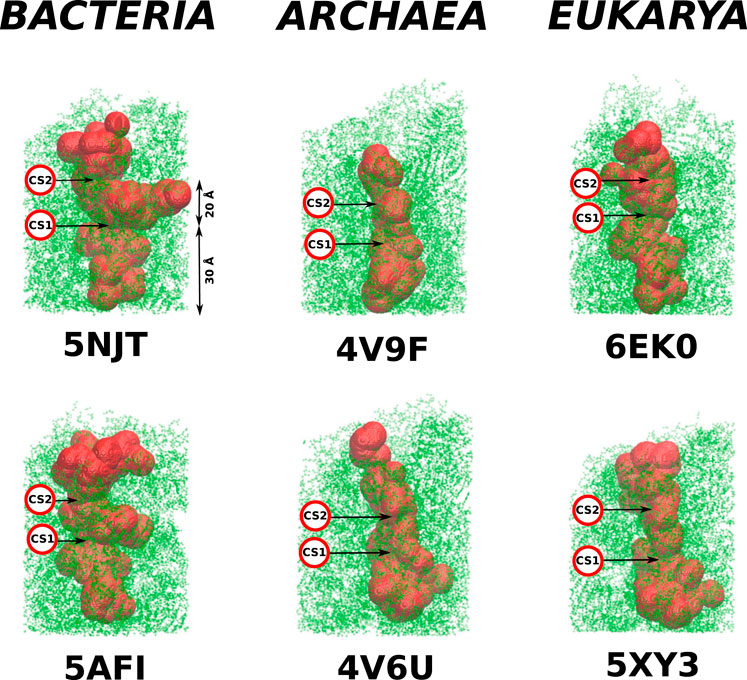
FIGURE 3. Structures of the cylindrical cut-outs around the ribosomal exit tunnels from the three different domains of life. Each of the six panels shows the all-atom representation of the cylinder. The colors are meant just to generate a sense of perspective. The structures shown below the main picture represents the very exit of the cylinder. Up to five colors are used to indicate the vertical positions. The ball-like structure on the right of the cylinder represents the top view of the exit mouth.

FIGURE 4

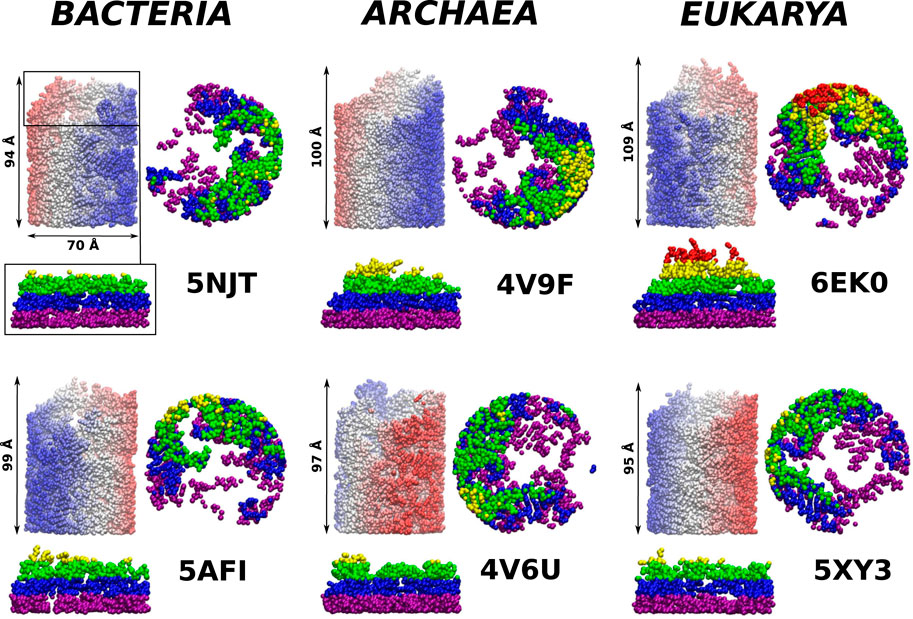
FIGURE 4. The ribosomal exit tunnels (the red shape) detected by the SPACEBALL algorithm (Chwastyk et al., 2014; Chwastyk et al., 2016a; Chwastyk et al., 2016b) within the ribosomal structures from different domains of life. The arrows point to the constriction sites (CS1 and CS2). The green shadow represents the all atoms that are present in the cut-out part of the ribosomes. The PTC is always at the bottom of each panel.

The location of the PTC was determined based on the data presented by Dao Duc et al. (2019)—it is found at the extension of the L22 and L4 proteins (Trylska, 2009; Dao Duc et al., 2019). In order to identify the tunnels and their volumes, we used the SPACEBALL algorithm (Chwastyk et al., 2014; Chwastyk et al., 2016a; Chwastyk et al., 2016b). The algorithm involves sending probing particles along main directions of a grid (at ten rotations of the ribosome) and checking which grid sites are accessible. Usually, one takes the radius of the probing particles to be 1.4 Å which is equal to the diameter of the water molecule. Here, we use primarily the radius of 4 Å in order not to penetrate the all-atom representation of the walls of the tunnel, but we also make comparisons to calculations done with the radius of 3 Å.

Our calculated volumes are somewhat smaller in comparison to the results obtained by Dao Duc et al. (2019). They got (3.85 ± 0.37)×10⁴ ų by considering 10 bacteria and (2.78 ± 0.13)×10⁴ ų for nine eukarya. When we decreased the radius of our probe to 3 Å we got very similar results, listed in Table 1. The difference in our algorithm is that we do not specify the position of the tunnel before undertaking the volume calculation. In addition, we make rotations of the grid. In the first step, Dao Duc et al. (2019) search for the tunnel position by using MOLE 2.0 (Sehnal et al., 2013) program and then implement HOLLOW (Ho and Gruswitz, 2008) approach to determine the volume. The HOLLOW approach is very similar to our method but for well defined structure. This allows for the usage of smaller probes and thus to obtain larger volumes.

We observe that the bacterial ribosomes are associated with tunnels of the largest volume and are thus expected to obstruct the motion toward the exit the least. The SPACEBALL-derived tunnel spaces are shown in Figure 4 in the red color. Despite the existence of pronounced side channels, the bacterial tunnels come with much fewer regions that are difficult to access. This was confirmed just by looking at the detected exit tunnel and by calculating the surface-area-to-volume ratio for the exit tunnels (see Table 1). The smallest value of this parameter was obtained for the bacterial exit tunnels and the largest one, for the eukaryotic tunnels.

The details of the cylindrical structures are shown in Figure 3. They are focused on the mouth regions and demonstrate that the openings are fairly irregular—they are not smooth funnel-like surfaces. The panels in Figure 3 also show the vertical distances from the PTC plane to the most distant atoms. These distances vary between 94 Å and 109 Å and do not distinguish between the domains of life.

As in Dao Duc et al. (2019), we find that there are several constriction sites (CS) in the ribosomes. The first of these, CS1, is located around 30 Å from the PTC for each of the six ribosomes studied. The second, CS2, is at 20 Å farther away from CS1. The width of CS2 depends on the domain of life: it is narrow in the eukaryotic case (the radius is around 8 Å), a bit wider for the archaea ribosomes (the average radius is around 11 Å), and still wider for the bacterial case (the average radius is around 15 Å). The locations of the CS1 and CS2 are marked in Figure 4.

Cotranslational Folding

Description of the Molecular Dynamics Model

The protein is modeled within the structure-based approach, as described in refs (Sulkowska and Cieplak, 2008; Sikora et al., 2009). with a chirality potential being responsible for the backbone stiffness. The contact interactions are selected by using the overlap criterion (Wołek et al., 2015) between the atoms of the residues as determined in the fully folded native state. The contacts correspond to the potential wells between the effective residues are located at the α-C atoms. The depth of the wells is denoted as ε. The remaining interactions are softly repulsive with the characteristic length of 4 Å. When one starts from an extended conformation and studies folding then the process is declared accomplished if all contacts get established. i.e., the distance between the residues involved becomes smaller than 1.5 σ, where σ denotes the width of the corresponding well. The temperature is controlled by random forces and the room temperature, T_R is around 0.35ε/k_B. Each of the ribosomal atoms is a source of the soft repulsive potential that is cut at 4 Å and has the amplitude of ε.

Dynamically, the bottom of the cylinder is represented by a repulsive wall with the potential $\frac{3\sqrt{3}}{2}\epsilon {\left({\sigma }_0/z\right)}^9$, where z denotes the distance away from the plate and ${\sigma }_0=4\cdot 2^{-1/6}$. This wall prevents making any backward steps. The models that incorporate the sequential growth consider it taking place either at the PTC or, effectively, at the mouth.

The most common practice is to place a fully synthesized chain near the PTC (Frank and Gonzalez, 2010; Elcock, 2006; Dabrowski-Tumanski et al., 2018; Nissley et al., 2020) and then to monitor folding (Nilsson et al., 2015; Kudva et al., 2018; Bock et al., 2018). The exit through the mouth can be helped computationally by switching from a CG simulation to a steered all-atom molecular dynamics approach with a steady motion of a pulling cantilever (Nissley et al., 2020). Another method is to apply a constant force (Dabrowski-Tumanski et al., 2018). Here, we incorporate the sequential growth at the PTC. Each of the amino acids emerges with some time interval after the previous one created earlier. The direction of the amino acid motion is given by the repulsive potential accelerating the created bead toward the exit of the tunnel. Since the mRNA is translated from the 5’ to 3’ ends, the proteins are synthesized from the N terminus to the C terminus, so the N terminus emerges first, as presented in Figure 1. This method is similar to the one considered in ref (Bui and Hoang, 2020). There are several differences, however: 1) all protein and RNA atoms of the walls provide repulsion (not just the α-C atoms), 2) the backward motion is prevented by the repulsion from the bottom wall, 3) the growth is implemented in a quasi-continuous fashion, 4) in one variant of the model, used for the YibK protein, we introduce electrostatics-mimicking contacts at the mouth of the ribosome, similarly to Dabrowski-Tumanski et al. (2018). The strength of these contacts is the same as in the case of the intramolecular contacts. We declare that the contacts can be created between two amino acids with opposed electric charge. We have found that the presence of such contacts do not impact the knotting process, but impedes the dissociation of the protein from the ribosome, so the results presented here have been obtained without these attractive contacts.

We represent our results as in Figure 5. It shows the histograms of distances of the N-terminal points of the proteins awya from the PTC. The bin size was chosen so that the first bin corresponds to the trajectories that are stuck between the PTC and CS1, the second one—between CS1 and CS2 and the others—the trajectories that resulted in proteins leaving the ribosome.

FIGURE 5

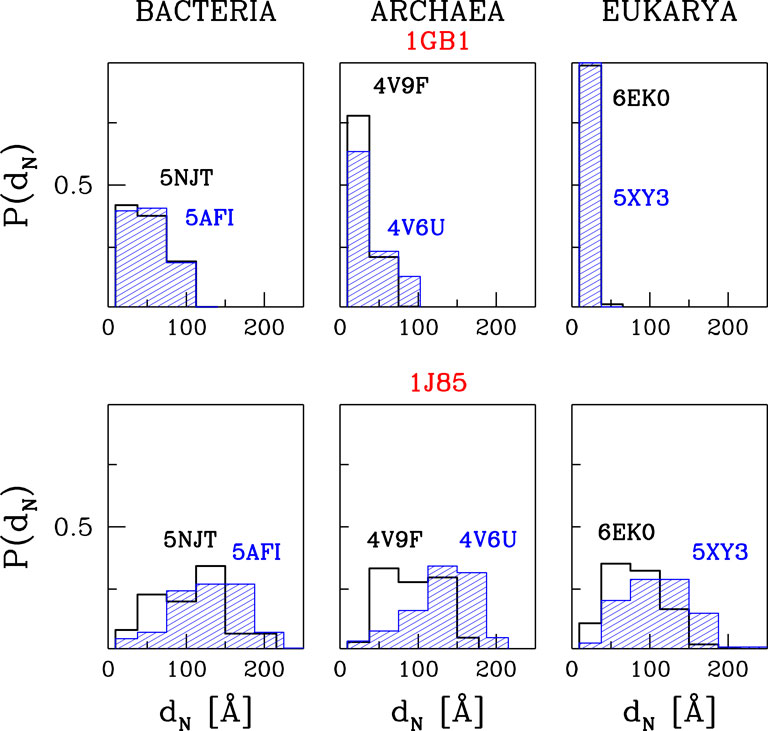
FIGURE 5. The histograms of the distances between PTC and the N-terminus after time t_E of simulations at T_R = 0.35ε/k_B and with t_w = 100τ. The results are for three different domains of life. The upper panels are for 1GB1, with t_E = 50000τ, and the lower ones for 1J85, with t_E = 150000τ.

Protein G

The upper panels of Figure 5 are for protein G. The temperature is equal to T_R and t_w is set to 100 τ, similarly to ref. (O'Brien et al., 2011). The panels show that the most difficult part of the movement of the growing protein is to pass through constriction CS1. For the two eukaryotic ribosomes, almost all of the trajectories get stuck at CS1. In the case of the two archaea ribosomes, this happens with 60–80% of the trajectories and around 20% get stuck at CS2. However, the bacterial ribosomes offer an easier passage for protein G: 40% of the trajectories stop at CS1, another 40% at CS2. Thus around 20% reach the mouth of the ribosome. Folding takes place after the exit and the median folding time of protein G in the 5NJT and 5AFI ribosomes is 7747τ and 7566τ respectively. An illustration of the various stages of the process is given in Figure 6. The folding process is considered to be accomplished when all native contacts are established for the first time (the distance between the corresponding α-C atoms is smaller than 1.5 σ where σ is the length parameter associated with the potential well. We considered 90 folding trajectories for each of the ribosomes.

FIGURE 6

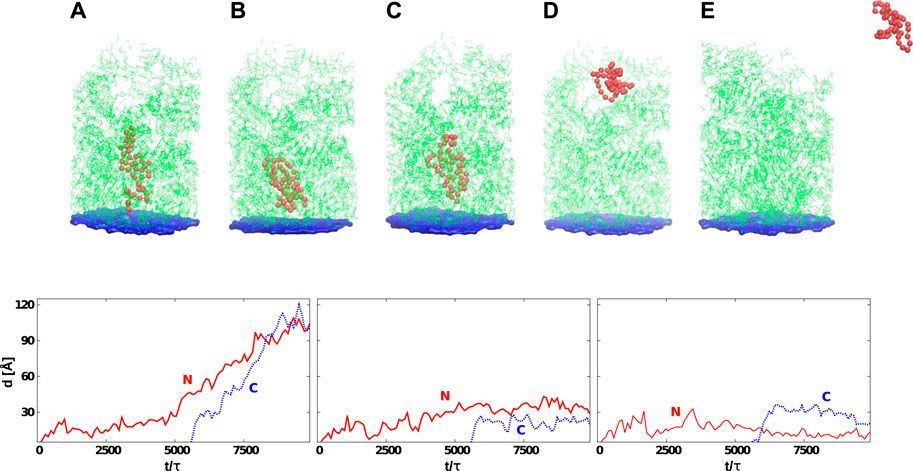
FIGURE 6. Top: Six snapshots of protein G (the red color) at various stages of its development that start at its synthesis (A) and, in many cases, end with the detachment (E). The average time needed by the ribosome to release the protein depends on t_w. The exit tunnel (in green) corresponds to the eukaryotic structure PDB:6EK0. The blue plane represents the origin of the repulsive potential. The PTC is located at the center of the plane. In (B), the protein is stuck permanently at the CS1. In (C), the jamming is at CS2. In (D), the protein has reached the mouth of the tunnel. Bottom: Distances between the PTC and the N-terminus (solid-red line) or C-terminus (dotted-blue line) as a function of time. The left panel corresponds to the situation presented in (D) (protein is leaving the ribosome). The graph in the center corresponds to the situation shown in (C) (the protein gets stuck at CS2). The last graph shows the situation corresponding to (B) (the protein is stuck between PTC and CS1). In all cases, the C-terminus gets released after the synthesis of the 56-residue protein which, for t_w = 100τ, corresponds to 5,600 τ.

When t_w is increased to 500τ, the number of trajectories that get stuck at the CS1 becomes similar for the two eukaryotic ribosomes and for the 4V6U archaea ribosome. However, it gets halved for the bacterial ribosomes while it increases from 80 to 100% for 4V9F (archaea). A further increase in t_w results in an increased probability of stopping at CS1 because there is more time to penetrate the exit tunnel nooks. The eukarya ribosomes do not allow for proteins leaving the ribosomal exit tunnel. We expect that when the walls are made flexible the protein will have a better chance of negotiating the constrictions at any t_w, but this remains to be demonstrated. These results are based on 60 trajectories for each ribosome.

Protein YibK

We now consider the knotted YibK protein. The knot ends are at LEU-75 and LYS-119 in the native state. We examine the impact of the full ribosomal structure on the knotting process. Unfortunately, it was impossible to reach t_w = 5000τ, as in ref (Chwastyk and Cieplak, 2015). that this time gives the highest value of the percentage-wise success of reaching the properly knotted folded conformation. t_w longer than 100τ decreases the number of trajectories with the full exit of the protein. To be able to examine the knotting process we did a numerical trick and we allowed for a fast growth (with t_w = 100τ) at the beginning of the protein synthesis and then switched to a slower process with t_w = 1000τ when the process reached LEU-75. This trick generates between 63 to 70 trajectories out of 100, depending on the ribosome, that manage to escape from the tunnel.

For this set of successful trajectories, about 10% resulted in formation of non-native temporal knots with one knot end at LYS-119. Another ∼10% resulted in temporal knots with improperly located knot ends. We expect, however, that an extension of the simulation will eventually move the ends to the proper locations. The most interesting situation is observed for the 5AFI ribosome. Only in this case, 1% of 1,000 trajectories resulted with the properly folded and knotted conformations. The knotting mechanism was based on a slipknot transient conformation, the same as observed in ref. (Chwastyk and Cieplak, 2015). In addition, 10% of the trajectories resulted in one temporal knot end located at LYS-119 and 5% of the trajectories with temporal knot elsewhere. Again, an extension of the simulations is expected to move the knot ends to their native locations. When we increased the temperature from T_R to 0.45 ε/k_B the total number of trajectories that escape the tunnel got decreased, but the success in folding and knotting was similar to the one at T_R.

Trp-Cage Miniprotein

In the case of the very short protein (1L2Y) which we also examined, all of the 100 trajectories got stuck at the CS1. Nevertheless, there is enough space between PTC and CS1 for this short protein to accomplish correct folding. This happens for all trajectories and the average folding time is 1979τ. The average here is over the trajectories and the six ribosomes.

Conclusion

We have demonstrated the existence of differences in the dynamical behavior of nascent proteins across the domains of life. These differences result from the dissimilarities in the ribosomal geometries. The tight eukarya ribosomal exit tunnels impede the protein movement towards the exit. The wider constrictions sites found in the two other domains of life allow for proteins for an easier squeezing through away from the PTC. It is important to mention that the percentage-wise success of reaching the properly knotted and folded conformations was found to be the highest for 5AFI ribosome that originates from the E. coli bacterium. The YibK protein is also bacterial (Haemophilus influenzae). The two bacteria have one common ancestor (de Rosa and Labedan, 1998) which suggests that the 5AFI ribosome is evolution-related to the one that makes YibK. It is thus natural to consider YibK in this ribosome and expect the best folding results in this case.

If the longer sequences manage to exit the mouth and start making globular structures then this process, in principle, should be helped by attractive contacts at the mouth by generating an extracting mechanism. However, we find such contacts to be disruptive to the process because they also capture the extracted protein at the mouth. The reason why the attractive patches at the mouth appear to promote knotting in Dabrowski-Tumanski et al. (2018). may be related to the fact that the bulk driving force used also eliminates the capture. This point needs to be elucidated further.

In our current model, the ribosomal molecules are considered to be rigid. Relaxing this condition should result in better escape rates and possibly also in a stronger knotting success. Moreover, it will allow for usage of the all-atom protein model, because right now the side chains block the protein that attempt to squeeze through away from the PTC. The flexibility can be introduced either by connecting the atoms to fixed centers by harmonic springs or by coarse-graining the RNA and protein chains of the ribosome (Kudva et al., 2018). We hope to address these issues in future research. We also plan to use the Dynamical Structure-Based model (Mioduszewski and Cieplak, 2018) to consider the exit times for selected intrinsically disordered proteins and study their behavior in the tunnel.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Both authors developed the model and wrote the paper. MCh performed the simulations.

Funding

This work has been supported by the National Science Centre (NCN), Poland, under grant No. 2018/31/B/NZ1/00,047. This work results within the collaboration of the COST Action CA17139 Eutopia. The computer resources were supported by the PL-GRID infrastructure.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Armache, J.-P., Anger, A. M., Márquez, V., Franckenberg, S., Fröhlich, T., Villa, E., et al. (2012). Promiscuous Behaviour of Archaeal Ribosomal Proteins: Implications for Eukaryotic Ribosome Evolution. Nucleic Acids Res. 41, 1284–1293. doi:10.1093/nar/gks1259

PubMed Abstract | CrossRef Full Text | Google Scholar

Beckert, B., Abdelshahid, M., Schäfer, H., Steinchen, W., Arenz, S., Berninghausen, O., et al. (2017). Structure of the Bacillus Subtilis Hibernating 100S Ribosome Reveals the Basis for 70S Dimerization. EMBO J. 36, 2061–2072. doi:10.15252/embj.201696189

PubMed Abstract | CrossRef Full Text | Google Scholar

Bock, L. V., Kolář, M. H., and Grubmüller, H. (2018). Molecular Simulations of the Ribosome and Associated Translation Factors. Curr. Opin. Struct. Biol. 49, 27–35. doi:10.1016/j.sbi.2017.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Boström, K., Wettesten, M., Borén, J., Bondjers, G., Wiklund, O., and Olofsson, S. O. (1986). Pulse-chase Studies of the Synthesis and Intracellular Transport of Apolipoprotein B-100 in Hep G2 Cells. J. Biol. Chem. 261, 13800–13806. doi:10.1016/s0021-9258(18)67090-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bui, P. T., and Hoang, T. X. (2020). Protein Escape at the Ribosomal Exit Tunnel: Effect of the Tunnel Shape. J. Chem. Phys. 153, 045105. doi:10.1063/5.0008292

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabrita, L. D., Dobson, C. M., and Christodoulou, J. (2010). Protein Folding on the Ribosome. Curr. Opin. Struct. Biol. 20, 33–45. doi:10.1016/j.sbi.2010.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Chwastyk, M., Cieplak, M., and Faisca, P. F. N. (2021). Ribosome- and Chaperonin-Assisted Knotting of Proteins. (submitted).

Google Scholar

Chwastyk, M., and Cieplak, M. M. (2015). Cotranslational Folding of Deeply Knotted Proteins. J. Phys. Condens. Matter 27, 354105. doi:10.1088/0953-8984/27/35/354105

PubMed Abstract | CrossRef Full Text | Google Scholar

Chwastyk, M., Jaskólski, M., and Cieplak, M. (2014). Structure-based Analysis of Thermodynamic and Mechanical Properties of Cavity-Containing Proteins - Case Study of Plant Pathogenesis-Related Proteins of Class 10. FEBS J. 281, 416–429. doi:10.1111/febs.12611

PubMed Abstract | CrossRef Full Text | Google Scholar

Chwastyk, M., Jaskólski, M., and Cieplak, M. (2016). The Volume of Cavities in Proteins and Virus Capsids. Proteins 84, 1275–1286. doi:10.1002/prot.25076

PubMed Abstract | CrossRef Full Text | Google Scholar

Chwastyk, M., Panek, E. A., Malinowski, J., Jaskólski, M., and Cieplak, M. (2016). Properties of Cavities in Biological Structures – A Survey of the Protein Data Bank. Front. Mol. Biosci. 7, 591381.

PubMed Abstract | CrossRef Full Text | Google Scholar

Dabrowski-Tumanski, P., Piejko, M., Niewieczerzal, S., Stasiak, A., and Sulkowska, J. I. (2018). Protein Knotting by Active Threading of Nascent Polypeptide Chain Exiting from the Ribosome Exit Channel. J. Phys. Chem. B 122, 11616–11625. doi:10.1021/acs.jpcb.8b07634

PubMed Abstract | CrossRef Full Text | Google Scholar

Dao Duc, K., Batra, S. S., Bhattacharya, N., Cate, J. H. D., and Song, Y. S. (2019). Differences in the Path to Exit the Ribosome across the Three Domains of Life. Nucl. Acids Res. 47, 4198–4210. doi:10.1093/nar/gkz106

PubMed Abstract | CrossRef Full Text | Google Scholar

de Rosa, R., and Labedan, B. (1998). The Evolutionary Relationships between the Two Bacteria Escherichia coli and Haemophilus Influenzae and Their Putative Last Common Ancestor. Mol. Biol. Evol. 15, 17–27. doi:10.1093/oxfordjournals.molbev.a025843

PubMed Abstract | CrossRef Full Text | Google Scholar

Elcock, A. H. (2006). Molecular Simulations of Cotranslational Protein Folding: Fragment Stabilities, Folding Cooperativity, and Trapping in the Ribosome. Plos Comput. Biol. 2, e98. doi:10.1371/journal.pcbi.0020098

PubMed Abstract | CrossRef Full Text | Google Scholar

Especial, J., Nunes, A., Rey, A., and Faísca, P. F. (2019). Hydrophobic Confinement Modulates thermal Stability and Assists Knotting in the Folding of Tangled Proteins. Phys. Chem. Chem. Phys. 21, 11764–11775. doi:10.1039/c9cp01701a

PubMed Abstract | CrossRef Full Text | Google Scholar

Faísca, P. F. N. (2015). Knotted Proteins: A Tangled Tale of Structural Biology. Comput. Struct. Biotechnol. J. 13, 459–468. doi:10.1016/j.csbj.2015.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Fischer, N., Neumann, P., Konevega, A. L., Bock, L. V., Ficner, R., Rodnina, M. V., et al. (2015). Structure of the E. coli Ribosome-EF-Tu Complex at Å Resolution by C S-Corrected Cryo-EM. Nature 520, 567–570. doi:10.1038/nature14275

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank, J., and Gonzalez, R. L. (2010). Structure and Dynamics of a Processive Brownian Motor: the Translating Ribosome. Annu. Rev. Biochem. 79, 381–412. doi:10.1146/annurev-biochem-060408-173330

PubMed Abstract | CrossRef Full Text | Google Scholar

Gabdulkhakov, A., Nikonov, S., and Garber, M. (2013). Revisiting theHaloarcula marismortui50S Ribosomal Subunit Model. Acta Crystallogr. D Biol. Cryst. 69, 997–1004. doi:10.1107/s0907444913004745

CrossRef Full Text | Google Scholar

Gronenborn, A., Filpula, D., Essig, N., Achari, A., Whitlow, M., Wingfield, P., et al. (1991). A Novel, Highly Stable Fold of the Immunoglobulin Binding Domain of Streptococcal Protein G. Science 253, 657–661. doi:10.1126/science.1871600

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, B. K., and Gruswitz, F. (2008). HOLLOW: Generating Accurate Representations of Channel and interior Surfaces in Molecular Structures. BMC Struct. Biol. 8, 49. doi:10.1186/1472-6807-8-49

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoang, T. X., and Cieplak, M. (2000). Molecular Dynamics of Folding of Secondary Structures in Go-type Models of Proteins. J. Chem. Phys. 112, 6851–6862. doi:10.1063/1.481261

CrossRef Full Text | Google Scholar

Ingolia, N. T., Lareau, L. F., and Weissman, J. S. (2011). Ribosome Profiling of Mouse Embryonic Stem Cells Reveals the Complexity and Dynamics of Mammalian Proteomes. Cell 147, 789–802. doi:10.1016/j.cell.2011.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaiser, C. M., Goldman, D. H., Chodera, J. D., Tinoco, I., and Bustamante, C. (2011). The Ribosome Modulates Nascent Protein Folding. Science 334, 1723–1727. doi:10.1126/science.1209740

PubMed Abstract | CrossRef Full Text | Google Scholar

Krobath, H., Shakhnovich, E. I., and Faísca, P. F. N. (2013). Structural and Energetic Determinants of Co-translational Folding. J. Chem. Phys. 138, 215101. doi:10.1063/1.4808044

PubMed Abstract | CrossRef Full Text | Google Scholar

Kudva, R., Tian, P., Pardo-Avila, F., Carroni, M., Best, R. B., Bernstein, H. D., et al. (2018). The Shape of the Bacterial Ribosome Exit Tunnel Affects Cotranslational Protein Folding. eLife 7, e36326. doi:10.7554/eLife.36326

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Guo, Q., Zheng, L., Ji, Y., Xie, Y.-T., Lai, D.-H., et al. (2017). Cryo-EM Structures of the 80S Ribosomes from Human Parasites Trichomonas Vaginalis and Toxoplasma Gondii. Cell Res 27, 1275–1288. doi:10.1038/cr.2017.104

PubMed Abstract | CrossRef Full Text | Google Scholar

Lim, K., Zhang, H., Tempczyk, A., Krajewski, W., Bonander, N., Toedt, J., et al. (2003). Structure of the YibK Methyltransferase fromHaemophilus Influenzae (HI0766): A Cofactor Bound at a Site Formed by a Knot. Proteins 51, 56–67. doi:10.1002/prot.10323

PubMed Abstract | CrossRef Full Text | Google Scholar

Liutkute, M., Samatova, E., and Rodnina, M. V. (2020). Cotranslational Folding of Proteins on the Ribosome. Biomolecules 10, 97. doi:10.3390/biom10010097

PubMed Abstract | CrossRef Full Text | Google Scholar

Mallam, A. L., and Jackson, S. E. (2011). Knot Formation in Newly Translated Proteins Is Spontaneous and Accelerated by Chaperonins. Nat. Chem. Biol. 8, 147–153. doi:10.1038/nchembio.742

PubMed Abstract | CrossRef Full Text | Google Scholar

Melnikov, S., Ben-Shem, A., Garreau de Loubresse, N., Jenner, L., Yusupova, G., and Yusupov, M. (2012). One Core, Two Shells: Bacterial and Eukaryotic Ribosomes. Nat. Struct. Mol. Biol. 19, 560–567. doi:10.1038/nsmb.2313

PubMed Abstract | CrossRef Full Text | Google Scholar

Mioduszewski, Ł., and Cieplak, M. (2018). Disordered Peptide Chains in an α-C-based Coarse-Grained Model. Phys. Chem. Chem. Phys. 20, 19057–19070. doi:10.1039/c8cp03309a

PubMed Abstract | CrossRef Full Text | Google Scholar

Natchiar, S. K., Myasnikov, A. G., Kratzat, H., Hazemann, I., and Klaholz, B. P. (2017). Visualization of Chemical Modifications in the Human 80S Ribosome Structure. Nature 551, 472–477. doi:10.1038/nature24482

PubMed Abstract | CrossRef Full Text | Google Scholar

Neidigh, J. W., Fesinmeyer, R. M., and Andersen, N. H. (2002). Designing a 20-residue Protein. Nat. Struct. Biol. 9, 425–430. doi:10.1038/nsb798

PubMed Abstract | CrossRef Full Text | Google Scholar

Nilsson, O. B., Hedman, R., Marino, J., Wickles, S., Bischoff, L., Johansson, M., et al. (2015). Cotranslational Protein Folding inside the Ribosome Exit Tunnel. Cel Rep. 12, 1533–1540. doi:10.1016/j.celrep.2015.07.065

PubMed Abstract | CrossRef Full Text | Google Scholar

Nissley, D. A., Vu, Q. V., Trovato, F., Ahmed, N., Jiang, Y., Li, M. S., et al. (2020). Electrostatic Interactions Govern Extreme Nascent Protein Ejection Times from Ribosomes and Can Delay Ribosome Recycling. J. Am. Chem. Soc. 142, 6103–6110. doi:10.1021/jacs.9b12264

PubMed Abstract | CrossRef Full Text | Google Scholar

O'Brien, E. P., Christodoulou, J., Vendruscolo, M., and Dobson, C. M. (2011). New Scenarios of Protein Folding Can Occur on the Ribosome. J. Am. Chem. Soc. 133 (3), 513–526. doi:10.1021/ja107863z

PubMed Abstract | CrossRef Full Text | Google Scholar

Prosdocimi, F., Zamudio, G. S., Palacios-Pérez, M., Torres de Farias, S., and V. José, M. (2020). The Ancient History of Peptidyl Transferase center Formation as Told by Conservation and Information Analyses. Life 10, 134–151. doi:10.3390/life10080134

PubMed Abstract | CrossRef Full Text | Google Scholar

Sehnal, D., Svobodová Vařeková, R., Berka, K., Pravda, L., Navrátilová, V., Banáš, P., et al. (2013). MOLE 2.0: Advanced Approach for Analysis of Biomacromolecular Channels. J. Cheminform. 5, 39. doi:10.1186/1758-2946-5-39

PubMed Abstract | CrossRef Full Text | Google Scholar

Sikora, M., Sułkowska, J. I., and Cieplak, M. (2009). Mechanical Strength of 17 134 Model Proteins and Cysteine Slipknots. Plos Comput. Biol. 5, e1000547. doi:10.1371/journal.pcbi.1000547

PubMed Abstract | CrossRef Full Text | Google Scholar

Soler, M. A., Rey, A., and Faísca, P. F. N. (2016). Steric Confinement and Enhanced Local Flexibility Assist Knotting in Simple Models of Protein Folding. Phys. Chem. Chem. Phys. 18, 26391–26403. doi:10.1039/c6cp05086g

PubMed Abstract | CrossRef Full Text | Google Scholar

Sulkowska, J. I., and Cieplak, M. (2008). Selection of Optimal Variants of Go-like Models of Proteins through Studies of Stretching. Biophys. J. 95, 3174–3191.

PubMed AbstractGoogle Scholar

Takagi, F., Koga, N., and Takada, S. (2003). How Protein Thermodynamics and Folding Mechanisms Are Altered by the Chaperonin Cage: Molecular Simulations. Proc. Natl. Acad. Sci. 100, 11367–11372. doi:10.1073/pnas.1831920100

PubMed Abstract | CrossRef Full Text | Google Scholar

Trylska, J. (2009). Simulating Activity of the Bacterial Ribosome. Quart. Rev. Biophys. 42, 301–316. doi:10.1017/s0033583510000028

CrossRef Full Text | Google Scholar

Voss, N. R., Gerstein, M., Steitz, T. A., and Moore, P. B. (2006). The Geometry of the Ribosomal Polypeptide Exit Tunnel. J. Mol. Biol. 360, 893–906. doi:10.1016/j.jmb.2006.05.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Wołek, K., Gómez-Sicilia, À., and Cieplak, M. (2015). Determination of Contact Maps in Proteins: a Combination of Structural and Chemical Approaches. J. Chem. Phys. 143, 243105. doi:10.1063/1.4929599

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, R., and Bremer, H. (1976). Polypeptide-chain-elongation Rate in Escherichia coli B/r as a Function of Growth Rate. Biochem. J. 160, 185–194. doi:10.1042/bj1600185

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Dabrowski-Tumanski, P., Niewieczerzal, S., and Sulkowska, J. I. (2017). The Exclusive Effects of Chaperonin on the Behavior of Proteins with 52 Knotknot. Plos Comput. Biol. 14, e1005970. doi:10.1371/journal.pcbi.1005970

CrossRef Full Text | Google Scholar