- 1Department of Physics, University of Houston, Houston, TX, United States
- 2Center for Theoretical Biological Physics, Rice University, Houston, TX, United States
Calmodulin (CaM) is a calcium-binding protein that transduces signals to downstream proteins through target binding upon calcium binding in a time-dependent manner. Understanding the target binding process that tunes CaM’s affinity for the calcium ions (Ca2+), or vice versa, may provide insight into how Ca2+-CaM selects its target binding proteins. However, modeling of Ca2+-CaM in molecular simulations is challenging because of the gross structural changes in its central linker regions while the two lobes are relatively rigid due to tight binding of the Ca2+ to the calcium-binding loops where the loop forms a pentagonal bipyramidal coordination geometry with Ca2+. This feature that underlies the reciprocal relation between Ca2+ binding and target binding of CaM, however, has yet to be considered in the structural modeling. Here, we presented a coarse-grained model based on the Associative memory, Water mediated, Structure, and Energy Model (AWSEM) protein force field, to investigate the salient features of CaM. Particularly, we optimized the force field of CaM and that of Ca2+ ions by using its coordination chemistry in the calcium-binding loops to match with experimental observations. We presented a “community model” of CaM that is capable of sampling various conformations of CaM, incorporating various calcium-binding states, and carrying the memory of binding with various targets, which sets the foundation of the reciprocal relation of target binding and Ca2+ binding in future studies.
Introduction
Calmodulin (CaM) is a calcium-binding protein that is present in all eukaryotic cells (Berchtold and Villalobo, 2014; Villalobo et al., 2018; Chin and Means, 2000). CaM is composed of two globular domains separated by a central linker. The two domains (N- and C-domains) are constituted of two calcium-binding helix-loop-helix motifs each, namely, EF-hand motifs (Chattopadhyaya et al., 1992; Fernandes and Oliveira-Brett, 2017). Upon sufficient increase in Ca2+ concentration, Ca2+-free CaM transitions to the Ca2+-loaded CaM (Figure 1), exposing the hydrophobic target-binding surfaces of CaM to the solvent (Figure 2) (Barton et al., 2002; Vetter and Leclerc, 2003; Park et al., 2008; Gromiha and Gromiha, 2010; Wu et al., 2012; Fernandes and Oliveira-Brett, 2017). This transition is accompanied by large conformational changes mutually induced by the conformational changes in the CaM-binding target (CaMBT) peptides (Wang et al., 2013; Liu et al., 2017a; Archer et al., 2019; Bekker et al., 2020). The most unique feature of CaM is its reciprocal relation between Ca2+ binding and target binding (Meador et al., 1993; Weinstein and Mehler, 1994; Wall et al., 1997; Wriggers et al., 1998; Chin and Means, 2000; Hoeflich and Ikura, 2002; Westerlund and Delemotte, 2018), where the conformational changes in the CaM/CaMBT compound further tune CaM’s affinity for the Ca2+ ions (Hoffman et al., 2014; Zhang et al., 2017). The important feature that the net charges of Ca2+ ions vary with the conformations of a calcium-binding loop (Zhang et al., 2021), however, has not been accurately captured in molecular dynamics simulations on calcium-binding proteins.
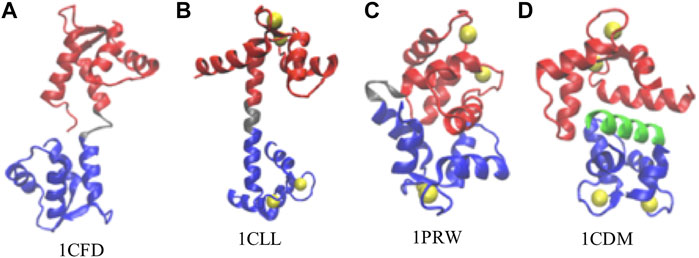
FIGURE 1. Representative conformations of calmodulin (CaM). (A) Ca2+-free CaM, or apoCaM (PDB ID: 1CFD); (B) Ca2+-bound CaM, or holoCaM, in the extended conformation (PDB ID: 1CLL); (C) holoCaM in the collapsed conformation without a target peptide (PDB ID: 1PRW); (D) holoCaM with a target peptide (PDB ID 1CDM). We visualized the structures using the Visual Molecular Dynamics (VMD) program (Humphrey et al., 1996). Ca2+ ions are shown in yellow spheres, the N-terminal and C-terminal domains of CaM are shown in red and blue, respectively, the central linker is shown in grey, and the target peptide is in green.
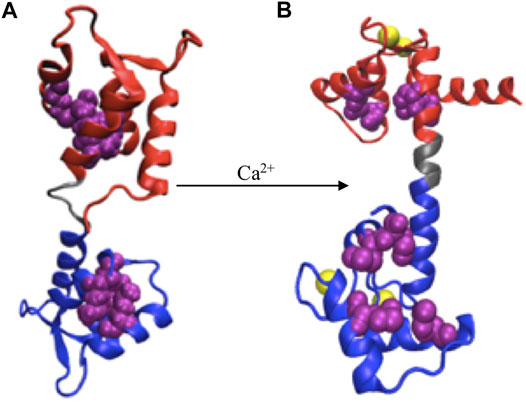
FIGURE 2. Ca2+ induced conformational change. (A) apoCaM, (B) holoCaM. Ca2+ ions are shown in yellow spheres, the N-terminal and C-terminal domains of CaM are shown in red and blue, respectively, and the central linker is shown grey. Upon conformational change, the four methionine residues (shown as beads in purple), initially buried inside the EF-hands, are exposed to the solvent.
The 148-amino acid CaM is an evolutionarily conserved protein across all vertebrates (Davis and Thorner, 1989; Tripathi et al., 2015a), while it is capable of binding more than 300 variations of CaMBTs (Yamniuk and Vogel, 2004). Such structural variability permits its regulation upon the stimulation of calcium ions processes (Clapham, 2007; Carafoli, 2002; Bootman, 2012) in a wide range of biological activities (Chin and Means, 2000; Hoeflich and Ikura, 2002) including cellular motility, neurogenesis, memory formation, muscle contraction, and neuronal transmission (Bootman, 2012; Marambaud et al., 2009; Berridge, 2006). A large and growing body of literature has investigated the structures and dynamics of CaM upon calcium binding (Wriggers et al., 1998; Mehler et al., 1991; Her et al., 2018; Anthis et al., 2011). The crystal structure of the Ca2+-CaM shows a dumbbell-like structure with a central α-helical linker (Figure 1B). However, in solution, the central linker demonstrates higher flexibility (Wriggers et al., 1998; Her et al., 2018; Anthis et al., 2011; Ikura et al., 1992; Chou et al., 2001), which enables the two globular domains of CaM to orient independently from each other (Wriggers et al., 1998; Shepherd and Vogel, 2004; Qin and Squier, 2001). Moreover, this flexibility of the central linker could justify the compact structure of the Ca2+-CaM (Figure 1D) upon target binding (Barton et al., 2002; Shepherd and Vogel, 2004). Additionally, Ca2+-CaM has been shown to crystallize in the collapsed conformation in the absence of the target (Figure 1C), indeed providing more evidence of the backbone plasticity of the Ca2+-CaM (Fallon and Quiocho, 2003) and domain-domain interactions. The structural distribution between the collapsed and extended conformations is roughly 1:9 (Anthis et al., 2011).
A myriad of computational approaches, ranging from all-atom to coarse-grained (Weinstein and Mehler, 1994; Spoel et al., 1996; Wriggers et al., 1998; Vigil et al., 2001; Yang et al., 2001; Barton et al., 2002; Komeiji et al., 2002; Yang et al., 2004; Zuckerman, 2004; Monticelli et al., 2008; Nandigrami and Portman, 2016; Liu et al., 2017b; Gong and Sun, 2017; Robustelli et al., 2018; Delfino et al., 2019; Sun and Kekenes-Huskey, 2021), have been employed to model the structural dynamics of CaM. However, these models have yet to capture the reciprocal relation between Ca2+ binding and target binding. The modeling of CaM is often limited for a specific purpose to either bind the target or the calcium ions. As such, CaM is treated as a folded protein (Shepherd and Vogel, 2004; Yang et al., 2004; Zuckerman, 2004) or a folded protein with intrinsically disordered regions (Robustelli et al., 2018), where, in most cases, Ca2+ effects are ignored for simplicity (Spoel et al., 1996; Yang et al., 2001; Shepherd and Vogel, 2004; Robustelli et al., 2018). When Ca2+ is considered, it is treated as a particle with fixed charges as in an aqueous solution (Monticelli et al., 2008; Gong and Sun, 2017). When Ca2+ ions are implicitly included, their charges are often distributed to all the negatively charged residues present in the EF-hand motifs (Nandigrami and Portman, 2016) without any consideration of the coordination geometry of the Ca2+ ion, which is influenced by the conformation of a calcium-binding loop (Zhang et al., 2021). Our group has recently proposed a coarse-grained model to study the dynamics of CaM that accounts for both considerations (Wang et al., 2013; Zhang et al., 2017), but it is yet to reproduce the reciprocal relationship between calcium binding and target binding as both require intensive data-driven efforts.
One of the main challenges for developing an appropriate force field involving Ca2+ is that CaM is a structurally flexible protein about its central linker while the binding of Ca2+ to the two domains of CaM increases the rigidity of the local domains. A compromise between rigidity and softness has to be considered in order for CaM to accurately select, bind, and activate its binding targets. We, therefore, turned to the coarse-grained approach that adopts the Associative memory, Water mediated, Structure, and Energy Model (AWSEM) force field (Wang et al., 2011; Zhang et al., 2017) to fulfill these requirements. The next challenge is to properly include the Ca2+ ions in the force field of a coarse-grained model since this would allow us to understand the reciprocal relationship between calcium binding to CaM and binding of a target (Wang et al., 2013; Tripathi et al., 2015b). Although in separate studies, there have been development in AWSEM force fields on structurally flexible proteins (Wu et al., 2018) or on di-valent ions (Tsai et al., 2016), both features, however, have yet to be combined for modeling CaM. Particularly, the coordination chemistry of Ca2+ ions and the structural flexibility allowing CaM to flex according to its binding targets and surrounding environment is important in modeling the adaptive behavior of CaM (Wang et al., 2013; Liu et al., 2017a; Archer et al., 2019; Bekker et al., 2020). By taking into account the coordination chemistry of the Ca2+ ions as well as the flexible nature of the central linker of CaM, our proposed model for Ca2+-CaM elucidates the many-body effects of calcium binding on the geometrical shape of the calcium-binding loop and allows large conformational changes for binding various targets.
Materials and Methods
Coarse-Grained Modeling Using the AWSEM Force Field
We used the AWSEM force field (Davtyan et al., 2012; Tsai et al., 2016) to build the model of Ca2+-CaM. AWSEM is a transferable coarse-grained protein model, which uses three beads (
which is composed of two main terms: the physics-based terms,
(a) The backbone term,
(b) The many-body potential of mean force
The contact term
where
(c) The electrostatic interactions in solution with implicit solvent are described by the Debye–Hückel term (Tsai et al., 2016)
where
(d)
where the outer sum is over the aligned memory (from
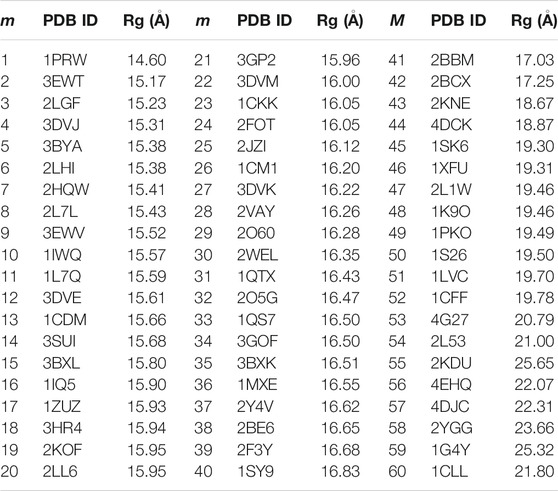
TABLE 1. The PDB IDs of the 60 non-redundant CaM memory structures for the AWSEM model and the Rg of the CaM. In the case of CaM complexes, only the coordinates of CaM were used for memory. m is the index for the memories.
We used 60 non-redundant structures of CaM taken from our prior study (Tripathi et al., 2015c) (Table 1), either free or in complex with the target peptides, to build the memory fragments for the coarse-grained model of CaM. We used the 60 sequence homologs of Ca2+-CaM since we are interested in studying the dynamics and the folding properties of CaM. We divided each memory into three segments: N-domain of CaM, from residue 5 to residue 76; the flexible central linker, from residue 77 through residue 81; and C-domain of CaM, from residue 82 to residue 147 (as illustrated in Figure 1). The weight of each segment is controlled by a memory weight parameter
We summarized CaM models using various values of
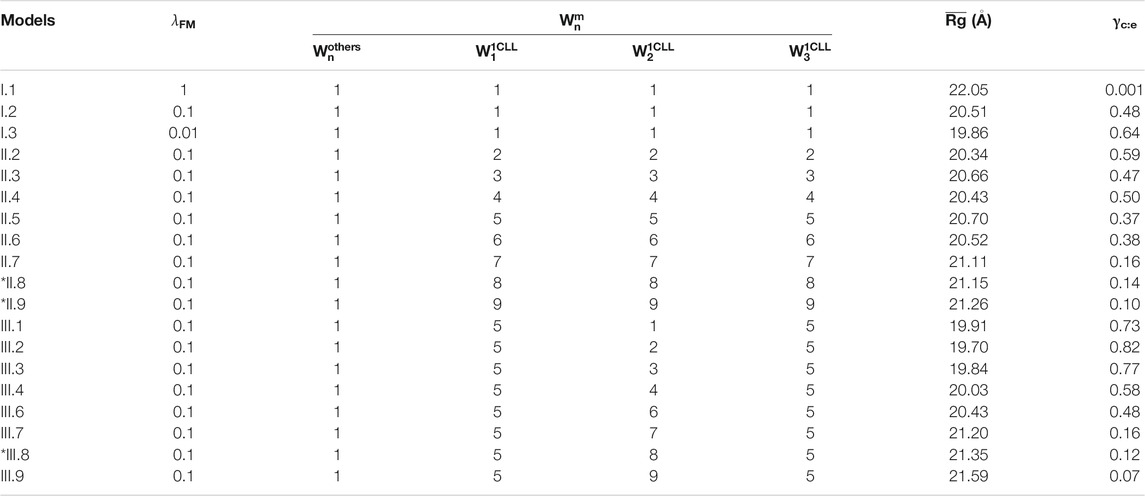
TABLE 2. Summary of Ca2+-CaM models with different values of the global and local memory weight and the average Rg (
Modeling Ca2+ Ions in ASWEM Force Field
Calcium-binding proteins in most cases contain the EF-hand calcium-binding motif which is formed by the pentagonal bipyramidal geometry (Figure 3; Supplementary Figure S1 in the SI) (Drake et al., 1997; Yang et al., 2002). The literature on modeling those proteins, in general, does not clearly explain how Ca2+-binding effects are considered during the simulations. We developed an implicit Ca2+ model that evenly splits the Ca2+ charges to a selection of residues. Partial charges on the sidechain beads of the negatively charged residues that coordinate Ca2+ collectively in the Ca2+ binding loops (Figure 3) were adjusted to reflect the Ca2+- binding effect (Table 3). To note, charges on those acidic residues which do not coordinate (Ca2+) remain intact (−1 e). This simple approach incorporates the coordination geometry of the Ca2+ and allows us to improve the modeling of many-body effects in the local Ca2+ binding loops which furthermore controls the open/close state of the helix-loop-helix EF-hand and the global conformation of calmodulin.
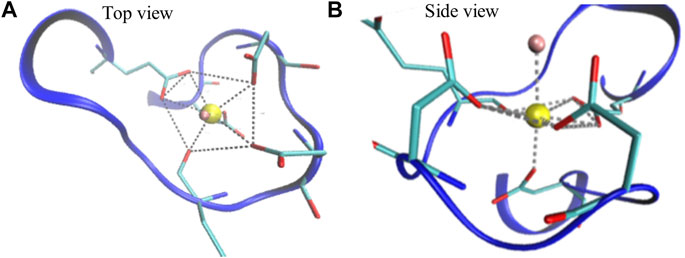
FIGURE 3. Illustration of a Ca2+ binding loop at the fourth EF-hand of CaM (PDB ID: 1CLL). The pentagonal bipyramidal geometry of the Ca2+ coordination is represented with the dotted lines in the top view (A) and side view (B). The red sticks linked with the dotted lines represent oxygen atoms that participate in coordination. The water molecule, shown in pink, completes the spherical coordination through hydrogen bonding.

TABLE 3. The adjusted partial charges of the negatively charged residues participated in calcium coordination in the four calcium-binding loops of CaM. The amino acid sequences of the calcium-binding loops are provided as a reference. The subscript indices stand for the positions of the starting/ending residues in the CaM sequence. Underscored residues are the selected amino acids with negative charges as shown in the third column. We adjusted the partial charges on the sidechain beads of those residues based on the bipyramidal pentagonal coordination geometry of the calcium ion.
In this study, we compared the abovementioned approach (approach III) with two other calcium models:
I. Splitting the Ca2+ charges evenly to the neighboring negatively charged residues (Tsai et al., 2016).
II. Splitting the Ca2+ charges evenly to the residues that participate with the calcium coordination and the radius of gyration of the sidechain beads are constrained by a stiff harmonic potential with a force constant of 30 kcal/mol/Å2.
III. The same with approach II except that the harmonic constraint is removed.
Comparing to approach I of Ca2+ in AWSEM (Tsai et al., 2016), in approach III calcium charges were split according to the coordination chemistry of calcium; comparing to approach II, in approach III more degrees of freedom to the Ca2+ coordination residues allow sampling of more different conformations of CaM.
Simulation Details
We performed the coarse-grained simulations with the open-source MD package LAMMPS, in which AWSEM code was implemented (Davtyan et al., 2012). We used the periodic boundary conditions on the cubic box of 400 Å on each side so that even unfolded CaM can fit in the box. Initial velocities were chosen randomly from a Boltzmann distribution with the average squared velocity equal to 3
Simulated annealing: firstly, we denatured the protein at 450 K using the initial structure built from the crystal structure (PDB ID: 1CLL) (Chattopadhyaya et al., 1992); then, we performed simulated annealing on Ca2+-CaM by cooling down the system to a low temperature (280 K) for 2,000,000 time steps for each value of
Production simulation: we employed the umbrella sampling (US) method (Roux, 1995) to evaluate the thermodynamic properties of Ca2+-CaM using different memory parameters. We conducted the production simulations in canonical ensemble (NVT) at the constant temperature of 300 K. Radius of gyration (Rg) of Ca2+-CaM was used as the reaction coordinate, which was restrained by a harmonic potential
Data Analysis
We described the conformational changes of the Ca2+-CaM during the simulations by calculating the radius of gyration (
Radius of Gyration (
Rg describes the compactness of the protein, and its definition is given in Eq. 7:
In the case of PDB structures,
Pairwise Comparison
where
Definition of Collapsed and Extended Conformations of CaM
In our analyses, we used the parameter Rg to define a collapsed or extended conformation. The Rg cutoff was set according to the potential of mean force (PMF) and distribution of Rg in our simulations (Figures 4–8). A collapsed conformation is defined if Rg < 18.5Å; otherwise, an extended conformation is defined.
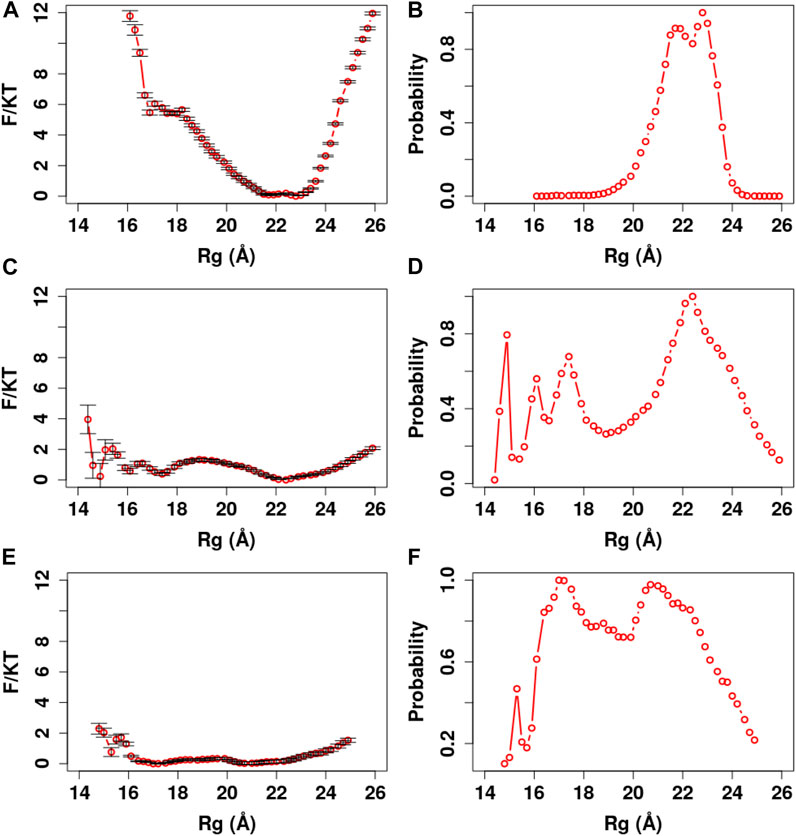
FIGURE 4. PMF and Rg distribution of the Ca2+-CaM models using the global memory weight of different order of magnitudes. The memory weight parameters of the Ca2+-CaM models are listed in Table 2 (model I;
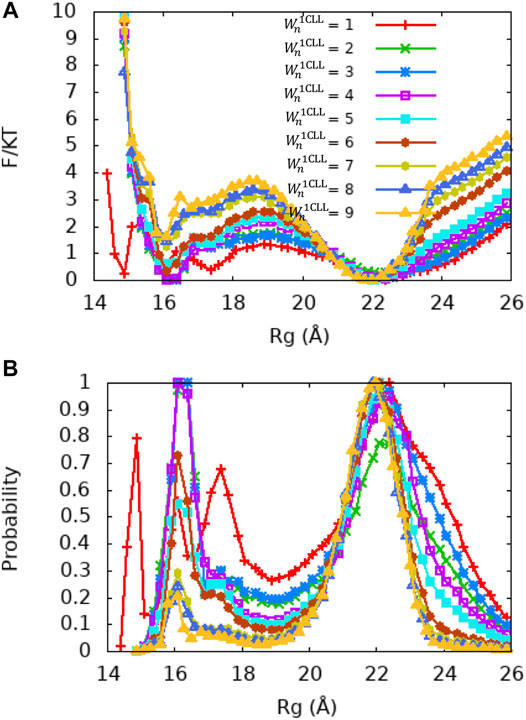
FIGURE 5. PMF and Rg distribution of the Ca2+-CaM models for different values of the local memory weight
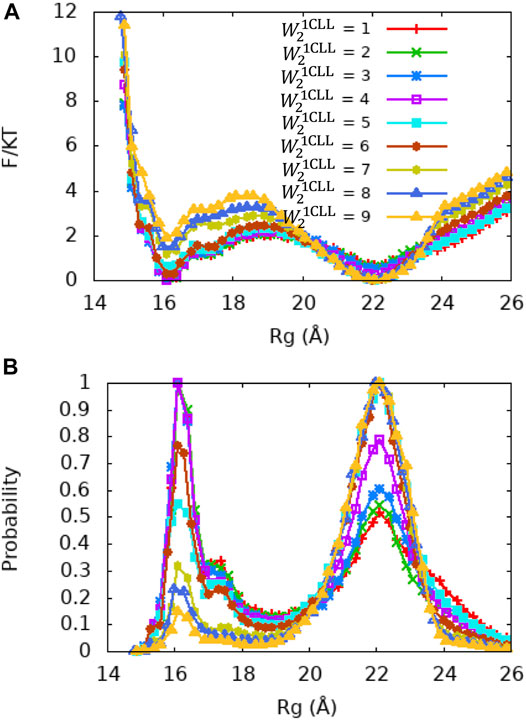
FIGURE 6. PMF and Rg distribution of the Ca2+-CaM models for different values of the local memory weight
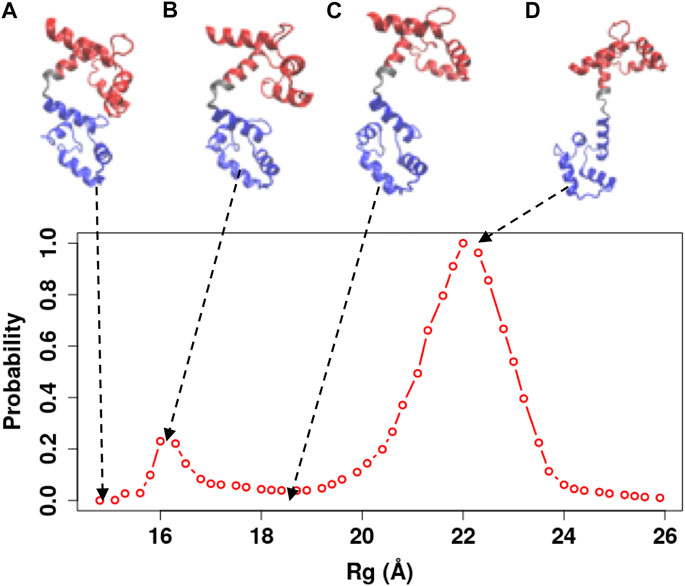
FIGURE 7. Representative snapshots of the Ca2+-CaM model obtained from our simulations. The model that best reproduces experimental measurements was used (
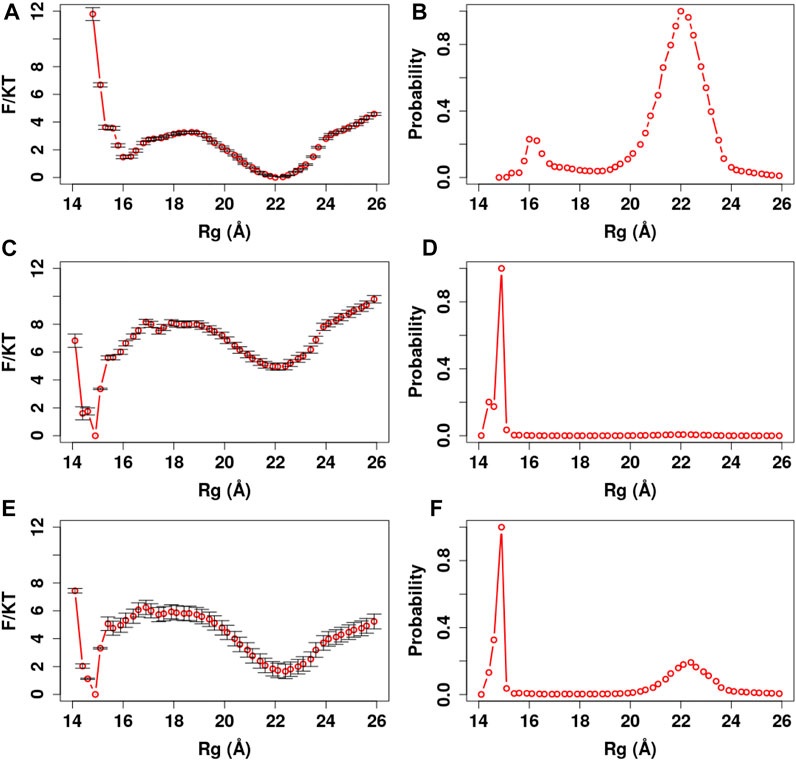
FIGURE 8. PMF and Rg distribution of the Ca2+-CaM for different Ca2+ models. The optimized memory parameters for the Ca2+-CaM model were used (
Results and Discussion
The goal is to create a computational model for CaM accommodating its several key functions including divalent ion binding, conformational dynamics, and target recognition. In order to achieve this, we adopted a pool of 60 CaM or CaM complex structures from our previous study (Tripathi et al., 2015c) representing full-length CaM without mutations and its complex with 24 unique target proteins/peptides. As stated in the Materials and Methods Simulation Details, our approach is to tune the two scaling parameters
Each of the 60 memories has a specific conformation of calmodulin which could be helpful in target recognition and target selection; therefore, clustering the 60 memories may leave out important conformations that accommodate recognition of a specific target protein. Potentially, there could be as many as 181 fragment memory parameters to be determined in the most complicated scenario. However, in the general practice of AWSEM modeling, a search in the available determined structures in the database according to the match in the desired amino acid sequence is conducted to generate a library of memory structures. Therefore, to avoid excessive tuning of the parameters, the individual memory weight Wnm is kept as a constant default value. Because the unbound extended form of the Ca2+/CaM (PDB code: 1CLL) was found to be most dominant experimentally, we adjusted its local memory weight parameter correspondingly, while keeping others the default
Parameterization of our CG model was guided by the existing following experimental measures:
The Global Parameter Weight Controls the Energy Barrier Between Extended and the Collapsed States of Ca2+-CaM
Firstly, we determined the magnitude of the fragment memory interaction by investigating its effect on the folding properties of Ca2+-CaM. We carried out simulated annealing using the unfolded structure of the Ca2+-CaM (
In addition, we carried out US simulations to evaluate thermodynamic properties of Ca2+-CaM with the global scaling parameter in three orders of magnitudes
In summary, the global memory parameter
Single Memory Optimization Captures the Dynamics of Ca2+-CaM
Although the global fragment memory weight of
Since the crystal structure of Ca2+-CaM (PDB ID: 1CLL) demonstrates a value of Rg that is closest to the experimentally measured values and does not bind a target, we first examined whether variation in single memory weight of this structure (
Central Linker of the Ca2+-CaM Determines the Conformational Change of Ca2+-CaM
Although the X-ray crystallography experiment shows that the central linker that connects the two domains of Ca2+-CaM has a helical structure, numerous studies including NMR have shown its high flexibility in solution. To explore the relationship between the flexible linker and the dynamics of Ca2+-CaM in more detail, we carried out a series of US molecular simulations with the memory weight of the central linker of the Ca2+-CaM,
In order to illustrate the conformational changes of Ca2+-CaM in solution, we selected representative snapshots from the simulations using the Ca2+-CaM model with
Coordination Geometry Is Necessary for Representing Divalent Ions in Coarse-Grained Models
Although it can be tempting to use the available intrinsically disordered protein (IDP) force fields such as AWSEM-IDP (Wu et al., 2018) (due to the disordered nature of the central linker) to study the dynamics of Ca2+-CaM, the heterogeneity of CaM needs to be considered. The high rigidity of the two domains upon calcium-binding limits the use of IDP force fields, thus making the computational investigation of CaM even more complex.
We further manifest the importance of coordination chemistry by comparing the three approaches to modeling Ca2+ as described in Method Modeling Ca2+Ions in ASWEM Force Field in Figure 8. With approach I, the Ca2+ charges were evenly distributed to all the negatively charged residues (Tsai et al., 2016) and Ca2+-CaM presents an equal probability of sampling the completely collapsed conformation and the extended conformation (γc:e = 1.01).
Force field development for Ca2+ ion is mostly limited to the aqueous solution rather than in protein-bound environments (Probst et al., 1985). One of the main challenges in computer simulations of macromolecules remains the development of force fields with the appropriate implementation of the metal ion (Gifford et al., 2007; Duarte et al., 2014; Li and Merz, 2017; Liao et al., 2017; Fracchia et al., 2018; Huang and MacKerell, 2018). Due to the high sensibility of the molecules upon bivalent metal ion binding, taking the Ca2+-induced conformational changes in CaM as an example, a lack of appropriate approach to model its effects on the molecules could impede the capability of the target molecule to transduce its signals, thus, leading to the inactivation and/or malfunction of the signaling pathways (Gaertner et al., 2004; Wang et al., 2011).
Most calcium-binding proteins such as CaM contain the EF-hand (helix-loop-helix) structural domain as the calcium-binding motif (Lepšík and Field, 2007; Capozzi et al., 2006). In this motif, the calcium ion is coordinated in a pentagonal bipyramidal configuration (Figure 3). The canonical positions 1, 3, 5, 7, 9, and 12 represent the positions of the residues involved in calcium coordination (Clapham, 2007; Gifford et al., 2007). Table 3 shows simple and efficient ways to consider the effect of the Ca2+ ions in the force field, where we distributed its charges to the negatively charged residues present in the pentagonal bipyramidal configuration. In contrast to other approaches where the harmonic constraint is applied to the calcium coordinated residues in the loop, or the charges are distributed to all the negatively charged residues in the system, our approach (III) not only considers the heterogeneity of CaM but also takes into account the coordination chemistry of calcium by giving the coordinated residues the freedom to participate to the different conformations of the system, which are relevant to the target selectivity of Ca2+-CaM.
The Distribution of Ca2+-CaM Conformations Is Beyond the Extended and the Collapsed Structures
Ca2+-CaM undergoes substantial conformational changes upon binding to a target, in most cases, the Ca2+-CaM develops a collapsed form that wraps around the target peptide with the two domains coming in proximity (Meador et al., 1993; Westerlund and Delemotte, 2018; Tidow and Nissen, 2013). For various CaMBT molecules, CaM undergoes structural rearrangement to different degrees during the complex formation. Thus, the collapsed conformation of the intact Ca2+-CaM (e.g., Figure 7) assembles a vast variety of structures including a structure that resembles the compact conformation of a specific Ca2+-CaM/target complex (Figure 1D). This was also observed by X-ray crystallography (Fallon and Quiocho, 2003) and NMR studies (Anthis et al., 2011). This collapsed structure of the Ca2+-CaM (Figure 7A) confirms the earlier experiments that show multiple conformations of the Ca2+-CaM in solution, as well as the interaction between opposing domains of CaM (Johnson, 2006; Anthis et al., 2011; Her et al., 2018).
Previous studies have shown that the high flexibility of the linker in solution allows the two domains to independently undergo multiple conformations (Malmendal et al., 1999; Chou et al., 2001; Barton et al., 2002; Hoeflich and Ikura, 2002; Komeiji et al., 2002; Park et al., 2008; Wu et al., 2012). Structural differences can be inferred from crystallography, but the dynamical insights are pivotal to understand Ca2+-CaM interactions with the targets. Experimental and computational studies including NMR spectroscopy, X-ray crystallography, small-angle X-ray scattering, and molecular dynamics simulations unveil important details of the dynamics of Ca2+-CaM and paint a clear portrait of its conformational motions at the origin of the binding selectivity. The available structures of Ca2+-CaM show that it crystallizes into two major conformations: extended (Chattopadhyaya et al., 1992) and collapsed (Fallon and Quiocho, 2003), while in solution, Ca2+-CaM adopts multiple conformations (Project et al., 2006; Park et al., 2008; Wu et al., 2012; McCarthy et al., 2015; Fernandes and Oliveira-Brett, 2017; Jing et al., 2017; Her et al., 2018; Villalobo et al., 2018; Shimoyama, 2019). The conformational changes of CaM upon Ca2+ binding have been under intensive investigation (Weinstein and Mehler, 1994; Gilli et al., 1998; Project et al., 2006; Park et al., 2008; Wu et al., 2012). The goal of such studies is to understand the molecular mechanism that leads to the Ca2+-CaM target binding selectivity. How Ca2+-CaM interacts with its CaMBTs is of major interest. This presented community model of CaM allows transitions between a rich set of states beyond the two major extended or the collapsed conformations and are applicable for various Ca2+ bound conditions; this further could improve the interpretation of how target binding may tune CaM’s affinity for Ca2+ ions (Gaertner et al., 2004; Zhang et al., 2017).
Conclusion
Here, we developed a “community model” of CaM that samples various conformations of CaM, incorporates various calcium-binding states, and carries the memory of binding with various targets. The model would be useful for studying the reciprocal relationship interplay between target binding and calcium binding through CaM’s conformational changes as the next step. We demonstrated a workflow of the development of the AWSEM model for CaM guided by physical knowledge and experimental data. Should new structures of CaM (or CaM/CaMBT complex) structures become available, the model can be easily expanded by including these structures in the memory library.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
MC conceived and designed the research. JN performed the simulations and prepared the figures. MC, JN, PZ, JE, WL, and KK performed data analysis and wrote the article. PW provided critical advice. All authors contributed to the manuscript, read, and approve the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Drs. Neal M. Waxham, Piotr Cieplak, and Qian Wang for stimulating discussions. The work was supported by a grant from the National Institutes of Health (2R01GM097553). MSC and PGW are grateful for the funding support from the National Science Foundation (PHY2019745). PGW is grateful for the support from the D. R. Bullard-Welch Chair at Rice University, Grant C-0016. The authors acknowledge the computing resources from the computing clusters uHPC and Sabine at the University of Houston.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2021.661322/full#supplementary-material
References
Anthis, N. J., Doucleff, M., and Clore, G. M. (2011). Transient, Sparsely Populated Compact States of Apo and Calcium-Loaded Calmodulin Probed by Paramagnetic Relaxation Enhancement: Interplay of Conformational Selection and Induced Fit. J. Am. Chem. Soc. 133 (46), 18966–18974. doi:10.1021/ja2082813
Archer, C. R., Enslow, B. T., Taylor, A. B., De la Rosa, V., Bhattacharya, A., and Shapiro, M. S. (2019). A Mutually Induced Conformational Fit Underlies Ca2+-Directed Interactions between Calmodulin and the Proximal C Terminus of KCNQ4 K+ Channels. J. Biol. Chem. 294 (15), 6094–6112. doi:10.1074/jbc.ra118.006857
Barton, N. P., Verma, C. S., and Caves, L. S. D. (2002). Inherent Flexibility of Calmodulin Domains: A Normal-Mode Analysis Study. J. Phys. Chem. B 106 (42), 11036–11040. doi:10.1021/jp026692q
Bekker, G. J., Fukuda, I., Higo, J., and Kamiya, N. (2020). Mutual Population-Shift Driven Antibody-Peptide Binding Elucidated by Molecular Dynamics Simulations. Sci. Rep. 10 (1), 1406. doi:10.1038/s41598-020-58320-z
Berchtold, M. W., and Villalobo, A. (2014). The many Faces of Calmodulin in Cell Proliferation, Programmed Cell Death, Autophagy, and Cancer. Biochim. Biophys. Acta (Bba) - Mol. Cel Res. 1843 (2), 398–435. doi:10.1016/j.bbamcr.2013.10.021
Berridge, M. J. (2006). Calcium Microdomains: Organization and Function. Cell Calcium 40 (5), 405–412. doi:10.1016/j.ceca.2006.09.002
Bootman, M. D. (2012). Calcium Signaling. Cold Spring Harbor Perspect. Biol. 4 (7). doi:10.1101/cshperspect.a011171
Capozzi, F., Casadei, F., and Luchinat, C. (2006). EF-hand Protein Dynamics and Evolution of Calcium Signal Transduction: an NMR View. J. Biol. Inorg. Chem. 11 (8), 949–962. doi:10.1007/s00775-006-0163-0
Carafoli, E. (2002). Calcium Signaling: A Tale for All Seasons. Proc. Natl. Acad. Sci. 99 (3), 1115–1122. doi:10.1073/pnas.032427999
Chattopadhyaya, R., Meador, W. E., Means, A. R., and Quiocho, F. A. (1992). Calmodulin Structure Refined at 1.7 Å Resolution. J. Mol. Biol. 228 (4), 1177–1192. doi:10.1016/0022-2836(92)90324-d
Chin, D., and Means, A. R. (2000). Calmodulin: a Prototypical Calcium Sensor. Trends Cel Biol. 10 (8), 322–328. doi:10.1016/s0962-8924(00)01800-6
Chou, J. J., Li, S., Klee, C. B., and Bax, A. (2001). Solution Structure of Ca(2+)-Calmodulin Reveals Flexible Hand-like Properties of its Domains. Nat. Struct. Biol. 8 (11), 990–997. doi:10.1038/nsb1101-990
Davis, T. N., and Thorner, J. (1989). Vertebrate and Yeast Calmodulin, Despite Significant Sequence Divergence, Are Functionally Interchangeable. Proc. Natl. Acad. Sci. 86 (20), 7909–7913. doi:10.1073/pnas.86.20.7909
Davtyan, A., Schafer, N. P., Zheng, W., Clementi, C., Wolynes, P. G., and Papoian, G. A. (2012). AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 116 (29), 8494–8503. doi:10.1021/jp212541y
Delfino, F., Porozov, Y., Stepanov, E., Tamazian, G., and Tozzini, V. (2019). Structural Transition States Explored with Minimalist Coarse Grained Models: Applications to Calmodulin. Front. Mol. Biosciences 6 (104). doi:10.3389/fmolb.2019.00104
Drake, S. K., Zimmer, M. A., Kundrot, C., and Falke, J. J. (1997). Molecular Tuning of an EF-hand-like Calcium Binding Loop. J. Gen. Physiol. 110 (2), 173–184. doi:10.1085/jgp.110.2.173
Duarte, F., Bauer, P., Barrozo, A., Amrein, B. A., Purg, M., Åqvist, J., et al. (2014). Force Field Independent Metal Parameters Using a Nonbonded Dummy Model. J. Phys. Chem. B 118 (16), 4351–4362. doi:10.1021/jp501737x
Fallon, J. L., and Quiocho, F. A. (2003). A Closed Compact Structure of Native Ca2+-Calmodulin. Structure 11 (10), 1303–1307. doi:10.1016/j.str.2003.09.004
Fernandes, I. P. G., and Oliveira-Brett, A. M. (2017). Calcium-induced Calmodulin Conformational Change. Electrochemical Evaluation. Bioelectrochemistry 113, 69–78. doi:10.1016/j.bioelechem.2016.10.002
Fracchia, F., Del Frate, G., Mancini, G., Rocchia, W., and Barone, V. (2018). Force Field Parametrization of Metal Ions from Statistical Learning Techniques. J. Chem. Theor. Comput. 14 (1), 255–273. doi:10.1021/acs.jctc.7b00779
Gaertner, T. R., Putkey, J. A., and Waxham, M. N. (2004). RC3/Neurogranin and Ca2+/calmodulin-dependent Protein Kinase II Produce Opposing Effects on the Affinity of Calmodulin for Calcium. J. Biol. Chem. 279 (38), 39374–39382. doi:10.1074/jbc.m405352200
Gifford, J. L., Gifford, M. P., and Walsh, H. J. (2007). Structures and Metal-Ion-Binding Properties of the Ca2+-Binding helix-loop-helix EF-Hand Motifs. Biochem. J. 405 (2), 199–221. doi:10.1042/BJ20070255
Gilli, R., Lafitte, D., Lopez, C., Kilhoffer, M.-C., Makarov, A., Briand, C., et al. (1998). Thermodynamic Analysis of Calcium and Magnesium Binding to Calmodulin. Biochemistry 37 (16), 5450–5456. doi:10.1021/bi972083a
Gong, Z., and Sun, H. (2017). A Coarse-Grained Force Field Parameterized for MgCl2 and CaCl2 Aqueous Solutions. J. Chem. Inf. Model. 57 (7), 1599–1608. doi:10.1021/acs.jcim.7b00206
Gromiha, M. M. (2010). “Chapter 6 - Protein Stability,” in Protein Bioinformatics. Editor M. M. Gromiha (Singapore: Academic Press).
Heidorn, D. B., and Trewhella, J. (1988). Comparison of the crystal and Solution Structures of Calmodulin and Troponin C. Biochemistry 27 (3), 909–915. doi:10.1021/bi00403a011
Her, C., Thompson, A. R., Karim, C. B., and Thomas, D. D. (2018). Structural Dynamics of Calmodulin-Ryanodine Receptor Interactions: Electron Paramagnetic Resonance Using Stereospecific Spin Labels. Scientific Rep. 8 (1), 10681. doi:10.1038/s41598-018-29064-8
Hoeflich, K. P., and Ikura, M. (2002). Calmodulin in Action. Cell 108 (6), 739–742. doi:10.1016/s0092-8674(02)00682-7
Hoffman, L., Chandrasekar, A., Wang, X., Putkey, J. A., and Waxham, M. N. (2014). Neurogranin Alters the Structure and Calcium Binding Properties of Calmodulin. J. Biol. Chem. 289 (21), 14644–14655. doi:10.1074/jbc.m114.560656
Homouz, D., Sanabria, H., Waxham, M. N., and Cheung, M. S. (2009). Modulation of Calmodulin Plasticity by the Effect of Macromolecular Crowding. J. Mol. Biol. 391 (5), 933–943. doi:10.1016/j.jmb.2009.06.073
Huang, J., and MacKerell, A. D. (2018). Force Field Development and Simulations of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol. 48, 40–48. doi:10.1016/j.sbi.2017.10.008
Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: Visual Molecular Dynamics. J. Mol. Graphics 14 (1), 33–38. doi:10.1016/0263-7855(96)00018-5
Ikura, M., Clore, G., Gronenborn, A., Zhu, G., Klee, C., and Bax, A. (1992). Solution Structure of a Calmodulin-Target Peptide Complex by Multidimensional NMR. Science 256 (5057), 632–638. doi:10.1126/science.1585175
Jing, Z., Qi, R., Liu, C., and Ren, P. (2017). Study of Interactions between Metal Ions and Protein Model Compounds by Energy Decomposition Analyses and the AMOEBA Force Field. J. Chem. Phys. 147 (16), 161733. doi:10.1063/1.4985921
Johnson, C. K. (2006). Calmodulin, Conformational States, and Calcium Signaling. A Single-Molecule Perspective. Biochemistry 45 (48), 14233–14246. doi:10.1021/bi061058e
Kataoka, M., Head, J. F., Vorherr, T., Krebs, J., and Carafoli, E. (1991). Small-angle X-ray Scattering Study of Calmodulin Bound to Two Peptides Corresponding to Parts of the Calmodulin-Binding Domain of the Plasma Membrane Calcium Pump. Biochemistry 30 (25), 6247–6251. doi:10.1021/bi00239a024
Komeiji, Y., Ueno, Y., and Uebayasi, M. (2002). Molecular Dynamics Simulations Revealed Ca2+ -dependent Conformational Change of Calmodulin. FEBS Lett. 521 (1), 133–139. doi:10.1016/s0014-5793(02)02853-3
Lepšík, M., and Field, M. J. (2007). Binding of Calcium and Other Metal Ions to the EF-Hand Loops of Calmodulin Studied by Quantum Chemical Calculations and Molecular Dynamics Simulations. The J. Phys. Chem. B 111 (33), 10012–10022.
Li, P., and Merz, K. M. (2017). Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 117 (3), 1564–1686. doi:10.1021/acs.chemrev.6b00440
Liao, Q., Pabis, A., Strodel, B., and Kamerlin, S. C. L. (2017). Extending the Nonbonded Cationic Dummy Model to Account for Ion-Induced Dipole Interactions. J. Phys. Chem. Lett. 8 (21), 5408–5414. doi:10.1021/acs.jpclett.7b02358
Liu, F., Chu, X., Lu, H. P., and Wang, J. (2017). Molecular Mechanism of Multispecific Recognition of Calmodulin through Conformational Changes. Proc. Natl. Acad. Sci. U S A. 114, E3927. doi:10.1073/pnas.1615949114
Liu, F., Chu, X., Lu, H. P., and Wang, J. (2017). Molecular Mechanism of Multispecific Recognition of Calmodulin through Conformational Changes. Proc. Natl. Acad. Sci. USA 114 (20), E3927–E3934. doi:10.1073/pnas.1615949114
Malmendal, A., Evenäs, J., Forsén, S., and Akke, M. (1999). Structural Dynamics in the C-Terminal Domain of Calmodulin at Low Calcium Levels 1 1Edited by P. E. Wright. J. Mol. Biol. 293 (4), 883–899. doi:10.1006/jmbi.1999.3188
Marambaud, P., Dreses-Werringloer, U., and Vingtdeux, V. (2009). Calcium Signaling in Neurodegeneration. Mol. Neurodegeneration 4 (1), 20. doi:10.1186/1750-1326-4-20
McCarthy, M. R., Thompson, A. R., Nitu, F., Moen, R. J., Olenek, M. J., Klein, J. C., et al. (2015). Impact of Methionine Oxidation on Calmodulin Structural Dynamics. Biochem. Biophysical Res. Commun. 456 (2), 567–572. doi:10.1016/j.bbrc.2014.11.091
Meador, W., Means, A., and Quiocho, F. (1993). Modulation of Calmodulin Plasticity in Molecular Recognition on the Basis of X-ray Structures. Science 262 (5140), 1718–1721. doi:10.1126/science.8259515
Mehler, E. L., Pascual-Ahuir, J.-L., and Weinstein, H. (1991). Structural Dynamics of Calmodulin and Troponin C. Protein Eng. Des. Sel 4 (6), 625–637. doi:10.1093/protein/4.6.625
Monticelli, L., Kandasamy, S. K., Periole, X., Larson, R. G., Tieleman, D. P., and Marrink, S.-J. (2008). The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theor. Comput. 4 (5), 819–834. doi:10.1021/ct700324x
Nandigrami, P., and Portman, J. J. (2016). Coarse-grained Molecular Simulations of Allosteric Cooperativity. J. Chem. Phys. 144 (10), 105101. doi:10.1063/1.4943043
Park, H. Y., Kim, S. A., Korlach, J., Rhoades, E., Kwok, L. W., Zipfel, W. R., et al. (2008). Conformational Changes of Calmodulin upon Ca2+ Binding Studied with a Microfluidic Mixer. Proc. Natl. Acad. Sci. 105 (2), 542–547. doi:10.1073/pnas.0710810105
Probst, M. M., Radnai, T., Heinzinger, K., Bopp, P., and Rode, B. M. (1985). Molecular Dynamics and X-ray Investigation of an Aqueous Calcium Chloride Solution. J. Phys. Chem. 89 (5), 753–759. doi:10.1021/j100251a007
Project, E., Friedman, R., Nachliel, E., and Gutman, M. (2006). A Molecular Dynamics Study of the Effect of Ca2+ Removal on Calmodulin Structure. Biophysical J. 90 (11), 3842–3850. doi:10.1529/biophysj.105.077792
Qin, Z., and Squier, T. C. (2001). Calcium-Dependent Stabilization of the Central Sequence between Met76 and Ser81 in Vertebrate Calmodulin. Biophysical J. 81 (5), 2908–2918. doi:10.1016/s0006-3495(01)75931-0
Robustelli, P., Piana, S., and Shaw, D. E. (2018). Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. USA 115 (21), E4758–E4766. doi:10.1073/pnas.1800690115
Roux, B. (1995). The Calculation of the Potential of Mean Force Using Computer-Simulations. Comput. Phys. Commun. 91 (1-3), 275–282. doi:10.1016/0010-4655(95)00053-i
Seaton, B. A., Head, J. F., Engelman, D. M., and Richards, F. M. (1985). Calcium-induced Increase in the Radius of Gyration and Maximum Dimension of Calmodulin Measured by Small-Angle X-ray Scattering. Biochemistry 24 (24), 6740–6743. doi:10.1021/bi00345a002
Shepherd, C. M., and Vogel, H. J. (2004). A Molecular Dynamics Study of Ca2+-Calmodulin: Evidence of Interdomain Coupling and Structural Collapse on the Nanosecond Timescale. Biophysical J. 87 (2), 780–791. doi:10.1529/biophysj.103.033266
Shimoyama, H. (2019). A Structural Comparison of 'real' and 'model' Calmodulin Clarified Allosteric Interactions Regulating Domain Motion. J. Biomol. Struct. Dyn. 37 (6), 1567–1581. doi:10.1080/07391102.2018.1462730
Shirts, M. R., and Chodera, J. D. (2008). Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 129 (12), 124105. doi:10.1063/1.2978177
Spoel, D. V. D., Groot, B. L. D., Hayward, S., Berendsen, H. J. C., and Vogel, H. J. (1996). Bending of the Calmodulin central helix: a Theoretical Study. Protein Sci. 5 (10), 2044–2053. doi:10.1002/pro.5560051011
Sun, B., and Kekenes-Huskey, P. M. (2021). Assessing the Role of Calmodulin's Linker Flexibility in Target Binding. Int. J. Mol. Sci. 22 (9). doi:10.3390/ijms22094990
Tidow, H., and Nissen, P. (2013). Structural Diversity of Calmodulin Binding to its Target Sites. Febs j 280 (21), 5551–5565. doi:10.1111/febs.12296
Tripathi, S., Wang, Q., Zhang, P., Hoffman, L., Waxham, M. N., and Cheung, M. S. (2015). Conformational Frustration in Calmodulin-Target Recognition. J. Mol. Recognit. 28 (2), 74–86. doi:10.1002/jmr.2413
Tripathi, S., Waxham, M. N., Cheung, M. S., and Liu, Y. (2015). Lessons in Protein Design from Combined Evolution and Conformational Dynamics. Sci. Rep. 5, 14259. doi:10.1038/srep14259
Tripathi, S., Waxham, M. N., Cheung, M. S., and Liu, Y. (2015). Lessons in Protein Design from Combined Evolution and Conformational Dynamics. Scientific Rep. 5 (1), 14259. doi:10.1038/srep14259
Tsai, M.-Y., Zheng, W., Balamurugan, D., Schafer, N. P., Kim, B. L., Cheung, M. S., et al. (2016). Electrostatics, Structure Prediction, and the Energy Landscapes for Protein Folding and Binding. Protein Sci. 25 (1), 255–269. doi:10.1002/pro.2751
Vetter, S. W., and Leclerc, E. (2003). Novel Aspects of Calmodulin Target Recognition and Activation. Eur. J. Biochem. 270 (3), 404–414. doi:10.1046/j.1432-1033.2003.03414.x
Vigil, D., Gallagher, S. C., Trewhella, J., and García, A. E. (2001). Functional Dynamics of the Hydrophobic Cleft in the N-Domain of Calmodulin. Biophysical J. 80 (5), 2082–2092. doi:10.1016/s0006-3495(01)76182-6
Villalobo, A., Ishida, H., Vogel, H. J., and Berchtold, M. W. (2018). Calmodulin as a Protein Linker and a Regulator of Adaptor/scaffold Proteins. Biochim. Biophys. Acta (Bba) - Mol. Cel Res. 1865 (3), 507–521. doi:10.1016/j.bbamcr.2017.12.004
Wall, M. E., Clarage, J. B., and Phillips, G. N. (1997). Motions of Calmodulin Characterized Using Both Bragg and Diffuse X-ray Scattering. Structure 5 (12), 1599–1612. doi:10.1016/s0969-2126(97)00308-0
Wang, Q., Liang, K.-C., Czader, A., Waxham, M. N., and Cheung, M. S. (2011). The Effect of Macromolecular Crowding, Ionic Strength and Calcium Binding on Calmodulin Dynamics. PLOS Comput. Biol. 7 (7), e1002114. doi:10.1371/journal.pcbi.1002114
Wang, Q., Zhang, P., Hoffman, L., Tripathi, S., Homouz, D., Liu, Y., et al. (2013). Protein Recognition and Selection through Conformational and Mutually Induced Fit. Proc. Natl. Acad. Sci. 110 (51), 20545–20550. doi:10.1073/pnas.1312788110
Weinstein, H., and Mehler, E. L. (1994). Ca2+-Binding and Structural Dynamics in the Functions of Calmodulin. Annu. Rev. Physiol. 56, 213–236. doi:10.1146/annurev.ph.56.030194.001241
Westerlund, A. M., and Delemotte, L. (2018). Effect of Ca2+ on the Promiscuous Target-Protein Binding of Calmodulin. Plos Comput. Biol. 14 (4), e1006072. doi:10.1371/journal.pcbi.1006072
Wriggers, W., Mehler, E., Pitici, F., Weinstein, H., and Schulten, K. (1998). Structure and Dynamics of Calmodulin in Solution. Biophysical J. 74 (4), 1622–1639. doi:10.1016/s0006-3495(98)77876-2
Wu, G., Gao, Z., Dong, A., and Yu, S. (2012). Calcium-induced Changes in Calmodulin Structural Dynamics and Thermodynamics. Int. J. Biol. Macromolecules 50 (4), 1011–1017. doi:10.1016/j.ijbiomac.2012.02.017
Wu, H., Wolynes, P. G., and Papoian, G. A. (2018). AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins. J. Phys. Chem. B 122 (49), 11115–11125. doi:10.1021/acs.jpcb.8b05791
Yamniuk, A. P., and Vogel, H. J. (2004). Calmodulin's Flexibility Allows for Promiscuity in its Interactions with Target Proteins and Peptides. Mb 27 (1), 33–58. doi:10.1385/mb:27:1:33
Yang, C., Jas, G. S., and Kuczera, K. (2001). Structure and Dynamics of Calcium-Activated Calmodulin in Solution. J. Biomol. Struct. Dyn. 19 (2), 247–271. doi:10.1080/07391102.2001.10506736
Yang, C., Jas, G. S., and Kuczera, K. (2004). Structure, Dynamics and Interaction with Kinase Targets: Computer Simulations of Calmodulin. Biochim. Biophys. Acta (Bba) - Proteins Proteomics 1697 (1), 289–300. doi:10.1016/j.bbapap.2003.11.032
Yang, W., Lee, H.-W., Hellinga, H., and Yang, J. J. (2002). Structural Analysis, Identification, and Design of Calcium-Binding Sites in Proteins. Proteins 47 (3), 344–356. doi:10.1002/prot.10093
Zhang, P., Han, J., Cieplak, P., and Cheung, M. S. (2021). Determining the Atomic Charge of Calcium Ion Requires the Information of its Coordination Geometry in an EF-Hand Motif. J. Chem. Phys. 154 (12), 124104. doi:10.1063/5.0037517
Zhang, P., Tripathi, S., Trinh, H., and Cheung, M. S. (2017). Opposing Intermolecular Tuning of Ca2+ Affinity for Calmodulin by Neurogranin and CaMKII Peptides. Biophysical J. 112 (6), 1105–1119. doi:10.1016/j.bpj.2017.01.020
Keywords: calmodulin dynamics, calcium-binding protein, conformational changes, intrinsic disorder, AWSEM, community model
Citation: Nde J, Zhang P, Ezerski JC, Lu W, Knapp K, Wolynes PG and Cheung MS (2021) Coarse-Grained Modeling and Molecular Dynamics Simulations of Ca2+-Calmodulin. Front. Mol. Biosci. 8:661322. doi: 10.3389/fmolb.2021.661322
Received: 30 January 2021; Accepted: 21 July 2021;
Published: 24 August 2021.
Edited by:
Vojtech Spiwok, University of Chemistry and Technology in Prague, CzechiaReviewed by:
Jianhan Chen, University of Massachusetts Amherst, United StatesManuel N. Melo,Universidade Nova de Lisboa, Portugal
Sunita Negi, GD Goenka University, India
Copyright © 2021 Nde, Zhang, Ezerski, Lu, Knapp, Wolynes and Cheung. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Margaret S. Cheung, bXNjaGV1bmdAdWguZWR1
 Jules Nde
Jules Nde Pengzhi Zhang
Pengzhi Zhang Jacob C. Ezerski1
Jacob C. Ezerski1 Peter G. Wolynes
Peter G. Wolynes Margaret S. Cheung
Margaret S. Cheung