Gibbs Free Energy Calculation of Mutation in PncA and RpsA Associated With Pyrazinamide Resistance

A central approach for better understanding the forces involved in maintaining protein structures is to investigate the protein folding and thermodynamic properties. The effect of the folding process is often disturbed in mutated states. To explore the dynamic properties behind mutations, molecular dynamic (MD) simulations have been widely performed, especially in unveiling the mechanism of drug failure behind mutation. When comparing wild type (WT) and mutants (MTs), the structural changes along with solvation free energy (SFE), and Gibbs free energy (GFE) are calculated after the MD simulation, to measure the effect of mutations on protein structure. Pyrazinamide (PZA) is one of the first-line drugs, effective against latent Mycobacterium tuberculosis isolates, affecting the global TB control program 2030. Resistance to this drug emerges due to mutations in pncA and rpsA genes, encoding pyrazinamidase (PZase) and ribosomal protein S1 (RpsA) respectively. The question of how the GFE may be a measure of PZase and RpsA stabilities, has been addressed in the current review. The GFE and SFE of MTs have been compared with WT, which were already found to be PZA-resistant. WT structures attained a more stable state in comparison with MTs. The physiological effect of a mutation in PZase and RpsA may be due to the difference in energies. This difference between WT and MTs, depicted through GFE plots, might be useful in predicting the stability and PZA-resistance behind mutation. This study provides useful information for better management of drug resistance, to control the global TB problem.

GRAPHICAL ABSTRACT

Graphical Abstract. Most of the functions are performed by DNA, RNA, and proteins molecules. Mutations in these molecules may affect the dynamic properties and free energies, results in weak or loss of interactions.

Introduction

Evolution may have optimized proteins to perform proper functions, native to the host organism, in different environmental conditions. Pharmaceutical industries desire changes in the thermodynamic properties of a protein (Liszka et al., 2012; Gapsys et al., 2016) to enhance the thermal stability, improving the protein–protein interactions. These desired changes are oftenly accomplished by mutations, and the free-energy changes are predicted to gain the desired properties. However, natural mutation in drug target may cause a resistance to the therapeutic drugs. Such mutations pose a great threat to the treatment of major infectious diseases. Understanding the forces like thermodynamic properties and protein folding involved in maintaining the protein structures, is of central interest when working on drug resistance. The folding process is most often affected by mutations (Carra and Privalov, 1996). To explore the dynamic properties behind mutations, molecular dynamic (MD) simulations have been widely performed, and have been especially useful in unveiling the mechanism of drug failure behind mutation (Carter Childers and Daggett, 2017; Dong et al., 2018; Hashemzadeh et al., 2019; Kaushik et al., 2019). MD simulation studies of ligand-protein interactions are a widely applied approach for explaining the mechanisms of drug resistance behind mutations (Aggarwal et al., 2017; Carter Childers and Daggett, 2017; Bera et al., 2018; Liu et al., 2018; Pandey et al., 2018; Ishima et al., 2019). During in vivo analysis, the crystal structure is analyzed for drug resistance. However, it can be formed based on some experimental conditions where none of the protein-drug complexes provide the mechanism of resistance, and none of the structures can be attained by X-ray. Investigating the insight mechanism at molecular level, MD simulation has got a certain advantage over experimental approaches of exploring drug resistance behind mutations (Liu and Yao, 2010; Khalaf and Mansoori, 2018; Liu et al., 2018; Meng et al., 2018; Mehmood et al., 2019). Furthermore, the dynamics and residues level analysis could be performed which was difficult to achieve through experimental approaches (Hou et al., 2008; Xue et al., 2012; Ding et al., 2013; Khan et al., 2018).

The effect of mutations on a protein complex is experimentally performed by different methods including isothermal titration calorimetry (ITC) (Ghai et al., 2012), surface plasmon resonance (Masi et al., 2010), Fluorescence resonance energy transfer (FRET) (Phillip et al., 2012), and some other procedures as described earlier (Kastritis and Bonvin, 2013). However, all these techniques are considered to be time consuming as well as costly. The mechanism of resistance behind mutation is of key interest where free energy is commonly altered. To estimate changes in the thermodynamics of wild types and mutant proteins, MD-based free energy calculations allow a precise measurement of changes (Aldeghi et al., 2019). Gibbs free energy (GFE) or free enthalpy (Greiner et al., 1995; Matthews, 2000; Li et al., 2014; Rietman et al., 2016) can be used to estimate the maximum level at which the process is reversible, performed through a thermodynamic system. The GFE is the non-expansion work, calculated from a thermodynamically closed system where this maximum can be achieved individually in an entirely reversible procedure. The reversible transformation of a system is going to decrease in GFE, from initial state to a final state, equal to the work done by the system to its surroundings, minus the work of the pressure forces (Matthews, 2000).

The most common cause of drug resistance is mutation in the target proteins (Thomas et al., 1996; Bell et al., 2005; Wang et al., 2007; Ashworth, 2008; Yun et al., 2008; Tyagi et al., 2013; Reiche et al., 2017; Palzkill and Palzkill, 2018; Yang et al., 2018). Pyrazinamidase (PZase) has three major regions, 3–17, 61–85, and 132–142, associated with PZase catalytic activity (Lemaitre et al., 2001; Sheen et al., 2009). However, Yoon et al. reported that mutations which occurred far from the active site might be involved in altering the catalytic property by changing the protein folding and expression rate (Sheen et al., 2009; Rajendran and Sethumadhavan, 2013; Yoon et al., 2014; Yadon et al., 2017). Amino acid substitution of a protein’s structure may result in drastic effects, especially on the binding pockets and its surroundings (Worth et al., 2009; Ganesan and Ramalingam, 2018) or they may have long-ranging effects (Kosloff and Kolodny, 2008). The second major cause behind PZA resistance is mutations in RpsA. In MTB it has four S1 domains (amino acids from 36–105, 123–188, 209–277, and 294–363) (Salah et al., 2009). Residues, F307, F310, H322, D352, and R357 are present in RNA binding sites, involved in proper function (Bycroft et al., 1997). Residues in the fourth S1 domain, which is known as a highly conserved region and is able to interact with pyrazinoic acid (POA), the active form of PZA.

The internal motion of the system is measured using Principal Component Analysis (PCA), which is performed on the mass-weighted cartesian coordinates, and the long dynamics are able to recognize low modes in proteins (Jencks, 1981; Rajendran et al., 2018). In a long trajectory, PCA reduces the complicated motion (Novotny, 1991; Zídek et al., 1999; Datar et al., 2006). In a comparative analysis of two sets of proteins, a transformed set of variables z1, z2…, zp called principal components (PCs) where the PC1 and PC2 are the first two components, give the trajectories on the primary two principal components of motion (Verma et al., 2008; Martis et al., 2015).

Binding free energy calculations yield either absolute free energies (Molecular mechanics generalized Born surface area and Molecular mechanics Poisson–Boltzmann surface area) or relative free energies (Alchemical method) (Michel and Essex, 2010; Chodera et al., 2011; Mobley and Klimovich, 2012). Alchemical free energy calculations work by introducing a series of intermediate unphysical states spanning between the desired end states. Molecular docking combined with MD simulations followed by Molecular mechanics Poisson–Boltzmann surface area (MM/PBSA) analysis is an efficient approach for Free energy calculation. The results of MM/PBSA are in reasonable agreement with previous experiments (Wang and Kollman, 2000, 2001; Wang et al., 2001) and less computationally demanding than alchemical free energy methods. These two methods have been widely applied in biomolecules such as protein folding, protein–ligand binding, protein–protein interaction, etc. (Hou, 2010; Xu et al., 2013; Chen et al., 2015, 2019; Sun et al., 2018; Wang et al., 2019). MM-PBSA and Molecular Mechanics/Generalized Born Surface Area (MM/GBSA) have been the two most efficient methods to rapidly evaluate binding ability and to compute binding free energies (Hou, 2010; Sun et al., 2014a).

In previous studies, we have investigated the PZA drug sensitivity testing and then sequencing to find mutations in pncA and rpsA genes associated with PZA-resistance (Khan et al., 2018,a, Khan et al., 2019c) (Accession No. MH461111). MD simulation of some MTs in comparison with WT have been investigated as the cause behind resistance (Junaid et al., 2018; Khan et al., 2018,a,c, 2019b; Rehman et al., 2019). In the current paper, we aimed to reanalyze the free energy differences, predicted via MM/GBSA and MM/PBSA, of WT and MTs that may be applied as a measure of stability in the binding affinity of drug and targets.

Materials and Methods

Mutants Selection in pncA

The primary cause behind PZA resistance have been associated with mutations in the pncA gene. The majority of studies have been conducted to investigate the drug resistance mechanism behind mutation by analyzing the root mean square deviation, root mean square fluctuation, and motion of MTs and WT PZase. However, the comparison of free energy as a mechanism of changes that occur behind a mutation is required to be investigated for better understanding of PZA-resistance. Here we selected N11K, P69T, D126N, L19R, R140H, and E144K to analyze the effect of mutations on free energy by comparing the MTs and WT (Junaid et al., 2018; Khan et al., 2018,a). A three-dimensional structure (PDB ID 3pl1) was retrieved from the Brookhaven Raster Display (BRAD) protein data bank (PDB) (Berman et al., 2000). Using the mutate_Model script of Modeller (Webb and Sali, 2016) and PYMOL (DeLano, 2002), mutants were created at specific locations.

Mutants Selection in rpsA

In our previous study (Khan et al., 2018,b), we detected mutations, S324F, E325K, G341R, D342N, D343N, A344P, I351F, T370P, and W403G in the conserved region (292–363) called C-terminus RpsA (MtRpsA^CTD) of the rpsA gene in PZA resistance isolates. The crystal structure of RpsA (Yang et al., 2015) (PDB ID 4NNI) was retrieved from PDB Databank, and all the water of crystallization was removed. Mutants were generated at positions S324F, E325K, G341R, D342N, D343N, A344P, I351F, T370P, and W403G using PYMOL (DeLano, 2002). Free energy differences between MTs and WT RpsA from our previous papers (Khan et al., 2018c, 2019b; Rehman et al., 2019) were re-analyzed. PZA is a prodrug, activated by MTB encoded pncA into POA, targeting RpsA. POA-resistance may occur when mutations arise at the C-terminus of RpsA (MtRpsA^CTD), causing conformational changes (Yang et al., 2015; Huang et al., 2019; Khan et al., 2019a; Shi et al., 2019; Singh et al., 2019; Zhi et al., 2019). Residues in the fourth S1 domain, which is known as a highly conserved region, were able to interact with POA (Shi et al., 2011; Yang et al., 2015). The C-terminal region of RpsA is the drug binding site, replacing the transfer-messenger RNA (tmRNA) complex during the translation process (Shi et al., 2011).

Protein-Ligand Interaction

Protein and ligand structures were prepared as described in earlier studies (Aggarwal et al., 2017; Friesner et al., 2004) using MOE. Incorrect hydrogen atoms were corrected and selenomethionine were changed into methionine. Protein–drug interactions were examined in MOE as a flexible docking. WT and MTs structure were subjected to MD simulations in apo and complex with the drug.

Molecular Dynamics Simulation (MD)

MD simulation was performed on all the MTs and WT using the Amber14 package (Salomon-Ferrer et al., 2013; Sun et al., 2014a,b) with the ff14SB force field. The TIP3P water model was used to solvate each system and counterion were added to neutralize the system (Jorgensen et al., 1983). The neutralized systems were minimized with the steepest descent minimization step (6000 cycles) and conjugate gradient (3000 cycles) followed by heating upto 300K. The systems were equilibrated at 1 atm and 300 K. For control of the temperature, the Langevin thermostat was turned on. For Long-range electrostatic interactions, the Particle Mesh Ewald algorithm was used (Darden et al., 1993; Essmann et al., 1995) and the treatment of the covalent bonds was performed with the SHAKE algorithm (Ryckaert et al., 1977). The production step of MD simulation was performed with pmemd code 30 (Götz et al., 2012). The cpptraj package in Amber 14 was used to analyze the trajectories.

Principal Component Analysis and Gibbs Free Energy Calculation

The high fluctuations in residues of protein were captured through principal component analysis (PCA) (Amadei et al., 1993) while variation in GFE values has been accounted for in the calculation of stability level in proteins molecules to perform proper function (Rajendran et al., 2018; Martis and Coutinho, 2019; Sohaib Shahzan et al., 2019). GFE calculation is a useful process for understanding the thermodynamic properties of antibody-antigen complex formation and proteins-proteins interactions (Jencks, 1981; Novotny, 1991; Zídek et al., 1999). Using a cpptraj package, the covariance matrix was calculated considering only the Cα coordinates followed by the diagonalization to calculate the eigenvectors and eigenvalues. PCA was calculated from the trajectory, containing 5000 snapshots. PC1 and PC2, the first two components, were used for the plotting. The binding free energy was calculated as described in previous studies (Sun et al., 2014a,b; Martis and Coutinho, 2019).

$\mathrm{\Delta }{G}_{bind}=G_{complex}-(G_{protein}+G_{ligand})(1)$

The binding events involved many interactions (Wang and Wade, 2001; Datar et al., 2006; Verma et al., 2008; Martis et al., 2015), therefore the classical binding free energy equation may be written as follows:

$\mathrm{\Delta }{G}_{bind}=G_{sol}+G_{conf}+G_{int}+G_{motion}(2)$

In equation 2, Gs_ol: solvation energy, G_conf: conformational energy, G_int energy due to interaction with residues in the vicinity, G_motion: energy of motions (translational, rotational, and vibrational).

The free energy landscape (FEL) was developed using g_sham module to capture the lowest energy stable state. The deep valleys on a plot show the stable state while the boundaries between deep valleys represent the intermediate conformations (Hoang et al., 2004). The first two principal components were used to calculate the FEL based on the equation:

$\mathrm{\Delta }\mathrm{G}(\mathrm{PC1},\mathrm{PC2})=-\mathrm{KBTlnP}(\mathrm{PC1},\mathrm{PC2})(3)$

PC1 and PC2 are reaction coordinates, KB symbolizes the Boltzmann constant, and P (PC1, PC2) illustrate the probability distribution of the system along the first two principal components.

The changes in enthalpy (ΔH), standard free energy (ΔG), and entropy (ΔS) are calculated using the following equation (Basu, 2010; Gautam and Chattopadhyaya, 2016);

$\mathrm{\Delta }\mathrm{G}=\mathrm{\Delta }\mathrm{H}--\mathrm{T}\mathrm{\Delta }\mathrm{S}(4)$

Where, ΔH = Enthalpy, T = temperature in Kelvin, ΔS = entropy, ΔG = Gibbs Free Energy.

In the current review we analyzed the GFE of MTs and WT PZase and RpsA that might be useful to measure the resistance among drug target proteins for better management of drug resistance.

Solvation Free Energies of Wild Type and Mutants

The solvation free energy is the product of the atomic solvation parameter and the accessibility of the atom to the solvent. This method estimates the relative stability of protein conformations, and estimates the free energy of proteins binding to ligands (Eisenberg and McLachlan, 1986). The stability and fluctuation of protein are measured through the solvation. Protein and solvent interactions at atomic level is quantified by solvation free energy (SFE). Free energy of protein hydration (solvation) is carried out with explicit solvent and all-atom treatment (Weber and Asthagiri, 2012; Kokubo et al., 2013; Matubayasi, 2017). Here we calculated the Solvation Free Energy (ΔGsolv) of WT and MTs PZase and RpsA to find the effect of mutation on the proteins solvation free energy.

Results and Discussion

PCA and Entropy

Intra-protein information is transmitted over distances via allosteric processes. This ubiquitous protein process allows for protein function changes due to ligand binding events. Understanding protein allostery is essential in protein functions. Allostery in the protein has been inspected using a rigid residue scan method along with configurational entropy calculation and PCA. Based on a covariance correlation analysis of simulations, the contributions from individual residues to whole-protein dynamics have been systematically assessed and the entropic contributions of individual residues to whole-protein dynamics were also evaluated. When individual residues are held rigid, the variations of overall protein entropy favor the rigidity/flexibility equilibrium in protein structure. Further, the change of entropic contribution from each residue has been linked to the intrinsic differences among all the residues. These findings provide a systematic approach to dig out the contribution of individual residue’s internal motion to overall protein dynamics and allostery (Bhakat et al., 2014; Kalescky et al., 2016).

Gibbs Free Energy Comparison Between Wild Type and Mutant in PncA

Geographically distinct and novel mutations have been detected in our recent studies (Khan et al., 2018,b, Khan et al., 2019c) after the drug susceptibility testing followed by pncA and rpsA sequencing of PZA resistance Mycobacterium tuberculosis isolates. Changes in values of GFE might be important in calculating the stability of proteins’ confirmation. In order to explore the protein conformational shift from WT to mutant, the GFE for the first two principal components (PC1 and PC2) has been calculated. The energy landscape of both the apo and complex states of WT, and three mutants, N11K, P69T and D126N have been shown in Figure 1. The minimum energy area is indicated by the blue color. WT protein shows a clear large global energy minima basin (in blue), whereas the MTs reveal several different energy minima states. The blue areas depict more stability while more blue areas indicate transitions in the protein conformation followed by the thermodynamically more favorable state. The WT shows low energy state as compared to the MTs. The result demonstrates that native PZase has a more stable cluster as compared to the MTs that might be involved in low binding affinity with PZA, causing resistance (Junaid et al., 2018; Yang et al., 2018). Calculating the GFE in case of PZA resistance might be a useful way to analyze the MTs stability and also aid in alternative drug discovery.

FIGURE 1

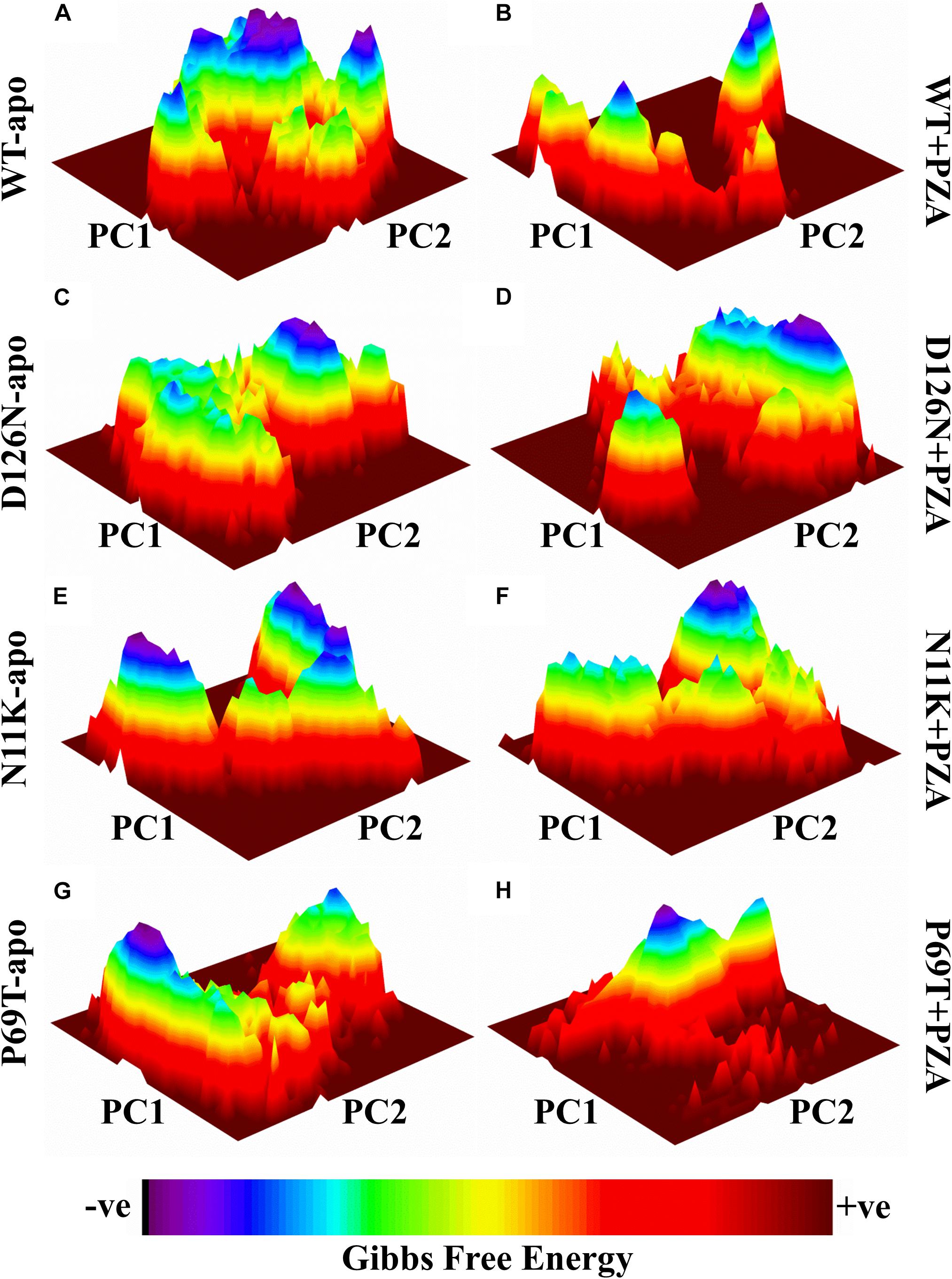
Figure 1. Gibbs free energy of PZase and mutants (N11K, P69T and D126N) in apo and complex state with PZA. The Gibbs free energy landscape for wild and mutated proteins in their apo and wild states is depicted along with their value bars against PC1 and PC2. Noticeable differences can be observed. The red color represents the high energy state, yellow and green low and blue represents the lowest stable state. (A) WT apo (without bound PZA) in comparison with MTs apo have been shown (C,E,G). (B) WT complex (bound with PZA) in comparison with MTs complex (D,F,H).

The differences in GFE values of WT and MTs PZase, L19R, R140H, and E144K showed that mutations may alter the stability (Figure 2) which could be a measure to evaluate the PZA resistance.

FIGURE 2

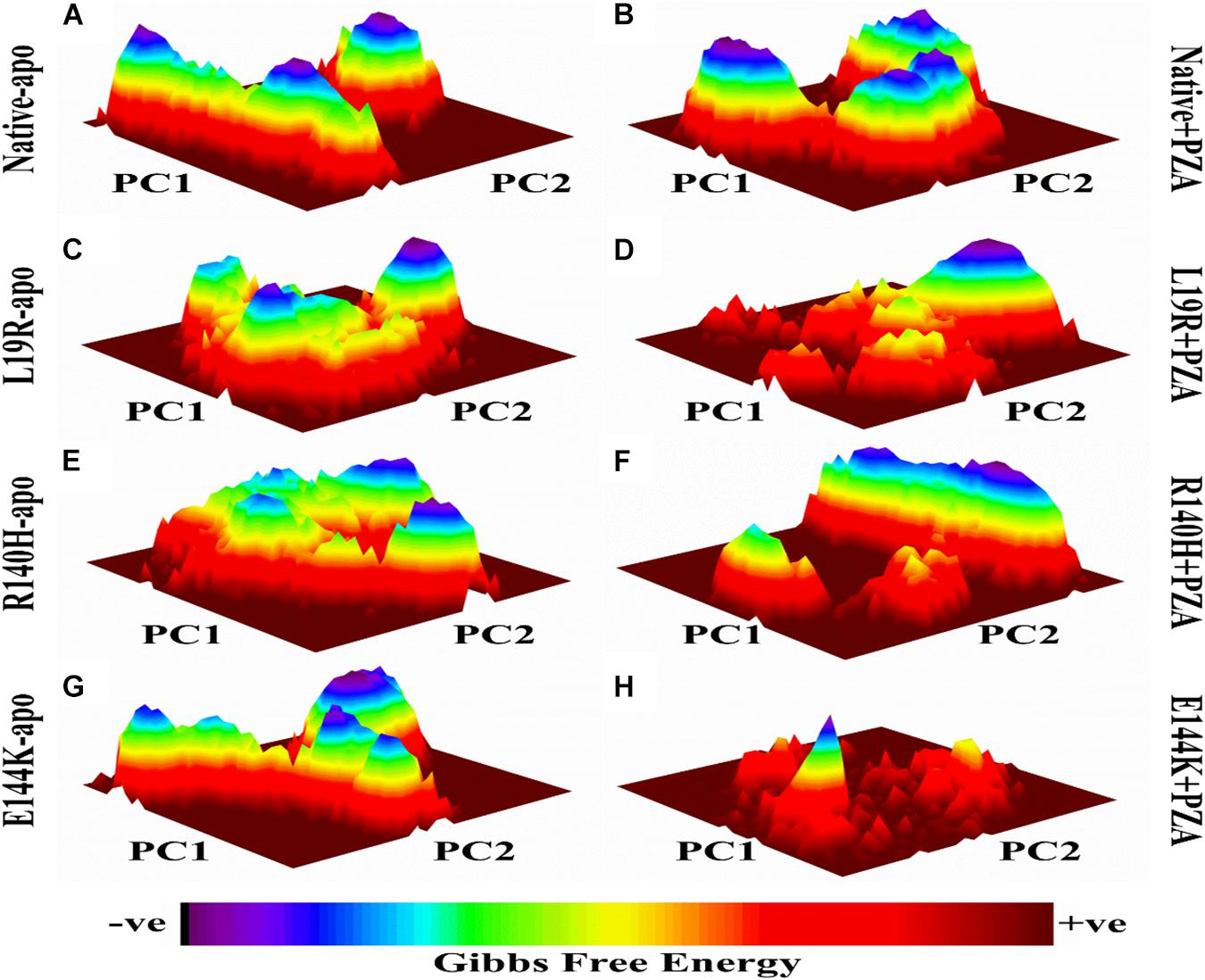
Figure 2. Gibbs free energy of PZase and MTs (L19R, R140H, and E144K) in apo and complex state with PZA. (A,B) GFE peaks of WT apo and complex with PZA. (C,E,F) MTs apo. (D,F,H) MTs complex with PZA. GFE plots of WT and MTs shows a significant difference in stability states behind mutations involved in PZA resistance (Khan, 2019).

Gibbs Free Energy Comparison Between Wild Type and Mutants RpsA

A number of mutations, S24Phe, E325K, G341R, D342N, D343N, A344P, I351F, T370P, and W403G have been detected in the conserved region (292-363) called C-terminal domain (MtRpsA^CTD) of the RpsA (Table 1) in our previous studies among PZA resistance isolates of Mycobacterium tuberculosis (MTB) (Khan et al., 2018,b, Khan et al., 2019b; Rehman et al., 2019). The MtRpsA^CTD is the POA binding site. All these MTs at 100 and 50 ns of MD simulations showed significant change in the structure and activity of RpsA (Figures 3–5).

TABLE 1

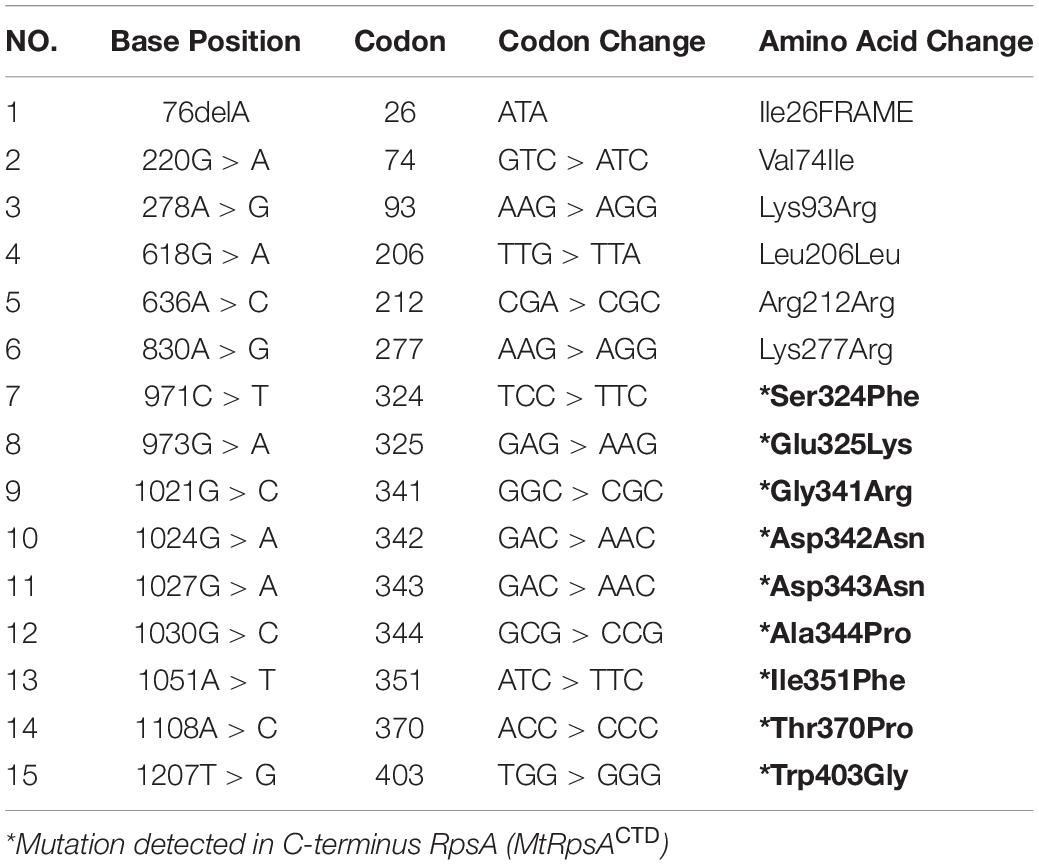
Table 1. Mutations in RpsA gene in PZA resistant pncA^WT isolates (Khan et al., 2018,c).

FIGURE 3

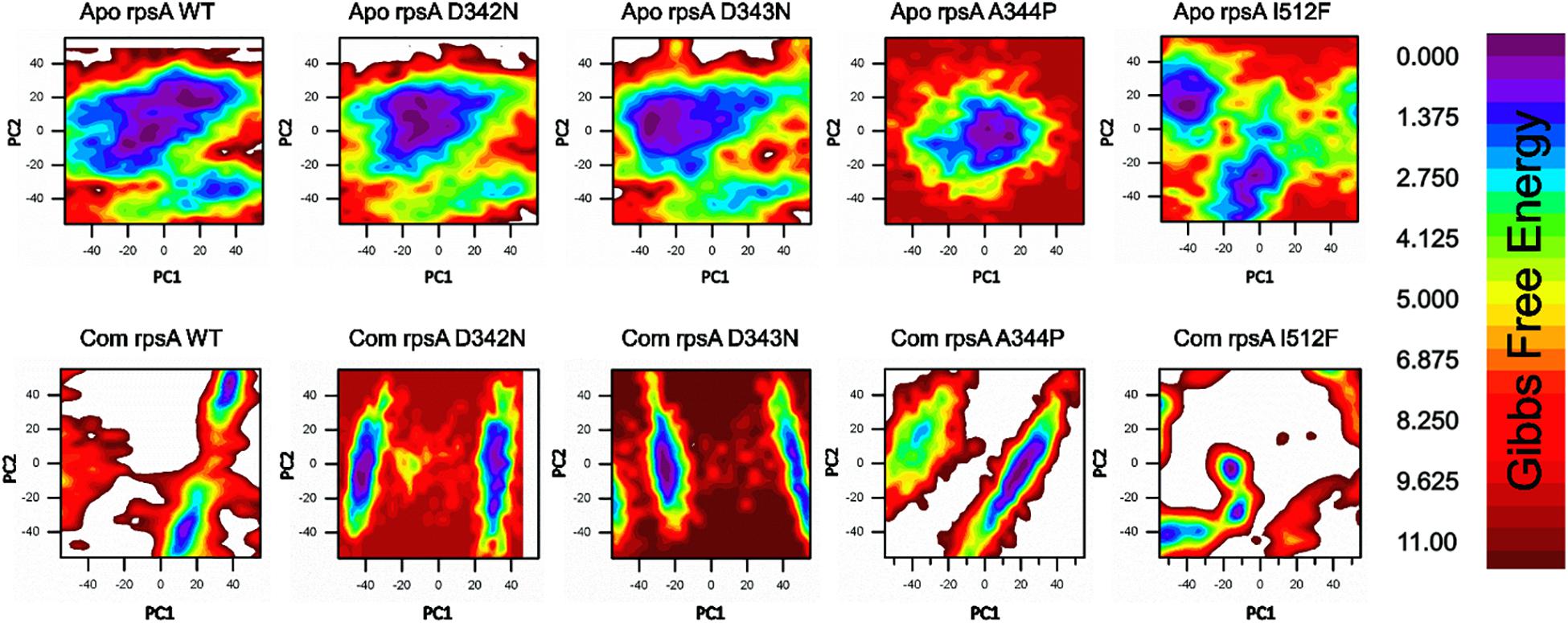
Figure 3. Gibbs free energy (GFE) of WT and MTS, D342N, D343N, A344P, and I351F in apo and complex states. Wild type has a significant GFE difference to MTs as indicated by the color of the GFE plot. WT exhibited a more stable state as compared to mutants. POA resistance might be due the GFE states altering the affinity of RpsA (Khan et al., 2019b).

FIGURE 4

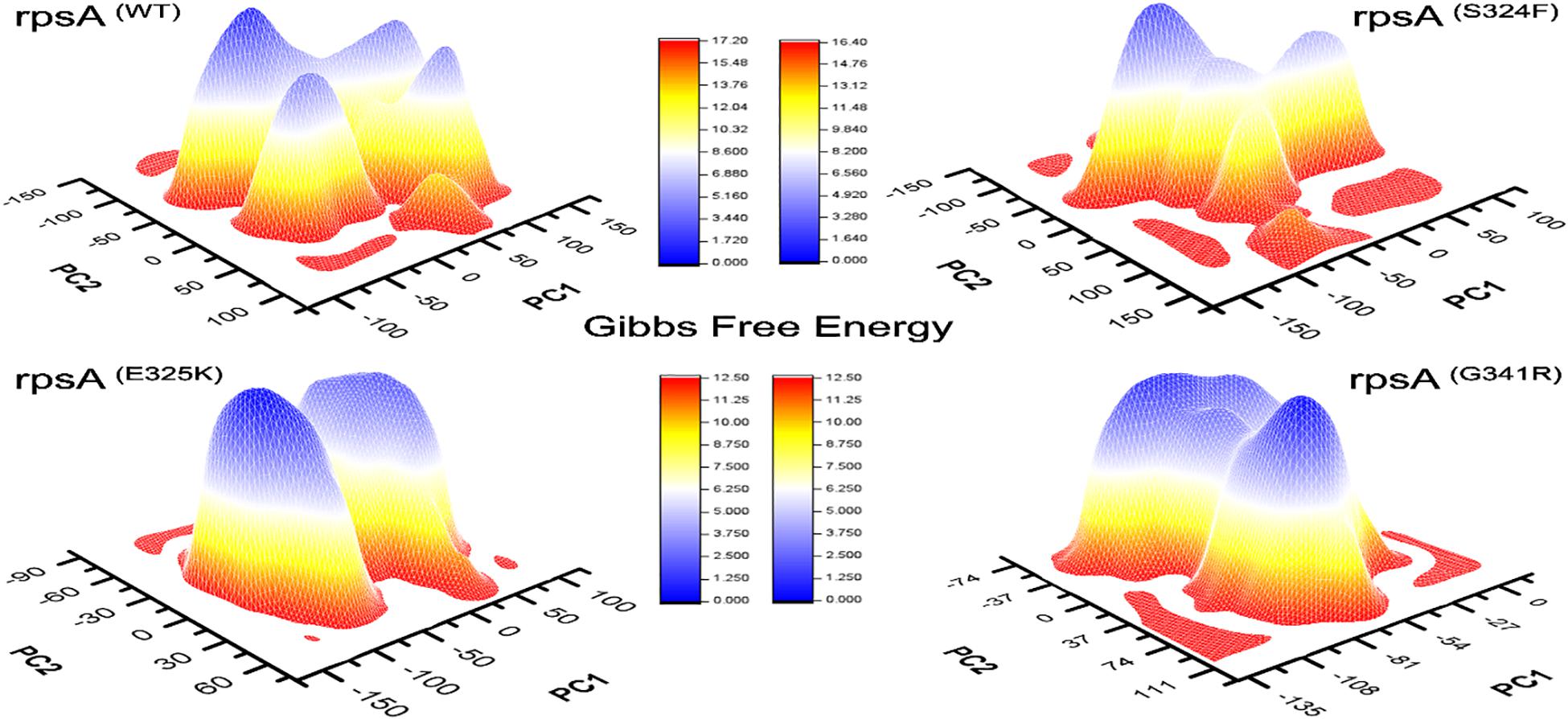
Figure 4. Comparison of Gibbs free energy of MTs and wild type RpsA. WT exhibited a significant difference in GFE as indicated by the peak color of GFE plot.

FIGURE 5

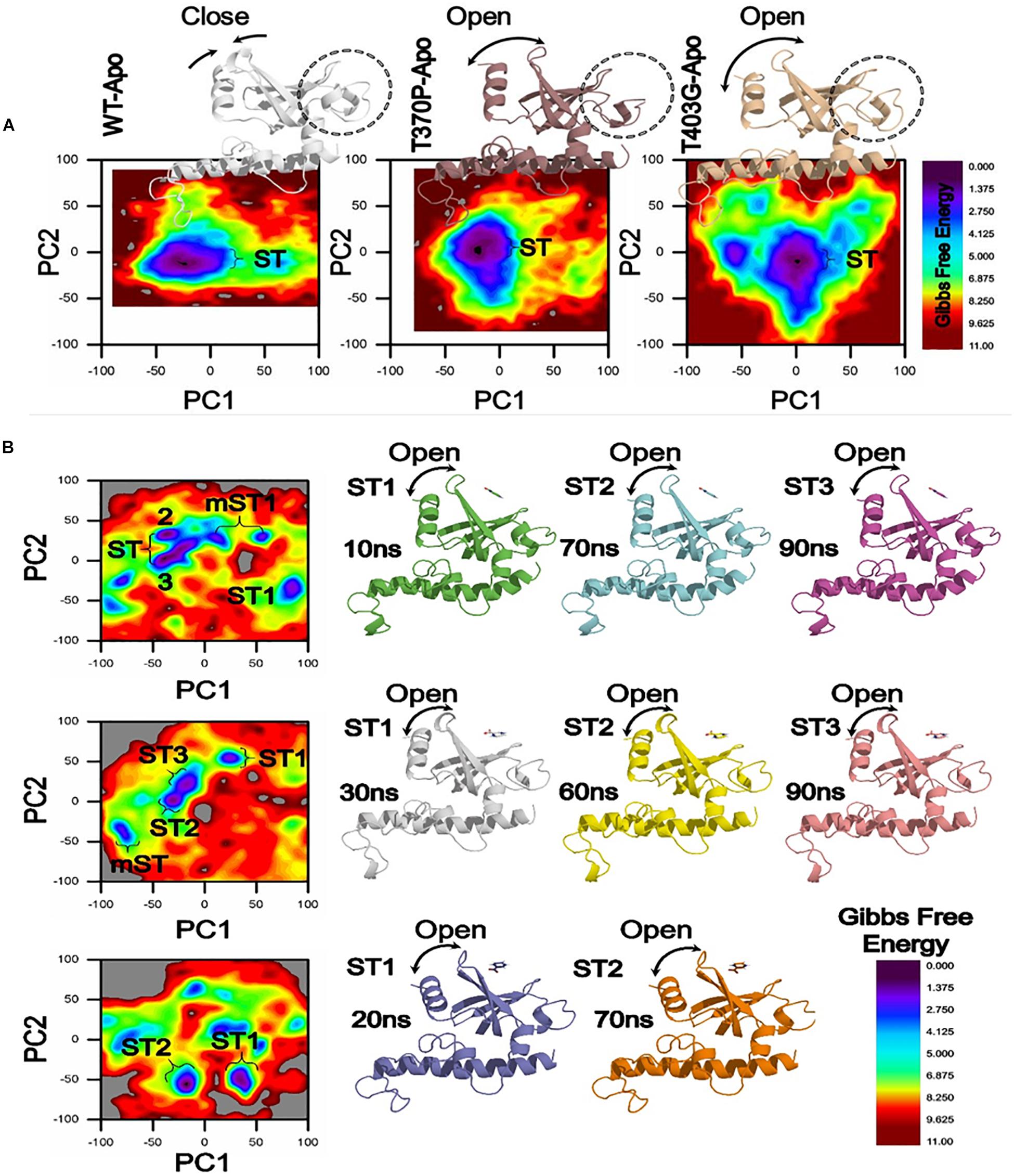
Figure 5. Gibbs Free energy Landscape of WT and MTs (T370P and W403G) in apo (A) and complex states (B). WT exhibited a GFE difference as indicated by the color of the plot. RpsA structure was analyzed at 10, 20, 30, 60, 70, and 90 ns shows variation among the loop and starting residues in ST1, ST2, ST3. The loop and starting residues of proteins are more open at 90 and 70 ns. ST, stable state; mST, metastable state.

A native RpsA structure has the minimum GFE, exhibiting significant variations when compared with MTs, D342N, D343N, A344P and I351F (Figure 3). The color (red) in the plot is more prevalent in mutants, and seems less stable when compared with WT.

The differences in GFE values of other MTs RpsA (S324F, E325K, and G341R) has been shown (Figure 4), revealing that they may have altered the stability of MTs RpsA. WT attained a significant value in comparison with MTs (Figure 5). The peak color in both states of the native is seems to be more stable, indicating the importance of GFE calculation when measuring the effect of mutation on proteins dynamics characteristics.

In a more insightful study of WT and MTs, T370P and W403G RpsA, the comparison shows a significant difference not only in GFE states but also a difference in the loop structure (Figure 5). The loop structure in MTs is seemed to be more open in both apo and complex with POA. These changes may cause POA resistance, resulting in weak or no binding with RpsA. Further, the high energy state might be involved to exhibit a more open loop residue. However, further confirmation through experimental approaches will enhance the understanding of low, medium, and high levels of POA resistance.

The differences in GFE values may have effects on the binding affinity and the stability calculation, resulting in weak interactions or loss of interactions with POA. In a farther site mutation, WT exhibited a significant difference in GFE in comparison with mutants, T370P and W403G (Figure 5). Mutations in C-terminal site of RpsA might be involved in the alteration of GFE, resulting in a loss of binding affinity with the drug.

Solvation Free Energies of Wild Type and Mutant PZase and RpsA

Hydrogen bonding is an important part of molecular interactions where the solvent is water. Free energy of protein hydration (solvation) is carried out with explicit solvent and all-atom treatment (Weber and Asthagiri, 2012; Kokubo et al., 2013; Matubayasi, 2017). The solvation free energy is the product of the atomic solvation parameter and the accessibility of the atom to the solvent. This method estimates the relative stability of protein conformations, and free energy of proteins binding to ligands (Eisenberg and McLachlan, 1986). Protein and solvent interactions at an atomic level is quantified by solvation free energy (SFE). The Solvation Free Energy (ΔGsolv) of WT and MTs have been given (Table 2). Interestingly the MTs PZase exhibited a decreased level of SFE than WT except P69T (−681.60) and D126N (−385.29). Similarly during the investigation of protein kinetics and thermodynamics, the MTs, Y91Q exhibited a decreased SFE and hydrophobicity compared to WT. This may be due to the more exposed and solvated hydrophilic side chains in the R1-region in acylphosphatase (Chong et al., 2011). Another important property while studying the protein thermodynamics is the energy of solvation (ES), recorded when dissolving a solute in a solvent. A positive and negative SE represents endothermic and exothermic processes respectively. This process of solvation is thermodynamically favored only when the overall GFE of the solution is decreased, as compared to the GFE of separated solvent and solute. A negative value is obtained when the change in enthalpy minus the change in entropy is multiplied by the absolute temperature or GFE of the system decreases. All the MTs exhibited lower ES than WT except P69T and D126N (Table 2). Similarly MTs RpsA attained a much lower ES than WT except E325K. Entropy of WT and MTs has been found in significant variation, a measure of a system’s thermal energy per unit temperature, unavailable for useful work. Molecular disorder, or randomness, of a system may also be measured through entropy (Chong and Ham, 2012; Caro et al., 2017; Verteramo et al., 2019).

TABLE 2

Table 2. Comparison of solvation energies of wild types and mutants PZase and RpsA.

Overall, SFE changes by point mutation in PZase and RpsA casusing PZA-resistance during TB treatment regime. The SFE is commonly influenced by the hydrophilic residues. In a previous study the SFE of Y91Q has been found lower by 25.1 kcal/mol than WT acylphosphatase, indicating that Y91Q is less hydrophobic (Chong and Ham, 2011; Chong et al., 2011). Two mutations (R1s40H, E144K) that have been detected in α-helix of PZase exhibited the lowest SFE and SE as shown (Table 2 and Figures 6, 7). All the MTs RpsA attained lower SFE and SE than WT except E325K and G341R. Further, the solvation entropy of all the MTs is higher than WT (−3664.43 kcal/mol) except E325K (−3682.23 kcal/mol) and G341R (−3705.82 kcal/mol). The standard deviation of total free energy has also been given in Table 1 and along with Supplementary Table 1.

FIGURE 6

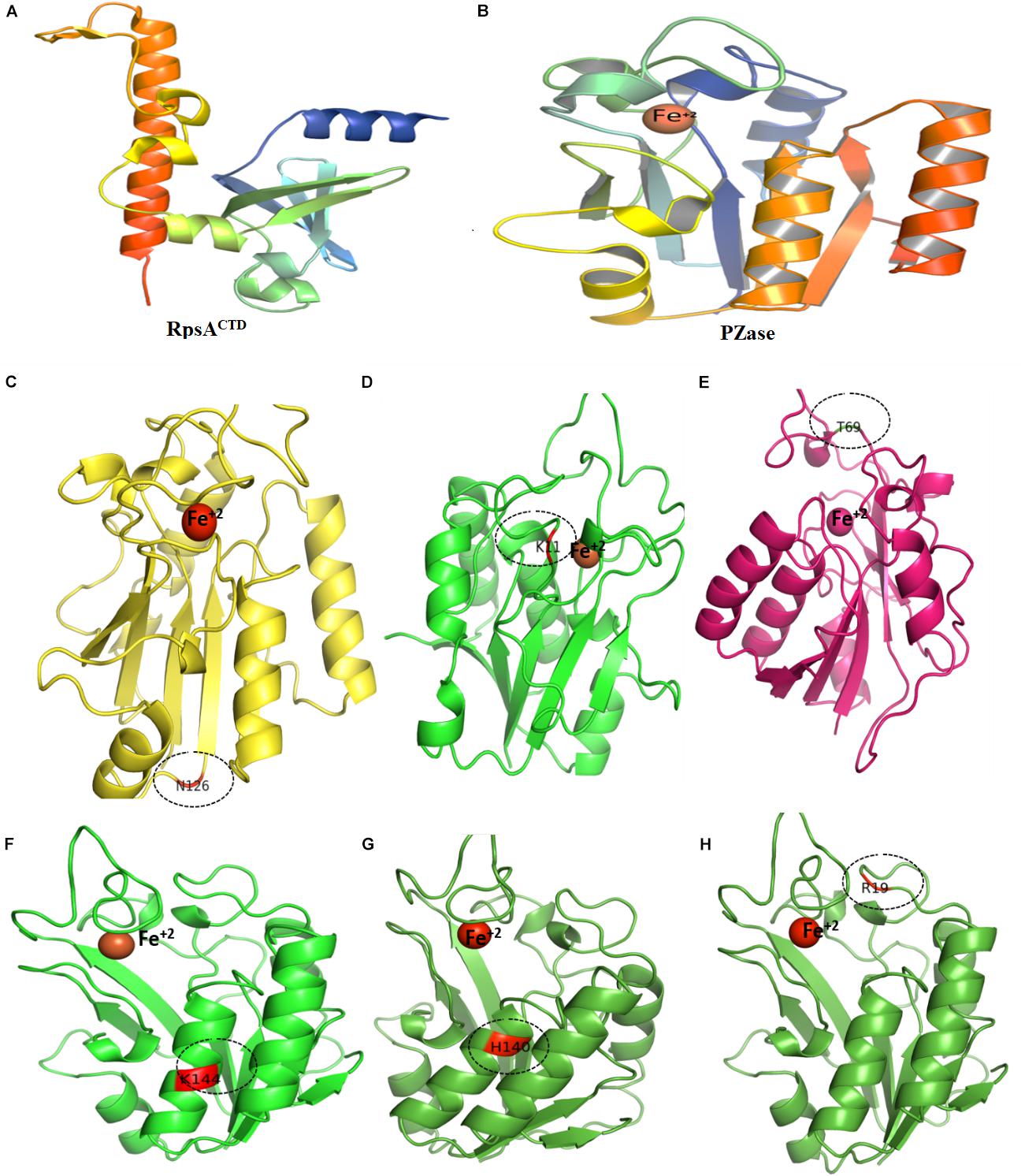
Figure 6. Wild type and mutants PZase structures. Majority of the MTs have been detected in the loop region except (F,G). Fe⁺² ion parameters have been adjusted in Supplementary Table 1.

FIGURE 7

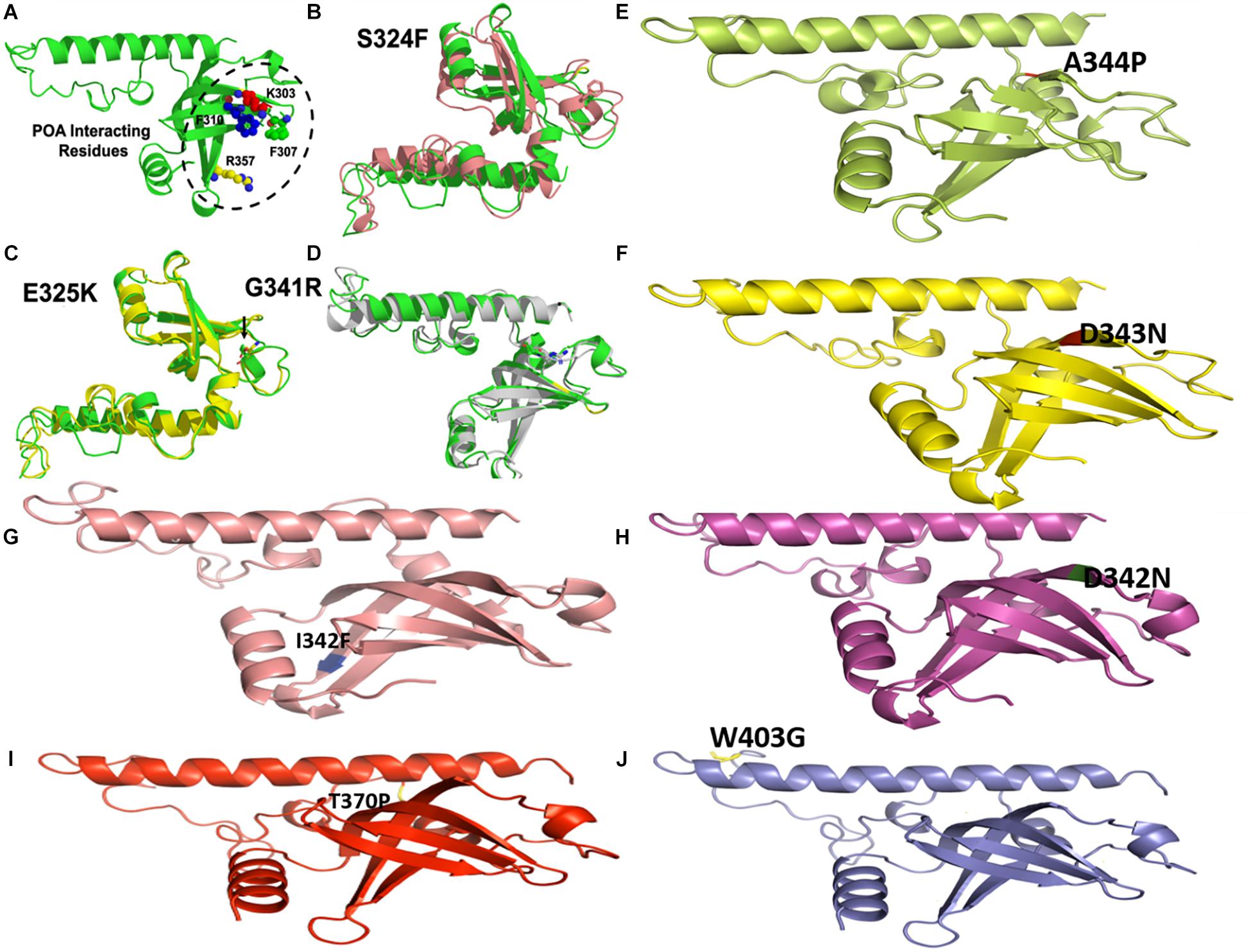
Figure 7. Wild type and mutants RpsA structures. MTs have been highlighted at their original positions. (A) POA interacting residues have been shown. (E,I,J) Mutations in loop region. (B–D) Superimposed MTs and WT. (F–H) Mutations in helix regions.

Conclusion

In the current analysis GFE along with SFE and SE of WT and MTs exhibited a significant difference which might be useful in predicting the drug resistance level behind mutations in PZase and RpsA. Molecular dynamics simulations, binding free energy, and PCA clearly show the impact of mutations on thr thermodynamics of proteins. These findings depict that mutations affect the overall enzyme’s conformational landscape and distort the atomic interaction network. The GFE differences provide rapid potential, key for further designing of novel inhibitors to combat MTB resistant strains. The physiological effect of mutations in drug targets might be due to the energy differences. Evolutionary pressures might have maintained a protein folding integrity and stability while mutations may have decreased and posed severe consequences in disturbing bonds of intrinsic energy. The level of resistance might be analyzed through further experimental analysis and alternative drug discovery for better achieving the goals of the global TB eradication program 2030.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

D-QW: manuscript design. MK, AK, and SA: manuscript analysis. SM, MZ, MK and SA: manuscript writing. D-QW and AK: manuscript approval.

Funding

D-QW was supported by the grants from the Key Research Area Grant 2016YFA0501703 of the Ministry of Science and Technology of China, the National Natural Science Foundation of China (Contract no. 61832019, 61503244), the Science and Technology Commission of Shanghai Municipality (Grant: 19430750600), the Natural Science Foundation of Henan Province (162300410060) and Joint Research Funds for Medical and Engineering and Scientific Research at Shanghai Jiao Tong University (YG2017ZD14). The computations were partially performed at the Pengcheng Lab. And the Center for High-Performance Computing, Shanghai Jiao Tong University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are thankful for technical support of Dr. Qasim Abbas, project director provincial TB control Programme. The simulations in this work were supported by the Center for High-Performance Computing, Shanghai Jiao Tong University.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmolb.2020.00052/full#supplementary-material

References

Aggarwal, M., Singh, A., Grover, S., Pandey, B., Kumari, A., Grover, A., et al. (2017). Role of pnc A gene mutations W68R and W68G in pyrazinamide resistance. J. Cell Biochem. 13:593.

Google Scholar

Aldeghi, M., de Groot, B. L., and Gapsys, V. (2019). Accurate calculation of free energy changes upon amino acid mutation. Methods Mol. Biol. 1851, 19–47. doi: 10.1007/978-1-4939-8736-8_2

PubMed Abstract | CrossRef Full Text | Google Scholar

Amadei, A., Linssen, A. B., and Berendsen, H. J. (1993). Essential dynamics of proteins. Proteins 17, 412–425. doi: 10.1002/prot.340170408

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashworth, A. (2008). Drug resistance caused by reversion mutation. Cancer Res. 68, 10021–10023. doi: 10.1158/0008-5472.can-08-2287

PubMed Abstract | CrossRef Full Text | Google Scholar

Basu, P. (2010). “Chapter 5 - gasification theory and modeling of gasifiers,” in Biomass Gasification and Pyrolysis, ed. P. Basu (Boston: Academic Press).

Google Scholar

Bell, D. W., Gore, I., Okimoto, R. A., Godin-Heymann, N., Sordella, R., Mulloy, R., et al. (2005). Inherited susceptibility to lung cancer may be associated with the T790M drug resistance mutation in EGFR. Nat. Genet. 37, 1315–1316. doi: 10.1038/ng1671

PubMed Abstract | CrossRef Full Text | Google Scholar

Bera, K., Rani, P., Kishor, G., Agarwal, S., Kumar, A., Singh, D. V., et al. (2018). Structural elucidation of transmembrane domain zero (TMD0) of EcdL: a multidrug resistance-associated protein (MRP) family of ATP-binding cassette transporter protein revealed by atomistic simulation. J. Biomol. Struct. Dyn. 36, 2938–2950. doi: 10.1080/07391102.2017.1372311

PubMed Abstract | CrossRef Full Text | Google Scholar

Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., et al. (2000). The protein data bank. Nucleic Acids Res. 28, 235–242.

Google Scholar

Bhakat, S., Martin, A. J. M., and Soliman, M. E. S. (2014). An integrated molecular dynamics, principal component analysis and residue interaction network approach reveals the impact of M184V mutation on HIV reverse transcriptase resistance to lamivudine. Mol. Biosyst. 10, 2215–2228. doi: 10.1039/c4mb00253a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bycroft, M., Hubbard, T. J., Proctor, M., Freund, S. M., and Murzin, A. G. (1997). The solution structure of the S1 RNA binding domain: a member of an ancient nucleic acid-binding fold. Cell 88, 235–242. doi: 10.1016/s0092-8674(00)81844-9

CrossRef Full Text | Google Scholar

Caro, J. A., Harpole, K. W., Kasinath, V., Lim, J., Granja, J., Valentine, K. G., et al. (2017). Entropy in molecular recognition by proteins. Proc. Natl. Acad. Sci. U.S.A. 114, 6563–6568.

Google Scholar

Carra, J. H., and Privalov, P. L. (1996). Thermodynamics of denaturation of staphylococcal nuclease mutants: an intermediate state in protein folding. FASEB J. 10, 67–74. doi: 10.1096/fasebj.10.1.8566550

CrossRef Full Text | Google Scholar

Carter Childers, M., and Daggett, V. (2017). Insights from molecular dynamics simulations for computational protein design. Mol. Syst. Des. Eng. 2, 9–33. doi: 10.1039/c6me00083e

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Wang, J., Yin, B., Pang, L., Wang, W., Zhu, W., et al. (2019). Molecular mechanism of binding selectivity of inhibitors toward BACE1 and BACE2 revealed by multiple short molecular dynamics simulations and free-energy predictions. ACS Chem. Neurosci. 10, 4303–4318. doi: 10.1021/acschemneuro.9b00348

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Wang, X., Zhu, T., Zhang, Q., and Zhang, J. Z. H. (2015). A comparative insight into amprenavir resistance of mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 protease based on thermodynamic integration and MM-PBSA methods. J. Chem. Inf. Model. 55, 1903–1913. doi: 10.1021/acs.jcim.5b00173

PubMed Abstract | CrossRef Full Text | Google Scholar

Chodera, J. D., Mobley, D. L., Shirts, M. R., Dixon, R. W., Branson, K., Pande, V. S., et al. (2011). Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol. 21, 150–160. doi: 10.1016/j.sbi.2011.01.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Chong, S.-H., and Ham, S. (2011). Atomic decomposition of the protein solvation free energy and its application to amyloid-beta protein in water. J. Chem. Phys. 135:034506. doi: 10.1063/1.3610550

PubMed Abstract | CrossRef Full Text | Google Scholar

Chong, S.-H., and Ham, S. (2012). Component analysis of the protein hydration entropy. Chem. Phys. Lett. 535, 152–156. doi: 10.1016/j.cplett.2012.03.033

CrossRef Full Text | Google Scholar

Chong, S.-H., Lee, C., Kang, G., Park, M., and Ham, S. (2011). Structural and thermodynamic investigations on the aggregation and folding of acylphosphatase by molecular dynamics simulations and solvation free energy analysis. J. Am. Chem. Soc. 133, 7075–7083. doi: 10.1021/ja1116233

PubMed Abstract | CrossRef Full Text | Google Scholar

Darden, T., York, D., Pedersen, L., and An, N. (1993). Particle mesh ewald: log (N) method for ewald sums in large systems. J. Chem. Phys. 98:10089. doi: 10.1063/1.464397

CrossRef Full Text | Google Scholar

Datar, P. A., Khedkar, S. A., Malde, A. K., and Coutinho, E. C. (2006). Comparative residue interaction analysis (CoRIA): a 3D-QSAR approach to explore the binding contributions of active site residues with ligands. J. Comput. Aided Mol. Des. 20, 343–360. doi: 10.1007/s10822-006-9051-5

PubMed Abstract | CrossRef Full Text | Google Scholar

DeLano, W. L. (2002). The PyMOL Molecular Graphics System. Palo Alto, CA: DeLano Scientific.

Google Scholar

Ding, B., Li, N., and Wang, W. (2013). Characterizing binding of small molecules. II. Evaluating the potency of small molecules to combat resistance based on docking structures. J. Chem. Inf. Model. 53, 1213–1222. doi: 10.1021/ci400011c

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, Y., Liao, M., Meng, X., and Somero, G. N. (2018). Structural flexibility and protein adaptation to temperature: molecular dynamics analysis of malate dehydrogenases of marine molluscs. Proc. Natl. Acad. Sci. U.S.A. 115, 1274–1279. doi: 10.1073/pnas.1718910115

PubMed Abstract | CrossRef Full Text | Google Scholar

Eisenberg, D., and McLachlan, A. D. (1986). Solvation energy in protein folding and binding. Nature 319, 199–203. doi: 10.1038/319199a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Essmann, U., Perera, L., Berkowitz, M. L., Darden, T., Lee, H., Pedersen, L. G., et al. (1995). A smooth particle mesh Ewald method. J. Chem. Phys. 103, 8577–8593. doi: 10.1063/1.470117

CrossRef Full Text | Google Scholar

Friesner, R., Banks, J., Murphy, R., Halgren, T., Klicic, J., Mainz, D., et al. (2004). Glide: a new approach for rapid, accurate docking and scoring 2. Enrichment factors in database screening. J. Med. Chem. 47, 1739–1749. doi: 10.1021/jm0306430

PubMed Abstract | CrossRef Full Text | Google Scholar

Ganesan, P., and Ramalingam, R. (2018). Investigation of structural stability and functionality of homodimeric gramicidin towards peptide-based drug: a molecular simulation approach. J. Cell Biochem. 120, 4903–4911. doi: 10.1002/jcb.27765

PubMed Abstract | CrossRef Full Text | Google Scholar

Gapsys, V., Michielssens, S., Seeliger, D., and de Groot, B. L. (2016). Accurate and rigorous prediction of the changes in protein free energies in a large-scale mutation scan. Angew. Chem. Int. Ed. Engl. 55, 7364–7368. doi: 10.1002/anie.201510054

PubMed Abstract | CrossRef Full Text | Google Scholar

Gautam, R. K., and Chattopadhyaya, M. C. (2016). “Chapter 5 - kinetics and equilibrium isotherm modeling: graphene-based nanomaterials for the removal of heavy metals from water,” in Nanomaterials for Wastewater Remediation, eds R. K. Gautam and M. C. Chattopadhyaya (Boston: Butterworth-Heinemann).

Google Scholar

Ghai, R., Falconer, R. J., and Collins, B. M. (2012). Applications of isothermal titration calorimetry in pure and applied research–survey of the literature from 2010. J. Mol. Recognit. JMR 25, 32–52. doi: 10.1002/jmr.1167

PubMed Abstract | CrossRef Full Text | Google Scholar

Götz, A. W., Williamson, M. J., Xu, D., Poole, D., Le Grand, S., Walker, R. C., et al. (2012). Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized born. J. Chem. Theory Comput. 8, 1542–1555. doi: 10.1021/ct200909j

PubMed Abstract | CrossRef Full Text | Google Scholar

Greiner, W., Neise, L., and Stöcker, H. (1995). Thermodynamics and Statistical Mechanics. New York: Springer-Verlag.

Google Scholar

Hashemzadeh, S., Ramezani, F., and Rafii-Tabar, H. (2019). Study of molecular mechanism of the interaction between MEK1/2 and trametinib with docking and molecular dynamic simulation. Interdiscip. Sci. Comput. Life Sci. 11, 115–124. doi: 10.1007/s12539-018-0305-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoang, T. X., Trovato, A., Seno, F., Banavar, J. R., and Maritan, A. (2004). Geometry and symmetry presculpt the free-energy landscape of proteins. Proc. Natl. Acad. Sci. U.S.A. 101, 7960–7964. doi: 10.1073/pnas.0402525101

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, T. (2010). Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J. Chem. Inf. Model. 51, 69–82. doi: 10.1021/ci100275a

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, T., McLaughlin, W. A., and Wang, W. (2008). Evaluating the potency of HIV-1 protease drugs to combat resistance. Proteins 71, 1163–1174. doi: 10.1002/prot.21808

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, B., Fan, S., Liu, Y., Zhao, Y., Lin, D., Liao, X., et al. (2019). Solution structure and backbone dynamics for S1 domain of ribosomal protein S1 from Mycobacterium tuberculosis. Eur. Biophys. J. 48, 491–501. doi: 10.1007/s00249-019-01372-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishima, R., Kurt Yilmaz, N., and Schiffer, C. A. (2019). NMR and MD studies combined to elucidate inhibitor and water interactions of HIV-1 protease and their modulations with resistance mutations. J. Biomol. NMR 73, 365–374. doi: 10.1007/s10858-019-00260-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Jencks, W. P. (1981). On the attribution and additivity of binding energies. Proc. Natl. Acad. Sci. U.S.A. 78, 4046–4050. doi: 10.1073/pnas.78.7.4046

PubMed Abstract | CrossRef Full Text | Google Scholar

Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi: 10.1063/1.445869

CrossRef Full Text | Google Scholar

Junaid, M., Khan, M. T., Malik, S. I., and Wei, D.-Q. (2018). Insights into the mechanisms of pyrazinamide resistance of three pyrazinamidase mutants N11K, P69T and D126N. J. Chem. Inf. Model. 59, 498–508. doi: 10.1021/acs.jcim.8b00525

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalescky, R., Zhou, H., Liu, J., and Tao, P. (2016). Rigid residue scan simulations systematically reveal residue entropic roles in protein allostery. PLoS Comput. Biol. 12:e1004893. doi: 10.1371/journal.pcbi.1004893 doi: 10.1371/journal.pcbi.1004893

PubMed Abstract | PubMed Abstract | CrossRef Full Text

Kastritis, P. L., and Bonvin, A. M. J. J. (2013). On the binding affinity of macromolecular interactions: daring to ask why proteins interact. J. R. Soc. Interf. 10:20120835. doi: 10.1098/rsif.2012.0835

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaushik, A. C., Gautam, D., Nangraj, A. S., Wei, D.-Q., and Sahi, S. (2019). Protection of primary dopaminergic midbrain neurons through impact of small molecules using virtual screening of gpr139 supported by molecular dynamic simulation and systems biology. Interdiscip. Sci. Comput. Life Sci. 11, 247–257. doi: 10.1007/s12539-019-00334-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Khalaf, M. H., and Mansoori, G. A. (2018). A new insight into asphaltenes aggregation onset at molecular level in crude oil (an MD simulation study). J. Pet. Sci. Eng. 162, 244–250. doi: 10.1016/j.petrol.2017.12.045

CrossRef Full Text | Google Scholar

Khan, M. (2019). Pyrazinamide resistance and mutations L19R, R140H, and E144K in pyrazinamidase of Mycobacterium tuberculosis. J. Cell Biochem. Proc. 120, 7154–7166. doi: 10.1002/jcb.27989

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, M. K. A., Akhtar, S., and Arif, J. M. (2018). Development of in silico protocols to predict structural insights into the metabolic activation pathways of xenobiotics. Interdiscip. Sci. Comput. Life Sci. 10, 329–345. doi: 10.1007/s12539-017-0237-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, M. T., Junaid, M., Mao, X., Wang, Y., Hussain, A., Malik, S. I., et al. (2018a). Pyrazinamide resistance and mutations L19R, R140H, and E144K in pyrazinamidase of Mycobacterium tuberculosis. J. Cell Biochem. 120, 7154–7166.

Google Scholar

Khan, M. T., Malik, S. I., Bhatti, A. I., Ali, S., Khan, A. S., Zeb, M. T., et al. (2018b). Pyrazinamide-resistant mycobacterium tuberculosis isolates from Khyber pakhtunkhwa and rpsA mutations. J. Biol. Regul. Homeost. Agents 32, 705–709.

Google Scholar

Khan, M. T., Rehaman, A. U., Junaid, M., Malik, S. I., and Wei, D.-Q. (2018c). Insight into novel clinical mutants of RpsA-S324F, E325K, and G341R of Mycobacterium tuberculosis associated with pyrazinamide resistance. Comput. Struct. Biotechnol. J. 16, 379–387. doi: 10.1016/j.csbj.2018.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, M. T., Kaushik, A. C., Bhatti, A. I., Zhang, Y.-J., Zhang, S., Wei, A. J., et al. (2019a). Marine natural products and drug resistance in latent tuberculosis. Mar. Drugs 17:E549.

Google Scholar

Khan, M. T., Khan, A., Rehman, A. U., Wang, Y., Akhtar, K., Malik, S. I., et al. (2019b). Structural and free energy landscape of novel mutations in ribosomal protein S1 (rpsA) associated with pyrazinamide resistance. Sci. Rep. 9:7482.

Google Scholar

Khan, M. T., Malik, S. I., Ali, S., Masood, N., Nadeem, T., Khan, A. S., et al. (2019c). Pyrazinamide resistance and mutations in pncA among isolates of Mycobacterium tuberculosis from Khyber pakhtunkhwa, Pakistan. BMC Infect. Dis. 19:116. doi: 10.1186/s12879-019-3764-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kokubo, H., Harris, R. C., Asthagiri, D., and Pettitt, B. M. (2013). Solvation free energies of alanine peptides: the effect of flexibility. J. Phys. Chem. B 117, 16428–16435. doi: 10.1021/jp409693p

PubMed Abstract | CrossRef Full Text | Google Scholar

Kosloff, M., and Kolodny, R. (2008). Sequence-similar, structure-dissimilar protein pairs in the PDB. Proteins 71, 891–902. doi: 10.1002/prot.21770

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemaitre, N., Callebaut, I., Frenois, F., Jarleir, V., and Sougakof, W. (2001). Study of the structure–activity relationships for the pyrazinamidase (PncA) from Mycobacterium tuberculosis. Biochem. J. 353, 453–458. doi: 10.1042/bj3530453

CrossRef Full Text | Google Scholar

Li, T., Verma, D., Tracka, M. B., Casas-Finet, J., Livesay, D. R., Jacobs, D. J., et al. (2014). Thermodynamic stability and flexibility characteristics of antibody fragment complexes. Protein Pept. Lett. 21, 752–765. doi: 10.2174/09298665113209990051

PubMed Abstract | CrossRef Full Text | Google Scholar

Liszka, M. J., Clark, M. E., Schneider, E., and Clark, D. S. (2012). Nature versus nurture: developing enzymes that function under extreme conditions. Annu. Rev. Chem. Biomol. Eng. 3, 77–102. doi: 10.1146/annurev-chembioeng-061010-114239

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., and Yao, X. (2010). Molecular basis of the interaction for an essential subunit PA-PB1 in influenza virus RNA polymerase: insights from molecular dynamics simulation and free energy calculation. Mol. Pharm. 7, 75–85. doi: 10.1021/mp900131p

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, X., Shi, D., Zhou, S., Liu, H., Liu, H., Yao, X., et al. (2018). Molecular dynamics simulations and novel drug discovery. Expert. Opin. Drug Discov. 13, 23–37. doi: 10.1080/17460441.2018.1403419

PubMed Abstract | CrossRef Full Text | Google Scholar

Martis, E. A. F., Chandarana, R. C., Shaikh, M. S., Ambre, P. K., D’Souza, J. S., Iyer, K. R., et al. (2015). Quantifying ligand-receptor interactions for gorge-spanning acetylcholinesterase inhibitors for the treatment of Alzheimer’s disease. J. Biomol. Struct. Dyn. 33, 1107–1125. doi: 10.1080/07391102.2014.931824

PubMed Abstract | CrossRef Full Text | Google Scholar

Martis, E. A. F., and Coutinho, E. C. (2019). “Free energy-based methods to understand drug resistance mutations,” in Structural Bioinformatics: Applications in Preclinical Drug Discovery Process, ed. C. G. Mohan (Cham: Springer International Publishing).

Google Scholar

Masi, A., Cicchi, R., Carloni, A., Pavone, F. S., and Arcangeli, A. (2010). Optical methods in the study of protein-protein interactions. Adv. Exp. Med. Biol. 674, 33–42.

Google Scholar

Matthews, M. A. (2000). A to Z of thermodynamics by pierre perrot (Université des sciences et technologies de Lille). J. Am. Chem. Soc. 122, 3799–3800. doi: 10.1021/ja995706b

CrossRef Full Text | Google Scholar

Matubayasi, N. (2017). Free-energy analysis of protein solvation with all-atom molecular dynamics simulation combined with a theory of solutions. Curr. Opin. Struct. Biol. 43, 45–54. doi: 10.1016/j.sbi.2016.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehmood, A., Kaushik, A. C., and Wei, D.-Q. (2019). Prediction and validation of potent peptides against herpes simplex virus type 1 via immunoinformatic and systems biology approach. Chem. Biol. Drug Des. 94, 1868–1883. doi: 10.1111/cbdd.13602

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, F., Bellaiche, M. M. J., Kim, J.-Y., Zerze, G. H., Best, R. B., Chung, H. S., et al. (2018). Highly disordered Amyloid-β monomer probed by single-molecule FRET and MD simulation. Biophys. J. 114, 870–884. doi: 10.1016/j.bpj.2017.12.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Michel, J., and Essex, J. W. (2010). Prediction of protein-ligand binding affinity by free energy simulations: assumptions, pitfalls and expectations. J. Comput. Aided Mol. Des. 24, 639–658. doi: 10.1007/s10822-010-9363-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Mobley, D. L., and Klimovich, P. V. (2012). Perspective: alchemical free energy calculations for drug discovery. J. Chem. Phys. 137:230901. doi: 10.1063/1.4769292

PubMed Abstract | CrossRef Full Text | Google Scholar

Novotny, J. (1991). Protein antigenicity: a thermodynamic approach. Mol. Immunol. 28, 201–207. doi: 10.1016/0161-5890(91)90062-o

CrossRef Full Text | Google Scholar

Palzkill, T., and Palzkill, T. (2018). Structural and mechanistic basis for extended-spectrum drug-resistance mutations in altering the specificity of TEM, CTX-M, and KPC β-lactamases. Front. Mol. Biosci. 5:16. doi: 10.3389/fmolb.2018.00016

PubMed Abstract | CrossRef Full Text | Google Scholar

Pandey, B., Grover, S., Tyagi, C., Goyal, S., Jamal, S., Singh, A., et al. (2018). Dynamics of fluoroquinolones induced resistance in DNA gyrase of Mycobacterium tuberculosis. J. Biomol. Struct. Dyn. 36, 362–375. doi: 10.1080/07391102.2016.1277784

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillip, Y., Kiss, V., and Schreiber, G. (2012). Protein-binding dynamics imaged in a living cell. Proc. Natl. Acad. Sci. U.S.A. 109, 1461–1466. doi: 10.1073/pnas.1112171109

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajendran, V., Gopalakrishnan, C., and Sethumadhavan, R. (2018). Pathological role of a point mutation (T315I) in BCR-ABL1 protein—a computational insight. J. Cell Biochem. 119, 918–925. doi: 10.1002/jcb.26257

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajendran, V., and Sethumadhavan, R. (2013). Drug resistance mechanism of PncA in Mycobacterium tuberculosis. J. Biomol. Struct. Dyn. 32, 209–221. doi: 10.1080/07391102.2012.759885

PubMed Abstract | CrossRef Full Text | Google Scholar

Rehman, A. U., Khan, M. T., Liu, H., Wadood, A., Malik, S. I., and Chen, H.-F. (2019). Exploring the pyrazinamide drug resistance mechanism of clinical mutants T370P and W403G in ribosomal protein s1 of Mycobacterium tuberculosis. J. Chem. Inf. Model. 59, 1584–1597. doi: 10.1021/acs.jcim.8b00956

PubMed Abstract | CrossRef Full Text | Google Scholar

Reiche, M. A., Warner, D. F., and Mizrahi, V. (2017). Targeting DNA replication and repair for the development of novel therapeutics against tuberculosis. Front. Mol. Biosci. 4:75. doi: 10.3389/fmolb.2017.00075

CrossRef Full Text | Google Scholar

Rietman, E. A., Platig, J., Tuszynski, J. A., and Lakka Klement, G. (2016). Thermodynamic measures of cancer: Gibbs free energy and entropy of protein–protein interactions. J. Biol. Phys. 42, 339–350. doi: 10.1007/s10867-016-9410-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryckaert, J.-P., Ciccotti, G., and Berendsen, H. J. C. (1977). Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341. doi: 10.1016/0021-9991(77)90098-5

CrossRef Full Text | Google Scholar

Salah, P., Bisaglia, M., Aliprandi, P., Uzan, M., Sizun, C., Bontems, F., et al. (2009). Probing the relationship between gram-negative and gram-positive S1 proteins by sequence analysis. Nucleic Acids Res. 37, 5578–5588. doi: 10.1093/nar/gkp547

PubMed Abstract | CrossRef Full Text | Google Scholar

Salomon-Ferrer, R., Case, D. A., and Walker, R. C. (2013). An overview of the amber biomolecular simulation package. WIREs Comput. Mol. Sci. 3, 198–210. doi: 10.1002/wcms.1121

CrossRef Full Text | Google Scholar

Sheen, P., Ferrer, P., Gilman, R. H., López-Llano, J., Fuentes, P., Valencia, E., et al. (2009). Effect of pyrazinamidase activity on pyrazinamide resistance in Mycobacterium tuberculosis. Tuberculosis 89, 109–113. doi: 10.1016/j.tube.2009.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, W., Cui, P., Niu, H., Zhang, S., Tønjum, T., Zhu, B., et al. (2019). Introducing RpsA point mutations Δ438A and D123A into the chromosome of Mycobacterium tuberculosis confirms their role in causing resistance to pyrazinamide. Antimicrob Agents Chemother 63:e02681-18.

Google Scholar

Shi, W., Zhang, X., Jiang, X., Yuan, H., Lee, J. S., Barry, C. E., et al. (2011). Pyrazinamide inhibits trans-translation in Mycobacterium tuberculosis. Science 333, 1630–1632. doi: 10.1126/science.1208813

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., Somvanshi, P., and Grover, A. (2019). Pyrazinamide drug resistance in RpsA mutant (?438A) of Mycobacterium tuberculosis: dynamics of essential motions and free-energy landscape analysis. J. Cell Biochem. 120, 7386–7402. doi: 10.1002/jcb.28013

PubMed Abstract | CrossRef Full Text | Google Scholar

Sohaib Shahzan, M., Smiline Girija, A. S., and Vijayashree Priyadharsini, J. (2019). A computational study targeting the mutated L321F of ERG11 gene in C. albicans, associated with fluconazole resistance with bioactive compounds from Acacia nilotica. J. Mycol. Méd. 29, 303–309. doi: 10.1016/j.mycmed.2019.100899

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, H., Duan, L., Chen, F., Liu, H., Wang, Z., Pan, P., et al. (2018). Assessing the performance of MM/PBSA and MM/GBSA methods. 7. Entropy effects on the performance of end-point binding free energy calculation approaches. Phys. Chem. Chem. Phys. 20, 14450–14460. doi: 10.1039/c7cp07623a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, H., Li, Y., Shen, M., Tian, S., Xu, L., Pan, P., et al. (2014a). Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. PCCP 16, 22035–22045. doi: 10.1039/c4cp03179b

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, H., Li, Y., Tian, S., Xu, L., and Hou, T. (2014b). Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. PCCP 16, 16719–16729. doi: 10.1039/c4cp01388c

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, A., El, S. R., Reed, J. C., Krajewski, S., Silber, R., Potmesil, M., et al. (1996). Drug-induced apoptosis in B-cell chronic lymphocytic leukemia: relationship between p53 gene mutation and bcl-2/bax proteins in drug resistance. Oncogene 12, 1055–1062.

Google Scholar

Tyagi, R. K., Das, M. K., Singh, S. S., and Sharma, Y. D. (2013). Discordance in drug resistance-associated mutation patterns in marker genes of Plasmodium falciparum and Plasmodium knowlesi during coinfections. J. Antimicrob. Chemother. 68, 1081–1088. doi: 10.1093/jac/dks508

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, J., Khedkar, V. M., Prabhu, A. S., Khedkar, S. A., Malde, A. K., Coutinho, E. C., et al. (2008). A comprehensive analysis of the thermodynamic events involved in ligand-receptor binding using CoRIA and its variants. J. Comput. Aided Mol. Des. 22, 91–104. doi: 10.1007/s10822-008-9172-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Verteramo, M. L., Stenström, O., Ignjatoviæ, M. M., Caldararu, O., Olsson, M. A., Manzoni, F., et al. (2019). Interplay between conformational entropy and solvation entropy in protein–ligand binding. J. Am. Chem. Soc. 141, 2012–2026. doi: 10.1021/jacs.8b11099

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Mitsuya, Y., Gharizadeh, B., Ronaghi, M., and Shafer, R. W. (2007). Characterization of mutation spectra with ultra-deep pyrosequencing: application to HIV-1 drug resistance. Genome Res. 17, 1195–1201. doi: 10.1101/gr.6468307

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, E., Sun, H., Wang, J., Wang, Z., Liu, H., Zhang, J. Z. H., et al. (2019). End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chem. Rev. 119, 9478–9508. doi: 10.1021/acs.chemrev.9b00055

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Morin, P., Wang, W., and Kollman, P. A. (2001). Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 123, 5221–5230. doi: 10.1021/ja003834q

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, T., and Wade, R. C. (2001). Comparative binding energy (COMBINE) analysis of influenza neuraminidase-inhibitor complexes. J. Med. Chem. 44, 961–971. doi: 10.1021/jm001070j

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., and Kollman, P. A. (2000). Free energy calculations on dimer stability of the HIV protease using molecular dynamics and a continuum solvent model11Edited by B. Honig. J. Mol. Biol. 303, 567–582. doi: 10.1006/jmbi.2000.4057

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., and Kollman, P. A. (2001). Computational study of protein specificity: The molecular basis of HIV-1 protease drug resistance. Proc. Natl. Acad. Sci. U.S.A. 98, 14937–14942. doi: 10.1073/pnas.251265598

PubMed Abstract | CrossRef Full Text | Google Scholar

Webb, B., and Sali, A. (2016). Comparative protein structure modeling using modeller. Curr. Protoc. Bioinform. 54, 5.6.1–5.6.37. doi: 10.1002/cpbi.3

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, V., and Asthagiri, D. (2012). Regularizing binding energy distributions and the hydration free energy of protein cytochrome c from all-atom simulations. J. Chem. Theory Comput. 8, 3409–3415. doi: 10.1021/ct300505b

PubMed Abstract | CrossRef Full Text | Google Scholar

Worth, C. L., Gong, S., and Blundell, T. L. (2009). Structural and functional constraints in the evolution of protein families. Nat. Rev. Mol. Cell Biol. 10, 709–720. doi: 10.1038/nrm2762

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, L., Sun, H., Li, Y., Wang, J., and Hou, T. (2013). Assessing the performance of MM/PBSA and MM/GBSA Methods. 3. The impact of force fields and ligand charge models. J. Phys. Chem. B 117, 8408–8421. doi: 10.1021/jp404160y

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, W., Pan, D., Yang, Y., Liu, H., and Yao, X. (2012). Molecular modeling study on the resistance mechanism of HCV NS3/4A serine protease mutants R155K, A156V and D168A to TMC435. Antiviral Res. 93, 126–137. doi: 10.1016/j.antiviral.2011.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Yadon, A. N., Maharaj, K., Adamson, J. H., Lai, Y.-P., Sacchettini, J. C., Ioerger, T. R., et al. (2017). A comprehensive characterization of PncA polymorphisms that confer resistance to pyrazinamide. Nat. Commun. 8:588.

Google Scholar

Yang, F., Zheng, G., Fu, T., Li, X., Tu, G., Li, Y. H., et al. (2018). Prediction of the binding mode and resistance profile for a dual-target pyrrolyl diketo acid scaffold against HIV-1 integrase and reverse-transcriptase-associated ribonuclease H. Phys. Chem. Chem. Phys. 20, 23873–23884. doi: 10.1039/c8cp01843j

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Liu, Y., Bi, J., Cai, Q., Liao, X., Li, W., et al. (2015). Structural basis for targeting the ribosomal protein S1 of Mycobacterium tuberculosis by pyrazinamide. Mol. Microbiol. 95, 791–803. doi: 10.1111/mmi.12892

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoon, J.-H., Nam, J.-S., Kim, K.-J., and Ro, Y.-T. (2014). Characterization of pncA mutations in pyrazinamide-resistant Mycobacterium tuberculosis isolates from Korea and analysis of the correlation between the mutations and pyrazinamidase activity. World J. Microbiol. Biotechnol. 30, 2821–2828. doi: 10.1007/s11274-014-1706-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yun, C.-H., Mengwasser, K. E., Toms, A. V., Woo, M. S., Greulich, H., Wong, K.-K., et al. (2008). The T790M mutation in EGFR kinase causes drug resistance by increasing the affinity for ATP. Proc. Natl. Acad. Sci. U.S.A. 105, 2070–2075. doi: 10.1073/pnas.0709662105

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhi, Y., Dai, Y., Yang, J., Tan, S., Lin, D., Lin, K., et al. (2019). Lead compounds and key residues of ribosomal protein S1 in drug-resistant Mycobacterium tuberculosis. Bioorgan. Chem. 82, 58–67. doi: 10.1016/j.bioorg.2018.09.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Zídek, L., Novotny, M. V., and Stone, M. J. (1999). Increased protein backbone conformational entropy upon hydrophobic ligand binding. Nat. Struct. Biol. 6, 1118–1121.

Google Scholar