Development of extensive growth and growth boundary models for mesophilic and psychrotolerant Bacillus cereus in dairy products (Part 1)

Guidelines for combinations of product characteristics to prevent unacceptable growth of Bacillus cereus in foods are lacking, and models are therefore valuable for predicting these responses. B. cereus isolates of dairy origin were used to generate a comprehensive dataset to develop two cardinal parameter growth and growth boundary models for mesophilic and psychrotolerant B. cereus, respectively. Each model incorporated the inhibitory effect of 11 environmental factors, i.e., temperature, pH, NaCl/a_w, organic acids (acetic, benzoic, citric, lactic, and sorbic), phosphate salts (orthophosphate, diphosphate, and triphosphate), and the effect of interactions between these factors. Cardinal parameter values for mesophilic and psychrotolerant strain cocktails were estimated using 231 and 203 maximum specific growth rates (μ_max values), respectively, generated in a standard liquid laboratory medium (BHI broth). Furthermore, an additional 113 and 100 μ_max values were generated for the two strain cocktails using a dairy-specific liquid medium (an ultra-filtration permeate from whey) to evaluate growth responses obtained in BHI broth. Cardinal parameter values for the two extensive growth boundary models were selected conservatively using data from BHI broth or UF permeate, such that the widest growth range was obtained for each environmental factor. The studied cocktail of six vegetative mesophilic B. cereus isolates exhibited greater acid tolerance in UF permeate than in BHI broth with lower pH_min (pH_min values of 4.75 versus 4.98), higher minimum inhibitory concentrations (MIC) of undissociated lactic acid (MIC_u,LAC of 2.99 versus 2.34 mM) and total citric acid (MIC_T,CAC of 169.1 versus 82.5 mM). The psychrotolerant B. cereus strain cocktail also had lower pH_min and higher values for MIC_LAC and MIC_T,CAC in UF permeate than in BHI broth. The remaining cardinal parameter values were determined from growth rates in BHI broth. The two new models can predict the combined effect of storage temperature and a wide range of dairy product characteristics, including combinations of organic acids and phosphate melting salts. These growth and growth boundary models can support the evaluation and management of the two B. cereus subgroups in various dairy products. However, product validation of the two predictive models is required to determine their performance and range of applicability.

1 Introduction

Bacillus cereus sensu lato is a group of closely related species that are widespread in the environment and many types of food, including dairy products (Vos et al., 2011; Tirloni et al., 2022; Maktabdar et al., 2024). Most B. cereus s.l. isolates include one or more toxin genes and may pose a public health concern, although the ability to cause foodborne illness varies among subgroups (Ehling-Schulz et al., 2019). Classification of B. cereus s.l. into panC groups has been used to cluster B. cereus isolates as thermotolerant (panC group VII), mesophilic (panC groups I, III, and IV), or psychrotolerant (panC groups II, V, and VI) (Guinebretière et al., 2008; Carroll et al., 2020). Growth temperatures to differentiate these subgroups may vary depending on the media and atmospheres used for incubation. However, isolates capable of growing ≤8–10°C are typically considered psychrotolerant (Guinebretière et al., 2008; Webb et al., 2019; Carroll et al., 2021).

If B. cereus in food is not inhibited by chilled storage or specific product formulations, the spores may germinate and grow to critical concentrations. It is important to manage the growth of both mesophilic and psychrotolerant B. cereus as this will reduce safety concerns associated with critical cell concentrations. Currently, regulations for the management of B. cereus growth are limited to specific infant formula and dairy powders (EC, 2007; Watterson et al., 2014). EFSA (2005) suggested that B. cereus concentrations at the time of consumption should not exceed 1,000 CFU/g, while others consider concentrations of 5 log CFU/g (or CFU/ml) as critical (EFSA, 2016; Webb et al., 2019). Challenge tests, storage trials, and predictive models can identify combinations of storage conditions and product characteristics that reduce or prevent the growth of pathogens in various foods. Validated growth models, when available, are useful to support product development or reformulation. These models can provide information to assess and manage microbial growth more rapidly and less costly than traditional approaches such as challenge tests and storage trials (NACMCF, National Advisory Committee on Microbiological Criteria for Foods, 2010; Dalgaard and Mejlholm, 2019; Bergis et al., 2021). This is particularly relevant for B. cereus in dairy products. However, new models that incorporate the growth-inhibiting effects of a wider range of dairy product characteristics may need to be developed and validated. Available B. cereus growth models include the effects of temperature combined with one to four other factors (pH, water activity (a_w), lactic acid, acetic acid, nitrite, or CO₂). These models were developed based on growth responses in laboratory broth, milk, paneer cheese, or other foods. Validation studies with dairy products have primarily focused on milk and reconstituted infant formula (Zwietering et al., 1996; Ölmez and Aran, 2005; Carlin et al., 2013; Buss da Silva et al., 2017; Ellouze et al., 2021; Le Marc et al., 2021a,b, 2024; Sarkar et al., 2023). Compared to available B. cereus growth models, dairy products contain several additional factors likely to influence the growth of B. cereus subgroups. These factors include benzoic, citric, formic, propionic, and sorbic acids resulting from fermentation or added as preservatives (Bevilacqua and Califano, 1989; Biesta-Peters et al., 2010; Dorko et al., 2014; Østergaard et al., 2014; Han et al., 2016; Martinez-Rios et al., 2016, 2019a; Koukou et al., 2022). Furthermore, phosphate melting salts used in processed cheese to achieve desired texture properties (Fusieger et al., 2022, 2024), and compounds produced by lactic acid bacteria (Wong and Chen, 1988; Røssland, 2003; Soria and Audisio, 2014) can also influence growth of B. cereus. To obtain unbiased B. cereus growth predictions across a wide range of dairy products, not just milk and reconstituted infant formula, it seems relevant to consider several additional growth-reducing factors not currently included in existing models. Cardinal parameter models can quantify the impact of multiple factors and their interactions on the growth and growth boundary of microorganisms (Augustin and Carlier, 2000; Le Marc et al., 2002; Ross and Dalgaard, 2004). However, such extensive growth and growth boundary models have not yet been developed for B. cereus.

The objective of the present study was to develop two extensive models with the potential to predict the growth and growth boundary of mesophilic and psychrotolerant B. cereus under conditions found in a broad range of dairy products. Strain cocktails for each subgroup of B. cereus isolates were studied. Cardinal parameter values for the effects of temperature, pH, NaCl/a_w, organic acids, and phosphate melting salts were determined using two liquid media: BHI broth and an ultra-filtration permeate from whey (UF permeate). Two cardinal parameter growth and growth boundary models were formulated for the combined effect of all 11 environmental factors. These models were developed using a conservative approach, where the widest range of growth conditions, as determined with BHI broth or UF permeate, were used for model development.

2 Materials and methods

2.1 Bacterial isolates, pre-cultures, and strain cocktails

A cocktail of vegetative cells comprising six mesophilic B. cereus s.l. strains (RIC-2, SML-1, WHY-4, AP7.4, AP10.2, and 0109.0074) belonging to panC group III were used for the development of a mesophilic model. Another cocktail of vegetative cells including seven B. cereus strains with psychrotolerant characteristics (HML-5, JRD-1, MP-3, TDS-9, BRI-4, MRB-6, and GDN-1) and belonging to panC groups II, III, VI, and VIII were used for the development of a psychrotolerant model. These strains were previously isolated from various dairy products and were selected based on their fast growth rates at a temperature of 45°C or 10°C, their tolerance to pH 5.1, and low a_w equivalent to 6% NaCl (Maktabdar et al., 2024). All these isolates have at least one of the genes for the production of non-hemolytic (nhe), hemolytic (hbl), cytotoxic (cytK), or cereulide (ces) toxins. Half of the mesophilic isolates (SML-1, WHY1.4, and AP10.2) and two of the psychrotolerant isolates (MP-3 and BRI-4) ferment lactose, a prevalent carbohydrate in dairy products (Maktabdar et al., 2024). Individual strains kept at −80°C were grown overnight in brain heart infusion (BHI, Oxoid, CM1135, Hampshire, United Kingdom) broth at 30°C. Pre-cultures of mesophilic isolates were then prepared at 30°C by transferring 500 μL of the overnight cultures to 10 mL of BHI broth. Pre-cultures of psychrotolerant isolates were prepared by transferring 10, 100, and 500 μL aliquots of the overnight cultures to new BHI tubes and incubating at 15°C to minimize temperature shifts when later studied at low temperatures. Pre-cultures were incubated until the absorbance at 540 nm (Novaspec II, Pharmacia Biotech, Allerød, Denmark) increased by 0.05–0.2 units equivalent to the late exponential phase. Equal concentrations of the six mesophilic or seven psychrotolerant individual pre-cultures were mixed for the mesophilic (Mix-Bc_mes) or psychrotolerant (Mix-Bc_psy) cocktails. The cell density of the strain cocktails was determined by direct phase-contrast microscopy prior to dilution and inoculation of liquid media to determine growth rates.

2.2 Determination of growth cardinal parameter values

Two different liquid media were used to estimate cardinal parameter values for the 11 environmental factors in each of the two models. A conservative approach was applied, selecting the cardinal parameter values resulting in the widest growth range (worst-case scenario). As an example, the lowest of the pH_min values determined with the two liquid media was selected for the final growth and growth boundary models. A total of 344 maximum specific growth rates (μ_max, h⁻¹) for Mix-Bc_mes and 303 μ_max values for Mix-Bc_psy were determined in the two liquid media using absorbance detection times measured at 540 nm (Bioscreen C, Labsystems, Helsinki, Finland). Serial 10-fold diluted pre-cultures of Mix-Bc_mes or Mix-Bc_psy with approximately 10¹ to 10⁵ CFU/mL were used to determine μ_max values as previously suggested by Dalgaard and Koutsoumanis (2001). Bioscreen C Honeycomb plates with 300 μL medium per well were incubated aerobically, and a maximum storage time was fixed to limit evaporation, particularly at higher temperatures.

First, the meat-based BHI broth was applied to quantify the effects of the 11 studied environmental factors on μ_max values of Mix-Bc_mes and Mix-Bc_psy. These factors were as follows: temperature, pH, NaCl/water activity (a_w), acetic, benzoic, citric, lactic, and sorbic acid, and orthophosphate, diphosphate, and triphosphates. Second, the effect of pH, a_w and the aforementioned five different organic acids were also quantified using a UF permeate solution, prepared with 1.45% (w/w) UF permeate powder. This dairy-based powder contained 87% lactose, 2.8% protein, and 0.75% calcium (Arla Foods Ingredients). Initially, to determine a suitable UF permeate concentration for B. cereus growth and accurate measurement of growth by absorbance using Bioscreen C, solutions with concentrations ranging from 1.38 to 13.9% (w/w) were tested. The 1.45% (w/w) UF permeate was then selected as an appropriate concentration. BHI broth was sterilized at 121°C for 15 min, and the UF permeate solution was heat-treated at 80°C for 10 min to limit precipitation.

The effect of temperature and phosphate salts on the growth rates of Mix-Bc_mes and Mix-Bc_psy was exclusively quantified using BHI broth. This decision was based on challenge testing with UF permeate and the use of viable counting to quantify growth. These studies showed comparable growth rates between BHI and whey permeate at different temperatures (Maktabdar et al., 2025; Part 2). Moreover, the addition of phosphates to the UF permeate resulted in turbidity, making the solution unsuitable for accurate absorbance measurement with the Bioscreen C instrument.

2.2.1 Effect of temperature

The effect of temperature on μ_max values of Mix-Bc_mes or Mix-Bc_psy was quantified in BHI broth with pH adjusted to 6.00 ± 0.05. To determine cardinal parameter values, 13 different temperatures (13–45°C) and 12 different temperatures (8–40°C), where growth was observed, were studied for Mix-Bc_mes and Mix-Bc_psy, respectively. Growth was studied during storage periods of up to 25 days. At each tested temperature, four to five repetitions were studied resulting in 58 μ_max values for Mix-Bc_mes and 51 μ_max values for Mix-Bc_psy. A gamma concept model was used to fit the square root-transformed μ_max values obtained at different temperatures (Equation 1). In this equation, X is the temperature (°C) and μ_opt (h⁻¹) is the growth rate at the optimum temperature and at pH 6.00 ± 0.05. Cardinal parameter values for temperature were estimated by Equation 2 (Rosso et al., 1995).

$\begin{array}{ll}\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{\mathit{opt}}CM\left(X\right)}& (1)\end{array}$

$\begin{array}{l}CM\left(X\right)\\ =\{\begin{array}{l}0\hfill \\ \frac{\left(X-X_{\text{max}}\right){\left(X-X_{\text{min}}\right)}^n}{\left(X_{\mathit{opt}}-X_{\text{min}}\right)\left[\left(X_{\mathit{opt}}-X_{\text{min}}\right)\left(x-X_{\mathit{opt}}\right)-\left(X_{\mathit{op}\mathrm{t}}-X_{\text{max}}\right)\left(\left(n-1\right)X_{\mathit{opt}}+X_{\text{min}}-nX\right)\right]}\hfill \\ 0\hfill \end{array}\begin{array}{c}X\le X_{\text{min}}\\ X_{\text{min}}<X<X_{\text{max}}\\ X\ge X_{\text{max}}\end{array}\end{array}\text{ (2)}$

where X_min (°C), X_max (°C), and X_opt (°C) are the fitted and theoretical minimum, maximum, and optimum temperature, respectively. The shape parameter n was set to 2 as suggested by Rosso et al. (1995).

2.2.2 Effect of pH

The effect of pH on μ_max values of Mix-Bc_mes or Mix-Bc_psy was quantified using both BHI and the UF permeate (see Section 2.2). For both these liquid media, pH was adjusted with HCl/NaOH to achieve different pH values as shown in Figure 1. To determine the pH cardinal parameter values, growth experiments were conducted at 37°C for up to 10 days with Mix-Bc_mes and at 15°C for up to 29 days with Mix-Bc_psy. Using BHI broth, pH ranges from 5.0 to 8.0 were studied for Mix-Bc_mes and between 5.25 and 8.01 for Mix-Bc_psy, where growth was observed. The square root-transformed μ_max values (17 values for Mix-Bc_mes and 13 values for Mix-Bc_psy) were used to estimate the cardinal parameter values for pH in BHI broth by fitting Equation 2, where X is the pH and X_min and X_opt are the fitted values for theoretical minimum pH allowing growth and optimum pH, respectively. X_max is the theoretical maximum pH allowing growth, and it was fixed at 9.5. The shape parameter n was set to 1 (Rosso et al., 1995). Model parameters were obtained by fitting $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,pH}CM\left(pH\right)}$ , where μ_ref,pH is a parameter for the optimal growth rate at 37°C for Mix-Bc_mes and at 15°C for Mix-Bc_psy. A similar experimental approach was used for the UF permeate. pH was adjusted to achieve levels between 4.80 and 6.90 for Mix-Bc_mes and between 4.62 and 6.92 for Mix-Bc_psy, within the pH range where growth was observed; 20 and 23 μ_max values were obtained for Mix-Bc_mes and Mix-Bc_psy, respectively, which were used to estimate pH_min and pH_opt values with Equation 2, following the same fitting procedure as for BHI broth.

Figure 1

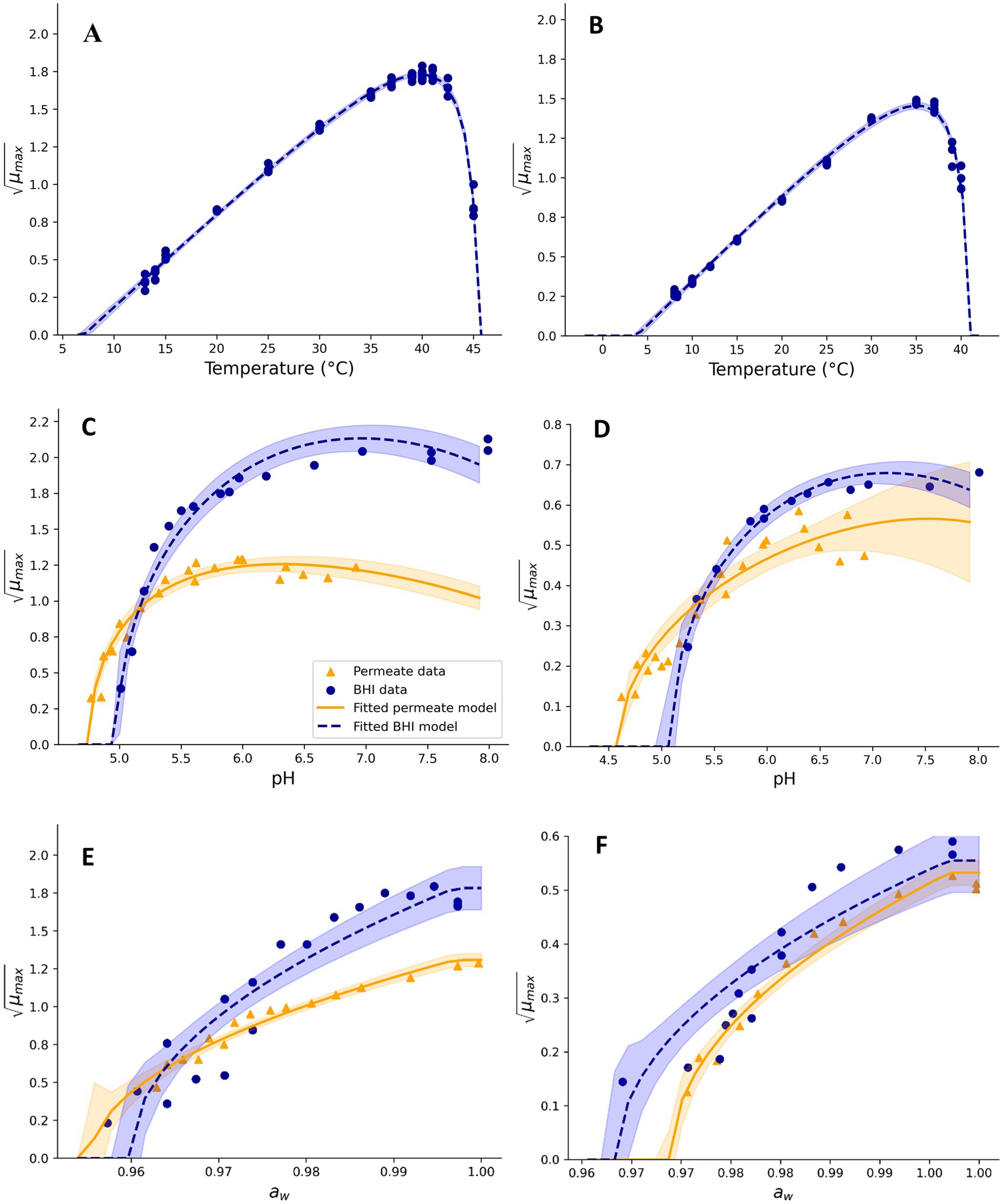
Figure 1. Effect of temperature (A,B), pH (C,D), and a_w (E,F), on square root-transformed maximum specific growth rates (μ_max, h^−0.5) of mesophilic (A,C,E) and psychrotolerant (B,D,F) B. cereus in BHI broth and UF permeate solution. Fitted model terms for BHI (dashed blue lines) and UF permeate (solid yellow lines) were obtained by fitting Equations 2, 3, respectively, to the observed μ_max values in BHI (blue dots) and UF permeate (yellow triangles). 95% confidence intervals of the fits are shown in blue and yellow shades.

2.2.3 Effect of water activity

BHI broth and UF permeate with different concentrations of NaCl (Figure 1) and at pH 6.00 ± 0.05 were used to estimate the effect of a_w on μ_max values of, respectively, Mix-Bc_mes (37°C) during 6 days or Mix-Bc_psy (15°C) during 16 days. NaCl was added to BHI broth and to the 1.45% w/w UF permeate solution in the range of 0.5–7% to study the effect of different levels of a_w on Mix-Bc_mes growth (Figure 1). To evaluate these effects on Mix-Bc_psy growth, NaCl concentrations ranging from 0.5 to 6% in BHI broth and between 0.0 and 5.2% in UF permeate were studied. The a_w equivalent to each NaCl concentration was calculated as previously described (Resnik and Chirife, 1988; Ross and Dalgaard, 2004). Square root-transformed μ_max values from BHI broth (17 values for Mix-Bc_mes and 15 values for Mix-Bc_psy) or UF permeate (17 values for Mix-Bc_mes and 12 values for Mix-Bc_psy) were used to estimate a_{w, min} by fitting Equation 3 (Koukou et al., 2021). Model parameter values were estimated by fitting $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,a_w}CM\left(a_w\right)}$ , where μ_ref,aw is the optimal growth rate at pH 6.00 ± 0.05 and 37°C for Mix-Bc_mes and at pH 6.00 ± 0.05 and 15°C for Mix-Bc_psy.

$CM\left(a_w\right)=\left\{\begin{array}{cc}1& a_w\ge a_{w,\mathit{opt}}\\ 1-\frac{a_{w,\mathit{opt}}-a_w}{a_{w,\mathit{opt}}-a_{w,min}}& a_{w,min}<a_w<a_{w,\mathit{opt}}\\ 0& a_w\le a_{w,min}\end{array}\right.\text{ (3)}$

where a_w,min is the theoretical minimum a_w allowing growth and a_w,opt is the optimum a_w for growth which was set to 0.997.

2.2.4 Effect of organic acids

The effect of acetic acid (5.43808, LiChropur), benzoic acid (sodium benzoate, 71,300, Sigma), citric acid (sodium citrate, C0909, Sigma), lactic acid (sodium DL lactate, L1375, Sigma), and sorbic acid (potassium sorbate, 85,520, Sigma) on growth was assessed at 37°C for Mix-Bc_mes during up to 8 days and at 15°C for Mix-Bc_psy during up to 30 days. Experiments with different concentrations of the studied organic acids (Figures 2, 3) were conducted in both BHI broth and UF permeate at pH 6.00 ± 0.05 adjusted using HCl or NaOH. A pH of 6.0 allows a fraction of the studied organic acids to remain in their undissociated forms and pH values of 6.0 and 6.2 have been previously used to determine cardinal parameter values for growth models that were successfully validated with dairy products or other foods (Mejlholm and Dalgaard, 2009; Martinez-Rios et al., 2019a; Koukou et al., 2022). Concentrations of organic acids as indicated below are calculated for the pure acids and not for the sodium or potassium salts mentioned above and used to prepare the solutions.

Figure 2

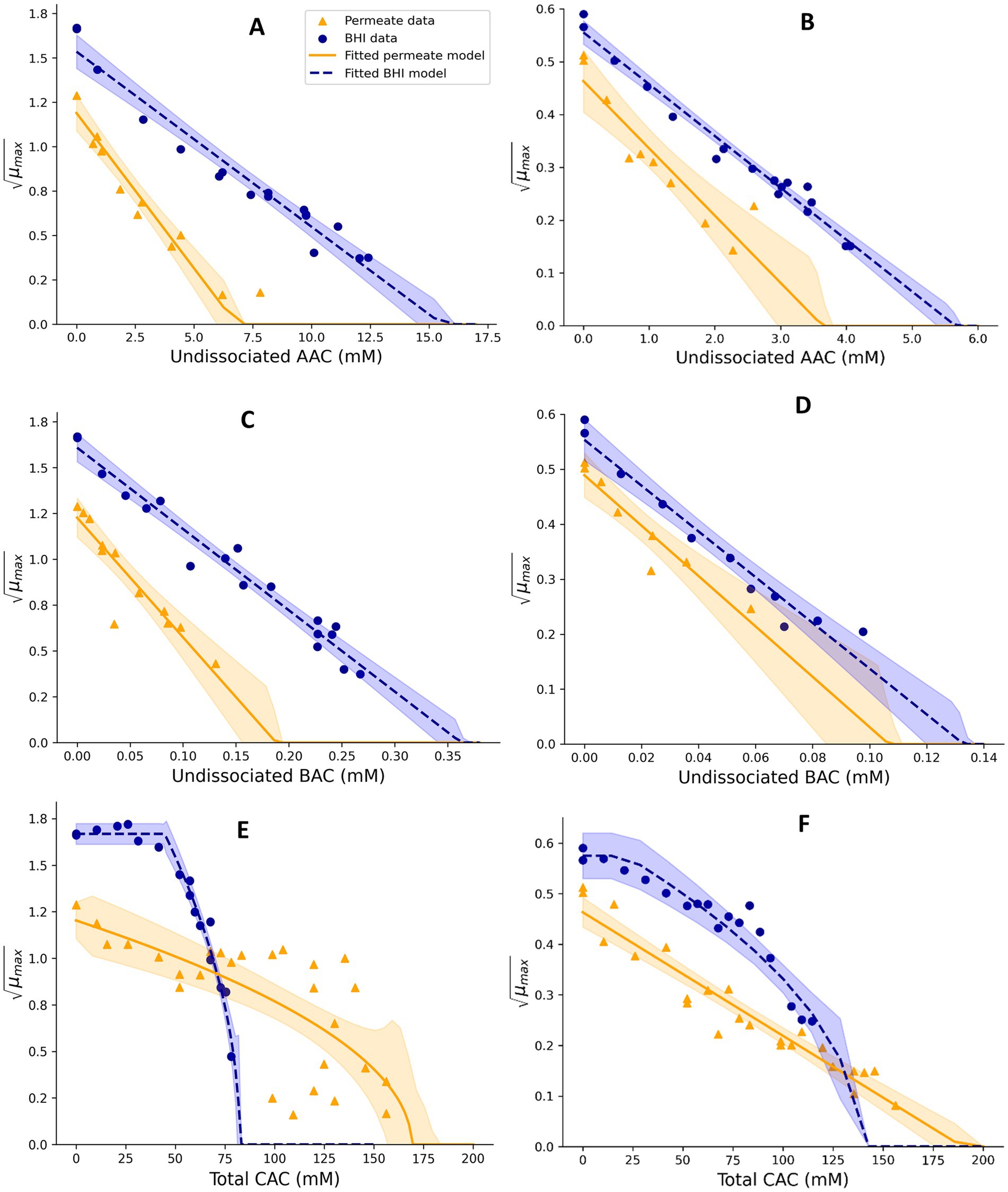
Figure 2. Effect of undissociated acetic acid (A,B), undissociated benzoic acid (C,D), and total citric acid (E,F) on the square root-transformed maximum specific growth rates (μmax, h^−0.5) of mesophilic (A,C,E) and psychrotolerant (B,D,F) B. cereus in BHI broth and UF permeate solution. Fitted model terms for BHI (dashed blue lines) and UF permeate (solid yellow lines) were obtained by fitting Equations 4, 7, respectively, with the observed μ_max values in BHI (blue dots) and UF permeate (yellow triangles). 95% confidence intervals of the fits are shown in blue and yellow shades.

Figure 3

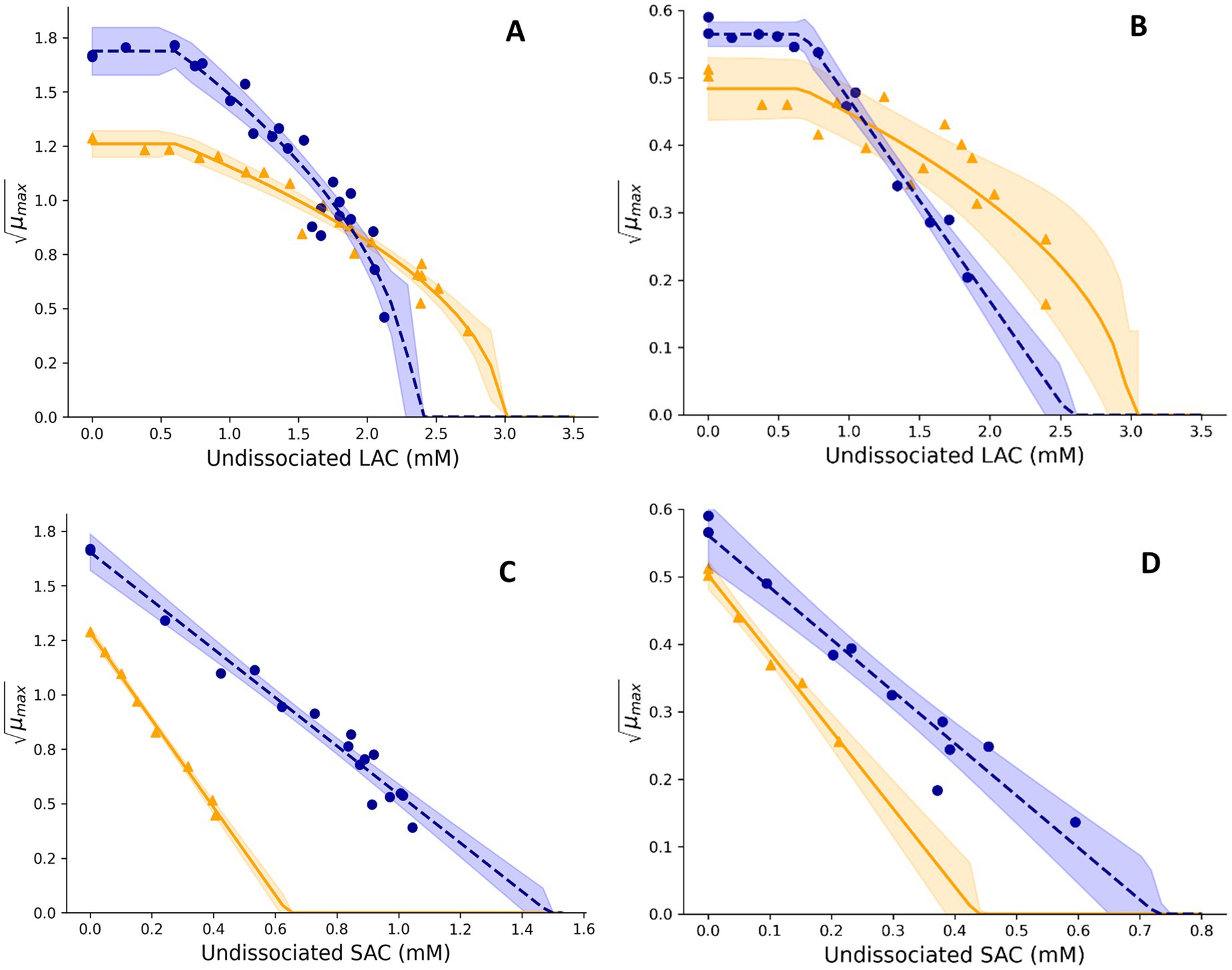
Figure 3. Effect of undissociated lactic acid (A,B) and undissociated sorbic acid (C,D) on the square root-transformed maximum specific growth rates (μmax, h^−0.5) of mesophilic (A,C) and psychrotolerant (B,D) B. cereus in BHI broth and UF permeate solution. Fitted model terms for BHI (dashed blue lines) and UF permeate (solid yellow lines) were obtained by fitting Equations 4, 6, respectively, to the observed μ_max values in BHI (blue dots) and UF permeate (yellow triangles). 95% confidence intervals of the fits are shown in blue and yellow shades.

2.2.4.1 Cardinal parameter values for acetic, benzoic, and sorbic acids

For Mix-Bc_mes, the effect of acetic acid (AAC) was determined for different constant concentrations between 0.0 and 1.4% (w/w) in BHI broth and 0.0 to 0.9% in UF permeate, resulting in 17 and 12 μ_max values, respectively. Benzoic acid (BAC) concentrations of 0.0–0.2% and 0.0–0.13% (w/w) were studied in BHI broth and UF permeate to generate 17 and 13 μ_max values, respectively. Sorbic acid (SAC) with concentrations between 0.0–0.22% and 0.0–0.08% (w/w) were analyzed in BHI broth and UF permeate resulting in 17 and nine μ_max values, respectively (Figures 2, 3). For Mix-Bc_psy, the effects of AAC with concentrations ranging from 0.0 to 0.5% in BHI broth and between 0.0 and 0.3% (w/w) in UF permeate were evaluated, resulting in 18 and 11 μ_max values, respectively. BAC concentrations up to 0.08% in BHI broth and up to 0.05% in UF permeate were studied, to generate 11 and eight μ_max values, respectively. Similarly, a range of SAC concentrations from 0.0 to 0.11% in BHI broth and up to 0.04% (w/w) in UF permeate were examined, leading to 11 and six μ_max values, respectively (Figures 2, 3).

Cardinal parameter values for AAC, BAC, and SAC were determined by fitting square root-transformed μ_max values obtained with different concentrations of these organic acids using Equation 4 (Presser et al., 1997) and the procedure $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,OA}CM\left(OA\right)}$ . This fitting procedure was used for data from both BHI broth and UF permeate.

$\begin{array}{ll}CM\left(OA\right)={\left(1-\frac{O{A}_u}{MI{C}_{u,OA}}\right)}^2& (4)\end{array}$

where OA_u is the concentration of undissociated acetic, benzoic, or sorbic acids (mM) and MIC_u,OA (mM) is the fitted minimum inhibitory concentration for each undissociated organic acid (acetic, benzoic, or sorbic acids). μ_ref,oA is a fitted parameter for the optimal growth rate at pH 6.00 ± 0.05 and 37°C for Mix-Bc_mes and at pH 6.00 ± 0.05 and 15°C for Mix-Bc_psy.

The concentration of undissociated acids (OA_u, mM) was calculated based on concentrations of total organic acids (OA, mM), pH of 6.00, pK_a of 4.76 for AAC and SAC, and pK_a of 4.20 for BAC (Equation 5) (Budavari, 1989).

$\begin{array}{ll}O{A}_u\left(mM\right)=\frac{OA\left(mM\right)}{1+{10}^{\left(pH-p{K}_a\right)}}& (5)\end{array}$

2.2.4.2 Cardinal parameters for lactic acid

Lactic acid (LAC) concentrations ranging from 0.0 to 2.6% in BHI broth and from 0.0 to 3.5% (w/w) in UF permeate were used to determine the effect of LAC on μ_max values of Mix-Bc_mes, resulting in 24 μ_max values in BHI and 18 μ_max values in UF permeate (Figure 3). For Mix-Bc_psy, LAC concentrations between 0.0 and 2.1% in BHI broth and concentrations up to 2.8% (w/w) in UF permeate were studied, resulting in, respectively, 13 and 17 μ_max values (Figure 3). Concentrations of undissociated acid were calculated from total LAC using Equation 5 with pH 6.0 and a pKa value of 3.86. The obtained μ_max values were used to estimate cardinal values for lactic acid (Equation 6) with the fitting procedure $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,\mathit{LAC}}.CM\left(\mathit{LAC}\right)}$ (Koukou et al., 2021).

$CM\left(\mathit{LAC}\right)=\{\begin{array}{l}1LA{C}_u<LA{C}_{u,\mathit{opt}}\hfill \\ {\left(1-{\left(\frac{LA{C}_u-LA{C}_{u,\mathit{opt}}}{MI{C}_{u,\mathit{LAC}}-LA{C}_{u,\mathit{opt}}}\right)}^{n1}\right)}^{n2}LA{C}_u\ge LA{C}_{u,\mathit{opt}}\hfill \end{array}\text{ (6)}$

where μ_{ref, LAC} is the optimal growth rate with lactic acid at pH 6.00 ± 0.05 and 37°C for Mix-Bc_mes and at pH 6.00 ± 0.05 and 15°C for Mix-Bc_psy. LAC_u is the concentration of undissociated lactic acid (mM) corresponding to the growth, and MIC_u,LAC is the fitted minimum inhibitory concentration of undissociated lactic acid (mM) that prevents growth. LAC_u,opt is the fitted concentration of undissociated lactic acid below which the growth rate was optimal (Figure 3). When Equation 6 was fitted, values of n1 were set to 0.5 or 1.0 and n2 to 1.0 or 2.0 in four combinations. The best fit was then determined from the lowest root mean square error (RMSE) value as previously described (Koukou et al., 2021).

2.2.4.3 Cardinal parameters for citric acid

The inhibitory effect of citric acid was evaluated by using both BHI broth and UF permeate. A model term for the effect of total citric acid was developed (Equation 7) because a term based on the effect of undissociated citric acid overestimated the inhibitory effect of this acid in dairy products (Maktabdar et al., 2025; Part 2). Different concentrations of citric acid (CAC), ranging from 0.0 to 1.5% in BHI broth and 0.0–3.0% (w/w) in UF permeate, where growth was observed, were studied for Mix-Bc_mes, resulting in 17 and 24 μ_max values, respectively. The growth-inhibiting effect of CAC on Mix-Bc_psy was studied for different CAC concentrations up to 2.1% in BHI broth and up to 3% (w/w) in UF permeate, resulting in 18 and 24 μ_max values, respectively. The cardinal parameter values for CAC were estimated by fitting square root transformed μ_max values obtained for different concentrations (mM) of CAC using Equation 7 (Koukou et al., 2021) and the fitting procedure $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,CAC}CM\left(CAC\right)}$ .

$CM\left(CAC\right)=\{\begin{array}{l}1CA{C}_T<CA{C}_{T,\mathit{opt}}\hfill \\ {\left(1-{\left(\frac{CA{C}_T-CA{C}_{T,\mathit{opt}}}{MI{C}_{T,CAC}-CA{C}_{T,\mathit{opt}}}\right)}^{n1}\right)}^{n2}CA{C}_T\ge CA{C}_{T,\mathit{opt}}\hfill \end{array}\text{ (7)}$

where μ_{ref, CAC} is the optimal growth rate at pH 6.00 ± 0.05 and 37°C for Mix-Bc_mes and at pH 6.00 ± 0.05 and 15°C for Mix-Bc_psy. CAC_T is the concentration of total citric acid (concentration of dissociated and undissociated citric acid; mM), MIC_T,CAC is the fitted minimum concentration of total citric acid (mM) at which growth is prevented. CAC_T,opt is the fitted value for the concentration of total citric acid (mM) below which the growth rate is optimal (Figure 2). Equation 7 was fitted as described above for Equation 6.

2.2.5 Inhibitory effect of phosphate melting salts

Sodium phosphate monobasic dehydrate (P1; 04269, Sigma-Aldrich), sodium pyrophosphate decahydrate (P2; 221,368, Sigma-Aldrich), and sodium tripolyphosphate (P3; 72,061, Sigma-Aldrich) were used to evaluate the effect of these phosphate salts on μ_max values of Mix-Bc_mes and Mix-Bc_psy. Experiments were performed using BHI broth with pH adjusted to 6.00 ± 0.5 by HCl/NaOH. For Mix-Bc_mes, growth was studied at 37°C for up to 8 days and for Mix-Bc_psy at 15°C for 10 days. Different constant concentrations of orthophosphate (P1) between 0 and 4% of PO₄³⁻, diphosphate (P2) between 0 and 1.8% of P₂O₇⁴⁻, and triphosphate (P3) ions between 0 and 1.7% of H₄O₁₀P₃⁻ were studied using BHI broth, to estimate phosphate cardinal parameters values for Mix-Bc_mes, resulting in 15, 15, and 17 μ_max values, respectively (Figure 4). P1 concentrations up to 4.5% (w/w), P2 concentrations up to 1.8%, and P3 concentrations up to 1.9% (w/w) in BHI broth were evaluated, for estimation of cardinal parameter values of Mix-Bc_psy, resulting in 17, 16, and 20 μ_max values, respectively (Figure 4). Square root-transformed μ_max values for P1, P2, and P3 concentrations were used to estimate the cardinal parameter values with Equation 8 and by fitting $\sqrt{{\mu }_{\text{max}}}=\sqrt{{\mu }_{ref,P}.CM\left(P\right)}$ (Martinez-Rios et al., 2019b; Koukou et al., 2022).

$\begin{array}{ll}CM\left(P\right)=1-\left(\frac{P}{MI{C}_P}\right)& (8)\end{array}$

where P is the concentration (% ions; w/w) of P1, P2, or P3 corresponding to the growth, MIC_P (%) is the fitted minimum inhibitory concentrations of phosphate ions inhibiting growth, and μ_{ref, P} is the fitted optimal growth rate corresponding to μ_max values at pH 6.00 ± 0.05 and 37°C for Mix-Bc_mes and at 15°C for Mix-Bc_psy.

Figure 4

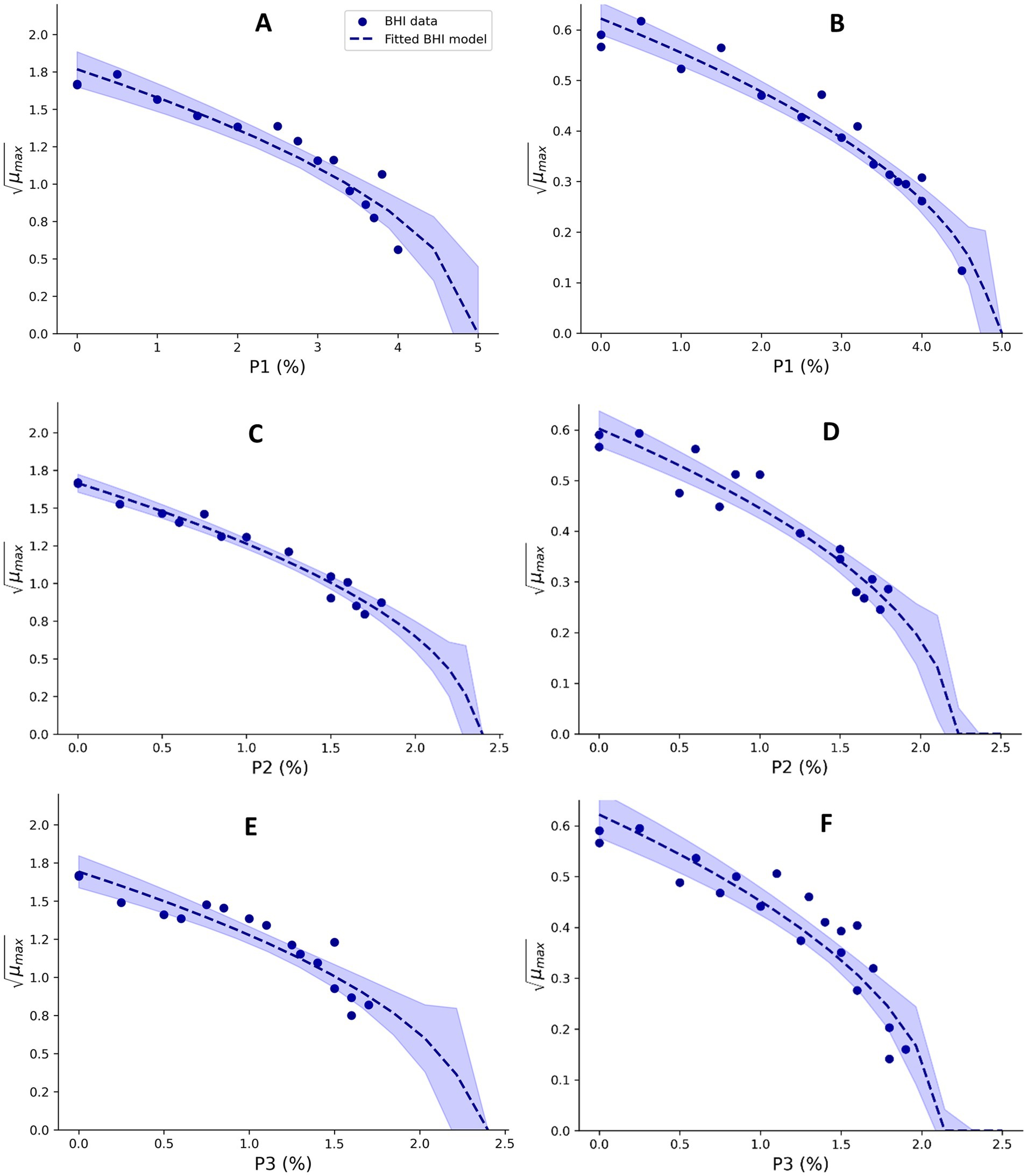
Figure 4. Effect of orthophosphate (A,B), diphosphate (C,D), and triphosphate (E,F), on the square root-transformed maximum specific growth rates (μ_max, h^−0.5) of mesophilic (A,C,E) and psychrotolerant (B,D,F) B. cereus in BHI broth. Fitted model terms for BHI (dashed blue lines) were obtained by fitting Equation 8 to the observed μ_max values in BHI (blue dots). 95% confidence intervals of the fits are shown in blue shades.

2.3 Development of a secondary model

Two secondary models were developed with cardinal model terms (CM; Equations 2–8) for Mix-Bc_mes and Mix-Bc_psy as explained above (see Section 2.2) and their corresponding cardinal parameter values for the effect of temperature, pH, a_w, acetic, benzoic, citric, lactic, and sorbic acid, and orthophosphate, diphosphate, and triphosphate ions (Equation 9; Koukou et al., 2022). The value of each CM-term is between 0 and 1, with lower values indicating a stronger effect of that factor to inhibit growth.

$\begin{array}{l}{\mu }_{\text{max}}={\mu }_{\mathit{opt}}·CM\left(T\right)·CM\left(pH\right)·CM\left(a_w\right)·CM\left(\mathit{AA}{C}_u\right)·\\ CM\left(\mathit{BA}{C}_u\right)·CM\left(CA{C}_T\right)·CM\left(LA{C}_u\right)·\\ CM\left(SA{C}_u\right)·CM\left(P_1\right)·CM\left(P_2\right)·CM\left(P_3\right)·\xi \end{array}\text{ (9)}$

where μ_opt was determined at optimum temperature and pH 6.0 (Equations 1, 2). ξ with a value between 0 and 1 quantified the growth-inhibiting effect of interactions between CM terms in the model (Equations 10, 11; Le Marc et al., 2002). This Le Marc approach quantifies the effect of interactions between environmental factors. The value of ξ is calculated without requiring any model parameters to be fitted. Instead, Equations 10–13 determine the effect of interactions such that an additional inhibitory effect is included due to interaction between environmental factors. The calculated effect of interaction is particularly important close to the growth boundary. This approach was originally suggested for a Listeria monocytogenes cardinal parameter model, and it has later been used and validated for different microorganisms including B. cereus, Clostridium botulinum, and lactic acid bacteria (Dalgaard and Mejlholm, 2019; Le Marc et al., 2002, 2024; Koukou et al., 2021, 2022).

$\xi \left(\phi \left(T,pH,a_w,\mathit{organic}\mathit{acids},P1,P2,P3\right)\right)=\{\begin{array}{cc}1& \psi \le 0.5\\ 2\left(1-\psi \right)& 0.5<\psi <1\\ 0& \psi \ge 1\end{array}\text{ (10)}$

$\begin{array}{ll}\Psi ={\displaystyle \sum }_i\frac{{{\phi }_e}_i}{2{{\displaystyle \prod }}_{j\ne i}\left(1-{{\phi }_e}_j\right)}& (11)\end{array}$

where the ψ value represents the proximity of environmental conditions to the growth boundary (ψ = 1). Ψ values below and above 1.0 correspond to conditions that, respectively, support or prevent growth. The contribution of CM terms (φ values) for temperature, pH, a_w, and phosphate salts on ψ was, respectively, calculated using Equation 12 (Le Marc et al., 2002).

$\begin{array}{ll}{\phi }_{T,pH,a_w,P}={\left(1-\sqrt{C{M}_{\mathit{term}}}\right)}^2& (12)\end{array}$

The φ value for organic acid CM terms was calculated by the multiplicative approach (Equation 13) as proposed by Coroller et al. (2005).

$\begin{array}{ll}{\phi }_{\mathit{organic}\mathit{acids}}={\left(1-C{M}_{AAC}.C{M}_{BAC}.C{M}_{CAC}.C{M}_{\mathit{LAC}}.C{M}_{SAC}\right)}^2& (13)\end{array}$

2.4 Data analysis

Calculation of μ_max values from absorbance data determined by Bioscreen C as described in Section 2.2 was performed with an in-house Python script (Maktabdar et al., 2024; https://github.com/maktabdar/bioscreen). Curve fitting to estimate cardinal parameter values was performed using Python 3.11. Data in MS Excel files were read by the Pandas package (McKinney, 2010; The Pandas development team, 2020) and fitted with the lmfit package (Newville et al., 2014) using the non-linear least squares minimization method.

3 Results

CM terms appropriately fitted growth rate data for Mix-Bc_mes and Mix-Bc_psy in both BHI broth and UF permeate (Figures 1–4) as also indicated by the fitted parameter values and their standard errors (Tables 1, 2). The MIC_T,CAC value determined using UF permeate for Mix-Bc_mes was less accurate due to the high variability of growth rates at high citric acid concentrations (Figure 2E; Table 1). Both Mix-Bc_mes and Mix-Bc_psy grew faster in BHI broth than in UF permeate with added AAC, BAC, and SAC (Figures 2A–D, 3C,D). However, interestingly, both Mix-Bc_mes and Mix-Bc_psy showed greater tolerance to low pH and high concentrations of CAC and LAC in UF permeate than in BHI broth (Figures 1C,D, 2E,F, 3A,B). Consequently, following a worst-case approach, the cardinal parameters values for pH (pH_min; pH_opt), CAC (MIC_{T, CAC}; CAC_T,opt), and LAC (MIC_U,LAC; LAC_U,opt) as determined using UF permeate were included in the secondary models (Tables 1, 2). The effect of NaCl/a_w on μ_max values of Mix-Bc_mes and Mix-Bc_psy was similar for both media, with a slightly lower a_w,min value estimated using UF permeate (a_{w, min} = 0.955) for Mix-Bc_mes and a slightly lower a_{w, min} value estimated using BHI broth (a_{w, min} = 0.963) for Mix-Bc_psy (Figures 1E,F; Tables 1, 2).

Table 1

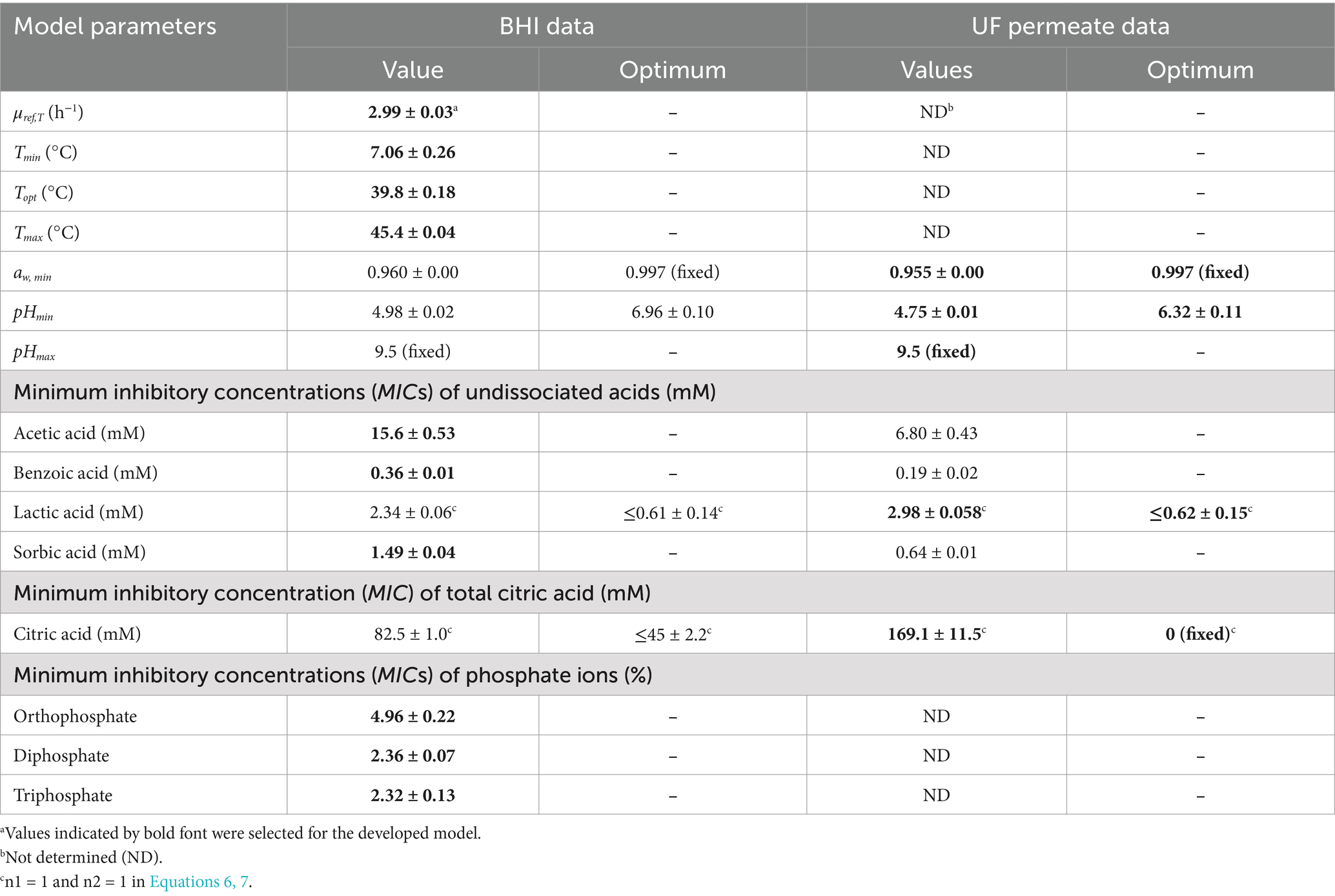
Table 1. Fitted cardinal parameter values and their standard errors estimated for a cocktail of mesophilic B. cereus (Mix-Bc_mes) using both BHI broth and UF permeate from whey.

Table 2

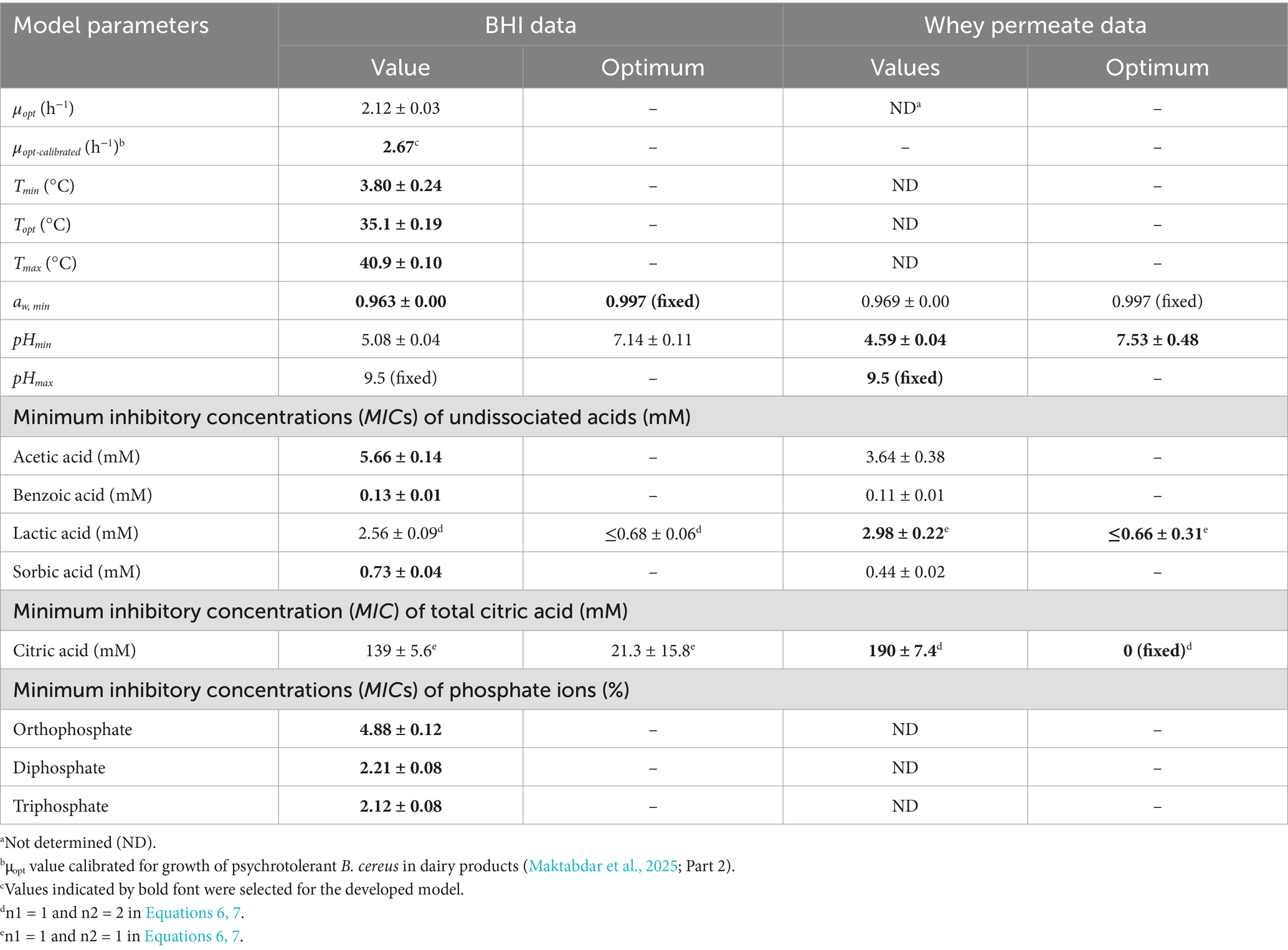
Table 2. Cardinal parameters and their standard errors estimated for a cocktail of psychrotolerant B. cereus (Mix-Bc_psy) using both BHI broth and UF permeate from whey.

The two developed models highlighted differences between the tolerance of mesophilic and psychrotolerant B. cereus to different inhibitory conditions. Mesophilic B. cereus, despite being more sensitive to low temperatures, showed a higher tolerance to acetic, benzoic, and sorbic acids. Mesophilic and psychrotolerant B. cereus showed similar tolerance to high concentrations of lactic and citric acids (Tables 1, 2). The MIC_T,CAC value of 169.1 ± 11.5 mM included in the mesophilic model was estimated using UF permeate and was markedly higher than the 82.5 ± 1.0 mM estimated using BHI broth (Table 1). A higher tolerance of mesophilic isolates was also observed for a_w. The estimated a_w,min for mesophilic isolates was 0.955, equivalent to 7.2% NaCl, whereas for psychrotolerant isolates, it was 0.963, equivalent to 6.1% NaCl. However, mesophilic isolates were more sensitive to low pH than psychrotolerant isolates (pH_min value of 4.75 versus 4.59) (Tables 1, 2). The inhibitory effects of phosphate salts were exclusively studied using BHI broth. Among the evaluated phosphate salts, P1 had the weakest inhibitory effect, whereas P2 and P3 exhibited similar growth inhibitory effects on Mix-Bc_mes and Mix-Bc_psy (Figure 4; Tables 1, 2).

4 Discussion

4.1 Potential of the developed models to predict growth boundaries in dairy product

The two extensive models developed in the present study for mesophilic (Mix-Bc_mes) and psychrotolerant (Mix-Bc_psy) strain cocktails can predict the combined effect of 11 environmental factors on growth rates and growth boundaries for these two subgroups. However, at this stage, the two models are not yet ready to be directly applied to predict the growth kinetics of B. cereus in food, such as during the storage of various dairy products or solutions. Prior to such applications of the models, further product validation studies, using dairy matrices with known product characteristics, are needed to evaluate and determine (i) lag times, including potential differences between vegetative cells and spores, (ii) the need for calibration of μ_opt to obtain unbiased predictions of growth rates in matrices of interest, (iii) water-phase concentrations of the lipophilic benzoic and sorbic acids in fat containing products, and (iv) the models range of applicability where they have been successfully validated with respect to types of matrices and product characteristics. These dairy-related aspects were studied and discussed by Maktabdar et al. (2025; Part 2), and after calibrating the μ_opt value for the psychrotolerant model, they found that both models provided acceptable predictions for a broad range of dairy matrices and product characteristics. However, in the present study, we exclusively discuss the development of these models and their potential to be applied to dairy matrices.

Available models for B. cereus growth do not account for the inhibitory effects of benzoic, citric, and sorbic acids or the effects of phosphate melting salts. The new models developed in the present study can potentially be applicable to a broader range of dairy products, as they can predict the effect of these six environmental factors, along with five others, and their interaction on growth rates and growth boundaries (Equation 9). The environmental factors included in the new models are relevant for products such as cottage cheese, cream cheese, dairy desserts, and processed cheese. These models also have the potential to be used for products where fewer environmental factors influence B. cereus growth, such as milk, fermented milk, and chemically acidified cheese (Bevilacqua and Califano, 1989; Dorko et al., 2014; Østergaard et al., 2014; Han et al., 2016; Martinez-Rios et al., 2016, 2019a; Koukou et al., 2022).

For liquid laboratory media at 30°C, ICMSF (1996) reported B. cereus pH–growth boundaries of 4.8–5.0 with HCl, above 5.6 with 0.1 M lactic acid and above 6.1 with 0.1 M acetic acid. This suggests a strong interaction effect between pH and each of the organic acids as their concentrations were below reported MIC values for both lactic and acetic acids (Tables 1, 2; Biesta-Peters et al., 2010; Le Marc et al., 2024). For chemically acidified white cheese at 25°C, with 4.5% water-phase NaCl, and assuming no growth-inhibiting effect of the acidulant glucono-delta-lactone (Martinez-Rios et al., 2019a), the new models predicted pH–growth boundaries of 4.76 and 4.62 for Mix-Bc_mes and Mix-Bc_psy, respectively. These predicted pH-growth boundaries were similar to both the corresponding pH_min values of 4.75 and 4.59 (Tables 1, 2) and the pH of 4.8–5.0 reported by ICMSF (1996). In this case, little effect of interaction between NaCl and pH at 25°C was predicted. For cream cheese at 25°C, with 2.0% water-phase NaCl, and containing 1,000 ppm, 2000 ppm, and 3,000 ppm of acetic, citric, and lactic acids in the water phase (Martinez-Rios et al., 2019b), the new models predicted pH–growth boundary of 5.04 and 5.32 for mesophilic and psychrotolerant B. cereus, respectively. The new models also predicted pH–growth boundaries of 5.67 and 5.74 for the B. cereus subgroups in processed cheese at 25°C, with 55% moisture, 2,0% WPS, 2.0% water-phase orthophosphate, and the following concentrations of water-phase organic acids (1,500 ppm acetic acid, 4,500 ppm citric acid, and 14,000 ppm lactic acid) (Martinez-Rios et al., 2019b; Koukou et al., 2022). These pH-growth-boundary predictions, modeled using the Le Marc et al. (2002) approach, highlight the significance of interactions between several growth-inhibiting factors. For a complex dairy product such as processed cheese, the new models predicted growth boundaries (Ψ = 1.00) and other boundary conditions (e.g., Ψ = 2.00) that are far from the cardinal parameter values (Figure 5). Biesta-Peters et al. (2010) reported a pH–growth boundary of 4.8 with H₂SO₄ for a mesophilic B. cereus isolate in BHI broth at 30°C. This pH–growth boundary increased to 5.0–5.4 when combined with acetic, formic, lactic, or propionic acids (Biesta-Peters et al., 2010). While this modest interaction effect does not contradict the models developed in the present study, it is important to note that Biesta-Peters et al. (2010) studied the effect of only two growth-inhibiting factors at near-optimal temperatures. In dairy and other foods, multiple environmental factors can contribute to reduced growth, particularly for chilled products. Therefore, considering the effects of interactions between these factors, as demonstrated in Figure 5, can be crucial. The two newly developed models, which include the effect of interaction between their environmental factors, were successfully validated by Maktabdar et al. (2025; Part 2) for processed cheese and various other dairy foods. Similarly, other extensive models that account for interaction effects have been successfully validated for other microorganisms and foods (Mejlholm et al., 2010; Mejlholm and Dalgaard, 2013; Koukou et al., 2021, 2022; Martinez-Rios et al., 2019a,b). These models can help identify combinations of environmental factors that prevent microbial growth, facilitating the formulation or reformulation of dairy products and other foods.

Figure 5

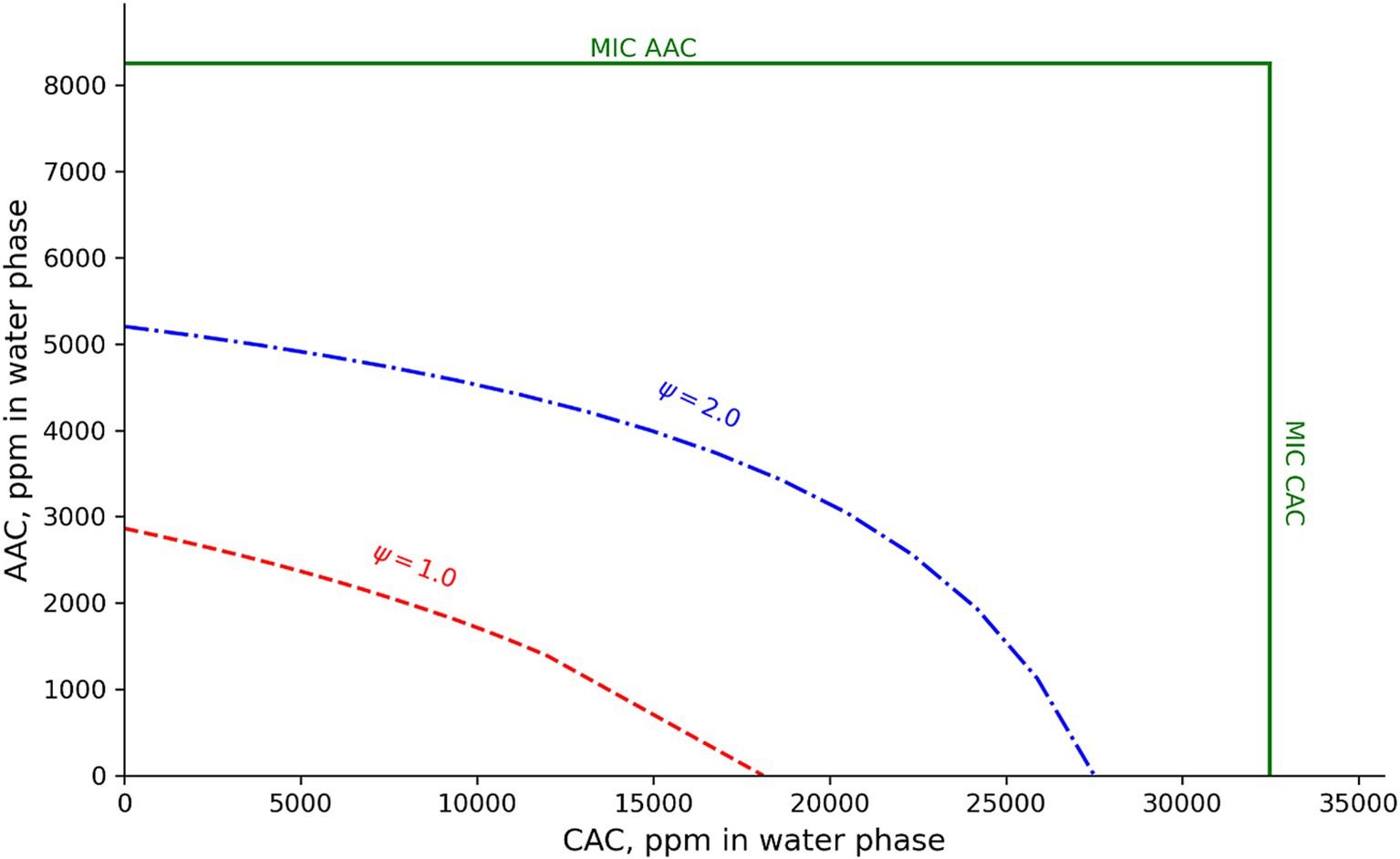
Figure 5. Effect of acetic (AAC) and citric acid (CAC) concentrations on predicted growth boundary (Ψ = 1.00) and boundary conditions with Ψ = 2.00 for mesophilic B. cereus. Predictions were for processed cheese at 25°C and with pH 5.67, 2.0% WPS, 2.0% water-phase orthophosphate, and 14,000 ppm water-phase lactic acids. MIC values of the new mesophilic B. cereus model (15.6 mM for undissociated acetic acid and 169.1 mM total citric acid) were expressed as water-phase concentrations of the acids at pH 5.67.

4.2 Cardinal parameter values and model terms for organic acids, pH, and a_w

Mesophilic B. cereus isolates were more tolerant to acetic, benzoic, and sorbic acids than psychrotolerant isolates (Tables 1, 2). This may be related to more unsaturated fatty acid and higher membrane fluidity of psychrotolerant isolates (Pol and Smid, 1999; Carlin et al., 2010), but this was not evaluated in the present study. The enhanced stress tolerance of B. cereus in UF permeate (Figures 1C,D, 2E,F, 3A,B; Tables 1, 2) may be due to compounds that reduce the inhibitory effect of low pH and high concentrations of lactic and citric acids. Previously, milk protein has been reported to reduce the inhibitory effect of low pH on the growth of C. botulinum (Smelt et al., 1982). Furthermore, calcium and other divalent metal ions have been shown to reduce the inhibitory effect of citric acid on the growth of C. botulinum by the formation of ion–citrate complexes (Graham and Lund, 1986). The difference in tolerance to citric acid between BHI broth and UF permeate was more pronounced for mesophilic B. cereus at 37°C than for psychrotolerant B. cereus at 15°C, suggesting the underlying mechanism is temperature-dependent or quantitatively different for the two strain cocktails. Vavrusova et al. (2014) reported that concentrations of calcium complexes with organic acid ions increased with increasing temperature, potentially explaining the lower inhibitory effect of citric acid at higher temperatures (Figures 2E,F). However, we have found no studies on these effects for B. cereus. The studied UF permeate powder contained 0.75% calcium (see Section 2.2), corresponding to 2.7 mM in the 1.45% UF permeate solution used to determine cardinal parameter values. This is markedly lower than the calcium concentrations found in dairy products such as milk, cheese, and desserts, which range from approximately 15 mM to over 100 mM (Guinee et al., 2002; Guinee and O’Kennedy, 2009; NEVO, 2024). Even considering that some calcium in dairy is bound to other components (Walstra et al., 2005; Pereira et al., 2019), the difference remains substantial. Maktabdar et al. (2025; Part 2) found that the developed models predicted unbiased growth rates of Mix-Bc_mes and Mix-Bc_psy in various dairy products, including products with water-phase concentrations of up to 42 mM of citric acid and up to 194 mM of lactic acids. This suggests that the inhibitory effects of citric and lactic acids on B. cereus are similar in UF permeate and dairy products, despite their markedly different calcium concentrations. Therefore, it seems unlikely that calcium alone can explain the increased tolerance of Mix-Bc_mes and Mix-Bc_psy to citric and lactic acids in UF permeate compared to BHI broth (Figures 2E,F, 3A,B; Tables 1, 2). Further research is needed to identify the specific components or interactions within dairy products and UF permeate that might enhance B. cereus tolerance to low pH and high concentrations of lactic and citric acids. Such future studies should include the effects of lactose, dairy proteins, and divalent metal ions due to their concentrations and potential effects in both dairy products and UF permeate.

T_min values of 5.8°C to 9.1°C and of 0.97°C to 5.2°C have been reported for individual isolates of mesophilic and psychrotolerant B. cereus isolates, respectively (Carlin et al., 2013; Ellouze et al., 2021; Le Marc et al., 2021a,b; Le Marc et al., 2024). The determined T_min values of 7.06°C for Mix-Bc_mas and of 3.80°C for Mix-Bc_psy therefore do not represent extreme values although determined for cocktails rather than individual isolates (Tables 1, 2).

Carlin et al. (2013) and Le Marc et al. (2024) reported pH_min values of 4.59 to 4.65 for mesophilic B. cereus from the panC groups III and IV and pH_min values of 4.62 to 4.96 for psychrotolerant panC group II, V, and VI strains when determined at 30°C using BHI broth supplemented with yeast extract and glucose. We found higher pH_min values of 4.98 for Mix-Bc_mes at 37°C and 5.08 for Mix-Bc_psy at 15°C using BHI broth (Tables 1, 2). This discrepancy might be attributed to differences between strains or to the temperatures used for the determination of the pH_min values. Le Marc et al. (2021a) observed the lowest pH_min values at suboptimum growth temperatures (27–29°C for mesophilic and 21–25°C for psychrotolerant isolates) as also previously observed for L. monocytogenes (Augustin and Carlier, 2000; Martinez-Rios et al., 2019a).

The a_{w, min} values of 0.955 to 0.963 (equivalent to 6.1–7.2% WPS) determined in the present study (Tables 1, 2) align with those determined by Carlin et al. (2013) and Le Marc et al. (2024). These values were higher than the aw-growth boundaries of 0.92 to 0.95 (equivalent to 8.0–11.9% WPS) indicated by NACMCF, National Advisory Committee on Microbiological Criteria for Foods (2010) and ICMSF (1996) for B. cereus. Nevertheless, the dairy product validation studies by Maktabdar et al. (2025; Part 2) suggest the determined a_{w, min} values (Tables 1, 2) are relevant for the growth-inhibiting effect of water-phase salt on mesophilic and psychrotolerant B. cereus isolates in dairy matrices.

For mesophilic B. cereus, we found higher acetic acid tolerance (MIC values of 15.6 mM versus 7.5 mM) and similar lactic acid tolerance (MIC values of 2.34 mM versus 2.6 mM) than previous studies (Table 1; Biesta-Peters et al., 2010). For psychrotolerant B. cereus, Le Marc et al. (2024) reported MIC of undissociated acetic acid to be between 7.12 and 7.77 mM and MIC of undissociated lactic to be 3.20 mM when estimated in BHI broth and at 25°C and 30°C, respectively. The lower MIC values determined using BHI broth in the present study (5.66 mM for acetic and 2.56 for lactic acid; Table 2) may be due to lower experimental temperatures at 15°C. For benzoic, citric, and sorbic acids, as well as for phosphate melting salts, we could not find any studies reporting MIC values in BHI broth for comparison. Additionally, no cardinal parameter or MIC values for B. cereus in UF permeate have been previously reported.

Several models have successfully predicted microbial growth by incorporating the undissociated acid concentrations as inputs (Ross and Dalgaard, 2004; Coroller et al., 2005; Mejlholm and Dalgaard, 2013; Martinez-Rios et al., 2016, 2019b). The present study confirmed this approach (Equations 4, 6). However, using the determined MIC values for undissociated citric acid overestimated its inhibitory effect when evaluating the performance of the developed models (Maktabdar et al., 2025; Part 2). To obtain unbiased predictions and to avoid fail-dangerous prediction of growth/no-growth responses specifically related to citric acid, we used the total concentration of citric acid, rather than the undissociated form, when modeling its inhibitory effect on mesophilic and psychrotolerant B. cereus (see Section 2.2.4.3).

4.3 Conservative approach to formulate cardinal parameter models

BHI broth, with or without added yeast extract and glucose, has been extensively used as a nutrient-rich medium to generate growth responses for B. cereus (Guinebretière et al., 2008; Biesta-Peters et al., 2010; Carlin et al., 2013; Le Marc et al., 2021a,b). The present study confirmed that high growth rates of mesophilic and psychrotolerant B. cereus can be obtained in BHI broth and that these data allowed the estimation of several cardinal parameter values of relevance for dairy products (Figures 1A,B,F, 2A–D, 3C,D, 4; Tables 1, 2). However, the different cardinal parameter values determined in the present study using BHI broth or UF permeate were taken into account using a conservative approach. In this way, the developed growth models included cardinal parameter values determined using BHI broth or UF permeate to obtain the widest growth range for the factors in the two models (Tables 1, 2). This approach resulted in growth and growth boundary models that performed better for dairy products than models developed exclusively with cardinal parameter values from BHI broth (Maktabdar et al., 2025; Part 2). The applied conservative approach is not optimal for the development of models to predict B. cereus growth in dairy products as several cardinal parameter values had to be determined by using two different liquid media. Automated absorbance measurement facilitated the determination of growth rates in both BHI broth and UF permeate, but a better understanding of why cardinal parameter values for some environmental factors differed between the two media is needed for more efficient model development as discussed above (see Section 3.2). Previously, other studies observed that cardinal parameter values determined using liquid laboratory media did not always correspond to growth responses in foods, but an efficient approach to handle this challenge when developing growth models remains to be formulated. Within predictive food microbiology, cardinal parameter growth models have often been developed from growth rates generated using liquid laboratory media such as BHI broth or tryptone soy broth. The developed models have then been evaluated, calibrated, and validated by comparison of predictions with growth responses in foods of interest (Dalgaard and Mejlholm, 2019; Garre et al., 2025). Growth responses in foods can be used directly to develop growth models. For B. cereus in milk and paneer, models including primarily the effect of temperature on growth responses have been developed in this way (Zwietering et al., 1996; Sarkar et al., 2023). For L. monocytogenes, more extensive models have been developed using growth responses and properties of various meat products (Gunvig et al., 2007; Gowda et al., 2024). Markedly fewer B. cereus growth responses and corresponding accurate product characteristics are available for dairy products (Maktabdar et al., 2025; Part 2). Much more data are needed before extensive B. cereus models, as formulated in the present study, can be developed directly from growth responses in dairy products. However, cardinal parameter values can be determined in dairy matrices rather than in liquid laboratory media. This has, for example, been applied for the effect of different organic acids (acetic, benzoic, citric, gluconic, or sorbic) on the growth of lactic acid bacteria or L. monocytogenes in cheeses or seafood where cardinal parameter values from liquid laboratory media did not correspond to growth in food. Furthermore, growth rates in foods of interest can be described using an extensive cardinal parameter model where exclusively selected cardinal parameter values are fitted and others are fixed, e.g., as determined using liquid laboratory media (Mejlholm and Dalgaard, 2009, 2013; Martinez-Rios et al., 2019a; Tirloni et al., 2019). These techniques and the conservative approach from the present study may be useful to expand the new extensive B. cereus models (Tables 1, 2) or for the development of other models to predict growth responses in dairy products.

5 Conclusion

This study developed two extensive predictive models for growth and growth boundaries of both mesophilic and psychrotolerant B. cereus. These models included the combined inhibitory effect of 11 environmental factors relevant to dairy products and ingredients. The importance of the growth medium to quantify the inhibiting effect of environmental factors on B. cereus was demonstrated. While the meat-based BHI broth provided a suitable medium for some factors, a dairy-based UF permeate offered a more realistic representation of B. cereus growth boundaries in dairy products for other factors. A conservative approach allowed the widest growth range as determined using data from BHI broth and UF permeate to be applied for the development of the two extensive models.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

MM: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Project administration, Validation, Visualization, Writing – original draft, Writing – review & editing. EW: Conceptualization, Funding acquisition, Resources, Writing – review & editing. EG: Conceptualization, Funding acquisition, Resources, Writing – review & editing. PD: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The Danish Dairy Research foundation funded the present study as part of the project “Predictive tool for dairy products (Bacillus-Predict; grant no. 2021-20).”

Acknowledgments

We thank Rannvá Høgnadóttir Houmann and Nanna Hulbæk Scheel from DTU Food for their skillful assistance in Bioscreen C experiments, and Ali A. Eftekhari from DTU Sustain for their contribution to data analysis using Python. Edgar Remmet Snoeck from DTU Food contributed to discuss the potential effect of calcium.

Conflict of interest

EW and EG were employed by, respectively, Arla Foods Ingredients and Arla Foods amba.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Augustin, J.-C., and Carlier, V. (2000). Modelling the growth rate of Listeria monocytogenes with a multiplicative type model including interactions between environmental factors. Int. J. Food Microbiol. 56, 53–70. doi: 10.1016/S0168-1605(00)00224-5

PubMed Abstract | Crossref Full Text | Google Scholar

Bergis, H., Bonanno, L., Asséré, A., and Lombard, B. (2021). EURL lm technical guidance document on challenge tests and durability studies for assessing shelf-life of ready-to-eat foods related to Listeria monocytogenes. Maisons-Alfort, France: Anses – Food Safety Laboratory.

Google Scholar

Bevilacqua, A. E., and Califano, A. N. (1989). Determination of organic acids in dairy products by high performance liquid chromatography. J. Food Sci. 54:1076. doi: 10.1111/j.1365-2621.1989.tb07948.x

Crossref Full Text | Google Scholar

Biesta-Peters, E. G., Reij, M. W., Gorris, L. G. M., and Zwietering, M. H. (2010). Comparing nonsynergistic gamma models with interaction models to predict growth of emetic Bacillus cereus when using combinations of pH and individual undissociated acids as growth-limiting factors. Appl. Environ. Microbiol. 76, 5791–5801. doi: 10.1128/AEM.00355-10

PubMed Abstract | Crossref Full Text | Google Scholar

Budavari, S. (1989). The Merck index: An encyclopedia of chemicals. Drugs and biologicals. 11th Edn. Rahway, N.J., USA: Merck & Co. Inc.

Google Scholar

Buss da Silva, N., Baranyi, J., Carciofi, B. A. M., and Ellouze, M. (2017). From culture-medium-based models to applications to food: predicting the growth of B. cereus in reconstituted infant formulae. Front. Microbiol. 8:1799. doi: 10.3389/fmicb.2017.01799

PubMed Abstract | Crossref Full Text | Google Scholar

Carlin, F., Albagnac, C., Rida, A., Guinebretière, M.-H., Couvert, O., and Nguyen-the, C. (2013). Variation of cardinal growth parameters and growth limits according to phylogenetic affiliation in the Bacillus cereus group. Consequences for risk assessment. Food Microbiol. 33, 69–76. doi: 10.1016/j.fm.2012.08.014

PubMed Abstract | Crossref Full Text | Google Scholar

Carlin, F., Brillard, J., Broussolle, V., Clavel, T., Duport, C., Jobin, M., et al. (2010). Adaptation of Bacillus cereus, an ubiquitous worldwide-distributed foodborne pathogen, to a changing environment. Food Res. Int. 43, 1885–1894. doi: 10.1016/j.foodres.2009.10.024

Crossref Full Text | Google Scholar

Carroll, L. M., Cheng, R. A., and Kovac, J. (2020). No assembly required: using BTyper3 to assess the congruency of a proposed taxonomic framework for the Bacillus cereus group with historical typing methods. Front. Microbiol. 11:580691. doi: 10.3389/fmicb.2020.580691

PubMed Abstract | Crossref Full Text | Google Scholar

Carroll, L. M., Cheng, R. A., Wiedmann, M., and Kovac, J. (2021). Keeping up with the Bacillus cereus group: taxonomy through the genomics era and beyond. Crit. Rev. Food Sci. Nutr. 62, 7677–7702. doi: 10.1080/10408398.2021.1916735

PubMed Abstract | Crossref Full Text | Google Scholar

Coroller, L., Guerrot, V., Huchet, V., Le Marc, Y., Mafart, P., Sohier, D., et al. (2005). Modelling the influence of single acid and mixture on bacterial growth. Int. J. Food Microbiol. 100, 167–178. doi: 10.1016/j.ijfoodmicro.2004.10.014

Crossref Full Text | Google Scholar

Dalgaard, P., and Koutsoumanis, K. (2001). Comparison of maximum specific growth rates and lag times estimated from absorbance and viable count data by different mathematical models. J. Microbiol. Methods 43, 183–196. doi: 10.1016/S0167-7012(00)00219-0

PubMed Abstract | Crossref Full Text | Google Scholar

Dalgaard, P., and Mejlholm, O. (2019). “Modeling growth of Listeria and lactic acid bacteria in food environments” in Foodborne bacterial pathogens. ed. A. Bridier (New York: Springer), 247–264.

Google Scholar

Dorko, C. L., Ford, G. T. Jr., Baggett, M. S., Behling, A. R., and Carmen, H. E.by Staff, U (2014). “Sorbic acid” in Kirk-Othmer encyclopedia of chemical technology (John Wiley & Sons, Ltd.), 1–19.

Google Scholar

EC (2007). Commission regulation No. 1441/2007 of 5 Dec. 2007 Amendment of regulation EC No. 2073/2005. Microbiological criteria for foodstuffs. Off. J. Eur. Commun. https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2007:322:0012:0029:EN:PDF (Accessed February 22, 2023).

Google Scholar

EFSA (2005). Opinion of the scientific panel on biological hazards (BIOHAZ) on Bacillus cereus and other Bacillus spp in foodstuffs. EFSA J. 3:175. doi: 10.2903/j.efsa.2005.175

PubMed Abstract | Crossref Full Text | Google Scholar

EFSA (2016). Risks for public health related to the presence of Bacillus cereus and other Bacillus spp. including Bacillus thuringiensis in foodstuffs. EFSA J. 14:e04524. doi: 10.2903/j.efsa.2016.4524

PubMed Abstract | Crossref Full Text | Google Scholar

Ehling-Schulz, M., Lereclus, D., and Koehler, T. M. (2019). The Bacillus cereus group: Bacillus species with pathogenic potential. Microbiol. Spectr. 7, 7–3. doi: 10.1128/microbiolspec.GPP3-0032-2018

PubMed Abstract | Crossref Full Text | Google Scholar

Ellouze, M., Buss Da Silva, N., Rouzeau-Szynalski, K., Coisne, L., Cantergiani, F., and Baranyi, J. (2021). Modeling Bacillus cereus growth and cereulide formation in cereal-, dairy-, meat-, vegetable-based food and culture medium. Front. Microbiol. 12:155. doi: 10.3389/fmicb.2021.639546

PubMed Abstract | Crossref Full Text | Google Scholar

Fusieger, A., da Silva, R. R., Cavicchioli, V. Q., Rodrigues, R. D. S., Honorato, J. A., De Jesus Silva, S. R., et al. (2022). Influence of emulsifying salts on the growth of Bacillus thuringiensis CFBP 3476 and Clostridium perfringens ATCC 13124 in processed cheese. Food Secur. 11:3217. doi: 10.3390/foods11203217

PubMed Abstract | Crossref Full Text | Google Scholar

Fusieger, A., Russo, N., Nero, L. A., De Carvalho, A. F., Randazzo, C., and Caggia, C. (2024). Emulsifying salts and P₂O₅ content as promising strategies to control Bacillus cereus growth during storage of processed cheese. Int. J. Dairy Technol. 77, 198–211. doi: 10.1111/1471-0307.13023

Crossref Full Text | Google Scholar

Garre, A., Fernández, P., Grau-Noguer, E., Guillén, S., Portaña, S., Possas, A., et al. (2025). Predictive microbiology through the last century. From paper to excel and towards AI. Adv. Food Nutr. Res. 113, 1–63. doi: 10.1016/bs.afnr.2024.09.012

Crossref Full Text | Google Scholar

Gowda, N. A. N., Singh, M., Lommerse, G., Kumar, S., Heintz, E., and Subbiah, J. (2024). Predictive model for Listeria monocytogenes in RTE meats using exclusive food matrix data. Food Secur. 13:3948. doi: 10.3390/foods13233948

PubMed Abstract | Crossref Full Text | Google Scholar

Graham, A. F., and Lund, B. M. (1986). The effect of citric acid on growth of proteolytic strains of Clostridium botulinum. J. Appl. Bacteriol. 61, 39–49. doi: 10.1111/j.1365-2672.1986.tb03756.x

PubMed Abstract | Crossref Full Text | Google Scholar

Guinebretière, M.-H., Thompson, F. L., Sorokin, A., Normand, P., Dawyndt, P., Ehling-Schulz, M., et al. (2008). Ecological diversification in the Bacillus cereus group. Environ. Microbiol. 10, 851–865. doi: 10.1111/j.1462-2920.2007.01495.x

Crossref Full Text | Google Scholar

Guinee, T. P., Feeney, E. P., Auty, M. A. E., and Fox, P. F. (2002). Effect of pH and calcium concentration on some textural and functional properties of mozzarella cheese. J. Dairy Sci. 85, 1655–1669. doi: 10.3168/jds.S0022-0302(02)74238-0

PubMed Abstract | Crossref Full Text | Google Scholar

Guinee, T. P., and O’Kennedy, B. T. (2009). The effect of calcium content of Cheddar-style cheese on the biochemical and rheological properties of processed cheese. Dairy Sci. Technol. 89, 317–333. doi: 10.1051/dst/2009009

Crossref Full Text | Google Scholar

Gunvig, A., Blom-Hanssen, J., Jacobsen, T., Hansen, F., and Borggaard, C. (2007). “A predictive model for growth of Listeria monocytogenes in meat products with seven hurdle variables” in 5th Int. Conf. Predictive modelling in foods—Conference proceedings. eds. G.-J. E. Nychas, P. Taoukis, K. Koutsoumanis, J. Van Impe, and A. Geeraerd. (Athens: Agricultural University of Athens), 197–200.

Google Scholar

Han, N., Park, S.-Y., Kim, S.-Y., Yoo, M.-Y., Paik, H.-D., and Lim, S.-D. (2016). Change of naturally occurring benzoic acid during skim milk fermentation by commercial cheese starters. J. Dairy Sci. 99, 8633–8637. doi: 10.3168/jds.2016-10890

PubMed Abstract | Crossref Full Text | Google Scholar

ICMSF (1996). Microorganisms in foods 5: Characteristics of microbial pathogens. New York, NY: Springer. Available online at: https://link.springer.com/book/9780412473500 (accessed November 18, 2024).

Google Scholar

Koukou, I., Mejlholm, O., and Dalgaard, P. (2021). Cardinal parameter growth and growth boundary model for non-proteolytic Clostridium botulinum – effect of eight environmental factors. Int. J. Food Microbiol. 346:109162. doi: 10.1016/j.ijfoodmicro.2021.109162

PubMed Abstract | Crossref Full Text | Google Scholar

Koukou, I., Stergioti, T., la Cour, R., Gkogka, E., and Dalgaard, P. (2022). Clostridium sporogenes as surrogate for proteolytic C. botulinum – development and validation of extensive growth and growth-boundary model. Food Microbiol. 107:104060. doi: 10.1016/j.fm.2022.104060

PubMed Abstract | Crossref Full Text | Google Scholar

Le Marc, Y., Baert, L., Buss da Silva, N., Postollec, F., Huchet, V., Baranyi, J., et al. (2021a). The effect of pH on the growth rate of Bacillus cereus sensu lato: quantifying strain variability and modelling the combined effects of temperature and pH. Int. J. Food Microbiol. 360:109420. doi: 10.1016/j.ijfoodmicro.2021.109420

PubMed Abstract | Crossref Full Text | Google Scholar

Le Marc, Y., Buss da Silva, N., Postollec, F., Huchet, V., Baranyi, J., and Ellouze, M. (2021b). A stochastic approach for modelling the effects of temperature on the growth rate of Bacillus cereus sensu lato. Int. J. Food Microbiol. 349:109241. doi: 10.1016/j.ijfoodmicro.2021.109241

PubMed Abstract | Crossref Full Text | Google Scholar

Le Marc, Y., Huchet, V., Bourgeois, C. M., Guyonnet, J. P., Mafart, P., and Thuault, D. (2002). Modelling the growth kinetics of Listeria as a function of temperature, pH and organic acid concentration. Int. J. Food Microbiol. 73, 219–237. doi: 10.1016/S0168-1605(01)00640-7

PubMed Abstract | Crossref Full Text | Google Scholar

Le Marc, Y., Petton, E., Lochardet, A., Postollec, F., and Huchet, V. (2024). Growth limits of psychrotrophic Bacillus cereus as a function of temperature, pH, water activity, and lactic or acetic acid. Microb. Risk Anal. 27-28:100310. doi: 10.1016/j.mran.2024.100310

PubMed Abstract | Crossref Full Text | Google Scholar

Maktabdar, M., Houmann, R. H., Scheel, N. H., Skytthe, K. B., Wemmenhove, E., Gkogka, E., et al. (2025). Evaluation and validation of two extensive growth and growth boundary models for mesophilic and psychrotolerant Bacillus cereus in dairy products (part 2). Front. Microbiol. 16:1559303. doi: 10.3389/fmicb.2025.1553903

Crossref Full Text | Google Scholar

Maktabdar, M., Truelstrup Hansen, L., Wemmenhove, E., Gkogka, E., and Dalgaard, P. (2024). Prevalence, characteristics, and selection of Bacillus cereus subgroups from dairy products for challenge testing and predictive model development. J. Food Prot. 87:100367. doi: 10.1016/j.jfp.2024.100367

PubMed Abstract | Crossref Full Text | Google Scholar

Martinez-Rios, V., Gkogka, E., and Dalgaard, P. (2019a). New term to quantify the effect of temperature on pH_min-values used in cardinal parameter growth models for Listeria monocytogenes. Front. Microbiol. 10:1510. doi: 10.3389/fmicb.2019.01510

PubMed Abstract | Crossref Full Text | Google Scholar

Martinez-Rios, V., Jørgensen, M. Ø., Koukou, I., Gkogka, E., and Dalgaard, P. (2019b). Growth and growth boundary model with terms for melting salts to predict growth responses of Listeria monocytogenes in spreadable processed cheese. Food Microbiol. 84:103255. doi: 10.1016/j.fm.2019.103255

PubMed Abstract | Crossref Full Text | Google Scholar

Martinez-Rios, V., Østergaard, N. B., Gkogka, E., Rosshaug, P. S., and Dalgaard, P. (2016). Modelling and predicting growth of psychrotolerant pseudomonads in milk and cottage cheese. Int. J. Food Microbiol. 216, 110–120. doi: 10.1016/j.ijfoodmicro.2015.09.020

PubMed Abstract | Crossref Full Text | Google Scholar

McKinney, W. (2010). "Data structures for statistical computing in Python." In Proceedings of the 9th Python in Science Conference, eds. S. WaltVan Der and J. Millman, (SCIPY) 56–61.

Google Scholar

Mejlholm, O., and Dalgaard, P. (2009). Development and validation of an extensive growth and growth boundary model for Listeria monocytogenes in lightly preserved and ready-to-eat shrimp. J. Food Prot. 72, 2132–2143. doi: 10.4315/0362-028X-72.10.2132

PubMed Abstract | Crossref Full Text | Google Scholar

Mejlholm, O., and Dalgaard, P. (2013). Development and validation of an extensive growth and growth boundary model for psychrotolerant Lactobacillus spp. in seafood and meat products. Int. J. Food Microbiol. 167, 244–260. doi: 10.1016/j.ijfoodmicro.2013.09.013

PubMed Abstract | Crossref Full Text | Google Scholar

Mejlholm, O., Gunvig, A., Borggaard, C., Blom-Hanssen, J., Mellefont, L., Ross, T., et al. (2010). Predicting growth rates and growth boundary of Listeria monocytogenes — an international validation study with focus on processed and ready-to-eat meat and seafood. Int. J. Food Microbiol. 141, 137–150. doi: 10.1016/j.ijfoodmicro.2010.04.026

PubMed Abstract | Crossref Full Text | Google Scholar

NACMCF, National Advisory Committee on Microbiological Criteria for Foods (2010). Parameters for determining dnoculated pack/challenge study protocols. J. Food Prot. 73, 140–202. doi: 10.4315/0362-028X-73.1.140

Crossref Full Text | Google Scholar

NEVO (2024). Dutch food composition database (NEVO), National Institute for Public Health and the Environment, Ministry of Health, Welfare and Sport, The Netherlands. Available online at: https://www.rivm.nl/en/dutch-food-composition-database (accessed December 8, 2024).

Google Scholar

Newville, M., Stensitzki, T., Allen, D. B., and Ingargiola, A. (2014). LMFIT: Non-linear least-square minimization and curve-fitting for Python. The Panda development team: Zenodo.

Google Scholar

Ölmez, H. K., and Aran, N. (2005). Modeling the growth kinetics of Bacillus cereus as a function of temperature, pH, sodium lactate and sodium chloride concentrations. Int. J. Food Microbiol. 98, 135–143. doi: 10.1016/j.ijfoodmicro.2004.05.018

PubMed Abstract | Crossref Full Text | Google Scholar

Østergaard, N. B., Eklöw, A., and Dalgaard, P. (2014). Modelling the effect of lactic acid bacteria from starter- and aroma culture on growth of Listeria monocytogenes in cottage cheese. Int. J. Food Microbiol. 188, 15–25. doi: 10.1016/j.ijfoodmicro.2014.07.012

PubMed Abstract | Crossref Full Text | Google Scholar

Pereira, J. P. F., Mageste, A. C., Campos, N. D. S., Francisquini, J. D. A., Perrone, I. T., Carvalho, A. F. D., et al. (2019). Calcium partition in Minas Padrão cheese and its bioaccessibility during ripening time. Food Sci. Technol. 39, 859–866. doi: 10.1590/fst.12518

Crossref Full Text | Google Scholar

Pol, I. E., and Smid, E. J. (1999). Combined action of nisin and carvacrol on Bacillus cereus and Listeria monocytogenes. Lett. Appl. Microbiol. 29, 166–170. doi: 10.1046/j.1365-2672.1999.00606.x

Crossref Full Text | Google Scholar

Presser, K. A., Ratkowsky, D. A., and Ross, T. (1997). Modelling the growth rate of Escherichia coli as a function of pH and lactic acid concentration. Appl. Environ. Microbiol. 63, 2355–2360. doi: 10.1128/aem.63.6.2355-2360.1997

PubMed Abstract | Crossref Full Text | Google Scholar

Resnik, S. L., and Chirife, J. (1988). Proposed theoretical water activity values at various temperatures for selected solutions to be used as reference sources in the range of microbial growth. J. Food Prot. 51, 419–423. doi: 10.4315/0362-028X-51.5.419

PubMed Abstract | Crossref Full Text | Google Scholar

Ross, T., and Dalgaard, P. (2004). “Secondary models” in Modeling microbial responses in foods. eds. R. C. McKellar and X. Lu (Boca Raton, Fl: CRC Press), 63–150.

Google Scholar

Røssland, E. (2003). Inhibition of Bacillus cereus by strains of Lactobacillus and Lactococcus in milk. Int. J. Food Microbiol. 89, 205–212. doi: 10.1016/S0168-1605(03)00149-1

PubMed Abstract | Crossref Full Text | Google Scholar

Rosso, L., Lobry, J. R., Bajard, S., and Flandrois, J. P. (1995). Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 61, 610–616. doi: 10.1128/aem.61.2.610-616.1995

PubMed Abstract | Crossref Full Text | Google Scholar

Sarkar, D., Hunt, I., Macdonald, C., Wang, B., Bowman, J. P., and Tamplin, M. L. (2023). Modelling growth of Bacillus cereus in paneer by one-step parameter estimation. Food Microbiol. 112:104231. doi: 10.1016/j.fm.2023.104231

PubMed Abstract | Crossref Full Text | Google Scholar

Smelt, J. P. P. M., Raatjes, G. J. M., Crowther, J. S., and Verrips, C. T. (1982). Growth and toxin formation by Clostridium botulinum at low pH values. J. Appl. Bacteriol. 52, 75–82. doi: 10.1111/j.1365-2672.1982.tb04375.x

Crossref Full Text | Google Scholar

Soria, M. C., and Audisio, M. C. (2014). Inhibition of Bacillus cereus strains by antimicrobial metabolites from Lactobacillus johnsonii CRL1647 and Enterococcus faecium SM21. Probiotics Antimicrob. Proteins 6, 208–216. doi: 10.1007/s12602-014-9169-z

PubMed Abstract | Crossref Full Text | Google Scholar

The Pandas development team (2020). pandas-dev/pandas: Pandas. (Zenodo).

Google Scholar

Tirloni, E., Stella, S., Bernardi, C., Dalgaard, P., and Rosshaug, P. S. (2019). The Panda development team: Zenodo. Predicting growth of Listeria monocytogenes in fresh ricotta. Food Microbiol. 78, 123–133. doi: 10.1016/j.fm.2018.10.004

PubMed Abstract | Crossref Full Text | Google Scholar

Tirloni, E., Stella, S., Celandroni, F., Mazzantini, D., Bernardi, C., and Ghelardi, E. (2022). Bacillus cereus in dairy products and production plants. Food Secur. 11:2572. doi: 10.3390/foods11172572

PubMed Abstract | Crossref Full Text | Google Scholar

Vavrusova, M., Liang, R., and Skibsted, L. H. (2014). Thermodynamics of dissolution of calcium hydroxycarboxylates in water. J. Agric. Food Chem. 62, 5675–5681. doi: 10.1021/jf501453c

PubMed Abstract | Crossref Full Text | Google Scholar

Vos, P., Garrity, G., Jones, D., Krieg, N. R., Ludwig, W., Rainey, F. A., et al. (2011). Bergey’s manual of systematic bacteriology, volume 3: The Firmicutes. 2nd Edn. Springer New York: New York.

Google Scholar

Walstra, P., Walstra, P., Wouters, J. T. M., and Geurts, T. J. (2005). Dairy science and technology. 2nd Edn. Boca Raton: CRC Press.

Google Scholar

Watterson, M. J., Kent, D. J., Boor, K. J., Wiedmann, M., and Martin, N. H. (2014). Evaluation of dairy powder products implicates thermophilic spore formers as the primary organisms of interest. J. Dairy Sci. 97, 2487–2497. doi: 10.3168/jds.2013-7363

PubMed Abstract | Crossref Full Text | Google Scholar

Webb, M. D., Barker, G. C., Goodburn, K. E., and Peck, M. W. (2019). Risk presented to minimally processed chilled foods by psychrotrophic Bacillus cereus. Trends Food Sci. Technol. 93, 94–105. doi: 10.1016/j.tifs.2019.08.024

PubMed Abstract | Crossref Full Text | Google Scholar

Wong, H.-C., and Chen, Y.-L. (1988). Effects of lactic acid bacteria and organic acids on growth and germination of Bacillus cereus. Appl. Environ. Microbiol. 54, 2179–2184. doi: 10.1128/aem.54.9.2179-2184.1988

PubMed Abstract | Crossref Full Text | Google Scholar

Zwietering, M. H., de Wit, J. C., and Notermans, S. (1996). Application of predictive microbiology to estimate the number of Bacillus cereus in pasteurised milk at the point of consumption. Int. J. Food Microbiol. 30, 55–70. doi: 10.1016/0168-1605(96)00991-9

PubMed Abstract | Crossref Full Text | Google Scholar