Jing Chen1*†
Beiyan Nan2*†- 1Department of Biological Sciences, Virginia Polytechnic Institute and State University, Blacksburg, VA, United States
- 2Department of Biology, Texas A&M University, College Station, TX, United States
Many bacteria move on solid surfaces using gliding motility, without involvement of flagella or pili. Gliding of Myxococcus xanthus is powered by a proton channel homologous to the stators in the bacterial flagellar motor. Instead of being fixed in place and driving the rotation of a circular protein track like the flagellar basal body, the gliding machinery of M. xanthus travels the length of the cell along helical trajectories, while mechanically engaging with the substrate. Such movement entails a different molecular mechanism to generate propulsion on the cell. In this perspective, we will discuss the similarities and differences between the M. xanthus gliding machinery and bacterial flagellar motor, and use biophysical principles to generate hypotheses about the operating mechanism, efficiency, sensitivity to control, and mechanosensing of M. xanthus gliding.
Introduction
Bacteria navigate their environments using diverse motility systems, yet many distinct mechanisms can find homology between each other, possibly as a result of divergent evolution. Such systems could use analogous energy sources and be subject to similar physical and chemical constraints. For example, rotary bacterial flagella, regardless of their localization (inside or outside of the cell wall) and energy sources (proton motive force or other ion gradient across the membrane), are all subject to comparable mechanochemical and hydrodynamic limits. In this perspective, we will focus on the gliding machinery of Myxococcus xanthus, which mediates linear cellular translocation on solid surfaces, yet uses a proton channel that is homologous to the energy-harvesting unit in rotary flagella (Nan et al., 2011; Sun et al., 2011).
Myxococcus xanthus is a rod-shaped gram-negative bacterium that cannot swim due to the lack of flagella. Instead, it moves on surfaces using two motility systems, a social (S)-motility system that works more effectively in cells within groups, and an adventurous (A)-motility system that predominates in isolated cells. S-motility, also termed twitching motility, depends on extension and retraction of the Type IV pili (Wu and Kaiser, 1995; Chang et al., 2016), while A-motility, also termed gliding motility, is driven by a rather unique system. The entire gliding machinery consists of about 20 proteins and spans across the cytoplasm, inner membrane, peptidoglycan (PG) wall and outer membrane to interact with the substrate (Figure 1). The energy-harvesting unit in the inner membrane consists of AglR, AglQ, and AglS, which show significant homology with the MotA/B proteins in the flagellar stator of Escherichia coli (AglR is homologous to MotA, whereas AglQ and AglS are homologous to MotB; Nan et al., 2011; Sun et al., 2011). As a conserved proton-binding site on AglQ is essential for gliding, AglR/Q/S, similar to MotA/B, are predicted to form proton channels that convert the proton motive force into mechanical forces (Sun et al., 2011). For brevity, hereafter we will refer to the energy-harvesting proton channel as the “motor”, to be distinguished from the fully assembled gliding machinery. In contrast to the flagellar MotA/B stator, however, the AglR/Q/S motors are not fixed in the cell envelop, but rather travel the length of the cell along helical trajectories (Nan et al., 2011; Fu et al., 2018). When the motors travel to the sites where the cell contacts the substrate, they interact with the substrate through a group of Glt proteins that span the periplasm (Figure 1; Nan et al., 2010; Faure et al., 2016). In order to propel the cell forward, the motors must exert opposite mechanical forces on the substrate and the cell to cause relative motion between the two.
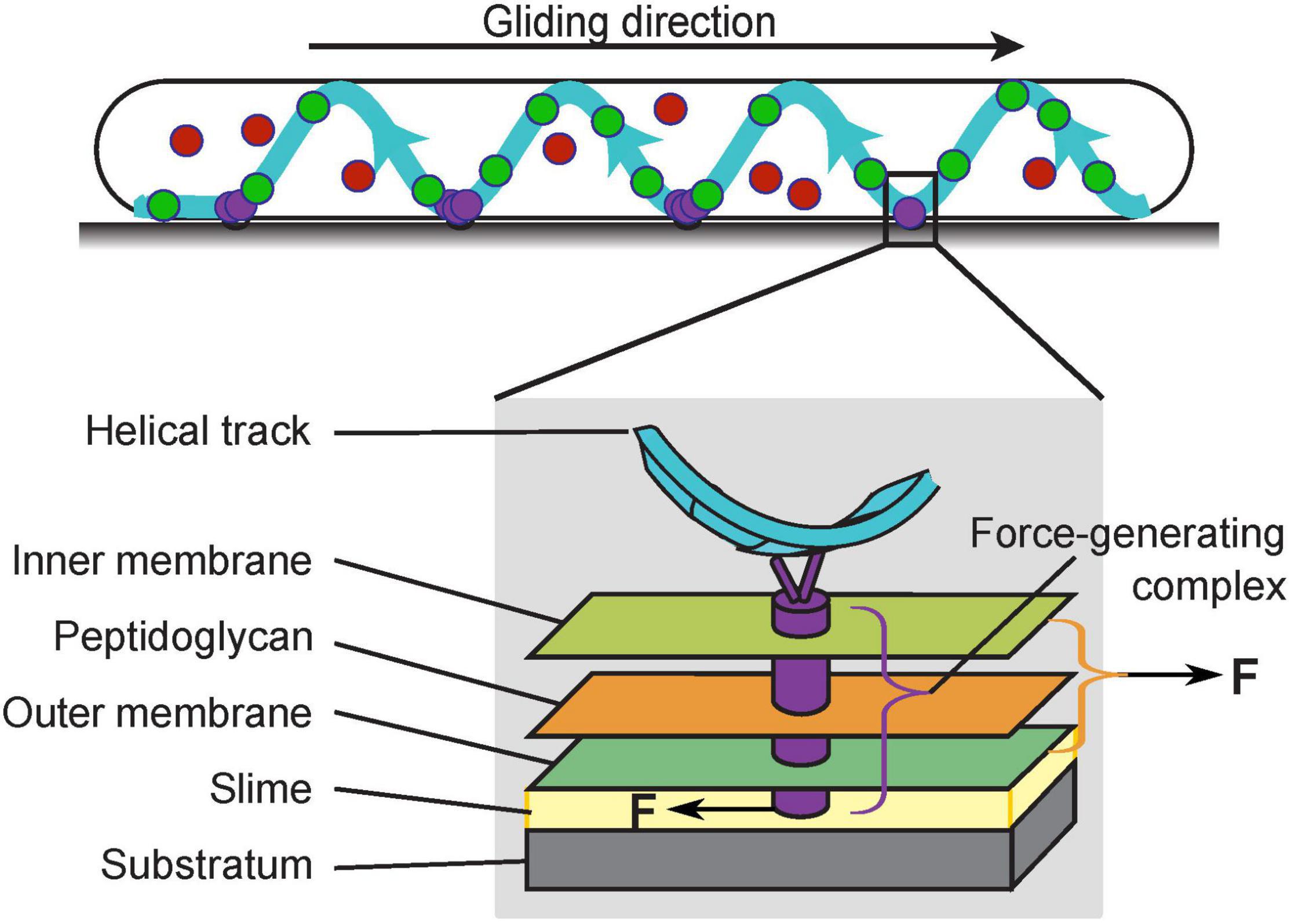
Figure 1. The gliding machinery of Myxococcus xanthus. The AglR/Q/S motors can be categorized into three subpopulations: those in the stationary force-generating complexes (purple), those undergoing directed motion along helical trajectories (green), and those that are diffusive (red). The fully assembled force-generating complexes span the entire cell envelop (gray box). To propel the cell forward, the force-generating complexes must exert opposite forces on the cell and substrate.
Single molecules of the motor and motor-associated proteins typically exhibit three subcellular dynamic patterns, stationary, directed motion, and diffusion. Current data suggest that the force-generating units are stationary, in which the motors assemble with other gliding proteins into fully functional gliding machineries (Nan et al., 2013; Faure et al., 2016; Nan, 2017). Most prominently, the stationary subpopulation aggregate in regularly spaced “focal adhesion” sites where the substrate interfaces with a helical intracellular track (Figure 1, purple circles; Nan et al., 2013). As the cell moves forward, these motor aggregations remain static with respect to the substrate; relative to the cell, they move toward the trailing pole at the speed of the cell (Mignot et al., 2007; Nan et al., 2010, 2013; Faure et al., 2016). Another subpopulation of motors travel along the helical track. The helical pattern of the motors (Figure 1, green circles) colocalizes with that of MreB, a bacterial cytoskeletal protein and homolog of eukaryotic actin. Disruption of MreB abolishes the helical motion of the motors and blocks gliding motility (Mauriello et al., 2010; Nan et al., 2011; Fu et al., 2018). However, it is yet unclear whether MreB directly provides the intracellular track for the motors, or rather, guides the helical motion of the motors indirectly. Although the helical motion of motors depends on the proton motive force and can reach ∼2 μm/s (Nan et al., 2013, 2015), the motors in directed motion could be in an intermediate state before the complete assembly of the force-generating units at the “focal adhesion” sites. Such incomplete machineries probably lack mechanical engagement with the substrate, and are thus not likely to provide propulsion for gliding (Nan et al., 2013; Faure et al., 2016; Nan, 2017). The third subpopulation of motor proteins are diffusive (Figure 1, red circles). As this subpopulation increases when either the proton motive force or MreB is disrupted1, it may be composed of incomplete motors, which are unable to harvest the proton motive force (Nan et al., 2013). Individual gliding proteins switch among the three states dynamically, out of which the switch into the stationary state likely reflects the assembly of the force-generating machineries and their engagement with the substrate. Notably, this assembly responds to substrate stiffness: the aggregation of stationary motors and motor-associated proteins intensifies on harder substrates and nearly all motors become stationary when the whole cell is embedded in the substrate (Nan et al., 2010, 2013). This phenomenon suggests that external mechanical cues can influence the gliding of M. xanthus, which is a hallmark of cellular mechanosensing.
Although the proteins constituting the M. xanthus gliding machinery are largely known, it remains unclear how the gliding machinery generates propulsion and drives linear motion of the cell. Based on prominent biophysical characteristics, such as the velocities of the motors and the intracellular helical track, a number of studies have proposed physical models for various aspects of gliding (Wolgemuth et al., 2002; Nan et al., 2011; Balagam et al., 2014; Tchoufag et al., 2019). As increasing amount of experimental data become available, we will review the similarities and differences between the gliding machinery in M. xanthus and the well-studied bacterial flagellar system in E. coli. Based on these comparisons, we will leverage biophysical principles to make hypotheses about the elusive mechanistic aspects of the M. xanthus gliding machinery, such as its assembly, force transmission, and sensitivity to control.
Open Questions on the Mechanism of M. Xanthus Gliding
How Does the Gliding Machinery Move Without Tearing the Cell Wall?
The envelop-spanning force-generating units at the “focal adhesion” sites are stationary relative to the substrate, while the cell wall moves forward at the cell velocity. Intuitively, the relative motion between the force-generating units and the cell wall would tear the wall and compromise its mechanical integrity. Yet, the cell wall is not broken in moving M. xanthus cells. How does the gliding machinery move without tearing the cell wall? This is a challenge that the statically positioned flagellar motor does not face.
The answer to the above question depends on how the gliding machineries interact with the substrate. An early theory proposes a viscous coupling between the gliding machinery and the substrate, which entirely avoids penetrating the PG cell wall (Nan et al., 2011; Nan and Zusman, 2011; Tchoufag et al., 2019; Figure 2A). Particularly, some motor-associated proteins are of extraordinary sizes. For instance, AgmK, a transmembrane protein, contains 3,812 amino acids. Such proteins could form a bulky complex beneath the PG layer and deform the cell envelop locally. As the gliding machinery moves, the resulting bump at the surface of the cell would push against the extracellular slime, a putative layer of polysaccharides between the cell surface and the substrate (Figure 2A). The viscous drag from the slime thereby imposes thrust on the cell. This theory readily explains the correlation between the aggregation of motors at the “focal adhesion” sites and the stiffness of substrate: harder substrates presumably exert higher viscous drag on the gliding machineries and slow them down to create stronger aggregations (Nan et al., 2010, 2011, 2013). However, this viscous coupling cannot explain the cell’s resistance to sideway collisions (Balagam et al., 2014), unless the viscous drag between the cell and the substrate is highly anisotropic, with a much stronger drag perpendicular to the cell body. Currently, there is no evidence for such a strong anisotropy.
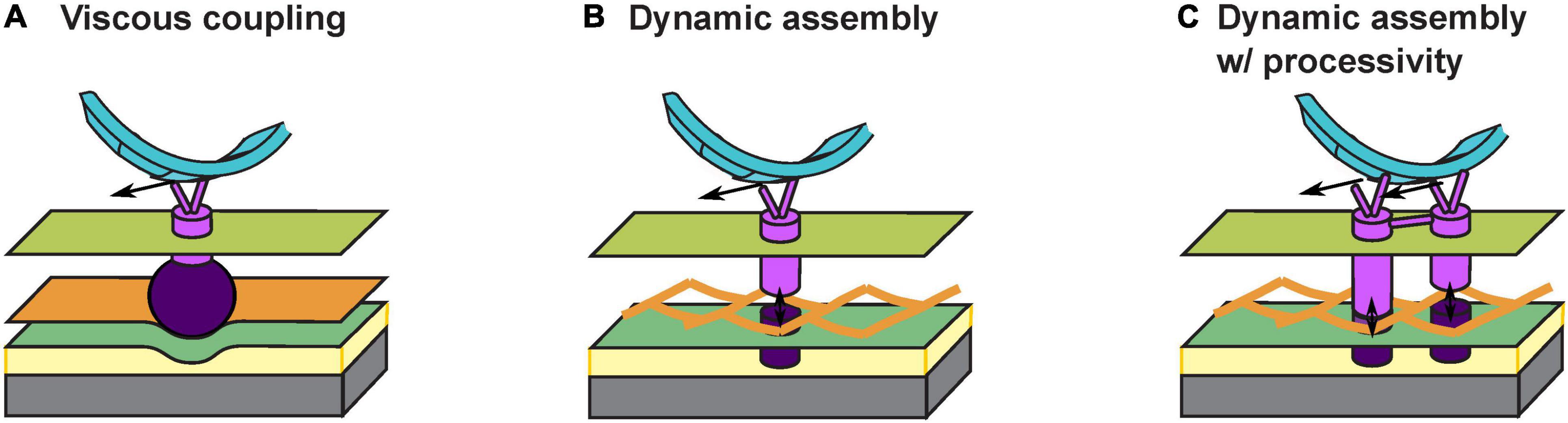
Figure 2. Models for interaction between the gliding machinery and substrate. (A) Viscous coupling between the gliding machinery and substrate. Large motor-associated proteins (dark purple) may deform the PG and the resulting bump exerts a viscous force on the substrate as the proton channel motor (bright purple) moves. (B) Dynamic assembly of the force-generating gliding machinery. An inner subcomplex (bright purple) that includes the motor and an outer subcomplex (dark purple) that binds with the substrate bind with each other dynamically across the PG mesh to allow force generation without tearing the PG. (C) Dynamic assembly of coupled gliding machineries confers processivity. The dynamic binding between the inner (bright purple) and outer (dark purple) subcomplexes is similar to (B). Coordinated activities of coupled motors keep the motors on the helical track and/or at the “focal adhesion” sites for an extended period of time.
Recently, an updated theory proposes that the gliding machinery may consists of two subcomplexes inside and outside the PG wall, respectively (Faure et al., 2016; Figure 2B). The inner subcomplex contains the proton channel motor and the outer subcomplex directly binds the substrate. Transient association between the two subcomplexes across the mesh-like structure of PG (Hughes et al., 1975; Demchick and Koch, 1996; Vollmer et al., 2008) forms a fully assembled gliding machinery at the “focal adhesion” site. The fully assembly machinery is mechanically engaged with the substrate and generates propulsion (Figure 2B). Meanwhile, constant disassociation between the inner and outer subcomplexes allows the inner subcomplex to move relative to PG. Whereas this attractive hypothesis successfully circumvents the breach of PG, it also incurs a new problem: once the inner subcomplex disassociates from the outer subcomplex, without resistance from the substrate it may quickly escape from the “focal adhesion” site, causing a low duty ratio of the motor (i.e., the fraction of time a motor actually contributes to force generation). This also conflicts with the observation that most motors become stationary and stay engaged with the substrate under certain conditions, e.g., on very hard substrates (Nan et al., 2013). How do the inner and outer subcomplexes re-associate sufficiently fast across the PG so that the motors remain at the “focal adhesion” sites?
To address the above question, here we hypothesize that individual inner subcomplexes are coupled with each other: they bind with the outer subcomplexes alternately and hence help each other stay on the track (Figure 2C). Similar processive mechanisms are widely observed in well studied molecular motors, with the best example found in the hand-over-hand mechanism in dimeric kinesins (Yildiz et al., 2004; Gennerich and Vale, 2009). In M. xanthus, aggregation of motor proteins at the “focal adhesion” sites could reflect such coupling among multiple motors. Alternatively, the two MotB homologs, AglQ and AglS, may each constitute one of two coupled subunits, giving rise to a hand-over-hand mechanism within a single motor.
How Do Motors Propel the Cell Body?
As motors reside in the fluid membrane, they require a certain structure to transmit the force onto the cell body. Part of this structure must be localized inside the cytoplasm, such that the motors in the inner membrane can exert opposite forces on the cell and the substrate. The helical track along which the motors travel is a candidate for such a mechanical structure (Figure 1). But how exactly is the force transmitted? Generally speaking, the intracellular track may transmit force to the cell body in four ways (Figure 3): (i) through mechanical tethering with the cell envelop, (ii) through interaction with the membrane and cell envelop, (iii) through viscous drag against the cytoplasm, and (iv) by direct pushing against the cell pole. Note that the four mechanisms are not exclusive to each other, and may co-contribute to cell propulsion.
Figure 3. Hypotheses about transmission of motor force to the cell body. (A) Mechanical tethering between the intracellular track and cell envelop. The mechanical tethering can be mediated either through non-motor components of the gliding machinery (i) or directly through the motor components (ii). In case (ii), the “feet” of the motor are on the periplasmic side because the motor must travel with respect to the PG to stay static to the substrate. Bright purple: proton channel motor. Dark purple: outer subcomplex. Orange cylinder in case (i) mechanical tethering between the intracellular track and PG. Gray cylinder in case (ii) molecules connecting the intracellular track to the outer subcomplex (through dynamic binding/unbinding to avoid tearing the PG). Black arrows illustrate the moving direction of the motor. (B) Interaction between the intracellular track and cell membrane/envelop. (C) Viscous drag between the intracellular track and cytoplasm. (D) Direct push on the cell pole by the intracellular track.
The first mechanism, tethering between the intracellular track and cell envelop, may effectively transmit the force from the former to the latter, thereby pushing the cell forward. Note that the intracellular track can tether to the cell envelop either indirectly through non-motor components of the gliding machinery, such as through the Rod PG synthesis complex associated with MreB (Garner, 2021; Rohs and Bernhardt, 2021; Figure 3A(i)) or directly through AglQ and AglS, if these proteins interact with PG mechanically (Figure 3A(ii)). In the former case, the motors push the intracellular track toward the leading pole, and the track in turn, pushes the PG forward. Whereas in the latter case, the intracellular track acts as a mechanical extension of the substrate and is pushed by the motors toward the trailing pole. These two mechanisms predict opposite directions of motion in the track relative to the cell, and can be tested by future experiments. In both cases, PG strands, if oriented helically, can guide the helical motion of the motors without MreB forming a continuous cytoplasmic track, as a recent report speculates (Faure et al., 2016); in the latter case, the PG even provides the direct track for the motors to move on.
The second mechanism, interaction between the intracellular track and cell membrane/envelop (Figure 3B), can effectively transmit the force from the intracellular track to the cell body, only if the interaction is sufficiently strong and the cell membrane exhibits glass-like properties in terms of its mechanical resistance against the motion of the track. The latter is possible if the membrane is crowded (Munguira et al., 2016). If the cell membrane behaves like fluid, as in in vitro membrane systems like the giant unilamellar vesicle (GUV), or the track interacts with the membrane too weakly, the mechanism would be insufficient for transmitting the motor force onto the cell. Verification of this hypothesis requires data on the physical properties and molecular components of the membranes in M. xanthus.
The third mechanism, viscous drag between the intracellular track and cytoplasm (Figure 3C), is unlikely to transmit significant force, because such a viscous drag is typically orders of magnitude lower than the force required to move a cell on a substrate surface (∼102 pN (Wolgemuth, 2005; Sabass et al., 2017; Tchoufag et al., 2019). For example, a 10-μm microtubule traveling at ∼1 μm/s (observed speed of fluorescent MreB particles in M. xanthus (Fu et al., 2018) in the cytoplasm would encounter a sub-piconewton (pN) viscous drag force.
The fourth mechanism, the intracellular track directly pushing on the cell pole (Figure 3D), can only transmit the force effectively if the track is a continuous and relatively rigid structure, like the rotor ring in the bacterial flagellar motor. However, such a track may not exist, as MreB, the most likely constituent of the track, only forms patchy filaments (Fu et al., 2018), which probably lack the continuity and mechanical rigidity to generate a push on the cell pole.
How Does the Gliding Machinery Switch Its Direction?
M. xanthus is known for periodic reversal of its direction of gliding, which is crucial for its “social” behaviors (Wu et al., 2007; Berleman and Kirby, 2009; Patra et al., 2016). Many previous models have investigated how intercellular coordination of gliding and reversals mediates formation of complex patterns and structures in the M. xanthus populations, e.g., rippling waves and fruiting bodies (Igoshin et al., 2001; Borner et al., 2002; Alber et al., 2004; Igoshin et al., 2004; Borner et al., 2006; Sliusarenko et al., 2007; Wu et al., 2009; Holmes et al., 2010; Harvey et al., 2012; Zhang et al., 2012a; Janulevicius et al., 2015; Patra et al., 2016). At the single-cell level, reversals are achieved by switching the cell’s polarity, which in turn, is determined by a group of polarity-setting molecules localized at the cell poles. Particularly, MglA is concentrated at the leading pole, and MglB, its antagonist, at the trailing pole (Leonardy et al., 2010; Zhang et al., 2010). MglA and MglB periodically switch between the two poles, causing cell polarity to switch (Leonardy et al., 2010; Zhang et al., 2010, 2012b; Keilberg and Sogaard-Andersen, 2014; Rashkov et al., 2014; Guzzo et al., 2018; Carreira et al., 2020). Moreover, the frequency of polarity switching is modulated by the Frz chemosensory pathway (Guzzo et al., 2018). This is reminiscent of the clockwise-counterclockwise switches in the bacterial flagellar motor, which is also controlled by the chemosensory pathway. We do not intend to discuss here the chemosensory pathway or polarity switching itself. Rather, we would like to raise the question of how the gliding machineries change the direction of force in response to the switched cell polarity.
This question may seem trivial at first sight, because MglA directly binds the gliding motor and likely mediates its activation (Nan et al., 2015; Treuner-Lange et al., 2015). One may envision that the gliding motor is activated at the MglA-concentrated pole and deactivated at the MglB-concentrated pole; traveling from the MglA pole to the MglB pole would generate a propulsion on the cell in the direction of the MglA pole. Hence, as the polar localization of MglA and MglB switches, the direction of propulsion also switches. This straightforward model, however, is challenged by the observation of constant reversals of single gliding motors as they travel along the intracellular track (Figure 4A; Nan et al., 2013, 2015). Due to the constant reversals, the gliding machinery cannot generate force consistently in one direction. Even though polarized activation and deactivation can bias the motion of gliding machineries in the productive direction (i.e., bound for the MglB pole), a large fraction of gliding machineries still generate counter-productive forces on the cell, with a 2∼20% estimated relative difference between motors in the two directions (the relative difference is roughly the ratio between the average time for motor reversal, ∼1 s (Nan et al., 2013, 2015) and the time for a motor to traverse the cell length without reversing, 5 s∼1 min (Sun et al., 2011; Nan et al., 2013, 2015). This makes the motility mechanism highly inefficient. With significant noise, this could also incur random switches of the cell’s direction of motion, which further reduces the efficiency of directional gliding.
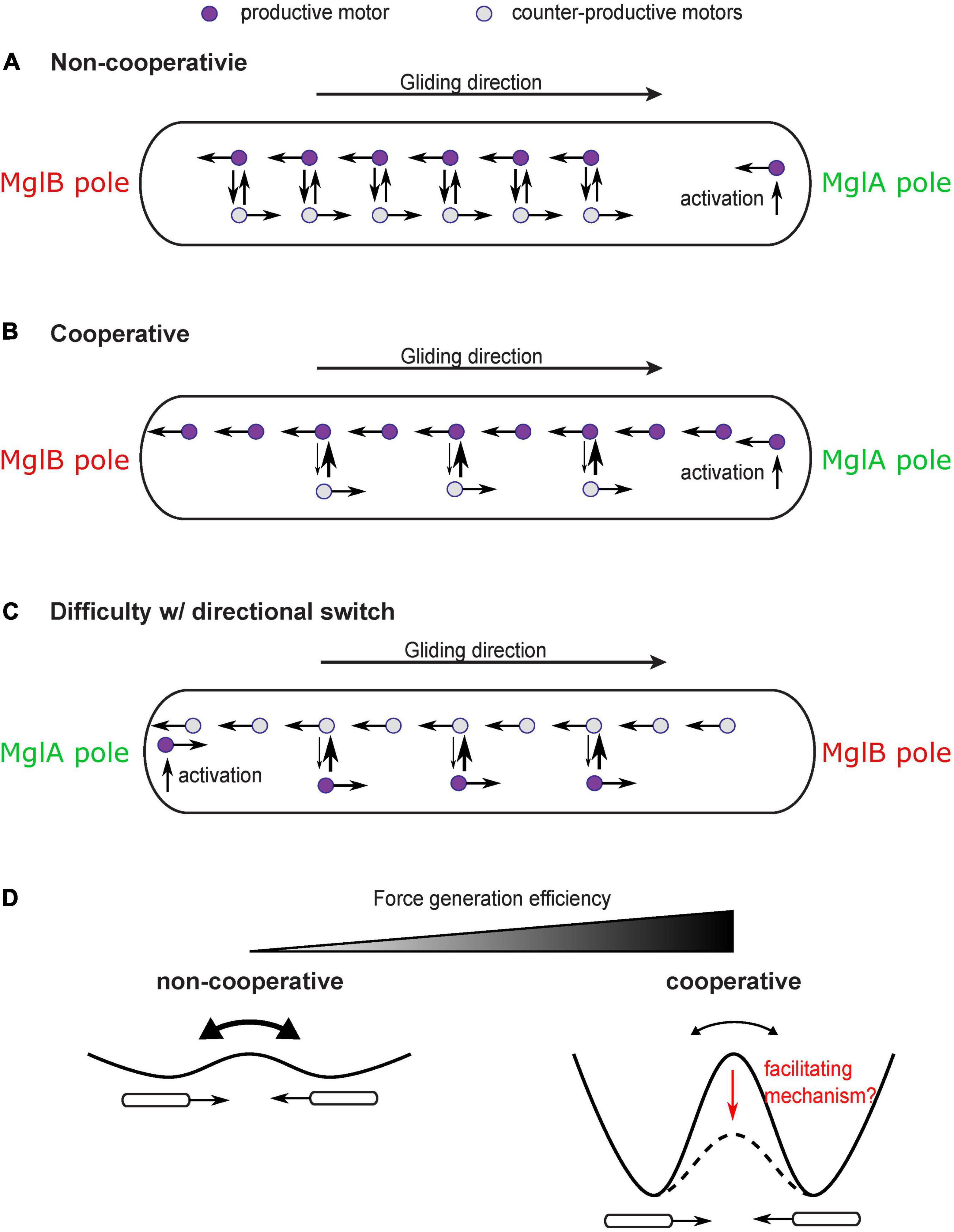
Figure 4. Cooperativity of gliding motors and issue with directional switch. (A) Constant reversal of gliding motors diminishes efficiency and stability of force generation. A large number of motors would travel in the counter-productive direction and produce forces in the counter-productive direction. (B) A cooperativity mechanism makes motors more likely to convert to the direction in which more motors are traveling, which enhances the bias toward productive motors and significantly increases the efficiency and stability of force generation. (C) The cooperativity mechanism may inhibit the reversal of the moving direction of the cell after the switch of cell polarity. The motors which are activated at the new MglA pole and travel in the new productive direction may be forced by the cooperativity mechanism to join the majority that remains traveling in the old productive direction. (D) Cooperativity among motors increases efficiency and stability of force generation at the price of inhibiting reversals. Reversals can be regarded as transitions between two symmetric states with equal energy. Cooperativity increases the energy barrier between the two states. A facilitating mechanism may be needed to reduce the energy barrier and promote state transition despite cooperativity.
In order to increase efficiency and stability of the gliding mechanism, a cooperativity mechanism is required to magnify the bias of motors in the productive direction (Figure 4B). For example, those gliding machineries traveling in the same direction as the cell may have a disadvantage in engaging with the substrate because they move at a higher speed relative to the substrate (relative speed to the cell + speed of cell). Therefore, the gliding machinery is more likely to stay in the productive direction. Cooperativity can also be boosted by intermolecular interactions among aggregated motors. In any case, the cooperativity can bring an asymmetry between motors traveling in opposite directions, which can magnify the directional bias induced by the established cell polarity and increase the fraction of productive gliding machineries over the counter-productive ones.
While significantly improving the efficiency and stability of force generation, such cooperativity has a down side: it may inhibit reversal of the cell’s moving direction even after cell polarity switches (Figure 4C). This is because the gliding machineries which are activated at the new MglA pole and travel in the new productive direction can be forced by the cooperativity mechanism to rejoin the majority that are still traveling in the old productive direction. The rate at which the new MglA pole generates productive motors is physically limited by the active motion and diffusion of motors. Therefore, it may not be strong enough to overcome the cooperativity mechanism and tip the balance in the new direction. Similar conflict between cooperativity and sensitivity of the directional switch was studied in the bacterial flagellar motor (Duke et al., 2001; Bai et al., 2010). Reversing the direction of rotation entails a switch of the C-ring—the rotor part of the flagellar motor (Chang et al., 2020). The switch requires cooperative conformational changes in all the rotor subunits that constitute the C-ring. Strong cooperativity among these subunits can suppress random switch of their conformation, promote structural homogeneity of the C-ring, and hence gauge the motor forces toward one direction. However, the cooperativity also imposes a challenge in switching the entire ring from one conformation to another in response to chemotactic signals (Duke et al., 2001; Bai et al., 2010). To circumvent this problem, Bai et al. (2010) proposed a mechanism: as a stator exerts force on a rotor subunit, it also promotes conformational changes in the latter and hence facilitate the switch of the rotor ring. It remains to be investigated if the force generated by the gliding machinery of M. xanthus plays a similar role in facilitating directional switch and overcoming the efficiency-boosting cooperativity (Figure 4D).
How Does the Gliding Machinery Respond to Mechanical Load?
The observation that aggregations of gliding proteins at the “focal adhesion” sites intensify on harder substrates (Nan et al., 2010, 2013) implies that external mechanical cues can influence assembly and/or activity of the gliding machinery. This phenomenon is reminiscent of the observation that external load on the bacterial flagellar motor boosts the recruitment of stators into the motor complex (Lele et al., 2013; Tipping et al., 2013). The underlying molecular mechanism for the mechanosensing in the bacterial flagellar motor is known: the stators are dynamically recruited to and released from the motor and a “catch bond” mechanism retains the stators in the motor for longer time in response to a higher load (Nord et al., 2017; Wadhwa et al., 2019). Sharing homologous energy-harvesting proteins with the bacterial flagellar motor, the M. xanthus gliding machinery may exploit a similar force-sensitive mechanism that strengthens the engagement with the substrate upon higher load.
Interestingly, substrate stiffness also affects the reversal frequency of the M. xanthus cell (Zhou and Nan, 2017). It is possible that the gliding machinery further transduces the external mechanical cues into a signal that controls polarity switching. Currently, the most promising candidate that mediates the transduction from mechanical cues to regulatory signals for polarity switching is probably MglA, as it is not only a key molecule of the polarity-switching mechanism but also an essential component of the gliding machinery (Nan et al., 2015; Treuner-Lange et al., 2015). As the gliding machineries travel from the leading pole to the trailing pole, they carry the MglA along. The directed transport of MglA toward the trailing pole could affect the dynamics of polarity switching. Hence, the external mechanical cues could affect the reversal frequency through modulating the activity of the gliding machineries. Future investigations are needed to test this hypothesis.
Conclusion
The M. xanthus gliding machinery exploits similar energy-harvesting units as the rotary flagellar motor, yet operates on a helical intracellular track. This is yet another testimony on the versatility of flagellar motors in biological systems. In this article, we brought up a few unresolved questions on the mechanism of M. xanthus gliding. As rotary motors are ubiquitous in nature and helical-tracking motors are also found in a number of bacteria (Nan et al., 2014), we predict that the answers to these questions will make wide impacts, much beyond the gliding motility in M. xanthus.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author Contributions
JC and BN conceptualized and designed the work, curated and interpreted the relevant literature, and drafted the article. Both authors contributed to the article and approved the submitted version.
Funding
National Institutes of Health R35GM138370 to JC and R01GM129000 to BN.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
- ^ In Nan et al., 2013, the authors simplified the data analysis, in which particles are only categorized as stationary or in directed motion. The increase of the “slow-moving” particles actually corresponds to an increase in the diffusive population in a three-population analysis.
References
Alber, M. S., Kiskowski, M. A., and Jiang, Y. (2004). Two-stage aggregate formation via streams in myxobacteria. Phys. Rev. Lett. 93, 068102. doi: 10.1103/PhysRevLett.93.068102
Bai, F., Branch, R. W., Nicolau, D. V. Jr., Pilizota, T., Steel, B. C., Maini, P. K., et al. (2010). Conformational spread as a mechanism for cooperativity in the bacterial flagellar switch. Science 327, 685–689. doi: 10.1126/science.1182105
Balagam, R., Litwin, D. B., Czerwinski, F., Sun, M., Kaplan, H. B., Shaevitz, J. W., et al. (2014). Myxococcus xanthus gliding motors are elastically coupled to the substrate as predicted by the focal adhesion model of gliding motility. PLoS Comput. Biol. 10:e1003619. doi: 10.1371/journal.pcbi.1003619
Berleman, J. E., and Kirby, J. R. (2009). Deciphering the hunting strategy of a bacterial wolfpack. FEMS Microbiol. Rev. 33, 942–957. doi: 10.1111/j.1574-6976.2009.00185.x
Borner, U., Deutsch, A., and Bar, M. (2006). A generalized discrete model linking rippling pattern formation and individual cell reversal statistics in colonies of myxobacteria. Phys. Biol. 3, 138–146. doi: 10.1088/1478-3975/3/2/006
Borner, U., Deutsch, A., Reichenbach, H., and Bar, M. (2002). Rippling patterns in aggregates of myxobacteria arise from cell-cell collisions. Phys. Rev. Lett. 89:078101. doi: 10.1103/PhysRevLett.89.078101
Carreira, L. A. M., Tostevin, F., Gerland, U., and Sogaard-Andersen, L. (2020). Protein-protein interaction network controlling establishment and maintenance of switchable cell polarity. PLoS Genet. 16:e1008877. doi: 10.1371/journal.pgen.1008877
Chang, Y., Zhang, K., Carroll, B. L., Zhao, X., Charon, N. W., Norris, S. J., et al. (2020). Molecular mechanism for rotational switching of the bacterial flagellar motor. Nat. Struct. Mol. Biol. 27, 1041–1047. doi: 10.1038/s41594-020-0497-2
Chang, Y. W., Rettberg, L. A., Treuner-Lange, A., Iwasa, J., Sogaard-Andersen, L., and Jensen, G. J. (2016). Architecture of the type IVa pilus machine. Science. 351:aad2001.
Demchick, P., and Koch, A. L. (1996). The permeability of the wall fabric of Escherichia coli and Bacillus subtilis. J. Bacteriol. 178, 768–773. doi: 10.1128/jb.178.3.768-773.1996
Duke, T. A., Le Novere, N., and Bray, D. (2001). Conformational spread in a ring of proteins: a stochastic approach to allostery. J. Mol. Biol. 308, 541–553. doi: 10.1006/jmbi.2001.4610
Faure, L. M., Fiche, J. B., Espinosa, L., Ducret, A., Anantharaman, V., Luciano, J., et al. (2016). The mechanism of force transmission at bacterial focal adhesion complexes. Nature 539:530. doi: 10.1038/nature20121
Fu, G., Bandaria, J. N., Le Gall, A. V., Fan, X., Yildiz, A., Mignot, T., et al. (2018). MotAB-like machinery drives the movement of MreB filaments during bacterial gliding motility. Proc. Natl. Acad. Sci. U.S.A. 115, 2484–2489. doi: 10.1073/pnas.1716441115
Garner, E. C. (2021). Toward a mechanistic understanding of bacterial rod shape formation and regulation. Annu. Rev. Cell Dev. Biol. 37, 1–21. doi: 10.1146/annurev-cellbio-010521-010834
Gennerich, A., and Vale, R. D. (2009). Walking the walk: how kinesin and dynein coordinate their steps. Curr. Opin. Cell Biol. 21, 59–67. doi: 10.1016/j.ceb.2008.12.002
Guzzo, M., Murray, S. M., Martineau, E., Lhospice, S., Baronian, G., My, L., et al. (2018). A gated relaxation oscillator mediated by FrzX controls morphogenetic movements in Myxococcus xanthus. Nat. Microbiol. 3, 948–959. doi: 10.1038/s41564-018-0203-x
Harvey, C. W., Du, H., Xu, Z., Kaiser, D., Aranson, I., and Alber, M. (2012). Interconnected cavernous structure of bacterial fruiting bodies. PLoS Comput. Biol. 8:e1002850. doi: 10.1371/journal.pcbi.1002850
Holmes, A. B., Kalvala, S., and Whitworth, D. E. (2010). Spatial simulations of myxobacterial development. PLoS Comput. Biol. 6:e1000686. doi: 10.1371/journal.pcbi.1000686
Hughes, R. C., Thurman, P. F., and Stokes, E. (1975). Estimates of the porosity of Bacillus licheniformis and Bacillus subtilis cell walls. Z. Immunitatsforsch. Exp. Klin. Immunol. 149, 126–135.
Igoshin, O. A., Mogilner, A., Welch, R. D., Kaiser, D., and Oster, G. (2001). Pattern formation and traveling waves in myxobacteria: theory and modeling. Proc. Natl. Acad. Sci. U.S.A. 98, 14913–14918. doi: 10.1073/pnas.221579598
Igoshin, O. A., Welch, R., Kaiser, D., and Oster, G. (2004). Waves and aggregation patterns in myxobacteria. Proc. Natl. Acad. Sci. U.S.A. 101, 4256–4261. doi: 10.1073/pnas.0400704101
Janulevicius, A., van Loosdrecht, M., and Picioreanu, C. (2015). Short-range guiding can result in the formation of circular aggregates in myxobacteria populations. PLoS Comput. Biol. 11:e1004213. doi: 10.1371/journal.pcbi.1004213
Keilberg, D., and Sogaard-Andersen, L. (2014). Regulation of bacterial cell polarity by small GTPases. Biochemistry 53, 1899–1907. doi: 10.1021/bi500141f
Lele, P. P., Hosu, B. G., and Berg, H. C. (2013). Dynamics of mechanosensing in the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 110, 11839–11844. doi: 10.1073/pnas.1305885110
Leonardy, S., Miertzschke, M., Bulyha, I., Sperling, E., Wittinghofer, A., and Sogaard-Andersen, L. (2010). Regulation of dynamic polarity switching in bacteria by a Ras-like G-protein and its cognate GAP. EMBO J. 29, 2276–2289. doi: 10.1038/emboj.2010.114
Mauriello, E. M., Mouhamar, F., Nan, B., Ducret, A., Dai, D., Zusman, D. R., et al. (2010). Bacterial motility complexes require the actin-like protein, MreB and the Ras homologue, MglA. EMBO J. 29, 315–326. doi: 10.1038/emboj.2009.356
Mignot, T., Shaevitz, J. W., Hartzell, P. L., and Zusman, D. R. (2007). Evidence that focal adhesion complexes power bacterial gliding motility. Science 315, 853–856. doi: 10.1126/science.1137223
Munguira, I., Casuso, I., Takahashi, H., Rico, F., Miyagi, A., Chami, M., et al. (2016). Glasslike membrane protein diffusion in a crowded membrane. ACS Nano 10, 2584–2590. doi: 10.1021/acsnano.5b07595
Nan, B. (2017). Bacterial gliding motility: rolling out a consensus model. Curr. Biol. 27, R154–R156. doi: 10.1016/j.cub.2016.12.035
Nan, B., Chen, J., Neu, J. C., Berry, R. M., Oster, G., and Zusman, D. R. (2011). Myxobacteria gliding motility requires cytoskeleton rotation powered by proton motive force. Proc. Natl. Acad. Sci. U.S.A. 108, 2498–2503. doi: 10.1073/pnas.1018556108
Nan, B., Mauriello, E. M., Sun, I. H., Wong, A., and Zusman, D. R. (2010). A multi-protein complex from Myxococcus xanthus required for bacterial gliding motility. Mol. Microbiol. 76, 1539–1554. doi: 10.1111/j.1365-2958.2010.07184.x
Nan, B., McBride, M. J., Chen, J., Zusman, D. R., and Oster, G. (2014). Bacteria that glide with helical tracks. Curr. Biol. 24, R169–R173. doi: 10.1016/j.cub.2013.12.034
Nan, B., and Zusman, D. R. (2011). Uncovering the mystery of gliding motility in the myxobacteria. Annu. Rev. Genet. 45, 21–39. doi: 10.1146/annurev-genet-110410-132547
Nan, B. Y., Bandaria, J. N., Guo, K. Y., Fan, X., Moghtaderi, A., Yildiz, A., et al. (2015). The polarity of myxobacterial gliding is regulated by direct interactions between the gliding motors and the Ras homolog MglA. Proc. Natl. Acad. Sci. U.S.A. 112, E186–E193. doi: 10.1073/pnas.1421073112
Nan, B. Y., Bandaria, J. N., Moghtaderi, A., Sun, I. H., Yildiz, A., and Zusman, D. R. (2013). Flagella stator homologs function as motors for myxobacterial gliding motility by moving in helical trajectories. Proc. Natl. Acad. Sci. U.S.A. 110, E1508–E1513. doi: 10.1073/pnas.1219982110
Nord, A. L., Gachon, E., Perez-Carrasco, R., Nirody, J. A., Barducci, A., Berry, R. M., et al. (2017). Catch bond drives stator mechanosensitivity in the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 114, 12952–12957. doi: 10.1073/pnas.1716002114
Patra, P., Kissoon, K., Cornejo, I., Kaplan, H. B., and Igoshin, O. A. (2016). Colony expansion of socially motile Myxococcus xanthus cells is driven by growth, motility, and exopolysaccharide production. PLoS Comput. Biol. 12:e1005010. doi: 10.1371/journal.pcbi.1005010
Rashkov, P., Schmitt, B. A., Keilberg, D., Beck, K., Sogaard-Andersen, L., and Dahlke, S. (2014). A model for spatio-temporal dynamics in a regulatory network for cell polarity. Math. Biosci. 258, 189–200. doi: 10.1016/j.mbs.2014.10.005
Rohs, P. D. A., and Bernhardt, T. G. (2021). Growth and division of the peptidoglycan matrix. Annu. Rev. Microbiol. 75, 315–336. doi: 10.1146/annurev-micro-020518-120056
Sabass, B., Koch, M. D., Liu, G. N., Stone, H. A., and Shaevitz, J. W. (2017). Force generation by groups of migrating bacteria. Proc. Natl. Acad. Sci. U.S.A. 114, 7266–7271. doi: 10.1073/pnas.1621469114
Sliusarenko, O., Zusman, D. R., and Oster, G. (2007). Aggregation during fruiting body formation in Myxococcus xanthus is driven by reducing cell movement. J. Bacteriol. 189, 611–619. doi: 10.1128/JB.01206-06
Sun, M., Wartel, M., Cascales, E., Shaevitz, J. W., and Mignot, T. (2011). Motor-driven intracellular transport powers bacterial gliding motility. Proc. Natl. Acad. Sci. U.S.A. 108, 7559–7564. doi: 10.1073/pnas.1101101108
Tchoufag, J., Ghosh, P., Pogue, C. B., Nan, B., and Mandadapu, K. K. (2019). Mechanisms for bacterial gliding motility on soft substrates. Proc. Natl. Acad. Sci. U.S.A. 116, 25087–25096. doi: 10.1073/pnas.1914678116
Tipping, M. J., Delalez, N. J., Lim, R., Berry, R. M., and Armitage, J. P. (2013). Load-dependent assembly of the bacterial flagellar motor. mBio 4, e00551–13.
Treuner-Lange, A., Macia, E., Guzzo, M., Hot, E., Faure, L. M., Jakobczak, B., et al. (2015). The small G-protein MglA connects to the MreB actin cytoskeleton at bacterial focal adhesions. J. Cell Biol. 210, 243–256. doi: 10.1083/jcb.201412047
Vollmer, W., Blanot, D., and de Pedro, M. A. (2008). Peptidoglycan structure and architecture. FEMS Microbiol Rev. 32, 149–167. doi: 10.1111/j.1574-6976.2007.00094.x
Wadhwa, N., Phillips, R., and Berg, H. C. (2019). Torque-dependent remodeling of the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 116, 11764–11769. doi: 10.1073/pnas.1904577116
Wolgemuth, C., Hoiczyk, E., Kaiser, D., and Oster, G. (2002). How myxobacteria glide. Curr. Biol. 12, 369–377. doi: 10.1016/s0960-9822(02)00716-9
Wolgemuth, C. W. (2005). Force and flexibility of flailing myxobacteria. Biophys. J. 89, 945–950. doi: 10.1529/biophysj.105.062513
Wu, S. S., and Kaiser, D. (1995). Genetic and functional evidence that type IV pili are required for social gliding motility in Myxococcus xanthus. Mol. Microbiol. 18, 547–558. doi: 10.1111/j.1365-2958.1995.mmi_18030547.x
Wu, Y., Jiang, Y., Kaiser, D., and Alber, M. (2007). Social interactions in myxobacterial swarming. PLoS Comput. Biol. 3:e253. doi: 10.1371/journal.pcbi.0030253
Wu, Y., Kaiser, A. D., Jiang, Y., and Alber, M. S. (2009). Periodic reversal of direction allows Myxobacteria to swarm. Proc. Natl. Acad. Sci. U.S.A. 106, 1222–1227. doi: 10.1073/pnas.0811662106
Yildiz, A., Tomishige, M., Vale, R. D., and Selvin, P. R. (2004). Kinesin walks hand-over-hand. Science 303, 676–678. doi: 10.1126/science.1093753
Zhang, H., Vaksman, Z., Litwin, D. B., Shi, P., Kaplan, H. B., and Igoshin, O. A. (2012a). The mechanistic basis of Myxococcus xanthus rippling behavior and its physiological role during predation. PLoS Comput. Biol. 8:e1002715. doi: 10.1371/journal.pcbi.1002715
Zhang, Y., Franco, M., Ducret, A., and Mignot, T. (2010). A bacterial Ras-like small GTP-binding protein and its cognate GAP establish a dynamic spatial polarity axis to control directed motility. PLoS Biol. 8:e1000430. doi: 10.1371/journal.pbio.1000430
Zhang, Y., Guzzo, M., Ducret, A., Li, Y. Z., and Mignot, T. (2012b). A dynamic response regulator protein modulates G-protein-dependent polarity in the bacterium Myxococcus xanthus. PLoS Genet. 8:e1002872. doi: 10.1371/journal.pgen.1002872
Keywords: myxobacteria, bacterial motility, bacterial gliding, proton channel, cell polarity, mechanosensing, force transmission
Citation: Chen J and Nan B (2022) Flagellar Motor Transformed: Biophysical Perspectives of the Myxococcus xanthus Gliding Mechanism. Front. Microbiol. 13:891694. doi: 10.3389/fmicb.2022.891694
Received: 08 March 2022; Accepted: 13 April 2022;
Published: 06 May 2022.
Edited by:
Ronald Mark Wooten, University of Toledo, United StatesReviewed by:
Abhishek Shrivastava, Arizona State University, United StatesDaisuke Nakane, The University of Electro-Communications, Japan
Copyright © 2022 Chen and Nan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jing Chen, chenjing@vt.edu; Beiyan Nan, bnan@tamu.edu
†These authors have contributed equally to this work