Modeling Bacterial Flagellar Motor With New Structure Information: Rotational Dynamics of Two Interacting Protein Nano-Rings

In this article, we develop a mathematical model for the rotary bacterial flagellar motor (BFM) based on the recently discovered structure of the stator complex (MotA₅MotB₂). The structure suggested that the stator also rotates. The BFM is modeled as two rotating nano-rings that interact with each other. Specifically, translocation of protons through the stator complex drives rotation of the MotA pentamer ring, which in turn drives rotation of the FliG ring in the rotor via interactions between the MotA ring of the stator and the FliG ring of the rotor. Preliminary results from the structure-informed model are consistent with the observed torque-speed relation. More importantly, the model predicts distinctive rotor and stator dynamics and their load dependence, which may be tested by future experiments. Possible approaches to verify and improve the model to further understand the molecular mechanism for torque generation in BFM are also discussed.

1. Introduction

The swimming motion of many bacteria is powered by the rotary bacterial flagellar motor (BFM). As a canonical example, the motors in E. coli are fueled by electrochemical potential difference of protons (H⁺) across the cytoplasmic membrane, i.e., the proton motive force (PMF) (Larsen et al., 1974; Hirota et al., 1981; Berg, 2003). The BFM can rotate bidirectionally. Without binding to the phosphorylated response regulator CheY protein (CheY-P), the BFM rotates in a counter-clockwise (CCW, viewed from the filament to the motor) direction. There are ~4 − 6 BFMs in an E. coli cell. The CCW rotation of the BFMs causes their flagellar filaments to form a coherent bundle and propels the swimming cells in a roughly straight line that is called a “run.” However, the binding of CheY-P to BFM causes it to rotate in the clockwise (CW) direction, which disrupts the filament bundle. As a result, the rod-shaped E. coli cell changes its orientation randomly without translational movement in an event called a “tumble.”

The bacterial flagellar motor consists of a rotor and a number of stators that can vary from 0 to 11 depending on gene expression and mechanical load (Blair and Berg, 1988; Lele et al., 2013; Tipping et al., 2013; Nord et al., 2017; Wadhwa et al., 2019, 2021). The rotor consists of FliF, FliG, FliM, and FliN. FliF forms the MS-ring embedded within the cytoplasmic membrane (Asai et al., 1997; Sato and Homma, 2000; Yorimitsu et al., 2004; Morimoto and Minamino, 2014; Baker et al., 2016). The cytoplasmic face of the MS-ring is attached to the C-ring, which comprises the FliG, FliM, and FliN proteins. The diameter of the C-ring is ~45nm. The C-ring is responsible for coupling the rotor to the stator units and for switching rotational directions. The membrane-bound stators, which consist of the MotA and MotB proteins, are powered by the PMF to drive the rotation of the rotor via direct interaction between MotA and FliG (Chun and Parkinson, 1988; Blair and Berg, 1990; Kojima and Blair, 2004; Roujeinikova, 2008).

The molecular mechanism of torque generation by the stator units has been suggested by two recent Cryo-EM studies of the stator structure (Deme et al., 2020; Santiveri et al., 2020). Both studies report that a stator unit consists of a MotB dimer surrounded by a MotA pentamer ring with a diameter of ~ 5 − 7.5nm. The position of the MotB dimer, which is bound to the peptidoglycan layer in the rigid cell wall, remains fixed, while the MotA pentamer forms a ring that can rotate around the MotB dimer. Each MotB monomer progressively engages with each MotA monomer to form an ion channel through which one proton can pass to drive the rotation of the MotA pentamer ring.

Brownian ratchet models have attracted physicists' attention for modeling molecular motors since Richard Feynman popularized the idea more than half a century ago (Feynman et al., 1966; Parrondo et al., 1998; Astumian, 2010; Golubeva et al., 2012). Among all variants of the ratchet models, only isothermal chemical ratchets are relevant for biological motors (Jülicher et al., 1997; Parrondo and de Cisneros, 2002). A minimal model for the rotational ratchet model can be found in Xing et al. (2006), Meacci and Tu (2009), and Meacci et al. (2011). This model has two types of coordinates: the “physical” coordinate that describes the motion of the motor in physical space (angles for rotary motor); and the “chemical” coordinate that describes the different conformational states of the motor. For the BFM, the motor moves in a periodic potential in which torque, which is the gradient of the potential, is generated as the motor slide down from a position of high potential energy toward its equilibrium position, which has the lowest potential energy. The passage of an ion triggers a conformational change (stepping) of the motor. Because the landscape of potential energy is different for different conformational states of the motor, the conformational change driven by the PMF changes the potential energy landscape and can bring the motor to a position of high potential energy in the new potential energy landscape. The newly gained potential energy continues to drive the physical rotation of the motor. This continuous process drives the system toward a sequence of new equilibrium positions and gives rise to a directed stepwise rotation (Sowa et al., 2005).

One of the most important characteristics of a rotary motor is its torque-speed dependence (or force-speed dependence for linear motors). The measured torque-speed curve for the CCW BFM has a downward concave shape with a roughly constant high torque at low to medium speeds and a rapid and nearly linear decrease of torque at high speeds (Chen and Berg, 2000; Lo et al., 2013). This concave torque-speed curve has the advantage of generating high power output (or, equivalently, a high torque for a given speed) in a wide range of physiologically relevant loads. The minimal ratchet model can reproduce the observed torque-speed curve when certain general constraints for the rotor-stator interaction potential and the proton-assisted transition rate between different conformational states are applied (Tu and Cao, 2018).

Before the recent availability of an accurate picture of the structure of the stator (Deme et al., 2020; Santiveri et al., 2020), previous structure-based modeling studies assumed that the stator unit has a MotA₄MotB₂ composition (Braun et al., 2004; Kim et al., 2008). For example, it was proposed (Mandadapu et al., 2015; Nirody et al., 2016) that the power stroke for each rotational direction of the rotor (CCW or CW) is delivered by two of the four MotA subunits through a steric force generated by a “kink and swivel” conformational change of MotA induced by the binding of a proton to a corresponding MotB. The newly discovered structure of the stator complex has the different stoichiometry of MotA₅MotB₂ (Deme et al., 2020; Santiveri et al., 2020). The structure of the stator complex immediately led to an important new insight into the molecular mechanism by which the BFM operates: the MotA ring in the stator unit rotates. Consequently, all of the five MotA subunits are involved in torque generation independent of the rotational direction of the rotor, and the power stroke is generated directly by the rotational motion of the MotA subunits themselves instead of their internal conformational changes.

In terms of modeling, the new insight gained from the stator complex structure means that the stator unit must be described by its physical state in terms of the relative angle between the MotA pentamer ring and the MotB dimer in addition to its chemical (conformational) states. In the following section, we present an updated model for the BFM based on the general modeling framework described before (Tu and Cao, 2018), but now in the context of the new structure of the stator complex. Some preliminary results predicted by the model will also be described.

2. A Structure-Informed Model and Some Preliminary Results

Our new model describes the dynamics of the two coupled rotating nano-rings (the MotA ring and the FliG ring) as shown in Figures 1A,B. The stator unit is the active part of the motor. It can generate torque as a rotational ratchet powered by the PMF. Rotation of the MotA ring drives the rotation of the passive FliG ring through a coupling potential V_R(θ_S, θ_R), where θ_S and θ_R are the rotational angles of the stator and the rotor, which have a periodicity of Δθ_S = 2π/5, Δθ_R = 2π/26, respectively. It is assumed that there are 26 FliG proteins in the C-ring (Thomas et al., 2006). The rotational motion of the rotor is described by a Langevin equation for the rotor angle θ_R:

$\begin{array}{ll}{\xi }_R\frac{d{\theta }_R}{dt}=-\frac{\partial V_R({\theta }_S,{\theta }_R)}{\partial {\theta }_R}+{\eta }_R(t),& (1)\end{array}$

where ξ_R is the load on the rotor, the first term on the right hand side of Equation 1 is the torque exerted on the rotor from the stator via the MotA-FliG interaction, and η_R(t) is the rotor thermal noise: $<{\eta }_R(t){\eta }_R(t^{\prime })>=2k_{B}T{\xi }_R\delta (t-t^{\prime })$ with k_B the Boltzmann constant and T the temperature. The coupling potential V_R(θ_S, θ_R) should be periodic in both θ_S and θ_R. To satisfy this dual periodicity, we write V_R(θ_S, θ_R) = V_R(φ) where φ = θ_R − kθ_S is the scaled relative angle, with $k=\Delta {\theta }_R/\Delta {\theta }_S=\frac{5}{26}$, which is the gear ratio between the two rotating rings in E. coli.

FIGURE 1

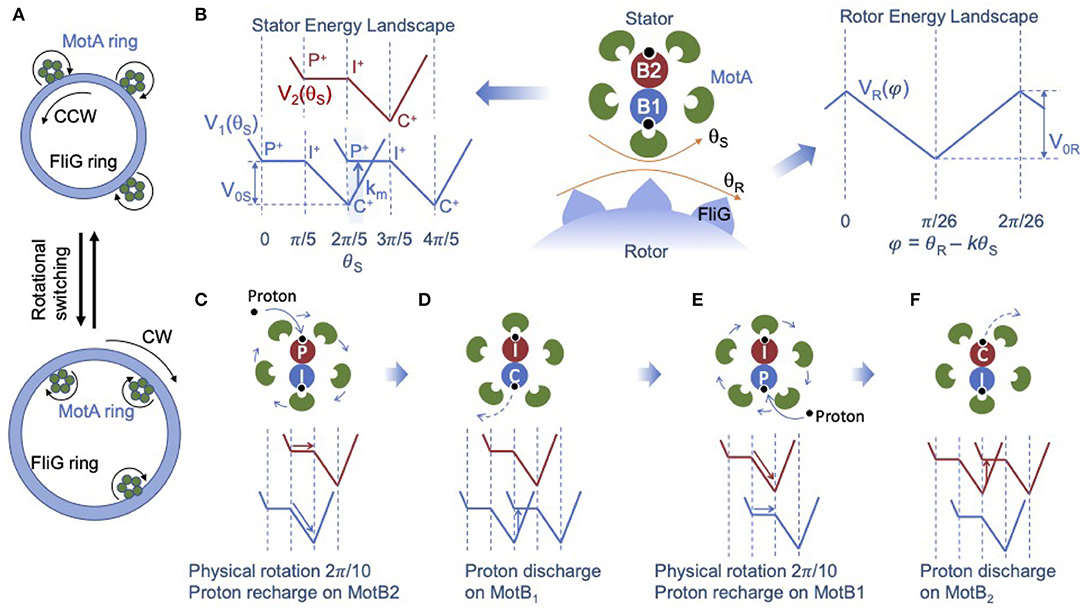
Figure 1. A structure-informed model for the bacterial flagellar motor (BFM). (A) Illustration of the bidirectional rotation of the BFM. In counter-clovkwise (CCW) mode (top), the C- ring adapts a compact conformation, and the MotA ring on stator units contacts the FliG subunits on the outside of the C-ring. In the CW mode (bottom), the C-ring expands, and the MotA rings contact the FliG subunits on the inside of the C-ring. (B) Illustration of the two-rotating-ring model for the BFM (center panel). The stator energy landscape (left panel) shows the two interaction potentials between the MotA pentamer ring and the MotB dimer: V₁(θ_S) from MotB₁ (blue) and V₂(θ_S) from MotB₂ (red), which have the same shape but are shifted from each other by half a period Δθ_S/2 = 2π/10. The blue and red energy landscapes are shifted vertically only for clarity. P and C stand for the two conformational states of MotB in which the proton acceptor residue faces the periplasm and the cytoplasm, respectively, and I stands for an intermediate state between P-state and C-state. The plus (or minus) superscript indicates the proton-bound (or proton-unbound) state. Transition (stepping) from one MotA-MotB interaction potential to another interaction potential occurs with a probability rate k_m near the potential minimum (shaded region in the left panel), which is driven by the proton discharge-recharge chain reaction P⁺ → P ⁻ → C ⁻ → C⁺. For brevity, only the initial and final states (P⁺ and C⁺) are shown, and the intermediate discharged states C ⁻ and P ⁻ are omitted (see text for the full description). The rotor energy landscape (right panel) shows the interaction potential (V_R) between MotA and FliG, which depends only on the scaled angle difference φ = θ_R − kθ_S. For simplicity, we used a piece-wise linear form for V_{1, 2} and V_R. To the left of the P → I plateau in V_{1, 2}, a barrier is added to prevent back flow. The four stages of stator dynamics during one full power stroke as described in Equation 2 are illustrated in C-F. (C) Physical rotation of the MotA pentamer ring, which is driven dominantly by MotB₁ and proton recharge (the black dot) on MotB₂. (D) Proton discharge on MotB₁, which causes the transition of the MotA-MotB₁ interaction potential and effectively shifts V₁ (blue line) by one period (Δθ_S). (E) Physical rotation of the MotA pentamer ring, which is driven dominantly by MotB₂ and proton recharge on MotB₁. (F) Proton discharge on MotB₂, which shifts the MotA-MotB₂ potential V₂ (red line) by one period.

We model the stator unit as a rotational ratchet driven by the PMF. Based on the new structural information, the MotA pentamer ring rotates around the fixed MotB dimer. Given the incommensurate stoichiometry (5:2) within the stator unit, the two MotB monomers engage with MotA monomers alternately – when one MotB is engaged directly with one MotA monomer the other MotB is positioned between two MotA monomers. Consequently, the two MotB monomers generate two different energy potentials shifted by half a period (Δθ_S/2). To account for this effect, the overall stator potential can be written as the sum of two identical periodic potentials shifted by an angle difference of Δθ_S/2: V_S(θ_S) = V₁(θ_S)+V₂(θ_S) with V₂(θ_S) = V₁(θ_S+Δθ_S/2) as shown in Figure 1B.

During one power stroke, the MotA pentamer ring rotates one period (2π/5). Each full power stroke consists of two half strokes, each of which is powered by a proton passing through one of the two ion channels alternately. During each half stroke, the proton acceptor residue (D32 for E. coli) on the corresponding MotB monomer becomes protonated, which drives rotation of the MotA ring. At the same time, the protonated MotB undergoes a conformational change in which the proton acceptor residue changes from a periplasm-facing position to a cytoplasm-facing position, from which the proton can be released to the cytoplasm. To describe this process, we define three conformational states for each MotB: a periplasm-facing state called the P-state, a cytoplasm-facing state called the C-state, and an intermediate state between the P-state and C-state, which we call the I-state. Each MotB can be either protonated or unprotonated (indicated by a plus or minus sign). A proton can bind with MotB when it is in the P-state; and a bound proton can enter the cytoplasm when the MotB is in the C-state.

As suggested by the recent Cryo-EM study (Santiveri et al., 2020), different conformational states occur at different relative positions between MotB and the closest MotA monomer, or, equivalently, at different locations within the MotA-MotB landscape of interaction energy potential, as shown in Figure 1B (left). In particular, the P-state occurs near the peak potential and the C-state occurs near the minimum. For simplicity, we used a simple piece-wise linear potential (V_{1, 2}) that is flat over half of the period and linear in the other half, as shown in Figure 1B (left). Using this simple representation of the internal chemical states of the stator, evolution of the internal states of the two MotB monomers in a stator unit during one full rotational period (2π/5) can be described by the reaction cycle:

$\begin{array}{l}{P}_2^{+}\underset{\text{Rotation}}{\underbrace{I_1^{+}\to I_2^{+}}}\underset{{\text{Proton discharge and recharge on MotB}}_{\text{1}}}{\underbrace{C_1^{+}\to I_2^{+}{C}_1^{-}\to I_2^{+}{P}_1^{-}\to I_2^{+}}}\underset{\text{Rotation}}{\underbrace{P_1^{+}\to C_2^{+}}}\\ \underset{{\text{Proton discharge and recharge on MotB}}_{\text{2}}}{\underbrace{I_1^{+}\to C_2^{-}{I}_1^{+}\to P_2^{-}{I}_1^{+}\to P_2^{+}}}{I}_1^{+},& (2)\end{array}$

where the subscripts (1,2) indicate the two MotB monomers. For each MotB, torque is generated during the transitions P⁺→I⁺→C⁺, which drives the physical rotation of the MotA ring. After reaching the C⁺-state near the potential energy minimum, MotB is rejuvenated by the release of the proton to the cytoplasm followed by a conformational change from the C-state to the P-state and subsequent addition of a new proton to the P-state: C⁺→C ⁻ →P ⁻ →P⁺. This chain reaction returns MotB to its high-energy protonated P-state (P⁺) to continue driving the rotation of the stator. It is clear from the reaction cycle (Equation 2) that one full power stroke is powered by translocation of two protons (or 2PMF), each “consumed” by one MotB. The four stages of the alternating physical rotations and proton discharge-charge reactions during one full power stroke as described in Equation 2 are illustrated in Figures 1C–F, respectively.

In our model, the rotation dynamics of the MotA ring can also be described by a Langevin equation for the stator angle θ_S:

$\begin{array}{ll}{\xi }_S\frac{d{\theta }_S}{dt}=-\frac{\partial V_R({\theta }_S,{\theta }_R)}{\partial {\theta }_S}-\frac{\partial V_S({\theta }_S)}{\partial {\theta }_S}+{\eta }_S(t),& (3)\end{array}$

where ξ_S is the load (viscosity) of the stator, the first and the second terms on the right hand side of Equation 4 are the torque exerted on the stator from the rotor via the MotA-FliG interaction and the torque generated by the MotA-MotB interaction, respectively, and η_S(t) is the stator thermal noise with $<{\eta }_S(t){\eta }_S(t^{\prime })>=2k_{B}T{\xi }_S\delta (t-t^{\prime })$. The shape of V_S(θ_S) is given in Figure 1B. To prevent back flow at the maximum potential energy, we introduce an additional energy barrier which extends to the left of the P→I plateau.

The key chemical reaction that powers rotation of the stator is the proton discharge-recharge chain reaction (C⁺→C ⁻ →P ⁻ →P⁺), which leads to the transition (stepping) from one potential landscape, in which the system has a low (near minimum) potential energy, to another potential landscape where the system has a high (near maximum) potential energy. For simplicity, this chain reaction is modeled here by an overall transition rate k_m(θ_S) that depends on the MotA-MotB relative angle θ_S (see Figure 1B for an illustration of k_m, the blue arrow in the left panel). Specifically,

$\begin{array}{l}\text{Prob }(\text{transition from low to high potential energy during}\\ t\to t+dt)=k_m({\theta }_S)dt.& (4)\end{array}$

In summary, our model considers the coupled rotations of both the active stator and the passive rotor as well as the key chemical reactions that power the rotation of the stator. The dynamics of the BFM are fully described by Equations 1, 3 and 4, which depend on three biologically meaningful functions: two interaction energy (potential) functions - V_R(θ_S − kθ_R) between the FliG-ring of the rotor and the MotA ring, V_S(θ_S) between the MotB dimer and the MotA ring, and the chemical transition rate function k_m(θ_S). Next, we present some preliminary results based on simulations of the model with simple choices for these functions to demonstrate the general utility of the model.

In our simulations, we set the stator load ξ_S to be a small constant and change the rotor load ξ_R to obtain the torque and speed for different values of ξ_R. The motor dynamics depend on the relative strength between the MotA-FliG coupling interaction potential V_R and the torque-generating potential V_S. In Figure 2, we present the results for a case in which these two potentials are comparable. As shown in Figure 2A, the torque-speed curve shows a downward concave shape consistent with experiments. In addition to the torque-speed relationship, our model allows us to investigate the rotational dynamics of both the rotor and the stator. In Figure 2B, we plot the time trajectories of the stator (dashed lines) and rotor (solid lines) angles for different loads. At a low load, the two trajectories are close to each other, whereas, at a high load, the trajectory of the rotor is almost flat, even though the stator still rotates at a finite speed. As shown in Figure 2C, as load increases, the rotor's speed quickly decreases to zero, while the stator's speed approaches a constant speed (reduced but still finite). Our results indicate that the rotations of the stator and the rotor are in-sync at low load: when the stator rotates at an angle of Δθ, the rotor rotates at approximately kΔθ, i.e., there is no slippage between the two rotating rings. However, slippage between the two rings increases with the load. Near stall, the rotor speed vanishes while the stator still rotates at a finite speed. The existence of the stator-rotor slippage depends on the strength of the stator-rotor (MotA-FliG) coupling (V_R) relative to that of the MotA-MotB coupling (V_S). When we used a V_R that is much stronger than V_S, slippage disappears. Here, we choose to show a case in which V_R and V_S are comparable to highlight the possibility of slippage between the two rotating protein nano-rings.

FIGURE 2

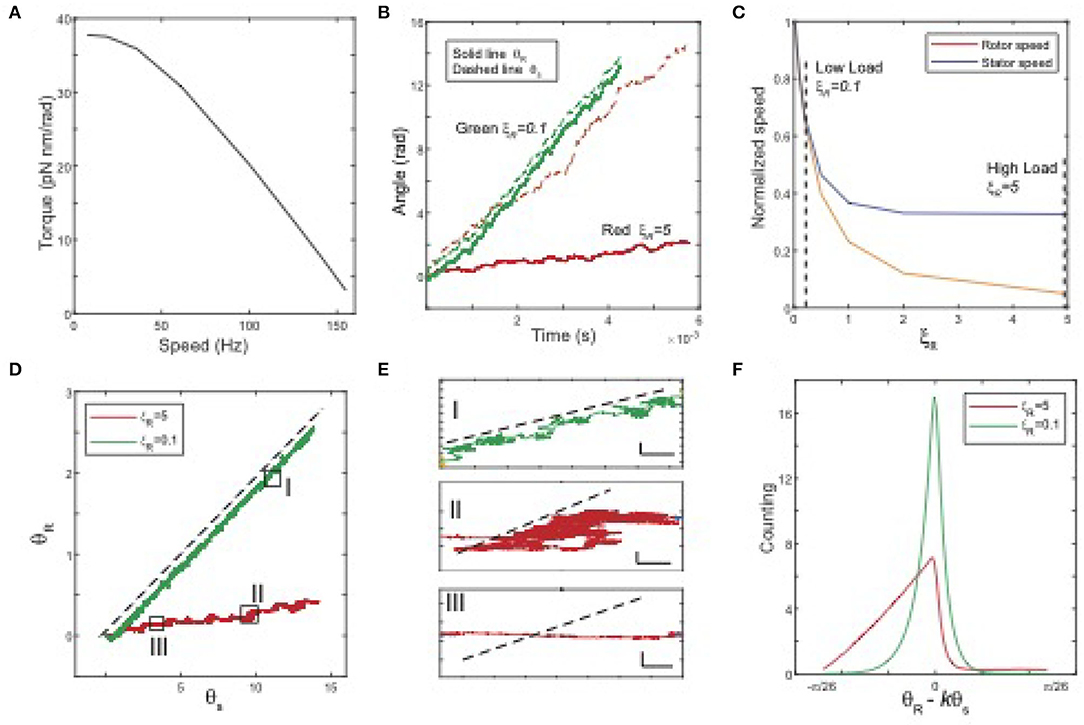
Figure 2. Model results. (A) The torque-speed curve from the model with simple choices of the interaction potentials (V_R and V_S) and the transition (stepping) rate k_m (parameters are given at the end of the caption). (B) Time series of θ_R (solid line) and θ_S (dashed line) for different rotor loads. Red: high load ξ_R = 5, green: low load ξ_R = 0.1. (C) The normalized average speeds of the rotor (yellow) and stator (blue) vs. the rotor load ξ_R. (D) Trajectories in (θ_R, θ_S) space for different loads. Dashed black line: θ_R = kθ_S, with k = Δθ_R/Δθ_S = 5/26. The three boxes highlight the three different types of motions. (E) Three typical movements with zoom-in trajectories [highlighted in (D)]. I: rotor moves along with stator without slipping; II: reduced net speed for both rotor and stator; III: stator rotates while rotor speed is near zero. The black dashed lines indicate the no-slip motion θ_R = kθ_S. Horizontal scale bar: 0.3 rad; vertical scale bar: 0.1 rad. (F) The distributions (histogram) of φ = θ_R − kθ_S for a high load and a low load. Parameters and simulation methods are given in the Supplementary Materials.

To investigate the relative motion (rotation) of the stator and rotor in details, we plot the trajectories of θ_R(t) vs. θ_S(t) for different loads in Figure 2D, where the dashed black line indicates the tight coupling (no slippage) limit when θ_R = kθ_S (dotted black line). At low load (the green line), the trajectory is almost a straight line parallel to the tight coupling limit, while at high load (the red line), the trajectory wiggles closer to the horizontal direction. We can categorize the relative stator-rotor motion by coarse-graining the trajectories in the θ_S − θ_R space. We found three types of relative motion, which are shown in the zoom-in plots in Figure 2E. In type I movement, the rotor moves with the stator without slippage; in type II movement, the rotor-stator system follows a biased random walk in the (θ_S, θ_R) space with net motion lower for both the stator and the rotor; in type III movement, the stator rotates at a finite speed but the rotor has almost no net motion, which indicates a high degree of slippage between the rotor and the stator. Type III movement can be considered as the extreme case of type II movement. From the results of our simulation, we find that as load increases, the motor spends more time in the type II&III movements, i.e., slipping. This observation is further confirmed by the distributions of the scaled angle difference between the rotor and stator, i.e., φ = θ_R − kθ_S, as shown in Figure 2F. At low load, the distribution is concentrated around φ = 0, indicating the absence of slippage. As load increases, the distribution of φ becomes more populated in the region with φ <0, which shows that the stator leaves the rotor behind more often, i.e., the motor spends more time slipping.

The most unique feature of our model is its ability to investigate the rotational motion of the stator in addition to the rotational motion of the rotor, which was the main focus of previous modeling studies. The model predictions, such as the dependence of the stator speed on the rotor load (Figure 2C) and the distributions of the relative rotor-stator angle (Figure 2F), can be tested by future experiments that directly measure the rotational motion of the stator in addition to the existing measurements of the rotor motion. These experiments together with our model can also be used to infer the interaction potentials (V_S and V_R) as well as the proton-assisted transition rate (k_m).

3. Discussion

In this article, we propose a new model for BFM based on a general modeling framework and the recently discovered molecular structure of the stator complex. The most important update in our model is that the stator is now modeled as an active rotating nano-machine that consumes PMF and drives the rotation of the rotor. The model can generate the characteristic torque-speed curve observed in experiments. More importantly, our model can be used to investigate and predict the dynamics of both the rotor and the stator, which can be tested in experiments.

It is generally believed that proton flux and motor rotation are “tightly coupled” in the BFM, which implies that there is no proton flux at stall and the efficiency of the BFM is close to 1 near stall (Berg, 2003). Here, we find that if the MotA-FliG interaction is comparable to (or weaker than) the MotA-MotB interaction, there is slippage between the rotor and the stator. The probability of slippage increases as the load increases, which leads to a motor efficiency that is less than 1 near stall. On the other hand, we also find that slippage can be suppressed by increasing the rotor-stator interaction strength. Thus, our study poses a simple but important question. Does the BFM slip? Ultimately, this question needs to be answered experimentally by measuring the rotation of the stator (MotA-ring) at different loads, especially at the high load where the probability of slippage is expected to be the highest if it exists. Alternatively, one may be able to look for signatures of slipping by measuring fluctuations of the rotor's instantaneous speed at a high load. In the absence of slipping, the rotor should run smoothly at a high load with the dominant fluctuations coming from thermal fluctuations (Meacci and Tu, 2009). However, if there is slipping, then fluctuations in the rotor speed can be much larger with additional contributions coming from the slipping events.

Our model can be extended to cases with multiple stators. At low load, the stators and rotor rotate in sync without slippage, so the rotor's maximum speed is determined by the maximum speed of the individual stator units independent of the number of stators. However, at high load (e.g., near stall), the effective duty ratio of the stator can be far below 1 due to the higher probability of slippage and/or the relatively long time spent at the energy potential minima waiting for the conformational change (Meacci and Tu, 2009). Note that the effective duty ratio during slipping is zero although the stator is not disengaged with the rotor. Assuming no direct coordination among stators, there should be little overlap among the duty cycles of each stator. Thus, the maximum torque at stall is simply the sum of torques generated by all the stators. The dependence of maximum speed and maximum torque on the number of stators has been reported before (Blair and Berg, 1988; Yuan and Berg, 2008), and our model may provide a natural explanation for these experimental observations.

The rotation of the stator units is also essential for understanding switching between CW and CCW rotation of the rotor. As pointed out in Santiveri et al. (2020) and illustrated in Figure 1A here, the MotA ring always rotates clockwise around the MotB dimer, and the switch between the CW and CCW rotation of the rotor ring is determined by conformational changes of the C-ring. In the CCW mode, the C-ring adopts a compact conformation, and the stator units contact FliG subunits on the outside of the C-ring; thus, the C-ring rotates CCW. Upon binding of CheY-P to FliM in the C-ring, the C-ring expands, and the stator units are now in contact with FliG subunits on the inside of the C-ring, so the C-ring rotates clockwise. In this manner, the unidirectional rotation of the stator drives the bidirectional rotation of the motor. In our modeling framework, the coupling between rotor and stator is modeled by V_R(θ_R, θ_S). We hypothesize that the CW and CCW rotation modes correspond to different forms of the interaction potential V_R, which can lead to the different torque-speed curves for the BFM in CCW and CW rotation observed experimentally (Yuan et al., 2010).

The BFM, like all other biological motors, converts chemical energy (e.g. from ATP hydrolysis or ion translocations) into mechanical work. A fundamental question is whether there are thermodynamic bounds to the power generation and energy efficiency for these highly non-equilibrium molecular engines (Parmeggiani et al., 1999; Parrondo and de Cisneros, 2002; Astumian, 2010). A related question is what microscopic design principles allow a molecular motor to approach these bounds under realistic constraints. In our model, the motor design space is spanned by three functions: V_S(θ_S), V_R(φ), and k_m(θ_S), which determine the motor dynamics. For example, as we showed in this paper, depending on the relative strength of V_R and V_S, there could be slippage between the stator and the rotor, which strongly affects the efficiency of the motor. Each of these functions contains information about the molecular details of the motor, which, in principle, can be estimated from or constrained by the structural data. A systematical exploration of the motor design space will lead to a better understanding of the fundamental limits and possible design principles for optimal motor performance.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YT originated the study. YC and TL performed all simulations. YC and YT prepared the manuscript. All authors read and approved the final manuscript.

Funding

The work by YT is supported by a NIH grant (R35GM131734).

Conflict of Interest

YT is employed by IBM T. J. Watson Research Center.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

YT would like to express deepest thanks to Howard Berg for introducing the bacterial flagellar motor—a biotechnological marvel (Berg, 2003) to him more than a decade ago and for Howard's constant enlightenment and encouragement on the topic till his untimely passing at the end of 2021. We dedicate this work in the memory of Howard—it was Howard and members of the Berg lab who first told us about the new stator structure (Deme et al., 2020; Santiveri et al., 2020), who launched this study. YT would also like to thank Nicholas Taylor for an insightful discussion on details of the stator structure and proton translocation process.

References

Asai, Y., Kojima, S., Kato, H., Nishioka, N., Kawagishi, I., and Homma, M. (1997). Putative channel components for the fast-rotating sodium-driven flagellar motor of a marine bacterium. J. Bacteriol. 179, 5104–5110. doi: 10.1128/jb.179.16.5104-5110.1997

PubMed Abstract | CrossRef Full Text | Google Scholar

Astumian, R.. (2010). Thermodynamics and kinetics of molecular motors. Biophys. J. 98, 2401–2409. doi: 10.1016/j.bpj.2010.02.040

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, M. A. B., Hynson, R. M. G., Ganuelas, L. A., Mohammadi, N. S., Liew, C. W., Rey, A. A., et al. (2016). Domain-swap polymerization drives the self-assembly of the bacterial flagellar motor. Nat. Struct. Mol. Biol. 23, 197–203. doi: 10.1038/nsmb.3172

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, H. C.. (2003). The rotatory motor of bacterial flagella. Annu. Rev. Biochem. 72, 19–54. doi: 10.1146/annurev.biochem.72.121801.161737

PubMed Abstract | CrossRef Full Text | Google Scholar

Blair, D. F., and Berg, H. C. (1988). Restoration of torque in defective flagellar motors. Science 242, 1678–1681. doi: 10.1126/science.2849208

PubMed Abstract | CrossRef Full Text | Google Scholar

Blair, D. F., and Berg, H. C. (1990). The mota protein of E. coli is a proton-conducting component of the flagellar motor. Cell 60, 439–449. doi: 10.1016/0092-8674(90)90595-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, T. F., Al-Mawsawi, L. Q., Kojima, S., and Blair, D. F. (2004). Arrangement of core membrane segments in the mota/motb proton-channel complex of escherichia coli. Biochemistry 43, 35–45. doi: 10.1021/bi035406d

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., and Berg, H. C. (2000). Torque-speed relationship of the flagellar rotary motor of escherichia coli. Biophys. J. 78, 1036–1041. doi: 10.1016/S0006-3495(00)76662-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Chun, S. Y., and Parkinson, J. S. (1988). Bacterial motility: membrane topology of the escherichia coli motb protein. Science 239, 276–278. doi: 10.1126/science.2447650

PubMed Abstract | CrossRef Full Text | Google Scholar

Deme, J. C., Johnson, S., Vickery, O., Aron, A., Monkhouse, H., Griffiths, T., et al. (2020). Structures of the stator complex that drives rotation of the bacterial flagellum. Nat. Microbiol. 5, 1553–1564. doi: 10.1038/s41564-020-0788-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Feynman, R. P., Leighton, R. B., and Sands, M. (1966). The Feynman Lectures on Physics, Vol. I. Reading, MA: Addison-Wesley.

Google Scholar

Golubeva, N., Imparato, A., and Peliti, L. (2012). Efficiency of molecular machines with continuous phase space. EPL 97, 60005. doi: 10.1209/0295-5075/97/60005

CrossRef Full Text | Google Scholar

Hirota, N., Kitada, M., and Imae, Y. (1981). Flagellar motors of alkalophilic bacillus are powered by an electrochemical potential gradient of na+. FEBS Lett. 132, 278–280. doi: 10.1016/0014-5793(81)81178-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Jülicher, F., Ajdari, A., and Prost, J. (1997). Modeling molecular motors. Rev. Mod. Phys. 69, 1269–1282. doi: 10.1103/RevModPhys.69.1269

CrossRef Full Text | Google Scholar

Kim, E. A., Price-Carter, M., Carlquist, W. C., and Blair, D. F. (2008). Membrane segment organization in the stator complex of the flagellar motor: Implications for proton flow and proton-induced conformational change? Biochemistry 47, 11332–11339. doi: 10.1021/bi801347a

PubMed Abstract | CrossRef Full Text | Google Scholar

Kojima, S., and Blair, D. F. (2004). Solubilization and purification of the mota/motb complex of escherichia coli. Biochemistry 43, 26–34. doi: 10.1021/bi035405l

PubMed Abstract | CrossRef Full Text | Google Scholar

Larsen, S. H., Adler, J., Gargus, J. J., and Hogg, R. W. (1974). Chemomechanical coupling without atp: the source of energy for motility and chemotaxis in bacteria. Proc. Natl. Acad. Sci. U.S.A. 71, 1239–1243. doi: 10.1073/pnas.71.4.1239

PubMed Abstract | CrossRef Full Text | Google Scholar

Lele, P. P., Hosu, B. G., and Berg, H. C. (2013). Dynamics of mechanosensing in the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 110, 11839–11844. doi: 10.1073/pnas.1305885110

PubMed Abstract | CrossRef Full Text | Google Scholar

Lo, C.-J., Sowa, Y., Pilizota, T., and Berry, R. M. (2013). Mechanism and kinetics of a sodium-driven bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 110, E2544–2551. doi: 10.1073/pnas.1301664110

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandadapu, K. K., Nirody, J. A., Berry, R. M., and Oster, G. (2015). Mechanics of torque generation in the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 112, E4381–4389. doi: 10.1073/pnas.1501734112

PubMed Abstract | CrossRef Full Text | Google Scholar

Meacci, G., Lan, G., and Tu, Y. (2011). Dynamics of the bacterial flagellar motor: the effects of stator compliance, back steps, temperature, and rotational asymmetry. Biophys. J. 100, 1986–1995. doi: 10.1016/j.bpj.2011.02.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Meacci, G., and Tu, Y. (2009). Dynamics of the bacterial flagellar motor with multiple stators. Proc. Natl. Acad. Sci. U.S.A. 106, 3746–3751. doi: 10.1073/pnas.0809929106

PubMed Abstract | CrossRef Full Text | Google Scholar

Morimoto, Y. V., and Minamino, T. (2014). Structure and function of the bi-directional bacterial flagellar motor. Biomolecules 4, 217–234. doi: 10.3390/biom4010217

PubMed Abstract | CrossRef Full Text | Google Scholar

Nirody, J. A., Berry, R. M., and Oster, G. (2016). The limiting speed of the bacterial flagellar motor. Biophys. J. 111, 557–564. doi: 10.1016/j.bpj.2016.07.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Nord, A. L., Gachon, E., Perez-Carrasco, R., Nirody, J. A., Barducci, A., Berry, R. M., et al. (2017). Catch bond drives stator mechanosensitivity in the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 114, 12952–12957. doi: 10.1073/pnas.1716002114

PubMed Abstract | CrossRef Full Text | Google Scholar

Parmeggiani, A., Julicher, F., Ajdari, A., and Prost, J. (1999). Energy transduction of isothermal ratchets: generic aspects and specific examples close to and far from equilibrium. Phys. Rev. E 60, 2127. doi: 10.1103/PhysRevE.60.2127

PubMed Abstract | CrossRef Full Text | Google Scholar

Parrondo, J., and de Cisneros, B. (2002). Energetics of brownian motors: a review. Appl. Phys. A 75, 179–191. doi: 10.1007/s003390201332

PubMed Abstract | CrossRef Full Text | Google Scholar

Parrondo, J. M., Blanco, J., Cao, F., and Brito, R. (1998). Efficiency of brownian motors. Europhys. Lett. 43, 248–254. doi: 10.1209/epl/i1998-00348-5

CrossRef Full Text | Google Scholar

Roujeinikova, A.. (2008). Crystal structure of the cell wall anchor domain of motb, a stator component of the bacterial flagellar motor: implications for peptidoglycan recognition. Proc. Natl. Acad. Sci. U.S.A. 105, 10348–10353. doi: 10.1073/pnas.0803039105

PubMed Abstract | CrossRef Full Text | Google Scholar

Santiveri, M., Roa-Eguiara, A., Kühne, C., Wadhwa, N., Hu, H., Berg, H. C., et al. (2020). Structure and function of stator units of the bacterial flagellar motor. Cell 183, 244–257. doi: 10.1016/j.cell.2020.08.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, K., and Homma, M. (2000). Functional reconstitution of the Na+-driven polar flagellar motor component of vibrio alginolyticus. J. Biol. Chem. 275, 5718–5722. doi: 10.1074/jbc.275.8.5718

PubMed Abstract | CrossRef Full Text | Google Scholar

Sowa, Y., Rowe, A. D., Leake, M. C., Yakushi, T., Homma, M., Ishijima, A., et al. (2005). Direct observation of steps in rotation of the bacterial flagellar motor. Nature 437, 916–919. doi: 10.1038/nature04003

PubMed Abstract | CrossRef Full Text | Google Scholar

Thomas, D. R., Francis, N. R., Xu, C., and DeRosier, D. J. (2006). The three-dimensional structure of the flagellar rotor from a clockwise-locked mutant of salmonella enterica serovar typhimurium. J. bacteriol. 188, 7039–7048. doi: 10.1128/JB.00552-06

PubMed Abstract | CrossRef Full Text | Google Scholar

Tipping, M. J., Delalez, N. J., Lim, R., Berry, R. M., and Armitage, J. P. (2013). Load-dependent assembly of the bacterial flagellar motor. mBio. 4, e00551–13. doi: 10.1128/mBio.00551-13

PubMed Abstract | CrossRef Full Text | Google Scholar

Tu, Y., and Cao, Y. (2018). Design principles and optimal performance for molecular motors under realistic constraints. Phys. Rev. E 97, 022403. doi: 10.1103/PhysRevE.97.022403

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadhwa, N., Phillips, R., and Berg, H. C. (2019). Torque-dependent remodeling of the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 116, 11764–11769. doi: 10.1073/pnas.1904577116

PubMed Abstract | CrossRef Full Text | Google Scholar

Wadhwa, N., Tu, Y., and Berg, H. C. (2021). Mechanosensitive remodeling of the bacterial flagellar motor is independent of direction of rotation. Proc. Natl. Acad. Sci. U.S.A. 118, e2024608118. doi: 10.1073/pnas.2024608118

PubMed Abstract | CrossRef Full Text | Google Scholar

Xing, J., Bai, F., Berry, R., and Oster, G. (2006). Torque-speed relationship of the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 103, 1260–1265. doi: 10.1073/pnas.0507959103

PubMed Abstract | CrossRef Full Text | Google Scholar

Yorimitsu, T., Kojima, M., Yakushi, T., and Homma, M. (2004). Multimeric structure of the poma/pomb channel complex in the Na+-driven flagellar motor of vibrio alginolyticus. J. Biochem. 135, 43–51. doi: 10.1093/jb/mvh005

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, J., and Berg, H. C. (2008). Resurrection of the flagellar rotary motor near zero load. Proc. Natl. Acad. Sci. U.S.A. 105, 1182–1185. doi: 10.1073/pnas.0711539105

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, J., Fahrner, K. A., Turner, L., and Berg, H. C. (2010). Asymmetry in the clockwise and counterclockwise rotation of the bacterial flagellar motor. Proc. Natl. Acad. Sci. U.S.A. 107, 12846–12849. doi: 10.1073/pnas.1007333107

PubMed Abstract | CrossRef Full Text | Google Scholar

Supplementary Material

Piece-wise linear forms for V_R and V_{1, 2} are used. V_{1, 2}: k_BT = 4.11pN × nm, V_0S = 10k_BT, ${\tau }_S^{+}=2V_{0S}/\Delta {\theta }_S$, ${\tau }_S^{-}=4V_{0S}/\Delta {\theta }_S$, where ${\tau }_S^{\pm }$ is the positive and negative torque on stator potential V_{1, 2}, respectively, and the extended potential to the left of P→I has the same slope as ${\tau }_S^{+}$. V_R: a symmetric form is used with V_0R = 10k_BT. Load on the stator ξ_S = 0.01(pN nm rad ^{− 1} s). The transition rate is $k_m=10^5{s}^{-1}$ for θ_S ≥ 2π/5 and 0 otherwise.

Equations 1 and 3 are solved with discrete time step dt = 5 × 10 ^{− 6}, and in the format of ${\theta }_{R,S}^{i+1}={\theta }_{R,S}^i+dt(\cdots )/{\xi }_{R,S}+\sqrt{2k_{B}Tdt/{\xi }_{R,S}}N(0,1)$, where (⋯ ) is the drift term, and N(0, 1) is a random number with standard normal distribution. During each step, the transition from low to high energy potential happens when k_m(θ)dt > U(0, 1), where U(0, 1) is a random number with uniform distribution on (0,1).