- Departments of Electrical and Computer Engineering, Biomedical Engineering, Mathematical Sciences University of Delaware, Newark, DE, United States
The inherent stochasticity in the gene product levels can drive single cells within an isoclonal population to different phenotypic states. The dynamic nature of this intercellular variation, where individual cells can transition between different states over time, makes it a particularly hard phenomenon to characterize. We reviewed recent progress in leveraging the classical Luria–Delbrück experiment to infer the transient heritability of the cellular states. Similar to the original experiment, individual cells were first grown into cell colonies, and then, the fraction of cells residing in different states was assayed for each colony. We discuss modeling approaches for capturing dynamic state transitions in a growing cell population and highlight formulas that identify the kinetics of state switching from the extent of colony-to-colony fluctuations. The utility of this method in identifying multi-generational memory of the both expression and phenotypic states is illustrated across diverse biological systems from cancer drug resistance, reactivation of human viruses, and cellular immune responses. In summary, this fluctuation-based methodology provides a powerful approach for elucidating cell-state transitions from a single time point measurement, which is particularly relevant in situations where measurements lead to cell death (as in single-cell RNA-seq or drug treatment) or cause an irreversible change in cell physiology.
1. Introduction
Advances in single-cell technologies have exposed remarkable differences in phenotype and expression patterns between individual cells within the same isogenic cell population (Raj and van Oudenaarden, 2008; Brandt et al., 2020; Foreman and Wollman, 2020; Lyu et al., 2021; SoRelle et al., 2021; Van Eyndhoven et al., 2021; Topolewski et al., 2022). While some of this variation can be linked to extrinsic factors (i.e., cell-cycle stage, cell size, and local extracellular environment), a growing body of evidence points to the role of stochastic processes inherent to gene expression in driving random fluctuations (noise) in the gene product levels (Süel et al., 2006; Maamar et al., 2007; Eldar and Elowitz, 2010; Singh et al., 2010; Chalancon et al., 2012; Johnston et al., 2012; Neuert et al., 2013; Dar et al., 2014; Magklara and Lomvardas, 2014; Battich et al., 2015; Larsson et al., 2019, 2021; Rodriguez et al., 2019; Ochiai et al., 2020; Fraser et al., 2021). Intercellular phenotypic heterogeneity is physiologically relevant and has important implications for both biology and medicine from driving genetically identical cells to different cell fates (Chang et al., 2008; Losick and Desplan, 2008; St-Pierre and Endy, 2008; Singh and Weinberger, 2009; Thompson et al., 2009; Kim and Sauro, 2012; Norman et al., 2013; Abranches et al., 2014; Balázsi et al., 2014; Torres-Padilla and Chambers, 2014) to facilitating the survival and adaptation of cells to detrimental environmental changes (Kussell and Leibler, 2005; Bishop et al., 2007; Acar et al., 2008; Veening et al., 2008a; Shu et al., 2013; Ackermann, 2015; Doganay et al., 2017; Gasch et al., 2017; Zheng et al., 2018; Evans and Zhang, 2020; Sampaio and Dunlop, 2020; Vasdekis and Singh, 2021).
While single-cell sequencing tools can probe phenotypic heterogeneity within a given cell population, they only provide a static picture of different cell states. Characterizing the dynamics of individual cells transitioning between different states with multi-generational time scales remains a fundamental challenge in advancing the field of single-cell biology. In this regard, a recent innovation leverages the Luria–Delbrück experiment (also called the fluctuation test) in conjunction with mathematical modeling for inferring the switching dynamics between the cellular states. We briefly reviewed this seminal work published 80 years ago.
The classical Luria–Delbrück experiment was designed to discriminate whether genetic mutations arise in response to selection or mutations arise randomly in the population in the absence of selection (Figure 1). In an ideal experiment, single E. coli cells are grown into clonal colonies and then exposed to the selection pressure (in this case, viral infection by bacteriophage T1). If each bacterial cell has a small and independent probability of gaining a phage-induced mutation, then the number of mutant cells should follow a Poisson distribution across clones (Figure 1, left). Alternatively, if mutations occur randomly, then the number of mutant cells will vary considerably across colonies depending on when the mutation arose in the population expansion (Figure 1, right). The data clearly showed a non-Poissonian skewed distribution for the number of resistant bacteria, validating the hypothesis of pre-existing mutants arising randomly before viral exposure (Luria and Delbrück, 1943). Subsequent mathematical modeling and development of statistical methods allow for the accurate estimation of mutation rates from measured fluctuations across colonies (Koch, 1982; Sarkar, 1991; Jones et al., 1993; Zheng, 1999; Hall et al., 2009; Houchmandzadeh, 2015; Holmes et al., 2017). Apart from its biological significance, this elegant experiment shows how fluctuation-based analysis can reveal hidden random processes that are not directly observable.
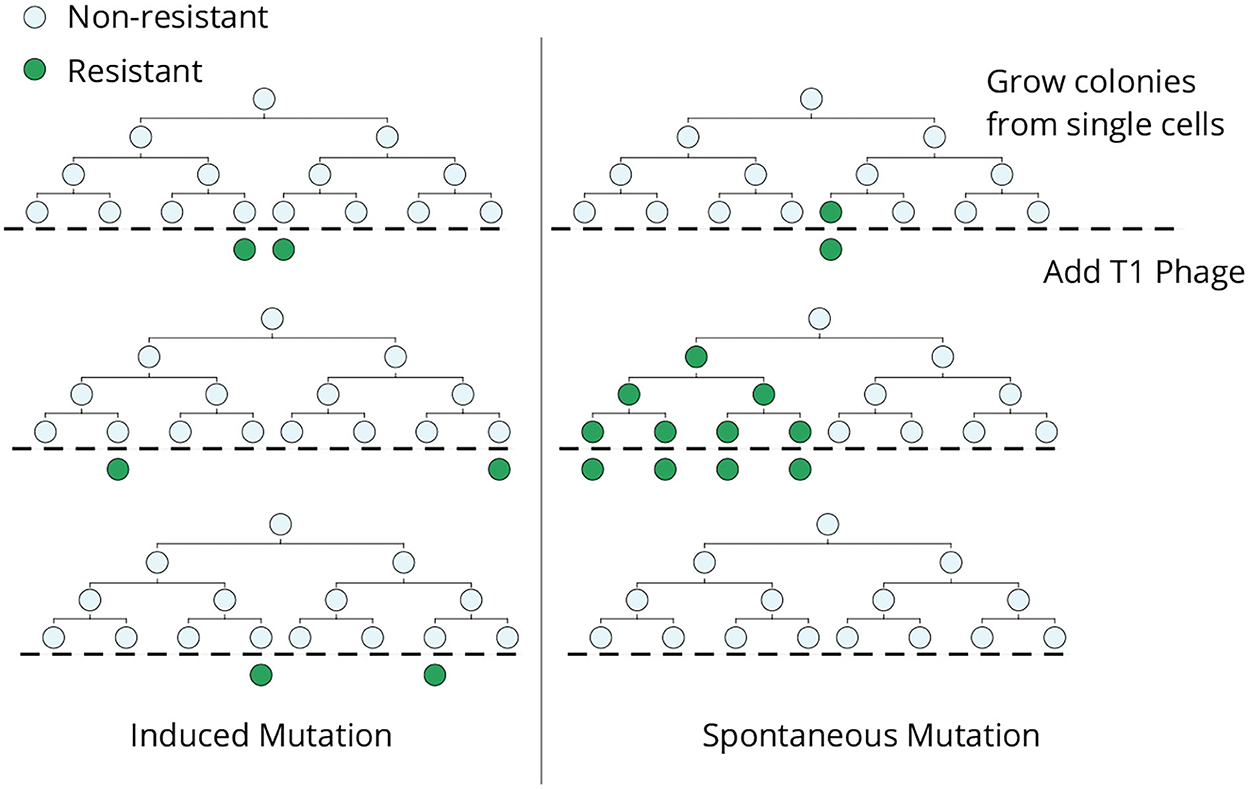
Figure 1. The original Luria–Delbrück fluctuation test. Individual E. coli cells were isolated, grown into colonies, and then infected by bacteriophage T1. In the induced mutation hypothesis (left), each cell independently acquires a phage-resistant mutation in response to the infection, and the resulting colony-to-colony variation in the resistant cells would follow a Poisson distribution. In contrast, mutant cells arising spontaneously during lineage expansion prior to viral exposure will lead to large skewed colony-to-colony fluctuations in the number of surviving cells (right)—including “jackpot” colonies, where mutations occurred in the early phase of colony expansion leading to a large fraction of resistant cells.
While the original Luria–Delbrück experiment considers an irreversible change from a non-resistant to resistant phenotype using genetic mutations, this approach can be generalized to consider reversible switching between cellular states. We reviewed recent progress in this direction for inferring the transient heritability of cell states (i.e., the number of generations a cell resides in a state before exiting it) from a Luria–Delbrück style experiment. Finally, we highlight several experimental works exploiting this methodology to reveal the plasticity of the drug-tolerant states in cancer cells and discuss its applications to microbiology.
2. Fluctuation-test approach to infer cell-state switching
Considering a scenario as in Figure 2 where cells within a population can reside in two states (States 1 and 2), cells proliferate and reversibly switch between states, and the rates of switching determine the transient heritability of a state. Let f denote the average fraction of cells in State 2 in the original population. Single cells are randomly drawn from the population (through serial dilutions or FACS sorting or single-cell barcoding) and expanded into colonies. Note that the state of the starting single cell is unobservable, as we only considered a single endpoint measurement. After growing the colonies for a certain duration of time, each colony is assayed for the fraction of cells in State 2 (or State 1). The basic idea is that if switching between states is relatively fast (several switches happen in the growth duration), then the fraction of State 2 cells will rapidly equilibrate to f in each colony, and colony-to-colony fluctuations will be minimal (Figure 2). In contrast, if switching is slow, then, based on the memory of the initial cell, colonies will primarily be composed of cells in either State 1 or State 2 by generating large colony-to-colony fluctuations (Figure 2). In essence, fluctuations in colony cell-state composition reveal the timescale of switching, with slower relaxation kinetics driving higher fluctuations.
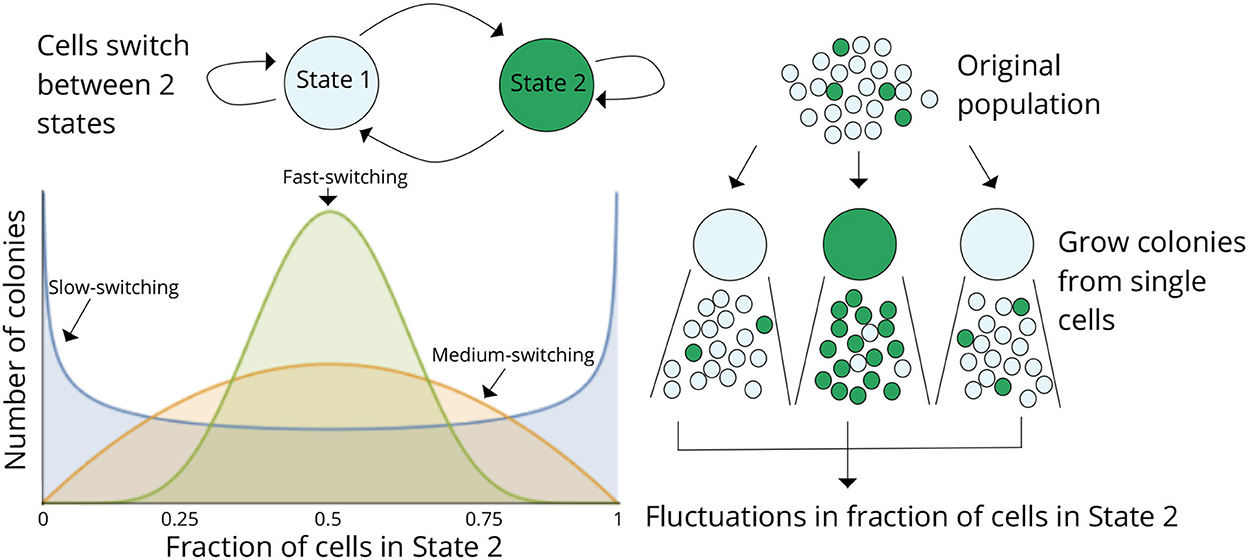
Figure 2. The fluctuation test approach for deciphering switching between two cellular states. Schematic showing cells in two different states (States 1 and 2) together with reversible switching between states and proliferation in each state. Individual cells are randomly chosen from the original population and assayed for the fraction of cells in State 2 after a certain duration of lineage expansion. If switching between states is relatively fast, then the colonies will show similar fractions of State 2 cells as the original population, and variance across colonies will be minimal. On the contrary, if switching is slow, then colony composition will heavily depend on the state of the initial cell, and there would be large colony-to-colony fluctuations based on differences in the initial condition. Thus, statistical fluctuations in colony composition can be exploited to infer the transient heritability of cellular states.
In a recent study, we developed several mathematical formulas connecting the magnitude of inter-colony fluctuations to the switching kinetics (Saint-Antoine et al., 2022). We next highlight these formulas that are derived under the following assumptions:
• Cells proliferate at a constant rate kx that is assumed to be the same irrespective of the cellular state.
• Starting from a single cell, the colony expands exponentially with the average colony size at time t being .
• Cells in State 1 transition to State 2 with a rate k1 and switch back to State 1 with a rate k2 resulting in the average fraction as follows:
• The transition rates are assumed to be constants over time and also the same across single-cell colonies.
• The initial cell is chosen randomly from the original bulk population and is either in State 2 with probability f or in State 1 with probability 1−f.
Let the random process f(t) denote the fraction of cells in State 2 at time t of colony expansion. Our goal is to quantify statistical fluctuation in f(t) as measured by its coefficient of variation:
Where 〈f(t)〉 and 〈f2(t)〉−〈f(t)〉2 denote the mean and variance of f(t) across colonies, respectively.
2.1. Modeling cell proliferation and switching as deterministic processes
In the simplest formulation of this problem, we considered a Bernoulli cell-state assignment of the initial cell where f(0) = 1 with probability f (starting cell is in State 2) and f(0) = 0 with probability 1−f (starting cell is in State 1). Conditioned on this random initial condition, everything else is modeled deterministically using differential equations. More specifically, the total number of cells over time is , and the fraction of cells in State 2 is given by the following first-order differential equation:
Solving Equation (3) results in the solution as follows:
A straightforward analysis of Equation (4) shows that 〈f(t)〉 = f, which is intuitively expected—the average fraction of cells in State 2 across clones is the same as that in the original population. Note that this time invariant 〈f(t)〉 is fundamentally different from the classical Luria–Delbrück experiment where the average fraction of mutant cells monotonically increases over time (Luria and Delbrück, 1943).
The colony-to-colony fluctuations can be derived from Equation (4) as follows:
where the dimensionless quantity
is a relative measure of the speed of switching with respect to the cell proliferation rate, and tkx can be interpreted as the average number of generations of colony expansion. Some key features of the fluctuation Equation (5) are as follows:
• At t = 0, , which is expected from the Bernoulli distributed cell-state assignment of the initial single cell.
• For a given fixed time point t and average fraction f, a slower speed of switching will lead to larger values of Z and CVf.
• As t → ∞, with the fraction of State 2 cells converging to f across colonies.
From a practical perspective, given a measured value of CVf at a given time t of colony expansion, a priori knowledge of the cell proliferation rate and f (that can also be estimated from 〈f(t)〉 = f), the switching rates can be estimated by simultaneously solving Equations (1), (5). It is important to point out that this approach for determining transient heritability of cellular states does not require tracking of individual proliferating cells by microscopy over longer period of time to know the exact kinship between cells (Hormoz et al., 2016). To take into account technical fluctuations that are inevitable in an experimental setting, Equation (5) can be modified to
Lu et al. (2021). Here, represents technical fluctuations measured using a noise control experiment where random cell populations (of similar size as in the fluctuation test) are drawn from the bulk population and assayed for state fractions. The coefficient of variation of state fractions between these technical repeats determines . In the limit of rapid switching between cell states (corresponding to non-heritable states), .
2.2. Modeling cell proliferation and switching as random processes
Perhaps a more accurate modeling approach would be to consider stochasticity in cell proliferation and state switching. Toward that end, for analytical tractability, we considered the cell-cycle time as an independent and identically distributed random variable that follows an exponential distribution with a mean value of 1/kx. While actual cell-cycle times are better captured by Gamma or lognormal distributed random variables, our simulation results show that fluctuations in the fraction of cell states are quite robust to the exact form of the cell-cycle time distribution (Saint-Antoine et al., 2022). The stochastic dynamics of state switching is also modeled as a memoryless process with the time spent in State 2 (State 1) being exponentially distributed with means 1/k2 (1/k1), respectively.
Let the integer-value random processes x(t) and x2(t) denote the total number of cells and the number of cells in State 2, respectively, and now
It turns out that, for this stochastic system, one can obtain an exact analytical expression for the statistical moments of x(t) and x2(t) (see Saint-Antoine et al., 2022) for a detailed derivation of population count moment). To connect fluctuations in absolute cell numbers to fluctuations in f(t), two different approximations have been employed.
Independent variable approximation
Assuming that the fraction of cells in State 2 in a colony is independent of the colonies, population size
Exploiting this independence and substituting the moments of absolute cell numbers in Equation (9) results in
and in the limit Z → 2, Equation (10) reduces to
As seen earlier, for a fixed f and t, CVf monotonically increases with slower switching (Figure 3). Moreover, Equation (10) provides a more accurate estimation of the magnitude of inter-colony fluctuations compared with the deterministically formulated Equation (5) (Figure 4).
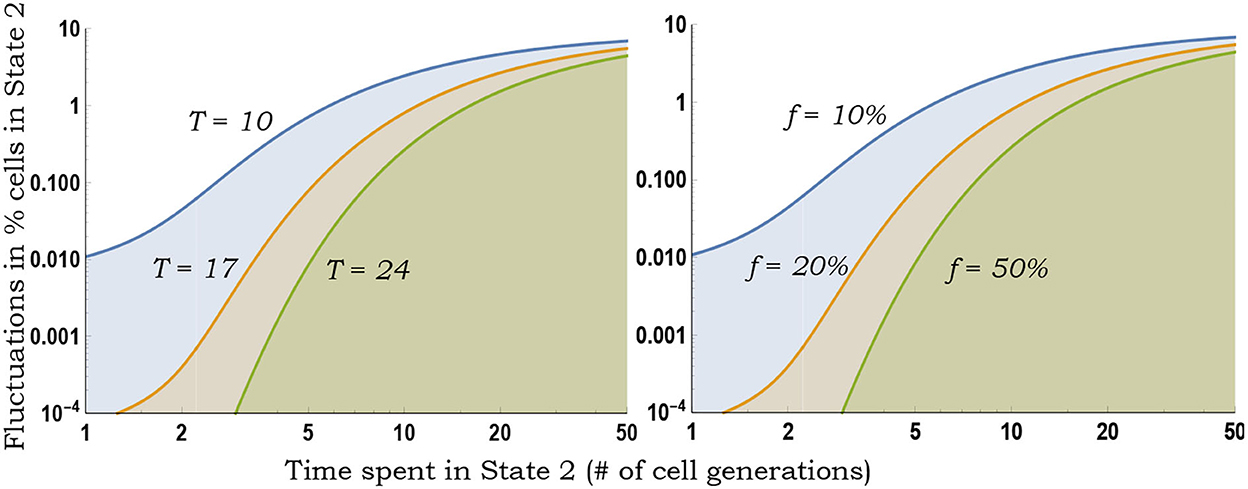
Figure 3. Inferring switching rates from the generalized fluctuation test. Left: Colony-to-colony fluctuations in the fraction of State 2 cells as predicted by Equation (10) for fixed f = 0.1, as a function of 1/k2 (average time spent in State 2) for different durations T of colony expansion. With decreasing k2, k1 is changed to ensure a fixed f = 0.1. Slower switching (decreasing k2) generates larger colony-to-colony fluctuations. Right: Same plot as on the left except T = 10 (fixed number of cell generations of colony growth) and colony-to-colony fluctuations are plotted for different fractions f.
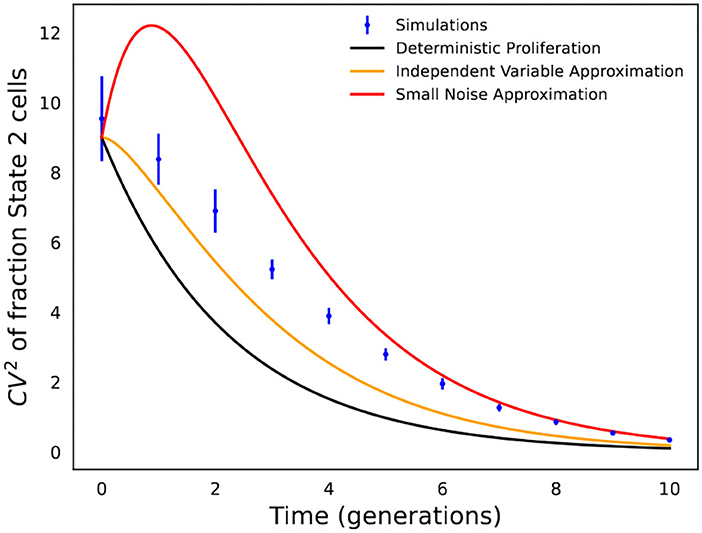
Figure 4. Comparison of analytical formulas predicting fluctuations in state fractions across single-cell colonies. Stochastic simulations of the cell proliferation and switching process were used to perform an in silico fluctuation test experiment with f = 0.1, kx = 1, and k2 = 1/5 (i.e., cells spend an average of 5 generations in State 2). CVf is computed based on 1,000 colonies, and simulations were repeated 20 times to generate error bars that show one standard deviation. The fluctuation in State 2 fractions across colonies as obtained from stochastic simulations are compared with formulas in Equations (5), (10), and (13).
Small noise approximation
Considering small fluctuations in x(t) and x2(t) around their respective average population counts, one can use the Taylor series to approximate the coefficient of variation of f(t) as
which results in the following formula
The accuracy of the different formulas in Equations (5), (10), and (13) is shown in Figure 4, which is not surprising, and the formula based on deterministic modeling significantly underestimates fluctuations in State 2 fractions. In contrast, the formulas based on stochastic modeling provide a much better approximation, with Equation (10) (independent variable approximation) performing better at earlier time points when fluctuations are large, while Equation (13) (small noise approximation) works better at longer time points when fluctuations are small.
Recently, Saint-Antoine et al. (2022) performed a benchmarking investigation where in silico data were generated using a simulated fluctuation test with 40 single-cell colonies expanded as per a gamma or lognormally distributed cell-cycle time, and matching fluctuations in the data with Equation (10) were used to identify the transient heritability of cell states. This benchmarking indeed shows the utility of this approach in effectively discriminating between fast and slow cell-state switching (Saint-Antoine et al., 2022). However, the estimated average time spent in State 2 was slightly larger than that assumed in the simulations due to the fact that Equation (10) underestimates the actual extent of fluctuations (Figure 4). More rigorous inference approaches are clearly warranted, and a good direction would be to combine formula-based fluctuation-matching with maximum-likelihood approaches that directly fit the model-predicted distribution of state fractions to data.
3. Inferring transient heritable across biology systems
Drug resistance in response to targeted therapy is a major obstacle in curing a patient with cancer. The fluctuation test methodology was used to study cancer drug resistance, where single melanoma cells were expanded into colonies for a few weeks and then treated with a chemotherapy drug, vemurafenib (Shaffer et al., 2017). After treatment, each cell was phenotypically classified into two states:
• Drug-sensitive (the cell becomes nonviable in response to treatment).
• Drug-tolerant (the cell survives treatment and later develops into a drug-resistant colony).
Intriguingly, the colony-to-colony fluctuations in the number of surviving cells were significantly larger than a Poisson distribution with Fana factors (variance/mean) reported in the range of ≈10 − 25 (Shaffer et al., 2017). Recalling that the Fana factor of Poisson-distributed random variables is one, we observed that the Fana factors were orders of magnitude smaller than that predicted by a model where drug-tolerant cells arose using an irreversible genetic mutation prior to treatment. These observed fluctuations were consistent with a model of pre-treatment reversible switching between drug-sensitive and drug-tolerant states, and cells in the tolerant state can transform to become drug-resistant after long-term drug exposure (Shaffer et al., 2017; Harmange et al., 2022). In summary, a rare subpopulation of drug-tolerant melanoma cells (≈ one out of a thousand cells) are transiently primed to respond to drug therapy even in the absence of the drug. The study also identified several resistance markers that were expressed in rare cells, and stochastic modeling of interconnected networks of such genes mechanistically captured transient entry and exit from the drug-tolerant state (Schuh et al., 2020). These insights from the fluctuation assay add to the growing understanding of reversible and non-genetic mechanisms leading to the survival of drug-tolerant persister cells that are major drivers of therapy relapse across cancer types (Sharma et al., 2010; Raha et al., 2014; Mu et al., 2017; Duy et al., 2021; Rehman et al., 2021).
Combining the colony-to-colony fluctuations in the number of surviving melanoma cells with the formula in Equation (5) revealed a drug-tolerant state with a transient heritability of roughly five to eight generations before melanoma cells switch back to being drug-sensitive (Saint-Antoine and Singh, 2022). From a therapeutic point of view, knowing these rates of switching can aid the design of drug therapy schedules to delay the emergence of cancer drug resistance (Paryad-Zanjani et al., 2021). These mathematical results also facilitated the development of a novel approach, Memory Sequencing (MemorySeq), that identifies all slowly fluctuating expression programs in rare cells (Shaffer et al., 2020). The basic idea of MemorySeq is to perform bulk RNA sequencing on each single-cell lineage and then find all genes that exhibit much higher fluctuations in their expression levels across lineages as compared with its noise control (fluctuations in expression levels across randomly selected cell populations). MemorySeq facilitated a genome-wide identification of drug-tolerant expression programs and single-molecule fluorescence in situ hybridization (smFISH) confirmed the upregulation of these genes in rare single melanoma cells (Shaffer et al., 2017). Inferred switching rates were validated in two ways: i) The drug-tolerant genes identified in MemorySeq were fluorescently tagged at the protein level. Following single cells using time-lapse microscopy indeed showed individual cells stochastically switching to a high-expression state that persisted transiently for several cell divisions (Shaffer et al., 2020); ii) FACS sorted outlier cells with high expression of these genes exhibited enhanced drug tolerance, with both expression and drug-tolerance levels slowly reverting to corresponding levels in the original unsorted population consistent with model-predicted relaxation kinetics (Shaffer et al., 2017).
Recent advances in barcoding technologies allow single-cell lineage tracing both in culture and in vivo (Echeverria et al., 2019; Bowling et al., 2020; Rodriguez-Fraticelli et al., 2020; Leeper et al., 2021; Umkehrer et al., 2021) providing fertile grounds for applications of the fluctuation test. Recently, the fluctuation test has been applied to barcoded data from both melanoma and breast cancer cell lines (Chang et al., 2021; Harmange et al., 2022). In the latter study, barcoded single breast cancer cells were first expanded for several generations and then treated with the tyrosine kinase inhibitor, tucatinib, for 2 weeks. Modeling lineage-to-lineage fluctuations in cell survival revealed a rare subpopulation of drug-tolerant cells that existed even before treatment (Chang et al., 2021). Interestingly, the transient heritability of the tolerant state significantly differed between cell lines ranging from six generations to only two generations (Figure 5).
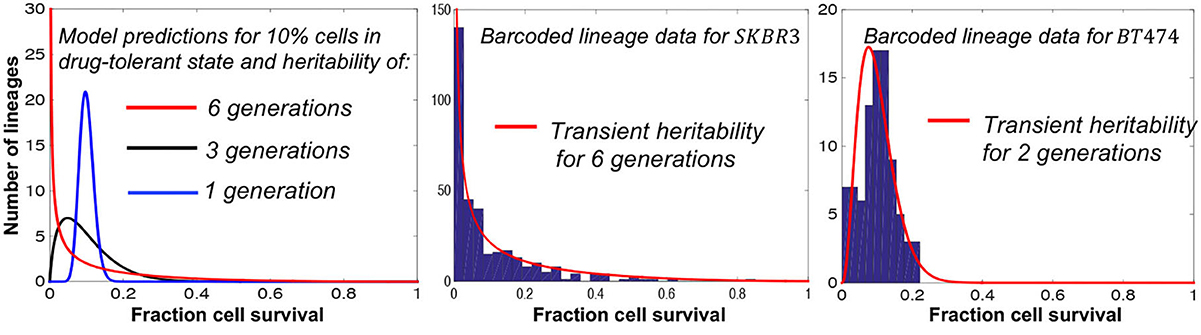
Figure 5. Fluctuation assay on barcoded breast cancer cell lines shows different plasticities for the drug-tolerant state. Left: The model predicted fluctuations for different transient heritabilities of the drug-tolerant state. Right: The model fits lineage-to-lineage fluctuations in the fraction of cells surviving targeted therapy for two different cell lines (Chang et al., 2021).
Along the same theme of reversible non-genetic switching between states, working with a human epithelial cell line time-lapse microscopy to trace single cells within a population to derive lineage trees, these cells were subsequently challenged with microbial signatures (Clark et al., 2021). Data showed a digital all-or-none immune response at the single-cell level, with a subpopulation of cells (≈15%) responding to the challenge (Figure 6). Modeling the number of responders across lineages revealed reversible switching between the responder and non-responder cell states that occurred even before exposure to microbial signatures and was mechanistically mapped to dynamic epigenetic regulation of the toll-like receptor 2 (TLR2) (Clark et al., 2021). Similar digital responses in subpopulations were also seen in primary organoids with individual cells showing switch-like epigenetic modifications of the TLR2 locus (Clark et al., 2021). Cell density can alter the fraction of responding cells, and the fluctuation test was recently used to show that this phenomenon arises from a higher switching rate into responder cell states at lower densities, indicating a form of immune quorum sensing (Antonioli et al., 2018; Van Eyndhoven et al., 2021, 2022).
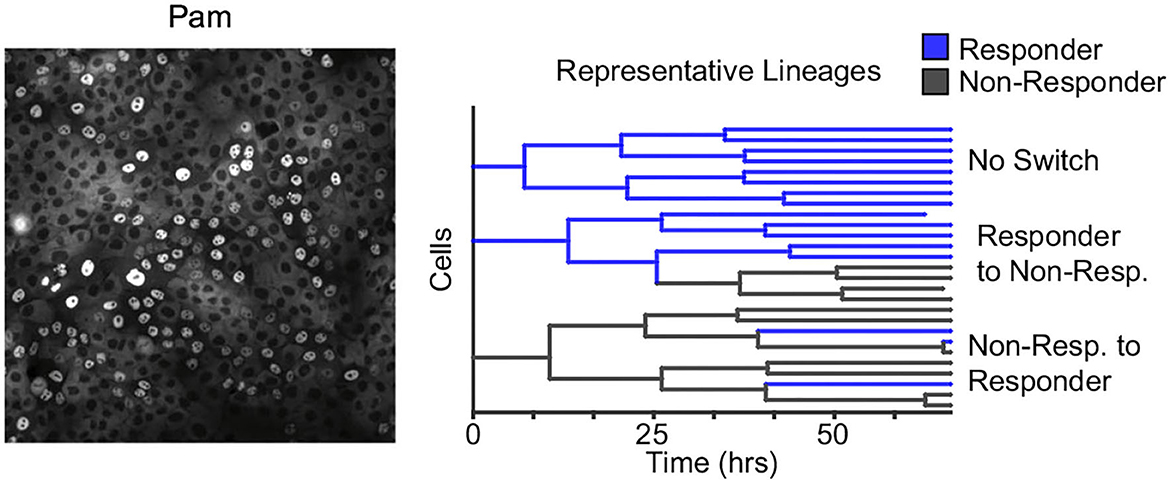
Figure 6. Reversible epigenetic states regulate the innate immune response of single epithelial cells. Left: Human epithelial cells when challenged with bacterial microbe-associated molecular patterns (pam) show a digital all-or-nothing activation of NF-κB at the single-cell level. Right: The fluctuation test was performed by tracking single-cell derived lineages using time-lapse microscopy and then challenged with pam. The response of single cells was highly correlated within lineages. Subsequent modeling revealed switching between responder and non-responder cell states that in turn are controlled by epigenetic regulation at the promoters of toll-like receptors (Clark et al., 2021).
The fluctuation-test approach has also been used to study the reactivation of human immunodeficiency virus (HIV) from latency in T cells (Lu et al., 2021). Latency refers to a dormant state of HIV inside infected cells, and these cells can evade drug treatment, creating a barrier to curing patients (Han et al., 2007; Singh and Weinberger, 2009; Razooky et al., 2015). This study used a specific T-cell line (Jurkat cells) that has a single copy of HIV integrated at the same genome location in all cells. While it is well-known that exposing latent cells to latency reversal agents (LRA) leads to a viral reactivation in a subpopulation (despite cells being isoclonal and receiving the same LRA dosage), it remains a mystery if these cells arise randomly or are a result of a pre-treatment cell state. Performing the fluctuation test at 5 weeks of colony expansion revealed large colony-to-colony fluctuation in the fraction of reactivation cells that was significantly higher than the noise control (Figure 7). However, by 10 weeks of colony growth, the inter-colony fluctuations had attenuated to noise control levels. These data from the fluctuation assay performed for different duration of colony growth were consistent with a model of pre-treatment switching of single cells between the unresponsive and responsive states, with cells residing in the latter state for several weeks (Lu et al., 2021). The long-timescale switching found here indicates an epigenetic mechanism where slow turnover of histone marks at the HIV integration site drives all-or-none reactivation in individual cells. Consistent with this finding, previous studies implicated HIV-promoter methylation patterns as key determinants of viral reactivation in response to LRAs (Blazkova et al., 2009).
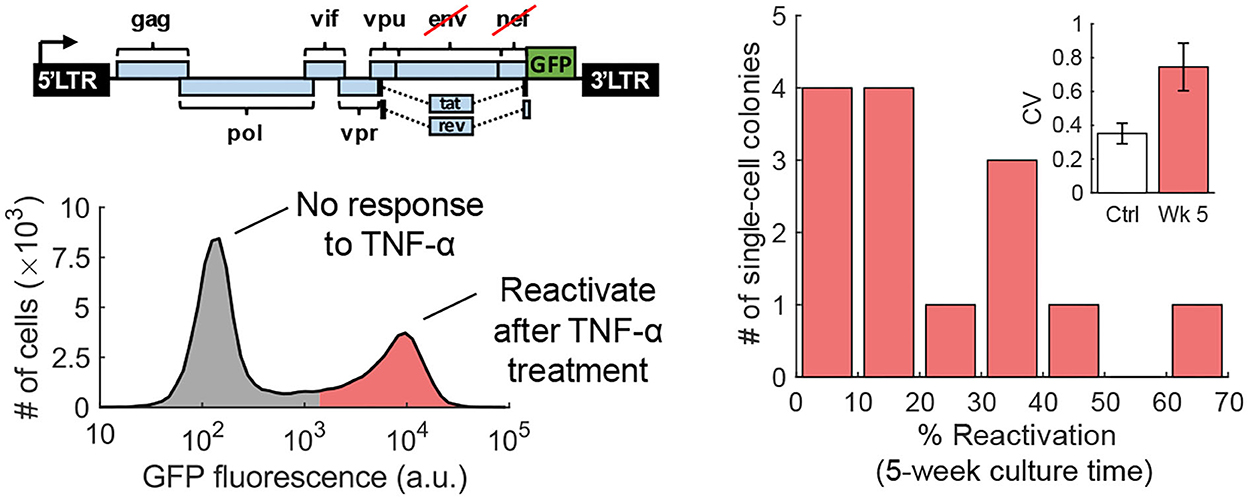
Figure 7. Transient cell state regulates HIV reactivation from latency. Left: An isoclonal population of Jurkat cells with a latently infected GFP-tagged HIV-1 gene circuit (one copy of the virus at the same integration site in all cells) when uniformly stimulated with TNF-α causes viral reactivation in a fraction of cells. Right: The fluctuation test was performed by first growing single Jurkat cells into colonies and then treating them with TNF-α. The fraction of reactivated cells showed a skewed distribution across colonies consistent with pre-exposure responsive and unresponsive cell states that reversibly switch within several weeks (Lu et al., 2021).
4. Conclusion
The original Luria–Delbrück fluctuation experiment done 80 years ago revolutionized the field of bacterial genetics and led to an innovative method for estimating mutation rates. In this study, we reviewed a generalization of this approach to elucidate the transient heritability of cellular states, which has important implications for both biology and medicine. The approach relies on using the inter-colony variation, as quantified analytically using CVf through the various approximations in Equations (5), (10), and (13), together with a priori knowledge on the average of fraction cells in different states in Equation (1), to estimate the interconversion rate between two given cellular states. Thus, the kinetics of reversible switching can be identified from the magnitude of fluctuations using a single endpoint measurement. In many cases, more information can be acquired by repeating the fluctuation test at different time points of colony expansion (Lu et al., 2021) or the lineage tracking of cells in an expanding colony to know the exact kinship between cells (Veening et al., 2008b; Hormoz et al., 2016; Wheat et al., 2020; Clark et al., 2021; Vertti-Quintero et al., 2022). This can be used to further test the model predictions (for example, the colony-to-colony variation in f(t) monotonically decreasing over time) and expand the model by relaxing many of the assumptions made in its formulation. We discussed this latter point in more detail below.
While much of this analytical study used simplifying assumptions, it can be extended along several fronts:
1. Considering different proliferative potential of cellular states, which is especially important given that drug persisters can in some cases grow significantly slower than drug-sensitive cells (Balaban et al., 2004; Maisonneuve et al., 2013; Feng et al., 2014; Meouche et al., 2016; Fisher et al., 2017; Manuse et al., 2021).
2. Inclusion of density-dependent effects where transition rates themselves depend on the local cell density. For example, the rates k1 and k2 can depend on the fraction of cells in State 2 capturing some form of quorum sensing, which is well-known in microbial populations and also reported in immune cells (Antonioli et al., 2018; Van Eyndhoven et al., 2022).
3. Allowing for irreversible transformations, as seen in our work with melanoma cells, where reversible drug-tolerant cells proceed irreversibly to a resistant phenotype upon drug exposure (Shaffer et al., 2017), and some recent work has been done in this direction (Bokes and Singh, 2021).
4. Modeling a continuum of cell states using a partial differential equation-based framework, with the inference of forward and backward diffusion rates based on the generalized fluctuation test.
5. More realistic models of colony growth are needed where the cell-cycle times themselves have multi-generational memory. Preliminary study suggests that this can lead to very different stochastic variations of colony sizes as compared with simplistic approaches where cell-cycle times are considered independent and identically distributed random variables (Nieto et al., 2022).
Relaxing many of these assumptions will result in nonlinear stochastic dynamical systems, which may not be amenable to analytical approaches. In such cases, exact stochastic simulations of the underlying processes can be used to obtain the statistical distributions that can then be fitted to data using a maximum-likelihood approach to infer model parameters.
An important generalization of this approach will be to infer switching topologies and rates for an arbitrary number of cell states. There is an increasing body of research that uses expression profiles to classify individual cells in different cell states (Trapnell, 2015; Hormoz et al., 2016; Hejna et al., 2017; Lieberman et al., 2018; Neftel et al., 2019; Andreatta et al., 2021; Li et al., 2021; Shao et al., 2021). While these methods only provide a static distribution of cell states, fluctuation analysis can shed rich insights into the plasticity of states by characterizing dynamical transitions between them. To appreciate the complexity of the problem, note that, for n cell states, there are 2n(n−1) possible network topologies. While n = 2 yields four topologies (reversible switching, irreversible transitions between either state, and the trivial case of no transitions), this number increases quite sharply to 64 (n = 3) and 4,096 topologies (n = 4). With multiple cell states, the data obtained from the fluctuation assay are also richer—one measures both the variances and covariances in the fraction of different states across colonies. Given the data from a fluctuation assay, mathematical tools can combine stochastic modeling of state transition with likelihood-based methods to rank all plausible topologies based on their likelihood of occurrence with corresponding transition rates. These predictions can then be used to design further experiments to discriminate between the most probable topologies and to validate the model by sorting cells in a given state and following the redistribution of states over time.
Cognizant of the fact that the fluctuation test requires the expansion of cells, its application in human cells has primarily been in well-established cell line model systems uncovering fundamental questions in cancer biology, immunology, and virology. However, we believe that the true potential of this generalized fluctuation test is in microbial systems, where (unlike mammalian cells) cells are readily grown from single cells with relatively fast doubling times, and there is a longstanding tradition of performing the Luria–Delbrück experiment. Working in this direction, we currently have several ongoing collaborations probing antibiotic tolerance across bacterial species (Mycobacterium tuberculosis, Vibrio cholerae, Enterobacter cloacae, and Salmonella enterica), and a recent study characterizes the transient priming of bacterial cells even before lethal antibiotic stress (Hossain et al., 2022).
The rapid growth of microbial cells allows for an ingenious experiment to validate the transient heritability of cellular states. More specifically, each single-cell colony is split into two colonies, and one split is assayed for survival to antibiotics, and the other split is assayed after dilution and further growth for several generations. If antibiotic tolerance is transient, then the correlation in bacterial survival between the initial and later splits will weaken as the second split is allowed to grow for more generations before treatment. Moreover, considering several splits of the same population can allow for multiplexing responses to different stress conditions. For example, two splits of the same colony can be treated with two different classes of antibiotics, and the correlation in fraction survival across colonies can point toward similar or different biochemical pathways at work. Finally, one split (both post-treatment and pre-treatment) can also be used for proteomic/transcriptomic/metabolomic studies, which can aid in a mechanistic mapping of stress-tolerant states to expression programs using the MemorySeq approach (Shaffer et al., 2020). In summary, building up on this transformative fluctuation-based tool combined with mechanistic stochastic modeling of underlying gene networks can significantly advance the field of single-cell biology and have tremendous applications across life science disciplines.
Author contributions
AS and MS-A contributed to the writing and revision of this review article. All authors contributed to the article and approved the submitted version.
Funding
AS acknowledges support from the NIH-NIGMS grant R01GM124446.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abranches, E., Guedes, A. M. V., Moravec, M., Maamar, H., Svoboda, P., Raj, A., et al. (2014). Stochastic nanog fluctuations allow mouse embryonic stem cells to explore pluripotency. Development 141, 2770–2779. doi: 10.1242/dev.108910
Acar, M., Mettetal, J. T., and van Oudenaarden, A. (2008). Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 40, 471–475. doi: 10.1038/ng.110
Ackermann, M. (2015). A functional perspective on phenotypic heterogeneity in microorganisms. Nat. Rev. Microbiol. 13, 497–508. doi: 10.1038/nrmicro3491
Andreatta, M., Corria-Osorio, J., Müller, S., Cubas, R., Coukos, G., and Carmona, S. J. (2021). Interpretation of t cell states from single-cell transcriptomics data using reference atlases. Nat. Commun. 12, 1–19. doi: 10.1038/s41467-021-23324-4
Antonioli, L., Blandizzi, C., Pacher, P., Guilliams, M., and Haskó, G. (2018). Quorum sensing in the immune system. Nat. Rev. Immunol. 18, 537–538. doi: 10.1038/s41577-018-0040-4
Balaban, N., Merrin, J., Chait, R., Kowalik, L., and Leibler, S. (2004). Bacterial persistence as a phenotypic switch. Science 305, 1622–1625. doi: 10.1126/science.1099390
Balázsi, G., van Oudenaarden, A., and Collins, J. J. (2014). Cellular decision making and biological noise: From microbes to mammals. Cell 144, 910–925. doi: 10.1016/j.cell.2011.01.030
Battich, N., Stoeger, T., and Pelkmans, L. (2015). Control of transcript variability in single mammalian cells. Cell 163, 1596–1610. doi: 10.1016/j.cell.2015.11.018
Bishop, A. L., Rab, F. A., Sumner, E. R., and Avery, S. V. (2007). Phenotypic heterogeneity can enhance rare-cell survival in stress-sensitive yeast populations. Mol. Microbiol. 63, 507–520. doi: 10.1111/j.1365-2958.2006.05504.x
Blazkova, J., Trejbalova, K., Gondois-Rey, F., Halfon, P., Philibert, P., Guiguen, A., et al. (2009). Cpg methylation controls reactivation of hiv from latency. PLoS Pathog. 5, e1000554. doi: 10.1371/journal.ppat.1000554
Bokes, P., and Singh, A. (2021). A modified fluctuation test for elucidating drug resistance in microbial and cancer cells. Eur. J. Control 62, 130–135. doi: 10.1016/j.ejcon.2021.06.018
Bowling, S., Sritharan, D., Osorio, F. G., Nguyen, M., Cheung, P., Rodriguez-Fraticelli, A., et al. (2020). An engineered crispr-cas9 mouse line for simultaneous readout of lineage histories and gene expression profiles in single cells. Cell 181, 1410–1422. doi: 10.1016/j.cell.2020.04.048
Brandt, L., Cristinelli, S., and Ciuffi, A. (2020). Single-cell analysis reveals heterogeneity of virus infection, pathogenicity, and host responses: HIV as a pioneering example. Ann. Rev. Virol. 7, 333–350. doi: 10.1146/annurev-virology-021820-102458
Chalancon, G., Ravarani, C. N., Balaji, S., Martinez-Arias, A., Aravind, L., Jothi, R., et al. (2012). Interplay between gene expression noise and regulatory network architecture. Trends Genet. 28, 221–232. doi: 10.1016/j.tig.2012.01.006
Chang, C. A., Jen, J., Jiang, S., Sayad, A., Mer, A. S., Brown, K. R., et al. (2021). Ontogeny and vulnerabilities of drug-tolerant persisters in HER2+ breast cancer. Cancer Discov. 12, 1022–1045. doi: 10.1101/2020.08.28.273029
Chang, H. H., Hemberg, M., Barahona, M., Ingber, D. E., and Huang, S. (2008). Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature 453, 544–547. doi: 10.1038/nature06965
Clark, H. R., McKenney, C., Livingston, N. M., Gershman, A., Sajjan, S., Chan, I. S., et al. (2021). Epigenetically regulated digital signaling defines epithelial innate immunity at the tissue level. Nat. Commun. 12, 1–13. doi: 10.1038/s41467-021-22070-x
Dar, R. D., Hosmane, N. N., Arkin, M. R., Siliciano, R. F., and Weinberger, L. S. (2014). Screening for noise in gene expression identifies drug synergies. Science 344, 1392–1396. doi: 10.1126/science.1250220
Doganay, S., Lee, M. Y., Baum, A., Peh, J., Hwang, S.-Y., Yoo, J.-Y., et al. (2017). Single-cell analysis of early antiviral gene expression reveals a determinant of stochastic IFNB1 expression. Integrat. Biol. 9, 857–867. doi: 10.1039/C7IB00146K
Duy, C., Li, M., Teater, M., Meydan, C., Garrett-Bakelman, F. E., Lee, T. C., et al. (2021). Chemotherapy induces senescence-like resilient cells capable of initiating aml recurrence. Cancer Discov. 11, 1542–1561. doi: 10.1158/2159-8290.CD-20-1375
Echeverria, G. V., Ge, Z., Seth, S., Zhang, X., Jeter-Jones, S., Zhou, X., et al. (2019). Resistance to neoadjuvant chemotherapy in triple-negative breast cancer mediated by a reversible drug-tolerant state. Sci. Transl. Med. 11, eaav0936. doi: 10.1126/scitranslmed.aav0936
Eldar, A., and Elowitz, M. B. (2010). Functional roles for noise in genetic circuits. Nature 467, 167–173. doi: 10.1038/nature09326
Evans, T. D., and Zhang, F. (2020). Bacterial metabolic heterogeneity: origins and applications in engineering and infectious disease. Curr. Opin. Biotechnol. 64, 183–189. doi: 10.1016/j.copbio.2020.04.007
Feng, J., Kessler, D. A., Ben-Jacob, E., and Levine, H. (2014). Growth feedback as a basis for persister bistability. Proc. Natl. Acad. Sci. U.S.A. 111, 544–549. doi: 10.1073/pnas.1320396110
Fisher, R. A., Gollan, B., and Helaine, S. (2017). Persistent bacterial infections and persister cells. Nat. Rev. Microbiol. 15, 453. doi: 10.1038/nrmicro.2017.42
Foreman, R., and Wollman, R. (2020). Mammalian gene expression variability is explained by underlying cell state. Mol. Syst. Biol. 16, e9146. doi: 10.15252/msb.20199146
Fraser, L. C., Dikdan, R. J., Dey, S., Singh, A., and Tyagi, S. (2021). Reduction in gene expression noise by targeted increase in accessibility at gene loci. Proc. Natl. Acad. Sci. U.S.A. 118, e2018640118. doi: 10.1073/pnas.2018640118
Gasch, A. P., Yu, F. B., Hose, J., Escalante, L. E., Place, M., Bacher, R., et al. (2017). Single-cell rna sequencing reveals intrinsic and extrinsic regulatory heterogeneity in yeast responding to stress. PLoS Biol. 15, e2004050. doi: 10.1371/journal.pbio.2004050
Hall, B. M., Ma, C.-X., Liang, P., and Singh, K. K. (2009). Fluctuation analysis calculator: a web tool for the determination of mutation rate using luria- delbrück fluctuation analysis. Bioinformatics 25, 1564–1565. doi: 10.1093/bioinformatics/btp253
Han, Y., Wind-Rotolo, M., Yang, H.-C., Siliciano, J. D., and Siliciano, R. F. (2007). Experimental approaches to the study of HIV-1 latency. Nat. Rev. Microbiol. 5, 95–106. doi: 10.1038/nrmicro1580
Harmange, G., Hueros, R. A. R., Schaff, D. L., Emert, B. L., Saint-Antoine, M. M., Nellore, S., et al. (2022). Disrupting cellular memory to overcome drug resistance. bioRxiv. doi: 10.1101/2022.06.16.496161
Hejna, M., Jorapur, A., Song, J. S., and Judson, R. L. (2017). High accuracy label-free classification of single-cell kinetic states from holographic cytometry of human melanoma cells. Sci. Rep. 7, 1–12. doi: 10.1038/s41598-017-12165-1
Holmes, C. M., Ghafari, M., Abbas, A., Saravanan, V., and Nemenman, I. (2017). Luria- delbrück, revisited: the classic experiment does not rule out lamarckian evolution. Phys. Biol. 14, 055004. doi: 10.1088/1478-3975/aa8230
Hormoz, S., Singer, Z. S., Linton, J. M., Antebi, Y. E., Shraiman, B. I., and Elowitz, M. B. (2016). Inferring cell-state transition dynamics from lineage trees and endpoint single-cell measurements. Cell Syst. 3, 419–433. doi: 10.1016/j.cels.2016.10.015
Hossain, T., Singh, A., and Butzin, N. C. (2022). Escherichia coli cells are primed for survival before lethal antibiotic stress. bioRxiv. doi: 10.21203/rs.3.rs-2264630/v1
Houchmandzadeh, B. (2015). General formulation of luria- delbrück distribution of the number of mutants. Phys. Rev. E 92, 012719. doi: 10.1103/PhysRevE.92.012719
Johnston, I. G., Gaal, B., das Neves, R. P., Enver, T., Iborra, F. J., and Jones, N. S. (2012). Mitochondrial variability as a source of extrinsic cellular noise. PLoS Comput. Biol. 8, e1002416. doi: 10.1371/journal.pcbi.1002416
Jones, M., Wheldrake, J., and Rogers, A. (1993). Luria- delbrück fluctuation analysis: estimating the poisson parameter in a compound poisson distribution. Comput. Biol. Med. 23, 525–534. doi: 10.1016/0010-4825(93)90099-M
Kim, K. H., and Sauro, H. M. (2012). Adjusting phenotypes by noise control. PLoS Comput. Biol. 8, e1002344. doi: 10.1371/journal.pcbi.1002344
Koch, A. L. (1982). Mutation and growth rates from luria- delbrück fluctuation tests. Mutat. Res. Fundament. Mol. Mech. Mutagenesis 95, 129–143. doi: 10.1016/0027-5107(82)90252-4
Kussell, E., and Leibler, S. (2005). Phenotypic diversity, population growth, and information in fluctuating environments. Science 309, 2075–2078. doi: 10.1126/science.1114383
Larsson, A. J., Johnsson, P., Hagemann-Jensen, M., Hartmanis, L., Faridani, O. R., Reinius, B., et al. (2019). Genomic encoding of transcriptional burst kinetics. Nature 565, 251–254. doi: 10.1038/s41586-018-0836-1
Larsson, A. J., Ziegenhain, C., Hagemann-Jensen, M., Reinius, B., Jacob, T., Dalessandri, T., et al. (2021). Transcriptional bursts explain autosomal random monoallelic expression and affect allelic imbalance. PLoS Comput. Biol. 17, e1008772. doi: 10.1371/journal.pcbi.1008772
Leeper, K., Kalhor, K., Vernet, A., Graveline, A., Church, G. M., Mali, P., et al. (2021). Lineage barcoding in mice with homing crispr. Nat. Protoc. 16, 2088–2108. doi: 10.1038/s41596-020-00485-y
Li, Y., Nowak, C. M., Pham, U., Nguyen, K., and Bleris, L. (2021). Cell morphology-based machine learning models for human cell state classification. NPJ Syst. Biol. Appl. 7, 1–9. doi: 10.1038/s41540-021-00180-y
Lieberman, Y., Rokach, L., and Shay, T. (2018). Castle-classification of single cells by transfer learning: harnessing the power of publicly available single cell rna sequencing experiments to annotate new experiments. PLoS ONE 13, e0205499. doi: 10.1371/journal.pone.0205499
Losick, R., and Desplan, C. (2008). Stochasticity and cell fate. Science 320, 65–68. doi: 10.1126/science.1147888
Lu, Y., Singh, H., Singh, A., and Dar, R. D. (2021). A transient heritable memory regulates HIV reactivation from latency. Iscience 24, 102291. doi: 10.1016/j.isci.2021.102291
Luria, S. E., and Delbrück, M. (1943). Mutations of bacteria from virus sensitivity to virus resistance. Genetics 28, 491. doi: 10.1093/genetics/28.6.491
Lyu, Z., Yang, A., Villanueva, P., Singh, A., and Ling, J. (2021). Heterogeneous flagellar expression in single salmonella cells promotes diversity in antibiotic tolerance. MBio. 12, e02374-e02321. doi: 10.1128/mBio.02374-21
Maamar, H., Raj, A., and Dubnau, D. (2007). Noise in gene expression determines cell fate in bacillus subtilis. Science 317, 526–529. doi: 10.1126/science.1140818
Magklara, A., and Lomvardas, S. (2014). Stochastic gene expression in mammals: lessons from olfaction. Trends Cell Biol. 23, 449–456. doi: 10.1016/j.tcb.2013.04.005
Maisonneuve, E., Castro-Camargo, M., and Gerdes, K. (2013). (p)ppGpp controls bacterial persistence by stochastic induction of toxin-antitoxin activity. Cell 154, 1140–1150. doi: 10.1016/j.cell.2013.07.048
Manuse, S., Shan, Y., Canas-Duarte, S. J., Bakshi, S., Sun, W.-S., Mori, H., et al. (2021). Bacterial persisters are a stochastically formed subpopulation of low-energy cells. PLoS Biol. 19, e3001194. doi: 10.1371/journal.pbio.3001194
Meouche, I. E., Siu, Y., and Dunlop, M. J. (2016). Stochastic expression of a multiple antibiotic resistance activator confers transient resistance in single cells. Sci. Rep. 6, 19538. doi: 10.1038/srep19538
Mu, P., Zhang, Z., Benelli, M., Karthaus, W. R., Hoover, E., Chen, C.-C., et al. (2017). Sox2 promotes lineage plasticity and antiandrogen resistance in tp53-and rb1-deficient prostate cancer. Science 355, 84–88. doi: 10.1126/science.aah4307
Neftel, C., Laffy, J., Filbin, M. G., Hara, T., Shore, M. E., Rahme, G. J., et al. (2019). An integrative model of cellular states, plasticity, and genetics for glioblastoma. Cell 178, 835–849. doi: 10.1016/j.cell.2019.06.024
Neuert, G., Munsky, B., Tan, R. Z., Teytelman, L., Khammash, M., and van Oudenaarden, A. (2013). Systematic identification of signal-activated stochastic gene regulation. Science 339, 584–587. doi: 10.1126/science.1231456
Nieto, C., Vargas-Garcia, C., Pedraza, J., and Singh, A. (2022). Cell size regulation and proliferation fluctuations in single-cell derived colonies. bioRxiv. doi: 10.1101/2022.07.05.498901
Norman, T. M., Lord, N. D., Paulsson, J., and Losick, R. (2013). Memory and modularity in cell-fate decision making. Nature 503, 481–486. doi: 10.1038/nature12804
Ochiai, H., Hayashi, T., Umeda, M., Yoshimura, M., Harada, A., Shimizu, Y., et al. (2020). Genome-wide kinetic properties of transcriptional bursting in mouse embryonic stem cells. Sci. Adv. 6, eaaz6699. doi: 10.1126/sciadv.aaz6699
Paryad-Zanjani, S., Saint-Antoine, M. M., and Singh, A. (2021). Optimal scheduling of therapy to delay cancer drug resistance. IFAC-PapersOnLine 54, 239–244. doi: 10.1016/j.ifacol.2021.10.262
Raha, D., Wilson, T. R., Peng, J., Peterson, D., Yue, P., Evangelista, M., et al. (2014). The cancer stem cell marker aldehyde dehydrogenase is required to maintain a drug-tolerant tumor cell subpopulation. Cancer Res. 74, 3579–3590. doi: 10.1158/0008-5472.CAN-13-3456
Raj, A., and van Oudenaarden, A. (2008). Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216–226. doi: 10.1016/j.cell.2008.09.050
Razooky, B. S., Pai, A., Aull, K., Rouzine, I. M., and Weinberger, L. S. (2015). A hardwired HIV latency program. Cell 160, 990–1001. doi: 10.1016/j.cell.2015.02.009
Rehman, S. K., Haynes, J., Collignon, E., Brown, K. R., Wang, Y., Nixon, A. M., et al. (2021). Colorectal cancer cells enter a diapause-like dtp state to survive chemotherapy. Cell 184, 226–242. doi: 10.1016/j.cell.2020.11.018
Rodriguez, J., Ren, G., Day, C. R., Zhao, K., Chow, C. C., and Larson, D. R. (2019). Intrinsic dynamics of a human gene reveal the basis of expression heterogeneity. Cell 176, 213–226. doi: 10.1016/j.cell.2018.11.026
Rodriguez-Fraticelli, A. E., Weinreb, C., Wang, S.-W., Migueles, R. P., Jankovic, M., Usart, M., et al. (2020). Single-cell lineage tracing unveils a role for tcf15 in haematopoiesis. Nature 583, 585–589. doi: 10.1038/s41586-020-2503-6
Saint-Antoine, M. M., Grima, R., and Singh, A. (2022). A fluctuation-based approach to infer kinetics and topology of cell-state switching. bioRxiv. doi: 10.1101/2022.03.30.486492
Saint-Antoine, M. M., and Singh, A. (2022). Moment-based estimation of state-switching rates in cell populations. bioRxiv. doi: 10.1101/2022.01.06.475260
Sampaio, N. M. V., and Dunlop, M. J. (2020). Functional roles of microbial cell-to-cell heterogeneity and emerging technologies for analysis and control. Curr. Opin. Microbiol. 57, 87–94. doi: 10.1016/j.mib.2020.08.002
Sarkar, S. (1991). Haldane's solution of the luria-delbrück distribution. Genetics 127, 257. doi: 10.1093/genetics/127.2.257
Schuh, L., Saint-Antoine, M., Sanford, E. M., Emert, B. L., Singh, A., Marr, C., et al. (2020). Gene networks with transcriptional bursting recapitulate rare transient coordinated high expression states in cancer. Cell Syst. 10, 363–378. doi: 10.1016/j.cels.2020.03.004
Shaffer, S. M., Dunagin, M. C., Torborg, S. R., Torre, E. A., Emert, B., Krepler, C., et al. (2017). Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance. Nature 546, 431–435. doi: 10.1038/nature22794
Shaffer, S. M., Emert, B. L., Hueros, R. A. R., Cote, C., Harmange, G., Schaff, D. L., et al. (2020). Memory sequencing reveals heritable single-cell gene expression programs associated with distinct cellular behaviors. Cell 182, 947–959. doi: 10.1016/j.cell.2020.07.003
Shao, X., Yang, H., Zhuang, X., Liao, J., Yang, P., Cheng, J., et al. (2021). scdeepsort: a pre-trained cell-type annotation method for single-cell transcriptomics using deep learning with a weighted graph neural network. Nucleic Acids Res. 49, e122-e122. doi: 10.1093/nar/gkab775
Sharma, S. V., Lee, D. Y., Li, B., Quinlan, M. P., Takahashi, F., Maheswaran, S., et al. (2010). A chromatin-mediated reversible drug-tolerant state in cancer cell subpopulations. Cell 141, 69–80. doi: 10.1016/j.cell.2010.02.027
Shu, C., Chatterjee, A., Hu, W.-S., and Ramkrishna, D. (2013). Role of intracellular stochasticity in biofilm growth. Insights from population balance modeling. PLoS ONE 8, e79196. doi: 10.1371/journal.pone.0079196
Singh, A., Razooky, B., Cox, C. D., Simpson, M. L., and Weinberger, L. S. (2010). Transcriptional bursting from the HIV-1 promoter is a significant source of stochastic noise in HIV-1 gene expression. Biophys. J. 98:L32-L34. doi: 10.1016/j.bpj.2010.03.001
Singh, A., and Weinberger, L. S. (2009). Stochastic gene expression as a molecular switch for viral latency. Curr. Opin. Microbiol. 12, 460–466. doi: 10.1016/j.mib.2009.06.016
SoRelle, E. D., Dai, J., Bonglack, E. N., Heckenberg, E. M., Zhou, J. Y., Giamberardino, S. N., et al. (2021). Single-cell rna-seq reveals transcriptomic heterogeneity mediated by host-pathogen dynamics in lymphoblastoid cell lines. Elife 10, e62586. doi: 10.7554/eLife.62586
St-Pierre, F., and Endy, D. (2008). Determination of cell fate selection during phage lambda infection. Proc. Natl. Acad. Sci. U.S.A. 105, 20705–20710. doi: 10.1073/pnas.0808831105
Süel, G. M., Garcia-Ojalvo, J., Liberman, L. M., and Elowitz, M. B. (2006). An excitable gene regulatory circuit induces transient cellular differentiation. Nature 440, 545–550. doi: 10.1038/nature04588
Thompson, R. L., Preston, C. M., and Sawtell, N. M. (2009). De novo synthesis of VP16 coordinates the exit from HSV latency in vivo. PLoS Pathog. 5, e1000352. doi: 10.1371/journal.ppat.1000352
Topolewski, P., Zakrzewska, K. E., Walczak, J., Nienałtowski, K., Müller-Newen, G., Singh, A., et al. (2022). Phenotypic variability, not noise, accounts for most of the cell-to-cell heterogeneity in ifn-γ and oncostatin m signaling responses. Sci. Signal. 15, eabd9303. doi: 10.1126/scisignal.abd9303
Torres-Padilla, M. E., and Chambers, I. (2014). Transcription factor heterogeneity in pluripotent stem cells: a stochastic advantage. Development 141, 2173–2181. doi: 10.1242/dev.102624
Trapnell, C. (2015). Defining cell types and states with single-cell genomics. Genome Res. 25, 1491–1498. doi: 10.1101/gr.190595.115
Umkehrer, C., Holstein, F., Formenti, L., Jude, J., Froussios, K., Neumann, T., et al. (2021). Isolating live cell clones from barcoded populations using crispra-inducible reporters. Nat. Biotechnol. 39, 174–178. doi: 10.1038/s41587-020-0614-0
Van Eyndhoven, L. C., Singh, A., and Tel, J. (2021). Decoding the dynamics of multilayered stochastic antiviral ifn-i responses. Trends Immunol. 42, 824–839. doi: 10.1016/j.it.2021.07.004
Van Eyndhoven, L. C., Verberne, V. P., Bouten, C. V., Singh, A., and Tel, J. (2022). Transiently heritable fates and quorum sensing drive early ifn-i response dynamics. bioRxiv. doi: 10.1101/2022.09.11.507479
Vasdekis, A. E., and Singh, A. (2021). Microbial metabolic noise. WIREs Mech. Dis. 13, e1512. doi: 10.1002/wsbm.1512
Veening, J.-W., Smits, W. K., and Kuipers, O. P. (2008a). Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 62, 193–210. doi: 10.1146/annurev.micro.62.081307.163002
Veening, J.-W., Stewart, E. J., Berngruber, T. W., Taddei, F., Kuipers, O. P., and Hamoen, L. W. (2008b). Bet-hedging and epigenetic inheritance in bacterial cell development. Proc. Natl. Acad. Sci. U.S.A. 105, 4393–4398. doi: 10.1073/pnas.0700463105
Vertti-Quintero, N., Levien, E., Poggi, L., Amir, A., Richard, G.-F., and Baroud, C. N. (2022). Single-cell microfluidic analysis unravels individual cellular fates during double-strand break repair. bioRxiv. doi: 10.1101/2022.03.10.483811
Wheat, J. C., Sella, Y., Willcockson, M., Skoultchi, A. I., Bergman, A., Singer, R. H., et al. (2020). Single-molecule imaging of transcription dynamics in somatic stem cells. Nature 583, 431–436. doi: 10.1038/s41586-020-2432-4
Zheng, Q. (1999). Progress of a half century in the study of the luria- delbrück distribution. Math. Biosci. 162, 1–32. doi: 10.1016/S0025-5564(99)00045-0
Keywords: fluctuation test, cell-state transitions, transient memory, cancer drug resistance, phenotypic heterogeneity, stochastic expression
Citation: Singh A and Saint-Antoine M (2023) Probing transient memory of cellular states using single-cell lineages. Front. Microbiol. 13:1050516. doi: 10.3389/fmicb.2022.1050516
Received: 21 September 2022; Accepted: 22 December 2022;
Published: 07 February 2023.
Edited by:
Hanna Salman, University of Pittsburgh, United StatesReviewed by:
Yuichi Wakamoto, The University of Tokyo, JapanAriel Amir, Harvard University, United States
Copyright © 2023 Singh and Saint-Antoine. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abhyudai Singh,  YWJzaW5naEB1ZGVsLmVkdQ==
YWJzaW5naEB1ZGVsLmVkdQ==
 Abhyudai Singh
Abhyudai Singh Michael Saint-Antoine
Michael Saint-Antoine