Investigating the Physical Effects in Bacterial Therapies for Avascular Tumors

Tumor-targeting bacteria elicit anticancer effects by infiltrating hypoxic regions, releasing toxic agents and inducing immune responses. Although current research has largely focused on the influence of chemical and immunological aspects on the mechanisms of bacterial therapy, the impact of physical effects is still elusive. Here, we propose a mathematical model for the anti-tumor activity of bacteria in avascular tumors that takes into account the relevant chemo-mechanical effects. We consider a time-dependent administration of bacteria and analyze the impact of bacterial chemotaxis and killing rate. We show that active bacterial migration toward tumor hypoxic regions provides optimal infiltration and that high killing rates combined with high chemotactic values provide the smallest tumor volumes at the end of the treatment. We highlight the emergence of steady states in which a small population of bacteria is able to constrain tumor growth. Finally, we show that bacteria treatment works best in the case of tumors with high cellular proliferation and low oxygen consumption.

1. Introduction

Cancers display huge variability between different patients and even in the same patient. Nonetheless, cancer cells share a finite set of hallmarks such as sustained proliferation, invasion and metabolic reprogramming, which shape their behavior in solid tumors (Hanahan and Weinberg, 2011). Among other hallmarks, tumor cells are known to recruit new blood vessels to sustain their proliferation, in a process known as tumor angiogenesis (Folkman, 1971). This neovasculature is generally altered in terms of architecture and morphology of the vessels, leading to poor perfusion of certain areas of the tumor (Carmeliet and Jain, 2000). Hypoxic regions are thus created and maintained during tumor development, concurring to the progression of cancer cells toward malignant phenotypes (Vaupel and Mayer, 2007). Moreover, low nutrient levels can lead to cell quiescence, a situation in which tumor cells delay metabolic activities and become less sensitive to standard chemotherapies (Challapalli et al., 2017). Such hypo-perfused areas are generally associated with poor patient outcome but, on the other hand, could be exploited for tumor targeting (Wilson and Hay, 2011). The same hypoxic areas provide indeed a niche for bacteria to colonize the tumor and exert a therapeutic action (Forbes, 2010; Zhou et al., 2018). The use of bacteria for cancer therapy dates back hundreds of years, with doctors reporting tumor regression in several patients (Kramer et al., 2018). However, such treatments also caused some fatalities and the limited understanding of the therapeutic mechanisms of action shifted research efforts toward other strategies - especially radiotherapy (Kramer et al., 2018). In the last few years the use of live bacteria for cancer treatment has regained interest, and several bacterial strains have been tested in animal models and even advanced to clinical trials (Torres et al., 2018). Nevertheless, clinical development of such therapies is still facing significant issues due to infection-associated toxicities and incomplete knowledge of infection dynamics (Kramer et al., 2018; Zhou et al., 2018). As much research was focused on the immune responses after bacteria administration, a clear picture of the interaction between cancer and bacterial cells is still lacking.

Mathematical modeling emerges as a promising candidate to assist the understanding of bacterial therapy mechanism of action in cancer. Mathematical models have been applied in the context of cancer to elucidate its progression and treatment (Byrne, 2010; Altrock et al., 2015). Recent examples combining experimental and modeling work in bacterial therapies are given in Kasinskas and Forbes (2006), Jean et al. (2014), Hatzikirou et al. (2017), and Suh et al. (2018), featuring in vitro as well in vivo experiments.

Here we describe a mathematical model for bacteria-based cancer therapy within avascular tumors, focusing on the influence of physical effects on therapy outcomes. Such effects are present in every biological system but are often concealed by the complexity of the interactions between molecular and cellular players. Here, we show through a simple mathematical model that these effects take an important part in bacterial therapies and are able to influence their outcomes. The model is formulated in the context of mixture theory, a framework with a long history of applications to biological problems—see for example Ambrosi and Preziosi (2002); Breward et al. (2001, 2002, 2003); Byrne and Preziosi (2003); Chaplain et al. (2006); Preziosi and Tosin (2009) and the recent reviews of Siddique et al. (2017) and Pesavento et al. (2017). Our aim is to evaluate the impact of bacterial chemotaxis and anti-tumor activity on cancer cells, using spheroids as a prototype of avascular tumors. We consider bacterial administration after full formation of the spheroid, when hypoxic areas are present. We describe the effects of the treatment on the behavior of the spheroid constituents, e.g., tumor cells and bacteria volume fractions, at different time points and over the spheroid radius.

The remainder of the paper is organized as follows. In section 2, we describe the mathematical model and its derivation. In section 3 we present model results, analyzing the impact of different model parameters. Finally, in section 4 we discuss the biological implications of the results and suggest new research directions.

2. Materials and Methods

We propose a mathematical model describing the impact of bacterial cells on tumor spheroid growth. The model is based on mixture theory, a continuum theory that allows to describe the chemo-mechanical interactions between different tissue components. We follow the approach discussed in Preziosi (2003) and Byrne (2012) and, specifically, adapt the derivation in Boemo and Byrne (2019) to our problem. In the following we present the final form of the equations, leaving the full derivation in the Supplementary Information.

We describe the tumor as being composed of three main constituents (or phases in the language of mixture theory): tumor cells (TCs), bacteria and extracellular material. The variables referring to these quantities will be identified by the indexes c, b, and f, respectively. We also consider the presence of a nutrient, i.e., oxygen, diffusing over the spheroid domain. The model equations are derived by applying conservation of mass and linear momentum to each phase, and enforcing the saturation constraint (i.e., all the space in the spheroid is occupied by the phases, there are no voids). Then, we impose suitable assumptions regarding the mechanical properties of the model constituents and their interaction terms.

2.1. Model Equations

In the following we will be interested in the case of tumor spheroids, for which the assumption of spherical symmetry applies. The problem reduces to the set of Partial Differential Equations (PDEs):

$\begin{array}{l}\frac{\partial {\varphi }_{\text{c}}}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left\{r^2\left[D_{\text{c}}(1-{\varphi }_{\text{c}})\frac{\partial {\varphi }_{\text{c}}}{\partial r}-D_{\text{b}}{\varphi }_{\text{c}}\frac{\partial {\varphi }_{\text{b}}}{\partial r}-\chi {\varphi }_{\text{c}}{\varphi }_{\text{b}}\frac{\partial n}{\partial r}\right]\right\}\\ +S_{\text{c}},& (1)\end{array}$

$\begin{array}{l}\frac{\partial {\varphi }_{\text{b}}}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\{r^2[D_{\text{b}}\left(1-{\varphi }_{\text{b}}\right)\frac{\partial {\varphi }_{\text{b}}}{\partial r}-D_{\text{c}}{\varphi }_{\text{b}}\frac{\partial {\varphi }_{\text{c}}}{\partial r}\\ +\chi {\varphi }_{\text{b}}\left(1-{\varphi }_{\text{b}}\right)\frac{\partial n}{\partial r}]\}+S_{\text{b}},& (2)\end{array}$

$\begin{array}{ll}\frac{\partial n}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2{D}_{\text{n}}\frac{\partial n}{\partial r}\right)+S_{\text{n}}.& (3)\end{array}$

Here, ϕ_c, ϕ_c, and n are the tumor cell and bacteria volume fractions and normalized nutrient concentration, respectively. These quantities depend on the radial coordinate r ∈ [0, R] and time t ∈ [0, t_f]. In addition, D_i are the phases motility coefficients (i = c,b), D_n the nutrient diffusion coefficient, and χ the bacterial chemotactic coefficient. The mass exchange terms S_i (i = c,b,n), regulating the transfer of mass between the different components, will be detailed in the next subsection. Note that we do not solve explicitly for ϕ_f (i.e., the volume fraction of extracellular material) since this quantity can be obtained as ϕ_f = 1−ϕ_c−ϕ_b due to the saturation constraint (see the Supplementary Information). We model growth of the spheroid as a free-boundary problem, in which the outer tumor radius r = R(t) moves with the same velocity as the TC phase,

$\begin{array}{ll}\frac{dR}{dt}=v_{\text{c}}(R,t)=D_{\text{b}}\frac{\partial {\varphi }_{\text{b}}}{\partial r}+D_{\text{c}}\left(1-\frac{1}{{\varphi }_{\text{c}}}\right)\frac{\partial {\varphi }_{\text{c}}}{\partial r}+\chi {\varphi }_{\text{b}}\frac{\partial n}{\partial r}{|}_{r=R}.& (4)\end{array}$

Finally, we define a set of boundary and initial conditions to close the differential problem in Equations (1)–(3). Due to the problem symmetry no-flow boundary conditions are enforced at the spheroid center, whereas we fix the values of TC volume fraction, bacterial volume fraction and normalized nutrient concentration on the spheroid boundary:

$\begin{array}{ll}{\partial }_r{\varphi }_{\text{c}}={\partial }_r{\varphi }_{\text{b}}={\partial }_{r}n=0,r=0& (5)\end{array}$

$\begin{array}{ll}{\varphi }_{\text{c}}={\varphi }_{\text{c}0},{\varphi }_{\text{b}}={\varphi }_{\text{b}0},n=1,r=R(t).& (6)\end{array}$

We assume a uniform initial tumor volume fraction ϕ_c0 = 0.8 across the spheroid (Byrne and Preziosi, 2003) and, to model bacteria administration, we consider a time dependent value for the bacterial volume fraction at the spheroid outer radius:

$\begin{array}{ll}{\varphi }_{\text{b}}=\{\begin{array}{ll}0,& \text{for }0\le t<t_0\\ {\varphi }_{\text{b}0},& \text{for }{t}_0\le t<t_{\text{a}}\\ 0,& \text{for }{t}_{\text{a}}\le t\le t_{\text{f}},\end{array}& (7)\end{array}$

where ϕ_b0 is the administered volume fraction of bacteria, t₀ is the time of administration and t_a its duration. Regarding the initial conditions, we consider a spheroid devoid of bacteria and displaying a uniform TC volume fraction and nutrient concentration over its radius:

$\begin{array}{ll}{\varphi }_{\text{c}}(r,0)={\varphi }_{\text{c}0},{\varphi }_{\text{b}}=0,n=1.& (8)\end{array}$

Finally, we prescribe an initial spheroid radius, i.e., R(0) = 90μm. The equations of the model are discretized through the Finite Element Method and solved using the commercial software COMSOL Multiphysics (COMSOL AB, 2019).

2.2. Choice of Mass Exchange Terms

To formulate the mass exchange terms in Equations (1)–(3) we assume the following assumptions (see Figure 1):

A1 TCs proliferate when oxygen is available. As soon as the latter decreases below a critical threshold, they stop proliferating and start necrosis (Chaplain et al., 2006; Gerlee and Anderson, 2007; Agosti et al., 2018).

A2 Bacteria compete with TCs for space and exert an anti-tumor effect by a variety of mechanisms (e.g., by realizing toxins and therapeutic agents, or stimulating an immune response) (Forbes, 2010; Osswald et al., 2015; Torres et al., 2018; Zhou et al., 2018).

A3 Bacteria die when oxygen is above a critical threshold and thrive in hypoxic conditions (anaerobic bacteria) (Toley and Forbes, 2011; Osswald et al., 2015; Phaiboun et al., 2015).

A4 TCs consume oxygen provided by the culture medium (Matzavinos et al., 2009; Grimes et al., 2014).

FIGURE 1

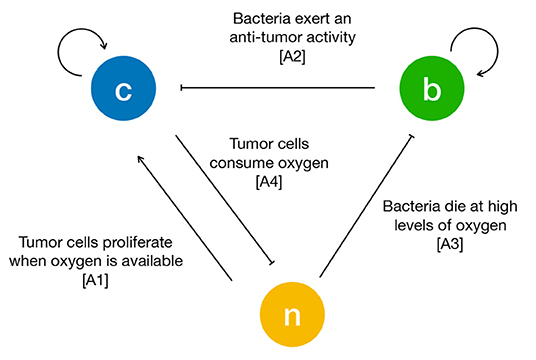
Figure 1. Schematic of the interactions between tumor cells (c), bacteria (b) and oxygen (n). The arrows are drawn according to the biological hypotheses detailed in the main text.

The resulting mass exchange terms read:

$\begin{array}{ll}{S}_{\text{c}}={\gamma }_{\text{c}}{\varphi }_{\text{c}}\frac{{\varphi }_{\text{f}}}{{\varphi }_{\text{f}0}}{H}\left(\frac{n}{n_{\text{cr}}}-1\right)-{\delta }_{\text{c}}{\varphi }_{\text{c}}{H}\left(1-\frac{n}{n_{\text{cr}}}\right)-\kappa {\varphi }_{\text{c}}{\varphi }_{\text{b}},& \left(9\right)\end{array}$

$\begin{array}{ll}{S}_{\text{b}}={\gamma }_{\text{b}}{\varphi }_{\text{b}}\frac{{\varphi }_{\text{f}}}{{\varphi }_{\text{f}0}}{H}\left(1-\frac{n}{n_{\text{cr}}}\right)-{\delta }_{\text{b}}{\varphi }_{\text{b}}{H}\left(\frac{n}{n_{\text{cr}}}-1\right),& \left(10\right)\end{array}$

$\begin{array}{ll}{S}_{\text{n}}=-{\delta }_{\text{n}}{\varphi }_{\text{c}}n.& (11)\end{array}$

Here γ_i and δ_i are the proliferation and death rate of the i-th phase respectively (i = c, b), whereas δ_n is the oxygen consumption rate. In addition, ϕ_f0 is the initial volume fraction of extracellular material and we indicate with ${H}(·)$ a smooth version of the step function, and with n_cr the critical oxygen value below which hypoxic conditions develop. Finally, we do not consider a specific form for the anti-tumor effect of bacteria and introduce an effective TC killing rate κ in the equation for S_c.

2.3. Model Parametrization

The parameters used in the model simulations are reported in Table 1. In the following we will compare model results with a set of published experiments on the U87 glioma cell line (Mascheroni et al., 2016). Colombo and colleagues (Colombo et al., 2015) estimated cell motility for glioma cells in the brain to be in the range [0.16, 0.5] mm²d⁻¹. Since we deal with in vitro experiments where cells experience less constraints with respect to tissues, we assume the largest value in the range for the motility coefficient D_c. We take the TC proliferation rate from the available data provided from the Bioresource Core Facility of the Physical Sciences-Oncology Center (PBCF, 2012), where the cell duplication time for U87 cells cultured in vitro is reported to be of 34 h. TC death rate in anoxic conditions has been estimated in Mart́ınez-González et al. (2012) to be on average of about 48 h. In their work, Toley and Forbes (2011) performed in vitro experiments for the migration of different bacteria strains inside tumor tissues. They estimated the motility of a Salmonella strain to be in the range [0.02, 0.05] mm²d⁻¹ and its growth rate of about 6 h⁻¹. Regarding bacteria death rate under starvation, Phaiboun et al. (2015) quantified bacterial death in a starving population of E. coli. They reported a mean value of 0.018 h⁻¹, which we rounded up to 0.24 d⁻¹ in our simulations. The oxygen diffusion coefficient has been quantified in several in vitro experiments and we assume a value for D_n of 100 mm²d⁻¹, according to the estimates in Schaller and Meyer-Hermann (2005), Matzavinos et al. (2009), Grimes et al. (2014), Colombo et al. (2015), and Alfonso et al. (2016). For the oxygen consumption rate we make use of the arguments in Frieboes et al. (2009), where the authors estimated δ_n in spheroids from measuring the oxygen penetration length L and the diffusion coefficient D_n through the relation ${\delta }_n=D_n/L^2$. Since L was found in the order of 100μm, they estimated ${\delta }_n=8,640{\text{d}}^{-1}$, a value that falls in the range reported in Alfonso et al. (2016) for gliomas. In the case of bacteria, two parameters were difficult to assess in tissues namely the chemotactic coefficient χ and the rate of anti-tumor activity. For the first, this is generally calculated for suspensions of bacteria that are stimulated from some kind of attractant. Ford and colleagues reported the chemotactic and random motility coefficients for bacteria solutions from different strains (Ford et al., 1991; Lewus and Ford, 2001). They provided values for Salmonella, which we used to estimate the range of chemotaxis in spheroids. We considered the value for the motility coefficient that they provided and divided it by the motility that we found for Salmonella in tissues (D_b). Then, we scaled their chemotaxis coefficient with this value to obtain the chemotactic coefficient χ for bacteria in spheroids. For the bacteria anti-tumor activity rate, we were not able to find any estimate in the literature. Therefore, we varied κ over the range [0, 5] d⁻¹, which includes processes that span multiple days to a few hours. Finally, we fitted the parameter for the critical oxygen concentration n_cr from the spheroid experiments in Mascheroni et al. (2016). The value that we found is similar to the one reported in Gerlee and Anderson (2007); Agosti et al. (2018) for tumor aggregates, which is in the range [0.15, 0.5].

TABLE 1

Table 1. Summary of the parameter values considered in the model simulations.

3. Results

3.1. Model Calibration on Spheroid Experiments

We start the analysis by considering the growth of a spheroid suspended in culture medium, in the absence of bacteria. We compare the results of the model with the data for radial growth of U87 tumor spheroids available from Mascheroni et al. (2016). We use the model to fit the critical oxygen concentration parameter n_cr, keeping all the other quantities as defined in Table 1.

Figure 2 shows a good agreement between the model and the experiments, over all the growth curve. The model is able to reproduce the two phases of spheroid growth usually described in the literature (Conger and Ziskin, 1983; Sutherland, 1988; Vinci et al., 2012). The spheroid radius (see Figure 2A) displays a first stage of rapid increase, followed by a saturation phase. This behavior is detailed in Figures 2B,C, showing the evolution of the tumor volume fraction and oxygen concentration over the spheroid radius at different time points. The tumor volume fraction, i.e., ϕ_c, increases over the spheroid at early time points (Figure 2B). Then, as TCs consume oxygen to proliferate, its concentration decreases in the center of the aggregate (Figure 2C). When the oxygen level drops below the critical threshold n_cr (dashed line in Figure 2C), TCs stop proliferating and die. This results in a decrease of ϕ_c in the spheroid core, displayed at longer times in Figure 2B. Close to saturation, the amount of cells that proliferate is balanced by the number of cells that die, turning into extracellular material. Therefore, even if cell growth continues to take place in the outer rim of the spheroid, it is not enough to advance the spheroid front, which reaches a steady state. These results match qualitatively what is observed in the experimental (Landry et al., 1982; Montel et al., 2011; Grimes et al., 2014; Sarkar et al., 2018) and modeling (Ward and King, 1999; Byrne and Preziosi, 2003; Ambrosi and Mollica, 2004; Schaller and Meyer-Hermann, 2005; Mascheroni et al., 2016; Boemo and Byrne, 2019) literature for tumor spheroids and will serve as a basis for the discussion in the next sections.

FIGURE 2

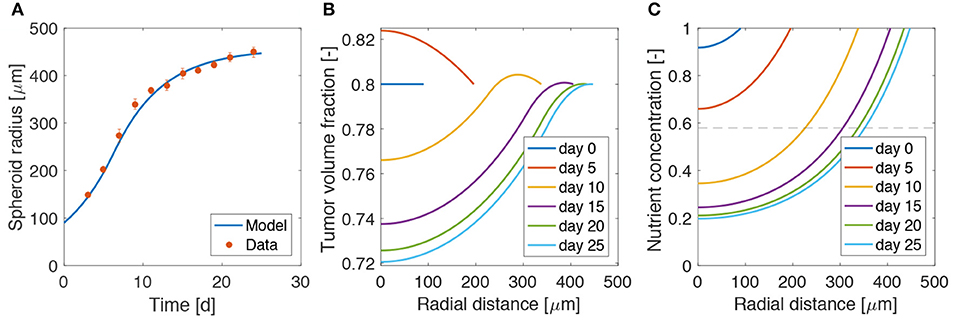
Figure 2. Calibration of the model on tumor spheroid data. (A) Fit of the mathematical model to the experimental data for the spheroid growth curve. The experimental points are taken from Mascheroni et al. (2016) and represent the growth of U87 spheroids. Dots are mean values and bars standard deviation of the measurements. Tumor volume fraction (B) and oxygen concentration (C) at different times of spheroid growth. The dashed line in the last plot displays the critical oxygen concentration.

3.2. Administration of Bacteria Leads to Tumor Remission but Not Eradication

Figure 3 shows the influence of bacterial therapy on tumor spheroid composition for an example case. We evaluate the effects of adding bacteria to the culture medium after the spheroid is fully formed, i.e., when hypoxic regions have developed. In particular, we select an administration time of t₀ = 26d and a treatment duration of t_a = 2d. We consider an intermediate value for both the bacterial chemotactic coefficient and killing rate (χ = 0.432 mm²d⁻¹, κ = 2.5 d⁻¹). As shown by the low TC volume fraction in Figure 3A at later times, bacteria administration leads to spheroids less populated by TCs. This space is occupied by bacteria (Figure 3B), which thrive in the hypoxic region located in the spheroid core. After bacterial therapy the spheroid shrinks and is less populated by cancer cells. This leads to higher values of oxygen concentration at the center of the aggregate, as displayed in Figure 3C. Finally, Figure 3D shows the evolution of TC (V_c) and bacteria (V_b) volumes over time. These quantities are calculated as

$\begin{array}{ll}{V}_{\text{i}}={\displaystyle {\int }_{V_{\text{sf}}}}{\varphi }_{\text{i}}dV,& (12)\end{array}$

where the integral is performed over the spheroid volume V_sf (i = c,b). At early time points, V_c is in a phase of fast growth, since the nutrient is available throughout the spheroid and no bacteria are present. After administration, there is a fast increase of bacteria volume together with a rapid decrease of TC volume. At later time points the system evolves toward a steady state in which both bacteria and TCs coexist in the tumor aggregate. Even though the TCs are not completely removed, the spheroid persists in an equilibrium state, where an asymptotic size is kept for long times.

FIGURE 3

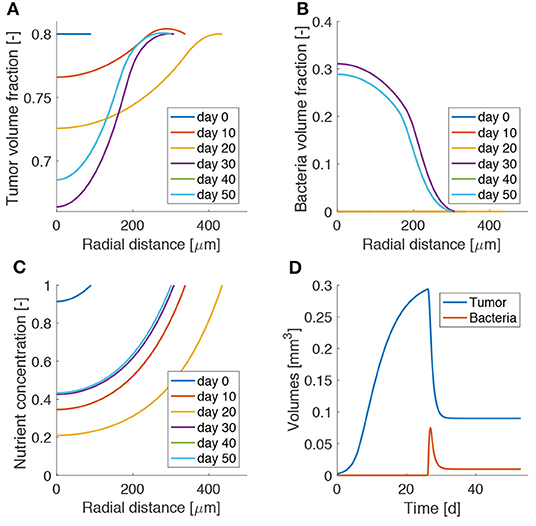
Figure 3. Model results for bacteria administration to tumor spheroids. Spatio-temporal evolution of tumor (A) and bacteria (B) volume fractions and oxygen concentration (C). (D) Temporal evolution of tumor and bacteria volumes in the spheroid. The lines for day 40 are behind those for day 50, as the spheroid has reached a steady state.

3.3. High Chemotaxis Allows for Maximal Reduction of Tumor Size

We investigated the impact of different bacterial chemotactic and anti-tumor strengths on spheroid composition at the end of the simulations, i.e., at day 50 (Figure 4). We found that the highest reduction in tumor volume is obtained for the highest values of the chemotactic coefficient and killing rate, as shown in Figure 4A. On the other hand, highly chemotactic bacteria without an anti-tumor activity lead to the highest tumor volume. Interestingly, the tumor is never completely eradicated over all the explored parameter sequence. A similar result is obtained for the bacteria volume at the end of the simulations (Figure 4). Here, no matter the strength of chemotaxis or anti-tumor activity, bacterial cells are always present in the final spheroid volume. High bacterial volumes are present for high chemotactic coefficients, whereas high killing rates lead to small bacterial volumes independent of the chemotactic strength. Indeed, even though the tumor volume considerably varies over the chemotactic space for high killing rates, the bacterial volume is almost independent of this quantity (see Figure S1). Finally, Figures 4C,D show the temporal variation of tumor and bacterial volumes for two extreme cases occurring for high chemotaxis and low (Case 1) or high (Case 2) killing rate. The first plot shows that after the administration of bacteria the tumor volume is reduced, even in the absence of anti-tumor activity. The two populations in the spheroid reach an equilibrium at later times, with bacteria representing a significant portion of the spheroid. In the second case, the high anti-tumor activity of the bacteria is responsible for a sharp decrease of the tumor population, leading also to oscillations in the TC volume. Although bacteria now constitute a small part of the overall spheroid volume, they are still able to keep the tumor size under control.

FIGURE 4

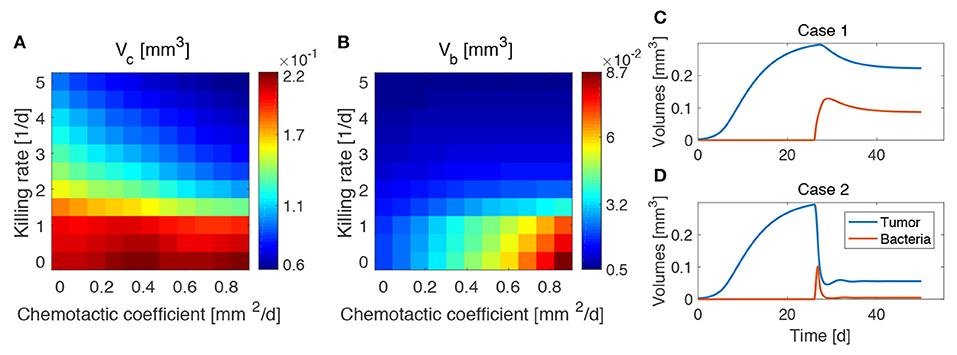
Figure 4. Influence of bacteria chemotactic coefficient and anti-tumor activity on tumor (A) and bacteria (B) volumes at the end of the simulations (day 50). Temporal evolution of tumor and bacteria volumes for a high chemotactic coefficient and a low (Case 1, C) and high (Case 2, D) killing rate.

3.4. Highly Proliferating and Low Oxygen Consuming Tumors Are Mostly Benefited From Bacterial Therapy

The results obtained in the previous subsection are insensitive of the administration time t₀, the duration of the administration t_a and the administered bacteria volume fraction ϕ_b0, even for large variations of these parameters (see Figures S2–S4). This made us investigate whether the steady states reached at the end of the simulations and displayed in Figure 4 were therefore a function of the mechanisms regulating the tumor/bacteria dynamics. To check this hypothesis we simulated the behavior of TCs with a lower or higher proliferation and oxygen consumption rates with respect of the one shown in Figure 4. We report our findings in Figures 5, 6.

FIGURE 5

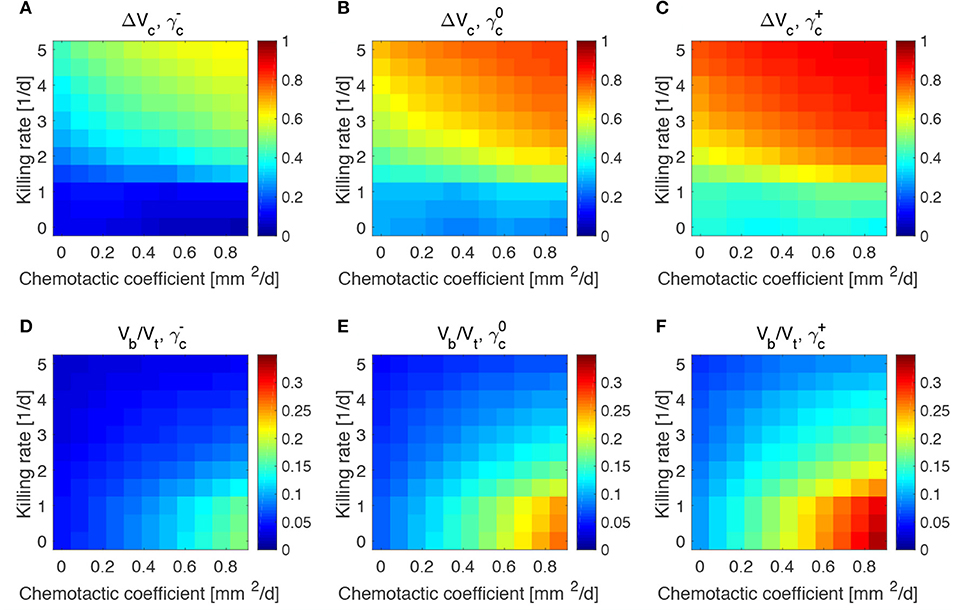
Figure 5. Impact of tumor proliferation rate on tumor and bacteria volumes at the end of the simulations (day 50). Relative tumor volume change and relative bacteria volume for low (A,D), nominal (B,E) and high (C,F) tumor cell proliferation rate.

FIGURE 6

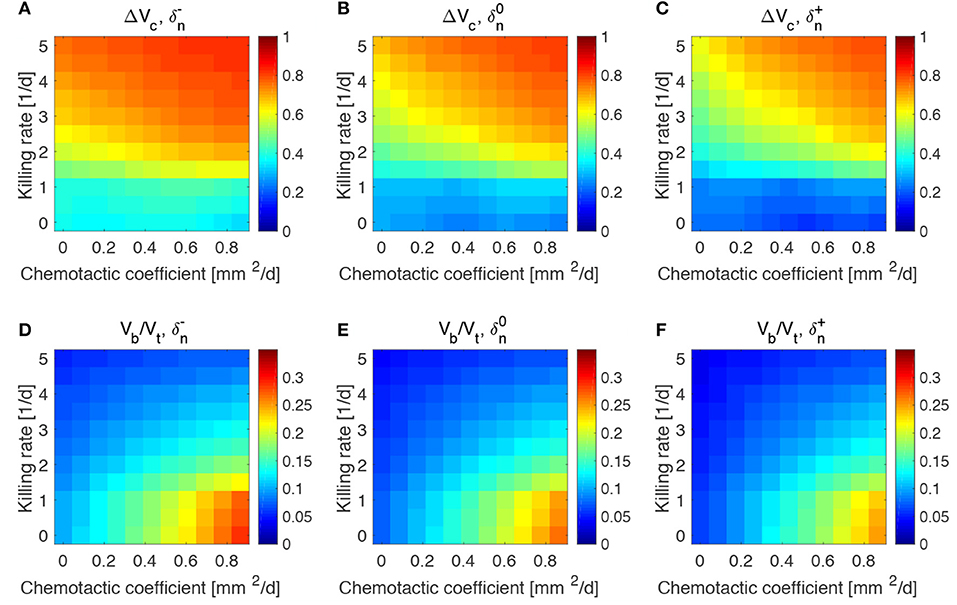
Figure 6. Impact of tumor oxygen consumption rate on tumor and bacteria volumes at the end of the simulations (day 50). Relative tumor volume change and relative bacteria volume for low (A,D), nominal (B,E) and high (C,F) tumor cell proliferation rate.

We considered a variation of ±50% with respect to the nominal value of the parameters in Table 1, and labeled the cases using the plus or minus in the superscript accordingly. All the other parameters keep the nominal values. We evaluated the spheroid response in terms of relative tumor reduction by introducing the quantity:

$\begin{array}{ll}\Delta V_{\text{c}}=\frac{V_0-V_{\text{c}}}{V_0},& (13)\end{array}$

where V_c is the final tumor volume and V₀ the tumor volume at the time of bacteria administration. We also analyzed the relative bacteria volume at the end of the simulation, plotting the ratio of bacteria volume V_b to the total spheroid volume V_t.

Tumors in which cells proliferate at a higher rate display the highest tumor reductions (Figures 5A–C). This is particularly true for the treatment with bacteria characterized by high chemotaxis and killing rate. Highly proliferative tumors are the ones that also show higher colonization by bacteria, as displayed in Figures 5D–F. Treatments with high chemotactic bacteria with low killing rates provide the highest relative bacteria volumes. Low oxygen consumption by TCs leads to results similar to highly proliferative tumors (Figure 6). Again, treatment using bacteria with high chemotaxis and high killing rate produces the best results in terms of tumor reduction. Regarding the final bacterial content, both high and low oxygen consuming tumors show considerable bacteria colonization. As before, the relative bacteria volume is higher for highly chemotactic bacteria with low anti-tumor activity. Even though highly proliferative and low oxygen consuming TCs originate the highest final spheroid volumes (Figure S5), they benefit the most from bacteria treatment and display the higher final bacteria content.

4. Discussion

We proposed a mathematical model to study the influence of bacteria treatment on avascular tumor growth. We considered anaerobic bacteria which thrive in hypoxic environments and actively migrate toward nutrient deprived regions in solid tumors. The model was calibrated to reproduce published tumor spheroid data and then used to evaluate the impact of bacteria chemotaxis and killing rate on spheroid response.

Model results show preferential bacteria accumulation in the hypoxic spheroid core, with tumor cells more localized toward the external spheroid surface. In general, highly chemotactic bacteria possessing increased anti-tumor activity provide the highest tumor reduction after treatment. On the other hand, high chemotaxis but low anti-tumor activity lead to smaller tumor reduction but higher bacteria colonization at the end of the simulations. When varying the tumor parameters, we found that bacteria treatment works best for highly proliferative and low oxygen consuming tumors.

For simplicity, we considered a general effective anti-tumor activity of TCs by bacteria without focusing on specific mechanisms, e.g., cytotoxic agents, prodrug-converting enzymes, etc. (Kramer et al., 2018; Torres et al., 2018; Zhou et al., 2018). Such treatment modalities could be incorporated by extending the model, to provide a more accurate description of the therapeutic action. Moreover, we focused on tumor spheroids, an in vitro approximation of avascular tumors. As such, they lack all the interactions between the tumor and its immune environment. On the one hand, this approach allows to investigate the mutual dynamics of bacteria and tumor cells without external influences, but on the other including the cross-talk between bacteria and the components of the immune system would be a fundamental step to address questions coming from in vivo tumors. Following Boemo and Byrne (2019), we modeled the mechanical response of cells and bacteria in the simplest way considering the phases as inviscid fluids. Although this description is still able to qualitatively describe the experimental results, more detailed constitutive assumptions for the mechanical behavior of the phases would lead to new insights into the interactions between bacteria and TCs in the aggregate (Sciumè et al., 2013; Giverso et al., 2015; Ambrosi et al., 2017; Fraldi and Carotenuto, 2018; Mascheroni et al., 2018; Giverso and Preziosi, 2019). We also considered ideal spherical spheroids to reduce the mathematical problem to one dimension. Even if the qualitative results will be maintained in a three-dimensional geometry, adopting the latter will be crucial to translate the model to in vivo situations. Finally, a note should be made about model parametrization. Generally, mathematical models in the biological framework require several parameters to be determined (Alber et al., 2019) and this work is no exception. We listed the source of the parameters used in the simulations and performed a sensitivity analysis on tumor and bacterial parameters in Figures S6, S7, but a thorough analysis on this topic has been not carried out for the sake of brevity. We believe that a dedicated study on this aspect, particularly in terms of the “Sloppy” model framework (White et al., 2016), could be extremely interesting for this model and for all the biomedical mixture model class.

In this modeling approach, space competition between bacteria and tumor cells arises naturally from the conservation of mass and momentum imposed by the governing equations. As no void regions are allowed into the spheroid, when cells move or die one of the model components automatically fills the space. Bacteria and TCs compete for space in the spheroid and the expansion of the tumor becomes limited, especially when the anti-tumor activity of bacteria is strong. However, for increasing values of the chemotactic coefficient and low values of the killing rate, bacteria localize predominantly in the spheroid core and displace TCs to the outer region of the spheroid. Both types of cell can proliferate in each of the two spheroid areas (hypoxic for spheroids, well-oxygenated for TCs), giving rise to high spheroid volumes and considerable bacteria colonization.

As a matter of fact, chemotaxis could be a target for bacteria-based anticancer therapies and diagnostic tools. For example, TCs that become restricted to outer spheroid areas after administration of highly chemotactic bacteria are more oxygenated and could benefit from standard chemotherapeutic or radiation treatments in the context of synergistic treatments (Zhou et al., 2018). We highlight that this is an example showing that mathematical models could help to identify situations when TC sensitization to therapies might be possible - see also (Owen et al., 2004; Kim et al., 2013; Michor and Beal, 2015; Mascheroni et al., 2017). On the other hand, highly chemotactic bacteria could be used as tracers to identify necrotic regions in spheroid, exploiting their targeting efficiency. Moreover, the simulations show the existence of steady states in which a small population of bacteria is in dynamical equilibrium with cancer cells, leading to tumor size control over time. All these mechanisms arise as a pure physical effect from the competition for space between cancer and bacteria cells and could be optimized to obtain the highest tumor volume reduction or bacteria colonization. Currently, even though researchers are aware of the benefits coming from active bacteria migration toward hypoxic regions in tumors (Forbes, 2010; Kramer et al., 2018), this knowledge has not been efficiently exploited in the clinical trials carried out so far (Torres et al., 2018).

Finally, we point out a few straightforward developments that emerge from the findings of this work. Firstly, our theoretical results advocate for experiments with tumor spheroids. With such a simplified experimental setup, several bacterial strains could be tested on different cancer cell lines to validate model findings. Secondly, the model could be extended to consider different synergistic treatments combined to bacterial administration. Chemotherapy or radiation therapy could be easily included in the model framework, exploiting the modular nature of the equations. The action of the immune system (in a co-culture in spheroids or for an in vivo situation) could be also integrated in future model versions. Lastly, we believe that the tight coupling between the dynamics of TCs and bacteria in terms of regulating their reciprocal environment could be suitably addressed via mathematical models, in order to control the bacterial infection or identify the optimal timing of the therapy.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author's Note

This manuscript has been released as a pre-print at BioRxiv (Mascheroni et al., 2020).

Author Contributions

PM, HH, and MM-H contributed conception and design of the study. PM derived the model and performed the computational analysis. PM wrote the first draft of the manuscript. HH and MM-H wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

MM-H and HH gratefully acknowledge the funding support of the Helmholtz Association of German Research Centers—Initiative and Networking Fund for the project on Reduced Complexity Models (ZT-I-0010). HH and PM acknowledge the funding support of MicMode-I2T (01ZX1710B) by the Federal Ministry of Education and Research (BMBF).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Raimondo Penta (University of Glasgow) for the help with the COMSOL simulations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2020.01083/full#supplementary-material

References

Agosti, A., Cattaneo, C., Giverso, C., Ambrosi, D., and Ciarletta, P. (2018). A computational framework for the personalized clinical treatment of glioblastoma multiforme. ZAMM J. Appl. Math. Mech. 98, 2307–2327. doi: 10.1002/zamm.201700294

CrossRef Full Text | Google Scholar

Alber, M., Tepole, A. B., Cannon, W. R., De, S., Dura-Bernal, S., Garikipati, K., et al. (2019). Integrating machine learning and multiscale modeling-perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digital Med. 2, 1–11. doi: 10.1038/s41746-019-0193-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Alfonso, J., Köhn-Luque, A., Stylianopoulos, T., Feuerhake, F., Deutsch, A., and Hatzikirou, H. (2016). Why one-size-fits-all vaso-modulatory interventions fail to control glioma invasion: in silico insights. Sci. Rep. 6:37283. doi: 10.1038/srep37283

PubMed Abstract | CrossRef Full Text | Google Scholar

Altrock, P. M., Liu, L. L., and Michor, F. (2015). The mathematics of cancer: integrating quantitative models. Nat. Rev. Cancer 15:730. doi: 10.1038/nrc4029

CrossRef Full Text | Google Scholar

Ambrosi, D., and Mollica, F. (2004). The role of stress in the growth of a multicell spheroid. J. Math. Biol. 48, 477–499. doi: 10.1007/s00285-003-0238-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ambrosi, D., Pezzuto, S., Riccobelli, D., Stylianopoulos, T., and Ciarletta, P. (2017). Solid tumors are poroelastic solids with a chemo-mechanical feedback on growth. J. Elastic. 129, 107–124. doi: 10.1007/s10659-016-9619-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Ambrosi, D., and Preziosi, L. (2002). On the closure of mass balance models for tumor growth. Math. Models Methods Appl. Sci. 12, 737–754. doi: 10.1142/S0218202502001878

CrossRef Full Text | Google Scholar

Boemo, M. A., and Byrne, H. M. (2019). Mathematical modelling of a hypoxia-regulated oncolytic virus delivered by tumour-associated macrophages. J. Theoret. Biol. 461, 102–116. doi: 10.1016/j.jtbi.2018.10.044

PubMed Abstract | CrossRef Full Text | Google Scholar

Breward, C., Byrne, H., and Lewis, C. (2001). Modelling the interactions between tumour cells and a blood vessel in a microenvironment within a vascular tumour. Eur. J. Appl. Math. 12, 529–556. doi: 10.1017/S095679250100448X

CrossRef Full Text | Google Scholar

Breward, C., Byrne, H., and Lewis, C. (2002). The role of cell-cell interactions in a two-phase model for avascular tumour growth. J. Math. Biol. 45, 125–152. doi: 10.1007/s002850200149

PubMed Abstract | CrossRef Full Text | Google Scholar

Breward, C. J., Byrne, H. M., and Lewis, C. E. (2003). A multiphase model describing vascular tumour growth. Bull. Math. Biol. 65, 609–640. doi: 10.1016/S0092-8240(03)00027-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrne, H. (2012). Mathematics and life sciences (Berlin).

Byrne, H., and Preziosi, L. (2003). Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. J. IMA 20, 341–366. doi: 10.1093/imammb/20.4.341

PubMed Abstract | CrossRef Full Text | Google Scholar

Byrne, H. M. (2010). Dissecting cancer through mathematics: from the cell to the animal model. Nat. Rev. Cancer 10:221. doi: 10.1038/nrc2808

PubMed Abstract | CrossRef Full Text | Google Scholar

Carmeliet, P., and Jain, R. K. (2000). Angiogenesis in cancer and other diseases. Nature 407:249. doi: 10.1038/35025220

PubMed Abstract | CrossRef Full Text | Google Scholar

Challapalli, A., Carroll, L., and Aboagye, E. O. (2017). Molecular mechanisms of hypoxia in cancer. Clin. Transl. Imaging 5, 225–253. doi: 10.1007/s40336-017-0231-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaplain, M. A., Graziano, L., and Preziosi, L. (2006). Mathematical modelling of the loss of tissue compression responsiveness and its role in solid tumour development. Math. Med. Biol. J. IMA 23, 197–229. doi: 10.1093/imammb/dql009

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombo, M. C., Giverso, C., Faggiano, E., Boffano, C., Acerbi, F., and Ciarletta, P. (2015). Towards the personalized treatment of glioblastoma: integrating patient-specific clinical data in a continuous mechanical model. PLoS ONE 10:e0132887. doi: 10.1371/journal.pone.0132887

CrossRef Full Text | Google Scholar

COMSOL AB (2019). Comsol Multiphysics. Stockholm.

Google Scholar

Conger, A. D., and Ziskin, M. C. (1983). Growth of mammalian multicellular tumor spheroids. Cancer Res. 43, 556–560.

PubMed Abstract | Google Scholar

Folkman, J. (1971). Tumor angiogenesis: therapeutic implications. N. Engl. J. Med. 285, 1182–1186. doi: 10.1056/NEJM197111182852108

PubMed Abstract | CrossRef Full Text | Google Scholar

Forbes, N. S. (2010). Engineering the perfect (bacterial) cancer therapy. Nat. Rev. Cancer 10:785. doi: 10.1038/nrc2934

PubMed Abstract | CrossRef Full Text | Google Scholar

Ford, R. M., Phillips, B. R., Quinn, J. A., and Lauffenburger, D. A. (1991). Measurement of bacterial random motility and chemotaxis coefficients: I. stopped-flow diffusion chamber assay. Biotechnol. Bioeng. 37, 647–660. doi: 10.1002/bit.260370707

CrossRef Full Text | Google Scholar

Fraldi, M., and Carotenuto, A. R. (2018). Cells competition in tumor growth poroelasticity. J. Mech. Phys. Solids 112, 345–367. doi: 10.1016/j.jmps.2017.12.015

CrossRef Full Text | Google Scholar

Frieboes, H. B., Edgerton, M. E., Fruehauf, J. P., Rose, F. R., Worrall, L. K., Gatenby, R. A., et al. (2009). Prediction of drug response in breast cancer using integrative experimental/computational modeling. Cancer Res. 69, 4484–4492. doi: 10.1158/0008-5472.CAN-08-3740

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerlee, P., and Anderson, A. R. (2007). An evolutionary hybrid cellular automaton model of solid tumour growth. J. Theor. Biol. 246, 583–603. doi: 10.1016/j.jtbi.2007.01.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Gibson, B., Wilson, D. J., Feil, E., and Eyre-Walker, A. (2018). The distribution of bacterial doubling times in the wild. Proc. R. Soc. B Biol. Sci. 285:20180789. doi: 10.1098/rspb.2018.0789

PubMed Abstract | CrossRef Full Text | Google Scholar

Giverso, C., and Preziosi, L. (2019). Influence of the mechanical properties of the necrotic core on the growth and remodelling of tumour spheroids. Int. J. Nonlinear Mech. 108, 20–32. doi: 10.1016/j.ijnonlinmec.2018.10.005

CrossRef Full Text | Google Scholar

Giverso, C., Scianna, M., and Grillo, A. (2015). Growing avascular tumours as elasto-plastic bodies by the theory of evolving natural configurations. Mech. Res. Commun. 68, 31–39. doi: 10.1016/j.mechrescom.2015.04.004

CrossRef Full Text | Google Scholar

Grimes, D. R., Kelly, C., Bloch, K., and Partridge, M. (2014). A method for estimating the oxygen consumption rate in multicellular tumour spheroids. J. R. Soc. Interface 11:20131124. doi: 10.1098/rsif.2013.1124

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanahan, D., and Weinberg, R. A. (2011). Hallmarks of cancer: the next generation. Cell 144, 646–674. doi: 10.1016/j.cell.2011.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatzikirou, H., Alfonso, J. C. L., Leschner, S., Weiss, S., and Meyer-Hermann, M. (2017). Therapeutic potential of bacteria against solid tumors. Cancer Res. 77, 1553–1563. doi: 10.1158/0008-5472.CAN-16-1621

PubMed Abstract | CrossRef Full Text | Google Scholar

Jean, A. T. S., Swofford, C. A., Panteli, J. T., Brentzel, Z. J., and Forbes, N. S. (2014). Bacterial delivery of Staphylococcus aureus α-hemolysin causes regression and necrosis in murine tumors. Mol. Ther. 22, 1266–1274. doi: 10.1038/mt.2014.36

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasinskas, R. W., and Forbes, N. S. (2006). Salmonella typhimurium specifically chemotax and proliferate in heterogeneous tumor tissue in vitro. Biotechnol. Bioeng. 94, 710–721. doi: 10.1002/bit.20883

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, M., Gillies, R. J., and Rejniak, K. A. (2013). Current advances in mathematical modeling of anti-cancer drug penetration into tumor tissues. Front. Oncol. 3:278. doi: 10.3389/fonc.2013.00278

PubMed Abstract | CrossRef Full Text | Google Scholar

Kramer, M. G., Masner, M., Ferreira, F. A., and Hoffman, R. M. (2018). Bacterial therapy of cancer: promises, limitations, and insights for future directions. Front. Microbiol. 9:16. doi: 10.3389/fmicb.2018.00016

PubMed Abstract | CrossRef Full Text | Google Scholar

Landry, J., Freyer, J., and Sutherland, R. (1982). A model for the growth of multicellular spheroids. Cell Proliferat. 15, 585–594. doi: 10.1111/j.1365-2184.1982.tb01065.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lewus, P., and Ford, R. M. (2001). Quantification of random motility and chemotaxis bacterial transport coefficients using individual-cell and population-scale assays. Biotechnol. Bioeng. 75, 292–304. doi: 10.1002/bit.10021

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-González, A., Calvo, G. F., Romasanta, L. A. P., and Pérez-García, V. M. (2012). Hypoxic cell waves around necrotic cores in glioblastoma: a biomathematical model and its therapeutic implications. Bull. Math. Biol. 74, 2875–2896. doi: 10.1007/s11538-012-9786-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mascheroni, P., Boso, D., Preziosi, L., and Schrefler, B. A. (2017). Evaluating the influence of mechanical stress on anticancer treatments through a multiphase porous media model. J. Theor. Biol. 421, 179–188. doi: 10.1016/j.jtbi.2017.03.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Mascheroni, P., Carfagna, M., Grillo, A., Boso, D., and Schrefler, B. (2018). An avascular tumor growth model based on porous media mechanics and evolving natural states. Math. Mech. Solids 23, 686–712. doi: 10.1177/1081286517711217

CrossRef Full Text | Google Scholar

Mascheroni, P., Meyer-Hermann, M., and Hatzikirou, H. (2020). Investigating the physical effects in bacterial therapies for avascular tumors. bioRxiv 683839. doi: 10.1101/683839

CrossRef Full Text | Google Scholar

Mascheroni, P., Stigliano, C., Carfagna, M., Boso, D. P., Preziosi, L., Decuzzi, P., et al. (2016). Predicting the growth of glioblastoma multiforme spheroids using a multiphase porous media model. Biomech. Model. Mechanobiol. 15, 1215–1228. doi: 10.1007/s10237-015-0755-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Matzavinos, A., Kao, C.-Y., Green, J. E. F., Sutradhar, A., Miller, M., and Friedman, A. (2009). Modeling oxygen transport in surgical tissue transfer. Proc. Natl. Acad. Sci. U.S.A. 106, 12091–12096. doi: 10.1073/pnas.0905037106

PubMed Abstract | CrossRef Full Text | Google Scholar

Michor, F., and Beal, K. (2015). Improving cancer treatment via mathematical modeling: surmounting the challenges is worth the effort. Cell 163, 1059–1063. doi: 10.1016/j.cell.2015.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Montel, F., Delarue, M., Elgeti, J., Malaquin, L., Basan, M., Risler, T., et al. (2011). Stress clamp experiments on multicellular tumor spheroids. Phys. Rev. Lett. 107:188102. doi: 10.1103/PhysRevLett.107.188102

PubMed Abstract | CrossRef Full Text | Google Scholar

Osswald, A., Sun, Z., Grimm, V., Ampem, G., Riegel, K., Westendorf, A. M., et al. (2015). Three-dimensional tumor spheroids for in vitro analysis of bacteria as gene delivery vectors in tumor therapy. Microb. Cell Factor. 14:199. doi: 10.1186/s12934-015-0383-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Owen, M. R., Byrne, H. M., and Lewis, C. E. (2004). Mathematical modelling of the use of macrophages as vehicles for drug delivery to hypoxic tumour sites. J. Theor. Biol. 226, 377–391. doi: 10.1016/j.jtbi.2003.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

PBCF (2012). PBCF Product guide.

Pesavento, F., Schrefler, B. A., and Sciumè, G. (2017). Multiphase flow in deforming porous media: a review. Arch. Comput. Methods Eng. 24, 423–448. doi: 10.1007/s11831-016-9171-6

CrossRef Full Text | Google Scholar

Phaiboun, A., Zhang, Y., Park, B., and Kim, M. (2015). Survival kinetics of starving bacteria is biphasic and density-dependent. PLoS Comput. Biol. 11:e1004198. doi: 10.1371/journal.pcbi.1004198

PubMed Abstract | CrossRef Full Text | Google Scholar

Preziosi, L. (2003). Cancer Modelling and Simulation. Boca Raton, FL: CRC Press. doi: 10.1201/9780203494899

CrossRef Full Text | Google Scholar

Preziosi, L., and Tosin, A. (2009). Multiphase modelling of tumour growth and extracellular matrix interaction: mathematical tools and applications. J. Math. Biol. 58:625. doi: 10.1007/s00285-008-0218-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Sarkar, S., Peng, C.-C., Kuo, C. W., Chueh, D.-Y., Wu, H.-M., Liu, Y.-H., et al. (2018). Study of oxygen tension variation within live tumor spheroids using microfluidic devices and multi-photon laser scanning microscopy. RSC Adv. 8, 30320–30329. doi: 10.1039/C8RA05505J

CrossRef Full Text | Google Scholar

Schaller, G., and Meyer-Hermann, M. (2005). Multicellular tumor spheroid in an off-lattice Voronoi-Delaunay cell model. Phys. Rev. E 71:051910. doi: 10.1103/PhysRevE.71.051910

PubMed Abstract | CrossRef Full Text | Google Scholar

Sciumè, G., Shelton, S., Gray, W. G., Miller, C. T., Hussain, F., Ferrari, M., et al. (2013). A multiphase model for three-dimensional tumor growth. N. J. Phys. 15:015005. doi: 10.1088/1367-2630/15/1/015005

PubMed Abstract | CrossRef Full Text | Google Scholar

Siddique, J., Ahmed, A., Aziz, A., and Khalique, C. (2017). A review of mixture theory for deformable porous media and applications. Appl. Sci. 7:917. doi: 10.3390/app7090917

CrossRef Full Text | Google Scholar

Suh, S., Leaman, E., Zhan, Y., and Behkam, B. (2018). “Mathematical modeling of bacteria-enabled drug delivery system penetration into multicellular tumor spheroids, in 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (Honolulu: IEEE), 6162–6165. doi: 10.1109/EMBC.2018.8513596

PubMed Abstract | CrossRef Full Text | Google Scholar

Sutherland, R. M. (1988). Cell and environment interactions in tumor microregions: the multicell spheroid model. Science 240, 177–184. doi: 10.1126/science.2451290

PubMed Abstract | CrossRef Full Text | Google Scholar

Toley, B. J., and Forbes, N. S. (2011). Motility is critical for effective distribution and accumulation of bacteria in tumor tissue. Integr. Biol. 4, 165–176. doi: 10.1039/c2ib00091a

PubMed Abstract | CrossRef Full Text | Google Scholar

Torres, W., Lameda, V., Olivar, L. C., Navarro, C., Fuenmayor, J., Pérez, A., et al. (2018). Bacteria in cancer therapy: beyond immunostimulation. J. Cancer Metastasis Treat. 4:4. doi: 10.20517/2394-4722.2017.49

CrossRef Full Text | Google Scholar

Vaupel, P., and Mayer, A. (2007). Hypoxia in cancer: significance and impact on clinical outcome. Cancer Metastasis Rev. 26, 225–239. doi: 10.1007/s10555-007-9055-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinci, M., Gowan, S., Boxall, F., Patterson, L., Zimmermann, M., Lomas, C., et al. (2012). Advances in establishment and analysis of three-dimensional tumor spheroid-based functional assays for target validation and drug evaluation. BMC Biol. 10:29. doi: 10.1186/1741-7007-10-29

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, J., and King, J. (1999). Mathematical modelling of avascular-tumour growth II: modelling growth saturation. Math. Med. Biol. J. IMA 16, 171–211. doi: 10.1093/imammb/16.2.171

PubMed Abstract | CrossRef Full Text | Google Scholar

White, A., Tolman, M., Thames, H. D., Withers, H. R., Mason, K. A., and Transtrum, M. K. (2016). The limitations of model-based experimental design and parameter estimation in sloppy systems. PLoS Comput. Biol. 12:e1005227. doi: 10.1371/journal.pcbi.1005227

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, W. R., and Hay, M. P. (2011). Targeting hypoxia in cancer therapy. Nat. Rev. Cancer 11:393. doi: 10.1038/nrc3064

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, S., Gravekamp, C., Bermudes, D., and Liu, K. (2018). Tumour-targeting bacteria engineered to fight cancer. Nat. Rev. Cancer 18:1. doi: 10.1038/s41568-018-0070-z

PubMed Abstract | CrossRef Full Text | Google Scholar