- 1Department of Molecular and Cell Biology, University of Connecticut, Storrs, CT, USA
- 2Institute for Systems Genomics, University of Connecticut, Storrs, CT, USA
Cells without Complete Genomes
Cells have long been recognized as life's building blocks (e.g., Virchow's dictum “omnis cellula e cellula,” Virchow, 1860). Specifically, a cell's genome is considered the repository of genetic information that pairs with the cellular machinery to determine the organism's phenotype. Except for rare circumstances, the majority of a genome is passed on from ancestor to descendant, although the acquisition of genes from organisms that are not direct ancestors is recognized to play an important role in evolution (Swithers et al., 2012).
Jeffrey Lawrence, in discussing minimal genome size proposed a meta-cell model (Lawrence, 1999), in which many micelles (small vesicles containing resources, products, and genes) exchange genes frequently. Genes temporarily reside in a micelle and direct the synthesis of compounds important for replication. A micelle only can replicate when all compounds necessary for division have been generated. However, at each point in time only a fraction of the necessary genes are present in an individual micelle. This model relies on gene transfer being so frequent that each of the genes that encode necessary functions visits the individual micelles often enough to allow for sufficient synthesis of the necessary gene products for future micelle divisions. The meta-cell can be considered an organism, whose genome is divided into a network of micelles. Lawrence's meta-cell model is reminiscent of Woese's progenote (Woese, 1998) and Kandler's pre-cell populations (Kandler, 1994) that were postulated to have existed early in evolution before genes coalesced into genomes.
The Pan-Genome as a Shared Genomic Resource
For most bacterial and archaeal species different strains contain non-overlapping gene sets. The pan-genome of a taxon or group refers to the sum of all genes that are present in members of the group (Tettelin et al., 2005; Lapierre and Gogarten, 2009). Pan-genomes comprise the core genome, i.e., the genes that are found in all members, and the accessory genome, i.e., genes that are present in only one or a few members of the group. Welch et al. (2002) provided the first illustration that genome content in bacteria changes rapidly. Comparing three Escherichia coli strains they found the shared core to be less than 40% of the gene families present in all three genomes. More recently the size of this core was further reduced to only 6% of gene families present in 61 E. coli genomes (Lukjancenko et al., 2010). Baumdicker et al. (2012) estimate that the Prochlorococcus pan-genome contains about 58,000 genes, whereas the individual genomes encode only about 2000 genes each.
The pan-genome concept was originally developed to explore the fluidity of prokaryotic genomes (Tettelin et al., 2005). Because HGT is more frequent between close relatives (Andam and Gogarten, 2011), the pan-genome may also represent the set of genes that is potentially available via HGT to any member of the group. The function of the pan-genome may then be thought of as a shared resource. This is supported by the observation that genes encoding weakly selected functions are frequently lost from bacterial genomes, when they do not provide selective advantages, only to be re-acquired through HGT, when new conditions provide a selective advantage to carriers (Lawrence and Roth, 1996). The idea of the pan-genome of a population as a shared genomic resource is similar to the description of meta-cells and pre-cell populations. In particular, these concepts have in common that the individual genome of a cell or micelle does not represent a sufficient description of the genomic resources of the population. The following paragraphs discuss some factors that contribute to the large size of pan-genomes.
The Strong Black Queen Hypothesis
The black queen hypothesis proposed by Morris et al. (2012) is built on the premise of “leaky” common good functions, which cannot be restricted to benefit only the producer. The hypothesis suggests that these functions combined with selection for small genomes may lead to a situation in which these leaky functions are encoded in only a fraction of the genomes comprising the community. Under the black queen hypothesis a cell's evolution can follow one of two pathways (see Figure 1): (1) the cell can retain all genes encoding leaky functions (in the game of hearts, from which the name for the black queen hypothesis derives, this strategy is known as “shooting the moon”). The cost is a large genome maintaining and expressing many genes that are not essential to central metabolism, growth, and reproduction. Consequently, maintaining these genes and expression of extra proteins competes for cellular resources that could be put toward replication and results in a lower growth rate (Dong et al., 1995; Scott et al., 2010; Weiße et al., 2015). The advantage of the “shooting the moon” strategy is that following a population bottleneck all genes encoding leaky functions are available in the genome. These members of a community following this strategy may be thought of as analogous to a keystone species. (2) The cell looses some or all of its leaky functions and increases its growth rate (in hearts, this represents the usual strategy of taking as few point cards as possible). Traditionally this is described as cheating, as the second strategy relies upon other cells in the population for the leaky functions it has lost. If a bottleneck occurs, a single cheating cell is unlikely to survive on its own. A possible outcome of all cells in a population following strategy #2 is that all members of a population cheat on some leaky functions. The members in the population then become mutually dependent on one another (Figure 1). In this scenario there are no keystone members providing all of the leaky functions. For the population to establish itself in a new environment several members of the population are required for the migration to be successful, as no single cell has all the components necessary to sustain itself. We term this the “strong” version of the black queen hypothesis. If all members of a population follow the second strategy, this may under some conditions lead to instability, the tragedy of the commons, and extinction of the population; however, experimental work by Morris et al. (2014) has shown that partitioning of a leaky common-goods function can enable the stable co-existence of two very similar organisms that use the same resources. Additionally, under natural conditions cells do rarely exist in homogeneous mixture (Davey and O'toole, 2000). Cells existing in biofilms or small aggregates are likely to be proximal to cells with which they share recent ancestry, and therefore proximal cells will have the same genotype with respect to shared functions. Drescher et al. (2014) show that Vibrio cholera can avoid the public goods dilemma by strengthening relationships between cells of the same genotype through creation of a thick biofilm, thereby providing a local selective advantage to producers of a particular common good in case this good becomes an overall limiting resource. It seems likely that genes encoding common goods are under frequency dependent selection, leading to local feedback loops that contribute to a long-term co-existence of the different types of cheaters.
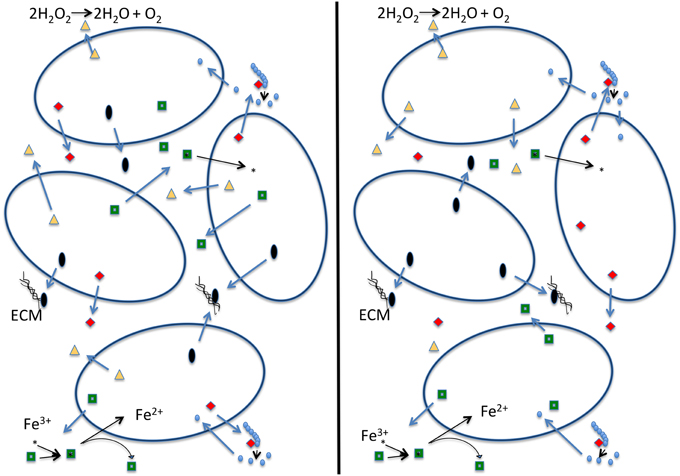
Figure 1. Schematic depiction of a strong version of the black queen hypothesis (Morris et al., 2012). Each cell in the left panel contains all the genes that produce the four depicted common goods. Cells on the right, due to selection to minimize genome size, each produce only one of the common goods, and rely on the presence of other cells to produce the other ones. We consider this a strong version of the black queen hypothesis because it no longer contains exclusive helper strains; rather all individuals in the population described in the right hand panel are simultaneously helpers and beneficiaries. In this example dark open ovals represent individual cells; red diamonds: hydrolases that digest an extracellular polymer (e.g., phosphatase, sialidase, glucanase); green squares: siderophores that allow cells to acquire iron; black ovals: building blocks of the extracellular matrix (ECM) or enzymes that produce and assemble these building blocks; yellow triangles: enzymes that destroy oxygen radicals (e.g., catalase—reaction given; or peroxidase—reaction: ROOR' + electron donor (2 e−) + 2H+ → ROH + R'OH).
Black vs. the Red Queen
Bacteria are under severe predation by phage (Thurber, 2009). They need to constantly change to evade predation, hence the analogy to the red queen from Lewis Carroll's (Carroll and Gardner, 1999) Through the Looking-Glass, who needs to run as fast as she can just to stay in place (Van Valen, 1973). The analysis of phage metagenomes and rank abundance curves indicated that the phage predation follows the kill the winner strategy (Hoffmann et al., 2007), where successful strains are targeted more frequently. The surprising long term stability of species composition despite phage predation suggests that cycling between different susceptible target cells occurs within a population and not between populations from different species (Rodriguez-Brito et al., 2010). Consequently, within a population, host genes that encode receptors utilized by phage and virus to enter the cell are expected to turn over quickly, creating within population diversity (Chaturongakul and Ounjai, 2014).
Random Acquisition of Genes
Genes are constantly acquired by genomes, and many of the transferred genes do not find a long term home in the recipient genome (Lawrence and Ochman, 1997). Among these genes are parasites (prophages) and selfish genetic elements. Most, but certainly not all (Lobkovsky et al., 2013), of the transferred genes are selectively neutral or nearly neutral to the recipient (Gogarten and Townsend, 2005; Baumdicker et al., 2010; Haegeman and Weitz, 2012). Though these genes may not find long term homes in the genomes they “visit,” selfish genes especially can affect the rates of gene sharing and thus the size of the pan-genome in a population. Furthermore, many selfish elements induce genome rearrangements that can promote the loss and gain of genes, and thus may have a significant impact on the initiation of the loss of leaky functions.
Generation of paralogs may play a role in facilitation of loss of leaky functions. Additional copies increase gene dosage, ameliorating the loss of function in other members of the population by providing more of the common good. However, the pressure to delete genes from genomes is much stronger than to duplicate them (Mira et al., 2001) and an increase in gene transcription can have a similar or greater effect on the overall expression level (Weiße et al., 2015). Regardless of whether the increased production comes from paralogy or regulation it would need to be countered by a greater decrease in production from other common good functions to overcome the cost of increased protein expression.
Conclusion
Random acquisition of genes and selfish genetic elements, selection by predators, and cheating on common goods, all undoubtedly play a role in generating diversity within populations of bacteria and archaea. The conjecture of the strong black queen hypothesis is that mutual cheating leads to mutual dependencies and therefore cooperation. Under this hypothesis individual cells would be integrated into a meta-organism, whose genome is the pan-genome of the population, similar to Lawrence's meta-cells whose genome is distributed over individual micelles.
The pan-genome of a population as shared genomic resource could explain part of the “genome of Eden” paradox (Doolittle et al., 2003), where estimations of ancestral genomes are far larger and more complex than those of any extant individual genome. Large estimates of archaeal ancestors' genome sizes (Csurös and Miklós, 2009; Wolf et al., 2012) could actually represent the pan-genome of the ancestral population rather than any single cell. If this is the case, the complexity of the progenitor cells in a lineage/population might often be at a similar level of complexity as their extant relatives. We hypothesize the large estimates of progenitor genome size might in part reflect a “strong” black queen scenario where genome variation creates a large pan-genome, but no single cell contains a “keystone genome” with all genes in the population represented. More extensive studies of individual and population genomes, and rates of within population transfer are needed to confirm that master genomes, encoding all the leaky functions needed for survival of the population, can be and often are absent from a population.
If the hypothesis of the population pan-genome as a shared genomic resource is borne out, then the scientific community will need to continue to increase its appreciation for the import of pan- and meta-genomes. Likewise, we may need to more seriously consider populations as the operative units in which genes are selected in rather than exclusively individual organisms. Similar to how Richard Dawkins (1976) advocated thinking of an organism as a collection of generally agreeable, but selfish, genes perhaps we should be thinking of lineages and populations as the collections of genes, i.e., pan-genomes, rather than the individual cells.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Michael Stephens, Joerg Graf, and Thane Papke for Discussion. Work in the Gogarten-lab was supported through grants from the National Science Foundation (AToL DEB0830024), the National Aeronautics and Space Agency (Exobiology NNX13AI03G), and the Bi-national Science Foundation (BSF 2013061).
References
Andam, C. P., and Gogarten, J. P. (2011). Biased gene transfer in microbial evolution. Nat. Rev. Microbiol. 9, 543–555. doi: 10.1038/nrmicro2593
Baumdicker, F., Hess, W. R., and Pfaffelhuber, P. (2010). The diversity of a distributed genome in bacterial populations. Ann. Appl. Probab. 20, 1567–1606. doi: 10.1214/09-AAP657
Baumdicker, F., Hess, W. R., and Pfaffelhuber, P. (2012). The infinitely many genes model for the distributed genome of bacteria. Genome Biol. Evol. 4, 443–456. doi: 10.1093/gbe/evs016
Carroll, L., and Gardner, M. (1999). The Annotated Alice: The Definitive Edition. New York, NY: Norton.
Chaturongakul, S., and Ounjai, P. (2014). Phage-host interplay: examples from tailed phages and Gram-negative bacterial pathogens. Front. Microbiol. 5:442. doi: 10.3389/fmicb.2014.00442
Csurös, M., and Miklós, I. (2009). Streamlining and large ancestral genomes in Archaea inferred with a phylogenetic birth-and-death model. Mol. Biol. Evol. 26, 2087–2095. doi: 10.1093/molbev/msp123
Davey, M. E., and O'toole, G. A. (2000). Microbial biofilms: from ecology to molecular genetics. Microbiol. Mol. Biol. Rev. 64, 847–867. doi: 10.1128/MMBR.64.4.847-867.2000
Dong, H., Nilsson, L., and Kurland, C. G. (1995). Gratuitous overexpression of genes in Escherichia coli leads to growth inhibition and ribosome destruction. J. Bacteriol. 177, 1497–1504.
Doolittle, W. F., Boucher, Y., Nesbø, C. L., Douady, C. J., Andersson, J. O., and Roger, A. J. (2003). How big is the iceberg of which organellar genes in nuclear genomes are but the tip? Philos. Trans. R. Soc. B Biol. Sci. 358, 39–58. doi: 10.1098/rstb.2002.1185
Drescher, K., Nadell, C. D., Stone, H. A., Wingreen, N. S., and Bassler, B. L. (2014). Solutions to the public goods dilemma in bacterial biofilms. Curr. Biol. 24, 50–55. doi: 10.1016/j.cub.2013.10.030
Gogarten, J. P., and Townsend, J. P. (2005). Horizontal gene transfer, genome innovation and evolution. Nat. Rev. Microbiol. 3, 679–687. doi: 10.1038/nrmicro1204
Haegeman, B., and Weitz, J. S. (2012). A neutral theory of genome evolution and the frequency distribution of genes. BMC Genomics 13:196. doi: 10.1186/1471-2164-13-196
Hoffmann, K. H., Rodriguez-Brito, B., Breitbart, M., Bangor, D., Angly, F., Felts, B., et al. (2007). Power law rank-abundance models for marine phage communities. FEMS Microbiol. Lett. 273, 224–228. doi: 10.1111/j.1574-6968.2007.00790.x
Kandler, O. (1994). “The early diversification of life,” in Early Life on Earth, ed S. Bengston (New York, NY: Columbia University Press), 152–509.
Lapierre, P., and Gogarten, J. P. (2009). Estimating the size of the bacterial pan-genome. Trends Genet. 25, 107–110. doi: 10.1016/j.tig.2008.12.004
Lawrence, J. G. (1999). “Gene transfer and minimal genome size,” in Size Limits of Very Small Microorganisms, eds A. Knoll, M. J. Osborn, J. Baross, H. C. Berg, N. R. Pace, and M. Sogin (Washington, DC: National Research Council), 32–38.
Lawrence, J. G., and Ochman, H. (1997). Amelioration of bacterial genomes: rates of change and exchange. J. Mol. Evol. 44, 383–397. doi: 10.1007/PL00006158
Lawrence, J. G., and Roth, J. R. (1996). Selfish operons: horizontal transfer may drive the evolution of gene clusters. Genetics 143, 1843–1860.
Lobkovsky, A. E., Wolf, Y. I., and Koonin, E. V. (2013). Gene frequency distributions reject a neutral model of genome evolution. Genome Biol. Evol. 5, 233–242. doi: 10.1093/gbe/evt002
Lukjancenko, O., Wassenaar, T. M., and Ussery, D. W. (2010). Comparison of 61 sequenced Escherichia coli genomes. Microb. Ecol. 60, 708–720. doi: 10.1007/s00248-010-9717-3
Mira, A., Ochman, H., and Moran, N. A. (2001). Deletional bias and the evolution of bacterial genomes. Trends Genet. 17, 589–596. doi: 10.1016/S0168-9525(01)02447-7
Morris, J. J., Lenski, R. E., and Zinser, E. R. (2012). The Black Queen hypothesis: evolution of dependencies through adaptive gene loss. MBio 3:e00036–12. doi: 10.1128/mbio.00036-12
Morris, J. J., Papoulis, S. E., and Lenski, R. E. (2014). Coexistence of evolving bacteria stabilized by a shared black queen function. Evolution 68, 2960–2971. doi: 10.1111/evo.12485
Rodriguez-Brito, B., Li, L., Wegley, L., Furlan, M., Angly, F., Breitbart, M., et al. (2010). Viral and microbial community dynamics in four aquatic environments. ISME J. 4, 739–751. doi: 10.1038/ismej.2010.1
Scott, M., Gunderson, C. W., Mateescu, E. M., Zhang, Z., and Hwa, T. (2010). Interdependence of cell growth and gene expression: origins and consequences. Science 330, 1099–1102. doi: 10.1126/science.1192588
Swithers, K. S., Soucy, S. M., and Gogarten, J. P. (2012). The role of reticulate evolution in creating innovation and complexity. Int. J. Evol. Biol. 2012:418964. doi: 10.1155/2012/418964
Tettelin, H., Masignani, V., Cieslewicz, M. J., Donati, C., Medini, D., Ward, N. L., et al. (2005). Genome analysis of multiple pathogenic isolates of Streptococcus agalactiae: implications for the microbial “pan-genome”. Proc. Natl. Acad. Sci. U.S.A. 102, 13950–13955. doi: 10.1073/pnas.0506758102
Thurber, R. V. (2009). Current insights into phage biodiversity and biogeography. Curr. Opin. Microbiol. 12, 582–587. doi: 10.1016/j.mib.2009.08.008
Virchow, R. L. K. (1860). Cellular Pathology (Google eBook). London: John Churchill. Available online at: https://play.google.com/store/books/details/Rudolf_Ludwig_Karl_Virchow_Cellular_Pathology?id=JUth7ntb0_AC
Weiße, A. Y., Oyarzún, D. A., Danos, V., and Swain, P. S. (2015). Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. U.S.A. 112, E1038–E1047. doi: 10.1073/pnas.1416533112
Welch, R. A., Burland, V., Plunkett, G., Redford, P., Roesch, P., Rasko, D., et al. (2002). Extensive mosaic structure revealed by the complete genome sequence of uropathogenic Escherichia coli. Proc. Natl. Acad. Sci. U.S.A. 99, 17020–17024. doi: 10.1073/pnas.252529799
Woese, C. (1998). The universal ancestor. Proc. Natl. Acad. Sci. U.S.A. 95, 6854–6859. doi: 10.1073/pnas.95.12.6854
Keywords: pan-genome, black queen hypothesis, red queen hypothesis, social cheating, gene transfer
Citation: Fullmer MS, Soucy SM and Gogarten JP (2015) The pan-genome as a shared genomic resource: mutual cheating, cooperation and the black queen hypothesis. Front. Microbiol. 6:728. doi: 10.3389/fmicb.2015.00728
Received: 27 April 2015; Accepted: 03 July 2015;
Published: 21 July 2015.
Edited by:
Luis Delaye, Centro de Investigación y de Estudios Avanzados - Unidad Irapuato, MexicoReviewed by:
Luis David Alcaraz, Universidad Nacional Autónoma de México, MexicoLuisa I. Falcon, Universidad Nacional Autónoma de México, Mexico
Copyright © 2015 Fullmer, Soucy and Gogarten. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Johann Peter Gogarten,Z29nYXJ0ZW5AdWNvbm4uZWR1;anBnb2dhcnRlbkBnbWFpbC5jb20=
 Matthew S. Fullmer
Matthew S. Fullmer Shannon M. Soucy
Shannon M. Soucy Johann Peter Gogarten
Johann Peter Gogarten