Machine learning prediction of the mechanical properties of refractory multicomponent alloys based on a dataset of phase and first principles simulation

In this work, a dataset including structural and mechanical properties of refractory multicomponent alloys was developed by fusing computations of phase diagram (CALPHAD) and density functional theory (DFT). The refractory multicomponent alloys, also named refractory complex concentrated alloys (CCAs) which contain 2–5 types of refractory elements were constructed based on Special Quasi-random Structure (SQS). The phase of alloys was predicted using CALPHAD and the mechanical property of alloys with stable and single body-centered cubic (BCC) at high temperature (over 1,500°C) was investigated using DFT-based simulation. As a result, a dataset with 393 refractory alloys and 12 features, including volume, melting temperature, density, energy, elastic constants, mechanical moduli, and hardness, were produced. To test the capability of the dataset on supporting machine learning (ML) study to investigate the property of CCAs, CALPHAD, and DFT calculations were compared with principal components analysis (PCA) technique and rule of mixture (ROM), respectively. It is demonstrated that the CALPHAD and DFT results are more in line with experimental observations for the alloy phase, structural and mechanical properties. Furthermore, the data were utilized to train a verity of ML models to predict the performance of certain CCAs with advanced mechanical properties, highlighting the usefulness of the dataset for ML technique on CCA property prediction.

1 Introduction

Complex concentrated alloys (CCAs) (Yeh et al., 2004a; Tsai and Yeh, 2014; Ye et al., 2016; Miracle and Senkov, 2017), the multicomponent alloys containing five or more elements with equal or near-equal concentrations, have recently received increased attention due to their new and important properties, such as high strength at both room temperature and elevated temperatures (Senkov et al., 2011; Kang et al., 2018), exceptional ductility (Yao et al., 2014), and toughness (Patriarca et al., 2016). Numerous studies on CCAs were motivated by the possibility that the high configurational entropy may simply favor a single phase, such as face-centered cubic (FCC) or body-centered cubic (BCC) phases (Yeh et al., 2004b). Thus, research on CCAs has become tightly associated with finding single-phase solid solutions by controlling their configurational entropy.

Based on the elements contained in CCAs, they can be classified into: 1) 3d transition metal alloys (formed of 4 or more of the following elements: Al, Co, Cr, Cu, Fe, Mn, Ni, Ti, and V), 2) refractory metal alloys (formed of 4 or more of the following elements: Cr, Hf, Mo, Nb, Ta, Ti, V, W, Re, and Zr), and 3) other alloys that include light metal and lanthanide transition metal (Miracle and Senkov, 2017). 3d transition metal alloys, for example, Ni-based alloys have been developed for high temperature applications in aircrafts, power generation turbines, rocket engines and other challenging environments (Ezugwu et al., 1999; Griffiths, 2019; Morinaga, 2019). A recent key goal for generating metallic alloys with high melting temperatures, which could potentially be employed in nuclear reactors and comparable applications, has motivated the development of refractory alloys. Alloys with single phase or dual phase were reported to have high strength (Li et al., 2016; Singh et al., 2018; Maresca and Curtin, 2020) and high hardness (Borkar et al., 2016). Additionally, the variety of refractory elemental characteristics offers significant design flexibility for refractory multicomponent alloys. For instance, BCC MoNbTaVW has demonstrated high Vickers micro-hardness of 11.4 GPa at 1,150°C (Xin et al., 2018) and strong yield strength of 1,246 MPa at room temperature which decreases to 842 MPa at 1,000°C (Senkov et al., 2011). This demonstrates promising mechanical property of refractory CCAs.

CCAs with simple crystal symmetry and remarkable mechanical properties is one of the areas that draw attention of scientists worldwide. The principal components analysis (PCA) technique was employed to predict the single phase of the multicomponent alloys (Zhang et al., 2008; Guo et al., 2011; Guo and Liu, 2011; Murty et al., 2014; Zhang et al., 2014). By using this statistical technique, the variables of the dataset can be reduced into principal components. The original database is preserved as much as correlation will allow in the principal components, which are made up of orthogonal linear combinations of the original variables. Based on the PCA technique, the mixing entropy ($∆S_{mix}$), valence electron concentration (VEC), atomic size difference ($\delta$), and mixing enthalpy ($∆H_{mix}$) were utilized as critical conditions for the formation of the CCA solid solutions. The formation of BCC CCAs requires that the following conditions are satisfied (Zhang et al., 2008; Guo et al., 2011; Guo and Liu, 2011; Zhang et al., 2014): −15 ≤ $∆H_{mix}$ ≤ 5 kJ/mol, $\delta$ ≤ 6.6%, 12 ≤ $∆S_{mix}$ ≤ 17.5 J/(Kmol) for CCAs that contain 5 or more elements, and VEC < 6.87. On the other hand, the calculation of phase diagrams using CALPHAD was widely used to predict phase stability of CCAs and to understand their formation mechanisms. Thermo-Calc’s High Entropy Alloy database (Andersson et al., 2002; Chen et al., 2018) was used in CALPHAD software along with the high entropy alloy database. These have been claimed to lead to good agreement with the experimental observations on the phase of refractory CCAs, such as MoNbTaTiVW and Ti_xNbMoTaW (Andersson et al., 2002; Gao et al., 2015; Zhang et al., 2015; Yao et al., 2016b; Yao et al., 2017; Chen et al., 2018; Han et al., 2018).

Thanks to the increase of computational capacity, the utilization of machine learning (ML) accelerates the study of CCA phases (Lederer et al., 2018; Huang et al., 2019; Zhou et al., 2019; Zhang et al., 2020). Additionally, ML has also been used in prediction of CCAs with predefined properties, such as high strength and high hardness, (Chang et al., 2019; Himanen et al., 2019; Wen et al., 2019; Hu et al., 2022; Vazquez et al., 2022) and high elasticity (Kim et al., 2019). However, designing CCAs with desirable properties by ML urgently requires statistical analysis of these alloys. Many of the current databases for ML studies were built using only mathematical models such as rule of mixture (ROM) (Couzinié et al., 2018; Roy et al., 2020; Li et al., 2021). ROM is a weighted mean method used to predict the properties of alloys, the parameter of an alloy $f_{mix}$ can be estimated by equation $f_{mix}=\sum C_i{f}_i$ , where $C_i$ and $f_i$ are the atomic fraction and the parameter of element i. While forming alloys lattice distortion may occur because of atomic level mismatches between components (e.g., atom size, valence electrons, etc.). In this case, the potentially novel mechanical, electronic, and thermal properties of CCAs may be missed, leading to significant deviation of mathematical models from reality. Therefore, physics-based optimizations which accurately characterize atomic interactions and atomic scale features are critically needed for building databases. For example, Lederer et al. (2018) used the Lederer-Toher-Vecchio-Curtarolo (LTVC) method to create a dataset for predicting refractory alloys with stable single phase by incorporating ab initio computed energies into a mean-field statistical mechanics model. To create a comprehensive dataset that can be used to train ML models to predict performance, more computational studies of CCAs are needed.

In a recent research, the phase and melting temperature of quaternary and quinary refractory CCAs with equivalent atomic numbers were reported by using CALPHAD, and the results were compared with those obtained by ROM (Shaikh et al., 2020), demonstrating the advance of CALPHAD in CCA prediction. In this work, we integrated CALPHAD and the density functional theory (DFT) to examine the structural and mechanical properties for not only quaternary and quinary, but many more binary and ternary refractory alloys with stable single phase as well. The calculated structural and mechanical properties were compared with ROM and experimental observations. A dataset was built based on the calculations, and it was used to train ML models to predict mechanical properties of CCAs such as hardness and elastic constants.

2 Methodology

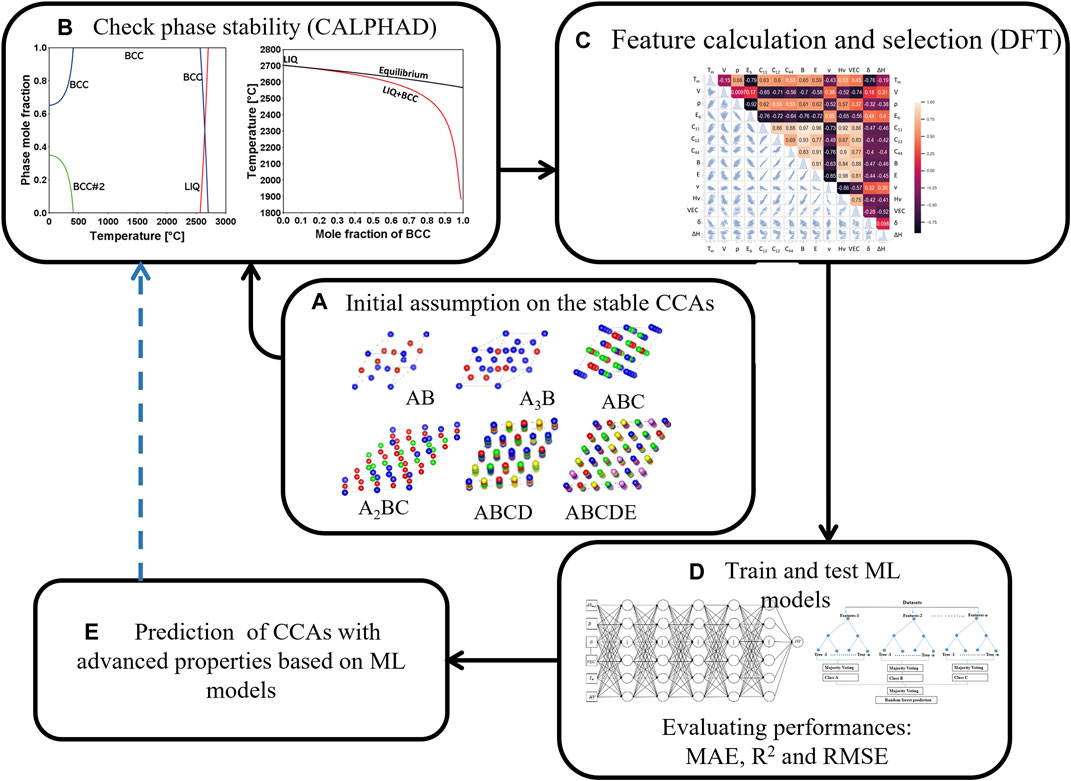
Since most pure refractory metals have stable BCC crystals, it is desirable that multicomponent alloys which contain only refractory elements have a predominantly BCC crystal structure. In this paper, the general procedures for building the dataset of structural and mechanical properties for BCC refractory multicomponent alloys are described as follows: 1) construct possible prototype binary, ternary, quaternary, and quinary alloys based on the Special Quasi-random Structure (SQS) (Zunger et al., 1990). The binary and ternary SQSs were provided by MedeA software, and the quaternary and quinary SQSs were generated through Alloy Theoretic Automated Toolkit (ATAT) (van de Walle et al., 2002; van de Walle, 2009) (Figure 1A). The reliability of SQS models on calculating the vibrational, electronic, and mechanical properties of alloys were validated by Gao et al. (2016) through hybrid Monte Carlo/molecular dynamics simulations. 2) analyze the possibility of forming stable solid state for each configuration based on the critical factors for forming solid solutions of high entropy alloys; 3) calculate phase diagram using CALPHAD to determine the solid solution phases at various thermodynamic conditions, screen out the alloys that have only BCC phase at high temperature (Figure 1B); and 4) predict the structural and mechanical properties of alloys with stable BCC phase by DFT calculations (Figure 1C). The dataset would be used to train ML models to anticipate CCAs with advanced mechanical properties once it had been built (Figures 1D, E). When building the dataset by DFT calculation, two questions that have come up are answered: 1) Do alloys with less than five different types of elements still adhere to the critical factors (VEC, , $∆S_{mix}$ , and $∆H_{mix}$) obtained by PCA? 2) How much of an advantage do DFT calculations have over the ROM method?

FIGURE 1

FIGURE 1. Workflow of machine learning based prediction of CCAs with advanced performance.

The possible SQS configurations of the alloys include AB, A₃B, ABC, A₂BC, ABCD, and ABCDE, in which A, B, C, D, E represent the refractory elements Cr, Hf, Mo, Nb, Re, Ta, Ti, V, W, and Zr. There were 1,077 alloys altogether, with initial configurations for 135 binary, 480 ternary, 210 quaternary, and 252 quinary alloys. CALPHAD calculations helped to eliminate alloys with stable single BCC phase at high temperature.

The structural and mechanical properties of BCC refractory multicomponent alloys at ground states were checked by the DFT (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) calculations. The unit cell of each BCC alloys defined by SQS was analyzed using Vienna Ab Initio Simulation Package (VASP 5.4) (Kresse and Furthmuller, 1996). The electron-ion interactions were described by the projector augmented wave (PAW) (Perdew et al., 1992), while electron exchange-correlation interactions were described by the generalized gradient approximation (GGA) (Perdew et al., 1996) in the Perdew-Burke-Ernzerhof (PBE) scheme (Monkhorst and Pack, 1976). The relaxation of the alloy atomic structures was performed using congregate-gradient algorithm (Gonze, 1997) implemented in VASP. An energy cutoff was set to be 300 eV for the plane wave basis in all calculations, and the criteria for the convergences of energy and force in relaxation processes were set to be 10^–5 eV and 10^–5 eV/Å, respectively. A smearing parameter of ∼0.2 eV was used for the Methfessel-Paxton (Methfessel and Paxton, 1989) technique.

Bulk modulus (B), shear modulus (G), and Pugh’s ratio (B/G) (Pugh, 1954) of all alloys screened out by CALPHAD were calculated at 0 K, using the Voigt-Reuss-Hill averaging scheme (Zuo et al., 1992). In addition, Young’s modulus (E) and Poisson’s ratio (ν) were calculated using the following equations: $E=9BG/\left(3B+G\right)$ and $=\left(3B-2G\right)/2\left(3b+G\right)$ . The Vickers hardness (H_v) was obtained by Tian’s model (Tian et al., 2012). Consequently, a dataset of alloys which contains properties including the mentioned features can be built. In this dataset, T_m implies the alloy temperature resistance, E describes the tendency of alloys to deform when stress is applied along a given axis, B denotes the deformation in all directions, and G represents deformation at constant volume. All features are essential for quantifying the alloy resistance to deformation.

The dataset was further screened by the Pearson correlation coefficient (Schober et al., 2018) in Pandas library to determine the association between any two features:

${\mathit{r}}_{\mathit{x}\mathit{y}}=\frac{\mathbf{1}}{\mathit{n}-\mathbf{1}}\frac{{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}\left({\mathit{x}}_{\mathit{i}}-\overline{\mathit{x}}\right)-\left({\mathit{y}}_{\mathit{i}}-\overline{\mathit{y}}\right)}{{\mathit{\sigma }}_{\mathit{x}}{\mathit{\sigma }}_{\mathit{y}}}(1)$

where n is the sample size, $\overline{x}$ and $\overline{y}$ are the mean values of two input features, ${\sigma }_x$ and ${\sigma }_y$ are the standard deviation of the two features. When the correlation coefficient’s absolute value is near to 1, it suggests that the properties are tightly connected. A correlation coefficient that is close to zero, on the other hand, indicates completely unconnected facts.

Through the Scikit-learn library (Pedregosa et al., 2011), the dataset was used to train the ML models, which comprise the Neural Network (NN), Random Forest (RF) regressor, Gradient Boosting Regressor (GBR), and XGBoost (XGB) (Chen and Guestrin, 2016). Information is sent from the input layer, hidden layer, and output layer by the NN model in order to create the output. The RF model uses a large number of decision trees in an ensemble technique to increase prediction accuracy and decrease over-fitting by averaging the trees. The GBR model is a kind of ensemble model that consists of an iterative collection of tree models and is able to draw lessons from the mistakes made by the preceding model. The XGB mode is a potent machine learning technique that quickly decides by efficiently and effectively deploying boosted decision trees. 90% of the data were used for training ML models that were used to predict the performance of refractory alloys, and 10% were used for testing and validating the outcomes. With a cross-validation score of 5, the GridSearchCV function from the Sklearn package was utilized to enhance the machine learning model. Each ML model’s performance is assessed using the mean absolute error, average coefficient of determination, and root-mean-squared error.

3 Results

According to the PCA technique as mentioned before, the parameters VEC, and $∆H_{mix}$ of alloy should reach the following requirement to have stable BCC phase: VEC < 6.87, −15 ≤ $∆H_{mix}$ ≤ 5 kJ/mol, and $\delta$ ≤ 6.6%. 545 out of 1,077 alloys were predicted to have stable BCC phase based on the PCA analysis. CALPHAD was then employed to calculate the phase diagram of alloys. It was found that most alloys, especially at low temperature, have more than one stable phase. Possible phase at low temperature may include BCC, hexagonal close-packed (HCP), sigma phase, and so on. Given that some pure refractory metals (Hf, Re, Ti, and Zr) are HCP crystals and others (Cr, Mo, Nb, Ta, V, and W) are BCC crystals, the observation is probable. Alloys made up of different element types tend to have more stable phases at low temperature due to their complex interactions. While the proportion of BCC phase increase with temperature for most refractory alloys. As a result, 393 refractory alloys appeared to have only BCC phase at high temperature.

Figure 2 demonstrates the transition temperature and melting temperature of alloys with only BCC phase present prior to melting, where the transition temperature represents the temperature at which other phases dissolve. The binary alloys were marked by black triangles; ternary alloys were marked by red triangles; quaternary alloys were marked by green triangles; and quinary alloys were marked by blue triangles, respectively. It has been found that BCC crystal formation in multicomponent alloys is promoted when only BCC type elements are present. In this work, the phase diagram of alloys was investigated in the temperature range 0°C–3,500°C, where the transition temperature is 0°C for 111 out of 393 alloys. It indicates that 111 multicomponent alloys exclusively contain BCC phase.

FIGURE 2

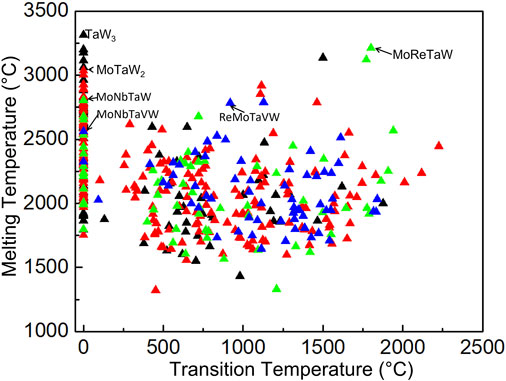
FIGURE 2. Melting and Transition temperature of (▲) binary, (▲) ternary, (▲) quaternary, and (▲) quinary multicomponent alloys. The 111 alloys (which appear lined-up at transition temperature equals to 0°C) have only BCC phase.

As shown in Figure 2, the melting temperature of all multicomponent alloys are above 1,300°C. These refractory alloys exhibit extremely high temperature resistance, 245 of them even have high melting temperature above 2000°C. Some of high melting temperature alloys are shown in the figure for reference. It should be noticed refractory alloys with high concentrations of W, Re, and Ta are anticipated to also have high melting temperatures since W has a high melting temperature above 3,000°C, followed by Re and Ta. For instance, the TaW₃ alloy has the highest melting temperature of 3,315°C. The ternary alloy MoTaW₂ has the highest melting temperature of 3,036°C. Even quaternary and quinary alloys MoReTaW, MoReTaVW and MoNbReTaW, also show high melting temperature above 2,500°C.

4 Discussion

4.1 Phase prediction by CALPHAD and PCA

Significant mismatch was found between PCA and CALPHAD on predicting phase of alloys. As mentioned above, 545 alloys out of 1,077 appeared to have stable BCC structure based on PCA correlation studies of VEC, $∆H_{mix}$ and $\delta$ . While according to the CALPHAD prediction, only 393 alloys have stable single BCC phase before melting. In detail, 18.7% binary, 20.5% trinary, 26.5% quaternary and 22.1% quinary alloys from the PCA estimation do not have a stable BCC single phase based on the CALPHAD calculations. Especially, the two methods differed significantly in predicting the phase of alloys containing Re, Hf, and Zr. It is reasonable since the PCA were studied based on only a small group of CCAs (Guo et al., 2011; Guo and Liu, 2011) (less than 100 alloys), in which insufficient data related to the Re, Hf, and Zr in their database were collected. While the database of CALPHAD calculation was built for CCAs involving a 15-element thermodynamic database. Meanwhile, nearly all of the stable solution phases of refractory binaries and trinaries in each of the evaluated systems are present in the database (Chen et al., 2018). In this case, the phases predicted by CALPHAD are more reliable.

4.2 Structure and mechanical properties by DFT and ROM

The SQS models for BCC crystal structures are shown in Figure 1A, where elements are represented in different colors. Based on SQS, there are 8 atoms per unit cell for AB binary alloys, 16 atoms in AB3, 36 atoms in ABC, 32 atoms in A2BC, 64 atoms in ABCD, and 125 atoms in ABCDE. The calculated structural and mechanical properties, as well as the melting temperature obtained by CALPHAD, are listed in the Supplementary Table S1. The structural properties of refractory alloys, including density and volume, obtained by DFT and ROM are compared in Figures 3A,B. The diagonal line in Figure 3 indicates excellent matching of the density and volume calculated by DFT and ROM, respectively. It is no surprise that the obtained refractory alloys are made of refractory elements with large densities. Both density and volume data are very close to the diagonal lines with trend functions of Density_DFT = 1.007 × Density_ROM + 0.131 and Volume_ROM = 0.939 × Volume_DFT + 0.859, and correlation coefficients of 0.996 and 0.995, respectively. These indicate that structural properties predicted by DFT and ROM are similar. The maximum difference of density between DFT and ROM calculation is 7.54%, and the maximum difference of volume between these two methods is 6.82%. Table 1 lists the DFT, ROM, and experimental density of selected refractory alloys. The error percentage (%), which accounts for the deviation of DFT/ROM from experimental data are also listed for comparison. The low error percentages are less than 5.5%, indicating that both DFT and ROM calculations are close to experimental data. Particularly, the overall error percentages for DFT to experiment data are less than 1%, whereas they are greater than 2% for ROM estimation, demonstrating higher accuracy of DFT.

FIGURE 3

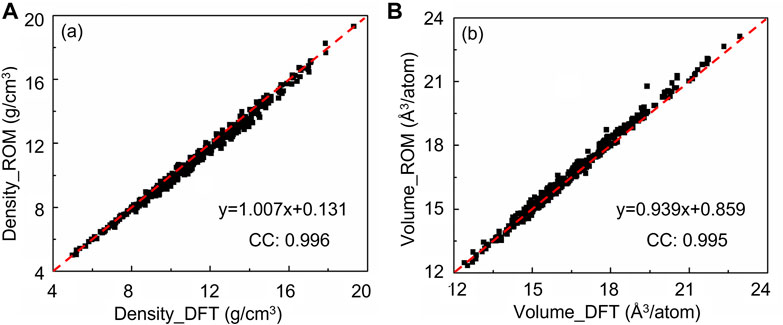
FIGURE 3. (A) Density and (B) Volume of refractory alloys calculated by ROM as a function of those calculated by DFT; red lines are the trends for each dataset.

TABLE 1

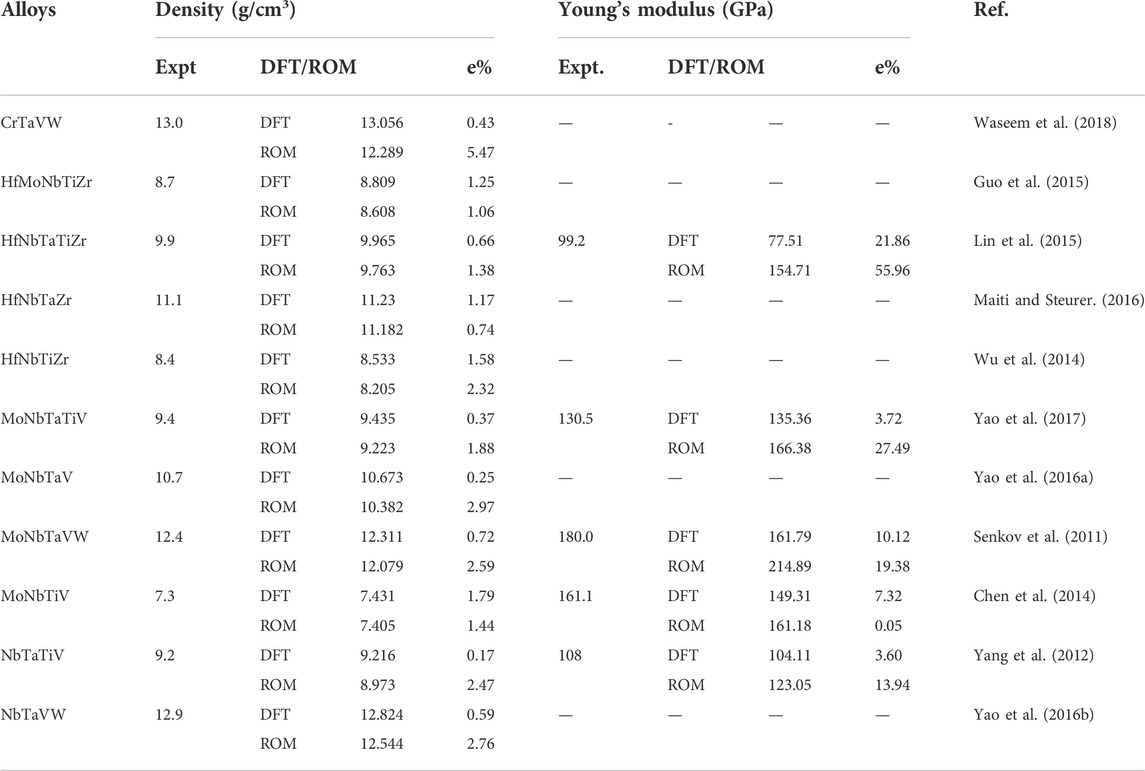
TABLE 1. The experimental observation (expt) of density and Young’s moduli of refractory alloys. The error percentage (e%) for DFT and ROM to experiments are listed in the table.

Different understanding of the mechanical properties based on DFT and ROM are presented in Figure 4, where the elastic constants C₁₁, C₁₂, and C₄₄, bulk moduli, shear moduli and Young’s moduli determined by DFT and ROM are demonstrated. Even through the correlation coefficients of certain parameters are close to 1, The significant difference between DFT and ROM can be obtained. The data in each figure are scattered with the correlation coefficients less than 0.97. The correlation coefficients of shear moduli and Young’s moduli are much lower, which represent that DFT and ROM simulation produced unrelated results. Furthermore, the tendencies of data in each figure are off the diagonal line with the coefficient of tendency less than 0.925, therefore indicating difference of DFT and ROM on calculating the mentioned property of alloys. The poor correlation coefficients, especially for C₄₄, shear moduli and Young’s moduli, represent the difference between DFT and ROM for predicting mechanical properties.

FIGURE 4

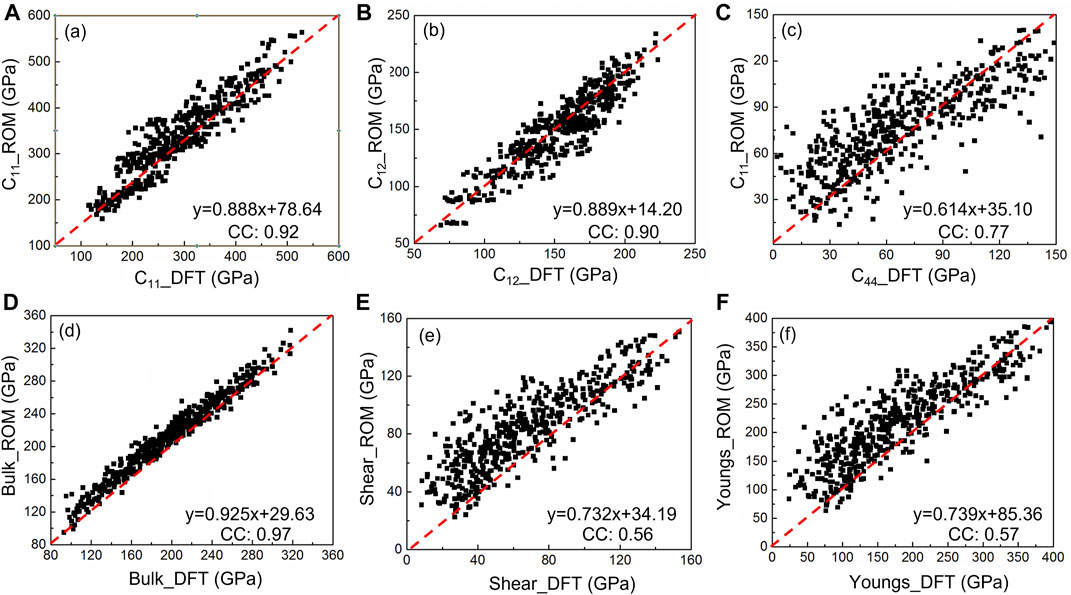
FIGURE 4. Ratios of DFT and ROM calculated elastic constants (A) C₁₁, (B) C₁₂, and (C) C₄₄, (D) bulk, (E) shear, and (F) Young’s moduli.

Table 1 lists Young’s moduli of various refractory alloys that were determined experimentally, by DFT, and ROM calculations in order to more thoroughly assess the predictions made by these methods. It is clearly shown that DFT calculations have a lower error percentage than that of ROM, is much lower than that of ROM, which indicates that DFT calculations are more in line with experimental data for Young’s modulus. This is reasonable since DFT takes into account how atoms interact physically while ROM calculations average the mechanical properties mathematically.

4.3 Evaluation of the quality of the dataset

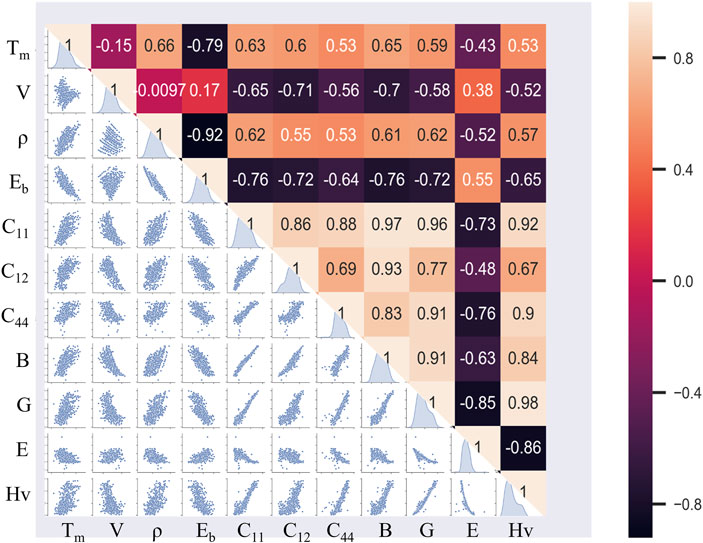
As discussed above, in this paper, a dataset that contains phase, structural, and mechanical properties of refractory alloys was built based on CALPHAD and DFT calculations. The correlation between each key parameters in the dataset are shown in the Heatmap diagram in the upper part of Figure 5, and the associated data scatter plots are given at the lower part of the matrix. In the heatmap diagram, the data dots in scatter plots matrix that are near to the diagonal or anti-diagonal lines show the absolute value of correlation coefficient close to 1, which implies features are highly correlated. On the other hand, the correlation coefficient close to 0 represents disordered data in the scatter plots matrix, which indicates the feature pairs are not correlated or, at most, weakly correlated. As shown in Figure 5, the majority of the analyzed traits had correlations between 0.3 and 0.8. These findings show that no irrelevant or redundant features exist in the developed database, suggesting that the DFT dataset of refractory alloy properties could yield reliable predictions for brand-new high-performance CCAs by ML.

FIGURE 5

FIGURE 5. Heatmap diagram and scatter plots matrix for one to one correlation between features.

4.4 ML study based on the dataset

The ML method is a rapidly developed technique for predicting materials with advanced performance. The dataset produced in this study has been utilized to predict the properties of CCAs such as hardness and elastic constants based on the workflow as shown in Figure 1. Various ML models were trained to investigate the mechanical properties of CCAs as illustrated in Figure 1D. Based on the dataset, the Neural Network (NN) model was trained to predict the Vickers hardness of alloys. It was predicted that C_0.1Cr₃Mo_11.9Nb₂₀Re₁₅Ta₃₀W₂₀ have hardness of 686 HV by (Bhandari et al., 2021), which lead to an error around 10% to the experimental test of 622.60 HV(Tian et al., 2012). The dataset was further used to train various ML models, including random forest regressor, gradient boosting regressor, and XGBoost regression models, to predict the mechanical properties of CCAs. For example, the elastic constants in the dataset were used to train those ML models (Bhandari et al., 2022) which were evaluated by the root-mean-squared error, the average coefficient of determination, and mean absolute error. It is found that gradient boosting regressor has higher prediction accuracy on elastic constants. The elastic constants of NbTaTiV predicted by gradient boosting regressor based on the dataset matches the experimental values well (Lee et al., 2020). Both examples highlight the excellent quality of the dataset and the potential of training ML models to predict CCA properties.

5 Conclusion

In this work, a dataset for 393 refractory alloys containing 2 to 5 different element types was assembled by combing CALPHAD and DFT simulations. For each refractory alloy, the phase type, atomic structure, and mechanical properties were determined, which include melting temperature (T_m), volume (V), density (ρ), total energy (E_tot), elastic constant (C₁₁, C₁₂, and C₄₄), bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (ν) and Vickers hardness (H_v). For predicting the stable single-phase of alloys under high temperature, CALPHAD and PCA techniques were evaluated. Since its database includes more information about the phase of refractory alloys, CALPHAD calculations are more trusted than the current PCA results for predicting the phase of alloys at various temperatures. The structural and mechanical properties were determined by DFT and ROM were compared. It is found that the DFT prediction of the structural properties of refractory alloy are comparable to those predicted by ROM, while the DFT prediction are more precise on mechanical property predictions. The dataset has been employed on predicting CCAs with advanced mechanical properties by ML technique such as hardness and elastic constants. Since CCAs performance predicted by ML trained by the refractory alloy dataset are compatible with experiments, the refractory alloys dataset can support the refractory alloy design based on ML model training and property prediction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CZ: Conceptualization, methodology, data curation, original draft preparation. XG: Resources. UB: Machine learning prediction. JL: Computational simulation. SG: Resources. MK: Resources. AK: Conceptualization, methodology. SY: Conceptualization, supervision. All authors: Review and editing the manuscript.

Funding

We acknowledge supports from DOE/NNSA (Grant No. DE-NA0003979) and DoD (Grant No. W911NF1910005). NSF award No. 2216805, NSF award No. 2154344, NSF award No. OIA-2019511, NSF award No. OIA-1946231, Louisiana BoR award No. LEQSF (2021-22)-ENH-DEC-22, and NSF/LA BoR award No. LEQSF-EPS(2022)-LAMDASeed-Track1C-09.

Acknowledgments

The computational simulations were supported by the Louisiana Optical Network Infrastructure (LONI) with the supercomputer allocation loni_mat_bio17.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ftmal.2022.1036656/full#supplementary-material

References

Andersson, J. O., Helander, T., Höglund, L., Shi, P., and Sundman, B. (2002). Thermo-Calc & DICTRA, computational tools for materials science. Calphad 26 (2), 273–312. doi:10.1016/S0364-5916(02)00037-8

CrossRef Full Text | Google Scholar

Bhandari, U., Ghadimi, H., Zhang, C., Yang, S., and Guo, S. (2022). Predicting elastic constants of refractory complex concentrated alloys using machine learning approach. Materials 15 (14), 4997. doi:10.3390/ma15144997

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhandari, U., Zhang, C., Zeng, C., Guo, S., Adhikari, A., and Yang, S. (2021). Deep learning-based hardness prediction of novel refractory high-entropy alloys with experimental validation. Crystals 11 (1), 46. doi:10.3390/cryst11010046

CrossRef Full Text | Google Scholar

Borkar, T., Gwalani, B., Choudhuri, D., Mikler, C. V., Yannetta, C. J., Chen, X., et al. (2016). A combinatorial assessment of AlxCrCuFeNi2 (0 < x < 1.5) complex concentrated alloys: Microstructure, microhardness, and magnetic properties. Acta Mater. 116, 63–76. doi:10.1016/j.actamat.2016.06.025

CrossRef Full Text | Google Scholar

Chang, Y.-J., Jui, C.-Y., Lee, W.-J., and Yeh, A.-C. (2019). Prediction of the composition and hardness of high-entropy alloys by machine learning. JOM 71 (10), 3433–3442. doi:10.1007/s11837-019-03704-4

CrossRef Full Text | Google Scholar

Chen, H.-L., Mao, H., and Chen, Q. (2018). Database development and Calphad calculations for high entropy alloys: Challenges, strategies, and tips. Mater. Chem. Phys. 210, 279–290. doi:10.1016/j.matchemphys.2017.07.082

CrossRef Full Text | Google Scholar

Chen, S. Y., Yang, X., Dahmen, K. A., Liaw, P. K., and Zhang, Y. (2014). Microstructures and crackling noise of AlxNbTiMoV high entropy alloys. Entropy 16 (2), 870–884. doi:10.3390/e16020870

CrossRef Full Text | Google Scholar

Chen, T., and Guestrin, C. (2016). “XGBoost: A scalable tree boosting system,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, California, USA, 13-17 August, 2016 (Association for Computing Machinery).

Google Scholar

Couzinié, J. P., Senkov, O. N., Miracle, D. B., and Dirras, G. (2018). Comprehensive data compilation on the mechanical properties of refractory high-entropy alloys. Data Brief 21, 1622–1641. doi:10.1016/j.dib.2018.10.071

PubMed Abstract | CrossRef Full Text | Google Scholar

Ezugwu, E. O., Wang, Z. M., and Machado, A. R. (1999). The machinability of nickel-based alloys: A review. J. Mater. Process. Technol. 86 (1), 1–16. doi:10.1016/S0924-0136(98)00314-8

CrossRef Full Text | Google Scholar

Gao, M. C., Carney, C. S., Doğan, Ö. N., Jablonksi, P. D., Hawk, J. A., and Alman, D. E. (2015). Design of refractory high-entropy alloys. JOM 67 (11), 2653–2669. doi:10.1007/s11837-015-1617-z

CrossRef Full Text | Google Scholar

Gao, M. C., Niu, C., Jiang, C., and Irving, D. L. (2016). “Applications of special quasi-random structures to high-entropy alloys,” in High-entropy alloys: Fundamentals and applications. Editors M. C. Gao, J.-W. Yeh, P. K. Liaw, and Y. Zhang (Cham: Springer International Publishing), 333–368.

CrossRef Full Text | Google Scholar

Gonze, X. (1997). First-principles responses of solids to atomic displacements and homogeneous electric fields: Implementation of a conjugate-gradient algorithm. Phys. Rev. B 55 (16), 10337–10354. doi:10.1103/PhysRevB.55.10337

CrossRef Full Text | Google Scholar

Griffiths, M. (2019). “Chapter 9 - Ni-based alloys for reactor internals and steam generator applications,” in Structural alloys for nuclear energy applications. Editors G. R. Odette, and S. J. Zinkle (Boston: Elsevier), 349–409.

CrossRef Full Text | Google Scholar

Guo, N. N., Wang, L., Luo, L. S., Li, X. Z., Su, Y. Q., Guo, J. J., et al. (2015). Microstructure and mechanical properties of refractory MoNbHfZrTi high-entropy alloy. Mater. Des. 81, 87–94. doi:10.1016/j.matdes.2015.05.019

CrossRef Full Text | Google Scholar

Guo, S., and Liu, C. T. (2011). Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 21 (6), 433–446. doi:10.1016/S1002-0071(12)60080-X

CrossRef Full Text | Google Scholar

Guo, S., Ng, C., Lu, J., and Liu, C. T. (2011). Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 109 (10), 103505. doi:10.1063/1.3587228

CrossRef Full Text | Google Scholar

Han, Z. D., Luan, H. W., Liu, X., Chen, N., Li, X. Y., Shao, Y., et al. (2018). Microstructures and mechanical properties of Ti NbMoTaW refractory high-entropy alloys. Mater. Sci. Eng. A 712, 380–385. doi:10.1016/j.msea.2017.12.004

CrossRef Full Text | Google Scholar

Himanen, L., Geurts, A., Foster, A. S., and Rinke, P. (2019). Data-driven materials science: Status, challenges, and perspectives. Adv. Sci. (Weinh). 6 (21), 1900808. doi:10.1002/advs.201900808

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136 (3), B864–B871. doi:10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

Hu, J., Stefanov, S., Song, Y., Omee, S. S., Louis, S.-Y., Siriwardane, E. M. D., et al. (2022). MaterialsAtlas.org: A materials informatics web app platform for materials discovery and survey of state-of-the-art. npj Comput. Mat. 8 (1), 65. doi:10.1038/s41524-022-00750-6

CrossRef Full Text | Google Scholar

Huang, W., Martin, P., and Zhuang, H. L. (2019). Machine-learning phase prediction of high-entropy alloys. Acta Mater. 169, 225–236. doi:10.1016/j.actamat.2019.03.012

CrossRef Full Text | Google Scholar

Kang, B., Lee, J., Ryu, H. J., and Hong, S. H. (2018). Ultra-high strength WNbMoTaV high-entropy alloys with fine grain structure fabricated by powder metallurgical process. Mater. Sci. Eng. A 712, 616–624. doi:10.1016/j.msea.2017.12.021

CrossRef Full Text | Google Scholar

Kim, G., Diao, H., Lee, C., Samaei, A. T., Phan, T., de Jong, M., et al. (2019). First-principles and machine learning predictions of elasticity in severely lattice-distorted high-entropy alloys with experimental validation. Acta Mater. 181, 124–138. doi:10.1016/j.actamat.2019.09.026

CrossRef Full Text | Google Scholar

Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140 (4), A1133–A1138. doi:10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmuller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54(16), 11169–11186. doi:10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Lederer, Y., Toher, C., Vecchio, K. S., and Curtarolo, S. (2018). The search for high entropy alloys: A high-throughput ab-initio approach. Acta Mater. 159, 364–383. doi:10.1016/j.actamat.2018.07.042

CrossRef Full Text | Google Scholar

Lee, C., Kim, G., Chou, Y., Musicó, B. L., Gao, M. C., An, K., et al. (2020). Temperature dependence of elastic and plastic deformation behavior of a refractory high-entropy alloy. Sci. Adv. 6 (37), eaaz4748. doi:10.1126/sciadv.aaz4748

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Xie, B., Fang, Q., and Li, J. (2021). Machine learning approach to design high entropy alloys with heterogeneous grain structures. Metall. Mat. Trans. A 52 (2), 439–448. doi:10.1007/s11661-020-06099-z

CrossRef Full Text | Google Scholar

Li, Z., Pradeep, K. G., Deng, Y., Raabe, D., and Tasan, C. C. (2016). Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 534 (7606), 227–230. doi:10.1038/nature17981

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, C.-M., Juan, C.-C., Chang, C.-H., Tsai, C.-W., and Yeh, J.-W. (2015). Effect of Al addition on mechanical properties and microstructure of refractory AlxHfNbTaTiZr alloys. J. Alloys Compd. 624, 100–107. doi:10.1016/j.jallcom.2014.11.064

CrossRef Full Text | Google Scholar

Maiti, S., and Steurer, W. (2016). Structural-disorder and its effect on mechanical properties in single-phase TaNbHfZr high-entropy alloy. Acta Mater. 106, 87–97. doi:10.1016/j.actamat.2016.01.018

CrossRef Full Text | Google Scholar

Maresca, F., and Curtin, W. A. (2020). Mechanistic origin of high strength in refractory BCC high entropy alloys up to 1900K. Acta Mater. 182, 235–249. doi:10.1016/j.actamat.2019.10.015

CrossRef Full Text | Google Scholar

Methfessel, M., and Paxton, A. T. (1989). High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 40 (6), 3616–3621. doi:10.1103/PhysRevB.40.3616

PubMed Abstract | CrossRef Full Text | Google Scholar

Miracle, D. B., and Senkov, O. N. (2017). A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511. doi:10.1016/j.actamat.2016.08.081

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Morinaga, M. (2019). “3 - nickel alloys,” in A quantum approach to alloy design. Editor M. Morinaga (Boston: Elsevier), 19–45.

CrossRef Full Text | Google Scholar

Murty, B. S., Yeh, J. W., and Ranganathan, S. (2014). “Chapter 3 - phase selection in high-entropy alloys,” in High entropy alloys. Editors B. S. Murty, J. W. Yeh, and S. Ranganathan (Boston: Butterworth-Heinemann), 37–56.

CrossRef Full Text | Google Scholar

Patriarca, L., Ojha, A., Sehitoglu, H., and Chumlyakov, Y. I. (2016). Slip nucleation in single crystal FeNiCoCrMn high entropy alloy. Scr. Mater. 112, 54–57. doi:10.1016/j.scriptamat.2015.09.009

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830. doi:10.5555/1953048.2078195

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Chevary, J. A., Vosko, S. H., Jackson, K. A., Pederson, M. R., Singh, D. J., et al. (1992). Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46 (11), 6671–6687. doi:10.1103/PhysRevB.46.6671

PubMed Abstract | CrossRef Full Text | Google Scholar

Pugh, S. F. (1954). XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philosophical Mag. J. Sci. 45 (367), 823–843. doi:10.1080/14786440808520496

CrossRef Full Text | Google Scholar

Roy, A., Babuska, T., Krick, B., and Balasubramanian, G. (2020). Machine learned feature identification for predicting phase and Young's modulus of low-medium- and high-entropy alloys. Scr. Mater. 185, 152–158. doi:10.1016/j.scriptamat.2020.04.016

CrossRef Full Text | Google Scholar

Schober, P., Boer, C., and Schwarte, L. A. (2018). Correlation coefficients: Appropriate use and interpretation. Anesth. Analgesia 126 (5), 1763–1768. doi:10.1213/ane.0000000000002864

PubMed Abstract | CrossRef Full Text | Google Scholar

Senkov, O. N., Wilks, G. B., Scott, J. M., and Miracle, D. B. (2011). Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 19 (5), 698–706. doi:10.1016/j.intermet.2011.01.004

CrossRef Full Text | Google Scholar

Shaikh, S. M., Hariharan, V. S., Yadav, S. K., and Murty, B. S. (2020). CALPHAD and rule-of-mixtures: A comparative study for refractory high entropy alloys. Intermetallics 127, 106926. doi:10.1016/j.intermet.2020.106926

CrossRef Full Text | Google Scholar

Singh, P., Sharma, A., Smirnov, A. V., Diallo, M. S., Ray, P. K., Balasubramanian, G., et al. (2018). Design of high-strength refractory complex solid-solution alloys. npj Comput. Mat. 4 (1), 16. doi:10.1038/s41524-018-0072-0

CrossRef Full Text | Google Scholar

Tian, Y., Xu, B., and Zhao, Z. (2012). Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Metals Hard Mater. 33, 93–106. doi:10.1016/j.ijrmhm.2012.02.021

CrossRef Full Text | Google Scholar

Tsai, M.-H., and Yeh, J.-W. (2014). High-entropy alloys: A critical review. Mater. Res. Lett. 2 (3), 107–123. doi:10.1080/21663831.2014.912690

CrossRef Full Text | Google Scholar

van de Walle, A., Asta, M., and Ceder, G. (2002). The alloy theoretic automated toolkit: A user guide. Calphad 26 (4), 539–553. doi:10.1016/S0364-5916(02)80006-2

CrossRef Full Text | Google Scholar

van de Walle, A. (2009). Multicomponent multisublattice alloys, nonconfigurational entropy and other additions to the Alloy Theoretic Automated Toolkit. Calphad 33 (2), 266–278. doi:10.1016/j.calphad.2008.12.005

CrossRef Full Text | Google Scholar

Vazquez, G., Singh, P., Sauceda, D., Couperthwaite, R., Britt, N., Youssef, K., et al. (2022). Efficient machine-learning model for fast assessment of elastic properties of high-entropy alloys. Acta Mater. 232, 117924. doi:10.1016/j.actamat.2022.117924

CrossRef Full Text | Google Scholar

Waseem, O. A., Lee, J., Lee, H. M., and Ryu, H. J. (2018). The effect of Ti on the sintering and mechanical properties of refractory high-entropy alloy TixWTaVCr fabricated via spark plasma sintering for fusion plasma-facing materials. Mater. Chem. Phys. 210, 87–94. doi:10.1016/j.matchemphys.2017.06.054

CrossRef Full Text | Google Scholar

Wen, C., Zhang, Y., Wang, C., Xue, D., Bai, Y., Antonov, S., et al. (2019). Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 170, 109–117. doi:10.1016/j.actamat.2019.03.010

CrossRef Full Text | Google Scholar

Wu, Y. D., Cai, Y. H., Wang, T., Si, J. J., Zhu, J., Wang, Y. D., et al. (2014). A refractory Hf25Nb25Ti25Zr25 high-entropy alloy with excellent structural stability and tensile properties. Mater. Lett. 130, 277–280. doi:10.1016/j.matlet.2014.05.134

CrossRef Full Text | Google Scholar

Xin, S. W., Zhang, M., Yang, T. T., Zhao, Y. Y., Sun, B. R., and Shen, T. D. (2018). Ultrahard bulk nanocrystalline VNbMoTaW high-entropy alloy. J. Alloys Compd. 769, 597–604. doi:10.1016/j.jallcom.2018.07.331

CrossRef Full Text | Google Scholar

Yang, X., Zhang, Y., and Liaw, P. K. (2012). Microstructure and compressive properties of NbTiVTaAlx high entropy alloys. Procedia Eng. 36, 292–298. doi:10.1016/j.proeng.2012.03.043

CrossRef Full Text | Google Scholar

Yao, H., Qiao, J.-W., Gao, M. C., Hawk, J. A., Ma, S.-G., and Zhou, H. (2016a). MoNbTaV medium-entropy alloy. Entropy 18 (5), 189. doi:10.3390/e18050189

CrossRef Full Text | Google Scholar

Yao, H., Qiao, J. W., Gao, M. C., Hawk, J. A., Ma, S. G., Zhou, H. F., et al. (2016b). NbTaV-(Ti, W) refractory high-entropy alloys: Experiments and modeling. Mater. Sci. Eng. A 674, 203–211. doi:10.1016/j.msea.2016.07.102

CrossRef Full Text | Google Scholar

Yao, H. W., Qiao, J. W., Hawk, J. A., Zhou, H. F., Chen, M. W., and Gao, M. C. (2017). Mechanical properties of refractory high-entropy alloys: Experiments and modeling. J. Alloys Compd. 696, 1139–1150. doi:10.1016/j.jallcom.2016.11.188

CrossRef Full Text | Google Scholar

Yao, M. J., Pradeep, K. G., Tasan, C. C., and Raabe, D. (2014). A novel, single phase, non-equiatomic FeMnNiCoCr high-entropy alloy with exceptional phase stability and tensile ductility. Scr. Mater. 72-73, 5–8. doi:10.1016/j.scriptamat.2013.09.030

CrossRef Full Text | Google Scholar

Ye, Y. F., Wang, Q., Lu, J., Liu, C. T., and Yang, Y. (2016). High-entropy alloy: Challenges and prospects. Mater. Today 19 (6), 349–362. doi:10.1016/j.mattod.2015.11.026

CrossRef Full Text | Google Scholar

Yeh, J.-W., Chen, S.-K., Lin, S.-J., Gan, J.-Y., Chin, T.-S., Shun, T.-T., et al. (2004a). Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mat. 6 (5), 299–303. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Yeh, J.-W., Lin, S.-J., Chin, T.-S., Gan, J.-Y., Chen, S.-K., Shun, T.-T., et al. (2004b). Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements. Metall. Mat. Trans. A 35 (8), 2533–2536. doi:10.1007/s11661-006-0234-4

CrossRef Full Text | Google Scholar

Zhang, B., Gao, M. C., Zhang, Y., Yang, S., and Guo, S. M. (2015). Senary refractory high entropy alloy MoNbTaTiVW. Mater. Sci. Technol. 31 (10), 1207–1213. doi:10.1179/1743284715Y.0000000031

CrossRef Full Text | Google Scholar

Zhang, Y., Wen, C., Wang, C., Antonov, S., Xue, D., Bai, Y., et al. (2020). Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 185, 528–539. doi:10.1016/j.actamat.2019.11.067

CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, Y. J., Lin, J. P., Chen, G. L., and Liaw, P. K. (2008). Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mat. 10 (6), 534–538. doi:10.1002/adem.200700240

CrossRef Full Text | Google Scholar

Zhang, Y., Zuo, T. T., Tang, Z., Gao, M. C., Dahmen, K. A., Liaw, P. K., et al. (2014). Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93. doi:10.1016/j.pmatsci.2013.10.001

CrossRef Full Text | Google Scholar

Zhou, Z., Zhou, Y., He, Q., Ding, Z., Li, F., and Yang, Y. (2019). Machine learning guided appraisal and exploration of phase design for high entropy alloys. npj Comput. Mat. 5 (1), 128. doi:10.1038/s41524-019-0265-1

CrossRef Full Text | Google Scholar

Zunger, A., Wei, S. H., Ferreira, L. G., and Bernard, J. E. (1990). Special quasirandom structures. Phys. Rev. Lett. 65 (3), 353–356. doi:10.1103/PhysRevLett.65.353

PubMed Abstract | CrossRef Full Text | Google Scholar

Zuo, L., Humbert, M., and Esling, C. (1992). Elastic properties of polycrystals in the Voigt-Reuss-Hill approximation. J. Appl. Crystallogr. 25(6), 751–755. doi:10.1107/S0021889892004874

CrossRef Full Text | Google Scholar