Transport in reverse osmosis membranes: observations and comments on the pore flow model versus the solution‒diffusion model

Sixty-four years have passed since the announcement of the cellulose acetate membrane for seawater desalination by Loeb and Sourirajan at UCLA on 23 Aug 1960. Reverse osmosis (RO) is now well established as a process for desalination of seawater, brackish water, as well as for wastewater treatment. The number of research papers on RO is growing. In contrast to the numerous publications on RO membrane preparation and applications, studies on transport mechanisms have been largely neglected. However, this changed recently when M. Elimelech’s research group from Yale University published several papers challenging the applicability of the solution‒diffusion (S‒D) model. Especially, in the most recent paper published in 2024, they have shown seven reasons why the well-accepted S‒D model appears to be wrong. It is interesting to note that, according to Srinivasa Sourirajan, one of the co-inventors of cellulose acetate RO membrane, their work was guided by the Preferential Sorption‒Capillary Flow model. Moreover, he wrote that this pore model was based on the presence of a pure water layer at the salt solution‒air interface, which could be predicted by the Gibbs Adsorption Isotherm. The purpose of this short communication is to present some observations and discussion in response to the 2024 paper published by Elimelech’s group in Desalination journal. In addition, the Gibbs Adsorption Isotherm was revisited to examine if there is a pure water layer at the sodium chloride‒cellulose acetate membrane interface.

1 Introduction

Sixty-four years have passed since the breakthrough announcement of the cellulose acetate membrane for seawater desalination by Sydney Loeb and Srinivasa Sourirajan at the University of California, Los Angeles (UCLA) on 23 Aug 1960. Sourirajan moved to the National Research Council Canada (NRC, Ottawa site) in 1961, where he set up a membrane program that lasted for 25 years, attracting membrane researchers worldwide. Takeshi Matsuura and Michael D. Guiver were two of those who had the opportunity of working at NRC on the fundamentals of reverse osmosis (RO) processes and RO membrane development while Sourirajan was active at NRC.

Since then, the reverse osmosis (RO) desalination process has steadily advanced, producing approximately 100 million m³ of drinking water per day in 2019 (Wikipedia, 2024). However, the transport of solvent (mostly water) and solute (sodium chloride, NaCl as the major component of seawater) is still not fully understood.

In the book “Reverse Osmosis” written by Srinivasa Sourirajan (Sourirajan, 1970) the author mentioned that the development of RO membranes was motivated by the Gibbs Adsorption Isotherm (GAI), employing Equation 1:

$\mathit{\Gamma }=-\frac{1}{RT}\frac{\partial \sigma }{\partial a}(1)$

where Γ, R, T, σ and a are the surface excess, gas constant, absolute temperature, surface tension of solution and activity of solute, respectively.

Since the surface tension of sodium chloride solution increases with an increase in activity (concentration) of sodium chloride, the surface excess becomes negative according to Equation 1, which means that sodium chloride is deficient at the air-solution interface.

Thus, the above equation predicts the presence of a thin layer of pure water, with a thickness on the order of a fraction of a nanometer (nm), at the interface between air and sodium chloride solution. Based on this equation, Sourirajan developed the Preferential Sorption‒Capillary Flow (PS‒CF) model, which became at that time, the guiding principle for the development of RO membrane for seawater desalination. According to this pore model, a pure water layer is assumed to be formed at the solution‒membrane interface as an analogue to the air‒solution interface. When pressure is applied on the feed salt solution, pure water flows through the pore whose radius is smaller than the thickness of the pure water layer, t, and pure water can be obtained as the permeate. When the pore radius is larger than t, salty water flows at the center of the pore and the removal of salt is incomplete (see Figure 1).

Figure 1

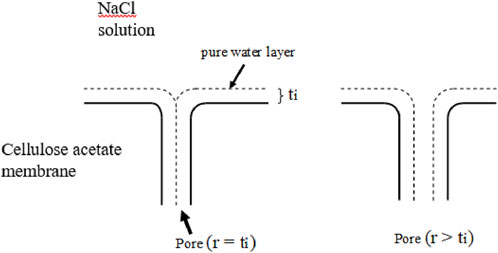
Figure 1. Principle of the PS‒CF model. Left, the pore radius (r) is equal to the thickness of the pure water layer (t), allowing complete salt rejection. Right, r is >t, allowing the passage of solute or salt.

Obviously, according to the model, the formation of many small pores is one of the prerequisites for the preparation of a viable RO membrane with appropriate water flux and high salt rejection. This contradicts the solution-diffusion (S‒D) model, which assumes uniform distribution of water in a rigid dense polymeric material without any pores. Soon after the development of the Loeb‒Sourirajan cellulose acetate membrane, Glückauf proposed an RO transport model based on the presence of subnano-sized pores (Glückauf, 1965). In the model it was mentioned that the lower dielectric constant of the polymer compared with water caused a repulsive force against the entry of electrolyte solutes into the subnano-sized pores of the RO membrane. Another paper based on the pore model was published by Jonsson and Boesen much later (Jonsson and Boesen, 1975). In their model, they considered the pore radius and pore length as the parameters that affect the solute rejection. Moreover, they incorporated friction parameters that are functions of the ratio of solute and pore radius.

A year after Glückauf’s paper was published, the Solution‒Diffusion (S‒D) model was proposed (Lonsdale, 1966), which has subsequently become the mainstream theory of RO membrane transport due to its greater simplicity. According to the model, both water and salt 1) are sorbed to the membrane at the feed side, 2) diffuse through the membrane under a pressure gradient and 3) are desorbed on the permeate side of the membrane. Thus, the S‒D model regards the membrane as a rigid polymeric material without any pores and diffusion takes place due to the concentration gradient in the membrane. The S‒D model was further originally supported by electron microscope images of the membrane surface, which showed no visible pores.

But deep in the minds of many researchers in that period, it seemed that the presence of pores was accepted intuitively. At one of the earlier Gordon Research Conferences on Membranes, W. Pusch, one of the advocates of the S‒D model, asked of the audience those who are pore-philic, meaning those who agree with the presence of pores, to raise their hands. Surprisingly, more than half of the audience raised their hands. It is also remembered that H. Ohya of National Yokohama University mentioned “If you prepare RO membranes yourself, you cannot help believing that there are pores in the membrane”.

Many years have passed since then, and the S‒D model became firmly entrenched in the membrane community to the extent that arguments supporting pore models were difficult to get published in mainstream journals. Subsequently, the dominant material for RO membranes has shifted from cellulose acetate to aromatic polyamides in the form of thin-film composite (TFC) membranes. Enormous improvements in instrumentation have enabled advanced characterization methods, which can now detect sub-nm pores and water channels in these new membranes.

In contrast to numerous publications on RO membrane preparation and applications, the study of transport has been largely overlooked in the intervening years, until recently, when M. Elimelech’s research group from Yale University published several papers (Heiranian et al., 2023; Wang et al., 2023; Wang et al., 2021; Fan et al., 2024) in which they challenged the applicability of the well-established S‒D model for RO transport. Especially, in the most recent paper of 2024, they presented seven reasons why the S‒D model appears to be incorrect (Fan et al., 2024). Understanding the true mechanism of RO transport, whether it is by the well-established S‒D model, by pore transport, or by a combination of both, has major implications with regards to the design of membranes, since it will be influential for their fabrication processes.

In this short communication, we provide some discussion points and observations related to their paper published in the journal Desalination (Fan et al., 2024). As well, the Gibbs Adsorption Isotherm (GAI) will be revisited to examine if there exists a pure water layer at the sodium chloride‒cellulose acetate membrane interface.

2 Discussion

2.1 Observations and comments on the findings of Fan et al.’s paper

2.1.1 RO membranes are not homogeneous, nonporous polymer phases

As mentioned by Fan et al. (2024), instrument characterization techniques such as small angle neutron scattering (SANS), positron annihilation lifetime spectroscopy (PALS), transmission electron microscopy (TEM) and atomic force microscopy (AFM) have supported the presence of “pores” of sub-nanometer size in aromatic polyamide and cellulose acetate RO membranes. Among these, PALS has made a major impact on membrane characterization. In this technique, a positron or positronium (Ps) (a bound atomic system consisting of an electron and the positron) will annihilate when it interacts with the surrounding electrons in the surrounding polymer matrix, releasing Gamma rays that can be detected; The time between the emission of positrons from a radioactive source and the detection of Gamma rays is thought to be the lifetime of the positrons. When positrons are injected to a solid body such as a polymeric material, positrons interact with the electrons in the material and annihilate rapidly. However, in the presence of voids or pores, the annihilation is delayed by up to 1 ns. Thus, from the lifetime of the positron, the size of the void (pore) can be evaluated. PALS is capable of determining the free-volume (FV) and hole properties directly at the atomic and nanoscale. Positronium tends to be localized or trapped before its annihilation within FV, or, in other words, in areas with reduced electron density such as in pores. Accordingly, annihilation characteristics, such as life-times and intensities of longer lifetime components of annihilation radiation, give information on concentrations, sizes and distribution of the void volume.

As well, when a log-normal plot was made for solute separation vs. solute size, two inflection points appeared, implying a bimodal distribution of nanoscale pores, which was corroborated by PALS (Kim et al., 2005). This observation cannot be explained by the S‒D model which requires a uniform distribution of the solute in the membrane matrix.

Recent progress in RO transport has been made mostly by Molecular Dynamics Simulation (MDS) applied for aromatic polyamide TFC membranes. MDS uses computer simulations to study the structure of water in a membrane and the movement of water molecules through a membrane at the molecular level, allowing insights into the interactions of individual water molecules with the membrane material as they pass through channels or pores. Harder et al. (2009) simulated the formation of the cross-linked polyamide layer by progressive cross-linking and concluded that there were two peaks in the pore size distribution at the radii of 0.3 and 0.5 nm, which are, respectively, network pores and aggregate pores. Shen et al. (2016) simulated the formation of cross-linked FT-30 TFC membrane by allowing trimesoyl chloride (TMC) and m-phenylenediamine (MPD) monomers move about randomly in a computational box. They also showed a bimodal pore distribution in dry membrane with diameters of 0.42–0.48 nm and 0.70–0.90 nm. Ding et al. (2014) conducted MDS for polyamide RO membrane in its hydrated state and obtained an average pore radius of 0.25 nm. Araki et al. (2015) ran an MDS of carbon nanotube‒polyamide RO membranes and found a strong orientation of MPD monomer near single walled carbon nanotubes (SWCNTs). When the membrane was hydrated, the membrane with SWCNT retained a single pore distribution with a radius of 0.231 nm, while the membrane without SWCNT exhibited a bimodal pore distribution with peaks at 0.15 and 0.25 nm.

Thus, MDS also detected sub-nanometer pores in polyamide TFC membranes and the data agreed well with those obtained by instrument characterization methods.

2.1.2 Hydrostatic pressure across RO membranes is not uniform

Lonsdale employed the S‒D model to analyse the transport of water and salt in RO membrane. He has shown the following chemical potential gradient of water by Equation 2, also called the extended chemical potential gradient (Song et al., 2021), as the driving force for the water flow.

$\nabla {\mu }_{Bm}=RT\nabla \ln a_{Bm}+{\nu }_B\nabla p_m(2)$

where μ, R, T, a, ν_B and p are chemical potential, gas constant, absolute temperature, activity, partial molar volume and pressure, respectively. The subscripts B and m are for water and inside the membrane, respectively.

Integrating from the feed to permeate side of the membrane with an assumption that ${\nu }_B$ is constant, gives Equation 3

${\mu }_{Bm,p}-{\mu }_{Bm,f}=RT\left(\ln a_{Bm,p}-\ln a_{Bm,f}\right)+{\nu }_B\left(p_{m,p}-p_{m,f}\right)(3)$

where the subscripts f and p are for feed and permeate side, respectively.

Now, it is assumed that thermodynamic equilibrium is established at the feed solution‒membrane interface, then Equation 4 holds

${\mu }_{Bm,f}={\mu }_{B,f}(4)$

where ${\mu }_{B,f}$ is the chemical potential of water in the feed solution. Further assuming that the pressure in the membrane is equal to the feed solution pressure, $p_f$ at the interface, leads to Equation 5

$p_{m,f}=p_f(5)$

Then, the activity, a, of water in the membrane should be equal to the activity of water in the feed solution, which is related to the osmotic pressure, π, by Equation 6

$\ln a_{Bm,f}=\ln a_{B,f}=-\frac{{\nu }_B}{RT}{\pi }_f(6)$

Therefore, rewriting Equation 6 gives Equation 7

$RT\ln a_{Bm,f}=-{\nu }_B{\pi }_f(7)$

Similarly, at the membrane‒permeate solution interface, the conditions can be expressed by Equation 8

${\mathit{p}}_{\mathit{m},\mathit{p}}={\mathit{p}}_{\mathit{p}}\text{\hspace{0.17em}and\hspace{0.17em}}\mathit{RT}\ln {\mathit{a}}_{\mathit{B}\mathit{m},\mathit{p}}=-{\mathit{\nu }}_{\mathit{B}}{\mathit{\pi }}_{\mathit{p}}(8)$

Thus, the difference in chemical potential of water between the permeate and feed side can be represented by Equation 9

${\mu }_{Bm,p}-{\mu }_{Bm,f}={\nu }_B\left\{-\left({\pi }_p-{\pi }_f\right)+\left(p_p-p_f\right)\right\}(9)$

or more simply by Equation 10

$∆\mu =∆p-∆\pi (10)$

where these terms are defined by Equation 11

$∆\mu ={\mu }_{Bm,f}-{\mu }_{Bm,p},∆p=p_f-p_p\text{\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}∆\pi ={\pi }_f-{\pi }_p(11)$

$∆\mu$ is well known as the driving force for the water flow in RO.

It should be noted that the p values at the two ends of the membrane, i.e., $p_{m,f}\text{\hspace{0.17em}and\hspace{0.17em}}{p}_{m,p}$, are set equal to those of the solutions, i.e., $p_f\text{\hspace{0.17em}and\hspace{0.17em}}{p}_p$, respectively (Equations 5, 8), but the profile of $p_m$ across the membrane is not given. Therefore, it cannot be said that the S‒D model for the water transport in the RO membrane is based on a constant pressure across the membrane.

The profiles of $a_{Bm}$ and $p_m$ are not independent but they are bound to each other by Equation 2. Rosenbaum and Cotton reported in their 1969 paper that the water concentration in the membrane changed linearly across the membrane, which is possible only when the pressure is constant across the membrane (Rosenbaum and Cotton, 1969). But their experimental results may not be applicable for all RO membranes.

As for the solute transport of RO, the chemical potential is written as Equation 12

$\nabla {\mu }_{Am}=RT\nabla \ln a_{Am}+{\nu }_B\nabla p_m(12)$

where subscript A is for the solute.

Integrating from feed to permeate side gives Equation 13

$∆{\mu }_{Am}=RT∆\ln a_{Am}+{\nu }_B∆p_m(13)$

Lonsdale dropped the pressure term and the chemical potential change was approximated by Equation 14

$∆{\mu }_{Am}=RT∆\ln a_{Am}(14)$

This approximation was justified not by the assumption of constant $p_m$ across the membrane, but because $RT∆\ln a_{Am}\gg {\nu }_B∆p_m$. Again, Lonsdale did not assume a constant pressure across the membrane.

On the other hand, Lee assumed that the pressure is constant across the membrane and equal to the feed solution pressure when he interpreted RO and pervaporation combined into one transport theory (Lee, 1975). Greenlaw et al. (1977) also adopted the same assumption in their study on pervaporation. It should be noted that there are two ways of ignoring the pressure term in the chemical potential equation. In the first, it is mentioned that the contribution of the pressure term is too small compared with that of the activity term. In the second, the pressure is constant across the cross-section of the membrane. In both cases, the activity (concentration) gradient becomes the sole contributor to the chemical potential gradient and RO transport occurs only by diffusive flow. It should also be noted that dropping the pressure term converts the partial differential equation to an ordinary differential equation, which renders the mathematics easier.

Thus, Lonsdale did not necessarily assume constant pressure across the RO membrane but other researchers (Lee, 1975; Greenlaw et al., 1977) used constant pressure, particularly for pervaporation transport.

2.1.3 Water molecules are not dispersed in the membrane

Zimm and Lundberg proposed the cluster function defined by Equation 15

$\frac{G_{11}}{{\overline{v}}_1}=-{\varnothing }_2{\left[\frac{\partial \left(\frac{a_1}{{\varnothing }_1}\right)}{\partial a_1}\right]}_{P,T}-1(15)$

where $G_{11}$ is cluster integral, ${\overline{v}}_1$ is partial molar volume of water, ${\varnothing }_1$ and ${\varnothing }_2$ are volume fractions of water and polymer, respectively and $a_1$ is the activity of water (Zimm and Lundberg, 1956). Furthermore, $1+{\varnothing }_1\frac{G_{11}}{{\overline{v}}_1}$ is called the cluster size. For the ideal solution, $\frac{G_{11}}{{\overline{v}}_1}$ is supposed to be −1 and therefore the cluster size should be less than 1. Strathmann and Von Mylius (1976) plotted $1+{\varnothing }_1\frac{G_{11}}{{\overline{v}}_1}$ versus solubility parameter for a number of polymers. They demonstrated that the cluster size was smallest with a solubility parameter range of 15–20 ${\left(\text{cal}/{\text{cm}}^3\right)}^{1/2}$, where polymers such as aromatic polyamide, polyamide hydrazide, polybenzpyrrolidone and polyimide are found. Note that RO membranes could be made from some of those polymers. In particular, aromatic polyamide and polyamide-hydrazide showed cluster sizes of about 2.5. Vieth et al. (1969) plotted $1+{\varnothing }_1\frac{G_{11}}{{\overline{v}}_1}$ versus effective diffusivity and stated that the cluster sizes of cellulose acetates are in a range of 1–2.

Both Strathmann and Von Mylius and Vieth et al. showed that water is well dispersed in the polymers from which RO membranes are fabricated. However, water and polymer do not form ideal solution.

2.1.4 A concentration gradient of water molecules in the membrane does not exist

According to the S‒D model, diffusion is the only mechanism for water transport in the RO membrane. Therefore, it is important to know if there is any concentration gradient of water molecules, which is the driving force for the diffusive flow, in the RO membrane. Currently, the only experimental result that supports the presence of a water concentration gradient is that of Rosenbaum and Cotton, who measured the water content at each layer of stacked dense cellulose acetate films (Rosenbaum and Cotton, 1969). However, as Fan et al. (2024) correctly pointed out, the total thickness of the films was 500 μm, which is orders of magnitude thicker than the skin layer of the asymmetric RO membrane, and the decrease in water content from the feed to the permeate side was only a few percent. Therefore, Rosenbaum and Cotton’s experimental result does not necessarily justify the assumption of a water concentration gradient that is required for the S‒D model.

Currently, there is no practical experimental technique that can determine the concentration profile across the selective layer of polyamide TFC membranes, which is as low as 100 nm. Therefore, Fan et al. (2024) used the data obtained from their own MDS to reject the existence of a water concentration gradient. Much work has been reported in the literature on MDS of desalination by polyamide TFC membranes during the last decade. However, we could find only a few studies in which the water concentration profile was recorded under the RO operational conditions of hydrated polyamide TFC membranes.

He et al. (2023) reported their study on the relationships between synthesis/preparation (membrane thickness and morphology), atomic-scale transport mechanism and separation performance (permeability and selectivity) for 3D-printed polyamide membranes. Their study employed non-equilibrium molecular simulations across a membrane thickness range of 4–32.4 nm and an extremely high transmembrane pressure difference of 30–150 MPa (equivalent to 300–1,500 bar). In Figure 2A of their paper, they reported the change of water content across the dense layer of the membrane whose thickness was 32.5 nm. Because the data scatter considerably along the z-axis, it is difficult to observe any trend in the water content profile. However, it appears there is a slight decrease from above 0.25 g/cm³ at the feed side to below 0.25 g/cm³ at the permeate side. It should be noted that the salt concentration in the feed solution and the cross-membrane pressure difference were not given in Figure 2A. It is interesting to note that they also reported the bimodal pore size distribution with network and aggregate pore.

Thus, Rosenbaum and Cotton’s experiments with stacked cellulose acetate layers are currently the only proof for the presence of concentration gradient in RO membrane. MDS, on the other hand, has demonstrated that water concentration did not change across the cross-section of RO membrane.

2.1.5 Water transport in osmosis does not follow a solution‒diffusion mechanism

Again, looking into Lonsdale’s work, when the thermodynamic equilibrium is established at the solution‒membrane interface on the feed side, ${\mu }_{Bm,f}={\mu }_{B,f}$ (Equation 4) is obviously acceptable.

However, they assumed that the pressure within the membrane, $p_{m,f}$ is equal to the feed solution pressure, $p_f$ at the interface (i.e., $p_{m,f}=p_f$ as expressed in (Equation 5). This leads to $\ln a_{Bm,f}=\ln a_{B,f}=-\frac{{\nu }_B}{RT}{\pi }_f$ as expressed in Equation 6.

This implies that both the pressure and activity term remain unchanged at the interface, which is a highly simplified assumption. It seems more precise to deal with Equation 4 assuming that the sum of the pressure and activity term remain unchanged, shown by Equation 16, especially for forward osmosis, i.e.,

$p_{m,f}-\frac{{\nu }_B}{RT}{\pi }_{m,f}=p_f-\frac{{\nu }_B}{RT}{\pi }_f(16)$

Applying the van’t Hoff Equation 17, gives Equation 18

$\pi =RTc(17)$

$\left(p_{m,f}-p_f\right)={\nu }_B\left(c_{m,f}-c_f\right)(18)$

Since in forward osmosis $c_{m,f}=c_f=0$. Therefore,

$p_{m,f}=p_f\left(=\text{usually\hspace{0.17em}}1\text{\hspace{0.17em}atmosphere\hspace{0.17em}pressure}\right)$

On the permeate side, this gives Equation 19, similar to Equation 18

$\left(p_{m,p}-p_p\right)={\nu }_B\left(c_{m,p}-c_p\right)(19)$

Since in the semipermeable membrane, $c_{m,p}=0$, but $c_p>0$, this gives the relationship shown by Equation 20

$p_{m,p}=p_p-{\nu }_B{c}_p(20)$

Equation 20 is exactly the same as the equation derived by Debye and Manning and Kay (Debye, 1923; Manning and Kay, 2023). In other words, water flows across the semipermeable membrane due to a pressure gradient.

2.1.6 Diffusion is a misused concept in the solution diffusion model

Among the papers quoted in this section of the work of Fan et al. (2024), the study by Yasuda et al. (1971) particularly drew our attention. They evaluated the permeability, P, that is related to the diffusive transport of water through the membrane, by measuring the diffusion rate of tritiated water that contains a hydrogen isotope having two neutrons and one proton in the nucleus. Tritiated water behaves essentially the same as regular water in terms of diffusion, due to its similar molecular size and structure, thus allowing the measurement of water movement without applying pressure. They also evaluated the hydraulic permeability of water, K, measuring the water flux under hydraulic pressure gradient. They reported, $\omega =KRT/v_{1}P$, where R is the gas constant, T is the absolute temperature and $v_1$ is the molar volume of water, as the ratio of total (diffusive + hydraulic) permeability to diffusive permeability for various polymeric membranes. The volumetric fraction of water, H, in the membrane was in the range of 0.01–0.86. Interestingly, $\omega$ was 2.01 for the film made of cellulose acetate, with 39.8 wt% acetyl content (the polymer used to prepare cellulose acetate RO desalination membrane) with H = 0.12, meaning the contribution of hydraulic and diffusive flow to the water transport is nearly equal. This ratio is much smaller than glycerol methacrylate (GMA) film (H = 0.86) of $\omega$ = 179 and those of synthetic collodion membranes, 36–730, which was reported in Manning and Kay’s paper.

Thus, it appears unlikely that RO transport takes place solely by diffusive flow.

2.1.7 Water and salt are treated independently in the solution diffusion model

Indeed, in the transport model presented by Lonsdale, solvent (water) and solute transport were treated independently. Later, Michaels et al. (1965) analysed the data of salt passage through cellulose acetate membrane and concluded that the salt passage occurs by the following three mechanisms.

a) Sorption and diffusion of ions in the polymer matrix

b) Diffusion of ions in near molecular sized pores

c) Hydrodynamic flow of saline solution through large pores

Obviously, the salt transport by the third mechanism deals with the coupling of water and salt transport. They plotted $J_2/C_2^{\alpha }$ vs. pressure of the experimental data, where $J_2$ is the salt flux and $C_2^{\alpha }$ is the salt concentration in the feed solution. Based on the plot, they made the statement “Diffusive transport of salt in the polymer accounts for a significant fraction of the ion flux, the balance being accounted for by bulk flow of saline solution through a very small number of rather large pores”, which implies that the salt transport took place by the combined mechanisms of a) and c). However, they did not mention the relative proportions of diffusive and bulk flow in the total salt flow.

Sherwood et al. (1967) used the following two Equations 20, 21 for the transport of salt and water through RO membrane.

$N_s=k_s{M}_s\left(c_i-c_p\right)+k_2{M}_s∆P{c}_i(21)$

$N_w=k_1\left(∆P-∆\pi \right)+k_2{M}_w∆P{c}_w(22)$

where $N_s\text{\hspace{0.17em}and\hspace{0.17em}}{N}_w$ are the weight flux of solute and water, respectively. $k_1,k_2\text{and}{k}_s$ are the membrane coefficients for the diffusion of water, pore flow and diffusion of salt, respectively. c_i and c_w are salt and water concentrations at the upstream membrane surface and c_p is the downstream salt concentration. Obviously, the first term of Equations 21, 22 is concerned with the diffusive flow through the polymer matrix and the second term convective flow in the pore. Even though coupling of water and salt is taken into consideration, especially in the second term of Equation 21, the water and salt transport are uncoupled in the first term of Equations 21, 22 that are based on the S‒D model.

Thus, attempts have been made by these authors to incorporate the coupling of water and salt transport, but their approach seems more practical than fundamental.

Additional evidence is that the Staverman reflection coefficient $\mathrm{\sigma }$ in the following Equation 23 is often less than one for RO membranes, indicating that the solute and water flow are coupled.

$Waterflux=B\left\{\left(p_f-p_p\right)-\mathrm{\sigma }\left({\pi }_f-{\pi }_p\right)\right\}(23)$

where $B$ is the permeability of water.

2.2 On the surface excess of cellulose acetate membrane

From the above discussions, it is noted that in the thermodynamic approach for membrane transport, the equilibrium between bulk phases (solution and membrane phase) are considered, while the interfacial phase between the solution and membrane has been largely overlooked, in most cases. It has to be again emphasized that the presence of a pure water layer at the interface predicted by the Gibbs Adsorption Isotherm (GAI) guided early research for the development of cellulose acetate RO membranes. Therefore, it seems prudent to pay more attention to the interfacial water structure. Litman et al. (2024) reported recently that the outermost surface is ion-depleted, and the subsurface layer is ion-enriched, causing ion-induced water reorganization at the outermost air/water interface, by combining surface-specific heterodyne-detected vibrational sum-frequency generation with neural network-assisted ab initio MDS. This paper has cast new light on the detailed structure of electrolyte solutions at the air‒solution interface.

There is also a need to revisit the GAI and investigate the state of the solution‒membrane interface. The question especially arises whether a similar interfacial pure water layer forms between cellulose acetate membrane and NaCl solution. To answer this question, GAI is now rewritten as Equation 24

$\mathit{\Gamma }=-\frac{1}{RT}\frac{\partial {\sigma }_{sl}}{\partial a}(24)$

where ${\sigma }_{sl}$ is the interfacial tension between solid (cellulose acetate) and liquid (water).

Applying the Young equation to the case of RO gives Equation 25

${\sigma }_{sg}={\sigma }_{sl}+\sigma \cos \theta (25)$

where σ_sg is the surface tension of solid (cellulose acetate), σ_sl is the interfacial tension between the liquid and the solid, σ is the surface tension of liquid (NaCl solution), and θ is the contact angle of NaCl solution at the cellulose acetate surface.

Rearranging the above equation gives Equation 26,

${\mathit{\sigma }}_{\mathit{sl}}={\mathit{\sigma }}_{\mathit{sg}}-\mathit{\sigma }\cos \mathit{\theta }(26)$

${\sigma }_{sg}$ does not depend on NaCl concentration and $\sigma$ is known to be a function of increasing NaCl concentration. Therefore, $\mathit{\Gamma }$ can be obtained by measuring the contact angle, $\theta$, of NaCl solution at different NaCl concentrations.

The contact angles were measured for a commercial cellulose triacetate membrane (CTA-NW) from Hydration Technology Innovations LLC (HTI), which is used in forward osmosis applications. $\mathit{\Gamma }$ was found to be −1.43 $\times$ 10^–6 mol/m² at 3.5 wt% NaCl solution, which is six times as large as that at the solution‒air interface (see Supplementary Material for the detailed calculation).

As shown in Supplementary Table S1 of the Supplementary Materials, the maximum error in contact angle measurement is 5.74° (0.1 radian). The average contact angle changed from 52.53° to 63.08° as NaCl concentration increased from 0 to 5 wt%. The error in the estimation of cosine (contact angle) change caused by the error of contact angle measurement is ±7%, which is also the error range of the surface excess assessment.

3 Conclusion and future directions

Considering all of the above work, we conclude that it appears unlikely that diffusive flow driven by the concentration gradient of water (which is homogeneously distributed in the membrane, an assumption underlying the S‒D model) can be either the sole or correct mechanism describing RO transport. Hydraulic flow is also an important component of water flow in the membrane. It is also noted that the RO transport in polyamide TFC membrane has subsequently been studied by using more advanced characterization instruments such as PALS and also by MDS, but the classical experiments such as the diffusion of tritiated water and the measurement of water content across the membrane still remain to be done for polyamide TFC membranes. GAI was applied to calculate the surface excess at the NaCl solution‒cellulose triacetate interface. It was found that the surface excess so calculated was 6 times as large as that at the NaCl solution‒air interface, implying a thicker pure water layer at the cellulose triacetate surface. Thus, there is a need to incorporate solution membrane interfacial phenomena into membrane transport models.

The solution-diffusion (S‒D) model has been mainstream among membrane scientists in describing the water transport mechanism in RO membranes for many years. In the S‒D model, water is sorbed into the membrane and then diffuses through the RO membrane by a concentration gradient of water. However, Fan et al. (2024) challenged these widely-accepted S‒D model assumptions recently by their own experimental and theoretical findings, enumerating the following seven flaws in the S‒D model: 1) disregarding the porous structure of RO membranes, 2) assuming a constant pressure profile along membranes, 3) using a water concentration gradient as the driving force, 4) assuming dispersed water molecules in RO membranes, 5) violating the physical nature of osmosis, 6) misusing the concept of diffusion, and 7) neglecting the coupling between water and salt transport. Thus, they justified the pore model, in which water flows through the pores driven by the pressure gradient in the membrane. They also mentioned that research efforts are needed to better understand the frictional interactions between solute, membrane and water to aid in the development of next-generation RO membranes.

Undoubtedly, recent publications by the prominent Elimelech group [e.g., Fan et al., 2024] questioning the applicability of the well-established S‒D model in favor of the controversial pore model will reignite vigorous and sometimes contentious scientific debate on the mechanism of RO transport, that has laid dormant for so long.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

TM: Methodology, Writing–review and editing, Conceptualization, Data curation, Formal Analysis, Investigation, Validation, Writing–original draft. MDG: Methodology, Writing–review and editing, Project administration. WL: Data curation, Investigation, Methodology, Validation, Writing–review and editing. AI: Investigation, Methodology, Supervision, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors extend their gratitude to Rickson Jun Jay Chia for conducting the contact angle analysis on the CTA membrane samples.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frmst.2025.1513591/full#supplementary-material

References

Araki, T., Cruz Silva, R., Tejima, S., Takeuchi, K., Hayashi, T., Inukai, S., et al. (2015). Molecular Dynamics study of carbon nanotubes/polyamide reverse osmosis membranes: polymerization, structure, and hydration. ACS Appl. Mater. Interfaces 7, 24566–24575. doi:10.1021/acsami.5b06248

PubMed Abstract | CrossRef Full Text | Google Scholar

Debye, P. (1923). Théorie Cinétique des Lois de la Pression Osmotique des Électrolytes Forts. Recl. Trav. Chim. Pays-Bas 42, 597–604. doi:10.1002/recl.19230420711

CrossRef Full Text | Google Scholar

Ding, M., Szymczyk, A., Goujon, F., Soldera, A., and Ghoufi, A. (2014). Structure and Dynamics of water confined in a polyamide reverse-osmosis membrane: a molecular-simulation study. J. Membr. Sci. 458, 236–244. doi:10.1016/j.memsci.2014.01.054

CrossRef Full Text | Google Scholar

Fan, H., Heiranian, M., and Elimelech, M. (2024). The solution-diffusion model for water transport in reverse osmosis: what went wrong? Desalination 580, 117575. doi:10.1016/j.desal.2024.117575

CrossRef Full Text | Google Scholar

Glückauf, E. (1965). On the mechanism of osmotic desalting with porous membranes. Proc. First Int. Symposium Water Desalination 1, 143–156.

Google Scholar

Greenlaw, F. W., Prince, W. D., Shelden, R. A., and Thompson, E. V. (1977). Dependence of diffusive permeation rates on upstream and downstream pressures: I. Single component permeant. J. Membr. Sci. 2, 141–151. doi:10.1016/S0376-7388(00)83240-8

CrossRef Full Text | Google Scholar

Harder, E., Walters, D. E., Bodnar, Y. D., Faibish, R. S., and Roux, B. (2009). Molecular Dynamics study of a polymeric reverse osmosis membrane. J. Phys. Chem. B 113, 10177–10182. doi:10.1021/jp902715f

PubMed Abstract | CrossRef Full Text | Google Scholar

He, J., Arbaugh, T., Nguyen, D., Xian, W., Hoek, E. M. W., McCutcheon, J. R., et al. (2023). Molecular mechanisms of thickness-dependent water desalination in polyamide reverse-osmosis membranes. J. Membr. Sci. 674, 121498. doi:10.1016/j.memsci.2023.121498

CrossRef Full Text | Google Scholar

Heiranian, M., Fan, H., Wang, L., Lu, X., and Elimelech, M. (2023). Mechanisms and models for water transport in reverse osmosis membranes: history, critical assessment, and recent developments. Chem. Soc. Rev. 52, 8455–8480. doi:10.1039/D3CS00395G

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonsson, G., and Boesen, C. E. (1975). Water and solute transport through cellulose acetate reverse osmosis membranes. Desalination 17, 145–165. doi:10.1016/S0011-9164(00)84054-0

CrossRef Full Text | Google Scholar

Kim, S. H., Kwak, S.-Y., and Suzuki, T. (2005). Positron annihilation spectroscopic evidence to demonstrate the flux-enhancement mechanism in morphology-controlled thin-film-composite (TFC) membrane. Environ. Sci. Technol. 30, 1764–1770. doi:10.1021/es049453k

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, C. H. (1975). Theory of reverse osmosis and some other membrane permeation operations. J. Appl. Polym. Sci. 19, 83–95. doi:10.1002/app.1975.070190107

CrossRef Full Text | Google Scholar

Litman, Y., Chiang, K.-Y., Seki, T., Nagata, Y., and Bonn, M. (2024). Surface stratification determines the interfacial water structure of simple electrolyte solutions. Nat. Chem. 16, 644–650. doi:10.1038/s41557-023-01416-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lonsdale, H. K. (1966). “Properties of cellulose acetate membranes,” in Desalination in reverse osmosis. Editor U. Merten (Cambridge, MA: The MIT Press). Chap. 4.

Google Scholar

Manning, G. S., and Kay, A. R. (2023). The physical basis of osmosis. J. Gen. Physiol. 155, e202313332. doi:10.1085/jgp.202313332

PubMed Abstract | CrossRef Full Text | Google Scholar

Michaels, A. S., Bixler, H. J., and Hodges, R. M. (1965). Kinetics of water and salt transport in cellulose acetate reverse osmosis desalination membranes. J. Colloid Sci. 20, 1034–1056. doi:10.1016/0095-8522(65)90072-3

CrossRef Full Text | Google Scholar

Rosenbaum, S., and Cotton, O. (1969). Steady-state distribution of water in cellulose acetate membrane. J. Polym. Sci. Part A-1 7, 101–109. doi:10.1002/pol.1969.150070110

CrossRef Full Text | Google Scholar

Shen, M., Keten, S., Richard, M., and Lueptow, R. M. (2016). Dynamics of water and solute transport in polymeric reverse osmosis membranes via molecular Dynamics simulations. J. Membr. Sci. 506, 95–108. doi:10.1016/j.memsci.2016.01.051

CrossRef Full Text | Google Scholar

Sherwood, T. K., Brian, P. L. T., and Fisher, R. E. (1967). Desalination by reverse osmosis. Ind. Eng. Chem. Fundam. 6, 2–12. doi:10.1021/i160021a001

CrossRef Full Text | Google Scholar

Song, L., Heiranian, M., and Elimelech, M. (2021). True driving force and characteristics of water transport in osmotic membranes. Desalination 520, 115360. doi:10.1016/j.desal.2021.115360

CrossRef Full Text | Google Scholar

Sourirajan, S. (1970). Reverse osmosis. NY: Academic Press.

Google Scholar

Strathmann, H., and Von Mylius, O. (1976). Proc. 5th Int. Symp. on Fresh Water from the Sea, Alghero, May 9–14. Vol. 4 (Athens), p. 189.

Google Scholar

Vieth, W., Douglas, A. S., and Block, R. (1969). Membrane-water structural interactions in reverse osmosis transport. J. Macromol. Sci. Part B 3, 737–749. doi:10.1080/00222346908217117

CrossRef Full Text | Google Scholar

Wang, L., Cao, T., Dykstra, J. E., Porada, S., Biesheuvel, P. M., and Elimelech, M. (2021). Salt and water transport in reverse osmosis membranes: beyond the solution-diffusion model. Environ. Sci. Technol. 55, 16665–16675. doi:10.1021/acs.est.1c05649

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., He, J., Heiranian, M., Fan, H., Song, L., Li, Y., et al. (2023). Water transport in reverse osmosis membranes is governed by pore flow, not a solution-diffusion mechanism. Sci. Adv. 9, eadf8488. doi:10.1126/sciadv.adf8488

PubMed Abstract | CrossRef Full Text | Google Scholar

Wikipedia (2024). Reverse osmosis. Available at: https://en.wikipedia.org/wiki/Reverse_osmosis#:∼:text=Almost%20all%20commercial%20RO%20membrane,billion%20US%20gallons%20per%20day (Accessed December 22, 2024. 241–412. doi:10.1016/b978-0-443-13904-8.00003-9

CrossRef Full Text | Google Scholar

Yasuda, H., Lamaze, C. E., and Perterlin, A. (1971). Diffusive and hydraulic permeabilities of water in water swollen polymer membranes. J. Polym. Sci. Part 9, 1117–1131. doi:10.1002/pol.1971.160090608

CrossRef Full Text | Google Scholar

Zimm, B. H., and Lundberg, J. L. (1956). Sorption of vapors by high polymers. J. Phys. Chem. 60, 425–428. doi:10.1021/j150538a010

CrossRef Full Text | Google Scholar