Modeling pore wetting in direct contact membrane distillation—effect of interfacial capillary pressure

In this study, we aimed to develop a model for computing direct contact membrane distillation (DCMD) performance, taking into account capillary pressure effects at the liquid–gas interface within membrane pores. We developed a simulation model to investigate how factors such as pore radius, feed/permeate temperature, pressure, and contact angle influenced the distance of liquid intrusion into the pore, the weight flow rate in a single pore, and the temperature at the liquid–gas interface. The model predicted that the permeation rate would decrease with an increase in the feed pressure when the permeate pressure was kept constant and also when the pressure difference between the feed and permeate was kept constant. It also predicted that the permeation rate would increase with an increase in the permeate pressure when the feed pressure was kept constant. The model also indicated that partial pore wetting would be enhanced with an increase in feed pressure when the pore size was as large as 1 μm but would diminish when the pore size was as small as 0.1 μm. According to the model, partial pore wetting diminished with a decrease in the permeate pressure. The model’s predictions were in line with the trends observed in the experimental DCMD flux data by many authors, particularly those regarding the effects of feed and permeate temperature and the effect of contact angle. The model’s predictions were compared with the experimental data recorded in the literature, validating the model’s accuracy.

1 Introduction

Membrane distillation (MD) is a thermally driven separation process utilizing microporous membranes and operating on the principle of liquid–vapor equilibrium. In this process, only the volatile component (typically water) of the feed solution evaporates at the pore inlet, transfers through the pore, and exits from the pore outlet in either vapor or condensed form. The membrane material must be hydrophobic to prevent liquid water from entering the pore.

MD finds applications in the desalination of seawater and brackish water and treating concentrated brine from the reverse osmosis (RO) process (Rácz et al., 2014; Ibrar et al., 2022). Despite its impressive performance, commercialization faces challenges due to pore wetting, causing a significant decrease in MD flux and selectivity (Peña et al., 1993; Alklaibi and Lior, 2005; Gryta, 2005; 2007; Karakulski and Gryta, 2005; Peng et al., 2005; Tun et al., 2005; He et al., 2008; Qtaishat et al., 2009; Pangarkar et al., 2011; Camacho et al., 2013; Guillen-Burrieza et al., 2013; Peng et al., 2013; Saffarini et al., 2013; Rezaei and Samhaber, 2016).

Efforts have been made to mitigate MD pore wetting, including methods like liquid entry pressure (LEP) evaluation, introducing air bubbles into the feed solution, and dewetting the pores for regeneration and reuse (Baghbanzadeh et al., 2016; Warsinger et al., 2017; Ibrar et al., 2022; Hou et al., 2023). One of the most useful methods to evaluate the membrane’s resistance against pore wetting is LEP, which is related to the contact angle and pore geometry (Rácz et al., 2014; Yazgan-Birgi et al., 2018). New devices have been designed and constructed to introduce air bubbles into the feed solution (Rezaei et al., 2018), and the pores have been dewetted to regenerate and reuse the membrane (Shin et al., 2016; Warsinger et al., 2017).

The principle of LEP is based on the following Laplace equation:

$∆\mathit{p}=\frac{\mathbf{2}\mathit{\sigma }\mathbf{cos}\mathit{\theta }}{\mathit{r}},(\mathrm{1a})$

where $∆p$ is the pressure required to make liquid (usually water) enter into a cylindrical pore of radius r, $\sigma$ is the surface tension of water, and $\theta$ is the contact angle (CA). Note that $\theta$ is usually measured on a flat surface of the material of which the membrane is made and considered intrinsic to the material.

The contact angle in MD is integral to understanding surface properties and wetting behavior and is closely linked to thermodynamics. Surface energy, a key thermodynamic concept, delineates the energy at interfaces between phases. In MD, the contact angle, a representation of equilibrium between cohesive and adhesive forces, is mathematically expressed by the Young–Laplace equation, connecting the contact angle (θ) with surface tensions (γSL, γSG, and γLG). Hydrophobic behavior, characterized by contact angles exceeding 90°, implies reduced wetting, while contact angles below 90° indicate hydrophilic behavior, signaling increased wetting. This alignment with thermodynamics underscores the tendency of systems to seek lower energy states. Hydrophobic surfaces minimize solid–liquid interfacial energy, while hydrophilic surfaces minimize liquid–gas interfacial energy. In DCMD, thermodynamics governs the vapor–liquid equilibrium. The contact angle influences membrane surface wetting, impacting mass transfer and overall MD performance. Designing and optimizing MD systems for efficiency hinges on thermodynamic principles.

Consideration of small capillaries introduces confinement effects that alter water behavior. While thermodynamics still governs wetting, capillary size, roughness, and confinement modify equilibrium conditions. The meniscus formed in capillaries may deviate from the flat surface scenario due to these effects. The Young–Laplace equation (ΔP = $\mathrm{\gamma }\mathrm{LG}/R$ + γLG/R_s − γSLG/R_l) elucidates the equilibrium of forces at a curved liquid interface. Regarding changes in the meniscus at high pressure in trapped air, an increase in pressure (ΔP) impacts the curvature of the liquid–gas interface (ΔR), potentially altering meniscus shape. The specific impact depends on factors like material interfaces, trapped air characteristics, and system geometry, emphasizing the need for experimental validation to comprehensively understand these interactions.

In DCMD, a capillary is in contact with the feed and permeate water stream at the pore entrance and exit, respectively, and gas is trapped in between. When a capillary made of hydrophobic material is placed between two water phases, both at room temperature (see Figure 1A), the meniscus formed at the pore entrance is convex rightward, and the meniscus at the pore exit is convex leftward (Ashoor et al., 2016). The liquid phase pressure is slightly higher than the gas phase pressure to counterbalance the capillary pressure. If the temperature of the feed water is gradually increased, the gas phase pressure near the pore entrance will increase due to the evaporation of water, and it may surpass that of the liquid pressure when the feed water temperature is high enough. Then, in order to counterbalance the pressure difference, the meniscus at the pore entrance should change to concave leftward (Figure 1B); otherwise, the gas would appear in the feed water as gas bubbles. Thus, it is possible for the meniscus to change from the convex right (Figure 1A) to the concave left (Figure 1B), particularly at the pore entrance (Biswas and Kartha, 2019). This effect is negligible at the pore exit because the permeate stream is maintained at room temperature.

Figure 1

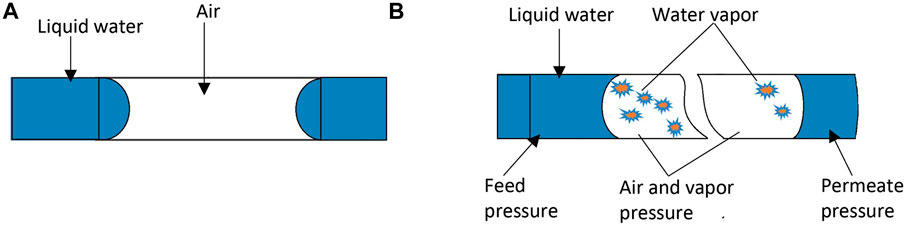
Figure 1. Meniscus change under high-pressure in the trapped air. (A) Pore entrance: convex right; exit: convex left. (B) Entrance shifts to concave left; exit to concave right.

Based on this conceptual experiment, the discussions in this work use contact angles below 90^o in the pore, in most cases, which allows drawing water into the capillary pore at the feed side of the pore, even when the pore is made of hydrophobic material.

Indeed, Gryta (2007) reported the possibility of partial pore wetting based on experiments conducted using hydrophobic MD membranes. Gryta’s comprehensive investigation identified a spectrum of pore-wetting phenomena encompassing four distinct categories:

1) Non-wetted: The entire membrane pore is filled with gas/vapor.

2) Surface-wetted: The pore is partially filled with liquid. A gas/vapor layer remains between the liquid layers at the entrance and exit of the pore.

3) Partial-wetted: As pore wetting proceeds, some pores are completely filled with liquid.

4) Wetted: The pore is completely filled with liquid, and the feed solution leaks to the permeate.

Confirmation of the concept of partial pore wetting is supported by Gryta’s work, where SEM/EDX analysis revealed concentration profiles of magnesium and calcium within the membrane pore (Gryta, 2007). Zhu et al. (2015) also observed the partial pore wetting of the PVA/PVDF composite hollow fiber membrane used for DCMD by applying SEM/EDX.

In wetting experiments involving PVDF, understanding channel geometry is paramount for grasping the interaction dynamics between liquids and PVDF membranes, as well as the influence of different geometrical features on wetting behavior. Research on PVDF hollow fiber membranes immersed in various solutions has yielded valuable insights into wetting behavior (Ritter, 2022). Moreover, investigations into the impact of channel wettability and geometry on water plug wetting underscore the importance of these factors in wetting phenomena (Pfeiffer et al., 2017). Consequently, examining the channel geometry of PVDF in wetting experiments becomes crucial for comprehending liquid–membrane interactions, understanding the influence of geometrical features on wetting behavior, and discerning how membrane properties are influenced by channel geometry.

Parameter screening studies on PVDF/PVP multi-channel capillary membranes further highlight the significance of channel geometry in shaping membrane properties and performance. Essential factors such as PVDF content, PVP molecular weight, pore size, and surface roughness play pivotal roles in determining membrane characteristics and behavior in wetting experiments (Back et al., 2019). In summary, when discussing wetting phenomena, it is imperative to consider parameters such as feed salinity, feed cross velocity, and channel geometry, as they significantly impact how liquids spread on a solid substrate. It is essential to note, however, that this particular study introduces an assumption regarding the simplification of pores as simple cylindrical channels. This simplification mirrors a similar geometric representation observed in previous studies, ensuring consistency and comparability in the analytical approach.

Jacob et al. (2018) made a very detailed study of pore wetting of vacuum membrane distillation (VMD), also using SEM/EDX, and proposed two pore wetting indicators: 1) the proportion of totally wetted membrane area (ω_s) and 2) the average rate of liquid intrusion in the pore (called pore wetting) (ω_p). Eljaddi and Cabassud (2022) applied the same method to a photoplasmonic PVDF membrane, incorporating Ag-nanoparticles, and unveiled that the integration of Ag-nanoparticles enhances partial pore wetting.

Typically, the occurrence of pore wetting in hydrophobic membranes is attributed to the hydrophilization of the pore entrance. This transformation is often triggered by the deposition of salt crystals or hydrophilic foulants, alongside the conversion of a hydrophobic material to a hydrophilic state through various chemical reactions. This rationale further supports the assumption of a contact angle of less than 90° in the model prediction. However, despite the widespread acceptance of these mechanisms, a comprehensive interpretation of pore wetting based on mass and heat transport remains elusive.

Notably, the groundbreaking work by Chamani et al. (2019) on vacuum membrane distillation (VMD) provides a remarkable exception. Their research delves into the intricacies of pore wetting with a distinct focus on mass and heat transport dynamics. This stands in stark contrast to the prevailing trends in the advancement of membrane materials, fabrication methods, and characterization techniques for MD. Chamani et al.'s findings underscore the need for a nuanced understanding of pore-wetting mechanisms, challenging conventional perspectives and stimulating further exploration in this crucial aspect of membrane science and technology.

The objective of this work is to present a model for DCMD transport in which simultaneous mass and heat transfer is considered, particularly under the influence of the capillary pressure at the liquid–gas interface. Using the model, the effects of pore radius, contact angle in the pore, feed and permeate pressure on the length of water uptake in the pore, the temperature at the water–gas interface, and the MD flux are studied. The results obtained by the model simulation are further compared with the trends observed by the experimental data and reported in the literature.

2 Theory

The following assumptions are made to simplify the model:

• The feed contains only water. Hence, in the model development, liquid means water.

• The pore is straight and cylindrical.

• The thermal conductivity of the membrane material is so low that only the heat transfer in the pore is considered. This assumption and the following two assumptions are made to examine purely the effects of mass and heat transfer occurring in the pore on the MD mass flux without the effects of other factors.

• The heat enters into the water inside the pore only from the pore entrance. The heat does not enter from the pore wall.

• Boundary layer resistance of the feed liquid is ignored.

• The liquid mass transfer inside the pore follows the Poiseuille flow.

• The vapor mass transfer inside the pore follows the combined Knudsen/molecular diffusion mechanism.

• The meniscus of the liquid–vapor interface does not affect saturation vapor pressure.

• Heat transfer in the longitudinal direction is dominant.

• The liquid is incompressible

2.1 Mass transfer

The MD transport model in a single pore is developed for the steady state at which the liquid–vapor phase boundary remains inside the pore (Figure 2).

Figure 2

Figure 2. Transport behavior model in DCMD.

In DCMD, both ends of the pore are in contact with liquid, and it seems possible that liquid enters from both sides. However, for the reason given in the introduction, it is assumed that the liquid enters only from the pore entrance that is in contact with the feed stream.

There is some evidence to support the water entry from the feed side. For example, Gryta (2007) reported that water partially filled the pore from the feed side to the distance of 15 µm in the total 400 µm of membrane thickness by showing the Mg and Ca content profile in the longitudinal direction of the pore by EDX, wherein DCMD was performed by polypropylene membrane using tap water as a feed. Jiang and co-workers also showed the presence of Na on the feed side by EDX when DCMD was performed by their hydrophilic–hydrophobic hybrid membrane (Zhu et al., 2015; Feng et al., 2017). Based on this assumption, the model is also applicable for air gap membrane distillation (AGMD) with some changes in the transport parameters.

2.1.1 Liquid transport

For the liquid phase $N_l$, the weight flow rate (kg/s) in a single pore is given according to the Poiseuille flow mechanism as

${\mathit{N}}_{\mathit{l}}=\frac{\mathit{\pi }\mathit{\rho }{\mathit{r}}^{\mathbf{4}}}{\mathbf{8}\mathit{\eta }{\mathit{\delta }}_{\mathit{l}}}∆{\mathit{p}}_{\mathit{l},}(\mathrm{1b})$

where $\rho$ (kg/m³) is the density of the liquid, $\eta$ (Pa s) is the viscosity of the liquid, ${\delta }_l$ (m) is the length of the liquid phase in the pore, and $∆p_l$ (Pa) is the driving force for the liquid movement, given by

$∆{\mathit{p}}_{\mathit{l}}={\mathit{p}}_{\mathit{f}}-{\mathit{p}}_{\mathit{i}}={\mathit{p}}_{\mathit{f}}-{\mathit{p}}_{\mathit{g}}+{\mathit{p}}_{\mathit{c}},(2)$

where $p_f$ (Pa) is the pressure of the liquid at the pore entrance, $p_g$ is the pressure of the gas phase (given later by Eq. 10) trapped between two liquid phases, and $p_c$ (Pa) is the capillary pressure at the interface (Chesworth et al., 2008), given by

${\mathit{p}}_{\mathit{c}}=\frac{\mathbf{2}\mathit{\sigma }\mathit{cos}\mathit{\theta }}{\mathit{r}},(3)$

where $\sigma$ (N/m) and $\theta$ (^o) are the liquid surface tension and contact angle, respectively.

In the above equations, the temperature dependence of the liquid properties is considered. Thus,

$\mathit{\rho }=\frac{\mathbf{0.14395}}{{\mathbf{0.0112}}^{\mathbf{1}+{\left(\mathbf{1}-\frac{\left({\mathit{T}}_{\mathit{f}}+{\mathit{T}}_{\mathit{i}}\right)/\mathbf{2}}{\mathbf{649.727}}\right)}^{\mathbf{0.05107},}}}(4)$

$\mathit{\eta }={\mathbf{0.001}\mathit{e}}^{-\mathbf{3.7188}+\frac{\mathbf{578.919}}{-\mathbf{137.546}+\left({\mathit{T}}_{\mathit{f}}+{\mathit{T}}_{\mathit{i}}\right)/\mathbf{2}}},(5)$

$\mathit{\sigma }=\mathbf{0.13415}{\left(\mathbf{1}-{\mathit{T}}_{\mathit{r}}\right)}^{\mathbf{1.6146}-\mathbf{2.035}{\mathit{T}}_{\mathit{r}}+\mathbf{1.5598}{\mathit{T}}_{\mathit{r}}^{\mathbf{2}}},{\mathit{T}}_{\mathit{r}}=\frac{\left({\mathit{T}}_{\mathit{f}}+{\mathit{T}}_{\mathit{i}}\right)/\mathbf{2}}{\mathbf{647.3}},(6)$

where $T_f$ and $T_i$ are the temperature at the pore entrance and at the liquid–gas interface. Thus, $\left(T_f+T_i\right)/2$ is the average liquid phase temperature.

2.1.2 Transport in the gas phase

In this work, the membrane pore sizes in a range of 0.01–1 × 10⁻⁶ m are considered for DCMD. Because the mean free path of water at an atmospheric pressure and 50°C is 0.14 × 10⁻⁶ m (Khayet and Matsuura, 2011), the Knudsen numbers for such pores are 0.07–7.1. Hence, the combined Knudsen/ordinary diffusion mechanism is used for the transport of water vapor in air that is trapped between two liquid phases.

Then, $N_v,$ the mass flux in the gas phase is given by

${\mathit{N}}_{\mathit{v}}=\left(\frac{\mathit{\pi }}{\mathit{R}{\mathit{T}}_{\mathit{g}}{\mathit{\delta }}_{\mathit{g}}}\right){\left[{\left\{\frac{\mathbf{2}}{\mathbf{3}}{\left(\frac{\mathbf{8}\mathit{R}{\mathit{T}}_{\mathit{g}}}{\mathit{\pi }\mathit{M}}\right)}^{\mathbf{1}/\mathbf{2}}{\mathit{r}}^{\mathbf{3}}\right\}}^{-\mathbf{1}}+{\left(\frac{{\mathit{p}}_{\mathit{g}}\mathit{D}}{{\mathit{p}}_{\mathit{a}}}{\mathit{r}}^{\mathbf{2}}\right)}^{-\mathbf{1}}\right]}^{-\mathbf{1}}\left({\mathit{p}}_{\mathit{s},\mathit{i}}-{\mathit{p}}_{\mathit{s},\mathit{p}}\right),(7)$

where $R$ and $T_g$ are the gas constant (8.314 J/mol K) and the temperature of the gas phase (K), respectively; ${\delta }_g$ is the length of the gas phase; $M$ is the molecular weight of water (18.02 × 10⁻³ kg/mol); $p_g$ and $p_a$ are the total pressure (Pa) of the gas phase and the partial pressure of the compressed air (Pa) in the gas phase, respectively; and $p_{s,i}$ and $p_{s,p}$ are the saturation vapor pressure of water at the water–gas interface and at the pore exit, respectively.

The following equations are used in Eq. 7:

${\mathit{p}}_{\mathit{a}}=\left(\frac{\mathit{\delta }}{{\mathit{\delta }}_{\mathit{g}}}\right)\left(\frac{{\mathit{p}}_{\mathit{f}}+{\mathit{p}}_{\mathit{p}}}{\mathbf{2}}\right),(8)$

where $\delta$ is the total pore length (m) and $p_f$ and $p_p$ are the feed and permeate pressure (Pa), respectively.

${\mathit{p}}_{\mathit{s}}=\frac{{\mathit{p}}_{\mathit{s}\mathit{i}}+{\mathit{p}}_{\mathit{s}\mathit{p}}}{\mathbf{2}},(9)$

where $p_s$ is the average vapor pressure of water (Pa) in the gas phase.

${\mathit{p}}_{\mathit{g}}={\mathit{p}}_{\mathit{a}}+{\mathit{p}}_{\mathit{s},}(10)$

${\mathit{T}}_{\mathit{g}}=\frac{{\mathit{T}}_{\mathit{i}}+{\mathit{T}}_{\mathit{p},}}{\mathbf{2}}(11)$

where $T_i$ and $T_p$ are the temperatures at the liquid–gas interface (K) and at the pore exit (K), respectively.

As for the diffusivity of water vapor in air D (m²/s),

$D=D_{atm}\left(1.013\mathrm{x}{10}^5/{\mathit{p}}_{\mathit{g}}\right),(12)$

where D_atm is the diffusivity (m²/s) at an atmospheric pressure, which is calculated by Bolz (1973):

$D_{atm}=-2.775\mathrm{x}{10}^{-6}+4.479\mathrm{x}{10}^{-}8{\mathit{T}}_{\mathit{g}}+1.656\mathrm{x}{10}^{-10}{{\mathit{T}}_{\mathit{g}}}^2.(13)$

Furthermore,

$\mathit{N}={\mathit{N}}_{\mathit{l}}={\mathit{N}}_{\mathit{g}},(14)$

where N is the mass flux of water (kg/s) through the liquid and gas phases.

$\mathit{\delta }={\mathit{\delta }}_{\mathit{l}}+{\mathit{\delta }}_{\mathit{g}}.(15)$

As for the saturation vapor pressure of water,

${\mathit{p}}_{\mathit{s}\mathit{i}}=\mathbf{133.3}\times {\mathbf{10}}^{\mathbf{8.07131}-\frac{\mathbf{1730.63}}{{\mathit{T}}_{\mathit{i}}-\mathbf{39.7240}}}.(16)$

${\mathit{p}}_{\mathit{s}\mathit{p}}=\mathbf{133.3}\times {\mathbf{10}}^{\mathbf{8.07131}-\frac{\mathbf{1730.63}}{{\mathit{T}}_{\mathit{p}}-\mathbf{39.7240}}}.(17)$

are used at the liquid–gas interface and at the pore exit, respectively.

2.2 Heat transfer

For the heat transfer in the liquid phase, the following differential equation is used at the steady state:

$\frac{{\mathit{d}}^{\mathbf{2}}\mathit{T}}{\mathit{d}{\mathit{x}}^{\mathbf{2}}}+\mathit{a}\frac{\mathit{d}\mathit{T}}{\mathit{d}\mathit{x}}=\mathbf{0},(18)$

where $T$ is the temperature in the liquid phase (K) and $x$ is the distance from the pore inlet (m) in the longitudinal direction, and

$\mathit{\alpha }=\frac{{\mathit{k}}_{\mathit{l}}}{\mathit{\rho }{\mathit{c}}_{\mathit{p}},}(19)$

where $k_l$ and $c_p$ are thermal conductivity (W/m K) and specific heat capacity (J/kg K) of the liquid, respectively.

The general solution of the differential equation is

$\mathit{T}={\mathit{C}}_{\mathbf{1}}+{\mathit{C}}_{\mathbf{2}}\mathbf{exp}\left(-\mathit{a}\mathit{x}\right),(20)$

where $C_1$ and $C_2$ are the integration constants.

Using the boundary conditions

$\mathbf{B}\mathbf{1}:\mathit{T}={\mathit{T}}_{\mathit{f}}\text{\hspace{0.17em}at\hspace{0.5em}}\mathit{x}=\mathbf{0},(21)$

$\mathrm{B}2:\frac{\mathit{d}\mathit{T}}{\mathit{d}\mathit{x}}=-\frac{\mathit{N}∆{\mathit{H}}_{\mathit{v}}}{{\mathit{k}}_{\mathit{l}}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}}-{\mathit{h}}_{\mathit{g}}\left({\mathit{T}}_{\mathit{i}}-{\mathit{T}}_{\mathit{p}}\right)\text{\hspace{0.17em}at\hspace{0.17em}}\mathit{x}={\mathit{\delta }}_{\mathit{g}},(22)$

where $∆H_v$ is the heat of evaporation of liquid (J/kg) and $h_g$ is the heat transfer coefficient of the gas phase (W/m² K).

$C_1$ and $C_2$ can be calculated from the above boundary conditions, resulting in the specific solution of the differential equation,

$\mathit{T}={\mathit{T}}_{\mathit{f}}+\left(-\frac{\mathit{\alpha }}{\mathit{u}}\right)\left\{-\frac{\mathit{N}∆{\mathit{H}}_{\mathit{v}}}{{\mathit{k}}_{\mathit{l}}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}}-{\mathit{h}}_{\mathit{g}}\left({\mathit{T}}_{\mathit{i}}-{\mathit{T}}_{\mathit{p}}\right)\right\}\left\{\mathbf{exp}\left(-\frac{\mathit{u}{\mathit{\delta }}_{\mathit{l}}}{\mathit{\alpha }}\right)-\mathbf{exp}\left(-\frac{\mathit{u}}{\mathit{\alpha }}\left({\mathit{\delta }}_{\mathit{l}}-\mathit{x}\right)\right)\right\},(23)$

where

$\mathit{u}=\frac{\mathit{N}}{\mathit{\rho }\mathit{\pi }{\mathit{r}}^{\mathbf{2}}}.(24)$

Furthermore, because $T=T_i$ at $x={\delta }_l$,

${\mathit{T}}_{\mathit{i}}={\mathit{T}}_{\mathit{f}}+\left(-\frac{\mathit{\alpha }}{\mathit{u}}\right)\left\{-\frac{\mathit{N}∆{\mathit{H}}_{\mathit{v}}}{{\mathit{k}}_{\mathit{l}}\mathit{\pi }{\mathit{r}}^{\mathbf{2}}}-{\mathit{h}}_{\mathit{g}}\left({\mathit{T}}_{\mathit{i}}-{\mathit{T}}_{\mathit{p}}\right)\right\}\left\{\mathbf{exp}\left(-\frac{\mathit{u}{\mathit{\delta }}_{\mathit{l}}}{\mathit{\alpha }}\right)-\mathbf{1}\right\}.(25)$

In Eq. 25, the temperature dependence of ${∆H}_v$ is considered as

${∆\mathit{H}}_{\mathit{v}}=\mathbf{8.314}\times \mathbf{647.3}\left(\mathbf{5.6297}{{\mathit{\tau }}_{\mathit{r}}}^{\frac{\mathbf{1}}{\mathbf{3}}}+\mathbf{13.962}{{\mathit{\tau }}_{\mathit{r}}}^{\frac{\mathbf{2}}{\mathbf{3}}}-\mathbf{11.673}{\mathit{\tau }}_{\mathit{r}}+\mathbf{2.1784}{{\mathit{\tau }}_{\mathit{r}}}^{\mathbf{2}}-\mathbf{0.31666}{{\mathit{\tau }}_{\mathit{r}}}^{\mathbf{6}}\right)\times \mathbf{1000}/\mathbf{18}.\mathbf{02},(26)$

where ${\tau }_r$ is

${\mathit{\tau }}_{\mathit{r}}=\mathbf{1}-\frac{{\mathit{T}}_{\mathit{i}}}{\mathbf{647.3}.}(27)$

$N_l=N,T_i\text{\hspace{0.17em}and\hspace{0.17em}}{\delta }_l$ can be given by solving Eqs 1a, 1b, (2), (3), (7), and (25) simultaneously.The following equations (Eqs 8–17) are used in Eq. 7:

The simulation was performed using Microsoft Excel, and the algorithm is presented in Figure 3.

Figure 3

Figure 3. Simulation algorithm for DCMD transport.

3 Results and discussion

In addition to the temperature-dependent properties of water, as shown in Eqs. (4)–(6), the following parameters were used in the simulation; that is, $k_l\text{and\hspace{0.17em}}{c}_p$ are 0.6406 W/m K and 4180 J/kg K, respectively. Both of them are used at 50°C (323.2 K). Even though both parameters depend on the temperature, their changes within a temperature range of 20–80°C (293.2–353.2 K) were found to have negligible effects on the results of the simulation.

The heat transfer was calculated using Eqs. 18 through 27. Specifically, the heat transfer coefficient, $h_g,$ required in Eq. 25 was calculated by k_g/${\delta }_g$, using k_g = 0.0275 W/m K, which is the thermal conductivity of humid air. Even though k_g changes considerably with the change of temperature and humidity, it was found that it did not affect the simulation result because the heat transfer at the liquid–gas interface by the evaporation of the liquid is much larger than the heat transfer by conduction ($\frac{N∆H_v}{k_l\pi r^2}\gg h_g\left(T_i-T_p\right)$ in Eq. 25).

3.1 Effect of r

Figure 4 illustrates how varying the pore radius (r) affects ${\delta }_l$, N, and $T_i$, while maintaining fixed parameters: $T_f$ = 353.2 K, $T_p$ = 293.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, θ = 60°, and δ = 5 × 10⁻⁵ m. The pore radius, r, was adjusted from 0.01 to 1 × 10⁻⁶ m.

Figure 4

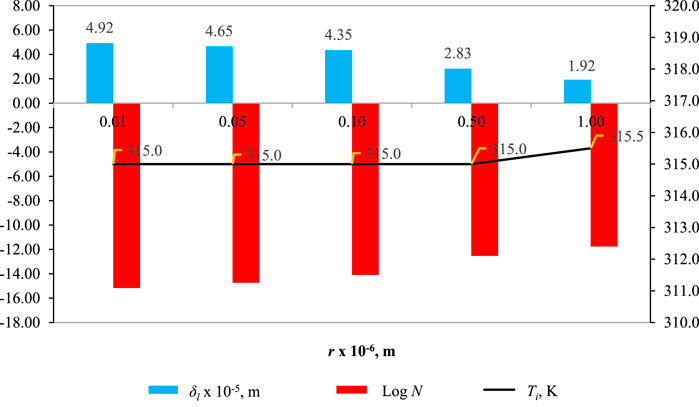
Figure 4. Effect of r on ${\delta }_l$, log N (kg/s), and $T_i$ with fixed parameters ($T_f$ = 353.2 K, $T_p$ = 293.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, $\theta$ = 60^o, and $\delta$ = 5 × 10⁻⁵ m).

In Figure 4, the influence of pore radius (r) on wetting characteristics, when the pore radius r = 0.01 × 10⁻⁶ m, ${\delta }_l$ reaches 4.92 × 10⁻⁵ m, signifying that over 90% of the pore space is occupied by the liquid phase due to the pronounced capillary force in such a small pore. As r increases to 1 × 10⁻⁶ m, ${\delta }_l$ progressively decreases to 1.92 × 10⁻⁵, accompanied by a significant rise in N from 6.69 × 10⁻¹⁶ kg/s to 1.73 × 10⁻¹² kg/s at the larger radius (r = 1 × 10⁻⁶ m, the red bars in Figure 4). This underscores the substantial impact of the r on N. Despite $T_i$ being nearly 40°C lower than T_f due to significant temperature polarization caused by the liquid phase in the pore, $T_i$ remains relatively constant with varying r. This constancy is attributed to the compensatory effect of the decrease in N countering the increase in ${\delta }_l$. In summary, the intricate interplay between pore size, capillary forces, and temperature dynamics shapes the wetting behavior within porous media.

3.2 Effect of T_f

Figure 5 illustrates the impact of feed temperature T_f on ${\delta }_l$, N and $T_i$, while maintaining fixed parameters: $T_p$ = 293.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, θ = 60°, and δ = 5 × 10⁻⁵ m.

Figure 5

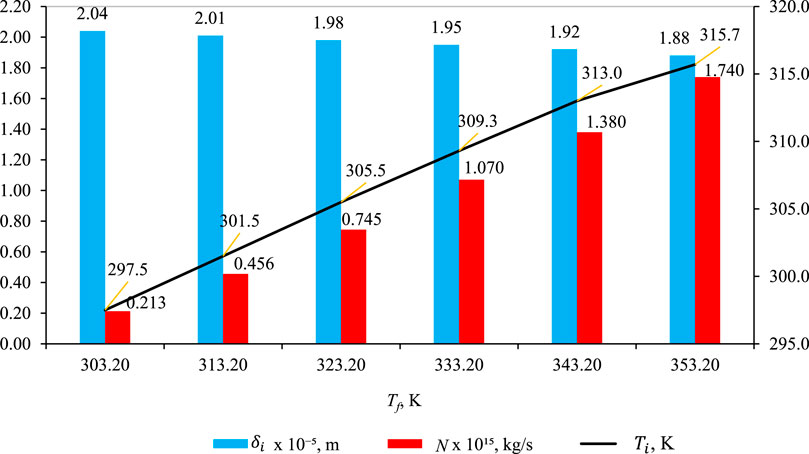
Figure 5. Effect of T_f on ${\delta }_l$, N, and $T_i$ with fixed parameters ($T_p$ = 293.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, $\theta$ = 60^o, and $\delta$ = 5 × 10⁻⁵ m).

In Figure 5, the effect of the impact of feed temperature (T_f) on wetting characteristics (blue bar), ${\delta }_l$ (blue bar) decreases with rising T_f, maintaining approximately 20% pore filling of the entire pore length with liquid. However, in Figure 5 (red bar), N deviates from the expected exponential increase tied to vapor pressure elevation with increasing feed temperature (T_f). This unexpected behavior is attributed to heightened temperature polarization at higher T_f. In Figure 5, ($T_i$ ) reveals the dynamics of temperature change, showing a mere 2% decrease (from 303.2 K to 297 K) when T_f is 303.2 K but a more significant 11% drop (from 353.2 K to 315 K) when T_f is 353.2 K. This contextualizes the observed deviation in N, underscoring the impact of temperature polarization on the anticipated exponential relationship between N and vapor pressure as T_f increases.

3.3 Effect of T_p

Figure 6 shows the effect of T_p on ${\delta }_l$, N, and $T_i$ when $T_f$, $p_f$, $p_p$, r, $\theta$, and $\delta$ are fixed to 353.2 K, 1 × 10⁵ Pa, 1 × 10⁵ Pa, 1 × 10⁻⁶ m, 60^o, and 5 × 10⁻⁵ m, respectively.

Figure 6

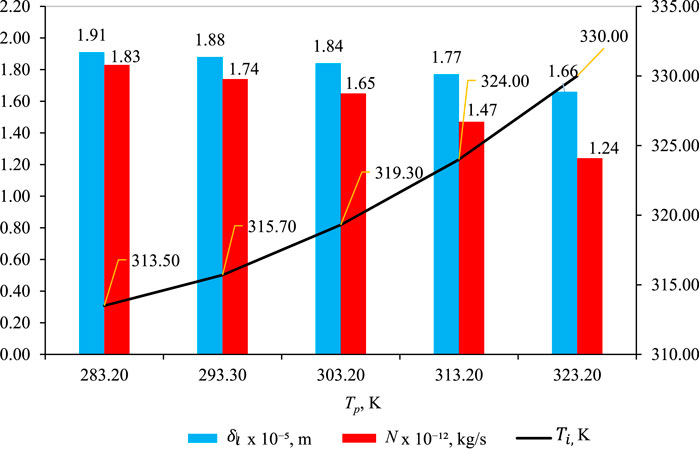
Figure 6. Effect of T_p on ${\delta }_l$, N, and $T_i$ with fixed parameters ($T_f$ = 353.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, $\theta$ = 60^o, and $\delta$ = 5 × 10⁻⁵ m).

As depicted in Figure 6, the liquid intrusion length ${\delta }_l$ decreases as the permeate temperature T_p increases. This trend can be attributed to the wettability of the membrane surface. At higher permeate temperatures, the membrane becomes more hydrophobic, leading to reduced liquid intrusion into the pores.

Temperature polarization (T_p): T_p represents the difference between the bulk feed temperature T_f and the temperature at the membrane/solution interface T_mf where the vapor–liquid transition occurs. As T_p increases, the temperature polarization, $T_f-T_i,$ decreases. This decrease in temperature polarization is noteworthy and can be linked to the heat transfer dynamics within the system.

Impact on mass flux (N): although temperature polarization decreases, there is also a decrease in mass flux (N) with increasing T_p. However, it is essential to recognize that the impact of T_p on mass flux is quantitatively smaller than the influence of feed temperature $T_f$ For instance, a 40 K increase in T_p results in a measured decrease in N of 0.59 × 10⁻¹² kg/s. In contrast, a similar increase in $T_f$ leads to a more substantial increase in N, specifically 1.17 × 10⁻¹² kg/s.

The discrepancy between the effects of T_p and $T_f$ suggests that the system is more sensitive to variations in $T_f$. The nuanced interplay between temperature parameters and mass flux underscores the complexity of the system dynamics. In summary, understanding the intricate balance between temperature, wettability, and mass transport is crucial for optimizing membrane-based processes. Further investigations will help uncover the underlying mechanisms governing these observed trends.

3.4 Effect of p_f

Figure 7 shows the effect of p_f on ${\delta }_l$, N, and $T_i$ when $T_f,T_p$, $p_p$, r, $\theta$, and $\delta$ are fixed to 353.2 K, 293.2 K, 1 × 10⁵ Pa, 0.1 × 10⁻⁶ m, 60^o, and 5 × 10⁻⁵ m, respectively.

Figure 7

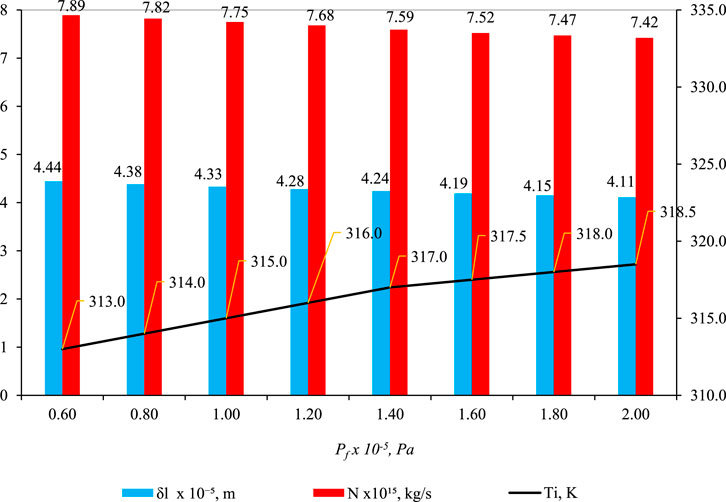
Figure 7. Effect of p_f on ${\delta }_l$, (blue), N (red), and $T_i$ (line), where $T_f=353.2\mathrm{K},T_p$ = 293.2 K, $p_p$ = 1 × 10⁵ Pa, r = 0.1 × 10⁻⁶ m, $\theta$ = 60^o, and $\delta$ = 5 × 10⁻⁵ m.

In Figure 7, a compelling pattern emerges: the parameter δ_l displays a decreasing trend as feed pressure (p_f) increases. This seemingly paradoxical observation results from various factors. Despite higher feed pressure propelling liquid deeper into the pore, a simultaneous rise in temperature at the liquid–gas interface (T_i) amplifies capillary pressure in the gas phase (p_g), diverting the liquid back toward the pore entrance. The findings in Figure 7 (blue bar) underscore that the influence of p_g on δ_l outweighs that of p_f. This pattern is also evident in the reduction of another parameter, N (mass flux of water through liquid and gas phases), as p_f increases (Figure 7, red bar).

The initially counterintuitive decrease in δ_l with increasing p_f becomes clear upon examining the role of capillary pressure (p_g). As p_f rises, more liquid infiltrates the pore structure, but the pivotal factor is the impact of p_g, controlled by T_i. Analyzing the relationship between T_i, we observe its increase with p_f, leading to an elevated saturation vapor pressure (ψpsi) (Eq. 16), subsequently influencing p_g (Eq. 10). The essence lies in the dominance of p_g over p_f in influencing δ_l. Essentially, capillary forces play a predominant role in determining δ_l, and a similar phenomenon is observed for parameter N. With an increase in p_f, T_i rises, causing an escalation in p_g, which, in turn, alters flow behavior and results in a decrease in N.

The core interaction driving the observed phenomena lies in the intricate relationship between capillary pressure in the gas phase (p_g) and feed pressure (p_f). The augmentation of p_f facilitates enhanced liquid entry into the pore space, yet the prevailing influence of capillary forces, particularly governed by T_i, ultimately dictates the behavior of the liquid phase. Eq. 10 and (16) are likely instrumental in comprehending this intricate interplay, encapsulating the dynamic involvement of surface tension, capillary pressure, and porosity.

To synthesize the findings, it becomes evident that the increase in T_i (and subsequently p_g) eclipses the impact of p_f, shedding light on the discernible trends in δ_l and N. This interdependence is graphically depicted in Figures 5–7 (as depicted by the blue bars), where an escalation in T_i, T_p, and pf precipitates a swift reduction in δ_l.

The decrease in δ_l is particularly conspicuous when T_f rises, as this prompts a rapid decline in wetting characteristics. Various factors related to wettability properties come into play as the temperature increases. Elevated temperatures induce a reduction in hydroxyl groups within cellulose chains, leading to diminished moisture uptake and decreased water adsorption, thereby influencing wettability properties (Sipahutar et al., 2021). Furthermore, heightened temperatures result in the expansion of membrane pores, escalating the risk of membrane wetting and enlarging pore sizes. This expansion is more pronounced at elevated temperatures due to an amplified temperature gradient and increased heat transfer rates. Additionally, the rise in temperature concurrently diminishes the surface tension and contact angle, further contributing to membrane wetting (Gryta, 2020). In summary, the collective impact of these factors at heightened temperatures manifests in a precipitous decline in wetting characteristics (δ_l).

Figure 8 elucidates the impact of feed pressure (p_f) on key parameters—${\delta }_l$, N, and $T_i$, while maintaining specific conditions: $T_f,$ $T_p$, $p_p$, r, and $\delta$ are fixed to 353.2 K, 293.2 K, 1 × 10⁵ Pa, 1 × 10⁻⁶ m, and 5 × 10⁻⁵ m, respectively. Two distinct contact angles, $\theta$ = 60° (blue shades) and $\theta$ = 82° (red shades), are considered. Notably, the pore radius (r) has been adjusted from 0.1 × 10⁻⁶ m to 0.1 × 10^–6 m in Figure 7 to 1 × 10^–6 m in Figure 8. Despite the different pressure ranges studied for 60° (0.5–1.5 × 10⁵ Pa) and 82° (1.4–2.0 × 10⁵ Pa), both contact angles exhibit consistent trends. A notable observation is the reversal in the trend of $T_i$ in Figure 8 compared to Figure 7. Specifically, $T_i$ decreases as p_f increases, resulting in an upswing in ${\delta }_l$ (Figure 8). In contrast, the flux, N, follows the same decreasing trend with increasing p_f in both Figures 7, 8.

Figure 8

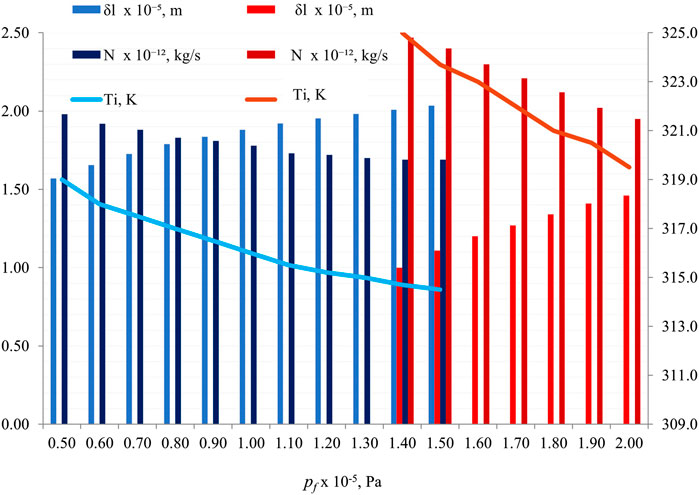
Figure 8. Effect of p_f on δ_l, N, and T_i , with fixed parameters (T_f = 353.2 K, T_p = 293.2 K, P_p= 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, and δ = 5 × 10⁻⁵ m). Two contact angles are represented: θ = 60° (blue shades) and θ = 82° (red shades).

Here, the contact angle values of 60° and 82° are commonly used in studies to represent different wetting properties of surfaces. A contact angle above 90° indicates hydrophobicity, where the surface repels water, while an angle below 90° signifies hydrophilicity, indicating good wetting by water (Danish, 2020). These specific angles are chosen to represent these distinct wetting behaviors for experimental and analytical purposes. Similarly, the values of 1.0×10⁵ Pa and 1.5 × 10⁵ Pa for p_f (pressure) are set to explore the impact of varying pressures on wetting characteristics and interfacial tension in fluid–rock systems. By using different pressure values within this range, researchers can analyze how changes in pressure affect contact angles and interfacial tension, providing insights into the behavior of fluids interacting with rock surfaces under different conditions. These specific pressure values are selected to study a range of scenarios and understand the nuances of fluid–rock interactions comprehensively (Taetz et al., 2016).

This reversal in $T_i$ behavior underscores the system’s sensitivity to variations in p_f, a shift that can be influenced by adjusting parameters such as pore radius and contact angle. The cohesion between fixed conditions and altered experimental factors in Figure 8 emphasizes the intricate dynamics governing the observed trends in ${\delta }_l$, N, and $T_i$. These findings contribute to a nuanced understanding of how the system responds to changes in feed pressure (p_f) under controlled conditions.

3.5 Effect of p_p

Figure 9 shows the effect of p_p on ${\delta }_l$, N, and $T_i$ when parameters $T_f$, ${T_p,p}_f$, and $\delta$ are fixed to $353.2\mathrm{K},$ 293.2 K, 1.5 × 10⁵ Pa, and 5 × 10⁻⁵ m, respectively. Again, $\theta$ is either 60^o (blue shades) or 82^o (red shades), and r is 1 × 10⁻⁶ m. Comparing Figures 8, 9, it is found that the decrease in $p_p$ has the same effect as the increase in $p_f$. As $p_f-p_p$ increases by either an increase in $p_f$ or a decrease in $p_p$, ${\delta }_l$ experiences an increase, while N and $T_i$ exhibit a decrease.

Figure 9

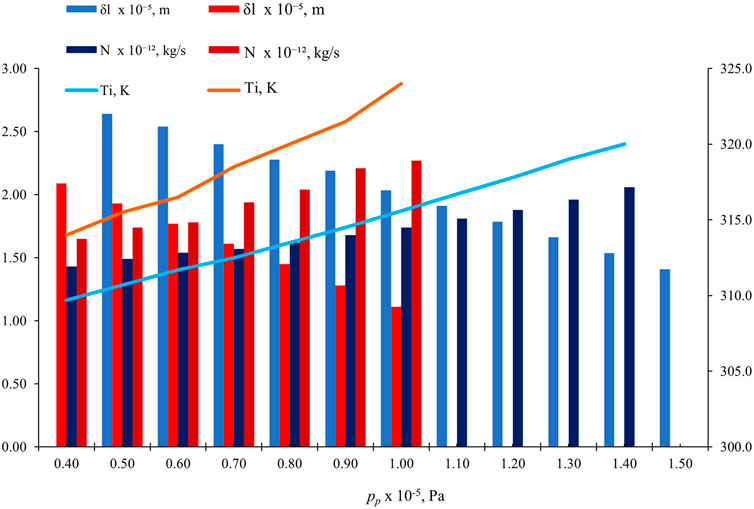
Figure 9. Effect of p_p on ${\delta }_l$, N, and $T_i$, with fixed parameters ($T_f=353.2\mathrm{K},T_p$ = 293.2 K, $p_p$ = 1.5 × 10⁻⁵ Pa, r = 1 × 10⁻⁶ m, and $\delta$ = 5 × 10⁻⁵ m). Two contact angles are represented: θ = 60° (blue shades) and θ = 82° (red shades).

In fluid flow, the significance of maintaining a consistent pressure difference ($p_f-p_p$) is evident in the relationship between flux (N) and permeate pressure ($p_p$). As permeate pressure increases, the flux also increases, indicating a direct correlation between these two parameters (Naidu et al., 2015). This consistency in pressure difference ensures predictable and controlled flux rates, which are crucial for optimizing system performance and efficiency in various applications like reverse osmosis, gas separation, and membrane processes (Stewart, 2014). By regulating this pressure difference, engineers can manipulate the flux of substances through membranes, leading to improved separation efficiency and overall system effectiveness.

3.6 Effect of ${\mathit{p}}_{\mathit{f}}$ when ${\mathit{p}}_{\mathit{f}}-{\mathit{p}}_{\mathit{p}}$ is fixed

Figure 10 shows the effect of p_f on ${\delta }_l$, N, and $T_i$ when $T_f$, $T_p$, ${p_f-p}_p$, r, $\theta ,$ and $\delta$ are fixed to 353.2 K, 293.2 K, 0.5 × 10⁵ Pa, 1 × 10⁻⁶ m, 60^o, and 5 × 10⁻⁵ m, respectively. In this specific scenario, an escalation in p_f leads to a concurrent decrease in ${\delta }_l$, a subtle augmentation in N, and an elevation in $T_i$. Remarkably, this dynamic unfolds while maintaining a consistent (${p_f-p}_p$).

Figure 10

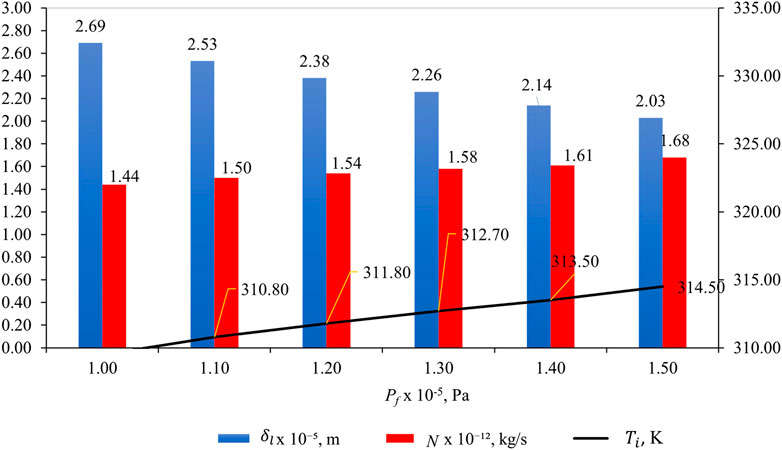
Figure 10. Effect of p_f on ${\delta }_l$, N, and $T_i$, with fixed parameters ($T_f=353.2\mathrm{K},T_p$ = 293.2 K, ${p_f-p}_p$ = 0.5 × 10⁵ Pa, r = 1 × 10⁻⁶ m, $\theta$ = 60^o, and $\delta$ = 5 × 10⁻⁵ m).

Understanding the relationship between liquid intrusion length (${\delta }_l$), feed pressure ($p_f$), mass flux (N), and liquid–gas interface temperature ($T_i$) is crucial in various engineering applications. As $p_f$ increases, a decrease in ${\delta }_l$ suggests improved heat transfer efficiency, with smaller values indicating more effective heat transfer. The subtle increase in mass flux (N) signifies a rise in fluid flow or mass flow rate. Additionally, the elevation in $T_i$ indicates that the system’s internal temperature rises with escalating $p_f$, which is essential for designing and optimizing temperature-controlled processes like those in chemical reactors or electronic devices (Rouquerol et al., 2011). In this case, we must balance the benefits of enhanced heat transfer and fluid flow against drawbacks like increased energy consumption or system complexity (Rouquerol et al., 2011).

3.7 Effect of $\mathit{\theta }$

Figure 11 shows the effect of $\theta$ on ${\delta }_l$, N, and $T_i$ , when $T_{f,}$ $T_p$, $p_f$, $p_p$, r, and $\delta$ are fixed to $353.2\mathrm{K},$ 293.2 K, 1 × 10⁵ Pa, 1 × 10⁵ Pa, 1 × 10⁻⁶ m, and 5 × 10⁻⁵ m, respectively.

Figure 11

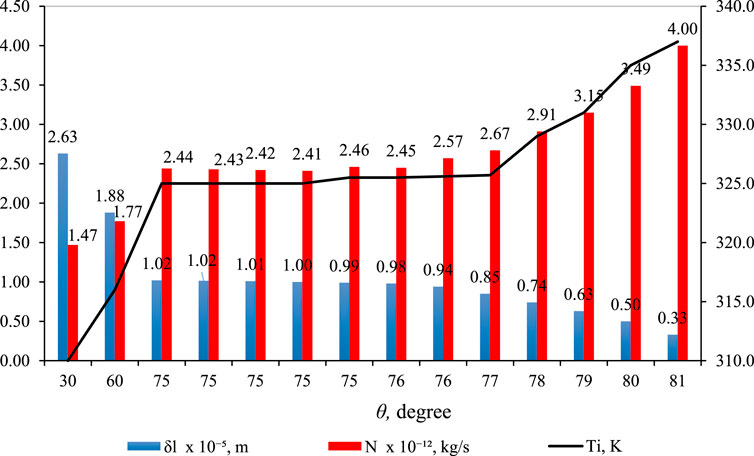
Figure 11. Effect of $\theta$ on ${\delta }_l$, N, and, $T_i$, with fixed parameters (${T_f=353.2\mathrm{K},T}_p$ = 293.2 K, $p_f$ = 1 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, and $\delta$ = 5 × 10⁻⁵ m).

In Figure 11 (blue bar), ${\delta }_l$ decreases as $\theta$ increases because less water is driven into the pore as the hydrophobicity of the membrane material increases. In Figure 11, the line shows that T_i increases as $\theta$ increases because of the decrease in temperature polarization with the decrease in the length of the liquid phase. A decrease in ${\delta }_l$ enhances the flow rate of the liquid phase (Eq. 1), and as a result, N increases (red bar). At $\theta$ = 81^o, ${\delta }_l$ and N become 0.326 × 10⁻⁵ m and 4 × 10⁻¹² kg/s, respectively. Even though it is not shown in the figure, $\theta$ may increase until it becomes 85.6^o, where ${\delta }_l$ becomes 0, and the pore is filled only with the gas phase. N becomes as high as 7.79 × 10⁻¹² kg/s. This scenario is more explicitly illustrated in Figure 13.

Figure 12 illustrates the impact of contact angle (θ) on ${\delta }_l$, N, and $T_i$ with fixed parameters ($T_f$ = 353.2 K, $T_p$ = 293.2 K, $p_f$ = 1.5 × 10⁵ Pa, $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, and δ = 5 × 10⁻⁵ m). It is important to note that $p_f$ has been increased to 1.5 × 10⁵ Pa from the 1 × 10⁵ Pa used in Figure 11. The observed patterns in Figure 12 align with those in Figure 11, where ${\delta }_l$ decreases, and N and $T_i$ increase with higher θ values.

Figure 12

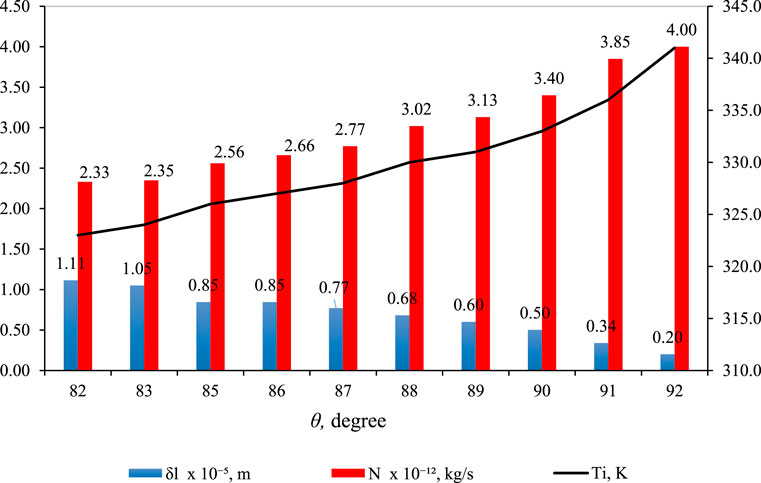
Figure 12. Effect of $\theta$ on ${\delta }_l$, N, and $T_i$, with fixed parameters ($T_f=353.2\mathrm{K},T_p$ = 293.2 K, $p_f$ = 1.5 × 10⁵ Pa $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, and $\delta$ = 5 × 10⁻⁵ m).

However, a key distinction is the use of larger θ values in Figure 12. This adjustment is necessitated by the higher hydrophobicity required in the membrane material to counteract the elevated feed pressure ($p_f$) and maintain the interface position. Remarkably, even with θ values exceeding 90°, indicating hydrophobicity in the pore, there is partial liquid filling, according to Figure 12. Notably, the maximum θ is 92° in this scenario, where ${\delta }_l$ and N are reported as 0.201 × 10⁻⁵ m and 4.73 × 10⁻¹² kg/s, respectively. It is worth mentioning that θ may further increase until it reaches 107.9°, leading to ${\delta }_l$ becoming 0 and N reaching 7.79 × 10⁻¹² kg/s, as revealed in the data.

In Figure 13, N is graphed against ${\delta }_l$ for two different feed pressures: p_f = 1.0 × 10⁵ Pa (blue) and p_f = 1.5 × 10⁵ Pa (red). Notably, the data for both feed pressures overlap, and there is a consistent increase in N as ${\delta }_l$ decreases. Particularly, N exhibits a steep increase when ${\delta }_l$ is below 0.5 × 10⁻⁵ m, reaching N = 7.79 × 10⁻¹² kg/s when ${\delta }_l$ = 0. This signifies a scenario where there is no liquid in the pore, and transport occurs solely in the vapor phase.

Figure 13

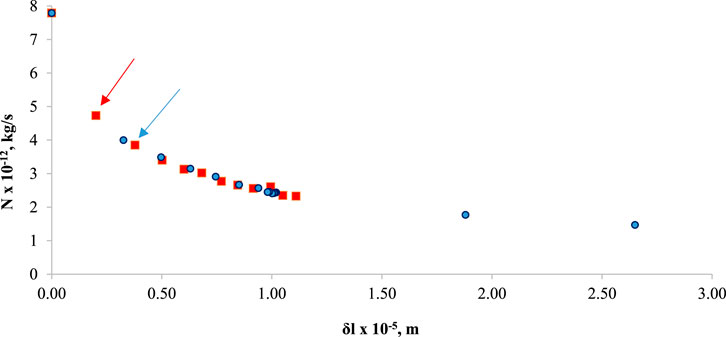
Figure 13. N versus ${\delta }_l$, with fixed parameters ($T_p$ = 293.2 K, $p_f$ = 1.0 × 10⁵ Pa (blue), $p_f$ = 1.5 × 10⁵ Pa (red), $p_p$ = 1 × 10⁵ Pa, r = 1 × 10⁻⁶ m, and $\delta$ = 5 × 10⁻⁵ m).

4 Comparison with the experimental data

The simulation model proposed in this work does not include some factors that would affect the DCMD performance, such as the heat transfer coefficient of the feed and permeate boundary layer and the thermal conductivity of the membrane polymer matrix. Therefore, the agreement of the computational results with the experimental data in their numerical values cannot be tested. Nevertheless, the validity of the model simulation can be examined by comparing the trends it predicts with those observed by experiments. The simulation predicts that the DCMD flux

1) Increases as r increases. (Figure 4)

2) Increases as T_f increases (Figure 5)

3) Decreases as p_f increases (Figure 7; Figure 8)

4) Increases as p_p increases (Figure 9)

5) Increases as θ increases (Figure 11; Figure 12).

Among those, 1), 2), and 5) are quite obvious and have been proven by many experiments (Khayet and Matsuura, 2011). The trends predicted by 3) and 4) are, however, not quite obvious because only a few studies have examined the effect of P_f and p_p on the MD flux. Some of those examples are as follows:

Park and Lee (2019) observed a decrease in the flux with an increase in the feed pressure p_f and attributed it to membrane compaction. They also noticed a sudden increase in the flux at a high pressure caused by the pore wetting.

Liu et al. (2022) observed a 62% increase in the initial flux of DCMD when the feed pressure (P_f) was changed from 1 kPa (gauge) to −30 kPa (gauge) for a commercial PVDF membrane. They have explained this phenomenon by 1) considering the contribution of the molecular diffusion and the Knudsen diffusion in the pore and 2) attributing to the increase in the heat transfer coefficient of the boundary layer at the feed side and the reduction in transmembrane heat conduction caused by the change of the meniscus shape from convex to concave.

In summary, the trends observed by the experiments were:

1) Park and Lee (2019) also observed a decrease in the flux with an increase in the feed pressure and attributed it to membrane compaction. They also noticed a sudden increase in the flux at a high pressure caused by the pore wetting.

2) The DCMD flux of the incompressible hollow fiber membrane did not change with an increase in p_f (Zhang et al., 2011).

3) The DCMD flux increased with a decrease in p_f. It is unlikely the pore deformation occurred when the feed pressure was decreased (Liu et al., 2022).

As for the effect of the increase in p_f, the simulation predicts the flux decrease (Figures 7, 8). Thus, the model prediction agrees with experimental results 1) but disagrees with the experimental results 2).

In Zhang et al.’s compression experiments (Zhang et al., 2011), however, pressure was applied to the hollow fiber on both sides, that is, the lumen and the shell side, but in the DCMD experiments, the pressure was applied only to the feed side (likely the lumen side of the hollow fiber according to their article (Zhang et al., 2010)). Then, it is possible that the hollow fiber expanded, resulting in an increase in DCMD flux. If such an expansion did not take place, the flux could decrease with an increase in p_f, as the model predicted. The model predicts a slight increase in flux as feed pressure rises, a condition where p_f–p_p is maintained constant, as depicted in Figure 10. The concept of the liquid intrusion length (${\delta }_l$) serves as an indicator of partial pore wetting. Larger values of ${\delta }_l$ suggest more pronounced pore wetting. Although, there has been no direct measurement of ${\delta }_l$ under various DCMD operating conditions to date, it is reasonable to speculate that the likelihood of wetting along the entire pore length increases as ${\delta }_l$ becomes larger.

The model simulation, on the other hand, predicts that ${\delta }_l$ increases with an increase in $p_f$, when the pore size is as large as 1 μm (Figure 8). Thus, the model prediction agrees with 1) of the above experimental results. However, ${\delta }_l$ tends to decrease with an increase in the feed pressure when the pore size is as small as 0.1 μm (Figure 7). It would be interesting to test this prediction experimentally. ${\delta }_l$ decreases with an increase in $p_p$ (Figure 9). This agrees with 2) of the above experimental results.

5 Conclusion

We developed a simulation model to investigate flux and partial pore wetting in DCMD while considering the influence of capillary pressure at the liquid–gas interface. In this context, we assumed that the contact angle inside the pore was less than 90° due to the high pressure in the gas phase or potential alterations in chemistry at the pore wall. The model predicts that the weight flow rate increases with an increase in the pore radius, rises with higher feed temperature, decreases with an increase in permeate temperature, and increases with an increase in the contact angle. These trends have already been experimentally confirmed by numerous authors.

Regarding the effect of feed pressure (p_f), the model predicts a decrease in the permeation rate as feed pressure increases while keeping the permeate pressure constant. This prediction generally aligns with experimental results, except in the case of hollow fibers, which are considered incompressible. Additionally, the model forecasts a decrease in permeation rate with increasing feed pressure while maintaining a constant pressure difference between the feed and permeate, a trend that contradicts certain experimental findings. However, these instances of disagreement can be attributed to the potential expansion of the pore during DCMD experiments.

Furthermore, the model suggests that partial pore wetting is enhanced with an increase in feed pressure when the pore size is as large as 1 μm, which is consistent with experimental results obtained from membranes with an average pore size of 0.67 μm. Conversely, the model predicts an opposite trend when the pore size is as small as 0.1 μm. This prediction warrants further experimental testing to validate its accuracy. According to the model, partial pore wetting diminishes as permeate pressure increases, a trend supported by experimental observations of pore wetting. These findings provide valuable insights into the complex interplay of feed and permeate pressure in the context of DCMD and its potential applications.

These insights deepen our comprehension of the nuanced dynamics within DCMD, shedding light on potential applications. Future research should prioritize rigorous experimental validation and refine the model to encompass diverse membrane characteristics and operating conditions, enhancing its predictive accuracy.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

SA: visualization, and writing–original draft. TM: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, resources, supervision, validation, visualization, writing–original draft, and writing–review and editing. JJ: conceptualization, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization, writing–review and editing, and data curation. LJ: validation and writing–review and editing. AI: validation and writing–review and editing. MO: validation and writing–review and editing. MA: validation and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article from the Ministry of Higher Education, Malaysia under HICoE grant, R.J090301.7851.4J433 and from Universiti Teknologi Malaysia under Hi-Tech (F4) grant Q.J130000.4609.00Q14.

Acknowledgments

The authors would like to express gratitude to the Ministry of Higher Education, Malaysia for funding under HICoE grant, R.J090301.7851.4J433 and to Universiti Teknologi Malaysia for the financial funding under Hi-Tech (F4) grant Q.J130000.4609.00Q14.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor MK declared a past co-authorship with the author TM.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alklaibi, A. M., and Lior, N. (2005). Membrane-distillation desalination: status and potential. Desalination 171, 111–131. doi:10.1016/j.desal.2004.03.024

CrossRef Full Text | Google Scholar

Ashoor, B. B., Mansour, S., Giwa, A., Dufour, V., and Hasan, S. W. (2016). Principles and applications of direct contact membrane distillation (DCMD): a comprehensive review. Desalination 398, 222–246. doi:10.1016/j.desal.2016.07.043

CrossRef Full Text | Google Scholar

Back, J. O., Brandstätter, R., Spruck, M., Koch, M., Penner, S., and Rupprich, M. (2019). Parameter screening of PVDF/PVP multi-channel capillary membranes. Polym. (Basel) 11, 463. doi:10.3390/polym11030463

PubMed Abstract | CrossRef Full Text | Google Scholar

Baghbanzadeh, M., Rana, D., Lan, C. Q., and Matsuura, T. (2016). Effects of hydrophilic silica nanoparticles and backing material in improving the structure and performance of VMD PVDF membranes. Sep. Purif. Technol. 157, 60–71. doi:10.1016/j.seppur.2015.11.029

CrossRef Full Text | Google Scholar

Biswas, D., and Kartha, S. A. (2019). Conceptual modeling of temperature effects on capillary pressure in dead-end pores. Sādhanā 44, 117. doi:10.1007/s12046-019-1108-y

CrossRef Full Text | Google Scholar

Bolz, R. E. (1973). CRC handbook of tables for applied engineering science. Boca Raton, Florida, United States: CRC Press. doi:10.1201/9781315214092

CrossRef Full Text | Google Scholar

Camacho, L. M., Dumée, L., Zhang, J., Li, J., Duke, M., Gomez, J., et al. (2013). Advances in membrane distillation for water desalination and purification applications. Water 5, 94–196. doi:10.3390/w5010094

CrossRef Full Text | Google Scholar

Chesworth, W., Camps Arbestain, M., Macías, F., Spaargaren, O., and Mualem, Y. (2015). Capillary pressure BT - encyclopedia of soil science. in, ed. W. Chesworth (Dordrecht: Springer Netherlands), 81–91. doi:10.1007/978-1-4020-3995-9_87

CrossRef Full Text | Google Scholar

Chamani, H., Matsuura, T., Rana, D., and Lan, C. Q. (2019). Modeling of pore wetting in vacuum membrane distillation. J. Memb. Sci. 572, 332–342. doi:10.1016/j.memsci.2018.11.018

CrossRef Full Text | Google Scholar

Danish, M. (2020). Contact angle studies of hydrophobic and hydrophilic surfaces BT - handbook of magnetic hybrid nanoalloys and their nanocomposites. Cham: Springer International Publishing, 1–22. doi:10.1007/978-3-030-34007-0_24-1

CrossRef Full Text | Google Scholar

Eljaddi, T., and Cabassud, C. (2022). Wetting of photoplasmonic PVDF/silver membranes in photothermal membrane distillation: identification of wetting mechanisms and comparison of wetting dynamics. Desalination 540, 116019. doi:10.1016/j.desal.2022.116019

CrossRef Full Text | Google Scholar

Feng, X., Jiang, L. Y., Matsuura, T., and Wu, P. (2017). Fabrication of hydrophobic/hydrophilic composite hollow fibers for DCMD: influence of dope formulation and external coagulant. Desalination 401, 53–63. doi:10.1016/j.desal.2016.07.026

CrossRef Full Text | Google Scholar

Gryta, M. (2005). Long-term performance of membrane distillation process. J. Memb. Sci. 265, 153–159. doi:10.1016/j.memsci.2005.04.049

CrossRef Full Text | Google Scholar

Gryta, M. (2007). Influence of polypropylene membrane surface porosity on the performance of membrane distillation process. J. Memb. Sci. 287, 67–78. doi:10.1016/j.memsci.2006.10.011

CrossRef Full Text | Google Scholar

Gryta, M. (2020). Mitigation of membrane wetting by applying a low temperature membrane distillation. Membr. (Basel) 10, 158. doi:10.3390/membranes10070158

CrossRef Full Text | Google Scholar

Guillen-Burrieza, E., Thomas, R., Mansoor, B., Johnson, D., Hilal, N., and Arafat, H. (2013). Effect of dry-out on the fouling of PVDF and PTFE membranes under conditions simulating intermittent seawater membrane distillation (SWMD). J. Memb. Sci. 438, 126–139. doi:10.1016/j.memsci.2013.03.014

CrossRef Full Text | Google Scholar

He, F., Gilron, J., Lee, H., Song, L., and Sirkar, K. K. (2008). Potential for scaling by sparingly soluble salts in crossflow DCMD. J. Memb. Sci. 311, 68–80. doi:10.1016/j.memsci.2007.11.056

CrossRef Full Text | Google Scholar

Hou, C., Pang, Z., Xie, S., Hing Wong, N., Sunarso, J., and Peng, Y. (2023). Enhanced permeability and stability of PVDF hollow fiber membrane in DCMD via heat-stretching treatment. Sep. Purif. Technol. 304, 122325. doi:10.1016/j.seppur.2022.122325

CrossRef Full Text | Google Scholar

Ibrar, I., Yadav, S., Naji, O., Alanezi, A. A., Ghaffour, N., Déon, S., et al. (2022). Development in forward Osmosis-Membrane distillation hybrid system for wastewater treatment. Sep. Purif. Technol. 286, 120498. doi:10.1016/j.seppur.2022.120498

CrossRef Full Text | Google Scholar

Jacob, P., Laborie, S., and Cabassud, C. (2018). Visualizing and evaluating wetting in membrane distillation: new methodology and indicators based on Detection of Dissolved Tracer Intrusion (DDTI). Desalination 443, 307–322. doi:10.1016/j.desal.2018.06.006

CrossRef Full Text | Google Scholar

Karakulski, K., and Gryta, M. (2005). Water demineralisation by NF/MD integrated processes. Desalination 177, 109–119. doi:10.1016/j.desal.2004.11.018

CrossRef Full Text | Google Scholar

Khayet, M., and Matsuura, T. (2011). Membrane distillation principles and applications. Amsterdam: Elsevier. doi:10.1016/B978-0-444-53126-1.10017-X

CrossRef Full Text | Google Scholar

Liu, Y., Horseman, T., Wang, Z., Arafat, H. A., Yin, H., Lin, S., et al. (2022). Negative pressure membrane distillation for excellent gypsum scaling resistance and flux enhancement. Environ. Sci. Technol. 56, 1405–1412. doi:10.1021/acs.est.1c07144

PubMed Abstract | CrossRef Full Text | Google Scholar

Naidu, L. D., Saravanan, S., Chidambaram, M., Goel, M., Das, A., and Babu, J. S. C. (2015). Nanofiltration in transforming surface water into healthy water: comparison with reverse osmosis. J. Chem. 2015, 1–6. doi:10.1155/2015/326869

CrossRef Full Text | Google Scholar

Pangarkar, B. L., Sane, M. G., Parjane, S. B., and Guddad, M. (2011). Vacuum membrane distillation for desalination of ground water by using flat sheet membrane. https://zenodo.org/records/1070211.

Google Scholar

Park, S.-M., and Lee, S. (2019). Influence of hydraulic pressure on performance deterioration of direct contact membrane distillation (DCMD) process. Membr. (Basel) 9, 37. doi:10.3390/membranes9030037

CrossRef Full Text | Google Scholar

Peña, L., de Zárate, J. M. O., and Mengual, J. I. (1993). Steady states in membrane distillation: influence of membrane wetting. J. Chem. Soc. Faraday Trans. 89, 4333–4338. doi:10.1039/FT9938904333

CrossRef Full Text | Google Scholar

Peng, P., Fane, A. G., and Li, X. (2005). Desalination by membrane distillation adopting a hydrophilic membrane. Desalination 173, 45–54. doi:10.1016/j.desal.2004.06.208

CrossRef Full Text | Google Scholar

Peng, Y., Dong, Y., Fan, H., Chen, P., Li, Z., and Jiang, Q. (2013). Preparation of polysulfone membranes via vapor-induced phase separation and simulation of direct-contact membrane distillation by measuring hydrophobic layer thickness. Desalination 316, 53–66. doi:10.1016/j.desal.2013.01.021

CrossRef Full Text | Google Scholar

Pfeiffer, A. M., Finnegan, N. J., and Willenbring, J. K. (2017). Sediment supply controls equilibrium channel geometry in gravel rivers. Proc. Natl. Acad. Sci. 114, 3346–3351. doi:10.1073/pnas.1612907114

PubMed Abstract | CrossRef Full Text | Google Scholar

Qtaishat, M., Khayet, M., and Matsuura, T. (2009). Novel porous composite hydrophobic/hydrophilic polysulfone membranes for desalination by direct contact membrane distillation. J. Memb. Sci. 341, 139–148. doi:10.1016/j.memsci.2009.05.053

CrossRef Full Text | Google Scholar

Rácz, G., Kerker, S., Kovács, Z., Vatai, G. N., Ebrahimi, M., and Czermak, P. (2014). Theoretical and experimental approaches of liquid entry pressure determination in membrane distillation processes. Period. Polytech. Chem. Eng. 58, 81–91. doi:10.3311/PPCH.2179

CrossRef Full Text | Google Scholar

Rezaei, M., and Samhaber, W. (2016). Wetting behaviour of superhydrophobic membranes coated with nanoparticles in membrane distillation. Chem. Eng. Trans. 47, 373–378. SE-Research Articles. doi:10.3303/CET1647063

CrossRef Full Text | Google Scholar

Rezaei, M., Warsinger, D. M., Lienhard V, J. H., Duke, M. C., Matsuura, T., and Samhaber, W. M. (2018). Wetting phenomena in membrane distillation: mechanisms, reversal, and prevention. Water Res. 139, 329–352. doi:10.1016/j.watres.2018.03.058

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritter, M. E. (2022). 18.2: channel Geometry and flow characteristics. Univ. Wisconsin-Stevens Point. Libr., Available at: https://geo.libretexts.org/@go/page/16641 (Accessed March 9, 2024).

Google Scholar

Rouquerol, J., Baron, G., Denoyel, R., Giesche, H., Groen, J., Klobes, P., et al. (2011). Liquid intrusion and alternative methods for the characterization of macroporous materials (IUPAC Technical Report). IUPAC Tech. Rep. 84, 107–136. doi:10.1351/PAC-REP-10-11-19

CrossRef Full Text | Google Scholar

Saffarini, R. B., Mansoor, B., Thomas, R., and Arafat, H. A. (2013). Effect of temperature-dependent microstructure evolution on pore wetting in PTFE membranes under membrane distillation conditions. J. Memb. Sci. 429, 282–294. doi:10.1016/j.memsci.2012.11.049

CrossRef Full Text | Google Scholar

Shin, Y., Choi, J., Lee, T., Sohn, J., and Lee, S. (2016). Optimization of dewetting conditions for hollow fiber membranes in vacuum membrane distillation. Desalin. Water Treat. 57, 7582–7592. doi:10.1080/19443994.2015.1044266

CrossRef Full Text | Google Scholar

Sipahutar, W. S., Maulana, S., Augustina, S., Murda, R. A., and Bindar, Y. (2021). Effects of heat treatment on the wettability and color properties of betung bamboo (dendrocalamus asper) strand. IOP Conf. Ser. Earth Environ. Sci. 830, 012071. doi:10.1088/1755-1315/830/1/012071

CrossRef Full Text | Google Scholar

Stewart, M. I. (2014). Chapter nine - gas sweetening. Boston: Gulf Professional Publishing, 433–539. doi:10.1016/B978-0-12-382207-9.00009-3

CrossRef Full Text | Google Scholar

Taetz, S., John, T., Bröcker, M., and Spandler, C. (2016). Fluid–rock interaction and evolution of a high-pressure/low-temperature vein system in eclogite from New Caledonia: insights into intraslab fluid flow processes. Contrib. Mineral. Petrol. 171, 90. doi:10.1007/s00410-016-1295-z

CrossRef Full Text | Google Scholar

Tun, C. M., Fane, A. G., Matheickal, J. T., and Sheikholeslami, R. (2005). Membrane distillation crystallization of concentrated salts—flux and crystal formation. J. Memb. Sci. 257, 144–155. doi:10.1016/j.memsci.2004.09.051

CrossRef Full Text | Google Scholar

Warsinger, D. M., Servi, A., Connors, G. B., Mavukkandy, M. O., Arafat, H. A., Gleason, K. K., et al. (2017). Reversing membrane wetting in membrane distillation: comparing dryout to backwashing with pressurized air. Environ. Sci. Water Res. Technol. 3, 930–939. doi:10.1039/C7EW00085E

CrossRef Full Text | Google Scholar

Yazgan-Birgi, P., Hassan Ali, M. I., and Arafat, H. A. (2018). Estimation of liquid entry pressure in hydrophobic membranes using CFD tools. J. Memb. Sci. 552, 68–76. doi:10.1016/j.memsci.2018.01.061

CrossRef Full Text | Google Scholar

Zhang, J., Li, J.-D., Duke, M., Xie, Z., and Gray, S. (2010). Performance of asymmetric hollow fibre membranes in membrane distillation under various configurations and vacuum enhancement. J. Memb. Sci. 362, 517–528. doi:10.1016/j.memsci.2010.07.004

CrossRef Full Text | Google Scholar

Zhang, J., Li, J.-D., and Gray, S. (2011). Effect of applied pressure on performance of PTFE membrane in DCMD. J. Memb. Sci. 369, 514–525. doi:10.1016/j.memsci.2010.12.033

CrossRef Full Text | Google Scholar

Zhu, J., Jiang, L., Matsuura, T., Zhang, J., Du, R., Ni, J., et al. (2015). New insights into fabrication of hydrophobic/hydrophilic composite hollow fibers for direct contact membrane distillation. Chem. Eng. Sci. 137, 79–90. doi:10.1016/j.ces.2015.05.064

CrossRef Full Text | Google Scholar