Microstructural orientation of anion exchange membrane through mechanical stretching for improved ion transport

Synthesis of anion exchange membranes (AEMs) with orientated nano/micro-structure and with tunable ion-channels is of great interest for applications in fuel cells, water electrolyzers, and redox flow batteries. However, there is still a dearth of work in the detailed understanding of anion conductivity from a polymer structure‒property perspective. Herein, we demonstrate an easy and versatile strategy to fabricate highly conductive AEMs. By stretching the AEMs, an improvement in OH⁻ conductivities of AEMs is achieved. The effect of elongation at different water contents on polymer structures and OH⁻ conductivities was investigated by a combination of molecular dynamics (MD) simulation and experimental study, giving insights into macromolecular orientation at the atomic level. The morphological changes, which consist of oriented polymer chains and elongated water clusters, are quantified by a combination of two dimensional small angle X-ray scattering (SAXS), scanning electron microscopy (SEM) and radial distribution functions. Detailed analyses of interatomic distances reveal morphological variations of hydrophilic domains and their interactions with water and OH⁻ under elongation at different hydration levels. Furthermore, the OH⁻ conductivities of our synthesized quaternized poly(2,6-dimethyl-1,4-phenylene oxide) (QPPO) AEMs increased significantly after stretching to 20% elongation at all water contents. Specifically, OH⁻ conductivity of stretched QPPO was 2.24 times more than the original AEM at 60% RH. The higher relative increase in OH⁻ conductivity at lower water content may be caused by the lower flexibility of side chains at lower hydrated level. This work verifies the significance of porous and/or oriented AEM structure in the improvement on anion conductivity and water transport efficiency.

1 Introduction

Anion exchange membranes (AEMs), as one of the core components of AEM fuel cells, are required to have high ion conductivity, a low degree of swelling, excellent mechanical properties, and robust chemical and thermal stabilities (Mustain et al., 2020; Chen and Lee, 2022). Many effects have been dedicated to the development of highly conductive AEMs. A variety of polymer backbones (Wang et al., 2013; Li et al., 2013) and cation groups (Zhu et al., 2016; Sun et al., 2018) have been employed in AEMs. Increasing the ion exchange capacity (IEC) and reducing AEM thickness are well-recognized approaches to improve the ion conductivity of AEMs. Nevertheless, many AEMs, especially those with IECs above 2.0 meq g⁻¹, do not survive the swelling and de-swelling cycles, and either fail during changes in relative humidity (RH) or delaminate from the electrodes (Hickner et al., 2013). In cases where the polymer is randomly functionalized, the AEM morphology is often ill-defined and difficult to control or quantify. Highly ordered structures and efficient ion channels are optimal for AEMs to achieve high conductivity (Huang et al., 2019). One popular vein of research of AEMs is the construction of microphase separated morphology (Wei et al., 2019; Pan et al., 2014; Lee et al., 2017; Huang et al., 2020), which shows some improvements in ion conductivity and mechanical properties, and reduced dimensional swelling. A different approach to achieve high conductivity AEMs is with microporous structures, using polymers of intrinsic microporosity (PIMs). Their inefficient packing of contorted polymer chains generates microporous structure to facilitate efficient ion transport, leading to excellent OH⁻ conductivity (Yang et al., 2016; Huang et al., 2021). The concept of structure design for alignment of ion channels has also been explored (Liu et al., 2019; Liu et al., 2020a). Magnetic field has been used to construct oriented ion-channel structures in electrolyte membranes. Highly conductive and durable membranes with aligned ion channels are obtained with ion-conducting paramagnetic compounds. Nevertheless, they are less convenient to scale-up for practical applications.

Membrane deformation occurs under assembly pressure, temperature and humidity changes during fuel cell operations (Ozmaian and Naghdabadi, 2015; Kusoglu et al., 2006; Zhou et al., 2009). Interestingly, an increase in proton conductivity of sulfonated poly(phenylene oxide) can be achieved by heating and stretching (Li et al., 2007). It is highly desirable to fundamentally understand the correlation between mechanical deformation and the morphology and ion conductivity of AEMs, to allow morphology‒conductivity relationships to be possibly quantified. Molecular dynamics (MD) simulation is a powerful tool to investigate the influence of mechanical stretching on macromolecular orientation at the atomic level (Ouma et al., 2022) especially to give insights into changes in structure and ion transport properties (Wei et al., 2015; Hofmann et al., 2010; Sengupta et al., 2017; Feng and Voth, 2019; Kurihara et al., 2019; Mabuchi and Tokumasu, 2014; Savage, 2021; Savage and Voth, 2014; Savage and Voth, 2016), membrane morphology (Petersen and Voth, 2006; Komarov et al., 2013; Kuo et al., 2016), water sorption and permeation (Daly et al., 2013; Daly et al., 2014), and mechanical properties (Sun et al., 2013; Li et al., 2018; Ozmaian and Naghdabadi, 2015 Xie et al., 2016).

Poly(2,6-dimethyl phenylene oxide) (PPO) is a commodity polymer widely used for its properties of thermal stability, mechanical strength and chemical durability (Liu et al., 2018; Zhang et al., 2022). PPO is readily brominated to access bromobenzyl groups for subsequent quaternization without chloromethylation (Hickner et al., 2013; Yang and Knauss, 2015). Many strategies have been developed with the aim of improving the anion conductivity and alkaline stability of positively charged PPO, including modifying the type and the position of the cationic moieties on the polymer backbone (Liu et al., 2018; Liu et al., 2020b), electrical treatment (Kim et al., 2018), and crosslinking with functionalized graphene oxide (Zhang et al., 2022). The objective of the present work is to study the effect of mechanical stretching-induced membrane orientation in poly(2,6-dimethyl-1,4-phenylene oxide)- trimethylammonium hydroxide (PPO-TMA)) AEM, with various water contents, λ, which is number of absorbed water molecules per hydroxide group (λ = H₂O/OH⁻). The small-angle X-ray scattering (SAXS), free volume and radial distribution functions are analyzed to evaluate the structural changes, which include backbone stretching, side chain extension, and also reformed water cluster distribution. The influence of structure deformation on ion transport is also investigated in detail. This is the first time that MD simulation and experimental work are combined to comprehensively investigate the effect of mechanical stretching on membrane morphology and properties.

2 Simulation methods

2.1 Modeling considerations

In the classical MD method, the ion conduction process is normally simulated with the following considerations: (i) A cubic computational domain with particles containing all of the material components needed in the actual operation of the ionic membrane is shown in Figure 1, which can be considered as a unit lattice. (ii) Each atom or atom group within the computational domain is treated as a single particle, and their interactions and motions are governed by Newton’s second law of mechanics. Therefore, the simulation depends on the type and number of the particles within the computational domain, and the forces acting on each particle.

FIGURE 1

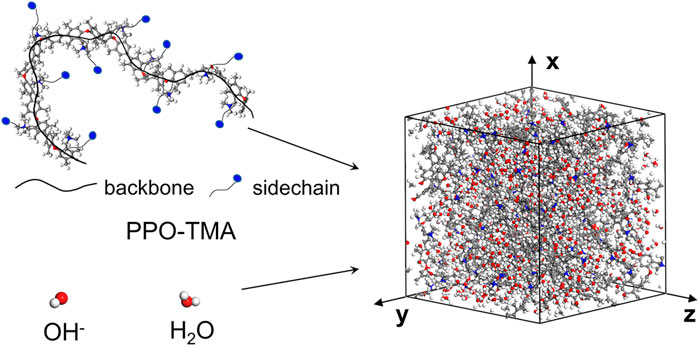
FIGURE 1. Schematic of the 3D molecular structure model in AEM, and the selected computational domain.

To balance statistical results and computational time within a domain, 10 polymer chains (or backbones, as illustrated by the black solid line in Figure 1) are considered along with the number of the ten repeat units in each backbone. An exact number of water molecules is specified by the hydration parameter λ, denoted as the absorbed water molecules per hydroxide group. Each hydroxide ion corresponds to a quaternary ammonium group of each side chain, resulting in a total of 100 hydroxy groups to maintain electrical neutrality. The size of the cubic domain was determined by the reference density. The total mass was set based on the polymer composition, as described above, and the density was set by adjusting the lattice size. The polymer chains, hydroxide anions, and water molecules were randomly packed within the computational domain in the initial state (Figure 1).

2.2 Model formulation

In MD simulation, atom interactions and motions are governed by Newton’s second law of mechanics as given in Eq. 1:

$F_i\left(t\right)=m_i{a}_i\left(t\right)(1)$

where $a_i\left(t\right)$ and $m_i$ are the acceleration at time t and the mass of atom i, and i = 1, 2 … N. Here, N represents the total number of atoms in the computational domain. The net force acting on the atom i at any instant of time t, $F_i\left(t\right)$, is expressed in terms of the position gradient of the potential energy the atom i has in the multi-atom system, $E_i\left(t\right)$, or

$F_i\left(t\right)=-\frac{d{E}_i}{d{r}_i}(2)$

such that

$-\frac{d{E}_i}{d{r}_i}=m_i\frac{d^2{r}_i}{d{t}^2}(3)$

where r_i is the position of the atom i at the instant of time t.

Parameterized complex functional forms, such as off-diagonal cross-coupling terms and high-order force constants, were taken into account by the COMPASS force field. The potential energy is expressed by Equations (S1)‒(S6) in the Supporting Material. Three-dimensional periodic boundary conditions (described in the Supporting Material) were adopted in this study. The initial position and initial velocity of each atom in the computational domain are described by Equation (S7).

The above equations form a conventional mathematical model for MD simulation. The simulation process was to solve the governing Newton’s equations of motion as shown in Equations (S8)‒(S10) and the simulation details are shown in the Supporting Material. Once the threshold reached the convergence tolerances of energy and force of geometry optimization shown in Equations (S15)‒(S16), the system was considered to be equilibrium, then model validation could be carried out as shown in Supplementary Figure S1.

In order to investigate the effect of mechanical stretching (deformation) in a given direction on the transport of ions in the membrane, a uniaxial deformation was applied in the z-direction (shown in Figure 1), after the unit lattice had reached thermodynamic equilibrium. The degree of deformation can be varied to assess the impact of the deformation on the oriented structure, morphology, and ion transport. The deformation in the z-direction was considered as the total atom number remains the same. Therefore, the deformation may be described as:

$L_{z1}=L_{z0}+\left(L_{z0}\times \mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\right)(4)$

$L_{x1}=L_{y1}={\left(V/L_{z1}\right)}^{1/2}(5)$

Similarly, the deformation for individual atoms have the effect of changing the inter-atom distance in the z, x and y directions such that

$z_{ij}=z_{ij,0}\left(1+\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\right)(6)$

$x_{ij}=\frac{x_{ij,0}}{L_{x1}};y_{ij}=\frac{y_{ij,0}}{L_{y1}}(7)$

where L and V is the side length and volume of the unit lattice, $x_{ij}$, $y_{ij}$, and $z_{ij}$ are the distances between the atoms i and j in the x, y and z directions, respectively. The subscript “0” represents the distance before deformation (strain). A series of strains were considered in the z-direction, with the corresponding compression in the other two directions (x and y) in order to maintain a constant density. Clearly, the strain mainly affects potential energy E_i in Eq. 2 through the change in the distance among the atoms in the computational domain, and the stress can be obtained through dividing the force given in Eq. 3 by the area ($L_{x1}\times L_{y1}$).

2.3 Simulation analysis: Statistical analysis of all the particles in the domain

2.3.1 Free volume

The free volume is defined as a unit lattice outside the defined surface. The isosurface representation of the aqueous domain includes water molecules, quaternary ammonium groups of the polymer, the PPO-TMA polymer chains and hydroxide ions. In the simulation, a probe with a radius of 1.4 Å was adopted (Kuo et al., 2018).

2.3.2 Radial distribution function

Radial distribution functions (RDFs) have been employed to study the interactions between different atoms in membrane systems, such as ammonium groups, hydroxide ions, and water molecules (Ennari, 2008):

$g_{A-B}\left(r\right)=\frac{V}{N_B}\cdot \frac{n_B}{4\pi r^{2}dr}(8)$

where n_B is the number of atoms B at the distance r from atoms A in a layer of thickness dr. N_B represents the number of particles B and V represents the domain total volume. It can be seen from the equation that the radial distribution function is the ratio of regional density to the average density of the domain.

The coordination numbers (CNs) of molecules around the nitrogen atom were calculated (Bahlakeh and Nikazar, 2012), which is the number of adjacent atoms around the nitrogen atoms, with the aim of investigating the relationship between water molecules and hydroxide ions with ammonium groups.

$\mathrm{C}\mathrm{N}=4\pi \frac{N_B}{V}\int r^2{g}_{A-B}\left(r\right)dr(9)$

2.3.3 Ion conductivity

The diffusion coefficient of hydroxide ions was calculated using the mean square displacement (MSD) by the following relationship (Chen et al., 2014), according to the Einstein formula (Blickle et al., 2007):

$MSD=\frac{1}{N_i}\langle {\displaystyle \sum _{i=1}^{N_i}}{\left|r_i\left(t\right)-r_i\left(t_0\right)\right|}^2\rangle (10)$

$D_i=\frac{1}{6}\underset{t\to \infty }{\mathit{lim}}\frac{dMSD}{dt}(11)$

where D_i is the diffusion coefficient of atom i and N_i refers to the total number of i atoms in the computational domain.

Ion conductivity (σ) was calculated using the hydroxide ion diffusion coefficient (Pozuelo et al., 2006):

$\sigma =\frac{N{z}^2{e}^{2}D}{VkT}(12)$

where k, z and e represent the Boltzmann constant, total charge and electronic charge, respectively. N is the number of hydroxide ions, D is the hydroxide ion diffusion coefficient, and T is the absolute temperature.

3 Experimental section

3.1 Materials

Poly(2,6-dimethyl-1,4-phenylene oxide) (PPO, M_n = 20,000), N-bromosuccinimide (NBS, 99%), 2-2′-azobisisobutyronitrile (AIBN, 98%), trimethylamine (TMA, 3.2 M solution in ethanol), chlorobenzene and N-methyl-2-pyrrolidone (NMP) were obtained from Sigma-Aldrich and used as received, except AIBN.

3.2 Modification of PPO and fabrication of membranes

Bromination and quaternization reactions were used to prepare trimethylamine functionalized PPO AEMs as shown in Figure 2. PPO was brominated using NBS according to a procedure outlined in the literature (Yang et al., 2018). In summary, NBS and recrystallized AIBN initiator (molar ratio 0.8:1) were added to a PPO solution in chlorobenzene. The mixture was heated and maintained at 135°C for 3 h under a nitrogen atmosphere, and then it was rapidly poured into methanol, resulting in a produce yellow precipitate. After washing with ethanol and drying in a vacuum oven at 30°C for 24 h, clean brominated PPO (BPPO) was obtained, having approximately 20% degree of bromination.

FIGURE 2

FIGURE 2. The synthesis route of PPO-TMA polymer.

The BPPO polymer and TMA were dissolved in NMP for 1 h at room temperature (RT) under ultrasonication. To ensure the benzyl bromine groups quaternization completely, the molar ratio of N in TMA to the bromobenzyl groups in BPPO was adjusted to 3:1. The solution was poured onto dry Petri plates sized 10 cm × 10 cm, then heated at 70°C to drive off TMA reagent and solvent. To convert the counter ions from bromide ions to hydroxide ions, the membranes were peeled off and submerged in 1 M KOH solution at room temperature for 48 h. The AEMs were then washed with deionized water until they were neutral pH. The synthesized quaternary ammonium membranes (approximately 10 cm × 10 cm, thickness approximately 50 μm) are denoted as PPO-TMA.

3.3 Membrane characterization and measurements

The IEC was measured experimentally by the Mohr method (Wang et al., 2019; Xu and Yang, 2001). Dried membranes in the Br⁻ form were immersed into Na₂SO₄ solution to release bromine ions. The released bromide ions were determined by titration with 0.01 M AgNO₃ aqueous solution with the indicator K₂CrO₄ solution. The IEC value was calculated as follows:

$IEC=\frac{0.01\times V_{\mathrm{A}\mathrm{g}\mathrm{N}{\mathrm{O}}_3}}{m_{\mathrm{d}\mathrm{r}\mathrm{y}}}(13)$

where VAgNO₃ is the volume of consumed AgNO₃ aqueous solution and m_dry is the weight of dried membrane.

The ion conductivity (σ, mS cm^-1) was measured in the in-plane direction by the four-electrode AC impedance method. The membrane was clamped in the test device and placed in an environmental chamber (Espec, SH-222) at different relative humidity (RH). The ion conductivity was calculated as follows:

$\sigma =\frac{L}{R\bullet A}(14)$

where L is the distance between the two reference electrodes (cm), R is the measured resistance, and A is the cross-sectional area of the membrane (cm²).

WU and λ were calculated from followed formulae:

$WU=\frac{W_{\mathrm{w}\mathrm{e}\mathrm{t}}-W_{\mathrm{d}\mathrm{r}\mathrm{y}}}{W_{\mathrm{d}\mathrm{r}\mathrm{y}}}\times 100(15)$

$\lambda =\frac{WU\times 1000}{IEC\times 18}(16)$

where W_wet is the weight of the wet membrane; W_dry is the weight of the dry membrane. The dried membrane was immersed in deionized water at a specified temperature for 24 h. After removing it and quickly blotting off the surface water, the weight was measured. Then, the membrane was placed in a vacuum oven at 60°C for 24 h and again weighed.

3.4 Tensile tests

The membranes were cut into strips (1 cm × 3 cm) and stretched mechanically by a tensile system (Instron, E1000). The loading was static and the stress state was uniaxial stretching. Mechanical stretching was conducted at RT with a constant strain rate (2 mm min⁻¹) to obtain the stress‒strain (SS) correlations and repeated three times.

3.5 Scanning electron microscopy (SEM)

The surfaces or cross-sections of membrane were characterized by an S4800 field emission scanning electron microscope (Hitachi, Japan) at an accelerating voltage of 5 kV. The observed areas were pre-sputtered with a thin layer of platinum under vacuum.

3.6 Small-angle X-ray scattering (SAXS)

The two-dimensional SAXS patterns were recorded using the Beijing Synchrotron Radiation Facility (BSRF) 1W2A experimental site using a Cu Kα (λ = 1.54 Å) radiation generator, with a distance of 1.5 m between the membrane sample and detector.

4 Results and discussion

4.1 The influence of molecular structure on ion conductivity of PPO-TMA

The effect of molecular oriented arrangement on ion transport in PPO-TMA was studied by MD simulation. The results show that the oriented ion transmission pathways improve conduction efficiency. Interestingly, the σ at λ = 5 of oriented-arranged PPO-TMA (inset in Figure 3) was 1.391 mS cm⁻¹ at 300 K, which is 2.4 higher than that of randomly-arranged PPO-TMA (0.405 mS cm⁻¹), suggesting that oriented polymer chains significantly promote ionic transport, which is consistent with the literature (Meng et al., 2019).

FIGURE 3

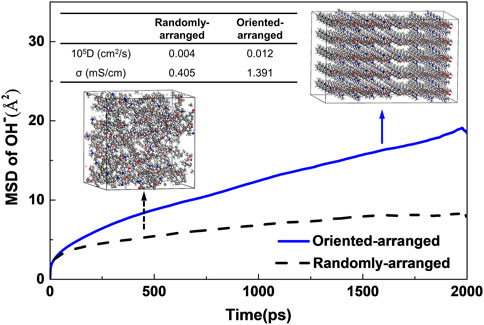
FIGURE 3. Mean square displacements (MSD) of OH⁻, diffusivity (cm² s^-1) of OH⁻ and anion conductivity in PPO-TMA membrane. The inset shows the diagram of the randomly-arranged structure and oriented-arranged structure of PPO-TMA.

4.2 Morphological changes under uniaxial stretching

The above-mentioned oriented arrangement is an idealized model, because it is difficult to achieve an absolutely oriented arrangement. Here we present that mechanical stretching induces relatively ordered arrangement, which results in improved anion conductivity. The effect of mechanical stretching on PPO-TMA AEMs (such as changes of polymer chain arrangement and water cluster distribution) was investigated by experimental work combined with MD simulation, as shown in Figure 4A. Young’s modulus (initial slope section) and yield stress can be obtained from the stress-strain curves. It should be noted that the experimental conditions and parameters were identical with those used in the MD simulation. For simulation, a linear elastic region is found at a strain of less than 2%, which correlates with the experimental results. The yield stress obtained from the experiment is also in the same order as the simulation results, although there are some slight deviations from the simulation due to statistical errors.

FIGURE 4

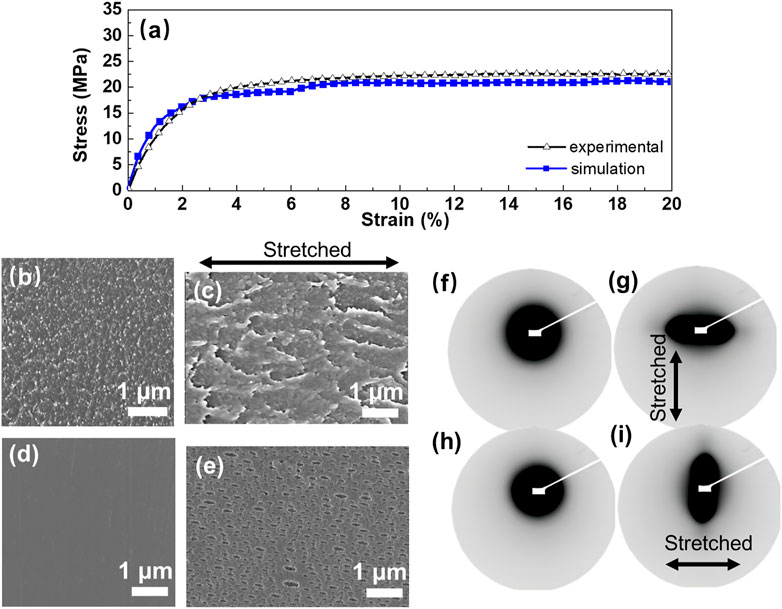
FIGURE 4. (A) Stress-strain curves of experimental and simulation results. SEM images (cross-sectional) of PPO-TMA (B) before and (C) after stretching; SEM images (surface) of PPO-TMA (D) before and (E) after stretching. Two-dimensional SAXS patterns of PPO-TMA membrane at (F) (H) initial and (G) (I) stretched state. Stretching direction is indicated with double sided arrow.

Morphology characteristics were measured using SEM and shown in Figures 4B–E. The polymer chain displays a relatively uniform structure morphology before stretching (Figure 4B), while the cross-sectional SEM image after stretching shows a relatively oriented structure (Figure 4C). The polymer molecular arrangement or aggregation can be described via simulation of the density field calculation, which is presented in Supplementary Figure S2. The color gradient from white to black shown in Supplementary Figure S2A, B corresponds to the increase in density of polymer chains. It is seen that after the tensile stretching simulation, the density value decreases and the polymer morphology tends to be stretched and extended toward the stretched direction. Figures 4D, E shows the surface morphology of un-stretched and stretched PPO-TMA. A relatively smooth surface of un-stretched membrane is observed in Figure 4D. A large number of submicroscopic pores are formed during stretching of PPO-TMA. The elliptical pores formed during this process are oriented with their major axes parallel to the stretching direction and the film surface (Figure 4E). The lengths of the slits are typically in the range from 53 nm to 419 nm. The porous structure provides a continuous configuration necessary for fast ion and water transport (Morehouse et al., 2006; Sarada et al., 1983). Two-dimensional SAXS characterization provides additional evidence for the oriented structure. The isotropic SAXS data show a diffuse outer ring in Figures 4F–H, which has been attributed to scattering from the polymer aggregates (phase-separation of hydrophilic‒hydrophobic domains). As the membrane was stretched, the initially isotropic scattering pattern transforms into a strongly anisotropic scattering pattern, as observed in Figures 4G–I. For the stretched membrane, evident anisotropism is observed in SAXS pattern, indicating oriented morphology. This is attributed to the alignment of elongated polymer aggregates in the direction of uniaxial stretching (van der Heijden et al., 2004).

Structure changes of PPO-TMA by stretching was simulated and is shown in Figure 5. The 10 colors represent 10 polymer chains in Figure 5A. As the membrane is stretched, the backbones become oriented in the direction of stretching, which coincides with the strain effect that has been found in proton exchange membranes (Cable et al., 1995). With the consideration of adsorbed water molecules (λ = 15), a dramatic change in structure due to stretching can also be observed in Figures 5C, D. Water clusters tend to be extended along the stretching direction. The simulation results of the density field of water clusters also shows the same phenomenon (Supplementary Figure S3).

FIGURE 5

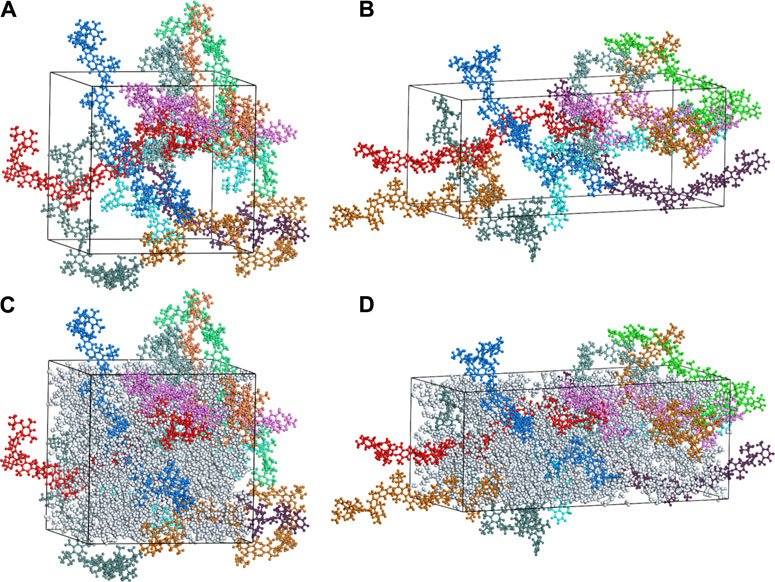
FIGURE 5. Schematic of the PPO-TMA membrane (A) and (C) before deformation, and (B) and (D) after uniaxial stretching with 60% strain deformation in the z-axis direction. Gray particles in (C) and (D) represent water molecules (λ = 15), and other colors correspond to polymer chains.

To further verify the increased porosity and connected channels of stretched PPO-TMA, the free volume of the unit lattice was calculated (Supplementary Figure S4). Free volume increased gradually with strains of up to 60% at all levels of water content. A high water content results in higher free volume for the same strain. The rapid increase in the free volume with increasing hydration levels is due to the increase in the number of water molecules in the membrane, causing a plasticizing effect and a larger distance between the polymer chains (Kuo et al., 2018).

4.3 Radial distribution functions

In order to probe the detailed changes in the lattice orders in the local structure during PPO-TMA deformation at different water contents, N−N (nitrogen atom in polymer), N−O_w (oxygen atom in water molecule), and N−O_h (oxygen atom in hydroxide ion) RDFs were analyzed (Supplementary Figure S5), followed by calculation of the quantitative coordination numbers (CNs), as shown Figure 6. The CNs of N‒N, N‒O_w, and N‒O_h indicate the interaction strength between TMAs, TMA and water, TMA and OH⁻, respectively.

FIGURE 6

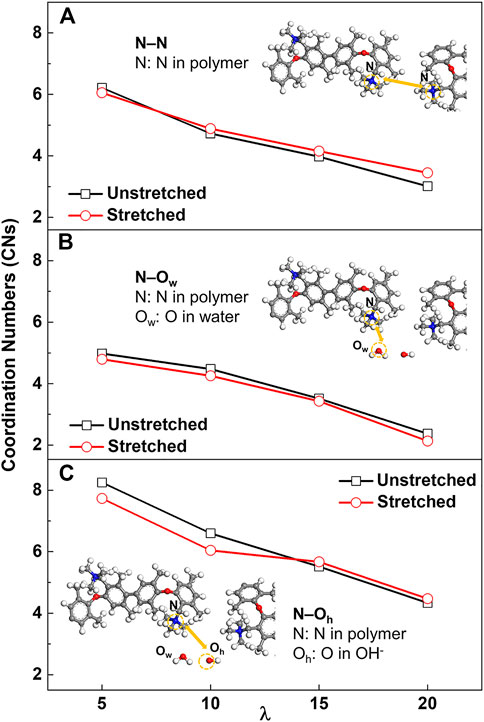
FIGURE 6. The coordination numbers (CNs) of (A) N‒N, (B) N‒O_w (oxygen atom in water molecule) and (C) N‒O_h (oxygen atom in hydroxide ion) in the un-stretched condition and 60% strain.

Supplementary Figure S5A shows the simulated RDFs of N−N linkage. The position of peaks at distances of <12 Å and >12 Å can be assigned to adjacent N−N between two chains as well as the N−N in the same chain, respectively (Dong et al., 2018). The differences among the RDFs at the prophase curves demonstrate the changes in the crystal lattice order of PPO-TMA. As the water content increases, the CNs for the un-stretched membrane decrease from 6.214 to 3.011 (Figure 6 and Supplementary Table S1), indicating that the nitrogen atoms tend to be separated at higher water content (Kuo et al., 2016). When the membrane was stretched, the CNs decrease for low water contents but increase for high water contents. At low water content, quaternary ammonium groups aggregate densely in the local hydrophilic phase, which is not conducive to conformational relaxation for the side chains in response to membrane deformation. Under uniaxial deformation, the side chains tend to align parallel to the stretching direction. At high water content, the quaternary ammonium groups are fully hydrated, resulting in flexible side chains, which allow rearrangement during membrane stretching. In addition, a decrease in the peak intensity at ∼13 Å indicates that the distance between N atoms in the same chain increases with stretching, also inducing a highly orientated polymer chain.

To investigate how the quaternary ammonium groups are solvated by water molecules, the RDFs of nitrogen and oxygen atoms in H₂O for different systems were investigated, as shown in Supplementary Figure S5B. Firstly, the peak intensity and CNs decrease as the water content increases, indicating that water molecules bind weakly with the quaternized groups with increasing water content. However, the peak positions do not change. This indicates that stretching mainly has an effect on the probability of the atoms in proximity with the quaternized groups. There is no significant change in the distribution of water molecules as the density decreases. Secondly, the CNs of water molecules surrounding each quaternary ammonium group are found to decrease with stretching for all water contents. This again confirms that the elongation of water clusters under mechanical stretching results in a decrease in the number of water molecules associated with the quaternized groups.

To investigate the relationship between R₄N⁺ groups and OH⁻, the CNs of the N−O_h were calculated and the results are shown in Figure 6C. At low water content, compared to the un-stretched membranes, the stretched membranes have lower CNs for N‒O_h. Hydroxide ions aggregate densely in the hydrophilic phase. As the water cluster extends due to uniaxial deformation, the number of water molecules and hydroxide ions correlated with the quaternary ammonium groups decreases. Therefore, at high water content, the polymer side chains have greater conformational flexibility and are more likely in a relaxed state when stretching the membrane, and thereby interact with free hydroxide ions. This leads to an increase in CNs and hydroxide ions around the quaternary ammonium group. Similar results have been reported in the literature (Kuo et al., 2017).

4.4 Dynamic properties of the hydrated membrane

To analyze the ion diffusion characteristics, the diffusion coefficients of hydroxide ions were calculated at various water contents and different strain. Supplementary Figure S6 shows the hydroxide ion MSD curves at 300 K. Figure 7 summarizes the diffusion coefficients calculated from the hydroxide ion MSD curves at different water contents. Notably, Supplementary Figure S6 shows the slope of hydroxide ion MSD curves increases apparently with an increase in strain. The slopes increase more significantly with the change in the water contents rather than the strain levels. The diffusion coefficients of hydroxide ion in the un-stretched membrane at different water contents are 0.006 × 10⁻⁵ to 0.286 × 10⁻⁵ cm² s⁻¹, with λ from 5–20, respectively. The corresponding calculated σ values are 0.608, 1.989, 11.75 and 16.63 mS cm⁻¹, respectively.

FIGURE 7

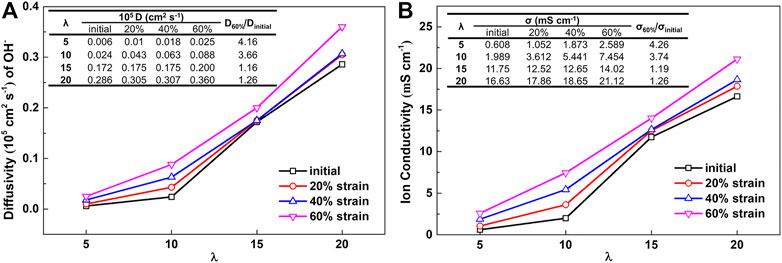
FIGURE 7. MD simulation results of (A) diffusivity of hydroxide ion and (B) hydroxide ion conductivity under different strain.

Compared with the effect of changes in strain, the influence of change in water content is more significant. When the membrane was stretched with different strain, the D values change. For λ = 5 with the strain of 0%–60%, the corresponding D values are in the range of 0.006 × 10⁻⁵ to 0.025 × 10⁻⁵ cm² s⁻¹, respectively. The calculated σ values are 0.608–2.589 mS cm⁻¹ (an increase of 326% compared with un-stretched membrane). At the condition of λ = 15, when the strain changes from 0% to 60%, D increases from 0.172 × 10⁻⁵ to 0.2 × 10⁻⁵ cm² s⁻¹; the corresponding ion conductivity is 11.75 mS cm⁻¹ (reference value 11.25 mS cm^-1 (Yang et al., 2018)) and 14.02 mS cm⁻¹ (an increase of less than 50% than that of the un-stretched membrane), respectively. It has also been reported that the proton conductivity of oriented membranes in the direction of the strain increased compared with un-stretched membranes (Dan et al., 2006).

The ratios of D and σ in stretched and un-stretched membranes are shown in Figure 7 as embedded tables. The stretching effect on σ is not obvious at high water content, which can be explained by the morphology changes. At low water contents, the enhancement in hydroxide transport can be attributed to the stretched membrane with a high orientation of polymer chain and water pathways (Park et al., 2011). For higher water contents of λ = 15 and 20, flexible hydrated side chains are strongly correlated with free hydroxide ions, reducing the increase in D. Thus, the effects of stretching on ion transport are noticeably different at different water contents. The σ reaches the maximum value at λ = 20 and at a strain of 60%. It can be concluded that the orientation of water clusters and polymer chains are extended in the stretching direction by the uniaxial stretching of the membrane. The above analysis also correlates with the analysis of the microscopic morphology diagram shown in Figure 4, resulting in pathways that facilitate hydroxide ion transport.

4.5 Experimental results of ion conductivity for un-stretched/stretched membranes

To further verify the simulation results, experimental conductivity tests were conducted at different RH with the membranes before and after mechanical stretching. From calculations based on experimental values of water uptake (WU) and IEC, λ is obtained, which represents the number of water molecules corresponding to each quaternary ammonium group, consistent with the definition of λ in the MD simulation. Therefore, we observe that when λ = 15.86, σ = 11.33 mS cm⁻², which is in good agreement with the simulation results in Figure 7B (λ = 15, σ = 11.75 mS cm^-2). In addition, the conductivity of membrane at 20% elongation in the stretching direction was also tested. In the stretched z-direction, the σ increased by 3.24, 2.61, 1.61 and 1.57 times with increasing λ (listed in Table 1), respectively. Such results well demonstrate that mechanical stretching has a positive effect on the ion conduction in the tensile direction, which further verifies the conclusion obtained in the above simulation.

TABLE 1

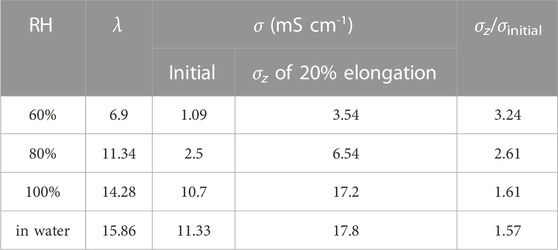
TABLE 1. The hydroxide ion conductivity of the PPO-TMA membrane in the stretching direction before and after stretching.

5 Conclusion

In this study, simulation models of quaternized poly(2,6-dimethyl-1,4-phenylene oxide) membranes with a range of water content were constructed to investigate the effect of mechanical stretching on structure deformation, anion conductivity and morphology‒conductivity relationships. During the elongation process, macromolecular orientation at the atomic level is shown to occur by molecular dynamics simulation. The oriented morphology was observed by scanning electron microscopy and two-dimensional small-angle X-ray scattering. Water clusters became elongated along the direction of stretching. The resulting continuous and oriented pathways effectively enhance hydroxide ion diffusivity in the direction of stretching at all water contents. The ion conductivities after mechanical stretching increased by 326% and 274% at hydration levels of λ = 5 and 10, respectively, which are similar to the experimental observations. However, at higher water contents (λ = 15 and 20), the ion conductivities increased by less than 50%. The abundant water induces greater conformational flexibility in the hydrated side chains, leading to structure relaxation in any direction when the membrane undergoes stretching. Therefore the incremental increase in ion conduction in the stretching direction at high water content is less than at low water content. This study provides insights into the micro-morphology of anion exchange membranes under mechanical stretching and explains the effect of macromolecular orientation on hydroxide conductivity of hydrated membranes, which is useful for providing a theoretical basis for the structure‒property relationship of AEMs. We are only in the early stages of understanding anion transport efficiency in ordered AEM systems and there remains more work to be done, especially in the development of innovative material strategies for the synthesis of highly ordered anion conducting membranes, and new methods to analyze their performance characteristics.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CZ contributed to investigation, methodology, data curation, formal analysis, visualization, writing—Original Draft. LW contributed to data curation, data analysis, writing—review and editing. SZ contributed to investigation. JZ contributed to methodology, project administration, writing—review and editing. YY contributed to conceptualization, writing—review and editing, supervision, funding acquisition. KJ contributed to project administration. QD contributed to project administration. Xianguo Li contributed to methodology, writing—review and editing, supervision. MG contributed to writing—review and editing, supervision. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors thank the National Natural Science Foundation of China (21875161) and the State Key Laboratory of Engines for financial support.

Conflict of interest

Author SZ was employed by the company CATARC New Energy Vehicle Test Center (Tianjin) Co., Ltd. The author(s) XL, YY and MDG declared that they were an editorial board member of Frontiers, at the time of submission.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frmst.2023.1193355/full#supplementary-material

References

Bahlakeh, G., and Nikazar, M. (2012). Molecular dynamics simulation analysis of hydration effects on microstructure and transport dynamics in sulfonated poly(2,6-dimethyl-1,4-phenylene oxide) fuel cell membranes. Int. J. Hydrogen Energy 37, 12714–12724. doi:10.1016/j.ijhydene.2012.06.034

CrossRef Full Text | Google Scholar

Blickle, V., Speck, T., Lutz, C., Seifert, U., and Bechinger, C. (2007). Einstein relation generalized to nonequilibrium. Phys. Rev. Lett. 98, 210601. doi:10.1103/PhysRevLett.98.210601

PubMed Abstract | CrossRef Full Text | Google Scholar

Cable, K. M., Mauritz, K. A., and Moore, R. B. (1995). Anisotropic ionic conductivity in uniaxially oriented perfluorosulfonate ionomers. Chem. Mat. 7, 1601–1603. doi:10.1021/cm00057a002

CrossRef Full Text | Google Scholar

Chen, L., He, Y., Tao, W., and Huang, X. (2014). A case of long-term survival after curative resection for synchronous solitary adrenal metastasis from rectal cancer. Numer. Heat. Tr. 65, 216–219. doi:10.12669/pjms.301.4341

CrossRef Full Text | Google Scholar

Chen, N., and Lee, Y. M. (2022). Anion-conducting polyelectrolytes for energy devices. Trends Chem. 4, 236–249. doi:10.1016/j.trechm.2021.12.009

CrossRef Full Text | Google Scholar

Daly, K. B., Benziger, J. B., Debenedetti, P. G., and Panagiotopoulos, A. Z. (2013). Molecular dynamics simulations of water sorption in a perfluorosulfonic acid membrane. J. Phys. Chem. B 117, 12649–12660. doi:10.1021/jp405440r

PubMed Abstract | CrossRef Full Text | Google Scholar

Daly, K. B., Benziger, J. B., Panagiotopoulos, A. Z., and Debenedetti, P. G. (2014). Molecular dynamics simulations of water permeation across Nafion membrane interfaces. J. Phys. Chem. B 118, 8798–8807. doi:10.1021/jp5024718

PubMed Abstract | CrossRef Full Text | Google Scholar

Dan, L., Hickner, M. A., Case, S. W., and Lesko, J. (2006). Relaxation of proton conductivity and stress in proton exchange membranes under strain. J. Eng. Mat. and Technol. 128, 503–508. doi:10.1115/1.2345441

CrossRef Full Text | Google Scholar

Dong, D., Wei, X., Hooper, J. B., Pan, H., and Bedrov, D. (2018). Role of cationic groups on structural and dynamical correlations in hydrated quaternary ammonium-functionalized poly(p-phenylene oxide)-based anion exchange membranes. Phys. Chem. Chem. Phys. 20, 19350–19362. doi:10.1039/c8cp02211a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ennari, J. (2008). Modelling of transport properties and state of water of polyelectrolytes containing various amounts of water. Polymer 49, 2373–2380. doi:10.1016/j.polymer.2008.03.019

CrossRef Full Text | Google Scholar

Feng, S., and Voth, G. A. (2019). Proton solvation and transport in hydrated Nafion. J. Phys. Chem. B 115, 5903–5912. doi:10.1021/jp2002194

PubMed Abstract | CrossRef Full Text | Google Scholar

Hickner, M. A., Herring, A. M., and Coughlin, E. B. (2013). Anion exchange membranes: Current status and moving forward. J. Polym. Sci. Pol. Phys. 51, 1727–1735. doi:10.1002/polb.23395

CrossRef Full Text | Google Scholar

Hofmann, D. W. M., Kuleshova, L. N., and Aguanno, B. D. (2010). Theoretical simulations of proton conductivity: Basic principles for improving the proton conductor. J. Power Sources 195, 7743–7750. doi:10.1016/j.jpowsour.2009.10.019

CrossRef Full Text | Google Scholar

Huang, G., Mandal, M., Peng, X., Yang-Neyerlin, A. C., Pivovar, B. S., Mustain, W. E., et al. (2019). Composite poly(norbornene) anion conducting membranes for achieving durability, water management and high power (3.4 W/cm²) in hydrogen/oxygen alkaline fuel cells. J. Electrochem. Soc. 166, F637–F644. doi:10.1149/2.1301910jes

CrossRef Full Text | Google Scholar

Huang, T., He, G., Xue, J., Otoo, O., He, X., Jiang, H., et al. (2020). Self-crosslinked blend alkaline anion exchange membranes with bi-continuous phase separated morphology to enhance ion conductivity. J. Membr. Sci. 597, 117769. doi:10.1016/j.memsci.2019.117769

CrossRef Full Text | Google Scholar

Huang, T., Zhang, J., Pei, Y., Liu, X., Xue, J., Jiang, H., et al. (2021). Mechanically robust microporous anion exchange membranes with efficient anion conduction for fuel cells. Chem. Eng. J. 418, 129311. doi:10.1016/j.cej.2021.129311

CrossRef Full Text | Google Scholar

Kim, J.-H., Ryu, S., Lee, J.-Y., Moon, S.-H., Cheung, D. Y., Chung, W. C., et al. (2018). Early detection is important to reduce the economic burden of gastric cancer. J. Membr. Sci. 553, 82–89. doi:10.5230/jgc.2018.18.e7

PubMed Abstract | CrossRef Full Text | Google Scholar

Komarov, P. V., Khalatur, P. G., and Khokhlov, A. R. (2013). Large-scale atomistic and quantum-mechanical simulations of a Nafion membrane: Morphology, proton solvation and charge transport. Beilstein J. Nanotech. 4, 567–587. doi:10.3762/bjnano.4.65

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuo, A. T., Shinoda, W., and Okazaki, S. (2016). Molecular dynamics study of the morphology of hydrated perfluorosulfonic acid polymer membranes. J. Phys. Chem. C 120, 25832–25842. doi:10.1021/acs.jpcc.6b08015

CrossRef Full Text | Google Scholar

Kuo, A. T., Takeuchi, K., Tanaka, A., Urata, S., Okazaki, S., and Shinoda, W. (2018). Exploring the effect of pendent side chain length on the structural and mechanical properties of hydrated perfluorosulfonic acid polymer membranes by molecular dynamics simulation. Polymer 146, 53–62. doi:10.1016/j.polymer.2018.05.033

CrossRef Full Text | Google Scholar

Kuo, A. T., Tanaka, A., Irisawa, J., Shinoda, W., and Okazaki, S. (2017). Molecular dynamics study on the mechanical deformation of hydrated perfluorosulfonic acid polymer membranes. J. Phys. Chem. C 121, 21374–21382. doi:10.1021/acs.jpcc.7b05719

CrossRef Full Text | Google Scholar

Kurihara, Y., Mabuchi, T., and Tokumasu, T. (2019). Molecular dynamics study of oxygen transport resistance through ionomer thin film on Pt surface. J. Power Sources 414, 263–271. doi:10.1016/j.jpowsour.2019.01.011

CrossRef Full Text | Google Scholar

Kusoglu, A., Karlsson, A. M., Santare, M. H., Cleghorn, S., and Johnson, W. B. (2006). Mechanical response of fuel cell membranes subjected to a hygro-thermal cycle. J. Power Sources 161, 987–996. doi:10.1016/j.jpowsour.2006.05.020

CrossRef Full Text | Google Scholar

Lee, W., Park, E. J., Han, J., Shin, D. W., Kim, Y. S., and Bae, C. (2017). Poly(terphenylene) anion exchange membranes: The effect of backbone structure on morphology and membrane property. ACS Macro Lett. 6, 566–570. doi:10.1021/acsmacrolett.7b00148

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, C., Liu, J., Guan, R., Zhang, P., and Zhang, Q. (2007). Effect of heating and stretching membrane on ionic conductivity of sulfonated poly(phenylene oxide). J. Membr. Sci. 287, 180–186. doi:10.1016/j.memsci.2006.10.015

CrossRef Full Text | Google Scholar

Li, L., Li, W., Geng, L., Chen, B., Mi, H., Hong, K., et al. (2018). Formation of stretched fibrils and nanohybrid shish-kebabs in isotactic polypropylene-based nanocomposites by application of a dynamic oscillatory shear. Chem. Eng. J. 348, 546–556. doi:10.1016/j.cej.2018.04.197

CrossRef Full Text | Google Scholar

Li, N., Leng, Y., Hickner, M. A., and Wang, C. (2013). Highly stable, anion conductive, comb-shaped copolymers for alkaline fuel cells. J. Am. Chem. Soc. 135, 10124–10133. doi:10.1021/ja403671u

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, L., Chu, X., Liao, J., Huang, Y., Li, Y., Ge, Z., et al. (2018). Tuning the properties of poly(2,6-dimethyl-1,4-phenylene oxide) anion exchange membranes and their performance in H₂/O₂ fuel cells. Energy Environ. Sci. 2, 435–446. doi:10.1039/c7ee02468a

CrossRef Full Text | Google Scholar

Liu, L., Liu, Z., Bai, L., Shao, C., Chen, R., Zhao, P., et al. (2020b). Quaternized poly (2, 6-dimethyl-1, 4-phenylene oxide) anion exchange membranes based on isomeric benzyltrimethylammonium cations for alkaline fuel cells. J. Membr. Sci. 606, 118133. doi:10.1016/j.memsci.2020.118133

CrossRef Full Text | Google Scholar

Liu, L., Zhang, J., Zheng, C., Xue, J., Huang, T., Yin, Y., et al. (2020a). Oriented proton-conductive nano-spongefacilitated polymer electrolyte membranes. Energy Environ. Sci. 13, 297–309. doi:10.1039/c9ee03301g

CrossRef Full Text | Google Scholar

Liu, X., Li, Y., Xue, J., Zhu, W., Zhang, J., Yin, Y., et al. (2019). Magnetic field alignment of stable proton-conducting channels in an electrolyte membrane. Nat. Commun. 10, 842. doi:10.1038/s41467-019-08622-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Mabuchi, T., and Tokumasu, T. (2014). Effect of bound state of water on hydronium ion mobility in hydrated Nafion using molecular dynamics simulations. J. Chem. Phys. 141, 104904. doi:10.1063/1.4894813

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, H., Yu, X., Feng, H., Xue, Z., and Yang, N. (2019). Superior thermal conductivity of poly (ethylene oxide) for solid-state electrolytes: A molecular dynamics study. Int. J. Heat. Mass Tran. 137, 1241–1246. doi:10.1016/j.ijheatmasstransfer.2019.04.021

CrossRef Full Text | Google Scholar

Morehouse, J. A., Lloyd, D. R., Freeman, B. D., Lawler, D. F., Liechti, K. M., and Becker, E. B. (2006). Modeling the stretching of microporous membranes. J. Membr. Sci. 283, 430–439. doi:10.1016/j.memsci.2006.07.024

CrossRef Full Text | Google Scholar

Mustain, W. E., Chatenet, M., Page, M., and Kim, Y. S. (2020). Durability challenges of anion exchange membrane fuel cells. Energy Environ. Sci. 13, 2805–2838. doi:10.1039/d0ee01133a

CrossRef Full Text | Google Scholar

Ouma, C. N. M., Obodo, K. O., and Bessarabov, D. (2022). Computational approaches to alkaline anion-exchange membranes for fuel cell applications. Membranes 12, 1051. doi:10.3390/membranes12111051

PubMed Abstract | CrossRef Full Text | Google Scholar

Ozmaian, M., and Naghdabadi, R. (2015). Properties of nafion under uniaxial loading at different temperatures: A molecular dynamics study. Polym-Plast Technol. 54, 806–813. doi:10.1080/03602559.2014.974192

CrossRef Full Text | Google Scholar

Pan, J., Chen, C., Li, Y., Wang, L., Tan, L., Li, G., et al. (2014). Angioarchitectural characteristics associated with complications of embolization in supratentorial brain arteriovenous malformation. Energy Environ. Sci. 7, 354–359. doi:10.3174/ajnr.A3643

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J. K., Li, J., Divoux, G. M., Madsen, L. A., and Moore, R. B. (2011). Oriented morphology and anisotropic transport in uniaxially stretched perfluorosulfonate ionomer membranes. Macromolecules 44, 5701–5710. doi:10.1021/ma200865p

CrossRef Full Text | Google Scholar

Petersen, M. K., and Voth, G. A. (2006). Characterization of the solvation and transport of the hydrated proton in the perfluorosulfonic acid membrane Nafion. J. Phys. Chem. B 110, 18594–18600. doi:10.1021/jp062719k

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozuelo, J., Riande, E., Saiz, E., and Compan, V. (2006). Molecular dynamics simulations of proton conduction in sulfonated poly(phenyl sulfone)s. Macromolecules 39, 8862–8866. doi:10.1021/ma062070h

CrossRef Full Text | Google Scholar

Sarada, T., Sawyer, L. C., and Ostler, M. I. (1983). Three dimensional structure of celgard® microporous membranes. J. Membr. Sci. 15, 97–113. doi:10.1016/s0376-7388(00)81364-2

CrossRef Full Text | Google Scholar

Savage, J. (2021). Molecular dynamics study on water and hydroxide transfer mechanisms in PSU-g-alkyl-TMA membranes at low hydration: Effect of side chain length. Int. J. Hydrogen Energy 46, 33915–33933. doi:10.1016/j.ijhydene.2021.07.081

CrossRef Full Text | Google Scholar

Savage, J., and Voth, G. A. (2014). Persistent subdiffusive proton transport in perfluorosulfonic acid membranes. J. Phys. Chem. Lett. 5, 3037–3042. doi:10.1021/jz5014467

PubMed Abstract | CrossRef Full Text | Google Scholar

Savage, J., and Voth, G. A. (2016). Proton solvation and transport in realistic proton exchange membrane morphologies. J. Phys. Chem. C 120, 3176–3186. doi:10.1021/acs.jpcc.5b11168

CrossRef Full Text | Google Scholar

Sengupta, S., Pant, R., Komarou, P., Venkatnathan, A., and Lyulin, A. V. (2017). Atomistic simulation study of the hydrated structure and transport dynamics of a novel multi acid side chain polyelectrolyte membrane. Int. J. Hydrogen Energy 42, 27254–27268. doi:10.1016/j.ijhydene.2017.09.078

CrossRef Full Text | Google Scholar

Sun, Y., Wang, C., and Chen, Y. (2013). Molecular dynamics simulations of the deformation behavior of gadolinia-doped ceria solid electrolytes under tensile loading. J. Power Sources 233, 131–138. doi:10.1016/j.jpowsour.2013.01.139

CrossRef Full Text | Google Scholar

Sun, Z., Lin, B., and Yan, F. (2018). Anion-exchange membranes for alkaline fuel-cell applications: The effects of cations. Chem. Sus. Chem. 11, 58–70. doi:10.1002/cssc.201701600

CrossRef Full Text | Google Scholar

van der Heijden, P. C., Rubatat, L., and Diat, O. (2004). Orientation of drawn Nafion at molecular and mesoscopic scales. Macromolecules 37, 5327–5336. doi:10.1021/ma035642w

CrossRef Full Text | Google Scholar

Wang, J., Zhao, Y., Setzler, B. P., Rojas-Carbonell, S., Yehuda, C. B., Amel, A., et al. (2019). Identification of a monoclonal antibody that targets PD-1 in a manner requiring PD-1 Asn58 glycosylation. Nat. Energy 4, 392–398. doi:10.1038/s42003-019-0642-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Qiao, J., Bakerb, R., and Zhang, J. (2013). Alkaline polymer electrolyte membranes for fuel cell applications. Chem. Soc. Rev. 42, 5768–5787. doi:10.1039/c3cs60053j

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, C., Srivastava, D., and Cho, K. J. (2015). Thermal expansion and diffusion coefficients of carbon nanotube-polymer composites. Nano Lett. 2, 647–650. doi:10.1021/nl025554+

CrossRef Full Text | Google Scholar

Wei, H., Li, Y., Wang, S., Tao, G., Wang, T., Cheng, S., et al. (2019). Side-chain-type imidazolium-functionalized anion exchange membranes: The effects of additional hydrophobic side chains and their hydrophobicity. J. Membr. Sci. 579, 219–229. doi:10.1016/j.memsci.2019.02.058

CrossRef Full Text | Google Scholar

Xie, J., Ban, S., Liu, B., and Zhou, H. (2016). A molecular simulation study of chemical degradation and mechanical deformation of hydrated Nafion membranes. Appl. Surf. Sci. 362, 441–447. doi:10.1016/j.apsusc.2015.11.144

CrossRef Full Text | Google Scholar

Xu, T., and Yang, W. (2001). Fundamental studies of a new series of anion exchange membranes: Membrane preparation and characterization. J. Membr. Sci. 190, 159–166. doi:10.1016/s0376-7388(01)00434-3

CrossRef Full Text | Google Scholar

Yang, Y., and Knauss, D. M. (2015). Poly (2,6-dimethyl-1,4-phenylene oxide)-b-poly(vinylbenzyltrimethylammonium) diblock copolymers for highly conductive anion exchange membranes. Macromolecules 48, 4471–4480. doi:10.1021/acs.macromol.5b00459

CrossRef Full Text | Google Scholar

Yang, Y., Xu, Y., Ye, N., Zhang, D., Yang, J., and He, R. (2018). Alkali resistant anion exchange membranes based on saturated heterocyclic quaternary ammonium cations functionalized poly(2,6-dimethyl-1,4-phenylene oxide)s. J. Electrochem. Soc. 165, F350–F356. doi:10.1149/2.1031805jes

CrossRef Full Text | Google Scholar

Yang, Z., Guo, R., Malpass-Evans, R., Carta, M., McKeown, N. B., Guiver, M. D., et al. (2016). Highly conductive anion-exchange membranes from microporous Troger's base polymers. Angew. Chem. Int. Ed. 55, 11499–11502. doi:10.1002/anie.201605916

CrossRef Full Text | Google Scholar

Zhang, D., Xu, S., Wan, R., Yang, Y., and He, R. (2022). Functionalized graphene oxide cross-linked poly (2,6-dimethyl-1,4-phenylene oxide)-based anion exchange membranes with superior ionic conductivity. J. Power Sources 517, 230720. doi:10.1016/j.jpowsour.2021.230720

CrossRef Full Text | Google Scholar

Zhou, Y., Lin, G., Shih, A. J., and Hu, S. J. (2009). Egr-1 is involved in the inhibitory effect of leptin on PPARgamma expression in hepatic stellate cell in vitro. J. Power Sources 192, 544–551. doi:10.1016/j.lfs.2009.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, L., Pan, J., Wang, Y., Han, J., Zhuang, L., and Hickner, M. A. (2016). Multication side chain anion exchange membranes. Macromolecules 49, 815–824. doi:10.1021/acs.macromol.5b02671

CrossRef Full Text | Google Scholar